1 Introduction

Synchronization is a typical form of group motion rhythm, which means the neurons of a system discharge at the same time, or their discharge rhythms have some kind of relationship [1, 2]. Neural synchrony activities are found not only among coupled neuron groups in the same brain region, but also among uncoupled neuron groups in the same brain region or among different cortical areas; moreover, it can cross over two hemispheres of the brain [3]. Synchronization processes are crucially important for the neural system; and well-coordinated synchrony within and between neuronal populations appears to play an important role in neuronal signaling and information processing [4]. There are many neuroscientists who have been mainly concentrated on the coupling system topology and stability, as well as the parameters for the coupled effects [5–9].

Noise is ubiquitous in linear system and electronic engineering applications; in most cases, noise is considered harmful, especially in signal measurement [10–12], but the phenomenon of Stochastic Resonance (SR) makes us recognize that noise is also beneficial, especially, the noise induced synchronization [13–16]. In different ways, the noise could influence the synchronization of a nonlinear system. The known approaches are noise induced synchronization and noise enhanced synchronization. These are very special aspects that noise could be utilized for a specific object.

Neurons are living in an environment that may be full of noise. The noise comes either from outside or from the inside of nerve cells, for example, from the temperature changes outside, neuronal interactions, various ion fluctuations, and so on [17]. Wang et al. [18] studied the properties of a chemical synaptic coupled neuronal system with exterior noise of a stochastic resonance and synchronization dynamics, the results show that the coupling term can enhance the system’s autonomous stochastic resonance, and when the coupling strength is big enough, the synchronization could be induced. Casado et al. [19, 20] have reported the phase synchronization of two electrically coupled Hodgkin–Huxley (HH) model neurons. They found that the internal noise makes two neurons discharge synchronously, including the discharge frequency and phase synchronization. Generalized synchronization induced by noise or parameter mismatch in two Hindmarsh–Rose (HR) model neurons is studied in [21], which illustrated that the two neurons can get into generalized synchronization by introducing noise and changing another parameter in one of the neurons. The relation between the noise induced synchronization and autonomous stochastic resonance was also found in the coupled mismatching excitable ML neurons with noise intensity as the control parameters [22].

The influence of the complete synchronization affected by noise has attracted particular attention extensively. Many independent excitatory and inhibitory synaptic currents are usually approximated by a Gaussian distribution. Zambrano et al. [23] studied the synchronization of uncoupled excitable systems with common noise both numerically and experimentally. They considered two identical FitzHugh–Nagumo (FHN) systems which display both spiking and non-spiking behaviors in chaotic or periodic regimes. An electronic circuit provides a laboratory implementation of these dynamics. Synchronization is tested with both white and colored noise, showing that colored noise is more effective in inducing synchronization of the system.

The ML neuron model is a model for the electrical activity in the barnacle muscle fiber; it is a simplified version of Hodgkin–Huxley neuron model for describing the discharge and the refractory properties of real neurons [24]. This model contains a Calcium current generating a fast action potential and a delayed potassium current, at the same time, a leakage current is considered to maintain a constant potential at the rest state. Dynamics of the reduced ML neuron is governed by the following differential equations:

(1)
$$ \frac{dW}{dt} = \lambda (V) \bigl(W_{\infty} (V) - W \bigr), $$
(2)
$$ \frac{dI}{dt} = \mu (0.2 + V), $$
(3)

where

and t is the time, V is the membrane action potential of the ML neuron model, W is the probability of potassium channel activation, I is a slow variable which could result in rich firing patterns in a single ML neuron model. The related parameters are: g Ca=1.2, g K=2.0, g L =0.5, V K=−1.1, V L =−0.5, V a =−0.01, V b =0.15, V c =0.1, V d =0.05, μ=0.005. Besides the noise intensity D, the reversal potential V Ca also be used as another control parameter.

2 Noise induced complete synchronization

Systems with two uncoupled ML neurons are given as follows:

(4)

Here indices 1 and 2 mark separate neurons with different initial conditions. The noises ξ V (t) and ξ I (t) are added to the variable V and variable I of the ML neuron model, respectively. In order to verify the degree of synchronization of the two neurons’ system, one real-time error of response of the two coupled neurons is defined as:

$$ e = \vert V_{2} - V_{1} \vert + \vert W_{2} - W_{1} \vert + \vert I_{2} - I_{1} \vert . $$
(5)

In this work, we propose discussing the synchronous behavior of the system governed by Eq. (4) in terms of the average error 〈e〉, additionally, with the average Maximal Lyapunov Exponent 〈λ 1〉, and the average Interspike Interval 〈ISI〉.

For the two uncoupled ML neurons (shown in Eq. (4)) with different initial conditions and two fixed reversal potentials V Ca, from the view of mathematics, with the passage of time, the behavior of the two neurons does not become the same. However, if the two identical systems use the same noise stimulation, the two nonlinear systems will achieve complete synchronization when the noise intensity is large enough after a period of time, i.e., noise can induce synchronization.

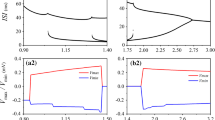
From Fig. 1(a), we can find that the exponent 〈λ 1〉 will change from positive to negative when the noise intensity is large enough; this means that the two uncoupled ML neurons can get completely synchronized. At the same time, compared with V, I is more sensitive to noise because the cross-noise intensity (the value of 〈λ 1〉 from positive to negative) of I is much less than that for V, therefore, white noise is only added to I in the following. The reversal potential V Ca is also a sensitive parameter, which significantly affects the system discharge patterns. Figures 1(b), (c), and (d) show the joint effects of the dynamic behavior with V ca and the white noise. Figure 1(b) indicates that a smaller V Ca yields a smaller 〈λ 1〉 in a certain D, which implies that it is more likely that in an uncoupled system with smaller intensity, noise can induce complete synchronization; moreover, this could be proved by the error 〈e〉 shown in Fig. 1(c). From Fig. 1(d), we can find that noise has a quite obvious relationship with the neuronal discharge frequency; generally, the average interspike interval of a sequence decreased with the increase of noise intensity. What is interesting is that a larger V Ca corresponds to a smaller 〈ISI〉 at the same noise intensity D, however, the conclusion to be drawn is that D is one of the main factors for the discharge frequency, and the strong noise could induce more discharges and activities.

Fig. 1
figure 1

Noise induced complete synchronization: (a) the average Maximum Lyapunov Exponent 〈λ 1〉 vs noise intensity D with noise in the variables V and I under V Ca=0.925; (b) 〈λ 1〉 vs noise intensity D under V Ca=0.925 and V Ca=0.6; (c) the average synchronization error 〈e〉 vs noise intensity D under V Ca=0.925 and V Ca=0.6; (d) the average Interspike Interval 〈ISI〉 vs noise intensity D under V Ca=0.925 and V Ca=0.6

Full size image

3 Noise enhanced complete synchronization

In this section, we focus on the effect of noise on a system with two coupled ML model neurons, and the coupling scheme is shown in the last part of the first equation of Eq. (6):

(6)

Here C is the coupling strength, the other variable being the same as in Eq. (4). In this work, a statistical index, called Similarity Function S(0), is introduced to test complete synchronization. It is given by

$$ S(0) = \sqrt{\frac{ \langle ( V_{1}(t) - V_{2}(t) )^{2} \rangle}{ \sqrt{ \langle V_{1}^{2}(t) \rangle \cdot \langle V_{2}^{2}(t) \rangle}}}, $$
(7)

where 〈⋅〉 represents the signal average value with respect to time. A smaller S(0) shows greater correlation between two signals. From the standpoint of synchronization, it means that the two coupled neurons’ phase synchronization is strengthened. The value S(0)=0 refers to the complete synchronization for the coupled system under identical parameters with different initial conditions.

Under the absence of noise and with the coupling strength C=0.01, the coupled ML neurons described in Eq. (6) could not be synchronized. Compared with Fig. 1, we can find that there is even a smaller noise intensity D for the system synchronization, shown in Fig. 2(a), due to the coupling with noise ξ(t). A smaller V Ca results in a bigger exponent 〈λ 1〉; this situation is contrary to the case in Fig. 1(b), indicating that the two ML neurons will be synchronized under weak noise and weak coupling, as shown in Fig. 2(b). The results shown in Fig. 2(c) are to examine the influence of synchronization by S(0), setting V Ca=0.925 and with C located in [0,0.065]. The coupled neuronal system could not be synchronized when D=0, but the majority of the section shows complete synchronization for D=10−6, even in the part of above 0.65, which proves that noise has a promoting effect for the synchronization of coupled neurons. We find that the minimum D (named the critical noise intensity D j ) which could induce complete synchronization under different weak coupling strength C shows different situations with the changing of V Ca under noise intensity D=1.0×10−6, seen from Fig. 2(d), while with the value of V Ca≤0.625, the smaller C corresponds to a larger D j . However, the situation is just the opposite when V Ca>0.625; this demonstrates that the activity of ML neurons in the strong coupling system will be reduced when V Ca increases to a certain extent, the stronger noise is needed to achieve complete synchronization.

Fig. 2
figure 2

Noise enhanced complete synchronization: (a) the average Maximum Lyapunov Exponent 〈λ 1〉 vs noise intensity D under V Ca=0.925 and V Ca=0.6 with C=0.01; (b) the average synchronization error 〈e〉 vs noise intensity D under V Ca=0.925 with C=0.01; (c) Similarity Index S(0) vs coupling strength C under noise intensity D=0 and D=1.0×10−6; (d) the minimum value of noise intensity (critical noise intensity) D j in ML neurons cause complete synchronization for different V Ca

Full size image

4 Conclusions

In summary, we have studied the effects of noise to the complete synchronization of ML neurons. The investigation indicates that the slow variable I is more sensitive to noise. Two uncoupled ML neurons can discharge completely synchronously when the noise intensity is large enough. The smaller the V Ca, the more it is likely that the weak noise can induce complete synchronization. A bigger noise can induce more discharge spikes. For a coupled neuronal system, even in the case of weak coupling, the two ML neurons will be synchronized under very small noise, based on the study of the Similarity Function S(0), which proves that noise has a promoting effect to the synchronization of coupled neurons, and there are different situations for critical noise intensity D j with the change of V Ca under different coupling strength C. Anyhow, the results prove that noise can enhance the complete synchronization in coupled ML neurons with the cooperation of other factors.