Computational study on neuronal activities arising in the pre-Bötzinger complex

Abstract

Experimental investigations have shown that the pre-Bötzinger complex (pre-BötC) within the mammalian brainstem generates the inspiratory phase of respiratory rhythm. Based on a single-compartment model of a pre-BötC inspiratory neuron, we, in this paper, use semi-analytical, numerical as well as fast-slow dynamical methods to investigate the effects of sodium conductance ($g_{\text{Na}}$) and potassium conductance ($g_{{\text{K}}}$) on the firing activities of pre-BötC and try to reveal the dynamical mechanisms behind them. We show how $g_{{\text{Na}}}$ and $g_{\text{K}}$ affect the bifurcations of the fast-subsystem and how the the firing patterns of pre-BötC transit according to the bifurcations.

Introduction

At the beginning of 1890s, researchers conducted experiments on neonatal rats. They found that the region between the Bötzinger complex (pre-BötC) located in the mammalian brainstem and the ventral respiratory group (VRG) may be essential for the generation of respiratory rhythm in newborn mammals (Smith et al. 1991). Subsequent studies show that a particular class of excitatory neurons with oscillating cluster similar to a heart pacemaker in the pre-BötC drives the inspiratory phase of the respiratory rhythm (Rekling and Feldman 1998). It is also shown that the network connection and interaction between inspiratory and pre-inspiratory neurons in the pre-BötC can cause the respiratory rhythm (Mellen et al. 2003).

The firing patterns of neurons in the respiratory system are very rich and can be divided into two categories: bursting and spiking (Rekling and Feldman 1998; Gray et al. 1999; Butera et al. 1997, 1988b, 1998a). The experimental results show that the mode of bursting can be presented in single cell or network (Rybak et al. 1997; Butera et al. 1999b; Jia et al. 2017). Based on a large number of experiments and investigation, researchers have proposed different computational models of respiratory rhythm of pre-BötC (Smith 1997; Balis et al. 1994; Botros and Brace 1990; Duffin 1991; Gottschalk et al. 1994; Ogilvie et al. 1992; Rybak et al. 1997). The two models proposed by Butera et al. (1999a, b) have played an important role in the later research. In model I, bursting starts with the rapid activation of the persistent sodium current and terminates in the slow inactivation of the persistent sodium current (Butera et al. 1999a). In model II, bursting produced by the rapid activation of persistent sodium currents which end in slow activation of sustained potassium currents (Butera et al. 1999b).

With the development of nonlinear science, bifurcation theory has become an important research tool in the study of the dynamics of neuronal firing activity. Using bifurcation analysis, Izhikevich studied the properties of neuronal excitability, spiking and bursting, revealed the characteristics of the firing activity of neurons, and at the same time, gave the classification of the bursting (Izhikevich 2000). Fast-slow decomposition is also an important approach in neurodynamics research (Rinzel 2007). Taking the excitatory neuron model in pre-Bötzinger complex as their research object, Best et al. (2005) studied the the dynamic range of the bursting by combing the geometry method with the fast-slow decomposition. Wang et al. applied fast-slow decomposition, phase plane analysis and bifurcation analysis to a pre-BötC inspiratory neuron model, and revealed the mechanisms underlying the novel mixed bursting solutions (Wang and Rubin 2016). By two parameter bifurcation analysis and fast-slow decomposition, Duan et al. (2008, 2010, 2012, 2015, 2017) studied the effects of different ion channels on the firing patterns of pre-BötC. Using numerical simulations, bifurcation methods, and fast-slow decomposition, Rubin et al. (2009, 2011) investigated the behavior of a neural network, and analyzed the state-dependent mechanisms for respiratory rhythm generation and control. The fast-slow decomposition has also been applied to study the properties of some crucial bifurcations, such as the Hopf bifurcation, which deeply related to the firing patterns of neurons (Sterpu and Rocṣoreanu 2005; Wang et al. 2011; Jia et al. 2012; Kim and Lim 2015; Kuznetsov 2013).

The delayed rectifier potassium current $I_{\text{K}}$ is considered of particular interest due to its role in neuronal after spike repolarization (Rybak et al. 2003). Higher conductance values of potassium ion K$^+$ enhance the value of $I_{\text{K}}$, which in turn affect the regimes of neuronal activity as well as the transitions between regular spiking and bursting. Currently both Na$^+$- and Ca$^{2+}$-based mechanisms are considered to contribute to inspiratory rhythm generation in the pre-BötC network (Bruce et al. 2013). The usual job of sodium channels is to make brief voltage signals, action potentials, for long distance propagation (Yu et al. 2012). Specifically, a transition from asynchronous firing to population bursting could be induced by a direct suppression of the potassium conductance or through an elevation of extracellular potassium concentration (Rybak et al. 2004). In this paper, we mainly discuss how the transition of firing patterns is related to the change of the conductance of sodium (Na$^+$), potassium (K$^+$) or other ions.

This paper is organized as follows. In “Model description” section, the pre-BötC model developed by Park and Rubin (2013) is introduced. In “Dynamics related to $g_{{\text{Na}}}$ and $g_{\text{K}}$ ” section, different bursting patterns in the pre-BötC model are investigated with the change of the conductances of sodium and potassium channels. Semi-analytical studies for Hopf bifurcation are also explored to investigate the firing activities of the model. Finally, conclusions are given in the last section. The bifurcation diagrams in this paper are performed by XPPAUT (Ermentrout 2002).

Model description

In this study, we consider a single-compartment model of a pre-BötC inspiratory neuron, which was introduced by Park and Rubin based on a two-compartment model developed by Park et al. (Park and Rubin 2013). The model features multiple currents, and dynamics of the membrane potential is described as follows:

$$\dot{V} = \left( -I_{{\text{Na}}}-I_{\text{K}}-I_L-I_{NaP}-I_{CAN}\right) /C$$

(1)

$$\begin{aligned} \dot{n}= \left( n_{\infty }(V)-n\right) /{\tau }_{n}(V) \end{aligned}$$

(2)

$$\begin{aligned} \dot{h}= \left( h_{\infty }(V)-h\right) /{\tau }_{h}(V) \end{aligned}$$

(3)

where $I_{{\text{Na}}}$, $I_{{\text{K}}}$, $I_{L}$, $I_{NaP}$, $I_{CAN}$ represent Na$^+$ current, delayed rectifier K$^+$ current, leakage current, persistent sodium current and calcium-activated nonspecific cationic current, respectively. Particularly, $I_{{\text{Na}}}=g_{{\text{Na}}}m_{\infty }^3(V)(1-n)(V-V_{{\text{Na}}})$, $I_{\text{K}}=g_{{\text{K}}}n^4(V-V_{\text{K}})$, $I_L=g_{L}(V-V_L)$, $I_{NaP}=g_{NaP}m_{p,\infty }h(V-V_{{\text{Na}}})$, $I_{CAN}=g_{CAN}f([{\text{Ca}}])(V-V_{{\text{Na}}})$, with $m_{\infty }(V)=1/(1+exp((V-\theta _m)/\sigma _m))$, $n_{\infty }(V)=1/(1+exp((V-\theta _n)/\sigma _n))$, $m_{p,\infty }(V)=1/(1+exp((V-\theta _{m,p})/\sigma _{m,p}))$, $h_{\infty }(V)=1/(1+exp((V-\theta _h)/\sigma _h)),$ $\tau _{n}(V)=\tau _{n}/cosh((v-\theta _n)/2\sigma _n))$, $\tau _{h}(V)=\tau _{h}/cosh((v-\theta _h)/2\sigma _h))$ and $f([{\text{Ca}}])=1/(1+(K_{CAN}/[{\text{Ca}}])^{n_{CAN}})$.

The calcium dynamics is given as:

$$\begin{aligned} d[{\text{Ca}}]/dt= f_{i}\left( J_{ER_{IN}}-J_{ER_{OUT}}\right) \end{aligned}$$

(4)

$$\begin{aligned} dl/dt= AK_{d}(1-l)-A[{\text{Ca}}]l \end{aligned}$$

(5)

where l indicates the fraction of $IP_3$ channels in the membrane of the ER that have not been inactivated, which depends on the intracellular calcium concentration ([Ca]). Equation (4) shows that [Ca] is determined by the flux into the cytosol from the ER ($J_{ER_{IN}}$) and the flux out of the cytosol into the ER ($J_{ER_{OUT}}$). These fluxes are regulated by the intracellular concentration of $IP_3$, $[IP_3]$, and $IP_3$ channel gating variable, l, and are described as follows:

$$\begin{aligned} J_{ER_{IN}}&= \left( L_{IP_3}+P_{IP_3}[\frac{[IP_3][{\text{Ca}}]l}{([IP_3]+K_I)([{\text{Ca}}]+K_a)}]^3\right) \times ([{\text{Ca}}]_{ER}-[{\text{Ca}}])\nonumber \\ J_{ER_{OUT}}&= V_{SERCA}\left( \frac{[{\text{Ca}}]^2}{K_{SERCA}^2+[{\text{Ca}}]^2}\right) \end{aligned}$$

(6)

where $L_{IP_3}$, $P_{IP_3}$, $K_I$ and $K_a$ represent ER leak permeability, maximum total ER permeability, dissociation constants for $IP_3$ receptor activation by $IP_3$ and Ca$^{2+}$ respectively. $V_{SERCA}$ is the maximal SERCA pump rate, $K_{SERCA}$ sets the half-activation of the SERCA pump. In Eq. (6), $[{\text{Ca}}]_{ER}$ is given as:

$$\begin{aligned} [{\text{Ca}}]_{ER}=\frac{[{\text{Ca}}]_{Tot}-[{\text{Ca}}]}{\sigma } \end{aligned}$$

(7)

where $\sigma$ is the ratio of cytosolic to ER volume. The other parameters used are listed in the Appendix Table 2.

Dynamics related to g _Na and g _K

In the model, h, [Ca] and l vary much more slowly than V and n. Therefore, we can perform the fast-slow dynamical analysis. Fixing $[IP_3]$ at 0.8, we can obtain a steady state calcium concentration $[{\text{Ca}}]=0.021040572$ and corresponding $l=0.950027209$ from Eqs. (4) to (5). With these fixed values, the full system of Eqs. (1)–(5) can be reduced to a fast-slow dynamical system of Eqs. (1)–(3) with the slow variable h. Based on this fast-slow system, in what follows, we investigate how the variation of $g_{{\text{Na}}}$ and $g_{{\text{K}}}$ affect firing activities of the pre-BötC.

Bifurcations and firings for g _Na = 5

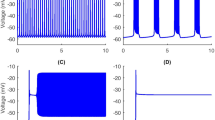
In this subsection, we fix $g_{{\text{Na}}}$ at $5\,nS$ and consider bifurcations and firings of the system for different values of $g_{\text{K}}$. The neuron can exhibit three types of bursting, which are, the “subHopf/subHopf” bursting (Fig. 1a), the “subHopf/homoclinic” bursting (Fig. 1b, c) and the “fold/homoclinic” bursting (Fig. 1d). The fast-slow decomposition for different bursting with different values of ${g}_{{\text{K}}}$ are shown in Fig. 2a–d respectively.

In the case ${g}_{{\text{K}}}=3$ nS, as shown in Fig. 2a, the equilibrium points form an “S”-shaped curve. The solid, dotted, and dashed lines represent the stable node (lower branch), the saddle (middle branch), and the un-stable focus and stable focus (upper branch), respectively. The interaction point F1 (or F2) between the middle and the lower (or upper) branches is a fold bifurcation point. With h increasing, the unstable focus becomes stable at the subcritical Hopf (subH) point where an unstable limit cycle is bifurcated from the subH. The maximum and minimum amplitudes of the unstable limit cycle are shown by upper and lower red open circles respectively. The unstable limit cycle intersects with the stable limit cycle (upper and lower red solid circles) at the fold bifurcation of a limit cycle (LPC). The stable limit cycle disappears via the homoclinic bifurcation (HC). The trajectory of the whole system (1)–(5) (the green curve) is also superimposed. We can see from the figure that the rest state disappears via subcritical Hopf bifurcation $\hbox {subH}$, and the active state disappears via subcritical Hopf bifurcation $\mathrm{subH}$ too. Such bursting is called the “subHopf/subHopf” type according to the classifications introduced by Izhikevich (2000).

When ${g}_{{\text{K}}}$ continuously increases to ${g}_{{\text{K}}}=4$ nS, the attracting of periodic orbits gradually appears. So the the rest state disappear via subcritical Hopf bifurcation $\mathrm{subH}$, then the trajectory damps and tends to stable focus. When the trajectory goes through the subHopf bifurcation (subH), it begins to oscillate around the stable limit cycle. Finally, the active state disappears via the homoclinic (HC) bifurcation. So the bursting is called the “subHopf/homoclinic” type via “fold/homoclinic” hysteresis loop (Fig. 2b, c).

With the value of ${g}_{{\text{K}}}$ increasing further, the subcritical Hopf (subH) bifurcation of the fast subsystem changes to supercritical (supH) and there is no fold bifurcation of limit cycle. When ${g}_{{\text{K}}}$ increases from 4.3 to 11.2 nS, the rest state disappears via fold bifurcation $F_1$, and the active state disappears via the homoclinic (HC) bifurcation. So the bursting is called the “fold/homoclinic” type, as shown in Fig. 2d.

Fig. 1

Fixing $g_{{\text{Na}}}$ at 5 nS, bursting pattern changes corresponding to different parameter values of $g_{{\text{K}}}$. a $g_{{\text{K}}}=3$ nS; b $g_{{\text{K}}}=4$ nS; c $g_{{\text{K}}}=4.3$ nS; d $g_{{\text{K}}}=11.2$ nS

Fig. 2

The fast-slow decomposition and bifurcation analysis. The parameter set is same as that in Fig. 1. The model exhibits a“subHopf/subHopf bursting; b “subHopf/homoclinic” bursting; c “subHopf/homoclinic” bursting; d “fold/homoclinic” bursting, respectively

As we known, Hopf bifurcation plays an important role in the dynamical analysis of the neuronal system. The numerical results about the Hopf bifurcations may be investigated by semi-analytical study.

When $g_{\text{K}}=11.2,$ numerical results show that supercritical Hopf bifurcation occurs at the equilibrium $supH_1(v_1, n_1, h_1)=supH_1(-26.21, 0.6679, 0.4734)$. In order to test this, we rewrite the fast subsystem (1) and (2) as:

$$\begin{aligned} \dot{V}= f_1(V,n,h) \end{aligned}$$

(8)

$$\begin{aligned} \dot{n}= f_2(V,n,h) \end{aligned}$$

(9)

where

$$\begin{aligned} f_1(V,n,h)& = (-g_{{\text{Na}}}m_{\infty }^3(V)(1-n)(V-V_{{\text{Na}}})-g_{{\text{K}}}n^4(V-V_{\text{K}})-g_{NaP}m_{p,\infty }h(V-V_{{\text{Na}}}) \\ &-g_{L}(V-V_L)-g_{CAN}f([{\text{Ca}}])(V-V_{{\text{Na}}}))/C \end{aligned}$$

(10)

$$\begin{aligned} f_2(V,n,h)= (n_{\infty }(V)-n)/{\tau }_{n}(V) \end{aligned}$$

(11)

The corresponding Jacobian matrix A can be written as:

$$\begin{aligned} A=\left( \begin{array}{cc} \frac{\partial f_1}{\partial V} & \frac{\partial f_1}{\partial n} \\ \frac{\partial f_2}{\partial V} & \frac{\partial f_2}{\partial n} \\ \end{array} \right) \end{aligned}$$

(12)

Then, we have

$$\begin{aligned} A|_{supH_1}=\left( \begin{array}{cc} 0.103028 & -47.5961 \\ 0.00588708 & -0.106143 \\ \end{array} \right) , \end{aligned}$$

(13)

which possesses a pair of pure imaginary eigenvalues $\lambda _{1, 2}=\pm i\,\omega$, with $\omega =0.518906$.

Let

$$\begin{aligned} A^T p=-i\omega p,\ \ A q=i\omega q, \ \ \langle p,q \rangle =\sum _{n=1}^2\overline{p_i}q_i=1, \end{aligned}$$

(14)

we have

$$\begin{aligned} p=\left( \begin{array}{c} 6.82503\times 10^{-6} + 0.000022887 I \\ 0.306874 - 89.9117 I \\ \end{array} \right) , \ \ q=\left( \begin{array}{c} -0.0000171871 - 0.000314737 I \\ 1.56428\times 10^{-6} - 0.011122 I \\ \end{array} \right) . \end{aligned}$$

(15)

Consider the following system

$$\begin{aligned} \dot{x}=Ax + F(x),\ \ x \in R^2. \end{aligned}$$

(16)

Let F(x) be expanded into

$$\begin{aligned} F(x)=\frac{1}{2} B(x,x) + \frac{1}{6} C(x,x,x)+ O(\Vert x\Vert ^4). \end{aligned}$$

(17)

In coordinate, we have

$$\begin{aligned} B_i(x,y)= \left. \sum _{j,k=1}^n \frac{\partial ^2 F_i(\xi )}{\partial \xi _j \partial \xi _k} \right| _{\xi =0} x_j y_k, \end{aligned}$$

(18)

$$\begin{aligned} C_i(x,y,z)= \left. \sum _{j,k,l=1}^n \frac{\partial ^3 F_i(\xi )}{\partial \xi _j \partial \xi _k \partial \xi _l} \right| _{\xi =0} x_j y_k z_l, \end{aligned}$$

(19)

where $\xi =(\xi _1, \xi _2)^T$, $\xi _0$ is the equilibrium. Therefore,we obtain

$$\begin{aligned} B_i(x,y)& = \left( \begin{array}{c} -0.0424508 x_1 y_1 - 1.56884 x_2 y_1 - 1.56884 x_1 y_2 - 167.844 x_2 y_2 \\ -4.4239\times 10^{-7} x_1 y_1 - 0.00444828 x_2 y_1 - 0.00444828 x_1 y_2 \\ \end{array} \right) , \end{aligned}$$

(20)

$$\begin{aligned} C_i(x,y,z)& = \left( \begin{array}{c} -0.00461131 x_1 y_1 z_1 + 0.0929698 (x_2 y_1 z_1 + x_1 y_2 z_1 + x_1 y_1 z_2) -\\ 2.85498 (x_1 y_2 z_2 + x_2 y_2 z_1 + x_2 y_1 z_2)- 502.603 x_2 y_2 z_2 \\ 0.0000919857 x_1 y_1 z_1 - 0.00165849 (x_2 y_1 z_1 + x_1 y_2 z_1 + x_1 y_1 z_2). \end{array}\right) \end{aligned}$$

(21)

Now, we can calculate the first Lyapunov coefficient at $supH_1$:

$$\begin{aligned} l_{1}(0)=\frac{1}{2\,\omega }Re[\langle p, C(q, q, \overline{q})\rangle - 2\langle p, B(q, A^{-1}B(q, \overline{q}))\rangle ] +\langle p, B(\overline{q}, (2i\omega I - A)^{-1}B(q, q))\rangle ] \end{aligned}$$

(22)

to get

$$\begin{aligned} l_{1}(0) = -5.45731\times 10^{-9} <0. \end{aligned}$$

(23)

Hence, $supH_1$ is a supercritical Hopf bifurcation point. This coincides with the numerical results.

The critical values of $g_{\text{K}}$ dividing the supercritical and subcritical Hopf bifurcations corresponding to different values of $g_{{\text{Na}}}$ are listed in Table 1, from which we can see for example, that when $g_{{\text{Na}}}=5$, the subcritical Hopf bifurcation transits to supercritical at $g_{\text{K}}=4.99$. That means, the “subHopf/subHopf” bursting transits to the “fold/homoclinic” type at the critical points, and we call the “subHopf/homoclinic” bursting as the “transition state” because it exists in a very small range of

Table 1 Critical values of $g_{\text{K}}$ dividing the supercritical and subcritical Hopf bifurcations corresponding to different values of $g_{{\text{Na}}}$

Bifurcations and firings for g _Na = 15

As $g_{{\text{Na}}}=15$ nS, the neurons exhibit different bursting when ${g}_{{\text{K}}}$ increases in a certain range. The oscillations of the whole system (green) are shown in Fig. 3a–d. The bifurcation structure of the fast subsystem (1), (2) with respect to the slow variable h is projected onto the (h, V))-plane, as shown in Fig. 4a–d. Similarly, the equilibrium points form an “S”-shaped curve. Note that a family of unstable periodic orbits (red open circle) emanate from the subcritical Hopf (subH) bifurcation on the upper branch. The unstable periodic orbits coincide with the stable limit cycles (red solid circle) and then disappear at fold bifurcation of limit cycle (LPC). The trajectory of the whole system (1)–(5) (the green curve) is also superimposed.

For different values of ${g}_{{\text{K}}}$, the neurons can exhibit three types of bursting, which are, the “subHopf/subHopf” bursting (Fig. 4a), the “fold cycle/homoclinic” bursting (Fig. 4b) and the “fold/homoclinic” bursting (Fig. 4c) and spiking (Fig. 4d). The fast-slow decomposition of different bursting are shown in Fig. 4a–d respectively.

Fig. 3

Bursting patterns and spiking when $g_{{\text{Na}}}=15$ nS with a $g_{{\text{K}}}=4$ nS; b $g_{{\text{K}}}=4.3$ nS; c $g_{{\text{K}}}=11.2$ nS; d $g_{{\text{K}}}=14$ nS

Fig. 4

The fast-slow decomposition and bifurcation analysis. The parameter values are same as that in Fig. 3. The model exhibits a “subHopf/subHopf bursting; b “fold cycle/homoclinic” bursting; c “fold/homoclinic” bursting; d spiking respectively

When $g_{{\text{Na}}}=15$ and $g_{\text{K}}=11.2$, numerical results show that subcritical Hopf bifurcation occurs at the equilibrium $subH_2(v_1, n_1, h_1)=subH_2(-23.91, 0.781, 0.7928).$

The Jacobian matrix A at $subH_2$ can be written as:

$$\begin{aligned} A|_{subH_2}=\left( \begin{array}{cc} 0.12814 & -98.3901 \\ 0.00516961 & -0.120933 \\ \end{array} \right) , \end{aligned}$$

(24)

which has a simple pair of complex eigenvalues $\lambda _{1, 2}=\pm i\,\omega$, with $\omega =0.703502.$ Then we can get

$$\begin{aligned} p=\left( \begin{array}{l} -0.00180447 - 0.00414688 I \\ 2.02861 - 138.097 I \\ \end{array} \right) , \quad \ q=\left( \begin{array}{l} 0.00161557 - 0.00276375 I \\ 0.000026669 - 0.00724036 I \\ \end{array} \right) , \end{aligned}$$

(25)

which satisfy

$$\begin{aligned} A^T p=-i\omega p,\ \ A q=i\omega q, \ \ \langle p,q \rangle =\sum _{n=1}^2\overline{p_i}q_i=1. \end{aligned}$$

(26)

Therefore, we have

$$\begin{aligned} B_i(x,y) & = \left( \begin{array}{c} -0.0889726 x_1 y_1 - 3.08083 x_2 y_1 - 3.08083 x_1 y_2 - 238.48 x_2 y_2 \\ 3.21995\times 10^{-7} x_1 y_1 - 0.00850068 x_2 y_1 - 0.00850068 x_1 y_2 \\ \end{array} \right) , \end{aligned}$$

(27)

$$\begin{aligned} C_i(x,y,z) & = \left( \begin{array}{c} 0.00142365 x_1 y_1 z_1 + 0.340426 (x_2 y_1 z_1 + x_1 y_2 z_1 + x_1 y_1 z_2) -\\ 3.90375 (x_2 y_2 z_1 + x_2 y_1 z_2 + x_1 y_2 z_2)- 610.705 x_2 y_2 z_2 \\ 0.0000807751 x_1 y_1 z_1 - 0.00188958 (x_2 y_1 z_1 + x_1 y_2 z_1 + x_1 y_1 z_2) \\ \end{array} \right) . \end{aligned}$$

(28)

Now, we can calculate the first Lyapunov coefficient at $subH_2$:

$$\begin{aligned} l_{1}(0)=\frac{1}{2\omega }Re[\langle p, C(q, q, \overline{q})\rangle - 2\langle p, B(q, A^{-1}B(q, \overline{q}))\rangle ]+\langle p, B(\overline{q}, (2i\omega I - A)^{-1}B(q, q))\rangle ] \end{aligned}$$

(29)

get

$$\begin{aligned} l_{1}(0) = 2.50533\times 10^{-7} >0. \end{aligned}$$

(30)

Hence, $subH_2$ is a subcritical Hopf point.

In this case, there is no transition from subcritical Hopf bifurcation to supercritical in a small range of $g_{\text{K}}$ (the transition occurs at $g_{\text{K}}=78.62$, as shown in Table 1). The “subHopf/subHopf” bursting transits to the “fold/homoclinic” type at certain value of $g_{\text{K}}$. The “transition state” in a very small range of $g_{\text{K}}$ is the “fold cycle/homoclinic” bursting in stead of the “subHopf/homoclinic” bursting compared with that in the case of $g_{{\text{Na}}}=5$.

By treating $g_{\text{K}}$ as the second bifurcation parameter for Eqs. (1)–(2) and following in $(h, g_{\text{K}})$ the HC, subH, LPC and $F_1$ points in the 1-parameter bifurcation diagram as shown in Figs. 2a and 4a, we obtain a 2-parameter bifurcation diagram in $(h, g_{\text{K}})$-space (Fig. 5). The 2-parameter bifurcation diagrams in our analysis will help us identify how variations of parameter $g_{\text{K}}$ and $g_{{\text{Na}}}$ affect the existence region of bursting or spiking solutions. We only consider the parameter region for $g_k \in (0,40]$. For a small value of $g_{{\text{Na}}}=5$ (Fig. 5a), the fold bifurcation curve f and Hopf bifurcation curve h have an intersect at $g_k=4.84$. And there is always a gap between the curve f and the homoclinic bifurcation curve homo in the $(h, g_{\text{K}})$ 2- parameter bifurcation diagram. That means for roughly $4.84\le g_k\le 40$, the system exhibits the “fold/homoclinic” bursting. For a big value of $g_{{\text{Na}}}=15$ (Fig. 5b), the fold bifurcation curve f and fold limit cycle bifurcation l curve intersect at roughly $g_k=4.37$. And there has a gap between the curves homo and f until roughly $g_k=13.3$ in the $(h, g_{\text{K}})$ 2-parameter bifurcation diagram. For $g_k>13.3$, the curves of homo and f both overlap completely with the green curve, and hence are not visible as separate entities in the figure (Fig. 5b). That means for $4.37<g_k<13.3$, the system exhibits the “fold/homoclinic” bursting. Then the bursting activities transit to spiking for $13.3\le g_k\le 40$.

Fig. 5

Homoclinic bifurcation curve homo (green), the Hopf bifurcation curve h (red), the fold limit cycle bifurcation l (blue) and the curve of fold bifurcations f (black) corresponding to the lower fold of the bifurcation diagram (Figs. 2a, 4a) in $(h, g_{\text{K}})$ parameter space for a $g_{{\text{Na}}}=5$; b $g_{{\text{Na}}}=15$. (Color figure online)

Discussions and conclusions

In this paper, we have studied the single cell model of Park and Rubin which yield different types of busting as $g_{{\text{Na}}}$ and $g_{{\text{K}}}$ vary. We have shown that for small values of $g_{{\text{Na}}}$, taking $g_{{\text{Na}}}=5$ as an example, the fast subsystem achieved the transition from subcritical to supercritical Hopf bifurcation with a small values of $g_{{\text{K}}}$ ($g_{{\text{K}}}=4.99$). The single cell undergoes the “subHopf/subHopf”, the “subHopf/homoclinic”, and the “fold/homoclinic” bursting with parameter $g_{{\text{K}}}$ increases. But for the bigger value of $g_{{\text{Na}}}$, for example, $g_{{\text{Na}}}=15$, the transition will take place at a much bigger value of $g_{{\text{K}}}$ ( $g_{{\text{K}}} =78.62$). In this case the single cell undergoes the “subHopf/subHopf”, the “fold cycle/homoclinic”, and the “fold/homoclinic” bursting and spiking with parameter $g_{{\text{K}}}$ increases.

We give the semi-analytical study for both the supercritical and subcritical Hopf bifurcation. According to the analysis of the Hopf bifurcation, we found that the transition of the supercritical and subcritical Hopf bifurcation point is closely related to $g_{{\text{Na}}}$. Although the types of fast-slow bursters are similar in both cases of small and big values of $g_{{\text{Na}}}$, the corresponding “transition states” of the bursting are different due to the difference of Hopf bifurcations. We also found that both supercritical and subcritical Hopf bifurcations can lead to the “fold/homoclinic” bursting, which implies that the relative position of bifurcation points is essential for the investigation of bursting patterns.

Higher $g_{{\text{Na}}}$ values enhance $I_{{\text{Na}}}$, which in turn affect regimes of bursting and spiking. With small values of $g_{{\text{Na}}}$, there is only bursting region. But for the bigger value of $g_{{\text{Na}}}$, there is a relative large region for spiking ($13.3\le g_k\le 40$). Previous work has suggested that the Na$^+$/K$^+$ pump plays an important role in the generation of the bursting solution. Our study show that both higher conductance values of potassium ion K$^+$ or sodium Na$^+$ can enhance their currents $I_{\text{K}}$ or $I_{{\text{Na}}}$, which in turn affects the regimes of neuronal activity and transitions between spiking and bursting. Although our study is motivated by the bursting patterns observed in the pre-BötC, it may also be applicable to other cells exhibiting rhythmic activity.

Appendix

See Table 2.

Table 2 Parameter values for Eqs. (1)–(7)