Abstract
Experimental results in rodent medullary slices containing the pre-Bötzinger complex (pre-BötC) have identified multiple bursting mechanisms based on persistent sodium current (I NaP) and intracellular Ca2+. The classic two-timescale approach to the analysis of pre-BötC bursting treats the inactivation of I NaP, the calcium concentration, as well as the Ca2+-dependent inactivation of IP 3 as slow variables and considers other evolving quantities as fast variables. Based on its time course, however, it appears that a novel mixed bursting (MB) solution, observed both in recordings and in model pre-BötC neurons, involves at least three timescales. In this work, we consider a single-compartment model of a pre-BötC inspiratory neuron that can exhibit both I NaP and Ca2+ oscillations and has the ability to produce MB solutions. We use methods of dynamical systems theory, such as phase plane analysis, fast-slow decomposition, and bifurcation analysis, to better understand the mechanisms underlying the MB solution pattern. Rather surprisingly, we discover that a third timescale is not actually required to generate mixed bursting solutions. Through our analysis of timescales, we also elucidate how the pre-BötC neuron model can be tuned to improve the robustness of the MB solution.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Certain neurons in the pre-Bötzinger complex (pre-BötC) of the mammalian brainstem exhibit bursting activity in the inspiratory phase of respiration, which has been extensively studied both experimentally and computationally. Two distinct bursting mechanisms have been identified in the pre-BötC, depending on the persistent sodium current (I NaP) or a nonspecific cation or CAN current (I CAN), respectively. The latter is activated by intracellular Ca2+ originating from the dendrite, where it may be influenced by synaptic input and intracellular calcium stores, regulated by IP 3 receptors (Mironov 2008). Motivated by these experimental results, Toporikova and Butera (2011) developed a two-compartment conductance-based pre-BötC neuron model (TB model) that encompasses both I NaP-dependent somatic bursting and dendritic calcium oscillations that activate the CAN current and thereby contribute to somatic voltage dynamics. This model produces not just two but three types of bursting; in addition to the I NaP-dependent somatic bursting and I CAN-dependent dendritic bursting, it produces a somato-dendritic bursting or mixed pattern that depends on both currents and is also seen experimentally (e.g., Dunmyre 2011). The focus of this paper is the analysis of the mechanisms underlying this mixed bursting, the elucidation of the timescales that are needed to produce it, and the determination of parameter changes that can enhance its robustness.
Neurons in the pre-BötC appear to be electronically compact (Dunmyre et al. 2011; Del Negro et al. 2011), and qualitatively similar dynamics arise when the model of Toporikova and Butera (TB model) is reduced to a single compartment. Thus, Park and Rubin (2013) used such a reduction and studied a single-compartment model of a pre-BötC inspiratory neuron featuring both Na P and CA N currents, as well as intracellular calcium oscillations that activate the CAN current but are themselves independent of somatic voltage, as in previous computational and experimental work (Mironov 2008; Toporikova and Butera 2011). The dynamics of this model is given by the following equations:
with
In system (1a)-(1e), V denotes voltage, n,h are voltage-dependent gating variables, [Ca] is intracellular calcium concentration, and l represents the fraction of IP 3 channels that have not been inactivated, which affects the flux of calcium between the cytosol and endoplasmic reticulum (ER) denoted by J ER IN,J ER OUT. Additional description of model components has been given previously (Toporikova and Butera 2011; Park and Rubin 2013).
Default parameter values and corresponding units for this system are given in Table 1. We refer to the system of Eqs. (1a)-(1e) as the full model. Following the terminology used in Park and Rubin (2013), we call the system of Eqs. (1a)-(1c) the somatic subsystem and the system of Eqs. (1d)-(1e) the dendritic subsystem; however, we emphasize that this is a one-compartment model and hence includes just one voltage variable. The somatic subsystem alone, with g CAN=0, is based on an earlier pre-BötC model (Butera et al. 1999) that can switch between quiescence in which no spikes occur, a second form of activity called square-wave bursting in which silent phases lacking voltage spikes rhythmically alternate with active phases of spiking, and a third activity pattern consisting of uninterrupted tonic or sustained spiking, depending on parameter choices. The dendritic subsystem variables ([Ca],l) act as a relaxation oscillator. In the full system, calcium still evolves independently from somatic activity patterns, and the dynamics of ([Ca],l) affects the dynamics of (V,n,h); the parameter g CAN controls the coupling strength.
Time series for bursting solutions of the full system (1a)–(2a). This model produces (A) somatic bursting (shown for [IP3]=0.9 μM and g NaP=2.5 nS), (B) dendritic bursting ([IP3]=1.2 μM and g NaP=1 nS), and (C) somato-dendritic bursting ([IP3]=0.95 μM and g NaP=2 nS), with other parameter values as in Table 1; all patterns repeat periodically
Similarly to the TB model (Toporikova and Butera 2011), the full model (1a)-(1e) can produce two types of intrinsic bursting behaviors, depending on chosen parameter values. One type of bursting (somatic bursting) depends on persistent sodium current inactivation, whereas the other type (dendritic bursting) relies on intracellular Ca2+. [IP3] and g NaP are two critical parameters that can be used to switch the bursting mechanism from one type to the other (Toporikova and Butera 2011; Park and Rubin 2013). Specifically, the level of [IP3] determines whether the ([Ca],l) system exhibits a stable steady state or a stable oscillation, while [Ca] and g NaP both affect the dynamics of the somatic subsystem. In the two extreme cases, bursting is driven by either somatic membrane properties or Ca2+ oscillations alone. However, in some region of (g NaP,[IP3]) parameter space, these mechanisms interact to produce a somato-dendritic bursting pattern. Figure 1 shows the three types of bursting.
One of the most interesting somato-dendritic bursting solution patterns presented in Park and Rubin (2013) is generated when [IP3]=0.95 and g NaP=2 (Fig. 1, bottom panel). This pattern consists of long bursts separated by sequences of short bursts and is observed experimentally (Dunmyre et al. 2011). For convenience, we refer to such solutions as mixed bursting (MB) solutions. Numerical simulations show that MB solutions of system (1a)-(1e) are quite sensitive to changes of values of parameters such as [IP3] and g NaP, to changes of timescale parameters, and to changes in timescale separation.
Since a regular bursting solution requires at least two timescales, it is natural to expect that MB solutions, which involve a gradual temporal progression of bursts, might need a third timescale. In this paper, we aim to better understand the mechanisms underlying the dynamics of the MB solution (Park and Rubin 2013) and to determine what mix of timescales is involved in generating this solution. More generally, we seek to analyze what combinations of timescales can support MB solutions and whether the full model can be tuned to make the MB solution more robust, corresponding to the fact that it is seen in experiments (Dunmyre et al. 2011). With this goal, we will nondimensionalize the equations to reveal the presence of different timescales; determine how to group the timescales that are present (in particular, whether to use two or three classes); set up reduced systems based on the separation of timescales; and use the reduced systems to explain the mechanisms underlying the dynamics of MB solutions.
By uncovering the mechanisms underlying the MB solution pattern in the full model, we deduce what combination of timescales can generally support MB solutions and conclude that a third timescale is not actually required to generate MB solutions in this model. In the course of our analysis, we also attain and illustrate important insights into how the full model can be tuned to make MB solutions more robust.
2 Methods and preliminary analysis
Since the dendritic system (1d)-(1e) evolves independently of Eqs. (1a)-(1c), it is useful to visualize its nullclines, namely the curves where d[Ca]/d t=0 and d l/d t=0, respectively, in the ([Ca],l) phase plane. With our default parameter values (Table 1), the nullcline of [Ca] is a cubic curve and that of l is sigmoidal (Fig. 2A). The dendritic subsystem generates relaxation oscillations involving jumps in [Ca] between branches of the [Ca]-nullcline alternating with drift in ([Ca],l) along these branches (Fig. 2A); the [Ca]-jumps appear to be fast relative to the slow drift.
Basic structures of the two subsystems (1a)-(1c) and (1d)-(1e) with parameter values as given in Table 1 but without coupling and with [IP3]=1 μM. (A): Nullclines of [Ca] (red) and l (cyan) for the dendritic subsystem (1d)-(1e). The attracting periodic orbit for this subsystem is shown in black (with clockwise flow passing through the numbered regions in increasing order). Yellow symbols mark key points along the solution trajectory (star: start of phase  ; circle: start of phase
; circle: start of phase  ; square: start of phase
; square: start of phase  ; triangle: start of phase
; triangle: start of phase  ). (B): Projection onto (h,V)-space of the bifurcation diagram for the somatic subsystem along with the h-nullcline shown in cyan. The curve S (black) denotes the fixed points of the Eqs. (1a)-(1b) with h taken as a constant parameter, and the blue curve shows the maximum and minimum V along the family of periodics (P). S and the h-nullcline intersect in a fixed point of the full model (1a), which is labeled. (C): Projection of a burst trajectory (black) of model (5a) onto the bifurcation diagram for the somatic subsystem generated with c=0.0171 fixed, along with the h-nullcline (cyan). The blue and red dashed lines indicate the h values where the lower fold and homoclinic bifurcations occur, respectively
). (B): Projection onto (h,V)-space of the bifurcation diagram for the somatic subsystem along with the h-nullcline shown in cyan. The curve S (black) denotes the fixed points of the Eqs. (1a)-(1b) with h taken as a constant parameter, and the blue curve shows the maximum and minimum V along the family of periodics (P). S and the h-nullcline intersect in a fixed point of the full model (1a), which is labeled. (C): Projection of a burst trajectory (black) of model (5a) onto the bifurcation diagram for the somatic subsystem generated with c=0.0171 fixed, along with the h-nullcline (cyan). The blue and red dashed lines indicate the h values where the lower fold and homoclinic bifurcations occur, respectively
Since the somatic subsystem (1a)-(1c) is influenced by the dendritic subsystem and the somatic subsystem includes more than two variables, it is not as useful to examine somatic subsystem nullclines and instead we turn to bifurcation diagrams based on an approach called fast-slow decomposition.
2.1 Fast-slow decomposition and bifurcation diagrams
In the classical fast-slow decomposition approach, which has been applied to a wide range of neuroscience models (see e.g. Rinzel 1987; Rubin and Terman 2002; Ermentrout and Terman 2010), variables in a model system are identified as fast or slow depending on the rates at which they evolve. The behavior of fast variables is analyzed with slow variables frozen. Once attractors for fast dynamics are identified, then one considers how the dynamics of the slow variables can yield drift along a family of fast subsystem attractors. If this family terminates, then fast dynamics are once again used to identify the next fast subsystem attractor that is reached. Indeed, interesting solutions often involve multiple fast and slow components. Trajectory segments corresponding to these epochs of fast and slow dynamics are concatenated to form a singular solution, which represents an estimate for an actual solution near the limit in which the rate of change of the slow variables goes to zero.
A standard bifurcation diagram is a representation of the equilibria and periodic orbits that are present for a system over a range of values of some parameter, known as the bifurcation parameter, as well as the bifurcations associated with changes in existence and stability of these structures (Strogatz 2014; Guckenheimer and Holmes 2013; Shilnikov et al. 2001). For example, in Section 3.4, we will consider a traditional 1-parameter diagram for the dendritic subsystem, with [IP 3] treated as a bifurcation parameter. For a system with a single slow variable, one way to complete a fast-slow analysis is to treat the slow variable as a parameter, compute the fast subsystem’s bifurcation diagram with respect to that variable (Rinzel 1987; Izhikevich 2000), and then consider how the slow variable’s dynamics moves a trajectory along the structures in the diagram.
In this vein, the first step of fast-slow decomposition analysis of the somatic subsystem (1a)-(1c) can be performed by treating the slowest variable, h, as a bifurcation parameter for the other, faster model (1a), (1b). The resulting bifurcation diagram (Fig. 2B) includes an S-shaped curve of equilibria (S) and a family of stable periodic orbits (P) for Eq. (1a), (1b). The bifurcations where S turns around are called saddle-node or fold bifurcations. The family P initiates in a homoclinic (HC) bifurcation at an h value where Eq. (1a), (1b) have a homoclinic orbit, which converges to a point called the homoclinic point on the middle branch of S as t→±∞. As h is increased above this value, the family P persists until it terminates in a saddle-node of periodic orbits (SNPO) bifurcation, which occurs where P coalesces with a second family of unstable periodic solutions. This unstable orbit family is born in a subcritical Andronov-Hopf (AH) bifurcation (the subcriticality refers to the fact that unstable orbits emanate from the bifurcation point). We sometimes refer to h A H , h L F and h H C as the h values where the AH, LF and HC bifurcations happen, respectively.
To complete the fast-slow analysis, we next consider the h dynamics relative to this bifurcation diagram. How h evolves depends on the location of its nullcline, which is V-dependent. If the h-nullcline intersects S on its lower branch, then the intersection point is a stable equilibrium point for the full model and hence the full system exhibits quiescence. To first approximation, if the intersection point lies on the middle branch of S yet below the homoclinic point, then the full system exhibits the square-wave bursting (Rinzel 1987) mentioned in the Introduction, consisting of slow drift to the right along the lower branch of S, a fast jump to elevated voltages at the lower fold or knee of S, fast oscillations along P accompanied by slow drift to the left in h, and a fast jump back down to the lower branch of S near HC on each cycle. An example of such a square-wave bursting solution, superimposed on the relevant bifurcation diagram for the nondimensionalized model (5a) derived below in Section 2.3, appears in Fig. 2C. Finally, if the intersection point lies above the homoclinic point on the middle branch of S, then the full system exhibits the sustained oscillations known as tonic spiking. The location of the intersection of the h-nullcline and S depends on the tuning of parameters (e.g. g NaP, g ton).
In a system with 3 disparate timescales, timescale decomposition can also be used (Nan et al. 2015). We refer to the three widespread timescales that will appear in model (1a) as fast, slow, and superslow. Note that for the fast-slow decomposition of the somatic subsystem alone, it does not matter if h is slow or superslow, as long as it is much slower than the other variables V,n.
2.2 2-parameter bifurcation diagrams
Suppose that in a 1-parameter bifurcation diagram as described in the previous section, generated with respect to a parameter p 1, a particular bifurcation occurs, say at \(p_{1}={p_{1}^{c}}\). Generally, although not always, it can be expected that if another parameter, say p 2, is perturbed by a small amount, then that bifurcation will still happen for some value of p 1 near \({p_{1}^{c}}\). When this holds, we can trace a curve of values in the (p 1,p 2) plane at which this bifurcation occurs. The resulting plot is called a 2-parameter bifurcation diagram. If there are multiple bifurcations that arise as p 1 is varied for each fixed p 2, then we can include multiple curves in our 2-parameter bifurcation diagram.
For example, by treating [Ca] as the second bifurcation parameter for Eq. (1a)-(1b) and following in (h,[Ca]) the HC and LF points in the 1-parameter bifurcation diagram as shown in Fig. 2B, we obtain a 2-parameter bifurcation diagram in (h,[Ca])-space (Fig. 3).
Homoclinic bifurcation curve (red) and the curve of saddle-node bifurcations (blue) corresponding to the lower fold of the bifurcation diagram (Fig. 2B) in (h, [Ca]) parameter space
We will make heavy use of 2-parameter bifurcation diagrams in our analysis because they can help us identify how variations in 2 slow variables affect fast variable dynamics and they can show us how variation of parameters related to timescales can promote or compromise the existence of mixed bursting (MB) solutions. First, as a final preliminary step before embarking on our main analysis, to better justify the fast-slow decomposition approach and to clearly identify the timescales that are present, we nondimensionalize the full system (1a)-(1e).
2.3 Nondimensionalization and simplification of timescales
Our analysis will depend heavily on exploiting the presence of different timescales. As a first step, it is helpful to rescale the variables so that the important timescales can be explicitly identified. To this end, we define new dimensionless variables (v, c, τ), and voltage, calcium and timescales Q v , Q c and Q t , respectively, such that
Note that n, h and l are already dimensionless in Eq. (1a).
Details of the nondimensionalization procedure, including the determination of appropriate values for Q v , Q c and Q t , are given in Appendix B. From this process, we obtain a dimensionless system of the form
with parameters R v , R n , R h , R c and R l given in Eq. (9a), where the functions f 1, f 2, g 1, g 2, h 1, t n and t h are specified in Eq. (10a), both of which appear in Appendix B. All functions on the right hands of these equations are of size O(1), except 1/t n and 1/t h , which are bounded by 1. We use the notation O to denote an order of magnitude estimate: x∼O(10n), where n is the nearest integer to log(x). The parameter values given in Table 1 yield R v ∼O(1), R c ∼O(10) and R l ∼O(1000) (note that these values are as given in earlier work (Toporikova and Butera 2011; Park and Rubin 2013) except that we reduced A from 0.005 μM −1⋅m s −1 to 0.001 μM −1⋅m s −1 to clarify the timescale separation).
To obtain \(R_{x}=\frac {1}{Q_{t}\cdot T_{x}}\) for x∈{n,h} in Appendix B, we followed the standard procedure of defining scaling factors T x = max (1/τ x (V)), where τ x (V) appears in system (1a). These factors turn out to be problematic, however, because both 1/τ n (V) and 1/τ h (V) depend heavily on voltage. Specifically, Fig. 4 shows the plots of 1/τ n (V) and 1/τ h (V) over the range V∈[−60,20]. This figure indicates that 1/τ n (V) varies from about 0.1 ms−1 to about 20 ms−1 and 1/τ h (V) varies from about 0.0001 ms−1 to about 0.04 ms−1. From the definition of T x , we then obtain T n ≈20 ms−1 and T h ≈0.04 ms−1. As a result, the terms \(1/t_{x}(V):=\frac {1/\tau _{x}(V)}{T_{x}}\) appearing on the right hand sides of the n and h equations in Eq. (4a) vary from O(0.001) to O(1). However, nondimensionlization requires the right hand sides to be O(1). Therefore, the quantities R n and R h , based on T n and T h , respectively, cannot capture the timescales for n and h. In other words, because the evolution rates of n and h depend on voltage V(t), these variables will have different timescales at different phases within a solution. As a first step in addressing this issue, we temporarily remove the reliance of the timescales of n and h on voltage by setting the two functions τ h (V), τ n (V) in (1a) to be constants, τ h , τ n , respectively. As a result, we obtain the following dimensionless full model, which we call the constant- τ model:
with relative rates of all variables:
From Eq. (6a) we conclude that v evolves on a fast timescale, c evolves on a slow timescale, and l evolves on a superslow timescale for the baseline parameter values, although the values R v , R c and R l can be varied by changing C m , K C a and A, respectively, as shown in Eq. (9a) in Appendix B. The constants τ n and τ h appearing in Eq. (6b), which control the timescales for n and h, will need to be determined. To start our analysis, we will set [IP3]=1 μM, although we will vary it again in Section 3.4. For our other parameter values fixed as in Table 1, this choice ensures that the dendritic subsystem acts as a standard relaxation oscillator, with simple nullcline interactions.
To analyze the dynamics of Eq. (5a), our approach is to use fast-slow decomposition, treating h as a bifurcation parameter for the somatic subsystem (5a)-(5b) and considering the effect of the dendritic system (c,l) on the resulting bifurcation diagram, in some cases by using 2-parameter bifurcation diagrams (Section 2.2). In the following, we will first determine what timescales for n and h, controlled by τ n and τ h , are needed for Eq. (5a) to generate an MB solution, while other timescales are as specified in Eq. (6a); second, we will ascertain which timescales can be combined without losing the qualitative features of MB solutions; and third, we will deduce what combinations of timescales can support MB solutions in general. For convenience, we henceforth omit units of parameter values.
3 Results
System (4a) is a nondimensionalized version of a 1-compartment pre-BötC neuron model (Park and Rubin 2013) derived from an earlier 2-compartment model (Toporikova and Butera 2011). This system exhibits a clear separation of timescales between v (fast), c (slow) and l (superslow), as described in Section 2.3. To analyze the system with a fast-slow decomposition approach (see Section 2.1), we also need a clear separation of timescales between n, h and the other variables. However, this separation is lacking, since the rate factors multiplying the equations for the gating variables depend on the voltage. Until we resolve this issue, we consider the adjusted system (5a), with τ n ,τ h constant, and we temporarily group n as a fast variable and h as a slow variable, as has been suggested in past studies of the Butera model, such as Best et al. (2005).
To explain the mechanisms underlying the dynamics of the model, we link various two-dimensional projections, each corresponding to either a 1-parameter bifurcation diagram with respect to some parameter, a 2-parameter bifurcation diagram, or the phase plane of one oscillator (Section 2). Since (c,l) oscillates independently of (v,n,h), it is useful to consider the system from the perspective of a fast-slow system driven by a slow-superslow oscillation (cf. (Nan et al. 2015)). There are three slow/superslow variables, h, c, l, in the full system. Changes in l affect the somatic subsystem (5a)-(5c) indirectly, in the sense that l is coupled to c and c is coupled to v, but l does not appear in the v equation. Thus, if we treat all slow or superslow variables as bifurcation parameters, then it is sufficient to consider only h and c when studying the dynamics of the somatic subsystem (Park and Rubin 2013). With these two parameters, it is convenient to treat h as a bifurcation parameter for the geometric analysis of the somatic subsystem and to consider the effect of c on the resulting bifurcation diagram. Instead of using c directly, we follow Park and Rubin (2013) and choose g CAN T o t =g CAN f(c) as a bifurcation parameter, where f is the Hill function of c given in Eq. (2c).
3.1 The constant- τ model generates MB under certain conditions
Based on simulations of the constant- τ model (5a) over a range of τ n and τ h values, we find that under the choice τ n =5 and τ h =1000, (5a) yields an MB solution, the time series of which is shown in Fig. 5A. In this case, h evolves on a superslow timescale, comparable to l. To generalize this result to other parameter values, we seek to derive conditions under which MB patterns occur.
Simulation of one cycle of the MB solution generated by (5a), together with corresponding bifurcation diagrams, for τ n =5, τ h =1000, [IP3]=1 and other parameter values as given in Table 1. Circled numbers and yellow symbols correspond to phases of the (c,l) oscillation and the points of transition between them, as shown in Fig. 2A. (A): Temporal evolution of v. (B): The effect of c on the bifurcation diagram for the (v,n) system, projected into (h,v)-space, along with the h-nullcline (cyan). Increasing c from 0.0171 to 1 results in a shift of the bifurcation diagram to the left (magenta to blue) and switches the homoclinic bifurcation to a SNIC. (C): Homoclinic bifurcation curve (red), the curve of saddle-node bifurcations corresponding to the lower fold of the bifurcation diagram (blue) and the trajectory (black) in (h,g CAN T o t ) parameter space
3.1.1 Coupling from the dendritic subsystem affects the somatic subsystem bifurcation diagram
As a first step, we investigate the coupling effect in Eq. (5a). When g
CAN=0, the constant- τ model decouples into two systems, each of which has a multiple-timescale structure. For the parameter values we have chosen, the bifurcation structure and the nullclines for the uncoupled systems are qualitatively as shown in Fig. 2. Since the coupling in our system is unidirectional, the oscillations in (c,l) are independent of g
CAN and of the dynamics of the (v,n,h) subsystem. Since c is slow and l is superslow, these are relaxation oscillations that can be described in terms of fast-slow (or here, slow-superslow) decomposition. Specifically, the oscillations consist of a superslow excursion through the silent phase (Fig. 2A,  ), a slow jump away from the c-nullcline up to the active phase (Fig. 2A,
), a slow jump away from the c-nullcline up to the active phase (Fig. 2A,  ), a superslow excursion through the active phase (Fig. 2A,
), a superslow excursion through the active phase (Fig. 2A,  ), and a slow jump back to the silent phase (Fig. 2A,
), and a slow jump back to the silent phase (Fig. 2A,  ).
).
In contrast, if g CAN>0 (e.g., g CAN=0.7 in Fig. 5A), then the (v,n,h) subsystem depends on g CAN and on the (c,l) oscillation. An example of the coupling effect can be seen in Fig. 5B: the magenta (respectively blue) curve denotes the bifurcation diagram of the somatic subsystem that is obtained for c at 0.0171 (respectively 1) and we can see that as c increases, the bifurcation diagram will shift to the left. This shift includes movement of the relevant bifurcations within the diagram, namely the lower fold (LF), the homoclinic (HC), and the Andronov-Hopf (AH) bifurcations; that is, the bifurcation points h A H , h L F and h H C depend on c.
To generalize this observation, we consider the 2-parameter bifurcation diagram of the (v,n) subsystem where we use h and g CAN T o t as bifurcation parameters (Section 2.2); see Fig. 5C. The red (respectively blue) curve in this panel is the curve of HC (respectively LF) bifurcations, which terminates (respectively initiates) each burst, as noted previously (Section 2.1). Since the increase of g CAN T o t moves the bifurcation diagram in the direction of decreasing h, both the LF and HC curves are negatively sloped in (h,g CAN T o t )-space. The two curves eventually meet, corresponding to the homoclinic occurring at the knee of S (also known as a SNIC bifurcation (Shilnikov et al. 2001; Ermentrout and Terman 2010)).
3.1.2 Low calcium permits small bursts while a jump in calcium terminates them
Superimposing the trajectory of the full model (5a) on the 2-parameter bifurcation diagram allows us to understand how the smaller bursts within the MB solution occur and terminate. Recall that for c fixed, the somatic subsystem generates a small square-wave burst, as can be seen in Fig. 2C, when c is fixed at 0.0171, corresponding to its value at the beginning of the first small burst of an MB solution (near the yellow star in Fig. 5A), with the (c,l) oscillation in phase  . Within each burst cycle, the trajectory evolves from the lower fold of S, where it jumps to higher v and starts to oscillate, to the HC bifurcation, where oscillations end, and back to the fold; in other words, h evolves through the same interval of values twice per cycle. In the 2-parameter bifurcation diagam of Fig. 5C, this corresponds to a trajectory segment traversing from LF to HC and back to LF. Now, what happens if c is not fixed?
. Within each burst cycle, the trajectory evolves from the lower fold of S, where it jumps to higher v and starts to oscillate, to the HC bifurcation, where oscillations end, and back to the fold; in other words, h evolves through the same interval of values twice per cycle. In the 2-parameter bifurcation diagam of Fig. 5C, this corresponds to a trajectory segment traversing from LF to HC and back to LF. Now, what happens if c is not fixed?
As long as (c,l) remain in phase  , we have f
2(c,l)=0. Thus, fast-slow decomposition tells us that the slower l dynamics governs this subsystem, with evolution occuring on a superslow timescale. Hence, during the first small burst period, which is relatively short, c only increases by a small amount. As a result, the bifurcation diagrams for c corresponding to the beginning and end of the first small burst lie extremely close to each other. Thus, another small burst can occur. In fact, we see from Fig. 5C that until the (c,l) system leaves phase
, we have f
2(c,l)=0. Thus, fast-slow decomposition tells us that the slower l dynamics governs this subsystem, with evolution occuring on a superslow timescale. Hence, during the first small burst period, which is relatively short, c only increases by a small amount. As a result, the bifurcation diagrams for c corresponding to the beginning and end of the first small burst lie extremely close to each other. Thus, another small burst can occur. In fact, we see from Fig. 5C that until the (c,l) system leaves phase  (yellow circle in Fig. 5C and A), a gap remains between LF and HC and the trajectory can continue to pass back and forth between these curves, yielding small bursts.
(yellow circle in Fig. 5C and A), a gap remains between LF and HC and the trajectory can continue to pass back and forth between these curves, yielding small bursts.
As the trajectory passes the yellow circle and moves into phase  , f
2=0 no longer applies, and the flow switches from superslow to slow. More precisely, the c coordinate starts to jump up on the slow timescale, while h remains on the superslow timescale. The 2-parameter bifurcation diagram shows that this jump in c, or correspondingly in g
CAN
T
o
t
, pulls the system out of the square-wave bursting region between the LF and HC curves. The fact that the trajectory in (h,g
CAN
T
o
t
)-space reaches the LF and HC curves six times before g
CAN
T
o
t
jumps up corresponds to the existence of the six small bursts (see Fig. 5A). In fact, since the l-nullcline lies close to the left knee of the c-nullcline, as discussed in the Remark of Appendix A, the jump up is gradual; a seventh small burst actually occurs during the initial part of the jump up (just after the yellow circle in Fig. 5A) and is followed by the start of an eighth small burst. In the singular limit, however, this additional bursting will be lost and all small bursts will occur within phase
, f
2=0 no longer applies, and the flow switches from superslow to slow. More precisely, the c coordinate starts to jump up on the slow timescale, while h remains on the superslow timescale. The 2-parameter bifurcation diagram shows that this jump in c, or correspondingly in g
CAN
T
o
t
, pulls the system out of the square-wave bursting region between the LF and HC curves. The fact that the trajectory in (h,g
CAN
T
o
t
)-space reaches the LF and HC curves six times before g
CAN
T
o
t
jumps up corresponds to the existence of the six small bursts (see Fig. 5A). In fact, since the l-nullcline lies close to the left knee of the c-nullcline, as discussed in the Remark of Appendix A, the jump up is gradual; a seventh small burst actually occurs during the initial part of the jump up (just after the yellow circle in Fig. 5A) and is followed by the start of an eighth small burst. In the singular limit, however, this additional bursting will be lost and all small bursts will occur within phase  .
.
3.1.3 Short bursts are followed by a long incrementing burst
As this jump of c occurs, it induces a burst of higher frequency spiking with gradually incrementing spike amplitudes (Fig. 5A). The increase in frequency arises because the trajectory pulls far away from the HC (or SNIC) curve, which is associated with slow oscillations. This deviation occurs because h, which is evolving superslowly, remains almost constant during phase  , while c evolves on the slow timescale. In other words, the increase in c shifts the HC/SNIC in the fast system bifurcation diagram to much lower h values (Fig. 5B), while h itself hardly changes. Thus, the trajectory now oscillates at an h value far away from the HC/SNIC. At this value, the periodic orbits have relatively small amplitude, as can also be seen near the AH bifurcation in Fig. 5B. Once the jump of c is complete and phase begins
, while c evolves on the slow timescale. In other words, the increase in c shifts the HC/SNIC in the fast system bifurcation diagram to much lower h values (Fig. 5B), while h itself hardly changes. Thus, the trajectory now oscillates at an h value far away from the HC/SNIC. At this value, the periodic orbits have relatively small amplitude, as can also be seen near the AH bifurcation in Fig. 5B. Once the jump of c is complete and phase begins  (Fig 5C, yellow square), c again evolves superslowly and h can gradually drift left towards the SNIC, with oscillation amplitude growing along P correspondingly.
(Fig 5C, yellow square), c again evolves superslowly and h can gradually drift left towards the SNIC, with oscillation amplitude growing along P correspondingly.
Finally, as phase  begins, c no longer tracks l on the superslow timescale and instead evolves on the slow timescale, just as during phase
begins, c no longer tracks l on the superslow timescale and instead evolves on the slow timescale, just as during phase  . Hence, the slow jump down in c will bring the trajectory far below the HC/SNIC curve (Fig. 5C), so the trajectory enters the silent phase and the long burst terminates. The overall duration of the long burst is set by the superslow time scale, since both c and h evolve on that scale in phase
. Hence, the slow jump down in c will bring the trajectory far below the HC/SNIC curve (Fig. 5C), so the trajectory enters the silent phase and the long burst terminates. The overall duration of the long burst is set by the superslow time scale, since both c and h evolve on that scale in phase  . After the long burst ends, the solution returns to our starting point (star in Fig. 5A and C) and one cycle of the MB solution is completed.
. After the long burst ends, the solution returns to our starting point (star in Fig. 5A and C) and one cycle of the MB solution is completed.
3.1.4 Conditions for MB activity
Based on the results so far, we have identified the following conditions that conspire to yield MB patterns:
-
(C1):
It is necessary that the somatic subsystem acts as a square-wave burster for c values arising during phase
 of the (c,l) oscillation, so that there exist small burst solutions before c jumps up to its active phase. In other words, there must be a gap in h between the LF and HC curves in the (h,g
CAN
T
o
t
) 2-parameter bifurcation diagram for c small (Fig. 5C).
of the (c,l) oscillation, so that there exist small burst solutions before c jumps up to its active phase. In other words, there must be a gap in h between the LF and HC curves in the (h,g
CAN
T
o
t
) 2-parameter bifurcation diagram for c small (Fig. 5C). -
(C2):
The trajectory needs to cross the gap between the LF and HC curves multiple times, with each crossing taking long enough to allow for a square-wave burst, so that there are multiple small bursts before the long burst; the timescales of h, v, and c should be related during the square-wave bursting (SW) period in a way that makes this outcome possible.
-
(C3):
The transition to the long burst occurs due to the jump up of c to the active phase, which requires the timescale for c to become faster than h and l after the SW phase.
We next use these three conditions to find the right combination of timescales that are generally needed to obtain an MB solution.
3.2 A certain combination of timescales supports MB solutions in the constant- τ model (5a)
3.2.1 (C1) ⇒v and n should evolve on the same timescale
(C1) requires that the (v,n,h) subsystem acts as a square-wave burster for c small, which is determined by the bifurcation diagram of the (v,n) subsystem with h treated as a bifurcation parameter. Note that the AH value and the position of the periodic orbit (P) branch of the bifurcation diagram for (v,n) depend on R v and R n , which determine the timescales of v and n. Thus, we investigate what mix of timescales for these two variables is needed.
R v and R n can be varied by changing the two parameters C m and τ n , respectively (see the Appendix B). In the following, we fix C m =21 and vary τ n to study how it will affect the (v,n) bifurcation diagram and under what condition the somatic subsystem can generate a square-wave bursting solution. Representative results are shown in Fig. 6A, where the 1-parameter bifurcation diagram of the (v,n) subsystem with respect to h for c=0.0171 is computed. While the curve of equilibria of the (v,n) subsystem, S (black), and the h-nullcline (cyan) are both independent of τ n , the periodic orbit branch, P, is sensitive to changes of τ n . Specifically, an increase of τ n moves the family of periodic orbits to the right in (h,v)-space (Fig. 6A).
Bifurcation diagrams for the somatic subsystem for various τ n values. (A): Bifurcation diagrams for the somatic subsystem with h as a parameter and c fixed at 0.0171. From the magenta curve to the blue to the red, τ n varies from 1 to 5 to 10. As τ n increases, AH and P move to the upper right, while the h-nullcline (cyan) and S (black) remain unchanged. (B): Two curves of HC bifurcations (red, τ n =5; green, τ n =10) in (h,g CAN T o t ) parameter space. The curves of LF bifurcations for τ n =5 and 10 are essentially identical; both overlap completely with the green curve and hence are not visible as separate entities in the figure. The horizontal line represents g CAN T o t =0.116, where the green and red curves meet
For τ n =1, the family of periodic orbits is almost vertical, as illustrated by the magenta curve in Fig. 6A, and is in a position where it will not influence the attracting solution. Indeed, under such a choice, the constant- τ model yields a solution lacking v spiking and MB cannot exist. Specifically, for c at its minimum, the h-nullcline and the equilibria branch S intersect at one stable fixed point on the upper branch of S and two unstable fixed points on the middle branch (Fig. 6A). Notice that the increase of c, which moves S (black) and P (magenta) to the left, will not change the stability of the equilibrium point on the upper branch of S. Hence, for the full range of c values, there is a stable equilibrium of (v,n,h), and the trajectory will eventually be attracted by this family of stable equilibria, yielding a plateau of v, rather than spiking or MB.
For τ n =5 (respectively τ n =10) and c=0.0171, the periodic orbit branch is given by the blue (respectively red) curve in Fig. 6A. In both cases, unlike when τ n =1, as h is increased, a stable family of periodic orbits is created in a HC bifurcation involving the middle branch of S and is destroyed in a supercritical AH bifurcation along the upper branch. Although these two stable periodic orbit branches appear to be quite similar, there is a crucial difference between them. For τ n =10, there is a SNIC bifurcation as the HC bifurcation meets with the LF bifurcation for c at its minimal value, and this bifurcation persists for all c values within a complete relaxation oscillation cycle, as can be seen in the 2-parameter bifurcation diagram in Fig. 6B (green curve). Thus there is only a tonic spiking solution, which violates (C1). For τ n =5, there is a gap in h between the LF and HC curves for c=0.0171 (Fig. 6A), persisting up to roughly c=0.14 (Fig. 6B), which will result in a square-wave bursting solution as required. Therefore, τ n =5 together with C m =21 is a parameter set that satisfies (C1).
In summary, among all three cases that we have discussed above, only τ n =5 (R n =5) can support the MB solution. Recall that we have chosen the timescale of voltage to be R v ∼O(1). To determine whether v and n truly can be coordinated as evolving on disparate timescales, a natural question to ask is: can we make the timescales of v and n more separated without losing the MB solution? To figure this out, we now fix τ n =5 and allow both C m and h to vary to find the somatic (v,n) subsystem 2-parameter bifurcation curves in the (C m ,h) parameter plane, as illustrated in Fig. 7A. The LF and HC curves are shown in blue and red, respectively, and the green curve denotes the AH bifurcation on the upper branch of S.
Bifurcation curves for the (v,n) subsystem of Eq. (5a) for c=0. The curves of AH bifurcations, LF bifurcations and HC bifurcations are given by the green, blue and red curves, respectively. Solid (respectively, dashed) black curves indicate stable (respectively, unstable) equilibria of the somatic subsystem. (C1) requires that for fixed C m , the curves progress from red to blue to green as h increases. (A): (C m ,h) parameter space with τ n =5. The two magenta vertical lines represent C m =12.87 and C m =35.62, at which the LF and HC bifurcation curves intersect and the LF and AH bifurcation curves intersect, respectively. (B): (τ n ,h) parameter space with C m =21. The two magenta vertical lines represent τ n =2.909 and τ n =8.116, with similar interpretations as in (A)
As we have seen, to allow square-wave bursting, we must have h A H >h L F >h H C . These inequalities hold between the two vertical dashed magenta lines in Fig. 7A. These lines demarkate C m =12.87 and C m =35.62, at which the SNIC bifurcation appears and at which the LF and AH bifurcation curves intersect, respectively. These two lines divide (C m ,h)-space into three regions, which we can call regions 1, 2, and 3 from left to right. Our analysis has shown that v engages in tonic spiking for parameter values chosen in region 1 and v asymptotes to a steady state in at least most of region 3 (other complicated behaviors may occur on small parameter intervals and are not considered here). In terms of the timescale parameters, (C1) requires the timescale of v to satisfy 0.4596≤R v ≤1.2721 with the timescale of n given by R n =5. Similarly, there is a bounded range of τ n values for which the bifurcation curves align properly for fixed C m (Fig. 7B). In other words, a certain difference in rate constants for v and n is required, but the extent of the timescale separation is bounded, and thus v,n should indeed be considered as evolving on the same timescale, albeit at different rates.
3.2.2 (C2) and (C3) ⇒ relationships among all remaining timescales
Using (C2) and (C3), we can obtain the relation among timescales for the other three variables, h, c and l, required to yield an MB solution. Imposing (C3), we require that the (c,l) system acts as a relaxation oscillator and so the timescale of c is determined by that of l during its silent phase. In other words, we have R
c
≈R
l
during phase  and phase
and phase  (Fig. 2A). Moreover, the fact that almost all small bursts happen during phase
(Fig. 2A). Moreover, the fact that almost all small bursts happen during phase  suggests that the SW phase lies in phase
suggests that the SW phase lies in phase  . As a result, to consider (C2), we compare R
h
with R
l
, rather than R
c
, during phase
. As a result, to consider (C2), we compare R
h
with R
l
, rather than R
c
, during phase  .
.
Based on (C1), (C3), and (6a), we set the timescales to be (R v ,R n )∼(1,5) and (R c ,R l )∼(10,1000), respectively.. By fixing R l =1000 and varying τ h , which controls R h , we study the influence of the relation between R h and R l on the dynamics of Eq. (5a). From numerical simulations over a range of τ h values, we find that (5a) can generate MB solutions when τ h =1000, but this pattern is lost when τ h =90 (Fig. 8A) or τ h =10000 (Fig. 8B). These numerical results suggest that h and l may need to evolve at comparable rates in order for the constant- τ model to generate MB solutions.
Time series for attracting solutions of the constant- τ model and associated bifurcation diagrams when R v =1, R n =5, R c =10, and R l =1000 (pattern shown repeats periodically). (A) and (C): R h =90; (B) and (D): R h =10000. Top row shows temporal evolution of v (black); bottom row shows the curves of HC bifurcations (red), LF bifurcations (blue) and the trajectory (black), projected into (h,g CAN T o t ) parameter space. The yellow symbols indicate transition points between different phases for the dendritic subsystem, as shown in Fig. 2A. Circled numbers in (D), which represent the four phases of the (c,l) oscillation as in Fig. 2A, are omitted in (C)
The top row in Fig. 8 shows the time series for v, while the bottom row shows the 2-parameter bifurcation diagrams in (h,g
CAN
T
o
t
)-space together with the projection of the solution shown in the top row. The left panel of Fig. 8 shows the case when R
h
=90<R
l
=1000 during phase  . Since the dendritic oscillation follows the c-nullcline on the superslow timescale in this phase, h is evolving faster than c and thus the trajectory crosses the curves of LF and HC bifurcations within only one spike. This process will continue until c jumps up to its maximum value (yellow square), after which a burst of higher frequency spiking begins via the mechanism discussed in Section 3.1 and terminates when c falls down during phase
. Since the dendritic oscillation follows the c-nullcline on the superslow timescale in this phase, h is evolving faster than c and thus the trajectory crosses the curves of LF and HC bifurcations within only one spike. This process will continue until c jumps up to its maximum value (yellow square), after which a burst of higher frequency spiking begins via the mechanism discussed in Section 3.1 and terminates when c falls down during phase  . Therefore, the spiking persists throughout the c oscillation, failing to yield an MB solution. In the other case, when h evolves on a timescale of O(10000), h is slower than l and c, and Eq. (5a) generates a non-mixed bursting solution as shown in Fig. 8B. This solution arises because the drift of the trajectory in the direction of decreasing h after passing the curve of LF bifurcations is too slow for the solution to reach the curve of HC bifurcations (see Fig. 8D). As a result, spiking continues throughout the silent and active phases of the (c,l) oscillation, corresponding to the active phase of a single burst, until the slow jump down of c during phase
. Therefore, the spiking persists throughout the c oscillation, failing to yield an MB solution. In the other case, when h evolves on a timescale of O(10000), h is slower than l and c, and Eq. (5a) generates a non-mixed bursting solution as shown in Fig. 8B. This solution arises because the drift of the trajectory in the direction of decreasing h after passing the curve of LF bifurcations is too slow for the solution to reach the curve of HC bifurcations (see Fig. 8D). As a result, spiking continues throughout the silent and active phases of the (c,l) oscillation, corresponding to the active phase of a single burst, until the slow jump down of c during phase  brings the flow below the HC curve, terminating the burst of v spiking. On the other hand, if we fix R
h
=1000 and slow down l (e.g., R
l
=10000), then the MB solution persists, with more small bursts produced within each MB cycle because phase
brings the flow below the HC curve, terminating the burst of v spiking. On the other hand, if we fix R
h
=1000 and slow down l (e.g., R
l
=10000), then the MB solution persists, with more small bursts produced within each MB cycle because phase  , during which small bursts occur, is prolonged; see Fig. 9A. Therefore, we conclude that for mixed bursting, the timescales should satisfy the following refined and extended version of condition (C2):
, during which small bursts occur, is prolonged; see Fig. 9A. Therefore, we conclude that for mixed bursting, the timescales should satisfy the following refined and extended version of condition (C2):
-
(C2)’:
The trajectory needs to cross the gap between the LF and HC curves multiple times, with each crossing taking long enough to allow for a square-wave burst, so that there are multiple small bursts before the long burst; for this to happen, h should be slow enough relative to v and n, and c should evolve at least as slowly as h during the SW phase.
Fig. 9 MB dynamics with altered timescales. (A) One period of an MB solution for R h =1000,R l =10000. The slowing of l results in additional small bursts within the cycle. (B) Two periods of an MB solution for R c =1,R h =1000,R l =1000, such that the model includes only 2 timescales. (C) Equilibrium curves for the (v,n,c) system with h as a parameter and l=0.8. In this view there are 3 different curves corresponding to c=0.97 (green), c=0.07 (red), and c=0.02 (blue), respectively, which are the 3 values where \(c^{\prime }=0\) with l=0.8. AH and HC points are labeled; periodic orbits emanating from AH points are not shown, to avoid cluttering the plot. (D) Two periods of an MB solution for R c =1,R h =10000,R l =10000. Note that the time axis is scaled by a factor of 10 relative to (B). The persistence of MB dynamics with larger R h ,R l emphasizes that h,l really do evolve on a separate, slower timescale from the other variables in the 2-timescale model
For the above analysis to apply, we require that c evolves faster than h and l, but we have not yet specified how fast. The discussion up to this point shows that if (C3) holds and we speed up c, then we do not affect (C1), (C2)’, or (C3). In fact, as long as the relaxation character of the (c,l) oscillations is maintained, the timescale of c, which determines how fast the jump up of c happens and hence determines how fast the transition from the small burst to the long burst occurs, will not affect the MB pattern qualitatively. This claim is supported by the simulation result that if we make R c ∼O(1)=R v so that c evolves on the same timescale as v, the MB pattern still occurs, as shown in Fig. 9B.
3.2.3 Summary: MB requires two but not three separate timescales
We summarize the choices about the timescales that support MB dynamics in Table 2. If MBs are truly a three timescale form of dynamics, then we should be able to separate variables into three timescale classes and spread the timescales out as much as we like while still maintaining the MB solution. However, this is not the case. In fact, the MB solution breaks down as we make (v,c) and n more separated. Hence, in a timescale decomposition, the timescales should be considered as segregating into two classes, as indicated in Table 2.
This grouping is supported by two additional observations. First, if we consider (v,n,c) as the fast variables and compute the bifurcation diagram of the fast subsystem with respect to h, analogous to Fig. 2B, we obtain a similar result, see for example Fig. 9C. (Actually, as shown in Fig. 9C, there is one subtle change: because c ′=0 has three solutions for each fixed l in some range as shown by the red nullcline in Fig. 2A, we get three S-shaped equilibrium curves, each with its own AH, HC and LF points, instead of one. The evolution of l modulates these curves, just as c modulated the bifurcation curves when it was slow as in Fig. 5, but the overall MB dynamics remains similar, as shown in Fig. 9B, and can be understood using similar arguments.) Second, as we exaggerate the separation between these two classes, the MB solution persists (Fig. 9D). Therefore, we conclude that the MB solution of the constant- τ model (5a) is not specifically a three-timescale phenomenon but rather can occur robustly with two timescales.
3.3 Conditions (C1),(C2)’,(C3) guide selection of timescales that support MB dynamics in the full model (1a)
Based on the timescales that we have found in Section 3.2, we can now modify the original full model (1a), the dimensionless version of which is given by Eq. (4a), to obtain MB solutions. Notice that the only difference between the full model and the constant- τ model is whether the timescales of n and h are the v-dependent functions τ n (v) and τ h (v) or the constants τ n and τ h . We set R c =O(1) by increasing K C a from 2.5×10−5 to 1.25×10−4 and keep timescales for v and l unchanged so that we have (R v ,R c ,R l )=(O(1),O(1),O(1000)). According to Table 2, we will need to modify τ n (v) and τ h (v) in order to obtain R n ≈5 and R h ≈1000 for MB solutions. Specifically, we require these two functions to be less dependent on v and so as close as possible to the size 5 or 1000. To this end, we introduce a new parameter a x with default value 0 and abuse notation to redefine \(1/\tau _{x}(V)=\bar {\tau }_{x}/\cosh ((V-\theta _{x})/2\sigma _{x})+a_{x}\), where x∈{n,h}. We constrain the timescales for n and h by varying the parameters (σ n ,a n ) and (σ h ,a h ), respectively.
Figure 10 shows both the original τ x functions and their modified versions with the new parameters we have chosen. The reciprocals of the original τ n and τ h functions are given by the dashed blue curves, while the reciprocals of the modified functions that are now less dependent on voltage are denoted by the solid curves. Two examples of τ n (v), the reciprocals of which are shown in Fig. 10A, illustrate the effects of modifying τ n on the robustness of MB solutions. In the case when σ n =−6, the upper branch of somatic subsystem equilibria (magenta) intersects the h-nullcline (cyan) at a stable fixed point (Fig. 11), leading to a bistability of silence and bursting and hence compromising the robustness of the bursting solution. There is no such issue in the other case, when σ n =−5. In fact, the resulting bifurcation diagram (Fig. 11, green) is qualitatively the same as the one denoted by the blue curve in Fig. 6A except that the AH bifurcation on the upper branch of S is now subcritical, and so we choose to modify τ n (v) with σ n =−5,a n =0.1.
The graphs of the functions 1/τ n (v) and 1/τ h (v), with both default and new choices of σ n , a n , σ h and a h . (A): The graph of 1/τ n (v) for the default parameter values (σ n ,a n )=(−4,0) (dashed blue), or for the modified parameter values (σ n ,a n )=(−5,0.1) (green) or (σ n ,a n )=(−6,0.1) (magenta). (B): The graph of 1/τ h (v) for the default parameter value (σ h ,a h )=(5,0) (dashed blue), or for the modified parameter value (σ h ,a h )=(7,0.001) (red)
Recall that it is not accurate to simply nondimensionalize 1/τ x (V) by dividing it by its maximum, T x = max(1/τ x (V)), due to its dependence on voltage. Taking into consideration the full range of 1/τ x (V) rather than just the maximum, we summarize the timescales of n and h in Table 3.
With (R v ,R c ,R l ) fixed at (O(1),O(1),O(1000)), the version of system (4a) derived with the modified τ n and τ h given in Table 3 is able to generate an MB solution (Fig. 12A). The HC and LF curves in the 2-parameter bifurcation diagram in (h,g CAN T o t ) parameter space, as shown in Fig. 12B, are qualitatively the same as those denoted by the red and blue curves in Fig. 5c in Section 3.1. Hence the mechanisms underlying the MB solution from Eq. (4a), the dimensionless version of the full model, are qualitatively the same as those underlying the MB solution from the constant- τ model as discussed in Section 3.1.
Time series for attracting solutions of Eq. (4a) and corresponding bifurcation diagrams, with modified τ n and τ h as shown in Fig. 10 and Table 3 and with the timescales for the other three variables given by (R v ,R c ,R l )=(O(1),O(1),O(1000)). Left panels: Temporal evolution of v. Right panels: Two-parameter bifurcation diagrams showing HC (red) and LF (blue) curves, together with the projection of the trajectory (black) from the left panel, in (h,g CAN T o t )-space. In the top row, h is evolving on a timescale of O(1000) according to Table 3, which is made 10 times as slow (respectively fast) as in the middle (respectively lower) row. The yellow symbols indicate transition points between different phases for the dendritic subsystem, as shown in Fig. 2A. Circled numbers in (B), which represent the four phases of the (c,l) oscillation as in Fig. 2A, are omitted in (D) and (F)
Further speeding up of h (e.g., dividing τ h by 10) will eliminate MB solutions (Fig. 12C), as will the slowing down of h (e.g., multiplying τ h by 10, see Fig. 12E). The bifurcation mechanisms involved are again similar to what happens to the constant- τ model, as seen by comparing Fig. 12D with Fig. 8C and F with Fig. 8D. Hence, the results from the constant- τ model give crucial insights into how to adjust and group timescales for the original full model to support MB solutions.
3.4 Robustness of the full model
For the original parameter values as given in Park and Rubin (2013), MB solutions of the full model have sensitive dependence to [IP3] and g NaP, two critical parameters that help control the relative contributions of I CAN and I NaP and are used in previous studies to switch between different forms of bursting dynamics (Toporikova and Butera 2011; Park and Rubin 2013). With the new mix of timescales chosen in Section 3.3, simulation results show that the full model can generate MB solutions that are significantly more robust to variations in both [IP3] and g NaP (Fig. 13). In the following, we will examine what happens to the system dynamics under variations of timescales to yield this great enhancement of robustness of MB solutions to [IP3] and g NaP.
Regions of MB solutions in ([IP 3],g NaP)-space for the full model. The region for MB solutions of the full model for its original parameter values as given in Park and Rubin (2013) is shown in red; the MB region for the new mix of timescales (R v ,R c ,R l )=(O(1),O(1),O(1000)), with R n and R h given in Table 3, obtained by making C m =21, K C a =1.25×10−4, σ n =−5 , a n =0.1, σ h =7 and a h =0.001, is shown in blue. While the right boundary of the blue region ends at [IP3]≈1.58 for g NaP∈[1.78,2.43], we only plot the part with [IP3]≤1 to allow better visibility of the red region
3.4.1 Robustness to [IP3]
To explore the dependence of MB solutions of system (4a) on [IP3], we fix g NaP=2. As [IP3] increases from 0.95 (Fig. 14A) to 1.5 (Fig. 14B), the number of small bursts per MB cycle decreases. If we keep increasing [IP3], the small bursts will eventually disappear and the MB solution will be lost. By understanding the effect, we can deduce what adjustments are needed to make MB solutions even more robust to changes in [IP3].
From Fig. 15, we find that an increase of [IP3] shifts the c-nullcline downward and therefore influences the dynamics of the (c,l) subsystem. A 1-parameter bifurcation diagram for the (c,l) system, with [IP3] as a parameter, summarizes the effects of [IP3] variations on the intracellular calcium dynamics more fully (Fig. 16). For each fixed [IP3], the c-nullcline is cubic and the l-nullcline intersects it in 1, 2, or 3 points (Fig. 2A). The intersection points are critical points, which occur along the red curve in Fig. 16 and may be stable (solid) or unstable (dashed). For each [IP3], the c-nullcline achieves a local maximum at a left fold or knee (Fig. 2A). The knees form the blue curve in Fig. 16, and the loss of stability of the fixed point occurs, in an AH bifurcation that yields oscillations, when the fixed point is very close to this knee.
Summary of how structures relevant to the activity of the dendritic subsystem depend on the parameter [IP3], with all other parameters involved in the calcium dynamics as given in Fig. 14. The red solid (respectively, dashed) curve indicates the l-coordinate of the stable (respectively, unstable) intersection of the c- and l-nullclines, i.e., fixed points (FP), for the dendritic subsysystem, while the blue curve denotes the l-coordinate of the left knee (LK) of the c-nullcline for the dendritic subsystem, both parametrized by [IP3]. The two black vertical lines indicate the [IP3] values of two AH bifurcations in the dendritic subsystem where the periodic oscillations (PO) of (c,l) begin ([IP3]=0.942602) and terminate ([IP3]=1.58101), respectively
The l-nullcline lies near the knee on a range of [IP3] values near the loss of stability, as exemplified in Fig. 15A. (c,l) evolve very slowly near the knee when the nullclines are so close together (data not shown). Thus, even though c evolves on the same timescale, determined by its slaving to l, during phase
 (Fig. 15: from the yellow star, c≈0.0175, to the yellow circle, c≈0.0293), for both [IP3] values in Fig. 15, this phase duration is much longer for [IP3]=0.95, where the trajectory spends on long time near the fold (yellow circle), than for [IP3]=1.5, as observed in Fig. 14. Recall that all small bursts occur during the silent phase before c gets large, as shown in Figs. 14 and 17; as a result, there are fewer small bursts for [IP3]=1.5. Specifically, in Fig. 17A when [IP3]=0.95, the silent phase time is long enough for the trajectory to pass between the LF and HC curves multiple times and hence v exhibits multiple small bursts. However, for the other case shown in Fig. 17B, the time available for generating small bursts is so short that only two small bursts occur before the yellow circle.
(Fig. 15: from the yellow star, c≈0.0175, to the yellow circle, c≈0.0293), for both [IP3] values in Fig. 15, this phase duration is much longer for [IP3]=0.95, where the trajectory spends on long time near the fold (yellow circle), than for [IP3]=1.5, as observed in Fig. 14. Recall that all small bursts occur during the silent phase before c gets large, as shown in Figs. 14 and 17; as a result, there are fewer small bursts for [IP3]=1.5. Specifically, in Fig. 17A when [IP3]=0.95, the silent phase time is long enough for the trajectory to pass between the LF and HC curves multiple times and hence v exhibits multiple small bursts. However, for the other case shown in Fig. 17B, the time available for generating small bursts is so short that only two small bursts occur before the yellow circle.
Therefore, one way to make the MB solution more robust to changes in [IP3] is by using another means to prolong the silent phase of the dendritic subsystem oscillation. To this end, we can make l slower so that it is more separated from c and h. In that way, the orbits adhere closer to the c-nullcline during the silent phase and are slaved to l on a slower timescale, resulting in a longer silent phase for each fixed [IP3].
On the other hand, according to (C1), the somatic subsystem must yield bursting for the full system to generate MB solutions, i.e., there must be a gap in h between the LF and HC curves in (h,g CAN T o t ) parameter space (Fig. 17). As τ n is modified according to Table 3, LF remains unchanged, while the HC curve moves further away from the LF curve (Fig. 18). Correspondingly, the range of \(g_{\text {CAN}_{tot}}\) values for which there exists a gap becomes wider and the gap also expands relative to the default case. Therefore, the \(g_{\text {CAN}_{tot}}\) interval over which bursting occurs in the somatic subsystem is broadened with the modified timescale for n.
Two curves of HC bifurcations (red solid, modified τ n : σ n =−5, a n =0.1; red dashed, default τ n : σ n =−4, a n =0) and two overlapping curves of LF bifurcations (blue, default and modified τ n ), in (h,g CAN T o t ) parameter space. The black curve denotes the trajectory for the default τ n function, with other parameters the same as in Figs. 14–17B. The yellow symbols have the same meanings as in Fig. 14
As a result, it is natural to expect that within the same amount of silent phase time of the dendritic subsystem oscillation, the full model with the modified τ n will be able to generate more small bursts. This is not the case, however. In fact, for [IP3]=1.5, the full model with the default τ n yields an MB solution consisting of the same number of small bursts (Fig. 18) as with the modified τ n (Fig. 17B). The effect of the adjustment of the timescale for n is to increase the duration and the number of spikes within each small burst, corresponding to the larger gap between the LF and HC curves, resulting in more biologically relevant small burst events.
3.4.2 Robustness to g NaP
To study the robustness of MB solutions to g NaP, we fix [IP3] at 0.95. Numerical simulations show that as g NaP is increased, the behavior of the somatic subsystem switches from quiescence to bursting to spiking, corresponding to the full system transitioning from bursting driven by the dendritic subsystem (dendritic bursting (Toporikova and Butera 2011; Park and Rubin 2013)) to mixed bursting to bursting that involves both the somatic and dendritic subsystems but without a mix of burst types (somato-dendritic bursting Toporikova and Butera 2011; Park and Rubin 2013).
A graphical summary of the effect of g NaP variations on the dynamics of the somatic subsystem is provided in a 1-parameter bifurcation diagram in Fig. 19A, where the bifurcation structure of the somatic subsystem with respect to g NaP for g CAN T o t =0 is displayed. In this case, we plot g NaP against the standard Euclidean norm of the solution, rather than against V. The hyperpolarized fixed point of somatic subsystem is stable (red solid), corresponding to quiescence, for the smaller g NaP values. The stability changes at an AH bifurcation and the spiking family (blue) becomes stable at a period doubling (PD) bifurcation. Moreover, the blue curve terminates at a homoclinic bifurcation involving the unstable equilibrium branch (red). Between the spiking and the quiescence is the g NaP interval where the somatic subsystem is available in participating in bursting. According to previous work on square-wave bursting (Butera et al. 1999), bursting patterns result for most of the g NaP interval between the AH and PD bifurcations. A similar bifurcation diagram for the modified τ n function, also for g CAN T o t =0, appears in Fig. 19B. The potential bursting interval is broadened substantially by the modification of τ n .
Effect of variations in g NaP on the behaviors of the somatic subsystem with g CAN T o t =0. (A) Default τ n (v). (B) Modified τ n (v) (denoted by the green curve in Fig. 10A). All other parameters are fixed at their standard values
Next we extend this bifurcation analysis and examine the dependence of MB solutions on both g NaP and g CAN T o t . To do this, we compute 2-parameter bifurcation diagrams in (g CAN T o t ,g NaP)-space (Fig. 20). The somatic subsystem’s spiking/bursting boundary (blue, PD) was calculated using AUTO (Doedel 1981; Doedel et al. 2009), by following the PD point in (g CAN T o t ,g NaP), while the boundary between bursting and quiescence was computed by following the AH point where the fixed points of the somatic subsystem lose stability (Fig. 20A). A similar 2-parameter bifurcation diagram for the modified τ n function was also computed (Fig. 20B). Comparing these two plots shows that for all g CAN T o t values below 0.05, i.e., for all c values within a complete relaxation oscillation cycle, the somatic subsystem after modification can generate bursting solutions for a wider range of g NaP. Recall that in order for the full system to generate MB solutions, (C1) requires the somatic subsystem to engage in bursting for c values arising during the silent phase of calcium. Hence with the new mix of timescales, MB solutions of the full model (4a) become more robust to g NaP.
Spiking/bursting and bursting/plateauing boundaries of the somatic subsystem for (A) default τ n (v) and (B) modified τ n (v) as in Fig. 19
In summary, through its effects on the somatic subsystem bifurcation diagrams with respect to both g NaP and \(g_{\text {CAN}_{tot}}\) (Figs. 18, 19, 20), the new timescale for n helps enlarge the bursting region in \((g_{\text {CAN}_{tot}}, g_{\text {NaP}})\)-space, which in turn enhances the robustness of MB solutions for the full system with respect to changes in g NaP for each fixed g CAN.
4 Discussion
We consider a single-compartment reduction (Park and Rubin 2013) of a two-compartment model of a pre-BötC neuron (Toporikova and Butera 2011), featuring both NaP and CAN currents, as well as intracellular calcium oscillations that modulate the CAN current. Previous work characterized the regions of ([IP3],g NaP) parameter space in which various types of solutions, namely somatic bursting, dendritic bursting, and somato-dendritic bursting, occur in these models (Toporikova and Butera 2011; Park and Rubin 2013). While (Park and Rubin 2013) presented a mathematical analysis explaining relevant bursting mechanisms, based on the Na P current, the CA N current, or both currents working together, limited analysis of MB solutions was provided and little consideration was given to identifying how many timescales are truly required to obtain these solutions or to their robustness.
In this paper, we have explained the mechanisms underlying MB solutions. Our method is based on the ideas of fast-slow decomposition, implemented by considering the interaction of two subsystems (one potentially bursting and the other intrinsically oscillating). This approach is commonly used in the two-timescale setting and has also recently been extended for a three-timescale system (Nan et al. 2015).
In the course of our analysis, we derive certain conditions on the timescales that together support MB solutions, based on which we obtain a non-intuitive result that the MB solution is in fact, at its simplest, a two-timescale phenomenon rather than actually requiring three timescales. Our analysis about how to group timescales in this system may provide useful information for future studies of irregular bursting solutions observed in other realistic biological models and in recordings from respiratory CPG neurons as well as subthalamic nucleus (STN) neurons in the basal ganglia that can exhibit somewhat similar bursting patterns (e.g. Beurrier et al. 1999; Jasinski et al. 2013; Dunmyre et al. 2011). Our approach may also prove helpful to modelers making choices about timescale groupings in other physical systems.
While parts of this work investigate rather specific details of the MB solution, we have also followed our analysis with an investigation of how the full model can be tuned to obtain more robust MB solutions. Notice that the transitions between regimes of different activity patterns yielded by varying system parameters (e.g. [IP3], g NaP, g CAN) have been studied in past works (Dunmyre et al. 2011; Toporikova and Butera 2011; Park and Rubin 2013), in all of which the MB solution only exists in a very small range of parameters. In our work, we have investigated why the new combination of timescales that we have found can support more robust MB solutions and hence have determined how to obtain a larger MB region in ([IP3],g NaP) parameter space by changing timescales. This analysis would also carry over similarly to the robustness analysis of the MB solution with respect to other parameters, such as g CAN, that are known to vary across pre-BötC neurons. Given that MB activity is observed in pre-BötC recordings, we propose that the modified model that we have derived would be a reasonable choice for incorporation in future studies of pre-BötC network dynamics. Based on this model, we predict that MB is likely to arise for pre-BötC neurons for which dendritic calcium oscillations contribute significantly to somatic membrane dynamics, such as through activation of a CAN current, over an intermediate range of g NaP values for which the somatic compartment is itself burst-capable at low Ca 2+. From an MB state, both increases and decreases of g NaP that are sufficiently large should yield non-mixed bursting. MB dynamics is predicted to be robust to slowing of IP 3 dynamics but not with respect to slowing of Ca 2+ dynamics. Furthermore, although the contribution of a SNIC bifurcation to MB dynamics is reminiscent of parabolic bursting (Rinzel 1987), we nonetheless do not expect pre-BötC neurons to exhibit behavior with the quantitative properties of parabolic bursting, because the fast jumps in Ca 2+, relative to the slower persistent sodium inactivation dynamics, will yield abrupt transitions to rapid spiking and to quiescence (e.g., Fig. 8A and E) even if there are two fast subsystem SNIC events per cycle.
As in other earlier work, we have considered only one-directional coupling, from the dendritic to the somatic subsystem, such that our model can be thought of as one oscillator forcing another. This simplification arises because we consider a one-compartment model, eliminating the coupling between compartmental voltages present in two-compartment models, and the original experiments and modeling underlying the system that we study did not highlight an influence of somatic voltage on the included calcium oscillations (Mironov 2008; Toporikova and Butera 2011). The independent calcium oscillation itself includes two disparate timescales, and this property significantly contributes to the generation of MB solutions, which would not arise, for example, with pure sinusoidal coupling. Nonetheless, similar MB dynamics could likely arise with other less biological but mathematically similar two-timescale forcing terms. Moreover, there are many variations on the coupling among timescales that arise in other model systems. For instance, Jasinski et al. recently presented a more detailed model for neurons in the pre-BötC, where each of membrane potential and cytoplasmic Ca2+ concentration can influence the evolution of the other, and showed that a heterogeneous population of these neurons can generate somewhat similar MB solution patterns associated with the generation of sighs (Jasinski et al. 2013). The bidirectional coupling could alter the relevant bifurcation structures and additional analysis would certainly be needed to explore this complication. Furthermore, previous work has suggested that the Na +/K + pump, in addition to I NaP and I CAN, plays an important role in the generation of the MB solution (Rubin et al. 2009; Jasinski et al. 2013), yet this is not considered in the system we have studied. Hence, the generalization of the analysis in this paper to more complicated models, including additional multi-scale forms of dynamics seen in respiratory neurons and possibly synaptic coupling as well, represent important open directions for future work.
On the analytical side, open problems from the perspective of fast-slow decomposition and bursting analysis include the development of systematic methods to treat equations that evolve on different timescales in different parts of phase space (Clewley et al. 2005), the study of effects of varying additional model parameters, as well as the identification of unfoldings that relate MB dynamics to other forms of bursting (Osinga et al. 2012). It is important to note that by using fast-slow decomposition, we miss the opportunity to capture more complicated behaviors where timescale separation breaks down (e.g., Desroches et al. 2012), including possible chaotic dynamics. By focusing on a specific solution pattern, mixed bursting, and on aspects of timescales needed to produce these solutions and to make them robust, we have not pursued a variety of other interesting and important mathematical directions. For example we have neglected the exploration of scenarios such as codimension-2 bifurcations and spike-adding mechanisms by which fundamental transitions in model dynamics could result from parameter variations as well as quite a range of phenomena that can be associated with homoclinic and SNIC bifurcations (Andronov and Vitt 1930; Andronov and Leontovich 1963; Shilnikov 1963; Afraimovich and Shilnikov 1974b; Lukyanov and Shilnikov 1978; Afraimovich et al. 2014; Terman 1992; Shilnikov et al. 2005; Shilnikov and Kolomiets 2008; Linaro et al. 2012; Desroches et al. 2013; Shilnikov et al. 2001).
While our study is motivated by the bursting patterns observed in the pre-BötC, it may also be applicable to other brain areas exhibiting rhythmic activity. In fact, we have carried out similar analysis on a heuristic model, consisting of a square-wave burster coupled to a general relaxation oscillator, which can generate similar MB solution patterns to the full pre-BötC model considered in this paper, and we found that qualitatiely similar mechanisms underlie these solution patterns in the heuristic model, again without the need for a third timescale. In other mammalian CPGs and rhythmic neural circuits, the Na P current and CAN current have been identified as playing critical roles in pattern generation (Wang et al. 2006; Tazerart et al. 2007; Zhong et al. 2007; Tazerart et al. 2008; Ziskind-Conhaim et al. 2008; Sheroziya et al. 2009; Brocard et al. 2013; Tsuruyama et al. 2013). Given that Na P and CA N currents are widespread and can be essential for the generation of bursts (Rubin et al. 2009; Dunmyre et al. 2011; Toporikova and Butera 2011; Park and Rubin 2013; Jasinski et al. 2013), it seems likely that the interaction of these currents is a fundamental component of the genesis of bursting solutions in other areas as well. Therefore, it is likely that our analysis of MB patterns can be extended and applied to these other rhythmic neuronal systems, both to explain the underlying dynamics and to assess its timescale requirements.
References
Afraimovich, V.S., Gonchenko, S.V., Lerman, L.M., Shilnikov, A.L., & Turaev, D.V.(2014). Scientific heritage of L.P. Shilnikov. Part 1. Regular and Chaotic Dynamics, 19(4), 435–460.
Afraimovich, V.S., & Shilnikov, L.P. (1974b). On some global bifurcations connected with the disappearance of a fixed point of saddle-node type. Soviet Mathematics - Doklady, 15, 1761–1765.
Andronov, A.A., & Leontovich, E.A. (1963). Generalization of limit cycles from a separatrix forming a loop and from the separatrix of an equilibrium state of saddle-node type. American Mathematics Society Translations: Series 2, 33, 189–231.
Andronov, A.A., & Vitt, A.A. (1930). Zur theorie des mitmehmens von van der Pol. Archiv für Elektrotechnik XXIV, 99–110.
Best, J., Borisyuk, A., Rubin, J., Terman, D., & Wechselberger, M. (2005). The dynamic range of bursting in a model respiratory pacemaker network. SIAM Journal on Applied Dynamical Systems, 4, 1107–1139.
Beurrier, C., Congar, P., Bioulac, B., & Hammond, C. (1999). Subthalamic nucleus neurosns switch from single-spike activity to burst-firing mode. The Journal of Neuroscience, 19(2), 599–609.
Brocard, F., Shevtsova, N.A., Bouhadfane, M., Tazerart, S., Heinemann, U., Rybak, I.A., & Vinay, L. (2013). Activity-dependent changes in extracellular Ca 2+ and K+ reveal pacemakers in the spinal locomotor-related network. Neuron, 77(6), 1047–1054.
Butera, R.J., Rinzel, J., & Smith, J.C. (1999). Models of respiratory rhythm generation in the pre-B,ötzinger complex. I. Bursting pacemaker neurons. Journal of Neurophysiology, 82(1), 382–397.
Clewley, R., Rotstein, H.G., & Kopell, N. (2005). A computational tool for the reduction of nonlinear ode systems possessing multiple scales. Multiscale Modeling and Simulation, 4, 732–759.
Del Negro, C.A., Hayes, J.A., & Rekling, J.C. (2011). Dendritic calcium activity precedes inspiratory bursts in pre-Bötzinger complex neurons. The Journal of Neuroscience, 31(3), 1017–1022.
Desroches, M., Guckenheimer, J., Krauskopf, B., Kuehn, C., Osinga, H., & Wechselberger, M. (2012). Mixed-mode oscillations with multiple time scales. SIAM Review, 54, 211–288.
Desroches, M., Kaper, T.J., & oscillations, M. Krupa. (2013). Mixed-mode bursting Dynamics created by a slow passage through spike-adding canard explosion in a square-wave burster. Chaos, 23, 046106.
Doedel, E.J. (1981). Auto: a program for the automatic bifurcation analysis of autonomous systems. Congressus Numerantum, 30, 265–284.
Doedel, E.J., Champneys, A.R., Fairgrieve, T.F., Kuznetsov, Y.A., Oldeman, K.E., Paffenroth, R.C., Sanstede, B., Wang, X.J., & Zhang, C. (2009). Auto-07p: continuation and bifurcation software for ordinary differential equations. available from: http://cmvl.cs.concordia.ca/.
Dunmyre, J.R., Del Negro, C.A., & Rubin, J.E. (2011). Interactions of persistent sodium and calcium-activated nonspecific cationic currents yield dynamically distinct bursting regimes in a model of respiratory neurons. Journal of Computational Neuroscience, 31(2), 305–328.
Ermentrout, G.B., & Terman, D.H. (2010). Mathematical foundations of neuroscience. New York: Springer.
Guckenheimer, J., & Holmes, P. (2013). Nonlinear oscillations, dynamical systems, and bifurcations of vector fields. Springer Science & Business Media, 42.
Hodgkin, A.L., & Huxley, A.F. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of Physiology, 117, 500–544.
Izhikevich, E.M. (2000). Neural excitability, spiking, and bursting. International Journal of Bifurcation and Chaos, 10, 1171–1266.
Jasinski, P.E., Molkov, Y.I., Shevtsova, N.A., Smith, J.C., & Rybak, I.A. (2013). Sodium and calcium mechanisms of rhythmic bursting in excitatory neural networks of the pre-Bötzinger complex: a computational modelling study. The European Journal of Neuroscience, 37, 212–230.
Linaro, D., Champneys, A., Desroches, M., & Storace, M. (2012). Codimension-two homoclinic bifurcations underlying spike adding in the Hindmarsh-Rose burster. SIAM Journal on Applied Dynamical Systems, 11(3), 939–962.
Lukyanov, V., & Shilnikov, L.P. (1978). Some bifurcations of dynamical system with homoclinic structures. Soviet Mathematics - Doklady, 19, 1314–1318.
Mironov, S.L. (2008). Metabotropic glutamate receptors activate dendritic calcium waves and TRPM channels which drive rhythmic respiratory patterns in mice. Journal of Physiology, 586, 2277–2291.
Morris, C., & Lecar, H. (1981). Voltage oscillations in the barnacle giant muscle fiber. Biophysical Journal, 35(1), 193–213.
Nan, P., Wang, Y., Kirk, V., & Rubin, J.E. (2015). Understanding and distinguishing three-timescale oscillations: case study in a coupled Morris-Lecar system. SIAM Journal on Applied Dynamical Systems, 14, 1518–1557.
Osinga, H.M., Sherman, A., & Tsaneva-Atanasova, K. (2012). Cross-currents between biology and mathematics: The codimension of pseudo-plateau bursting. Discrete and Continuous Dynamical Systems Series A, 32, 2853–2877.
Park, C., & Rubin, J.E. (2013). Cooperation of intrinsic bursting and calcium oscillations underlying activity patterns of model pre-bötzinger complex neurons. Journal of Computational Neuroscience, 34, 345–366.
Rinzel, J. (1987). A formal classification of bursting mechanisms in excitable systems. In Gleason, A.M. editor, Proceedings of the International Congress of Mathematicians, pp. 1578–1594. American Mathematical Society, Providence, RI.
Rinzel, J., & Ermentrout, G.B. (1998). Analysis of neural excitability and oscillations. In Koch, C., & Segev, I. (Eds.) Methods in Neuronal Modeling: From Synapses to Networks, second edition, pp. 251–291. MIT Press, Cambridge, MA.
Rubin, J.E., Hayes, J.A., Mendenhall, J.L., & Del Negro, C.A. (2009). Calcium-activated nonspecific cation current and synaptic depression promote network-dependent burst oscillations. Proceedings of the National Academy of Sciences of the United States of America, 106, 2939–2944.
Rubin, J.E., & Terman, D. (2002). Geometric singular perturbation analysis of neuronal dynamics. In Fiedler, B. (Ed.) Handbook of Dynamical Systems, (Vol. 2 pp. 93–146). Amsterdam: Elsevier.
Strogatz, S.H. (2014). Nonlinear Dynamics and Chaos: with Applications to Physics, Biology, Chemistry, and Engineering Westview press.
Sheroziya, M.G., von BOhlen, O., Unsicker, K., & Egorov, A.V. (2009). Spontaneous bursting activity in the developing entorhinal cortex. The Journal of Neuroscience, 29, 12131–12144.
Shilnikov, A.L., Calabrese, R.L., & Cymbalyuk, G. (2005). Mechanism of bistability: tonic spiking and bursting in a neuron model. Physics Review E, 71, 056214.
Shilnikov, A.L., & Kolomiets, M.L. (2008). Methods of the qualitative theory for the Hindmarsh-Rose model A case study. International Journal of Bifurcation and Chaos, 18, 1–27.
Shilnikov, L.P. (1963). Some cases of generation of periodic motion from singular trajectories. Mathematics of the USSR - Izvestiya, 61, 443–466.
Shilnikov, L.P., Shilnikov, A., Turaev, D., & Chua, L. (2001). Methods of qualitative theory in nonlinear dynamics. Parts I and II. World Sci.
Tazerart, S., Viemari, J.C., Darbon, P., Vinay, L., & Brocard, F. (2007). Contribution of persistent sodium current to locomotor pattern generation in neonatal rats. Journal of Neurophysiology, 98(2), 613.
Tazerart, S., Vinay, L., & Brocard, F. (2008). The persistent sodium current generates pacemaker activities in the central pattern generator for locomotion and regulates the locomotor rhythm. The Journal of Neuroscience, 28, 8577–8589.
Terman, D. (1992). The transition from bursting to continuous spiking in excitable membrane models. Journal of Nonlinear Science, 2(2), 135–182.
Toporikova, N., & Butera, R.J. (2011). Two types of independent bursting mechanisms in inspiratory neurons: an integrative model. Journal of Computational Neuroscience, 30(3), 515–528.
Tsuruyama, K., Hsiao, C. -F., & Chandler, S.H. (2013). Participation of a persistent sodium current and calcium-activated nonspecific cationic current to burst generation in trigeminal principal sensory neurons. Journal of Neurophysiology, 110(8), 1903– 1914.
Wang, D., Grillner, S., & Wallen, P. (2006). Effects of flufenamic acid on fictive locomotion, plateau potentials, calcium channels and NMDA receptors in the lamprey spinal cord. Neuropharmocology, 51, 1038–1046.
Zhong, G., Masino, M.A., & Harris-Warrick, R.M. (2007). Persistent sodium currents participate in fictive locomotion generation in neonatal mouse spinal cord. The Journal of Neuroscience, 27(17), 4507–4518.
Ziskind-Conhaim, L., Wu, L., & Wiesner, E.P. (2008). Persistent sodium current contributes to induced voltage oscillations in locomotor-related hb9 interneurons in the mouse spinal cord. Journal of Neurophysiology, 100 (4), 2254–2264.
Acknowledgments
This work was partially supported by NSF awards DMS 1312508, DMS 1612913.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interests
The authors declare that they have no conflict of interest.
Additional information
Action Editor: David Terman
Appendices
Appendix: A: Adjusting timescales in the dendritic subsystem
The full model (1a) is capable of generating an MB solution (Fig. 21A) using parameter values for which ([Ca],l) acts as a relaxation oscillator ([IP3]=0.95 μM, A=0.005 μM−1⋅m s −1 as in (Park and Rubin 2013)). However, since the l-nullcline lies extremely close to the left knee of [Ca]-nullcline (Fig. 21B), the trajectory projected to ([Ca],l)-space does not jump up to large [Ca] values and transition to the long burst (LB) phase immediately after passing the left knee (yellow circle). Instead, it slowly moves along the l-nullcline for a transient period before jumping up to the right branch (Fig. 21B and C: from the yellow circle to the green circle); this effect can be interpreted as the influence of the bifurcation in the dendritic subsystem that initiates the (c,l) oscillation, which occurs at a value of [IP3] just below 0.95 (Park and Rubin 2013). Numerically, we observe that small bursts occur during this period (Fig. 21A). Therefore, the existence of the MB solution relies heavily on the nullcline interactions, which can be tuned by changing [IP3]. To clarify the identification of the timescales involved in the MB behavior and the assessment of how to group timescales, and to eliminate the sensitivity of MB solutions to the precise value of [IP3], we increase [IP3] to 1. As a result, the [Ca]-nullcline moves downward and hence further from the l-nullcline. Furthermore, we also slow down l by decreasing A from 0.005 to 0.001 so that l∼O(1000) ms becomes more separated from [Ca], the delay time of the jump up of [Ca] at the left knee is significantly decreased, and the dendritic subsystem takes on a stronger relaxation character.
Time series for attracting solutions of the full model (1a) as well as the bifurcation structure of the dendritic subsystem with parameter values as in Table 1 except [IP3]=0.95[μM], A=0.005[μM−1⋅m s −1] as in (Park and Rubin 2013). Green and yellow symbols mark key points along the solution trajectory (green star: the point with minimum g CAN T o t ; yellow circle: the point when the trajectory passes the left knee of the [Ca]-nullcline; green circle: beginning of the long burst (LB).) (A): Time series for V. (B): Enlarged view of part of Fig. 2B showing the nullclines for [Ca] (red) and l (cyan) for the dendritic subsystem, together with the MB solution from the upper row. (C): Part of time series of [Ca]
Remark 1
Although the dendritic subsystem acts as a more standard relaxation oscillator with the new parameter values ([IP3]=1, A=0.001), [IP3] is not far enough from the bifurcation value for the influence of the bifurcation mentioned above to completely vanish. Hence, there is still a transient delay before [Ca] jumps up at the left knee, but it is much shorter than that with original parameter values.
Appendix: B: Nondimensionalization of the full model (1a)
From numerical simulations, we find that the membrane potential V typically lies between −60 mV and 20 mV. Correspondingly, for x∈{n,h}, we define T x = max(1/τ x (V)) over the range V∈[−60,20] and then define t x (V), a rescaled version of τ x (V), by t x (V)=T x τ x (V). We also define g max to be the maximum of the five conductances g L, g K, g Na, g NaP and g CAN. Furthermore, we let \(G([\text {Ca}])=\frac {[\mathrm {IP_{3}}][\text {Ca}]} {([\mathrm {IP_{3}}]+K_{I})([\text {Ca}]+K_{a})}\) and \(g_{\text {SERCA}}([\text {Ca}])=V_{\text {SERCA}}\frac {[\text {Ca}]}{K^{2}_{\text {SERCA}}+[\text {Ca}]^{2}}\). Substituting these expressions into Eq. (1a) and rearranging, we obtain the following system:
with dimensionless parameters \(\bar {g}_{x}=g_{x}/g_{\max }\) and \(\bar {V}_{x}=V_{x}/Q_{v}\). Note that we have now nondimensionalized the somatic subsystem (1a)-(1c).
Next we deal with Eqs. (1d)-(1e) by nondimensionalizing [Ca], which typically lies between 0 μM and 1 μM, based on numerical simulations. We define G c = max(G 3([Ca])) and G S = max(g SERCA(Ca)) over the range [Ca]∈[0,1] and then define P max to be the maximum of { L IP 3,P IP 3 G c ,G S }. From system (7a), we get the following dimensionless system:
with dimensionless parameters \(\bar {L}_{{\text {IP}}_{3}}=L_{{\text {IP}}_{3}}/P_{\max }\), \(\bar {P}_{{\text {IP}}_{3}}(c)=P_{{\text {IP}}_{3}}/P_{\max }\), \(\bar {g}_{\text {SERCA}}(c)=g_{\text {SERCA}}([\text {Ca}])/P_{\max }\) and \(\bar {K}_{\mathrm {d}}=K_{\mathrm {d}}/Q_{c}\) .
Since we expect V∈[−60,20] and [Ca]∈[0,1], suitable choices for the voltage and calcium scales are Q v =100 mV and Q c =1 μM, respectively. We also see that values of m ∞ (V), m p ∞ (V), f([Ca]), n ∞ (V), h ∞ (V), G([Ca]), \(\bar {g}_{\text {SERCA}}([\text {Ca}])\), n, h and l all lie in the range [0,1]. For the choice of parameters specified in Table 1, the maximum conductance is g Na=28 nS, so we have g max=g Na. Numerical evaluations of 1/τ n (V) and 1/τ h (V) for V∈[−60,20] show that T n ≈20 ms−1 and T h ≈0.04 ms−1. Similarly, we obtain G c ≈0.0421 and G S ≈1000 pL⋅m s −1, so we have P max≈1305 pL⋅m s −1. Using these values we see that all terms in the right hand sides of Eqs. (8a)–(8e) are bounded (in absolute value) by one.
The coefficients of the derivatives in the left hand sides of Eqs. (8a)–(8e) now reveal the relative rates of evolution of the variables. We find that C m /g max=0.75 ms∼O(1) m s, 1/T n =0.05 ms∼O(0.1) ms, 1/T h =25ms∼O(10) m s, \(\frac {\sigma }{P_{\max }\cdot K_{Ca}} = 5.67 \,\text {ms}\sim O(10)\, ms\) and \(\frac {1}{Q_{c}\cdot A} = 200 \,\text {ms} \sim \, O(100)\, ms\). We choose the fast timescale as our reference time, i.e., pick Q t =1 ms, and set
As a result, the dimensionless system (8a) becomes the system (4a) given in Section 3, namely
where R v , R n , R h , R c and R l are dimensionless parameters given in (9a).
Rights and permissions
About this article
Cite this article
Wang, Y., Rubin, J.E. Multiple timescale mixed bursting dynamics in a respiratory neuron model. J Comput Neurosci 41, 245–268 (2016). https://doi.org/10.1007/s10827-016-0616-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10827-016-0616-6


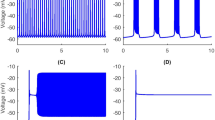
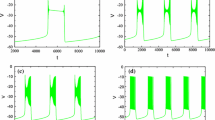






 of the (c,l) oscillation, so that there exist small burst solutions before c jumps up to its active phase. In other words, there must be a gap in h between the LF and HC curves in the (h,g
CAN
T
o
t
) 2-parameter bifurcation diagram for c small (Fig.
of the (c,l) oscillation, so that there exist small burst solutions before c jumps up to its active phase. In other words, there must be a gap in h between the LF and HC curves in the (h,g
CAN
T
o
t
) 2-parameter bifurcation diagram for c small (Fig. 














