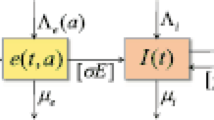1 Introduction

Tuberculosis (TB), a disease caused by Mycobacterium tuberculosis (Mtb) (Flynn and Chan 2001), has long been considered as a cause of mortality and is one of the top 10 diseases of mortality worldwide (World Health Organization 2018). Around 1.3 million died because of tuberculosis, and 10.0 million developed tuberculosis in 2017 (World Health Organization 2018). Patients with smear-positive will generally infect ten individuals annually and over 20 people during the natural period of the disease until death (Styblo 1991). In Hong Kong, tuberculosis dynamics have declined in recent years, but it persists (Fig. 1a) and causes various mortality in different age groups (Fig. 1b). The transmission dynamics of tuberculosis is a complicated process which includes latent phenomenon (Parrish et al. 1998; Selwyn et al. 1989; Vynnycky and Fine 2000; Anderson and Trewhella 1985; Ma et al. 2017), aging effect (Marais et al. 2004; Chan-Yeung et al. 2002; Mossong et al. 2008; Castillo-Chavez and Feng 1998), exogenous reinfection issue (Feng et al. 2000; Vynnycky and Fine 1997; Cohen et al. 2006; Kasaie et al. 2014) and several stochastic factors (Liu et al. 2018).

Fig. 1
figure 1

Tuberculosis tendency in Hong Kong. a Notification and death rates of tuberculosis in Hong Kong, 1947–2016 (data from Department of Health of the Government of the Hong Kong (2018)). b Tuberculosis induced mortality in Hong Kong for various age groups [data from Department of Health of the Government of the Hong Kong (2018)]

Full size image

Latent tuberculosis is the clinical syndrome that the immune system forces pathogens into a quiescent state after infection (Parrish et al. 1998; Barry et al. 2009; Houben and Dodd 2016). Through adapting the immune system of infected hosts, Mycobacterium tuberculosis-latent bacilli will break out several years later until encountering a favorable environment and further reactive to contribute tuberculosis break out (Cardona and Ruiz-Manzano 2004; Cardona 2016). Latent phenomenon contributes pressure in tuberculosis control (Selwyn et al. 1989), and the effect was studied in several susceptible-infected-infectious models (Castillo-Chavez and Feng 1998; Feng et al. 2000; Waaler et al. 1962; Jabbari et al. 2016; Kuniya 2011; Kapitanov 2015). This latent phenomenon was considered as the source of delay in tuberculosis control. Many factors (World Health Organization 2006; Cai et al. 2015) contribute to the delay phenomenon, and the longest total delay is larger than 120 days (Storla et al. 2008), which results in difficulty for tuberculosis diagnosis and treatment.

Demographic dynamics is another significant factor affecting tuberculosis transmission as individuals in various age groups may have different immune response levels to Mtb and various primary infection rates (Marais et al. 2004; Arregui et al. 2018). The probability of pulmonary disease for infants (less than one years old) is 30–40\(\%\), and then decreases (\(10\%\) for 1–2 years old, \(5\%\) for 2–5 years old, \(2\%\) for 5–10 years old), and increases for larger than ten years old (10–20\(\%\)) (Marais et al. 2004), which indirectly indicates the complicated relation between tuberculosis transmission and individuals’ age. In Hong Kong, longevity and the high rate of tuberculosis in the elderly are the significant factors for the persistence of tuberculosis, stated by Chan-Yeung et al. (2002). After infection by Mtb, extensive symptoms result in many concrete stages. In Aagaard et al. (2011), Aagaard et al. studied various vaccination methods for different stages to determine the efficient protection strategy before and after exposure to tuberculosis.

Mathematical and computational model can be used to study all these phenomenon with to provide new hypotheses and design therapeutic approaches to TB (Kirschner et al. 2017). Recently, Renardy and Kirschner (2020) considered a network-based model to study tuberculosis transmission in school, household and workplace. They obtained that the disease prevalence is sensitive to the contact weight assigned to transmissions between casual contacts. This result suggests a direction to prevent the spread of TB. Arregui et al. (2018) applied a data-driven model with demographic dynamics to demonstrate a greater burden level for those areas with heavy tuberculosis nowadays. The study in Okuonghae and Omosigho (2011) considered susceptible by two stages and infectious population by three stages to investigate how various stages affect tuberculosis transmission in the population.

Infection age is often utilized in mathematical systems for tuberculosis transmission (Castillo-Chavez and Feng 1998; Feng et al. 2002), but only a few mathematical models consider age structure coupling with disease stages of infectious individuals. Instead of using latent state in mathematical model (Feng et al. 2001), we utilize distributed delay to reflect latent phenomenon after infection as the distributed delay can capture the delay difference among individuals. In this paper, we develop a mathematical model for tuberculosis transmission, which involves age structure for all individuals and age-specific disease progression for infectious populations. Our model considers demographic structure coupling with the continuous development of disease stage, which is a crucial component for studying tuberculosis transmission. In this paper, we apply the local stability analysis to determine the basic reproduction number, demonstrating that the age-specific progression rate may affect tuberculosis permanence. Several numerical simulations are applied to investigate the influence of various progression rates on tuberculosis dynamics.

2 Mathematical Model

In our model, we differentiate the population into two groups, susceptible and infectious individuals, with demographic structure and multiple disease stages, and a delay term applied to represent the latent state.

Here, we let a and s be the individual’s age and the disease stage, respectively. To represent two types of population distribution at time t, we define the following two variables: S(t, a) for susceptible individuals, and I(t, a, s) for infectious individuals. We also consider several age-dependent parameters for modeling tuberculosis transmission as individuals of different ages may have different immune response levels and various transmission patterns after infection (Arregui et al. 2018; Makinodan and Kay 1980). The mathematical model for tuberculosis transmission in the population is based on the schematic diagram shown in Fig. 2.

Fig. 2
figure 2

Schematic diagram representing how tuberculosis are transmitted within the population. Population in the system is recruited through immigration and natural birth. Susceptible individuals (S(t, a)) are infected by infectious individuals (I(t, a, s)) and become new infectious individuals and this process exists with delay phenomenon (Makinodan and Kay 1980; World Health Organization 2006; Storla et al. 2008). Infectious individuals in I(t, a, s) will move back to susceptible state S(t, a) after effective treatment and may be reinfected later (Kasaie et al. 2014). The individuals in the population have natural mortality and tuberculosis-induced mortality (World Health Organization 2018)

Full size image

2.1 Susceptible Population

Here, we consider the interaction between susceptible individuals and infectious individuals to explain the susceptible population dynamics. Newly infected individuals in the population at time t depend on the number of effective interactions between susceptible and infectious individuals (Mossong et al. 2008) modeled by the following term

$$\begin{aligned} \int _0^{s_{\max }}\int _0^{a_{\max }}S(t,a)I(t,a',s)T(a,a',s)\mathrm {d}a'\mathrm {d}s, \end{aligned}$$

where \(a_{\max }\) and \(s_{\max }\) are the maximum survival age and stage, respectively. If an individual’s age is larger than \(a_{\max }\) or the disease stage is over \(s_{\max }\), we consider that the individual is dead or removed from the system. The term \(T(a,a',s)\) is the infection rate for a susceptible individual with age a infected by an infectious individual with age \(a'\) and stage s at time t. After successful treatment, an infectious individual will be recovered back to susceptible state (Feng et al. 2001; Castillo-Chavez and Song 2004) with the recovery rate \(\gamma (a,s)\) for an individual with age a and stage s and the process is modeled by the term

$$\begin{aligned} \int _0^{s_{\max }}\gamma (a,s)I(t,a,s)\mathrm {d}s. \end{aligned}$$

In addition, immigration, natural birth and death will be considered with rates \(\beta (t,a)\), \(\beta _0(t)\) and \(\delta _S(a)S(t,a)\), respectively. Hence, the following equation can be utilized to describe the dynamics of S(t, a):

$$\begin{aligned} \frac{\partial S(t,a)}{\partial t}+\frac{\partial S(t,a)}{\partial a} =&-\underbrace{\int _0^{s_{\max }}\int _0^{a_{\max }} S(t,a)I(t,a',s)T(a,a',s)\mathrm {d}a'\mathrm {d}s}_{\text {TB infection}}+\underbrace{\beta (t,a)}_{\text {Immigration}}\\&-\underbrace{\delta _S(a)S(t,a)}_{\text {Natural death}}+\underbrace{\int _0^{s_{\max }}\gamma (a,s)I(t,a,s) \mathrm {d}s}_{\text {Recovery}}, \end{aligned}$$

with the boundary condition \(S(t,0) = \beta _0(t)\) to represent the number of newborn in the population.

2.2 Infectious Population

After tuberculosis infection, individuals will either enter into a state that has no clinic symptom and noninfectious (World Health Organization 2018; Parrish et al. 1998; Blower et al. 1995) or directly become infectious (direct progression) (Okuonghae and Omosigho 2011; Blower et al. 1995) represented by I(t, a, s) with stage s. Reactivation (Cohen et al. 2006) and exogenous refection (Cohen et al. 2006; Kasaie et al. 2014) will transform quiescent individuals into infectious group again after several years, which also contributes to difficulty in tuberculosis control (World Health Organization 2018). Here, we utilize the delay phenomenon (World Health Organization 2006; Storla et al. 2008; Cai et al. 2015) to reflect latent phenomenon since various individuals may have different immune response levels after infection. Hence, the number of total new infectious individuals is modeled by the term

$$\begin{aligned} \int ^{\infty }_0\int _0^{s_{\max }}\int _0^{a_{\max }} S(t-\tau ,a-\tau )I(t-\tau ,a',s)T(a-\tau ,a',s)\mathrm {e}^{-\int ^a_{a-\tau } \delta _S(\mu )\mathrm {d}\mu }K(\tau )\mathrm {d}a'\mathrm {d}s\mathrm {d}\tau . \end{aligned}$$

In the delay period, individuals are still under the mortality process from \(a-\tau \) to a, which implies the term \(\mathrm {e}^{-\int ^a_{a-\tau }\delta _S(\mu )\mathrm {d}\mu }\). Moreover, we introduce the delay kernel function K(s) to describe the distribution of the influence under delay, which satisfies

$$\begin{aligned} \int ^{\infty }_0K(s)\mathrm {d}s = 1,\ \ \ \bar{\tau } = \int ^{\infty }_0sK(s)\mathrm {d}s. \end{aligned}$$

Here, \(\bar{\tau }\) is known as the average time delay for the kernel.

In biological models, the delay kernel with Gamma distribution is often utilized as follows (Macdonald 1978)

$$\begin{aligned} K(s) = \frac{s^n\alpha ^{n+1}\mathrm {e}^{-\alpha s}}{n!},\ \ s\in (0,\infty ), \end{aligned}$$

where \(\alpha >0\) is known as exponentially fading memory, and the integer \(n\ge 0\). Here, we consider the weak kernel function (\(n=0\) in the above formula), that is,

$$\begin{aligned} K(s) = \alpha \mathrm {e}^{-\alpha s}. \end{aligned}$$

After infected by Mtb, individuals will have an extensive spectrum of symptoms (World Health Organization 2018) since the antigens, such as Rv3407, are expressed in various states of tuberculosis infection (Ma et al. 2017). We apply the following term to represent the progression of disease stage:

$$\begin{aligned} v(a)\frac{\partial I(t,a,s)}{\partial s}, \end{aligned}$$

where v(a) is the age-dependent progression rate of disease stage. We assume that the progression rate v(a) is a non-decreasing function. Without loss of generality, we further assume that \(0\le v(a)\le 1\). Individuals flowed out from S(t, a) will be counted as the inflow of I(t, a, 0) at stage 0 and all newborn will be susceptible. Hence, the boundary conditions are

$$\begin{aligned}&I(t,0,s) = 0,\\&I(t,a,0)\\&\quad = \int ^{\infty }_0\int _0^{s_{\max }}\int _0^{a_{\max }} S(t-\tau ,a-\tau )I(t-\tau ,a',s)T(a-\tau ,a',s) \mathrm {e}^{-\int ^a_{a-\tau }\delta _S(\mu )\mathrm {d}\mu } \alpha \mathrm {e}^{-\alpha \tau } \mathrm {d}a'\mathrm {d}s\mathrm {d}\tau . \end{aligned}$$

There are two ways of outflow from an infectious state: recovery after successful treatment and mortality. Patients with various symptoms need different treatment methods (Nahid and Hopewell 2017), and hence we use the following terms to model recovery and mortality processes, respectively,

$$\begin{aligned} \gamma (a,s)I(t,a,s) \text { and } \delta _I(a,s)I(t,a,s), \end{aligned}$$

where \(\gamma (a,s)\) and \(\delta _I(a,s)\) depends on age and disease stage. Therefore, we have the following equation for modeling the dynamics of infectious individuals:

$$\begin{aligned}&\frac{\partial I(t,a,s)}{\partial t}+\frac{\partial I(t,a,s)}{\partial a} +\underbrace{v(a)\frac{\partial I(t,a,s)}{\partial s}}_{\text {Disease progression}} =-\underbrace{\delta _I(a,s)I(t,a,s)}_{\text {Death}}-\underbrace{\gamma (a,s) I(t,a,s)}_{\text {Recovery}},\\&I(t,a,0)\\&\quad = \underbrace{\int ^{\infty }_0\int _0^{s_{\max }}\int _0^{a_{\max }} S(t-\tau ,a-\tau )I(t-\tau ,a',s) T(a-\tau ,a',s)\mathrm {e}^{-\int ^a_{a-\tau }\delta _S(\mu )\mathrm {d}\mu }\alpha \mathrm {e}^{-\alpha \tau }\mathrm {d}a'\mathrm {d}s\mathrm {d}\tau } _{\text {Transmission from}\ S(t,a)},\\&I(t,0,s) = 0. \end{aligned}$$

2.3 Governing Equations

On the basis of the discussion above and combining all the equations, we have

$$\begin{aligned}&\frac{\partial S(t,a)}{\partial t}+\frac{\partial S(t,a)}{\partial a}\nonumber \\&\quad =-\int _0^{s_{\max }}\int _0^{a_{\max }} S(t,a)I(t,a',s)T(a,a',s)\mathrm {d}a'\mathrm {d}s+\beta (t,a)\nonumber \\&\qquad -\delta _S(a)S(t,a)+\int _0^{s_{\max }}\gamma (a,s)I(t,a,s)\mathrm {d}s,\nonumber \\&\frac{\partial I(t,a,s)}{\partial t}+\frac{\partial I(t,a,s)}{\partial a} +v(a)\frac{\partial I(t,a,s)}{\partial s}\nonumber \\&\quad =-\delta _I(a,s)I(t,a,s)-\gamma (a,s)I(t,a,s), \end{aligned}$$
(1)

for \(a\in (0,a_{\max })\) and \(s\in (0,s_{\max })\). Initial and boundary conditions are as follows

$$\begin{aligned} S(0,a)= & {} S_0(a),\ \ I(0,a,s) = I_0(a,s),\ \ S(t,0) = \beta _0(t),\ \ I(t,0,s) = 0,\\ I(t,a,0)= & {} \int ^{\infty }_0\int _0^{s_{\max }}\int _0^{a_{\max }} S(t-\tau ,a-\tau )I(t-\tau ,a',s)\\&\times T(a-\tau ,a',s) \mathrm {e}^{-\int ^a_{a-\tau }\delta _S(\mu )\mathrm {d}\mu } \alpha \mathrm {e}^{-\alpha \tau } \mathrm {d}a'\mathrm {d}s\mathrm {d}\tau . \end{aligned}$$

Here, \(S_0(a)\) and \(I_0(a,s)\) are the initial conditions for susceptible and infectious classes, respectively. In our simulations, the values of the initial conditions are based on the data obtained in Hong Kong (Department of Health of the Government of the Hong Kong 2018; Census and Statistics Department of the Government of the Hong Kong SAR 2018; Census and Statistics Department 2018). The biological meanings of the parameters are summarized in Table 1.

Table 1 Biological meaning of parameters
Full size table

3 Infection-free Equilibrium

For studying the equilibria, we assume that there exist \(\hat{\beta }(a)\) and \(\hat{\beta }_0\) such that

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }\beta (t,a) = \hat{\beta }(a),\ \ \lim \limits _{t\rightarrow \infty }\beta _0(t) = \hat{\beta }_0, \end{aligned}$$

that is, the immigration rate \(\beta (t,a)\) only depends on age a and the birth rate \(\beta _0(t)\) is a constant when time approaches infinity. The equilibria of system (1) satisfy following equations

$$\begin{aligned}&\frac{\mathrm {d}\hat{S}(a)}{\mathrm {d}a}\nonumber \\&\quad =-\hat{S}(a)\int _0^{s_{\max }}\int _0^{a_{\max }} \hat{I}(a',s)T(a,a',s)\mathrm {d}a' \mathrm {d}s+\hat{\beta }(a)-\delta _S(a)\hat{S}(a)\nonumber \\&\qquad +\int _0^{s_{\max }}\gamma (a,s)\hat{I}(a,s)\mathrm {d}s,\nonumber \\&\frac{\partial \hat{I}(a,s)}{\partial a}\ +v(a)\frac{\partial \hat{I}(a,s)}{\partial s}= -\delta _I(a,s)\hat{I}(a,s)-\gamma (a,s)\hat{I}(a,s), \end{aligned}$$
(2)

and

$$\begin{aligned} \hat{S}(0)= & {} \hat{\beta }_0,\ \ \hat{I}(0,s) = 0,\nonumber \\ \hat{I}(a,0)= & {} \int ^{\infty }_0\alpha \mathrm {e}^{-\alpha \tau }\mathrm {e}^{\int ^a_{a-\tau } \delta _S(\mu )\mathrm {d}\mu }\hat{S}(a-\tau )\nonumber \\&\times \int _0^{s_{\max }}\int _0^{a_{\max }}\hat{I}(a',s)T(a-\tau ,a',s) \mathrm {d}a'\mathrm {d}s\mathrm {d}\tau . \end{aligned}$$
(3)

For the infection-free equilibrium \(E_0=(S(a),0)\), we have the following equation

$$\begin{aligned} \frac{\mathrm {d}\hat{S}(a)}{\mathrm {d}a}= \hat{\beta }(a)-\delta _S(a)\hat{S}(a)\ \text {with}\ \hat{S}(0) = \hat{\beta }_0, \end{aligned}$$

then we obtain that

$$\begin{aligned} \hat{S}(a) = \mathrm {e}^{-\int ^a_0\delta _S(\sigma )\mathrm {d}\sigma }\left( \hat{\beta }_0+\int ^a_0\mathrm {e} ^{\int ^\xi _0\delta _S(\sigma )\mathrm {d}\sigma }\hat{\beta }(\xi )\mathrm {d}\xi \right) , \end{aligned}$$
(4)

for \(a\ge 0\). Without loss of generality, we assume \(\hat{S}(a)=0\) when \(a<0\). In the following subsection, we will discuss the local stability of \(E_0\).

3.1 Stability Analysis

To investigate the local stability of \(E_0 = (\hat{S}(a),0)\), we linearized model (1) at the equilibrium first. Consider the small perturbations around equilibrium as follows

$$\begin{aligned} S(t,a)&= \hat{S}(a)+ \epsilon \bar{S}(a)\mathrm {e}^{\lambda t},\\ I(t,a,s)&= 0 + \epsilon \bar{I}(a,s)\mathrm {e}^{\lambda t}, \end{aligned}$$

where the perturbation amplitude \(\epsilon \ll 1\). With the assumption \(T(a,a',s) = T_1(a)T_2(a',s)\), we obtain the following linearized system at \(E_0 = (\hat{S}(a),0)\):

$$\begin{aligned}&\lambda \bar{S}(a)+\frac{\mathrm {d}\bar{S}(a)}{\mathrm {d}a}\nonumber \\&\quad = -\int _0^{s_{\max }}\int _0^{a_{\max }} \hat{S}(a)\bar{I}(a',s)T(a,a',s)\mathrm {d}a'\mathrm {d}s+\beta (a)\nonumber \\&\qquad -\delta _S(a)\bar{S}(a)+\int _0^{s_{\max }}\gamma (a,s)\bar{I}(a,s)\mathrm {d}s,\nonumber \\&\lambda \bar{I}(a,s)+\frac{\partial \bar{I}(a,s)}{\partial a}+v(a)\frac{\partial \bar{I}(a,s)}{\partial s}\nonumber \\&\quad =-\delta _I(a,s)\bar{I}(a,s)-\gamma (a,s)\bar{I}(a,s), \end{aligned}$$
(5)

and

$$\begin{aligned} \bar{S}(0)&= 0,\ \ \bar{I}(0,s) = 0,\\ \bar{I}(a,0)&=\int ^{\infty }_0\hat{S}(a-\tau )T_1(a-\tau )\mathrm {e}^{-\lambda \tau }\alpha \mathrm {e}^{-\alpha \tau }\mathrm {e}^{-\int ^a_{a-\tau }\delta _S(\mu )\mathrm {d}\mu } \bar{\varLambda }\mathrm {d}\tau , \end{aligned}$$

where

$$\begin{aligned} \bar{\varLambda }=\int _0^{s_{\max }}\int _0^{a_{\max }}\bar{I}(a',s)T_2(a',s)\mathrm {d}a'\mathrm {d}s. \end{aligned}$$
(6)

We first calculate the second equation in (5), and rewrite this equation into following form

$$\begin{aligned} \frac{\partial \bar{I}(a,s)}{\partial a}+v(a)\frac{\partial \bar{I}(a,s)}{\partial s} =-\big [\lambda +\delta _I(a,s)+\gamma (a,s)\big ]\bar{I}(a,s). \end{aligned}$$

For the partial differential equation above, the characteristic curve passing through \((a_0,0)\) is

$$\begin{aligned} f(a):=\int ^a_0v(\mu )\mathrm {d}\mu = s+C, \end{aligned}$$

where \(C=f(a_0)\). Since v is a positive function, f is increasing and the curve and the inverse of f are well defined. By the boundary condition \(\bar{I}(0,s) = 0\) and integrating along the characteristic curves for \(C<0\), we obtain

$$\begin{aligned} \bar{I}(a,s) = 0, \ \ \ s>f(a)\ge 0; \end{aligned}$$

if \(C\ge 0\), that is, \(f(a)\ge s>0\), we have

$$\begin{aligned} \bar{I}(a,s) = \bar{I}(f^{-1}(f(a)-s),0)\exp \left( -\int ^a_{f^{-1}(f(a)-s)}\lambda +\mathscr {F}(\eta , a, s)\mathrm {d}\eta \right) , \end{aligned}$$

where

$$\begin{aligned} \mathscr {F}(\eta , a, s) = \delta _I(\eta ,f(\eta )-f(a)+s)+\gamma (\eta ,f(\eta )-f(a)+s). \end{aligned}$$
(7)

Equation (6) and the expression of \(\bar{I}(a,s)\) with the boundary conditions imply that

$$\begin{aligned} \bar{\varLambda }&= \int _0^{s_{\max }}\int _0^{a_{\max }} \bar{I}(a',s)T_2(a',s)\mathrm {d}a'\mathrm {d}s\\&= \int _0^{s_{\max }}\int _0^{a_{\max }} \bar{I}(f^{-1}(f(a')-s),0)\exp \\&\quad \times \left( -\int ^{a'}_{f^{-1}(f(a')-s)}\lambda +\mathscr {F}(\eta , a', s)\mathrm {d}\eta \right) T_2(a',s)\mathrm {d}a'\mathrm {d}s\\&= \int _0^{s_{\max }}\int _0^{a_{\max }} \left[ \int ^{\infty }_0\hat{S}(f^{-1}(f(a')-s)-\tau )T_1(f^{-1}(f(a')-s)-\tau ) \mathrm {e}^{-\lambda \tau }\right. \\&\quad \left. \times \alpha \mathrm {e}^{-\alpha \tau }\bar{\varLambda }\exp \left( -\int ^{f^{-1}(f(a')-s)}_{f^{-1}(f(a')-s)-\tau } \delta _S(\mu )\mathrm {d}\mu \right) \mathrm {d}\tau \right] \exp \\&\quad \times \left( -\int ^{a'}_{f^{-1}(f(a')-s)}\lambda +\mathscr {F}(\eta , a', s)\mathrm {d} \eta \right) T_2(a',s)\mathrm {d}a'\mathrm {d}s, \end{aligned}$$

which yields the following equation

$$\begin{aligned} g(\lambda ):= & {} \int _0^{s_{\max }}\int _0^{a_{\max }}\left[ \int ^{\infty }_0\hat{S}(f^{-1}(f(a')-s)-\tau )T_1(f^{-1}(f(a')-s)-\tau ) \right. \nonumber \\&\left. \times \mathrm {e}^{-\lambda \tau }\alpha \mathrm {e}^{-\alpha \tau }T_2(a',s)\exp \left( -\int ^{f^{-1}(f(a')-s)}_{f^{-1}(f(a')-s)-\tau } \delta _S(\mu )\mathrm {d}\mu \right) \mathrm {d}\tau \right] \exp \nonumber \\&\times \left( -\int ^{a'}_{f^{-1}(f(a')-s)}\lambda +\mathscr {F}(\eta , a', s)\mathrm {d} \eta \right) \mathrm {d}a'\mathrm {d}s\nonumber \\= & {} 1. \end{aligned}$$
(8)

Equation (8) is the characteristic equation of the system (1) at the infection-free equilibrium \(E_0\). Through investigating the behaviors of \(g(\lambda )\), we can obtain the condition of local stability for the boundary equilibrium \(E_0\) as the following theorem.

Theorem 1

Define

$$\begin{aligned} \mathcal {R}_0= & {} \int _0^{s_{\max }}\int _0^{a_{\max }} \left[ \int ^{\infty }_0\hat{S}(x(a',s) -\tau )T_1(x(a',s) -\tau )\alpha \mathrm {e}^{-\alpha \tau }\right. \nonumber \\&\left. \times \exp \left( -\int ^{x(a',s)}_{x(a',s)-\tau } \delta _S(\mu )\mathrm {d}\mu \right) \mathrm {d}\tau \right] \nonumber \\&\times \exp \left( -\int ^{a'}_{x(a',s)} \mathscr {F}(\eta , a', s)\mathrm {d}\eta \right) T_2(a',s)\mathrm {d}a'\mathrm {d}s \end{aligned}$$
(9)

where \(x(a',s) = f^{-1}(f(a')-s)\) which satisfies \( x=f^{-1}(f(a')-s)<a'\) as f is an increasing function; \(\mathscr {F}(\eta , a', s)\) is defined as (7). The infection-free equilibrium \(E_0 = (\hat{S}(a),0)\) for system (1) is locally asymptotically stable if \(\mathcal {R}_0<1\) and unstable if \(\mathcal {R}_0>1\).

Proof

From (8), it is easy to show that \(g(\lambda )\) is a continuous function which is monotone decreasing. In addition,

$$\begin{aligned} \lim \limits _{\lambda \rightarrow -\infty }g(\lambda )\rightarrow +\infty ,\ \ \lim \limits _{\lambda \rightarrow +\infty }g(\lambda )\rightarrow 0, \end{aligned}$$

and

$$\begin{aligned} g(0) = \mathcal {R}_0. \end{aligned}$$

If \(\mathcal {R}_0=g(0)<1\), the characteristic equation \(g(\lambda ) = 1\) exists at least one negative solution. Furthermore, let \(\hat{\lambda }\) be a negative solution of \(g(\lambda ) = 1\), and for any complex solution \(\lambda = z_1+iz_2\ (z_1, z_2\in R)\) of \(g(\lambda ) = 1\), we can check that

$$\begin{aligned} g(\hat{\lambda })=1 = g(\lambda ) = |g(z_1+iz_2)|\le g(z_1), \end{aligned}$$

which leads to \(0>\hat{\lambda }\ge z_1\) as g is a decreasing function. Therefore, we proved that the infection-free equilibrium \(E_0\) is locally asymptotically stable if \(\mathcal {R}_0<1\). On the contrary, if \(\mathcal {R}_0 = g(0)>1\), there exists a positive real solution for equation (8), and it implies that the infection-free equilibrium \(E_0\) is unstable. \(\square \)

3.2 Biological Meaning of \(\mathcal {R}_0\)

We can rewrite equation (9) into the following expression

$$\begin{aligned} \mathcal {R}_0 = \int ^{\infty }_0\left[ \int _0^{s_{\max }}\int _0^{a_{\max }} \hat{S}(x-\tau )T_1(x-\tau ) \mathrm {e}^{-\int ^{x}_{x-\tau }\delta _S(\mu )\mathrm {d}\mu }\mathrm {e}^{-\int ^{a'}_x \mathscr {F}(\eta , a',s)\mathrm {d}\eta }T_2(a',s)\mathrm {d}a'\mathrm {d}s\right] \alpha \mathrm {e}^{-\alpha \tau }\mathrm {d}\tau . \end{aligned}$$

In the above equation, the term \(\exp \left( -\int ^{a'}_x\mathscr {F}(\eta ,a',s)\mathrm {d} \eta \right) \) represents the probability that one individual who is infectious at age x and still stays in infectious state at age \(a'\). Hence,

$$\begin{aligned} \exp \left( -\int ^{a'}_x\mathscr {F}(\eta ,a',s)\mathrm {d}\eta \right) T_2(a',s) \end{aligned}$$

is the number of contacts for an infectious individual who survives from age x to age \(a'\) and stays in stage s. Meanwhile, \(\hat{S}(x-\tau )\) is the total susceptible individual with age \(x-\tau \), and \(\exp \left( -\int ^{x}_{x-\tau }\delta _S(\mu )\mathrm {d}\mu \right) \) stands for the probability that one susceptible individual survives at age \(x-\tau \) and is still survived at age x. Therefore,

$$\begin{aligned} \hat{S}(x-\tau )T_1(x-\tau )\exp \left( -\int ^{x}_{x-\tau }\delta _S(\mu )\mathrm {d}\mu \right) \end{aligned}$$

represents the number of susceptible individuals contacting one infectious individual with age \(x-\tau \) and surviving to age x. Here, \(T_1(x-\tau )\) is the infectiousness rate for susceptible at age \(x-\tau \). On the basis of the above discussion, the term

$$\begin{aligned} \int _0^{s_{\max }}\int _0^{a_{\max }} \hat{S}(x-\tau )T_1(x-\tau )\mathrm {e}^{-\int ^{x}_{x-\tau }\delta _S(\mu )\mathrm {d}\mu } \mathrm {e}^{-\int ^{a'}_x\mathscr {F}(\eta ,a',s)\mathrm {d}\eta }T_2(a',s)\mathrm {d}a'\mathrm {d}s \end{aligned}$$

is the total number of new contact individuals between susceptible with age \(x-\tau \) and infectious with age \(a'\) and stage s. These individuals will become infectious after time period \(\tau \in (0,\infty )\), and \(\alpha \mathrm {e}^{-\alpha \tau }\) is the influence for every point \(\tau \) to current time t. Overall, we showed that \(\mathcal {R}_0\) represents the basic reproduction number for system (1).

4 Numerical Simulations

The disease progression rate is critical for altering the transmission dynamics of tuberculosis in populations since the patients with severe symptoms may easily transmit disease to others. In this section, we will use numerical simulations to verify this observation. First, we will estimate the parameters for the simulations. Then, we will apply two types of functions to model disease progression rate, constant and age-specific linear functions. The latter one can capture the aging effect for tuberculosis transmission. The detailed numerical scheme can be found in Appendix.

4.1 Parameter Estimation

The natural mortality rate in system (1) is referred from Væth et al. (2018) and we utilize the following form

$$\begin{aligned} \delta _S(a) = 9.317\times 10^{-6}\mathrm {e}^{0.11a}. \end{aligned}$$

Moreover, for the tuberculosis induced death rate in system (1), we can fit it based on the information and data from the Census and Statistics Department of Hong Kong and Department of Health of Hong Kong (Department of Health of the Government of the Hong Kong 2018) and obtained the age-specific function for \(\delta _{I1}(a)\) listed in Table 2.

Table 2 Expression of \(\delta _{I1}(a)\)
Full size table

Here, we further suppose that the mortality rate \(\delta _I(a,s) = \delta _{I1}(a)\times \delta _{I2}(s)\), where \(\delta _{I1}(a)\) is represented in Table 2. We assume that the mortality rate may increase when the disease stage s is increasing, so \(\delta _{I2}(s)\) is assumed to be an increasing function, defined as

$$\begin{aligned} \delta _{I2}(s) = \left\{ \begin{array}{cc} 0.01, &{} 0<s<s_1, \\ 0.01+0.99(s-s_1)/(s_2-s_1), &{} s_1 \le s\le s_2, \\ 1, &{} s_2<s\le s_{\max }, \end{array} \right. \end{aligned}$$

where the maximum stage \(s_{\max }\) is 1. To match the results we observed in the data, we take \(s_1= 0.1\), and \(s_2=0.7\).

According to Census and Statistics Department of Hong Kong (Census and Statistics Department 2001, 2018) from 2001 to 2016, we have the data of immigration and birth. We use these data to estimate the birth rate and immigration rate and rescale them to make the steady state (4) to be around 100. The stage factor s in the infection rate matrix \(T(a,a',s)\) is assumed with the following function:

$$\begin{aligned} T(a,a',s) = T_1(a)T_1(a')T_s(s). \end{aligned}$$

The function \(T_1(a)\) will be estimated based on the contact rates in Arregui et al. (2018) for the numerical simulations later. We assume that the function \(T_s(s)\) is an increasing function as

$$\begin{aligned} T_s(s) = \left\{ \begin{array}{cc} 0.01, &{} 0<s<s_1, \\ 0.01+0.99(s-s_1)/(s_2-s_1), &{} s_1 \le s\le s_2, \\ 1, &{} s_2<s\le s_{\max }. \end{array} \right. \end{aligned}$$

We assume that the age- and stage-specific recovery rate \(\gamma (a,s)=\gamma _a(a)\gamma _s(s)\). The function \(\gamma _a(a)\) will be estimated based on the data from the Department of Health of Hong Kong Department of Health of the Government of the Hong Kong (2018), and the function \(\gamma _s(s)\) will be defined as

$$\begin{aligned} \gamma _s(s) = \left\{ \begin{array}{cc} \frac{s}{s_1}, &{} 0<s<s_1, \\ 1-\frac{s-s_1}{s_{\max }-s_1}, &{} s_1\le s\le s_{\max }, \end{array} \right. \end{aligned}$$

which is increasing when \(0<s<s_1\) and decreasing when \(s_1<s<s_2\).

The progression rate v(a) in system (1) plays an important role on the dynamics of infected population. The rate of disease progression is a key component for studying the disease transmission in the system because the patients with serious symptoms may easily transmit disease than the patients with light symptoms. In the next section, we will apply different kinds of functions to model the effect of progression rate v(a).

For the weak delay kernel function \(K(s) = \alpha \mathrm {e}^{-\alpha s}\), we have the average delay as follows

$$\begin{aligned} \bar{\tau } = \int ^{\infty }_0sK(s)\mathrm {d}s = \frac{1}{\alpha }, \end{aligned}$$

which implies that \(\alpha \) determines the average delay time from infected to infectious individuals. When the value of \(\alpha \) is small, the average delay time \(\frac{1}{\alpha }\) will be large, which reflects a long period from infected individuals to infectious because of latent phenomenon (World Health Organization 2018; Parrish et al. 1998; Blower et al. 1995) or self-immune system (Makinodan and Kay 1980). If the value of \(\alpha \) is large, then the average delay time will be small, which means that the susceptible individuals will immediately become infectious after contacting infectious individuals through direct progression (Okuonghae and Omosigho 2011; Blower et al. 1995). Consequently, the larger value of \(\alpha \) has a positive effect on tuberculosis transmission because of the short average delay period. World health organization (World Health Organization 2006) stated that the average delay period from one and half months to four months. Storla et al. (2008) also pointed out that the average delay time within the range from 60 to 90 days and the longest delay time is larger than 120 days (126 in high endemic countries). Therefore, the average delay time here is assumed as around 120 days. In the following numerical simulations, we set \(\alpha \approx 365/120\) per year.

We set the initial values for susceptible individuals (S(0, a)) as the steady state solution (4) and the infectious individuals (I(0, a, s)) is \(S(0,a)\times 10^{-4}\) for \(s=0\) and zero for \(s>0\).

4.2 Constant Progression Rate

Here, we simulate tuberculosis dynamics with the constant progression rate \(v(a) = v_0\). Based on the data in Okuonghae and Omosigho (2011); Blower et al. (1995), we set \(v_0 = 4.5\times 10^{-4}(a_{\max }/2)\), where \(a_{\max } = 100\). From (9), we obtain the value of reproduction number \(\mathcal {R}_0\approx 0.42<1\) and the solution of system A.10 will tend to the infection-free equilibrium, which means that disease will be eradicated at the end.

Figure 3 shows the dynamics of susceptible individuals \(\mathbf {S}(t)\) and infectious individuals \(\mathbf {I}(t)\) as time t increases, where

$$\begin{aligned} \mathbf {S}(t) = \int _0^{a_{\max }}S(t,a)\mathrm {d} a\ \text { and }\ \mathbf {I}(t) = \int _0^{a_{\max }}\int _0^{s_{\max }}I(t,a,s)\mathrm {d} s \mathrm {d} a. \end{aligned}$$

In Fig. 3, the susceptible individuals \(\mathbf {S}(t)\) slightly decreases and the number of infectious individuals \(\mathbf {I}(t)\) increases at the beginning. But, after certain time, \(\mathbf {I}(t)\) declines to zero and \(\mathbf {S}(t)\) increases back to the steady state. The simulation demonstrates the extinction of tuberculosis in the population if \(\mathcal {R}_0<1\). In this case, a system with a relatively low and age-independent progression rate does not have many infectious individuals with severe symptoms who transmit disease efficiently in the population. Combined with the effect of immune response to Mycobacterium tuberculosis, the disease will be eradicated with effective control strategies in this case.

Fig. 3
figure 3

Numerical simulations for \(v(a) = 4.5\times 10^{-4}(a_{\max }/2)\). The time series of \(\mathbf {I}(t)\) that the number of infectious individuals declines to zero

Full size image

The simulations in Fig. 4 display the population distribution of the infectious individuals I(t, a, s) at different times. Figure 4\((i)\) is the population distribution of infectious individuals at the initial time \(t=0\), and infectious individuals distribute in around all age groups with \(s=0\). From the result \(\mathcal {R}_0\approx 0.42<1\), we predict that the number of infectious individuals will decrease [Figs. 3 and 4(\(iii\))] to zero as time increases. Simulations in Figs. 3 and 4(\(iii\), \(iv\)) show that tuberculosis in the population will be controlled at the end, and Fig. 4(\(iv\)) is the population distribution of the infectious individuals under successful treatment at the end of the longtime simulation. The number of infectious individuals in the elderly age groups is much more than the number of infectious individuals in the other age groups since the elderly individuals have weaker immune systems compared with the other age groups (Makinodan and Kay 1980).

Now we consider a larger progression rate \(v_0 = 9\times 10^{-4}(a_{\max }/2)\) and simulate the corresponding disease dynamics. From (9), we obtain that \(\mathcal {R}_0\approx 1.30>1\), which implies that an outbreak of tuberculosis happens in the population. The numerical simulations in Fig. 5 show that the number of infectious individuals \(\mathbf {I}(t)\) increases again after a drop. This result is different from the simulation in the former example. Figure 6 displays the population distribution of infectious individuals I(t, a, s). The number of infectious individuals with elderly age groups keeps increasing (Figs. 6(\(i\))–(\(iii\))), which leads to the persistence of disease in the population. Compared with Fig. 4(\(iv\)), Fig. 6(\(iv\)) shows that Infections in the older population are in the region with large value of s. This observation is consistent with the results in Chan-Yeung et al. (2002); Department of Health of the Government of the Hong Kong (2018) that the high notification rate of tuberculosis in the elderly age groups contributes to the persistence of tuberculosis in the population.

Fig. 4
figure 4

Population distribution of infectious individuals I(t, a, s) for \(v(a) = 4.5\times 10^{-4}(a_{\max }/2)\)

Full size image
Fig. 5
figure 5

Numerical simulations for constant progression rate \(v(a) = 9\times 10^{-4}(a_{\max }/2)\). The time series of infectious individuals I(t) declines at the beginning and then keeps increasing

Full size image
Fig. 6
figure 6

Population distribution of infectious individuals I(t, a, s) with constant progression rate \(v(a) = 9\times 10^{-4}(a_{\max }/2)\)

Full size image

4.3 Age-specific Progression Rate

In this subsection, we introduce the aging factor to the disease progression rate and simulate the tuberculosis transmission with an age-specific progression rate \(v(a) = ca\). First, we take \(c = 4.5\times 10^{-4}\). In this case, we obtain that \(\mathcal {R}_0\approx 0.84<1\), which implies that the infection-free equilibrium is stable based on Theorem 1. Figures 7 and 8 are the numerical simulations of disease dynamics for this case.

Figure 7 displays that the number of infectious individuals \(\mathbf {I}(t)\) decreases to zero as time t increases, which demonstrates that the disease will die out at the end. The temporal dynamics of \(\mathbf {S}(t)\) and \(\mathbf {I}(t)\) in Fig. 7 are similar with that in Fig. 3 but the speed of the decrease of \(\mathbf {I}(t)\) is slower in Fig. 7.

Fig. 7
figure 7

Numerical simulations of disease with the progression rate \(v(a) = 4.5\times 10^{-4}a\). The time series of I(t) that the number of infectious individuals declines to zero

Full size image

Figure 8 is the population distribution of the infectious individuals for various time t. As time t increases, the number of infectious individuals tends to zero with a low level of \(10^{-6}\) at the end [Figure 8(\(iv\))]. It reflects the extinction of disease in the population. Compared with Fig. 4, Fig. 8 shows that the elderly age group is in an area with larger s due to the aging effect in the disease progression rate (Fig. 9).

Fig. 8
figure 8

Population distribution of infectious individuals I(t, a, s) with the progression rate \(v(a) = 4.5\times 10^{-4}a\)

Full size image
Fig. 9
figure 9

Comparison of I(50, a, s) for the model with different types of progression rate and values of a. Red dash-dotted line represents the case with constant progression rate; blue solid line represents the case with age-specific progression rate (Color figure online)

Full size image

Next, we increase the coefficient to \(c = 9\times 10^{-4}\). In this case, the value of reproduction number will increase to \(\mathcal {R}_0\approx 1.99>1\), which means that the infection-free equilibrium is unstable. Figure 10 shows that the number of infectious individuals \(\mathbf {I}(t)\) increases first and declines later. When \(t>15\), \(\mathbf {I}(t)\) increases rapidly as shown in Fig. 10.

Fig. 10
figure 10

Numerical simulations for \(v(a) = 9\times 10^{-4}a\). The time series of I(t) that the number of infectious individuals declines at the beginning and then keeps increasing

Full size image
Fig. 11
figure 11

Population distribution of infectious individuals I(t, a, s) for \(v(a) = 9\times 10^{-4}a\)

Full size image

Figure 11 is the population distribution of the infectious individuals at various times. The simulations in Fig. 11 display that the number of infectious individuals in the elderly age groups does not tend to zero and infectious individuals are mainly with high levels of a and s. This result is similar to Fig. 6 but the increased speed of I(t) is faster in Fig. 11.

The disease transmission may be underestimated from our simulations when we assume that the progression rate is independent of age. Now we compare the simulations of the models with the constant progression rate and age-specific progression rate. We consider the constant progression rate \(v(a) = v_0= 6\times 10^{-4}(a_{\max }/2)\) and the age-specific progression rate \(v(a) = 6\times 10^{-4}a\), which have same average value. Figure 12 displays the numbers of susceptible individuals and infectious individuals under two types of progression rates. In Fig. 12, the number of susceptible individuals with the constant progression rate is slightly more than the number of susceptible individuals with the age-specific progression rate. On the contrary, Fig. 12 shows that the number of infectious individuals with the constant progression rate is less than that with the age-specific progression rate after \(t>5\). We further observe that the number of patients under the constant progression rate is six times less than the number of patients with the age-specific progression rate after \(t>40\). As shown in the former simulations and Chan-Yeung et al. (2002); Department of Health of the Government of the Hong Kong (2018), the elderly age groups are the major population that contributes to the permanence of disease in the population. Using the constant progression rate may not capture this point, and the age-specific progression rate can accurately model the aging effect in disease transmission. Consequently, considering the progression rate with the aging factor will be more feasible for simulating the transmission dynamics of tuberculosis as it will avoid the underestimation in the number of infected population.

Fig. 12
figure 12

Numerical simulations for constant progression rate and age-specific progression rate. Red dashed line represents the case with constant progression rate; blue solid line represents the case with age-specific progression rate (Color figure online)

Full size image
Fig. 13
figure 13

The variation of \(\mathcal {R}_0\) for two kinds of progression rates. Red dashed line represents the case with constant progression rate; blue solid line represents the case with age-specific progression rate; black dotted line represents \(\mathcal {R}_0\)=1 (Color figure online)

Full size image

Figure 13 validates the increase of the basic reproduction number \(\mathcal {R}_0\) for the age-specific progression rate, \(3c\times 10^{-4}a\), and the constant progression rate, \(3c\times 10^{-4} \frac{a_{\max }}{2}\). The value of \(\mathcal {R}_0\) with the age-specific progression rate is greater than the case with constant progression rate as shown in Fig. 13. Consequently, as the value of c increases, tuberculosis may transmit faster with the age-specific progression rate.

5 Conclusion

In this paper, we have developed a tuberculosis system with demographic structure and delay effect after infection. The model involved a continuous disease progression process with an age-specific progression rate. In this work, stability analysis for the infection-free equilibrium was applied to determine the formula of the basic reproduction number, which is essential to study the condition of disease outbreak. During the transmission process of tuberculosis, the disease progression may be enhanced by aging. The formula of the basic reproduction number (9) provides a tool to understand how the age-specific progression affects the disease transmission dynamics through changing the stability of infection-free equilibrium. In our simulations, we observed that the age-specific progression rate would accelerate tuberculosis transmission. In fact, if the progression rate rapidly increases in the elderly population, the number of infectious individuals with severe symptoms will increase at the same time, which further contributes to more new patients in the population.

The system with a constant disease progression rate cannot capture the aging effect on the disease progression. Consequently, considering the disease progression rate with aging effect will avoid underestimating the number of infected population during prediction since infectious elderlies may quickly become patients with severe symptoms. Individuals with serious symptoms can easily infect susceptible individuals, which leads to a higher value of \(\mathcal {R}_0\) and further leads to more infectious individuals in the whole population. Therefore, to control tuberculosis, the government should take some strategies for elderly patients, such as regular checks and immediate treatment for elderly patients, to further control tuberculosis in the future.

The expression of \(\mathcal {R}_0\) obtained here depends on some functions, such as delay and disease progression rate. Our study can be generalized to study the basic reproduction number with other types of delay and disease progression functions. In addition, random contact in society may influence TB transmission dynamics. Some stochastic factors can be included to our model for understanding the transmission process of tuberculosis under random effects.