Global analysis of an age-structured tuberculosis model with an application to Jiangsu, China

Abstract

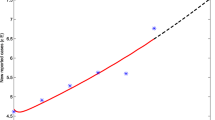
Diagnostic delay for TB infected individuals and the lack of TB vaccines for adults are the main challenges to achieve the goals of WHO by 2050. In order to evaluate the impacts of diagnostic delay and vaccination for adults on prevalence of TB, we propose an age-structured model with latent age and infection age, and we incorporate Mycobacterium TB in the environment and vaccination into the model. Diagnostic delay is indicated by the age of infection before receiving treatment. The threshold dynamics are established in terms of the basic reproduction number ${\mathcal {R}}_0$. When ${\mathcal {R}}_0<1$, the disease-free equilibrium is globally asymptotically stable, which means that TB epidemic will die out; When ${\mathcal {R}}_0=1$, the disease-free equilibrium is globally attractive; there exists a unique endemic equilibrium and the endemic equilibrium is globally attractive when ${\mathcal {R}}_0>1$. We estimate that the basic reproduction number ${\mathcal {R}}_{0}=0.5320$ (95% CI (0.3060, 0.7556)) in Jiangsu Province, which means that TB epidemic will die out. However, we find that the annual number of new TB cases by 2050 is 1,151 (95%CI: (138, 8,014)), which means that it is challenging to achieve the goal of WHO by 2050. To this end, we evaluate the possibility of achieving the goals of WHO if we start vaccinating adults and reduce diagnostic delay in 2025. Our results demonstrate that when the diagnostic delay is reduced from longer than four months to four months, or 20% adults are vaccinated, the goal of WHO in 2050 can be achieved, and 73,137 (95%CI: (23,906, 234,086)) and 54,828 (95%CI: (15,811, 206,468)) individuals will be prevented from being infected from 2025 to 2050, respectively. The modeling approaches and simulation results used in this work can help policymakers design control measures to reduce the prevalence of TB.

1 Introduction

Tuberculosis (TB) is a chronic infectious disease caused by infection with Mycobacterium TB (Wikipedia 2022). In 2020, approximately ten million people worldwide developed TB, including 5.6 million men, 3.3 million women and 1.1 million children, and 1.5 million people died from TB. Globally, TB ranks the 13th among all leading causes of deaths, and becomes the second leading infectious killer among all infectious diseases since COVID-19 (World Health Organization 2022b). In recent two decades, China has made great progress in the prevention and mitigation of TB (Wang et al. 2014). During this period, the incidence rate of TB is reduced by 42%, and the mortality rate of TB is reduced by more than 90%. However, China still had 833,000 TB infections and 38,800 TB deaths in 2019 (World Health Organization 2022a). Globally, the incidence rate of TB reduced about 2% per year and the cumulative reduction between 2015 and 2020 was 11%, which is more than half of 20% reduction milestone of the TB Eradication Strategy (World Health Organization 2022b). However, the speed is not fast enough to achieve the goals of World Health Organization (WHO), which is to reduce the incidence rate of TB by $50\%$, $80\%$, and $90\%$ in 2025, 2030, and 2035, respectively, compared with that in 2015, and there will be less than one case per million individuals per year in 2050 in China (Dye and Williams 2008; Harris et al. 2019, 2020; Houben et al. 2016; Huynh et al. 2015; Lin et al. 2015; Xu et al. 2017).

According to the current findings and predictions through mathematical models (Abu-Raddad et al. 2009; Feng et al. 2001, 2002; Guo et al. 2021; Harris et al. 2019, 2020; Sreeramareddy et al. 2009), the effectiveness of TB control strategies depends on several factors. First, many symptoms of TB are similar to those of other diseases. Hence, it is easy to diagnose TB as other diseases by mistakes so that diagnostic delay occurs. Diagnostic delay may increase the risk of deaths and facilitate the transmission of TB in the community (Sreeramareddy et al. 2009). The incidence data in Jiangsu Province show that the average diagnostic delay is 44 days (see Fig. 2A). Consequently, the age of infection (the time from being infected to being treated) is an important factor in disease progression (Feng et al. 2002). Second, there are no effective vaccines against TB for adults except the bacille Calmette-Guérin (BCG) vaccine. In the past few years, the development of new TB vaccines is rapid, with 14 candidates entering clinical trials, including four in phase 2B/3 (Harris et al. 2019, 2020). Therefore, vaccination strategy is essential in disease progression when adult vaccines are introduced. Third, Mycobacterium TB is resistant to dry, cold, acidic and alkaline environments. In particular, Mycobacterium TB adheres to dust and remains infectious for 8-10 days, can survive for 6-8 months in dry sputum, and can survive for 4-5 years when the temperature is minus $6^{\circ }$C or above, indicating that Mycobacterium TB can widely spread through the air, and everyone who is exposed to the air with Mycobacterium TB may be infected (Chinese Center for Disease Control and Prevention 2022). Thus, Mycobacterium TB in the environment is non-neglectable in TB transmission.

During the spread of TB, approximately 5% to 10% of people infected with Mycobacterium TB will develop active TB during their lifetime (World Health Organization 2022a). Some of these people develop TB very soon (within a few weeks) after being infected, while others may get sick several years later (Guo et al. 2021). In addition, the timings of diagnostic delays vary among countries, regions, and TB patients. The average diagnostic delays in high-income countries and low-income countries are 47 days and 60 days (Sreeramareddy et al. 2009), respectively. The durations of diagnostic delay reach hundreds of days (see Fig. 2A). Age structure is essential when modeling long-term disease (Magal et al. 2010; Qiu and Feng 2010; Shen et al. 2017; Wu and Zhao 2021; Yang and Wang 2019; Zhang and Liu 2020; Zou et al. 2010), because the time it takes for latent individuals to become infectious differs and the chances of receiving treatment for infectious individuals varies considerably (Iannelli and Milner 2017).

Many mathematical models have been used to study the dynamics of TB, including ordinary differential equation (ODE) models (Cai et al. 2021; Choi and Jung 2014; Huo and Zou 2016; Liu et al. 2010; Song et al. 2002), delay differential equation (DDE) models (Feng et al. 2001, 2007; Okuonghae 2015), age-structured models (Ainseba et al. 2017; Castillo-Chavez and Feng 1998; Feng et al. 2002; Guo et al. 2021; Harris et al. 2019, 2020; Liu et al. 2022; Li et al. 2020; Mu et al. 2022; Wang et al. 2017; Xue et al. 2022; Xu et al. 2019; Yang et al. 2011), and reaction-diffusion models (Català et al. 2020; Wang et al. 2022; Zhang et al. 2021). Motivated by the above work, we propose an age-structured model with latent age and infection age. Mycobacterium TB can survive in dry, cold, acidic, and alkaline environments (Chinese Center for Disease Control and Prevention 2022), especially in some special environments, Mycobacterium TB can survive for several years, which means that Mycobacterium TB can spread widely through air. Therefore, we incorporate Mycobacterium TB in the environment into our model. Since the vaccines for adults are under development and will be applied once they are available, we include vaccination for adults in the model, besides BCG-vaccination for children. In addition, we also consider the age of infection before receiving treatment to represent diagnostic delay, and the treated class is also introduced into the model. Our goals are to study the dynamic properties of the model, calibrate the transmission model according to the demographic and epidemiological data classified by the age of infection, as well as to evaluate the possibility of achieving the goals of WHO in Jiangsu Province, China.

The remaining sections of our work are structured as follows. In Sect. 2, we propose a TB model that takes into account various factors such as latent age, infection age, vaccination, treatment, and both indirect and direct transmission. We analyze the model to derive the basic reproduction number, ${\mathcal {R}}_0$, and study the boundedness and uniform persistence of the model, as well as the existence and stability of equilibrium solutions. In Sect. 3, we employ Markov Chain Monte Carlo (MCMC) to estimate the unknown parameters and initial values of the model. Through this estimation, we can also determine the value of the basic reproduction number, ${\mathcal {R}}_0$. In Sect. 4, we utilize Latin Hypercube Sampling (LHS) and the Partial Rank Correlation Coefficient (PRCC) to explore the uncertainty and sensitivity of the parameters. Additionally, we evaluate the possibility of achieving the goals of WHO in Jiangsu Province, China. In Sect. 5, we summarize and discuss the findings of our research.

2 The TB model with latent age and infection age

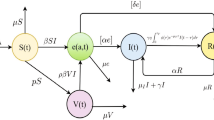
The total population is divided into six classes, namely, susceptible, vaccinated, latent, infected, treated, and recovered individuals. S(t), V(t), T(t), and R(t) represent the number of susceptible, vaccinated, treated, and recovered individuals, respectively. e(t, b) represents the density of latent individuals with latent age b. i(t, a) represents the density of infected individuals with infection age a. W(t) represents the density of Mycobacterium TB in environment, such as door handles, towels, handkerchiefs, toys, utensils, and beds, etc. The total population at time t is denoted by

$$\begin{aligned} N(t)=S(t)+V(t)+T(t)+R(t)+\int ^{+\infty }_{0}e(t,b)\text{ d }b +\int ^{+\infty }_{0}i(t,a)\text{ d }a. \end{aligned}$$

The total population, N(t), is born and dies at the rates $\varLambda$ and dN(t), respectively, where d represents the natural mortality rate. The baseline infection probability of susceptible and vaccinated individuals is defined as

$$\begin{aligned} \lambda (t)=\int ^{+\infty }_{0}\beta _{1}(a)i(t,a)\text{ d }a +\beta _{2}T(t)+g(W(t)), \end{aligned}$$

(1)

where $\beta _{1}(a)$ denotes the direct transmission rate of infected individuals at stage a; $\beta _{2}$ denotes the direct transmission rate of treated individuals. The function g(W(t)) represents the probability that a susceptible individual becomes infected through indirect contact with Mycobacterium TB in the environment. Obviously, higher Mycobacterium TB density increases the chance that a susceptible individual becomes infected. Thus, the transmittability of the disease, g(W(t)), is an increasing function of W(t) (Kong et al. 2014a, b; Posny and Wang 2014). In general, we assume that the function g(W(t)) satisfies the following conditions for all $t\ge 0$:

$$\begin{aligned} {g(0)=0,\;g'(W)>0,\;\text{ and }\;g''(W)\le 0,\;\;\text{ for }\;W\ge 0.} \end{aligned}$$

Susceptible individuals become exposed and active TB at the rates $(1-q)\lambda (t)S(t)$ and $q\lambda (t)S(t)$, respectively, where q denotes the proportion of new infections that directly develop into active TB. Similarly, Vaccinated individuals become exposed and active TB at the rates $(1-q)\eta \lambda (t)V(t)$ and $q\eta \lambda (t)V(t)$, respectively, where $1-\eta$ denotes the reduction in susceptibility to infection due to vaccination. Susceptible individuals, including children and adults who transfer to the vaccinated class at the rate $\alpha S(t)$, where $\alpha$ is the vaccination rate. Once the vaccine protection is lost, the vaccinated individuals transfer to the susceptible class at the rate $\tau V(t)$, where $1/\tau$ denotes the duration of vaccine protection. Exposed individuals can become infected at the rate $\rho \int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b$, where $\sigma (b)$ denotes the progression rate of the latent individuals at stage b, and $\rho$ denotes the proportion of new infections that develop into active TB from latent individuals. Infected individuals can be treated at the rate $\int ^{+\infty }_{0}\theta (a)i(t,a)\text{ d }a$, where $\theta (a)$ denotes the diagnostic rate of the infected individuals at stage a. All cases in T(t) will either recover or die at the rates $\gamma T(t)$ and dT(t), where $\gamma$ represents the recovery rate. Recovered individuals can also transfer to the susceptible class at the rate $\delta R(t)$, where $\delta$ is the rate at which a recovered individual loses immunity (becoming susceptible again). Note that we don’t consider relapse of the recovered individuals in this work. Eventually, $\xi _{1}(a)$ and $\xi _{2}$ are the virions of Mycobacterium TB released into the environment per unit time by infected individuals with infection age a and treated individuals, respectively; and c is the rate at which Mycobacterium TB is eliminated from the environment by any means (Li et al. 2009). The population flow among those compartments is shown in Fig. 1. We formulate the following system mixed with ordinary differential equations and partial differential equations:

$$\begin{aligned}{} & {} \frac{\text{ d }S(t)}{\text{ d }t}=\varLambda +\tau V(t)+\delta R(t)-\lambda (t)S(t)-(\alpha +d)S(t),\nonumber \\{} & {} \frac{\text{ d }V(t)}{\text{ d }t}=\alpha S(t)-\eta \lambda (t)V(t)-(\tau +d)V(t),\nonumber \\{} & {} \frac{\text{ d }T(t)}{\text{ d }t}=\int ^{+\infty }_{0}\theta (a)i(t,a)\text{ d }a-(\gamma +d)T(t),\nonumber \\{} & {} \frac{\text{ d }R(t)}{\text{ d }t}=\gamma T(t)-(\delta +d)R(t),\\{} & {} \frac{\text{ d }W(t)}{\text{ d }t}=\int ^{+\infty }_{0}\xi _{1}(a)i(t,a)\text{ d }a+\xi _{2}T(t)-cW(t),\nonumber \\{} & {} \frac{\partial e(t,b)}{\partial t}+\frac{\partial e(t,b)}{\partial b}=-(\rho \sigma (b)+d)e(t,b),\nonumber \\{} & {} \frac{\partial i(t,a)}{\partial t}+\frac{\partial i(t,a)}{\partial a}=-(\theta (a)+d)i(t,a).\nonumber \end{aligned}$$

(2)

Fig. 1

Schematic diagram of the mathematical model

The boundary and initial conditions for System (2) is as follows

$$\begin{aligned} \left. \begin{aligned}&e(t,0)=(1-q)\lambda (t)\big (S(t)+\eta V(t)\big ),\\&i(t,0)=q\lambda (t)\big (S(t)+\eta V(t)\big )+\rho \int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b,\\&S(0)=S_{0},V(0)=V_{0},T(0)=T_{0},R(0)=R_{0},W(0)=W_{0},\\&e(0,b)=e_{0}(b),i(0,a)=i_{0}(a), \end{aligned} \right. \end{aligned}$$

(3)

where $e_{0}(b),i_{0}(a)\in L^{1}_{+}(0,+\infty )$, and $S_{0},V_{0},T_{0},R_{0},W_{0}\in {\mathbb {R}}_{+}$. The definitions of all parameters are shown in Table 1.

Throughout this work, we make the following assumptions on the coefficients of System (2).

(A1)::

$\varLambda$, $\tau$, $\delta$, $\beta _{2}$, $\beta _{3}$, $\alpha$, d, $\eta$, $\gamma$, $\xi _{2}$, c, $\rho$, $\beta _{1}(a)$, $\theta (a)$, $\xi _{1}(a)$, $\sigma (b)>0$;

(A2)::

$\beta _{1}(a)$, $\theta (a)$, $\xi _{1}(a)$, $\sigma (b)\in L^{\infty }_{+}(0,+\infty )$ with essential upper bounds ${\bar{\beta }}_{1}$, ${\bar{\theta }}$, ${\bar{\xi }}_{1}$, ${\bar{\sigma }}>0$, respectively;

(A3)::

$\beta _{1}(a)$, $\theta (a)$, $\xi _{1}(a)$, and $\sigma (b)$ are Lipschitz continuous on ${\mathbb {R}}_{+}$, with Lipschitz coefficients $M_{\beta _{1}}$, $M_{\theta }$, $M_{\xi _{1}}$, and $M_{\sigma }$, respectively;

(A4)::

The stability analysis for general expressions of g(W(t)) is tedious. For simplicity, we assume that $g(W(t))=\beta _{3}W(t)$, where $\beta _{3}$ is the indirect transmission rate of Mycobacterium TB.

We define the phase space for System (2) by ${\mathcal {Y}}={\mathbb {R}}^{5}_{+}\times (L^{1}_{+}(0,+\infty ))^{2}$, with the norm

$$\begin{aligned} \Vert (x_{1},x_{2},x_{3},x_{4},x_{5},x_{6},x_{7})\Vert _{{\mathcal {Y}}} =\sum ^{5}_{i=1}|x_{i}|+\int ^{+\infty }_{0}|x_{6}(b)|\text{ d }b +\int ^{+\infty }_{0}|x_{7}(a)|\text{ d }a. \nonumber \\ \end{aligned}$$

(4)

Table 1 The parameter description of System (2)

In the following analysis, we assume that both (A1)-(A4) are valid.

2.1 Well-posedness

The continuous solution semiflow $\varPhi : {\mathbb {R}}_{+}\times {\mathcal {Y}}\rightarrow {\mathcal {Y}}$ is defined as

$$\begin{aligned} \varPhi (t,x_{0}):=(S(t),V(t),T(t),R(t),W(t),e(t,\cdot ),i(t,\cdot )), \;t\in {\mathbb {R}}_{+},\;x_{0}\in {\mathcal {Y}}, \end{aligned}$$

where $\varPhi (t,x_{0})$ is the solution to System (2) with $\varPhi (0,x_{0})=x_{0}$.

For $a,b\ge 0$, let

$$\begin{aligned}{} & {} k_{1}(b)=\text{ e}^{-\int ^{b}_{0}(\rho \sigma (s)+d)\text{ d }s}, \quad k_{2}(a)=\text{ e}^{-\int ^{a}_{0}(\theta (s)+d)\text{ d }s},\\{} & {} {\mathcal {K}}_{1}=\int ^{+\infty }_{0}\sigma (b)k_{1}(b)\text{ d }b, \quad {\mathcal {K}}_{2}=\int ^{+\infty }_{0}\beta _{1}(a)k_{2}(a)\text{ d }a,\\{} & {} {\mathcal {K}}_{3}=\int ^{+\infty }_{0}\theta (a)k_{2}(a)\text{ d }a, \quad {\mathcal {K}}_{4}=\int ^{+\infty }_{0}\xi _{1}(a)k_{2}(a)\text{ d }a. \end{aligned}$$

Integrating the equations for e(t, b) and i(t, a) in System (2) along the characteristic lines, $t-b=\text{ const }$ and $t-a=\text{ const }$, respectively, we obtain

$$\begin{aligned} e(t,b)= & {} \left\{ \begin{aligned}&e(t-b,0)k_{1}(b),{} & {} 0\le b\le t,\\&e_{0}(b-t)\frac{k_{1}(b)}{k_{1}(b-t)},{} & {} 0\le t\le b,\\ \end{aligned} \right. \nonumber \\ i(t,a)= & {} \left\{ \begin{aligned}&i(t-a,0)k_{2}(a),{} & {} 0\le a\le t,\\&i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)},{} & {} 0\le t\le a.\\ \end{aligned} \right. \end{aligned}$$

(5)

In what follows, we prove that the solution of System (2) is bounded.

Theorem 1

The solution of System (2) is bounded, that is,

$$\begin{aligned} \left. \begin{aligned} N(t)\le \max \Big \{N_{0},\frac{\varLambda }{d}\Big \}, \;\; W(t)\le \max \Big \{W_{0},\frac{\varLambda ({\bar{\xi }}_{1}+\xi _{2})}{dc}\Big \},\;\; \text{ for }\;\;t\in {\mathbb {R}}_{+}. \end{aligned} \right. \end{aligned}$$

Moreover, the upper bounds are eventually uniform,

$$\begin{aligned} \left. \begin{aligned} \underset{t\rightarrow \infty }{\lim \sup }\;N(t)\le \frac{\varLambda }{d}, \;\; \underset{t\rightarrow \infty }{\lim \sup } \;W(t)\le \frac{\varLambda ({\bar{\xi }}_{1}+\xi _{2})}{dc}. \end{aligned} \right. \end{aligned}$$

Proof

See “Appendix A”. $\square$

Hence, the trajectories of System (2) are ultimately bounded. Then we have the following proposition.

Proposition 1

Define

$$\begin{aligned} \left. \begin{aligned} {\mathcal {D}}&=\bigg \{(S(t),V(t),T(t),R(t),W(t),e(t,b),i(t,a)) \in {\mathcal {Y}}:0\le N(t)\le \frac{\varLambda }{d},\\&\quad 0\le W(t)\le \frac{\varLambda ({\bar{\xi }}_{1}+\xi _{2})}{dc}\bigg \} \end{aligned} \right. \end{aligned}$$

(6)

is positively invariant for System (2).

2.2 Equilibria and the basic reproduction number

We assume that $(S^{0},V^{0},T^{0},R^{0},W^{0},e^{0}(\cdot ),i^{0}(\cdot ))$ is disease-free equilibrium. We take $T^{0}=R^{0}=W^{0}=e^{0}(0)=i^{0}(0)=0$, then $e^{0}(b)={\textbf{0}}$ and $i^{0}(a)={\textbf{0}}$ can be obtained by $e^{0}(b)=e^{0}(0)k_{1}(b)$ and $i^{0}(a)=i^{0}(0)k_{2}(a)$, respectively, where ${\textbf{0}}\in L^{1}_{+}(0,+\infty )$ is the zero function. Let the disease-free equilibrium be given by ${\mathcal {P}}^{0}=(S^{0},V^{0},0,0,0,0_{L^{1}(0,+\infty )},0_{L^{1}(0,+\infty )})$. Using $\frac{\text{ d }S(t)}{\text{ d }t}=\frac{\text{ d }V(t)}{\text{ d }t}=0$, we obtain

$$\begin{aligned} {\mathcal {P}}^{0}=\bigg (\frac{\varLambda (\tau +d)}{d(\alpha +\tau +d)}, \frac{\varLambda \alpha }{d(\alpha +\tau +d)},0,0,0,0_{L^{1}(0,+\infty )},0_{L^{1}(0,+\infty )}\bigg ). \end{aligned}$$

In order to derive endemic equilibria, we first determine the basic reproduction number ${\mathcal {R}}_{0}$ using the next generation operator approach (Diekmann et al. 1990; Van den Driessche and Watmough 2002). We obtain

$$\begin{aligned} \left. \begin{aligned} {\mathcal {R}}_{0}&=\big (S^{0}+\eta V^{0}\big )\Bigg ({\mathcal {K}}_{2} +\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d}+\frac{\beta _{3}[(\gamma +d){\mathcal {K}}_{4}+ \xi _{2}{\mathcal {K}}_{3}]}{c(\gamma +d)}\Bigg )[q+\rho (1-q){\mathcal {K}}_{1}]\\&=\frac{\varLambda (\eta \alpha +\tau +d)}{d(\alpha +\tau +d)}\Bigg ({\mathcal {K}}_{2} +\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d} +\frac{\beta _{3}[(\gamma +d){\mathcal {K}}_{4}+\xi _{2}{\mathcal {K}}_{3}]}{c(\gamma +d)}\Bigg )[q+\rho (1-q){\mathcal {K}}_{1}]. \end{aligned} \right. \end{aligned}$$

(7)

An endemic equilibrium ${\mathcal {P}}^{*}=\big (S^{*},V^{*},T^{*},R^{*},W^{*},e^{*}(b),i^{*}(a)\big )$ satisfies the following equations:

$$\begin{aligned}{} & {} \varLambda +\tau V^{*}+\delta R^{*}-\lambda ^{*}S^{*}-(\alpha +d)S^{*}=0,\nonumber \\{} & {} \alpha S^{*}-\eta \lambda ^{*}V^{*}-(\tau +d)V^{*}=0,\nonumber \\{} & {} \int ^{+\infty }_{0}\theta (a)i^{*}(a)\text{ d }a-(\gamma +d)T^{*}=0,\nonumber \\{} & {} \gamma T^{*}-(\delta +d)R^{*}=0,\nonumber \\{} & {} \int ^{+\infty }_{0}\xi _{1}(a)i^{*}(a)\text{ d }a+\xi _{2}T^{*}-cW^{*}=0,\\{} & {} e^{*}(b)=e^{*}(0)k_{1}(b),\nonumber \\{} & {} i^{*}(a)=i^{*}(0)k_{2}(a),\nonumber \\{} & {} e^{*}(0)=(1-q)\lambda ^{*}\big (S^{*}+\eta V^{*}\big ),\nonumber \\{} & {} i^{*}(0)=q\lambda ^{*}\big (S^{*}+\eta V^{*}\big )+\rho \int ^{+\infty }_{0}\sigma (b)e^{*}(b)\text{ d }b,\nonumber \end{aligned}$$

(8)

where

$$\begin{aligned} \lambda ^{*}=\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a)\text{ d }a+\beta _{2}T^{*} +\beta _{3}{W^{*}}. \end{aligned}$$

(9)

From Eq. (8), we have

$$\begin{aligned} T^{*}= & {} \frac{i^{*}(0){\mathcal {K}}_{3}}{\gamma +d}, \end{aligned}$$

(10)

$$\begin{aligned} R^{*}= & {} \frac{i^{*}(0)\gamma {\mathcal {K}}_{3}}{(\delta +d)(\gamma +d)},\end{aligned}$$

(11)

$$\begin{aligned} W^{*}= & {} \frac{i^{*}(0)[(\gamma +d){\mathcal {K}}_{4}+\xi _{2}{\mathcal {K}}_{3}]}{c(\gamma +d)},\end{aligned}$$

(12)

$$\begin{aligned} \lambda ^{*}= & {} i^{*}(0){\mathcal {K}}_{2}+\frac{\beta _{2}i^{*}(0){\mathcal {K}}_{3}}{\gamma +d}+\frac{\beta _{3}i^{*}(0)[(\gamma +d){\mathcal {K}}_{4}+\xi _{2}{\mathcal {K}}_{3}]}{c(\gamma +d)},\end{aligned}$$

(13)

$$\begin{aligned} V^{*}= & {} \frac{\alpha [\varLambda (\delta +d)(\gamma +d)+i^{*}(0)\delta \gamma {\mathcal {K}}_{3}]}{(\delta +d)(\gamma +d)[(\lambda ^{*}+d)(\eta \lambda ^{*}+\tau +d)+\alpha (\eta \lambda ^{*}+d)]},\end{aligned}$$

(14)

$$\begin{aligned} S^{*}= & {} \frac{(\eta \lambda ^{*}+\tau +d)[\varLambda (\delta +d)(\gamma +d)+i^{*}(0)\delta \gamma {\mathcal {K}}_{3}]}{(\delta +d)(\gamma +d)[(\lambda ^{*}+d)(\eta \lambda ^{*}+\tau +d)+\alpha (\eta \lambda ^{*}+d)]}. \end{aligned}$$

(15)

Substituting Eqs.(10)–(15) into the last two equations of Eq. (8) gives

$$\begin{aligned} \left. \begin{aligned} i^{*}(0)&=\big (S^{*}+\eta V^{*}\big )\bigg \{i^{*}(0){\mathcal {K}}_{2} +\frac{\beta _{2}i^{*}(0){\mathcal {K}}_{3}}{\gamma +d} +\frac{\beta _{3}i^{*}(0)[(\gamma +d){\mathcal {K}}_{4}+ \xi _{2}{\mathcal {K}}_{3}]}{c(\gamma +d)}\bigg \}\\&\quad \times \Big [q+\rho (1-q){\mathcal {K}}_{1}\Big ]. \end{aligned} \right. \end{aligned}$$

By calculation, we obtain the following equation satisfied by the endemic equilibrium

$$\begin{aligned} \left. \begin{aligned} \big (S^{*}+\eta V^{*}\big )\bigg \{{\mathcal {K}}_{2} +\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d}+\frac{\beta _{3}[(\gamma +d){\mathcal {K}}_{4}+ \xi _{2}{\mathcal {K}}_{3}]}{c(\gamma +d)}\bigg \}[q+\rho (1-q){\mathcal {K}}_{1}]-1=0. \end{aligned} \right. \nonumber \\ \end{aligned}$$

(16)

The above equation can be expressed as

$$\begin{aligned} a_{2}(i^{*}(0))^{2}+a_{1}i^{*}(0)+a_{0}=0, \end{aligned}$$

(17)

where

$$\begin{aligned} a_{2}= & {} \eta \bigg ({\mathcal {K}}_{2}+\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d}+\frac{\beta _{3}[(\gamma +d){\mathcal {K}}_{4}+ \xi _{2}{\mathcal {K}}_{3}]}{c(\gamma +d)}\bigg )^{2}\Big \{[q+\rho (1-q) {\mathcal {K}}_{1}]{\mathcal {K}}_{3}\delta \gamma \\{} & {} -(\delta +d)(\gamma +d)\Big \},\\ a_{1}= & {} \bigg ({\mathcal {K}}_{2}+\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d}+\frac{\beta _{3}[(\gamma +d){\mathcal {K}}_{4}+ \xi _{2}{\mathcal {K}}_{3}]}{c(\gamma +d)}\bigg )\bigg \{\varLambda \eta (\delta +d)(\gamma +d)\\{} & {} \times \bigg ({\mathcal {K}}_{2}+\frac{\beta _{2} {\mathcal {K}}_{3}}{\gamma +d}+\frac{\beta _{3}[(\gamma +d){\mathcal {K}}_{4}+ \xi _{2}{\mathcal {K}}_{3}]}{c(\gamma +d)}\bigg )[q+\rho (1-q){\mathcal {K}}_{1}]\\{} & {} +[q+\rho (1-q){\mathcal {K}}_{1}]{\mathcal {K}}_{3}\delta \gamma (d+\tau +\alpha \eta )-(\delta +d)(\gamma +d)(\eta d+d+\tau +\alpha \eta )\bigg \},\\ a_{0}= & {} (\delta +d)(\gamma +d)({\mathcal {R}}_{0}-1). \end{aligned}$$

Note that ${\mathcal {K}}_{1}\le \frac{{\bar{\sigma }}}{\rho {\bar{\sigma }}+d}$ and ${\mathcal {K}}_{3}\le \frac{{\bar{\theta }}}{{\bar{\theta }}+d}<1$. Thus, we have

$$\begin{aligned} a_{2}= & {} \eta \bigg ({\mathcal {K}}_{2}+\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d}+\frac{\beta _{3}[(\gamma +d){\mathcal {K}}_{4}+ \xi _{2}{\mathcal {K}}_{3}]}{c(\gamma +d)}\bigg )^{2} \Big \{[q+\rho (1-q){\mathcal {K}}_{1}]{\mathcal {K}}_{3}\delta \gamma \\{} & {} -(\delta +d)(\gamma +d)\Big \}\\< & {} \eta \bigg ({\mathcal {K}}_{2}+\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d} +\frac{\beta _{3}[(\gamma +d){\mathcal {K}}_{4}+ \xi _{2}{\mathcal {K}}_{3}]}{c(\gamma +d)}\bigg )^{2} \Big [\delta \gamma -(\delta +d)(\gamma +d)\Big ]\\< & {} 0. \end{aligned}$$

According to the basic properties of the quadratic equation, Eq. (17) has a unique positive root if ${\mathcal {R}}_{0}>1$. Then, System (2) has a unique positive endemic equilibrium ${\mathcal {P}}^{*}$. When ${\mathcal {R}}_{0}<1$, according to Eqs. (7) and (16), we notice that

$$\begin{aligned} \left. \begin{aligned} \frac{S^{*}+\eta V^{*}}{S^{0}+\eta V^{0}}=\frac{1}{{\mathcal {R}}_{0}}>1, \end{aligned} \right. \end{aligned}$$

which contradicts with $S^{*}+\eta V^{*}\le S^{0}+\eta V^{0}$. Hence, when ${\mathcal {R}}_{0}<1$, the endemic equilibrium of System (2) does not exist.

2.3 Local stability of the disease-free equilibrium

In this section, we prove the local stability of the equilibria of System (2). We consider the linearized system of System (2) at an equilibrium $\widetilde{{\mathcal {P}}}=\big ({\widetilde{S}},{\widetilde{V}},{\widetilde{T}},{\widetilde{R}},{\widetilde{W}},{\widetilde{e}}(b),{\widetilde{i}}(a)\big )$. Let

$$\begin{aligned} {\bar{S}}(t)= & {} S(t)-{\widetilde{S}},\;\;{\bar{V}}(t)=V(t)-{\widetilde{V}}, \;\;{\bar{T}}(t)=T(t)-{\widetilde{T}}, \;\; {\bar{R}}(t)=R(t)-{\widetilde{R}}, \\ {\bar{W}}(t)= & {} W(t)-{\widetilde{W}},\;\;{\bar{e}}(t,b)=e(t,b)-{\widetilde{e}}(b), \;\;{\bar{i}}(t,a)=i(t,a)-{\widetilde{i}}(a), \end{aligned}$$

we then drop “−” of ${\bar{S}}(t)$, ${\bar{V}}(t)$, ${\bar{T}}(t)$, ${\bar{R}}(t)$, ${\bar{W}}(t)$, ${\bar{e}}(t,b)$, and ${\bar{i}}(t,a)$ for simplicity, the linearized system becomes

$$\begin{aligned}{} & {} \frac{\text{ d }S(t)}{\text{ d }t}=\tau V(t)+\delta R(t) -{\widetilde{\lambda }}S(t)-\lambda (t){\widetilde{S}}-(\alpha +d)S(t),\nonumber \\{} & {} \frac{\text{ d }V(t)}{\text{ d }t}=\alpha S(t)-\eta {\widetilde{\lambda }}V(t)-\eta \lambda (t){\widetilde{V}}-(\tau +d)V(t),\nonumber \\{} & {} \frac{\text{ d }T(t)}{\text{ d }t}=\int ^{+\infty }_{0}\theta (a)i(t,a) \text{ d }a-(\gamma +d)T(t),\nonumber \\{} & {} \frac{\text{ d }R(t)}{\text{ d }t}=\gamma T(t)-(\delta +d)R(t),\\{} & {} \frac{\text{ d }W(t)}{\text{ d }t}=\int ^{+\infty }_{0}\xi _{1}(a) i(t,a)\text{ d }a+\xi _{2}T(t)-cW(t),\nonumber \\{} & {} \frac{\partial e(t,b)}{\partial t}+\frac{\partial e(t,b)}{\partial b} =-(\rho \sigma (b)+d)e(t,b),\nonumber \\{} & {} \frac{\partial i(t,a)}{\partial t}+\frac{\partial i(t,a)}{\partial a} =-(\theta (a)+d)i(t,a),\nonumber \end{aligned}$$

(18)

where

$$\begin{aligned} {\widetilde{\lambda }}=\int ^{+\infty }_{0}\beta _{1}(a){\widetilde{i}} (a)\text{ d }a+\beta _{2}{\widetilde{T}}+\beta _{3}{\widetilde{W}}, \end{aligned}$$

(19)

and $\lambda (t)$ is given by Eq. (1). System (18) with boundary and initial conditions is as follows

$$\begin{aligned} \left. \begin{aligned}&e(t,0)=(1-q){\widetilde{\lambda }}\big (S(t)+\eta V(t)\big )+(1-q)\lambda (t)\big ({\widetilde{S}}+\eta {\widetilde{V}}\big ),\\&i(t,0)=q{\widetilde{\lambda }}\big (S(t)+\eta V(t)\big )+q\lambda (t)\big ({\widetilde{S}}+\eta {\widetilde{V}}\big )+\rho \int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b,\\&S(0)=S_{0},V(0)=V_{0},T(0)=T_{0},R(0)=R_{0},W(0)=W_{0},\\&e(0,b)=e_{0}(b),i(0,a)=i_{0}(a). \end{aligned} \right. \end{aligned}$$

(20)

To study System (18), we seek the solutions in the form

$$\begin{aligned} S(t)= & {} {\widehat{S}}\text{ e}^{\iota t},\;\; V(t)={\widehat{V}} \text{ e}^{\iota t}, \;\;T(t)={\widehat{T}}\text{ e}^{\iota t}, \;\; R(t)={\widehat{R}}\text{ e}^{\iota t}, \\ W(t)= & {} {\widehat{W}}\text{ e}^{\iota t}, \;\;e(t,b)={\widehat{e}}(b) \text{ e}^{\iota t}, \;\;i(t,a)={\widehat{i}}(a)\text{ e}^{\iota t}, \end{aligned}$$

where ${\widehat{S}}$, ${\widehat{V}}$, ${\widehat{T}}$, ${\widehat{R}}$, ${\widehat{W}}$, ${\widehat{e}}(b)$, ${\widehat{i}}(a)$, and $\iota$ have to be determined in such a way that ${\widehat{S}}$, ${\widehat{V}}$, ${\widehat{T}}$, ${\widehat{R}}$, ${\widehat{W}}$, ${\widehat{e}}(b)$, ${\widehat{i}}(a)$ are not all zeros. Substituting the constitutive form of the solutions into System (18), we obtain

$$\begin{aligned}{} & {} \iota {\widehat{S}}=\tau {\widehat{V}}+\delta {\widehat{R}} -{\widetilde{\lambda }}{\widehat{S}}-{\widehat{\lambda }}{\widetilde{S}} -(\alpha +d){\widehat{S}},\nonumber \\{} & {} \iota {\widehat{V}}=\alpha {\widehat{S}}-\eta {\widetilde{\lambda }} {\widehat{V}}-\eta {\widehat{\lambda }}{\widetilde{V}}-(\tau +d){\widehat{V}},\nonumber \\{} & {} \iota {\widehat{T}}=\int ^{+\infty }_{0}\theta (a){\widehat{i}}(a)\text{ d }a -(\gamma +d){\widehat{T}},\nonumber \\{} & {} \iota {\widehat{R}}=\gamma {\widehat{T}}-(\delta +d){\widehat{R}},\\{} & {} \iota {\widehat{W}}=\int ^{+\infty }_{0}\xi _{1}(a){\widehat{i}}(a)\text{ d }a +\xi _{2}{\widehat{T}}-c{\widehat{W}},\nonumber \\{} & {} \frac{\text{ d } {\widehat{e}}(b)}{\text{ d } b}=-(\rho \sigma (b) +d+\iota ){\widehat{e}}(b),\nonumber \\{} & {} \frac{\text{ d } {\widehat{i}}(a)}{\text{ d } a}=-(\theta (a) +d+\iota ){\widehat{i}}(a),\nonumber \end{aligned}$$

(21)

where ${\widehat{\lambda }}=\int ^{+\infty }_{0}\beta _{1}(a){\widehat{i}}(a)\text{ d }a+\beta _{2}{\widehat{T}}+\beta _{3}{\widehat{W}}$ and ${\widetilde{\lambda }}$ is given by Eq. (19). The initial conditions of System (21) are as follows

$$\begin{aligned} \left. \begin{aligned} {\widehat{e}}(0)&=(1-q){\widetilde{\lambda }}\big ({\widehat{S}} +\eta {\widehat{V}}\big )+(1-q){\widehat{\lambda }}\big ({\widetilde{S}} +\eta {\widetilde{V}}\big ),\\ {\widehat{i}}(0)&=q{\widetilde{\lambda }}\big ({\widehat{S}} +\eta {\widehat{V}}\big )+q{\widehat{\lambda }}\big ({\widetilde{S}} +\eta {\widetilde{V}}\big )+\rho \int ^{+\infty }_{0}\sigma (b){\widehat{e}}(b)\text{ d }b. \end{aligned} \right. \end{aligned}$$

(22)

Let

$$\begin{aligned} \left. \begin{aligned} {\mathcal {H}}_{1}(\iota )&=\int ^{+\infty }_{0}\sigma (b)k_{1}(b)\text{ e}^{-\iota b} \text{ d }b,\;\;\; {\mathcal {H}}_{2}(\iota )=\int ^{+\infty }_{0}\beta _{1}(a)k_{2}(a) \text{ e}^{-\iota a}\text{ d }a,\\ {\mathcal {H}}_{3}(\iota )&=\int ^{+\infty }_{0}\theta (a)k_{2}(a)\text{ e}^{-\iota a} \text{ d }a,\;\;\; {\mathcal {H}}_{4}(\iota )=\int ^{+\infty }_{0}\xi _{1}(a)k_{2}(a) \text{ e}^{-\iota a}\text{ d }a. \end{aligned} \right. \end{aligned}$$

(23)

According to Systems (21) and (22), we have

$$\begin{aligned} {\widehat{\lambda }}(\iota )= & {} {\widehat{i}}(0)\bigg \{{\mathcal {H}}_{2}(\iota ) +\frac{\beta _{2}{\mathcal {H}}_{3}(\iota )}{\iota +\gamma +d}+ \frac{\beta _{3}[(\iota +\gamma +d){\mathcal {H}}_{4}(\iota ) +\xi _{2}{\mathcal {H}}_{3}(\iota )]}{(\iota +c)(\iota +\gamma +d)}\bigg \}:= {\widehat{i}}(0){\widehat{\lambda }}_{1}(\iota ),\\ {\widehat{S}}= & {} \frac{{\widehat{i}}(0)\left\{ \begin{aligned}&\delta \gamma {\mathcal {H}}_{3}(\iota )(\iota +\eta {\widetilde{\lambda }} +\tau +d)-{\widehat{\lambda }}_{1}(\iota )(\iota +\delta +d)(\iota +\gamma +d)\\&\quad \times \big [\tau \eta {\widetilde{V}}+(\iota +\eta {\widetilde{\lambda }} +\tau +d){\widetilde{S}}\big ] \end{aligned}\right\} }{(\iota +\delta +d)(\iota +\gamma +d)[(\iota +{\widetilde{\lambda }}+d)(\iota +\eta {\widetilde{\lambda }}+\tau +d)+\alpha (\iota +\eta {\widetilde{\lambda }}+d)]},\nonumber \\ {\widehat{V}}= & {} \frac{{\widehat{i}}(0)\Big \{\alpha \delta \gamma {\mathcal {H}}_{3}(\iota )-{\widehat{\lambda }}_{1}(\iota )(\iota +\delta +d)(\iota +\gamma +d) \big [\alpha {\widetilde{S}}+\eta (\iota +{\widetilde{\lambda }}+\alpha +d) {\widetilde{V}}\big ]\Big \}}{(\iota +\delta +d)(\iota +\gamma +d)[(\iota +{\widetilde{\lambda }}+d)(\iota +\eta {\widetilde{\lambda }}+\tau +d)+\alpha (\iota +\eta {\widetilde{\lambda }}+d)]},\nonumber \end{aligned}$$

(24)

and

$$\begin{aligned} {\widehat{i}}(0)=\Big [{\widetilde{\lambda }}\big ({\widehat{S}} +\eta {\widehat{V}}\big )+{\widehat{\lambda }}\big ({\widetilde{S}} +\eta {\widetilde{V}}\big )\Big ]\big [q+\rho (1-q){\mathcal {H}}_{1}(\iota )\big ]. \end{aligned}$$

By calculation, we obtain the characteristic equation at an equilibrium $\widetilde{{\mathcal {P}}}$, which is

$$\begin{aligned} \left. \begin{aligned} G(\iota )&=\frac{G_{1}(\iota )\big [q+\rho (1-q){\mathcal {H}}_{1}(\iota )\big ]}{G_{2} (\iota )}+{\widehat{\lambda }}_{1}(\iota )\big ({\widetilde{S}} +\eta {\widetilde{V}}\big )\big [q+\rho (1-q){\mathcal {H}}_{1}(\iota )\big ]-1, \end{aligned} \right. \nonumber \\ \end{aligned}$$

(25)

where

$$\begin{aligned} \begin{aligned} G_{1}(\iota )&={\widetilde{\lambda }}\delta \gamma {\mathcal {H}}_{3}(\iota ) (\iota +\eta {\widetilde{\lambda }}+\tau +d+\eta \alpha )-{\widetilde{\lambda }} {\widehat{\lambda }}_{1}(\iota )(\iota +\delta +d)(\iota +\gamma +d)\\&\quad \times \big [\tau \eta {\widetilde{V}}+\eta ^{2}{\widetilde{V}}(\iota +{\widetilde{\lambda }}+\alpha +d)+{\widetilde{S}}(\iota +\eta {\widetilde{\lambda }} +\tau +d+\eta \alpha )\big ],\\ G_{2}(\iota )&=(\iota +\delta +d)(\iota +\gamma +d)[(\iota +{\widetilde{\lambda }} +d)(\iota +\eta {\widetilde{\lambda }}+\tau +d)+\alpha (\iota +\eta {\widetilde{\lambda }}+d)]. \end{aligned} \end{aligned}$$

Thus, we establish the following result.

Theorem 2

If ${\mathcal {R}}_{0}<1$, then the disease-free equilibrium ${\mathcal {P}}^{0}$ of System (2) is locally asymptotically stable. If ${\mathcal {R}}_{0}>1$, it is unstable.

Proof

The local asymptotic stability of ${\mathcal {P}}^{0}$ is determined by the sign of the eigenvalues. More details can be found in “Appendix B”. $\square$

2.4 Asymptotic smoothness

Lemma 1

(see Theorem 2.46 in Smith and Thieme 2011) The semiflow $\varPhi$ is asymptotically smooth if there are maps $\varPsi , \Theta : {\mathbb {R}}_{+}\times {\mathcal {Y}}\rightarrow {\mathcal {Y}}$ such that

$$\begin{aligned} \varPhi (t,x) =\Theta (t,x) + \varPsi (t,x) \end{aligned}$$

and the following properties hold for any bounded closed set ${\mathcal {B}}$ that is forward invariant under $\varPhi :$

• (i) $\underset{t\rightarrow \infty }{\lim }\;{\textrm{diam}}\;\Theta (t, {\mathcal {B}})= 0$;

• (ii) there exists $t_{{\mathcal {B}}}\in {\mathbb {R}}_{+}$ such that $\varPsi (t,{\mathcal {B}})$ has a compact closure for all $t\in {\mathbb {R}}_{+},\;t\ge t_{{\mathcal {B}}}$.

Lemma 2

(see Theorem B.2 in Smith and Thieme 2011) Let ${\mathcal {A}}$ be a subset of $L^{1}_{+}(0,\infty )$. Then ${\mathcal {A}}$ has a compact closure if and only if the following four conditions hold:

• (i) $\underset{f\in {\mathcal {A}}}{\sup }\int ^{\infty }_{0}|f(s)|{\textrm{d}}s<\infty$;

• (ii) $\underset{h\rightarrow \infty }{\lim }\int ^{\infty }_{h}|f(s)|{\textrm{d}}s\rightarrow 0$ uniformly in $f\in {\mathcal {A}}$;

• (iii) $\underset{h\rightarrow 0^{+}}{\lim }\int ^{\infty }_{0}|f(s+h)-f(s)|{\textrm{d}}s\rightarrow 0$ uniformly in $f\in {\mathcal {A}}$;

• (iv) $\underset{h\rightarrow 0^{+}}{\lim }\int ^{h}_{0}|f(s)|{\textrm{d}}s\rightarrow 0$ uniformly in $f\in {\mathcal {A}}$.

We now prove that the semiflow $\{\varPhi (t,\cdot )\}_{t\ge 0}$ generated by System (2) is asymptotically smooth.

Theorem 3

The semiflow $\{\varPhi (t,\cdot )\}_{t\ge 0}$ generated by System (2) is asymptotically smooth.

Proof

According to Lemmas 1 and 2, we prove that each forward invariant bounded closed set under $\{\varPhi (t,\cdot )\}_{t\ge 0}$ is attracted by a non-empty compact set. More details can be found in “Appendix C”. $\square$

According to Theorem 2.6 in Magal and Zhao (2005) and Theorem 2.4 in D’Agata et al. (2006), $\{\varPhi (t,\cdot )\}_{t\ge 0}$ has a global attractor.

2.5 Uniform persistence

In this section, we demonstrate that System (2) is uniformly persistent when ${\mathcal {R}}_{0} > 1$. To this end, we define the following symbols.

$$\begin{aligned} {\mathcal {D}}_{0}=\bigg \{(x_{1},x_{2},x_{3},x_{4},x_{5},x_{6},x_{7}) \in {\mathcal {Y}}:x_{3}+x_{5}+\int ^{+\infty }_{0}x_{6}(b)\text{ d }b +\int ^{+\infty }_{0}x_{7}(a)\text{ d }a>0\bigg \}, \end{aligned}$$

and $\partial {\mathcal {D}}_{0}={\mathcal {Y}}\backslash {\mathcal {D}}_{0}$.

Theorem 4

The sets ${\mathcal {D}}_{0}$ and $\partial {\mathcal {D}}_{0}$ are positively invariant under the semiflow $\{\varPhi (t,\cdot )\}_{t\ge 0}$. Besides, the disease-free equilibrium ${\mathcal {P}}^{0}$ of System (2) is globally asymptotically stable for the semiflow $\{\varPhi (t,\cdot )\}_{t\ge 0}$ restricted to $\partial {\mathcal {D}}_{0}$.

Proof

We use the comparison principle to prove that the sets ${\mathcal {D}}_{0}$ and $\partial {\mathcal {D}}_{0}$ are positively invariant under the semiflow $\{\varPhi (t,\cdot )\}_{t\ge 0}$. For the global asymptotic stability of ${\mathcal {P}}^{0}$, we first prove the local asymptotic stability of ${\mathcal {P}}^{0}$, then prove the global attractivity of ${\mathcal {P}}^{0}$. More details can be found in “Appendix D”. $\square$

By applying the results in Hale and Waltman (1989) and Magal and Zhao (2005), we obtain the following theorem.

Theorem 5

If ${\mathcal {R}}_{0}>1$, the semiflow $\{\varPhi (t,\cdot )\}_{t\ge 0}$ is uniformly persistent with respect to $({\mathcal {D}}_{0},\;\partial {\mathcal {D}}_{0})$; that is, there exists $\nu >0$ such that

$$\begin{aligned} \underset{t\rightarrow +\infty }{\liminf }\;d(\varPhi (t,x),\partial {\mathcal {D}}_{0})\ge \nu \;\text{ for } \;\text{ any }\;x\in {\mathcal {D}}_{0}. \end{aligned}$$

Proof

Since the disease-free equilibrium ${\mathcal {P}}^{0}$ is globally asymptotically stable restricted to $\partial {\mathcal {D}}_{0}$. Applying Theorem 4.2 in Hale and Waltman (1989), the semiflow $\{\varPhi (t,\cdot )\}_{t\ge 0}$ is uniformly persistent if and only if

$$\begin{aligned} W^{s}({\mathcal {P}}^{0})\cap {\mathcal {D}}_{0}=\emptyset , \end{aligned}$$

(26)

where $W^{s}({\mathcal {P}}^{0})=\Big \{x\in {\mathcal {Y}}:\;\underset{t\rightarrow +\infty }{\lim }\varPhi (t,x)={\mathcal {P}}^{0}\Big \}$. More details can be found in “Appendix E”. $\square$

2.6 Global stablility of the disease-free equilibrium

In this section, we prove the global asymptotic stability of the disease-free equilibrium ${\mathcal {P}}^{0}$ when $\delta =0$.

Theorem 6

If ${\mathcal {R}}_{0}<1$, then the disease-free equilibrium ${\mathcal {P}}^{0}$ of System (2) is globally asymptotically stable, and if ${\mathcal {R}}_{0}=1$, then the disease-free equilibrium ${\mathcal {P}}^{0}$ of System (2) is globally attractive.

Proof

We prove Theorem 6 by constructing the Lyapunov function (see “Appendix F”). $\square$

2.7 Global attractivity of the endemic equilibrium

According to Eq. (25), the characteristic equation corresponding to ${\mathcal {P}}^{*}$ is

$$\begin{aligned} G(\iota )&=\frac{G^{*}_{1}(\iota )\big [q+\rho (1-q){\mathcal {H}}_{1}(\iota )\big ] }{G^{*}_{2}(\iota )}+{\widehat{\lambda }}_{1}(\iota )\big (S^{*} +\eta V^{*}\big )\big [q+\rho (1-q){\mathcal {H}}_{1}(\iota )\big ]-1, \end{aligned}$$

(27)

where

$$\begin{aligned} \begin{aligned} G^{*}_{1}(\iota )&=\lambda ^{*}\delta \gamma {\mathcal {H}}_{3}(\iota ) (\iota +\eta \lambda ^{*}+\tau +d+\eta \alpha )-\lambda ^{*}{\widehat{\lambda }}_{1} (\iota )(\iota +\delta +d)(\iota +\gamma +d)\\&\quad \times \big [\tau \eta V^{*}+\eta ^{2}V^{*}(\iota +\lambda ^{*} +\alpha +d)+S^{*}(\iota +\eta \lambda ^{*}+\tau +d+\eta \alpha )\big ],\\ G^{*}_{2}(\iota )&=(\iota +\delta +d)(\iota +\gamma +d)[(\iota +\lambda ^{*} +d)(\iota +\eta \lambda ^{*}+\tau +d)+\alpha (\iota +\eta \lambda ^{*}+d)], \end{aligned} \end{aligned}$$

$\lambda ^{*}$ and ${\widehat{\lambda }}_{1}(\iota )$ are given by Eqs. (9) and (24), respectively. We only need to prove that all the eigenvalues of the characteristic equation (27) have negative real parts when ${\mathcal {R}}_{0}>1$. However, it is difficult to confirm it. In the following, we only prove that the endemic equilibrium ${\mathcal {P}}^{*}$ is globally attractive when $\delta =0$.

Theorem 7

The endemic equilibrium ${\mathcal {P}}^{*}$ of System (2) is globally attractive if ${\mathcal {R}}_{0}>1$.

Proof

We also prove Theorem 7 by constructing the Lyapunov function (see “Appendix G”). $\square$

3 Fitting the model to the TB data of Jiangsu Province

In this section, we estimate the unknown parameters and initial values of System (2) using the number of new TB cases with infection age from 2009 to 2018 in Jiangsu Province, and we obtain the mean value and confidence interval of the basic reproduction number, ${\mathcal {R}}_{0}$.

3.1 Data collection

To parameterize the mathematical model for the transmission dynamics of TB in Jiangsu Province, we collect 351,401 data points from January 2009 to December 2018 in Jiangsu Province. The data was collected from the Jiangsu Provincial Center for Disease Control and Prevention, including symptom-onset date, confirmed date, and diagnostic result, etc. (see Table 2). We set the age of infection as the difference between the symptom-onset date and confirmed date (see Fig. 2A). The number of new TB cases varying with infection age and time is shown in Fig. 2B.

It can be seen from Fig. 2A that the mean age of infection is 44.3 days, ranging from 0 to 24,726 days. We find 220,399 infected individuals with an infection age of less than one month, accounting for 66% of the total infected individuals, and 10,532 infected individuals with an infection age of more than six months, accounting for 3% of the total infected individuals.

Table 2 The incidence data of TB in Jiangsu Province from January 2009 to December 2018

Fig. 2

A Frequency distribution of delay time. B The number of new TB cases in Jiangsu Province from January 2009 to December 2018 changing with infection age and time

3.2 Parameter estimation

To simulate the number of new TB cases in Jiangsu Province, the feasibility of the model is verified by the actual number of newly infected cases. System (2) is solved numerically using the forward/backward finite difference method for time and age (see “Appendix H”) (implemented by the Python Programming Language). Next, we estimate all the parameters and initial values of System (2).

• (I) The recruitment rate of the population (i.e., $\varLambda$): According to the statistics of the Jiangsu Statistical Yearbook (2022), we obtain that the annual numbers of births from 2009 to 2018 was 743600, 763100, 756100, 746700, 748600, 751300, 721100, 779600, 778200, and 749300, respectively. Therefore, we can obtain that the monthly average number of newborns of Jiangsu Province is about 62,813, that is, $\varLambda =62813\;\text{ number }/\text{month }$.

• (II) The natural mortality rate (i.e., d): According to the statistics of the National Bureau of Statistics of China (2022), we conclude that the monthly natural mortality rate of the population in Jiangsu Province in 2020 is approximately $d=1/(79\times 12)\;\text {per month}$, where the constant 79 represents the average life expectancy of the population in Jiangsu Province.

• (III) The proportion of new infections that develop into active TB (i.e., q): Since approximately 10% of infected individuals will develop active TB during their lifetime (World Health Organization 2022b), and around $5\%$ of these infected individuals will develop active TB during the first two years of infection (Ziv et al. 2001). Therefore, we choose $q=0.05$.

• (IV) The proportion of new infections that develop into active TB from latent individuals (i.e., $\rho$): According to the statement in (III), we know that approximately $10\%$ of infected individuals will develop active TB during their lifetime. Hence, we estimate the parameter $\rho$ to be 0.1.

• (V) The recovery rate (i.e., $\gamma$): TB patients can be cured after six months of drug treatment (World Health Organization 2022b). Thus, we choose $\gamma =1/6\;\text {per month}$.

• (VI) The rate at which a recovered individual loses immunity (i.e., $\delta$): Since TB antibodies in the human body last for more than ten years (Aronson et al. 2004). Therefore, we choose $\delta =1/(12\times 10)\;\text {per month}$.

• (VII) The clearance rate of the Mycobacterium TB in the environments (i.e., c): Mycobacterium TB can survive for several months or years in dry environments. Thus, we assume that the average survival time of TB is six months, then $c=1/6$ per month.

• (VIII) The vaccination rate of the susceptible individuals (i.e., $\alpha$): In addition to BCG vaccine, there are no effective vaccines against TB for adults. Therefore, we only consider the scenario of BCG vaccination. According to the statistics of the Jiangsu Statistical Yearbook (2022), we obtain that the proportion of people under ten years old is 0.084 in Jiangsu Province, then we let $V(t)/(S(t)+V(t))$ approximately equal to 0.084 by changing the parameter $\alpha$ when the disease becomes extinct. At this time, we have $\alpha =0.00086$.

• (IX) The level of protection for vaccinated individuals due to immunity (i.e., $1-\eta$): BCG has 60%-80% protective efficacy against severe forms of TB in children (Roy et al. 2014). Thus, we assume $1-\eta =0.8$.

• (X) The duration of vaccine protection (i.e., $1/\tau$): As part of the childhood immunization program, BCG vaccine has a high protection rate and remains effective for about ten years (Aronson et al. 2004; Xue et al. 2022). Therefore, we choose $\tau =1/(12\times 10)$ per month.

• (XI) The progression rate of the latent individuals at stage b (i.e., $\sigma (b)$): According to the estimates from previous literature (Borgdorff et al. 2011; Yan and Cao 2019), we obtain that the progression rate of latent individuals gradually decreases with the increase of latent age. Therefore, we choose exponential function $\sigma (b)=\sigma _{1}\text{ e}^{-\sigma _{2}b}$ as the progression rate of the latent individuals, where $\sigma _{1}$ and $\sigma _{2}$ are parameters to be estimated.

• (XII) The diagnotic rate of the infected individuals at stage a (i.e., $\theta (a)$): We approximate the diagnotic rate of the infected individuals by Erlang-distributed diagnostic period using the frequency distribution of delay time (Champredon et al. 2018) (see Fig. 2A). We assume that the maximum delay time is ${\hat{n}}$ months and divide the infected compartment into ${\hat{n}}$ sub-compartments. Let ${\hat{A}}$ denote the total number of cases from January 2009 to December 2018. ${\hat{B}}_{i}$ represents the total number of cases with delay that is no longer than i months. Then the diagnostic rate of the infected individuals in the i-th month can be expressed as

  $$\begin{aligned} {\hat{\theta }}_{i}=\left\{ \begin{aligned}&\frac{{\hat{B}}_{i}}{{\hat{A}}}{\hat{n}}\frac{1}{{\hat{n}}},\quad i=1,\\&\frac{{\hat{B}}_{i}-{\hat{B}}_{i-1}}{{\hat{A}}-{\hat{B}}_{i-1}}{\hat{n}} \frac{1}{{\hat{n}}},\quad i>1, \end{aligned} \right. \end{aligned}$$

  which is shown in Fig. 3A. The diagnotic rate of the infected individuals is a decreasing function. Hence, we choose the exponential function $\theta (a)=\theta _{1}\text{ e}^{-\theta _{2}a}$ to approximate the discretized data (${\hat{\theta }}_{i}$), where $\theta _{1}$ and $\theta _{2}$ are parameters to be estimated. The fitting result of the diagnotic rate of the infected individuals is shown in Fig. 3A.

• (XIII) The transmission rate of infected individuals at stage a (i.e., $\beta _{1}(a)$): Since it is difficult to characterize the transmission rate that depends on the age of infection (Ainseba et al. 2017; Feng et al. 2002), we assume that $\beta _{1}(a)$ is a constant, that is, $\beta _{1}(a)\equiv \beta _{1}$, where $\beta _{1}$ is derived by fitting the actual incidence.

• (XIV) The transmission rate of treated individuals (i.e., $\beta _{2}$): TB patients have reduced transmission rates due to treatment, and we assume $\beta _{2}=\omega \beta _{1}$, where $\omega \in (0,1)$ is the coefficient that reduces the transmission rate due to treatment. According to the estimation of Guo et al. (2021), we choose $\omega =0.4387$.

• (XV) The Mycobacterium TB shedding rates from infected and treated individuals at stage a (i.e., $\xi _{1}(a)$ and $\xi _{2}$): In order to reduce the complexity of estimating parameters, we assume that $\xi _{1}(a)$ is a constant, that is, $\xi _{1}(a)\equiv \xi _{1}$. Since the W(t) variable is of a different order of magnitude compared with the population variable, we let $\xi _{1}=1$, which means that an infected individual releases one unit of Mycobacterium TB per month (Cai et al. 2021). In general, the Mycobacterium TB shedding rate from treated individuals at stage a is $\xi _{2}\le \xi _{1}$ due to treatment.

• (XVI) The initial values of System (2): According to the relevant data reported by the Jiangsu Statistical Yearbook (2022), we choose the initial value of the total population as $N(0)=85,\!000,\!000$. We also obtain that the proportion of people under ten years old is 0.084 in Jiangsu Province, then $V(0)=0.084N(0)=7,\!140,\!000$. According to recent estimation, approximately 350 million people are infected with Mycobacterium TB in China (Cui et al. 2020), we approximate that the initial value of the latent individuals is

  $$\begin{aligned} \int ^{+\infty }_{0}e(0,b)\text{ d }b=\frac{3.5}{14}\times N(0)=21250000, \end{aligned}$$

  where 14 means that average total population is 1.4 billion in China. Hence, we choose

  $$\begin{aligned} e(0,b)=21250000\zeta _{1}\text{ e}^{-\zeta _{1}b} \end{aligned}$$

  to satisfy $\int ^{+\infty }_{0}e(0,b)\text{ d }b=21,\!250,\!000$, where $\zeta _{1}$ is the parameter to be estimated. The initial value i(0, a) of the density of the infected individuals, the initial value of treated individuals T(0), the initial value of recovered individuals R(0), and the initial value of the density of Mycobacterium TB in the environment W(0) are obtained by fitting the data. For the functional form of i(0, a), we choose i(0, a) as an exponential function through Fig. 2B, that is, $i(0,a)=\varpi _{1}\text{ e}^{-\varpi _{2}a}$, where $\varpi _{1}$ and $\varpi _{2}$ are parameters to be estimated. The initial value of susceptible individuals is estimated as

  $$\begin{aligned} S(0)=N(0)-V(0)-\int ^{+\infty }_{0}e(0,b)\text{ d }b -\int ^{+\infty }_{0}i(0,a)\text{ d }a-T(0)-R(0). \end{aligned}$$

The set of unknown parameters and initial values is

$$\begin{aligned} {\widehat{\chi }}=\big (\sigma _{1},\sigma _{2},\beta _{1},\beta _{3}, \xi _{2},\zeta _{1},T(0),R(0),W(0)\big ). \end{aligned}$$

The density of new TB cases with infection age a at time t is

$$\begin{aligned} {\mathcal {Z}}_{1}(t,a)=\theta (a)i(t,a), \end{aligned}$$

where the time step and age step are 0.5 and 1 in the simulation, respectively. We choose the maximum time, maximum latent age and maximum infection age in the simulation to be 120, 120 and 24 months, respectively. Since the monthly number of new TB cases shows seasonality, we fit the model using the annual number of new TB cases. The annual number of new TB cases is an annual integral in the form

$$\begin{aligned} {\mathcal {Z}}_{2}(j,a)=\int _{\text{ year }\,j}\theta (a)i(t,a)\text{ d }t. \end{aligned}$$

In order to simplify our simulation, we first use MCMC method to fit ${\mathcal {Z}}_{1}(0,a)$ to the TB data at the initial time, which allows us to estimate the parameters $\varpi _{1}$ and $\varpi _{2}$, as shown in Fig. 3B. ${\mathcal {Z}}_{1}(0,a)$ is represented as follows

$$\begin{aligned} {\mathcal {Z}}_{1}(0,a)=\theta (a)i(0,a)=\theta _{1}\text{ e}^{-\theta _{2}a} \varpi _{1}\text{ e}^{-\varpi _{2}a}. \end{aligned}$$

We then use the MCMC method (Haario et al. 2006) to fit System (2) for 200,000 iterations with a burn-in of 180,000  iterations. We estimate the unknown parameters and initial conditions for System (2), using the MCMC package provided by Miles (2019). More details on MCMC method can be found in “Appendix I”.

The mean and standard deviation of the parameters, and initial values are shown in Table 3. Figure 4A shows the 3D graph of the fitting results of the annual number of new TB cases from 2009 to 2018. Figure 4B shows the fitting results of the annual number of new TB cases accumulated by age of infection from 2009 to 2018. The simulated data is quite similar to the corresponding reported TB data.

Fig. 3

A The fitting result of the diagnotic rate of the infected individuals. B The fitting result of initial reported data. The solid red lines denote simulation median. Black circles represent actual data. The $95\%$ confidence and prediction intervals are shown in light green and blue, respectively

Table 3 The unknown parameters and initial values of System (2)

4 Results

In this section, we aim to explore the possibility of achieving the goals of WHO if we start diagnostic strategies and vaccinations for adults in 2025, as well as the significance of incorporating age into the model.

4.1 Basic reproduction number and sensitivity analysis

Based on the estimated parameter values in the previous section, we calculate the mean values of the basic reproduction number, ${\mathcal {R}}_{0}$, is 0.5320 (95% CI (0.3060, 0.7556)). Since ${\mathcal {R}}_{0}<1$, the disease-free equilibrium ${\mathcal {P}}^{0}$ of System (2) is globally asymptotically stable, which indicates that TB will die out in Jiangsu Province. However, according to the fitting results, we find that the annual number of new TB cases by 2050 will be 1,151 (95%CI: (138, 8,014)), which means that it is challenging to achieve the goal of WHO by 2050. Next, to investigate how the parameters affect the dynamics of System (2), we use the PRCC (Marino et al. 2008) to evaluate the impact of ten main parameters on the basic reproduction number (${\mathcal {R}}_0$). The input parameters are $\theta _{1}$, $\theta _{2}$, $\beta _{1}$, $\beta _{2}$, $\beta _{3}$, $\xi _{1}$, $\xi _{2}$, $\alpha$, $\eta$, and c, and the output is the basic reproduction number (${\mathcal {R}}_0$). We take 2000 samples for each parameter to conduct sensitivity analysis, and repeat 1000 times to get 1000 sets of PRCCs for each parameter, then take the average. All input parameters are normally distributed, with the mean and standard deviation of $\theta _{1}$, $\theta _{2}$, $\beta _{1}$, $\beta _{3}$, and $\xi _{2}$ given in Table 3, and the mean and standard deviation of $\beta _{2}$ and $\xi _{1}$ are consistent with $\beta _{1}$ and $\xi _{2}$. We also assume that the mean values of $\alpha$, $\eta$, and c are 0.00086, 0.2 and 1/6, respectively, and their standard deviations are 1/5 times of the means. The results of the sensitivity analysis of parameters are shown in Table 4.

Fig. 4

A 3D graph of the fitting results of the annual numbers of new TB cases from 2009 to 2018. The colored surface represents the simulation median. The black plus signs represent actual data. B The fitting result of the annual number of new TB cases. The solid red lines denote the simulation median. Black circles represent actual data. The $95\%$ confidence and prediction intervals are shown in light green and blue, respectively

Table 4 The PRCCs of the parameters with respect to the basic reproduction number (${\mathcal {R}}_0$)

Table 4 shows the sensitivity of the parameters $\theta _{1}$, $\theta _{2}$, $\beta _{1}$, $\beta _{2}$, $\beta _{3}$, $\xi _{1}$, $\xi _{2}$, $\alpha$, $\eta$, and c with respect to the basic reproduction number (${\mathcal {R}}_0$). Firstly, our results show that the direct transmission rate of infected and treated individuals ($\beta _{1}$ and $\beta _{2}$) and the indirect transmission rate of Mycobacterium TB ($\beta _{3}$) are highly positively correlated with the basic reproduction number (${\mathcal {R}}_0$). In particular, the correlation coefficient between the indirect transmission rate of Mycobacterium TB ($\beta _{3}$) and the basic reproduction number (${\mathcal {R}}_0$) is greater than 0.9, which means that Mycobacterium TB in the environment has a great influence on the TB epidemic. Next, we find that both parameters $\theta _{2}$ and $\xi _{1}$ are moderately positively correlated with the basic reproduction number (${\mathcal {R}}_0$), which indicates that the diagnotic rate of the infected individuals and the Mycobacterium TB shedding rate from infected individuals also have an impact on the TB epidemic. Moreover, the clearance rate of the Mycobacterium TB in the environments (c) is highly negatively correlated with the basic reproduction number (${\mathcal {R}}_0$). In particular, $\alpha$ has a lower correlation with the basic reproduction number (${\mathcal {R}}_0$) than $\beta _{1}$, $\beta _{2}$, $\beta _{3}$, c, $\theta _{2}$, and $\xi _{1}$, but improving the vaccination rate will also effectively control the TB epidemic.

4.2 The impact of diagnostic strategies

Diagnostic delay of TB results in increasing cases, mortality, infection time and transmission (Sreeramareddy et al. 2009). In order to shorten the duration of infectiousness to decrease the annual number of new TB cases. We reduce the annual number of new TB cases by decreasing the diagnostic delay. To this end, we redefine the diagnostic rate as

$$\begin{aligned} \theta (a)=\left\{ \begin{aligned}&\theta _{1}\text{ e}^{-\theta _{2}a},\quad a\le T_{a},\\&\theta _{1}\text{ e}^{-\theta _{2}T_{a}},\quad a> T_{a}. \end{aligned} \right. \end{aligned}$$

The above equation indicates that when the diagnostic delay time is greater than $T_{a}$, the diagnotic rate of infected individuals remains consistent with the diagnotic rate at $T_{a}$, which means that the diagnotic rate has been increased. We set $T_{a}$ to 5 and 4 to estimate the annual number of new TB cases, respectively. Using these estimated parameters, our simulations show that the annual number of new TB cases will be 274 (95% CI (22, 3000)) and 52 (95% CI (2, 932)) by 2050, respectively, which means that the goal of WHO in 2050 can be achieved when $T_{a}=4$. In particular, we find that setting $T_{a}$ to 5 and 4 can reduce the annual number of new TB cases by 74.88% (95% CI (47.42%, 86.77%)) and 95.28% (95% CI (77.55%, 98.79%)) by 2050, respectively (see Fig. 5A), and can prevent 45,351 (95%CI: (13,997, 150,655)) and 73,137 (95%CI: (23,906, 234,086)) individuals from being infected from 2025 to 2050, respectively (see Fig. 5B), which indicates that reducing the diagnostic delay can shorten the duration of infection, thereby reducing the number of new TB cases.

Fig. 5

A The impact of improved diagnostic strategies starting from 2025 on the annual number of new TB cases by year up to 2050. B The number of TB cases averted per year under improved diagnostic strategies

4.3 The impact of vaccinations for adults

Currently, there are no effective vaccines against TB for adults. In the simulations, we assume that TB vaccinations for adults will start in 2025. We assume that the level and duration of TB vaccine protection for adults vaccines and BCG vaccines are the same, that is, we set the level of vaccine protection to be $80\%$ (i.e., $1-\eta =0.8$) and the duration of vaccine protection to be ten years (i.e., $1/\tau =10\times 12$), and assume that the vaccine coverage of susceptible individuals is $V/(S+V)$ by changing the vaccination rate $\alpha$. We set the vaccine coverage of susceptible individuals over ten years old to $10\%$ and $20\%$ to estimate the annual number of new TB cases, respectively. Using these estimated parameters, our simulations find that the annual number of new TB cases will be 262 (95% CI (25, 2602)) and 46 (95% CI (3, 590)) by 2050, respectively, which means that the goal of WHO in 2050 can be achieved when vaccine coverage is 20%. In particular, we further predict that increasing vaccine coverage of susceptible individuals over ten years old to $10\%$ and $20\%$ can reduce the annual number of new TB cases by 77.34% (95% CI (67.42%, 83.36%)) and 95.97% (95% CI (91.58%, 97.88%)) by 2050, respectively (see Fig. 6A), and can prevent 33,931 (95%CI: (9,140, 130,171)) and 54,828 (95 infected from 2025 to 2050, respectively (see Fig. 6B), which indicates that vaccinating susceptible individuals over ten years old can effectively reduce the annual number of new TB cases.

Fig. 6

A The impact of adult vaccinations starting from 2025 on the annual number of new TB cases by year up to 2050. B The number of TB cases averted per year when adults are vaccinated

4.4 The significance of incorporating age into the model

The class-age is an important factor in the prevention and control of infectious diseases when modeling long-term diseases (Iannelli and Milner 2017). Firstly, the symptoms of TB are atypical, that is, the early symptoms of TB are not obvious and can resemble other illnesses such as colds and pneumonia, leading to missed diagnotic and misdiagnotic (Sreeramareddy et al. 2009). Especially in Jiangsu Province, the duration of diagnotic delay range from a few days to several hundred days. Therefore, the diagnotic rate of TB individuals varies from person to person, and this phenomenon can be characterized by an age structure model. Secondly, the duration of the latent period of TB varies greatly depending on the individual physical condition, immune response, the route and level of exposure to Mycobacterium TB. Some of these people can remain in a latent state after infection for their entire lives and may never develop active disease, while others may develop TB disease shortly after infection, which means that progression rate of the latent individuals depends on the latent age (Wikipedia 2022). During modeling, we captured the age of infection before receiving treatment and latent age. Our model is very consistent with the TB data in Jiangsu Province, which varies with the infection age and time (see Fig. 4A). In Sect. 4.2, we evaluate the possibility of achieving the goals of WHO in Jiangsu Province by changing the diagnostic rate function $(\theta (a))$, which can not be studied with a standard model that has no diagnostic delay. Our model not only allows more detailed grouping of latent individuals and infected individuals to obtain more accurate transmission models, but also introduces the class-age in the modeling process to predict the trend of epidemics at different infection ages, providing guidance for formulating prevention and control policies.

5 Discussion

The effectiveness of TB control strategies depends on many factors, of which the most important ones are diagnostic delay, adult vaccination, and the survival time of Mycobacterium TB in the environment, etc., (Chinese Center for Disease Control and Prevention 2022; Harris et al. 2019, 2020; Sreeramareddy et al. 2009), which presents a challenge for achieving the goal of WHO by 2050. In this work, we propose an age-structured model with latent age and infection age, and we incorporate Mycobacterium TB in the environment into the model. Since the development of new TB vaccines is rapid, we also introduce vaccination into the model. In particular, we consider the age of infection before receiving treatment to represent diagnostic delay. To start with, we derive the basic reproduction number (${\mathcal {R}}_{0}$) of the System (2), which is a very important threshold parameter for the persistence and extinction of the disease. Using the theories of infinite-dimensional systems and Lyapunov functions, we have obtained a threshold for the global stability of the System (2) with respect to ${\mathcal {R}}_{0}$, that is, when ${\mathcal {R}}_{0}$ is less than 1, the disease-free equilibrium is globally asymptotically stable and the disease eventually dies out; when ${\mathcal {R}}_{0}$ is equal to 1, the disease-free equilibrium is globally attractive; there exists a unique endemic equilibrium and the endemic equilibrium is globally attractive when ${\mathcal {R}}_{0}$ is greater than 1. Besides, we conduct a case study based on the epidemiological data stratified by the age of infection in Jiangsu Province and evaluate the possibility of achieving the goals of WHO in Jiangsu Province.

The study consists of 351,401 TB cases from January 2009 to December 2018 in Jiangsu Province. The data include symptom-onset date, confirmed date, and diagnostic result, etc. We set the age of infection as the difference between the symptom-onset date and confirmed date, allowing us to obtain the epidemiological data classified by the age of infection. We also find an average delay of 44 (95% CI (1, 189)) days in Jiangsu Province, which means that the risk of TB transmission in the community is high.

According to the estimated parameter values, we calculate that the basic reproduction number, ${\mathcal {R}}_{0}$, is estimated to be 0.5320 (95% CI (0.3060, 0.7556)), which indicates that TB will die out in Jiangsu Province. Regrettably, we obtain that the annual number of new TB cases by 2050 is 1,151 (95%CI: (138, 8,014)), which means that it is challenging to achieve the goal of WHO by 2050. Our sensitivity analysis indicates that the parameter $\theta _{2}$ is moderately positively correlated with the basic reproduction number (${\mathcal {R}}_0$), which indicates that the diagnotic rate of the infected individuals also has an impact on the TB epidemic, and the parameter $\alpha$ has a lower correlation with the basic reproduction number (${\mathcal {R}}_0$) than $\beta _{1}$, $\beta _{2}$, $\beta _{3}$, c, $\theta _{2}$, and $\xi _{1}$, but improving the vaccination rate will also effectively control the TB epidemic. According to the results of sensitivity analysis, we find that the correlation between the diagnotic rate or vaccination rate and the basic reproduction number (${\mathcal {R}}_0$) is not the highest. Because other non-pharmaceutical interventions other than surgery are not feasible for TB, we can only mitigate TB transmission by varying diagnostic rate and vaccination coverage (NEWTON 1912; Riquelme-Miralles et al. 2019).

Furthermore, we also evaluate the possibility of achieving the goals of WHO if we start diagnostic strategies and adult vaccinations in 2025. We find that when the diagnostic delay is reduced from longer than four months to four months, the annual number of new TB cases will be 52 (95% CI (2, 932)) by 2050, and 73,137 (95%CI: (23,906, 234,086)) individuals will be prevented from being infected from 2025 to 2050, which means that the goal of WHO by 2050 can be achieved. In addition, we also find that the goal of WHO in 2050 can be achieved and 54,828 (95%CI: (15,811, 206,468)) individuals will be prevented from being infected from 2025 to 2050 when 20% adults are vaccinated.

Our work provides a framework for determining how to quickly diagnose populations with prolonged infections and better vaccinate adults when more advanced diagnostic strategies and more effective vaccines for adults are available. Our research results utilize a wide range of datasets. Specifically, we extract the diagnostic rate from the dataset and fit the diagnostic rate function, which provided convenience for us to study the impact of diagnostic strategies in Jiangsu Province. We discuss the effectiveness of the diagnostic strategies and vaccinations for adults on the prevalence of TB. Both the diagnotic strategy and vaccination for adults are likely to achieve the goal of WHO in Jiangsu Province. In summary, reducing the delayed diagnotic time can shorten the infection time of infected individuals, and vaccinating adults can protect susceptible individuals from infection, thereby reducing the number of new TB cases, which is of great significance for reducing the prevalence of TB.

Our study still has several limitations. First, in the modeling, we don’t consider relapses in recovered individuals in order to obtain the completed mathematical theoretical results. Second, we assume that the global attractivity of the equilibria are obtained when the average period of immunity $\delta =0$. Third, since there is not enough data to fit the progression rate of the latent individuals ($\sigma (b)$), we assume the progression rate of the latent individuals to be $\sigma (b)=\sigma _{1}\text{ e}^{-\sigma _{2}b}$, which will be studied in future work when relevant data become publicly available.

Appendices

Appendix A: Proof of Theorem 1

Note that the total population size N(t) satisfies

$$\begin{aligned} \left. \begin{aligned} \frac{\text{ d }N(t)}{\text{ d }t}&=\frac{\text{ d }S(t)}{\text{ d }t} +\frac{\text{ d }V(t)}{\text{ d }t}+\frac{\text{ d }T(t)}{\text{ d }t}+ \frac{\text{ d }R(t)}{\text{ d }t}+\frac{\text{ d }}{\text{ d }t} \int ^{+\infty }_{0}e(t,b)\text{ d }b\\&\quad +\frac{\text{ d }}{\text{ d }t} \int ^{+\infty }_{0}i(t,a)\text{ d }a. \end{aligned} \right. \end{aligned}$$

(28)

According to Eq. (5), we have

$$\begin{aligned} \int ^{+\infty }_{0}e(t,b)\text{ d }b= & {} \int ^{t}_{0}e(t-b,0)k_{1}(b)\text{ d }b +\int ^{+\infty }_{t}e_{0}(b-t)\frac{k_{1}(b)}{k_{1}(b-t)}\text{ d }b\\= & {} \int ^{t}_{0}e(\tau _{1},0)k_{1}(t-\tau _{1})\text{ d }\tau _{1} +\int ^{+\infty }_{0}e_{0}(\tau _{2})\frac{k_{1}(t+\tau _{2})}{k_{1}(\tau _{2})}\text{ d }\tau _{2}. \end{aligned}$$

Then

$$\begin{aligned} \frac{\text{ d }}{\text{ d }t}\int ^{+\infty }_{0}e(t,b)\text{ d }b= & {} \frac{\text{ d }}{\text{ d }t}\int ^{t}_{0}e(\tau _{1},0)k_{1}(t-\tau _{1})\text{ d }\tau _{1}+ \frac{\text{ d }}{\text{ d }t}\int ^{+\infty }_{0}e_{0}(\tau _{2}) \frac{k_{1}(t+\tau _{2})}{k_{1}(\tau _{2})}\text{ d }\tau _{2}\\= & {} e(t,0)k_{1}(0)+\int ^{t}_{0}e(\tau _{1},0)\frac{\text{ d }}{\text{ d }t} k_{1}(t-\tau _{1})\text{ d }\tau _{1}\\{} & {} +\int ^{+\infty }_{0}\frac{e_{0} (\tau _{2})}{k_{1}(\tau _{2})}\frac{\text{ d }}{\text{ d }t}k_{1}(t+\tau _{2})\text{ d }\tau _{2}.\\ \end{aligned}$$

Note that $k_{1}(0)=1$ and $\frac{\text{ d }}{\text{ d }b}k_{1}(b)=-(\rho \sigma (b)+d)k_{1}(b)$ for almost all $b\ge 0$. Thus, we have

$$\begin{aligned} \frac{\text{ d }}{\text{ d }t}\int ^{+\infty }_{0}e(t,b)\text{ d }b= & {} e(t,0)-\int ^{t}_{0}e(\tau _{1},0)(\rho \sigma (t-\tau _{1}) +d)k_{1}(t-\tau _{1})\text{ d }\tau _{1}\\{} & {} -\int ^{+\infty }_{0}\frac{e_{0}(\tau _{2})}{k_{1}(\tau _{2})} (\rho \sigma (t+\tau _{2})+d)k_{1}(t+\tau _{2})\text{ d }\tau _{2}\\= & {} e(t,0)-\int ^{+\infty }_{0}(\rho \sigma (b)+d)e(t,b)\text{ d }b. \end{aligned}$$

Similarly, we obtain

$$\begin{aligned} \begin{aligned} \frac{\text{ d }}{\text{ d }t}\int ^{+\infty }_{0}i(t,a)\text{ d }a=i(t,0) -\int ^{+\infty }_{0}(\theta (a)+d)i(t,a)\text{ d }a. \end{aligned} \end{aligned}$$

We deduce that N(t) satisfies the following equation

$$\begin{aligned} \begin{aligned} \frac{\text{ d }N(t)}{\text{ d }t}=\varLambda -dN(t). \end{aligned} \end{aligned}$$

Solving the above equation, we have $N(t)=\frac{\varLambda }{d}-\text{ e}^{-dt}(\frac{\varLambda }{d}-N_{0})$ and $\underset{t\rightarrow \infty }{\lim \sup }\;N(t)\le \frac{\varLambda }{d}$ for $t\in {\mathbb {R}}_{+}$, where $N_{0}$ represents the total population at time $t = 0$.

Through the fifth equation of System (2), we obtain

$$\begin{aligned} \frac{\text{ d }W(t)}{\text{ d }t}=\int ^{+\infty }_{0}\xi _{1}(a)i(t,a) \text{ d }a+\xi _{2}T(t)-cW(t)\le \frac{\varLambda ({\bar{\xi }}_{1}+\xi _{2})}{d}-cW(t). \end{aligned}$$

Solving the above equation, we have that $W(t)=\frac{\varLambda ({\bar{\xi }}_{1}+\xi _{2})}{dc}-\text{ e}^{-ct} \Big (\frac{\varLambda ({\bar{\xi }}_{1}+\xi _{2})}{dc}-W_{0}\Big )$ and $\underset{t\rightarrow \infty }{\lim \sup }\;W(t)\le \frac{\varLambda ({\bar{\xi }}_{1}+\xi _{2})}{dc}$ for $t\in {\mathbb {R}}_{+}$, where $W_{0}$ indicates the density of Mycobacterium TB at time $t=0$. This completes the proof. $\square$

Appendix B: Proof of Theorem 2

The characteristic equation corresponding to ${\mathcal {P}}^{0}$ is

$$\begin{aligned} \begin{aligned} G(\iota )&=\big (S^{0}+\eta V^{0}\big )\bigg \{{\mathcal {H}}_{2}(\iota ) +\frac{\beta _{2}{\mathcal {H}}_{3}(\iota )}{\iota +\gamma +d}+ \frac{\beta _{3}[(\iota +\gamma +d){\mathcal {H}}_{4}(\iota ) +\xi _{2}{\mathcal {H}}_{3}(\iota )]}{(\iota +c)(\iota +\gamma +d)}\bigg \}\\&\quad \big [q+\rho (1-q){\mathcal {H}}_{1}(\iota )\big ]-1. \end{aligned} \end{aligned}$$

When $\iota$ is real, we can acquire some basic properties of $G(\iota )$ as follows

$$\begin{aligned} \begin{aligned} G(0)={\mathcal {R}}_{0}-1,\;G'(\iota )<0,\;\underset{\iota \rightarrow - \infty }{\lim }G(\iota )=+\infty ,\;\underset{\iota \rightarrow +\infty }{\lim }G(\iota )=-1. \end{aligned} \end{aligned}$$

Hence, when ${\mathcal {R}}_{0}>1$, the characteristic equation $G(\iota )=0$ has a real positive root. Then, the disease-free equilibrium is unstable. When ${\mathcal {R}}_{0}<1$, the characteristic equation $G(\iota )=0$ does not have a solution with non-negative real part. Otherwise, $G(\iota )=0$ has at least one root $\iota _{0}=\alpha _{0}+i\beta _{0}$ satisfying $\alpha _{0}\ge 0$. Then, we have

$$\begin{aligned} 0=|G(\iota _{0})|\le {\mathcal {R}}_{0}-1, \end{aligned}$$

which contradicts with ${\mathcal {R}}_{0}<1$. Hence, when ${\mathcal {R}}_{0}<1$, the disease-free equilibrium is locally asymptotically stable. This completes the proof. $\square$

Appendix C: Proof of Theorem 3

For $t\ge 0$, let

$$\begin{aligned} \varPsi (t,x)=(S(t),V(t),T(t),R(t),W(t),{\tilde{e}}(t,\cdot ),{\tilde{i}}(t,\cdot )), \end{aligned}$$

and

$$\begin{aligned} \Theta (t,x)=(0,0,0,0,0,\varphi _{e}(t,\cdot ),\varphi _{i}(t,\cdot )), \end{aligned}$$

where

$$\begin{aligned} {\tilde{e}}(t,b)= & {} \left\{ \begin{array}{ll} e(t-b,0)k_{1}(b),&{}\quad 0\le b\le t,\\ 0,&{}\quad 0\le t\le b,\\ \end{array}\right. \quad {\tilde{i}}(t,a)=\left\{ \begin{array}{ll} i(t-a,0)k_{2}(a),&{}\quad 0\le a\le t,\\ 0,&{}\quad 0\le t\le a,\\ \end{array} \right. \\ \varphi _{e}(t,b)= & {} \left\{ \begin{array}{ll} 0,&{}\quad 0\le b\le t,\\ e_{0}(b-t)\frac{k_{1}(b)}{k_{1}(b-t)}, &{}\quad 0\le t\le b,\\ \end{array}\right. \quad \varphi _{i}(t,a)=\left\{ \begin{array}{ll} 0,&{}\quad 0\le a\le t,\\ i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)},&{}\quad 0\le t\le a,\\ \end{array} \right. \end{aligned}$$

for $x=(S(0),V(0),T(0),R(0),W(0),e_{0}(b),i_{0}(a))$. Clearly, we have $\varPhi (t,x) =\Theta (t,x) + \varPsi (t,x)$. Let ${\mathcal {B}}$ be a bounded subset of ${\mathcal {Y}}$, ${\mathcal {M}}$ is constants greater than $\max \Big \{N_{0},\frac{\varLambda }{d},W_{0},\frac{\varLambda ({\bar{\xi }}_{1}+\xi _{2})}{dc}\Big \}$, for each $x\in {\mathcal {B}}$. Hence, we can derive

$$\begin{aligned} \Vert \Theta (t,x)\Vert _{{\mathcal {Y}}}= & {} \int ^{+\infty }_{t}e_{0}(b-t) \frac{k_{1}(b)}{k_{1}(b-t)}\text{ d }b+ \int ^{+\infty }_{t}i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)}\text{ d }a\\= & {} \int ^{+\infty }_{0}e_{0}(\tau _{1})\frac{k_{1}(\tau _{1}+t)}{k_{1} (\tau _{1})}\text{ d }\tau _{1}+ \int ^{+\infty }_{0}i_{0}(\tau _{1})\frac{k_{2}(\tau _{1}+t)}{k_{2} (\tau _{1})}\text{ d }\tau _{1}\\= & {} \int ^{+\infty }_{0}e_{0}(\tau _{1})\text{ e}^{-\int ^{\tau _{1} +t}_{\tau _{1}}(\rho \sigma (s)+d)\text{ d }s}\text{ d }\tau _{1}+ \int ^{+\infty }_{0}i_{0}(\tau _{1})\text{ e}^{-\int ^{\tau _{1} +t}_{\tau _{1}}(\theta (s)+d)\text{ d }s}\text{ d }\tau _{1}\\\le & {} \text{ e}^{-dt}\bigg (\int ^{+\infty }_{0}e_{0}(\tau _{1}) \text{ d }\tau _{1}+\int ^{+\infty }_{0}i_{0}(\tau _{1})\text{ d } \tau _{1}\bigg )\le {\mathcal {M}}\text{ e}^{-dt}. \end{aligned}$$

This implies $\underset{t\rightarrow \infty }{\lim }\;{\textrm{diam}}\;\Theta (t, {\mathcal {B}})= 0$. In the following, we will show that $\varPsi (t,x)$ has a compact closure for each $t\ge 0$. We know that S(t), V(t), T(t), R(t), and W(t) remain in the compact set $[0,{\mathcal {M}}]$ for all $t\ge 0$. Thus, we only need to prove that ${\tilde{e}}(t,b)$ and ${\tilde{i}}(t,a)$ remain in a pre-compact subset of $L^{1}_{+}(0,+\infty )$, which is independent of $x\in {\mathcal {B}}$. According to

$$\begin{aligned} 0\le {\tilde{e}}(t,b)=\left\{ \begin{array}{ll} e(t-b,0)k_{1}(b),&{}\quad 0\le b\le t,\\ 0,&{}\quad 0\le t\le b,\\ \end{array} \right. \end{aligned}$$

and assumption (A2), it is easy to show that

$$\begin{aligned} 0\le {\tilde{e}}(t,b)\le (1-q)(1+\eta )({\bar{\beta }}_{1}+\beta _{2} +\beta _{3}){\mathcal {M}}^{2}\text{ e}^{-db}. \end{aligned}$$

Therefore, the conditions (i), (ii) and (iv) of Lemma 2 are satisfied. Next, we verify that condition (iii) of Lemma 2 is satisfied.

$$\begin{aligned} \begin{aligned} \int ^{+\infty }_{0}|{\tilde{e}}(t,b+h)-{\tilde{e}}(t,b)|\text{ d }b&=\int ^{t-h}_{0}|{\tilde{e}}(t,b+h)-{\tilde{e}}(t,b)|\text{ d }b +\int ^{t}_{t-h}|{\tilde{e}}(t,b)|\text{ d }b\\&\le \int ^{t-h}_{0}|e(t-b-h,0)||k_{1}(b+h)-k_{1}(b)|\text{ d }b\\&\quad +\int ^{t-h}_{0}|e(t-b-h,0)-e(t-b,0)||k_{1}(b)|\text{ d }b\\&\quad +(1-q)(1+\eta )({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}){\mathcal {M}}^{2}h, \end{aligned} \end{aligned}$$

where

$$\begin{aligned}{} & {} \int ^{t-h}_{0}|e(t-b-h,0)||k_{1}(b+h)-k_{1}(b)|\text{ d }b\\{} & {} \quad \le (1-q)(1+\eta )({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}){\mathcal {M}}^{2} \bigg (\int ^{t-h}_{0}k_{1}(b)\text{ d }b-\int ^{t-h}_{0}k_{1}(b+h)\text{ d }b\bigg )\\{} & {} \quad =(1-q)(1+\eta )({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}){\mathcal {M}}^{2} \bigg (\int ^{h}_{0}k_{1}(b)\text{ d }b-\int ^{h}_{t-h}k_{1}(b)\text{ d }b -\int ^{t}_{h}k_{1}(s)\text{ d }s\bigg )\\{} & {} \quad =(1-q)(1+\eta )({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}){\mathcal {M}}^{2} \bigg (\int ^{h}_{0}k_{1}(b)\text{ d }b-\int ^{t}_{t-h}k_{1}(s)\text{ d }s\bigg )\\{} & {} \quad \le (1-q)(1+\eta )({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}){\mathcal {M}}^{2}h. \end{aligned}$$

According to System (2), the following inequalities,

$$\begin{aligned}{} & {} \Big |\frac{\text{ d }S(t)}{\text{ d }t}\Big |\le \varLambda +\big [\tau +\delta +\alpha +d+({\bar{\beta }}_{1}+\beta _{2} +\beta _{3}){\mathcal {M}}\big ]{\mathcal {M}},\\{} & {} \Big |\frac{\text{ d }V(t)}{\text{ d }t}\Big |\le \big [\alpha +\eta ({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}){\mathcal {M}}+\tau +d\big ]{\mathcal {M}},\\{} & {} \Big |\frac{\text{ d }T(t)}{\text{ d }t}\Big |\le ({\bar{\theta }} +\gamma +d){\mathcal {M}},\\{} & {} \Big |\frac{\text{ d }R(t)}{\text{ d }t}\Big |\le (\gamma +\delta +d){\mathcal {M}},\\{} & {} \Big |\frac{\text{ d }W(t)}{\text{ d }t}\Big |\le ({\bar{\xi }}_{1}+\xi _{2}+c){\mathcal {M}}, \end{aligned}$$

can be obtained. Next, we prove that $\int ^{+\infty }_{0}\beta _{1}(a)i(t,a)\text{ d }a$ is Lipschitz continuous.

$$\begin{aligned}{} & {} \bigg |\int ^{+\infty }_{0}\beta _{1}(a)i(t+h,a)\text{ d }a-\int ^{+\infty }_{0} \beta _{1}(a)i(t,a)\text{ d }a\bigg |\\{} & {} \quad =\bigg |\int ^{h}_{0}\beta _{1}(a)i(t+h,a)\text{ d }a +\int ^{+\infty }_{h}\beta _{1}(a)i(t+h,a)\text{ d }a-\int ^{+\infty }_{0} \beta _{1}(a)i(t,a)\text{ d }a\bigg |\\{} & {} \quad =\bigg |\int ^{h}_{0}\beta _{1}(a)i(t+h-a,0)k_{2}(a)\text{ d }a +\int ^{+\infty }_{h}\beta _{1}(a)i(t+h,a)\text{ d }a-\int ^{+\infty }_{0} \beta _{1}(a)i(t,a)\text{ d }a\bigg |\\{} & {} \quad \le \Big [q(1+\eta )({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}) {\mathcal {M}}+\rho {\bar{\sigma }}\Big ]{\bar{\beta }}_{1}{\mathcal {M}}h\\{} & {} \qquad +\bigg |\int ^{+\infty }_{0}\beta _{1}(\tau _{1}+h)i(t+h, \tau _{1}+h)\text{ d }\tau _{1}-\int ^{+\infty }_{0}\beta _{1}(a)i(t,a)\text{ d }a\bigg |\\{} & {} \quad =\Big [q(1+\eta )({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}) {\mathcal {M}}+\rho {\bar{\sigma }}\Big ]{\bar{\beta }}_{1}{\mathcal {M}}h\\{} & {} \qquad +\bigg |\int ^{+\infty }_{0}\beta _{1}(\tau _{1}+h)i(t, \tau _{1})\frac{k_{2}(\tau _{1}+h)}{k_{2}(\tau _{1})}\text{ d } \tau _{1}-\int ^{+\infty }_{0}\beta _{1}(a)i(t,a)\text{ d }a\bigg |. \end{aligned}$$

According to assumption (A3), we note that

$$\begin{aligned}{} & {} \bigg |\int ^{+\infty }_{0}\beta _{1}(a+h)i(t,a)\frac{k_{2}(a+h)}{k_{2}(a)} \text{ d }a-\int ^{+\infty }_{0}\beta _{1}(a)i(t,a)\text{ d }a\bigg |\\{} & {} \quad =\bigg |\int ^{+\infty }_{0}\Big (\beta _{1}(a+h)\frac{k_{2}(a+h)}{k_{2}(a)} -\beta _{1}(a)\Big )i(t,a)\text{ d }a\bigg |\\{} & {} \quad =\bigg |\int ^{+\infty }_{0}\beta _{1}(a+h)i(t,a)\Big (\frac{k_{2}(a +h)}{k_{2}(a)}-1\Big )\text{ d }a\\{} & {} \qquad +\int ^{+\infty }_{0}(\beta _{1}(a+h) -\beta _{1}(a))i(t,a)\text{ d }a\bigg |\\{} & {} \quad =\bigg |\int ^{+\infty }_{0}\beta _{1}(a+h)i(t,a)\Big (\text{ e}^{-\int ^{a +h}_{a}(\theta (s)+d)\text{ d }s}-1\Big )\text{ d }a\\{} & {} \qquad +\int ^{+\infty }_{0} (\beta _{1}(a+h)-\beta _{1}(a))i(t,a)\text{ d }a\bigg |\\{} & {} \quad \le {\bar{\beta }}_{1}({\bar{\theta }}+d){\mathcal {M}}h+\bigg |\int ^{ +\infty }_{0}(\beta _{1}(a+h)-\beta _{1}(a))i(t,a)\text{ d }a\bigg |\\{} & {} \quad \le {\bar{\beta }}_{1}({\bar{\theta }}+d){\mathcal {M}}h+\int ^{ +\infty }_{0}\big |\beta _{1}(a+h)-\beta _{1}(a)\big |\big |i(t,a)\big |\text{ d }a\\{} & {} \quad \le \big [{\bar{\beta }}_{1}({\bar{\theta }}+d)+M_{\beta _{1}}\big ]{\mathcal {M}}h. \end{aligned}$$

Hence, we obtain

$$\begin{aligned}{} & {} \bigg |\int ^{+\infty }_{0}\beta _{1}(a)i(t+h,a)\text{ d }a -\int ^{+\infty }_{0}\beta _{1}(a)i(t,a)\text{ d }a\bigg |\\{} & {} \quad \le \Big \{\Big [q(1+\eta )({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}) {\mathcal {M}}+\rho {\bar{\sigma }}\Big ]{\bar{\beta }}_{1}+{\bar{\beta }}_{1} ({\bar{\theta }}+d)+M_{\beta _{1}}\Big \}{\mathcal {M}}h. \end{aligned}$$

According to the above inequality, we have

$$\begin{aligned}{} & {} \big |e(t-b-h,0)-e(t-b,0)\big |\\{} & {} \quad =(1-q)\big |\lambda (t-b-h)\big (S(t-b-h)+\eta V(t-b-h)\big )\\{} & {} \qquad -\lambda (t-b)\big (S(t-b)+\eta V(t-b)\big )\big |\\{} & {} \quad \le (1-q)\bigg (\Big |S(t-b-h)\int ^{+\infty }_{0}\beta _{1}(a)i (t-b-h,a)\text{ d }a\\{} & {} \qquad -S(t-b)\int ^{+\infty }_{0}\beta _{1}(a)i(t-b,a)\text{ d }a\Big |\\{} & {} \qquad +\beta _{2}\big |S(t-b-h)T(t-b-h)-S(t-b)T(t-b)\big |\\{} & {} \qquad +\beta _{3}\Big |S(t-b-h)W(t-b-h)-S(t-b)W(t-b)\Big |\\{} & {} \qquad +\eta \Big |V(t-b-h)\int ^{+\infty }_{0}\beta _{1}(a)i(t-b-h,a) \text{ d }a-V(t-b)\int ^{+\infty }_{0}\beta _{1}(a)i(t-b,a)\text{ d }a\Big |\\{} & {} \qquad +\eta \beta _{2}\big |V(t-b-h)T(t-b-h)-V(t-b)T(t-b)\big |\\{} & {} \qquad +\eta \beta _{3}\Big |V(t-b-h)W(t-b-h)-V(t-b)W(t-b)\Big |\bigg )\le \varUpsilon h, \end{aligned}$$

where

$$\begin{aligned} \varUpsilon= & {} (1-q){\mathcal {M}}^{2}\Big \{\Big [q(1+\eta )({\bar{\beta }}_{1} +\beta _{2}+\beta _{3}){\mathcal {M}}+\rho {\bar{\sigma }}\Big ]{\bar{\beta }}_{1} +{\bar{\beta }}_{1}({\bar{\theta }}+d)+M_{\beta _{1}}\Big \}\\{} & {} +(1-q){\bar{\beta }}_{1}{\mathcal {M}}\Big \{\varLambda +\big [\tau +\delta +\alpha +d+({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}){\mathcal {M}}\big ]{\mathcal {M}}\Big \}\\{} & {} +(1-q)\beta _{2}{\mathcal {M}}\Big \{\varLambda +\big [{\bar{\theta }}+\gamma +d+\tau +\delta +\alpha +d+({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}) {\mathcal {M}}\big ]{\mathcal {M}}\Big \}\\{} & {} +(1-q)\beta _{3}{\mathcal {M}}\bigg \{\varLambda +\big [{\bar{\xi }}_{1} +\xi _{2}+c+\tau +\delta +\alpha +d+({\bar{\beta }}_{1}+\beta _{2} +\beta _{3}){\mathcal {M}}\big ]{\mathcal {M}}\bigg \}\\{} & {} +(1-q)\eta {\mathcal {M}}^{2}\Big \{\Big [q(1+\eta )({\bar{\beta }}_{1} +\beta _{2}+\beta _{3}){\mathcal {M}}+\rho {\bar{\sigma }}\Big ]{\bar{\beta }}_{1} +{\bar{\beta }}_{1}({\bar{\theta }}+d)+M_{\beta _{1}}\Big \}\\{} & {} +(1-q)\eta {\bar{\beta }}_{1}{\mathcal {M}}^{2}\Big \{\alpha +\eta ({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}){\mathcal {M}}+\tau +d\Big \}\\{} & {} +(1-q)\eta \beta _{2}{\mathcal {M}}^{2}\big \{{\bar{\theta }} +\gamma +d+\alpha +\eta ({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}){\mathcal {M}}+\tau +d\big \}\\{} & {} +(1-q)\eta \beta _{3}{\mathcal {M}}^{2}\Big \{{\bar{\xi }}_{1} +\xi _{2}+c+\alpha +\eta ({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}){\mathcal {M}}+\tau +d\Big \}. \end{aligned}$$

Then, we obtain

$$\begin{aligned} \begin{aligned} \int ^{t-h}_{0}|e(t-b-h,0)-e(t-b,0)||k_{1}(b)|\text{ d }b\le \varUpsilon h\int ^{t-h}_{0}e^{-db}\text{ d }b\le \frac{\varUpsilon h}{d}. \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \left. \begin{aligned} \int ^{+\infty }_{0}|{\tilde{e}}(t,b+h)-{\tilde{e}}(t,b)|\text{ d }b \le \Big [2(1-q)(1+\eta )({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}) {\mathcal {M}}^{2}+\frac{\varUpsilon }{d}\Big ]h. \end{aligned} \right. \end{aligned}$$

We have verified that ${\tilde{e}}(t,b)$ satisfies the conditions of Lemma 2. In a similar way, ${\tilde{i}}(t,a)$ also satisfies the conditions of Lemma 2. As a result, ${\tilde{e}}(t,b)$ and ${\tilde{i}}(t,a)$ remain in pre-compact subsets ${\mathcal {A}}^{e}_{{\mathcal {M}}}$ and ${\mathcal {A}}^{i}_{{\mathcal {M}}}$ of $L^{1}_{+}(0,+\infty )$, respectively. Therefore, $\varPsi (t,{\mathcal {B}})\subseteq [0,{\mathcal {M}}]\times [0,{\mathcal {M}}]\times [0,{\mathcal {M}}]\times [0,{\mathcal {M}}]\times [0,{\mathcal {M}}]\times {\mathcal {A}}^{e}_{{\mathcal {M}}}\times {\mathcal {A}}^{i}_{{\mathcal {M}}}$, which has a compact closure in ${\mathcal {Y}}$. This implies that $\varPsi (t,{\mathcal {B}})$ has a compact closure, satisfying the second condition of Lemma 1. Therefore, we conclude that $\{\varPhi (t,\cdot )\}_{t\ge 0}$ is asymptotically smooth. This completes the proof. $\square$

Appendix D: Proof of Theorem 4

Let

$$\begin{aligned} J(t)=T(t)+W(t)+\int ^{+\infty }_{0}e(t,b)\text{ d }b +\int ^{+\infty }_{0}i(t,a)\text{ d }a. \end{aligned}$$

(29)

For any $\varPhi (0,x_{0})\in {\mathcal {D}}_{0}$, we have

$$\begin{aligned} \frac{\text{ d }J(t)}{\text{ d }t}= & {} -(\gamma +d)T(t)+\int ^{+\infty }_{0} \xi _{1}(a)i(t,a)\text{ d }a+\xi _{2}T(t)-cW(t)\\{} & {} -d\int ^{+\infty }_{0}e(t,b)\text{ d }b+\lambda (t)\big (S(t)+\eta V(t) \big )-d\int ^{+\infty }_{0}i(t,a)\text{ d }a\\\ge & {} -(\gamma +d)T(t)-cW(t)-d\int ^{+\infty }_{0}e(t,b)\text{ d }b -d\int ^{+\infty }_{0}i(t,a)\text{ d }a\\\ge & {} -{\bar{a}}J(t), \end{aligned}$$

where ${\bar{a}}=\max \{\gamma +d,c\}$. Then, we obtain $J(t)\ge J(0)\text{ e}^{-{\bar{a}}t}>0$. This implies that $\varPhi (t,{\mathcal {D}}_{0})\in {\mathcal {D}}_{0}$, i.e., ${\mathcal {D}}_{0}$ is positively invariant under the semiflow $\{\varPhi (t,\cdot )\}_{t\ge 0}$.

In addition, for any $\varPhi (0,x_{0})\in \partial {\mathcal {D}}_{0}$, we consider the following system

$$\begin{aligned}{} & {} \frac{\text{ d }T(t)}{\text{ d }t}=\int ^{+\infty }_{0}\theta (a)i(t,a) \text{ d }a-(\gamma +d)T(t),\nonumber \\{} & {} \frac{\text{ d }W(t)}{\text{ d }t}=\int ^{+\infty }_{0}\xi _{1}(a)i(t,a) \text{ d }a+\xi _{2}T(t)-cW(t),\nonumber \\{} & {} \frac{\partial e(t,b)}{\partial t}+\frac{\partial e(t,b)}{\partial b} =-(\rho \sigma (b)+d)e(t,b),\nonumber \\{} & {} \frac{\partial i(t,a)}{\partial t}+\frac{\partial i(t,a)}{\partial a} =-(\theta (a)+d)i(t,a),\\{} & {} e(t,0)=(1-q)\lambda (t)\big (S(t)+\eta V(t)\big ),\nonumber \\{} & {} i(t,0)=q\lambda (t)\big (S(t)+\eta V(t)\big )+\rho \int ^{+\infty }_{0} \sigma (b)e(t,b)\text{ d }b,\nonumber \\{} & {} T(0)=0,W(0)=0,e(0,b)=e_{0}(b),i(0,a)=i_{0}(a),\nonumber \end{aligned}$$

(30)

where $\lambda (t)$ is given by Eq. (1). Since $S(t)+\eta V(t)\le \max \Big \{N_{0},\frac{\varLambda }{d}\Big \}:=\aleph$, then we set up the following comparison system

$$\begin{aligned}{} & {} \frac{\text{ d }{\overline{T}}(t)}{\text{ d }t}=\int ^{+\infty }_{0} \theta (a){\overline{i}}(t,a)\text{ d }a-(\gamma +d){\overline{T}}(t),\nonumber \\{} & {} \frac{\text{ d }{\overline{W}}(t)}{\text{ d }t}=\int ^{+\infty }_{0} \xi _{1}(a){\overline{i}}(t,a)\text{ d }a+\xi _{2}{\overline{T}}(t) -c{\overline{W}}(t),\nonumber \\{} & {} \frac{\partial {\overline{e}}(t,b)}{\partial t}+\frac{\partial {\overline{e}}(t,b)}{\partial b}=-(\rho \sigma (b)+d){\overline{e}}(t,b),\nonumber \\{} & {} \frac{\partial {\overline{i}}(t,a)}{\partial t}+\frac{\partial {\overline{i}}(t,a)}{\partial a}=-(\theta (a)+d){\overline{i}}(t,a),\\{} & {} {\overline{e}}(t,0)=(1-q){\overline{\lambda }}(t)\aleph ,\nonumber \\{} & {} {\overline{i}}(t,0)=q{\overline{\lambda }}(t)\aleph +\rho \int ^{+\infty }_{0} \sigma (b){\overline{e}}(t,b)\text{ d }b,\nonumber \\{} & {} {\overline{T}}(0)=0,{\overline{W}}(0)=0,{\overline{e}}(0,b) =e_{0}(b),{\overline{i}}(0,a)=i_{0}(a),\nonumber \end{aligned}$$

(31)

where ${\overline{\lambda }}(t)=\int ^{+\infty }_{0}\beta _{1}(a){\overline{i}}(t,a)\text{ d }a+\beta _{2}{\overline{T}}(t)+\beta _{3}{{\overline{W}}(t)}$.

Integrating the equations for ${\overline{e}}(t,b)$ and ${\overline{i}}(t,a)$ in System (31) along the characteristic lines, $t-b=\text{ const }$ and $t-a=\text{ const }$, respectively, we obtain

$$\begin{aligned} {\overline{e}}(t,b)=\left\{ \begin{array}{ll} {\overline{e}}(t-b,0)k_{1}(b),&{}\quad 0\le b\le t,\\ e_{0}(b-t)\frac{k_{1}(b)}{k_{1}(b-t)},&{}\quad 0\le t\le b,\\ \end{array}\right. \quad {\overline{i}}(t,a)=\left\{ \begin{array}{ll} {\overline{i}}(t-a,0)k_{2}(a),&{}\quad 0\le a\le t,\\ i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)},&{}\quad 0\le t\le a.\\ \end{array} \right. \nonumber \\ \end{aligned}$$

(32)

Substituting Eq. (32) into System (31), we obtain

$$\begin{aligned}{} & {} \frac{\text{ d }{\overline{T}}(t)}{\text{ d }t} =\int ^{t}_{0}\theta (a){\overline{i}}(t-a,0)k_{2}(a)\text{ d }a +\int ^{+\infty }_{t}\theta (a)i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a -t)}\text{ d }a-(\gamma +d){\overline{T}}(t),\nonumber \\{} & {} \frac{\text{ d }{\overline{W}}(t)}{\text{ d }t} =\int ^{t}_{0}\xi _{1}(a){\overline{i}}(t-a,0)k_{2}(a)\text{ d }a +\int ^{+\infty }_{t}\xi _{1}(a)i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a -t)}\text{ d }a+\xi _{2}{\overline{T}}(t)-c{\overline{W}}(t),\nonumber \\{} & {} {\overline{T}}(0)=0,{\overline{W}}(0)=0. \end{aligned}$$

(33)

According to assumption (A2), one can obtain

$$\begin{aligned}{} & {} \int ^{+\infty }_{t}\theta (a)i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)} \text{ d }a\le {\bar{\theta }}\int ^{+\infty }_{0}i_{0}(a)\text{ d }a,\\{} & {} \int ^{+\infty }_{t}\xi _{1}(a)i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)} \text{ d }a\le {\bar{\xi }}_{1}\int ^{+\infty }_{0}i_{0}(a)\text{ d }a,\\{} & {} \int ^{+\infty }_{t}\sigma (b)e_{0}(b-t)\frac{k_{1}(b)}{k_{1}(b-t)} \text{ d }b\le {\bar{\sigma }}\int ^{+\infty }_{0}e_{0}(b)\text{ d }b,\\{} & {} \int ^{+\infty }_{t}\beta _{1}(a)i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)} \text{ d }a\le {\bar{\beta }}_{1}\int ^{+\infty }_{0}i_{0}(a)\text{ d }a. \end{aligned}$$

For any $\varPhi (0,x_{0})\in \partial {\mathcal {D}}_{0}$, we have

$$\begin{aligned}{} & {} \int ^{+\infty }_{t}\theta (a)i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)}\text{ d }a=0, \quad \int ^{+\infty }_{t}\xi _{1}(a)i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)}\text{ d }a=0,\\{} & {} \int ^{+\infty }_{t}\sigma (b)e_{0}(b-t)\frac{k_{1}(b)}{k_{1}(b-t)}\text{ d }b=0, \quad \int ^{+\infty }_{t}\beta _{1}(a)i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)}\text{ d }a=0. \end{aligned}$$

Let

$$\begin{aligned}{} & {} \overline{L_{e}}(t)={\overline{e}}(t,0)=(1-q){\overline{\lambda }}(t)\aleph ,\\{} & {} \overline{L_{i}}(t)={\overline{i}}(t,0)=q{\overline{\lambda }}(t)\aleph +\rho \int ^{+\infty }_{0}\sigma (b){\overline{e}}(t,b)\text{ d }b, \end{aligned}$$

we have

$$\begin{aligned} \overline{L_{e}}(t)= & {} (1-q)\bigg [\int ^{t}_{0}\beta _{1}(a)\overline{L_{i}}(t-a) k_{2}(a)\text{ d }a+\beta _{2}{\overline{T}}(t)+\beta _{3}{{\overline{W}}(t)}\bigg ]\aleph ,\\ \overline{L_{i}}(t)= & {} q\bigg [\int ^{t}_{0}\beta _{1}(a)\overline{L_{i}}(t-a)k_{2} (a)\text{ d }a+\beta _{2}{\overline{T}}(t)+\beta _{3}{{\overline{W}}(t)}\bigg ] \aleph \\{} & {} +\rho \int ^{t}_{0}\sigma (b)\overline{L_{e}}(t-b)k_{1}(b)\text{ d }b. \end{aligned}$$

Then, System (33) can be rewritten as

$$\begin{aligned} \overline{L_{e}}(t)= & {} (1-q)\bigg [\int ^{t}_{0}\beta _{1}(a)\overline{L_{i}} (t-a)k_{2}(a)\text{ d }a+\beta _{2}{\overline{T}}(t)+\beta _{3}{{\overline{W}}(t)} \bigg ]\aleph ,\nonumber \\ \overline{L_{i}}(t)= & {} q\bigg [\int ^{t}_{0}\beta _{1}(a)\overline{L_{i}} (t-a)k_{2}(a)\text{ d }a+\beta _{2}{\overline{T}}(t)+\beta _{3}{{\overline{W}}(t)} \bigg ]\aleph \nonumber \\{} & {} +\rho \int ^{t}_{0}\sigma (b)\overline{L_{e}}(t-b)k_{1}(b)\text{ d }b,\nonumber \\ \frac{\text{ d }{\overline{T}}(t)}{\text{ d }t}= & {} \int ^{t}_{0}\theta (a) \overline{L_{i}}(t-a)k_{2}(a)\text{ d }a-(\gamma +d){\overline{T}}(t),\\ \frac{\text{ d }{\overline{W}}(t)}{\text{ d }t}= & {} \int ^{t}_{0}\xi _{1}(a) \overline{L_{i}}(t-a)k_{2}(a)\text{ d }a+\xi _{2}{\overline{T}}(t) -c{\overline{W}}(t),\nonumber \\ \overline{L_{e}}(0)= & {} 0,\overline{L_{i}}(0)=0,{\overline{T}}(0)=0, {\overline{W}}(0)=0.\nonumber \end{aligned}$$

(34)

It is easy to show that System (34) has a unique solution $\overline{L_{e}}(t)=0$, $\overline{L_{i}}(t)=0$, ${\overline{T}}(t)=0$, and ${\overline{W}}(t)=0$.

From System (31) and Eq. (32), we obtain that ${\overline{e}}(t,{\overline{t}})=0$ and ${\overline{i}}(t,{\overline{t}})=0$ for $0\le {\overline{t}}\le t$. Hence,

$$\begin{aligned} \Vert {\overline{e}}(t,b)\Vert _{L^{1}_{+}}=\int ^{+\infty }_{t}e_{0}(b-t) \frac{k_{1}(b)}{k_{1}(b-t)}\text{ d }b\le \Vert e_{0}({\bar{t}})\Vert _{L^{1}_{+}}=0. \end{aligned}$$

Similarly, we can also obtain $\Vert {\overline{i}}(t,a)\Vert _{L^{1}_{+}}=0$. Since $T(t)\le {\overline{T}}(t)$, $W(t)\le {\overline{W}}(t)$, $e(t,b)\le {\overline{e}}(t,b)$, and $i(t,a)\le {\overline{i}}(t,a)$, we have

$$\begin{aligned} T(t)=0,\; W(t)=0,\; \Vert e(t,b)\Vert _{L^{1}_{+}}=0,\; \Vert i(t,a)\Vert _{L^{1}_{+}}=0. \end{aligned}$$

This implies that $\partial {\mathcal {D}}_{0}$ is positively invariant under the semiflow $\{\varPhi (t,\cdot )\}_{t\ge 0}$.

Next, we prove that the disease-free equilibrium ${\mathcal {P}}^{0}$ of System (2) is globally asymptotically stable for the semiflow $\{\varPhi (t,\cdot )\}_{t\ge 0}$ restricted to $\partial {\mathcal {D}}_{0}$. Obviously, System (2) can be represented as

$$\begin{aligned}{} & {} \frac{\text{ d }S(t)}{\text{ d }t}=\varLambda +\tau V(t)+\delta R(t)-(\alpha +d)S(t),\nonumber \\{} & {} \frac{\text{ d }V(t)}{\text{ d }t}=\alpha S(t)-(\tau +d)V(t),\\{} & {} \frac{\text{ d }R(t)}{\text{ d }t}=-(\delta +d)R(t).\nonumber \end{aligned}$$

(35)

Obviously, the unique equilibrium $(S^{0},V^{0},0)$ of System (35) is locally asymptotically stable. By solving System (35), we obtain

$$\begin{aligned} S(t)= & {} -\frac{C_{3}\tau }{\alpha +\tau }\text{ e}^{-(d+\delta )t} +\frac{\varLambda (\tau +d)}{d(\alpha +\tau +d)}+\frac{\alpha \delta C_{3}}{(\alpha +\tau )(\alpha -\delta +\tau )}\text{ e}^{-(d+\delta )t}\\{} & {} -C_{1}\text{ e}^{-(\alpha +\tau +d)t}-\frac{\tau C_{1}}{\alpha }\text{ e}^{-dt},\\ V(t)= & {} C_{2}\text{ e}^{-dt}+C_{1}\text{ e}^{-(\alpha +\tau +d)t} -\frac{\alpha \delta }{(\alpha +\tau )(\alpha -\delta +\tau )}\text{ e}^{-(d+\delta )t}\\{} & {} -\frac{\alpha C_{3}}{\alpha +\tau }\text{ e}^{-(d+\delta )t} +\frac{\varLambda \alpha }{d(\alpha +\tau +d)},\\ R(t)= & {} C_{3}\text{ e}^{-(d+\delta )t}, \end{aligned}$$

where $C_{1}, C_{2}, C_{3}$ are constants. Thus, $\lim _{t\rightarrow \infty } S(t)=\frac{\varLambda (\tau +d)}{d(\alpha +\tau +d)}=S^{0}$, $\lim _{t\rightarrow \infty } V(t)=\frac{\varLambda \alpha }{d(\alpha +\tau +d)}=V^{0}$, and $\lim _{t\rightarrow \infty } R(t)=0$. Then, the disease-free equilibrium ${\mathcal {P}}^{0}$ is globally asymptotically stable restricted to $\partial {\mathcal {D}}_{0}$. This completes the proof. $\square$

Appendix E: Proof of Theorem 5

We assume by contradiction that there exists $x_{0}\in W^{s}({\mathcal {P}}^{0})\cap {\mathcal {D}}_{0}$. In this case, one can find a sequence $\{x_{n}\}\in {\mathcal {D}}_{0}$ such that

$$\begin{aligned} \big \Vert \varPhi (t,x_{n})-{\mathcal {P}}^{0}\big \Vert _{{\mathcal {Y}}}<\frac{1}{n},\;t\ge 0. \end{aligned}$$

Here, $\varPhi (t,x_{n}):=(S_{n}(t),V_{n}(t),T_{n}(t),R_{n}(t),W_{n}(t),e_{n}(t,\cdot ),i_{n}(t,\cdot ))$.

Now, we choose $n>0$ large enough to ensure $S^{0}-\frac{1}{n}>0$ and $V^{0}-\frac{1}{n}>0$. For the above given $n>0$, there exists a $t_{1}>0$ such that for $t>t_{1}$,

$$\begin{aligned} S^{0}-\frac{1}{n}<S_{n}(t)<S^{0}+\frac{1}{n},\;V^{0} -\frac{1}{n}<V_{n}(t)<V^{0}+\frac{1}{n}. \end{aligned}$$

Then, System (2) can be written as

$$\begin{aligned}{} & {} \frac{\text{ d }T(t)}{\text{ d }t}\ge \int ^{+\infty }_{0} \theta (a)i(t,a)\text{ d }a-(\gamma +d)T(t),\\{} & {} \frac{\text{ d }W(t)}{\text{ d }t}\ge \int ^{+\infty }_{0} \xi _{1}(a)i(t,a)\text{ d }a+\xi _{2}T(t)-cW(t),\\{} & {} \frac{\partial e(t,b)}{\partial t}+\frac{\partial e(t,b)}{\partial b}\ge -(\rho \sigma (b)+d)e(t,b),\\{} & {} \frac{\partial i(t,a)}{\partial t}+\frac{\partial i(t,a)}{\partial a}\ge -(\theta (a)+d)i(t,a),\\{} & {} e(t,0)\ge (1-q)\lambda (t)\bigg (S^{0}-\frac{1}{n}+\eta (V^{0} -\frac{1}{n})\bigg ),\\{} & {} i(t,0)\ge q\lambda (t)\bigg (S^{0}-\frac{1}{n}+\eta (V^{0}-\frac{1}{n})\bigg )+\rho \int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b,\\{} & {} T(0)=T_{0},W(0)=W_{0},e(0,b)=e_{0}(b),i(0,a)=i_{0}(a), \end{aligned}$$

where $\lambda (t)$ is given by Eq. (1). We consider the following auxiliary system

$$\begin{aligned}{} & {} \frac{\text{ d }{\underline{T}}(t)}{\text{ d }t}=\int ^{+\infty }_{0} \theta (a){\underline{i}}(t,a)\text{ d }a-(\gamma +d){\underline{T}}(t),\nonumber \\{} & {} \frac{\text{ d }{\underline{W}}(t)}{\text{ d }t}=\int ^{+\infty }_{0} \xi _{1}(a){\underline{i}}(t,a)\text{ d }a+\xi _{2}{\underline{T}}(t) -c{\underline{W}}(t),\nonumber \\{} & {} \frac{\partial {\underline{e}}(t,b)}{\partial t}+\frac{\partial {\underline{e}}(t,b)}{\partial b}=-(\rho \sigma (b)+d){\underline{e}}(t,b),\nonumber \\{} & {} \frac{\partial {\underline{i}}(t,a)}{\partial t}+\frac{\partial {\underline{i}}(t,a)}{\partial a}=-(\theta (a)+d){\underline{i}}(t,a),\\{} & {} {\underline{e}}(t,0)=(1-q){\underline{\lambda }}(t)\bigg (S^{0} -\frac{1}{n}+\eta (V^{0}-\frac{1}{n})\bigg ),\nonumber \\{} & {} {\underline{i}}(t,0)= q{\underline{\lambda }}(t)\bigg (S^{0} -\frac{1}{n}+\eta (V^{0}-\frac{1}{n})\bigg )+\rho \int ^{+\infty }_{0} \sigma (b){\underline{e}}(t,b)\text{ d }b,\nonumber \\{} & {} {\underline{T}}(0)=T_{0},{\underline{W}}(0)=W_{0}, {\underline{e}}(0,b)=e_{0}(b),{\underline{i}}(0,a)=i_{0}(a),\nonumber \end{aligned}$$

(36)

where ${\underline{\lambda }}(t)=\int ^{+\infty }_{0}\beta _{1}(a){\underline{i}}(t,a)\text{ d }a+\beta _{2}{\underline{T}}(t)+\beta _{3}{{\underline{W}}(t)}$. By Volterra formulation (5), we have

$$\begin{aligned} {\underline{e}}(t,b)=\left\{ \begin{aligned} {\underline{e}}(t-b,0)k_{1}(b),&\quad 0\le b\le t,\\ e_{0}(b-t)\frac{k_{1}(b)}{k_{1}(b-t)},&\quad 0\le t\le b,\\ \end{aligned}\right. \quad {\underline{i}}(t,a)=\left\{ \begin{aligned} {\underline{i}}(t-a,0)k_{2}(a),&\quad 0\le a\le t,\\ i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)},&\quad 0\le t\le a.\\ \end{aligned} \right. \nonumber \\ \end{aligned}$$

(37)

By direct calculation, the characteristic equation of System (36) at ${\mathcal {P}}^{0}$ is

$$\begin{aligned} \begin{aligned}&\bigg (S^{0}-\frac{1}{n}+\eta (V^{0}-\frac{1}{n})\bigg )\\&\quad \bigg \{{\mathcal {H}}_{2}(\iota )+\frac{\beta _{2}{\mathcal {H}}_{3}(\iota )}{\iota +\gamma +d}+ \frac{\beta _{3}[(\iota +\gamma +d){\mathcal {H}}_{4}(\iota ) +\xi _{2}{\mathcal {H}}_{3}(\iota )]}{(\iota +c)(\iota +\gamma +d)}\bigg \}\big [q+\rho (1-q){\mathcal {H}}_{1}(\iota )\big ]=1, \end{aligned} \end{aligned}$$

where ${\mathcal {H}}_{1}(\iota )$, ${\mathcal {H}}_{2}(\iota )$, ${\mathcal {H}}_{3}(\iota )$, and ${\mathcal {H}}_{4}(\iota )$ are given by Eq. (23). Let

$$\begin{aligned} \begin{aligned} {\underline{f}}(\iota )&=\bigg (S^{0}-\frac{1}{n}+\eta (V^{0} -\frac{1}{n})\bigg )\bigg \{{\mathcal {H}}_{2}(\iota ) +\frac{\beta _{2}{\mathcal {H}}_{3}(\iota )}{\iota +\gamma +d}+ \frac{\beta _{3}[(\iota +\gamma +d){\mathcal {H}}_{4}(\iota ) +\xi _{2}{\mathcal {H}}_{3}(\iota )]}{(\iota +c)(\iota +\gamma +d)}\bigg \}\\&\qquad \big [q+\rho (1-q){\mathcal {H}}_{1}(\iota )\big ]. \end{aligned} \end{aligned}$$

Clearly, we have ${\underline{f}}'(\iota )<0$ and $\underset{\iota \rightarrow +\infty }{\lim }{\underline{f}}(\iota )=0$. Furthermore, we also have ${\underline{f}}(0)>1$ for sufficiently large n. Hence, when ${\mathcal {R}}_{0}>1$, the characteristic equation of System (36) has a real positive root. This implies that the solution $({\underline{T}}(t),{\underline{W}}(t),{\underline{e}}(t,\cdot ),{\underline{i}}(t,\cdot ))$ of System (36) is unbounded. Since $T(t)\ge {\underline{T}}(t)$, $W(t)\ge {\underline{W}}(t)$, $e(t,\cdot )\ge {\underline{e}}(t,\cdot )$, and $i(t,\cdot )\ge {\underline{i}}(t,\cdot )$, by comparison principle, we obtain that $(T(t),W(t),e(t,\cdot ),i(t,\cdot ))$ is unbounded, which contradicts with Proposition 1. Therefore, $W^{s}({\mathcal {P}}^{0})\cap {\mathcal {D}}_{0}=\emptyset$. By Theorem 4.2 in Hale and Waltman (1989), we conclude that semiflow $\{\varPhi (t,\cdot )\}_{t\ge 0}$ generated by System (2) is uniformly persistent. This completes the proof. $\square$

Appendix F: Proof of Theorem 6

Define a Lyapunov function

$$\begin{aligned} \begin{aligned} {\mathcal {L}}(t)={\mathcal {L}}_{s}(t)+{\mathcal {L}}_{v}(t) +{\mathcal {L}}_{e}(t)+{\mathcal {L}}_{i}(t)+{\mathcal {L}}_{t}(t)+{\mathcal {L}}_{w}(t) \end{aligned} \end{aligned}$$

(38)

where

$$\begin{aligned} {\mathcal {L}}_{s}(t)= & {} \frac{1}{2S^{0}}(S(t)-S^{0})^{2},\;\;{\mathcal {L}}_{v}(t) =\frac{1}{2V^{0}}(V(t)-V^{0})^{2},\\ {\mathcal {L}}_{e}(t)= & {} {\mathcal {F}}_{b}\int ^{+\infty }_{0}{\mathcal {F}}_{e}(b) e(t,b)\text{ d }b,\;\;{\mathcal {L}}_{i}(t)=\big (S^{0}+\eta V^{0}\big ) \int ^{+\infty }_{0}{\mathcal {F}}_{i}(a)i(t,a)\text{ d }a,\\ {\mathcal {L}}_{t}(t)= & {} \big (S^{0}+\eta V^{0}\big )\Bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\Bigg )T(t),\;\;{\mathcal {L}}_{w}(t)=\big (S^{0}+\eta V^{0}\big )\frac{\beta _{3}}{c}W(t). \end{aligned}$$

The nonnegative function ${\mathcal {L}}(t)$ is defined with respect to the disease-free equilibrium ${\mathcal {P}}^{0}$, which is a global minimum. We choose

$$\begin{aligned} {\mathcal {F}}_{b}= & {} \big (S^{0}+\eta V^{0}\big )\Bigg ({\mathcal {K}}_{2} +\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d} +\frac{\beta _{3}{\mathcal {K}}_{4}}{c}+\frac{\beta _{3}\xi _{2} {\mathcal {K}}_{3}}{c(\gamma +d)}\Bigg ),\\ {\mathcal {F}}_{e}(b)= & {} \int ^{+\infty }_{b}\rho \sigma (\upsilon ) \text{ e}^{-\int ^{\upsilon }_{b}(\rho \sigma (\varrho )+d)\text{ d }\varrho }\text{ d }\upsilon ,\\ {\mathcal {F}}_{i}(a)= & {} \int ^{+\infty }_{a}\Bigg (\beta _{1}(\upsilon ) +\frac{\beta _{2}\theta (\upsilon )}{\gamma +d}+ \frac{\beta _{3}\xi _{1}(\upsilon )}{c}+\frac{\beta _{3}\xi _{2} \theta (\upsilon )}{c(\gamma +d)}\Bigg )\text{ e}^{-\int ^{\upsilon }_{a} (\theta (\varrho )+d)\text{ d }\varrho }\text{ d }\upsilon . \end{aligned}$$

By direct calculations, one obtains that

$$\begin{aligned} {\mathcal {F}}_{e}(0)= & {} \int ^{+\infty }_{0}\rho \sigma (\upsilon ) \text{ e}^{-\int ^{\upsilon }_{0}(\rho \sigma (\varrho )+d)\text{ d }\varrho } \text{ d }\upsilon =\rho {\mathcal {K}}_{1},\\ {\mathcal {F}}_{i}(0)= & {} \int ^{+\infty }_{0}\Bigg (\beta _{1}(\upsilon ) +\frac{\beta _{2}\theta (\upsilon )}{\gamma +d}+ \frac{\beta _{3}\xi _{1}(\upsilon )}{c}+\frac{\beta _{3}\xi _{2} \theta (\upsilon )}{c(\gamma +d)}\Bigg )\text{ e}^{-\int ^{\upsilon }_{0} (\theta (\varrho )+d)\text{ d }\varrho }\text{ d }\upsilon \\= & {} {\mathcal {K}}_{2}+\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d} +\frac{\beta _{3}{\mathcal {K}}_{4}}{c}+\frac{\beta _{3}\xi _{2} {\mathcal {K}}_{3}}{c(\gamma +d)},\\ \frac{\text{ d }{\mathcal {F}}_{e}(b)}{\text{ d }b}= & {} -\rho \sigma (b) +(\rho \sigma (b)+d){\mathcal {F}}_{e}(b),\\ \frac{\text{ d }{\mathcal {F}}_{i}(a)}{\text{ d }a}= & {} -\Bigg (\beta _{1}(a) +\frac{\beta _{2}\theta (a)}{\gamma +d}+ \frac{\beta _{3}\xi _{1}(a)}{c}+\frac{\beta _{3}\xi _{2}\theta (a)}{c(\gamma +d)}\Bigg )+(\theta (a)+d){\mathcal {F}}_{i}(a). \end{aligned}$$

Calculating the derivative of ${\mathcal {L}}_{s}(t)$, ${\mathcal {L}}_{v}(t)$, ${\mathcal {L}}_{e}(t)$, ${\mathcal {L}}_{i}(t)$, ${\mathcal {L}}_{t}(t)$, and ${\mathcal {L}}_{w}(t)$ along solutions of System (2), respectively. We can obtain

$$\begin{aligned} \frac{\text{ d }{\mathcal {L}}_{s}(t)}{\text{ d }t}= & {} \frac{1}{S^{0}}(S(t) -S^{0})\frac{\text{ d }S(t)}{\text{ d }t}=\frac{1}{S^{0}}(S(t)-S^{0}) \Big (\varLambda +\tau V(t)-\lambda (t)S(t)-(\alpha +d)S(t)\Big )\\= & {} \frac{1}{S^{0}}(S(t)-S^{0})\Big [-(\alpha +d)(S(t)-S^{0})+\tau (V(t) -V^{0})-\lambda (t)(S(t)-S^{0})-\lambda (t)S^{0}\Big ]\\= & {} -\frac{\alpha +d}{S^{0}}(S(t)-S^{0})^{2}+\frac{\tau }{S^{0}}(S(t) -S^{0})(V(t)-V^{0})\\{} & {} -\frac{1}{S^{0}}\lambda (t)(S(t)-S^{0})^{2}-\lambda (t)S(t)+\lambda (t)S^{0}, \end{aligned}$$

where $\lambda (t)$ is given by Eq. (1).

$$\begin{aligned} \frac{\text{ d }{\mathcal {L}}_{v}(t)}{\text{ d }t}= & {} \frac{1}{V^{0}}(V(t) -V^{0})\frac{\text{ d }V(t)}{\text{ d }t} =\frac{1}{V^{0}}(V(t)-V^{0})\big (\alpha S(t)-\eta \lambda (t)V(t)-(\tau +d)V(t)\big )\\= & {} \frac{1}{V^{0}}(V(t)-V^{0})\Big [\alpha (S(t)-S^{0}) -(\tau +d)(V(t)-V^{0})\\{} & {} -\eta \lambda (t)(V(t)-V^{0})-\eta \lambda (t)V^{0}\Big ]\\= & {} \frac{\alpha }{V^{0}}(S(t)-S^{0})(V(t)-V^{0})-\frac{\tau +d}{V^{0}}(V(t) -V^{0})^{2}-\frac{\eta }{V^{0}}\lambda (t)(V(t)-V^{0})^{2}\\{} & {} -\eta \lambda (t)V(t)+\eta \lambda (t)V^{0},\\ \frac{\text{ d }{\mathcal {L}}_{e}(t)}{\text{ d }t}= & {} {\mathcal {F}}_{b} \int ^{+\infty }_{0}{\mathcal {F}}_{e}(b)\frac{\text{ d }e(t,b)}{\text{ d }t}\text{ d }b=-{\mathcal {F}}_{b}\int ^{+\infty }_{0} {\mathcal {F}}_{e}(b)\bigg [(\rho \sigma (b)+d)e(t,b)+\frac{\partial e(t,b)}{\partial b}\bigg ]\text{ d }b\\= & {} {\mathcal {F}}_{b}\bigg (-\int ^{+\infty }_{0}{\mathcal {F}}_{e}(b) (\rho \sigma (b)+d)e(t,b)\text{ d }b-\int ^{+\infty }_{0}{\mathcal {F}}_{e}(b)\text{ d }e(t,b)\bigg )\\= & {} {\mathcal {F}}_{b}\bigg (-\int ^{+\infty }_{0}{\mathcal {F}}_{e}(b) (\rho \sigma (b)+d)e(t,b)\text{ d }b-{\mathcal {F}}_{e}(b)e(t,b) \Big |^{+\infty }_{0}+\int ^{+\infty }_{0}e(t,b)\text{ d }{\mathcal {F}}_{e}(b)\bigg )\\= & {} {\mathcal {F}}_{b}\bigg (-\int ^{+\infty }_{0}{\mathcal {F}}_{e}(b) (\rho \sigma (b)+d)e(t,b)\text{ d }b+{\mathcal {F}}_{e}(0)e(t,0)\\{} & {} +\int ^{+\infty }_{0}e(t,b)\big [-\rho \sigma (b)+(\rho \sigma (b) +d){\mathcal {F}}_{e}(b)\big ]\text{ d }b\bigg )\\= & {} {\mathcal {F}}_{b}\bigg ({\mathcal {F}}_{e}(0)e(t,0)-\int ^{ +\infty }_{0}\rho \sigma (b)e(t,b)\text{ d }b\bigg )\\= & {} {\mathcal {F}}_{b}\bigg (\rho {\mathcal {K}}_{1}e(t,0)-\rho \int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b\bigg )\\= & {} {\mathcal {F}}_{b}\bigg (\rho {\mathcal {K}}_{1}(1-q)(S(t) +\eta V(t))\lambda (t)-\rho \int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b\bigg ),\\ \end{aligned}$$

$$\begin{aligned}= & {} \big (S^{0}+\eta V^{0}\big )\Bigg ({\mathcal {K}}_{2} +\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d} +\frac{\beta _{3}{\mathcal {K}}_{4}}{c}+\frac{\beta _{3}\xi _{2} {\mathcal {K}}_{3}}{c(\gamma +d)}\Bigg )\rho {\mathcal {K}}_{1}(1-q)(S(t)+\eta V(t))\lambda (t)\\{} & {} -\big (S^{0}+\eta V^{0}\big )\Bigg ({\mathcal {K}}_{2} +\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d} +\frac{\beta _{3}{\mathcal {K}}_{4}}{c}+\frac{\beta _{3}\xi _{2}{\mathcal {K}}_{3}}{c(\gamma +d)}\Bigg ) \rho \int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b,\\ \frac{\text{ d }{\mathcal {L}}_{i}(t)}{\text{ d }t}= & {} \big (S^{0} +\eta V^{0}\big )\int ^{+\infty }_{0}{\mathcal {F}}_{i}(a) \frac{\text{ d }i(t,a)}{\text{ d }t}\text{ d }a\\= & {} -\big (S^{0}+\eta V^{0}\big )\int ^{+\infty }_{0}{\mathcal {F}}_{i}(a) \bigg [(\theta (a)+d)i(t,a)+\frac{\partial i(t,a)}{\partial a}\bigg ]\text{ d }a\\= & {} \big (S^{0}+\eta V^{0}\big )\bigg (-\int ^{+\infty }_{0} {\mathcal {F}}_{i}(a)(\theta (a)+d)i(t,a)\text{ d }a-\int ^{+\infty }_{0} {\mathcal {F}}_{i}(a)\text{ d }i(t,a)\bigg )\\= & {} \big (S^{0}+\eta V^{0}\big )\bigg (-\int ^{+\infty }_{0} {\mathcal {F}}_{i}(a)(\theta (a)+d)i(t,a)\text{ d }b-{\mathcal {F}}_{i} (a)i(t,a)\Big |^{+\infty }_{0}\\{} & {} +\int ^{+\infty }_{0}i(t,a)\text{ d }{\mathcal {F}}_{i}(a)\bigg )\\= & {} \big (S^{0}+\eta V^{0}\big )\Bigg \{-\int ^{+\infty }_{0} {\mathcal {F}}_{i}(a)(\theta (a)+d)i(t,a)\text{ d }b+{\mathcal {F}}_{i}(0)i(t,0)\\{} & {} +\int ^{+\infty }_{0}i(t,a)\Bigg [-\Bigg (\beta _{1}(a) +\frac{\beta _{2}\theta (a)}{\gamma +d}+ \frac{\beta _{3}\xi _{1}(a)}{c}+\frac{\beta _{3}\xi _{2} \theta (a)}{c(\gamma +d)}\Bigg )\\{} & {} +(\theta (a)+d){\mathcal {F}}_{i}(a)\Bigg ]\text{ d }a\Bigg \}\\= & {} \big (S^{0}+\eta V^{0}\big )\bigg ({\mathcal {F}}_{i}(0)i(t,0) -\int ^{+\infty }_{0}\beta _{1}(a)i(t,a)\text{ d }a- \frac{\beta _{2}}{\gamma +d}\int ^{+\infty }_{0}\theta (a)i(t,a)\text{ d }a\\{} & {} -\frac{\beta _{3}}{c}\int ^{+\infty }_{0}\xi _{1}(a)i(t,a) \text{ d }a-\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\int ^{+\infty }_{0}\theta (a)i(t,a)\text{ d }a\bigg )\\ \end{aligned}$$

$$\begin{aligned}= & {} \big (S^{0}+\eta V^{0}\big )\Bigg ({\mathcal {K}}_{2} +\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d} +\frac{\beta _{3}{\mathcal {K}}_{4}}{c}+\frac{\beta _{3}\xi _{2} {\mathcal {K}}_{3}}{c(\gamma +d)}\Bigg )q(S(t)+\eta V(t))\lambda (t)\\{} & {} +\big (S^{0}+\eta V^{0}\big )\Bigg ({\mathcal {K}}_{2} +\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d} +\frac{\beta _{3}{\mathcal {K}}_{4}}{c}+\frac{\beta _{3}\xi _{2} {\mathcal {K}}_{3}}{c(\gamma +d)}\Bigg )\rho \int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b\\{} & {} -\big (S^{0}+\eta V^{0}\big )\bigg (\int ^{+\infty }_{0} \beta _{1}(a)i(t,a)\text{ d }a+ \frac{\beta _{2}}{\gamma +d}\int ^{+\infty }_{0}\theta (a)i(t,a)\text{ d }a\\{} & {} +\frac{\beta _{3}}{c}\int ^{+\infty }_{0}\xi _{1}(a)i(t,a) \text{ d }a+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\int ^{+\infty }_{0} \theta (a)i(t,a)\text{ d }a\bigg ),\\ \frac{\text{ d }{\mathcal {L}}_{t}(t)}{\text{ d }t}= & {} \big (S^{0}+\eta V^{0}\big )\Bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3} \xi _{2}}{c(\gamma +d)}\Bigg )\frac{\text{ d }T(t)}{\text{ d }t}\\= & {} \big (S^{0}+\eta V^{0}\big )\Bigg (\frac{\beta _{2}}{\gamma +d} +\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\Bigg )\bigg (\int ^{+\infty }_{0} \theta (a)i(t,a)\text{ d }a-(\gamma +d)T(t)\bigg )\\= & {} \big (S^{0}+\eta V^{0}\big )\Bigg (\frac{\beta _{2}}{\gamma +d} +\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\Bigg )\int ^{+\infty }_{0} \theta (a)i(t,a)\text{ d }a\\{} & {} -\big (S^{0}+\eta V^{0}\big )\Bigg (\beta _{2} T(t)+\frac{\beta _{3}\xi _{2}}{c}T(t)\Bigg ),\\ \frac{\text{ d }{\mathcal {L}}_{w}(t)}{\text{ d }t}= & {} \big (S^{0}+\eta V^{0} \big )\frac{\beta _{3}}{c}\frac{\text{ d }W(t)}{\text{ d }t}\\= & {} \big (S^{0}+\eta V^{0}\big )\frac{\beta _{3}}{c} \bigg (\int ^{+\infty }_{0}\xi _{1}(a)i(t,a)\text{ d }a+\xi _{2}T(t)-cW(t)\bigg )\\= & {} \big (S^{0}+\eta V^{0}\big )\frac{\beta _{3}}{c} \int ^{+\infty }_{0}\xi _{1}(a)i(t,a)\text{ d }a+\big (S^{0} +\eta V^{0}\big )\frac{\beta _{3}\xi _{2}}{c}T(t)-\big (S^{0}+\eta V^{0}\big ){\beta _{3}}W(t). \end{aligned}$$

Therefore,

$$\begin{aligned} \frac{\text{ d }{\mathcal {L}}(t)}{\text{ d }t}= & {} -\frac{\alpha +d}{S^{0}}(S(t)-S^{0})^{2}+\bigg (\frac{\tau }{S^{0}} +\frac{\alpha }{V^{0}}\bigg )(S(t)-S^{0})(V(t)-V^{0})\\{} & {} -\frac{\tau +d}{V^{0}}(V(t)-V^{0})^{2}-\frac{1}{S^{0}}\lambda (t) (S(t)-S^{0})^{2}-\frac{\eta }{V^{0}}\lambda (t)(V(t)-V^{0})^{2}\\{} & {} -\lambda (t)(S(t)+\eta V(t))+\lambda (t)(S^{0}+\eta V^{0} )+{\mathcal {R}}_{0}\lambda (t)(S(t)+\eta V(t))-\lambda (t)(S^{0}+\eta V^{0}), \end{aligned}$$

where $\lambda (t)$ is given by Eq. (1). To confirm that $\frac{\text{ d }{\mathcal {L}}(t)}{\text{ d }t}$ is a negative semidefinite function, we obtain

$$\begin{aligned}{} & {} -\frac{\alpha +d}{S^{0}}(S(t)-S^{0})^{2}+\bigg (\frac{\tau }{S^{0}} +\frac{\alpha }{V^{0}}\bigg )(S(t)-S^{0})(V(t)-V^{0})-\frac{\tau +d}{V^{0}}(V(t)-V^{0})^{2}\nonumber \\{} & {} \quad =-\frac{\alpha +d}{S^{0}}\bigg [(S(t)-S^{0})^{2}-\frac{\tau V^{0} +\alpha S^{0}}{(\alpha +d)V^{0}}(S(t)-S^{0})(V(t)-V^{0})\nonumber \\{} & {} \qquad +\frac{(\tau +d)S^{0}}{(\alpha +d)V^{0}}(V(t)-V^{0})^{2}\bigg ]\nonumber \\{} & {} \quad =-\frac{\alpha +d}{S^{0}}\Bigg \{(S(t)-S^{0})^{2}-\frac{\tau V^{0} +\alpha S^{0}}{(\alpha +d)V^{0}}(S(t)-S^{0})(V(t)-V^{0})\nonumber \\{} & {} \qquad +\frac{(\tau V^{0}+\alpha S^{0})^{2}}{4(\alpha +d)^{2}(V^{0} )^{2}}(V(t)-V^{0})^{2}-\frac{(\tau V^{0}+\alpha S^{0})^{2}}{4 (\alpha +d)^{2}(V^{0})^{2}}(V(t)-V^{0})^{2}\nonumber \\{} & {} \qquad +\frac{(\tau +d)S^{0}}{(\alpha +d)V^{0}}(V(t)-V^{0})^{2}\Bigg \}\nonumber \\{} & {} \quad =-\frac{\alpha +d}{S^{0}}\Bigg \{\bigg [(S(t)-S^{0})^{2} -\frac{\tau V^{0}+\alpha S^{0}}{2(\alpha +d)V^{0}}(V(t)-V^{0})\bigg ]^{2}\nonumber \\{} & {} \qquad +\frac{4(\tau +d)(\alpha +d)S^{0}V^{0}-(\tau V^{0} +\alpha S^{0})^{2}}{4(\alpha +d)^{2}(V^{0})^{2}}(V(t)-V^{0})^{2}\Bigg \}. \end{aligned}$$

(39)

Substituting $S^{0}=\frac{\tau +d}{\alpha }V^{0}$ into Eq. (39), we have

$$\begin{aligned}{} & {} -\frac{\alpha +d}{S^{0}}\bigg \{\bigg [(S(t)-S^{0})^{2}-\frac{\tau V^{0} +\alpha S^{0}}{2(\alpha +d)V^{0}}(V(t)-V^{0})\bigg ]^{2}\\{} & {} \quad +\frac{4(\tau +d)(\alpha +d)S^{0}V^{0}-(\tau V^{0} +\alpha S^{0})^{2}}{4(\alpha +d)^{2}(V^{0})^{2}}(V(t)-V^{0})^{2}\bigg \}\\{} & {} \quad =-\frac{\alpha +d}{S^{0}}\bigg \{\bigg [(S(t)-S^{0})^{2} -\frac{\tau V^{0}+\alpha S^{0}}{2(\alpha +d)V^{0}}(V(t)-V^{0})\bigg ]^{2}\\{} & {} \qquad +\frac{\alpha d(4\tau +3d)+4d(\tau +d)^{2}}{4 \alpha (\alpha +d)^{2}}(V(t)-V^{0})^{2}\bigg \}\le 0. \end{aligned}$$

Hence, we obtain

$$\begin{aligned} \frac{\text{ d }{\mathcal {L}}(t)}{\text{ d }t}= & {} -\frac{\alpha +d}{S^{0}} \bigg \{\bigg [(S(t)-S^{0})^{2}-\frac{\tau V^{0}+\alpha S^{0}}{2( \alpha +d)V^{0}}(V(t)-V^{0})\bigg ]^{2}\\{} & {} +\frac{\alpha d(4\tau +3d) +4d(\tau +d)^{2}}{4\alpha (\alpha +d)^{2}}(V(t)-V^{0})^{2}\bigg \}\\{} & {} -\frac{1}{S^{0}}\lambda (t)(S(t)-S^{0})^{2}-\frac{\eta }{V^{0}} \lambda (t)(V(t)-V^{0})^{2}+({\mathcal {R}}_{0}-1)(S(t)+\eta V(t))\lambda (t), \end{aligned}$$

where $\lambda (t)$ is given by Eq. (1). Notice that if ${\mathcal {R}}_{0} \le 1$, then $\frac{\text{ d }{\mathcal {L}}(t)}{\text{ d }t}\le 0$, and the equality holds only for $S(t)=S^0$, $V(t)=V^0$, $e(t,b)=0$, $i(t,a)=0$, $T(t)=0$, $R(t)=0$, and $W(t)=0$. LaSalle’s Invariance Principle (LaSalle 1960) implies that the bounded solutions of System (2) converges to the largest compact invariant set of $\big \{(S(t),V(t),T(t),R(t),W(t),e(t,b),i(t,a))\in {\mathcal {D}}:\;{\text{ d }{\mathcal {L}}(t)}/{\text{ d }t}=0\big \}$. Since the disease-free equilibrium ${\mathcal {P}}^{0}$ is the only invariant set of System (2) contained entirely in $\big \{(S(t),V(t),T(t),R(t),W(t),e(t,b),i(t,a))\in {\mathcal {D}}:\;{\text{ d }{\mathcal {L}}(t)}/{\text{ d }t}=0\big \}$. Hence, the disease-free equilibrium ${\mathcal {P}}^{0}$ is globally attractive. By Theorem 2, we obtain that the disease-free equilibrium ${\mathcal {P}}^{0}$ is globally asymptotically stable when ${\mathcal {R}}_{0}<1$, and the disease-free equilibrium ${\mathcal {P}}^{0}$ is globally attractive when ${\mathcal {R}}_{0}=1$. This completes the proof. $\square$

Appendix G: Proof of Theorem 7

Let ${\textbf{p}}(x)=x-1-\ln x$, note that ${\textbf{p}}(x)$ is non-negative and continuous in $(0,+\infty )$ with a unique root at $x = 1$. Define a Lyapunov function

$$\begin{aligned} \begin{aligned} {\mathcal {G}}(t)={\mathcal {G}}_{s}(t)+{\mathcal {G}}_{v}(t)+ {\mathcal {G}}_{e}(t)+{\mathcal {G}}_{i}(t)+{\mathcal {G}}_{t}(t) +{\mathcal {G}}_{w}(t), \end{aligned} \end{aligned}$$

(40)

where

$$\begin{aligned} {\mathcal {G}}_{s}(t)= & {} S^{*}{\textbf{p}}\bigg (\frac{S(t)}{S^{*}}\bigg ), \;\;{\mathcal {G}}_{v}(t)=V^{*}{\textbf{p}}\bigg (\frac{V(t)}{V^{*}}\bigg ),\\ {\mathcal {G}}_{e}(t)= & {} \big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a} \int ^{+\infty }_{0}{\mathcal {F}}_{e}(b)e^{*}(b){\textbf{p}} \bigg (\frac{e(t,b)}{e^{*}(b)}\bigg )\text{ d }b,\\ {\mathcal {G}}_{i}(t)= & {} \big (S^{*}+\eta V^{*}\big )\int ^{+\infty }_{0} {\mathcal {F}}_{i}(a)i^{*}(a){\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)} \bigg )\text{ d }a,\\ {\mathcal {G}}_{t}(t)= & {} \big (S^{*}+\eta V^{*}\big ) \Bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\Bigg )T^{*}{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg ),\\ {\mathcal {G}}_{w}(t)= & {} \big (S^{*}+\eta V^{*}\big ) \frac{\beta _{3}}{c}W^{*}{\textbf{p}}\bigg (\frac{W(t)}{W^{*}}\bigg ). \end{aligned}$$

The nonnegative function ${\mathcal {G}}(t)$ is defined with respect to the endemic equilibrium ${\mathcal {P}}^{*}$, which is a global minimum. We choose

$$\begin{aligned} {\mathcal {F}}_{a}= & {} {\mathcal {K}}_{2}+\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d} +\frac{\beta _{3}{\mathcal {K}}_{4}}{c}+\frac{\beta _{3}\xi _{2}{\mathcal {K}}_{3}}{c(\gamma +d)},\\ {\mathcal {F}}_{e}(b)= & {} \int ^{+\infty }_{b}\rho \sigma (\upsilon )\text{ e}^{-\int ^{\upsilon }_{b}(\rho \sigma (\varrho )+d)\text{ d }\varrho }\text{ d }\upsilon ,\\ {\mathcal {F}}_{i}(a)= & {} \int ^{+\infty }_{a}\Bigg (\beta _{1}(\upsilon )+\frac{\beta _{2}\theta (\upsilon )}{\gamma +d}+ \frac{\beta _{3}\xi _{1}(\upsilon )}{c}+\frac{\beta _{3}\xi _{2}\theta (\upsilon )}{c(\gamma +d)}\Bigg )\text{ e}^{-\int ^{\upsilon }_{a}(\theta (\varrho )+d)\text{ d }\varrho }\text{ d }\upsilon . \end{aligned}$$

Calculating the derivative of ${\mathcal {G}}_{s}(t)$, ${\mathcal {G}}_{v}(t)$, ${\mathcal {G}}_{e}(t)$, ${\mathcal {G}}_{i}(t)$, ${\mathcal {G}}_{t}(t)$, and ${\mathcal {G}}_{w}(t)$ along solutions of System (2), respectively, we can obtain

$$\begin{aligned} \frac{\text{ d }{\mathcal {G}}_{s}(t)}{\text{ d }t}= & {} \bigg (1-\frac{S^{*}}{S(t)}\bigg )\frac{\text{ d }S(t)}{\text{ d }t}\nonumber \\= & {} \varLambda \bigg (2-\frac{S(t)}{S^{*}}-\frac{S^{*}}{S(t)}\bigg )+\tau \bigg (V(t)-\frac{V(t)S^{*}}{S(t)}-\frac{V^{*}S(t)}{S^{*}}+V^{*}\bigg )\nonumber \\{} & {} -\int ^{+\infty }_{0}\beta _{1}(a)\Big (S(t)i(t,a)-S^{*}i(t,a)-S(t)i^{*}(a)+S^{*}i^{*}(a)\Big )\text{ d }a\nonumber \\{} & {} -\beta _{2}\big (T(t)S(t)-T(t)S^{*}-T^{*}S(t)+T^{*}S^{*}\big )\nonumber \\{} & {} -\beta _{3}\big (W(t)S(t)-W(t)S^{*}-W^{*}S(t)+W^{*}S^{*}\big ).\end{aligned}$$

(41)

$$\begin{aligned} \frac{\text{ d }{\mathcal {G}}_{v}(t)}{\text{ d }t}= & {} \bigg (1-\frac{V^{*}}{V(t)}\bigg )\frac{\text{ d }V(t)}{\text{ d }t}\nonumber =\alpha \bigg (S(t)-\frac{S(t)V^{*}}{V(t)}-\frac{S^{*}V(t)}{V^{*}}+S^{*}\bigg )\nonumber \\{} & {} -\eta \int ^{+\infty }_{0}\beta _{1}(a)\Big (V(t)i(t,a)-V^{*}i(t,a)-V(t)i^{*}(a)+V^{*}i^{*}(a)\Big )\text{ d }a\nonumber \\{} & {} -\eta \beta _{2}\big (T(t)V(t)-T(t)V^{*}-T^{*}V(t)+T^{*}V^{*}\big )\nonumber \\{} & {} -\eta \beta _{3}\big (W(t)V(t)-W(t)V^{*}-W^{*}V(t)+W^{*}V^{*}\big ). \end{aligned}$$

(42)

We note that

$$\begin{aligned}{} & {} \frac{\partial }{\partial b}{\textbf{p}}\bigg (\frac{e(t,b)}{e^{*}(b)}\bigg ) =\frac{1}{e^{*}(b)}\bigg (1-\frac{e^{*}(b)}{e(t,b)}\bigg )\bigg (\frac{\partial e(t,b)}{\partial b}+(\rho \sigma (b)+d)e(t,b)\bigg ),\\{} & {} \frac{\partial }{\partial a}{\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg ) =\frac{1}{i^{*}(a)}\bigg (1-\frac{i^{*}(a)}{i(t,a)}\bigg )\bigg (\frac{\partial i(t,a)}{\partial a}+(\theta (a)+d)i(t,a)\bigg ). \end{aligned}$$

Thus, we obtain

$$\begin{aligned} \frac{\text{ d }{\mathcal {G}}_{e}(t)}{\text{ d }t}= & {} \big (S^{*}+\eta V^{*}\big ) {\mathcal {F}}_{a}\int ^{+\infty }_{0}{\mathcal {F}}_{e}(b)\bigg (1 -\frac{e^{*}(b)}{e(t,b)}\bigg )\frac{\partial e(t,b)}{\partial t}\text{ d }b\\= & {} -\big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\int ^{+\infty }_{0} {\mathcal {F}}_{e}(b)\bigg (1-\frac{e^{*}(b)}{e(t,b)}\bigg ) \bigg (\frac{\partial e(t,b)}{\partial b}+(\rho \sigma (b)+d)e(t,b)\bigg )\text{ d }b\\= & {} -\big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\int ^{+\infty }_{0} {\mathcal {F}}_{e}(b)e^{*}(b)\frac{\partial }{\partial b}{\textbf{p}} \bigg (\frac{e(t,b)}{e^{*}(b)}\bigg )\text{ d }b\\= & {} \big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\bigg [{\mathcal {F}}_{e} (0)e^{*}(0){\textbf{p}}\bigg (\frac{e(t,0)}{e^{*}(0)}\bigg ) -\rho \int ^{+\infty }_{0}\sigma (b)e^{*}(b){\textbf{p}}\bigg (\frac{e(t, b)}{e^{*}(b)}\bigg )\text{ d }b\bigg ]\\= & {} \big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\rho {\mathcal {K}}_{1} \bigg [(1-q)(S(t)+\eta V(t))\bigg (\int ^{+\infty }_{0}\beta _{1}(a)i(t,a) \text{ d }a+\beta _{2}T(t)\\{} & {} +\beta _{3}W(t)\bigg )-(1-q)(S^{*}+\eta V^{*})\bigg (\int ^{+\infty }_{0} \beta _{1}(a)i^{*}(a)\text{ d }a+\beta _{2}T^{*}+\beta _{3}W^{*}\bigg )\\{} & {} -(1-q)(S^{*}+\eta V^{*})\bigg (\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a) \text{ d }a+\beta _{2}T^{*}+\beta _{3}W^{*}\bigg )\ln \bigg (\frac{e(t,0)}{e^{*}(0)}\bigg )\bigg ]\\{} & {} -\big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\rho \int ^{+\infty }_{0} \sigma (b)e^{*}(b){\textbf{p}}\bigg (\frac{e(t,b)}{e^{*}(b)}\bigg )\text{ d }b.\\ \frac{\text{ d }{\mathcal {G}}_{i}(t)}{\text{ d }t}= & {} \big (S^{*}+\eta V^{*}\big ) \int ^{+\infty }_{0}{\mathcal {F}}_{i}(a)\bigg (1-\frac{i^{*}(a)}{i(t,a)} \bigg )\frac{\partial i(t,a)}{\partial t}\text{ d }a\\= & {} -\big (S^{*}+\eta V^{*}\big )\int ^{+\infty }_{0}{\mathcal {F}}_{i}(a) \bigg (1-\frac{i^{*}(a)}{i(t,a)}\bigg )\bigg (\frac{\partial i(t,a)}{\partial a}+(\theta (a)+d)i(t,a)\bigg )\text{ d }a\\ \end{aligned}$$

$$\begin{aligned}= & {} -\big (S^{*}+\eta V^{*}\big )\int ^{+\infty }_{0}{\mathcal {F}}_{i} (a)i^{*}(a)\frac{\partial }{\partial a}{\textbf{p}}\bigg (\frac{i(t, a)}{i^{*}(a)}\bigg )\text{ d }a\\= & {} \big (S^{*}+\eta V^{*}\big )\bigg [{\mathcal {F}}_{i}(0)i^{*}(0) {\textbf{p}}\bigg (\frac{i(t,0)}{i^{*}(0)}\bigg ) -\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a){\textbf{p}}\bigg (\frac{i(t, a)}{i^{*}(a)}\bigg )\text{ d }a\\{} & {} -\bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\bigg )\int ^{+\infty }_{0}\theta (a)i^{*}(a){\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a\\{} & {} -\frac{\beta _{3}}{c}\int ^{+\infty }_{0} \xi _{1}(a)i^{*}(a){\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a\bigg ]\\= & {} \big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\bigg \{q(S(t)+\eta V(t))\bigg (\int ^{+\infty }_{0}\beta _{1}(a)i(t,a)\text{ d }a+\beta _{2}T(t) +\beta _{3}W(t)\bigg )\\{} & {} +\rho \int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b-\bigg [q(S^{*} +\eta V^{*})\bigg (\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a)\text{ d }a+\beta _{2}T^{*}+\beta _{3}W^{*}\bigg )\\{} & {} +\rho \int ^{+\infty }_{0}\sigma (b)e^{*}(b)\text{ d }b\bigg ]-\bigg [q(S^{*}+\eta V^{*})\bigg (\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a)\text{ d }a+\beta _{2}T^{*}+\beta _{3}W^{*}\bigg )\\{} & {} +\rho \int ^{+\infty }_{0}\sigma (b)e^{*}(b)\text{ d }b\bigg ]\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\bigg \}\\{} & {} -\big (S^{*}+\eta V^{*}\big )\bigg [\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a){\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a\\{} & {} +\bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\bigg )\int ^{+\infty }_{0}\theta (a)i^{*}(a){\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a\\{} & {} +\frac{\beta _{3}}{c}\int ^{+\infty }_{0}\xi _{1}(a)i^{*}(a){\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a\bigg ],\\ \frac{\text{ d }{\mathcal {G}}_{t}(t)}{\text{ d }t}= & {} \big (S^{*}+\eta V^{*}\big )\Bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\Bigg )\bigg (1-\frac{T^{*}}{T(t)}\bigg )\frac{\text{ d }T(t)}{\text{ d }t}\\= & {} \big (S^{*}+\eta V^{*}\big )\Bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\Bigg )\int ^{+\infty }_{0}\theta (a)i^{*}(a)\\{} & {} \bigg [\frac{i(t,a)}{i^{*}(a)}-\frac{T(t)}{T^{*}}-\frac{T^{*}i(t,a)}{T(t)i^{*}(a)}+1\bigg ]\text{ d }a\\= & {} \big (S^{*}+\eta V^{*}\big )\Bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\Bigg )\int ^{+\infty }_{0}\theta (a)i^{*}(a)\\{} & {} \bigg [{\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )-{\textbf{p}}\bigg (\frac{T^{*}i(t,a)}{T(t)i^{*}(a)}\bigg )\bigg ]\text{ d }a\\ \end{aligned}$$

$$\begin{aligned}{} & {} -\big (S^{*}+\eta V^{*}\big )\beta _{2}T^{*}{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg )-\big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}\xi _{2}}{c}T^{*}{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg ),\\ \frac{\text{ d }{\mathcal {G}}_{w}(t)}{\text{ d }t}= & {} \big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}}{c}\bigg (1-\frac{W^{*}}{W(t)}\bigg )\frac{\text{ d }W(t)}{\text{ d }t}\\= & {} \big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}}{c}\int ^{+\infty }_{0}\xi _{1}(a)i^{*}(a) \bigg [\frac{i(t,a)}{i^{*}(a)}-\frac{W(t)}{W^{*}}-\frac{W^{*}i(t,a)}{W(t)i^{*}(a)}+1\bigg ]\text{ d }a\\{} & {} +\big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}\xi _{2}}{c}\bigg [\frac{T(t)}{T^{*}}-\frac{W(t)}{W^{*}}-\frac{W^{*}T(t)}{W(t)T^{*}}+1\bigg ]\\= & {} \big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}}{c}\int ^{+\infty }_{0}\xi _{1}(a)i^{*}(a) \bigg [{\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )-{\textbf{p}}\bigg (\frac{W^{*}i(t,a)}{W(t)i^{*}(a)}\bigg )\bigg ]\text{ d }a\\{} & {} +\big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}\xi _{2}}{c}T^{*}\bigg [{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg )-{\textbf{p}}\bigg (\frac{W^{*}T(t)}{W(t)T^{*}}\bigg )\bigg ]-\big (S^{*}+\eta V^{*}\big )\beta _{3}W^{*}{\textbf{p}}\bigg (\frac{W(t)}{W^{*}}\bigg ). \end{aligned}$$

From the first two equations of System (2) and Eq. (16), we obtain

$$\begin{aligned}{} & {} \big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}[q+\rho (1-q){\mathcal {K}}_{1}]=1,\\{} & {} \varLambda =(S^{*}+\eta V^{*})\bigg (\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a)\text{ d }a+\beta _{2}T^{*}+\beta _{3}W^{*}\bigg )+dS^{*}+dV^{*},\\{} & {} \alpha =\frac{\eta V^{*}\Big (\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a)\text{ d }a+\beta _{2}T^{*}+\beta _{3}W^{*}\Big )+(\tau +d)V^{*}}{S^{*}}. \end{aligned}$$

Substituting the expressions of $\varLambda$ and $\alpha$ into Eqs. (41) and (42), respectively, we have

$$\begin{aligned} \frac{\text{ d }{\mathcal {G}}(t)}{\text{ d }t}= & {} \frac{\text{ d }{\mathcal {G}}_{s}(t)}{\text{ d }t}+\frac{\text{ d }{\mathcal {G}}_{v}(t)}{\text{ d }t} +\frac{\text{ d }{\mathcal {G}}_{e}(t)}{\text{ d }t}+\frac{\text{ d } {\mathcal {G}}_{i}(t)}{\text{ d }t} +\frac{\text{ d }{\mathcal {G}}_{t}(t)}{\text{ d }t}+\frac{\text{ d } {\mathcal {G}}_{w}(t)}{\text{ d }t}\\= & {} \tau V^{*}\bigg (2-\frac{S^{*}V(t)}{S(t)V^{*}}-\frac{S(t)V^{*}}{S^{*}V(t)}\bigg )+d V^{*}\bigg (3-\frac{S^{*}}{S(t)}-\frac{V(t)}{V^{*}} -\frac{S(t)V^{*}}{S^{*}V(t)}\bigg )\\{} & {} +dS^{*}\bigg (2-\frac{S(t)}{S^{*}}-\frac{S^{*}}{S(t)}\bigg )+(S^{*} +\eta V^{*})\bigg (\int ^{+\infty }_{0}\beta _{1}(a)i(t,a)\text{ d }a +\beta _{2}T(t)+\beta _{3}W(t)\bigg )\\{} & {} -\bigg (\frac{S^{*}S^{*}}{S(t)}+\eta \frac{S^{*}V^{*}}{S(t)}\bigg ) \bigg (\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a)\text{ d }a+\beta _{2}T^{*}+\beta _{3}W^{*}\bigg )\\{} & {} +\eta \bigg (V^{*}-\frac{S(t)V^{*}V^{*}}{S^{*}V(t)}\bigg ) \bigg (\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a)\text{ d }a+\beta _{2}T^{*}+\beta _{3}W^{*}\bigg )\\{} & {} -(S^{*}+\eta V^{*})\bigg [{\mathcal {F}}_{a}\rho {\mathcal {K}}_{1}(1 -q)\ln \bigg (\frac{e(t,0)}{e^{*}(0)}\bigg )+{\mathcal {F}}_{a}q\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\bigg ]\\{} & {} \times (S^{*}+\eta V^{*})\bigg (\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a) \text{ d }a+\beta _{2}T^{*}+\beta _{3}W^{*}\bigg )\\{} & {} -\big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\rho \int ^{+\infty }_{0} \sigma (b)e^{*}(b){\textbf{p}}\bigg (\frac{e(t,b)}{e^{*}(b)}\bigg )\text{ d }b +\big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\rho \\{} & {} \times \bigg [\int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b -\int ^{+\infty }_{0}\sigma (b)e^{*}(b)\text{ d }b -\int ^{+\infty }_{0}\sigma (b)e^{*}(b)\text{ d }b\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\bigg ]\\{} & {} -\big (S^{*}+\eta V^{*}\big )\bigg [\int ^{+\infty }_{0} \beta _{1}(a)i^{*}(a){\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a +\frac{\beta _{3}}{c}\int ^{+\infty }_{0}\xi _{1}(a)i^{*}(a) {\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a\\{} & {} +\bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\bigg )\int ^{+\infty }_{0}\theta (a)i^{*}(a){\textbf{p}} \bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a\bigg ]\\{} & {} +\big (S^{*}+\eta V^{*}\big )\Bigg (\frac{\beta _{2}}{\gamma +d} +\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\Bigg )\int ^{+\infty }_{0}\theta (a)i^{*}(a)\\{} & {} \bigg [{\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg ) -{\textbf{p}}\bigg (\frac{T^{*}i(t,a)}{T(t)i^{*}(a)}\bigg )\bigg ]\text{ d }a\\{} & {} -\big (S^{*}+\eta V^{*}\big )\beta _{2}T^{*}{\textbf{p}} \bigg (\frac{T(t)}{T^{*}}\bigg )-\big (S^{*}+\eta V^{*}\big ) \frac{\beta _{3}\xi _{2}}{c}T^{*}{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg )\\{} & {} +\big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}}{c}\int ^{+\infty }_{0}\xi _{1}(a)i^{*}(a) \bigg [{\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )-{\textbf{p}} \bigg (\frac{W^{*}i(t,a)}{W(t)i^{*}(a)}\bigg )\bigg ]\text{ d }a\\{} & {} +\big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}\xi _{2}}{c}T^{*} \bigg [{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg )-{\textbf{p}} \bigg (\frac{W^{*}T(t)}{W(t)T^{*}}\bigg )\bigg ]-\big (S^{*}+\eta V^{*}\big ) \beta _{3}W^{*}{\textbf{p}}\bigg (\frac{W(t)}{W^{*}}\bigg ). \end{aligned}$$

For simplicity, we let

$$\begin{aligned} \frac{\text{ d }{\mathcal {G}}(t)}{\text{ d }t}= & {} \frac{\text{ d }{\mathcal {G}}_{s}(t )}{\text{ d }t}+\frac{\text{ d }{\mathcal {G}}_{v}(t)}{\text{ d }t}+ \frac{\text{ d }{\mathcal {G}}_{e}(t)}{\text{ d }t}+\frac{\text{ d }{\mathcal {G} }_{i}(t)}{\text{ d }t}+\frac{\text{ d }{\mathcal {G}}_{t}(t)}{\text{ d }t} +\frac{\text{ d }{\mathcal {G}}_{w}(t)}{\text{ d }t}\\= & {} {\mathcal {G}}_{1}+{\mathcal {G}}_{2}+{\mathcal {G}}_{3}+{\mathcal {G}}_{4} +{\mathcal {G}}_{5}+{\mathcal {G}}_{6}, \end{aligned}$$

where

$$\begin{aligned} {\mathcal {G}}_{1}= & {} \tau V^{*}\bigg (2-\frac{S^{*}V(t)}{S(t)V^{*}} -\frac{S(t)V^{*}}{S^{*}V(t)}\bigg )+dV^{*}\bigg (3-\frac{S^{*}}{S(t)} -\frac{V(t)}{V^{*}}-\frac{S(t)V^{*}}{S^{*}V(t)}\bigg )\\{} & {} +dS^{*}\bigg (2-\frac{S(t)}{S^{*}}-\frac{S^{*}}{S(t)}\bigg )\le 0,\\ {\mathcal {G}}_{2}= & {} (S^{*}+\eta V^{*}){\mathcal {F}}_{a}q \Bigg \{\int ^{+\infty }_{0}\beta _{1}(a)S^{*}i^{*}(a)\bigg [\frac{i(t,a)}{i^{*}(a)} -\frac{S^{*}}{S(t)}-\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\bigg ]\text{ d }a\\{} & {} +\beta _{2}S^{*}T^{*}\bigg [\frac{T(t)}{T^{*}} -\frac{S^{*}}{S(t)}-\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\bigg ] +\beta _{3}S^{*}W^{*}\bigg [\frac{W(t)}{W^{*}} -\frac{S^{*}}{S(t)}-\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\bigg ]\\{} & {} +\eta \int ^{+\infty }_{0}\beta _{1}(a)V^{*}i^{*}(a)\bigg [\frac{i(t,a)}{i^{*}(a)} -\frac{V^{*}}{V(t)}-\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\bigg ]\text{ d }a\\{} & {} +\eta \beta _{2}V^{*}T^{*}\bigg [\frac{T(t)}{T^{*}} -\frac{V^{*}}{V(t)}-\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\bigg ] +\eta \beta _{3}V^{*}W^{*}\bigg [\frac{W(t)}{W^{*}} -\frac{V^{*}}{V(t)}-\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\bigg ]\Bigg \}\\= & {} (S^{*}+\eta V^{*}){\mathcal {F}}_{a}q\Bigg \{\int ^{+\infty }_{0} \beta _{1}(a)S^{*}i^{*}(a)\bigg [{\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg ) -{\textbf{p}}\bigg (\frac{S^{*}}{S(t)}\bigg )\\{} & {} -{\textbf{p}}\bigg (\frac{S(t)i(t,a)i^{*}(0)}{S^{*}i^{*}(a)i(t,0)}\bigg )\bigg ]\text{ d }a\\{} & {} +\beta _{2}S^{*}T^{*}\bigg [{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg ) -{\textbf{p}}\bigg (\frac{S^{*}}{S(t)}\bigg )-{\textbf{p}} \bigg (\frac{S(t)T(t)i^{*}(0)}{S^{*}T^{*}i(t,0)}\bigg )\bigg ]\\ \end{aligned}$$

$$\begin{aligned}{} & {} +\beta _{3}S^{*}W^{*}\bigg [{\textbf{p}}\bigg (\frac{W(t)}{W^{*}}\bigg ) -{\textbf{p}}\bigg (\frac{S^{*}}{S(t)}\bigg )-{\textbf{p}} \bigg (\frac{S(t)W(t)i^{*}(0)}{S^{*}W^{*}i(t,0)}\bigg )\bigg ]\\{} & {} +\eta \int ^{+\infty }_{0}\beta _{1}(a)V^{*}i^{*}(a) \bigg [{\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg ) -{\textbf{p}}\bigg (\frac{V^{*}}{V(t)}\bigg )-{\textbf{p}} \bigg (\frac{V(t)i(t,a)i^{*}(0)}{V^{*}i^{*}(a)i(t,0)}\bigg )\bigg ]\text{ d }a\\{} & {} +\eta \beta _{2}V^{*}T^{*}\bigg [{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg ) -{\textbf{p}}\bigg (\frac{V^{*}}{V(t)}\bigg )-{\textbf{p}} \bigg (\frac{V(t)T(t)i^{*}(0)}{V^{*}T^{*}i(t,0)}\bigg )\bigg ]\\{} & {} +\eta \beta _{3}V^{*}W^{*}\bigg [{\textbf{p}}\bigg (\frac{W(t)}{W^{*}}\bigg ) -{\textbf{p}}\bigg (\frac{V^{*}}{V(t)}\bigg )-{\textbf{p}} \bigg (\frac{V(t)W(t)i^{*}(0)}{V^{*}W^{*}i(t,0)}\bigg )\bigg ]\Bigg \}\\{} & {} +(S^{*}+\eta V^{*}){\mathcal {F}}_{a}\rho \int ^{+\infty }_{0} \sigma (b)e^{*}(b)\text{ d }b-(S^{*}+\eta V^{*}){\mathcal {F}}_{a} \rho \frac{i^{*}(0)}{i(t,0)}\int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b,\\ {\mathcal {G}}_{3}= & {} (S^{*}+\eta V^{*}){\mathcal {F}}_{a}\rho (1-q){\mathcal {K}}_{1}\Bigg \{\int ^{+\infty }_{0}\beta _{1}(a)S^{*}i^{*}(a)\bigg [\frac{i(t,a)}{i^{*}(a)} -\frac{S^{*}}{S(t)}-\ln \bigg (\frac{e(t,0)}{e^{*}(0)}\bigg )\bigg ]\text{ d }a\\{} & {} +\beta _{2}S^{*}T^{*}\bigg [\frac{T(t)}{T^{*}} -\frac{S^{*}}{S(t)}-\ln \bigg (\frac{e(t,0)}{e^{*}(0)}\bigg )\bigg ] +\beta _{3}S^{*}W^{*}\bigg [\frac{W(t)}{W^{*}} -\frac{S^{*}}{S(t)}-\ln \bigg (\frac{e(t,0)}{e^{*}(0)}\bigg )\bigg ]\\{} & {} +\eta \int ^{+\infty }_{0}\beta _{1}(a)V^{*}i^{*}(a)\bigg [\frac{i(t,a)}{i^{*}(a)} -\frac{V^{*}}{V(t)}-\ln \bigg (\frac{e(t,0)}{e^{*}(0)}\bigg )\bigg ]\text{ d }a\\{} & {} +\eta \beta _{2}V^{*}T^{*}\bigg [\frac{T(t)}{T^{*}} -\frac{V^{*}}{V(t)}-\ln \bigg (\frac{e(t,0)}{e^{*}(0)}\bigg )\bigg ]\\{} & {} +\eta \beta _{3}V^{*}W^{*}\bigg [\frac{W(t)}{W^{*}} -\frac{V^{*}}{V(t)}-\ln \bigg (\frac{e(t,0)}{e^{*}(0)}\bigg )\bigg ]\Bigg \}\\= & {} (S^{*}+\eta V^{*}){\mathcal {F}}_{a}\rho (1-q){\mathcal {K}}_{1} \Bigg \{\int ^{+\infty }_{0}\beta _{1}(a)S^{*}i^{*}(a)\bigg [{\textbf{p}} \bigg (\frac{i(t,a)}{i^{*}(a)}\bigg ) -{\textbf{p}}\bigg (\frac{S^{*}}{S(t)}\bigg )\\{} & {} -{\textbf{p}}\bigg (\frac{S(t)i(t,a)e^{*}(0)}{S^{*}i^{*}(a)e(t,0)} \bigg )\bigg ]\text{ d }a+\beta _{2}S^{*}T^{*}\bigg [{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg ) -{\textbf{p}}\bigg (\frac{S^{*}}{S(t)}\bigg )-{\textbf{p}} \bigg (\frac{S(t)T(t)e^{*}(0)}{S^{*}T^{*}e(t,0)}\bigg )\bigg ]\\{} & {} +\beta _{3}S^{*}W^{*}\bigg [{\textbf{p}}\bigg (\frac{W(t)}{W^{*}}\bigg ) -{\textbf{p}}\bigg (\frac{S^{*}}{S(t)}\bigg )-{\textbf{p}} \bigg (\frac{S(t)W(t)e^{*}(0)}{S^{*}W^{*}e(t,0)}\bigg )\bigg ]\\{} & {} +\eta \int ^{+\infty }_{0}\beta _{1}(a)V^{*}i^{*}(a)\bigg [{\textbf{p}} \bigg (\frac{i(t,a)}{i^{*}(a)}\bigg ) -{\textbf{p}}\bigg (\frac{V^{*}}{V(t)}\bigg )-{\textbf{p}} \bigg (\frac{V(t)i(t,a)e^{*}(0)}{V^{*}i^{*}(a)e(t,0)}\bigg )\bigg ]\text{ d }a\\ \end{aligned}$$

$$\begin{aligned}{} & {} +\eta \beta _{2}V^{*}T^{*}\bigg [{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg ) -{\textbf{p}}\bigg (\frac{V^{*}}{V(t)}\bigg )-{\textbf{p}} \bigg (\frac{V(t)T(t)e^{*}(0)}{V^{*}T^{*}e(t,0)}\bigg )\bigg ]\\{} & {} +\eta \beta _{3}V^{*}W^{*}\bigg [{\textbf{p}}\bigg (\frac{W(t)}{W^{*}}\bigg ) -{\textbf{p}}\bigg (\frac{V^{*}}{V(t)}\bigg )-{\textbf{p}} \bigg (\frac{V(t)W(t)e^{*}(0)}{V^{*}W^{*}e(t,0)}\bigg )\bigg ]\Bigg \},\\ {\mathcal {G}}_{4}= & {} \eta \bigg (1+\frac{V^{*}}{V(t)}-\frac{S^{*}}{S(t)} -\frac{S(t)V^{*}}{S^{*}V(t)}\bigg ) \bigg (\int ^{+\infty }_{0}\beta _{1}(a)V^{*}i^{*}(a)\text{ d }a +\beta _{2}V^{*}T^{*}+\beta _{3}V^{*}W^{*}\bigg )\\= & {} \eta \bigg [{\textbf{p}}\bigg (\frac{V^{*}}{V(t)}\bigg ) -{\textbf{p}}\bigg (\frac{S^{*}}{S(t)}\bigg ) -{\textbf{p}}\bigg (\frac{S(t)V^{*}}{S^{*}V(t)}\bigg )\bigg ]\\{} & {} \bigg (\int ^{+\infty }_{0}\beta _{1}(a)V^{*}i^{*}(a)\text{ d }a +\beta _{2}V^{*}T^{*}+\beta _{3}V^{*}W^{*}\bigg ),\\ {\mathcal {G}}_{5}= & {} \big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\rho \bigg [\int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b-\int ^{+\infty }_{0} \sigma (b)e^{*}(b){\textbf{p}}\bigg (\frac{e(t,b)}{e^{*}(b)}\bigg )\text{ d }b\\{} & {} -\int ^{+\infty }_{0}\sigma (b)e^{*}(b)\text{ d }b-\int ^{+\infty }_{0} \sigma (b)e^{*}(b)\text{ d }b\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\bigg ]\\{} & {} -\big (S^{*}+\eta V^{*}\big )\bigg [\int ^{+\infty }_{0}\beta _{1}(a)i^{*} (a){\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a +\frac{\beta _{3}}{c}\int ^{+\infty }_{0}\xi _{1}(a)i^{*}(a){\textbf{p}} \bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a\\{} & {} +\bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\bigg )\int ^{+\infty }_{0}\theta (a)i^{*}(a){\textbf{p}} \bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a\bigg ],\\ {\mathcal {G}}_{6}= & {} \big (S^{*}+\eta V^{*}\big )\Bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\Bigg )\int ^{+\infty }_{0}\theta (a)i^{*}(a) \bigg [{\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )-{\textbf{p}} \bigg (\frac{T^{*}i(t,a)}{T(t)i^{*}(a)}\bigg )\bigg ]\text{ d }a\\{} & {} -\big (S^{*}+\eta V^{*}\big )\beta _{2}T^{*}{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg )-\big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}\xi _{2}}{c} T^{*}{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg )\\{} & {} +\big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}}{c}\int ^{+\infty }_{0} \xi _{1}(a)i^{*}(a) \bigg [{\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )-{\textbf{p} }\bigg (\frac{W^{*}i(t,a)}{W(t)i^{*}(a)}\bigg )\bigg ]\text{ d }a\\{} & {} +\big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}\xi _{2}}{c}T^{*} \bigg [{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg )-{\textbf{p}} \bigg (\frac{W^{*}T(t)}{W(t)T^{*}}\bigg )\bigg ]-\big (S^{*}+\eta V^{*}\big )\beta _{3}W^{*}{\textbf{p}}\bigg (\frac{W(t)}{W^{*}}\bigg ). \end{aligned}$$

Note that

$$\begin{aligned}{} & {} \big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\rho \bigg [\int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b-\int ^{+\infty }_{0}\sigma (b)e^{*}(b){\textbf{p}}\bigg (\frac{e(t,b)}{e^{*}(b)}\bigg )\text{ d }b\\{} & {} \quad -\int ^{+\infty }_{0}\sigma (b)e^{*}(b)\text{ d }b-\int ^{+\infty }_{0}\sigma (b)e^{*}(b)\text{ d }b\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\\{} & {} \quad +\int ^{+\infty }_{0}\sigma (b)e^{*}(b)\text{ d }b-\frac{i^{*}(0)}{i(t,0)}\int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b\bigg ]\\{} & {} \quad =\big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\rho \int ^{+\infty }_{0}\sigma (b)e^{*}(b)\bigg [-\frac{i^{*}(0)e(t,b)}{i(t,0)e^{*}(b)}+1+\ln \bigg (\frac{i^{*}(0)e(t,b)}{i(t,0)e^{*}(b)}\bigg )\bigg ]\text{ d }b\\{} & {} \quad =-\big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\rho \int ^{+\infty }_{0}\sigma (b)e^{*}(b){\textbf{p}}\bigg (\frac{i^{*}(0)e(t,b)}{i(t,0)e^{*}(b)}\bigg )\text{ d }b. \end{aligned}$$

Hence, we have

$$\begin{aligned} \sum ^{6}_{i=2}{\mathcal {G}}_{i}= & {} -(S^{*}+\eta V^{*}){\mathcal {F}}_{a}q\Bigg [\int ^{+\infty }_{0}\beta _{1}(a)S^{*}i^{*}(a) {\textbf{p}}\bigg (\frac{S(t)i(t,a)i^{*}(0)}{S^{*}i^{*}(a)i(t,0)}\bigg )\text{ d }a\nonumber \\{} & {} +\beta _{2}S^{*}T^{*}{\textbf{p}}\bigg (\frac{S(t)T(t)i^{*}(0)}{S^{*}T^{*}i(t,0)}\bigg ) +\beta _{3}S^{*}W^{*}{\textbf{p}}\bigg (\frac{S(t)W(t)i^{*}(0)}{S^{*}W^{*}i(t,0)}\bigg )\nonumber \\{} & {} +\eta \int ^{+\infty }_{0}\beta _{1}(a)V^{*}i^{*}(a){\textbf{p}}\bigg (\frac{V(t)i(t,a)i^{*}(0)}{V^{*}i^{*}(a)i(t,0)}\bigg )\text{ d }a +\eta \beta _{2}V^{*}T^{*}{\textbf{p}}\bigg (\frac{V(t)T(t)i^{*}(0)}{V^{*}T^{*}i(t,0)}\bigg )\nonumber \\{} & {} +\eta \beta _{3}V^{*}W^{*}{\textbf{p}}\bigg (\frac{V(t)W(t)i^{*}(0)}{V^{*}W^{*}i(t,0)}\bigg )\Bigg ]-(S^{*}+\eta V^{*}){\mathcal {F}}_{a}\rho (1-q){\mathcal {K}}_{1}\nonumber \\{} & {} \times \Bigg [\int ^{+\infty }_{0}\beta _{1}(a)S^{*}i^{*}(a){\textbf{p}}\bigg (\frac{S(t)i(t,a)e^{*}(0)}{S^{*}i^{*}(a)e(t,0)}\bigg )\text{ d }a+\beta _{2}S^{*}T^{*}{\textbf{p}}\bigg (\frac{S(t)T(t)e^{*}(0)}{S^{*}T^{*}e(t,0)}\bigg )\nonumber \\{} & {} +\beta _{3}S^{*}W^{*}{\textbf{p}}\bigg (\frac{S(t)W(t)e^{*}(0)}{S^{*}W^{*}e(t,0)}\bigg ) +\eta \int ^{+\infty }_{0}\beta _{1}(a)V^{*}i^{*}(a){\textbf{p}}\bigg (\frac{V(t)i(t,a)e^{*}(0)}{V^{*}i^{*}(a)e(t,0)}\bigg )\text{ d }a\nonumber \\{} & {} +\eta \beta _{2}V^{*}T^{*}{\textbf{p}}\bigg (\frac{V(t)T(t)e^{*}(0)}{V^{*}T^{*}e(t,0)}\bigg ) +\eta \beta _{3}V^{*}W^{*}{\textbf{p}}\bigg (\frac{V(t)W(t)e^{*}(0)}{V^{*}W^{*}e(t,0)}\bigg )\Bigg ]\\{} & {} -S^{*}{\textbf{p}}\bigg (\frac{S^{*}}{S(t)}\bigg )\bigg (\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a)\text{ d }a +\beta _{2}T^{*}+\beta _{3}W^{*}\bigg )\nonumber \\{} & {} -\eta V^{*}\bigg [{\textbf{p}}\bigg (\frac{S^{*}}{S(t)}\bigg ) +{\textbf{p}}\bigg (\frac{S(t)V^{*}}{S^{*}V(t)}\bigg )\bigg ] \bigg (\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a)\text{ d }a +\beta _{2}T^{*}+\beta _{3}W^{*}\bigg )\nonumber \\{} & {} -\big (S^{*}+\eta V^{*}\big )\Bigg [{\mathcal {F}}_{a}\rho \int ^{+\infty }_{0}\sigma (b)e^{*}(b){\textbf{p}}\bigg (\frac{i^{*}(0)e(t,b)}{i(t,0)e^{*}(b)}\bigg )\text{ d }b\nonumber \\{} & {} +\Bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\Bigg )\int ^{+\infty }_{0}\theta (a)i^{*}(a) {\textbf{p}}\bigg (\frac{T^{*}i(t,a)}{T(t)i^{*}(a)}\bigg )\text{ d }a\nonumber \\{} & {} +\frac{\beta _{3}}{c}\int ^{+\infty }_{0}\xi _{1}(a)i^{*}(a) {\textbf{p}}\bigg (\frac{W^{*}i(t,a)}{W(t)i^{*}(a)}\bigg )\text{ d }a +\frac{\beta _{3}\xi _{2}}{c}T^{*}{\textbf{p}}\bigg (\frac{W^{*}T(t)}{W(t)T^{*}}\bigg )\Bigg ].\nonumber \end{aligned}$$

(43)

We find that all terms in Eq. (43) have the property of the function ${\textbf{p}}(x)=x-1-\ln x$. This means that positive-definite function ${\mathcal {G}}(t)$ has negative derivative $\text{ d }{\mathcal {G}}(t)/\text{d }t$. Furthermore, the equality $\text{ d }{\mathcal {G}}(t)/\text{d }t=0$ holds if and only if $S(t)=S^{*}$, $V(t)=V^{*}$, $e(t,b)=e^{*}(b)$, $i(t,a)=i^{*}(a)$, $T(t)=T^{*}$, $R(t)=R^{*}$, and $W(t)=W^{*}$. LaSalle’s Invariance Principle (LaSalle 1960) implies that the bounded solutions of System (2) converge to the largest compact invariant set of $\big \{(S(t),V(t),T(t),R(t),W(t),e(t,b),i(t,a))\in {\mathcal {D}}:\;{\text{ d }{\mathcal {G}}(t)}/{\text{ d }t}=0\big \}$. Since the endemic equilibrium ${\mathcal {P}}^{*}$ is the only invariant set of System (2) contained entirely in $\big \{(S(t),V(t),T(t),R(t),W(t),e(t,b),i(t,a))\in {\mathcal {D}}:\;{\text{ d }{\mathcal {G}}(t)}/{\text{ d }t}=0\big \}$. Hence, every solution of System (2) in set ${\mathcal {D}}\backslash \{{\mathcal {P}}^{0}\}$ tends to the endemic equilibrium ${\mathcal {P}}^{*}$, which is globally attractive when it exists. This completes the proof. $\square$

Appendix H: Numerical method for System (2)

To compute the numerical solution, we use the forward/backward finite difference method for time and age to discretize System (2) (Kenne et al. 2021; Martcheva 2015). We define the finite domain with respect to time and age as follows

$$\begin{aligned} \overline{{\textbf{D}}}=\Big \{(t,a,b):0\le t\le {\mathbb {T}},\;0\le a\le {\mathbb {K}}_{a},\;0\le b\le {\mathbb {K}}_{b}\Big \}. \end{aligned}$$

To discretize the model, we divide the time interval $(0,{\mathbb {T}})$ into ${\mathcal {T}}$ subintervals $(t_{n}, t_{n+1})$ with a time step $\varDelta t=t_{n+1}-t_{n}$, for $n = 0, 1, 2,\cdots , {\mathcal {T}}-1$. Similarly, we also divide the latent age interval $(0,{\mathbb {K}}_{b})$ and the infected age interval $(0,{\mathbb {K}}_{a})$ into $K_{b}$ subintervals $(b_{k},b_{k+1})$ with a time step $\varDelta b=b_{k+1}-b_{k}$ and $K_{a}$ subintervals $(a_{j},a_{j+1})$ with a time step $\varDelta a=a_{j+1}-a_{j}$, respectively, for $k=0, 1, 2, \cdots , K_{b}-1$, $j=0, 1, 2, \cdots , K_{a}-1$. We define the symbol substitution rules as follows

$$\begin{aligned}{} & {} S_{n}=S(t_{n}),\;V_{n}=V(t_{n}),\;T_{n}=T(t_{n}),\;R_{n}=R(t_{n}), \;W_{n}=W(t_{n}),\;i^{j}_{n}=i(t_{n},a_{j}),\\{} & {} e^{k}_{n}=e(t_{n},b_{k}),\;\beta ^{j}_{1}=\beta _{1}(a_{j}), \;\theta ^{j}=\theta (a_{j}),\;\xi ^{j}_{1}=\xi _{1}(a_{j}),\; \sigma ^{k}=\sigma (b_{k}). \end{aligned}$$

Next, we use the trapezoidal rule to approximate several integral expressions in System (2), that is,

$$\begin{aligned}{} & {} \int ^{+\infty }_{0}\beta _{1}(a)i(t,a)\text{ d }a\approx \varDelta a\bigg (\frac{\beta ^{0}_{1}i(t,a_{0})+\beta ^{K_{a}-1}_{1}i(t,a_{K_{a}-1})}{2}\bigg )+\varDelta a\sum ^{K_{a}-2}_{j=1}\beta ^{j}_{1}i(t,a_{j}),\\{} & {} \int ^{+\infty }_{0}\theta (a)i(t,a)\text{ d }a\approx \varDelta a\bigg (\frac{\theta ^{0}i(t,a_{0})+\theta ^{K_{a}-1}i(t,a_{K_{a}-1})}{2}\bigg )+\varDelta a\sum ^{K_{a}-2}_{j=1}\theta ^{j}i(t,a_{j}),\\{} & {} \int ^{+\infty }_{0}\xi _{1}(a)i(t,a)\text{ d }a\approx \varDelta a\bigg (\frac{{\xi ^{0}_{1}}i(t,a_{0})+{\xi ^{K_{a}-1}_{1}}i(t,a_{K_{a}-1})}{2}\bigg )+\varDelta a\sum ^{K_{a}-2}_{j=1}{\xi ^{j}_{1}}i(t,a_{j}),\\{} & {} \int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b\approx \varDelta b\bigg (\frac{{\sigma }^{0}e(t,b_{0})+{\sigma }^{K_{b}-1}e(t,b_{K_{b}-1})}{2}\bigg )+\varDelta b\sum ^{K_{b}-2}_{k=1}{\sigma }^{k}e(t,b_{k}). \end{aligned}$$

Hence, the discrete form of System (2) can be expressed as

$$\begin{aligned}{} & {} \frac{S_{n+1}-S_{n}}{\varDelta t}=\varLambda +\tau V_{n}+\delta R_{n}-\lambda _{n}S_{n}-(\alpha +d)S_{n},\nonumber \\{} & {} \frac{V_{n+1}-V_{n}}{\varDelta t}=\alpha S_{n}-\eta \lambda _{n}V_{n}-(\tau +d)V_{n},\nonumber \\{} & {} \frac{T_{n+1}-T_{n}}{\varDelta t}=\varDelta a\bigg (\frac{\theta ^{0}i^{0}_{n}+\theta ^{K_{a}-1}i^{K_{a}-1}_{n}}{2}\bigg )+\varDelta a\sum ^{K_{a}-2}_{j=1}\theta ^{j}i^{j}_{n}-(\gamma +d)T_{n},\nonumber \\{} & {} \frac{R_{n+1}-R_{n}}{\varDelta t}=\gamma T_{n}-(\delta +d)R_{n},\nonumber \\{} & {} \frac{W_{n+1}-W_{n}}{\varDelta t}=\varDelta a\bigg (\frac{{\xi ^{0}_{1}}i^{0}_{n}+{\xi ^{K_{a}-1}_{1}}i^{K_{a}-1}_{n}}{2}\bigg )+\varDelta a\sum ^{K_{a}-2}_{j=1}{\xi ^{j}_{1}}i^{j}_{n}+\xi _{2}T_{n}-cW_{n},\nonumber \\{} & {} \frac{e^{k}_{n+1}-e^{k}_{n}}{\varDelta t}+\frac{e^{k}_{n}-e^{k-1}_{n}}{\varDelta b}=-(\rho \sigma ^{k}+d)e^{k}_{n},\nonumber \\{} & {} \frac{i^{j}_{n+1}-i^{j}_{n}}{\varDelta t}+\frac{i^{j}_{n}-i^{j-1}_{n}}{\varDelta a}=-(\theta ^{j}+d)i^{j}_{n},\nonumber \\{} & {} e^{0}_{n}=(1-q)\lambda _{n}\big (S_{n}+\eta V_{n}\big ),\nonumber \\{} & {} i^{0}_{n}=q\lambda _{n}\big (S_{n}+\eta V_{n}\big )+\rho \varDelta b\bigg (\frac{{\sigma }^{0}e^{0}_{n}+{\sigma }^{K_{b}-1}e^{K_{b}-1}_{n}}{2}\bigg )+\rho \varDelta b\sum ^{K_{b}-2}_{k=1}{\sigma }^{k}e^{k}_{n},\nonumber \\{} & {} e^{k}_{0}=e_{0}(b_{k}),i^{j}_{0}=i_{0}(a_{j}), \end{aligned}$$

(44)

where $\lambda _{n}=\varDelta a\Big (\frac{\beta ^{0}_{1}i^{0}_{n}+\beta ^{K_{a}-1}_{1}i^{K_{a}-1}_{n}}{2}\Big )+\varDelta a\sum ^{K_{a}-2}_{j=1}\beta ^{j}_{1}i^{j}_{n}+\beta _{2}T_{n}+\beta _{3}W_{n}$. After some algebraic manipulation, the first seven equations of System (44) can be rewritten as

$$\begin{aligned}{} & {} S_{n+1}=S_{n}+\varDelta t\big [\varLambda +\tau V_{n}+\delta R_{n}-\lambda _{n}S_{n}-(\alpha +d)S_{n}\big ],\\{} & {} V_{n+1}=V_{n}+\varDelta t\big [\alpha S_{n}-\eta \lambda _{n}V_{n}-(\tau +d)V_{n}\big ],\\{} & {} T_{n+1}=T_{n}+\varDelta t\bigg [\varDelta a\bigg (\frac{\theta ^{0}i^{0}_{n}+\theta ^{K_{a}-1}i^{K_{a}-1}_{n}}{2}\bigg )+\varDelta a\sum ^{K_{a}-2}_{j=1}\theta ^{j}i^{j}_{n}-(\gamma +d)T_{n}\bigg ],\\{} & {} R_{n+1}=R_{n}+\varDelta t\big [\gamma T_{n}-(\delta +d)R_{n}\big ],\\{} & {} W_{n+1}=W_{n}+\varDelta t\bigg [\varDelta a\bigg (\frac{{\xi ^{0}_{1}}i^{0}_{n}+{\xi ^{K_{a}-1}_{1}}i^{K_{a}-1}_{n}}{2}\bigg )+\varDelta a\sum ^{K_{a}-2}_{j=1}{\xi ^{j}_{1}}i^{j}_{n}+\xi _{2}T_{n}-cW_{n}\bigg ],\\{} & {} e^{k}_{n+1}=\bigg [1-\frac{\varDelta t}{\varDelta b}-\varDelta t(\rho \sigma ^{k}+d)\bigg ]e^{k}_{n}+\frac{\varDelta t}{\varDelta b}e^{k-1}_{n},\\{} & {} i^{j}_{n+1}=\bigg [1-\frac{\varDelta t}{\varDelta a}-\varDelta t(\theta ^{j}+d)\bigg ]i^{j}_{n}+\frac{\varDelta t}{\varDelta a}i^{j-1}_{n},\\{} & {} i^{0}_{n}=q\lambda _{n}\big (S_{n}+\eta V_{n}\big )+\rho \varDelta b\bigg (\frac{{\sigma }^{0}e^{0}_{n}+{\sigma }^{K_{b}-1}e^{K_{b}-1}_{n}}{2}\bigg )+\rho \varDelta b\sum ^{K_{b}-2}_{k=1}{\sigma }^{k}e^{k}_{n},\\{} & {} e^{0}_{n}=(1-q)\lambda _{n}\big (S_{n}+\eta V_{n}\big ). \end{aligned}$$

The explicit expressions for $i^{0}_{n}$ and $e^{0}_{n}$ are as follows

$$\begin{aligned} i^{0}_{n}=\frac{\left( \begin{aligned}&\Bigg [\frac{\rho \varDelta b\sigma ^{0}(1-q)(S_{n}+\eta V_{n})}{2}+q(S_{n}+\eta V_{n})\Bigg ]\Bigg (\varDelta a\frac{\beta ^{K_{a}-1}_{1}i^{K_{a}-1}_{n}}{2}+\varDelta a\sum ^{K_{a}-2}_{j=1}\beta ^{j}_{1}i^{j}_{n}+\beta _{2}T_{n}+\beta _{3}W_{n}\Bigg )\\&+\rho \varDelta b\Bigg (\frac{{\sigma }^{K_{b}-1}e^{K_{b}-1}_{n}}{2}+\sum ^{K_{b}-2}_{k=1}{\sigma }^{k}e^{k}_{n}\Bigg ) \end{aligned}\right) }{1-\frac{q(S_{n}+\eta V_{n})\varDelta a\beta ^{0}_{1}}{2}-\frac{\rho \sigma ^{0}(1-q)(S_{n}+\eta V_{n})\varDelta a\varDelta b\beta ^{0}_{1}}{4}}, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} e^{0}_{n}=(1-q)(S_{n}+\eta V_{n})\Bigg (\varDelta a\frac{\beta ^{0}_{1}i^{0}_{n} +\beta ^{K_{a}-1}_{1}i^{K_{a}-1}_{n}}{2}+\varDelta a\sum ^{K_{a}-2}_{j=1}\beta ^{j}_{1} i^{j}_{n}+\beta _{2}T_{n}+\beta _{3}W_{n}\Bigg ). \end{aligned} \end{aligned}$$

Appendix I: MCMC method for parameter estimation

Let $\varepsilon$ be the fitting error, and $\varepsilon$ follows the additive independent Gaussian distribution with mean zero and unknown variance $\xi ^{2}$, which is based on the result of the Central Limit Theorem. Then, the observations y can be expressed as follows

$$\begin{aligned} y=f(x,{\widehat{\chi }})+\varepsilon ,\;\;\varepsilon \sim N(0,I\xi ^{2}), \end{aligned}$$

(45)

where $f(x,{\widehat{\chi }})$ is the nonlinear model ($\theta (a)$, ${\mathcal {Z}}_{1}(0,a)$, or ${\mathcal {Z}}_{2}(j,a)$); x are the independent variables; ${\widehat{\chi }}$ are the unknown parameters and initial values.

For ${\hat{\varPsi }}$ independent identically distributed observations, the likelihood function $p(y|{\hat{\chi }}, \xi ^{2})$ from Eq. (45) with a Gaussian error model is

$$\begin{aligned} p(y|{\hat{\chi }}, \xi ^{2})=\Bigg (\frac{1}{\sqrt{2\pi \xi ^2}}\Bigg )^{{\hat{\varPsi }}}\exp \Bigg [\frac{-\textrm{SS}({\hat{\chi }})}{2\xi ^{2}}\Bigg ], \end{aligned}$$

where $\textrm{SS}({\hat{\chi }})$ represents the sum of squares function

$$\begin{aligned} \textrm{SS}({\hat{\chi }})=\overset{{\hat{\varPsi }}}{\underset{i=1}{\sum }} \Big [(y_{i}-f({\hat{\chi }})_{i})^{2}\Big ]. \end{aligned}$$

For simplicity, we assume that the unknown parameters ${\hat{\chi }}$ are an independent Gaussian prior specification, that is,

$$\begin{aligned} {\hat{\chi }}_{j}\sim N(\nu _{j}, \varphi ^{2}_{j}),\;\;j = 1,\ldots , {\hat{M}}. \end{aligned}$$

where ${\hat{M}}$ is the number of unknown parameters. For $\xi ^{-2}$, a Gamma distribution is used as a prior, that is,

$$\begin{aligned} p(\xi ^{-2})\sim \Gamma \Bigg (\frac{n_{0}}{2}, \frac{n_{0}}{2}S^{2}_{0}\Bigg ), \end{aligned}$$

where $S^2_0$ and $n_0$ are the prior mean and prior accuracy of variance $\xi ^{2}$, respectively.

The conditional distribution $p(\xi ^{-2}|y, {\hat{\chi }})$ can be expressed as follows

$$\begin{aligned} \begin{aligned} p(\xi ^{-2}|y, {\hat{\chi }})\propto \big (\xi ^{-2}\big )^{-\frac{{\hat{\varPsi }} +n_{0}}{2}-1}\exp \bigg [-\frac{\textrm{SS}({\hat{\chi }})+n_{0}S^{2}_{0}}{2\xi ^{-2}}\bigg ]. \end{aligned} \end{aligned}$$

Using the conditional conjugacy property of the Gamma distribution, the conditional distribution $p(\xi ^{-2}|y, {\hat{\chi }})$ is also a Gamma distribution with

$$\begin{aligned} p(\xi ^{-2}|y, {\hat{\chi }})=\Gamma \Bigg (\frac{{\hat{\varPsi }}+n_{0}}{2}, \frac{\textrm{SS}({\hat{\chi }})+n_{0}S^{2}_{0}}{2}\Bigg ), \end{aligned}$$

according to which we sample and update $\xi ^{-2}$ for other parameters within each run of Metropolis Hastings simulations. Since we assume independent Gaussian prior specification for parameters ${\hat{\chi }}$, the prior sum of squares for the given parameters ${\hat{\chi }}$ can be calculated as follows

$$\begin{aligned} \textrm{SS}_{\textrm{pri}}({\hat{\chi }})=\overset{{\hat{M}}}{\underset{i=1}{\sum }} \Bigg [\frac{{\hat{\chi }}_{i}-\nu _{i}}{\varphi _{i}}\Bigg ]^{2}. \end{aligned}$$

Then the posterior for the unknown parameters ${\hat{\chi }}$ can be estimated as

$$\begin{aligned} \begin{aligned} p({\hat{\chi }}|y, \xi ^{2})\propto \exp \Bigg [-\frac{1}{2} \bigg (\frac{\textrm{SS}({\hat{\chi }})}{\xi ^2}+\textrm{SS}_{\textrm{pri}}({\hat{\chi }})\bigg )\Bigg ]. \end{aligned} \end{aligned}$$

In the simulation, we use Delayed Rejection Adaptive Metropolis (DRAM) algorithm to generate efficient chains of estimated parameters (Haario et al. 2006). The variance of measured components $\theta (a)$, ${\mathcal {Z}}_{1}(0,a)$, and ${\mathcal {Z}}_{2}(j,a)$ are given by inverse gamma distribution with hyper-parameters (0.01, 0.04), where 0.01 is the initial error variance, which is updated by inverse gamma distribution (Tang et al. 2018). Prior information of unknown parameters is given by $\theta _{1}\in (0, 1000)$, $\theta _{2}\in (0, 1000)$, $\varpi _{1}\in (0, 10000)$, $\varpi _{2}\in (0, 1000)$, $\sigma _{1}\in (0, 10)$, $\sigma _{2}\in (0, 1000)$, $\beta _{1}\in (0, 1\times 10^{-7})$, $\beta _{3}\in (0, 1\times 10^{-7})$, $\xi _{2}\in (0.6, 1)$, $\zeta _{1}\in (0, 1000)$, $T(0)\in (10000, 50000)$, $R(0)\in (2\times 10^{6}, 1\times 10^{7})$, $W(0)\in (1\times 10^{4}, 1\times 10^{5})$, and the proposal density follows a multivariate normal distribution.