Evaluating Strategies For Tuberculosis to Achieve the Goals of WHO in China: A Seasonal Age-Structured Model Study

Abstract

Although great progress has been made in the prevention and mitigation of TB in the past 20 years, China is still the third largest contributor to the global burden of new TB cases, accounting for 833,000 new cases in 2019. Improved mitigation strategies, such as vaccines, diagnostics, and treatment, are needed to meet goals of WHO. Given the huge variability in the prevalence of TB across age-groups in China, the vaccination, diagnostic techniques, and treatment for different age-groups may have different effects. Moreover, the statistics data of TB cases show significant seasonal fluctuations in China. In view of the above facts, we propose a non-autonomous differential equation model with age structure and seasonal transmission rate. We derive the basic reproduction number, ${\mathcal {R}}_{0}$, and prove that the unique disease-free periodic solution, ${\mathcal {P}}_{0}$ is globally asymptotically stable when ${\mathcal {R}}_{0}<1$, while the disease is uniformly persistent and at least one positive periodic solution exists when ${\mathcal {R}}_{0}>1$. We estimate that the basic reproduction number ${\mathcal {R}}_{0}=1.3935$ ($95\%\text{ CI }:(1.3729, 1.4087)$), which means that TB is uniformly persistent. Our results demonstrate that vaccinating susceptible individuals whose ages are over 65 and between 20 and 24 is much more effective in reducing the prevalence of TB, and each of the improved vaccination strategy, diagnostic strategy, and treatment strategy leads to substantial reductions in the prevalence of TB per 100,000 individuals compared with current approaches, and the combination of the three strategies is more effective. Scenario A (i.e., coverage rate $85\%$, diagnosis rate $5\theta _{k}$, relapse rate $0.1\chi _{k}$) is the best and can reduce the prevalence of TB per 100,000 individuals by $98.91\%$ and $99.07\%$ in 2035 and 2050, respectively. Although the improved strategies will significantly reduce the incidence rate of TB, it is challenging to achieve the goal of WHO in 2050. Our findings can provide guidance for public health authorities in projecting effective mitigation strategies of TB.

1 Introduction

Tuberculosis (TB) is a chronic infectious disease caused by Mycobacterium TB infection (Wikipedia 2021). Mycobacterium TB may invade various organs of the body, but mainly invade the lungs, which is called pulmonary TB (Grange et al. 2001; World Health Organization 2021b). TB is one of the top ten causes of death worldwide and the leading cause of death from a single infectious agent, ranking above HIV/AIDS as a cause of death (Grange et al. 2001; Ren et al. 2020). In 2019, about 8.9–11 million individuals developed TB in the world (World Health Organization 2021a). Globally, an average of 130 per 100,000 individuals developed into TB patients, and the annual incidence rate is 5 to 500 per 100,000 individuals in 2019 (World Health Organization 2021a). A total of 1.4 million individuals died from TB in 2019, including 208,000 individuals infected by HIV (Grange et al. 2001; World Health Organization 2021b). Among the people suffering from TB in 2019, 30 countries with a high burden of TB accounted for $87\%$ of global cases, of which eight countries accounted for two-thirds of the global total number of TB cases: India ($26\%$), Indonesia ($8.5\%$), China ($8.4\%$), Philippines ($6.0\%$), Pakistan ($5.7\%$), Nigeria ($4.4\%$), Bangladesh ($3.6\%$), and South Africa ($3.6\%$) (World Health Organization 2021a; Ren et al. 2020).

Although great progress has been made in the prevention and mitigation of TB in the past 20 years (Wang et al. 2014), China is still the third largest contributor to the global burden of new TB cases, accounting for 833,000 new cases in 2019 and the incidence rate of 58 per 100,000 individuals (World Health Organization 2021a). Globally, the incidence rate of TB is declining, but the speed is not fast enough to achieve the goals of WHO, which is to reduce the incidence rate of TB by $50\%$, $80\%$, and $90\%$ in 2025, 2030, and 2035, respectively, compared with 2015, and less than one case per million individuals per year in 2050 compared with 2015 in China (Dye and Williams 2008; Harris et al. 2019, 2020; Houben et al. 2016; Huynh et al. 2015; Lin et al. 2015; Xu et al. 2017). From the results of the current research and the prediction of mathematical models (Abu-Raddad et al. 2009; Guo et al. 2021; Harris et al. 2019, 2020), it is impossible to control TB further from the existing nursing and preventive measures. Therefore, improved vaccination, diagnostics, and treatment drugs will be the key of achieving the goals of WHO (Harris et al. 2019, 2020; Huynh et al. 2015; Lin et al. 2015). In the past few years, the development of new TB vaccines is rapid, with 14 candidates entering clinical trials, including four in phase 2B/3 (Harris et al. 2019, 2020). The improved vaccination can effectively prevent infection in susceptible individuals and reinfection in latent individuals and recovered individuals to replace neonatal BCG (Skeiky and Sadoff 2006). The improved diagnostics can shorten the duration of infection and increase the probability of case detection before death from TB disease (Abu-Raddad et al. 2009; Keeler et al. 2006). The improved treatment drugs can shorten the time of treatment and reduce the relapse rate of the recovered individuals (Abu-Raddad et al. 2009).

Many mathematical models have studied the dynamics of TB (Bhunu et al. 2008; Cai et al. 2021; Feng et al. 2002; Guo et al. 2021; Harris et al. 2019, 2020; Liu et al. 2010; Renardy and Kirschner 2020; Song et al. 2002; Zhang et al. 2015, 2019; Zhao et al. 2017; Zhou et al. 2008), and explored strategies for improved vaccination, diagnostics, and treatment drugs (Abu-Raddad et al. 2009; Harris et al. 2019, 2020; Liu et al. 2017; Renardy and Kirschner 2019). There is evidence showing that the number of TB cases is highly age-dependent (Abu-Raddad et al. 2009; Ainseba et al. 2017; Castillo-Chavez and Feng 1998; Harris et al. 2019, 2020). Thus, age-structured models are often used to study the transmission dynamics of TB. Abu-Raddad et al. (2009) used an age-structured mathematical model of TB; they focused on the WHO Southeast Asia region and explore the potential benefits with a set of new interventions under development. Harris et al. (2016) introduced the results of studies comparing infant vaccination with adolescents or people of all ages. Harris et al. (2019) used an age-structured mathematical model to compare the impact of new vaccination targeting the older adults (60–64 years) and adolescents (15–19 years) in China. Their conclusions proved that providing effective vaccinations to the older adults (60–64 years) is more effective than the adolescents (15–19 years). However, the seasonal age-structured model has not been applied to explore the potential impact of vaccination strategy, diagnostic strategy, and treatment strategy on TB in China. In order to evaluate the current status of TB epidemic and the impact of the improved strategies on the incidence rate of TB in China, we propose a non-autonomous differential equation model with age structure. The real reason for the seasonal pattern of TB is still unknown, but the higher infection rate in winter may be relevant to the increased periods spent in overcrowded and poorly ventilated housing conditions; these phenomena are much more easily seen than in the other three seasons (Liu et al. 2010; Rios et al. 2000; Zhang et al. 2016). Next, highly infectious viruses such as influenza and lack of vitamin D lead to immune deficiency, causing Mycobacterium TB to be reactivated in winter and spring (Rios et al. 2000; Zhang et al. 2016). In addition, the diagnosis delay also has certain seasonal characteristics (Zhang et al. 2016). In the model, we introduce the periodic transmission rate to characterize the seasonality of TB. Our goals are to calibrate the Mycobacterium TB transmission model based on age-stratified demographic and epidemiological data, as well as to evaluate the possibility of achieving the goals of WHO under improved strategies in China.

The rest of the work is organized as follows. In Sect. 2, we propose the TB model with age structure and seasonal transmission rate. We derive the basic reproduction number ${\mathcal {R}}_0$ and study the boundedness, existence, uniqueness, and stability of the equilibrium solutions. In Sect. 3, we use Markov chain Monte Carlo (MCMC) to estimate the unknown parameters and initial values of the model and estimate the basic reproduction number ${\mathcal {R}}_0$. In Sect. 4, we evaluate the possibility of vaccination strategy, diagnostic strategy, and treatment strategy, and combination strategies to achieve the goals of WHO in China. In Sect. 5, we summarize and discuss our findings.

2 The Seasonal TB Model with Age Structure and Vaccination

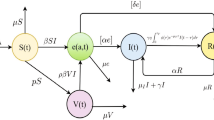
We divide the total population into n age-groups. Each age-group is further divided into seven classes, namely susceptible individuals ($S_{k}$), vaccinated individuals ($V_{k}$), latent individuals ($E_{k}$), infected individuals ($I_{k}$), treated individuals ($T_{k}$), recovered individuals ($R_{k}$), and deceased individuals ($D_{k}$). The population size of the kth age-group is denoted by $N_{k}(t)=S_{k}(t)+V_{k}(t)+E_{k}(t)+I_{k}(t)+T_{k}(t)+R_{k}(t)$, and the total population size is $N(t)=\sum ^{n}_{k=1}N_{k}(t)$. For demographic dynamics in the absence of disease and vaccination, we adopt the framework of Hethcote (2000) to derive an ordinary differential equation model of a discrete age structure with aging population from a partial differential equation system with continuous age. In this framework, we divide the population age into n intervals and define an ordinary differential equation model on each interval of age $[{\bar{x}}_{k-1}, {\bar{x}}_{k}]$, where $0={\bar{x}}_{0}<{\bar{x}}_{1}<{\bar{x}}_{2}<\cdots<{\bar{x}}_{n-1}<{\bar{x}}_{n}=\infty$. For ${\bar{x}}\in [{\bar{x}}_{k-1}, {\bar{x}}_{k}]$, we assume that the birth and death rates of the population are constants, denoted by $b_{k}$ and $d_{k}$, respectively. Let $\alpha _{k}$ denote the rate at which individuals of age-group k transfer into age-group $k+1$. We assume that the population has reached an equilibrium age distribution with exponential growth in the form $N_{k}(t)=\text{ e}^{ut}P_{k}$, where u represents constant growth rate and $P_{k}$ represents the initial size of the kth age-group; $P_{k}$ are constants satisfying

$$\begin{aligned} P_{k}=\frac{\alpha _{k-1}P_{k-1}}{\alpha _{k}+d_{k}+u},\; k=2,3,\cdots ,n. \end{aligned}$$

The birth function can be expressed as

$$\begin{aligned} \sum ^{n}_{k=1}b_{k}P_{k}=(\alpha _{1}+d_{1}+u)P_{1}. \end{aligned}$$

Hence, the birth population per unit time is

$$\begin{aligned} \sum ^{n}_{k=1}b_{k}N_{k}=\text{ e}^{ut}\sum ^{n}_{k=1}b_{k}P_{k}=(\alpha _{1}+d_{1}+u)\text{ e}^{ut}P_{1}=(\alpha _{1}+d_{1}+u)N_{1}, \end{aligned}$$

where $P_{1}=N_{1}(0)$.

The forces of infection among individuals (susceptible, vaccinated, latent, and recovered individuals) in age-group k are defined as

$$\begin{aligned} \varLambda _{k}(t)=\beta _{k}(t)\sum ^{n}_{j=1}c_{kj}\frac{I_{j}+\omega _{j}T_{j}}{N_{j}},\;1\le k\le n, \end{aligned}$$

where $c_{kj}$ is the average number of contacts between individuals in age-group k and individuals in age-group j, $\beta _{k}(t)$ is the probability of infection upon contacting an infectious person, and $I_{j}/N_{j}$ is the probability that a randomly encountered an infectious member of age-group j, $\omega _{j}$ represents the coefficient that reduces the transmission rate due to treatment in age-group j. We assume that the newborn is vaccinated, and the proportion of vaccination is $p_{1}$. For the kth age-group, susceptible individuals infected with Mycobacterium TB transfer to latent class and infected class at the rates $(1-q_{k})\varLambda _{k}$ and $q_{k}\varLambda _{k}$, respectively, where $q_{k}$ represents the proportion of new infections that develop into active TB. Latent individuals can become infected class and recovered class at the rates $\mu _{k}\sigma _{k}$ and $(1-\mu _{k})\sigma _{k}$, respectively, where $1-\mu _{k}$ is the proportion of latent class receiving treatment and $\sigma _{k}$ represents risk of reactivation in latently infected class. Latent individuals can transfer to infected class through ‘fast progression’ upon reinfection ($q_{k}\varLambda _{k}\varrho _{k}$), where $\varrho _{k}\in (0,\;1)$ represents that primary infection confers some degree of immunity (Bhunu et al. 2008; Feng et al. 2000; Harris et al. 2019, 2020). Infected individuals transfer to treated class and recovered class at the rates $(1-\xi _{k})\theta _{k}$ and $\xi _{k}\theta _{k}$, respectively, where $\xi _{k}$ represents the proportion of infected class entering the treated class due to treatment, $1-\xi _{k}$ represents the proportion of infected class who recover naturally, and $1/\theta _{k}$ represents time delays in diagnosis of TB. Treated individuals transfer to recovered class and deceased class at the rates $\rho _{k}\gamma _{k}$ and $(1-\rho _{k})\gamma _{k}$, respectively, where $\rho _{k}$ and $1-\rho _{k}$ represent the proportion of recovered class and deceased class, respectively, $\gamma _{k}$ represents the recovery rate of treated class. Recovered individuals are not totally immune to Mycobacterium TB infection and transfer to latent class and infected class at the rates $(1-q_{k})\varLambda _{k}\delta _{k}$ and $q_{k}\varLambda _{k}\delta _{k}$, respectively, where $\delta _{k}\in (0,\;1)$ represents the level of immunity of recovered individuals (Bhunu et al. 2008; Harris et al. 2019, 2020). Vaccinated individuals transfer to latent class and infected class at the rates $(1-q_{k})\varLambda _{k}\eta _{k}$ and $q_{k}\varLambda _{k}\eta _{k}$, respectively, where $\eta _{k}\in (0,\;1)$ represents that the immunity generated by the vaccine has a protective effect on individuals. $\chi _{k}$ represents the relapse rate of recovered class. $\nu _{k}\;(2\le k\le n)$ represents the vaccination rate for susceptible class, $\tau _{k}$ represents the duration of vaccine-induced immunity in age-group k. The population flow among those compartments is shown in Fig. 1. The model is described by the following system of ordinary differential equations:

$$\begin{aligned} \left\{ \begin{aligned} \frac{\text{ d }S_{1}}{\text{ d }t}&=(1-p_{1})(\alpha _{1}+d_{1}+u)\text{ e}^{ut}P_{1}+\tau _{1}V_{1}-(\varLambda _{1}(t)+d_{1}+\alpha _{1})S_{1},\\ \frac{\text{ d }S_{k}}{\text{ d }t}&=\alpha _{k-1}S_{k-1}+\tau _{k}V_{k}-(\varLambda _{k}(t)+\nu _{k}+d_{k}+\alpha _{k})S_{k},&2\le k\le n,\\ \frac{\text{ d }V_{1}}{\text{ d }t}&=p_{1}(\alpha _{1}+d_{1}+u)e^{ut}P_{1}-(\eta _{1}\varLambda _{1}(t)+\tau _{1}+d_{1}+\alpha _{1})V_{1},\\ \frac{\text{ d }V_{k}}{\text{ d }t}&=\alpha _{k-1}V_{k-1}+\nu _{k}S_{k}-(\eta _{k}\varLambda _{k}(t)+\tau _{k}+d_{k}+\alpha _{k})V_{k},&2\le k\le n,\\ \frac{\text{ d }E_{1}}{\text{ d }t}&=(1-q_{1})\varLambda _{1}(t)(S_{1}+\eta _{1}V_{1}+\delta _{1}R_{1})-(q_{1}\varLambda _{1}(t)\varrho _{1}+\sigma _{1}+d_{1}+\alpha _{1})E_{1},\\ \frac{\text{ d }E_{k}}{\text{ d }t}&=\alpha _{k-1}E_{k-1}+(1-q_{k})\varLambda _{k}(t)(S_{k}+\eta _{k}V_{k}+\delta _{k}R_{k})\\&\quad -(q_{k}\varLambda _{k}(t)\varrho _{k}+\sigma _{k}+d_{k}+\alpha _{k})E_{k},&2\le k\le n,\\ \frac{\text{ d }I_{1}}{\text{ d }t}&=q_{1}\varLambda _{1}(t)(S_{1}+\eta _{1}V_{1}+\delta _{1}R_{1}+\varrho _{1}E_{1})+\mu _{1}\sigma _{1}E_{1}+\chi _{1}R_{1}\\&\quad -(\theta _{1}+d_{1}+\alpha _{1})I_{1},\\ \frac{\text{ d }I_{k}}{\text{ d }t}&=\alpha _{k-1}I_{k-1}+q_{k}\varLambda _{k}(t)(S_{k}+\eta _{k}V_{k}+\delta _{k}R_{k}+\varrho _{k}E_{k})+\mu _{k}\sigma _{k}E_{k}+\chi _{k}R_{k}\\&\quad -(\theta _{k}+d_{k}+\alpha _{k})I_{k},&2\le k\le n,\\ \frac{\text{ d }T_{1}}{\text{ d }t}&=\xi _{1}\theta _{1}I_{1}-(\gamma _{1}+d_{1}+\alpha _{1})T_{1},\\ \frac{\text{ d }T_{k}}{\text{ d }t}&=\alpha _{k-1}T_{k-1}+\xi _{k}\theta _{k}I_{k}-(\gamma _{k}+d_{k}+\alpha _{k})T_{k},&2\le k\le n,\\ \frac{\text{ d }R_{1}}{\text{ d }t}&=\rho _{1}\gamma _{1}T_{1}+(1-\mu _{1})\sigma _{1}E_{1}+(1-\xi _{1})\theta _{1}I_{1}-(\chi _{1}+\delta _{1}\varLambda _{1}(t)+d_{1}+\alpha _{1})R_{1},\\ \frac{\text{ d }R_{k}}{\text{ d }t}&=\alpha _{k-1}R_{k-1}+\rho _{k}\gamma _{k}T_{k}+(1-\mu _{k})\sigma _{k}E_{k}+(1-\xi _{k})\theta _{k}I_{k}\\&\quad -(\chi _{k}+\delta _{k}\varLambda _{k}(t)+d_{k}+\alpha _{k})R_{k},&2\le k\le n,\\ \frac{\text{ d }D_{1}}{\text{ d }t}&=(1-\rho _{1})\gamma _{1}T_{1},\\ \frac{\text{ d }D_{k}}{\text{ d }t}&=(1-\rho _{k})\gamma _{k}T_{k},&2\le k\le n. \end{aligned} \right. \nonumber \\ \end{aligned}$$

(1)

Here, we assume that $\alpha _{n} = 0$ for simplicity. Consider the fractions $s_{k}(t)=\frac{S_{k}(t)}{\text{ e}^{ut}P_{k}}$, $v_{k}(t)=\frac{V_{k}(t)}{\text{ e}^{ut}P_{k}}$, $e_{k}(t)=\frac{E_{k}(t)}{\text{ e}^{ut}P_{k}}$, $i_{k}(t)=\frac{I_{k}(t)}{\text{ e}^{ut}P_{k}}$, $f_{k}(t)=\frac{T_{k}(t)}{\text{ e}^{ut}P_{k}}$, $r_{k}(t)=\frac{R_{k}(t)}{\text{ e}^{ut}P_{k}}$, and let $a_{kj}=\frac{P_{k}}{P_{j}}$ denote the ratio of the age-group k and j. Then, System (1) becomes

Fig. 1

Schematic diagram of the mathematical model (Color figure online)

$$\begin{aligned} \left\{ \begin{aligned} \frac{\text{ d }s_{1}}{\text{ d }t}&=(1-p_{1})(\alpha _{1}+d_{1}+u)+\tau _{1}v_{1}-({\lambda }_{1}(t)+u+d_{1}+\alpha _{1})s_{1},\\ \frac{\text{ d }s_{k}}{\text{ d }t}&=a_{(k-1)k}\alpha _{k-1}s_{k-1}+\tau _{k}v_{k}-({\lambda }_{k}(t)+\nu _{k}+u+d_{k}+\alpha _{k})s_{k},&2\le k\le n,\\ \frac{\text{ d }v_{1}}{\text{ d }t}&=p_{1}(\alpha _{1}+d_{1}+u)-(\eta _{1}{\lambda }_{1}(t)+\tau _{1}+u+d_{1}+\alpha _{1})v_{1},\\ \frac{\text{ d }v_{k}}{\text{ d }t}&=a_{(k-1)k}\alpha _{k-1}v_{k-1}+\nu _{k}s_{k}-(\eta _{k}{\lambda }_{k}(t)+\tau _{k}+u+d_{k}+\alpha _{k})v_{k},&2\le k\le n,\\ \frac{\text{ d }e_{1}}{\text{ d }t}&=(1-q_{1}){\lambda }_{1}(t)(s_{1}+\eta _{1}v_{1}+\delta _{1}r_{1})-(q_{1}{\lambda }_{1}(t)\varrho _{1}+\sigma _{1}+u+d_{1}+\alpha _{1})e_{1},\\ \frac{\text{ d }e_{k}}{\text{ d }t}&=a_{(k-1)k}\alpha _{k-1}e_{k-1}+(1-q_{k}){\lambda }_{k}(t)(s_{k}+\eta _{k}v_{k}+\delta _{k}r_{k})\\&\quad -(q_{k}{\lambda }_{k}(t)\varrho _{k}+\sigma _{k}+u+d_{k}+\alpha _{k})e_{k},&2\le k\le n,\\ \frac{\text{ d }i_{1}}{\text{ d }t}&=q_{1}{\lambda }_{1}(t)(s_{1}+\eta _{1}v_{1}+\delta _{1}r_{1}+\varrho _{1}e_{1})+\mu _{1}\sigma _{1}e_{1}+\chi _{1}r_{1}-(\theta _{1}+u+d_{1}+\alpha _{1})i_{1},\\ \frac{\text{ d }i_{k}}{\text{ d }t}&=a_{(k-1)k}\alpha _{k-1}i_{k-1}+q_{k}{\lambda }_{k}(t)(s_{k}+\eta _{k}v_{k}+\delta _{k}r_{k}+\varrho _{k}e_{k})+\mu _{k}\sigma _{k}e_{k}+\chi _{k}r_{k}\\&\quad -(\theta _{k}+u+d_{k}+\alpha _{k})i_{k},&2\le k\le n,\\ \frac{\text{ d }f_{1}}{\text{ d }t}&=\xi _{1}\theta _{1}i_{1}-(\gamma _{1}+u+d_{1}+\alpha _{1})f_{1},\\ \frac{\text{ d }f_{k}}{\text{ d }t}&=a_{(k-1)k}\alpha _{k-1}f_{k-1}+\xi _{k}\theta _{k}i_{k}-(\gamma _{k}+u+d_{k}+\alpha _{k})f_{k},&2\le k\le n,\\ \frac{\text{ d }r_{1}}{\text{ d }t}&=\rho _{1}\gamma _{1}f_{1}+(1-\mu _{1})\sigma _{1}e_{1}+(1-\xi _{1})\theta _{1}i_{1}-(\chi _{1}+\delta _{1}{\lambda }_{1}(t)+u+d_{1}+\alpha _{1})r_{1},\\ \frac{\text{ d }r_{k}}{\text{ d }t}&=a_{(k-1)k}\alpha _{k-1}R_{k-1}+\rho _{k}\gamma _{k}f_{k}+(1-\mu _{k})\sigma _{k}e_{k}+(1-\xi _{k})\theta _{k}i_{k}\\&\quad -(\chi _{k}+\delta _{k}{\lambda }_{k}(t)+u+d_{k}+\alpha _{k})r_{k},&2\le k\le n. \end{aligned} \right. \nonumber \\ \end{aligned}$$

(2)

where ${\lambda }_{k}(t)=\beta _{k}(t)\sum ^{n}_{j=1}c_{kj}(i_{j}+\omega _{j}f_{j})$. The fraction of the kth age-group $n_{k}(t)$ for System (2) satisfies the following equation:

$$\begin{aligned} \left\{ \begin{aligned} \frac{\text{ d }n_{1}}{\text{ d }t}&=(\alpha _{1}+d_{1}+u)-(u+d_{1}+\alpha _{1})n_{1}-(1-\rho _{1})\gamma _{1}f_{1},\\ \frac{\text{ d }n_{k}}{\text{ d }t}&=a_{(k-1)k}\alpha _{k-1}n_{k-1}-(u+d_{k}+\alpha _{k})n_{k}-(1-\rho _{k})\gamma _{k}f_{k},&2\le k\le n. \end{aligned} \right. \end{aligned}$$

Thus, the following inequality holds:

$$\begin{aligned} \left\{ \begin{aligned} \frac{\text{ d }n_{1}}{\text{ d }t}&\le (\alpha _{1}+d_{1}+u)-(u+d_{1}+\alpha _{1})n_{1},\\ \frac{\text{ d }n_{k}}{\text{ d }t}&\le a_{(k-1)k}\alpha _{k-1}n_{k-1}-(u+d_{k}+\alpha _{k})n_{k},&2\le k\le n. \end{aligned} \right. \end{aligned}$$

Solving the above equations, we have

$$\begin{aligned}&\underset{t\rightarrow \infty }{\lim \sup }\;n_{1}(t)\le \frac{\alpha _{1}+d_{1}+u}{u+d_{1}+\alpha _{1}}=1, \\&\underset{t\rightarrow \infty }{\lim \sup }\;n_{k}(t)\le \frac{a_{(k-1)k}\alpha _{k-1}}{u+d_{k}+\alpha _{k}}=1, \;\;2\le k\le n. \end{aligned}$$

Hence, the trajectories of System (2) are ultimately bounded.

For simplicity, we define

$$\begin{aligned} \left. \begin{aligned}&{\mathbf {S}}=(s_{1},\cdots ,s_{k},\cdots ,s_{n}), \;{\mathbf {V}}=(v_{1},\cdots ,v_{k},\cdots ,v_{n}),\\&{\mathbf {E}}=(e_{1},\cdots ,e_{k},\cdots ,e_{n}), \;{\mathbf {I}}=(i_{1},\cdots ,i_{k},\cdots ,i_{n}),\\&{\mathbf {F}}=(f_{1},\cdots ,f_{k},\cdots ,f_{n}), \;{\mathbf {R}}=(r_{1},\cdots ,r_{k},\cdots ,r_{n}),\\&{\mathbf {N}}=(n_{1},\cdots ,n_{k},\cdots ,n_{n}). \end{aligned} \right. \end{aligned}$$

Thus, we can obtain the following results:

Theorem 1

The solution of System (2) is ultimately bounded with the initial value

$$\begin{aligned} \big ({\mathbf {S}}(0),{\mathbf {V}}(0),{\mathbf {E}}(0),{\mathbf {I}}(0),{\mathbf {F}}(0),{\mathbf {R}}(0)\big )\in {\mathbb {R}}_{+}^{6n}. \end{aligned}$$

Further, the set

$$\begin{aligned} \varOmega =\Big \{({\mathbf {S}},{\mathbf {V}},{\mathbf {E}},{\mathbf {I}},{\mathbf {F}},{\mathbf {R}})\in {\mathbb {R}}_{+}^{6n}: 0\le s_{k},v_{k},e_{k},i_{k},f_{k},r_{k},n_{k} \le 1,\;1\le k\le n\Big \} \end{aligned}$$

is a positively invariant set.

2.1 Basic Reproduction Number

Taking into account the seasonality of TB (Liu et al. 2010; Rios et al. 2000), we introduce the basic reproduction number ${\mathcal {R}}_{0}$ for System (2) according to the general procedure presented in Wang and Zhao (2008). System (2) has a disease-free periodic solution

$$\begin{aligned} {\mathcal {P}}_{0}=\big ({\mathbf {S}}^{0},{\mathbf {V}}^{0},{\mathbf {E}}^{0},{\mathbf {I}}^{0},{\mathbf {F}}^{0},{\mathbf {R}}^{0}\big ), \end{aligned}$$

where

$$\begin{aligned} s^{0}_{1}= & {} \frac{(1-p_{1})(u+d_{1}+\alpha _{1})+\tau _{1}v^{0}_{1}}{u+d_{1}+\alpha _{1}}, \\ s^{0}_{k}= & {} \frac{(\tau _{k}+u+d_{k}+\alpha _{k})a_{(k-1)k}\alpha _{k-1}s^{0}_{k-1}+\tau _{k}a_{(k-1)k}\alpha _{k-1}v^{0}_{k-1}}{(u+d_{k}+\alpha _{k})(\tau _{k}+u+d_{k}+\alpha _{k}+\nu _{k})},\;2\le k\le n, \\ v^{0}_{1}= & {} \frac{p_{1}(u+d_{1}+\alpha _{1})}{\tau _{1}+u+d_{1}+\alpha _{1}}, \\ v^{0}_{k}= & {} \frac{(u+d_{k}+\alpha _{k}+\nu _{k})a_{(k-1)k}\alpha _{k-1}v^{0}_{k-1}+\nu _{k}a_{(k-1)k}\alpha _{k-1}s^{0}_{k-1}}{(u+d_{k}+\alpha _{k})(\tau _{k}+u+d_{k}+\alpha _{k}+\nu _{k})},\;2\le k\le n, \\ e^{0}_{k}= & {} i^{0}_{k}=f^{0}_{k}=r^{0}_{k}=0,\;1\le k\le n. \end{aligned}$$

The linearized system of System (2) at ${\mathcal {P}}_{0}$ is as follows:

$$\begin{aligned} \left\{ \begin{aligned} \frac{\text{ d }e_{1}}{\text{ d }t}&=(1-q_{1})\beta _{1}(t)\sum ^{n}_{j=1}c_{1j}(i_{j}+\omega _{j}f_{j})(s^{0}_{1}+\eta _{1}v^{0}_{1})-(\sigma _{1}+u+d_{1}+\alpha _{1})e_{1},\\ \frac{\text{ d }e_{k}}{\text{ d }t}&=a_{(k-1)k}\alpha _{k-1}e_{k-1}+(1-q_{k})\beta _{k}(t)\sum ^{n}_{j=1}c_{kj}(i_{j}+\omega _{j}f_{j})(s^{0}_{k}+\eta _{k}v^{0}_{k})\\&\quad -(\sigma _{k}+u+d_{k}+\alpha _{k})e_{k},&2\le k\le n,\\ \frac{\text{ d }i_{1}}{\text{ d }t}&=q_{1}\beta _{1}(t)\sum ^{n}_{j=1}c_{1j}(i_{j}+\omega _{j}f_{j})(s^{0}_{1}+\eta _{1}v^{0}_{1})+\mu _{1}\sigma _{1}e_{1}+\chi _{1}r_{1}\\&\quad -(\theta _{1}+u+d_{1}+\alpha _{1})i_{1},\\ \frac{\text{ d }i_{k}}{\text{ d }t}&=a_{(k-1)k}\alpha _{k-1}i_{k-1}+q_{k}\beta _{k}(t)\sum ^{n}_{j=1}c_{kj}(i_{j}+\omega _{j}f_{j})(s^{0}_{k}+\eta _{k}v^{0}_{k})+\mu _{k}\sigma _{k}e_{k}\\&\quad +\chi _{k}r_{k}-(\theta _{k}+u+d_{k}+\alpha _{k})i_{k},&2\le k\le n,\\ \frac{\text{ d }f_{1}}{\text{ d }t}&=\xi _{1}\theta _{1}i_{1}-(\gamma _{1}+u+d_{1}+\alpha _{1})f_{1},\\ \frac{\text{ d }f_{k}}{\text{ d }t}&=a_{(k-1)k}\alpha _{k-1}f_{k-1}+\xi _{k}\theta _{k}i_{k}-(\gamma _{k}+u+d_{k}+\alpha _{k})f_{k},&2\le k\le n,\\ \frac{\text{ d }r_{1}}{\text{ d }t}&=\rho _{1}\gamma _{1}f_{1}+(1-\mu _{1})\sigma _{1}e_{1}+(1-\xi _{1})\theta _{1}i_{1}-(\chi _{1}+u+d_{1}+\alpha _{1})r_{1},\\ \frac{\text{ d }r_{k}}{\text{ d }t}&=a_{(k-1)k}\alpha _{k-1}r_{k-1}+\rho _{k}\gamma _{k}f_{k}+(1-\mu _{k})\sigma _{k}e_{k}+(1-\xi _{k})\theta _{k}i_{k}\\&\quad -(\chi _{k}+u+d_{k}+\alpha _{k})r_{k},&2\le k\le n. \end{aligned} \right. \nonumber \\ \end{aligned}$$

(3)

Let $x=({\mathbf {E}},{\mathbf {I}},{\mathbf {F}},{\mathbf {R}})^{{\mathbf {T}}}$, System (3) can be rewritten as

$$\begin{aligned} \frac{\text{ d }x}{\text{ d }t}=({{{\mathcal {F}}}}(t)-{{{\mathcal {V}}}}(t))x, \end{aligned}$$

where

$$\begin{aligned} {{{\mathcal {F}}}}(t)=\left[ \begin{array}{cccc} {\mathbf {0}}&{}f_{12}&{}f_{13}&{}{\mathbf {0}}\\ {\mathbf {0}}&{}f_{22}&{}f_{23}&{}{\mathbf {0}}\\ {\mathbf {0}}&{}{\mathbf {0}}&{}{\mathbf {0}}&{}{\mathbf {0}}\\ {\mathbf {0}}&{}{\mathbf {0}}&{}{\mathbf {0}}&{}{\mathbf {0}}\\ \end{array} \right] , \;\text{ and }\; {{{\mathcal {V}}}}(t)=\left[ \begin{array}{cccc} v_{11}&{}{\mathbf {0}}&{}{\mathbf {0}}&{}{\mathbf {0}}\\ v_{21}&{}v_{22}&{}{\mathbf {0}}&{}v_{24}\\ {\mathbf {0}}&{}v_{32}&{}v_{33}&{}{\mathbf {0}}\\ v_{41}&{}v_{42}&{}v_{43}&{}v_{44}\\ \end{array} \right] . \end{aligned}$$

The expressions of $f_{ij}$ and $v_{ij}$ are in Appendix A.

It is very clear that ${{{\mathcal {F}}}}(t)$ is nonnegative and $-{{{\mathcal {V}}}}(t)$ is cooperative in the sense that the off-diagonal elements of $-{{{\mathcal {V}}}}(t)$ are nonnegative.

Let $Y (t, s), t \ge s$, be the evolution operator of the linear ${\mathcal {T}}$-periodic system

$$\begin{aligned} \frac{\text{ d }y}{\text{ d }t}=-{{{\mathcal {V}}}}(t)y. \end{aligned}$$

Hence, for each $s\in {\mathbb {R}}$, the $4n\times 4n$ matrix Y(t, s) satisfies

$$\begin{aligned} \frac{\text{ d }Y(t,s)}{\text{ d }t}=-{{{\mathcal {V}}}}(t)Y(t,s),\;\; {\forall }t\ge s, \;\;Y(s,s)=I, \end{aligned}$$

where I is a $4n\times 4n$ identity matrix. Let $\varPhi _{-{{{\mathcal {V}}}}}(t)$ be the monodromy matrix of the linear ${\mathcal {T}}$-periodic system $\frac{\text{ d }y}{\text{ d }t}=-{{{\mathcal {V}}}}(t)y$.

Following the method established by Wang and Zhao (2008), we assume that $\phi (s)$, ${\mathcal {T}}$-periodic in s, is the initial distribution of infectious individuals. Then, ${{{\mathcal {F}}}}(s)\phi (s)$ is the distribution of new infections produced by infected individuals who were introduced at time s. Given $t\ge s$, then $Y(t,s){{{\mathcal {F}}}}(s)\phi (s)$ gives the distribution of those infected individuals who were newly infected at time s and remain in infected compartments at time t. We define that

$$\begin{aligned} \psi (t):=\int ^{t}_{-\infty }Y(t, s){{{\mathcal {F}}}}(s)\phi (s)ds=\int ^{\infty }_{0}Y(t, t-a){{{\mathcal {F}}}}(t-a)\phi (t-a)da, \end{aligned}$$

where $\psi (t)$ represents the distribution of accumulated newly infectious individuals at time t produced by all infectious individuals $\phi (s)$ introduced at previous time to t.

Let $C_{{\mathcal {T}}}$ be the ordered Banach space of all ${\mathcal {T}}$-periodic functions from ${\mathbb {R}}$ to ${\mathbb {R}}^{4n}$ with the maximum norm $\parallel \cdot \parallel$ and the positive cone $C_{{\mathcal {T}}}^{+}:=\{\phi \in C_{{\mathcal {T}}}: \;\phi (t)\ge 0,\; {\forall }t\in {\mathbb {R}}\}$. According to the method in Wang and Zhao (2008), we define a linear operator $L:\;C_{{\mathcal {T}}}\rightarrow C_{{\mathcal {T}}}$ as follows

$$\begin{aligned} (L\phi )(t)=\int ^{\infty }_{0}Y(t, t-a){{{\mathcal {F}}}}(t-a)\phi (t-a)da,\;{\forall }t\in {\mathbb {R}},\;\phi \in C_{T}. \end{aligned}$$

L is called the next-generation infection operator and the spectral radius of L is defined as the basic reproduction number, ${\mathcal {R}}_{0}$. Therefore, ${\mathcal {R}}_{0}$ of System (2) can be expressed as follows:

$$\begin{aligned} {\mathcal {R}}_{0}:=\rho (L). \end{aligned}$$

In order to calculate the basic reproduction number ${\mathcal {R}}_{0}$ of System (2), according to Theorem 2.1 in Wang and Zhao (2008), we introduce the linear ${\mathcal {T}}$-periodic system as follows:

$$\begin{aligned} \frac{\text{ d }\omega }{\text{ d }t}=\Big [-{{{\mathcal {V}}}}(t) +\frac{{{{\mathcal {F}}}}(t)}{\lambda }\Big ]\omega ,\;t\in {\mathbb {R}}, \end{aligned}$$

(4)

where parameter $\lambda \in (0, \infty )$. Let the evolution operator of System (4) on ${\mathbb {R}}^{4n}$ be $W(t, s, \lambda ),\; t \ge s,\; s \in {\mathbb {R}}$. It is clear that $\varPhi _{{{{\mathcal {F}}}}-{{{\mathcal {V}}}}}(t)=W(t, 0, 1),\;t\ge 0$ can be obtained. Hence, we derive

$$\begin{aligned} \varPhi _{\frac{{{{\mathcal {F}}}}}{\lambda }-{{{\mathcal {V}}}}}(t)=W(t, 0, \lambda ),\;t\ge 0, \end{aligned}$$

where

$$\begin{aligned} -{{{\mathcal {V}}}}(t)+\frac{{{{\mathcal {F}}}}(t)}{\lambda }=\left[ \begin{array}{cccc} v_{11}&{}\frac{f_{12}}{\lambda }&{}\frac{f_{13}}{\lambda }&{}{\mathbf {0}}\\ -v_{21}&{}-v_{22}+\frac{f_{22}}{\lambda }&{}\frac{f_{23}}{\lambda }&{}-v_{24}\\ {\mathbf {0}}&{}-v_{32}&{}-v_{33}&{}{\mathbf {0}}\\ -v_{41}&{}-v_{42}&{}-v_{43}&{}-v_{44}\\ \end{array} \right] . \end{aligned}$$

It is easy to verify that System (2) satisfies the assumptions A(1)-A(7) in Wang and Zhao (2008). Therefore, we have the following two lemmas.

Lemma 1

(see Theorem 2.1 in Wang and Zhao (2008)). The following statements are valid:

• (1) If $\rho (W({\mathcal {T}}, 0, \lambda )) = 1$ has a positive solution $\lambda _{0}$, then $\lambda _{0}$ is an eigenvalue of L. Therefore, ${\mathcal {R}}_0 > 0$.

• (2) If ${\mathcal {R}}_0 > 0$, then $\lambda = {\mathcal {R}}_0$ is the unique solution of $\rho (W({\mathcal {T}}, 0, \lambda )) = 1$.

• (3) ${\mathcal {R}}_0 = 0$ if and only if $\rho (W({\mathcal {T}}, 0, \lambda ))<1$ for all $\lambda > 0$.

Lemma 2

(see Theorem 2.2 in Wang and Zhao (2008)). The following statements are valid:

• (1) ${\mathcal {R}}_0 = 1$ if and only if $\rho (\varPhi _{{{{\mathcal {F}}}}-{{{\mathcal {V}}}}}({\mathcal {T}}))=1$.

• (2) ${\mathcal {R}}_0 > 1$ if and only if $\rho (\varPhi _{{{{\mathcal {F}}}}-{{{\mathcal {V}}}}}({\mathcal {T}}))>1$.

• (3) ${\mathcal {R}}_0 < 1$ if and only if $\rho (\varPhi _{{{{\mathcal {F}}}}-{{{\mathcal {V}}}}}({\mathcal {T}}))<1$.

2.2 Extinction of the Disease

In order to prove the globally asymptotic stability of the disease-free periodic solution of System (2), we assume that $\varrho _{k}=0,\;\delta _{k}=0,\;1\le k\le n$, and we introduce the following theorem.

Theorem 2

The disease-free periodic solution ${\mathcal {P}}_{0}$ of System (2) is globally asymptotic stable if ${\mathcal {R}}_{0}<1$ and is unstable if ${\mathcal {R}}_{0}>1$.

Proof

By Lemma 2, we obtain that the disease-free periodic solution ${\mathcal {P}}_{0}$ is locally asymptotic stable when ${\mathcal {R}}_{0}<1$ and the disease-free periodic solution ${\mathcal {P}}_{0}$ is unstable when ${\mathcal {R}}_{0}>1$. Thus, we only need to prove that the disease-free periodic solution ${\mathcal {P}}_{0}$ is globally attractive when ${\mathcal {R}}_{0}<1$. Clearly,

$$\begin{aligned} \underset{t\rightarrow \infty }{\lim \sup }\;s_{k}(t)\le s^{0}_{k},\;\underset{t\rightarrow \infty }{\lim \sup }\;v_{k}(t)\le v^{0}_{k},\;1\le k\le n. \end{aligned}$$

Thus, for ${\forall }{\bar{\epsilon }}>0$, there exists ${\bar{t}}>0$, such that $s_{k}(t)\le s^{0}_{k}+\frac{{\bar{\epsilon }}}{2}$, and $\eta _{k}v_{k}(t)\le \eta _{k}v^{0}_{k}+\frac{{\bar{\epsilon }}}{2}$ for $t>{\bar{t}}$. We set up the following comparison system:

$$\begin{aligned} \left\{ \begin{aligned} \frac{\text{ d }{\bar{e}}_{1}}{\text{ d }t}&=(1-q_{1}){\bar{\lambda }}_{1}(t)(s^{0}_{1}+\eta _{1}v^{0}_{1}+{\bar{\epsilon }})-(\sigma _{1}+u+d_{1}+\alpha _{1}){\bar{e}}_{1},\\ \frac{\text{ d }{\bar{e}}_{k}}{\text{ d }t}&=a_{(k-1)k}\alpha _{k-1}{\bar{e}}_{k-1}+(1-q_{k}){\bar{\lambda }}_{k}(t)(s^{0}_{k}+\eta _{k}v^{0}_{k}+{\bar{\epsilon }})\\&\quad -(\sigma _{k}+u+d_{k}+\alpha _{k}){\bar{e}}_{k},&2\le k\le n,\\ \frac{\text{ d }{\bar{i}}_{1}}{\text{ d }t}&=q_{1}{\bar{\lambda }}_{1}(t)(s^{0}_{1}+\eta _{1}v^{0}_{1}+{\bar{\epsilon }})+\mu _{1}\sigma _{1}{\bar{e}}_{1}+\chi _{1}{\bar{r}}_{1}-(\theta _{1}+u+d_{1}+\alpha _{1}){\bar{i}}_{1},\\ \frac{\text{ d }{\bar{i}}_{k}}{\text{ d }t}&=a_{(k-1)k}\alpha _{k-1}{\bar{i}}_{k-1}+q_{k}{\bar{\lambda }}_{k}(t)(s^{0}_{k}+\eta _{k}v^{0}_{k}+{\bar{\epsilon }})+\mu _{k}\sigma _{k}e_{k}\\&\quad +\chi _{k}{\bar{r}}_{k}-(\theta _{k}+u+d_{k}+\alpha _{k}){\bar{i}}_{k},&2\le k\le n,\\ \frac{\text{ d }{\bar{f}}_{1}}{\text{ d }t}&=\xi _{1}\theta _{1}{\bar{i}}_{1}-(\gamma _{1}+u+d_{1}+\alpha _{1}){\bar{f}}_{1},\\ \frac{\text{ d }{\bar{f}}_{k}}{\text{ d }t}&=a_{(k-1)k}\alpha _{k-1}{\bar{f}}_{k-1}+\xi _{k}\theta _{k}{\bar{i}}_{k}-(\gamma _{k}+u+d_{k}+\alpha _{k}){\bar{f}}_{k},&2\le k\le n,\\ \frac{\text{ d }{\bar{r}}_{1}}{\text{ d }t}&=\rho _{1}\gamma _{1}{\bar{f}}_{1}+(1-\mu _{1})\sigma _{1}{\bar{e}}_{1}+(1-\xi _{1})\theta _{1}{\bar{i}}_{1}-(\chi _{1}+u+d_{1}+\alpha _{1}){\bar{r}}_{1},\\ \frac{\text{ d }{\bar{r}}_{k}}{\text{ d }t}&=a_{(k-1)k}\alpha _{k-1}{\bar{r}}_{k-1}+\rho _{k}\gamma _{k}{\bar{f}}_{k}+(1-\mu _{k})\sigma _{k}{\bar{e}}_{k}+(1-\xi _{k})\theta _{k}{\bar{i}}_{k}\\&\quad -(\chi _{k}+u+d_{k}+\alpha _{k}){\bar{r}}_{k},&2\le k\le n, \end{aligned} \right. \nonumber \\ \end{aligned}$$

(5)

where ${\bar{\lambda }}_{k}(t)=\beta _{k}(t)\sum ^{n}_{j=1}c_{kj}({\bar{i}}_{j}+\omega _{j}{\bar{f}}_{j})$. Let ${\bar{h}}=({\bar{\mathbf {E}}},{\bar{\mathbf {I}}},{\bar{\mathbf {F}}},{\bar{\mathbf {R}}})^{{\mathbf {T}}}$, System (5) is equivalent to the following equation:

$$\begin{aligned} \frac{\text{ d }{\bar{h}}}{\text{ d }t}=\big ({\mathcal {F}}(t)-{\mathcal {V}}(t)+{\bar{\epsilon }} \varpi (t)\big ){\bar{h}}, \end{aligned}$$

where

$$\begin{aligned} \varpi (t)=\left[ \begin{array}{cccc} {\mathbf {0}}&{}\varpi _{12}&{}\varpi _{13}&{}{\mathbf {0}}\\ {\mathbf {0}}&{}\varpi _{22}&{}\varpi _{23}&{}{\mathbf {0}}\\ {\mathbf {0}}&{}{\mathbf {0}}&{}{\mathbf {0}}&{}{\mathbf {0}}\\ {\mathbf {0}}&{}{\mathbf {0}}&{}{\mathbf {0}}&{}{\mathbf {0}}\\ \end{array} \right] , \end{aligned}$$

(6)

$\varpi _{12}$, $\varpi _{13}$, $\varpi _{22}$, and $\varpi _{23}$ are expressed as follows:

$$\begin{aligned} \varpi _{12}= & {} \left[ \begin{array}{cccc} (1-q_{1})\beta _{1}(t)c_{11}&{} (1-q_{1})\beta _{1}(t)c_{12}&{} \cdots &{}(1-q_{1})\beta _{1}(t)c_{1n}\\ (1-q_{2})\beta _{2}(t)c_{21}&{} (1-q_{2})\beta _{2}(t)c_{22}&{} \cdots &{}(1-q_{2})\beta _{2}(t)c_{2n}\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ (1-q_{n})\beta _{n}(t)c_{n1}&{} (1-q_{n})\beta _{n}(t)c_{n2}&{} \cdots &{}(1-q_{n})\beta _{n}(t)c_{nn}\\ \end{array} \right] , \\ \varpi _{13}= & {} \left[ \begin{array}{cccc} (1-q_{1})\beta _{1}(t)c_{11}\omega _{1}&{} (1-q_{1})\beta _{1}(t)c_{12}\omega _{2}&{} \cdots &{}(1-q_{1})\beta _{1}(t)c_{1n}\omega _{n}\\ (1-q_{2})\beta _{2}(t)c_{21}\omega _{1}&{} (1-q_{2})\beta _{2}(t)c_{22}\omega _{2}&{} \cdots &{}(1-q_{2})\beta _{2}(t)c_{2n}\omega _{n}\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ (1-q_{n})\beta _{n}(t)c_{n1}\omega _{1}&{} (1-q_{n})\beta _{n}(t)c_{n2}\omega _{2}&{} \cdots &{}(1-q_{n})\beta _{n}(t)c_{nn}\omega _{n}\\ \end{array} \right] , \\ \varpi _{22}= & {} \left[ \begin{array}{cccc} q_{1}\beta _{1}(t)c_{11}&{} q_{1}\beta _{1}(t)c_{12}&{} \cdots &{}q_{1}\beta _{1}(t)c_{1n}\\ q_{2}\beta _{2}(t)c_{21}&{} q_{2}\beta _{2}(t)c_{22}&{} \cdots &{}q_{2}\beta _{2}(t)c_{2n}\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ q_{n}\beta _{n}(t)c_{n1}&{} q_{n}\beta _{n}(t)c_{n2}&{} \cdots &{}q_{n}\beta _{n}(t)c_{nn}\\ \end{array} \right] , \\ \varpi _{23}= & {} \left[ \begin{array}{cccc} q_{1}\beta _{1}(t)c_{11}\omega _{1}&{} q_{1}\beta _{1}(t)c_{12}\omega _{2}&{} \cdots &{}q_{1}\beta _{1}(t)c_{1n}\omega _{n}\\ q_{2}\beta _{2}(t)c_{21}\omega _{1}&{} q_{2}\beta _{2}(t)c_{22}\omega _{2}&{} \cdots &{}q_{2}\beta _{2}(t)c_{2n}\omega _{n}\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ q_{n}\beta _{n}(t)c_{n1}\omega _{1}&{} q_{n}\beta _{n}(t)c_{n2}\omega _{2}&{} \cdots &{}q_{n}\beta _{n}(t)c_{nn}\omega _{n}\\ \end{array} \right] . \end{aligned}$$

According to Lemma 2.1 in Zhang and Zhao (2007), there exists a positive ${\mathcal {T}}$-periodic function h(t), such that ${\bar{h}}(t)=e^{{\bar{b}}t}h(t)$ is a solution of System (5), where ${\bar{b}}=\frac{1}{{\mathcal {T}}}\ln \rho (\varPhi _{{\mathcal {F}}-{\mathcal {V}}+{\bar{\epsilon }} \varpi }({\mathcal {T}}))$. We know that $\rho (\varPhi _{{\mathcal {F}}-{\mathcal {V}}+{\bar{\epsilon }} \varpi }({\mathcal {T}}))<1$ when ${\mathcal {R}}_0<1$. Therefore, we have ${\bar{h}}(t)\rightarrow 0$ as $t\rightarrow \infty$, which implies that the zero solution of System (5) is globally asymptotically stable. Applying the comparison principle (Smith and Waltman 1995), we know that for System (2),

$$\begin{aligned} \underset{t\rightarrow \infty }{\lim } e_{k}(t)=0,\;\underset{t\rightarrow \infty }{\lim } i_{k}(t)=0,\;\underset{t\rightarrow \infty }{\lim } f_{k}(t)=0,\;\underset{t\rightarrow \infty }{\lim } r_{k}(t)=0,\;(1\le k\le n). \end{aligned}$$

By the theory of asymptotic autonomous systems (Thieme 1992), we also know that

$$\begin{aligned} \underset{t\rightarrow \infty }{\lim } s_{k}(t)=s^{0}_{k},\;\underset{t\rightarrow \infty }{\lim } v_{k}(t)=v^{0}_{k},\;(1\le k\le n). \end{aligned}$$

Hence, the disease-free periodic solution ${\mathcal {P}}_{0}$ is globally asymptotically stable when ${\mathcal {R}}_{0}<1$. This completes the proof. $\square$

Remark 1

Since exogenous reinfection and reinfection of recovered individuals, that is, $\varrho _{k}\ne 0,\;\delta _{k}\ne 0,\;1\le k\le n$, we know that ${\mathcal {R}}_{0}$ is not a threshold parameter between the persistence and extinction of the disease (Bhunu et al. 2008). This implies that even if ${\mathcal {R}}_{0}<1$, the epidemic may take off. We verify the above conclusions through numerical simulations (see Fig. 8).

2.3 Uniform Persistence of the Disease

In this section, we demonstrate the uniform persistence of System (2) by using uniform persistence theory of the periodic epidemic model in Zhao (2003). First, we assume that $\varrho _{k}=0,\;\delta _{k}=0,\;1\le k\le n$, and we define the following symbols.

$$\begin{aligned} X:= & {} \Big \{({\mathbf {S}},{\mathbf {V}},{\mathbf {E}},{\mathbf {I}},{\mathbf {F}}, {\mathbf {R}})\in \varOmega : s_{k}>0,v_{k}>0,e_{k}\ge 0,i_{k}\ge 0,f_{k}\ge 0,r_{k}\ge 0,\\&\quad 1\le k\le n\Big \}, \\ X_{0}:= & {} \Big \{({\mathbf {S}},{\mathbf {V}},{\mathbf {E}},{\mathbf {I}}, {\mathbf {F}},{\mathbf {R}})\in \varOmega : e_{k}> 0,i_{k}> 0,f_{k}> 0,r_{k}> 0,\;1\le k\le n\Big \}, \\ \partial X_{0}:= & {} X \backslash X_{0}=\Big \{({\mathbf {S}},{\mathbf {V}}, {\mathbf {E}},{\mathbf {I}},{\mathbf {F}},{\mathbf {R}})\in \varOmega : e_{k}=0,i_{k}=0, f_{k}=0,r_{k}=0,\\&1\le k\le n\Big \}. \end{aligned}$$

Let $\varphi (t, x_{0})$ be the unique solution of System (2) with an initial value of $x_{0}:=({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0}, {\mathbf {F}}_{0},{\mathbf {R}}_{0})$. Let $F :X\rightarrow X$ be the $\text{ Poincar }\acute{\text{ e }}$ map associated with System (2), that is,

$$\begin{aligned} F(x_{0})=\varphi ({\mathcal {T}},x_{0}),\;\; {\forall }x_{0}\in X, \end{aligned}$$

where ${\mathcal {T}}$ represents the period, and $\varphi ({\mathcal {T}},x_{0})$ is the only solution of System (2) that satisfies $\varphi (0,x_{0})=x_{0}$. It is very clear that

$$\begin{aligned} F^{m}({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0},{\mathbf {R}}_{0})=\varphi (m{\mathcal {T}},({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0},{\mathbf {R}}_{0})),\;\; {\forall }m\ge 0. \end{aligned}$$

According to Theorem 1, we obtain that the solution of System (2) is uniformly bounded, which means that F is the point dissipative on X.

Lemma 3

(see Theorem 1.3.1 in Zhao (2003)) Assume that

• (C1) $F(X_{0})\subset X_{0}$ and F has a global attractor ${\mathcal {A}}$;

• (C2) The maximal compact invariant set ${\mathcal {A}}_{\partial } = {\mathcal {A}} \cap M_{\partial }$ of F in $\partial X_{0}$, possibly empty, admits a Morse decomposition $\{M_{1},..., M_{k}\}$ with the following properties:

  • (a) $M_{i}$ is isolated in X.

  • (b) $W^{s}(M_{i}) \cap X_{0} = \emptyset$ for each $1 \le i \le k$.

  Then, there exists $\delta > 0$ such that for any compact internally chain transitive set L with $L\not \subset M_{i}$, for all $1 \le i \le k$, we have $\inf _{x\in L}d(x,\partial X_{0}) > \delta$, that is to say $F: X \rightarrow X$ is uniformly persistent with respect to $(X_{0}, \partial X_{0})$.

Lemma 4

(see Theorem 1.3.6 in Zhao (2003)) Let $F:X\rightarrow X$ be a continuous map with $F(X_{0})\subset X_{0}$. Assume that

• (1) $F:X\rightarrow X$ is point dissipative;

• (2) F is compact; or alternatively, F is a-condensing and $\gamma ^{+}(U)$ is strongly bounded in $X_{0}$ if U is strongly bounded in $X_{0}$;

• (3) F is uniformly persistent with respect to $(X_{0},\partial X_{0})$.

  Then, there exists a global attractor $A_{0}$ for F in $X_{0}$ that attracts strongly bounded sets in $X_{0}$, and F has a coexistence state $x_{0}\in A_{0}$.

Theorem 3

If the basic reproduction number ${\mathcal {R}}_{0}>1$, then there is a positive constant $\varepsilon >0$ such that when

$$\begin{aligned} \big \Vert ({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0},{\mathbf {R}}_{0})-{\mathcal {P}}_{0}\big \Vert \le \varepsilon \end{aligned}$$

for any $({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0},{\mathbf {R}}_{0})\in X_{0}$, we have

$$\begin{aligned} \underset{m\rightarrow \infty }{\lim \sup }\; d\big (F^{m}({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0},{\mathbf {R}}_{0}),{\mathcal {P}}_{0}\big )\ge \varepsilon , \end{aligned}$$

where d(x, y) represents the distance between x and y.

Proof

Since ${\mathcal {R}}_{0} > 1$, $\rho (\varPhi _{{{{\mathcal {F}}}}-{{{\mathcal {V}}}}}({\mathcal {T}}))>1$ can be inferred from Lemma 2. Thus, we can choose ${\hat{\epsilon }}$ small enough such that $\rho (\varPhi _{{{{\mathcal {F}}}}-{{{\mathcal {V}}}}-{\hat{\epsilon }}\varpi }({\mathcal {T}}))>1$, where $\varpi$ and Eq.(6) are equal. Next, we proceed by contradiction to prove that

$$\begin{aligned} \underset{m\rightarrow \infty }{\lim \sup }\; d\big (F^{m}({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0},{\mathbf {R}}_{0}),{\mathcal {P}}_{0}\big )\ge \varepsilon . \end{aligned}$$

Using the counter-evidence method, we assume that the following formula holds:

$$\begin{aligned} \underset{m\rightarrow \infty }{\lim \sup }\; d\big (F^{m}({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0},{\mathbf {R}}_{0}),{\mathcal {P}}_{0}\big )< \varepsilon \end{aligned}$$

for some $({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0},{\mathbf {R}}_{0})\in X_{0}$. Without loss of generality, there exists a natural number $M>0$ such that for all $m\ge M$, we have

$$\begin{aligned} d\big (F^{m}({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0},{\mathbf {R}}_{0}),{\mathcal {P}}_{0}\big )< \varepsilon . \end{aligned}$$

By the continuous dependence of solutions with respect to initial values, we know that

$$\begin{aligned} \big \Vert \varphi (t, F^{m}({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0},{\mathbf {R}}_{0})),\varphi (t, {\mathcal {P}}_{0})\big \Vert < {\hat{\varepsilon }},\;\;{\forall }t\in [0, {\mathcal {T}}]. \end{aligned}$$

For any $t\ge 0$, let $t = m{\mathcal {T}}+t'$, where $t'\in [0,{\mathcal {T}})$, and m is the largest integer less than or equal to $\frac{t}{{\mathcal {T}}}$ . Therefore, we have

$$\begin{aligned} \left. \begin{aligned}&\big \Vert \varphi (t, ({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0},{\mathbf {R}}_{0})),\varphi (t, {\mathcal {P}}_{0})\big \Vert \\&=\big \Vert \varphi (t', F^{m}({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0},{\mathbf {R}}_{0})),\varphi (t', {\mathcal {P}}_{0})\big \Vert < {\hat{\varepsilon }},\;\;{\forall }t\ge 0, \end{aligned} \right. \end{aligned}$$

which implies that when $t\ge 0$, we have $s^{0}_{k}-{\hat{\varepsilon }}\le s_{k}(t)\le s^{0}_{k}+{\hat{\varepsilon }}$, $v^{0}_{k}-{\hat{\varepsilon }}\le v_{k}(t)\le v^{0}_{k}+{\hat{\varepsilon }}$, $0\le e_{k}(t)\le {\hat{\varepsilon }}$, $0\le i_{k}(t)\le {\hat{\varepsilon }}$, $0\le f_{k}(t)\le {\hat{\varepsilon }}$, and $0\le r_{k}(t)\le {\hat{\varepsilon }}$. Since $0\le \eta _{k}\le 1$, we obtain that $\eta _{k}v^{0}_{k}-{\hat{\varepsilon }}\le \eta _{k}(v^{0}_{k}-{\hat{\varepsilon }})\le \eta _{k}v_{k}(t)\le \eta _{k}(v^{0}_{k}+{\hat{\varepsilon }})\le \eta _{k}v^{0}_{k}+{\hat{\varepsilon }}$. Let ${\hat{\epsilon }}=2{\hat{\varepsilon }}$, we can obtain the following system:

$$\begin{aligned} \left\{ \begin{aligned} \frac{\text{ d }e_{1}}{\text{ d }t}&\ge (1-q_{1})\lambda _{1}(t)(s ^{0}_{1}+\eta _{1}v^{0}_{1}-{\hat{\epsilon }})-(\sigma _{1}+u+d_{1}+\alpha _{1})e_{1},\\ \frac{\text{ d }e_{k}}{\text{ d }t}&\ge a_{(k-1)k}\alpha _{k-1}e_{k-1}+(1-q_{k})\lambda _{k}(t)(s^{0}_{k}+\eta _{k}v^{0}_{k}-{\hat{\epsilon }})\\&-(\sigma _{k}+u+d_{k}+\alpha _{k})e_{k},&2\le k\le n,\\ \frac{\text{ d }i_{1}}{\text{ d }t}&\ge q_{1}\lambda _{1}(t)(s^{0}_{1}+\eta _{1}v^{0}_{1}-{\hat{\epsilon }})+\mu _{1}\sigma _{1}e_{1}+\chi _{1}r_{1}-(\theta _{1}+u+d_{1}+\alpha _{1})i_{1},\\ \frac{\text{ d }i_{k}}{\text{ d }t}&\ge a_{(k-1)k}\alpha _{k-1}i_{k-1}+q_{k}\lambda _{k}(t)(s^{0}_{k}+\eta _{k}v^{0}_{k}-{\hat{\epsilon }})+\mu _{k}\sigma _{k}e_{k}+\chi _{k}r_{k}\\&-(\theta _{k}+u+d_{k}+\alpha _{k})i_{k},&2\le k\le n,\\ \frac{\text{ d }f_{1}}{\text{ d }t}&= \xi _{1}\theta _{1}i_{1}-(\gamma _{1}+u+d_{1}+\alpha _{1})f_{1},\\ \frac{\text{ d }f_{k}}{\text{ d }t}&= a_{(k-1)k}\alpha _{k-1}f_{k-1}+\xi _{k}\theta _{k}i_{k}-(\gamma _{k}+u+d_{k}+\alpha _{k})f_{k},&2\le k\le n,\\ \frac{\text{ d }r_{1}}{\text{ d }t}&=\rho _{1}\gamma _{1}f_{1}+(1-\mu _{1})\sigma _{1}e_{1}+(1-\xi _{1})\theta _{1}i_{1}-(\chi _{1}+u+d_{1}+\alpha _{1})r_{1},\\ \frac{\text{ d }r_{k}}{\text{ d }t}&= a_{(k-1)k}\alpha _{k-1}r_{k-1}+\rho _{k}\gamma _{k}f_{k}+(1-\mu _{k})\sigma _{k}e_{k}+(1-\xi _{k})\theta _{k}i_{k}\\&-(\chi _{k}+u+d_{k}+\alpha _{k})r_{k},&2\le k\le n, \end{aligned} \right. \end{aligned}$$

where $\lambda _{k}(t)=\beta _{k}(t)\sum ^{n}_{j=1}c_{kj}(i_{j}+\omega _{j}f_{j})$. Next, we consider the following system:

$$\begin{aligned} \left\{ \begin{aligned} \frac{\text{ d }{\hat{e}}_{1}}{\text{ d }t}&=(1-q_{1}){\hat{\lambda }}_{1}(t)(s^{0}_{1}+\eta _{1}v^{0}_{1}-{\hat{\epsilon }})-(\sigma _{1}+u+d_{1}+\alpha _{1}){\hat{e}}_{1},\\ \frac{\text{ d }{\hat{e}}_{k}}{\text{ d }t}&=a_{(k-1)k}\alpha _{k-1}{\hat{e}}_{k-1}+(1-q_{k}){\hat{\lambda }}_{k}(t)(s^{0}_{k}+\eta _{k}v^{0}_{k}-{\hat{\epsilon }})\\&\quad -(\sigma _{k}+u+d_{k}+\alpha _{k}){\hat{e}}_{k},&2\le k\le n,\\ \frac{\text{ d }{\hat{i}}_{1}}{\text{ d }t}&=q_{1}{\hat{\lambda }}_{1}(t)(s^{0}_{1}+\eta _{1}v^{0}_{1}-{\hat{\epsilon }})+\mu _{1}\sigma _{1}{\hat{e}}_{1}+\chi _{1}{\hat{r}}_{1}-(\theta _{1}+u+d_{1}+\alpha _{1}){\hat{i}}_{1},\\ \frac{\text{ d }{\hat{i}}_{k}}{\text{ d }t}&=a_{(k-1)k}\alpha _{k-1}{\hat{i}}_{k-1}+q_{k}{\hat{\lambda }}_{k}(t)(s^{0}_{k}+\eta _{k}v^{0}_{k}-{\hat{\epsilon }})+\mu _{k}\sigma _{k}{\hat{e}}_{k}+\chi _{k}{\hat{r}}_{k}\\&\quad -(\theta _{k}+u+d_{k}+\alpha _{k}){\hat{i}}_{k},&2\le k\le n,\\ \frac{\text{ d }{\hat{f}}_{1}}{\text{ d }t}&=\xi _{1}\theta _{1}{\hat{i}}_{1}-(\gamma _{1}+u+d_{1}+\alpha _{1}){\hat{f}}_{1},\\ \frac{\text{ d }{\hat{f}}_{k}}{\text{ d }t}&=a_{(k-1)k}\alpha _{k-1}{\hat{f}}_{k-1}+\xi _{k}\theta _{k}{\hat{i}}_{k}-(\gamma _{k}+u+d_{k}+\alpha _{k}){\hat{f}}_{k},&2\le k\le n,\\ \frac{\text{ d }{\hat{r}}_{1}}{\text{ d }t}&=\rho _{1}\gamma _{1}{\hat{f}}_{1}+(1-\mu _{1})\sigma _{1}{\hat{e}}_{1}+(1-\xi _{1})\theta _{1}{\hat{i}}_{1}-(\chi _{1}+u+d_{1}+\alpha _{1}){\hat{r}}_{1},\\ \frac{\text{ d }{\hat{r}}_{k}}{\text{ d }t}&=a_{(k-1)k}\alpha _{k-1}{\hat{r}}_{k-1}+\rho _{k}\gamma _{k}{\hat{f}}_{k}+(1-\mu _{k})\sigma _{k}{\hat{e}}_{k}+(1-\xi _{k})\theta _{k}{\hat{i}}_{k}\\&\quad -(\chi _{k}+u+d_{k}+\alpha _{k}){\hat{r}}_{k},&2\le k\le n, \end{aligned} \right. \nonumber \\ \end{aligned}$$

(7)

where ${\hat{\lambda }}_{k}(t)=\beta _{k}(t)\sum ^{n}_{j=1}c_{kj}({\hat{i}}_{j}+\omega _{j}{\hat{f}}_{j})$. By Lemma 2.1 in Zhang and Zhao (2007), we know that there is a positive ${\mathcal {T}}$-periodic function g(t), such that ${\hat{g}}(t)=e^{{\hat{b}}t}g(t)$ is a solution of System (7), where ${\hat{b}}=\frac{1}{{\mathcal {T}}}\ln \rho (\varPhi _{{\mathcal {F}}-{\mathcal {V}}-{\hat{\epsilon }} \varpi }({\mathcal {T}}))$. We know that $\rho (\varPhi _{{\mathcal {F}}-{\mathcal {V}}-{\hat{\epsilon }} \varpi }({\mathcal {T}}))>1$ when ${\mathcal {R}}_0>1$. Therefore, we have ${\hat{g}}(t)\rightarrow \infty$ as $t\rightarrow \infty$ when ${\hat{g}}(0)>0$. Applying the comparison principle (Smith and Waltman 1995), when $e_{k}(0)>0$, $i_{k}(0)>0$, $f_{k}(0)>0$, and $r_{k}(0)>0$, we know that

$$\begin{aligned} \underset{t\rightarrow \infty }{\lim } e_{k}(t)=\infty ,\;\underset{t\rightarrow \infty }{\lim } i_{k}(t)=\infty ,\;\underset{t\rightarrow \infty }{\lim } f_{k}(t)=\infty ,\;\underset{t\rightarrow \infty }{\lim } r_{k}(t)=\infty ,\;(1\le k\le n), \end{aligned}$$

which is a contradiction with Theorem 3. Thus, $\underset{m\rightarrow \infty }{\lim \sup }\; d(F^{m}({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0},{\mathbf {R}}_{0}),{\mathcal {P}}_{0})\ge \varepsilon$. This completes the proof. $\square$

Theorem 4

If the basic reproduction number ${\mathcal {R}}_{0}>1$, then there exists a $\varsigma >0$ such that the solution $({\mathbf {S}}(t),{\mathbf {V}}(t),{\mathbf {E}}(t),{\mathbf {I}}(t),{\mathbf {F}}(t),{\mathbf {R}}(t))$ of System (2) with initial value condition $({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0},{\mathbf {R}}_{0})\in X_{0}$ satisfies

$$\begin{aligned}&\underset{t\rightarrow \infty }{\lim \inf }\;e_{k}(t)\ge \varsigma ,\;\underset{t\rightarrow \infty }{\lim \inf }\;i_{k}(t)\ge \varsigma ,\;\underset{t\rightarrow \infty }{\lim \inf }\;f_{k}(t)\ge \varsigma ,\\&\underset{t\rightarrow \infty }{\lim \inf }\;r_{k}(t)\ge \varsigma ,\;(1\le k\le n), \end{aligned}$$

and System (2) admits at least one positive periodic solution.

Proof

First, we prove that F is uniformly persistent with respect to $(X_{0}, \partial X_{0})$. For any initial value condition $({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0},{\mathbf {R}}_{0})\in X_{0}$, solving the equations of System (2), we obtain that

$$\begin{aligned} s_{1}(t)= & {} \text{ e}^{-\int ^{t}_{0}A_{s_{1}}(\vartheta )d\vartheta }\nonumber \\&\times \Bigg (s_{1_0}+\int ^{t}_{0}\big [(1-p_{1})(\alpha _{1}+d_{1}+u)+\tau _{1}v_{1}({\bar{\vartheta }})\big ] \text{ e}^{\int ^{{\bar{\vartheta }}}_{0}A_{s_{1}}(\vartheta )d\vartheta }d{\bar{\vartheta }}\Bigg )\nonumber \\> & {} \text{ e}^{-\int ^{t}_{0}A_{s_{1}}(\vartheta )d\vartheta }\int ^{t}_{0}\big [(1-p_{1})(\alpha _{1}+d_{1}+u)+\tau _{1}v_{1}({\bar{\vartheta }})\big ] \text{ e}^{\int ^{{\bar{\vartheta }}}_{0}A_{s_{1}}(\vartheta )d\vartheta }d{\bar{\vartheta }}\nonumber \\> & {} 0,\;\;{\forall }t\ge 0, \end{aligned}$$

(8)

where $A_{s_{1}}(\vartheta )=\lambda _{1}(\vartheta )+u+d_{1}+\gamma _{1}$.

$$\begin{aligned} s_{k}(t)= & {} \text{ e}^{-\int ^{t}_{0}A_{s_{k}}(\vartheta )d\vartheta }\Bigg (s_{k_0}+\int ^{t}_{0}\big [a_{(k-1)k}\alpha _{k-1}s_{k-1}({\bar{\vartheta }})+\tau _{k}v_{k}({\bar{\vartheta }})\big ] \text{ e}^{\int ^{{\bar{\vartheta }}}_{0}A_{s_{k}}(\vartheta )d\vartheta }d{\bar{\vartheta }}\Bigg )\nonumber \\> & {} \text{ e}^{-\int ^{t}_{0}A_{s_{k}}(\vartheta )d\vartheta }\int ^{t}_{0}\big [a_{(k-1)k}\alpha _{k-1}s_{k-1}({\bar{\vartheta }})+\tau _{k}v_{k}({\bar{\vartheta }})\big ] \text{ e}^{\int ^{{\bar{\vartheta }}}_{0}A_{s_{k}}(\vartheta )d\vartheta }d{\bar{\vartheta }}\nonumber \\> & {} 0,\;\; 2\le k\le n,\;\;{\forall }t\ge 0, \end{aligned}$$

(9)

where $A_{s_{k}}(\vartheta )={\lambda }_{k}(\vartheta )+\nu _{k}+u+d_{k}+\alpha _{k}$.

$$\begin{aligned} v_{1}(t)= & {} \text{ e}^{-\int ^{t}_{0}A_{v_{1}}(\vartheta )d\vartheta }\Bigg (v_{1_0}+\int ^{t}_{0}p_{1}(\alpha _{1}+d_{1}+u) \text{ e}^{\int ^{{\bar{\vartheta }}}_{0}A_{v_{1}}(\vartheta )d\vartheta }d{\bar{\vartheta }}\Bigg )\nonumber \\> & {} p_{1}(\alpha _{1}+d_{1}+u)\text{ e}^{-\int ^{t}_{0}A_{v_{1}}(\vartheta )d\vartheta }\int ^{t}_{0} \text{ e}^{\int ^{{\bar{\vartheta }}}_{0}A_{v_{1}}(\vartheta )d\vartheta }d{\bar{\vartheta }}\nonumber \\> & {} 0,\;\;{\forall }t\ge 0, \end{aligned}$$

(10)

where $A_{v_{1}}(\vartheta )=\eta _{1}{\lambda }_{1}(\vartheta )+\tau _{1}+u+d_{1}+\alpha _{1}$.

$$\begin{aligned} v_{k}(t)= & {} \text{ e}^{-\int ^{t}_{0}A_{v_{k}}(\vartheta )d\vartheta }\Bigg (v_{k_0}+\int ^{t}_{0}\big [a_{(k-1)k}\alpha _{k-1}v_{k-1}({\bar{\vartheta }})+\nu _{k}s_{k}({\bar{\vartheta }})\big ] \text{ e}^{\int ^{{\bar{\vartheta }}}_{0}A_{v_{k}}(\vartheta )d\vartheta }d{\bar{\vartheta }}\Bigg )\nonumber \\> & {} \text{ e}^{-\int ^{t}_{0}A_{v_{k}}(\vartheta )d\vartheta }\int ^{t}_{0}\big [a_{(k-1)k}\alpha _{k-1}v_{k-1}({\bar{\vartheta }})+\nu _{k}s_{k}({\bar{\vartheta }})\big ] \text{ e}^{\int ^{{\bar{\vartheta }}}_{0}A_{v_{k}}(\vartheta )d\vartheta }d{\bar{\vartheta }}\nonumber \\> & {} 0,\;\; 2\le k\le n,\;\;{\forall }t\ge 0, \end{aligned}$$

(11)

where $A_{v_{k}}(\vartheta )=\eta _{k}{\lambda }_{k}(\vartheta )+\tau _{k}+u+d_{k}+\alpha _{k}$.

$$\begin{aligned} e_{1}(t)= & {} \text{ e}^{-A_{e_{1}}t}\Bigg (e_{1_0}+\int ^{t}_{0}\big [(1-q_{1}){\lambda }_{1}({\bar{\vartheta }})(s_{1}({\bar{\vartheta }})+\eta _{1}v_{1}({\bar{\vartheta }})+\delta _{1}r_{1}({\bar{\vartheta }}))\big ] \text{ e}^{A_{e_{1}}{\bar{\vartheta }}}d{\bar{\vartheta }}\Bigg )\nonumber \\> & {} \text{ e}^{-A_{e_{1}}t}\int ^{t}_{0}\big [(1-q_{1}){\lambda }_{1}({\bar{\vartheta }})(s_{1}({\bar{\vartheta }})+\eta _{1}v_{1}({\bar{\vartheta }})+\delta _{1}r_{1}({\bar{\vartheta }}))\big ] \text{ e}^{A_{e_{1}}{\bar{\vartheta }}}d{\bar{\vartheta }}\nonumber \\\ge & {} 0,\;\;{\forall }t\ge 0, \end{aligned}$$

(12)

where $A_{e_{1}}=\sigma _{1}+u+d_{1}+\alpha _{1}$.

$$\begin{aligned} e_{k}(t)= & {} \text{ e}^{-A_{e_{k}}t}\Bigg (e_{1_k}+\int ^{t}_{0}\big [a_{(k-1)k}\alpha _{k-1}e_{k-1}({\bar{\vartheta }})+B_{e_{k}}({\bar{\vartheta }})\big ] \text{ e}^{A_{e_{k}}{\bar{\vartheta }}}d{\bar{\vartheta }}\Bigg )\nonumber \\> & {} \text{ e}^{-A_{e_{k}}t}\int ^{t}_{0}\big [a_{(k-1)k}\alpha _{k-1}e_{k-1}({\bar{\vartheta }})+B_{e_{k}}({\bar{\vartheta }})\big ] \text{ e}^{A_{e_{k}}{\bar{\vartheta }}}d{\bar{\vartheta }}\nonumber \\> & {} 0,\;\; 2\le k\le n,\;\;{\forall }t\ge 0, \end{aligned}$$

(13)

where $A_{e_{k}}=\sigma _{k}+u+d_{k}+\alpha _{k}$, $B_{e_{k}}({\bar{\vartheta }})=(1-q_{k}){\lambda }_{k}({\bar{\vartheta }})(s_{k}({\bar{\vartheta }})+\eta _{k}v_{k}({\bar{\vartheta }})+\delta _{k}r_{k}({\bar{\vartheta }}))$.

$$\begin{aligned} i_{1}(t)= & {} \text{ e}^{-(\theta _{1}+u+d_{1}+\alpha _{1})t}\Bigg (i_{1_0}+\int ^{t}_{0}B_{i_{1}}({\bar{\vartheta }}) \text{ e}^{(\theta _{1}+u+d_{1}+\alpha _{1}){\bar{\vartheta }}}d{\bar{\vartheta }}\Bigg )\nonumber \\> & {} \text{ e}^{-(\theta _{1}+u+d_{1}+\alpha _{1})t}\int ^{t}_{0}B_{i_{1}}({\bar{\vartheta }}) \text{ e}^{(\theta _{1}+u+d_{1}+\alpha _{1}){\bar{\vartheta }}}d{\bar{\vartheta }}\nonumber \\\ge & {} 0,\;\;{\forall }t\ge 0, \end{aligned}$$

(14)

where $B_{i_{1}}({\bar{\vartheta }})=q_{1}{\lambda }_{1}({\bar{\vartheta }})(s_{1}({\bar{\vartheta }})+\eta _{1}v_{1}({\bar{\vartheta }}))+\mu _{1}\sigma _{1}e_{1}({\bar{\vartheta }})+\chi _{1}r_{1}({\bar{\vartheta }})$.

$$\begin{aligned} i_{k}(t)= & {} \text{ e}^{-(\theta _{k}+u+d_{k}+\alpha _{k})t}\nonumber \\&\times \Bigg (i_{k_0}+\int ^{t}_{0}\big [a_{(k-1)k}\alpha _{k-1}i_{k-1}({\bar{\vartheta }})+B_{i_{k}}({\bar{\vartheta }})\big ] \text{ e}^{(\theta _{k}+u+d_{k}+\alpha _{k}){\bar{\vartheta }}}d{\bar{\vartheta }}\Bigg )\nonumber \\> & {} \text{ e}^{-(\theta _{k}+u+d_{k}+\alpha _{k})t}\int ^{t}_{0}\big [a_{(k-1)k}\alpha _{k-1}i_{k-1}({\bar{\vartheta }})+B_{i_{k}}({\bar{\vartheta }})\big ] \text{ e}^{(\theta _{k}+u+d_{k}+\alpha _{k}){\bar{\vartheta }}}d{\bar{\vartheta }}\nonumber \\> & {} 0,\;\; 2\le k\le n,\;\;{\forall }t\ge 0, \end{aligned}$$

(15)

where $B_{i_{k}}({\bar{\vartheta }})=q_{k}{\lambda }_{k}({\bar{\vartheta }})(s_{k}({\bar{\vartheta }})+\eta _{k}v_{k}({\bar{\vartheta }}))+\mu _{k}\sigma _{k}e_{k}({\bar{\vartheta }})+\chi _{k}r_{k}({\bar{\vartheta }})$.

$$\begin{aligned} f_{1}(t)= & {} \text{ e}^{-(\gamma _{1}+u+d_{1}+\alpha _{1})t}\Bigg (f_{1_0}+\int ^{t}_{0}\xi _{1}\theta _{1}i_{1}({\bar{\vartheta }}) \text{ e}^{(\gamma _{1}+u+d_{1}+\alpha _{1}){\bar{\vartheta }}}d{\bar{\vartheta }}\Bigg )\nonumber \\> & {} \text{ e}^{-(\gamma _{1}+u+d_{1}+\alpha _{1})t}\int ^{t}_{0}\xi _{1}\theta _{1}i_{1}({\bar{\vartheta }}) \text{ e}^{(\gamma _{1}+u+d_{1}+\alpha _{1}){\bar{\vartheta }}}d{\bar{\vartheta }}\nonumber \\> & {} 0,\;\;{\forall }t\ge 0. \end{aligned}$$

(16)

$$\begin{aligned} f_{k}(t)= & {} \text{ e}^{-(\gamma _{k}+u+d_{k}+\alpha _{k})t}\nonumber \\&\times \Bigg (f_{k_0}+\int ^{t}_{0}\big [a_{(k-1)k}\alpha _{k-1}f_{k-1}({\bar{\vartheta }})+\xi _{k}\theta _{k}i_{k}({\bar{\vartheta }})\big ] \text{ e}^{(\gamma _{k}+u+d_{k}+\alpha _{k}){\bar{\vartheta }}}d{\bar{\vartheta }}\Bigg )\nonumber \\> & {} \text{ e}^{-(\gamma _{k}+u+d_{k}+\alpha _{k})t}\int ^{t}_{0}\big [a_{(k-1)k}\alpha _{k-1}f_{k-1}({\bar{\vartheta }})+\xi _{k}\theta _{k}i_{k}({\bar{\vartheta }})\big ] \text{ e}^{(\gamma _{k}+u+d_{k}+\alpha _{k}){\bar{\vartheta }}}d{\bar{\vartheta }}\nonumber \\> & {} 0,\;\; 2\le k\le n,\;\;{\forall }t\ge 0. \end{aligned}$$

(17)

$$\begin{aligned} r_{1}(t)= & {} \text{ e}^{-A_{r_{1}}t}\nonumber \\&\times \Bigg (r_{1_0}+\int ^{t}_{0}\big [\rho _{1}\gamma _{1}f_{1}({\bar{\vartheta }})+(1-\mu _{1})\sigma _{1}e_{1}({\bar{\vartheta }})+(1-\xi _{1})\theta _{1}i_{1}({\bar{\vartheta }})\big ] \text{ e}^{A_{r_{1}}{\bar{\vartheta }}}d{\bar{\vartheta }}\Bigg )\nonumber \\> & {} \text{ e}^{-A_{r_{1}}t}\int ^{t}_{0}\big [\rho _{1}\gamma _{1}f_{1}({\bar{\vartheta }})+(1-\mu _{1})\sigma _{1}e_{1}({\bar{\vartheta }})+(1-\xi _{1})\theta _{1}i_{1}({\bar{\vartheta }})\big ] \text{ e}^{A_{r_{1}}{\bar{\vartheta }}}d{\bar{\vartheta }}\nonumber \\> & {} 0,\;\;{\forall }t\ge 0, \end{aligned}$$

(18)

where $A_{r_{1}}=\chi _{1}+u+d_{1}+\alpha _{1}$.

$$\begin{aligned} r_{k}(t)= & {} \text{ e}^{-A_{r_{k}}t}\Bigg (r_{k_0}+\int ^{t}_{0}\big [a_{(k-1)k}\alpha _{k-1}r_{k-1}({\bar{\vartheta }})+B_{r_{k}}({\bar{\vartheta }})\big ] \text{ e}^{A_{r_{k}}{\bar{\vartheta }}}d{\bar{\vartheta }}\Bigg )\nonumber \\> & {} \text{ e}^{-A_{r_{k}}t}\int ^{t}_{0}\big [a_{(k-1)k}\alpha _{k-1}r_{k-1}({\bar{\vartheta }})+B_{r_{k}}({\bar{\vartheta }})\big ] \text{ e}^{A_{r_{k}}{\bar{\vartheta }}}d{\bar{\vartheta }}\nonumber \\> & {} 0,\;\; 2\le k\le n,\;\;{\forall }t\ge 0, \end{aligned}$$

(19)

where $A_{r_{k}}=\chi _{k}+u+d_{k}+\alpha _{k}$, $B_{r_{k}}({\bar{\vartheta }})=\rho _{k}\gamma _{k}f_{k}({\bar{\vartheta }})+(1-\mu _{k})\sigma _{k}e_{k}({\bar{\vartheta }})+(1-\xi _{k})\theta _{k}i_{k}({\bar{\vartheta }})$. Thus, both X and $X_0$ are positively invariant. Clearly, $\partial X_0$ is relatively closed in X.

We let

$$\begin{aligned} M_{\partial }= & {} \Big \{({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0},{\mathbf {R}}_{0})\in \partial X_{0}: F^{m}({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0},{\mathbf {R}}_{0})\in \partial X_{0},\nonumber \\&{\forall }m\ge 0\Big \}. \end{aligned}$$

(20)

Next, we prove that $M_{\partial } = \{({\mathbf {S}},{\mathbf {V}},{\mathbf {0}},{\mathbf {0}},{\mathbf {0}},{\mathbf {0}})\in X:s_{k}\ge 0,v_{k}\ge 0,\;1\le k\le n\}$ holds, where ${\mathbf {0}}$ represents the zero vector of n dimensions. Obviously, we obtain that

$$\begin{aligned} \{({\mathbf {S}},{\mathbf {V}},{\mathbf {0}},{\mathbf {0}},{\mathbf {0}},{\mathbf {0}})\in X:s_{k}\ge 0,v_{k}\ge 0,\;1\le k\le n\} \subseteq M_{\partial }. \end{aligned}$$

Thus, we only need to prove that

$$\begin{aligned} M_{\partial }\subseteq \big \{({\mathbf {S}},{\mathbf {V}},{\mathbf {0}},{\mathbf {0}},{\mathbf {0}},{\mathbf {0}})\in X:s_{k}\ge 0,v_{k}\ge 0,\;1\le k\le n\big \}. \end{aligned}$$

Otherwise, if $M_{\partial }\backslash \{({\mathbf {S}},{\mathbf {V}},{\mathbf {0}},{\mathbf {0}},{\mathbf {0}},{\mathbf {0}})\in X:s_{k}\ge 0,v_{k}\ge 0,\;1\le k\le n\}\ne \emptyset$, then at least a point $({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0}, {\mathbf {R}}_{0})\in M_{\partial }$ satisfies that at least one of $e_{k_0}$, $i_{k_0}$, $f_{k_0}$, and $r_{k_0}$ is greater than 0, where $1\le k\le n$.

If $e_{1_0}>0$, we obtain that inequality (12) holds. From $e_{k_0}>0,(2\le k\le n)$ and inequality (13), we have $e_{k}(t)>0,(2\le k\le n)$ for all $t > 0$. Similarly, we also obtain that $s_{k}(t)>0,(1\le k\le n)$, $v_{k}(t)>0,(1\le k\le n)$, $i_{k}(t)>0,(1\le k\le n)$, $f_{k}(t)>0,(1\le k\le n)$, and $r_{k}(t)>0,(1\le k\le n)$ for all $t > 0$, which contradicts that $F^{m}({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0},{\mathbf {R}}_{0})\in \partial X_{0},{\forall }m\ge 0$ when $({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0},{\mathbf {R}}_{0})\in \partial X_{0}$. Similarly, if $i_{1_0}>0$, we also obtain that $s_{k}(t)>0$, $v_{k}(t)>0$, $e_{k}(t)>0$, $i_{k}(t)>0$, $f_{k}(t)>0$, and $r_{k}(t)>0$ for all $t > 0$, where $1\le k\le n$, which leads to a contradiction. Therefore, we have $M_{\partial }\subseteq \big \{({\mathbf {S}},{\mathbf {V}},{\mathbf {0}},{\mathbf {0}},{\mathbf {0}},{\mathbf {0}})\in X:s_{k}\ge 0,v_{k}\ge 0,\;1\le k\le n\big \}$, which implies that Eq.(20) holds. Moreover, there only exists one fixed point ${\mathcal {P}}_{0}$ of F in $M_{\partial }$.

According to Theorem 3, we know that ${\mathcal {P}}_{0}$ is an isolated invariant set in X and $W^{s}({\mathcal {P}}_{0})\cap X_{0}=\emptyset$, where the set $W^{s}({\mathcal {P}}_{0})$ is the stable set of ${\mathcal {P}}_{0}$. Note that every orbit in $M_{\partial }$ approaches ${\mathcal {P}}_{0}$, and ${\mathcal {P}}_{0}$ is acyclic in $M_{\partial }$. According to Lemma 3, F is uniformly persistent with respect to $(X_{0}, \partial X_{0})$. Thus, the solution of System (2) is uniformly persistent, i.e., there exists a $\varsigma >0$ such that the solution $({\mathbf {S}}(t),{\mathbf {V}}(t),{\mathbf {E}}(t),{\mathbf {I}}(t),{\mathbf {F}}(t),{\mathbf {R}}(t))$ of System (2) with initial value condition $({\mathbf {S}}_{0},{\mathbf {V}}_{0},{\mathbf {E}}_{0},{\mathbf {I}}_{0},{\mathbf {F}}_{0},{\mathbf {R}}_{0})\in X_{0}$ satisfies

$$\begin{aligned}&\underset{t\rightarrow \infty }{\lim \inf }\;e_{k}(t)\ge \varsigma ,\;\underset{t\rightarrow \infty }{\lim \inf }\;i_{k}(t)\ge \varsigma ,\;\underset{t\rightarrow \infty }{\lim \inf }\;f_{k}(t)\ge \varsigma ,\\&\underset{t\rightarrow \infty }{\lim \inf }\;r_{k}(t)\ge \varsigma ,\;(1\le k\le n). \end{aligned}$$

Next, we prove the existence of a positive ${\mathcal {T}}$-period solution of System (2). According to Lemma 4, we know that F has a fixed point $({\mathbf {S}}^{*}(0),{\mathbf {V}}^{*}(0),{\mathbf {E}}^{*}(0),{\mathbf {I}}^{*}(0),{\mathbf {F}}^{*}(0),{\mathbf {R}}^{*}(0)) \in X_{0}$. Then, $s^{*}_{k}(0)\ge 0$, $v^{*}_{k}(0)\ge 0$, $e^{*}_{k}(0)>0$, $i^{*}_{k}(0)> 0$, $f^{*}_{k}(0)> 0$ and $r^{*}_{k}(0)> 0$, where $1\le k\le n$. We now prove that $s^{*}_{1}(0)> 0$. If it is not the case, then $s^{*}_{1}(0)=0$. From the first equation of System (2), we obtain that

$$\begin{aligned} s^{*}_{1}(t)= & {} \text{ e}^{-\int ^{t}_{0}A_{s_{1}}(\vartheta )d\vartheta }\\&\times \Bigg (s^{*}_{1}(0)+\int ^{t}_{0}\big [(1-p_{1})(\alpha _{1}+d_{1}+u)+\tau _{1}v_{1}({\bar{\vartheta }})\big ] \text{ e}^{\int ^{{\bar{\vartheta }}}_{0}A_{s_{1}}(\vartheta )d\vartheta }d{\bar{\vartheta }}\Bigg )\\= & {} \text{ e}^{-\int ^{t}_{0}A_{s_{1}}(\vartheta )d\vartheta }\int ^{t}_{0}\big [(1-p_{1})(\alpha _{1}+d_{1}+u)+\tau _{1}v_{1}({\bar{\vartheta }})\big ] \text{ e}^{\int ^{{\bar{\vartheta }}}_{0}A_{s_{1}}(\vartheta )d\vartheta }d{\bar{\vartheta }}\\> & {} 0,\;\;{\forall }t\in [0,{\mathcal {T}}], \end{aligned}$$

where $A_{s_{1}}(t)=\lambda _{1}(t)+u+d_{1}+\gamma _{1}$. The periodicity of $s^{*}_{1}(t)$ implies that $s^{*}_{1}(0)=s^{*}_{1}(m{\mathcal {T}})=0$, which is a contradiction. Thus, it follows that $s^{*}_{1}(0)>0$. Similarly, we also obtain that $s^{*}_{k}(0)>0,(2\le k\le n)$, and $v^{*}_{k}(0)>0,(1\le k\le n)$. Following the processes as in inequalities (8)-(19), we obtain that $s^{*}_{k}(t)> 0$, $v^{*}_{k}(t)>0$, $e^{*}_{k}(t)>0$, $i^{*}_{k}(t)> 0$, $f^{*}_{k}(t)> 0$ and $r^{*}_{k}(t)> 0$ for all $t>0$, where $1\le k\le n$. Thus, $({\mathbf {S}}^{*}(t),{\mathbf {V}}^{*}(t),{\mathbf {E}}^{*}(t),{\mathbf {I}}^{*}(t),{\mathbf {F}}^{*}(t),{\mathbf {R}}^{*}(t))$ is the positive ${\mathcal {T}}$-period solution of System (2). This completes the proof. $\square$

3 Fitting the Model to the TB Data of Mainland China

In this section, we estimate unknown parameters and initial values of System (1) using monthly number of new TB cases for 14 age-groups from January 2005 to December 2017 in mainland China, and we obtain the mean value and confidence interval of the basic reproduction number, ${\mathcal {R}}_{0}$.

3.1 Data Collection and Analysis

To parameterize the mathematical model for the transmission dynamics of TB in mainland China, we use observations of reported cases from January 2005 to December 2017, provided by the Data-Center of China Public Health Science (2021). This database collects all TB data reported since 2004, and the main content of the database includes the number of cases, morbidity, deaths, and death rates by region and age. We focus on the number of monthly new cases for each age-group. Figure 2A shows the prevalence of TB per 100,000 individuals in each age-group from January 2005 to December 2017, where

$$\begin{aligned} \text{ Prevalence } \text{ of } \text{ the } \text{ kth } \text{ age-group }= & {} \frac{\text{ Number } \text{ of } \text{ new } \text{ cases } \text{ of } \text{ the } \text{ kth } \text{ age-group }}{\text{ The } \text{ total } \text{ population } \text{ of } \text{ the } \text{ kth } \text{ age-group }}\\&\times 100000. \end{aligned}$$

The total population of China from 2005 to 2019 is provided by the China Statistical Yearbook (National Bureau of Statistics 2021a), as shown in Table 6. The population pyramids by age and gender are provided by the tabulation on the 2010 Population Census Office of the State Council of the People’s Republic of China (2021), as shown in Fig. 2B.

Fig. 2

A TB prevalence per 100,000 individuals. B The population pyramids by age and gender in China (Color figure online)

It can be seen from Fig. 2(A) that the prevalence of TB per 100,000 individuals of all age-groups shows periodic variations with peak in late spring to early summer each year. The mean monthly TB prevalence per 100,000 individuals is 84.2783 for all age-groups, 0.2851 for 0–4 years old, 0.3288 for 5–9 years old, 0.7130 for 10–14 years old, 4.8932 for 15–19 years old, 6.5233 for 20–24 years old, 6.5874 for 25–29 years old, 5.7410 for 30–34 years old, 4.9694 for 35–39 years old, 5.2128 for 40–44 years old, 5.9061 for 45–49 years old, 8.4524 for 50–54 years old, 8.1967 for 55–59 years old, 11.6263 for 60–64 years old, 14.8427 for 65+ years old (see Table 1). The prevalence of TB per 100,000 individuals is the highest among people over 65 years old, and the prevalence of TB per 100,000 individuals is the lowest among people under 15 years old. Further, Pearson’s correlation analysis showed that the prevalence of TB per 100,000 individuals was highly positively correlated with the age of individuals infected with TB from 2005 to 2017, as shown in Fig. 3. More specifically, the correlation coefficient between the prevalence of TB per 100,000 individuals and the age of individuals infected with TB was greater than $0.85\;(p<0.01)$ from 2005 to 2017, which indicates that older people are more likely to be infected by Mycobacterium TB.

Table 1 Distribution of monthly TB prevalence per 100,000 individuals in mainland China from January 2005 to December 2017. Q1 represents 25th percentile, Q3 represents 75th percentile

Fig. 3

Correlation between the age of the population and the prevalence of TB per 100,000 individuals from 2005 to 2017. The 14 age-groups represent 0–4 years old 5–9 years old, 10–14 years old, 15–19 years old, 20–24 years old, 25–29 years old, 30–34 years old, 35–39 years old, 40–44 years old, 45–49 years old, 50–54 years old, 55–59 years old, 60–64 years old, and 65+ years old, respectively (Color figure online)

3.2 Parameter Estimation

To simulate the number of new TB cases in mainland China, the rationality of the model is verified by the actual number of newly infected cases. We divide the population into 14 age-groups: 0–4 years old 5–9 years old, 10–14 years old, 15–19 years old, 20-24 years old, 25–29 years old, 30–34 years old, 35–39 years old, 40–44 years old, 45–49 years old, 50–54 years old, 55–59 years old, 60–64 years old, and over 65 years old. Next, we estimate all parameters and initial values of System (1).

(I) The birth rate of the population (i.e., $b_{k}$): According to the statistics of the China Statistical Yearbook (2014), we assume that the birth rate of people under age 15 and over 50 is 0, that is, $b_{1}=0$, $b_{2}=0$, $b_{3}=0$, $b_{11}=0$, $b_{12}=0$, $b_{13}=0$, and $b_{14}=0$. The birth rates of other age-groups are $b_{4}=0.98\times 10^{-3}$, $b_{5}=6.85\times 10^{-3}$, $b_{6}=7.61\times 10^{-3}$, $b_{7}=4.08\times 10^{-3}$, $b_{8}=1.44\times 10^{-3}$, $b_{9}=0.33\times 10^{-3}$, and $b_{10}=0.09\times 10^{-3}$ (Feng et al. 2020; Su et al. 2021).

(II) The natural mortality rate of the population (i.e., $d_{k}$): According to the China Statistical Yearbook (National Bureau of Statistics 2021b), we obtain that the average lifetime of Chinese is 76 years. Thus, we conclude that the monthly natural mortality rates of Chinese are $d_{1}={1}/{(76\times 12)}$, $d_{2}={1}/{(71\times 12)}$, $d_{3}={1}/{(66\times 12)}$, $d_{4}={1}/{(61\times 12)}$, $d_{5}={1}/{(56\times 12)}$, $d_{6}={1}/{(51\times 12)}$, $d_{7}={1}/{(46\times 12)}$, $d_{8}={1}/{(41\times 12)}$, $d_{9}={1}/{(36\times 12)}$, $d_{10}={1}/{(31\times 12)}$, $d_{11}={1}/{(26\times 12)}$, $d_{12}={1}/{(21\times 12)}$, $d_{13}={1}/{(16\times 12)}$, and $d_{14}={1}/{(11\times 12)}$.

(III) The rate of aging (i.e., $\alpha _{k}$): Since the maximum difference of age for each age-group is 5 years, the monthly aging rate of individuals is ${1}/{(5\times 12)}$. Therefore, we have

$$\begin{aligned} \alpha _{k}=\left\{ \begin{aligned}&\frac{1}{5\times 12},&1\le k \le 13,\\&0,&k=14. \end{aligned} \right. \end{aligned}$$

(IV) The proportion of BCG vaccination (i.e., $p_{1}$): In 2019, 153 countries reported providing BCG vaccination as a standard part of childhood immunization programs, of which 87 reported coverage of $\ge 90\%$. Since BCG vaccine has a higher coverage rate in China (Ren et al. 2020), we assume $p_{1}=0.99$ in the simulation.

(V) The vaccination rate for susceptible individuals (i.e., $\nu _{k}$): In addition to BCG vaccine, there are no effective vaccines against TB for adults. Therefore, in the simulation, we assume $\nu _{k}=0\;(2\le k \le 14)$.

(VI) The proportion of new infections that develop into active TB (i.e., $q_{k}$): Since approximately 10% of infected individuals will develop active TB in their lifetime (World Health Organization 2021a), around $5\%$ of these infected individuals will develop active TB during the first 2 years of infection (Ziv et al. 2001). Therefore, we choose $q_{k}=0.05\;(1\le k \le 14)$.

(VII) The level of protection for vaccinated individuals due to immunity (i.e., $1-\eta _{k}$): As part of the childhood immunization program, BCG vaccine has a high protection rate and is effective for about 10 years (Roy et al. 2014; Mangtani et al. 2014). Therefore, BCG vaccine is only effective for individuals between 0 and 10 years old. We choose

$$\begin{aligned} 1-\eta _{k}=\left\{ \begin{aligned}&0.85,&1\le k\le 2,\\&0,&3\le k\le 14. \end{aligned} \right. \end{aligned}$$

(VIII) The level of protection for latent individuals due to immunity (i.e., $1-\varrho _{k}$): The latent individuals progress to active TB, and the rate of exogenous reinfection is $\varrho _{k}\varLambda _{k}\;(1\le k \le 14)$. Since primary infection confers some degree of immunity, we have $0<1-\varrho _{k}<1$. According to the estimation of Harris et al. (2019), we have

$$\begin{aligned} 1-\varrho _{k}=[0.25,0.37], \;1\le k \le 14. \end{aligned}$$

(IX) The level of protection of the recovered individuals due to immunity (i.e., $1-\delta _{k}$): The recovered individuals are not completely immune to Mycobacterium TB, and the rate of reinfection is $\delta _{k}\varLambda _{k}\;(1\le k \le 14)$. Since the recovered individuals have a certain level of immunity, we have $0<1-\delta _{k}<1$. According to the estimation of Harris et al. (2019), we have

$$\begin{aligned} 1-\delta _{k}=[0.25,0.37], \;1\le k \le 14. \end{aligned}$$

(X) The risk of reactivation in latently infected individuals (i.e., $\sigma _{k}$): According to Harris et al.’s estimation of the risk of reactivation in latently infected individuals (Harris et al. 2019), we re-quantified the monthly risk of reactivation in latently infected individuals as follows:

$$\begin{aligned} \sigma _{k}=\left\{ \begin{aligned}&\Big [\frac{0.0001}{12},\frac{0.0002}{12}\Big ],&1\le k\le 3,\\&\Big [\frac{0.00018}{12},\frac{0.00028}{12}\Big ],&4\le k\le 11,\\&\Big [\frac{0.00020}{12},\frac{0.00193}{12}\Big ],&12\le k\le 13,\\&\Big [\frac{0.00020}{12},\frac{0.00365}{12}\Big ],&k=14. \end{aligned} \right. \end{aligned}$$

(XI) The time delays in diagnosis of TB (i.e., $1/\theta _{k}$): The clinical manifestations of TB are mostly non-specific symptoms, such as cough and fever, which are easily confused with other respiratory diseases, and its differential diagnosis is difficult, which may cause a certain delay in diagnosis. In China, the shortest total delay is 25 days and the longest total delay is 71 days (Sreeramareddy et al. 2009). Therefore, we choose

$$\begin{aligned} \theta _{k}=\Big [\frac{30}{71},\frac{30}{25}\Big ], \;1\le k \le 14. \end{aligned}$$

(XII) The recovery rate (i.e., $\gamma _{k}$): TB patients can be successfully cured after 6 months of drug treatment (World Health Organization 2021a). Thus, we have $\gamma _{k}=1/6\;(1\le k \le 14)$.

(XIII) The validity period of the vaccine (i.e., $1/\tau _{k}$): The immune function of BCG vaccine gradually declines after about 10 years (Lawn and Zumla 2011). Therefore, the vaccine failure rates for individuals under 5 years old and individuals 5–9 years old are $1/(10\times 12)$ and $1/(5\times 12)$, respectively. The vaccine failure rate for individuals over 10 years old is infinite. Therefore, we choose

$$\begin{aligned} \tau _{k}=\left\{ \begin{aligned}&\frac{1}{10\times 12},&k=1,\\&\frac{1}{5\times 12},&k=2,\\&\infty ,&3\le k\le 14. \end{aligned} \right. \end{aligned}$$

(XIV) The proportion of recovered individuals (i.e., $\rho _{k}$): According to the TB report of WHO (Harris et al. 2019; World Health Organization 2021a), we obtain that the proportion of successful TB treatment is $95\%$. Thus, for each age-group, we assume that the proportion of recovered individuals is $\rho _{k}=0.95\;(1\le k \le 14)$.

(XV) The proportion of infected individuals entering the treated class due to treatment (i.e., $\xi _{k}$): The WHO reported that the proportion of new active TB cases detected and started treatment was $89\%$ (Harris et al. 2019; World Health Organization 2021a). Thus, for each age-group, we choose $\xi _{k}=0.89\;(1\le k \le 14)$.

(XVI) The proportion of latent individuals receiving treatment (i.e., $1-\mu _{k}$): We assume that the proportion of latent individuals who develop active TB without treatment is $\mu _{k}=1-\rho _{k}\xi _{k}$, then the proportion of latent individuals who are tested and successfully treated is $1-\mu _{k}=\rho _{k}\xi _{k}$. Therefore, for each age-group, $\mu _{k}=1-0.8455\;(1\le k \le 14)$.

(XVII) The relapse rate of recovered individuals (i.e., $\chi _{k}$): Since the recovered TB individuals have a high relapse rate, and the relapse rate varies with age (Harris et al. 2019; Knight et al. 2014), we choose

$$\begin{aligned} \chi _{k}=\left\{ \begin{aligned}&\Big [\frac{0.005}{12},\frac{0.010}{12}\Big ],&1\le k\le 3,\\&\Big [\frac{0.005}{12},\frac{0.007}{12}\Big ],&4\le k\le 11,\\&\Big [\frac{0.005}{12},\frac{0.016}{12}\Big ],&12\le k\le 13,\\&\Big [\frac{0.005}{12},\frac{0.025}{12}\Big ],&k=14,\\ \end{aligned} \right. \end{aligned}$$

(XVIII) The contact matrix (i.e., $c_{kj}$): Since contact matrix is split into 16 age-groups in China (Prem et al. 2017), we aggregate it into the 14 age-groups used in our models (Meltzer et al. 2015). Next, we demonstrate how to aggregate 16 age-groups into 14 age-groups. The detailed derivation of the modified contact matrix is in B. The modified contact matrix is shown in Fig. 4.

Fig. 4

A The daily average number of contacts per person in the participant age-group. B The monthly average number of contacts per person in the participant age-group (Color figure online)

(XIX) The coefficient that reduces the transmission rate due to treatment (i.e., $\omega _{k}$): According to the estimation of Guo et al. (2021), we choose $\omega _{k}=0.4387, \;1\le k \le 14$.

(XX) The probability of infection upon contacting an infectious person (i.e., $\beta _{k}(t)$): Anderson and May (1992) conclude that the direct measurement of the transmission coefficient is essentially impossible for most infections. To predict the changes wrought by public health programs, we need to know the transmission coefficient. Pollicott et al. (2012) also state that large-scale transmission experiments (e.g., influenza transmission in ferrets) are useful in understanding the transmission dynamics, but are usually impractical (due to economic and ethical reasons). In order to fit the seasonal fluctuation of TB, we use wavelet analysis (Torrence and Compo 1998) to study the periodicity of monthly new TB cases for 14 age-groups from January 2005 to December 2017. Morlet wavelet is chosen as the ‘mother wavelet’ and continuous wavelet transform is performed (Yang and Jin 2021). The wavelet power spectrum indicates that the time series of monthly new TB cases in the 14 age-groups show obvious annual period. The annual period is surrounded by the black line that denotes the 5% significance level (see Fig. 9). Thus, we choose $\beta _{k}(t)$ as the periodic function for each age-group as follows:

$$\begin{aligned} \beta _{k}(t)={\hat{\beta }}_{k}\bigg (1+{\bar{\beta }}_{k}\sin \Big (\frac{2\pi t}{12}+\phi _{k}\Big )\bigg ),\;1\le k \le 14, \end{aligned}$$

where ${\hat{\beta }}_{k}$ is called the baseline level of transmission, ${\bar{\beta }}_{k}$ is known as the amplitude of seasonal variation or simply the strength of seasonality (Cintrón-Arias et al. 2009), and $\phi _{k}$ indicates the phase of the ${\mathcal {T}}$-periodic function.

(XXI) The initial values of System (1): According to the relevant data reported by tabulation on the 2010 Population Census Office of the State Council of the People’s Republic of China (2021), we obtain the total population of the age-group as $N_{k}$, as shown in Table 5. According to recent estimation, approximately 350 million people are infected with Mycobacterium TB in China (Cui et al. 2020); therefore, we approximate that the initial value of the latent individuals is $E_{k}(0)={300000000N_{k}}/{\sum ^{14}_{k=1}N_{k}}\;(1\le k \le 14)$. The initial value $I_{k}(0)\;(1\le k \le 14)$ of the infected individuals, the initial value $R_{k}(0)\;(1\le k \le 14)$ of the recovered individuals, and the initial value $V_{k}(0)\;(1\le k \le 2)$ of the vaccinated individuals are obtained by fitting the data. Since there is no improved vaccination for adults, we assume that the initial value of the vaccinated individuals is $V_{k}(0)=0\;(3\le k \le 14)$. The WHO reported that the proportion of new active TB cases detected and started on treatment was $89\%$ (Harris et al. 2019; World Health Organization 2021a), we assume that the initial value of the treated individuals is $T_{k}(0)=0.89I_{k}(0)\;(1\le k \le 14)$. The initial value of susceptible individuals is estimated as $S_{k}(0)=N_{k}-V_{k}(0)-E_{k}(0)-I_{k}(0)-T_{k}(0)-R_{k}(0)\;(1\le k \le 14)$.

Next, we use the MCMC method (Haario et al. 2006) to fit System (1) for 800000 iterations with a burn-in of 750000 iterations. We estimate the unknown parameters and initial conditions for System (1), using the monthly number of new TB cases in mainland China. The unknown parameters and initial values set is

$$\begin{aligned} {\hat{\chi }}=({\hat{\chi }}_{1},\cdots ,{\hat{\chi }}_{k},\cdots ,{\hat{\chi }}_{n}), \end{aligned}$$

where

$$\begin{aligned} {\hat{\chi }}_{k}=\left\{ \begin{aligned}&\big ({\hat{\beta }}_{k}, {\bar{\beta }}_{k}, \phi _{k}, \delta _{k},\varrho _{k},\theta _{k}, \sigma _{k}, \chi _{k}, I_{k}(0), R_{k}(0), V_{k}(0)\big ),&1\le k \le 2,\\&\big ({\hat{\beta }}_{k}, {\bar{\beta }}_{k}, \phi _{k}, \delta _{k},\varrho _{k},\theta _{k}, \sigma _{k}, \chi _{k}, I_{k}(0), R_{k}(0)\big ),&3\le k \le 14. \end{aligned} \right. \end{aligned}$$

Let ${\hat{C}}_{k}(t,{\hat{\chi }}),(1\le k\le 14)$ represent the cumulative number of TB cases, then the cumulative infection cases of the kth age-group can be expressed as follows:

$$\begin{aligned} \frac{\text{ d }{\hat{C}}_{k}(t,{\hat{\chi }})}{\text{ d }t}=\xi _{k}\theta _{k}I_{k},\;(1\le k\le n). \end{aligned}$$

The number of new TB cases of the kth age-group can be expressed as follows:

$$\begin{aligned} {\hat{P}}_{k}(t,{\hat{\chi }})=\xi _{k}\theta _{k}I_{k},\;(1\le k\le n), \end{aligned}$$

where ${\hat{P}}_{k}$ represents the number of new TB cases of the kth age-group; the time step is month in the simulations. We obtain $\varPsi$ independent observation data from the kth age-group, representing the number of new TB cases at the ith month. The data from 2005 to 2016 were used for training the model, and the data from 2017 were used for testing and validation purposes. The new observation data can be expressed as ${\mathbf {Y}}=(Y_{1}(t),Y_{2}(t),\cdots ,Y_{n}(t)),$ where ${\mathbf {Y}}$ is a $\varPsi \times n$ matrix. The error matrix, ${\hat{\epsilon }}$, is of dimension $\varPsi \times n$ and follows a matrix-variate normal distribution, i.e., ${\hat{\epsilon }}\sim N(0, I_{\varPsi }, \varSigma )$ (Gamerman et al. 2008). Thus, the observations ${\mathbf {Y}}$ can be expressed as follows:

$$\begin{aligned} {\mathbf {Y}}={\mathbf {P}}+{\hat{\epsilon }},\;{\hat{\epsilon }}\sim N(0,I_{\varPsi },\varSigma ), \end{aligned}$$

(21)

where ${\mathbf {P}}$ is a $\varPsi \times n$ matrix and ${\mathbf {P}}$ represents the numerical solution of the number of new TB cases of System (1), that is, ${\mathbf {P}}=({\hat{P}}_{1}(t,{\hat{\chi }}),{\hat{P}}_{2}(t,{\hat{\chi }}),\cdots ,{\hat{P}}_{n}(t,{\hat{\chi }}))$. For simplicity, we assume that $\varSigma =\text{ diag }({\hat{\sigma }}_{1},{\hat{\sigma }}_{2},\cdots ,{\hat{\sigma }}_{n})$ throughout the work.

We assume that the unknown parameter ${\hat{\chi }}$ of System (1) is an independent Gaussian prior specification. Hence, we obtain

$$\begin{aligned} {\hat{\chi }}_{j}\sim N({\hat{\nu }}_{j}, {\hat{\varphi }}^{2}_{j}),\;\;j = 1,2,\cdots ,M, \end{aligned}$$

where M is the number of unknown parameters. We also assume that the inverse of the error variance follows a gamma distribution as prior with the form

$$\begin{aligned} {\hat{\sigma }}^{-2}_{i}\sim \varGamma \Bigg (\frac{n_{0}}{2}, \frac{n_{0}S^{2}_{0}}{2}\Bigg ),\;i=1,2,\cdots ,n, \end{aligned}$$

where $S^2_0$ and $n_0$ are the prior mean and prior accuracy of variance ${\hat{\sigma }}^{2}_{i}$, respectively.

The likelihood function $L({\mathbf {Y}}|{\hat{\chi }},\varSigma )$ for $\varPsi$ independent and identically distributed observations from Eq.(21) with a Gaussian error model is

$$\begin{aligned} \begin{aligned} L({\mathbf {Y}}|{\hat{\chi }}, \varSigma )=\Big (\frac{1}{2\pi }\Big )^{\frac{\varPsi n}{2}}|\varSigma |^{-\frac{\varPsi }{2}}\exp \bigg [\text{ trace }\bigg (\frac{-\varSigma ^{-1}\mathrm{SS}({\hat{\chi }})}{2}\bigg )\bigg ], \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \mathrm{SS}({\hat{\chi }})=({\mathbf {Y}}-{\mathbf {P}})^{{\mathbf {T}}}({\mathbf {Y}}-{\mathbf {P}}). \end{aligned}$$

The joint posterior distribution of ${\hat{\sigma }}^{2}_{i}\;(i=1,2,\cdots ,n$) is

$$\begin{aligned} \begin{aligned}&L({\hat{\sigma }}^{2}_{1},{\hat{\sigma }}^{2}_{2},\cdots ,{\hat{\sigma }}^{2}_{n}|{\mathbf {Y}}, {\hat{\chi }})\propto L({\mathbf {Y}}|{\hat{\sigma }}^{2}_{1},{\hat{\sigma }}^{2}_{2},\cdots ,{\hat{\sigma }}^{2}_{n}, {\hat{\chi }})L({\hat{\sigma }}^{2}_{1},{\hat{\sigma }}^{2}_{2},\cdots ,{\hat{\sigma }}^{2}_{n})\\&\quad =L({\mathbf {Y}}|{\hat{\sigma }}^{2}_{1},{\hat{\sigma }}^{2}_{2},\cdots ,{\hat{\sigma }}^{2}_{n}, {\hat{\chi }})\prod ^{n}_{i=1}L({\hat{\sigma }}^{2}_{i})\\&\quad =\Big (\frac{1}{2\pi }\Big )^{\frac{\varPsi n}{2}}|\varSigma |^{-\frac{\varPsi }{2}}\exp \bigg [\text{ trace }\bigg (\frac{-\varSigma ^{-1}\mathrm{SS}({\hat{\chi }})}{2}\bigg )\bigg ]\\&\qquad \qquad \prod ^{n}_{i=1}\frac{\Big (\frac{n_{0}S^{2}_{0}}{2}\Big )^{\frac{n_{0}}{2}}}{\varGamma (\frac{n_{0}}{2})} ({\hat{\sigma }}^{2}_{i})^{-\frac{n_{0}}{2}-1}\exp \bigg [-\frac{n_{0}S^{2}_{0}}{2{\hat{\sigma }}^{2}_{i}}\bigg ]\\&\quad =\Big (\frac{1}{2\pi }\Big )^{\frac{\varPsi n}{2}}|\varSigma |^{-\frac{\varPsi }{2}}\exp \bigg [\text{ trace }\bigg (\frac{-\varSigma ^{-1}\mathrm{SS}({\hat{\chi }})}{2}\bigg )\bigg ]\\&\qquad \quad \times \frac{\Big (\frac{n_{0}S^{2}_{0}}{2}\Big )^{\frac{n_{0}n}{2}}}{(\varGamma (\frac{n_{0}}{2}))^{n}} |\varSigma |^{-\frac{n_{0}}{2}-1}\exp \bigg [\text{ trace }\bigg (\frac{-\varSigma ^{-1}{n_{0}S^{2}_{0}}}{2}\bigg )\bigg ]\\&\quad \propto |\varSigma |^{-\frac{\varPsi }{2}-\frac{n_{0}}{2}-1}\exp \bigg [\text{ trace }\bigg (\frac{-\varSigma ^{-1}\mathrm{SS}({\hat{\chi }})}{2}\bigg )+\text{ trace }\bigg (\frac{-\varSigma ^{-1}{n_{0}S^{2}_{0}}}{2}\bigg )\bigg ]. \end{aligned} \end{aligned}$$

Since we assume independent Gaussian prior specification for parameters ${\hat{\chi }}$, the prior sum of squares for the given parameters ${\hat{\chi }}$ can be calculated as follows:

$$\begin{aligned} \mathrm{SS}_{\mathrm{pri}}({\hat{\chi }})=\overset{M}{\underset{j=1}{\sum }}\Bigg [\frac{{\hat{\chi }}_{j}-{\hat{\nu }}_{j}}{{\hat{\varphi }}_{j}}\Bigg ]^{2}. \end{aligned}$$

Then, for a fixed value of variance ${\hat{\sigma }}^{2}_{i}\;(i=1,2,\cdots ,n$), the posterior distribution of parameters ${\hat{\chi }}$ can be expressed as follows:

$$\begin{aligned} \begin{aligned}&L({\hat{\chi }}|{\mathbf {Y}},\varSigma )\propto L({\mathbf {Y}}|{\hat{\chi }},\varSigma )L({\hat{\chi }}_{1})L({\hat{\chi }}_{2})\cdots L({\hat{\chi }}_{M})\\&\quad =L({\mathbf {Y}}|{\hat{\chi }},\varSigma )\prod ^{M}_{i=1}L({\hat{\chi }}_{i})\\&\quad =\Big (\frac{1}{2\pi }\Big )^{\frac{\varPsi n}{2}}|\varSigma |^{-\frac{\varPsi }{2}}\exp \bigg [\text{ trace }\bigg (\frac{-\varSigma ^{-1}\mathrm{SS}({\hat{\chi }})}{2}\bigg )\bigg ]\prod ^{M}_{j=1}\frac{1}{\sqrt{2\pi }\varphi _{j}} \exp \bigg [\!-\frac{({\hat{\chi }}_{j}-{\hat{\nu }}_{j})^{2}}{2{\hat{\varphi }}^{2}_{j}}\bigg ]\\&\quad =\Big (\frac{1}{2\pi }\Big )^{\frac{\varPsi n}{2}}|\varSigma |^{-\frac{\varPsi }{2}}\exp \bigg [\text{ trace }\bigg (\frac{-\varSigma ^{-1}\mathrm{SS}({\hat{\chi }})}{2}\bigg )\bigg ]\bigg (\frac{1}{\sqrt{2\pi }}\bigg )^{M}\\&\qquad \times \frac{1}{\varphi _{1}\varphi _{2}\cdots \varphi _{M}} \exp \bigg [-\frac{1}{2}\overset{M}{\underset{j=1}{\sum }}\Big (\frac{{\hat{\chi }}_{j}-{\hat{\nu }}_{j}}{{\hat{\varphi }}_{j}}\Big )^{2}\bigg ]\\&\quad \qquad \propto \exp \bigg [-\frac{1}{2}\Big (\text{ trace }\big ({\varSigma ^{-1}\mathrm{SS}({\hat{\chi }})}\big )+\mathrm{SS}_{\mathrm{pri}}({\hat{\chi }})\Big )\bigg ]. \end{aligned} \end{aligned}$$

and the posterior ratio needed in the Metropolis–Hastings acceptance probability can be written as follows:

$$\begin{aligned} \frac{L(\hat{\chi ^{1}}|{\mathbf {Y}},\varSigma )}{L(\hat{\chi ^{2}}|{\mathbf {Y}},\varSigma )}= & {} \exp \bigg [-0.5\Big (\varSigma ^{-1}{\mathrm{SS}(\hat{\chi ^{2}})}-\varSigma ^{-1}{\mathrm{SS}(\hat{\chi ^{1}})}\Big )\\&+0.5\Big (\mathrm{SS}_{\mathrm{pri}}(\hat{\chi ^{2}})-\mathrm{SS}_{\mathrm{pri}}(\hat{\chi ^{1}})\Big )\bigg ], \end{aligned}$$

where $\hat{\chi ^{1}}$ is the value of the current parameter set and $\hat{\chi ^{2}}$ represents the value of generating a new parameter set. Accordingly, the new unknown parameter value $\hat{\chi ^{2}}$ will be accepted with probability

$$\begin{aligned} \min \Bigg (1,\;\frac{L(\hat{\chi ^{1}}|{\mathbf {Y}},\varSigma )}{L(\hat{\chi ^{2}}|{\mathbf {Y}},\varSigma )}\Bigg ). \end{aligned}$$

Prior information of unknown parameters is given by

$$\begin{aligned} \left. \begin{aligned}&{\hat{\beta }}_{k}\in [0,1],\; {\bar{\beta }}_{k}\in [-1,1],\;\phi _{k}\in [-12,12],&1\le k \le 14,\\&\delta _{k}\in [0.63,0.75],\;\varrho _{k}\in [0.63,0.75],\;\theta _{k}\in \Big [\frac{30}{71},\frac{30}{25}\Big ],&1\le k \le 14,\\&I_{k}(0)\in [0,2\times 10^{5}], \;R_{k}(0)\in [0,1\times 10^{7}],&1\le k \le 14,\\&V_{k}(0)\in [4\times 10^{7},4.9\times 10^{7}],&1\le k \le 2,\\&\sigma _{k}\in \Big [\frac{0.0001}{12},\frac{0.0002}{12}\Big ],\;\chi _{k}\in \Big [\frac{0.005}{12},\frac{0.010}{12}\Big ],&1\le k\le 3,\\&\sigma _{k}\in \Big [\frac{0.00018}{12},\frac{0.00028}{12}\Big ],\;\chi _{k}\in \Big [\frac{0.005}{12},\frac{0.007}{12}\Big ],&4\le k\le 11,\\&\sigma _{k}\in \Big [\frac{0.00020}{12},\frac{0.00193}{12}\Big ],\;\chi _{k}\in \Big [\frac{0.005}{12},\frac{0.016}{12}\Big ],&12\le k\le 13,\\&\sigma _{k}\in \Big [\frac{0.00020}{12},\frac{0.00365}{12}\Big ],\;\chi _{k}\in \Big [\frac{0.005}{12},\frac{0.025}{12}\Big ],&k=14, \end{aligned} \right. \end{aligned}$$

and the proposal density follows a multivariate normal distribution.

Fig. 5

The fitting results of monthly TB prevalence per 100,000 individuals from January 2005 to December 2017. The solid red line represents the simulated curve of System (1). Black circles represent training data, and green circles represent testing data. The $95\%$ confidence and prediction intervals are shown in light red and light blue, respectively (Color figure online)

We randomly select 10% of the last 50,000 samples as the final distribution of parameters by fitting System (1) to the time series of the monthly TB prevalence per 100,000 individuals reported in mainland China, as shown in Fig. 5. The fitting result of the age series is shown in Fig. 11. From Fig. 10, the fitted curve of TB prevalence per 100,000 individuals matches the reported data very well. We use Brooks and Roberts (1998) diagnostics to examine the convergence of the MCMC chains, and the values of Geweke are shown in Tables 7 and 8. The traces plots of unknown parameters and initial values for System (1) are obtained by MCMC sampling (see Fig. 12). The mean and standard deviation of the parameters and model initial values are shown in Tables 7 and 8. The ratio of our sample size to the free parameters of the model is 28.8:1>10:1 (Wikipedia 2022); thus, our training model has good performance.

4 Results

In this section, we calculate the basic reproduction number of System (1), conduct sensitivity analysis, and evaluate the possibility of achieving the goals of WHO if we start vaccination strategy, diagnostic strategy, and treatment strategy in 2025.

Fig. 6

A The blue dots indicate the value of ${\mathcal {R}}_{0}$ within the 95% confidence interval, the red pluses indicate the value of ${\mathcal {R}}_{0}$ outside the 95% confidence intervals, and the black lines indicate the upper and lower confidence limits. B The frequency distribution of ${\mathcal {R}}_{0}$. The red curve is the probability density function curve of ${\mathcal {R}}_{0}$ (Color figure online)

4.1 Basic Reproduction Number and Sensitivity Analysis

Through the estimated parameter values, we calculate that the basic reproduction number, ${\mathcal {R}}_{0}$, is estimated to be 1.3935 ($95\%\text{ CI }:(1.3729, 1.4087)$), as shown in Fig. 6. Since ${\mathcal {R}}_{0}>1$, System (1) is uniformly persistent, which indicates that TB will not go extinct in the future without additional control measures. System (1) is uniformly persistent, which indicates that TB will not go extinct in the future with current control measures. Next, we use the LHS (Latin hypercube sampling) and the PRCCs (partial rank correlation coefficients) (Marino et al. 2008) to study the global uncertainty and sensitivity of the parameters of System (1). The goal is to identify the most important parameters that affect the dynamics of TB infection. The input parameters are $\theta _k\;(1\le k\le 14)$, $\sigma _{k}\;(1\le k\le 3)$, $\sigma _{k}\;(4\le k\le 11)$, $\sigma _{k}\;(12\le k\le 13)$, $\sigma _{k}\;(k=14)$, $\chi _{k}\;(1\le k\le 3)$, $\chi _{k}\;(4\le k\le 11)$, $\chi _{k}\;(12\le k\le 13)$, $\chi _{k}\;(k=14)$, and $\nu _{k}\;(3\le k\le 14)$; the output variables are yearly new TB cases. All input parameters are normally distributed, with the mean and standard deviation of $\theta _k$, $\sigma _{k}$, and $\chi _{k}$ given in Table 7, and the mean and standard deviation of $\nu _{k}$ are assumed to be 0.1 and 0.01, respectively. The results of the sensitivity analysis of parameters are shown in Table 2.

Table 2 The PRCCs of the parameters with respect to the new cases in 2017

Table 2 shows the sensitivity of the parameters $\theta _{k}$, $\sigma _{k}$, $\chi _{k}$, and $\nu _{k}$ with respect to the new cases in 2017. Firstly, our results show that the relapse rate of recovered individuals over 15 years old (i.e., $\chi _{k}\;(4\le k\le 14)$) is highly positively correlated with the total number of new cases; the relapse rate of recovered individuals under 15 years old (i.e., $\chi _{k}\;(1\le k\le 3)$) is not correlated with the total number of new cases, which indicates that it is essential to prevent the relapse of recovered individuals over 15 years old. Next, we find that the risk of reactivation in latently infected individuals (i.e., $\sigma _{k}\;(4\le k\le 14)$) over 15 years old is higher than that in latently infected individuals (i.e., $\sigma _{k}\;(1\le k\le 3)$) under 15 years old. Moreover, the diagnosis rate of TB (i.e., $\theta _{k}\;(1\le k\le 14)$) is highly negatively correlated with the total number of new cases, which indicates that the use of diagnostic techniques to shorten the time of delayed diagnosis can effectively reduce the prevalence of TB. Finally, the vaccination rate for susceptible individuals (i.e., $\nu _{k}\;(4\le k\le 14)$) over 15 years old is highly negatively correlated with the total number of new cases. In particular, the vaccination rates of susceptible individuals over 65 and between 20 and 24 years old have the strongest correlation with the total number of new cases.

4.2 Vaccination Strategy

We simulate the impact of vaccination strategy on the prevalence of TB in susceptible individuals over 10 years old. We set the level of protection of the vaccine to $85\%$ (i.e., $1-\eta _{k}=0.85\;(3\le k\le 14)$) and the validity period of the vaccine to 10 years (i.e., $1/\tau _{k}=10\times 12\;(3\le k\le 14)$), and assume the vaccine coverage rate of susceptible individuals is ${\sum ^{14}_{k=1}V_{k}}/{\sum ^{14}_{k=1}(S_{k}+V_{k})}$ by changing the vaccination rate $\nu _{k}$ (Shen et al. 2021). Using these estimated parameters, we further predict that increasing the value of vaccine coverage rate of susceptible individuals to $65\%$ and $85\%$ can reduce the TB prevalence per 100,000 individuals by $47.44\%$ and $54.98\%$ by 2035, respectively (see Fig. 7A). Meanwhile, we obtain that increasing the value of vaccine coverage rate of susceptible individuals to level of $65\%$ and $85\%$ can reduce the TB prevalence per 100,000 individuals by $51.40\%$ and $58.66\%$ by 2050, respectively (see Fig. 7A), which indicates that vaccinating susceptible individuals over 10 years old can effectively reduce the prevalence of TB. However, our simulation results show that the goals of WHO will not be achieved by vaccinating susceptible individuals with the improved vaccine alone, because the reinfection of latent individuals and recovered individuals and the relapse of recovered individuals also affect the prevalence of TB.

4.3 Diagnosis Strategy

Delay in diagnosis of TB results in increasing severity, mortality, infection time, and transmission (Sreeramareddy et al. 2009). In order to shorten the duration of infectiousness to increase the prevalence of TB, we simulate the use of diagnostic techniques to increase the delayed diagnosis time by twice and five times (i.e., $2\theta _{k}$ and $5\theta _{k}$) to reduce the prevalence of TB, respectively. Using these estimated parameters, we predict that decreasing the delayed diagnosis time of infected individuals to two times and five times can reduce the TB prevalence per 100,000 individuals by $66.63\%$ and $88.74\%$ by 2035, respectively (see Fig. 7B). Meanwhile, we obtain that decreasing the delayed diagnosis time of infected individuals to twice and five times can reduce the TB prevalence per 100,000 individuals by $66.09\%$ and $88.59\%$ by 2050, respectively (see Fig. 7B), which indicates that reducing the delayed diagnosis time can shorten the infection time of infected individuals, thereby reducing the prevalence of TB.

Fig. 7

The impact of interventions and strategies begun in 2025 on TB prevalence per 100,000 individuals by year up to 2050. A Vaccination strategy. B Diagnostic strategy. C Treatment strategy. D The combination of vaccination strategy, diagnostic strategy, and treatment strategy (Color figure online)

4.4 Treatment Strategy

During the treatment of TB, the relapse rate is high due to the increased drug resistance and short treatment time. Therefore, the treatment drugs are needed to prevent the relapse of recovered individuals. We simulate two cases where the relapse rate decreased by 50% and 90% (i.e., $0.5\chi _{k}$ and $0.1\chi _{k}$). More specifically, we predict that decreasing the relapse rate of recovered individuals by 50% and 90% can reduce the TB prevalence per 100,000 individuals by $46.45\%$ and $85.61\%$ by 2035, respectively (see Fig. 7C). Meanwhile, we obtain that reducing the relapse rate of recovered individuals by 50% and 90% can reduce the TB prevalence per 100,000 individuals by $45.55\%$ and $86.33\%$ by 2050, respectively (see Fig. 7C), which shows that the use of treatment strategies to prevent the relapse of recovered individuals is a very effective measure.

4.5 Combination of multiple intervention strategies

In order to end the TB epidemic, we need to combine vaccination strategy, diagnostic strategy, and treatment strategy. We simulate the following eight scenarios:

Scenario A: Coverage rate is $85\%$, diagnosis rate is $5\theta _{k}$, relapse rate is $0.1\chi _{k}$;

Scenario B: Coverage rate is $85\%$, diagnosis rate is $5\theta _{k}$, relapse rate is $0.5\chi _{k}$;

Scenario C: Coverage rate is $85\%$, diagnosis rate is $2\theta _{k}$, relapse rate is $0.1\chi _{k}$;

Scenario D: Coverage rate is $85\%$, diagnosis rate is $2\theta _{k}$, relapse rate is $0.5\chi _{k}$;

Scenario E: Coverage rate is $65\%$, diagnosis rate is $5\theta _{k}$, relapse rate is $0.1\chi _{k}$;

Scenario F: Coverage rate is $65\%$, diagnosis rate is $5\theta _{k}$, relapse rate is $0.5\chi _{k}$;

Scenario G: Coverage rate is $65\%$, diagnosis rate is $2\theta _{k}$, relapse rate is $0.1\chi _{k}$;

Scenario H: Coverage rate is $65\%$, diagnosis rate is $2\theta _{k}$, relapse rate is $0.5\chi _{k}$.

Our simulation results show that scenarios A, B, C, D, E, F, G, and H lead to $98.91\%$, $95.71\%$, $97.17\%$, $88.92\%$, $98.81\%$, $95.32\%$, $96.81\%$, and $87.50\%$ reductions, respectively, in the TB prevalence per 100,000 individuals by 2035 compared with the baseline (see Fig. 7D and Table 3). Meanwhile, scenarios A, B, C, D, E, F, G, and H can reduce the TB prevalence per 100,000 individuals by $99.07\%$, $95.96\%$, $97.62\%$, $89.70\%$, $99.01\%$, $95.65\%$, $97.38\%$, and $88.61\%$ in 2050 (see Fig. 7D and Table 3). The above results show that the scenarios A, C, E, and G are the most effective scenarios, and the decline rate has reached more than $96\%$ in 2035 and 2050. However, all scenarios cannot achieve the goals of WHO by 2050, because the reinfection of latent individuals and recovered individuals also affects the prevalence of TB.

Table 3 The combination of vaccination strategy, diagnostic strategy, and treatment strategy

5 Discussion

The prevalence of TB varies greatly among different age-groups in China, which leads to different effects of vaccination strategy, diagnostic strategy, and treatment strategy for different age-groups. Moreover, the number of TB cases of all age-groups show seasonal variations with peak in late spring to early summer each year in China. In this work, in order to study the dynamic impact of vaccination strategy, diagnostic strategy, and treatment strategy on TB, we propose a non-autonomous differential equation model with age structure and seasonal transmission rate. Firstly, the basic reproduction number of the system is derived, the disease-free periodic solution is globally asymptotically stable, and the disease eventually disappears when ${\mathcal {R}}_{0}<1$, and there exists at least one positive periodic solution and the disease is uniformly persistent when ${\mathcal {R}}_{0}>1$. Secondly, the unknown parameters and initial values of the TB dynamics model are obtained by fitting the monthly number of new TB cases in mainland China by Markov chain Monte Carlo (MCMC). The ratio of the number of data points to the free parameters is greater than ten, which indicates that the training model is not overfitting. Thirdly, we calculate the basic reproduction number, perform a global sensitivity analysis of the main parameters, and simulate the possibility of achieving the goals of WHO.

The study consists of 13029219 TB cases from January 2005 to December 2017 in mainland China. It has been found that there is a seasonal pattern of the monthly TB prevalence per 100,000 individuals of all age-groups, and the monthly TB prevalence per 100,000 individuals peak in late spring to early summer (see Fig. 2A). The mean monthly TB prevalence per 100,000 individuals is 84.2783 for all age-groups. The TB prevalence per 100,000 individuals is the highest among people over 65 years of age, and the TB prevalence per 100,000 individuals is the lowest among people under 15 years old (see Table 1). We find that the TB prevalence per 100,000 individuals was highly positively correlated with the age of infected individuals from 2005 to 2017 (Pearson correlation coefficients: >0.85, $p <0.01$), as shown in Fig. 3.

Our model differs from previous age-structured models in being based on the seasonality of TB (Harris et al. 2019, 2020), which can more accurately quantify the basic reproduction number, and our model also incorporates vaccination strategy, diagnostic strategy, and treatment strategy. We calculate that the basic reproduction number, ${\mathcal {R}}_{0}$, is estimated to be 1.3935 ($95\%\text{ CI }:(1.3729, 1.4087)$), which indicates that the TB is uniformly persistent, and System (1) has at least one positive periodic solution. Sensitivity analysis shows that the vaccination rate of susceptible individuals over 15 years old and the diagnosis rate of TB are highly negatively correlated with the total number of new TB cases (see Table 2). Meanwhile, the relapse of recovered individuals over 15 years old is highly positively correlated with the total number of new TB cases (see Table 2).

Our results demonstrate that the vaccination rates of susceptible individuals over 65 and between 20 and 24 have the strongest correlation with the total number of new cases. Further, vaccination strategy, diagnostic strategy, and treatment strategy currently under development each offer substantial reductions in TB prevalence per 100,000 individuals compared with current approaches, and the combination of the three strategies is more effective. When scenario A (i.e., coverage rate $85\%$, diagnosis rate $5\theta _{k}$, relapse rate $0.1\chi _{k}$) is selected, the TB prevalence per 100,000 individuals can be reduced by $98.91\%$ and $99.07\%$ by 2035 and 2050, respectively. Scenario C (i.e., coverage rate $85\%$, diagnosis rate $2\theta _{k}$, relapse rate $0.1\chi _{k}$) can reduce the TB prevalence per 100,000 individuals by $97.17\%$ and $97.62\%$ by 2035 and 2050, respectively. Scenario E (i.e., coverage rate $65\%$, diagnosis rate $5\theta _{k}$, relapse rate $0.1\chi _{k}$) can reduce the TB prevalence per 100,000 individuals by $98.81\%$ and $99.01\%$ by 2035 and 2050, respectively. Scenario G (i.e., coverage rate $65\%$, diagnosis rate $2\theta _{k}$, relapse rate $0.1\chi _{k}$) can reduce the TB prevalence per 100,000 individuals by $96.81\%$ and $97.38\%$ by 2035 and 2050, respectively. The goals of WHO in 2050 cannot be achieved, according to our simulation results. The elimination of TB requires new strategies, such as large-scale vaccination of latent individuals and recovered individuals. In addition, vaccinating latent and recovered individuals may help achieve the goals of WHO in 2050. Further, we did not consider the emergence and spread of drug-resistant and multi-drug-resistant TB, which will be studied in future work when relevant data become publicly available.

Appendices

Appendix A The Expressions of $f_{ij}$, $v_{ij}$ and the Existence of Periodic Solutions

$$\begin{aligned} f_{12}= & {} \left[ \begin{array}{cccc} (1-q_{1})\beta _{1}(t)c_{11}(s^{0}_{1}+\eta _{1}v^{0}_{1})&{} (1-q_{1})\beta _{1}(t)c_{12}(s^{0}_{1}+\eta _{1}v^{0}_{1})&{} \cdots &{}(1-q_{1})\beta _{1}(t)c_{1n}(s^{0}_{1}+\eta _{1}v^{0}_{1})\\ (1-q_{2})\beta _{2}(t)c_{21}(s^{0}_{2}+\eta _{2}v^{0}_{2})&{} (1-q_{2})\beta _{2}(t)c_{22}(s^{0}_{2}+\eta _{2}v^{0}_{2})&{} \cdots &{}(1-q_{2})\beta _{2}(t)c_{2n}(s^{0}_{2}+\eta _{2}v^{0}_{2})\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ (1-q_{n})\beta _{n}(t)c_{n1}(s^{0}_{n}+\eta _{n}v^{0}_{n})&{} (1-q_{n})\beta _{n}(t)c_{n2}(s^{0}_{n}+\eta _{n}v^{0}_{n})&{} \cdots &{}(1-q_{n})\beta _{n}(t)c_{nn}(s^{0}_{n}+\eta _{n}v^{0}_{n})\\ \end{array} \right] , \\ f_{13}= & {} \left[ \begin{array}{cccc} (1-q_{1})\beta _{1}(t)c_{11}\omega _{1}(s^{0}_{1}+\eta _{1}v^{0}_{1})&{} (1-q_{1})\beta _{1}(t)c_{12}\omega _{2}(s^{0}_{1}+\eta _{1}v^{0}_{1})&{} \cdots &{}(1-q_{1})\beta _{1}(t)c_{1n}\omega _{n}(s^{0}_{1}+\eta _{1}v^{0}_{1})\\ (1-q_{2})\beta _{2}(t)c_{21}\omega _{1}(s^{0}_{2}+\eta _{2}v^{0}_{2})&{} (1-q_{2})\beta _{2}(t)c_{22}\omega _{2}(s^{0}_{2}+\eta _{2}v^{0}_{2})&{} \cdots &{}(1-q_{2})\beta _{2}(t)c_{2n}\omega _{n}(s^{0}_{2}+\eta _{2}v^{0}_{2})\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ (1-q_{n})\beta _{n}(t)c_{n1}\omega _{1}(s^{0}_{n}+\eta _{n}v^{0}_{n})&{} (1-q_{n})\beta _{n}(t)c_{n2}\omega _{2}(s^{0}_{n}+\eta _{n}v^{0}_{n})&{} \cdots &{}(1-q_{n})\beta _{n}(t)c_{nn}\omega _{n}(s^{0}_{n}+\eta _{n}v^{0}_{n})\\ \end{array} \right] , \\ f_{22}= & {} \left[ \begin{array}{cccc} q_{1}\beta _{1}(t)c_{11}(s^{0}_{1}+\eta _{1}v^{0}_{1})&{} q_{1}\beta _{1}(t)c_{12}(s^{0}_{1}+\eta _{1}v^{0}_{1})&{} \cdots &{}q_{1}\beta _{1}(t)c_{1n}(s^{0}_{1}+\eta _{1}v^{0}_{1})\\ q_{2}\beta _{2}(t)c_{21}(s^{0}_{2}+\eta _{2}v^{0}_{2})&{} q_{2}\beta _{2}(t)c_{22}(s^{0}_{2}+\eta _{2}v^{0}_{2})&{} \cdots &{}q_{2}\beta _{2}(t)c_{2n}(s^{0}_{2}+\eta _{2}v^{0}_{2})\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ q_{n}\beta _{n}(t)c_{n1}(s^{0}_{n}+\eta _{n}v^{0}_{n})&{} q_{n}\beta _{n}(t)c_{n2}(s^{0}_{n}+\eta _{n}v^{0}_{n})&{} \cdots &{}q_{n}\beta _{n}(t)c_{nn}(s^{0}_{n}+\eta _{n}v^{0}_{n})\\ \end{array} \right] , \\ f_{23}= & {} \left[ \begin{array}{cccc} q_{1}\beta _{1}(t)c_{11}\omega _{1}(s^{0}_{1}+\eta _{1}v^{0}_{1})&{} q_{1}\beta _{1}(t)c_{12}\omega _{2}(s^{0}_{1}+\eta _{1}v^{0}_{1})&{} \cdots &{}q_{1}\beta _{1}(t)c_{1n}\omega _{n}(s^{0}_{1}+\eta _{1}v^{0}_{1})\\ q_{2}\beta _{2}(t)c_{21}\omega _{1}(s^{0}_{2}+\eta _{2}v^{0}_{2})&{} q_{2}\beta _{2}(t)c_{22}\omega _{2}(s^{0}_{2}+\eta _{2}v^{0}_{2})&{} \cdots &{}q_{2}\beta _{2}(t)c_{2n}\omega _{n}(s^{0}_{2}+\eta _{2}v^{0}_{2})\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ q_{n}\beta _{n}(t)c_{n1}\omega _{1}(s^{0}_{n}+\eta _{n}v^{0}_{n})&{} q_{n}\beta _{n}(t)c_{n2}\omega _{2}(s^{0}_{n}+\eta _{n}v^{0}_{n})&{} \cdots &{}q_{n}\beta _{n}(t)c_{nn}\omega _{n}(s^{0}_{n}+\eta _{n}v^{0}_{n})\\ \end{array} \right] , \\ v_{11}= & {} \left[ \begin{array}{ccccc} \sigma _{1}+u+d_{1}+\alpha _{1}&{}0&{}\cdots &{}0&{}0\\ -a_{(k-1)k}\alpha _{1}&{} \sigma _{2}+u+d_{2}+\alpha _{2}&{}\cdots &{}0&{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ 0&{}0&{}\cdots &{}-a_{(k-1)k}\alpha _{n-1}&{}\sigma _{n}+u+d_{n}+\alpha _{n}\\ \end{array} \right] , \\ v_{21}= & {} \left[ \begin{array}{ccccc} -\mu _{1}\sigma _{1}&{}0&{}\cdots &{}0\\ 0&{} -\mu _{2}\sigma _{2}&{}\cdots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\cdots &{} -\mu _{n}\sigma _{n}\\ \end{array} \right] , \\ v_{22}= & {} \left[ \begin{array}{ccccc} \theta _{1}+u+d_{1}+\alpha _{1}&{}0&{}\cdots &{}0&{}0\\ -a_{(k-1)k}\alpha _{1}&{} \theta _{2}+u+d_{2}+\alpha _{2}&{}\cdots &{}0&{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ 0&{}0&{}\cdots &{}-a_{(k-1)k}\alpha _{n-1}&{} \theta _{n}+u+d_{n}+\alpha _{n}\\ \end{array} \right] , \\ v_{24}= & {} \left[ \begin{array}{ccccc} -\chi _{1}&{}0&{}\cdots &{}0\\ 0&{} -\chi _{2}&{}\cdots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\cdots &{} -\chi _{n}\\ \end{array} \right] ,\;\; v_{32}=\left[ \begin{array}{ccccc} -\xi _{1}\theta _{1}&{}0&{}\cdots &{}0\\ 0&{} -\xi _{2}\theta _{2}&{}\cdots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\cdots &{} -\xi _{n}\theta _{n}\\ \end{array} \right] , \\ v_{33}= & {} \left[ \begin{array}{ccccc} \gamma _{1}+u+d_{1}+\alpha _{1}&{}0&{}\cdots &{}0&{}0\\ -a_{(k-1)k}\alpha _{1}&{} \gamma _{2}+u+d_{2}+\alpha _{2}&{}\cdots &{}0&{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ 0&{}0&{}\cdots &{}-a_{(k-1)k}\alpha _{n-1}&{} \gamma _{n}+u+d_{n}+\alpha _{n}\\ \end{array} \right] , \\ v_{41}= & {} \left[ \begin{array}{ccccc} -(1-\mu _{1})\sigma _{1}&{}0&{}\cdots &{}0\\ 0&{} -(1-\mu _{2})\sigma _{2}&{}\cdots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\cdots &{} -(1-\mu _{n})\sigma _{n}\\ \end{array} \right] , \\ v_{42}= & {} \left[ \begin{array}{ccccc} -(1-\xi _{1})\theta _{1}&{}0&{}\cdots &{}0\\ 0&{} -(1-\xi _{2})\theta _{2}&{}\cdots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\cdots &{} -(1-\xi _{n})\theta _{n}\\ \end{array} \right] , \;\; v_{43}=\left[ \begin{array}{ccccc} -\rho _{1}\gamma _{1}&{}0&{}\cdots &{}0\\ 0&{}-\rho _{2}\gamma _{2}&{}\cdots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\cdots &{} -\rho _{n}\gamma _{n}\\ \end{array} \right] , \\ v_{44}= & {} \left[ \begin{array}{ccccc} \chi _{1}+u+d_{1}+\alpha _{1}&{}0&{}\cdots &{}0&{}0\\ -a_{(k-1)k}\alpha _{1}&{} \chi _{2}+u+d_{2}+\alpha _{2}&{}\cdots &{}0&{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ 0&{}0&{}\cdots &{}-a_{(k-1)k}\alpha _{n-1}&{} \chi _{n}+u+d_{n}+\alpha _{n}\\ \end{array} \right] . \end{aligned}$$

We divide the population into two age-groups and provide some numerical simulations to support Remark 1. The parameters of System (2) are fixed as $\beta _{1}(t)={\hat{\beta }}_{1}(1+0.99\sin (\frac{\pi }{6}t))$, ${\hat{\beta }}_{1}\in [0.03,0.08]$, $\beta _{2}(t)={\hat{\beta }}_{2}(1+0.99\sin (\frac{\pi }{6}t))$, ${\hat{\beta }}_{2}\in [0.03,0.08]$, $c_{11}=42$, $c_{12}=18$, $c_{21}=19$, $c_{22}=186$, $d_1=1/(100\times 12)$, $d_2=1/(50\times 12)$, $\alpha _1=1/(50\times 12)$, $\alpha _2=0$, $p_1=0.99$, $\nu _2=0.4$, $q_1=0.05$, $q_2=0.05$, $\sigma _1=1.5\times 10^{-4}$, $\sigma _2=2.3\times 10^{-4}$, $\theta _1=30/25$, $\theta _2=30/25$, $\gamma _1=1/6$, $\gamma _2=1/6$, $\rho _1=0.95$, $\rho _2=0.95$, $\mu _1=0.1545$, $\mu _2=0.1545$, $\xi _1=0.89$, $\xi _2=0.89$, $\omega _1=0.4387$, $\omega _2=0.4387$, $\eta _1=0.15$, $\eta _2=0.15$, $\tau _1=1/(10\times 12)$, $\tau _2=1/(5\times 12)$, $\delta _1=0.8$, $\delta _2=0.8$, $\varrho _1=0.8$, $\varrho _2=0.8$, $\chi _1=0.0075/12$, $\chi _2=0.006/12$, $a_{12}=1$, $u=0$. The initial values of System (2) are $(s_{1}(0),s_{2}(0),v_{1}(0),v_{2}(0),e_{1}(0),e_{2}(0),i_{1}(0),i_{2}(0),f_{1}(0),f_{2}(0),r_{1}(0),r_{2}(0)) = (0.5,0.5,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1)$. According to numerical simulation results, when ${\mathcal {R}}_{0}<1$, System (2) has at least one stable positive periodic solution and one stable disease-free periodic solution. When ${\mathcal {R}}_{0}>1$, System (2) has at least one stable positive periodic solution and one unstable disease-free periodic solution, as shown in Fig. 8.

Fig. 8

The existence of periodic solutions (Color figure online)

Appendix B Contact Matrix

Let ${\overline{A}}$ represent the known contact matrix, as shown in Table 4, and ${\bar{a}}_{ig},i,g=1,2,\cdots ,m$ represents the elements in the contact matrix, where i, g refers to rows and columns, respectively, and m is the number of age-groups in the contact matrix. We use $C=(c_{kj}),k,j=1,2,\cdots ,n$ to denote the modified contact matrix, then we let age-group ${\bar{u}}$ contain narrower age-groups $i=l(k)$ to g(k), where n is the number of age-groups in the modified contact matrix.

Table 4 Contact matrix (Prem et al. 2017)

Table 5 Number of individuals in each age-group (Population Census Office of the State Council of the People’s Republic of China 2021)

The contact rate between an individual in age-group i and another individual in age-group g can be expressed as

$$\begin{aligned} {\bar{d}}_{ij}=\sum ^{{\bar{u}}(j)}_{g=l(j)}{\bar{a}}_{ig}. \end{aligned}$$

Let $N_{i}$ denote the population in age-group i, as shown in Table 5, we can calculate the population weighted average of each element, ${\bar{d}}$, and derive the contact rate between age-group k and age-group j. For elements off-diagonal, we need to calculate the number of contacts between different age-groups. Therefore, the total number of contacts from k to j and j to k can be expressed as

$$\begin{aligned} {\bar{Y}}_{kj}=\sum ^{{\bar{u}}(k)}_{i=l(k)}N_{i}{\bar{d}}_{ij},\;{\bar{Y}}_{jk}=\sum ^{{\bar{u}}(j)}_{i=l(j)}N_{i}{\bar{d}}_{ik}. \end{aligned}$$

In order to ensure that ${\bar{Y}}_{kj}$ and ${\bar{Y}}_{jk}$ are equal, we averaged ${\bar{Y}}_{kj}$ and ${\bar{Y}}_{jk}$, namely

$$\begin{aligned} Z_{kj}=Z_{jk}=\frac{{\bar{Y}}_{kj}+{\bar{Y}}_{jk}}{2}. \end{aligned}$$

In summary, the modified contact matrix element can be expressed as

$$\begin{aligned} c_{kj}=\frac{Z_{kj}}{\sum ^{{\bar{u}}(k)}_{i=l(k)}N_{i}},\;c_{jk}=\frac{Z_{jk}}{\sum ^{{\bar{u}}(j)}_{i=l(j)}N_{i}}, \end{aligned}$$

where $c_{kj}$ is the rate at which an individual in age-group k makes contacts with anyone in age-group j per day. The total contact rate on the diagonal is

$$\begin{aligned} c_{kk}=\frac{\sum ^{{\bar{u}}(k)}_{i=l(k)}N_{i}{\bar{d}}_{ik}}{\sum ^{{\bar{u}}(k)}_{i=l(k)}N_{i}}. \end{aligned}$$

Appendix C Data Collection and Wavelet Analysis

Table 6 Population data from 2005 to 2019 (National Bureau of Statistics 2021a)

Fig. 9

Temporal periodicity analysis of monthly new TB cases for 14 age-groups from January 2005 to December 2017 in mainland China using the wavelet method. (A) The wavelet spectrum analysis corresponding to time series of monthly new TB cases. High power values are colored in red; orange and yellow denote intermediate power; cyan and blue denote low one. Note the black line is the 95% confidence level. (B) The average wavelet spectrum (blue line) and the corresponding 95% confidence contour (red line) (Color figure online)

Fig. 10

3D graph of the fitting results of monthly TB prevalence per 100,000 individuals from January 2005 to December 2017. The 14 age-groups represent 0–4 years old 5–9 years old, 10–14 years old, 15–19 years old, 20–24 years old, 25–29 years old, 30–34 years old, 35–39 years old, 40–44 years old, 45–49 years old, 50–54 years old, 55–59 years old, 60–64 years old, and 65+ years old, respectively. The black circles represent the actual data (Color figure online)

Appendix D Parameter Estimation

Fig. 11

The fitting results of TB prevalence per 100,000 individuals vary with age-groups. The solid red line represents the simulated curve of System (1). The black circles represent training data, and the green circles represent testing data. The $95\%$ confidence and prediction intervals are shown as light red and light blue, respectively. The 14 age-groups represent 0–4 years old, 5–9 years old, 10–14 years old, 15–19 years old, 20–24 years old, 25–29 years old, 30–34 years old, 35–39 years old, 40–44 years old, 45–49 years old, 50–54 years old, 55–59 years old, 60–64 years old, and 65+ years old, respectively (Color figure online)

Fig. 12

Trace plots of unknown parameters and initial values for System (1), estimated by Markov chain Monte Carlo (MCMC) methods. The blue lines represent the $95\%$ confidence interval. The red line represents the mean value (Color figure online)

Table 7 The unknown parameters of System (1)

Table 8 The initial values of System (1)