1 Introduction

The goal of phylogenetics is to reconstruct the evolutionary history of a group of species from biological data. Most often, the data available are the aligned DNA sequences of the species under consideration. The descent of these species from a common ancestor is represented by a rooted phylogenetic tree which we call the species tree. However, it is well known that due to various biological phenomena, such as horizontal gene transfer and incomplete lineage sorting, the ancestry of individual genes will not necessarily match the tree of the species in which they reside (Pamilo and Nei 1988; Syvanen 1994; Maddison 1997). There are various phylogenetic reconstruction methods that account for this discrepancy in different ways. One approach is to reconstruct individual gene trees by some method and then utilize this information to infer the original species tree (Liu et al. 2009, 2010; Wu 2012; Mirarab et al. 2014; Mirarab and Warnow 2015).

The multispecies coalescent model incorporates incomplete lineage sorting directly. The tree parameter of the model is the species tree, an n-leaf rooted equidistant tree with branch lengths. The species tree yields a distribution on possible gene trees along which evolution is modeled by a \(\kappa \)-state substitution model. For a fixed choice of parameters, the multispecies coalescent returns a probability distribution on the \(\kappa ^n\) possible n-tuples of states that may be observed. In order to infer the species tree from data, one searches for model parameters yielding a distribution close to that observed, using, for example, maximum likelihood.

In Chifman and Kubatko (2015), the authors show that given a probability distribution from the multispecies coalescent model, it is possible to infer the unrooted topology of the species tree parameter. Unrooting the species tree and restricting to any four-element subset of the leaves yield an unrooted four-leaf binary phylogenetic tree called a quartet. For a given label set, there are only three possible quartets which each induce a flattening of the probability tensor. Given a probability distribution arising from the multispecies coalescent, the flattening matrix corresponding to the quartet compatible with the species tree will be rank \({\kappa + 1 \atopwithdelims ()2}\) or less while the other two will generically have rank strictly greater than this value. Since the topology of an unrooted tree is uniquely determined by quartets Semple and Steel (2003), these flattening matrices can be used to determine the unrooted topology of the species tree exactly. Of course, empirical and even simulated data produced by the multispecies coalescent will only approximate the distribution arising from the model. Therefore, the same authors also proposed a method called SVDQuartets Chifman and Kubatko (2014), which uses singular value decomposition to infer each quartet topology by determining which of the flattening matrices is closest to the set of rank \({\kappa + 1 \atopwithdelims ()2}\) matrices.

The method of SVDQuartets offers several advantages over other existing phylogenetic reconstruction methods. For example, it accounts for incomplete lineage sorting and is computationally much less expensive than Bayesian methods achieving the same level of accuracy. It is often underappreciated that this reconstruction method can be used to recover the species tree for several different underlying nucleotide substitution models without any modifications. It was shown in Chifman and Kubatko (2015) that the method of SVDQuartets is applicable when the underlying model for the evolution of sequence data along the gene trees is the four-state general time-reversible (GTR) model or any of the commonly used submodels thereof (e.g., JC69, K2P, K3P, F81, HKY85, TN93). Thus, the method does not require any a priori assumptions about the underlying nucleotide substitution process other than time reversibility.

In this paper, we show that the method of SVDQuartets has more theoretical robustness even than has already been shown. We will specifically focus on the case where the underlying nucleotide substitution model is one of the four-state models most widely used in phylogenetics. We describe several modifications to the classical multispecies coalescent model to allow for more realistic mechanisms of evolution. For example, we remove the assumption of a molecular clock by removing the restriction that the species tree be equidistant. We also allow the effective population size to vary on each branch of the species tree. Remarkably, we show that the unrooted topology of the species tree parameter of these modified models is still identifiable and that SVDQuartets is still an appropriate reconstruction method. Thus, despite the introduction of several parameters, effective and efficient methods for reconstructing the unrooted topology of the species tree for these modified coalescent models are already available off the shelf and implemented in \(\hbox {PAUP}^*\) (Swofford 2002).

In Sect. 2, we review the classical multispecies coalescent model and discuss some of its limitations in modeling certain biological phenomena. We then describe several modifications to the classical model to remedy these weaknesses. In Sect. 3, we establish the theoretical properties of identifiability for these families of modified coalescent models. Finally, in Sect. 4, we describe why SVDQuartets is a strong candidate for reconstructing the species tree under the multispecies coalescent and propose several other modifications that could be made to the multispecies coalescent.

2 The Multispecies Coalescent

2.1 Coalescent Models of Evolution

In this section, we briefly review the multispecies coalescent model and explain how the model yields a probability distribution on nucleotide site patterns. As our main results will parallel those found in Chifman and Kubatko (2015), we will import much of the notation from that paper and refer the reader there for a more thorough description of the model.

The Wright-Fisher model from population genetics models the convergence of multiple lineages backward in time toward a common ancestor. Beginning with j lineages from the current generation, the model assumes discrete generations with constant effective population size N. In each generation, each lineage is assigned a parent uniformly from the previous generation. For diploid species, there are 2N copies of each gene in each generation, and thus the probability of selecting any particular gene as a parent is \(\dfrac{1}{2N}\). Two lineages are said to coalesce when they share the same parent in a particular generation.

As an example, if we begin with two lineages in the same species, the probability they have the same parent in the previous generation, and hence coalesce, is \(\dfrac{1}{2N}\) and the probability that they do not coalesce in this generation is \((1 - \dfrac{1}{2N})\). Therefore, the probability that two lineages coalesce in exactly the ith previous generation is given by

$$\begin{aligned} \left( \dfrac{1}{2N} \right) \left( 1 - \dfrac{1}{2N} \right) ^{i-1}. \end{aligned}$$

For large N, the time at which the two lineages coalesce, t, approximately follows an exponential distribution with rate \((2N)^{-1}\), where time is measured in number of generations. Every 2N generation is called a coalescent unit, and time is typically measured in these units to simplify the formulas for time to coalescence. However, in this paper, we will introduce separate effective population size parameters for each branch of the species trees. So that our timescale is consistent across the tree we will work in generations rather than coalescent units. In these units, for j lineages, the time to the next coalescent event t has probability density,

$$\begin{aligned} f(t) = \dfrac{j(j-1)}{2} \left( \dfrac{1}{2N} \right) \exp \left( - \dfrac{j(j-1)}{2} \left( \dfrac{1}{2N} \right) t \right) , \ t > 0. \end{aligned}$$
(1)

This is typically referred to as Kingman’s coalescent (Kingman 1982a, b, c; Tajima 1983; Tavaré 1984; Takahata and Nei 1985).

The multispecies coalescent is based on the same framework, but we assume that the species tree of the sampled taxa is known. We let S denote the topology (without branch lengths) of the n-leaf rooted binary phylogenetic species tree. The tips of S represent distinct species and are labeled by uppercase letters. We assume here that one lineage is sampled from each species, and we label each lineage by the lowercase letter corresponding to the species from which it is sampled. We use \(e_X\) to denote the branch of S that is ancestral to exactly the species in X. The vector \(\varvec{\tau }\) specifies branch lengths where \(\tau _X\) is the length of \(e_X\). Thus, \((S,\varvec{\tau })\) denotes a rooted species tree with branch lengths. In the classical multispecies coalescent, the entries of \(\varvec{\tau }\) are chosen so that \((S,\varvec{\tau })\) is equidistant, meaning that the length of the path from the root to any tip of the species tree is the same. This is commonly referred to as the molecular clock assumption, and in what follows, we refer to the classical multispecies coalescent as the equidistant coalescent. For example, for the four-leaf species tree depicted in Fig. 1a, \(\varvec{\tau } = (\tau _A,\tau _B,\tau _C,\tau _D,\tau _{AB},\tau _{CD})\) and the entries satisfy \(\tau _A = \tau _B, \tau _C = \tau _D\), and \(\tau _A + \tau _{AB} = \tau _C + \tau _{CD}\). Later, we will introduce different effective population sizes in each population and we will use \(N_X\) to denote the size of the population in \(e_X\).

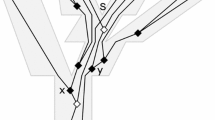
Once this species tree is fixed, the multispecies coalescent gives a probability density on possible gene trees, where here we use the term gene tree to mean both the topology and the branch lengths. All of the same assumptions above apply, except that it is now impossible for two lineages to coalesce if they are not part of the same population. Hence, lineages may only coalesce if they are in the same branch of S. We use the concept of a coalescent history, h (see, e.g., Degnan and Salter 2005) to indicate a particular sequence of coalescent events as well as the populations in which they occur (but not the precise times of the events). There are only finitely many possible coalescent histories compatible with S, and we call the set of all such histories \(\mathcal {H}\). We denote the topology of a rooted n-leaf binary phylogenetic gene tree by G and let \(\mathbf {t} = (t_1, \ldots , t_{n-1})\) be the vector that encodes the coalescent times. Thus, in the context of a specific species tree and history, \((G,\mathbf {t})\) encodes a gene tree with branch lengths. As for the species tree, we measure all branch lengths in units of generations. Note that any given history corresponds to infinitely many gene trees, though all will have the same topology. Likewise, a particular gene tree topology may correspond to only one history or (finitely) many histories. Figure 1 gives an example of a single gene tree topology with two distinct histories. Note, however, that in Fig. 1a, b, there are infinitely many choices for the values of \(t_1, t_2,\) and \(t_3\) that satisfy the constraints of each history.

For a particular history and a particular species tree \((S,\varvec{\tau })\), we can compute the probability density for gene trees \((G,\mathbf {t})\) with that history explicitly under the multispecies coalescent model. We denote this gene tree density by \(f_h((G,\mathbf {t})|(S,\varvec{\tau }))\). We demonstrate below how this is done for the history in Fig. 1a.

Fig. 1
figure 1

A species tree and two different coalescent histories that result in the same gene tree topology. The coalescent times \(t_j\) are measured from the most recent speciation event (looking backwards in time). a A gene tree with topology G and history h. b A gene tree with topology G and history \(h'\)

Full size image

Example 2.1

Let \((S,\varvec{\tau })\) be the four-leaf species tree depicted in Fig. 1a, and let h refer to the coalescent history in which the following events occur in order (looking backward from the present):

  1. (1)

    Lineages a and b coalesce in the population ancestral to A and B.

  2. (2)

    Lineages c and d coalesce in the population above the root.

  3. (3)

    Lineages ab and cd coalesce in the population above the root.

The probability of observing a gene tree with history h for the species tree \((S,\varvec{\tau })\) under the multispecies coalescent model can be found by integrating over all possible times at which the coalescent events consistent with h may occur. Note that the integrals must be taken with respect to the boundaries for the coalescent events specified by the history. Therefore, each history will have a unique region of integration, and each must be considered separately. For history h shown in Fig. 1a, we have

$$\begin{aligned} \int _\mathbf{t } \! f_h((G,{\mathbf {t}})|(S,\varvec{\tau })) \mathrm{d}{} \mathbf t&= \int _0^{\infty } \! \int _0^{t_3} \! \int _0^{\tau _{AB}} \! \exp \left( \dfrac{-\tau _{CD}}{2N} \right) \left( \left( \dfrac{1}{2N} \right) \exp \left( \dfrac{-t_1}{2N} \right) \right) \\&\quad \left( \left( \dfrac{1}{2N} \right) \exp \left( \dfrac{-3t_2}{2N} \right) \right) \left( \left( \dfrac{1}{2N} \right) \exp \left( \dfrac{-(t_3 - t_2)}{2N} \right) \right) \ \mathrm{d}t_1 \mathrm{d}t_2 \mathrm{d}t_3. \end{aligned}$$

We assume that the distribution of times to coalescent events is given by Kingman’s coalescent as in Eq. (1). We compute \(f_h((G,\mathbf {t})|(S,\varvec{\tau }))\) under the assumption that evolution occurs independently in each branch of the species tree. Thus, we multiply the contributions to the density of the events occurring in each species tree branch to obtain the probability density of the history. For example, the first term of \(f_h((G,\mathbf {t})|(S,\varvec{\tau }))\) is equal to

$$\begin{aligned} 1 - \int _0^{\tau _{CD}} \! \left( \dfrac{1}{2N} \right) \exp \left( \dfrac{-t}{2N} \right) \ \mathrm{d}t, \end{aligned}$$

the probability that lineages c and d do not coalesce in the population ancestral to C and D. The second term is the probability density for the event that lineages a and b coalesce at time \(t_1\). The third term is the probability density for the event that lineages c and d coalesce at time \(t_2\). Finally, the last term is the probability density for the event that the newly formed lineages ab and cd coalesce at time \(t_3 - t_2\) (measured relative to the time when lineages c and d coalesced). Notice that the coalescent history \(h'\) depicted in Fig. 1b results in the same gene tree, but the density function \(f_{h'}((G,\mathbf {t})|(S,\varvec{\tau }))\) will not be the same as \(f_{h}((G,\mathbf {t})|(S,\varvec{\tau }))\).

For a fixed gene tree at a given locus, we model the evolution along this gene tree as a continuous-time homogenous Markov process according to a nucleotide substitution model. The model gives a probability distribution on the set of all \(4^n\) possible n-tuples of observed states at the leaves of \((G,\mathbf {t})\). We can write the probability of observing the state \((i_1,\ldots ,i_n)\) as \(p^*_{i_1\ldots i_n|(G,\mathbf {t})}\). Precisely how this distribution is calculated is described in Chifman and Kubatko (2015). Here, we sketch the relevant details needed to introduce the modified multispecies coalescent model described in the next section.

For a four-state substitution model, there is a \(4 \times 4\) instantaneous rate matrix Q where the entry \(Q_{ij}\) encodes the rate of conversion from state i to state j. To compute the probability of observing a particular state at the leaves, we associate with each vertex v a random variable \(X_v\) with state space equal to the set of four possible states. The distribution of states at the root vertex is \(\varvec{\pi } = (\pi _A, \pi _G,\pi _C, \pi _T)\) where \(\varvec{\pi }\) is the stationary distribution of the rate matrix Q. Letting \(t_{e}\) be the length of edge \(e = uv\), \(P(t_e) = e^{Qt_{e}}\) is the matrix of transition probabilities along that edge. That is, \(P_{ij}(t_e) = P(X_v = j | X_u = i)\). Given an assignment of states to each vertex of the tree, we can compute the probability of observing this state using the Markov property and the appropriate entries of the transition matrices. To determine the probability of observing a particular state at the leaves, we marginalize over all possible states of the internal nodes.

In this paper, we are primarily interested in four-state models of DNA evolution where the four states correspond to the DNA bases. Different phylogenetic models place different restrictions on the entries of the rate matrices. The results that we prove in the next section will apply when the underlying nucleotide substitution model is any of the commonly used four-state time-reversible models. As an example, the rate matrices for two of these models, the Kimura three-parameter model (K3P) and the four-state general time-reversible model (GTR), are given in Fig. 2. We note here that because these models are time reversible, the location of the root in each gene tree is unidentifiable from the site pattern probability distribution for that gene tree Felsenstein (1981). In subsequent sections, we will introduce and describe similar results for the JC+I+\(\Gamma \) model that allows for invariable sites and gamma-distributed rates across sites.

Fig. 2
figure 2

Rate matrices for two commonly used models in phylogenetics. The diagonal entries are chosen so that the row sums are equal to zero. In the K3P model, the root distribution is uniform. a Kimura three-parameter model (K3P). b Four-state general time-reversible model (GTR)

Full size image

Now, given a species tree \((S,\varvec{\tau })\) and a choice of nucleotide substitution model, let \(p_{i_1\ldots i_n|(S,\varvec{\tau })}\) be the probability of observing the site pattern \(i_1\ldots i_n\) at the tips of \((S,\varvec{\tau })\). To compute \(p_{i_1\ldots i_n|(S,\varvec{\tau })}\), we must consider the contribution of each history to the site pattern probability distribution by integrating over branch lengths. So that we may write the formulas explicitly, and we first consider the contribution of gene trees matching a particular coalescent history,

$$\begin{aligned} p_{i_1\ldots i_n|h,(S,\varvec{\tau })}= \displaystyle \int _{\mathbf {t}} p^*_{i_1\ldots i_n|(G,\mathbf {t})} f_h((G,\mathbf {t})|(S,\varvec{\tau })) \ \mathrm{d}\mathbf {t}. \end{aligned}$$

As noted previously, there will be finitely many histories for any given species tree \((S,\varvec{\tau })\), and summing over these gives the probability of observing the site pattern \(i_1\ldots i_n\) at the tips of the species tree \((S,\varvec{\tau })\),

$$\begin{aligned} p_{i_1\ldots i_n|(S,\varvec{\tau })}&= \displaystyle \sum _{h \in \mathcal {H}} \displaystyle \int _{\mathbf {t}} p^*_{i_1\ldots i_n|(G,\mathbf {t})} f_h((G,\mathbf {t})|(S,\varvec{\tau })) \ \mathrm{d}\mathbf {t} \\&= \displaystyle \sum _{h \in \mathcal {H}} p_{i_1\ldots i_n|h,(S,\varvec{\tau })}. \end{aligned}$$

Note again that the bounds of integration in each term of the sum will depend on the history being considered.

2.2 A Modified Coalescent

In this section, we introduce various ways that we might alter the multispecies coalescent to better reflect the evolutionary process. Recall that the length of the path from the root of the species tree to each tip is the total number of generations that have occurred between the species at the root and that at the tip. Since the length of a generation may vary for different species Martin and Palumbi (1993), it may be desirable to allow the lengths of the paths from the root to each tip to differ. Therefore, we first consider expanding the allowable set of branch lengths so that \((S,\varvec{\tau })\) is not required to be equidistant.

Fix a nucleotide substitution model. Let \(\mathcal {C}(S) \subseteq \Delta ^{4^n - 1}\) be the set of site pattern probability distributions obtained from the equidistant multispecies coalescent model on the n-leaf topological rooted tree S. Let \(\mathcal {C}_n \subseteq \Delta ^{4^n - 1}\) denote the set of all distributions obtained by allowing \((S,\varvec{\tau })\) to be any equidistant n-leaf rooted tree. If \((S,\varvec{\tau })\) is not required to be equidistant, this removes the assumption of a molecular clock and we refer to this model as the clockless coalescent. The set of site pattern probabilities obtained from a single species tree topology in the clockless coalescent is \(\mathcal {C}^*(S)\), and the set of distributions obtained by allowing \((S,\varvec{\tau })\) to be any n-leaf rooted tree (not necessarily equidistant) is \(\mathcal {C}_n^*\).

We can also account for the fact that the effective population size, N, may vary for different species Charlesworth (2009) by introducing a separate effective population size parameter for each internal branch of the species tree. We call this model the p-coalescent and denote the set of all site pattern probabilities arising from the model as \(\mathcal {C}(S,N)\). Note that here we consider the species tree \((S,\varvec{\tau })\) to be equidistant. In analogy to our notation from above, we use \(\mathcal {C}_n(N)\) to denote the set of all site pattern probability distributions obtained from the p-coalescent and use \(\mathcal {C}^*(S,N)\) and \(\mathcal {C}^*_n(N)\) for the clockless p-coalescent.

Since we assume that coalescent events do not occur within terminal edges of the species tree, changing the effective population size on the terminal edges does not change the probability distribution on gene trees or the site pattern probabilities arising from a given gene tree. In the next section, we will show that, remarkably, the unrooted topologies of the species tree parameter of the clockless coalescent, p-coalescent, and the clockless p-coalescent are all generically identifiable. Conveniently, from the perspective of reconstruction, we also show that the method of SVDQuartets Chifman and Kubatko (2014) can be used to reconstruct the unrooted topology of the species tree based on a sample from the site pattern probability distribution given by the model.

It is well known that when considering the gene tree distribution from the coalescent model on a rooted tree S, the branch lengths and population sizes are confounded. For example, if a particular branch length is doubled and the population size on that branch halved, this will not affect the gene tree distribution. However, we note that the site pattern probability distributions induced by the clockless coalescent and by the p-coalescent on S are not necessarily equal (i.e., \(\mathcal {C}^*(S)\) does not necessarily equal \(\mathcal {C}(S,N)\)). Some intuition for why these are not necessarily the same can be obtained by comparing each of these modified coalescent models to the equidistant model. We can construct a species tree from the clockless coalescent by beginning with an equidistant species tree and either stretching or contracting certain branches. This alters the gene tree distribution by allowing more or less time, respectively, for coalescent events to occur along the affected branch. However, the probability density of the time to a fixed coalescent event will not necessarily be affected by this change. In contrast, the p-coalescent induces a change in the rate of coalescence, as can be seen by examining Eq. (1), which will alter the probability density of the time of a coalescent event that resides in any affected species tree branch. For example, if the branch e in Fig. 3 is from an equidistant tree \((S,\varvec{\tau })\), increasing \(\tau _e\) will not affect the probability density of the time to coalescence of lineages a and b, denoted by t in the figure and given by Eq. (1). However, changing the effective population size along this branch will affect the probability density of t, since the effective population size N appears in Eq. (1).

One might be interested in a generalization of the multispecies coalescent model in which a mutation rate is associated with each branch of the species tree. This is biologically realistic in that it would allow for mutation to accumulate at different rates along different branches of the species tree, in response to factors such as variations in climate or other ecological conditions. One might think of modeling this by generalizing the definition of the instantaneous rate matrix Q defined in Section 2.1, so that, rather than associating a single matrix Q with the entire species tree, the lineages within each species tree branch e evolve according to a species tree branch-specific matrix \(\rho _eQ\) (\(\rho _e\) is a scalar that modifies the mutation rate on branch e). The example below shows that we can obtain the same site pattern probability distribution obtained by scaling Q by \(\rho _e\) by instead scaling the length of e and the effective population size in e by \(\rho _e\). This illustrates that a model with a different mutation rate on each species tree edge is subsumed by the clockless p-coalescent.

Fig. 3
figure 3

Two lineages coalescing in a branch of a species tree

Full size image

Example 2.2

Let a and b be two lineages entering a branch e of a species tree as in Fig. 3. Let \(\tau _e\) be the length of this branch and N be the effective population size parameter. The probability that a and b do not coalesce in e is

$$\begin{aligned} 1 - \int _0^{\tau _e} \! \left( \dfrac{1}{2N} \right) \exp \left( \dfrac{-t}{2N} \right) \ \mathrm{d}t = \exp \left( \dfrac{-\tau _e}{2N} \right) . \end{aligned}$$
(2)

If a and b coalesce, then we can compute the probability of observing the state xy at a and b under a homogenous Markov model where the rate matrix on the branch e is scaled by a factor \(\rho _e\). We assume the distribution of states at the vertex u is the vector \(\varvec{\pi }\). Thus, we have,

$$\begin{aligned}&p_{xy} = \displaystyle \sum _{z_1,z_2} \displaystyle \int _0^{\tau _e} \! \left( \dfrac{1}{2N} \right) \exp \left( \dfrac{-t}{2N} \right) \pi _{z_1} \nonumber \\&\qquad \quad \exp (\rho _e Q(\tau _e - t))_{z_1,z_2} \exp (\rho _e Q(t))_{z_2,x} \exp (\rho _e Q(t))_{z_2,y} \ \mathrm{d}t. \end{aligned}$$
(3)

Instead of scaling the rate matrix Q by \(\rho _e\), we could scale the length of e and the effective population size by \(\rho _e\). Then, the probability that lineages a and b do not coalesce remains unchanged since

$$\begin{aligned} \exp \left( \dfrac{-\rho _e\tau _e}{2\rho _e N} \right) = \exp \left( \dfrac{-\tau _e}{2N} \right) . \end{aligned}$$

Likewise, the probability of observing state xy is given by the following formula, where we make the substitution \(t = \rho _e T\),

$$\begin{aligned} p_{xy}&= \displaystyle \sum _{z_1,z_2} \displaystyle \int _0^{\rho _e \tau _e} \! \left( \dfrac{1}{2\rho _e N} \right) \exp \left( \dfrac{-t}{2\rho _e N} \right) \pi _{z_1} \exp (Q(\rho _e \tau _e\\&\quad - t))_{z_1,z_2} \exp (Q(t))_{z_2,x} \exp (Q(t))_{z_2,y} \ \mathrm{d}t \\&= \displaystyle \sum _{z_1,z_2} \displaystyle \int _0^{\tau _e} \! \left( \dfrac{1}{2 N} \right) \exp \left( \dfrac{- T}{2 N} \right) \pi _{z_1} \exp (\rho _e Q(\tau _e \\&\quad - T))_{z_1,z_2} \exp (\rho _e Q(T))_{z_2,x} \exp (\rho _e Q(T))_{z_2,y} \ \mathrm{d}T. \end{aligned}$$

This expression is equal to (3), and thus we have the same distribution of site patterns at the leaves of the tree. Generalizing this example, we can obtain the site pattern probability distribution for a species tree with any branch-specific scaled rate matrices that we desire by appropriately adjusting population sizes and branch lengths across the tree. Thus, we consider only the clockless coalescent, p-coalescent, and clockless p-coalescent models in what follows.

3 Identifiability of the Modified Coalescent

One of the most fundamental concepts in model-based reconstruction is that of identifiability. A model parameter is identifiable if any probability distribution arising from the model uniquely determines the value of that parameter. For the purposes of phylogenetic reconstruction, it is particularly important that the tree parameter of the model be identifiable in order to make consistent inference.

In the following paragraphs, we will use the notation \(\mathcal {C}_{n}\) for the set of site pattern probability distributions obtained by varying the n-leaf tree parameter in the equidistant coalescent model, though the discussion applies equally to \(\mathcal {C}_n^*\), \(\mathcal {C}_n(N)\), and \(\mathcal {C}_n^*(N)\). To uniquely recover the unrooted topology of the species tree parameter of the n-leaf multispecies coalescent model, we would require that for all n-leaf rooted trees \(S_1\) and \(S_2\) that are topologically distinct when the root vertex of each is suppressed, \(\mathcal {C}({S_1}) \cap \mathcal {C}(S_2) = \emptyset \). This notion of identifiability is unobtainable in most instances and much stronger than is required in practice. Instead, we often wish to establish generic identifiability. A model parameter is generically identifiable if the set of parameters from which the original parameter cannot be recovered is a set of Lebesgue measure zero in the parameter space. In our case, although we cannot guarantee that \(\mathcal {C}(S_1) \cap \mathcal {C}(S_2) = \emptyset \), we will show that if we select parameters for either model, the resulting distribution will lie in \(\mathcal {C}(S_1) \cap \mathcal {C}(S_2)\) with probability zero.

In Chifman and Kubatko (2015), it was shown that the unrooted topology of the tree parameter for the coalescent model is generically identifiable when the nucleotide substitution model is GTR+I+ \(\Gamma \) or any of the commonly used submodels thereof, using the machinery of analytic functions and varieties. A function f with domain an open set \(U \subseteq \mathbb {R}^m\) and range \(\mathbb {R}\) is real analytic on U if it is given locally by a convergent power series. An analytic variety is the common zero set of a collection of analytic functions. For the purposes of this paper, we will only need to consider analytic varieties defined by a single function, that is, varieties of the form

$$\begin{aligned} {\mathcal {V}}(f) = \{ \mathbf{u} \in U | f(\mathbf{u}) = 0\}, \end{aligned}$$

where f is real analytic on U. The property of real analytic functions that we will use later is the following: For a real analytic function f with domain an open set \(U \subseteq \mathbb {R}^m\), either f is identically zero or \(\mathcal {V}(f)\) is a set of Lebesgue measure zero (Mityagin 2015).

To illustrate how we will use this property, we describe the strategy used in Chifman and Kubatko (2015) to prove the generic identifiability of the unrooted topology of the species tree parameter of the coalescent model. For the coalescent model with underlying \(\kappa \)-state nucleotide substitution model on an n-leaf rooted species tree S, let

$$\begin{aligned} \psi _{S}: \Theta _{S} \mapsto \Delta ^{\kappa ^n -1} \end{aligned}$$

be the map from the continuous parameter space for S, \(\Theta _{S}\), to the probability simplex with \(\text {Im}(\psi _{S}) = \mathcal {C}({S})\). Label the states of the model by the natural numbers \(\{1, \ldots , \kappa \}\). Given any two rooted species trees \(S_1\) and \(S_2\) that are topologically distinct when the root vertex of each is suppressed, the strategy is to find a polynomial

$$\begin{aligned} g \in \mathbb {R}[q_{i_1\ldots i_n}: 1 \le i_1, \ldots , i_n \le \kappa ] \end{aligned}$$

such that for all \(p_1 \in \mathcal {C}(S_1)\), \(g(p_1) = 0\), but for which there exists \(p_2 \in \mathcal {C}(S_2)\) such that \(g(p_2) \not = 0\). Then, since \(g(p_1) = 0\) for all \(p_1 \in \mathcal {C}(S_1)\), the set of parameters in \(\Theta _{S_2}\) mapping into \(\mathcal {C}(S_1) \cap \mathcal {C}(S_2)\), must be contained in the zero set of

$$\begin{aligned} g \circ \psi _{S_2}: \Theta _{S_2} \rightarrow \mathbb {R}. \end{aligned}$$

If it can then be shown that \(g \circ \psi _{S_2}\) is a real analytic function, then its zero set is the analytic variety \(\mathcal {V}(g \circ \psi _{S_2})\). The existence of \(p_2\) implies that \(g \circ \psi _{S_2}\) is not identically zero on \(\Theta _{S_2}\), and so the set of parameters in \(\Theta _{S_2}\) mapping into \(\mathcal {C}(S_1) \cap \mathcal {C}(S_2)\) must be measure zero. Doing this for all pairs of n-leaf trees that are topologically distinct when the root vertex of each is suppressed establishes the generic identifiability of the unrooted topology of the species tree parameter of \(\mathcal {C}_n\).

We will show that the species tree parameter of each of the modified models introduced above is generically identifiable using the same approach. In the discussion proceeding (Chifman and Kubatko 2015, Corollary 1), it was shown that for the equidistant multispecies coalescent, to establish identifiability of the species tree parameter of the coalescent model for trees with any number of leaves, it is enough to prove the identifiability of the species tree parameter for the four-leaf model. Essentially, the same proof of that theorem applies to the clockless coalescent giving us the following proposition.

Proposition 3.1

If the unrooted topology of the species tree parameter of \(\mathcal {C}^*_4\) is generically identifiable, then the unrooted topology of the species tree parameter of \(\mathcal {C}^*_n\) is generically identifiable for all n.

A similar proposition holds for the p-coalescent but a slight modification is required. The subtlety is illustrated in Fig. 4 where a species tree and its restriction to a four-leaf subset of the leaves are shown. Notice that on the restricted tree, the effective population size may now vary within a single branch. Therefore, to show the identifiability of the unrooted species tree parameter of the p-coalescent for n-leaf trees, we must show the identifiability of the unrooted topology of the species tree parameter of a model on four-leaf trees that allows for a finite number of bands on each branch with separate effective population sizes. We will revisit this point after the proof of Theorem 3.5, though it turns out to be rather inconsequential.

Fig. 4
figure 4

A five-leaf species tree with topology S with multiple effective population size parameters and its restriction to the four-leaf topological subtree \(S_{|\{A,B,D,E\}}\). The image of the marginalization map applied to the model for S will be the model for \(S_{|\{A,B,D,E\}}\) with different effective population size parameters on different portions of \(e_{AB}\)

Full size image

3.1 The analyticity of \(\psi _S\)

In the discussion preceding Proposition 3.1, we described how to use the properties of real analytic varieties to prove generic identifiability. One of the results needed was that the function \(g \circ \psi _S\) is a real analytic function. Since polynomial functions are real analytic and the composition of real analytic functions is again analytic, to prove this it is enough to show that for any tree S, each coordinate of \(\psi _S\) is a real analytic function in the continuous parameters of the model. That this is so may seem obvious to some and was stated without proof in Chifman and Kubatko (2015). However, this issue is slightly more subtle than it might first appear.

Recall that each coordinate of \(\psi _S: \Theta _S \rightarrow \Delta ^{\kappa ^n - 1}\) is defined by a function of the form

$$\begin{aligned} \displaystyle \sum _{h \in \mathcal {H}} \displaystyle \int _{\mathbf {t}} p^*_{i_1\ldots i_n|(G,\mathbf {t})} f_h((G,\mathbf {t})|(S,\varvec{\tau })) \ \mathrm{d}\mathbf {t}. \end{aligned}$$

The entries of the matrix exponential are defined by convergent power series on \(\Theta _S\) and so are real analytic functions on \(\Theta _S\). Moreover, since elementary functions are analytic, as are sums, products, and compositions of real analytic functions Krantz and Parks (2002), the function \(p^*_{i_1\ldots i_n|(G,\mathbf {t})}f_h((G,\mathbf {t})|(S,\varvec{\tau }))\) is also a real analytic function on the entire parameter space. However, notice that the integral may be improper as in Example 2.1. It is not in general true that taking an improper integral with respect to certain variables in a real analytic function results in a real analytic function. As a counterexample, consider the function \(f(\alpha ,t) = \dfrac{\mathrm{d}}{\mathrm{d}t}(\alpha \tanh (\alpha t))\) and define the function \(F(\alpha ) = \int _0^\infty f(\alpha ,t) \ \mathrm{d}t\). Then, \(f(\alpha ,t)\) is a real analytic function on its entire domain, but \(F(\alpha ) = | \alpha |\) and so is not analytic at \(\alpha = 0\).

For the models JC69, K2P, K3P, F81, HKY85, TN93, and the generalized \(\kappa \)-state JC, these issues become irrelevant, as we can diagonalize the rate matrices and obtain a closed-form expression for the entries of the transition matrices. The entries are then seen to be exponential functions of branch length, and we can solve the improper integrals from the multispecies coalescent and obtain exact formulas for each coordinate of \(\psi _S\) that are clearly analytic. Thus, we have the following proposition.

Proposition 3.2

Let S be a rooted four-leaf species tree. The parameterization map \(\psi _S\) is analytic when the underlying nucleotide substitution model is any of JC69, K2P, K3P, F81, HKY85, TN93, or the generalized \(\kappa \)-state JC.

The rate matrix for the four-state general time-reversible model is similar to a real symmetric matrix and is thus also diagonalizable. However, actually writing down a closed form for the entries of the transition matrix is not possible due to the large number of computations involved. Consequently, we cannot write down a closed-form expression for the coordinate functions of \(\psi _S\). Of course, this is not a necessary condition for these functions to be analytic, but it is difficult to argue that they are without such a closed-form expression. Therefore, in the proposition below, we will argue that around a generic choice of parameters for the GTR rate matrix, there exists a neighborhood on which the entries of the matrix exponential can be written as expressions involving only elementary functions of the rate matrix parameters, roots of the rate matrix parameters, and exponential functions. This allows us to argue that the coordinate functions of \(\psi _S\) can also be expressed in terms of well-known functions of the rate matrix parameters, and hence, that they are real analytic functions in a neighborhood around any generic choice of parameters from the modified coalescent models.

Proposition 3.3

Let S be a rooted four-leaf species tree. Let \(\psi _S\) be the parameterization map for the multispecies coalescent model when the underlying nucleotide substitution model is the four-state GTR model. For a generic choice of continuous parameters \(\varvec{\theta } \in \Theta _S\), there exists a neighborhood around \(\varvec{\theta }\) on which each coordinate of \(\psi _S\) is a real analytic function.

Proof

Let \(\varvec{\theta }\) be a generic point in \(\Theta _S\), and let Q be the rate matrix for the four-state GTR model. The matrix

$$\begin{aligned} A = \text {diag}(\varvec{\pi }^{1/2})Q\text {diag}(\varvec{\pi }^{-1/2}) \end{aligned}$$

is a real symmetric matrix that is similar to Q. Hence, all eigenvalues of A are real numbers that are less than or equal to zero and one of these eigenvalues is \(\lambda _1 = 0\). We can factor the degree four characteristic equation of A and use the cubic formula to write the other eigenvalues \(0 \ge \lambda _2 \ge \lambda _3 \ge \lambda _4\) in terms of the rate matrix parameters. For a generic choice of parameters, the eigenvalues will be distinct and the columns of \(\prod _{j \not = i}(A - \lambda _jI)\) will be eigenvectors of A with eigenvalue \(\lambda _i\). Define the vector \(V_i\) to be the first column of \(\prod _{j \not = i}(A - \lambda _jI)\) for \(1 \le i \le 4\), and let U be the \(4 \times 4\) matrix with i-th column equal to \(V_i/ \Vert {V_i} \Vert \). Since A is a real symmetric matrix, the eigenvectors corresponding to distinct eigenvalues are orthogonal Hoffman and Kunze (1971); hence, U is an orthonormal matrix. Therefore, \(A = U \text {diag}(0, \lambda _2, \lambda _3, \lambda _4) U^{T}\) and

$$\begin{aligned} e^{Qt} = (\text {diag}(\varvec{\pi }^{-1/2})U) \text {diag}(1, e^{\lambda _2t}, e^{\lambda _3t}, e^{\lambda _4t}) (U^{T}\text {diag}(\varvec{\pi }^{1/2})). \end{aligned}$$

Thus, in a neighborhood around \(\varvec{\theta }\), each entry of the matrix exponential can be written as

$$\begin{aligned} P_{ij}(t) = \displaystyle \sum _{1 \le k \le 4} f^{(ij)}_k(q)e^{\lambda _kt}, \end{aligned}$$

where the \(f^{(ij)}_k(q)\) are rational functions of the rate matrix parameters and roots of the rate matrix parameters coming from the cubic formula.

The functions \(p^*_{i_1\ldots i_n|(G,\mathbf {t})}\) are all sums of products of these functions which are exponential in the branch length t. The formulas coming from the coalescent process, \(f_h((G,\mathbf {t})|(S,\varvec{\tau }))\), are also exponential functions in t. Because each \(\lambda _i\) is guaranteed to be less than or equal to zero, when we integrate each \(p^*_{i_1\ldots i_n|(G,\mathbf {t})} f_h((G,\mathbf {t})|(S,\varvec{\tau }))\) with respect to branch length, the integral converges. Therefore, in a neighborhood around \(\varvec{\theta }\), each coordinate of \(\psi _S\) can be written in closed form as an expression involving rational functions of the model parameters, roots of the model parameters, and exponential functions of both of these. \(\square \)

3.2 Identifiability of the Modified Multispecies Coalescent for Four-Leaf Trees

We may encode the site pattern probability distribution associated with a \(\kappa \)-state phylogenetic model on an n-leaf species tree as an n-dimensional \(\kappa \times \ldots \times \kappa \) tensor P where the entry \(P_{i_1 \ldots i_n}\) is the probability of observing the state \(i_1 \ldots i_n\). In (Chifman and Kubatko 2015, Section 4), the authors explain how to construct tensor flattenings according to a bipartition of the taxa, or split, of the species tree. Our first result is the analogue of (Chifman and Kubatko 2015, Theorem 1) for the modified coalescent models. We use the notation \(P_{(S,\varvec{\tau },\varvec{\theta })}\) to denote the probability tensor that results from choosing a species tree S with vector of edge lengths \(\varvec{\tau }\) and continuous parameters \(\varvec{\theta }\).

Theorem 3.4

Let S be a four-taxon symmetric ((A, B), (C, D)) or asymmetric (A, (B, (C, D)) species tree with a cherry (C, D). Consider the clockless coalescent when the underlying nucleotide substitution model is any of the following: JC69, K2P, K3P, F81, HKY85, TN93, or GTR. Let \(L_1|L_2\) be the split AB|CD that is valid for S. Then, for all \(P_{(S,\varvec{\tau },\varvec{\theta })} \in \mathcal {C}^*(S)\),

$$\begin{aligned} rank(Flat_{L_1|L_2}(P_{(S,\varvec{\tau },\varvec{\theta })})) \le 10. \end{aligned}$$

Proof

Let \(L_1|L_2\) be the split AB|CD that is valid for S, and consider the distribution \(P_{(S,\varvec{\tau },\varvec{\theta })}\). Without loss of generality, suppose \(\tau _C \ge \tau _D\). Consider the new vector of edge lengths \(\varvec{\xi }\) where each entry is the same as in \(\varvec{\tau }\) except that \(\xi _C = \tau _D\). Thus, we can think of the tree \((S,\varvec{\tau })\) as an extension of the tree \((S,\varvec{\xi })\) as in Fig. 5.

First, we claim that

$$\begin{aligned} rank(Flat_{L_1|L_2}(P_{(S,\varvec{\tau },\varvec{\theta })})) \le rank(Flat_{L_1|L_2}(P_{(S,\varvec{\xi },\varvec{\theta })})) \end{aligned}$$

Notice that since coalescent events do not happen in the terminal edges of the species tree, the gene tree histories and the formulas for the gene tree distributions from \((S,\varvec{\tau })\) and \((S,\varvec{\xi })\) are identical. The only difference is that the leaf edge labeled by C in the gene tree \((G,\mathbf {t})\) from \((S,\varvec{\tau })\) is longer by \(\tau _C - \xi _C\) than the same edge in the gene tree \((G,\mathbf {t})\) from \((S,\varvec{\xi })\). The probability of observing the state \(i_1i_2i_3 i_4\) from these two gene trees will not be the same, so let us express this probability as \(p^*_{i_1i_2i_3 i_4|(G,\mathbf t ,\varvec{\theta })}\) when the species tree is \((S,\varvec{\xi })\) and \(q^*_{i_1i_2i_3 i_4|(G,\mathbf t ,\varvec{\theta })}\) when the species tree is \((S,\varvec{\tau })\). Extending the branch of a gene tree is equivalent to grafting a new edge onto the leaf edge to create an internal vertex of degree two. To compute the probability of observing a particular state at the leaves of the extended gene tree, we sum over all possible states of this vertex. For clarity of notation, let us represent the matrix of transition probabilities along the grafted edge by \(M = e^{Q(\tau _C - \xi _C)}\). Thus,

$$\begin{aligned} q^*_{i_1i_2i_3 i_4|(G,\mathbf t ,\varvec{\theta })}= \displaystyle \sum _{1 \le j \le 4} (M_{ji_3}) p^*_{i_1i_2ji_4|(G,\mathbf t ,\varvec{\theta })}. \end{aligned}$$
Fig. 5
figure 5

Extending one leaf in a cherry of S

Full size image

Therefore, the total probability for a particular history is given by

$$\begin{aligned} p_{i_1i_2i_3i_4|h,(S,\varvec{\tau },\varvec{\theta })}&= \displaystyle \int _{\mathbf {t}} q^*_{i_1i_2i_3i_4|(G,\mathbf t ,\varvec{\theta })} f_h((G,\mathbf {t})|(S,\varvec{\tau })) \ \mathrm{d}\mathbf {t} \\&= \displaystyle \int _{\mathbf {t}} \left( \displaystyle \sum _{1 \le j \le 4} (M_{ji_3}) p^*_{i_1i_2ji_4|(G,\mathbf t ,\varvec{\theta })} \right) f_h((G,\mathbf {t})|(S,\varvec{\xi })) \ \mathrm{d}\mathbf {t} \\&= \displaystyle \sum _{1 \le j \le 4} (M_{ji_3}) \displaystyle \left( \int _{\mathbf {t}} p^*_{i_1i_2ji_4|(G,\mathbf t ,\varvec{\theta })} f_h((G,\mathbf {t})|(S,\varvec{\xi })) \ \mathrm{d}\mathbf {t} \right) \\&= \displaystyle \sum _{1 \le j \le 4} \displaystyle (M_{ji_3}) p_{i_1i_2j i_4|h,(S,\varvec{\xi },\varvec{\theta })} \\ \end{aligned}$$

Summing over all histories, we also obtain

$$\begin{aligned} p_{i_1i_2i_3i_4|(S,\varvec{\tau },\varvec{\theta })}= \displaystyle \sum _{1 \le j \le 4} \displaystyle (M_{ji_3}) p_{i_1i_2j i_4|(S,\varvec{\xi },\varvec{\theta })}. \end{aligned}$$

Now consider the column of \(Flat_{L_1|L_2}(P_{(S,\varvec{\tau },\varvec{\theta })})\) indexed by the joint state \(i_3i_4\). The formula above shows that this column is a linear combination of the columns of \(Flat_{L_1|L_2}(P_{(S,\varvec{\xi },\varvec{\theta })})\) indexed by \(1i_4,2i_4, 3i_4,\) and \(4i_4\). Therefore,

$$\begin{aligned} rank(Flat_{L_1|L_2}(P_{(S,\varvec{\tau },\varvec{\theta })})) \le rank(Flat_{L_1|L_2}(P_{(S,\varvec{\xi },\varvec{\theta })})). \end{aligned}$$

Thus, any four-leaf species tree \((S,\varvec{\tau })\) with a (C, D) cherry can be constructed by lengthening one terminal edge in a tree \((S,\varvec{\xi })\) with a (C, D) cherry that satisfies \(\xi _C = \xi _D\). The tree \((S,\varvec{\xi })\) may not be equidistant, but it is still clear from the symmetry in the cherry that for any choice of continuous parameters, we will have

$$\begin{aligned} p_{i_1i_2i_3i_4|(S,\varvec{\xi },\varvec{\theta })}= p_{i_1i_2i_4i_3|(S,\varvec{\xi },\varvec{\theta })}, \end{aligned}$$

which implies that \( rank(Flat_{L_1|L_2}(P_{(S,\varvec{\xi },\varvec{\theta })})) \le 10\), and hence that \( rank(Flat_{L_1|L_2}(P_{(S,\varvec{\tau },\varvec{\theta })})) \le 10. \)\(\square \)

Theorem 3.5

Let S be a four-taxon symmetric ((A, B), (C, D)) or asymmetric (A, (B, (C, D)) species tree with a cherry (C, D). Let \(L_1|L_2\) be one of the splits AC|BD, or AD|BC. Consider the clockless coalescent when the underlying nucleotide substitution model is any of the following: JC69, K2P, K3P, F81, HKY85, TN93, or GTR. Then, for generic distributions \(P_{(S,\varvec{\tau },\varvec{\theta })} \in \mathcal {C}^*(S)\),

$$\begin{aligned} rank(Flat_{L_1|L_2}(P_{(S,\varvec{\tau },\varvec{\theta })})) =16. \end{aligned}$$

Proof

Consider the degree 16 polynomial \(\det (Flat_{L_1|L_2}(q))\) in the ring \(\mathbb {R}[q_{i_1\ldots i_n}: 1 \le i_1, \ldots , i_4 \le 4].\) Any choice of continuous parameters for the clockless coalescent that satisfies

$$\begin{aligned} rank(Flat_{L_1|L_2}(P_{(S,\varvec{\tau },\varvec{\theta })})) < 16, \end{aligned}$$

must be contained in the real analytic variety \(\mathcal {V}(\det (Flat_{L_1|L_2}(q)) \circ \psi _S)\). As per the discussion at the beginning of Section 3, to show that this is a set of measure zero, we need only verify that the function \(\det (Flat_{L_1|L_2}(q)) \circ \psi _S\) is not identically zero. To do so, we need only produce a single choice of parameters for both the symmetric and asymmetric trees for which \(Flat_{AC|BD}(P_{(S,\varvec{\tau },\varvec{\theta })})\) is rank 16 and likewise for \(Flat_{AD|BC}(P_{(S,\varvec{\tau },\varvec{\theta })})\). In fact, we can address both the symmetric and asymmetric cases with one tree by letting S be the symmetric tree and setting \(\tau _{AB} = 0\). In the supplemental materials, we choose parameters from the Jukes–Cantor model and show that both flattening matrices for the invalid splits are rank 16. Since the Jukes–Cantor model is contained in JC69, K2P, K3P, F81, HKY85, and TN93, this choice of parameters establishes the result for each of these.

The Jukes–Cantor model is of course also contained in the four-state GTR model. However, in light of Proposition 3.3, our choice of parameters must be sufficiently generic so that \(\det (Flat_{L_1|L_2}(q) \circ \psi _S\) is a real analytic function in a neighborhood around this point. In the supplemental materials, we also choose a set of sufficiently generic K3P parameters and show that both flattening matrices for the invalid splits are rank 16. \(\square \)

Suppose now that S is a four-leaf tree that displays the split \(L_1|L_2\) and that \(S'\) is a four-leaf trees with different unrooted topology than S. Then, \(S'\) does not display the split \(L_1|L_2\), and Theorem 3.5 shows that the determinant of \(Flat_{L_1|L_2}(q)\) is a degree 16 polynomial that does not vanish on the set \(\mathcal {C}^*(S')\). Hence, as per the discussion in Sect. 3, the set of parameters for \(S'\) mapping into \(\mathcal {C}^*(S) \cap \mathcal {C}^*(S')\) is a set of measure zero. Thus, the unrooted topology of the species tree parameter of the clockless coalescent is generically identifiable.

Following Proposition 3.1, we observed that showing the identifiability of the unrooted topology of the species tree parameter of the p-coalescent requires proving the identifiability of the unrooted topology of the species tree parameter for four-leaf trees in a model that allows multiple effective population size parameters on a single edge. Specifically, to prove the identifiability of the unrooted topology of the species tree parameter in \(\mathcal {C}^*_n(N)\), it is sufficient to prove the identifiability of the unrooted topology of the species tree parameter for four-leaf trees in a model with \(2n -3\) different effective population size parameters on each edge. This is because the effective population size parameters in the four-leaf tree are inherited from the original n-leaf tree, and the number of different effective population size parameters in an n-leaf tree is bounded above by the number of edges, \(2n -3\). All of the key ingredients needed to prove this result have already been presented in Theorems 3.4 and 3.5.

Since coalescent events do not occur in the terminal edges of the species tree, Theorem 3.4 applies equally to the p-coalescent and clockless p-coalescent models. Both distributions in the proof of Theorem 3.5 are still contained in the model where we allow multiple effective population size parameters on each edge since we can just choose all of the population size parameters on \(e_{CD}\) to be equal. We must still verify that the parameterization map for this model is analytic, but the argument from Sect. 3.1 remains unchanged when we allow multiple effective population size parameters on each edge. Thus, the same choices of parameters from the proof of Theorem 3.5 establish the result for the clockless p-coalescent. We also intentionally chose a point corresponding to an equidistant tree so that it applies to the p-coalescent. Thus, we have the following corollary.

Corollary 3.6

The unrooted topology of the species tree parameter of the clockless coalescent, the p-coalescent, and the clockless p-coalescent models on an n-leaf tree is generically identifiable for all n when the underlying nucleotide substitution model is any of the following: JC69, K2P, K3P, F81, HKY85, TN93, or GTR.

3.3 Identifiability with Invariable Sites and Gamma-Distributed Rates

It is well known that the rate of evolution may vary across sites (Yang 1993, 1994). One way to account for this is to let each site evolve according to the same model but where the rate matrix at each site is scaled by a random factor drawn from a specified gamma distribution. If the underlying nucleotide substitution model is assumed to be the GTR model, this is what is known as the GTR+\(\Gamma \) model.

In practice, the gamma distribution is approximated using m rate categories, each with probability \(\dfrac{1}{m}\), and \(\rho _i\) is defined to be the mean rate for category i (see Yang 1994 for details). From the formulas in Yang (1994), it is easy to see that the rates can be expressed as analytic functions in the parameters of the gamma distribution and consequently that the distributions from the GTR+\(\Gamma \) model are given by real analytic functions of the parameters.

It is also common to account for invariable sites by using the GTR+I+\(\Gamma \) model, where \(\delta \) is the proportion of invariable sites. The multispecies coalescent with the m-discrete \(\kappa \)-state GTR+I+\(\Gamma \) model was shown to exhibit the same flattening ranks as the multispecies coalescent with the \(\kappa \)-state GTR model in Chifman and Kubatko (2015). This is not terribly surprising as a probability distribution from the former is the sum of \(m+1\) distributions each satisfying the same linear relations. Explicitly, letting \(P^{I + \Gamma }\) be the site pattern probability distribution from a model with invariant sites and gamma-distributed rates,

$$\begin{aligned} p^{I + \Gamma }_{i_1i_2i_3i_4|(S, \tau , \varvec{\theta })} = \dfrac{(1 - \delta )}{m} (p^{\rho _1}_{i_1i_2i_3i_4|(S, \tau , \varvec{\theta })} + \cdots + p^{\rho _m}_{i_1i_2i_3i_4|(S, \tau , \varvec{\theta })}) + \delta (z_{i_1i_2i_3i_4|\varvec{\theta }}), \end{aligned}$$

where \(p^{\rho _j}_{i_1i_2i_3i_4|(S, \tau , \varvec{\theta })}\) is the probability of observing \(i_1i_2i_3i_4\) from the multispecies coalescent model with scaling factor \(\rho _j\) and \(z_{i_1i_2i_3i_4|\varvec{\theta }}\) is the probability of observing this state at an invariable site. If S has a (C, D) cherry as above, then each summand is contained in the linear space defined by the linear relations of the form \(p_{\star \star i_3i_4} - p_{\star \star i_4i_3}\) in the distribution space. The sum satisfies these relations as well, so we have

$$\begin{aligned} rank(Flat_{AB|CD}(P^{I + \Gamma }_{(S, \varvec{\tau }, \varvec{\theta })})) \le { \kappa + 1 \atopwithdelims ()2}. \end{aligned}$$

For a non-equidistant tree, the same result no longer applies. If we view \((S,\varvec{\tau })\) as an extension of \((S,\varvec{\xi })\) as we did in Theorem 3.4, we can see that

$$\begin{aligned} rank(Flat_{AB|CD}(P^{\rho _j}_{(S, \varvec{\tau }, \varvec{\theta })})) \le { \kappa + 1 \atopwithdelims ()2}, \end{aligned}$$

but the particular linear relationships satisfied by the columns of each flattening matrix will depend on the entries of the transition matrix on the extended edge, which in turn depend on the \(\rho _i\). However, we can obtain an analogous result for JC+I+\(\Gamma \), where the JC refers to the \(\kappa \)-state Jukes–Cantor model. When \(\kappa = 4\), we prove the result for \(m = 2,3,\) and 4, as four is the most common number of categories used in actual phylogenetic applications (Lio and Goldman 1998).

Theorem 3.7

Let S be a four-taxon symmetric ((A, B), (C, D)) or asymmetric (A, (B, (C, D)) species tree with a cherry (C, D). Let \(L_1|L_2\) be one of the splits AB|CD, AC|BD, or AD|BC. For \(\kappa \ge 4\), consider the \(\kappa \)-state m-discrete JC+I+\(\Gamma \) model under the coalescent with species tree S and \(m \le 4\).

  1. (1)

    If \(L_1|L_2\) is a valid split for S, then for all \(P^{I + \Gamma }_{(S,\varvec{\tau },\varvec{\theta })}\) from the clockless p-coalescent with invariant sites and gamma-distributed rates,

    $$\begin{aligned} rank(Flat_{L_1|L_2}(P_{(S,\varvec{\tau },\varvec{\theta })}^{I + \Gamma })) \le \kappa ^2 - {\kappa - 1 \atopwithdelims ()2} \end{aligned}$$
  2. (2)

    If \(L_1|L_2\) is not a valid split for S, then for a generic distribution \(P_{(S,\varvec{\tau },\varvec{\theta })}^{I + \Gamma }\) from the clockless p-coalescent with invariant sites and gamma-distributed rates,

    $$\begin{aligned} rank(Flat_{L_1|L_2}(P_{(S,\varvec{\tau },\varvec{\theta })}^{I + \Gamma }) ) > \kappa ^2 - {\kappa - 1 \atopwithdelims ()2}. \end{aligned}$$

Proof

Let \(L_1|L_2\) be the split AB|CD that is valid for S, and consider the distribution \(P_{(S,\varvec{\tau },\varvec{\theta })}\) from the Jukes-Cantor model. Without loss of generality, suppose \(\tau _C \ge \tau _D\). Construct the vector \(\varvec{\xi }\) with all entries equal to those of \(\varvec{\tau }\) but with \(\xi _C = \tau _D\). Again, by symmetry, we have

$$\begin{aligned} p_{\star \star i_3 i_4|(S,\varvec{\xi },\varvec{\theta })} = p_{\star \star i_4 i_3|(S,\varvec{\xi },\varvec{\theta })}. \end{aligned}$$

As in Theorem 3.4, we will identify the tree \((S,\varvec{\tau })\) as an extension of \((S,\varvec{\xi })\). For the JC model, there are only two distinct entries of \(M = e^{Q(\tau _C - \xi _C)}\). Let \(M_{ij} = a\) if \(i = j\) and b otherwise. Therefore, we have

$$\begin{aligned} p_{\star \star i_3i_4|(S,\varvec{\tau },\varvec{\theta })}= a p_{\star \star i_3 i_4|(S,\varvec{\xi },\varvec{\theta })} + \displaystyle \sum _{j \not = i_3} \displaystyle b p_{\star \star j i_4|(S,\varvec{\xi },\varvec{\theta })}, \end{aligned}$$

and one can check that for distinct \(k_1,k_2,k _3 \in [\kappa ]\), the distribution \(P_{|(S, \varvec{\tau }, \varvec{\theta })}\), satisfies

$$\begin{aligned} p_{\star \star k_1k_2} - p_{\star \star k_1k_3} - p_{\star \star k_2k_1} + p_{\star \star k_2k_3} + p_{\star \star k_3k_1} - p_{\star \star k_3k_2}=0. \end{aligned}$$

We obtain such a relation for any three-element subset of \([\kappa ]\). Moreover, since this linear relation does not depend on a or b, it is satisfied by \(P^{\rho _i}_{|(S, \xi , \varvec{\theta })}\). It is also satisfied by the matrix for invariable sites, \(Z_{|\varvec{\theta }}\), with entries given by \(z_{i_1i_2i_3i_4|\varvec{\theta }}\). Hence, this linear relation is also satisfied by any distribution from the m-discrete JC+I+\(\Gamma \) model. Consider the \({\kappa - 1 \atopwithdelims ()2}\) relations that come from choosing three-element subsets of the form \(\{k_1,k_2,\kappa \}\). For all \(k_1,k_2 \in [\kappa -1]\), exactly one of these relations involves the variable \(p_{\star \star k_1k_2}\). Therefore, these relations are linearly independent, and so the first claim of the theorem follows.

In (Chifman and Kubatko 2015, Theorem 1), the authors show that for all m, when \(\kappa \ge 4\), if \(L_1|L_2\) is not a valid split for S, then

$$\begin{aligned} rank(Flat_{L_1|L_2}(P_{(S,\varvec{\tau },\varvec{\theta })}^{I + \Gamma })) > \kappa ^2 - \kappa . \end{aligned}$$

When \(\kappa \ge 5 \), we have

$$\begin{aligned} \kappa ^2 - \kappa&\ge \kappa ^2 - {\kappa - 1 \atopwithdelims ()2}, \end{aligned}$$

which establishes our result. For \(\kappa = 4\), we must produce a choice of parameters to prove that the claim holds for \(m=2,3,\) and 4 and for both the symmetric and asymmetric trees. Choosing \(\alpha = \beta = 1\), \(\delta = 1/2\), and the same continuous JC69 parameters from Theorem 3.5 establishes the result. Code to verify these computations is contained in the supplementary materials. \(\square \)

Since all of the parameterization functions involved are analytic, this is enough to prove the identifiability of the unrooted topology of the species tree parameter of the JC+I+\(\Gamma \) model. Thus, we have the following corollary.

Corollary 3.8

The unrooted topology of the species tree parameter of the clockless coalescent, the p-coalescent, and the clockless p-coalescent models on an n-leaf tree is generically identifiable for all n when the underlying nucleotide substitution model is the m-discrete \(\kappa \)-state JC+I+\(\Gamma \) model with \(\kappa \ge 5\) and \(m \in \mathbb {N}\) and with \(\kappa = 4\) and \(m = 2,3,\) or 4.

Moreover, the parameters that we used to demonstrate that the invalid flattenings are full rank come from an exponential distribution, which is a special case of the gamma distribution. Therefore, the same result holds for a model where the m rates are constructed from an exponential distribution. In fact, this also applies to a more general variable rates model where the m rates are free parameters.

4 Conclusions

In the previous section, we have proven that the unrooted species tree parameter of several more generalized versions of the multispecies coalescent model is generically identifiable from the site pattern probability distributions on the species trees. Moreover, the means by which we have proven identifiability give us the necessary framework for reconstructing the unrooted topology of the species tree from data. In each case, we showed that we can reconstruct the unrooted quartets of the species tree parameter if we know the distribution exactly by taking ranks of the flattening matrices. Specifically, for a four-state model and generic choices of parameters, we showed that the rank of the flattening matrix for the quartet compatible with the species tree will be less than or equal to 10 while the other two flattening matrices will both be rank 16.

This gives a natural method for inferring the unrooted topology of the species from biological data. Specifically, for each quartet, we infer the unrooted quartets of the species tree by determining which of the three flattening matrices is closest to the set of rank 10 matrices. The method of singular value decomposition from linear algebra already provides a means of determining how close a matrix is to the set of matrices of a certain rank under the Frobenius norm (Golub and Loan 2013). This is exactly the procedure used by the method SVDQuartets, which is already fully implemented in the PAUP\(^*\) software (Swofford 2016). Hence, there is strong theoretical justification for applying SVDQuartets for phylogenetic reconstruction even when effective population sizes vary throughout the tree or when the molecular clock does not hold.

The model presented in Sect. 2, as well as that presented in Chifman and Kubatko (2015), describes the situation in which gene trees are randomly sampled under the multispecies coalescent model, and then sequence data for a single site evolve along each sampled gene tree according to one of the standard nucleotide substitution models. Data generated in this way have been termed “coalescent independent sites” Tian and Kubatko (2016) to distinguish them from SNP data. Although coalescent independent sites and SNP data refer to observations of single sites that are assumed to be conditionally independent samples from the model given the species tree, SNP data are generally biallelic, while coalescent independent sites may include three or four nucleotides at a site, or may be constant.

The other situation in which one might wish to apply these results is to multilocus data. Multilocus data are data in which individual genes are sampled from the species tree under the multispecies coalescent, but for each sampled gene tree, many individual sites are observed. Typical genes observed in phylogenomic studies range from 100 base pairs (bp) to 2000 bp in size, though most are \(<\,500\) bp. The site patterns observed within a gene are not independent observations under the model because they share the same gene tree, and thus it is not immediately obvious that the results presented here apply to this case. However, consider the case in which a large sample of genes, say W, is obtained, and for each gene, s sites are observed. Then, the flattening matrices of site pattern counts constructed from such data will be s times the flattening matrix of site pattern counts that would have been observed if only a single site had been observed from each gene tree, which does not change the matrix rank. It is clear that as \(W \rightarrow \infty \), the correct theoretical distribution will be well approximated by the observed site pattern frequencies, and the results presented here will hold. In practice, the genes will vary in their lengths and a more careful argument is required. We have elsewhere carried out thorough simulation studies to show that the methods used in SVDQuartets hold for multilocus data as well as for SNP data and for coalescent independent sites for the original model (Chifman and Kubatko 2014). We are currently working on a simulation study to compare the effectiveness of SVDQuartets to that of other species tree estimation methods on the models presented herein.

We note two possible criticisms of this method. The first is that, while we showed that generically the flattening matrices for the invalid splits will be rank 16, we have no theoretical guarantees that they are not arbitrarily close to the set of rank 10 matrices. Therefore, we do not know a priori that this method will provide any insight with a finite amount of either simulated or biological data. Along the same lines, determining that a flattening matrix is close to the set of rank 10 matrices does not necessarily mean that it is close to the set of distributions arising from a coalescent model, as the latter is properly contained in the former. While both are valid considerations, they appear to be academic, as SVDQuartets has already been shown to be an effective reconstruction method on several data sets, both real and simulated (Chifman and Kubatko 2014; Chou et al. 2015). As mentioned above, in a forthcoming paper, we will demonstrate that SVDQuartets also works well in practice by simulating data from these modified coalescent models and applying the method to real biological data sets known to violate the molecular clock.

In recent years, the amount of sequence data available for species tree inference has increased rapidly, presenting significant computational challenges for most model-based species tree inference methods that accommodate the coalescent process. The SVDQuartets method is fully model based but inference using this method is much more computationally efficient than methods that require evaluation of a likelihood function, such as \({}^*\hbox {BEAST}\) Heled and Drummond (2010) and SNAPP Bryant et al. (2012). This is because, for each quartet considered, all that is required is construction of the three flattening matrices, which involves the simple task of counting site patterns and computation of singular values from these \(16 \times 16\) matrices. In addition, increases in sequence length benefit the performance of the method (because site pattern probabilities are estimated more accurately) with almost no increased computational cost. However, increases in the number of sequences do incur a computational cost, in that more quartets must be evaluated and because the complexity of the algorithm for assembling the inferred quartets to form an overall species tree estimate increases. Even with these costs, however, computations can be carried out much more rapidly than with the likelihood-based methods referenced above. In the work presented here, we show that the theory underlying the SVDQuartets method holds in much more general settings than originally suggested. In particular, the method can be applied to data that violate the molecular clock and to the case in which each population has a distinct effective population size. Thus, this work is a significant advance that will contribute meaningfully to the collection of methods available to infer species-level phylogenies from phylogenomic data in very general settings.