1 Introduction

Modern sequencing technologies have provided a wealth of data to assist biologists in the inference of evolutionary relationships between species. It is now common to sequence thousands of genes, or entire genomes, simultaneously across a range of species. With this abundance of data comes new algorithmic and statistical challenges. One such challenge arises because phylogenomic inference entails dealing with the interplay of two processes. While a species phylogeny depicts the history of speciation of extant organisms, each gene within the genomes of these organisms has its own history. That history is captured by a gene tree. In practice, by contrasting the molecular sequences of a gene (or other genomic region) across species, one can reconstruct the corresponding gene tree. Indeed the accumulation of mutations along the gene tree reflects, if imperfectly, the underlying history. Much is known about the reconstruction of single-gene trees, a subject with a long history. See Steel (2016), Warnow (2017) for an overview.

But a gene tree does not necessarily coincide with the species phylogeny. In particular, various mechanisms lead to discordance between gene trees. These include the transfer of genetic material between species, hybrid speciation events and a population-genetic effect known as incomplete lineage sorting (Maddison 1997). The wide availability of genomic datasets has brought to the fore the major impact these discordances have on phylogenomic inference (Degnan and Rosenberg 2009). As a result, in addition to the stochastic process governing the evolution of molecular sequences on a fixed gene tree, one is led to model the structure of the gene tree itself, in relation to the species phylogeny, through a separate stochastic process. The inference of these complex, two-level evolutionary models is an active area of research.

We focus on incomplete lineage sorting (ILS) and consider the problem of reconstructing a species phylogeny from multiple genes under the multispecies coalescent (Rannala and Yang 2003), a standard population-genetic model. The problem is of great practical interest in computational evolutionary biology and is currently the subject of intense study; see e.g. Nakhleh (2013), Kapli et al. (2020), Scornavacca et al. (2020). There is in particular a growing body of theoretical results in this area (Degnan and Rosenberg 2006; Degnan et al. 2009; DeGiorgio and Degnan 2010; Mossel and Roch 2010; Liu et al. 2010; Allman et al. 2011; Roch 2013; Roch and Steel 2015; DeGiorgio and Degnan 2014; Dasarathy et al. 2015; Chifman and Kubatko 2015; Roch and Warnow 2015; Mossel and Roch 2017; Shekhar et al. 2017; Long and Kubatko 2017; Roch 2018; Roch et al. 2019; Allman et al. 2018, 2019; Long and Kubatko 2019; Rhodes 2019). A significant portion of prior rigorous work on species phylogeny estimation in the presence of ILS has been aimed at the case where true gene trees are assumed to be available. In reality, one needs to estimate gene trees from molecular sequences, leading to reconstruction errors, and indeed there has been a recent thrust towards understanding the effect of this important source of error in phylogenomic inference, both from empirical (Kubatko and Degnan 2007; Bayzid and Warnow 2013; Mirarab et al. 2014, 2016) and theoretical (DeGiorgio and Degnan 2014; Roch and Steel 2015; Bayzid et al. 2015; Roch and Warnow 2015) standpoints. Another option—which we further explore here—is to bypass the reconstruction of gene trees altogether and infer the species history directly from sequence data (Dasarathy et al. 2015; Mossel and Roch 2017; Chifman and Kubatko 2015; Rusinko and McPartlon February 2017; Allman et al. 2019; Long and Kubatko 2019).

In previous work (Mossel and Roch 2017), a surprising trade-off was derived between the number of genes m needed to accurately reconstruct a species phylogeny and the length of the genes k. Specifically, it was shown that m needs to scale like \(1/[f^{2} \sqrt{k}]\), where f is the length of the shortest branch in the tree (measured in expected number of substitutions per unit of time per site; see Sect. 2 for formal definitions). This result was obtained under a restrictive molecular clock assumption where the leaves are “equidistant” from the root; i.e., it was assumed that the mutation rates and population sizes do not vary across species.

In this work, we make progress towards designing species tree estimation methods that provably achieve the theoretical limit by relaxing the above assumption. Our key contribution is of independent interest. We show how to transform sequence data to appear as though it was generated under the multispecies coalescent with a molecular clock. We achieve this through a novel reduction which we call a stochastic Farris transform. Our construction relies on an identifiability result which is partly new: for any species phylogeny with \(n \ge 3\) species, the rooted topology of the species tree can be identified from the distribution of the unrooted weighted gene trees even in the absence of a molecular clock. We state our results in Sect. 2 and describe our reduction in Sect. 3. The main proofs are in Sects. 4 and 5.

Related work A common approach to species tree estimation that bypasses gene trees is to (1) concatenate the aligned gene sequences and (2) apply a standard phylogenetic reconstruction method (under the incorrect assumption that all sites have evolved on a fixed tree), such as maximum likelihood or a distance-based method, to the concatenated data. That approach has been shown to have serious theoretical drawbacks. Indeed, in Roch and Steel (2015), it was proved that, under the multispecies coalescent with a standard site substitution model (see Sect. 2), maximum likelihood on a concatenated alignment is statistically inconsistent, that is, it can converge on the wrong phylogeny even as the amount of data grows to infinity. The result in Roch and Steel (2015) allows for gene sequence lengths to vary with the number of genes. In follow-up work (Roch et al. 2019), it was shown that fully partitioned concatenated maximum likelihood (that is, maximizing the likelihood of the sequence data under the assumption that the tree topology is fixed across genes but allowing for branch lengths to vary) is also statistically inconsistent. That result was established under bounded gene sequence lengths.

On the other hand, positive results have also been obtained for some concatenation-based approaches under the multispecies coalescent. In Dasarathy et al. (2015), a notion of distance between taxa defined over a concatenated alignment was shown to satisfy the four-point condition (see, e.g., Semple and Steel (2003)) in the limit of infinitely many genes, for any fixed gene sequence length. The latter ensures that the unrooted topology of the species phylogeny is identifiable from the sequence data, that is, that species phylogenies with distinct unrooted topologies necessarily produce distinct data distributions. The results in Dasarathy et al. (2015) allow for varying population sizes and mutation rates across branches and were proved under the Jukes-Cantor substitution model. They also come with a data requirement guarantee: using an appropriate distance-based method, for any gene sequence length \(k \ge 1\), the correct unrooted species tree topology is guaranteed to be recovered with high probability provided the number of genes m scales roughly like \(\propto e^{C \Delta } \log n\) where \(\Delta \) is the depth of the tree (see, e.g., Erdos et al. 1999), n is the number of leaves and C is a universal constant.

The distance-based pipeline introduced in Dasarathy et al. (2015), specifically in combination with the reconstruction method Neighbor Joining (Saitou and Nei 1987) (but under a more general model of site substitution), was tested on simulated datasets in Rusinko and McPartlon (February 2017). Moreover, the theoretical identifiability results of Dasarathy et al. (2015) were extended to a significantly broader class of site substitution models in Allman et al. (2019) using the concept of log-det distance (see, e.g., Semple and Steel 2003). The model considered in Allman et al. (2019) allows for an arbitrary mixture of general time-reversible rate matrices across the genome and population sizes that vary on each branch of the species tree as a function of time.

There has also been closely related work on single nucleotide polymorphism (SNP)-based approaches (that is, the case \(k=1\)). In particular, it was shown in Chifman and Kubatko (2015) that the unrooted topology of the species phylogeny is identifiable given observed data at the leaves of the tree that are assumed to have arisen from the multispecies coalescent under a time-reversible substitution process with site-specific rate variation modeled by the discrete gamma distribution and a proportion of invariable sites. The results of Chifman and Kubatko (2015), which led to a practical SNP-based approach (Chifman and Kubatko 2014), were extended in Long and Kubatko (2019) to a modified model that allows for varying population sizes and mutation rates.

Finally, the data requirement bounds in Dasarathy et al. (2015) were substantially improved in Mossel and Roch (2017) using a different reconstruction approach, but under more restrictive assumptions (see Sect. 2). One of our main contributions here is to relax these assumptions while preserving roughly the same data requirements.

2 Background and results

We begin with a description of our modeling assumptions. More details on these standard models can be found for example in Steel (2016).

Species phylogeny v. gene trees A species phylogeny is a graphical depiction of the evolutionary history of a set of species. The leaves of the tree correspond to extant species while internal vertices indicate a speciation event. Each edge (or branch) corresponds to an ancestral population and will be described here by two numbers: one that indicates the amount of time that the corresponding population lived, and a second one that specifies the rate of genetic mutation in that population. Formally, we define the species phylogeny as follows. Throughout, we use the notation \([n] = \{1,\ldots ,n\}\).

Fig. 1
figure 1

Two samples from the MSC on a species phylogeny with 3 leaves. The topology of Gene 1 agrees with the topology of the underlying species phylogeny (i.e., species 1 and 2 are closest), while the topology of Gene 2 does not (here species 2 and 3 are closest instead)

Full size image

Definition 1

(Species phylogeny). A species phylogeny \(S = (V_s, E_s; r, \vec {\tau },\vec {\mu })\) is a directed tree rooted at \(r\in V_s\) with vertex set \(V_s\), edge set \(E_s\), and n labelled leaves \(L = [n]\) such that (a) the degree of all internal vertices is 3 except for the root r which has degree 2, and (b) each edge \(e\in E_s\) is associated with a length \(\tau _e\in (0,\infty )\) and a mutation rate \(\mu _e \in (0,\infty )\).

Our model involves several natural time scales, each of which can be used as a time unit. See, e.g., Allman et al. (2019) for a discussion. Here we choose to measure the length \(\tau _e\) of a branch \(e\in E_s\) in coalescent time units, which is the duration of the branch \(t_e\) in number of generations divided by twice its population size \(N_e\). That is, \(\tau _e = t_e/2 N_e\). The mutation rates \(\mu _e\) are expressed in expected number of substitutions per site per unit of time, where time is measured in coalescent units again. We pictorially represent species phylogenies as thick shaded trees; see Fig. 1. The goal in our applications will be to reconstruct the rooted topology of the species phylogeny \(S = (V_s, E_s; r, \vec {\tau },\vec {\mu })\), that is, the rooted tree \((V_s, E_s, r)\).

While a species phylogeny describes the history of speciation, each gene has its own history captured by a gene tree.

Definition 2

(Gene trees). Gene tree \(G^{(i)} = (V^{(i)}, E^{(i)}; {R}, \vec {\delta }^{(i)})\) of gene i is a directed tree rooted at R with vertex set \(V^{(i)}\) and edge set \(E^{(i)}\), and the same labeled leaf set \(L = [n]\) as S such that (a) the degree of each internal vertex is 3, except the root R whose degree is 2, and (b) each branch \(e\in E^{(i)}\) is associated with a branch length \(\delta _e^{(i)}\in (0,\infty )\).

The branch lengths \(\delta _e^{(i)}\) are expressed in expected number of substitutions per site. The precise relationship between the branch lengths of the species phylogeny and those of the gene trees under our modeling assumptions will be given below in (2).

Multispecies coalescent and Jukes-Cantor models While the species phylogeny is assumed to be fixed (but unknown), the gene trees are random. Their distribution depends on the species phylogeny. Specifically, we assume that a multispecies coalescent (MSC) process produces m independent gene trees \(G^{(1)}\), \(G^{(2)}\), \(\ldots ,\) \(G^{(m)}\). This process is parametrized by the species phylogeny S. In words, proceeding backwards in time, in each population, every pair of lineages entering from descendant populations merges at exponential rate one in coalescent time units. One key feature of the gene trees is the following: their topology may be distinct from that of the species phylogeny. This discordance, which in this context is referred to as incomplete lineage sorting, is a major challenge for species tree estimation from multiple genes. See again Figure 1 for an illustration.

Gene trees are not observed directly. They are inferred from sequence data evolving on the gene trees. We model this sequence generation process according to the standard Jukes-Cantor (JC) model. Given a gene tree \(G^{(i)} = (V^{(i)},E^{(i)}; r, \vec {\delta }^{(i)})\), we associate to each \(e\in E^{(i)}\), a probability \(p_{e}^{(i)} = \frac{3}{4}\left( 1 - e^{-\frac{4}{3}\delta _{e}^{(i)}} \right) \). In words, the corresponding gene i is a sequence of length k in \(\left\{ \mathtt{A, T, G, C}\right\} ^k\). Each position in the sequence evolves independently, starting from a uniform state in \(\left\{ \mathtt{A, T, G, C}\right\} \) at the root. Moving away from the root, a substitution occurs on edge e with probability \(p_{e}^{(i)}\), in which case the state changes uniformly at random. Repeating this process for each position produces a sequence of length k for all leaves of \(G^{(i)}\), for each \(i \in [m]\)—our input.

Tree metrics It remains to describe the relationship between the branch lengths of the species phylogeny and those of the gene trees. For this purpose, we recall some notions on tree metrics.

Definition 3

(Species metric). A species phylogeny \(S = (V_s, E_s; r, \vec {\tau }, \vec {\mu })\) induces the following metric on the leaf set L. For any pair of leaves \(a,b\in L\), we let

$$\begin{aligned} \mu _{ab} = \sum _{e\in \pi (a,b;S)}\tau _e\, \mu _e, \end{aligned}$$
(1)

where \(\pi (a,b;S)\) is the unique path connecting a and b in S interpreted as a set of edges. We will refer to \(\left\{ \mu _{ab} \right\} _{a,b\in L}\) as the species metric induced by S.

The species metric \(\mu \) can be naturally extended to the entire set \(V_s\) by using (1) for an arbitrary pair of vertices. The metric \(\left\{ \mu _{ab} \right\} _{a,b\in L}\) is said to be ultrametric when \(\mu _{ra} = \mu _{rb}\) for all \(a, b \in L\), that is, when the distance from the root to every leaf is the same. We do not make this assumption here. In particular, we allow mutation rates and population sizes to vary across branches of the species phylogeny. Instead, the key to our contribution is a transformation of the sequence data that mimics an ultrametric case. Details on this transformation are given below in Algorithm 1 and Defintion 5.

Recall from Definition 2 that each gene tree has an associated set of branch lengths. Under the MSC, a single branch of a gene tree may span across multiple branches of the species phylogeny; this can also be seen in Fig. 1. Let \(t_{\tilde{e}}\) denote the length of the branch \(\tilde{e}\in E^{(i)}\) in coalescent time units. For any species phylogeny branch \(e\in E_s\), let \(t_{\tilde{e}\cap e}\) denote the length of the branch \(\tilde{e}\) that overlaps with e. Then, \(\delta _{\tilde{e}}\) and \(t_{\tilde{e}}\) satisfy the following relationship

$$\begin{aligned} \delta _{\tilde{e}} = \sum _{e\in E_s} \mu _e t_{\tilde{e}\cap e}. \end{aligned}$$
(2)

This set of weights defines a different metric on the leaves. Note that, under the MSC, these weights are random. They also lead to a metric which will play a central role in our approach.

Definition 4

(Gene metric). A gene tree \(G^{(i)} = (V^{(i)}, E^{(i)}; {R^{(i)}}, \vec {\delta }^{(i)})\) induces the following metric on the leaf set L. For any pair of leaves \(a,b\in L\), we let \(\delta _{ab}^{(i)} = \sum _{e\in \pi (a,b;G^{(i)})}\delta _e^{(i)}\) where, again, \(\pi (a,b;G^{(i)})\) is the unique path connecting a and b in \(G^{(i)}\) interpreted as a set of edges. We will refer to \(\{ \delta _{ab}^{(i)} \}_{a,b\in L}\) as the gene metric induced by \(G^{(i)}\).

The gene metric \( \delta ^{(i)}\) can be extended to the entire set \(V_s\) and we say that it is ultrametric if \(\delta _{ra}^{(i)} = \delta _{rb}^{(i)}\) for all \(a, b \in L\). Throughout, the \(\mu _{ab}\)’s are deterministic (but unknown) while the \(\delta _{ab}\)’s are random.

Inference problem For gene i, we let \(\left\{ \xi ^{ij}_x \,:\, j\in [k], x\in L \right\} \) denote the data generated at the leaves L of the tree \(G^{(i)}\) by the Jukes-Cantor process, the superscript j runs across the positions of the gene sequence. To simplify the notation, we denote \(\xi ^{ij} = (\xi ^{ij}_x)_{x \in L}\). The species phylogeny estimation problem can then be stated as:

The \(n\times m\times k\) data array \(\left\{ \xi ^{ij} \right\} _{i\in [m], j\in [k]}\) is generated according to the Jukes-Cantor process on the m gene trees, each of which is generated by the multispecies coalescent on S. The goal is to recover the topology of the species phylogeny S from \(\left\{ \xi ^{ij} \right\} _{i\in [m], j\in [k]}\).

We refer to this two-step process as the MSC-JC(m, k) process on S.

A “stochastic” Farris transform Previous work in Mossel and Roch (2017) on tight data requirement trade-offs under the MSC-JC model was restricted to the case where mutation rates and population sizes do not vary across the species phylogeny. This results in the species metric \(\mu _{ab}\) being in fact ultrametric, as defined above. That, in turn, implies that the gene metrics \(\delta ^{(i)}\) are also ultrametric. That property produces symmetries that are useful in the design and analysis of reconstruction algorithms. Our main contribution here is a reduction to this ultrametric case.

figure a

That is, we transform the input sequences to appear as though they were generated (approximately) by a species phylogeny with an ultrametric species metric. This ultrametric reduction, inspired by a classical technique known as the Farris transform, may be of independent interest as it could be used to generalize other reconstruction algorithms. Further details and intuition about the Farris transform are given in Sect. 3.1. At a high level, this transform relates a general tree metric to an ultrametric over the same topology. Here we split the data and use one piece to estimate quantities necessary to perform a randomized version of the transform.

Although our reduction could be applied to a dataset of arbitrary size, for ease of presentation we fix a triple of leaves \(\mathcal {X} = [3]\). Specifically, Algorithm 1 takes as input a set of genes [m] divided into two disjoint subsets, \(\mathcal {M}_{\mathrm{R}}\) and \(\mathcal {M}_{\mathrm{Q}}\). The set \(\mathcal {M}_{\mathrm{R}}\) is used to estimate parameters needed for the reduction. The reduction is subsequently performed on \(\mathcal {M}_{\mathrm{Q}}\). For \(\phi >0\), we say that two metrics \(\mu '\) and \(\mu ''\) over \(\mathcal {X}\) are \(\phi \)-close if \(\left| \mu '_{xy} - \mu ''_{xy} \right| \le \phi \), for all \(x, y\in \mathcal {X}\). For convenience, we also say that two species phylogenies are \(\phi \)-close if their species metrics are. In essence, we show that \(m \ge 1/(k\phi ^2)\) genes suffice to output a dataset that is \(\phi \)-close to ultrametric. Given that \(1/\phi ^{2}\) independent sites are required to estimate distances within \(\phi \) Steel and Székely (2002), our bound on the total number of sites mk likely cannot be improved. Throughout, for \(a, b \in \mathbb {R}\), we use the notation \(a \vee b = \max \{a,b\}\).

Theorem 1

(Ultrametric reduction). Suppose we have sequence data \(\left\{ \xi ^{ij} \right\} _{i\in [m], j\in [k]}\) generated under the MSC-JC(m, k) process on a three-species phylogeny \(S = (V_s, E_s; r, \vec {\tau },\vec {\mu })\). The mutation rates, leaf-edge lengths and internal-edge lengths are respectively in the intervals \((\mu _L, \mu _U)\), \((f', g')\) and (f, g). Then, there are constants \(c_{}', c_{}'' > 0\) such that, for any \(\varepsilon , \phi \in (0,1)\) satisfying

$$\begin{aligned} k \ge c_{}' \left( \log \phi ^{-2} + \log \varepsilon ^{-1} \right) , \end{aligned}$$
(3)

with probability at least \(1-\varepsilon \), the output of Algorithm 1 is distributed according to the MSC-JC process on a species phylogeny \(S'\) that is \(\phi \)-close to a species phylogeny with an ultrametric species metric and a rooted topology identical to that of S, provided

$$\begin{aligned} m \ge c_{}'' \left( 1 \vee \frac{1}{k \phi ^{2}}\right) \log \varepsilon ^{-1}. \end{aligned}$$
(4)

Application: Data requirement trade-off Our main application of the ultrametric reduction is an extension of the data requirement trade-off in Mossel and Roch (2017) without the assumption that mutation rates and population sizes do not vary across the species phylogeny. After applying our reduction, we use the quantile triplet test developed in Mossel and Roch (2017). Roughly speaking this test, which is detailed in Algorithm 2 in the appendix, compares a well-chosen quantile of the sequence-based estimates of gene metrics \(\left\{ \delta _{ab}^{(i)} \right\} _{a,b\in \mathcal {X}}\) in order to determine which pair of leaves is closest.

For any leaves \(x, y, z \in L\), the species phylogeny S restricted to these three leaves has one of three possible rooted topologies: xy|z, xz|y, or yz|x. It is a classical phylogenetic result that if one is able to correctly reconstruct the topology of all triples of leaves in L, then the topology of the full species phylogeny can be correctly reconstructed as well (see e.g., Steel 2016). Hence, we restrict to the case \(\mathcal {X} = [3]\). Our data requirement applies to an unknown species phylogeny in the following class. We assume that: mutation rates are in the interval \((\mu _L, \mu _U)\); leaf-edge lengths are in \((f', g')\); and internal-edge lengths are in (f, g). We suppress the dependence on \(\mu _L, \mu _U, f', g', g\), which we think of as constants, and focus here on the role of f, which is known to play a critical role. Specifically, we answer the following question: as \(f \rightarrow 0\), how many genes m of length k are needed for a correct reconstruction with high probability? We obtain the same trade-off between m and k as in Mossel and Roch (2017), whose proof only applies to the ultrametric case.

Theorem 2

(Data requirement). Suppose that we have sequence data \(\left\{ \xi ^{ij} \right\} _{i\in [m], j\in [k]}\) generated according to the MSC-JC(m, k) process on a species phylogeny \(S = (V_s, E_s; r, \vec {\tau },\vec {\mu })\) . The mutation rates, leaf-edge lengths and internal-edge lengths are respectively in \((\mu _L, \mu _U)\), \((f', g')\) and (f, g). We assume further that there are \(C, C' > 0\) such that \(k = f^{-C}\) and \(\varepsilon , \phi \in (0,1)\) satisfy (3) with \(\phi = C' f/ \log f^{-1}\). Then, there exists a universal constant \(c''' > 0\) such that Algorithm 2 correctly identifies the rooted topology of S restricted to \(\mathcal {X} = [3]\) with probability at least \(1-\varepsilon \) provided that

$$\begin{aligned} m \ge c''' \left( \frac{1}{f} \vee \frac{1}{\sqrt{k} f^2}\right) \log \varepsilon ^{-1}. \end{aligned}$$
(5)

3 Main steps of the proof of Theorem 1

The goal of the ultrametric reduction step, Algorithm 1, is to transform the sequence data to appear statistically as though it is the output of an MSC-JC process on an ultrametric species phylogeny with the same topology as S restricted to \(\mathcal {X}\). Here we provide an overview of the key ideas behind this step.

3.1 Preliminary step: an identifiability result

Before diving into the description of Algorithm 1, we provide some insights into the algebra of our reduction by first proving an identifiability result, which is partly new.

It was shown in (Allman et al. 2011, Theorem 9) that the distribution of the unrooted topologies of the gene trees suffices to identify the rooted topology of the species phylogeny when the number of leaves exceeds 4. In fact, even more was shown in that case: the species metric (in coalescent time units, that is, taking \(\mu _e = 1\) for all e in our notation) can be recovered from the same information. On the other hand, it was also proved in (Allman et al. 2011, Proposition 3) that, when \(n=4\), the gene tree topologies are not enough to locate the root of the species phylogeny.

We complement these previous results by revisiting the cases \(n=3, 4\) when information about gene tree branch lengths is available. Here we show that, already with three species (and therefore when \(n \ge 3\)), this extra information allows to recover the rooted topology of the species phylogeny. Branch length information plays a critical role in achieving the data requirement in Theorem 2. We give a constructive proof of Theorem 3 below, leading to Algorithm 1.

Theorem 3

(Identifiability of rooted topology of species phylogeny from gene metrics). Let \(S = (V_s,E_s; r, \vec {\tau }, \vec {\mu })\) be a species phylogeny with \(n \ge 3\) leaves and root r and let \(G=(V,E; {R}, \vec {\delta })\) be a gene tree sampled from the MSC with corresponding (random) gene metric \(\{ \delta _{ab}\}_{a,b\in L}\). Then the rooted topology of the species phylogeny is identifiable from the distribution of the gene metric.

Our proof is inspired by the Farris transform (also related to the Gromov product; see e.g. Semple and Steel 2003), a classical technique to transform a general tree metric into an ultrametric. In a typical application of the Farris transform, one “roots” the species phylogeny S at an “outgroup” o (i.e., a species that is “far away” from the leaves of S) and then uses the quantities \(\mu _{ox}, x\in L\) to implicitly stretch the leaf edges appropriately, so as to make all inter-species distances to o equal, without changing the underlying topology. More specifically, let S be a species phylogeny. Suppose \(\mathcal {X} = [3]\) and let \(o \in L-\mathcal {X}\) be any leaf of S outside \(\mathcal {X}\). Assume that \( \mu _{o1} \ge \max \{\mu _{o2}, \mu _{o3}\} \) (the other cases being similar) and define the Farris transform

$$\begin{aligned} \dot{\mu }_{xy} := \mu _{xy} + 2\mu _{o1} - \mu _{ox} - \mu _{oy}, \qquad \forall x,y\in \mathcal {X}. \end{aligned}$$
(6)

A standard phylogenetic result (proved for instance in Semple and Steel 2003, Lemma 7.2.2) states that \(\{\dot{\mu }_{xy}\}_{x,y \in \mathcal {X}}\) is an ultrametric on \(\mathcal {X}\) consistent with the topology of S re-rooted at o and, then, restricted to \(\mathcal {X}\).

In the multi-gene context, however, we cannot apply a Farris transform in this manner. In particular, we do not have direct access to \(\{\mu _{xy}\}\); rather, we only estimate the gene metrics \(\{\delta _{xy}^{(i)}\}\). Moreover the latter vary across genes under the MSC.

Key idea 1: We artificially fix rooted gene tree topologies through conditioning. Doing so allows us to relate species and gene metrics.

We prove Theorem 3 for \(n=3\), which suffices.Footnote 1 Let S be a species phylogeny with three leaves and recall that r is the root of S. Let \(G=(V,E; {R}, \vec {\delta })\) be a gene tree sampled from the MSC with corresponding (random) gene metric \(\{ \delta _{ab}\}_{a,b\in L}\). Unlike the classical Farris transform above, we do not use an outgroup. Instead, we show how to achieve the same outcome by using only the distribution of G and, in particular, of \(\{ \delta _{ab}\}_{a,b\in L}\). Notice from (6) that we only need the differences \( \Delta _{xy} := \mu _{rx} - \mu _{ry}. \) It is these quantities that we derive from the distribution of the gene metric. The high-level idea is to:

  1. 1.

    Condition on an event such that the rooted topology of the gene tree is guaranteed to be equal to xy|z. Intuitively, we achieve this by considering an event where one pair of leaves is “somewhat close” while the other two pairs are “somewhat far.” We make the latter condition precise in Proposition 1 below.

  2. 2.

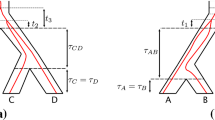
    Recover the species-based difference \(\Delta _{xy}=\mu _{rx} - \mu _{ry}\) from the gene-based difference \(\delta _{xz} - \delta _{yz}\). Indeed, when the rooted topology of G is xy|z, then the difference \(\delta _{xz} - \delta _{yz}\) is equal to \(\Delta _{xy}\) This is established in Proposition 2 below. See Fig. 2 for an illustration.

More formally, we establish the following two propositions, whose proofs are in Sect. 4. For \(x,y \in L\) and \(\beta \in [0,1]\), let \(\delta _{xy}^{(\beta )}\) be the \(\beta \)th quantile of \(\delta _{xy}\). That is, \(\delta _{xy}^{(\beta )}\) is the smallest number \(a\in [0,1]\) such that \(\mathbb {P}\left[ \delta _{xy} \le a \right] \ge \beta .\) Note that this quantile is a function of the distribution of G.

Fig. 2
figure 2

a Gene 1 (red gene) has the topology 12|3. Therefore, the gene distance on this gene satisfies the condition that \(\delta _{13} - \delta _{23} = \Delta _{12}\). b In this case, Gene 2 (blue gene) has the topology 1|23. Observe that therefore, \(\delta _{13} - \delta _{23} \ne \Delta _{12}\)

Full size image

Proposition 1

(Fixing the rooted topology of the gene tree). Let (x, y, z) be an arbitrary permutation of (1, 2, 3). The following event has positive probability and implies that the rooted topology of G is xy|z:

$$\begin{aligned} \mathscr {E}_{I} = \left\{ \delta _{xy} \le \delta _{xy}^{(1/2)}, \delta _{xz}> \delta _{xz}^{(1/2)}, \delta _{yz} > \delta _{yz}^{(1/2)}\right\} . \end{aligned}$$
(7)

Conditioning on \(\mathscr {E}_{I}\), we then show how to recover the difference \(\Delta _{xy}\) from \(\delta _{xz} - \delta _{yz}\).

Proposition 2

(A formula for the height difference). We have that, conditioned on \(\mathscr {E}_{I}\), almost surely

$$\begin{aligned} \delta _{xz} - \delta _{yz} = \Delta _{xy}. \end{aligned}$$
(8)

The quantity on the l.h.s. of (8) is a function of the distribution of G. From the \(\Delta _{xy}\) s, we can solve for \(\mu _{rx}\)’s. Combining the properties of the Farris transform with Propositions 1 and 2 leads to Theorem 3. The Proof of Theorem 3 can also be found in Sect. 4.

3.2 Algorithm 1: the reduction step

We are now ready to describe the reduction algorithm (Algorithm 1). Recall that we are restricting our attention to the case of three leaves \(\mathcal {X} = \left\{ 1,2,3 \right\} \) with rooted species tree topology 12|3. The main idea underlying the reduction algorithm is based on the proof of the identifiability result (Theorem 3). That is, we find a set of genes whose topology is highly likely to be a fixed triplet, we estimate the height differences on this set using (8), and we perform a type of Farris transform. However, given that we do not have access to the actual gene tree distribution but only to sequence data, there are several differences with the identifiability proof that make the analysis and the algorithm more involved. We explain these next in details.

A first challenge is that, in the regime where sequence length is “short,” i.e., when \(k \ll f^{-2}\), the sequence-based estimate of the gene tree metric is much less accurate than what is needed for our reduction step.

Key idea 2: We show how to combine genes satisfying a condition related to (7) to produce a much more accurate estimate of distance differences.

Fixing gene tree topologies Here we only have access to sequence data. In particular the \(\delta \)s are unknown. So, we work instead with the p-distances for gene i and \(x,y \in \mathcal {X}\), and their empirical quantiles \(\widehat{p}^{(\beta )}_{xy}\).Footnote 2 Similarly to Proposition 1, we then consider those genes for which the event

$$\begin{aligned} \left\{ \widehat{p}_{xy}^i \le \widehat{p}_{xy}^{(1/3)}, \widehat{p}_{xz}^{(2/3)} \le \widehat{p}_{xz}^i, \widehat{p}_{yz}^{(2/3)} \le \widehat{p}_{yz}^i\right\} \cap \left\{ \widehat{p}_{xz}^i \le \widehat{p}_{xz}^{(5/6)} \text { OR } \widehat{p}_{yz}^i \le \widehat{p}_{yz}^{(5/6)}\right\} .\nonumber \\ \end{aligned}$$
(9)

holds for some chosen permutation (x, y, z) of (1, 2, 3). We will call this set of genes I. We show that this set has a “non-trivial” size and that, with high probability, the genes satisfying (9) have topology xy|z (see Proposition 3).Footnote 3 In particular, letting \(p(x) = \frac{3}{4}\left( 1 - e^{-4x/3} \right) \), the analysis of this construction accounts for the “sequence noise” around the expected values

$$\begin{aligned} p^i_{xy} := \mathbb {E}\left[ \widehat{p}^i_{xy} | G^{(i)} \right] =\frac{3}{4}\left( 1 - e^{-4\delta ^i_{xy}/3} \right) =: p(\delta ^i_{xy}). \end{aligned}$$
(10)

Estimating distance differences Because we work with p-distances, we adapt formula (8) for the difference \(\Delta _{xy}\) as follows. Using \( \widehat{p}^I_{xz} = \frac{1}{\left| I \right| }\sum _{i\in I}\widehat{p}_{xz}^i\) and \(\widehat{p}^I_{yz} = \frac{1}{\left| I \right| }\sum _{i\in I}\widehat{p}_{yz}^i, \) our estimate of the distance differences is given by

$$\begin{aligned} \widehat{\Delta }_{xy} = \left\{ -\frac{3}{4}\log \left( 1 - \frac{4}{3}\widehat{p}_{xz}^I \right) \right\} - \left\{ -\frac{3}{4}\log \left( 1 - \frac{4}{3}\widehat{p}_{yz}^I \right) \right\} . \end{aligned}$$

Recall from Proposition 2 and Fig. 2 that, for this formula to be valid, we need to ensure that the topology of the gene trees used is xy|z. The logarithmic transforms in the curly brackets are the usual distance corrections in the Jukes-Cantor sequence model (see e.g. Semple and Steel (2003)). Note, however, that we perform an average over I before the correction; this is important to obtain the needed statistical power of our estimator. The non-trivial part of the analysis of this step is to bound the estimation error. Indeed, unlike the identifiability result, we have a finite amount of gene data and, moreover, we must account for the sequence noise. This is done using concentration inequalities in Proposition 4.

In Algorithm 1, we compute \(\widehat{\Delta }_{xy}\) with the formula above for two of the pairs in \(\mathcal {X}\), say (1, 2) and (1, 3), and then derive the third quantity consistently, i.e., \(\widehat{\Delta }_{23} = \widehat{\Delta }_{13} - \widehat{\Delta }_{12}\). We also set \(\widehat{\Delta }_{xy} = - \widehat{\Delta }_{yx}\) and \(\widehat{\Delta }_{xx} = 0\) for all x, y.

Stochastic Farris transform The quantile test (see Section 1) is not a distance-based method in the traditional sense of the term. Indeed we do not define a pairwise distance matrix on the leaves. Instead, we use the empirical distribution of the p-distances across genes. It is for this reason that we do not simply apply the classical Farris transform of (6) to the estimated distances. Rather, we perform what we call a “stochastic” Farris transform to ensure that we properly mimic the contributions from both the multispecies coalescent and the Jukes-Cantor model to the distribution of p-distances.

Key idea 3: We transform the sequence data itself to mimic the distribution under an ultrametric species phylogeny. This is done by adding the right amount of noise to the sequence data at each gene, as detailed next.

We will let \(\oplus \) denote addition mod-4 and identify \(\mathtt{A,T,G,C}\) with 0, 1, 2, 3 respectively in that order when doing this addition. For instance, this means that \(\mathtt{A} \oplus 1 = \mathtt{T}\) and \(\mathtt{G} \oplus 2 = \mathtt{A}\).

Definition 5

(Stochastic Farris transform). For a gene i, let \(\{\xi _x^{i}\}_{x\in \mathcal {X}}\) be a sequence dataset over the species \(\mathcal {X} = [3]\) and let \(\Delta _{xy} = \mu _{rx} - \mu _{ry}, x, y \in \mathcal {X}\). Assume without loss of generality that \(\min \{\Delta _{12},\Delta _{13}\} \ge 0\). The stochastic Farris transform defines a new set of sequences \(\{\xi ^i_{x,N}\}_{x \in \mathcal {X}}\) such that \(\xi _{x,N}^i = \xi _x^i \oplus \epsilon _x^i\), where \(\epsilon _x^i\in \{0,1,2,3\}^k\) is an independent random sequence whose jth coordinate is drawn according to: \(\epsilon _x^{ij} = 0\), w.p. \(1- p(\Delta _{1x})\); otherwise it is chosen uniformly among [3].

We write this as \(\{\xi _{x,N}^i\}_{x\in \mathcal {X}} = \mathcal {F}(\{\xi _{x}^i\}_{x\in \mathcal {X}}; \{\Delta _{xy}\}_{x,y\in \mathcal {X}})\).

By the Markov property, for \(x,y \in \mathcal {X}\), the “noisy” sequence data above satisfy

$$\begin{aligned} \mathbb {P}\left[ \xi _{x,N}^i \ne \xi _{y,N}^i \right]&= p \left( \delta _{xy}^i + \Delta _{1x} + \Delta _{1y}\right) =: r_{xy}^i. \end{aligned}$$

Notice that \(\delta _{xy}^i\), the random gene tree distance between x and y under gene i, can be decomposed as \(\mu _{xy} + \Gamma _{xy}^i\), where \(\Gamma _{xy}^i\) is the random component contributed by the multispecies coalescent. On the other hand, the set of distances \(\mu _{xy} + \Delta _{1x} + \Delta _{1y}\) is ultrametric by the properties of the classical Farris transform (see the Proof of Theorem 3). As a result, the stochastic Farris transform modifies the sequence data so that it appears as though it was generated from an ultrametric MSC-JC process.

In reality, we do not have access to the true differences \(\Delta _{xy}, x,y\in \mathcal {X}\). Instead, we employ our estimates \(\widehat{\Delta }_{xy}\) for all \(x,y \in \mathcal {X}\) in the previous step to obtain the following approximate stochastic Farris transform:

$$\begin{aligned} \{\xi _{x,N}^i\}_{x\in \mathcal {X}} = \mathcal {F}(\{\xi _x^{i}\}_{x\in \mathcal {X}};\{\widehat{\Delta }_{xy}\}_{x,y\in \mathcal {X}}). \end{aligned}$$
(11)

This is the output of the reduction. See Algorithm 1 for details. We prove Theorem 1 in Sect. 5.

4 Identifiability: detailed proofs

Proof

(Proposition 1) Recall the definition of the event \(\mathscr {E}_{I}\) from (7). Our goal is to show that it has positive probability and that it implies that the rooted topology of G is xy|z. This makes sense on an intuitive level because the event \(\mathscr {E}_{I}\) requires that \(\delta _{xy}\) is “somewhat small” and that \(\delta _{xz}\), \(\delta _{yz}\) are “somewhat large.” To prove this, we make crucial use of the following symmetry. Let w be the most recent common ancestor of x, y and z in S. By “above (respectively, below) w,” we refer to the times prior to (respectively, following) the species divergence at w (forward in time). Let

$$\begin{aligned} \Gamma _{xy} = \delta _{xy} - \mu _{xy}, \end{aligned}$$
(12)

and let \(\mathscr {B}_{xy}\) denote the event that the coalescence between the lineages of x and y occurs below w (which is only possible if x and y happen to be sister populations in the species phylogeny). For \(\beta \in [0,1]\), let \(\Gamma _{xy}^{(\beta )}\) be the \(\beta \)th quantile of \(\Gamma _{xy}\). We define the quantities and event above similarly for the other pairs. Under \(\mathscr {B}_{xy}^{c}\), note that \(\Gamma _{xy}\) is the contribution to \(\delta _{xy}\) coming from the path above w on G, and the same holds for the other pairs. Hence, by the exchangeability of the coalescent process above w, we have

$$\begin{aligned} \Gamma _{xy}\,|\,\mathscr {B}_{xy}^{c} {\mathop {=}\limits ^\mathrm{d}} \Gamma _{xz}\,|\,\mathscr {B}_{xz}^{c} {\mathop {=}\limits ^\mathrm{d}} \Gamma _{yz}\,|\,\mathscr {B}_{yz}^{c}. \end{aligned}$$
(13)

That observation will facilitate the comparison of quantiles.

We break up the proof into 3 cases depending on the rooted topology of S:

  • Rooted topology of S is yz|x. In that case, the lineages from the pairs (x, y) and (x, z) coalesce only above w. That is, the events \(\mathscr {B}_{xy}\) and \(\mathscr {B}_{xz}\) occur almost surely. By (13), we then get \(\Gamma _{xy} {\mathop {=}\limits ^\mathrm{d}} \Gamma _{xz}\) which implies that \(\Gamma _{xy}^{(1/2)} = \Gamma _{xz}^{(1/2)} =: \gamma \). Because \(\mu _{xy}\) and \(\mu _{xz}\) are deterministic, (12) guarantees further that

    $$\begin{aligned} \delta _{xy}^{(1/2)} = \mu _{xy} + \gamma , \qquad \delta _{xz}^{(1/2)} = \mu _{xz} + \gamma . \end{aligned}$$

    As a result, the event \(\mathscr {E}_{I}\) means that

    $$\begin{aligned} \mu _{xy} + \Gamma _{xy} = \delta _{xy} \le \delta _{xy}^{(1/2)} = \mu _{xy} + \gamma , \end{aligned}$$

    and

    $$\begin{aligned} \mu _{xz} + \Gamma _{xz} = \delta _{xz} > \delta _{xz}^{(1/2)} = \mu _{xz} + \gamma . \end{aligned}$$

    The last two inequalities are equivalent to \(\Gamma _{xy} \le \gamma < \Gamma _{xz}\) which is only possible if the rooted topology of G is xy|z. It remains to show that the event \(\mathscr {E}_{I}\) occurs with positive probability. What we have shown implies also that \(\Gamma _{yz} = \Gamma _{xz}\) almost surely. Moreover, conditioned on \(\mathscr {B}_{yz}\), the random variable \(\Gamma _{yz}\) is non-positive; hence, \(\Gamma _{yz}^{(1/2)} \le \gamma < \Gamma _{xz} = \Gamma _{yz}\). So \(\mathscr {E}_{I}\) is indeed possible and occurs with positive probability under the MSC.

  • Rooted topology of S is xz | y . This is case is similar to the previous one, and is therefore omitted.

  • Rooted topology of S is xy | z . In that case, the lineages from the pairs (x, z) and (y, z) coalesce only above w. On the other hand, conditioned on \(\mathscr {B}_{xy}\), the random variable \(\Gamma _{xy}\) is non-positive. Hence, combining these observations with (13), we get \(\Gamma _{xy}^{(1/2)} \le \Gamma _{xz}^{(1/2)} = \Gamma _{yz}^{(1/2)} =: \gamma \). The event \(\mathscr {E}_{I}\) then means that

    $$\begin{aligned} \mu _{xy} + \Gamma _{xy} = \delta _{xy} \le \delta _{xy}^{(1/2)} = \mu _{xy} + \Gamma _{xy}^{(1/2)} \le \mu _{xy} + \gamma , \end{aligned}$$

    and

    $$\begin{aligned} \mu _{xz} + \Gamma _{xz} = \delta _{xz} > \delta _{xz}^{(1/2)} = \mu _{xz} + \gamma , \end{aligned}$$

    and again \(\Gamma _{xy} \le \gamma < \Gamma _{xz}\), implying that the rooted topology of G is xy|z. The equality \(\Gamma _{xz} = \Gamma _{yz}\) holds as well almost surely. So \(\mathscr {E}_{I}\) has positive probability.

That proves the claim. \(\square \)

‘

Proof

(Proposition 2) We know from Proposition 1 that, conditioned on \(\mathscr {E}_{I}\), coalescence between the lineages of x and z necessarily occurs in the common ancestral population of x, y and z, irrespective of the species tree topology. The same holds for y and z. Further \(\Gamma _{xz} = \Gamma _{yz}\) almost surely, where the \(\Gamma \)s were defined in the proof of Proposition 1. Using (12) it follows that, conditioned on \(\mathscr {E}_{I}\), we have \( \delta _{xz} - \delta _{yz} = \mu _{xz} - \mu _{yz} = \Delta _{xy}\) with probability 1 as claimed.\(\square \)

Proof

(Theorem 3) By Proposition 2, conditioning on the event \(\mathscr {E}_{I}\)—which depends only on the gene metric—we have \( \delta _{xz} - \delta _{yz} = \mu _{xz} - \mu _{yz} = \Delta _{xy}\). Hence, from this information, we can construct

$$\begin{aligned} \dot{\mu }_{xy} = \mu _{xy} + \Delta _{1x} + \Delta _{1y}, \qquad x,y\in \mathcal {X}. \end{aligned}$$

assuming that \(\min \{\Delta _{12}, \Delta _{13}\}\ge 0\) (the other cases follow similarly). Recalling that \(\Delta _{xy} := \mu _{rx} - \mu _{ry}\), where r is the root of S, it follows that \(\dot{\mu }_{r1} = \dot{\mu }_{r2} = \dot{\mu }_{r3}\). That is, \(\dot{\mu }\) is ultrametric. From this, the rooted topology of the species tree can be reconstructed. See Fig. 2 for an illustration and, for instance (Semple and Steel 2003, Lemma 7.2.2) for more details on this last step. \(\square \)

5 Ultrametric reduction: detailed proofs

Before proving Theorem 1, we define \(S'\) formally. Given estimates \(\widehat{\Delta }_{xy}\) for all \(x,y \in \mathcal {X}\), and supposing that \(\min \{\widehat{\Delta }_{12}, \widehat{\Delta }_{13}\}\ge 0\) or equivalently that the quantity \(-\frac{3}{4}\log \left( 1 - \frac{4}{3}\widehat{p}_{xy}^I \right) \) is minimized for the pair \((x,y) = (2,3)\) (the other cases follow similarly), we let

$$\begin{aligned} \widehat{\dot{\mu }}_{xy} = \mu _{xy} + \widehat{\Delta }_{1x} + \widehat{\Delta }_{1y}, \qquad x,y\in \mathcal {X}. \end{aligned}$$

Note that this formula is consistent with the definition of \(\dot{\mu }_{xy}\) in (6). Observe further that we do not have access to \(\widehat{\dot{\mu }}_{xy}\), as \(\mu _{xy}\) is unknown—it is only used to define \(S'\) in the statement of the theorem.

Let \(S' = (V_s, E_s, r, \vec {\tau },\vec {\hat{\dot{\mu }}})\) be a species phylogeny with the same topology and branch lengths as S restricted to \(\mathcal {X}\), and with mutation rates \(\{\widehat{\dot{\mu }}\}_{e\in E_s}\) that are chosen such that:

  1. (a)

    If \(e\in E_s\) is an internal branch, we let \(\widehat{\dot{\mu }}_e = \mu _e\) ; and

  2. (b)

    Otherwise, that is, if \(e\in E_s\) is incident to a leaf x of S, we let \(\widehat{\dot{\mu }}_e\) be chosen to satisfy

    $$\begin{aligned} \widehat{\dot{\mu }}_e \tau _e = \mu _e \tau _e + \widehat{\Delta }_{1x}. \end{aligned}$$

The goal here is to “stretch” the leaf edges so that the modified species metric between any pair of leaves \(x, y \in \mathcal {X}\) is given by \(\widehat{\dot{\mu }}_{xy}\). Alternatively, we could have modified the branch lengths.

5.1 Proof of Theorem 1

Proof

(Theorem 1) Define two disjoint subsets \(\mathcal {M}_{\mathrm{R}1}, \mathcal {M}_{\mathrm{R}2}\) of [m] satisfying:

$$\begin{aligned} |\mathcal {M}_{\mathrm{R}1}| = c_{2} \log (4 \varepsilon ^{-1}),\qquad |\mathcal {M}_{\mathrm{R}2}| = \left( 1 \vee \frac{1}{k \phi ^{2}}\right) c_{2} \log (4 \varepsilon ^{-1}), \end{aligned}$$
(14)

for a constant \(c_{2}\) to be determined below, and let \(\mathcal {M}_{\mathrm{R}}\) and \(\mathcal {M}_{\mathrm{Q}}\) be such that \(\mathcal {M}_{\mathrm{R}} = \mathcal {M}_{\mathrm{R}1}\sqcup \mathcal {M}_{\mathrm{R}2}\) and \([m] = \mathcal {M}_{\mathrm{R}} \sqcup \mathcal {M}_{\mathrm{Q}}\). For a gene i and leaves \(x,y \in \mathcal {X}\), recall that In fact, we split this last average into two to avoid unwanted correlations as we explain below. Assuming k is even for simplicity, we denote these as

For \(\beta \in [0,1]\), let \(\widehat{p}^{(\beta )}_{xy}\) be the corresponding empirical quantiles computed based on the set \(\{\widehat{{p}}_{xy}^i: i\in \mathcal {M}_{\mathrm{R}1}\}\). Fix a permutation (x, y, z) of (1, 2, 3). Consider the following subset of genes in \(\mathcal {M}_{\mathrm{R}2}\):

$$\begin{aligned} I =&\left\{ i\in \mathcal {M}_{\mathrm{R}2}\,:\,\widehat{p}^{i\downarrow }_{xy} \le \widehat{p}_{xy}^{(1/3)}, \widehat{p}_{xz}^{(2/3)} \le \widehat{p}^{i\downarrow }_{xz}, \widehat{p}_{yz}^{(2/3)} \le \widehat{p}^{i\downarrow }_{yz}\right\} \\&\cap \left\{ i\in \mathcal {M}_{\mathrm{R}2}\,:\,\widehat{p}^{i\downarrow }_{xz} \le \widehat{p}_{xz}^{(5/6)} \text { OR } \widehat{p}^{i\downarrow }_{yz} \le \widehat{p}_{yz}^{(5/6)}\right\} . \end{aligned}$$

The proof of the theorem closely tracks that of the identifiability result (Theorem 3). We first show that the rooted topologies in I are highly likely to be xy|z and prove some technical claims that will be useful in the proof of Proposition 4 (proof in Sect. 5.2).\(\square \)

Proposition 3

(Fixing gene tree topologies) There are \(c_{9}, c_{10}, c_{10}', \varepsilon _0 > 0\) such that with probability at least

$$\begin{aligned} 1 - 10\exp (-2c_{9}^2 |\mathcal {M}_{\mathrm{R}1}|) - 6 |\mathcal {M}_{\mathrm{R}2}| \exp \left( - k \varepsilon _0^2 \right) - 2\exp \left( -2 c_{10}^2 |\mathcal {M}_{\mathrm{R}2}|\right) , \end{aligned}$$

the following hold:

  1. (a)

    The rooted topology of all gene trees in I is xy|z,

  2. (b)

    For all \(i\in I\), \(p^i_{xy} \le p^{(7/24)}_{xy}\), \(p^{(17/24)}_{xz} \le p^i_{xz} \le p^{(19/24)}_{xz}\), \(p^{(17/24)}_{yz} \le p^i_{yz} \le p^{(19/24)}_{yz}\),

  3. (c)

    The size of I is greater than \(c_{10}' |\mathcal {M}_{\mathrm{R}2}|\).

Let \(\mathscr {I}\) be the event that the conclusion of Proposition 3 holds. To simplify the notation, we use \(\widetilde{\mathbb {P}}\) and \(\widetilde{\mathbb {E}}\) to denote the probability and expectation operators conditioned on \(\mathscr {I}\). Using

$$\begin{aligned} \widehat{p}^I_{xz} = \frac{1}{\left| I \right| }\sum _{i\in I}\widehat{p}_{xz}^{i\uparrow } \qquad \text {and} \qquad \widehat{p}^I_{yz} = \frac{1}{\left| I \right| }\sum _{i\in I}\widehat{p}_{yz}^{i\uparrow }, \end{aligned}$$

let

$$\begin{aligned} \widehat{\Delta }_{xy} = \left\{ -\frac{3}{4}\log \left( 1 - \frac{4}{3}\widehat{p}_{yz}^I \right) \right\} - \left\{ -\frac{3}{4}\log \left( 1 - \frac{4}{3}\widehat{p}_{xz}^I \right) \right\} . \end{aligned}$$

Recall that \( \Delta _{xy} = \mu _{rx} - \mu _{ry}. \) We next show that \(\widehat{\Delta }_{xy}\) is a good approximation to \(\Delta _{xy}\) (proof in Sect. 5.2).

Proposition 4

(Estimating differences). There is a \(c_{11} \in (0,1)\) such that with \(\widetilde{\mathbb {P}}\)-probability at least \( 1 - 4\exp \left( - c_{11} k|\mathcal {M}_{\mathrm{R}2}| \phi ^2\right) , \) it holds that \( \left| \widehat{\Delta }_{xy} - \Delta _{xy} \right| \le \phi /2. \)

We repeat the height difference estimation above for all pairs in \(\mathcal {X}\). Therefore, by a union bound, we get the above guarantee for all pairs with probability at least \(1 - 12\exp \left( - c_{11} k|\mathcal {M}_{\mathrm{R}2}| \phi ^2\right) \).

Without loss of generality, assume that \( \mu _{r1} \ge \max \{\mu _{r2}, \mu _{r3}\}, \) and recall the Farris transform

$$\begin{aligned} \dot{\mu }_{xy} = \mu _{xy} + 2\mu _{r1}- \mu _{rx} - \mu _{ry} = \mu _{xy} + \Delta _{1x} + \Delta _{1y}, \qquad x, y \in \mathcal {X}, \end{aligned}$$

which defines an ultrametric, and consider the approximation

$$\begin{aligned} \widehat{\dot{\mu }}_{xy} = \mu _{xy} + \widehat{\Delta }_{1x} + \widehat{\Delta }_{1y}, \qquad x, y\in \mathcal {X}. \end{aligned}$$

Assuming that the conclusion of Proposition 4 holds for all \(x,y \in \mathcal {X}\), we have shown that \((\widehat{\dot{\mu }}_{xy})\) is \(\phi \)-close to the ultrametric \((\dot{\mu }_{xy})\). As we explained in Sect. 3.2, we produce a new sequence dataset using an approximate stochastic Farris transform \( \{\xi _{x,N}^i\}_{x\in \mathcal {X}} = \mathcal {F}(\{\xi _x^{i}\}_{x\in \mathcal {X}};\{\widehat{\Delta }_{xy}\}_{x,y\in \mathcal {X}}). \)

Hence, again by a union bound, we get the claim of Theorem 1 except with probability

$$\begin{aligned} 10\exp (-2c_{9}^2 |\mathcal {M}_{\mathrm{R}1}|)&+ 6 |\mathcal {M}_{\mathrm{R}2}| \exp \left( - 2 k \varepsilon _0^2 \right) + 2\exp \left( -2 c_{10}^2 |\mathcal {M}_{\mathrm{R}2}|\right) \\&+ 12\exp \left( - c_{11} k|\mathcal {M}_{\mathrm{R}2}| \phi ^2\right) . \end{aligned}$$

We get the data requirement by asking for the conditions under which the above quantity is less than \(\varepsilon \), which involves choosing \(c_{2}, c_{}', c_{}''\) large enough in (14) and in the statement of the theorem. \(\square \)

5.2 Proofs of Propositions 3 and 4

Proof

(Proposition 3) First fix \(0< \varepsilon _1 < 1/24\) and let \(\varepsilon _0 > 0\) be the largest value such that

$$\begin{aligned}&p_{xy}^{(7/24)} \le p_{xy}^{(1/3-\varepsilon _1)} - 2\varepsilon _0 \le p_{xy}^{(1/3 + \varepsilon _1)} + 2\varepsilon _0 \le p^{(9/24)}_{xy}\nonumber \\&p^{(15/24)}_{xz} \le p_{xz}^{(2/3-\varepsilon _1)} - 2\varepsilon _0 \le p_{xz}^{(2/3 + \varepsilon _1)} + 2\varepsilon _0 \le p^{(17/24)}_{xz}\nonumber \\&p^{(19/24)}_{xz} \le p_{xz}^{(5/6-\varepsilon _1)} - 2\varepsilon _0 \le p_{xz}^{(5/6 + \varepsilon _1)} + 2\varepsilon _0 \le p^{(21/24)}_{xz}\nonumber \\&p^{(15/24)}_{yz} \le p_{yz}^{(2/3-\varepsilon _1)} - 2\varepsilon _0 \le p_{yz}^{(2/3 + \varepsilon _1)} + 2\varepsilon _0 \le p^{(17/24)}_{yz}\nonumber \\&p^{(19/24)}_{yz} \le p_{yz}^{(5/6-\varepsilon _1)} - 2\varepsilon _0 \le p_{yz}^{(5/6 + \varepsilon _1)} + 2\varepsilon _0 \le p^{(21/24)}_{yz}. \end{aligned}$$
(15)

The fact that these inequalities hold is guaranteed by (27) in the Appendix which characterizes the behavior of the quantile functions of the random variables associated with the MSC. Note that \(\varepsilon _0\) depends on the parameters \(\mu _U\), \(g'\) and g.

Let (x, y, z) be an arbitrary permutation of the leaves (1, 2, 3). The idea of the proof is to rely on Proposition 1, which we rephrase in terms of p-distances. For a gene \(G_i\), let

$$\begin{aligned} p^i_{xy} = \frac{3}{4}\left( 1 - e^{-4\delta ^i_{xy}/3} \right) . \end{aligned}$$

And, for \(\beta \in [0,1]\), the corresponding \(\beta \)th quantile is given by

$$\begin{aligned} p^{(\beta )}_{xy} = \frac{3}{4}\left( 1 - e^{-4 \delta ^{(\beta )}_{xy}/3} \right) ; \end{aligned}$$

similarly for the other pairs. Then, by Proposition 1, the event

$$\begin{aligned} \mathscr {E}^i_{I} = \left\{ p^i_{xy} \le p_{xy}^{(1/2)}, p_{xz}^{(1/2)}< p^i_{xz} , p_{yz}^{(1/2)} < p^i_{yz} \right\} , \end{aligned}$$

implies that the rooted topology of \(G_i\) is xy|z.

Hence, our main goal is to show that

$$\begin{aligned} \mathscr {Q}_i \!=\! \left\{ \widehat{p}^{i\downarrow }_{xy} \le \widehat{p}_{xy}^{(1/3)}, \widehat{p}_{xz}^{(2/3)} \!\le \widehat{p}^{i\downarrow }_{xz}, \widehat{p}_{yz}^{(2/3)} \le \widehat{p}^{i\downarrow }_{yz}\right\} \cap \left\{ \widehat{p}^{i\downarrow }_{xz} \le \widehat{p}_{xz}^{(5/6)} \text { OR } \widehat{p}^{i\downarrow }_{yz} \le \widehat{p}_{yz}^{(5/6)}\!\right\} \!, \end{aligned}$$
(16)

implies \(\mathscr {E}^i_{I}\) with high probability. We do this by controlling the deviations of \(\widehat{p}_{uw}^{(\beta )}\) (Lemma 1 below) and \(\widehat{p}^{i\downarrow }_{uw}\) (Lemma 2 below). (The upper bounds on \(\widehat{p}^{i\downarrow }_{xz}\) and \(\widehat{p}^{i\downarrow }_{yz}\) in (16) are included for technical reasons that will be useful in proving Proposition 4.)

Recall that we use only the genes in \(\mathcal {M}_{\mathrm{R}}\) for the reduction step and this set in turn is divided into disjoint subsets \(\mathcal {M}_{\mathrm{R}1}\) and \(\mathcal {M}_{\mathrm{R}2}\). The quantiles are estimated using \(\mathcal {M}_{\mathrm{R}1}\), while \(\mathcal {M}_{\mathrm{R}2}\) is used to compute I. We do not argue about the deviation of \(\widehat{p}_{uw}^{(\beta )}\) from the true \(\beta \)th quantile of the distribution of \(\widehat{p}_{uw}^i\). Instead we show that \(\widehat{p}_{uw}^{(\beta )}\) is close to the \(\beta \)th quantile \(p_{uw}^{(\beta )}\) of the disagreement probability under the MSC, that is, the quantile without the sequence noise. We argue this way because the events that we are ultimately interested in (whether a certain coalescence event has occured in a particular population) are expressed in terms of the MSC. Note that, in order to obtain a useful bound of this type, we must assume that the sequence length is sufficiently long, that is, that the sequence noise is reasonably small. Hence this is one of the steps of our argument where we require a lower bound on k.

Lemma 1

(Deviation of \(\widehat{p}_{uw}^{(\beta )}\)). Fix a pair \(u,w \in \mathcal {X}\) and a constant \(\beta \in (0,1)\). For all \(\varepsilon _0 > 0\) and \(0< \varepsilon _1 < \min \{\beta ,1-\beta \}\), there is a constant \(c_9 > 0\) depending on \(\beta \), \(\varepsilon _0\) and \(\varepsilon _1\) such that

$$\begin{aligned} \mathbb {P}\left[ p_{uw}^{(\beta -\varepsilon _1)} - \varepsilon _0 \le \widehat{p}_{uw}^{(\beta )} \le p_{uw}^{(\beta + \varepsilon _1)} + \varepsilon _0 \right] \ge 1 - 2 \exp \left( - 2 c_{9}^2 |\mathcal {M}_{\mathrm{R}1}| \right) , \end{aligned}$$
(17)

provided that k is greater than a constant depending on \(\varepsilon _0\) and \(\varepsilon _1\).

Proof

We prove one side of the first equation (the other inequalities being similar). Define the random variable

$$\begin{aligned} M&= \left| \left\{ i \in \mathcal {M}_{\mathrm{R}1}: {\widehat{p}^{i}_{uw}}\le p^{(\beta + \varepsilon _1)}_{uw} + \varepsilon _0 \right\} \right| , \end{aligned}$$

and observe that

$$\begin{aligned} \mathbb {P}\left[ \widehat{p}^{(\beta )}_{uw} > p^{(\beta + \varepsilon _1)}_{uw} + \varepsilon _0 \right]&\le \mathbb {P}\left[ M < \beta |\mathcal {M}_{\mathrm{R}1}| \right] . \end{aligned}$$
(18)

Our goal is hence to bound the probability on the r.h.s.

For this, we first bound the expectation of M by noting that

$$\begin{aligned}&\mathbb {P}\left[ {\widehat{p}^{i}_{uw}} \le p^{(\beta + \varepsilon _1)}_{uw} + \varepsilon _0 \right] \nonumber \\&\ge \mathbb {P}\left[ {\widehat{p}^{i}_{uw}} \le p^{(\beta +\varepsilon _1)}_{uw} + \varepsilon _0 \,|\, p^i_{uw} \le p^{(\beta +\varepsilon _1)}_{uw}\right] \mathbb {P}\left[ p^i_{uw} \le p^{(\beta +\varepsilon _1)}_{uw} \right] \nonumber \\&\ge \left[ 1 - \exp \left( -k \varepsilon _0^2 \right) \right] \left( \beta + \varepsilon _1 \right) , \end{aligned}$$
(19)

by Hoeffding’s inequality Boucheron et al. (2013) applied to \(\widehat{p}^{i}_{uw}\) and the definition of \(p^{(\beta + \varepsilon _1)}_{uw}\); we also used that \(\mathbb {E}[{\widehat{p}^{i}_{uw}}\,|\,p_{uw}] = p_{uw}\).

We then apply Hoeffding’s inequality to M itself. From (19), it follows that

$$\begin{aligned} \mathbb {E}[M] \ge \left( \beta + \varepsilon _1 \right) \left[ 1 - \exp \left( - k \varepsilon _0^2 \right) \right] . \end{aligned}$$
(20)

Therefore, letting

$$\begin{aligned} c_9 = \left( \beta + \varepsilon _1 \right) \left[ 1 - \exp \left( - k \varepsilon _0^2 \right) \right] - \beta , \end{aligned}$$

we have that

$$\begin{aligned} \mathbb {P}\left[ M< \beta |\mathcal {M}_{\mathrm{R}1}| \right]&\le \mathbb {P}\left[ M - \mathbb {E}M < -c_9 |\mathcal {M}_{\mathrm{R}1}| \right] \\&\le \exp \left( - 2 c_{9}^2 |\mathcal {M}_{\mathrm{R}1}| \right) , \end{aligned}$$

where we used (20) on the first line. Observe moreover that \(c_9\) is strictly positive, provided that k is greater than a constant depending on \(\varepsilon _0\) and \(\varepsilon _1\). Combining with (18) gives the result.\(\square \)

We can also control the deviation of \(\widehat{p}^{i\downarrow }_{uw}\) around the random variable \(p^i_{uw}\).

Lemma 2

(Deviation of \(\widehat{p}^{i\downarrow }_{uw}\)). Fix a pair \(u, w \in \mathcal {X}\). For all i and \(\varepsilon _0 > 0\), almost surely

$$\begin{aligned} \mathbb {P}\left[ |\widehat{p}^{i\downarrow }_{uw} - p^i_{uw}| \ge \varepsilon _0 \,|\, p^i_{uw} \right] \le 2 \exp \left( - k \varepsilon _0^2 \right) . \end{aligned}$$
(21)

Proof

Conditioned on \(p^i_{uw}\), the random variable \((k/2) \widehat{p}^{i\downarrow }_{uw}\) is \(\mathrm {Bin}(k/2,p^i_{uw})\). The result follows again from Hoeffding.\(\square \)

Let \(\mathscr {E}_{\mathrm {qu}}\) be the event that the inequality in Lemma 1, i.e., \(p_{uw}^{(\beta -\varepsilon _1)} - \varepsilon _0 \le \widehat{p}_{uw}^{(\beta )} \le p_{uw}^{(\beta + \varepsilon _1)} + \varepsilon _0\), holds for \(\widehat{p}^{(1/3)}_{xy}\), \(\widehat{p}^{(2/3)}_{xz}\), \(\widehat{p}^{(5/6)}_{xz}\), \(\widehat{p}^{(2/3)}_{yz}\) and \(\widehat{p}^{(5/6)}_{yz}\), which occurs with probability at least \(1 - 10\exp (-2 c_0^2 |\mathcal {M}_{\mathrm{R}1}|)\) by a union bound over (17). Let \(\mathscr {D}_i\) be the event that the inequality in Lemma 2, i.e., \(|\widehat{p}^{i\downarrow }_{uw} - p^i_{uw}| {\le } \varepsilon _0\), holds for all pairs (u, w) in \(\mathcal {X}\), an event which occurs with probability at least \(1 - 6\exp (-k \varepsilon _0^2)\) by a union bound over (21).

Recall that our goal is to show that \(\mathscr {Q}_i\) (defined in (16)) implies \(\mathscr {E}^i_{I}\) with high probability. We also condition on \(\mathscr {E}_{\mathrm {qu}}\) and \(\mathscr {D}_i\), which occur with high probability. Given \(\mathscr {E}_{\mathrm {qu}}\), \(\mathscr {D}_i\) and \(\mathscr {Q}_i\), we have

$$\begin{aligned} p^i_{xy}\le & {} \widehat{p}^{i\downarrow }_{xy} + \varepsilon _0\\\le & {} \widehat{p}_{xy}^{(1/3)} + \varepsilon _0\\\le & {} p^{(1/3+\varepsilon _1)}_{xy} + 2\varepsilon _0\\\le & {} p^{(1/2)}_{xy}, \end{aligned}$$

and similarly for the other pairs, where the first inequality follows from \(\mathscr {D}_i\), the second inequality follows from \(\mathscr {Q}_i\), the third inequality follows from \(\mathscr {E}_{\mathrm {qu}}\), and the fourth inequality follows from (15). That is, \(\mathscr {E}^i_{I}\) holds. Finally, the probability that all \(i\in I\) satisfy \(\mathscr {E}^i_{I}\) simultaneously is at least

$$\begin{aligned} \mathbb {P}[\mathscr {E}^i_{I},\forall i \in I] \ge 1 - 10\exp (-2 c_0^2 |\mathcal {M}_{\mathrm{R}1}|) - 6 |\mathcal {M}_{\mathrm{R}2}| \exp \left( - k \varepsilon _0^2 \right) , \end{aligned}$$
(22)

where we bounded the probability that all i in I satisfy \(\mathscr {D}_i\) with the probability that all i in \(\mathcal {M}_{\mathrm{R}2}\) satisfy \(\mathscr {D}_i\).

It remains to bound the size of I.

Lemma 3

(Size of I). There are constants \(c_{10}, c_{10}'>0\) such that

$$\begin{aligned} \mathbb {P}[|I| \ge c_{10}' |\mathcal {M}_{\mathrm{R}2}|\,|\,\mathscr {E}_{\mathrm {qu}}] \ge 1- 2\exp \left( -2 c_{10}^2 |\mathcal {M}_{\mathrm{R}2}|\right) , \end{aligned}$$
(23)

provided k is greater than a constant depending on \(\varepsilon _0\).

Proof

We show that, under \( \mathscr {E}_{\mathrm {qu}}\), the event \(\mathscr {Q}_i\) has constant probability and we apply Hoeffding’s inequality to |I|, which counts the number of i in \(\mathcal {M}_{\mathrm{R}2}\) satisfying \(\mathscr {Q}_i\).

Observe that, by (15), the events \(\mathscr {D}_i\), \(\{p^i_{xy} \le p^{(7/24)}_{xy}\}\), and \(\mathscr {E}_{\mathrm {qu}}\) (applied in that order) imply

$$\begin{aligned} {\widehat{p}^{i\downarrow }_{xy}} \le p^i_{xy} + \varepsilon _0 \le p^{(7/24)}_{xy} + \varepsilon _0 \le p^{(1/3-\varepsilon _1)}_{xy} - \varepsilon _0 \le \widehat{p}^{(1/3)}_{xy}. \end{aligned}$$

A similar argument shows that, under \( \mathscr {E}_{\mathrm {qu}}\), for \(i \in \mathcal {M}_{\mathrm{R}2}\) the event \( \mathscr {D}_i \cap \mathscr {J}_i, \) implies \(\mathscr {Q}_i\), where we define

$$\begin{aligned} \mathscr {J}_i := \,&\{p^i_{xy} \le p^{(7/24)}_{xy}, p^{(17/24)}_{xz} \le p^i_{xz}, p^{(17/24)}_{yz} \le p^i_{yz}\}\\&\cap \{p^i_{xz} \le p^{(19/24)}_{xz} \text { OR } p^i_{yz} \le p^{(19/24)}_{yz} \}. \end{aligned}$$

This leads to the following lower bound on \(\mathbb {P}[\mathscr {Q}_i \,|\, \mathscr {E}_{\mathrm {qu}}]\):

$$\begin{aligned}&\quad \ge \mathbb {P}[\mathscr {D}_i \cap {\mathscr {J}_i}\,|\, \mathscr {E}_{\mathrm {qu}}]\\&\quad \ge \mathbb {P}[ {\mathscr {J}_i}\,|\, \mathscr {E}_{\mathrm {qu}}] \,\mathbb {P}[\mathscr {D}_i \,|\, {\mathscr {J}_i}\cap \mathscr {E}_{\mathrm {qu}}]\\&\quad = \mathbb {P}[ {\mathscr {J}_i}] \,\mathbb {P}[\mathscr {D}_i \,|\, {\mathscr {J}_i}\cap \mathscr {E}_{\mathrm {qu}}]\\&\quad \ge c_{10}'' \left[ 1 - 6 \exp \left( - k \varepsilon _0^2 \right) \right] , \end{aligned}$$

for some constant \(c_{10}'' > 0\), where we used Lemma 2 to bound the conditional probability of \(\mathscr {D}_i\) on the last line (recalling that Lemma 2 itself is conditioned on the \(p^i_{uw}\)’s). On the third line, we used the fact that \(\mathscr {E}_{\mathrm {qu}}\) depends on \(\mathcal {M}_{\mathrm{R}1}\), and is therefore independent of \(p^i_{xy}, p^i_{xz}, p^i_{yz}\) for \(i \in \mathcal {M}_{\mathrm{R}2}\). The existence of the constant \(c_{10}''\) follows from an argument similar to that leading up to (27) in the Appendix. The expression on the last line is a strictly positive constant provided k is greater than a constant depending on \(\varepsilon _0\).

Finally, applying Hoeffding’s inequality to |I|, we get the result.\(\square \)

Combining (22) and (23) concludes the proof. \(\square \)

Proof

(Proposition 4) Fix \(x,y \in \mathcal {X}\) and let z be the unique element in \(\mathcal {X}- \{x,y\}\). The proof idea is based on Proposition 2. Recall that \(\mathscr {I}\) is the event that the conclusion of Proposition 3 holds and that we use \(\widetilde{\mathbb {P}}\) and \(\widetilde{\mathbb {E}}\) to denote the probability and expectation operators conditioned on \(\mathscr {I}\). Let also \(\mathscr {G}_I\) be the event that the gene trees in I are \(\left\{ G_i \right\} _{i\in I}\). Similarly to the proof of Proposition 2 we note that, conditioned on \(\mathscr {I}\), in all genes in I the coalescences between the lineages of x and z happen in the common ancestral population of x, y and z, irrespective of the species tree topology. The same holds for y and z. That implies that, for \(i\in I\), \(\delta ^i_{xz} = \mu _{rx} + \mu _{rz} + \Gamma ^i_{xz}\), and \(\delta ^i_{yz} = \mu _{ry} + \mu _{rz} + \Gamma ^i_{yz}\), where the \(\Gamma ^i\)s are defined as in the proof of Lemma 1.

Hence

$$\begin{aligned} \widetilde{\mathbb {E}}\left[ \widehat{p}^I_{xz} \,|\, \mathscr {G}_I \right]&= \widetilde{\mathbb {E}}\left[ \frac{1}{\left| I \right| }\sum _{i\in I} \widehat{p}^i_{xz} \,|\, \mathscr {G}_I\right] \nonumber \\&= \frac{1}{\left| I \right| }\sum _{i\in I} p^i_{xz}\nonumber \\&= \frac{3}{4}\left( 1 - \frac{1}{\left| I \right| }\sum _{i\in I}e^{-4 \delta _{xz}^i /3 } \right) \nonumber \\&= \frac{3}{4}\left( 1 - e^{-4 \mu _{rx}/3 - 4 \mu _{rz}/3}\left( \frac{1}{\left| I \right| }\sum _{i\in I}e^{-4 \Gamma ^i_{xz}/3} \right) \right) , \end{aligned}$$

and similarly for the pair (y, z). Letting \(\ell (x) = -\frac{3}{4}\log \left( 1- \frac{4}{3}x\right) \), we get

$$\begin{aligned}&\ell \left( \widetilde{\mathbb {E}}\left[ \widehat{p}_{xz}^I \,|\, \mathscr {G}_I \right] \right) - \ell \left( \widetilde{\mathbb {E}}\left[ \widehat{p}_{yz}^I \,|\, \mathscr {G}_I \right] \right) \nonumber \\&= -\frac{3}{4}\log \left( \frac{1 - 4/3 \widetilde{\mathbb {E}}\left[ \widehat{p}_{xz}^I \,|\, \mathscr {G}_I \right] }{1 - 4/3 \widetilde{\mathbb {E}}\left[ \widehat{p}_{yz}^I \,|\, \mathscr {G}_I \right] } \right) \nonumber \\&= -\frac{3}{4}\log \left( \frac{e^{-4 \mu _{rx}/3-4 \mu _{rz}/3}\left( \frac{1}{\left| I \right| } \sum _{i\in I} e^{-4 \Gamma _{xz}^i /3 }\right) }{e^{-4 \mu _{ry}/3-4 \mu _{rz}/3}\left( \frac{1}{\left| I \right| } \sum _{i\in I} e^{-4 \Gamma _{yz}^i /3 }\right) } \right) \nonumber \\&= -\frac{3}{4}\log \left( e^{-4 \mu _{rx}/3 + 4 \mu _{ry}/3} \right) \nonumber \\&= \Delta _{xy},\nonumber \end{aligned}$$

where in the third equality we used that, conditioned on \(\mathscr {I}\), \(\Gamma ^i_{xz} = \Gamma ^i_{yz}\), for all \(i\in I\). Observe that the computation above relies crucially on the conditioning on \(\mathscr {G}_I\).

It remains to bound the deviation of \( \widehat{\Delta }_{xy} = \ell \left( \widehat{p}_{xz}^I\right) - \ell \left( \widehat{p}_{yz}^I\right) \) around \( \Delta _{xy} = \ell \left( \widetilde{\mathbb {E}}\left[ \widehat{p}_{xz}^I \,|\, \mathscr {G}_I \right] \right) - \ell \left( \widetilde{\mathbb {E}}\left[ \widehat{p}_{yz}^I \,|\, \mathscr {G}_I \right] \right) , \) and take expectations with respect to \(\mathscr {G}_I\). We do this by controlling the error on \(\widehat{p}^I_{xz}\) and \(\widehat{p}^I_{yz}\), conditionally on \(\mathscr {G}_I\). Indeed, observe that the function \(\ell \) satisfies the following Lipschitz property: for \(0 \le x \le y \le M < {3/4}\),

$$\begin{aligned} \left| \ell (x) - \ell (y) \right| = \int _x^y \frac{1}{1-4t/3}\,\mathrm{d}t\le \frac{\left| x-y \right| }{1-4M/3}. \end{aligned}$$
(24)

Hence, to control \(|\widehat{\Delta }_{xy} - \Delta _{xy}|\), it suffices to bound \(\left| \widehat{p}_{uz}^I - \widetilde{\mathbb {E}}\left[ \widehat{p}_{uz}^I \,|\, \mathscr {G}_I \right] \right| \) and \(\max \left\{ \widehat{p}_{uz}^I, \widetilde{\mathbb {E}}\left[ \widehat{p}_{uz}^I \,|\, \mathscr {G}_I \right] \right\} \) for \(u = x,y\).\(\square \)

Lemma 4

(Conditional expectation of \(\widehat{p}_{uz}^I\)). Fix \(u = x\) or y. There is a constant \(c_{12}' \in (0,{3/4})\) small enough such that almost surely

$$\begin{aligned} \widetilde{\mathbb {E}}\left[ \widehat{p}_{uz}^I \,|\, \mathscr {G}_I \right] \le {\frac{3}{4}} - c_{12}'. \end{aligned}$$

Proof

Using \(p_{uz}^i = \widetilde{\mathbb {E}}\left[ \widehat{p}_{uz}^i \,|\, \mathscr {G}_I \right] \) for \(i \in I\), by Proposition 3 (b), we have that

$$\begin{aligned} \widetilde{\mathbb {E}}\left[ \widehat{p}_{uz}^i \,|\, \mathscr {G}_I \right]&= p^i_{uz} = {\frac{3}{4}}\left( 1 - e^{-4\delta _{uz}^i/3} \right) \le {\frac{3}{4}} -c_{12}', \end{aligned}$$

for some constant \(c_{12}' \in (0,{3/4})\). This constant depends on the parameters \(\mu _U\), \(g'\) and g. Hence, the result follows from averaging over i.\(\square \)

Lemma 5

(Conditional deviation of \(\widehat{p}_{uz}^I\)). Fix \(u=x\) or y. For all \(\phi ' > 0\), almost surely

$$\begin{aligned} \widetilde{\mathbb {P}}\left[ \left| {\widehat{p}}_{uz}^I - \widetilde{\mathbb {E}}\left[ \widehat{p}_{uz}^I \,|\, \ \mathscr {G}_I \right] \right| \ge \phi ' \,|\, \mathscr {G}_I \right] \le 2\exp \left( -k|I|(\phi ')^2\right) . \end{aligned}$$

Proof

Observe first that, conditioned on \(\mathscr {G}_I\), the \(k \left| I \right| \) sites that are averaged over in the computation of

(25)

are independent. Secondly, each random variable in (25) is bounded by 1. Therefore, the result follows from Hoeffding’s inequality.\(\square \)

We set \(\phi ' = c_{12}' \phi / 6\), which is \(< c_{12}'\) since \(\phi \le 1\). Combining (24) and Lemmas 4 and 5, we get that conditioned on \(\mathscr {G}_I\)

$$\begin{aligned} \left| \widehat{\Delta }_{xy} - \Delta _{xy} \right|&\le \left| \ell \left( \widehat{p}_{xz}^I\right) - \ell \left( \widetilde{\mathbb {E}}\left[ \widehat{p}_{xz}^I \,|\, \mathscr {G}_I \right] \right) \right| + \left| \ell \left( \widehat{p}_{yz}^I\right) - \ell \left( \widetilde{\mathbb {E}}\left[ \widehat{p}_{yz}^I \,|\, \mathscr {G}_I \right] \right) \right| \\&\le \frac{\left| \widehat{p}_{xz}^I - \widetilde{\mathbb {E}}\left[ \widehat{p}_{xz}^I \,|\, \mathscr {G}_I \right] \right| }{1-4/3\max \left\{ \widehat{p}_{xz}^I, \widetilde{\mathbb {E}}\left[ \widehat{p}_{xz}^I \,|\, \mathscr {G}_I \right] \right\} }\! +\! \frac{\left| \widehat{p}_{yz}^I - \widetilde{\mathbb {E}}\left[ \widehat{p}_{yz}^I \,|\, \mathscr {G}_I \right] \right| }{1-4/3\max \left\{ \widehat{p}_{yz}^I, \widetilde{\mathbb {E}}\left[ \widehat{p}_{yz}^I \,|\, \mathscr {G}_I \right] \right\} }\\&\le 2 \frac{\phi '}{{4/3} (c_{12}'-\phi ')}\\&= {2 \frac{c_{12}' \phi / 6}{4/3 (c_{12}' - c_{12}' \phi / 6)}}\\&= {\frac{1}{4 - (2/3) \phi } \phi }\\&\le \phi /2, \end{aligned}$$

where we used again that \(\phi \le 1\), except with \(\widetilde{\mathbb {P}}\)-probability

$$\begin{aligned} 4\exp \left( -k|I|(\phi ')^2\right) \le 4\exp \left( - \frac{1}{8} (c_{12}')^2 c_{10}' k|\mathcal {M}_{\mathrm{R}2}| \phi ^2\right) = 4\exp \left( - c_{12} k|\mathcal {M}_{\mathrm{R}2}| \phi ^2\right) , \end{aligned}$$

by setting \(c_{12} = \frac{1}{8} (c_{12}')^2 c_{10}'\). Taking expectations with respect to \(\mathscr {G}_I\) gives the result.

6 Concluding remarks

Our main contribution is a novel transformation of sequence data under the MSC-JC that produces a new dataset mimicking a molecular clock. We use this reduction, which is of independent interest, to extend a previous data requirement trade-off for species tree estimation beyond the molecular clock case. Our second contribution is a delicate robustness analysis of the quantile-based triplet test of Mossel and Roch (2017). This represents a step towards the design of practical reconstruction algorithms that avoid gene tree estimation and achieve tight rigorous data requirement guarantees. Further issues must be addressed to achieve this goal. In particular, we have assumed here that the mutation rates and sequence lengths are the same across genes. Relaxing these assumptions is important. Identifiability issues may arise however (Matsen and Steel 2007; Steel 2009).