A Stochastic Tick-Borne Disease Model: Exploring the Probability of Pathogen Persistence

Abstract

We formulate and analyse a stochastic epidemic model for the transmission dynamics of a tick-borne disease in a single population using a continuous-time Markov chain approach. The stochastic model is based on an existing deterministic metapopulation tick-borne disease model. We compare the disease dynamics of the deterministic and stochastic models in order to determine the effect of randomness in tick-borne disease dynamics. The probability of disease extinction and that of a major outbreak are computed and approximated using the multitype Galton–Watson branching process and numerical simulations, respectively. Analytical and numerical results show some significant differences in model predictions between the stochastic and deterministic models. In particular, we find that a disease outbreak is more likely if the disease is introduced by infected deer as opposed to infected ticks. These insights demonstrate the importance of host movement in the expansion of tick-borne diseases into new geographic areas.

1 Introduction

Ticks are blood-feeding external parasites of mammals, birds and reptiles throughout the world. There are approximately 850 species of ticks worldwide and two main families namely Ixodidae (hard ticks) and Argasidae (soft ticks) (Furman and Loomis 1984). Ticks take blood meals by attaching themselves to a suitable host which is found through questing. The host might brush against the questing tick or walk near enough to allow the tick to latch onto or fall onto it. The length of a tick’s life depends on the species and the region in which they live. Ticks live longer in cold climates where they can enter a hibernation stage. Ticks in warm climates typically live less than a year but in general they have a 2-year life cycle. After hatching from an egg, ticks have three distinct life stages: larva, nymph and adult. The number and distribution of blood meals required in each life stage varies between tick species. The preferred hosts are also species-dependent and can be different for each life stage, adding complexity to the study of tick-borne diseases (Gaff and Gross 2013).

Ticks were the first arthropods to be established as vectors of pathogens, and currently they are recognised, along with mosquitoes, as the main vectors of disease agents to humans, domestic animals and wildlife globally (Jongejan and Uilenberg 2004). Tick-borne diseases (TBDs) have had an increasing impact on human health during the past 100 years (Gaff and Gross 2013). Ticks transmit pathogens that cause several diseases in humans, livestock and wildlife, for example, Lyme disease, Colorado tick fever, tick paralysis, human babesiosis, Rocky Mountain spotted fever, cowdriosis, anaplasmosis, human monocytic ehrlichiosis (HME), etc. Some of these diseases are capable of causing death (CDC 2015). The pathogens that cause these diseases include viruses, bacteria and protozoan (Gaff and Gross 2013). Ticks’ hosts have different levels of susceptibility to tick-borne pathogens, and as such the success of a pathogen is highly dependent on the suitability of the hosts on which the tick feeds. The spectrum of TBDs affecting domestic animals, wildlife and humans has increased in recent years and has gained more attention from physicians and veterinarians (Dantas-Torres et al. 2012). Ticks and TBDs are present throughout the world, but they are most prevalent and numerous in tropical and subtropical regions (Masika et al. 1997). For instance, large parts of South Africa are subtropical, and hence, animal husbandry is also severely constrained by tick-borne diseases.

Wildlife species are the main reservoirs of tick-borne pathogens of medical and veterinary concern (Piesman and Eisen 2008). The expanding range of tick-borne pathogens affecting domestic animals, wildlife and humans requires new studies on the epidemiology, diagnosis and ecology of these newly recognised diseases (Dantas-Torres et al. 2012). The vast majority of tick-borne diseases are maintained by wildlife reservoirs, and most cases of human parasitism are related to hard ticks. TBDs maybe difficult to control due to their complex epidemiology that may involve different tick vectors and animal hosts (Dantas-Torres et al. 2012). In this study, we focus on human monocytic ehrlichiosis (HME) that is caused by a rickettsial pathogen called Ehrlichia chaffeensis (Anderson et al. 1993). The lone star tick (Amblyomma americanum), of the Ixodidae family, is suspected to be one of the vectors that transmits pathogens that cause HME (Gaff and Gross 2013). The white-tailed deer (Odocoileus virginianus) is the reservoir host for Ehrlichia chaffeensis. Studies have shown that the lone star tick prefers the white-tailed deer as a blood meal host for all its life stages (Gaff and Gross 2013).

Mathematical models play a significant role in studies about TBDs and other vector-borne diseases. Different tick-borne disease models have been developed to address a variety of problems. Gaff and Gross (2013) formulated a deterministic metapopulation model to provide general methods to evaluate strategies for predicting and managing outbreaks of TBDs in a temporal and spatial context. They found parameter restrictions under which the susceptible and infected densities reach equilibrium. In 2013, Gaff and Nadolny formulated and used an agent-based model, TICKSIM, to identify key parameters that are predominant in driving the invasion of ticks and of tick-borne pathogens. They observed that if an area has competent hosts, an initial population of ten ticks is enough to always establish a new population. Wu et al. (2010) modelled the dynamical temperature influence on the tick Ixodes scapularis population’s influence on the transmission of pathogens that cause tick-borne disease Lyme disease. They found the threshold condition for tick persistence; showed existence, uniqueness and stability of the endemic equilibrium; and concluded that temperature can be used as a determining parameter to predict the distribution and establishment of tick populations and Lyme disease in new regions. Other model structures such as computer simulations using age-structured difference equations (Mount and Haile 1989; Mount et al. 1993, 1997), matrix-based models (Sandberg et al. 1992; Awerbuch and Sandberg 1995), remote sensing and GIS approaches (Randolph 1999; Glass et al. 1995; Das et al. 2002) and hybrid mathematical techniques (Ghosh and Pugliese 2004; Ding 2007) were also developed to address different issues pertaining to ticks and TBDs.

Ticks’ unique life history contributes to the complexity of mathematical studies of tick–host interactions as such models governing these interactions must incorporate stochasticity in the system (Gaff 2011). However, many models that have been used in tick-borne disease dynamics are deterministic, thereby neglecting the possible significance of stochasticity in the transmission of infection. For endemic infections, stochasticity leads to variation in prevalence about the endemic level which can result in disease extinction via endemic fade-out provided the fluctuations are large enough (Lloyd et al. 2007). One major significant difference between deterministic and stochastic epidemic models is that stochastic solutions (sample paths) converge to the disease-free equilibrium although the corresponding deterministic solution converges to an endemic equilibrium (Allen 2008). Unlike deterministic models, stochastic models predict the possibility of disease extinction in finite time and therefore the expected time to disease extinction can be calculated (Allen 2008; Allen and Burgin 2000). In addition, stochastic models capture the uncertainty and variability that is inherent in real-life epidemics due to demographics or the environment which are important when the initial number of infectives is small (Allen and Burgin 2000). Our goal in this study is to formulate and analyse a stochastic epidemic model for the transmission dynamics of a tick-borne disease, HME, in a single population using a continuous-time Markov chain (CTMC) model. The stochastic model is based on an existing deterministic metapopulation model by Gaff and Gross (2013). Their model tracked the host and tick population densities as well as the densities of infected individuals in each population. However, for CTMC models, numbers in each epidemiological class are nonnegative integers and not densities or proportions. Thus, to cater for stochastic transitions and assumptions, we modify the model by Gaff and Gross by re-writing the deterministic model into its equivalent form by using a standard incidence rate for infection terms in both the host and tick populations. The term for recovered hosts is added to the susceptible host class, and we incorporate density-dependent death in all the four classes. We shall then compare the dynamics of the deterministic and stochastic epidemic models in order to understand the effect of stochasticity in tick-borne disease dynamics.

This paper is organised as follows; in Sect. 2, we present a deterministic model which is equivalent to the model by Gaff and Gross (2013). We compute the basic reproduction number, ${\mathcal {R}}_0$, of the deterministic model using the next-generation matrix approach as well as presenting the equilibria of the deterministic model. The stochastic version of the deterministic model and its underlying assumptions necessary for model formulation are presented and discussed in Sect. 3. In Sect. 4, we compute the stochastic threshold for disease extinction or invasion by applying the multitype Galton–Watson branching process. We illustrate our results using numerical simulations in Sect. 5. We conclude with a discussion of the results in Sect. 6 which includes a comparison of the stochastic and deterministic models.

2 The Deterministic Model

2.1 Model Formulation

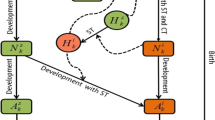
We consider an equivalent form of the model by Gaff and Gross (2013) in a single population. The model investigates transmission dynamics of a tick-borne disease in the case of a single host, a single pathogen and a single life stage. The assumptions in this model are not applicable to every tick species, but our model is suitable for the lone star tick because it prefers the same host (white-tailed deer) for all its life stages, thereby reducing the need to model multiple life stages. The total population sizes for the host and ticks are denoted by N(t) and V(t), respectively. The host (deer) population N(t) is divided into two epidemiological classes, namely susceptible and infected individuals denoted by T(t) and Y(t), respectively, with $N(t)=T(t)+Y(t)$. The tick population V(t) classes are denoted by S(t) and X(t) representing the susceptible and infected ticks, respectively, and $V(t)=S(t)+X(t)$. In both populations, there is no within-population structure except for infection status so that individuals of different locations, ages and sizes are equivalent. The disease is not spread from tick to tick or host to host, and it is not transmitted vertically from one generation to the next in either population. Thus, all offsprings are susceptible at the time of birth. The disease pathogen is assumed to pass from an infected tick to a susceptible host or from an infected host to a susceptible tick only during a blood meal. The ticks do not recover from the disease, while the hosts recover with temporary immunity at a rate $\nu$. Further, we assume that there is no disease-induced death for either population but there is density-dependent death in all classes. The flow diagram of the model is depicted in Fig. 1.

Fig. 1

(Color figure online) Schematic representation of the host–tick epidemic model

The model description is given by a system of nonlinear differential Eq. (1).

$$\begin{aligned} \dfrac{\mathrm{d}T}{\mathrm{d}t}= & {} \beta N-\beta \dfrac{TN}{K}-\hat{A}\dfrac{TX}{N} -bT+\nu Y ,\nonumber \\ \dfrac{\mathrm{d}Y}{\mathrm{d}t}= & {} \hat{A}\dfrac{TX}{N}-\beta \dfrac{YN}{K}-(b+\nu )Y,\nonumber \\ \dfrac{\mathrm{d}S}{\mathrm{d}t}= & {} \hat{\beta }V- \hat{\beta }\dfrac{SV}{MN}-A\dfrac{SY}{N}-\hat{b}S,\nonumber \\ \dfrac{\mathrm{d}X}{\mathrm{d}t}= & {} A\dfrac{SY}{N}-\hat{\beta }\dfrac{XV}{MN}-\hat{b}X. \end{aligned}$$

(1)

The total host and tick population sizes N(t) and V(t) can be determined by $N(t)=T(t)+Y(t)$ and $V(t)=S(t)+X(t)$.

Table 1 Description of parameters in model system (1)

The model parameters are explained in Table 1. The transmission rate from ticks to host and vice versa is $\hat{A}TX/N$ and AYS / N, respectively. Disease transmission in the model is restricted by the number of deer since the transmission rates depend on the proportion of T(t) and Y(t), that is, either T / N or Y / N. The deer have carrying capacity K and an external death rate b which is due to hunting or removal from the area. The growth rate for ticks $\hat{\beta }$ incorporates the actual birth rate, host-finding rate and survival rate. Ticks depend on their hosts for feeding as such the tick population is restricted by a maximum number of ticks per deer M and external death rate $\hat{b}$, which is due to desiccation and acaricide impacts. The second term in all equations of system (1) represents density-dependent death. In the following subsection, we present a brief analysis of model (1).

2.2 Existence and Stability of Model Equilibria

We investigate the existence and stability of equilibrium points of model (1). To do this, we scale the population sizes in terms of the proportions of individuals in each compartment in both populations and define $p=\frac{T}{N}, y=\frac{Y}{N}, s=\frac{S}{V}, x=\frac{X}{V}$ as proportions for individuals in classes T, Y, S and X, respectively. Let $h=\frac{V}{N}$ be the ratio of ticks to hosts which is taken as a constant because ticks have fixed number of blood meals per unit time which is independent of the host population density. Differentiating proportions p, y, s and x with respect to time t and simplifying leads to the scaled system of differential equations

$$\begin{aligned} \dfrac{\mathrm{d}p}{\mathrm{d}t}= & {} \beta -(\hat{A}hx+\beta )p +\nu y,\nonumber \\ \dfrac{\mathrm{d}y}{\mathrm{d}t}= & {} \hat{A}hpx -(\nu +\beta )y,\nonumber \\ \dfrac{\mathrm{d}s}{\mathrm{d}t}= & {} \hat{\beta }-Asy-\hat{\beta }s,\nonumber \\ \dfrac{\mathrm{d}x}{\mathrm{d}t}= & {} Asy-\hat{\beta }x, \end{aligned}$$

(2)

where $p+y=1$ and $s+x=1$.

The basic reproduction number, ${\mathcal {R}}_{0s}$, is defined as the number of secondary infections that one infective would produce in a completely susceptible population over the entire period of infectiousness (Van den Driessche and Watmough 2002; Hethcote 2000; Diekmann et al. 1990). We compute the basic reproduction number for the scaled model (2) using the next-generation matrix approach as described by Van den Driessche and Watmough (2002). The next-generation matrix, ${\mathbb {N}}$, of the infected classes y and x in model (2) is given by

$$\begin{aligned} {\mathbb {N}}=\begin{bmatrix} 0&\frac{\hat{A}h}{\hat{\beta }}\\ \frac{A}{\nu +\beta }&0 \end{bmatrix}, \end{aligned}$$

(3)

and the basic reproduction number ${\mathcal {R}}_{0s}$ is the spectral radius of matrix ${\mathbb {N}}$ (Van den Driessche and Watmough 2002; Diekmann et al. 1990). Thus,

$$\begin{aligned} {\mathcal {R}}_{0s}=\rho ({\mathbb {N}}) =\sqrt{\frac{\hat{A}Ah}{\hat{\beta }(\nu +\beta )}}. \end{aligned}$$

(4)

We reduce system (2) into a two-dimensional system in y and x by eliminating p and s because $p=1-y$ and $s=1-x$ respectively. We obtain

$$\begin{aligned} \dfrac{\mathrm{d}y}{\mathrm{d}t}= & {} \hat{A}h(1-y)x -(\nu +\beta )y,\nonumber \\ \dfrac{\mathrm{d}x}{\mathrm{d}t}= & {} A(1-x)y-\hat{\beta }x. \end{aligned}$$

(5)

All parameters and variables are nonnegative for $t>0$. Thus, system (5) is biologically and mathematically feasible in the domain

$$\begin{aligned} {\mathcal {C}}=\{(y, x) \in \mathbf {R}^2_+;\, 0\le y\le 1,\, 0\le x\le 1 \}. \end{aligned}$$

In addition, existence, uniqueness and continuation of solutions hold in this domain. For any initial conditions in ${\mathcal {C}}$, system (5) has unique solutions which start and remain in ${\mathcal {C}}$ for $t\ge 0$ (Maliyoni et al. 2012). To calculate the equilibrium points of system (5), we equate the derivatives with respect to time to zero and then solve for $y^*$ in terms of  $x^*$. After simplification, this gives

$$\begin{aligned} y^*&=\dfrac{\hat{A}hx^*}{\hat{A}hx^*+(\nu +\beta )}, \end{aligned}$$

(6)

$$\begin{aligned} x^*&=\dfrac{Ay^*}{Ay^*+\hat{\beta }}. \end{aligned}$$

(7)

Substituting (7) into (6) and simplifying yield a quadratic equation

$$\begin{aligned} F_1 (y^{*})^2 + F_2y^*=0, \end{aligned}$$

(8)

where $F_1=\hat{A}Ah+A\nu +A\beta$ and $F_2=\nu \hat{\beta }+\beta \hat{\beta }-\hat{A}Ah$.

From Eq. (8), the first root $y^*=0$ represents the disease-free equilibrium (DFE), $E_0$, while the second root

$$\begin{aligned} y^*=-\dfrac{F_2}{F_1}= \dfrac{\hat{\beta }(\nu +\beta )[{\mathcal {R}}^2_{0s} -1]}{\hat{A}Ah+(\nu +\beta )A} \end{aligned}$$

(9)

represents the endemic equilibrium, $E_1$, which is positive when ${\mathcal {R}}_{0s}>1$.

Thus, model (5) has a DFE, $E_0=(y^*, x^*)=(0, 0)$. When the disease persists in the population, there exists an endemic equilibrium, $E_1=(y^*, x^*)$ where

$$\begin{aligned} y^*= & {} \dfrac{\hat{\beta }(\nu +\beta )[{\mathcal {R}}^2_{0s} -1]}{\hat{A}Ah+(\nu +\beta )A},\nonumber \\ x^*= & {} \dfrac{(\nu +\beta )({\mathcal {R}}^2_{0s} -1)}{(\nu +\beta )[({\mathcal {R}}^2_{0s} -1)+\hat{\beta }]+\hat{\beta }\hat{A}Ah}. \end{aligned}$$

(10)

Applying Theorem 2 in (Van den Driessche and Watmough 2002), we establish the following result:

Theorem 1

The DFE, $E_0$, of model (5) is locally asymptotically stable if ${\mathcal {R}}_{0s}<1$ and unstable if ${\mathcal {R}}_{0s}>1$.

Note that the reproduction number (4) for the scaled model (2) can be reverted to the reproduction number of the original model (1) which is given by

$$\begin{aligned} {\mathcal {R}}_0=\sqrt{\frac{\bar{A}\hat{A}}{(\beta _t +\hat{b})(\beta _d +b+\nu )}}, \end{aligned}$$

(11)

where $\bar{A}=Ah$, $\beta _t=\frac{\hat{\beta }h}{M}$, $\beta _d=\frac{\beta T^*}{K}$ and $T^*$ is the DFE value for the variable T(t). The expression for ${\mathcal {R}}_0$ can also be obtained by applying the next-generation matrix approach to the original model (1).

The tick–deer model (1) is equivalent to the single patch model in (Gaff and Gross 2013), and our analytical results mirror those results. Their study provides a complete discussion of the deterministic single patch model.

3 Stochastic Epidemic Model

Stochastic models incorporate discrete movements of individuals between epidemiological classes and not average rates at which individuals move between classes (Bartlett 1956, 1960). In stochastic epidemic models, numbers in each class are integers and not continuously varying quantities. A significant possibility is that the last infected individual can recover before the disease is transmitted and the infection can only reoccur if it is reintroduced from outside the population (Lloyd et al. 2007). In contrast, most deterministic models have the flaw that infections can fall to very low levels well below the point at which there is only one infected individual only to rise up later (Allen 2008). In addition, the variability introduced in stochastic models may result in dynamics that differ from the predictions made by deterministic models (McCormack and Allen 2005).

3.1 Model Formulation and Properties

We derive the stochastic version of the deterministic model (1) using a CTMC model because time is continuous but the random variables are discrete (Allen 2008, 2010). The model takes into account random effects of individual birth and death processes, that is, demographic variability. We use the same notation for the state variables and parameters as used in the deterministic model (1) in order to simplify the analysis of the CTMC model. Let time be continuous, $t\in [0,\infty )$ and let T(t), Y(t), S(t) and X(t) be discrete random variables for the number of susceptible hosts, infected hosts, susceptible ticks and infected ticks, respectively, with finite state space,

$$\begin{aligned} T(t), Y(t), S(t), X(t) \in \{0, 1, 2, 3,\ldots , G\}, \end{aligned}$$

(12)

where G is a positive integer and represents the maximum size of the population in the finite space (Allen 2010).

For CTMC models, the transition from one state to a new state may occur at any time t. The state transitions and rates for the CTMC model are presented in Table 2.

Table 2 State transitions and rates of occurrence for the CTMC tick-host model

The stochastic process

$$\begin{aligned} \{T(t),\,Y(t),\,S(t),\,X(t):t\in [0,\,\infty )\} \end{aligned}$$

is a multivariate process. As such its joint probability function is given by

$$\begin{aligned} p_{(n,y,s,x)}(t)={\text {Prob}}\{ T(t)=n,\,Y(t)=y,\,S(t)=s,\,X(t)=x\}, \end{aligned}$$

(Allen 2010).

We assume that the stochastic process is homogeneous in time and satisfies the Markov property. The Markov property states that the future state of the process at time ($t+\varDelta t$) depends only on the current state of the process at time t and hence

$$\begin{aligned}&{\text {Prob}}\{[T(t+\varDelta t),Y(t+\varDelta t),S(t+\varDelta t),X(t+\varDelta t)]\,\,\vert \,\,[T(0),Y(0),S(0),X(0)],\\&\quad [T(\varDelta t),Y(\varDelta t),S(\varDelta t),X(\varDelta t)],\ldots , [T(t),Y(t),S(t),X(t)]\}\\&\quad ={\text {Prob}}\{[T(t+\varDelta t),Y(t{+}\varDelta t),S(t{+}\varDelta t),X(t+\varDelta t)]\,\,\vert \,\, [T(t),Y(t),S(t),X(t)]\}. \end{aligned}$$

The time to next event is exponentially distributed due to the Markov assumption (Allen 2010; Lahodny and Allen 2013; Lahodny et al. 2015). We assume that at most one event occurs during the time interval $\varDelta t$. The infinitesimal transition probabilities (ITPs) for the stochastic process from state $k=(n,y,s,x)$ at time t to a new state $k+m=(q, r, i, j)$ at time ($t+\varDelta t$), that is,

$$\begin{aligned} p_{k+m,\,k} (\varDelta t)= & {} \text {Prob}\{\varDelta T(t)=q,\varDelta Y(t)=r,\varDelta S(t)=i,\varDelta X(t)=j\\&\quad \quad \vert T(t)=n,Y(t)=y,S(t)=s,X(t)=x\} , \end{aligned}$$

are defined by

$$\begin{aligned} p_{k+m,\,k} (\varDelta t) = \left\{ \begin{array}{ll} \beta N \varDelta t + o(\varDelta t), &{} m=(1,0,0,0)\\ (\beta N/K + b)n\varDelta t + o(\varDelta t), &{} m=(-1,0,0,0)\\ \hat{A} nx/N \varDelta t+ o(\varDelta t), &{} m=(-1,1,0,0)\\ \nu y \varDelta t+ o(\varDelta t), &{} m=(1,-1,0,0)\\ (\beta N/K + b)y \varDelta t+ o(\varDelta t), &{} m=(0,-1,0,0)\\ \hat{\beta } V \varDelta t+ o(\varDelta t), &{} m=(0,0,1,0)\\ (\hat{\beta }V/MN +\hat{b})s \varDelta t+ o(\varDelta t), &{} m=(0,0,-1,0)\\ Ays/N \varDelta t+ o(\varDelta t), &{} m=(0,0,-1,1)\\ (\hat{\beta }V/MN +\hat{b})x \varDelta t+ o(\varDelta t), &{} m=(0,0,0,-1)\\ 1-C^\ominus \varDelta t + o(\varDelta t), &{} m=(0,0,0,0)\\ o(\varDelta t), &{} \text {otherwise}, \end{array} \right. \end{aligned}$$

(13)

where

$$\begin{aligned} C^\ominus= & {} \beta N + (\beta N/K + b)n+\hat{A} nx/N+\nu y+(\beta N/K + b)y+\hat{\beta } V\\&+(\hat{\beta }V/MN +\hat{b})s +\,\,Ays/N+(\hat{\beta }V/MN +\hat{b})x. \end{aligned}$$

The probability of no change in any of the state variables, $p(\varDelta t) =\pmb {0}$  is  $1-C^\ominus \varDelta t + o(\varDelta t)$. Applying the Markov property to the stochastic process and the ITPs in (13), we can express the state probabilities at time  ($t+\varDelta t$)  in terms of the state probabilities at time  t (Khan et al. 2013). Thus, at time  ($t+\varDelta t$), the state probabilities  $p_{(n,y,s,x)}(t)$  satisfy the following master equation:

$$\begin{aligned}&p_{(n,y,s,x)}(t+\varDelta t) =p_{(n-1,y,s,x)}(t)[\beta N \varDelta t +o(\varDelta t)]\\&\quad +\, p_{(n+1,y,s,x)}(t)[(\beta N/K + b)(n+1) \varDelta t +o(\varDelta t)]\\&\quad +\, p_{(n+1,y-1,s,x)}(t)[\hat{A} (n+1)x/N \varDelta t +o(\varDelta t)]\\&\quad +\, p_{(n-1,y+1,s,x)}(t)[\nu (y+1) \varDelta t +o(\varDelta t)]\\&\quad +\, p_{(n,y+1,s,x)}(t)[(\beta N/K + b)(y+1) \varDelta t +o(\varDelta t)]\\&\quad +\, p_{(n,y,s-1,x)}(t)[ \hat{\beta } V\varDelta t +o(\varDelta t)]\\&\quad +\, p_{(n,y,s+1,x)}(t)[(\hat{\beta }V/MN +\hat{b})(s+1) \varDelta t +o(\varDelta t)]\\&\quad +\, p_{(n,y,s+1,x-1)}(t)[Ay(s+1)/N \varDelta t +o(\varDelta t)]\\&\quad +\, p_{(n,y,s,x+1)}(t)[(\hat{\beta }V/MN +\hat{b})(x+1) \varDelta t +o(\varDelta t)]\\&\quad +\, p_{(n,y,s,x)}(t)[1-C^\ominus \varDelta t +o(\varDelta t)]+o(\varDelta t). \end{aligned}$$

4 Stochastic Threshold for Disease Extinction

In stochastic epidemic theory, predictions about occurrence of disease outbreak and extinction are possible and depend on the number of infectious individuals for each group. If a disease emerges from one infectious group with ${\mathcal {R}}_0>1$ and if i infectives are introduced into a wholly susceptible population, then the probability of a major disease outbreak is approximated by $1-(1/{\mathcal {R}}_0)^i$ while the probability of disease extinction is approximately $(1/{\mathcal {R}}_0)^i$ (Whittle 1955). However, this result does not hold if the infection emanates from multiple infectious groups (Allen 2012). For multiple infectious groups, the stochastic thresholds depend on two factors, namely the number of individuals in each group and the probability of disease extinction for each group. Further, the persistence of an infection into a wholly susceptible population is not guaranteed by having ${\mathcal {R}}_0$ greater than one (Lloyd et al. 2007). Disease extinction is possible during the period immediately following the introduction of an infection when there are few infected individuals. Stochastic models will in this case predict a minor outbreak unlike in deterministic models where a major outbreak may always result. After the introduction of an infection in the early stages of the epidemic process, little depletion of susceptibles will have occurred and so invasion probabilities can be derived using the linear model that arises by assuming that the whole population is susceptible (Bartlett 1964; Ball 1983). These invasion probabilities are often approximated by a multitype Galton–Watson branching process (GWbp) theory (Ball 1983; Ball and Donnelly 1995). In GWbp theory, individuals in the population are categorised into a finite number of types and each individual’s behaviour is independent of the other. An individual of a given type can produce offsprings of possibly all types, and individuals of the same type have the same offspring distribution (Karlin and Taylor 1975).

4.1 The Galton–Watson Branching Process

The GWbp theory is often used to calculate disease invasion and extinction probabilities. The theory addresses questions about extinction and survival in ecology and evolutionary biology (Allen 2012). If information about the number of infections produced by a single infectious deer or a single infectious tick is known, the GWbp theory is capable of approximating the probabilities of ultimate disease extinction and of a major disease outbreak. We first present a general theory for the branching process and then later apply it to our stochastic epidemic model in order to approximate the probability of disease extinction and of a major outbreak.

Definition 1

(Allen 2012) A multitype GWbp $\{\overrightarrow{I}(t)\}_{t=0}^\infty$ is a collection of vector random variables $\overrightarrow{I}(t)$, where each vector consists of k different types, $\overrightarrow{I}(t)=(I_1(t),I_2(t),\ldots , I_k(t))$ and each random variable $I_i(t)$ has k associated offspring random variables for the number of offsprings of type $j = 1, 2,\cdots ,k$ from a parent of type i.

The GWbp theory is applicable to infectious populations only and assumes that susceptible populations are at the DFE (Allen and van den Driessche 2013; Allen and Lahodny 2012; Lahodny and Allen 2013). The multitype branching process is linear near the disease-free equilibrium, it is time-homogeneous, and births and deaths/recovery are independent. Therefore, we can define offspring probability generating functions (pgfs) for the birth and death/recovery of the infectious populations, which are then used to approximate the probability of disease extinction and that of a major outbreak (Lahodny and Allen 2013).

Assuming that infectious individuals of type $i,\, I_i$, give birth (that is, successful disease transmission) to individuals of type $j,\, I_j$, and the number of offspring generated by an individual of type i is independent of the number of offspring generated by either type i or type j, $j\ne i$. Furthermore, infectious individuals of type i have the same offspring pgf. Let $\{Z_{ji}\}_ {j=1}^n$ be defined as the offspring random variables for type $i,\,i=1,2,3,\ldots ,n$ such that $Z_{ji}$ is the number of offspring of type j generated by an infective of type i.

The offspring pgf for infectious populations $I_i$ is defined when there is initially a single infectious individual at the start of an epidemic process, say, $I(0)=1$ and all other types are zero, $I_j(0)=0$. Thus, the offspring pgf $f_i :[0,1]^n \rightarrow [0,1],$ for type i given $I_i(0)=1$ and $I_j(0)=0, j\ne i$, is defined as

$$\begin{aligned} f_i(u_1, \ldots , u_n)= \displaystyle \sum _{k_n =0}^\infty \ldots \sum _{k_1 =0}^\infty {\text {P}}_i(k_1, \ldots , k_n)u_1^{k_1}\cdots u_n^{k_n}, \end{aligned}$$

(14)

where  $\text {P}_i(k_1, \ldots , k_n)={\text {Prob}}\{Z_{1i}=k_1, \ldots , Z_{ni}=k_n\}$ is the probability that one infected individual of type i gives birth to $k_j$ individuals of type j and there is always a fixed point at $f_i(1,1,\ldots ,1)=1$ (Allen 2012; Lahodny and Allen 2013; Allen 2015). $f_i(0,0,\ldots ,0)$ denotes the probability of extinction for $I_i$ given that $I_i(0)=1$ and $I_j(0)=0$ for all other types.

We define the expectation matrix $\pmb {M}=[m_{ji}]$ as an $n\times n$, nonnegative and irreducible matrix where the entry $m_{ji}$ is the expected number of offsprings of individuals of type j produced by an infective individual of type i. The elements of matrix $\pmb {M}$ are calculated from Eq. (14) by differentiating $f_i$ with respect to $u_j$ and then evaluating all the $\pmb {u}$ variables at 1, that is,

$$\begin{aligned} m_{ji}=\left. \dfrac{\partial f_i}{\partial u_j}\right| _{\pmb {u=1}}. \end{aligned}$$

The probability of disease extinction or persistence for the multitype GWbp is determined by the size of the spectral radius of expectation matrix $\pmb {M},\, \rho (\pmb {M})$. Thus, if $\rho (\pmb {M}) \le 1$, then the probability of ultimate disease extinction is one as $t\rightarrow \infty$ but if $\rho (\pmb {M})>1$, then there is a positive probability that the disease may persist (Karlin and Taylor 1975). Following (Allen and van den Driessche 2013; Lahodny and Allen 2013; Allen 2015; Allen and Lahodny 2012), the conditions for the probability of disease extinction or persistence are summarised in the following theorem:

Theorem 2

Let the initial sizes for each type be $I_i(0) = i_i,\, i = 1, 2,\ldots ,k$. Suppose the generating functions $f_i$ for each of the k types are nonlinear functions of $u_j$ with some $f_i(0, 0, \ldots , 0) > 0$. Also, suppose that the expectation matrix $\pmb {M}=[m_{ji}]$ is an $n\times n$ nonnegative and irreducible matrix, and $\rho (\pmb {M})$ is the spectral radius of matrix $\pmb {M}$.

• (i) If $\rho (\pmb {M}) <1\,\, or\,\,\rho (\pmb {M}) =1\,\, (\mathrm{subcritical}\, \mathrm{and} \, \mathrm{critical} \,\mathrm{case}\,\mathrm{respectively})$, then the probability of ultimate extinction is one:

  $$\begin{aligned} \displaystyle \lim _{t\rightarrow \infty } {\text {Prob}} \{\overrightarrow{I}(t)=\overrightarrow{0} \}=1. \end{aligned}$$

• (ii) If $\rho (\pmb {M}) > 1\, (\mathrm{supercritical}\, \mathrm{case})$, then the probability of ultimate disease extinction is less than one:

  $$\begin{aligned} \displaystyle \lim _{t\rightarrow \infty } \mathrm{Prob} \{\overrightarrow{I}(t)=\overrightarrow{0} \}=q_1^{i_1} q_2^{i_2} \ldots q_k^{i_k} < 1, \end{aligned}$$

  where $(q_1, q_2,\ldots ,q_k)$ is the unique fixed point of the k offspring pgf, $f_i(q_1, q_2,\ldots ,q_k) = q_i$ and $0< q_i < 1, i = 1, 2,\ldots , k$. The value of $q_i$ is the probability of disease extinction for infectives of type i and the probability of an outbreak is approximately

  $$\begin{aligned} 1-q_1^{i_1} q_2^{i_2} \ldots q_k^{i_k}. \end{aligned}$$

4.1.1 Application of the Multitype GWbp

In our CTMC model, the disease is spread by individuals of two types: infected deer and infected ticks. During tick feeding, infected ticks may infect susceptible deer or infected deer may infect susceptible ticks, thereby producing infected deer and ticks. Thus, the number of infected individuals in the tick–deer system during the early stages of the epidemic process can be approximated by a two-type GWbp. Let the infected deer be individuals of type 1 and infected ticks be of type 2.

We use the state transitions and rates for the CTMC epidemic model in Table 2 to define the offspring pgfs for the infectious populations Y and X. We assume that $T(0)=T^*$ and $S(0)=S^*$ are sufficiently large and are at the DFE. If initially there is a single infected deer, $Y(0)=1$, and no infected ticks, $X(0)=0$, then we define the offspring pgf for infected deer Y using Eq. (14). During tick feeding, an infected deer can infect a susceptible tick at a rate $\bar{A}$, but the infected deer does not die which results in two infectious individuals, that is, one infected deer and one infected tick, and we obtain $\bar{A} u_1^1 u_2^1=\bar{A} u_1 u_2$. The infected deer may also die or recover before transmitting the disease at a rate $(\beta _d +b+\nu )$ which results in zero infectious ticks and decreases the deer’s infected population by one while the tick population remains unchanged. Therefore, we obtain $(\beta _d +b+\nu )u_1^0 u_2^0=(\beta _d+b+\nu )$. The rates become probabilities when they are divided by the sum of the rate of birth and death or recovery. The probability of birth and of death or recovery is $P_2=\bar{A} u_1 u_2/(\bar{A}+\beta _d +b+\nu )$ and $P_0=(\beta _d +b+\nu )/(\bar{A}+\beta _d +b+\nu )$, respectively. Hence, the offspring pgf for Y is given by

$$\begin{aligned} f_1 (u_1,u_2)=P_0+P_2= \dfrac{\bar{A} u_1 u_2 +(\beta _d+b+\nu )}{\bar{A}+\beta _d+b+\nu }\quad u_1,u_2 \in [0,1]. \end{aligned}$$

(15)

Similarly, the offspring pgf for X given that $Y(0)=0$ and $X(0)=1$ is

$$\begin{aligned} f_2 (u_1,u_2)= \dfrac{\hat{A}u_1 u_2 + (\beta _t+\hat{b})}{\hat{A} + \beta _t+\hat{b}} \quad u_1,u_2 \in [0,1]. \end{aligned}$$

(16)

The elements $m_{ji}$ of the expectation matrix obtained from the offspring pgfs (15) and (16) are given by

$$\begin{aligned} \left. \begin{array}{lll} m_{11}=\left. \dfrac{\partial f_1(u_1,u_2)}{\partial u_1}\right| _{u_1=1, u_2=1}=\dfrac{\bar{A}}{\bar{A}+\beta _d+b+\nu }\\ \ \\ m_{12}=\left. \dfrac{\partial f_2(u_1,u_2)}{\partial u_1}\right| _{u_1=1, u_2=1}=\dfrac{\hat{A}}{\hat{A}+\beta _t+\hat{b}}\\ \ \\ m_{21}=\left. \dfrac{\partial f_1(u_1,u_2)}{\partial u_2}\right| _{u_1=1, u_2=1}=\dfrac{\bar{A}}{\bar{A}+\beta _d+b+\nu }\\ \ \\ m_{22}=\left. \dfrac{\partial f_2(u_1,u_2)}{\partial u_2}\right| _{u_1=1, u_2=1}=\dfrac{\hat{A}}{\hat{A}+\beta _t+\hat{b}} \\ \end{array}\right\} \end{aligned}$$

(17)

which leads to the expectation matrix

$$\begin{aligned} \pmb {M}= \begin{bmatrix} \dfrac{\bar{A}}{\bar{A}+\beta _d+b+\nu }&\dfrac{\hat{A}}{\hat{A}+\beta _t+\hat{b}}\\ \dfrac{\bar{A}}{\bar{A}+\beta _d+b+\nu }&\dfrac{\hat{A}}{\hat{A}+\beta _t+\hat{b}} \end{bmatrix}. \end{aligned}$$

(18)

We apply Theorem 2 to matrix (18). The eigenvalues of matrix $\pmb {M}$ are the roots of the characteristic equation

$$\begin{aligned} \lambda ^2 -(a + b)\lambda = 0, \end{aligned}$$

(19)

where $a=\dfrac{\bar{A}}{\bar{A}+\beta _d+b+\nu }$ and $b=\dfrac{\hat{A}}{\hat{A}+\beta _t+\hat{b}}$.

The spectral radius $\rho (\pmb {M})$ of matrix $\pmb {M}$ obtained from Eq. (19) is given by

$$\begin{aligned} \rho (\pmb {M})= \dfrac{\bar{A}(\hat{A}+\beta _t+\hat{b})+\hat{A}(\bar{A}+\beta _d+b+\nu )}{(\bar{A}+\beta _d+b+\nu )(\hat{A}+\beta _t+\hat{b})}. \end{aligned}$$

(20)

The probability of ultimate disease extinction is one if $\rho (\pmb {M})<1$ in (20) which is the case when

$$\begin{aligned} \bar{A}(\hat{A}+\beta _t+\hat{b})+\hat{A}(\bar{A}+\beta _d+b+\nu )<(\bar{A}+\beta _d+b+\nu )(\hat{A}+\beta _t+\hat{b}). \end{aligned}$$

(21)

Expanding and simplifying inequality (21) leads to

$$\begin{aligned} \bar{A}\hat{A} < (\beta _t +\hat{b})(\beta _d+b+\nu ), \end{aligned}$$

which reduces to

$$\begin{aligned} {\mathcal {R}}_0^2=\dfrac{\bar{A}\hat{A}}{(\beta _t +\hat{b})(\beta _d+b+\nu )}< 1 \Rightarrow {\mathcal {R}}_0<1. \end{aligned}$$

(22)

The result in (22) agrees with the deterministic threshold for disease elimination, and we conclude that the probability of disease extinction in the CTMC model is one if and only if

$$\begin{aligned} \rho (\pmb {M})<1 \Rightarrow {\mathcal {R}}_0 < 1. \end{aligned}$$

(23)

Allen and van den Driessche (2013) established the general relationship that exists between extinction threshold $\rho (M)$ and ${\mathcal {R}}_0$ in stochastic and deterministic epidemic models given by

$$\begin{aligned} {\mathcal {R}}_0< 1, =1,>1\quad {\text {if and only if}}\quad \rho (\pmb {M})< 1, =1, >1, \end{aligned}$$

(24)

It can be easily shown that our model satisfies this relationship. For the supercritical case, $\rho (\pmb {M})>1$ (and ${\mathcal {R}}_0>1$), there is a positive probability of a major disease outbreak occurring. This implies that there exists a fixed point of the offspring pgfs on $(0,1)^2$ which gives the probability of disease extinction of which one minus this probability is the probability of a major outbreak (Lahodny and Allen 2013). The fixed point can be found by setting $f_i(q_1,q_2)=q_i, q_i\in (0,1), \forall i=1,2$. From the pgfs (15) and (16), we compute the fixed point by simultaneously solving the pair of equations $f_1(q_1,q_2)=q_1$ and $f_2(q_1,q_2)=q_2$. The values $q_1$ and $q_2$ are the probabilities of ultimate disease extinction of infected deer and infected ticks respectively. The pair $(q_1,q_2)=(1,1)$ is always a solution but there may exist another fixed point (Allen and Lahodny 2012). Thus, we solve the following system of equations:

$$\begin{aligned}&\dfrac{\bar{A} q_1 q_2 +(\beta _d+b+\nu )}{\bar{A}+\beta _d+b+\nu }=q_1, \end{aligned}$$

(25)

$$\begin{aligned}&\dfrac{\hat{A}q_1 q_2 + (\beta _t+\hat{b})}{\hat{A} + \beta _t+\hat{b}}=q_2 . \end{aligned}$$

(26)

Expressing $q_2$ in terms of $q_1$ in Eq. (26) gives

$$\begin{aligned} q_2=\dfrac{\beta _t + \hat{b}}{\hat{A}(1-q_1)+\beta _t + \hat{b}}. \end{aligned}$$

(27)

Substituting Eq. (27) into Eq. (25) and then simplifying, we obtain the quadratic equation

$$\begin{aligned} H_1 q_1^2 + H_2q_1 + H_3=0, \end{aligned}$$

(28)

where

$$\begin{aligned} H_1= & {} \hat{A}(\bar{A}+\beta _d+b+\nu ), \\ H_2= & {} \bar{A}(\beta _t +\hat{b})-\hat{A}(\beta _d +b+\nu )-(\bar{A}+\beta _d+b+\nu )(\hat{A}+\beta _d+b+\nu ),\\ H_3= & {} (\beta _d+b+\nu )(\hat{A}+\beta _t +\hat{b}). \end{aligned}$$

Solving Eq. (28) for $q_1$ and then substituting its expression in Eq. (27) leads to the following expressions for $q_1$ and $q_2$:

$$\begin{aligned} q_1=\dfrac{(\beta _d + b+\nu )(\hat{A}+\beta _t +\hat{b})}{\hat{A}(\bar{A}+\beta _d+b+\nu )},\\ q_2=\dfrac{(\beta _t +\hat{b})(\bar{A}+\beta _d+b+\nu )}{\bar{A}(\hat{A}+\beta _t +\hat{b})}. \end{aligned}$$

We express  $q_1$  and  $q_2$  in terms of the basic reproduction number (11) to obtain

$$\begin{aligned} q_1= & {} \dfrac{\bar{A}}{\bar{A}+\beta _d+b+\nu }\left( \dfrac{1}{{\mathcal {R}}_0^2}\right) + \dfrac{\beta _d + b+\nu }{\bar{A}+\beta _d+b+\nu },\\ q_2= & {} \dfrac{\hat{A}}{\hat{A}+\beta _t +\hat{b}}\left( \dfrac{1}{{\mathcal {R}}_0^2}\right) + \dfrac{\beta _t +\hat{b}}{\hat{A}+\beta _t +\hat{b}}. \end{aligned}$$

The probability $q_1$ can be interpreted epidemiologically as follows: an infectious deer will either transmit the disease to a susceptible tick with probability $\bar{A}/(\bar{A}+\beta _d+b+\nu )$ or die or recover before transmitting the disease with probability $(\beta _d + b+\nu )/(\bar{A}+\beta _d+b+\nu )$. Likewise, the probability $q_2$ has the following interpretation: an infectious tick will either transmit the disease to a susceptible deer with probability $\hat{A}/(\hat{A}+\beta _t +\hat{b})$ or die before transmitting the disease with probability $(\beta _t +\hat{b})/(\hat{A}+\beta _t +\hat{b})$. If tick to deer transmission is successful, then the probability of transmission from an infectious tick to a susceptible tick is $(1/{\mathcal {R}}_0^2)$.

We compute the probability of disease extinction and of an outbreak using $q_1$ and $q_2$. If $Y(0)=y_0$ and $X(0)=x_0$ are the initial sizes of infected deer and infected ticks, respectively, then the probability of ultimate disease extinction is approximately

$$\begin{aligned} {\mathbb {P}}_0 =q_1^{y_0}q_2^{x_0} = \left[ \dfrac{\bar{A}+(\beta _d+b+\nu ){\mathcal {R}}_0^2}{(\bar{A}+\beta _d+b+\nu ){\mathcal {R}}_0^2}\right] ^{y_0}\left[ \dfrac{\hat{A}+(\beta _t +\hat{b}){\mathcal {R}}_0^2}{(\hat{A}+\beta _t +\hat{b}){\mathcal {R}}_0^2} \right] ^{x_0}. \end{aligned}$$

(29)

Hence, the probability of a major disease outbreak  ${\mathbb {P}}_m$  is given by

$$\begin{aligned} {\mathbb {P}}_m=1-{\mathbb {P}}_0 = 1- \left( \left[ \dfrac{\bar{A}+(\beta _d+b+\nu ){\mathcal {R}}_0^2}{(\bar{A}+\beta _d+b+\nu ){\mathcal {R}}_0^2}\right] ^{y_0}\left[ \dfrac{\hat{A}+(\beta _t +\hat{b}){\mathcal {R}}_0^2}{(\hat{A}+\beta _t +\hat{b}){\mathcal {R}}_0^2} \right] ^{x_0}\right) . \end{aligned}$$

The fixed point in $(0,1)^2$ of the offspring pgfs is $(q_1, q_2)=(0.5495, 0.9881)$. Table 3 summarises the probability of disease extinction ${\mathbb {P}}_0$ for different initial sizes of infected deer and infected ticks which is compared to the numerical approximation based on 5000 sample paths of the stochastic epidemic model. The approximation is accomplished by computing the proportion of sample paths out of 5000 sample paths of the stochastic model in which the number of infected individuals in both the deer and tick populations, $(Y(t)+X(t))$, reaches zero (implying disease extinction) before an outbreak takes off. The numerical approximation of the probabilities of extinction of the stochastic model is in excellent agreement with the calculated probability of disease extinction, ${\mathbb {P}}_0$.

Table 3 Probability of disease extinction ${\mathbb {P}}_0$ computed from the branching process ($q_1^{y_0}q_2^{x_0}$) and numerical approximation based on 5000 sample paths of the stochastic model for different initial sizes of infected deer and infected ticks with parameter values $\beta =0.2,\hat{\beta }=0.75,K=120,M=200,b=0.01,\hat{b}=0.01,\hat{A}=0.02,A=0.07,\nu =0$ and initial conditions $T(0)=114, S(0)=22496, Y(0)=y_0$ and $X(0)=x_0$

Fig. 2

(Color figure online) Probability of disease extinction ${\mathbb {P}}_0$, calculated from the branching process, for varying initial sizes of infected deer and infected ticks on a surface plot and b contour plot. Parameter values are: $\beta =0.2, \hat{\beta }=0.75, K=120,\,M=200, b=0.01, \hat{b}=0.01, \hat{A}=0.02, A=0.07$ and $\nu =0$

The probability of disease extinction is very high if the disease emerges from infected ticks with few ticks initially present at the beginning of the epidemic as shown in Table 3 and Figure 2. However, as the initial number of infected ticks becomes large, there is a high probability of a disease outbreak as illustrated by Fig. 2. The probability of disease extinction is significantly small if a few infected deer introduce the disease and it continues to decrease as the number of infected deer increases. Thus, the disease dynamics in this system at the beginning of the epidemic are being driven by the initial number of infected deer, $y_0$, as shown in Fig. 2 and Table 3. This behaviour is attributed to the situation where a single infected deer is capable of infecting at most 200 susceptible ticks (maximum number of ticks per deer, M) which may in turn infect more non-infected deer, thereby reducing the probability of disease extinction and increasing the probability of a major disease outbreak. In addition, deer are the reservoir host for the pathogens that cause the disease and it takes a long time for them to be disease free; hence, the high probability of an outbreak if the disease is introduced by them. Figure 2 shows the graphs of probability of disease extinction and disease outbreak for varying initial sizes of infected deer and infected ticks. The behaviour in Fig. 2 implies that any policy or intervention to halt the spread of the disease at the beginning of an outbreak must focus more on controlling the infected deer population. If more effort to control the disease is focussed on the infected ticks, then it is very unlikely that the disease can be eliminated.

5 Numerical Simulations

In this section, we illustrate the disease dynamics of the stochastic model using parameter values in Table 1. The multitype branching process assumes that susceptible populations are sufficiently large and are at the disease-free equilibrium. Therefore, initial conditions for susceptible host and ticks population are $T(0)=T^*=114$ and $S(0)=S^*=22496$ respectively. Initial conditions for the infectives are indicated in the caption of each graph.

Figures 3 and 4 show simulation results for sample paths of the stochastic epidemic model graphed with the corresponding deterministic solution for varying initial sizes of infectives of both populations.

Fig. 3

(Color figure online) Two sample paths of the stochastic model and the corresponding deterministic solution (dashed curve). Parameter values are: $\beta =0.2, \hat{\beta }=0.75, K=120, M=200, b=0.01, \hat{b}=0.01, \hat{A}=0.02, A=0.07, \nu =0$ with initial conditions $T(0)=114, S(0)=22496, Y(0)=0$ and $X(0)=1$. The value of the basic reproduction number ${\mathcal {R}}_0=1.3571$ and $\rho (\pmb {M})=1.0117$. The probability of a major outbreak is ${\mathbb {P}}_m=1-{\mathbb {P}}_0=0.0119$

Fig. 4

(Color figure online) Three sample paths of the stochastic epidemic model for the infected individuals in both populations and the corresponding deterministic solution (dashed curve). Parameter values are: $\beta =0.2, \hat{\beta }=0.75, K=120, M=200, b=0.01, \hat{b}=0.01, \hat{A}=0.02, A=0.07, \nu =0$ with initial conditions $T(0)=114, V(0)=22496; Y(0)=1, X(0)=0$ in graphs (a) and (b); $Y(0)=1, X(0)=1$  in graphs (c) and (d) and $Y(0)=2, X(0)=0$ in graphs (e) and (f). Some sample paths in the graphs go to zero rapidly (disease extinction). Disease extinction, ${\mathbb {P}}_0$, occurs with probability 0.5495, 0.5430 and 0.3019 (see Table 3) in graphs (a) and (b), (c) and (d) and (e) and (f), respectively. The value of the basic reproduction number ${\mathcal {R}}_0=1.3571$ and $\rho (\pmb {M})=1.0117$

For the given initial conditions and parameter values, the disease dynamics of the stochastic model are different but not far from those of the deterministic model as shown in Figs. 3 and 4. Some sample paths in Fig. 4 go to zero (that is, the population following these sample paths is quickly absorbed and eventually becomes disease-free) in finite time even though ${\mathcal {R}}_0=1.3571>1$ and $\rho (\pmb {M})=1.0117>1$ while the other sample paths illustrate occurrence of disease outbreak, similar to the prediction by the deterministic model. In other words, even if ${\mathcal {R}}_0>1$ the stochastic model predicts the possibility of disease extinction as shown in Fig. 4 while the deterministic model predicts with certainty that disease outbreak occurs as illustrated in Fig. 3. It is clear from Table 3 that the probability of disease extinction or of disease outbreak depends on the initial sizes of infected deer and infected ticks. Thus, increasing the number of initially infected deer at the beginning of an epidemic increases the probability of a disease outbreak. However, increasing the initial number of infected ticks has very little effect on the probability of a disease outbreak as illustrated in Table 3.

Figure 5 shows the approximate probability distribution of the sizes of infected deer and infected ticks using 5000 sample paths.

Fig. 5

(Color figure online) Approximate probability distribution for the number of infectives with initial conditions and parameter values $\beta =0.2,\hat{\beta }=0.75,K=120,M=200,b=0.01,\,\hat{b}=0.01,\hat{A}=0.02,A=0.07,\nu =0$; $T(0)=114, S(0)=22496, Y(0)=0$ and $X(0)=5$. On the $y-axis$, ${\text {Prob}}=P\times 10^4$ and n is the number of infectives. The basic reproduction number ${\mathcal {R}}_0=1.3571$ and $\rho (\pmb {M})=1.0117$

The graph in Fig. 5a is negatively skewed (skewed to the left) which implies that the impact of the disease is felt with only a few infected deer present. This behaviour is in agreement with the results in Table 3 that there is disease outbreak when a few infected deer are present at the beginning of an epidemic. In Fig. 5b, the graph is positively skewed (skewed to the right) and implies that the effect of infected ticks on the disease is noticeable when there are more infected ticks. In other words, as the number of infected ticks increases, the probability of disease extinction decreases.

6 Discussion

Tick-borne disease outbreaks have become a critical problem to human health, livestock and wildlife in tick-infested areas. We investigated the transmission dynamics of a tick-borne disease (HME) in a single population using a CTMC model. The stochastic model is based on an existing deterministic metapopulation model by Gaff and Gross (2013). The extinction threshold in the deterministic model provides information about disease extinction or occurrence of an outbreak. The corresponding stochastic model not only provides information about disease extinction or outbreak, but also the probability of occurrence of these outcomes. This is obtained by applying the multitype branching process theory when there are a few infectives at the beginning of an epidemic, a scenario deterministic models cannot handle (Allen and van den Driessche 2013).

Our analytical and numerical results showed that the probability of disease extinction, ${\mathbb {P}}_0$, calculated from the multitype branching process theory is in excellent agreement with the numerically approximated probability computed using a proportion of sample paths that go to zero before an outbreak occurs. Further, we derived the stochastic threshold for disease extinction $\rho (\pmb {M})$ and showed the relationship that exists between ${\mathcal {R}}_0$ and $\rho (\pmb {M})$ in terms of disease extinction and outbreak in the deterministic and stochastic models respectively. This relationship as shown in Eq. (24) is significant in the prediction of disease extinction and outbreak (Allen and van den Driessche 2013). It was also shown that both deterministic and stochastic models predict disease extinction when ${\mathcal {R}}_0$ and $\rho (\pmb {M})$ are less than unity, that is, ${\mathcal {R}}_0<1$ and $\rho (\pmb {M})<1$. However, the predictions by these models are different when ${\mathcal {R}}_0>1$ and $\rho (\pmb {M})>1$. In this case, the deterministic model predicts with certainty a stable endemic equilibrium and hence disease outbreak while the stochastic model has two possible outcomes, that is, either there is disease extinction, as shown by some sample paths in Fig. 4, or disease outbreak as shown in Figs. 3c, d and 4. Thus, with stochastic models, it is possible to attain a disease-free status in finite time even when ${\mathcal {R}}_0>1$. In addition, Fig. 4 indicates that initial conditions do not affect the dynamics of the deterministic model while the stochastic model is affected. Thus, the dynamics of the stochastic model are highly dependent on the initial conditions (see Table 3; Fig. 2) and should not be ignored.

The probabilities of disease extinction for different initial sizes of infected deer and infected ticks were approximated analytically and then compared to numerical approximations for disease extinction. Our results indicate that the probability of eliminating the disease in the deer-tick environment is very high if the disease emerges from infected ticks unlike if it emerges from infected deer at the beginning of the epidemic when there are few infectives. As a consequence, we propose that any control measure to reduce or eliminate the disease must target the infected deer population more than the infected tick population. We thus concur with Gaff and Gross’ (2013) suggestion that it is possible to reduce or eliminate the disease in the single population without wiping out the entire tick population. The model results indicate that it is highly unlikely for the establishment of the pathogen if the initial infected population is a single tick, but the probability of establishment is far higher if an infected host is introduced. This study can be extended by incorporating migration of individuals in one or both populations so that we investigate the effect of movement on the disease transmission dynamics of the stochastic model with regard to disease extinction and persistence.