1 Introduction

In recent years, tick-borne diseases, including Lyme disease, tick-borne encephalitis, babesiosis and anaplasmosis, are seriously threatening the health of humans living in the countryside or near woodlands. Lyme disease caused by the bacteria pathogen Borrelia burgdorferi is the most common tick-borne disease in the northern hemisphere (Kurtenbach et al. 2006). In USA, a total of 33,666 confirmed and probable cases of Lyme disease were reported in 2018 and the number of counties with an incidence of \(\ge 10\) confirmed cases per 100,000 persons increased from 324 in 2008 to 415 in 2018 (CDC 2019). In Europe, there may be more than 200,000 cases per year (O’Connell 2010). In Canada, 992 cases of Lyme disease were reported in 2016 compared with 114 in 2009, and the number of endemic areas is gradually increasing with the expanding range of ticks, which was attributed to climate change (Ogden et al. 2009, 2015).

Several tick-borne diseases are mainly transmitted by Ixodes ticks, which are most abundant in forests, woodlands and dense bushes and have three distinct post-egg stages: larva, nymph and adult (Dennis et al. 1998). The development from one stage to the next is processed by taking a blood meal. Immature ticks (larva and nymph) mainly feed on small animals such as rodents and other small vertebrates, and adult ticks prefer large mammals (Ostfeld 2010). Systemic and co-feeding transmissions (also called viraemic and non-viraemic transmissions) are two main routes for the widespread of tick-borne pathogens (Voordouw 2015).

Mathematical models have been formulated to extensively study various aspects of factors involving disease transmission. For example, Rosà et al. (2003) proposed a tick-borne infection dynamics model with two types of host species with differential competence of viraemic transmission, and derived the explicit threshold of disease persistence in terms of viraemic and non-viraemic transmissions. They further explored the impact of the dynamics of tick population and host densities on the persistence of tick-borne disease (Rosà and Pugliese 2007). Zhao (2012) employed a reaction-diffusion model to investigate the global dynamics of Lyme disease based on the reproduction number. Dunn et al. (2013) formulated a mechanistic model of tick-borne pathogens to obtain the specific form of the basic reproduction number, and evaluated the importance of parameters in conformity with the results of global sensitivity analysis. Tick population and tick-borne diseases pose a high level of seasonality, which can also be studied through models with seasonal weather variations. For example, Heffernan, Lou and Wu (2014) developed a tick-borne disease model incorporating climate change and seasonal bird migration and showed that bird migration may amplify the probability of pathogen establishment. Egyed et al. (2012) investigated the seasonal timing of questing by all developmental stages of Ixodes ricinus and its infection rate for the major tick-borne pathogens in Hungary. Hancock et al. (2011) proposed an age-structured tick population model and explored seasonal activity patterns of I. ricinus for disease persistence subject to temperature changes. Wu et al. (2015) and Liu, Lou and Wu (2017) studied age-structured models with time-dependent periodic maturation delays for tick populations. More models can be found in a brief review (Lou and Wu 2017).

It is well known that natural ecological environment has been separated into many patches due to human activities, such as the construction of highways and railways. Although ticks move only in a small spatial range by themselves, their hosts can freely move among various habitats. Hence, it is interesting and important to investigate the role of host movement on the spread of tick-borne diseases among different patches. A popular way to describe species movement in a fragmented environment is using the patch modeling framework. For instance, Arino et al. (2005) described a multi-species SEIR epidemic model with spatial dynamics consisting of s species and n patches. Wang and Mulone (2003) proposed an SIS epidemic model between two patches to describe the threshold of disease transmission. Gao and Ruan (2011) formulated an SIS patch model with variable spread coefficients to explore how human movement could affect the transmission of epidemic diseases in patchy environments. Recent extensive theoretical studies have been performed to study asymptotic profiles of the steady states for patch models, see for example, Allen et al. (2007).

Considering the possible impact of patchy environmental, systemic and co-feeding transmission routes and seasonal variations on disease transmission, in this paper, we are going to formulate a tick-borne disease transmission model. The net reproduction number of tick growth and the basic reproduction number for tick-borne pathogen transmission will be derived. Based on these two reproduction numbers, the global dynamics of tick-borne disease model can be characterized. The impact of host movement, co-feeding and seasonal variations on pathogen transmission will be evaluated through numerical simulations.

2 The model

In this section, we will construct a tick-borne disease model with co-feeding transmission in n-patches. Unlike models for tick-borne pathogen transmission reviewed in Lou and Wu (2017), which normally involve many variables, in particular, variables for infected larvae, infected nymphs and so on to capture the main features of stage-structure and infectivity of ticks, here we stratify tick and host populations by their infection status: susceptible (superscript s) and infected (superscript i). Three stages of tick population in an indexed patch (assume to be the kth patch), larvae (\(L_k\)), nymphs (\(N_k\)) and adults (\(A_k\)) are considered. The host population in the kth patch \(H_k\) is classified into two distinguished subgroups: susceptible hosts \(H_k^s\) and infectious hosts \(H_k^i\).

The model is formulated based on the following assumptions:

  1. (i)

    Since ticks can move by themselves only in a small range and the number of ticks that can be carried from one patch to another through feeding blood is small due to short biting period, we ignore the migration of tick population among n patches.

  2. (ii)

    Although many different species can serve as hosts for ticks and competent reservoirs for the pathogen (Ostfeld 2010), as a simplification, we classify them into the rodent compartment and use the averaged parameters in terms of growth, pathogen transmission and movement. We denote \(m_{ij}(t)\) as the rodent migration rate from jth patch to ith patch.

  3. (iii)

    Since transovarial transmission is low in tick population (Pettersson et al. 2014), we assume that all newly emerging larvae are susceptible and pathogen transmission are mainly due to the blood feeding of infectious rodents and/or co-feeding with infectious ticks on a host.

  4. (iv)

    Systemic transmission of pathogen involves three closely related paths: susceptible larvae feed on infectious rodents and get infection; infectious larvae develop into infected nymphs; infected nymphs transmit tick-borne pathogens to susceptible rodents through biting on them. Since adults mainly take blood feeding on large-size animals different from hosts for immature ticks, we ignore the transmission between infectious adults and non-viraemic deer (Hudson et al. 1995). Susceptible nymphs may also get infected through blood feeding on infectious rodents and develop to infectious adults.

  5. (v)

    A susceptible larva can also be infected by co-feeding transmission when it co-feeds on a rodent with an infected nymph in a proximity over a certain period of time. The co-feeding probability of a susceptible larval tick by infected nymphal ticks depends on the relative location of ticks on the host and the number of infected nymphal ticks. For the simplicity, here we assume that the number of infected ticks is equally distributed on all hosts and do not consider the relative distance between a larva and infected nymphs on one host. To describe the transmission rate through co-feeding transmission, let \(\eta _k\) be the probability that a susceptible larva gets infection from a co-feeding infected nymph through co-feeding transmission. Assume that feeding nymphs are evenly distributed in all rodents. Since the events that each infectious nymph launches co-feeding transmission to a susceptible larva are independent, the probability that a susceptible larva becomes infected through co-feeding with i number of infectious nymphs is \(1-(1-\eta _k)^i\) (see Nah et al. (2019) for more details on the derivation).

  6. (vi)

    Tick-borne pathogen transmission via systemic route from infected hosts and that via co-feeding route from infected nymphs are assumed to be independent events. That is, the incidence of one transmission route does not affect the probability of transmission through the other route.

Fig. 1
figure 1

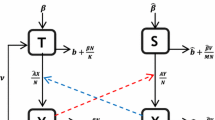
A schematic illustration of tick-borne disease dynamics with both systemic and co-feeding transmissions: the tick population is stratified into immature ticks (larvae and nymphs) and adults. All newly emerging larvae are assumed to be susceptible, may get infected by taking a blood meal from a host where systemic and co-feeding transmission can both occur, and then develop into nymphs. Susceptible nymphs can also get infection through biting an infectious host. Susceptible hosts can get infection through the bites of infected nymphs. ST systematic transmission, CT co-feeding transmission

Full size image

The transmission routes between multi-stage ticks and rodents can be depicted by the diagram in Fig. 1. Please note that in this diagram, \(L_k\) and \(N_k\) should be regarded as questing immature ticks looking for host for blood meal. Based on this diagram, a mechanistic model with less variables can be formulated to capture the complex cycle of systematic transmission of the pathogen between the multi-stage ticks and rodents. Considering the birth, stage-structured growth, pathogen transmission and seasonal variations on tick growth and activity, we can formulate the following model for the indexed kth patch where \({k} = 1, 2, \ldots , {n}\):

$$\begin{aligned} \small { \begin{array}{ll} \frac{d{{L}_{k}(t)}}{d{t}}=&{}\rho _k(t)A_k(t)-{d}^{L}_{k}({t}){L}_{k}({t}) -{\mu }^{L}_{k}(t){L}^{2}_{k}(t)-\beta ^{L}_{k}({t})H_k({t}){L}_{k}({t}),\\ \frac{d{{N}^{s}_{k}(t)}}{d{t}}=&{}{m}^{L}_{k}({t})\beta ^{L}_{k}({t})H_k({t}){L}_{k}({t}) -{d}^{N}_{k}({t}){N}^{s}_{k}({t})-{\mu }^{N}_{k}({t}){N}_{k}({t}){N}^{s}_{k}(t) -\beta ^{N}_{k}({t})H_{k}({t}){N}^{s}_{k}({t})\\ &{}-{\zeta }^{L}_{k}{m}^{L}_{k}({t})\beta ^{L}_{k}({t})H^{i}_{k}({t}){L}_{k}({t}) -{\begin{pmatrix}1-(1-\eta _{k})^{N_k^i(t)/H_k(t)}\end{pmatrix}{m}^{L}_{k}({t}) \beta ^{L}_{k}({t})H^{s}_{k}({t}){L}_{k}(t)}\\ &{}-{\begin{pmatrix}1-(1-\eta _{k})^{N_k^i(t)/H_k(t)}\end{pmatrix}({1}-{\zeta }^{L}_{k}) {m}^{L}_{k}({t})\beta ^{L}_{k}({t})H_{k}^i(t){L}_{k}(t)},\\ \frac{d{{N}^{i}_{k}(t)}}{d{t}}=&{}{\zeta }^{L}_{k}{m}^{L}_{k}({t})\beta ^{L}_{k}({t}) H^{i}_{k}({t}){L}_{k}({t}) +{\begin{pmatrix}1-(1-\eta _{k})^{N_k^i(t)/H_k(t)}\end{pmatrix}{m}^{L}_{k}({t}) \beta ^{L}_{k}({t})H^{s}_{k}({t}){L}_{k}(t)}\\ &{}+{\begin{pmatrix}1-(1-\eta _{k})^{N_k^i(t)/H_k(t)}\end{pmatrix}({1} -{\zeta }^{L}_{k}){m}^{L}_{k}({t})\beta ^{L}_{k}({t})H_{k}^i(t){L}_{k}(t)} -{d}^{N}_{k}({t}){N}^{i}_{k}({t})\\ &{}-{\mu }^{N}_{k}({t}){N}_{k}({t}){N}^{i}_{k}(t)-\beta ^{N}_{k}({t})H_{k}({t}) {N}^{i}_{k}({t}),\\ \frac{d{{A}^{s}_{k}(t)}}{d{t}}=&{}{m}^{N}_{k}({t})\beta ^{N}_{k}({t})H_{k}({t}) {N}^{s}_{k}({t})-{d}^{A}_{k}({t}){A}^{s}_{k}({t})-{\mu }^{A}_{k}({t}){A}_{k} ({t}){A}^{s}_{k}(t)\\ &{}-\beta ^{A}_{k}({t})D_k{A}^{s}_{k}({t})-{\zeta }^{N}_{k}{m}^{N}_{k}({t})\beta ^{N}_{k} ({t})H^{i}_{k}({t}){N}^{s}_{k}({t}),\\ \frac{d{{A}^{i}_{k}(t)}}{d{t}}=&{}{m}^{N}_{k}({t})\beta ^{N}_{k}({t})H_{k}({t}) {N}^{i}_{k}({t})+{\zeta }^{N}_{k}{m}^{N}_{k}({t})\beta ^{N}_{k}({t})H^{i}_{k}({t}) {N}^{s}_{k}({t})-{d}^{A}_{k}{A}^{i}_{k}({t})\\ &{}-{\mu }^{A}_{k}({t}){A}_{k}({t}){A}^{i}_{k}(t)-\beta ^{A}_{k}({t})D_k{A}^{i}_{k} ({t}),\\ \frac{d{H^{s}_{k}(t)}}{d{t}}=&{}{d}^{H}_{k}H_{k}({t})-{d}^{H}_{k}{H}^{s}_{k}({t}) -{\zeta }^{H}_{k}\beta ^{N}_{k}({t})H^{s}_{k}({t}){N}^{i}_{k}({t}) +\sum \limits _{{j=1},{j}\ne {k}}^{n}{m}_{kj}({t})H^{s}_{j}({t})\\ &{}-\sum \limits _{{j=1},{j}\ne {k}}^{n}{m}_{jk}({t})H^{s}_{k}({t}),\\ \frac{d{H^{i}_{k}(t)}}{d{t}}=&{}{\zeta }^{H}_{k}\beta ^{N}_{k}({t})H^{s}_{k} ({t}){N}^{i}_{k}({t})-{d}^{H}_{k}H^{i}_{k}({t})+\sum \limits _{{j}={1},{j}\ne {k}}^{n}{m}_{kj}({t})H^{i}_{j}({t})-\sum \limits _{{j}={1},{j}\ne {k}}^{n}{m}_{jk}({t})H^{i}_{k}({t}),\\ \end{array} } \end{aligned}$$
(1)

where \({L}_{k}({t})\) denotes the density of larvae at time t in kth patch, \({N}^{s}_{k}({t})\) and \({N}^{i}_{k}({t})\) represent the densities of susceptible and infected nymphs at time t in kth patch, respectively, \({A}^{s}_{k}({t})\) and \({A}^{i}_{k}({t})\) are the densities of susceptible and infected adults at time t in kth patch. \(H^{s}_{k}({t})\) and \(H^{i}_{k}({t})\) are the densities of susceptible and infected hosts in kth patch at time t, respectively. Please note that \({\zeta }^{L}_{k}{m}^{L}_{k}({t})\beta ^{L}_{k}({t})H^{i}_{k}({t}){L}_{k}({t})\) represents the incidence term of systemic transmission route, while \(\begin{pmatrix}1-(1-\eta _{k})^{N_k^i(t)/H_k(t)}\end{pmatrix}{m}^{L}_{k}({t})\beta ^{L}_{k}({t})H^{s}_{k}({t}){L}_{k}(t)\) and \(\begin{pmatrix}1-(1-\eta _{k})^{N_k^i(t)/H_k(t)}\end{pmatrix}({1}-{\zeta }^{L}_{k}){m}^{L}_{k}({t})\beta ^{L}_{k}({t})H_{k}^i(t){L}_{k}(t)\) represent the incidence rates of co-feeding transmission routes when larvae biting susceptible and infectious hosts, respectively. To describe the co-feeding incidence through sharing a same host, feeding nymphal ticks are supposed to distribute evenly on all rodents here. Actually, the distributions of ticks on hosts may obey other complicated forms, such as Poisson distribution, which may derive other incidence terms. All parameters are positive and their descriptions are shown in Table 1. Among them, those time-dependent parameters are assumed to be continuous and \(\omega =1\) year-periodic functions.

Table 1 Parameters and descriptions of model (1)
Full size table

In this model, we assume that there is no birth and death during rodents movement, and therefore, the total movement rate between immigration and emigration should satisfy

$$\begin{aligned} \sum \limits _{{k}={1}}^{n}\begin{pmatrix}\sum \limits _{{j}={1},{j} \ne {k}}^{n}{m}_{kj}({t})-\sum \limits _{{j}={1},{j}\ne {k}}^{n}{m}_{jk}({t}) \end{pmatrix} = {0}. \end{aligned}$$

Adding the equations of the host population in kth patch, we have

$$\begin{aligned} \frac{d{{H}_{k}(t)}}{d{t}}=\sum _{{j}={1},{j}\ne {k}}^{n}{m}_{kj}({t}){H}_{j}({t}) -\sum _{{j}={1},{j}\ne {k}}^{n}{m}_{jk}({t}){H}_{k}({t}).\\ \end{aligned}$$

The host population dynamics in n-patches can be described by the following system

$$\begin{aligned} \frac{d{H(t)}}{d{t}}={M(t)}H({t}), \end{aligned}$$
(2)

where \(H({t}) = (H_{1}({t}), H_{2}({t}), \ldots , H_{n}({t}))^{T}\) and the mobility matrix M(t) is represented as

$$\begin{aligned} M(t) = \left[ {\begin{array}{*{20}{c}} -\sum \limits _{j=1,j\ne 1}^{n}{m}_{j1}({t}) &{} {m}_{12}({t}) &{} \dots &{} {m}_{1n}({t}) \\ &{} \ddots &{} \vdots \\ {m}_{n1}({t}) &{} {m}_{n2}({t}) &{} \dots &{} -\sum \limits _{j=1,j\ne n}^{n}{m}_{jn}({t}) \end{array}} \right] . \end{aligned}$$

We assume that the mobility matrix M(t) consisting of the migration rates among various patches is irreducible. That is, the patches as vertices following the matrix M(t) as arcs of a directed digraph are strongly connected under the migration of host population.

By applying Smith (1995, Remark 5.2.1), as discussed in Lou et al. (2014), we can show that for a given nonnegative initial value for system (1), there is a unique solution which remains nonnegative for all \(t\ge 0\).

Let \({S_H}(t)=\sum \limits _{{k}=1}^n H_k(t)\) be the total density of hosts in all patches, and X be a set

$$\begin{aligned} X: =\{(H_1, H_2, \ldots , H_n)\in {\mathbb {R}}_+^n: \sum \limits _{{k}=1}^n H_k>0\}. \end{aligned}$$

Then we get the following result:

Theorem 1

Assume that the mobility matrix M(t) is irreducible in the host migration model (2). Then model (2) has a unique positive \(\omega \)-periodic solution \(H^*(t)=(H_1^*(t), H_2^*(t), \ldots , H_n^*(t))\) which is globally asymptotically stable to any positive solution.

Proof

Clearly, \(S_H(t)\) can be determined by \(\frac{dS_H(t)}{dt}=0\), namely, \(S_H(t)=S_H(0)\) which means total density of host population is a constant for all \(t\ge 0\). Let \(\varPhi (t)\) be the fundamental solution matrix of system (2) satisfying \(\frac{d\varPhi (t)}{dt}=M(t)\varPhi (t)\) and \(\varPhi (0)=I_{n}\) where \(I_n\) is the \(n\times n\) identity matrix. Notice that M(t) has nonnegative off-diagonal elements and its integral on the interval \([0,\omega ]\) is irreducible. Then \(\varPhi (t)\) is not only \(n\omega \)-periodic, but a strongly positive operator (see Smith 1995). Then Aronsson and Kellogg (1978) implies that system (2) has a positive \(n\omega \)-periodic solution \(H^*(t)\) which is globally attractive for any nonzero initial condition \(H(0)\in X\). Therefore, based on the similar argument in Weng and Zhao (2011), this \(n\omega \)-periodic solution is also a globally asymptotically stable \(\omega \)-periodic solution satisfying \(S_H^*(t)=S_H(0)\).

\(\square \)

Based on this result, without loss of generality, we may assume that the rodent population density stabilizes at the periodic positive solution, \(H_k^*(t)\), \(k=1,2,\ldots ,n\).

Considering the population densities of nymphs \(N_k(t)=N_k^s(t)+N_k^i(t)\), adult ticks \(A_k(t)=A_k^s(t)+A_k^i(t)\) and rodents \(H_k(t)=H_k^s(t)+H_k^i(t)\), we have the following system which is equivalent to model (1)

$$\begin{aligned} \small { \begin{aligned} \frac{d{{L}_{k}(t)}}{d{t}}=&\,\rho _{k}({t})A_k(t)-{d}^{L}_{k}({t}){L}_{k}({t}) -{\mu }^{L}_{k}(t){L}^{2}_{k}(t)-\beta ^{L}_{k}({t}){H}_{k}({t}){L}_{k}({t}),\\ \frac{d{{N}_{k}(t)}}{d{t}}=&\,{m}^{L}_{k}({t})\beta ^{L}_{k}({t}){H}_{k}({t}){L}_{k}({t}) -{d}^{N}_{k}({t}){N}_{k}({t})-{\mu }^{N}_{k}({t}){N}^{2}_{k}({t})-\beta ^{N}_{k}({t}) {H}_{k}({t}){N}_{k}({t}),\\ \frac{d{{A}_{k}(t)}}{d{t}}=&\,{m}^{N}_{k}({t})\beta ^{N}_{k}({t}){H}_{k}({t}){N}_{k}({t}) -{d}^{A}_{k}({t}){A}_{k}({t})-{\mu }^{A}_{k}({t}){A}^{2}_{k}({t})-\beta ^{A}_{k}({t}) {D}_{k}{A}_{k}({t}),\\ \frac{d{{N}^{i}_{k}(t)}}{d{t}}=&\,{\zeta }^{L}_{k}{m}^{L}_{k}({t})\beta ^{L}_{k}({t}) H^{i}_{k}({t}){L}_{k}({t})+\begin{pmatrix}1-(1-\eta _{k})^{N_k^i(t)/H_k(t)} \end{pmatrix}\begin{pmatrix}H_{k}({t})-{\zeta }^{L}_{k}H_{k}^i(t)\end{pmatrix}\\&\cdot {m}^{L}_{k}({t})\beta ^{L}_{k}({t}){L}_{k}(t) -{d}^{N}_{k}({t}){N}^{i}_{k}({t})-{\mu }^{N}_{k}({t}){N}_{k}({t}){N}^{i}_{k}(t) -\beta ^{N}_{k}({t})H_{k}({t}){N}^{i}_{k}({t}),\\ \frac{d{H^{i}_{k}(t)}}{d{t}}=&{\zeta }^{H}_{k}\beta ^{N}_{k}({t})(H_k(t) -H^{i}_{k}({t})){N}^{i}_{k}({t})-{d}^{H}_{k}H^{i}_{k}({t})+\sum \limits _{{j}={1},{j} \ne {k}}^{n}{m}_{kj}({t})H^{i}_{j}({t})\\ {}&-\sum \limits _{{j}={1},{j} \ne {k}}^{n}{m}_{jk}({t})H^{i}_{k}({t}) \end{aligned} } \end{aligned}$$
(3)

with \(k=1,2,\ldots ,n\).

3 Tick population dynamics

In this section, we assume all conditions in Theorem 1 holds. Therefore, we may assume \(H_k(t)=H_k^*(t)\), \(k=1,2,\ldots ,n\) to study the long-term behavior of tick population dynamics. From model (3), we have a decoupled system to describe stage-structured tick population growth in kth patch as follows:

$$\begin{aligned} \small { \begin{array}{ll} \frac{d{{L}_{k}(t)}}{d{t}}=\rho _{k}({t})A_k(t)-{d}^{L}_{k}({t}){L}_{k}({t}) -{\mu }^{L}_{k}(t){L}^{2}_{k}(t)-\beta ^{L}_{k}({t}){H}^*_{k}({t}){L}_{k}({t}),\\ \frac{d{{N}_{k}(t)}}{d{t}}={m}^{L}_{k}({t})\beta ^{L}_{k}({t}){H}^*_{k}({t}){L}_{k}({t}) -{d}^{N}_{k}({t}){N}_{k}({t})-{\mu }^{N}_{k}({t}){N}^{2}_{k}({t})-\beta ^{N}_{k}({t}) {H}^*_{k}({t}){N}_{k}({t}),\\ \frac{d{{A}_{k}(t)}}{d{t}}={m}^{N}_{k}({t})\beta ^{N}_{k}({t}){H}^*_{k}({t}){N}_{k}({t}) -{d}^{A}_{k}({t}){A}_{k}({t})-{\mu }^{A}_{k}({t}){A}^{2}_{k}({t})-\beta ^{A}_{k}({t}) {D}_{k}{A}_{k}({t}),\\ \end{array} } \end{aligned}$$
(4)

for \({k} = {{1}, {2}, ..., {n}}\).

Next, we will evaluate the net reproduction number \({\mathcal {R}}_{T}^{(k)}\) for system (4) in the kth patch through the procedure in Wang and Zhao (2008). The linearized system of (4) in the kth patch at the tick-free equilibrium (0, 0, 0) takes the following form

$$\begin{aligned} \begin{array}{ll} \frac{d{{L}_{k}(t)}}{d{t}}=\rho _{k}({t})A_k(t)-({d}^{L}_{k}({t})+\beta ^{L}_{k} ({t}){H}^*_{k}({t})){L}_{k}({t}),\\ \frac{d{{N}_{k}(t)}}{d{t}}={m}^{L}_{k}({t})\beta ^{L}_{k}({t}){H}^*_{k}({t}){L}_{k} ({t})-({d}^{N}_{k}({t})+\beta ^{N}_{k}({t}){H}^*_{k}({t})){N}_{k}({t}),\\ \frac{d{{A}_{k}(t)}}{d{t}}={m}^{N}_{k}({t})\beta ^{N}_{k}({t}){H}^*_{k}({t}){N}_{k} ({t})-({d}^{A}_{k}({t})+\beta ^{A}_{k}({t}){D}_{k}){A}_{k}({t}).\\ \end{array} \end{aligned}$$
(5)

Obviously, system (5) is cooperative. We introduce

$$\begin{aligned} F_T^{(k)}(t)=\begin{pmatrix}0 &{}\quad 0 &{}\quad \rho _k(t)\\ 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0\end{pmatrix}, \end{aligned}$$

and

$$\begin{aligned} V_T^{(k)}(t)=\begin{pmatrix} {d}^{L}_{k}({t})+\beta ^{L}_{k}({t}){H}^*_{k}({t}) &{}\quad 0 &{}\quad 0\\ -{m}^{L}_{k}({t})\beta ^{L}_{k}({t}){H}^*_{k}({t}) &{}\quad {d}^{N}_{k}({t})+\beta ^{N}_{k}({t}){H}^*_{k}({t}) &{}\quad 0\\ 0 &{}\quad -{m}^{N}_{k}({t})\beta ^{N}_{k}({t}){H}^*_{k}({t}) &{}\quad {d}^{A}_{k}({t})+\beta ^{A}_{k}({t}){D}_{k}\end{pmatrix}. \end{aligned}$$

Suppose \({Y_T^{(k)}}(t,s)\), \({t} \ge {s}\), is the evolution operator of the linear periodic system

$$\begin{aligned} \frac{d{y}}{d{t}} = - {V_T^{(k)}}({t}){y}. \end{aligned}$$

That is, for each \({s} \in {\mathbb {R}}\), the evolution operator \({Y_T^{(k)}}(t,s)\) satisfies

$$\begin{aligned} \frac{d{{Y_T^{(k)}}({t},{s})}}{d{t}} = - {V}_T^{(k)}({t}){Y_T^{(k)}}({t},{s}),~~~\forall {t} \ge {s},~~~{Y_T^{(k)}}({s},{s}) = {I}_{3}, \end{aligned}$$

where \({I}_{3}\) is the \({3} \times {3}\) identity matrix.

Let \({C}^T_{\omega }\) be the ordered Banach space of all \(\omega \)-periodic functions from \({\mathbb {R}}^{1}\) to \({\mathbb {R}}^{3}\), equipped with the maximum norm. In the periodic patchy environment, we assume that \(\phi (s) \in {C}^T_{\omega }\) represents the initial distribution of larval, nymphal and adult ticks. Then \({F_T^{(k)}}({s}){\phi }({s})\) represents the distribution of larvae produced by the adult ones who were introduced at time s in the kth patch. Given \({t} \ge {s}\), then \({Y_T^{(k)}}({t},{s}){F_T^{(k)}}({s})\phi ({s})\) denotes the distribution of those ticks who were newly born into the larval tick compartment at time s and remain alive as larval, nymphal or adult ticks at time t in the kth patch. It follows that

$$\begin{aligned} \psi ({t}): = {\int _{-\infty }^{t} {{Y}_T^{(k)}({t},{s}){F_T^{(k)}}({s})\phi ({s})ds} } = {\int _0^\infty {{Y_T^{(k)}}({t},{t-a}){F_T^{(k)}}({t-a})\phi ({t-a})da} } \end{aligned}$$

represents the distribution of accumulative new larval, nymphal and adult ticks at time t produced by all those larval, nymphal and adult ticks \(\phi ({s})\) introduced at previous time to t in the kth patch. Then, we can define a linear operator \({L_T^{(k)}} : {C}^T_{\omega } \rightarrow {C}^T_{\omega }\) by

$$\begin{aligned} ({L_T^{(k)}}{\phi })({t}) = {\int _0^\infty {{Y_T^{(k)}}({t},{t-a}){F_T^{(k)}}({t-a})\phi ({t-a})da} } ,~~~\forall {t} \in {\mathbb {R}},~~~\phi \in {C}^T_{\omega }. \end{aligned}$$

We call \(L_T^{(k)}\) the next population reproduction operator and define the net reproduction number in the kth patch as \({\mathcal {R}}_T^{(k)}:=\rho (L_T^{(k)})\), the spectral radius of \(L_T^{(k)}\). By using theories on monotone dynamical systems (Smith 1995; Zhao 2017) and results in Wang and Zhao (2008), as discussed in Heffernan, Lou and Wu (2014) and Lou et al. (2014), we have the following result on the tick growth in the kth patch.

Lemma 1

The following statements hold

  1. (i)

    If \({\mathcal {R}}_T^{(k)}\le 1\), the tick-free equilibrium of system (4) in the kth patch is globally asymptotically stable.

  2. (ii)

    If \({\mathcal {R}}_T^{(k)}>1\), system (4) in the kth patch has a unique positive \(\omega \)-periodic solution \((L_k^*(t),N_k^*(t),A_k^*(t))\) which is globally asymptotically stable for every nontrivial solution.

Without loss of generality, by relabelling each patch, we assume \({\mathcal {R}}_T^{(i)}\ge {\mathcal {R}}_T^{(j)}\) whenever \(i< j\). It is natural to introduce the maximum and minimum net reproduction number for all patches:

$$\begin{aligned} {\mathcal {R}}_T^{max}=\max \limits _{1\le k\le n} {\mathcal {R}}_T^{(k)} ={\mathcal {R}}_T^{(1)}~~\text {and}~~ {\mathcal {R}}_T^{min}=\min \limits _{1\le k\le n} {\mathcal {R}}_T^{(k)} ={\mathcal {R}}_T^{(n)}. \end{aligned}$$

Then we have the following results.

Theorem 2

  1. (i)

    If \({\mathcal {R}}_T^{max}\le 1\), the tick-free equilibrium of system (4) with n patches is globally asymptotically stable.

  2. (ii)

    If \({\mathcal {R}}_T^{min}>1\), system (4) with n patches has a unique \(\omega \)-periodic solution

    $$\begin{aligned} \begin{aligned}(L^*(t),N^*(t),A^*(t)) =({L}^{*}_{1}({t}), \ldots , {L}^{*}_{n}({t}), {N}^{*}_{1}({t}), \ldots , {N}^{*}_{n}({t}), {A}^{*}_{1}({t}), \ldots , {A}^{*}_{n}({t})),\end{aligned} \end{aligned}$$

    which is globally asymptotically attractive for each positive solution.

  3. (iii)

    If \( {\mathcal {R}}_T^{min}\le 1 <{\mathcal {R}}_T^{max}\), there exists a unique K with \(0< K< n\) such that \({\mathcal {R}}_T^{(K)}> 1\) while \({\mathcal {R}}_T^{(K+1)}\le 1\). Then system (4) with n patches satisfies

    $$\begin{aligned} \lim \limits _{t\rightarrow \infty }(L_{k}(t),N_{k}(t),A_{k}(t))=(L^{*}_{k}(t),N^{*}_{k}(t),A^{*}_{k}(t)) \end{aligned}$$

    and

    $$\begin{aligned} \lim \limits _{t\rightarrow \infty }(L_{p}(t),N_{p}(t),A_{p}(t))=(0,0,0) \end{aligned}$$

    for \(1\le k\le K\) and \(K+1\le p \le n\).

4 The dynamics of disease spread

For a patch with the net reproduction number smaller than or equal to unity, that is \({\mathcal {R}}_T^{(k)}\le 1\), there will be no ticks. For this unfavorable patch for ticks, we have \(\lim \limits _{t\rightarrow \infty }N^{i}_{k}(t)= \lim \limits _{t\rightarrow \infty }N_{k}(t)=0\) as \(N^{i}_{k}(t)\le N_{k}(t)\). To investigate the pathogen persistence in ticks in a habitat, we introduce another reproduction number for the pathogen. For the ease of explanation, we first investigate the scenario \({\mathcal {R}}_T^{min}>1\), and then the other two cases in Theorem 2 will be discussed later. In this case, the tick population in patch k will eventually follow the seasonal pattern \((L^*(t),N^*(t),A^*(t))\). Now consider the following asymptotic system of model (3) for infected compartments:

$$\begin{aligned} \small { \begin{aligned} \frac{d{{N}^{i}_{k}(t)}}{d{t}}=&\,{\zeta }^{L}_{k}{m}^{L}_{k}({t})\beta ^{L}_{k}({t}) H^{i}_{k}({t}){L}_{k}^*({t})+\begin{pmatrix}1-(1-\eta _{k})^{N_k^i(t)/H^*_k(t)} \end{pmatrix}\begin{pmatrix}H^*_{k}({t})-{\zeta }^{L}_{k}H_{k}^i(t)\end{pmatrix}\\&\cdot {m}^{L}_{k}({t})\beta ^{L}_{k}({t}){L}^*_{k}(t) -{d}^{N}_{k}({t}){N}^{i}_{k}({t})-{\mu }^{N}_{k}({t}){N}^*_{k}({t}){N}^{i}_{k}(t) -\beta ^{N}_{k}({t})H^*_{k}({t}){N}^{i}_{k}({t}),\\ \frac{d{H^{i}_{k}(t)}}{d{t}}=&\,{\zeta }^{H}_{k}\beta ^{N}_{k}({t})(H_k^*(t)-H^{i}_{k} ({t})){N}^{i}_{k}({t})-{d}^{H}_{k}H^{i}_{k}({t})+\sum \limits _{{j}={1},{j} \ne {k}}^{n}{m}_{kj}({t})H^{i}_{j}({t})\\ {}&-\sum \limits _{{j}={1},{j} \ne {k}}^{n}{m}_{jk}({t})H^{i}_{k}({t}), \end{aligned} } \end{aligned}$$
(6)

with \(k=1,2,\dots , n\).

We will derive the basic reproduction number based on the next generation operator approach in Wang and Zhao (2008) for system (6) of periodic ordinary differential equations. Let \({u(t)} = ({N}^{i}_{1}(t), \ldots , {N}^{i}_{n}(t), {H}^{i}_{1}(t), \ldots , {H}^{i}_{n}(t))^T\) be the vector which includes all infectious variables for system (6). Linearizing system (6) at the disease-free equilibrium, we produce the following system

$$\begin{aligned} \frac{d{u}}{d{t}} = ({{\widetilde{F}}}({t}) - \widetilde{V}({t})){u}, \end{aligned}$$

where

$$\begin{aligned} \widetilde{F}({t}) = \left[ \begin{array}{cccc} \widetilde{F}_{11}(t) &{} \widetilde{F}_{12}(t) \\ \widetilde{F}_{21}(t) &{} 0 \end{array} \right] , ~~~ \widetilde{V}({t}) = \left[ {\begin{array}{*{20}{c}} \widetilde{V}_{11}(t) &{} 0 \\ 0 &{} \widetilde{V}_{22}(t) \end{array}} \right] , \end{aligned}$$

and \(\small { \begin{aligned} \widetilde{F}_{11}(t)&= \left[ {\begin{array}{*{20}{c}} m_1^L(t)\beta _1^L(t)L_1^*(t)\ln (1-\eta _1)^{-1} &{} \dots &{} 0 \\ &{} \ddots &{} \vdots \\ 0 &{} \dots &{} m_n^L(t)\beta _n^L(t)L_n^*(t)\ln (1-\eta _n)^{-1} \end{array}} \right] ,\\ \widetilde{F}_{12}(t)&= \left[ \begin{array}{cccc} \zeta _1^Lm_1^L(t)\beta _1^L(t)L_1^*(t) &{} \dots &{} 0 \\ &{} \ddots &{} \vdots \\ 0 &{} \dots &{} \zeta _n^Lm_n^L(t)\beta _n^L(t)L_n^*(t) \end{array} \right] ,\\ \widetilde{F}_{21}(t)&= \left[ {\begin{array}{*{20}{c}} {\zeta }^{H}_{1}\beta ^{N}_{1}({t})H_1^*(t) &{} \dots &{} 0 \\ &{} \ddots &{} \vdots \\ 0 &{} \dots &{} {\zeta }^{H}_{n}\beta ^{N}_{n}({t})H_n^*(t) \end{array}} \right] , \end{aligned}}\)

\(\small { \begin{aligned} \widetilde{V}_{11}(t)&= \left[ \begin{array}{cccc} {d}^{N}_{1}({t})+{\mu }^{N}_{1}(t){N}^{*}_{1}(t)+\beta ^{N}_{1}({t}){H}^{*}_{1}({t}) &{} \dots &{} 0 \\ &{} \ddots &{} \vdots \\ 0 &{} \dots &{} {d}^{N}_{n}({t})+{\mu }^{N}_{n}(t){N}^{*}_{n}(t)+\beta ^{N}_{n}({t}){H}^{*}_{n}({t}) \end{array} \right] ,\\ \widetilde{V}_{22}(t)&= \left[ {\begin{array}{*{20}{c}} {d}^{H}_{1}+\sum \limits _{j=1,j\ne 1}^{n}{m}_{j1}({t}) &{} -{m}_{12}({t}) &{} \dots &{} -{m}_{1n}({t}) \\ &{} \ddots &{} \vdots \\ -{m}_{n1}({t}) &{} -{m}_{n2}({t}) &{} \dots &{} {d}^{H}_{n}+\sum \limits _{j=1,j\ne n}^{n}{m}_{jn}({t}) \end{array}} \right] . \end{aligned} } \)

Let \(\widetilde{Y}(t,s)\), \({t} \ge {s}\), be the evolution operator of the linear periodic system

$$\begin{aligned} \frac{d{y}}{d{t}} = - {\widetilde{V}}({t}){y}. \end{aligned}$$

For each \({s} \in {\mathbb {R}}\), the \({2n} \times {2n}\) matrix \(\widetilde{Y}(t,s)\) satisfies

$$\begin{aligned} \frac{d{\widetilde{Y}({t},{s})}}{d{t}} = - {\widetilde{V}}({t}){Y}({t},{s}),~~~\forall {t} \ge {s},~~~\widetilde{Y}({s},{s}) = {I}_{2n}, \end{aligned}$$

where \({I}_{2n}\) is the \({2n} \times {2n}\) identity matrix.

Let \(\widetilde{C}_{\omega }\) be the ordered Banach space of all \(\omega \)-periodic functions from \({\mathbb {R}}^{1}\) to \({\mathbb {R}}^{2n}\) equipped with the maximum norm. In the periodic patchy environment, if \(\psi \in \widetilde{C}_{\omega }\) is the initial distribution of infectious nymphs and hosts, then \({\widetilde{F}}({s}){\psi }({s})\) characterizes the distribution of new infections caused by the initial infectious nymphs and hosts who were introduced at time s. Given \({t} \ge {s}\), then \(\widetilde{Y}({t},{s}){\widetilde{F}}({s})\psi ({s})\) denotes the distribution of infectious nymphs and hosts who were newly infected at time s and remain infectious until time t. It follows that

$$\begin{aligned} {\int _{-\infty }^{t} {\widetilde{Y}({t},{s}){\widetilde{F}}({s})\psi ({s})ds} } = {\int _0^\infty {\widetilde{Y}({t},{t-a}){\widetilde{F}}({t-a})\psi ({t-a})da} } \end{aligned}$$

represents the distribution of accumulative new infectious nymphs and infectious hosts at time t produced by all those infections \(\psi ({s})\) introduced at previous time to t. Then a linear operator \(\widetilde{L} : \widetilde{C}_{\omega } \rightarrow \widetilde{C}_{\omega }\) can be introduced as

$$\begin{aligned} (\widetilde{L}{\psi })({t}) = {\int _0^\infty {{Y}({t},{t-a}){\widetilde{F}}({t-a})\psi ({t-a})da} } ,~~~\forall {t} \in {\mathbb {R}},~~~\psi \in \widetilde{C}_{\omega }. \end{aligned}$$

Then, the basic reproduction number of the periodic system (6) is defined as

$$\begin{aligned} {\mathcal {R}}_{0} := \rho (\widetilde{L}), \end{aligned}$$
(7)

the spectral radius of \(\widetilde{L}\). Based on Theorem 2.2 in Wang and Zhao (2008), the following result holds.

Lemma 2

The zero equilibrium of system (6) is locally asymptotically stable if \({\mathcal {R}}_{0} < {1}\), and unstable if \({\mathcal {R}}_{0} > {1}\).

Based on the observation that \(N_k^{i}({t})\le N_k(t)\) and \(H_k^i(t)<H_k(t)\) while \(\lim \limits _{t\rightarrow \infty } [(N_k(t),H_k(t))-(N^*_k(t),H^*_k(t))]=0\) , we have the boundedness of solutions for (6). Let

$$\begin{aligned} N^{i}({t})=(N_1^i(t),N_2^i(t),\ldots ,N_n^i(t)) \text { and } H^{i}({t})=(H_1^i(t),H_2^i(t),\ldots ,H_n^i(t)), \end{aligned}$$

then \({u}({t}) = ({N}^{i}({t}), {H}^{i}({t}))\). System (6) takes the following form

$$\begin{aligned} \frac{d{u}({t})}{d{t}} = {G}({t}, {u}({t})), \end{aligned}$$

where G(t, u) is the vector field of system (6) and it is periodic in time t. In what follows, we will further show the global dynamics of system (6).

Theorem 3

When \({\mathcal {R}}_T^{min}>1\), we can use the basic reproduction number defined in (7) to characterize the global dynamics of the asymptotic system (6):

  1. (i)

    If \({\mathcal {R}}_{0} \le {1}\), the zero equilibrium of system (6) is globally asymptotically stable.

  2. (ii)

    If \({\mathcal {R}}_{0} > {1}\), system (6) has a unique positive \(\omega \)-periodic solution \(({N}^{i*}({t}),\) \({H}^{i*}({t}))=({N}^{i*}_{1}(t), \ldots , {N}^{i*}_{n}({t}), {H}^{i*}_{1}({t}), \ldots , {H}^{i*}_{n}({t})),\) which is globally asymptotically attractive for each positive solution.

Proof

For every \({u} \ge {0}\) with \({N}^{i}_{k} = {0}\), \({k} = {1}, {2}, \ldots , {n}\), we have

$$\begin{aligned} {G}_{k}({t}, {u})= {\zeta }^{L}_{k}{m}^{L}_{k}({t})\beta ^{L}_{k}({t}){H}^{i}_{k}({t}){L}^{*}_{k}({t})\ge {0}. \end{aligned}$$

For every \({u} \ge {0}\) with \({H}^{i}_{k} = {0}\), \({k} = {1}, {2}, \ldots , {n}\), we have

$$\begin{aligned} {G}_{n+k}({t}, {u}) ={\zeta }^{H}_{k}\beta ^{N}_{k}({t}){H}^{*}_{k}({t}){N}^{i}_{k}({t}) + \sum \limits _{{j}={1},{j}\ne {k}}^{n}{m}_{kj}({t}){H}^{i}_{j}({t})\ge {0}. \end{aligned}$$

Let \(\varGamma (t)\): \((N^i(0),H^i(0))\rightarrow (N^i(t),H^i(t))\) be the solution map of system (6) for \(t>0\). Then \(\varGamma (\omega )\) is the Poincaré map of system (6) and \(\varGamma (t)\) is monotone as the system (6) is cooperative (Smith 1995). Moreover, the irreducibility of \((\int _0^{\omega }M(t)dt)_{n\times n}\) implies that the semiflow of system (6) is strongly monotone.

For every \({t} \ge {0}\) and \(u\gg 0\), \({k} = {1}, {2}, \ldots , {n}\), we can show that G(t, u) is strictly subhomogeneous on \({\mathbb {R}}^{2n}_{+}\). Therefore, Theorem 3.1.2 in Zhao (2017) implies the threshold dynamics in this theorem. \(\square \)

When \({\mathcal {R}}_T^{min}\le 1 <{\mathcal {R}}_T^{max}\), Lemma 1 implies that ticks establish in the first K patches while the remaining \(n-K\) patches are unfavorable patches for ticks. In this scenario, we have an asymptotic system for the model (3)

$$\begin{aligned} \small { \begin{aligned} \frac{d{{N}^{i}_{k}(t)}}{d{t}}=&{\zeta }^{L}_{k}{m}^{L}_{k}({t})\beta ^{L}_{k} ({t})H^{i}_{k}({t}){L}_{k}^*({t})+\begin{pmatrix}1-(1-\eta _{k})^{N_k^i(t)/H^*_k(t)} \end{pmatrix}\begin{pmatrix}H^*_{k}({t})-{\zeta }^{L}_{k}H_{k}^i(t)\end{pmatrix}\\&\cdot {m}^{L}_{k}({t})\beta ^{L}_{k}({t}){L}^*_{k}(t) -{d}^{N}_{k}({t}){N}^{i}_{k}({t})-{\mu }^{N}_{k}({t}){N}^*_{k}({t}){N}^{i}_{k}(t) -\beta ^{N}_{k}({t})H^*_{k}({t}){N}^{i}_{k}({t}),\\ \frac{d{H^{i}_{k}(t)}}{d{t}}=&{\zeta }^{H}_{k}\beta ^{N}_{k}({t})(H_k^*(t) -H^{i}_{k}({t})){N}^{i}_{k}({t})-{d}^{H}_{k}H^{i}_{k}({t})+\sum \limits _{{j}={1},{j} \ne {k}}^{n}{m}_{kj}({t})H^{i}_{j}({t})\\ {}&-\sum \limits _{{j}={1},{j} \ne {k}}^{n}{m}_{jk}({t})H^{i}_{k}({t}), \\ \frac{d{H^{i}_{p}(t)}}{d{t}}=&-{d}^{H}_{p}H^{i}_{p}({t})+\sum \limits _{{j}={1},{j} \ne {k}}^{n}{m}_{kj}({t})H^{i}_{j}({t})-\sum \limits _{{j}={1},{j}\ne {k}}^{n}{m}_{jk} ({t})H^{i}_{p}({t}) \end{aligned} } \end{aligned}$$
(8)

with \({k} = {1, 2, \ldots , K}\) and \(p = {K+1, K+2, \ldots , n}\). Then a similar argument as that for the system (6) can be used to define the basic reproduction number for this asymptotic system (8), denoted as \(\tilde{{\mathcal {R}}}_{0}\) . Furthermore, Lemma 2 and a similar result to Theorem 3 still hold.

Our next target is to characterize the global dynamics of the whole model system (3) by lifting the dynamics of the asymptotic systems with the aid of theories of internally chain transitive sets (Zhao 2017). For easy reference, we combine Lemma 1.2.1 and Theorem 1.2.1 of Zhao (2017) into the following Lemma:

Lemma 3

Let \({\mathcal {F}}:{\mathcal {X}}\rightarrow {\mathcal {X}}\) be a continuous map. Then the omega limit set of any precompact positive orbit is internally chain transitive. Let \({\mathcal {A}}\) be an attractor and \({\mathcal {C}}\) a compact internally chain transitive set for \({\mathcal {F}}\). If \({\mathcal {C}}\cap W^s({\mathcal {A}})\ne \emptyset \), then \({\mathcal {C}}\subset {\mathcal {A}}\). Here, \(W^s({\mathcal {A}})\) is the stable set of \({\mathcal {A}}\).

Based on this Lemma, we can establish the next result.

Theorem 4

The following statements hold

  1. (i)

    if \({\mathcal {R}}_T^{max}\le 1\), the zero equilibrium (0, 0, 0, 0, 0) of system (3) is globally attractive.

  2. (ii)

    When \({\mathcal {R}}_T^{min}> 1\), and furthermore

    1. (a)

      if \({\mathcal {R}}_{0} \le {1}\), the disease-free state \(({L}^{*}({t}), {N}^{*}({t}), {A}^{*}({t}), {0}, {0})\) of system (3) is globally attractive for all nontrivial solutions.

    2. (b)

      if \({\mathcal {R}}_{0} > {1}\), the unique positive \(\omega \)-periodic solution (\({L}^{*}({t})\), \({N}^{*}({t})\), \({A}^{*}({t})\), \({N}^{i*}({t})\), \({H}^{i*}({t})\)) of system (3) is globally attractive for each positive initial condition.

  3. (iii)

    When \({\mathcal {R}}_T^{max}>1\ge {\mathcal {R}}_T^{min}\), then

    $$\begin{aligned} \lim \limits _{t\rightarrow \infty }(N_{k}(t)-N^{*}_{k}(t))=0 \text { and } \lim \limits _{t\rightarrow \infty }N^{i}_{p}(t)= \lim \limits _{t\rightarrow \infty }N_{p}(t)=0 \end{aligned}$$

    for \(1\le k\le K\) and \(K+1\le p \le n\). Furthermore, we have

    1. (a)

      if \({\tilde{{\mathcal {R}}}_{0}} \le {1}\), then \(\lim \limits _{t\rightarrow \infty }N^i_{k}(t)=0\) and \(\lim \limits _{t\rightarrow \infty }H^{i}_{q}(t)=0\) for \(1\le k\le K\) and \(1\le q \le n\);

    2. (b)

      if \({\tilde{{\mathcal {R}}}_{0}} > {1}\), then there are unique positive \(\omega \)-periodic functions \(N^{i*}_{k}(t)\) and \(H^{i*}_{q}(t)\) such that \(\lim \limits _{t\rightarrow \infty }(N^i_{k}(t)-N^{i*}_{k}(t))=0\) and \(\lim \limits _{t\rightarrow \infty }(H^{i}_{q}(t)-H^{i*}_{q}(t))=0\) for \(1\le k\le K\) and \(1\le q \le n\) for all nontrivial solutions.

Proof

Let

$$\begin{aligned} P: P(L(0),N(0),A(0),N^i(0),H^i(0))=(L(\omega ),N(\omega ),A(\omega ),N^i(\omega ), H^i(\omega )) \end{aligned}$$

be the Poincaré map of system (3). Clearly, P is compact. Let \(\varOmega \) be the omega limit set of \(P^n(L(0),N(0),A(0),N^i(0),H^i(0))\). Then Lemma 3 implies that \(\varOmega \) is an internally chain transitive set for P. Next, we will prove three scenarios depending on the net reproduction number \({\mathcal {R}}_T^{min}\) (or \({\mathcal {R}}_T^{max}\)) and the basic reproduction number \({\mathcal {R}}_{0}\).

Scenario (i): \({\mathcal {R}}_T^{max}\le 1\).

From Theorem 2, tick-free equilibrium of system (4) is globally asymptotically stable. Then we have

$$\begin{aligned} \lim _{n\rightarrow \infty }P^n(L(0),N(0),A(0),N^i(0),H^i(0))=\lim _{n\rightarrow \infty }(0,0,0,0,P_5^n(H^i(0))), \end{aligned}$$

where \(P_5\) is the Poincaré solution map of the following system

$$\begin{aligned} \frac{d{H^{i}(t)}}{d{t}}=-{d}^{H}H^{i}({t}). \end{aligned}$$
(9)

That means \(\varOmega =\{(0,0,0,0)\}\times \varOmega _5\) where \(\varOmega _5\) is the omega limit set of \(P_5\). Since 0 is globally asymptotically stable for system (9), it is easy to see that \(\varOmega _5=\{0\}\). It follows that \(\varOmega =\{(0,0,0,0,0)\}\). This completes the proof of the first statement (i).

Scenario (iia): \({\mathcal {R}}_T^{min}> 1\) and \({\mathcal {R}}_{0} \le {1}\).

It can be seen from Theorem 2 that

$$\begin{aligned} \begin{aligned}&\lim _{n\rightarrow \infty }P^n(L(0),N(0),A(0),N^i(0),H^i(0)) \\ {}&=\lim _{n\rightarrow \infty }(L^*(0),N^*(0),A^*(0),{\tilde{P}}^n(N^i(0),H^i(0))),\end{aligned} \end{aligned}$$

where \({{\tilde{P}}}\) is the Poincaré solution map of system (6). It means that there exists the omega limit set \(\varOmega _2\in {\mathbb {R}}^{2n}\) corresponding to \({{\tilde{P}}}\) such that \(\varOmega =\{(L^*(0),N^*(0),A^*(0))\}\times \varOmega _2\). When \({\mathcal {R}}_{0} \le {1}\), Theorem 3 implies that for all \(\left( L(0),N(0),A(0),N^i(0),H^i(0)\right) \), we have

$$\begin{aligned} \begin{aligned}&\lim _{n\rightarrow \infty }\left( {{\tilde{P}}}^n(N^i(0),H^i(0))\right) =(0,0), \end{aligned} \end{aligned}$$

According to Lemma 3, we have \(\varOmega _2=\{(0,0)\}\). Therefore, the disease-free periodic solution \(({L}^{*}({t}), {N}^{*}({t}), {A}^{*}({t}), {0}, {0})\) of system (3) is globally attractive which completes the proof of statement (iia).

Scenario (iib): \({\mathcal {R}}_T^{min}> 1\) and \({\mathcal {R}}_{0} > {1}\).

In this case, the unique positive \(\omega \)-periodic solution \(({N}^{i*}({t}), {H}^{i*}({t}))\) of system (6) is globally asymptotically stable for each positive initial condition \((N^i(0),H^i(0))\in U(0)\) from Theorem 3. Since \(\varOmega _2\) is the omega limit set of Poincaré solution map \({\tilde{P}}\), there are two possible situations

$$\begin{aligned} \varOmega _2=\{({N}^{i*}({0}), {H}^{i*}({0}))\}~~ \text {or}~~ \varOmega _2=\{(0,0)\}. \end{aligned}$$

In what follows, we will rule out the second situation \(\varOmega _2=\{(0,0)\}\).

Assume, by contradiction, that \(\varOmega _2 = \{({0}, {0})\}\) for a positive initial condition \((N^i(0),H^i(0))\in U(0)\). Then, \(\varOmega = \{({L}^{*}({0}), {N}^{*}({0}), {A}^{*}({0}), {0}, {0})\}\) and the solution of system (3) guarantees

$$\begin{aligned} \lim _{t \rightarrow \infty } \begin{pmatrix}\left( {L}({t}), {N}({t}), {A}({t}), {N}^{i}({t}), {H}^{i}({t}))- ({L}^{*}({t}), {N}^{*}({t}), {A}^{*}({t}), {0}, {0}\right) \end{pmatrix}=0. \end{aligned}$$
(10)

Due to \({\mathcal {R}}_{0} > {1}\), there exists a small \(\epsilon > {0}\) such that the spectral radius of the Poincaré map associated with the following linear system

$$\begin{aligned} \begin{aligned} \frac{d{{{\overline{N}}}^{i}_{k}(t)}}{d{t}}=&\,[\ln (1-\eta _k)^{-1}m_k^L(t) \beta _k^L(t)(L_k^*(t)-\epsilon )-d_k^N(t)-\mu _k^N(t)(N_k^*(t)+\epsilon )\\&-\beta _k^N(t)H_k^*(t)]{\overline{N}}_k^i(t)+\zeta _k^Lm_k^L(t)\beta _k^L(t) (L_k^*(t)-\epsilon ){\overline{H}}_k^i(t),\\ \frac{d{{{\overline{H}}}^{i}_{k}(t)}}{d{t}} =&\,\zeta _k^H\beta _k^N(t)H_k^*(t) {\overline{N}}_k^i(t)-(d_k^H+\sum \limits _{{j}={1},{j}\ne {k}}^{n}{m}_{jk}({t})) {\overline{H}}_k^i(t)\\&+\sum \limits _{{j}={1},{j}\ne {k}}^{n}{m}_{kj}({t}){\overline{H}}^{i}_{j}({t})\\ \end{aligned} \end{aligned}$$
(11)

with \({k} = {1}, {2}, \ldots , {n}\) is greater than one. From (10), there exists some \({\tilde{t}}(\epsilon )> {0}\) such that \(L_k(t)>L_k^*(t)-\epsilon \) and \(N_k(t)<N_k^*(t)+\epsilon \) with \(k=1,2\ldots ,n\) for any \({t} > {\tilde{t}}\). For \({t} > {\tilde{t}}\), we have

$$\begin{aligned} \small { \begin{aligned} \frac{d{{N}^{i}_{k}(t)}}{d{t}}\ge&\,\zeta _k^Lm_k^L(t)\beta _k^L(t)H_k^i(t)(L_k^*(t)-\epsilon ) +(1-(1-\eta _k)^{N_k^i(t)/H_k^*(t)})\begin{pmatrix}H^*_k(t)-\zeta _k^LH_k^i(t) \end{pmatrix} \\ {}&\cdot m_k^L(t)\beta _k^L(t)(L_k^*(t)-\epsilon )-d_k^N(t)N_k^i(t) -\mu _k^N(t)(N_k^*(t)+\epsilon )N_k^i(t) \\ {}&-\beta _k^N(t)H_k^*(t)N_k^i(t),\\ \frac{d{{H}^{i}_{k}(t)}}{d{t}}=&\,\zeta _k^H\beta _k^N(t)(H_k^*(t)-H_k^i(t))N_k^i(t) -d_k^HH_k^i(t)+\sum \limits _{{j}={1},{j}\ne {k}}^{n}{m}_{jk}({t}) H_k^i(t)\\&+\sum \limits _{{j}={1},{j}\ne {k}}^{n}{m}_{kj}({t})H^{i}_{j}({t})\\ \end{aligned} } \end{aligned}$$

with \(k=1,2,\ldots ,n\). Since system (11) is unstable, by the similar argument to Theorem 3 (ii), the following comparison system

$$\begin{aligned} \small { \begin{aligned} \frac{d{{{\overline{N}}}^{i}_{k}(t)}}{d{t}}=&\,\zeta _k^Lm_k^L(t)\beta _k^L(t)H_k^i(t) (L_k^*(t)-\epsilon )+(1-(1-\eta _k)^{N_k^i(t)/H_k^*(t)})\begin{pmatrix}H^*_k(t) -\zeta _k^LH_k^i(t)\end{pmatrix}\\&\cdot m_k^L(t)\beta _k^L(t)(L_k^*(t)-\epsilon )-d_k^N(t)N_k^i(t)-\mu _k^N(t)(N_k^*(t) +\epsilon )N_k^i(t) \\ {}&-\beta _k^N(t)H_k^*(t)N_k^i(t),\\ \frac{d{{{\overline{H}}}^{i}_{k}(t)}}{d{t}}=&\,\zeta _k^H\beta _k^N(t)(H_k^*(t) -H_k^i(t))N_k^i(t)-d_k^HH_k^i(t)+\sum \limits _{{j}={1},{j}\ne {k}}^{n}{m}_{jk} ({t}) H_k^i(t)\\&+\sum \limits _{{j}={1},{j}\ne {k}}^{n}{m}_{kj}({t})H^{i}_{j}({t})\\ \end{aligned} } \end{aligned}$$

has a positive periodic solution

$$\begin{aligned} (\overline{N}^{i*}(t),\overline{H}^{i*}(t))=(\overline{N}^{i*}_{1}(t), \ldots , \overline{N}^{i*}_{n}({t}), \overline{H}^{i*}_{1}({t}), \ldots , \overline{H}^{i*}_{n}({t})). \end{aligned}$$

The comparison principle implies that

$$\begin{aligned} \lim _{t\rightarrow \infty } \inf (({N}^{i}(t),{H}^{i}(t))-(\overline{N}^{i*}(t),\overline{H}^{i*}(t)))\ge 0, \end{aligned}$$

which contradicts to (10). Then we must have \(\varOmega _2=\{({N}^{i*}({0}), {H}^{i*}({0}))\}\), namely, \(\varOmega = \{({L}^{*}({0}), {N}^{*}({0}), {A}^{*}({0}), {N}^{i*}({0}), {H}^{i*}({0}))\}\). Therefore, statement (iib) is valid.

The statements for the remaining scenarios (iiia) and (iiib) can be shown by using similar approaches to (iia) and (iib). \(\square \)

5 Numerical illustrations

In this section, we first perform simulations on model (1) with two patches to verify theoretical results and explore the effects of migration on population dynamics.

Some baseline parameter values are taken from existing literatures studying the tick population growth and tick-borne pathogen transmission (Dunn et al. 2013; Nonaka et al. 2010; Rosà et al. 2003; Rosà and Pugliese 2007), which are summarized in Table 1. To distinguish two patches, different parameter values are set to reflect the spatial and temporal heterogeneity in Table 2.

Table 2 Different parameter values of model (1) with 2 patches
Full size table

In Sects. 3 and 4, the net reproduction number and basic reproduction number for periodic ordinary differential systems are defined as the spectral radius of operators on functional spaces. Theoretically, it is hard to derive the analytic expressions for two reproduction numbers. In this section, numerical algorithms based on Theorem 2.1 in Wang and Zhao (2008) are used to compute the reproduction numbers.

Under this scenario, the net reproduction number of tick population \({\mathcal {R}}_T^{min}=1.27\) (\(R_T^{(1)}=1.56\) and \(R_T^{(2)}=1.27\)) which guarantees tick population will be persistent in both patches. Moreover, we can calculate the basic reproduction number of tick-borne diseases for each patch without host migration. Fix the probability of co-feeding transmission \(\eta _k=0.04\). For the first patch, the basic reproduction number is \({\mathcal {R}}_0^{1}=1.88\) which is greater than 1 and then the disease will remain persistent. For the second patch, the basic reproduction number is \({\mathcal {R}}_0^{2}=0.61\) and the disease will die out without migration. The corresponding numerical solutions are depicted in Fig. 2a. However, when the hosts are freely move between two patches with migration proportions \(m_{12}(t)=0.5\) and \(m_{21}(t)=0.2\), the basic reproduction number of tick-borne pathogen becomes to be greater than one, i.e., \({\mathcal {R}}_0=1.43\), indicating theoretically that the tick-borne pathogen persists in both patches, which is confirmed by the Fig. 2b. Therefore, in this scenario, host migration promotes persistence of the pathogen transmission in a wider range. Furthermore, it is interesting to see that the amplitudes of seasonal variations of infectious hosts become larger in the first patch.

Fig. 2
figure 2

Solutions of infected host population in each patch. a Without host migration, \(H_1^i(t)\) (red dashed line) approaches to a periodic solution and \(H_2^i(t)\) (blue solid line) tends to zero in the left panel. b When hosts are allowed to move between patches, infected host populations persist in both patches and approach to periodic solutions

Full size image
Fig. 3
figure 3

The basic reproduction numbers \({\mathcal {R}}_0\) vary with the host migration proportions and probability of co-feeding transmission. a The blue (red) curve shows the basic reproduction number is increasing (decreasing) with respect to \(m_{12}\in [0,1]\) (\(m_{21}\in [0,1]\)) when \(m_{21}=0.2\) (\(m_{12}=0.5\)), \(\eta _k=0.04\) and others parameters are fixed in Tables 1 and 2. b The basic reproduction number is increasing with respect to \(\eta _k\in [0,1]\) when \(m_{12}=0.15\), \(m_{21}=0.6\) and others parameters are fixed in Tables 1 and 2

Full size image
Fig. 4
figure 4

The contour plots of \({\mathcal {R}}_0\) depending on the host migration proportions \({m}_{12}\), \({m}_{21}\) with different co-feeding transmission probability a \(\eta _k=0.04\) and b \(\eta _k=0.25\) when the other parameters are fixed in Tables 1 and 2

Full size image

In order to explore the effects of host migrations, the relationship between the basic reproduction number and host migration proportions (\(m_{12}\) or \(m_{21}\)) is investigated in Fig. 3a. Fixing \(m_{21}=0.2\), we can see from the blue curve that the basic reproduction number \({\mathcal {R}}_{0}\) is increasing with respect to \({m}_{12}\), which indicates that tick-borne pathogen will appear to be endemic in both patches once the host migration proportion from patch 2 to 1 is greater than 0.12. Then we set \(m_{12}=0.5\) and investigate the effect of host migration proportion \(m_{21}\) on the basic reproduction number. The red curve shows that basic reproduction number \({\mathcal {R}}_{0}\) is decreasing with the increasing of host migration proportion \({m}_{21}\). Furthermore, the influence of co-feeding transmission on the basic reproduction number is illustrated in Fig. 3b when \(m_{12}=0.15\) and \(m_{21}=0.6\) are fixed. From Fig. 3b, the increasing of co-feeding transmission makes a greater contribution to the spread of tick-borne diseases.

Figure 4 presents contour plots for the basic reproduction number versus the migration proportions \({m}_{12}, {m}_{21}\in [0,1]\) when the co-feeding transmission probabilities are \(\eta _k=0.04\) and \(\eta _k=0.25\) respectively. It is easy to observe that the isolines move towards bottom right corner and dark red color area appears in the upper left corner while the probability of co-feeding transmission \(\eta _k\) increases from 0.04 to 0.25. From Fig. 4, we can see the parameter region satisfying \({\mathcal {R}}_{0}>1\) becomes larger when co-feeding transmission probability increases.

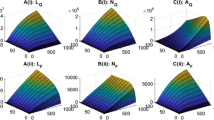
To better understand the effect of host migration on population persistence and disease spreading, simulations for 9 patches, \(P_1\), \(P_2\), \(\ldots \), \(P_9\), are performed. The movement rates are used to reflect the distributions of patches and the relative distances among them. In this case, all movement rates are set to be periodic. To reflect the variety of patches and generality of theoretical frameworks in this study, 9 patches are categorized into three classes: 5 patches (\(P_1\), \(P_2\), \(\ldots \), \(P_5\)) with net reproduction number and basic reproduction number both greater than one, two patches (\(P_6\) and \(P_7\)) with net reproduction number more than one and basic reproduction number less than one, and two patches (\(P_8\) and \(P_9\)) with net reproduction number less than one. Then there is no disease risk in patches \(P_6-P_9\) (see Fig. 5a for the accumulated yearly amounts of infected nymphal ticks). When host species are freely moving among 9 patches with parameters listed in the “Appendix” section, then accumulated yearly amounts of infected nymphal ticks for each patch \(P_i\), \(i=1,2,\ldots , 9\) can be simulated as Fig. 5b (also presented in the “Appendix” section). In this case, the basic reproduction number for the whole 9 patches is \({\mathcal {R}}_0=2.05\) which illustrates that tick-borne pathogen can spread. However for the patches with net reproduction numbers smaller than one (\(P_8\) and \(P_9\)), the pathogen transmission cycle is not established and there is no disease risk. This confirms the results in Theorem 4. Migration can reduce the severity of tick-borne diseases dramatically for some patches, such as the first patch \(P_1\) where the accumulated infected nymph number decreases from \(3.5098\times 10^5\) to \(5.694\times 10^4\). At the same time, migration may facilitate the establishment of pathogen spreading in those patches with the patch basic reproduction number smaller than one, such as \(P_6\) and \(P_7\). However, since the net reproduction numbers for \(P_8\) and \(P_9\) are both less than one, the pathogen fails to persist even with the help of infected host species migration. The last column of Table 6 in the “Appendix” section lists the comparison of accumulated yearly nymphal ticks and infected nymphal ticks across 9 patches for Fig. 5a, b, each corresponding to with and without host migration.

6 Discussions

Habitat fragmentation, a process of slowly altering the layout of the physical environment, may cause serious consequences on population dynamics. The current study evaluates the effect of spatial heterogeneity and host spatial movement on tick-borne pathogen transmission. In addition to that, seasonal factors on tick growth and co-feeding transmission factor are incorporated. Since the range tick population moves by itself is limited, the model is to uncover the relationship between rodent population dispersal and the spread of tick-borne diseases.

Unlike existing models involving many variables, this paper proposes a periodic tick-borne disease model with less variables in the consideration of patchy environment and co-feeding transmissions. Based on feeding behaviour of tick population, ticks are stratified into three stages: larvae, nymphs and adults. In modeling the co-feeding transmission, nymphs are assumed to obey uniform distribution on rodent population at time t. The global dynamics of tick population in each patch can be characterized by the net reproduction numbers \({\mathcal {R}}_T^{max}\) and \({\mathcal {R}}_T^{min}\) which can guarantee that tick-free equilibrium and the unique \(\omega \)-periodic solution with n patches are globally asymptotically stable, respectively. Furthermore, the basic reproduction number of tick-borne disease \({\mathcal {R}}_0\) is derived and the tick-borne disease transmission pattern is investigated through the theory of monotone dynamics systems. Further numerical simulations are performed to show that rodent migration can promote the disease spreading among all patches. This interesting result inspires us that migration restriction of host population among multiple patches can be used to control the breakout and spread of tick-borne disease.

Co-feeding transmission is another key factor which may make a significant contribution to the pathogen spread. The co-feeding transmission incidence term is formulated in the current model (1) by a uniform distribution assumption, that is, feeding nymphal ticks are supposed to distribute evenly on all rodents. The term of the probability of co-feeding transmission in tick-borne disease model (1) should be reformulated with other distribution assumptions, which will be our future work.

Another interesting aspect worthy to be investigated is the host immune response in the tick-borne disease transmission cycle. First, the host immune response to tick infestation may regulate the tick population dynamics. Many interesting models have been formulated to include the effect of this density-dependent aspect, for example, the models in Fan et al. (2015) and Rosà et al. (2003). This would be especially important to evaluate the effect of co-feeding since when many ticks are biting a single host, the density-dependent death of ticks due to host grooming should be counted. The current paper incorporates the host immunity to tick biting by density-dependent death rates of ticks. However, other types of self-regulations due to host immunity may be possible. Moreover, existing studies show that various types of host immune effector mechanisms could be induced by tick-borne pathogen (Torina et al. 2020). It would be interesting to include the effect of host immune response to infection with tick-transmitted pathogen in model formulation. However the modeling process involves careful biological justifications, and possible immunological- and epidemiological- modeling frameworks can be used.