Computational Modelling of Cancer Development and Growth: Modelling at Multiple Scales and Multiscale Modelling

Abstract

In this paper, we present two mathematical models related to different aspects and scales of cancer growth. The first model is a stochastic spatiotemporal model of both a synthetic gene regulatory network (the example of a three-gene repressilator is given) and an actual gene regulatory network, the NF-$\upkappa$B pathway. The second model is a force-based individual-based model of the development of a solid avascular tumour with specific application to tumour cords, i.e. a mass of cancer cells growing around a central blood vessel. In each case, we compare our computational simulation results with experimental data. In the final discussion section, we outline how to take the work forward through the development of a multiscale model focussed at the cell level. This would incorporate key intracellular signalling pathways associated with cancer within each cell (e.g. p53–Mdm2, NF-$\upkappa$B) and through the use of high-performance computing be capable of simulating up to $10^9$ cells, i.e. the tissue scale. In this way, mathematical models at multiple scales would be combined to formulate a multiscale computational model.

1 Introduction

Cancer is a complex, dynamic disease with underlying processes occurring over the full range of biological scales from genetic, through proteomic, cellular, tissue, organ, to organism and sometimes even the whole population level. The first detectable (palpable) symptoms are almost always macroscopic, but differences are also present a priori at the cellular level, and these in turn originate from changes in the individual’s DNA. Perhaps one of the most difficult questions of modern medicine is how to intervene and manipulate the complex system of the patient’s body to affect changes in dynamics, which can bring it back from a state of disease to either full remission or stabilisation. Given the complexity of the system, one way to answer that question should be sought by complementing the traditional clinical methods with mathematical and computational modelling and simulations. However, while developing “good” predictive models one should remember a few important points. The most crucial seems to be the consideration of one of the key features of the disease, if not the key feature, i.e. its multiscale character.

In one of the most influential papers of recent years, summarising our knowledge of the pathogenesis of cancer disease, Hanahan and Weinberg (2000) defined what they termed to be the six hallmarks of cancer: (1) sustaining proliferative signalling; (2) evading growth suppressors; (3) activating invasion and metastasis; (4) enabling replicative immortality; (5) inducing angiogenesis; (6) resisting cell death. More recently, the authors updated this list to also include two emerging hallmarks: (1) deregulating cellular energetics and (2) avoiding immune destruction, and two enabling characteristics: (1) genome instability and mutation and (2) tumour promoting inflammation (Hanahan and Weinberg 2011). These hallmarks are linked with phenotypic traits that give cancer cells an evolutionary advantage over healthy cells. Furthermore they provided a graphical representation of four main circuits regulating the operation of cells: (1) proliferation circuits; (2) viability circuits; (3) motility circuits; and (4) cytostasis and differentiation circuits (see Fig. 1). The failure or dysregulation of these four circuits jointly make up the characteristic phenotype of cancer cells, corresponding directly with four of the hallmarks given above. In contrast to healthy cells that carefully control the production of specific growth and proliferative signals, cancer cells have an abnormal progression through the cell cycle and divide rapidly. Equally they have much higher viability compared to normal cells, resisting cell death, avoiding immune destruction, genome instability and mutation, all of which make cancer cells somewhat “immortal”. The outcome of all of this is the formation of macroscopic structures such as solid tumours that can be observed clinically. Despite enormous progress, full understanding of these processes is difficult because we are dealing with a complex interplay between various subprocesses occurring with different dynamics at different spatial scales.

Fig. 1

Reprinted from Hanahan and Weinberg (2011), Copyright (2011), with permission from Elsevier

Key intracellular signalling pathways and the cell functions they are connected with, illustrating the connection between the intracellular scale and the cellular scale.

One of the most dangerous properties of malignant tumours is their ability to invade surrounding tissues and to metastasise. The invasion or infiltration of surrounding tissue by cancer cells can impair the tissue or organ function. However, a more dangerous aspect of invasion is the infiltration of blood and lymph vessels. When cancer cells penetrate the vessel lumen, they may migrate with blood or lymphatic fluid to distant sites in the body to form new tumours, i.e. metastases. It is worth mentioning that angiogenesis also contributes; through the formation of new blood vessels within the tumour, it facilitates the migration of tumour cells. Metastasis of cancer makes patient treatment very difficult. It prevents the effective resection of the primary tumour, and new outbreaks cause recurrence of the disease. There are many mechanisms that enable cancer cell invasion and metastasis, associated with the motility circuit. For example, the frequently occurring over-expression of genes encoding extracellular matrix-degrading enzymes such as matrix metalloproteinases (MMPs) that break down the extracellular matrix surrounding tumour cells and thus facilitate invasion. However, perhaps the most characteristic change is the loss of the functionality of the protein E-cadherin, which is the main molecule responsible for binding between epithelial cells.

While it is clear that there are many different, interconnected temporal and spatial scales that are important during the development of any tumour, within these there are three clearly demarcated “fundamental scales” linked to each other that, when considered together, provide a deeper understanding of the complex phenomenon that is cancer: the intracellular scale, the cellular scale and the tissue scale. At the level of intracellular processes, we must include within the description complicated but essential phenomena such as signal transduction cascades, gene regulatory networks and cell cycle regulation. Doing so aids our understanding of the differences at the intracellular level between normal and transformed cells and therefore improves the efficiency of anti-cancer cell-cycle-dependent drugs. Another challenge while modelling intracellular processes is to understand how the three-dimensional structure of DNA and chromatin affects gene expression within signalling pathways crucial for disease development. Although it is known that cancer is most often caused by the accumulation of mutations in genes involved in cell cycle regulation and apoptosis, another important issue is how disease progression is influenced by structural or epigenetic changes within the cell nucleus.

At the level of cellular colonies and tissue, there are two main approaches towards modelling complex biological processes like cancer: continuum and discrete. Continuum methods, which are derived from principles of continuum mechanics, have proved to be very useful in modelling phenomena at the tissue scale such as solid tumour growth. However, one of the main drawbacks of continuum modelling is the difficulty in representing individual cell properties. Including these and intracellular processes in multiscale phenomena such as cancer is becoming more and more important as experimental data across multiple scales become available. Alternative approaches rely on an individual-based description of single cells. The main advantage of such methods is related to the relative simplicity of incorporating detailed biological processes into dynamics and development of cell populations and tissue. The main disadvantage is the computational cost which increases rapidly with the number of simulated cells. However, the problem of high computational complexity can be addressed by selecting appropriate algorithms and by efficient implementation on high-performance computing (HPC) systems.

Further milestones related to cancer modelling will be adapting the models for specific cancer types and specific patients. The latter means not only the acquisition of biochemical parameters but also the acquisition of medical imaging data for individual patients. This will be a definite step towards personalised medicine, which has the potential to completely reform our approach to the patient and treatment. Already today imaging studies are of great importance in diagnosis and planning surgical procedures. However, especially for treatment of non-resectable tumours, such imaging studies could also be important in selecting the appropriate treatment or monitoring the disease dynamics.

In this paper, we intend to promote two specific avenues of cancer modelling, which consider processes at different scales. In Sect. 2, we discuss the modelling of intracellular dynamics, specifically gene regulatory networks (GRNs), using a spatial stochastic approach. Firstly, we apply this approach to so-called synthetic GRNs: repressilators, and explore the role of molecular movement in such systems. Secondly, we apply this approach to the NF-$\upkappa$B pathway, which is important in diseases such as cancer and the inflammatory response. In Sect. 3, we focus on the cell scale, in particular investigating cell–cell/cell–matrix dynamics using a force-based model. Specifically, we apply this to modelling avascular tumour cords around blood vessels. In Sect. 4, we remark on the importance of these two modelling approaches individually and discuss how coupling these techniques together to form a multiscale framework offers a new horizon for cancer modelling. In particular using high-performance computing (HPC), it would be possible to combine these two techniques while at the same time modelling $10^6$–$10^9$ cells, thereby enabling one to model at the tissue scale.

2 Intracellular Dynamics: GRNs

At the heart of cellular function and communication lie segments of DNA (genes) and their associated gene regulatory networks (GRNs). A GRN can be defined as a collection of genes in a cell which interact with each other indirectly through their RNA and protein products. GRNs are vital to intracellular signal transduction and indirectly control many important cellular functions such as cell division, apoptosis and adhesion. One specific class of GRN involves proteins called transcription factors, which alter the transcription rate of genes in response to intra- or extracellular cues. Transcription factors may reduce or increase the transcription rate of a given gene, respectively, inhibiting or promoting its production. If the inhibition (or promotion) is directed towards the transcription factor’s own gene, either directly or indirectly, there is negative (or positive) feedback. Negative feedback loops are an important component of many gene networks and are found within a wide range of biological processes, e.g. inflammation, meiosis, apoptosis and the heat shock response (Lahav et al. 2004). Mechanically speaking, systems that contain negative feedback should (and in fact are known to) exhibit oscillations in the levels of the molecules involved. Furthermore, in many biological processes, it is the oscillatory expression that is of particular importance.

Mathematical modelling of GRNs began with the papers of Goodwin (1965) and Griffith (1968), in which a negative feedback model for a simple, single mRNA-protein feedback system was proposed. However, while GRNs are known to exhibit periodic fluctuations in mRNA and protein concentrations (e.g. the results for the Hes1 system, cf. Hirata et al. 2002), these early models, which were restricted to purely temporal ordinary differential equations (ODEs), could not exhibit oscillatory behaviour. Since the late 1990s, there has been interest in the study of delay-differential equation models for GRNs (e.g. Smolen et al. 1999, 2001, 2002; Tiana et al. 2002; Jensen et al. 2003; Lewis 2003; Monk 2003; Bernard et al. 2006), following on from Mackey and Glass (1977) who introduced the idea of incorporating delays into differential equations two decades earlier. The inclusion of a delay in ODE models of GRNs (e.g. the Hes1 system, the p53–Mdm2 system and the NF-$\upkappa$B system) has been shown to produce the required oscillatory behaviour (e.g. Tiana et al. 2002; Jensen et al. 2003; Lewis 2003; Monk 2003; Bernard et al. 2006).

An alternate approach has been to model GRNs with reaction–diffusion partial differential equations (PDEs) rather than ODEs, to incorporate spatial aspects. The first such spatial models (for theoretical intracellular systems) were proposed in the 1970s by Glass and co-workers (Glass and Kauffman 1970; Shymko and Glass 1974) and similarly in the 1980s by Mahaffy and co-workers (Busenberg and Mahaffy 1985; Mahaffy 1988; Mahaffy and Pao 1984). The inclusion of spatial terms rather than a delay equally lead to the necessary oscillations (e.g. Sturrock et al. 2011, 2012; Szymańska et al. 2014; Lachowicz et al. 2016; Macnamara and Chaplain 2016). Furthermore, Chaplain et al. (2015) rigorously proved, for the Hes1 system, that molecular diffusion causes oscillations. It is worth noting that a few models incorporate both spatial aspects and delays (e.g. Momiji and Monk 2008). At a time when biologists are developing techniques to tag and monitor the movement of molecules in single cells (e.g. Betzig et al. 2006; Manley et al. 2008; Spiller et al. 2010; Linde et al. 2011; Won et al. 2011; Bar-On et al. 2012; Hiersemenzel et al. 2013), it is important to develop appropriate mathematical models that have the ability to analyse the spatial data that arise from such experiments.

The study of GRNs also plays both a theoretical and practical role in the field of synthetic biology. Since the pioneering work of Becskei and Serrano (2000) and Elowitz and Leibler (2000) on E. coli, there has been renewed interest in synthetic GRNs as a method of designing and constructing predictable biological systems (Balagadde et al. 2008; Chen et al. 2012; Yordanov et al. 2014) with concomitant studies of a more theoretical nature (Purcell et al. 2010; O’Brien et al. 2012; Macnamara and Chaplain 2016). Such activities could in future lead to the development of better drug design, more efficient crop yields and enhanced bioenergy production (Yordanov et al. 2014).

While previous work modelling GRNs has offered great insight (showing, for example, that spatial aspects are of key importance, e.g. Chaplain et al. 2015), biological systems are fundamentally noisy and as such it makes sense to consider them stochastically. While GRNs are observed to exhibit periodic fluctuations (e.g. Hirata et al. 2002; Nelson et al. 2004; Geva-Zatorsky et al. 2006), results from intracellular imaging show inherent stochasticity (e.g. Spiller et al. 2010). The noise may be caused by a combination of the underlying randomness of necessary events (such as the binding/unbinding of protein and promoter) and the natural variation of production and degradation rates (since transcription and translation occur in bursts rather than continually). Adding to that the fact that the molecular species involved are present in low numbers, continuum models are unlikely to provide an accurate description of the real-life situation. Burrage and co-workers (e.g. Barrio et al. 2006; Tian et al. 2007; Marquez-Lago et al. 2010) were among the first to seek oscillatory behaviour of GRNs using a stochastic approach. They used a delay SSA method, SSA being the stochastic simulation algorithm developed by Gillespie (1976), and discussed how a time delay could account for spatial aspects (Marquez-Lago et al. 2010), without the need to incorporate them explicitly. However, prompted to further investigate the importance of spatial aspects, Sturrock et al. (2013) designed a model of GRNs (specifically the Hes1 system) which accounts for the importance of both space and stochasticity. They used a continuous-time discrete-space Markov process to model the reaction–diffusion kinetics. Since cell populations are naturally heterogeneous, a stochastic description with spatial aspects built in allows us to incorporate a variety of differences and to look for emergent behaviour. The approach of Sturrock et al. (2013) can be applied to model other natural pathways or synthetic GRNs, and we give two such applications here.

At the heart of any model for GRNs lies a system of chemical/molecular reactions, which describe how different species interact. Within a continuum setting we are able to extrapolate from these a set of differential equations. A discrete approach by contrast relies on a chemical master equation; the spatial stochastic models we discuss here are continuous-time, discrete-space Markov processes governed by a reaction diffusion master equation (RDME). Model reactions (modelled with simple mass action kinetics) are localised at specific sites or regions within the cell. In the following section, we give some selected results from the simulations of specific RDMEs (see “Appendix 1” for more details of the basic model set-up).

2.1 GRN Simulation Results

2.1.1 Synthetic GRNs: n-Gene Repressilators

For a basic spatial stochastic model, we start with a single (or chain of) feedback(s) between mRNA(s) and protein(s). We consider a single stochastic reaction–diffusion model, which is developed from that of Sturrock et al. (2013), who modelled the single negative feedback Hes1 system. The model can be extended to one containing n-genes, i.e. n mRNAs and n proteins, connected in a cyclical arrangement in which a gene may activate or inhibit its following gene. Our model reactions are given in Table 1, for $i=\{1,2,\ldots n\}$. Consider a gene i, its mRNA is translated producing protein, within the cytoplasm, at a rate $\alpha _{pi}$. The $(i-1)$th protein is then available to bind with (and then unbind from) its ith promoter at a specific gene site, with binding and unbinding rates $b_1$ and $b_2$, respectively. Depending on whether the protein is bound with its promoter or not determines the rate of mRNA production for the following gene in the chain. A free (or unbound) promoter transcribes mRNA at the basal rate $\alpha _{mi}$, while an occupied (or bound) promoter either enhances or diminishes mRNA production depending on the value of $\gamma _i$. We assume that both species degrade (at rates $\mu _m$ and $\mu _p$, respectively) and diffuse throughout the domain.

Table 1 List of the ith molecular reactions in an n-gene repressilator system

This single description may be used to model a variety of synthetic GRNs, with the nuances of each captured by changes to specific parameters. In particular, we are able to model repression or activation of an mRNA by a preceding protein through changes to the parameter $\gamma _i$ (Sturrock et al. 2013). If $\gamma _i<1$, the basal rate of mRNA transcription is enhanced when the preceding protein is bound to its promoter (there is positive feedback), whereas the basal rate of mRNA transcription is reduced when the preceding protein is bound to its promoter for $\gamma _i>1$ (there is negative feedback).

Fig. 2

Computational 3D cellular domain used in the stochastic spatial simulations consisting of a cytoplasm (green), a nucleus (blue) and gene binding sites within the nucleus (red). The nucleus has radius 3 $\upmu$m, and the cell has radius 7.5 $\upmu$m. See text for full details

For this model with $n=1$, the system contains a single mRNA and protein pair. With $\gamma _1 > 1$, they are coupled by a simple negative feedback loop; this appropriately models the Hes1 system and was considered as such by Sturrock et al. (2013). Here we give here simulation results for a three-gene repressilator by taking $n=3$ and $\gamma _i>1$. Following Macnamara and Chaplain (2016), we consider a repressilator to be a loop of n-genes where each protein inhibits the production of the subsequent mRNA. We solve the system for a spherical domain, $\varOmega$, see Fig. 2. We approximate the cell as two concentric spheres centred on (0, 0) with radii 3 and 7.5 $\upmu$m, respectively; the inner sphere being the nucleus and the remainder of the domain the cytoplasm. Key to this modelling approach is the position of promoter sites, where the binding/unbinding and transcription reactions take place. How variations in the spatial location of the gene site (and also the protein production site) affect the levels of the molecules in GRNs has been explored in Sturrock et al. (2012) and Macnamara and Chaplain (2016, 2017). This aspect remains to be explored more fully in a spatial stochastic setting. For our simulations of the three-gene repressilator, the three promoter sites are located at single voxels tightly clustered together within the nucleus. In Table 2, we give the parameter values used in the simulations.

Table 2 List of parameter values used in the computational simulations (all parameters are within the ranges reported by Sturrock et al. 2013)

Simulation results are given in Fig. 3 where we depict the concentrations of mRNA and protein as they vary with time along with figures that indicate when each of the promoters is occupied. The individual gene/promoter sites are located in the x–y plane equidistant on a circle of radius 0.5 $\upmu$m as follows: promoter 1 site—$(0\,\upmu \hbox {m},g_y\,\upmu \hbox {m})$; promoter 2 site—$(g_y \cos (\pi /6)\,\upmu \hbox {m}, - g_y \sin (\pi /6)\,\upmu \hbox {m})$; promoter 3 site—$(-g_y \cos (\pi /6)\,\upmu \hbox {m},-g_y \sin (\pi /6)\,\upmu \hbox {m})$ where $g_y = 0.5$. We observe periodic fluctuations in mRNA and protein concentrations.

Fig. 3

Plots showing the copy numbers of mRNA and proteins obtained from a simulation of the three-gene repressilator system with individual gene sites (promoter sites) clustered together at the origin. The molecular species are colour coded as follows: mRNA1, protein1—red; mRNA2, protein2—blue; mRNA3, protein3—green. Top figure mRNA copy numbers; middle figure protein copy numbers; bottom figure the three promoters in either occupied (1) or free (0) state

2.1.2 Natural GRNs: The NF-$\upkappa$B Pathway

While a generic model of GRNs with simple feedback incorporated offers general insight into mRNA-protein dynamics, a spatial stochastic approach can easily be applied to more complex pathways that contain a variety of molecular interactions. Here, we give a few selected simulation results for a spatial stochastic model of the NF-$\upkappa$B pathway, which when it works correctly is responsible for coordinating processes such as adaptive and innate immunity, development and cell survival but if dysregulated may lead to chronic inflammatory diseases, autoimmune diseases and the initiation and progression of cancer. Nuclear factor $\upkappa$B (NF-$\upkappa$B) was discovered in 1986 as a nuclear factor in B lymphocytes responsible for regulating the gene encoding the immunoglobulin $\upkappa$ light polypeptide chain. It is found to be present in almost all mammalian cell types and is activated in response to many different stimuli, including environmental cues such as hypoxia and ultraviolet radiation; infectious agents, such as bacteria and viruses; and extra- and intracellular stress, such as inflammatory cytokines and DNA damage. Due to the diversity of the means to NF-$\upkappa$B activation, it is not surprising that NF-$\upkappa$B has been found to have the potential to control the transcriptional activity of over three hundred genes and to thus play a role in many different processes.

Nuclear–cytoplasmic oscillations of NF-$\upkappa$B have been observed in experiments (e.g. Nelson et al. 2004; Ashall et al. 2009; Lee et al. 2014), see, for example, Fig. 4, and have also been the subject of mathematical models (Hoffmann et al. 2002; Lipniacki and Kimmel 2007; Cheong et al. 2008; Pekalski et al. 2013). They are produced due to negative feedback from gene products such as its inhibitor I$\upkappa$Ba and the IKK deactivator A20 (Skaug et al. 2011). In the canonical NF-$\upkappa$B signalling pathway, NF-$\upkappa$B (predominantly experimentally observed to be RelA-NF-$\upkappa$B1 heterodimer) is held inactive in the cytoplasm of unstimulated cells by the family of inhibitor I$\upkappa$B proteins (predominantly I$\upkappa$Ba). The binding of I$\upkappa$B to NF-$\upkappa$B masks NF-$\upkappa$B’s nuclear localisation sequence (NLS), which in turn prevents the binding of NF-$\upkappa$B to nuclear pore complexes and hence nuclear translocation (O’Dea and Hoffmann 2010). I$\upkappa$B further spatially regulates NF-$\upkappa$B by actively translocating to the nucleus, binding to nuclear NF-$\upkappa$B and transporting it back to the cytoplasm (Arenzana-Seisdedos et al. 1997). Particular examples of extracellular stimuli that activate the canonical NF-$\upkappa$B signalling pathway are the pro-inflammatory cytokine, tumour necrosis factor $\upalpha$ (TNF$\upalpha$), and the bacterial product, lipopolysaccharide (LPS). Upon ligand binding to a specific cellular membrane receptor, such as tumour necrosis factor $\upalpha$ receptor 1 (TNFR1) or Toll like receptor 4 (TLR4), adaptor molecules, kinases and ubiquitin ligases are recruited, leading to the activation of the TAK–TAB complex [TGF (transforming growth factor) $\upbeta$ activated kinase—TAK associated binding protein]. TAK is essential for the activation of the trimeric complex, IKK (the inhibitor of I$\upkappa$B kinase), which in mammalian cells is composed by IKK$\upalpha$, IKK$\upbeta$ and IKK$\upgamma$. IKK activation leads to phosphorylation of the I$\upkappa$B$\upalpha$ within an I$\upkappa$B/NF-$\upkappa$B complex at amino acid residue serine 32 and serine 36. This phosphorylation of I$\upkappa$B is a marker for it to be tagged for ubiquitination. Once ubiquitinated, it is degraded by the proteasome, thus releasing NF-$\upkappa$B to translocate to the nucleus, where it binds to $\upkappa$B sites in the promoters and enhancers of its target genes. The full set of reactions/interactions for the NF-$\upkappa$B pathway is given in Tables 6, 7 and 8 in Appendix 2.

Fig. 4

From Nelson et al. (2004). Reprinted with permission from AAAS

Top panel. Experimental observation of temporal oscillations of key molecular species in the NF-$\upkappa$B system. Bottom panel. Experimental observation of spatiotemporal oscillations in NF-$\upkappa$B localisation in individual cells. This figure shows time-lapse confocal images of NF-$\upkappa$B-containing species fused to a red fluorescent protein and of I$\upkappa$Ba-containing species fused to a green fluorescent protein in SK-N-AS cells after stimulation with TNFa. The arrow marks one oscillating cell. Nuclear–cytoplasmic translocation of NF-$\upkappa$B-containing species is apparent. Time is shown in minutes, and the scale bar represents 50 $\upmu$m.

Here we give simulation results of the RDME for the NF-$\upkappa$B pathway. A single realisation of the experiment is shown in Fig. 5. Again, in this case the computational domain consists of two concentric spheres (the outer sphere representing the cytoplasm—radius 9.5 $\upmu$m—and the inner sphere representing the nucleus—radius 5 $\upmu$m) and three individual gene/promoter sites for NF-$\upkappa$B, I$\upkappa$B and A20 localised within the nucleus (specifically, the NF-$\upkappa$B gene site is located at the origin, and the I$\upkappa$B and A20 gene sites have displacements of 2.5 and −2.5 $\upmu$m, respectively, along the x Cartesian axis from the origin). The plots given in Fig. 5 show periodic fluctuations in the copy numbers of NF-$\upkappa$B, I$\upkappa$B (and the complex of the two) along with A20 as well as indicating periodicity in the NF-$\upkappa$B nuclear–cytoplasmic ratio that suggests nuclear–cytoplasmic oscillations.

Fig. 5

Plots showing temporal oscillations of key molecular species in the NF-$\upkappa$B system obtained from simulations of the spatial stochastic model. From top left to bottom left: time series (spanning 1600 min) for the copy number of (a) total NF-$\upkappa$B, (b) total I$\upkappa$B–NF-$\upkappa$B complex, (c) free NF-$\upkappa$B, (d) free I$\upkappa$B, (e) total A20, respectively. In the bottom right plot, (f) we give the NF-$\upkappa$B nuclear–cytoplasmic ratio. Where applicable (in Fig. 1d) the total number of cytoplasmic species is indicated in red and the total number of nuclear species is indicated in blue. Parameter values given in Appendix 2 in Tables 6, 7 and 8

Figure 6 indicates the cross-section through the middle of the cell from the full 3D simulation. We show the spatial distribution of NF-$\upkappa$B molecules inside a cell for discrete values of time. We note changes to the concentration over time both in general and with regard to location. Specifically, we note that the concentration of NF-$\upkappa$B alternates between being predominantly in the nucleus with being predominantly in the cytoplasm. These numerical simulations shown in Figs. 5 and 6 can be directly compared to experimental data, such as those given in Fig. 4. One way to achieve this in an objective manner is to estimate the underlying (mean) period of the oscillations. Figure 7 shows the mean period of total NF-$\upkappa$B for 100 different simulations of the spatial stochastic model. The (time-dependent) periods were estimated using a Morlet continuous-time wavelet transform as implemented in WAVOS, with Gaussian edge elimination used to minimise artefacts in the approximation of the period (cf. Harang et al. 2012; Sturrock et al. 2013). As can be seen from the plot, the period varies between 100 and 180 min, which is comparable to that observed by Nelson et al. (2004). Thus, our spatial stochastic model (SSM) is capable of capturing both the spatial–temporal experimental data within a single cell and the temporal data of molecular concentrations. As such, our SSM provides a very accurate in silico description of complex intracellular signalling pathways.

Fig. 6

Plots of the spatial distribution of NF-$\upkappa$B molecules inside a cell at times $t=0$, 42, 84, 128, 196, 292, 356, 400, 464 min. Cross-section through the middle of the cell from the full 3D simulation. Parameter values given in Appendix 2 in Tables 6, 7 and 8

Fig. 7

Plot showing the mean period (in minutes) of total NF-$\upkappa$B for 100 simulations of the spatial stochastic model. The periods were calculated using a Morlet continuous wavelet transform with Gaussian edge elimination. Parameter values given in Appendix 2 in Tables 6, 7 and 8

3 A Multiscale Individual-Based Model of Cancer Growth

While the model of the previous section focussed on (stochastic) spatiotemporal models of intracellular pathways, both synthetic and actual, as noted in Introduction, these intracellular pathways control cell-level activities. Therefore, in this section, we will focus on a model of cancer growth at the individual cell level. There are now a number of different individual-based modelling approaches that one can adopt, cf. cellular automata, Cellular Potts Model, hybrid discrete-continuum (Anderson and Chaplain 1998; Alarcón et al. 2003; Andasari et al. 2012; D’Antonio et al. 2013). Here we adopt an individual-based, force-based model of cell growth which is driven by forces acting upon the cell and is based upon the model of Ramis-Conde et al. (2008). More recently, this approach has been extended and implemented on a massively parallel system (IBM Blue Gene/Q system) allowing hybrid high-performance simulations to describe, for example, tumour growth in its early clinical stage. Details of the implementation can be found in Cytowski and Szymańska (2014, 2015a, b). Adopting this approach, we model each cell as an isotropic elastic object capable of migration and division and parameterise it by cell-kinetic, biophysical and cell-biological parameters that can be experimentally measured, from both in vitro and in vivo experiments (Chu et al. 2004; Gumbiner 2005; Jagiella et al. 2016; Miron-Mendoza et al. 2013; Näthke et al. 1995; Schlüter et al. 2012, 2015; Ritchie et al. 2001; Zaman et al. 2006). We assume that an individual cell $c_i$ in isolation is spherical and characterise the cell shape by its radius R. The position of the cell in 3D space is described by the Cartesian coordinates $(x_{c_i},y_{c_i},z_{c_i})$ of its centre.

Regarding cell kinetics, we assume that the cell cycle is divided into four phases, i.e. mitosis: M-phase, followed by $G_1$-, S-, and $G_2$-phases, after which mitosis occurs again. During a complete cell cycle, the cell must accurately duplicate its DNA once during S-phase and distribute an identical set of chromosomes equally to two progeny cells during M-phase. M-phase consists of two major events: the division of the nucleus, called mitosis, and subsequent cytoplasmic division, called cytokinesis. $G_1$-phase is an interval between mitosis and the initiation of nuclear DNA replication. It provides additional time for a cell to grow and to replicate its cytoplasmic organelles. $G_2$-phase is again an interval between the completion of nuclear DNA replication and mitosis. Over the course of both the $G_1$- and $G_2$-phases, the cell checks the internal and external environment to ensure that the conditions are suitable and complete preparation for entry into either S-phase or M-phase. When DNA is damaged, the cell cycle is arrested in $G_1$ or $G_2$ so that the cell can repair DNA damage prior to its duplication, or before cell division.

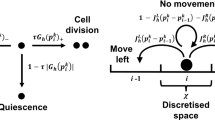
Cell cycle events must occur in a precise order, which should be maintained, even when one of the steps takes longer than usual. For instance, this means that cell division cannot start before DNA replication is complete. Similarly, when DNA is damaged the cell cycle is arrested so that the cell can repair the damage. This is possible because the cell is equipped with molecular mechanisms that can stop the cycle at various checkpoints. Two main checkpoints are located within the $G_1$- and $G_2$-phases. The $G_1$ checkpoint allows the cell to check whether its environment is conducive to divisions and whether its DNA is damaged. If environmental conditions make cell division impossible, instead of entering S-phase a cell can enter a resting state—$G_0$-phase—where it remains until conditions improve and it continues the cell cycle. The $G_2$ checkpoint ensures that the cell has no DNA damage, and DNA replication will be completed before the beginning of mitosis (Alberts et al. 2010). A simplified schematic of the cell-cycle model and cell interactions with the environment used in our computational simulations is given in Fig. 8.

Fig. 8

Schematic diagram showing the cell cycle and cell dependency upon availability of nutrients used in the individual-based model

Interactions between cells are modelled by taking into account the repulsive and attractive forces between cells. Upon compression, i.e. with decreasing distance $d_{c_{i}c_{j}}$ between the centres of two adjacent cells, $c_i$ and $c_j$, of radii, $r_{c_i}$ and $r_{c_j}$, both their surface contact area and the number of adhesive contacts increase, resulting in an attractive interaction. We assume that adhesive forces are proportional to $\rho _m$, which is the density of the surface adhesion molecules in the contact zone (which we assume is given for particular cell type), $k_\mathrm{B}$, which is the Boltzmann constant, T, which denotes temperature and $D_{c_ic_j}$, which measures the contact between cells $c_i$ and $c_j$ and is calculated as the volume of the common area of intersecting spheres representing those cells. Experiments suggest that cells only have a small compressibility—the Poisson numbers are close to 0.5 (Mahaffy et al. 2000; Alcaraz et al. 2003). In this instance, both the limited deformability and the limited compressibility give rise to a repulsive interaction. Repulsive forces are inversely proportional to the term $E_{c_{i},c_{j}}$, which is calculated from the Young moduli, $E_{c_i}$ and $E_{c_j}$, and Poisson ratios, $\nu _{c_i}$ and $\nu _{c_j}$. The precise formula is given by:

$$\begin{aligned} E_{c_{i},c_{j}} = \frac{3}{4}\left( \frac{1-\nu _{c_i}^2}{ E_{c_i} } + \frac{1-\nu _{c_j}^2}{ E_{c_j} } \right) . \end{aligned}$$

(1)

We model the combination of the repulsive and attractive energy contributions by a modified Hertz model (Galle et al. 2005; Schaller and Meyer-Hermann 2005) which has the advantage that both the interaction energy and the force can be represented as an analytical expression (Drasdo and Höhme 2005). Inertia terms are neglected due to the high friction of cells with their environment, and we also do not consider the existence of any memory term as in Galle et al. (2005):

$$\begin{aligned} V_{c_{i}c_{j}}=\underbrace{(r_{c_{i}}+r_{c_{j}}-d_{c_{i}c_{j}})^{\frac{5}{2}}\frac{1}{5E_{c_{i}c_{j}}}\sqrt{\frac{r_{c_{i}}r_{c_{j}}}{r_{c_{i}}+r_{c_{j}}}}}_{\text {repulsive interactions}}+\underbrace{\rho _m D_{c_{i}c_{j}}25k_{\mathrm{B}}T}_{\text {adhesion}}. \end{aligned}$$

(2)

Cells require access to oxygen from the circulatory system in order to grow and survive. It is well known that cancer cells grow preferentially around blood vessels. Those tumour cells that are located more than about 0.2 mm away from blood vessels were found to be quiescent, while others even farther away were found to be necrotic. This threshold of approximately 0.2 mm represents the distance that oxygen can effectively diffuse through living tissue (Weinberg 2007). Because of the low redox potential and high activation energy that occurs in living organisms, reactions involving molecular oxygen occur only in mitochondria. Therefore, we assume that the loss of oxygen in the tissue takes place only due to its consumption by the cells. The general equation governing the external oxygen concentration $Q(\mathbf{x}, t)$ in the cells’ environment may be written:

$$\begin{aligned} \frac{\partial }{\partial t}Q(\mathbf{x}, t) = D_Q \nabla ^2 Q(\mathbf{x}, t) - G(\mathbf x , t) + H(\mathbf x , t), \end{aligned}$$

(3)

where $D_Q$ is the oxygen diffusion coefficient. The function $G(\mathbf x , t)$ models the oxygen uptake by cells and the function $H(\mathbf x , t)$ models the production of oxygen by vessels. Both of these functions are computed in each time step of the simulation from the current spatial organisation of cells and vessels through interpolation. The force associated with a given cell, $c_i$, is then given by the expression:

$$\begin{aligned} F_{c_{i}}=\underbrace{\nabla V_{c_{i}}}_{\text {intercellular interactions}} + \underbrace{\lambda \nabla Q(x,t)}_{\text {chemotaxis}} \end{aligned}$$

(4)

where $\lambda$ is a measure of a cell’s chemotactic sensitivity to the oxygen concentration and $V_{c_{i}}$ is given by

$$\begin{aligned} V_{c_{i}} = \sum _{c_j\in B_{\epsilon _{c_i}}(c_i)}V_{c_{i}c_{j}} \end{aligned}$$

(5)

with $B_{\epsilon _{c_i}}(c_i)$ a sphere (i.e. a ball in $\mathbb {R}^3$) centred on $(x_{c_i},y_{c_i},z_{c_i})$, radius $\epsilon _{c_i}$, denoting the maximum intercellular interaction region.

Summing all the forces between the cells and assuming a frictional force/drag force proportional to a cell’s velocity and then applying Newton’s second law of motion allows us to integrate a Langevin-type equation to give the spatial location of the cells over time. The direct use of equations of motion for the cells permits one to include more easily the limiting case of very small (or no) noise and is more intuitive. In this approach, cells move under the influence of forces and a random contribution to the locomotion which results from the local exploration of space.

Solving the oxygen concentration (which is a global field) together with the individual-based particle system of up to $10^9$ cells is a challenging task in the context of parallel processing. First of all, it requires the use of appropriate data structures to optimise the computations of interactions between lattice-free cells. In our approach, the main data structure that stores information about cells is an octal tree. We assume that the domain of simulation is a 3D cube. The cells are arranged in a tree based on the position of their centres. The tree is built recursively starting from the whole domain of simulation, which corresponds to the root of the tree. Subsequently, the cubes are divided recursively into eight equal cubes with edges reduced by a factor of a half. This procedure is repeated until in the cube under consideration there is only one cell centre.

In order to perform large-scale simulations and to minimise the execution time and enable good parallel scalability on massively parallel systems, we need to perform an appropriate data partitioning across available processes. In our approach, we use two different domain decompositions. Firstly, we need to distribute the cells between the available processors. The solution we adopted is based on Peano–Hilbert space filling curves and is encoded in the following algorithm: for each cell in a 3D box we look for its corresponding value in the interval [0, 1]; then, the interval [0, 1] is divided into equal parts according to a given specific measure. Such a measure may be, for example, the number of cells contained in a given part. In our case, the measure is based on computed cell density. The particular parts are assigned to different processors. Such a load-balancing method (e.g. geometrical load-balancing method) has the very nice property of geometrical locality that is very important when computing cell–cell interactions in a given neighbourhood, see Fig. 9.

Fig. 9

A 2D example of domain decomposition assigning cells to different processors. Local cells of each process are denoted by the same colour. Our aim was to minimise the execution time and enable good parallel scalability on massively parallel systems. Our decomposition algorithm is based on Peano–Hilbert space filling curves. Such a method ensures the property of geometrical locality, which is very important when computing cell–cell interactions in a given neighbourhood

The equation governing the external oxygen concentration is equipped with Dirichlet boundary conditions and is discretised with an implicit in time finite difference scheme. The resulting linear system is then defined in the ParCSR parallel format and solved with the conjugate gradient method preconditioned by the BoomerAMG algebraic multigrid method (both available in the Hypre library, cf. Baker et al. 2012). The domain decomposition scheme used for the finite difference numerical scheme is different from the one used for a particle system. For data modelled in a continuous manner, the data decomposition is achieved by assigning 3D grid blocks to different processes.

The system is updated repeatedly as the program runs through a loop. During one time step, for each cell its cell-cycle phase is computed, i.e. its phase is checked and, if necessary, updated. The level of oxygen and nutrients available to a cell determines whether or not it dies (i.e. the probability of cell death increases as the oxygen and glucose concentrations decrease). A cell divides if it has sufficient space around it to place its daughter cell. Scheme 1 presents the computational algorithm followed during the simulation. Each iteration of the simulation begins with domain decomposition and a construction of an optimal data structure (i.e. an oct tree) for storing the cells and then follows the steps of the algorithm and ends with cells being moved to new spatial positions.

Fig. 10

From Hlatky et al. (2002), by permission of Oxford University Press

Tumour cells surrounding a central blood vessel from a Dunning rat prostate carcinoma xenograft (Hlatky et al. 2002). Regions of viable tumour cells (cuffs) are formed around the central vessel. The dashed black line indicates the boundary of the region. Cuff size is roughly indicative of the metabolic burden of the carcinoma cells. Tumour cells within approximately 110 $\upmu$m of the vasculature are viable. Beyond this zone, oxygen and nutrient levels drop below a critical threshold, and an area of necrosis is observed.

3.1 Application to Tumour Cords

In this section, we present the results of computational simulations carried out on our individual-based model. Previous work applying the individual-based model to cancer growth has already focussed on avascular multicell (multicellular) spheroids (Shirinifard et al. 2009; Cytowski and Szymańska 2014, 2015a, b), cancer invasion (Ramis-Conde et al. 2008) and metastasis (Ramis-Conde et al. 2009). However, here we choose to focus on a less well-studied solid tumour “structure” observed in vivo, that of “tumour cords” or “tumour cuffs”. In this case, tumour cells grow around a central blood vessel with those cells further away from the blood vessel experiencing lower nutrient levels. Since nutrient concentration (e.g. oxygen and glucose) decreases with increasing distance from the blood vessel, there is a region of viable cells close to the blood vessel, with necrosis appearing at a certain distance from the vessel. For example, in the Dunning rat model of prostate carcinoma, this is observed to be around 110 $\upmu$m, see Fig. 10 (Hlatky et al. 2002). Previous modelling work in this area has adopted a continuum approach (Bertuzzi and Gandolfi 2000 and Bertuzzi et al. 2005). This is the first time (to our knowledge) that an individual-based approach has been adopted for tumour cords.

Table 3 Description of the parameters used in the individual-based model and their values along with the relevant reference

3.2 Parameter Estimation

Whenever possible parameter values are estimated from available experimental data. Most of the parameters used in the simulations concern mouse breast cancer—EMT6 cell line. Given that the length of phases of the cell cycle is for cultivation of cells in favourable conditions, i.e. assuming adequate amounts of nutrients and space for development. We also assume that proliferating cells that lack oxygen stop at the $G_1$ checkpoint and become quiescent. Quiescent cells that are in $G_0$ need less oxygen than proliferating cells, see Table 3. If the level of oxygen available to the cells falls below the level needed to survive, the cells become necrotic. Because of the high permeability of cell membrane to oxygen (Alberts et al. 2010), we also assume that oxygen concentration inside the cell is equal to the extracellular concentration (Bertuzzi et al. 2010). The volume of a living EMT6 cell is about $4.975\times 10^{-9}\,\mathrm{cm}^{3}$ (Casciari et al. 1992) giving the cell diameter as approximately 10.6 $\upmu$m. A list of all the baseline parameters used in the individual-based model is given in Table 3.

Fig. 11

Plots showing results of numerical simulations of our model of a growing tumour cord around a central blood vessel at times 332, 443, 776 and 1332 h. As the tumour cord grows, cells further away from the vessel become necrotic (black). At the final time of 1332 h, there is a total of 10,279 cells comprising 3801 viable cancer cells and 6478 necrotic cells. See text for details

Fig. 12

Plot from our model simulations showing cross-sections of the growing tumour cord around a central blood vessel at times 332, 443, 776 and 1332 h. As the tumour cord grows, cells further away from the vessel become necrotic (black). At the final time of 1332 h, there is a total of 10,279 cells comprising 3801 viable cancer cells and 6478 necrotic cells. See text for details

3.3 Computational Simulation Results

In Figs. 11 and 12, we show computational simulation results for a tumour cord growing around a blood vessel for the baseline parameter case, as detailed in Table 3. Specifically the simulation is of an avascular cancer; the cancer cells are initiated around a central small blood vessel that secretes oxygen. The oxygen concentration is held constant on the vessel boundary and then diffuses to zero over a distance of around 200 $\upmu$m. We observe that as the mass of tumour cells grows, cells become hypoxic and then subsequently necrotic at which point they are coloured black. The numbers of viable and necrotic cells at various times from the computational simulation are given in Table 4. This mirrors the experimental findings of Hlatky et al. (2002), see Fig. 10.

Table 4 Numbers of viable and necrotic cells at various times from the computational simulation shown in Figs. 11 and 12

In Figs. 13 and 14, we repeat the simulation but this time with a reduced oxygen consumption rate for both quiescent and proliferating cells. Once again we observe that a mass of tumour cells develops around the blood vessel; again cells that are coloured black have become necrotic. In this case, the necrotic zone is of a smaller size and the overall diameter of the tumour cord is larger, as is to be expected from the reduction in $O_2$ consumption. At the level of the whole tumour cord, we see the evolution of a shorter but fatter structure around the central vessel. The numbers of viable and necrotic cells at various times from the computational simulation are given in Table 5.

Fig. 13

Plots showing results of numerical simulations of our model of a growing tumour cord around a central blood vessel under reduced oxygen consumption at times 332, 443, 776 and 1332 h. As the tumour cord grows, cells further away from the vessel become necrotic (black). At the final time of 1332 h, there is a total of 16,723 cells comprising 9271 viable cancer cells and 7452 necrotic cells. See text for details

Fig. 14

Plots from numerical simulations of our model showing cross-sections of the growing tumour cord around a central blood vessel under reduced oxygen consumption at times 332, 443, 776 and 1332 h. As the tumour cord grows, cells further away from the vessel become necrotic (black). At the final time of 1332 h, there is a total of 16,723 cells comprising 9271 viable cancer cells and 7452 necrotic cells. See text for details

In Fig. 15, we show the computational simulation results for the final structure of a tumour mass that has grown around two vessels—“double cuff”. This shows the ability of the code to simulate tumour growth around multiple vessels. This more closely aligns with a realistic tissue environment, which is perfused with many capillaries in close proximity with each other.

The figures shown in this section give an indication of the potential for this type of modelling. It offers the capability to determine how a tumour mass would grow and take shape in a given environment. This prospect is something we will discuss in more detail in the following discussion section.

4 Discussion and Conclusions

As noted in Introduction, the development of cancer is a true multiscale process connecting many scales through time and across space (cf. Hanahan and Weinberg 2000, 2011). In this paper, we have presented models for aspects of cancer growth at two of the “fundamental scales”; the intracellular level and the cellular level.

In Sect. 2, we considered spatial stochastic models of gene regulatory networks that permit the study of intracellular dynamics. In particular, through numerical simulations of reaction–diffusion master equations, we showed that it is possible to investigate time-dependent changes to concentration levels of genes and gene products, such as mRNA and proteins. The simulation results demonstrated the periodic fluctuations of these concentrations as well as capturing their noisy nature, offering a better match to experimental results than non-stochastic models. We have shown that this technique can be applied to relatively simple intracellular signalling systems (such as n-gene repressilators) and yet insight is not lost nor computational difficulty increased when we extend the approach to more complex systems of specific GRNs associated with cancer, such as the NF-$\upkappa$B pathway. We would encourage researchers working on GRN models to consider adopting such a modelling approach since it provides quantitative, as well as qualitative, connection to experimental data. Furthermore, we believe that coupling a model of intracellular behaviour with one based at the cell level, as we discuss next, would further strengthen our understanding of cancer dynamics.

Table 5 Numbers of viable and necrotic cells at various times from the computational simulation shown in Figs. 13 and 14

Fig. 15

Plots showing the computational simulation results of a tumour cord interacting with two blood vessels. (a) Tumour cord growing around two vessels, (b) tumour cord growing around two vessels later time. (c) Oxygen profile levels in the tumour cord, (d) cross-section showing corresponding development of tumour cells

In Sect. 3, we discussed a multiscale computational framework that focussed on the cell scale. At the heart of the framework is an individual-based, force-based model of cancer cell growth. The model was originally developed by Ramis-Conde et al. (2008) who in turn developed earlier work by Drasdo and Höhme (2005). By taking advantage of recent developments in high-performance computing techniques, we have carried out our simulations of the model on a massively parallel computer. This has enabled us to simulate up to the level of tens of thousands of cells in an acceptable timeframe. We have shown some simple proof of concept simulations to illustrate how the model can replicate solid tumour growth. In particular, we have considered the proliferation of cancer cells around blood vessels—so-called tumour cords.

The use of HPC will allow our computational framework for the individual-based model to reach the tissue scale (10$^9$ individual, interacting cells that translates into a volume of approximately 1 cm$^3$, i.e. a sizeable volume at the tissue scale), and as such it can be used to simulate tissue-level phenomena. The feasibility of such an approach in terms of computational time has been explored by Cytowski et al. (2017) where the growth of a solid tumour developing in healthy tissue was simulated. A single tumour cell was placed in the centre of an initial mass of 194,100,035 ($\approx$1.9 $\times$ 10$^8$) healthy cells and allowed to grow in response to an external oxygen field. The final tissue configuration consisted of 245,890,017 healthy cells ($\approx$2.5 $\times$ 10$^8$) and 73,836 cancer cells, with the simulation taking a single day using 128 cores of the IBM Power 775 system (Cytowski et al. 2017). The results of this study concluded that a single time step of the simulation, corresponding to 1 h in real time, took 100 s of computational time. Therefore, for example, to simulate a (real time) three-month growth period of a solid tumour would take $100\,\mathrm{s} \times (24\,\mathrm{h} \times 30\,\mathrm{days} \times 3) = 216{,}000\,\mathrm{s} = 60\,\mathrm{h}= 2.5\,\mathrm{days}$.

More importantly since the model itself considers cell–cell/cell–matrix interactions and can also incorporate intracellular data, coupling it with models of intracellular signalling pathways, as detailed above, allows a true multiscale investigation of tumour development. Specifically, we have formulated a multiscale mathematical model of cancer capable of simulating to a level at which solid tumours are distinctly palpable and so such a model has the potential to enable quantitative predictions of cancer growth and treatment. While in isolation the two models discussed in this paper offer insight into two different aspects of cancer progression, i.e. modelling at multiple scales, their incorporation into a single multiscale model is the natural next stage in this type of cancer modelling. Such a multiscale model will need to combine events occurring at the different spatial and temporal scales, from intracellular molecular interactions through to tissue scale phenomena, a challenging task from a modelling perspective with implications also for the time taken computationally. From a modelling perspective, there is a need to incorporate the interactions between the cancer cells and the microenvironment, i.e. the tissue/stroma surrounding the cancer cells (extracellular matrix and other cells, e.g. fibroblasts), explicitly (currently accounted for in the model implicitly through the external frictional/drag force). This could be done in several ways—model the tissue/stroma as a different cell type (Cytowski et al. 2017), model the tissue/stroma as a collection of individual fibres (Schlüter et al. 2015), model the tissue/stroma as another cell type and a collection of individual fibres, model the tissue/stroma as another external field satisfying a PDE similar to the external oxygen (Jagiella et al. 2016). Any one of these approaches would be more akin to modelling the cells moving through a porous medium. The approaches of Cytowski et al. (2017) and Jagiella et al. (2016) would have minimal increase in computational time, but the approach of Schlüter et al. (2015) is computationally more expensive. The computational cost of simulating large numbers of cells interacting with individual fibres in 3D would have to be explored, although initial estimates in 2D for small numbers of cells can be found in Schlüter et al. (2015). Incorporating intracellular signalling pathways into the multiscale model will also increase the computational simulation time. Indeed, embedding a system of stochastic PDEs within each cancer cell would be computationally prohibitive. However, it is also not necessary since many of the key gene regulatory networks associated with cancer (e.g. p53–Mdm2, NF-$\upkappa$B) are not operative continually, but begin to function and upregulate the molecules when there is some external stimulus—in the case of p53, when DNA damage occurs or a cell experiences hypoxia. The oscillations in the levels of the molecules in such systems are normally on the order of a few hours which is shorter than the growth timescale of a solid tumour. One approach that would be computationally feasible would be to exploit the difference in timescales, i.e. stop the growth of the cancer cells when an external stimulus was applied, carry out simulations of the intracellular GRNs modelling a period of several hours at which point the effect of the GRNs at a cell/phenotypic level could be determined. Key cell-level parameters connected to the activity of the GRNs, e.g. cell cycle arrest, cell proliferation rate, apoptosis, could then be modified in a number of the cancer cells. Modelling the intracellular activity would then be halted, and the modelling of the growth of the cells would then continue. A similar computational strategy has been successfully adopted by McDougall et al. (2006) in modelling the growth of blood vessel networks—the different time scales between blood flow dynamics and endothelial cell growth have been exploited to model a so-called dynamic-adaptive blood vessel network.

Further developments of the multiscale model presented in this paper could follow any one of several directions. The computational approach of the proposed multiscale model, coupled with developments in visualisation software, also enables the simulation of initial data and tissue structures (e.g. blood vessels), which have been imported from actual medical images and is therefore a significant milestone towards developing a system of personalised medicine. Clinical imaging data acquisition requires the use of sophisticated visualisation methods giving detailed insight into the anatomy of tissues and organs. The next step is to carry out a three-dimensional reconstruction of the relevant anatomical structures, such as blood vessels. For this purpose, it will be possible to use VisNow (http://visnow.icm.edu.pl), which is an open-access software developed at the Interdisciplinary Centre for Mathematical and Computational Modelling (ICM, Warsaw), allowing complex visual analysis and segmentation of the geometry to be studied. On the basis of the chosen geometry, we can develop digitised input data for our computational model. Figure 16 shows an example of a blood vessel geometry imported from heart microtomography. First, the relevant clinical/medical structures are segmented. Then, on the basis of the geometry obtained, again applying the VisNow package, we create a mesh that, after some smoothing and filtering procedures, is used as the input for the generation of the actual initial data. At each point of the mesh, we locate a cell. The final step consists of removing unnecessary cells, i.e. those that are too close to others. As imagining techniques develop further, they will be able to provide even finer detail, higher resolution and image smaller structures, and it should be possible to create “computational capillaries” at the correct spatial scale around which cancer is initiated. The model of solid tumour growth and interaction with blood vessels can also be further developed to explicitly include blood flow through the vessels and the impact that flow has on the vessel network structure through dynamic adaptation (cf. McDougall et al. 2006; Macklin et al. 2009). This in turn could lead to a multiscale model of chemotherapy treatment of cancer. In more general terms, the modelling approach can be applied to many other important processes such as wound healing, embryogenesis, tissue engineering and cardiac tissue modelling where tissue-level phenomena depend upon, and also in turn influence, interactions and phenomena at both the cell and intracellular levels.

Finally, given the timing of this special issue, it is perhaps apposite to end with a quotation from Professor Sir D’Arcy Wentworth Thompson, whose seminal book “On Growth and Form” was published exactly one century ago:

...numerical precision is the very soul of science, and its attainment affords the best, perhaps the only criterion of the truth of theories and the correctness of experiments ...I know that in the study of material things number, order, and position are the threefold clue to exact knowledge: and that these three, in the mathematician’s hands, furnish the first outlines for a sketch of the Universe. (Thompson 1917).

Fig. 16

Figure showing the three main steps in creating a “computational blood vessel” (input data) from an actual clinical image. (a) Actual vessel geometry from microtomography after segmentation procedure with VisNow software, (b) the mesh obtained after the segmentation procedure, and finally, (c) the vessel structure with individual (spherical) cells overlaid on the underlying mesh forming a “computational blood vessel”

While “sketching the universe” is on yet another completely different scale, the essence of the above quotation, that mathematical modelling can provide quantitative insight to biomedical systems, is still relevant and even more timely today. Echoing the words of D’Arcy Thompson, one century on, we may say that computational multiscale mathematical modelling furnishes not only the first outlines for a sketch of cancer growth but provides the basis for the development of a virtual solid tumour. Cura ex macchina—in silico oncology has arrived.

Appendices

Appendix 1: The Reaction–Diffusion Master Equation

Here we describe the formulation of the spatial stochastic model for intracellular GRN dynamics. We describe the computational domain and how reaction and diffusion events are incorporated into the reaction-diffusion master equation (RDME). We also provide some notes on how simulations are produced. For a more detailed description, see the supplementary material of Sturrock et al. (2013).

1.1 The Computational Domain

The computational domain (see Fig. 2, for example) is set up using COMSOL and a mesh is imposed. In general, the domain $\varOmega$ is meshed into V tetrahedra-shaped subvolumes, voxels, $\varOmega _k, k \in \{1,\ldots ,V\}$ such that,

$$\begin{aligned} \varOmega = \bigcup ^V_{k=1}{\varOmega _k}, \quad \text {and} \quad \varOmega _i \cap \varOmega _j = \emptyset , \forall i \ne j,\quad i,j \in \{1,\ldots ,V\}. \end{aligned}$$

At any given time, the state of the system is described by the number of each chemical species within the domain. Changes to the state will either be by the chemical reactions at the voxel level or the movement (diffusion jumps) of a molecule between neighbouring voxels.

1.2 Chemical Reactions

We consider reactions that occur due to molecular contact. We assume that the species of our system, within each subvolume, are uniformly distributed and in thermal equilibrium, such that the motion of each molecule is random. We consider the probability of a collision occurring between two reactant molecules. The likelihood of a reaction occurring, changing the state of the system from x to $x+N_r$, is determined by its reaction rate, described by the reaction propensity function $\omega _r(x)$. As such, reactions can be described by

$$\begin{aligned} {x} \xrightarrow {\omega _r(x)} {x} + {N}_{{r}}, \end{aligned}$$

where $N_r \in \mathbb {Z}^S$ is the transition step, defined by the rth column of the stoichiometric matrix M and $\omega _r(x)$ is the probability that the reaction occurs during a infinitesimal time interval, i.e.

$$\begin{aligned} \omega _r(x) = \lim _{\mathrm{d}t \rightarrow 0} \dfrac{P(x+N_r, t +\mathrm{d}t)-P(x, t)}{\mathrm{d}t} \end{aligned}$$

1.3 Molecular Diffusion

The movement of a chemical species $S_l$ from a voxel $\psi _i$ to a randomly selected adjacent voxel $\psi _j$ describes the molecular diffusion and is modelled as a first-order event. As such, we treat the diffusive process in a similar way to a reactive process and consider the probability of a transition taking place, i.e. the probability for one of the lth species to make a jump from the ith subvolume to an adjacent jth subvolume. Hence, we consider the following,

$$\begin{aligned} {S}_{{li}} \xrightarrow {{q}_{{lij}} {x}_{{li}}} {S}_{{lj}}, \end{aligned}$$

where $x_{{li}}$ is number of species l located in voxel i and $q_{lij}$ is the diffusion rate constant that depends on the macroscopic diffusion coefficient of species l ($D_l$) and the mesh of the domain, specifically the shape and size of voxels $\psi _i$ and $\psi _j$. Note each $q_{lij}$ is only non-zero for connected mesh elements and of the types of species we model only mRNAs and proteins diffuse, the free and occupied promoters remain permanently within the voxel assigned as the promoter site.

1.4 Solving the System

The temporal evolution of the probability distribution of each state in the state space is governed by the RDME. We complete the model set-up with zero-flux boundary conditions at the cell membrane, while we impose continuity of flux on the nuclear membrane. For initialisation, we suppose that there is only a single free promoter within each promoter site. All simulations found in this paper are produced using the URDME (Unstructured Reaction-Diffusion Master Equation) software framework (Drawert et al. 2012), which implements the next subvolume method (NSM) (Gibson and Bruck 2000); the NSM being far more computationally efficient than the classical SSA for a 3D domain such as ours. URDME uses unstructured tetrahedral and triangular meshes (such as shown in Fig. 2) for which diffusion rate constants $q_{lij}$ are automatically computed (Engblom et al. 2009; Drawert et al. 2012).

Appendix 2: NF-$\upkappa$B Reactions

Here we give the reactions for the NF-$\upkappa$B pathway (Tables 6, 7, 8).

Table 6 Cytoplasmic reactions

Table 7 Reactions at gene sites

Table 8 Global reactions