A Generalized Michaelis–Menten Equation in Protein Synthesis: Effects of Mis-Charged Cognate tRNA and Mis-Reading of Codon

Abstract

The sequence of amino acid monomers in the primary structure of a protein is decided by the corresponding sequence of codons (triplets of nucleic acid monomers) on the template messenger RNA (mRNA). The polymerization of a protein, by incorporation of the successive amino acid monomers, is carried out by a molecular machine called ribosome. We develop a stochastic kinetic model that captures the possibilities of mis-reading of mRNA codon and prior mis-charging of a tRNA. By a combination of analytical and numerical methods, we obtain the distribution of the times taken for incorporation of the successive amino acids in the growing protein in this mathematical model. The corresponding exact analytical expression for the average rate of elongation of a nascent protein is a ‘biologically motivated’ generalization of the Michaelis–Menten formula for the average rate of enzymatic reactions. This generalized Michaelis–Menten-like formula (and the exact analytical expressions for a few other quantities) that we report here display the interplay of four different branched pathways corresponding to selection of four different types of tRNA.

1 Introduction

Enzymes are known to play crucial roles in almost all kinds of intracellular processes (Rittie and Perbal 2008). For the simplest enzymatic reaction studied theoretically by Michaelis and Menten more than a century ago (Johnson and Goody 2011; Michaelis and Menten 2013), the rate of the formation of the product in bulk is given by the so-called Michaelis–Menten (MM) equation (Johnson 2013; Michel and Ruelle 2013). However, at extremely low population of an enzyme, the time taken for each enzymatic cycle fluctuates from one cycle to another; the time taken in each round is often referred to as the turnover time. The distribution of the turnover time is the key statistical characteristics of reactions studied by single-molecule enzymology (Grima et al. 2014). Interestingly, in spite of the fluctuations in the turnover time, the mean turnover time for a large class of enzymatic reactions still follows the MM equation (Xie 2013b). Over the last century, various generalizations of the MM equation have emerged in several different contexts (Schnell and Maini 2003). In this paper, we present a generalization that emerges naturally in the context of biophysical chemistry of protein synthesis.

Proteins are polymers whose monomeric subunits are amino acids. The specific sequence of the amino acid species in the primary linear structure of a given protein is directed by the corresponding sequence of codons (triplets of nucleotide monomers) on the corresponding template messenger RNA (mRNA). The template-directed polymerization of a protein, called translation, is carried out by a molecular machine called ribosome (Spirin 2002; Rodnina et al. 2011; Frank 2011; Frank and Gonzalez 2010; Chowdhury 2013a, b) that consists of two loosely connected subunits designated as large and small. Transfer RNA (tRNA) molecules play crucial roles in translation (Kim 2014). When “charged” (amino-acylated) by a specific enzyme, called amino-acyl tRNA synthetase (aa-tRNA synthetase) (Ling et al. 2009; Reynolds et al. 2010; Yadavalli and Ibba 2012), one end of each species of these “adapter” molecules carries a specific amino acid. The amino acid brought in by a correctly charged cognate tRNA is also the correct one, as directed by the corresponding template; the other end of the same cognate tRNA molecule, referred to as anticodon, matches perfectly, by complementary base pairing, with the codon on the template mRNA. In contrast, increasing degree of mismatch makes the tRNA near-cognate or non-cognate.

Most aa-tRNA synthetases employ editing mechanisms to ensure correct charging of the corresponding tRNA molecules. However, because of the intrinsic stochasticity of aminoacylation, and occasional failure of the editing mechanism of those aa-tRNA synthetase that are capable of correcting erroneous aminoacylation, a mis-charged tRNA may be produced (Ling et al. 2009; Yadavalli and Ibba 2012). Therefore, even when it turns out to be a cognate tRNA for a given codon, such a mis-charged tRNA compromises the translational fidelity by contributing an amino acid which is different from that dictated by the mRNA template. Erroneous substitution of one amino acid by another is called mis-sense error. Pre-translational mis-charging of tRNA is not the only possible cause of mis-sense error. Erroneous selection of a correctly charged near-cognate or non-cognate tRNA, i.e., a co-translational mis-reading of a codon, also contributes to mis-sense error (Parker 1989; Cochella and Green 2005; Zaher and Green 2009; Johansson et al. 2008; Rodnina 2012).

Thus, at the beginning of each elongation cycle the macromolecular complex consisting of the ribosome and accessory molecules select one of the four possible pathways indicated by the tRNA selected: (i) correctly charged cognate tRNA, (ii) incorrectly charged cognate tRNA, (iii) correctly charged near-cognate tRNA, and (iv) correctly charged non-cognate tRNA. Along each of these pathways, the sequence of intermediate steps is identical although the molecular identities of the complexes are different. In other words, the network of mechano-chemical states consists of four distinct cycles that shares the same initial state.

The time taken by a ribosome to incorporate a single amino acid in the growing protein is also the duration of the ribosome’s dwell at the corresponding codon on the mRNA template. The distribution of the dwell times (DDT) characterizes the intrinsic stochastic nature of the process of elongation of the nascent protein by the ribosome. Here, we develop a stochastic kinetic model for the elongation phase of translation capturing, within a single mathematical framework, all the four cycles that branch out from the initial state. Our model also distinguishes between the concentrations of four distinct types of tRNA molecules, namely correctly charged cognate tRNA, incorrectly charged cognate tRNA, correctly charged near-cognate tRNA and correctly charged non-cognate tRNA. Solving the corresponding master equations (a set of coupled ordinary differential equations), for an appropriate initial condition that captures the beginning of translation of a codon, we obtain the DDT of the ribosome. Moreover, using the steady-state solutions of these master equations, we derive the exact analytical expression for the average velocity of the ribosome which is also the average rate of amino acid incorporation (i.e., average rate of elongation of the nascent protein) catalyzed by the ribosomal machinery. This expression is a generalization of the MM equation and, as we demonstrate explicitly, it reduces to the standard form of MM equation in the appropriate special limits of our model. Few graphical plots of the average rate of elongation, corresponding to some typical values of the rate constants, are presented to provide an intuitive understanding of the relative contributions of the four competing cycles.

Three of the four pathways originating from the initial state lead to translational error if the cycle is completed by adding an amino acid to the growing protein. Therefore, as a by-product of our calculation, we also get exact expressions for the translation error. The more stringent is the mechanism of selection of incoming tRNA the lower is the mis-reading error. But, increasing the probability of rejecting near-cognate and non-cognate tRNAs would increase the likelihood of accepting not only correctly charged cognate tRNA but also that of a mis-charged cognate tRNA. A few illustrative plots display the interplay of the effects of micharging of tRNA and mis-reading of mRNA in the overall mis-sense error in translation.

2 Model

Sharma and Chowdhury (2010) developed a five-state stochastic kinetic model (from now onwards referred to as SC model) for the elongation cycle of translation (see Fig. 1). The arrival of a aa-tRNA molecule, bound to GTP and EF-Tu, and its rejection because of the codon-anticodon mismatch is captured by the forward and reverse transitions $1 \rightleftharpoons 2$. The second stage of quality control (kinetic proofreading) involves hydrolysis of GTP by EF-Tu ($2 \rightarrow 3$) followed by either rejection ($3 \rightarrow 1$) or incorporation ($3 \rightarrow 4$) in the growing protein by formation of a peptide bond [see Blomberg (2007) for a pedagogical introduction to kinetic proofreading]. The first of the two-step translocation process consists of the Brownian rotation of large subunit of the ribosome with respect to the small subunit and simultaneous reversible transitions of the tRNAs between the so-called classical and hybrid states. The second, and the final, step of translocation, driven by hydrolysis of another molecule of GTP by EF-G completes the cycle irreversibly. More detailed stochastic models of mechano-chemical kinetics of each elongation cycle have been developed [see, for example, Xie (2013a), Kinz-Thompson et al. (2015)]. However, in order to capture some other aspects of translational kinetics, we describe the kinetics of elongation cycle by the simpler SC model. Nevertheless, the strategy of modeling followed here can be implemented also using the more detailed descriptions as the basic models of elongation cycle.

Fig. 1

(Color figure online) Pictorial depiction of the elongation cycle in the SC model (see the text for details)

The SC model was used further to account for the stochastic alternating pause-and-translocation kinetics of a single ribosome (Sharma and Chowdhury 2011a) as well as for analyzing collective spatio-temporal organization of ribosomes in a polysome (Sharma and Chowdhury 2011b). Because of the extreme simplicity of the SC model model, no clear distinction could be made, in terms of different rate constants, between processes involving near-cognate and non-cognate tRNAs. More importantly, the SC model captured the possibility of mis-sense error arising from only mis-reading of the codons; it was not possible to incorporate the contributions from both mis-reading and mis-charging errors explicitly. The non-trivial extension of the SC model that we present here does not suffer from any of the above-mentioned limitations of the original SC model.

Fig. 2

(Color figure online) Pictorial depiction of the four possible alternative mutually exclusive pathways that open up, in each chemo-mechanical cycle of a single ribosome, upon the arrival of a correctly charged cognate aa-tRNA, b incorrectly charged cognate aa-tRNA, c correctly charged near-cognate tRNA, and d correctly charged non-cognate tRNA (see the text for details)

We begin formulation of the model with the four alternative elongation cycles shown in Fig. 2 which correspond to the four different mutually exclusive pathways that open up with the arrival of (a) correctly charged cognate tRNA, (b) incorrectly charged cognate tRNA, (c) correctly charged near-cognate tRNA, and (d) correctly charged non-cognate tRNA. Note that each of these cycles is formally identical to the only cycle that appeared in the original SC model. However, by opening up the possibility of four distinct pathways, each associated with a distinct identity of aa-tRNA, this model not only allows for a clear distinction between non-cognate, near-cognate and cognate tRNAs but also that between correctly and incorrectly charged cognate tRNAs.

Next, we simplify the model by exploiting some well known facts from the existing literature (Spirin 2002; Rodnina et al. 2011; Frank 2011). First, we note that $\omega _{a}, \omega _{a}', \omega _{a}''$ and $\omega _{a}'''$ are proportional to the concentrations of the corresponding aa-tRNA species; therefore, we assume:

$$\begin{aligned} \omega _{a}= & {} \omega ^{0}_{a,c1}[\text {tRNA}]_{c1} \;\text {(correctly charged cognate tRNA)}\nonumber \\ \omega _{a}'= & {} \omega ^{0}_{a,c2}[\text {tRNA}]_{c2} \;\text {(incorrectly charged cognate tRNA)}\nonumber \\ \omega _{a}''= & {} \omega ^{0}_{a,n}[\text {tRNA}]_{n} \;\text {(correctly charged near-cognate tRNA)}\nonumber \\ \omega _{a}'''= & {} \omega ^{0}_{a,N}[\text {tRNA}]_{N} \;\text {(correctly charged non-cognate tRNA)} \end{aligned}$$

(1)

where the symbol [.] denotes the concentration of the corresponding tRNA species and the prefactors are measures of the intrinsic rates of the reactions for unit concentration of the tRNA species. Thus, as stated in the introduction, concentrations of all the four types of tRNA molecules are incorporated explicitly.

Fig. 3

(Color figure online) Pictorial depiction of the full chemo-mechanical kinetics in the elongation cycle of a single ribosome, along with the corresponding rate constants. It is obtained from Fig. 2 by combining the four cycles (see the text for details)

The assumption (1) is valid under the “abundant substrate” condition, i.e., all four species of tRNA molecules are much more abundant than the ribosomes. This condition is commonly used in the stochastic models of enzyme kinetics although strong deviation from this condition can lead to drastically different results (Grima and Leier 2017).

We do not distinguish $4'$ from 4 and $5'$ from 5 because both the pathways $3 \rightarrow 4 \rightarrow 5$ and $3' \rightarrow 4' \rightarrow 5'$ involve movement of cognate tRNAs (see Fig. 3). Similarly, assuming the rates of translocation of near-cognate and non-cognate tRNA molecules to be comparable, but discriminating these from the corresponding cognate tRNAs, we assume $4'' \equiv 4'''=4^{*} \not \equiv 4$ and $5'' \equiv 5'''=5^{*} \not \equiv 5$ (see Fig. 3). These assumptions help in combining the four pathways shown in Fig. 2 within the single and simpler kinetic scheme depicted in Fig. 3 thereby also reducing the number of parameters (rate constants). From now onwards, unless stated otherwise, all our discussions will be based on the model kinetic scheme shown in Fig. 3.

We use the symbol $P_{\mu }(j,t)$ to denote the probability at time t that the ribosome is in the “chemical” state $\mu$ and is decoding the $j\mathrm{th}$ codon. In the steady state, all the probabilities $P_{\mu }(j,t)$ become independent of time. We define translational fidelity by the fraction

$$\begin{aligned} \phi= & {} \dfrac{\omega _{p} P_{3}}{\omega _{p} P_{3} + \omega ^{\prime }_{p} P^{\prime }_{3} + \Omega _{p} P^{\prime \prime }_{3} + \Omega _{p}^{\prime } P^{\prime \prime \prime }_{3}} = \dfrac{\omega _{p} P_{3}}{\omega _{p} P_{3} + \omega ^{\prime }_{p} P^{\prime }_{3} + \Omega _{h2} P^{*}_{5}} \end{aligned}$$

(2)

where we have used the relation $\Omega _{p} P^{\prime \prime }_{3}+\Omega ^{\prime }_{p} P^{\prime \prime \prime }_{3}=\Omega _{h2} P^{*}_{5}$.

The total mis-sense error $E=1-\phi$ is defined by the relation

$$\begin{aligned} E =\dfrac{\omega '_{p} P'_{3}+ \Omega _{h2} P^{*}_{5}}{\omega _{p} P_{3} + \omega '_{p} P'_{3}+ \Omega _{h2} P^{*}_{5}} \end{aligned}$$

(3)

which is the sum of the total mis-charged mis-sense error (i.e., mis-sense error arising solely from mis-charged tRNAs)

$$\begin{aligned} E_\mathrm{mc}=\dfrac{\omega '_{p} P'_{3}}{\omega _{p} P_{3} + \omega '_{p} P'_{3}+ \Omega _{h2} P^{*}_{5}} \end{aligned}$$

(4)

and the total mis-reading mis-sense error (i.e., mis-sense error arising only from mis-reading of codons)

$$\begin{aligned} E_\mathrm{mr} =\dfrac{\Omega _{h2} P^{*}_{5}}{\omega _{p} P_{3} + \omega '_{p} P'_{3}+ \Omega _{h2} P^{*}_{5}}. \end{aligned}$$

(5)

Similarly, the fraction

$$\begin{aligned} \epsilon _\mathrm{mc} = \dfrac{\omega ^{\prime }_{p} P^{\prime }_{3}}{\omega ^{\prime }_{p} P^{\prime }_{3} + \Omega _{h2} P^{*}_{5}} \end{aligned}$$

(6)

is the fraction of mis-sense error caused by mis-charged cognate tRNAs, while the corresponding fraction of mis-sense error caused by mis-reading is defined by

$$\begin{aligned} \epsilon _\mathrm{mr}=\dfrac{\Omega _{h2} P^{*}_{5}}{\omega '_{p} P'_{3} + \Omega _{h2} P^{*}_{5}} \end{aligned}$$

(7)

Obviously, the average velocity of a ribosome in the steady-state can be obtained by substituting the expressions of ${\mathcal {P}}_{5}$ and ${\mathcal {P}}_5^*$ into the defining relation

$$\begin{aligned} V= {\ell }_\mathrm{c} \left( \omega _{h2} {\mathcal {P}}_5 + \Omega _{h2} {\mathcal {P}}_5^*\right) \end{aligned}$$

(8)

where ${\ell }_\mathrm{c}$ is the length of a codon. We also note that the average velocity V of a ribosome is same as the average rate of elongation of the protein that it polymerizes.

We define the rejection factors

$$\begin{aligned} {\mathcal {R}}= & {} \biggl (\frac{\omega _{r1}}{\omega _{r1}+\omega _{h1}} \biggr )\biggl (\frac{\omega _{r2}}{\omega _{r2}+\omega _{p}} \biggr ) \nonumber \\ {\mathcal {R}}'= & {} \biggl (\frac{\omega '_{r1}}{\omega '_{r1}+\omega '_{h1}} \biggr )\biggl (\frac{\omega '_{r2}}{\omega '_{r2}+\omega '_{p}} \biggr ) \nonumber \\ {\mathcal {R}}''= & {} \biggl (\frac{\omega ''_{r1}}{\omega ''_{r1}+\omega ''_{h1}} \biggr )\biggl (\frac{\omega ''_{r2}}{\omega ''_{r2}+\Omega _{p}} \biggr ) \nonumber \\ {\mathcal {R}}'''= & {} \biggl (\frac{\omega '''_{r1}}{\omega '''_{r1}+\omega '''_{h1}} \biggr )\biggl (\frac{\omega '''_{r2}}{\omega '''_{r2}+\Omega '_{p}} \biggr ) \end{aligned}$$

(9)

The four rejection factors characterize the frequencies of rejection of the incoming charged tRNA molecules in the four alternative pathways depicted in Fig. 3. The higher the value of a rejection factor the more frequent is the corresponding futile cycles.

The analytical results for this model that we report here are exact, i.e., these are derived without making any mathematical approximations. The derivations of these analytical expressions do not require imposition of any condition on the numerical values of the rate constants. However, we now list some biologically motivated constraints on the relative magnitudes of the rate constants that we’ll use later in this paper only for presenting the results graphically for biologically relevant situations. Based on the levels of base-pair complementarity between the codon and the anticodon of the incoming tRNA, we expect that under normal physiological conditions the following conditions would be satisfied: $\omega _{r1}'''> \omega _{r1}'' > \omega _{r1}' = \omega _{r1}$. Motivated by similar considerations, for graphical plots, we also assume $\omega _{r2}'''> \omega _{r2}'' > \omega _{r2}' = \omega _{r2}$. Continuing similar justification for the reduction in the number of model parameters, we assume $\Omega _{p} \simeq \Omega _{p}' \simeq \omega _{p}' < \omega _{p}$.

3 Results

We begin our theoretical analysis by first solving the master equations (26) under steady-state conditions to get the corresponding expressions for $P_{\mu }$; the full analytical expressions are given in Appendix A. Then, using those expressions for $P_{\mu }$, we calculate the quantities of our interest namely, $\phi$, $E_\mathrm{mc}$, $E_\mathrm{mr}$, $\epsilon _\mathrm{mc}$, $\epsilon _\mathrm{mr}$ and V. The results are listed below.

$$\begin{aligned} \phi = \dfrac{A}{A+B+C+D} \end{aligned}$$

(10)

and, hence,

$$\begin{aligned} E = 1-\phi = \dfrac{B+C+D}{A+B+C+D} \end{aligned}$$

(11)

which is sum of the two contributions

$$\begin{aligned} E_\mathrm{mc} = \dfrac{B}{A+B+C+D} \end{aligned}$$

(12)

and

$$\begin{aligned} E_\mathrm{mr}=\dfrac{C+D}{A+B+C+D}. \end{aligned}$$

(13)

Similarly, we get

$$\begin{aligned} \epsilon _\mathrm{mc} = \dfrac{B}{B+C+D} \end{aligned}$$

(14)

and

$$\begin{aligned} \epsilon _\mathrm{mr} = 1-\epsilon _\mathrm{mc} = \dfrac{C+D}{B+C+D} . \end{aligned}$$

(15)

In all the expressions (10)–(15) A, B, C and D are given by

$$\begin{aligned} A = \frac{\omega _a}{\left[ 1+(\omega _{r1}/\omega _{h1})\right] \left[ 1+(\omega _{r2}/\omega _p)\right] }\nonumber \\ B = \frac{\omega _a'}{\left[ 1+(\omega _{r1}'/\omega _{h1}')\right] \left[ 1+(\omega _{r2}'/\omega _p')\right] }\nonumber \\ C = \frac{\omega _a''}{\left[ 1+(\omega _{r1}''/\omega _{h1}'')\right] \left[ 1+(\omega _{r2}''/\Omega _p)\right] }\nonumber \\ D = \frac{\omega _a'''}{\left[ 1+(\omega _{r1}'''/\omega _{h1}''')\right] \left[ 1+(\omega _{r2}'''/\Omega _p')\right] } \end{aligned}$$

(16)

The expressions (10)–(15) can be easily justified by intuitive physical arguments. Let us first consider the special case where $\omega _{r1} = \omega _{r1}' = \omega _{r1}'' = \omega _{r1}''' = 0 =\omega _{r2} = \omega _{r2}' = \omega _{r2}'' = \omega _{r2}'''$. In this case, the expressions for A, B, C and D reduce to $A=\omega _{a}, B=\omega _{a}', C=\omega _{a}''$ and $D=\omega _{a}'''$, respectively. Consequently, $\phi = \omega _{a}/(\omega _{a}+\omega _{a}'+\omega _{a}''+\omega _{a}''')$ is the probability of following the path $1 \rightarrow 2$, instead of the other three alternatives, namely $1 \rightarrow 2'$, $1 \rightarrow 2''$ and $1 \rightarrow 2'''$. Similarly, in this special case, the expression $\epsilon _\mathrm{mc} = \omega _{a}'/(\omega _{a}'+\omega _{a}''+\omega _{a}''')$ is expected because $\epsilon _\mathrm{mc}$ is the probability of following the path $1 \rightarrow 2'$, instead of the two alternatives $1 \rightarrow 2''$ and $1 \rightarrow 2'''$.

In the general case, the rate of transition $1 \rightarrow 2 \rightarrow 3 \rightarrow 4$ is given by

$$\begin{aligned} \omega _{a}~~ \underbrace{\frac{\omega _{h1}}{\omega _{h1}+\omega _{r1}}}_{\text {Prob. for } 2 \rightarrow 3 }~~ \underbrace{\frac{\omega _{p}}{\omega _{p}+\omega _{r2}}}_{\text {Prob. for } 3 \rightarrow 4 } = A \end{aligned}$$

(17)

The quantities B, C and D have similar interpretations as rates for the transitions $1 \rightarrow 2' \rightarrow 3' \rightarrow 4$, $1 \rightarrow 2'' \rightarrow 3'' \rightarrow 4^{*}$ and $1 \rightarrow 2''' \rightarrow 3''' \rightarrow 4^{*}$, respectively. Once the system reaches the state 4 it cannot return to state 1 without completing the full cycle. Therefore, fidelity $\phi$ is the ratio $A/(A+B+C+D)$. The expressions (12)–(15) for $E_\mathrm{mc}, E_\mathrm{mr}$ and $\epsilon _\mathrm{mc}, \epsilon _\mathrm{mr}$ also follow from the same interpretations of A, B, C and D.

Ribosome is an enzyme; interestingly, at any given instant of time its substrate-specificity depends on the codon that it is engaged in translating. In recent years, the average rate of translation has been shown to be a generalization of the rate of enzymatic reactions. Recall that for the Michaelis–Menten (MM) enzymatic reaction

$$\begin{aligned} E + S \mathop {\rightleftharpoons }^{k_{+1}}_{k_{-1}} \left[ \textit{ES}\right] \mathop {\rightarrow }^{k_{2}} E + P \end{aligned}$$

(18)

the rate of the reaction under steady-state condition is given by the MM equation

$$\begin{aligned} \frac{1}{V} = \frac{1}{V_\mathrm{max}} + \frac{K_M}{V_\mathrm{max}}\frac{1}{\left[ S\right] } \end{aligned}$$

(19)

where the Michaelis constant $K_{M} = (k_{-1}+k_{2})/k_{+1}$ and $V_\mathrm{max}=k_{2} [E]_{0}$, with $[E]_{0}$ being the initial (total) concentration of the enzyme. In the past, the average rate of translation by a ribosome has been shown to follow a generalized MM-like equation where the concentration of aa-tRNA is interpreted as the substrate concentration. For simpler models of translation reported earlier, the average rate of translation has been expressed as generalized MM equation (Garai et al. 2009; Chowdhury 2014).

For the full kinetic model shown in Fig. 3, the average rate of translation (i.e., the average velocity V of a ribosome) is given by

$$\begin{aligned} \dfrac{1}{V}= & {} \dfrac{1}{A+B+C+D} \nonumber \\&+ \dfrac{A}{A+B+C+D} \biggl (\frac{1}{V_{A}}\biggr ) + \dfrac{B}{A+B+C+D} \biggl (\frac{1}{V_{B}}\biggr )\nonumber \\&+\dfrac{C}{A+B+C+D} \biggl (\frac{1}{V_{C}}\biggr ) +\dfrac{D}{A+B+C+D} \biggl (\frac{1}{V_{D}}\biggr ) \end{aligned}$$

(20)

where

$$\begin{aligned} \frac{1}{V_{A}}= & {} \bigg [\dfrac{1}{\omega _{h1}}\bigg (1+\dfrac{\omega _{r2}}{\omega _p}\bigg )+\dfrac{1}{\omega _p} +\dfrac{1}{\omega _{bf}}\bigg (1+\dfrac{\omega _{br}}{\omega _{h2}}\bigg ) +\dfrac{1}{\omega _{h2}} \bigg ] \nonumber \\ \frac{1}{V_{B}}= & {} \bigg [\dfrac{1}{\omega _{h1}'}\bigg (1+\dfrac{\omega _{r2}'}{\omega _p'}\bigg )+\dfrac{1}{\omega _p'}+\dfrac{1}{\omega _{bf}}\bigg (1+\dfrac{\omega _{br}}{\omega _{h2}}\bigg )+\dfrac{1}{\omega _{h2}} \bigg ] \nonumber \\ \frac{1}{V_{C}}= & {} \bigg [\dfrac{1}{\omega _{h1}''}\bigg (1+\dfrac{\omega _{r2}''}{\Omega _p}\bigg )+\dfrac{1}{\Omega _p}+\dfrac{1}{\Omega _{bf}} \bigg (1+\dfrac{\Omega _{br}}{\Omega _{h2}}\bigg )+\dfrac{1}{\Omega _{h2}} \bigg ] \nonumber \\ \frac{1}{V_{D}}= & {} \bigg [\dfrac{1}{\omega _{h1}'''}\bigg (1+\dfrac{\omega _{r2}'''}{\Omega _p'}\bigg )+\dfrac{1}{\Omega _p'}+\dfrac{1}{\Omega _{bf}} \bigg (1+\dfrac{\Omega _{br}}{\Omega _{h2}}\bigg )+\dfrac{1}{\Omega _{h2}} \bigg ] \end{aligned}$$

(21)

Equation (20) is a generalized version of the MM equation (19) for our model. An intuitive derivation of the expression (20), that provides a deeper physical interpretation of this formula, is given in Appendix B.

The connection between the two can be elucidated by considering a special case of our model. In the limit $[\hbox {tRNA}]_{c2} = [\hbox {tRNA}]_{n} = [\hbox {tRNA}]_{N} = \omega _{r2} = \omega _{br} = 0$ and $\omega _{p} \rightarrow \infty$, $\omega _{bf} \rightarrow \infty$, $\omega _{h2} \rightarrow \infty$, the model reduces to

$$\begin{aligned} {\mathrm{Ribosome}}+\hbox {tRNA}_{c1} {\mathop {\rightleftharpoons }^{\omega ^{0}_{a,c1}}_{\omega _{r1}}} 2 \mathop {\rightarrow }^{\omega _{h1}} 5. \end{aligned}$$

(22)

which is, formally, identical to the MM reaction (18). In this limit, the expression (20) reduces to

$$\begin{aligned} \frac{1}{V} = \frac{1}{\omega _{h1}} + \biggl (\frac{\left( \omega _{h1}+\omega _{r1}\right) / \omega ^{0}_{a,c1}}{\omega _{h1}}\biggr )\frac{1}{\left[ \hbox {tRNA}\right] _{c1}} \end{aligned}$$

(23)

which is identical to MM equation (19) because of the correspondence $\omega _{h1} \longleftrightarrow k_{2} = V_\mathrm{max}$ and $(\omega _{h1}+\omega _{r1})/\omega ^{0}_{a,c1} \longleftrightarrow (k_{-1}+k_{2})/k_{1} = K_{M}$. Thus, on the right-hand side of the equation (20), the sum of the last four terms is the generalized counterpart of $1/V_\mathrm{max}$, while the first term is the generalized analog of $K_{M}/V_\mathrm{max}[S]$.

Fig. 4

(Color figure online) 1 / V is plotted against $1/[\hbox {tRNA}]_{c1}$ for our model; this plot is the analog of Lineweaver–Burk plot for the Michaelis–Menten reaction. For all the four plots (a–d), except for $\omega _{a}$, $\omega '_{a}$, $\omega ''_{a}$, $\omega '''_{a}$, the numerical values assigned to the rate constants for all the four tRNA species are those listed in the first column of Table 1 while $\omega _{a}$ is varied from $0\,\hbox {to}\,50\,\hbox {s}^{-1}$. The other parameters are as follows: a $\omega '_{a}=0$, $\omega ''_{a}=0$ and $\omega '''_{a}=0$; b $\omega '_{a}=25\; \hbox {s}^{-1}$, $\omega ''_{a}=0$ and $\omega '''_{a}=0$; c $\omega '_{a}=25\; \hbox {s}^{-1}$, $\omega ''_{a}=25\; \hbox {s}^{-1}$ and $\omega '''_{a}=0$; and d $\omega '_{a}=25\; \hbox {s}^{-1}$, $\omega ''_{a}=25\; \hbox {s}^{-1}$ and $\omega '''_{a}=25\; \hbox {s}^{-1}$

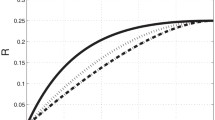
Note that, from the perspective of enzymatic reactions, in each elongation cycle four distinct species of substrates (tRNA molecules) compete for the same enzyme. In order to graphically demonstrate the effects of this competition among the substrates, in Fig. 4 we plot 1 / V as a function of $1/[\hbox {tRNA}]_{c1}$ under four different conditions.

Figure 4a corresponds to the simplest scenario where only correctly charged tRNA molecules are present. In this case, because of the absence competition among substrates, the plot is linear. This linear plot in Fig. 4a is the characteristic of MM equation displayed in what is known as the Lineweaver–Burk plot. By fitting the data of Fig. 4a to the MM equation (19), where the substrate concentration [S] is identified as $[\hbox {tRNA}]_{c1}$, we find $K_{m}/V_\mathrm{max}=1.44$ and $1/V_\mathrm{max}=0.208$; hence $K_{m} \simeq 6.9$ and $V_\mathrm{max} \simeq 4.8$ amino acids per second (or, equivalently, codons per second). The deviation from the linearity, as shown in Fig. 4b, arises from the presence of the competing second species of the tRNA molecules. The corresponding plots in Fig. 4c, d exhibit the increasing deviations from the single-substrate MM equation as the number of competing substrates increases. Interestingly, all the curves plotted in Fig. 4a–d have the same slope 1.44 in the limit $1/[\hbox {tRNA}]_{c1} \rightarrow 0$, i.e., $[\hbox {tRNA}]_{c1} \rightarrow \infty$. One way of characterizing the extent of the deviation of the curves in Fig. 4b–d from linearity, with the increasing number of competing substrates, is by computing the saturation values of these curve in the limit $1/[\hbox {tRNA}]_{c1} \rightarrow \infty$; these values are approximately 0.27, 0.24 and 0.23, respectively.

The numerical values assigned to the rate constants for the plots in Fig. 4 are not realistic in the sense that these do not reflect the intuitively expected relative strengths of the corresponding rates for the four different species of tRNA molecules. The sole purpose of treating all the four species of tRNA molecules on equal footing is to demonstrate the trend of increasing deviation from linearity on the Lineweaver–Burk plot with the increasing number of competing substrates. For plotting all the remaining graphs, we have used the parameter values as given in the Table 1.

Table 1 Values for different parameters

Fig. 5

(Color figure online) The fraction $\epsilon _\mathrm{mc}$ of error caused by mis-charged tRNA is plotted in 3D against the rejection factors ${\mathcal {R}}''$ and ${\mathcal {R}}'''$ of the near-cognate and non-cognate tRNAs, respectively. The parameters $\omega _{r2}''$ and $\omega _{r2}'''$ have been varied from 0 to 50 s$^{-1}$ keeping the values of all the other parameters fixed at those listed in Table 1

Fig. 6

(Color figure online) Same as in Fig. 5, except that the fraction $\epsilon _\mathrm{mr}$ of error caused by mis-reading of mRNA is plotted against ${\mathcal {R}}''$ and ${\mathcal {R}}'''$

Fig. 7

(Color figure online) The errors $E_\mathrm{mc}$, $E_\mathrm{mr}$ and E are plotted against the rejection factor ${\mathcal {R}}''$ for a fixed value of ${\mathcal {R}}'''$ The parameter $\omega _{r2}''$ has been varied from 0 to 25 s$^{-1}$ keeping the values of all the other parameters fixed at those listed in Table 1

The two-dimensional plots of the error fractions $\epsilon _\mathrm{mc}$ and $\epsilon _\mathrm{mr}$ against the rejection factors ${\mathcal {R}}''$ and ${\mathcal {R}}'''$ are shown in Figs. 5 and 6, respectively. Both show how the error fraction $\epsilon _\mathrm{mr}$ decreases, while the fraction $\epsilon _\mathrm{mc}$ increases with increasing ${\mathcal {R}}''$ and ${\mathcal {R}}'''$. The total mis-sense error can also decrease because, under favorable conditions, the increase of $E_\mathrm{mc}$ with ${\mathcal {R}}''$ is more than compensated by the simultaneous decrease of $E_\mathrm{mr}$, as shown in Fig. 7.

One of the main results reported above is the analytical expression for the average rate of translation, as given by Eq. 20, in the steady state. This average rate is the inverse of the mean time of dwell of a ribosome at successive codons (Sharma and Chowdhury 2011a) in the stochastic model reported in this paper. Ideally, for any such stochastic model of translational kinetics it is desirable to derive the full probability density for the dwell times of a ribosome. Therefore, we now give an outline of our derivation of the probability density f(t) of the dwell times of a ribosome in our model.

In order to simplify our calculations, following the trick used in Sharma and Chowdhury (2011a), we assume that the ribosome makes a transition to a hypothetical state $\tilde{1}$ at the $(j+1)$-th codon, after reaching the chemical state 5 or $5^{*}$ at the j-th codon. It then relaxes to the chemical state 1 at the same codon $j+1$ at a rate $\delta$. We can recover our original model by taking $\delta \rightarrow \infty$. The probability of finding the ribosome in this hypothetical state is denoted by $\widetilde{P_1}(j+1,t)$. Now, we define the dwell time of the ribosome at a particular codon, say the j-th, by the time taken by the ribosome to reach state $\tilde{1}$ at the $(j+1)$-th codon, starting from the state 1 at the j-th codon. The master equations governing the time evolution of the probabilities, the normalization condition as well as the initial conditions for the set of master equations are given in Appendix C. The probability of incorporation of one amino acid to the growing polypeptide in the time interval between t and $t+\Delta t$ is $f(t)\Delta t$ where f(t) is given by Sharma and Chowdhury (2011a)

$$\begin{aligned} f(t)=\dfrac{\Delta \widetilde{P_{1}}(t)}{\Delta t}= \omega _{h2}P_{5}(t) + \Omega _{h2}P^{*}_{5}(t). \end{aligned}$$

(24)

Since $P_{\mu }(t)$ are time-dependent solutions under the specific initial condition mentioned above, we cannot use the steady-state (i.e., time-independent) solutions derived in Appendix A. Instead, we adopted two alternative approaches for finding the probability density f(t). In the first, which is essentially an analytical approach, we found f(t) by the use of a standard technique (Sharma and Chowdhury 2011a) based on Laplace transform. However, the analytical expressions of $P_{5}(s)$ and $P_{5}^{*}(s)$ in the Laplace space are too long (covering several pages) to be reproduced here. Therefore, instead, we have substituted the numerical values of the parameters listed in Table 1 and, then, carried out the inverse Laplace transform that involved finding the roots of a 5th degree polynomial which were calculated numerically. The four curves plotted graphically (by lines) in Fig. 8 have been obtained by repeating this procedure for four different values of $\omega _{a}$. In the second approach, for the given initial condition, we numerically solved the master equations given in Appendix C (which are essentially a set of coupled ordinary differential equations) by a standard ODE solver in MATLAB and hence obtained f(t) by substituting $P_{5}(t)$ and $P^{*}_{5}(t)$ into (24). These numerical results for f(t) are plotted in Fig. 8 by discrete symbols. Results obtained by the two methods are in excellent agreement with each other.

Fig. 8

(Color figure online) The probability density of dwell times is plotted for four different values of $\omega _a$ keeping all the other parameters fixed at the values listed in Table 1. The lines have been obtained by inverse Laplace transform of analytically derived expressions in Laplace space for the specific parameter values listed in Table 1 (see the text for details). The data obtained from the alternative direct numerical solution of the master equations (see the text for details) have been plotted using discrete symbols

As $\omega _{a}$ increases the probability density f(t) becomes sharper. This trend of variation of the width of the distribution is consistent with the intuitive expectation that fluctuations in the dwell time, caused by the low concentration of tRNA, would become stronger with the decrease of $\omega _{a}$ which is directly proportional to $[\hbox {tRNA}]_{c1}$. To quantify the relative strength of the fluctuation and mean of the dwell times, we have computed the numerical values of the randomness parameter, defined as

$$\begin{aligned} r=\frac{\langle t^{2}\rangle -\langle t \rangle ^{2}}{\langle t \rangle ^{2}}, \end{aligned}$$

(25)

for the four curves plotted in Fig. 8; these data are presented in Table 2.

Table 2 The numerical values of the randomness parameter $r=(\langle t^{2} \rangle -\langle t \rangle ^{2})/\langle t \rangle ^{2}$ for the four curves plotted in Fig. 8

Naturally occurring mRNA templates in living cells consist of a heterogeneous sequence of nucleotides and, consequently, not all the codons are identical, in general. This feature of real mRNA templates can be captured in our theoretical model by assigning to each of rate constant different numerical values for translating different codons. However, only numerical results can be obtained in such cases. But, in order to derive the results analytically (in terms of closed form mathematical formulae), in this paper, we have considered the special case where the numerical values of each rate constant is independent of the type of the codon.

Fig. 9

(Color figure online) A mRNA template with a homogeneous (poly-U) coding sequence and the corresponding sequence of amino acids (Phe) are shown to propose an experimental test of our theoretical predictions (see the text for details)

We now propose an in vitro experimental setup for testing our theoretical predictions reported in this paper. A sequence homogeneous mRNA template (for example, a poly-U, as shown schematically in Fig. 9) would be ideally suited for this purpose. Such templates are used routinely for in vitro experiments (Uemura et al. 2010). The coding sequence in such a mRNA template that is actually translated consists of $N_\mathrm{c}$ number of identical codons UUU; in the poly-U template of Fig. 9, $N_\mathrm{c} = 6$. The coding sequence is preceded by a normal start codon (AUG) and is followed by a stop codon (UAA). The untranslated region (UTR) upstream from the start codon is required not only for assembling the ribosome from its subunits but also for stabilizing the pre-initiation complex. At the $3^{\prime }$-end, the stop codon is followed by a sequence of noncoding codons UUU; this region merely ensures the absence of any ‘edge effect’, i.e., the translation is not affected when the ribosome approaches the $3^{\prime }$-end of the codon sequence.

The optical method proposed here exploits labeling of the four species of tRNA molecules by four different fluorescent dyes of four distinct colors. Each UUU codon codes for the amino acid phenylalanine (abbreviated Phe or F). Targeted (site specific) mutation at the editing site of the aa-tRNA synthetase would produce a defective variant of the enzyme whose editing mechanism has been disabled. The cognate tRNA molecules labeled by red fluorescent dye should be charged with amino acid Phe by the wild-type aa-tRNA synthetase. In contrast, the cognate tRNA molecules labeled by green fluorescent dye should be separately charged with some amino acid other than Phe by the mutated aa-tRNA synthetase. Although the latter charging reaction is expected to proceed at a much slower rate than the former, yield can still be significant if the concentration of the amino acid substrate is sufficiently high. Thus, red and green fluorescence would signal correctly charged and mis-charged cognate tRNA species, respectively.

A good choice for the corresponding near-cognate tRNA would be tRNALeu because it is cognate for the codon CUU which codes for leucine (abbreviated L). The correctly charged near-cognate tRNA can be labeled by orange dye while the non-cognate tRNA can be labeled by yellow dye. The color of the fluorescence pulse identifies the monomer species that elongates the polypeptide by one unit; monitoring the colors of the fluorescence pulses, one would get an estimate of mis-sense error arising separately from mis-charging of tRNA and mis-reading of mRNA. Moreover, the time interval between the arrival of the successive aa-tRNA molecules provides an estimate of the dwell times of the ribosome. Usually, the coding sequence of such poly-U mRNA strands is quite short. Therefore, for collecting enough data to extract the DDT, the experiment has to be repeated sufficiently large number of times.

4 Summary and Conclusion

In this paper, we have developed a theoretical model that includes both the effects of mis-charging of tRNA and mis-reading of mRNA during the elongation cycle of gene translation. It also allows explicit distinction between (i) correctly charged cognate tRNA, (ii) incorrectly charged cognate tRNA, (iii) correctly charged near-cognate tRNA, and (iv) correctly charged non-cognate tRNA. For each of the four species, the master equations capture only the essential steps of the elongation cycle. From these equations, we obtain the distribution of the dwell times of the ribosome at successive codons which is identical to the distribution of the times taken to incorporate the successive amino acids in the growing protein. From the steady-state solutions of the master equations, we also derive exact analytical formulae (10)–(15) that characterize various aspects of the erroneous protein polymerization process, particularly the average speed and fidelity of polymerization. The average speed of the ribosome, i.e., the average rate (20) of elongation of the protein, is an interesting generalization of the Michaelis–Menten equation that governs the average rate of a very simple enzymatic reaction. Some important implications of the analytical results reported here have been emphasized by plotting the results graphically. In particular, the plots show how with increasing rates of rejection of the near-cognate and non-cognate tRNAs the relative contribution of the mis-charged cognate tRNAs to the overall mis-sense error increases.

Most of the experimental works on mis-reading error have been carried out for bacteria. So far as the eukaryotes are concerned, a comprehensive analysis of translational mis-reading error in budding yeast has been reported by Kramer et al. (2010). Mis-charging of tRNA and the failure of the editing mechanisms have been investigated separately for a long time (Ling et al. 2009; Yadavalli and Ibba 2012). However, to our knowledge, the relative contribution of mis-charging error to the overall mis-sense error has not been measured quantitatively in any experiment on translational kinetics. It is worth pointing out that a mis-charging error is not always detrimental for biological function of a cell and are believed to play some regulatory roles under special conditions (Pan 2013; de Pouplana et al. 2014; Ruan et al. 2008; Fan et al. 2015).

The dependence of the frequencies of mis-reading error on the codon usage and tRNA concentration have been investigated extensively in the past (Garai et al. 2009; Fluitt et al. 2007; Zouridis and Hatzimanikatis 2008; Basu and Chowdhury 2007; Shah and Gilchrist 2010; Rudorf and Lipowsky 2015); typical frequencies of mis-reading error can be as high as 1 in $10^{3}$ (Kramer and Farabaugh 2007). But, to our knowledge, mis-charging has not been incorporated so far in any mathematical model of kinetics of translation because under normal circumstances mis-charging error is as low as 1 in $10^5$ (or even lower). But, when subjected to various types of stress, at least ten fold increase in mis-charging has been observed (Netzer 2010). The model and the analytical formulae derived here will be useful in analyzing the data collected in future experiments that might be performed for investigation of the same phenomenon.

Next, we point out some features of the model that should be reflected in the experimental set up which may, in near future, be analyzed with the analytical formulae reported in this paper. For a natural mRNA molecule, because of its sequence inhomogeneity, the identity of the cognate tRNA keeps changing from one codon to another. On the other hand, the rate constants in our mathematical derivation is based on the assumption that the rates are independent of the position of the ribosome, i.e., independent of the identity of the codons. Thus, the sequence heterogeneity of natural mRNA molecules make those unsuitable for direct comparison with the analytical formulae reported here. Nevertheless, the model can be simply extended by assigning codon-dependent rate constants; but, in that case the results cannot be derived analytically (with closed form mathematical expressions) although all the quantities can be evaluated numerically. Since no experimental data for direct comparison is available at present, we have not carried out numerical study of the sequence-dependent model.

As an alternative to sequence inhomogeneous real mRNA, a synthetic mRNA with homogeneous sequence can be used to directly test the validity of our analytical formulae reported here. For example, poly-U, along with the necessary start-, stop codons and untranslated region (UTR) upstream from the start codon (Sharma and Chowdhury 2011a) could be a good candidate for this purpose. For any study of mis-sense error, the tRNA species which contribute the successive amino acids of the growing protein have to be identified. Fluorescence-based optical techniques (Uemura et al. 2010; Chen and Tsai 2012) seem to be ideally suited for this purpose. The model will have to be extended in future also to incorporate the effects of microenvironment, cell cycle phase, etc. on translation. We hope that the relative quantitative contributions of mis-charging of tRNA and mis-reading of mRNA will be measured experimentally in near future and the analytical formulae derived here will find use in analyzing the experimental data. The experimental data will also guide extension of the model to make it more realistic by capturing features that are missing from the simple version reported in this paper.

Appendices

Appendix A: Master Equations and Steady-State Probabilities

The master equations governing the time evolution of the probabilities can be written as:

$$\begin{aligned} \dfrac{\mathrm{d}P_{1}(t)}{\mathrm{d}t}= & {} -\left( \omega _{a}+\omega ^{\prime }_{a}+\omega ^{\prime \prime }_{a} +\omega ^{\prime \prime \prime }_{a}\right) P_{1}(t)\nonumber \\&+\, \omega _{r1} P_{2}(t) + \omega ^{\prime }_{r1}P^{\prime }_{2}(t) + \omega ^{\prime \prime }_{r1}P^{\prime \prime }_{2}(t) \nonumber \\&+\, \omega ^{\prime \prime \prime }_{r1}P^{\prime \prime \prime }_{2}(t) + \omega _{r2}P_{3}(t) + \omega ^{\prime }_{r2}P^{\prime }_{3}(t) \nonumber \\&+\, \omega ^{\prime \prime }_{r2}P^{\prime \prime }_{3}(t) + \omega ^{\prime \prime \prime }_{r2}P^{\prime \prime \prime }_{3}(t) \nonumber \\&+ \omega _{h2}P_{5}(t) + \Omega _{h2}P^{*}_{5}(t) \nonumber \\ \dfrac{\mathrm{d}P_{2}(t)}{\mathrm{d}t}= & {} \omega _{a}P_{1}(t) - \left( \omega _{r1} + \omega _{h1}\right) P_{2}(t) \nonumber \\ \dfrac{\mathrm{d}P_{3}(t)}{\mathrm{d}t}= & {} \omega _{h1}P_{2}(t) - \left( \omega _{p} + \omega _{r2}\right) P_{3}(t) \nonumber \\ \dfrac{\mathrm{d}P_{4}(t)}{\mathrm{d}t}= & {} \omega _{p}P_{3}(t) + \omega ^{\prime }_{p}P^{\prime }_{3}(t) + \omega _{br}P_{5}(t) - \omega _{bf}P_{4}(t) \nonumber \\ \dfrac{\mathrm{d}P_{5}(t)}{\mathrm{d}t}= & {} \omega _{bf}P_{4}(t) - \left( \omega _{h2} + \omega _{br}\right) P_{5}(t) \nonumber \\ \dfrac{\mathrm{d}P^{\prime }_{2}(t)}{\mathrm{d}t}= & {} \omega ^{\prime }_{a}P_{1}(t) - \left( \omega ^{\prime }_{r1} + \omega ^{\prime }_{h1}\right) P^{\prime }_{2}(t) \nonumber \\ \dfrac{\mathrm{d}P^{\prime }_{3}(t)}{\mathrm{d}t}= & {} \omega ^{\prime }_{h1}P^{\prime }_{2}(t) - \left( \omega ^{\prime }_{r2} + \omega ^{\prime }_{p}\right) P^{\prime }_{3}(t) \nonumber \\ \dfrac{\mathrm{d}P^{\prime \prime }_{2}(t)}{\mathrm{d}t}= & {} \omega ^{\prime \prime }_{a}P_{1}(t) - \left( \omega ^{\prime \prime }_{r1} + \omega ^{\prime \prime }_{h1}\right) P^{\prime \prime }_{2}(t) \nonumber \\ \dfrac{\mathrm{d}P^{\prime \prime }_{3}(t)}{\mathrm{d}t}= & {} \omega ^{\prime \prime }_{h1}P^{\prime \prime }_{2}(t) - \left( \Omega _{p} + \omega ^{\prime \prime }_{r2}\right) P^{\prime \prime }_{3}(t) \nonumber \\ \dfrac{\mathrm{d}P^{\prime \prime \prime }_{2}(t)}{\mathrm{d}t}= & {} \omega ^{\prime \prime \prime }_{a}P_{1}(t) - \left( \omega ^{\prime \prime \prime }_{h1} + \omega ^{\prime \prime \prime }_{r1}\right) P^{\prime \prime \prime }_{2}(t) \nonumber \\ \dfrac{\mathrm{d}P^{\prime \prime \prime }_{3}(t)}{\mathrm{d}t}= & {} \omega ^{\prime \prime \prime }_{h1}P^{\prime \prime \prime }_{2}(t) - \left( \Omega ^{\prime }_{p} + \omega ^{\prime \prime \prime }_{r2}\right) P^{\prime \prime \prime }_{3}(t) \nonumber \\ \dfrac{\mathrm{d}P^{*}_{4}(t)}{\mathrm{d}t}= & {} \Omega _{p}P^{\prime \prime }_{3}(t) + \Omega _{br} P^{*}_{5}(t) + \Omega ^{\prime }_{p}P^{\prime \prime \prime }_{3}(t) - \Omega _{bf}P^{*}_{4}(t) \nonumber \\ \dfrac{\mathrm{d}P^{*}_{5}(t)}{\mathrm{d}t}= & {} \Omega _{bf}P^{*}_{4}(t) - \left( \Omega _{br} + \Omega _{h2}\right) P^{*}_{5}(t) \end{aligned}$$

(26)

with the normalization condition

$$\begin{aligned}&P_{1}(t)+P_{2}(t)+P_{3}(t)+P_{4}(t)+P_{5}(t) +P'_{2}(t)+P'_{3}(t)+P''_{2}(t)+P''_{3}(t)\nonumber \\&\quad +P'''_{2}(t)+P'''_{3}(t)+P^{*}_{4}(t)+P^{*}_{5}(t)=1. \end{aligned}$$

(27)

The steady-state solutions $P_{\mu }$ of equations (26) are given by

$$\begin{aligned} P_{1}=\dfrac{1}{X1} \end{aligned}$$

(28)

where

$$\begin{aligned} X1= & {} A \bigg [\dfrac{1}{\omega _{h1}}\bigg (1+\dfrac{\omega _{r2}}{\omega _p}\bigg )+\dfrac{1}{\omega _p}+\dfrac{1}{\omega _{bf}} \bigg (1+\dfrac{\omega _{br}}{\omega _{h2}}\bigg ) +\dfrac{1}{\omega _{h2}}\bigg ] \\&+\, B \bigg [\dfrac{1}{\omega _{h1}'}\bigg (1 +\dfrac{\omega _{r2}'}{\omega _p'}\bigg )+\dfrac{1}{\omega _p'} +\dfrac{1}{\omega _{bf}}\bigg (1+\dfrac{\omega _{br}}{\omega _{h2}}\bigg ) +\dfrac{1}{\omega _{h2}}\bigg ] \\&+\, C \bigg [\dfrac{1}{\omega _{h1}''} \bigg (1+\dfrac{\omega _{r2}''}{\Omega _p}\bigg ) +\dfrac{1}{\Omega _p}+\dfrac{1}{\Omega _{bf}}\bigg (1+\dfrac{\Omega _{br}}{\Omega _{h2}}\bigg )+\dfrac{1}{\Omega _{h2}}\bigg ] \\&+\, D \bigg [\dfrac{1}{\omega _{h1}'''} \bigg (1+\dfrac{\omega _{r2}'''}{\Omega _p'}\bigg ) +\dfrac{1}{\Omega _p'}+\dfrac{1}{\Omega _{bf}}\bigg (1+\dfrac{\Omega _{br}}{\Omega _{h2}}\bigg )+\dfrac{1}{\Omega _{h2}}\bigg ] \end{aligned}$$

$$\begin{aligned} P_{2}= & {} A \bigg [\dfrac{1}{\omega _{h1}} \bigg (1+\dfrac{\omega _{r2}}{\omega _p}\bigg ) \bigg ]P_{1} \end{aligned}$$

(29)

$$\begin{aligned} P_{3}= & {} A \bigg [\dfrac{1}{\omega _{p}}\bigg ] P_{1} \end{aligned}$$

(30)

$$\begin{aligned} P_{4}= & {} (A+B) \bigg [\dfrac{1}{\omega _{bf}} \bigg (1+\dfrac{\omega _{br}}{\omega _{h2}}\bigg )\bigg ]P_{1} \end{aligned}$$

(31)

$$\begin{aligned} P_{5}= & {} (A+B) \bigg [\dfrac{1}{\omega _{h2}}\bigg ] P_{1} \end{aligned}$$

(32)

$$\begin{aligned} P_{2}'= & {} B \bigg [\dfrac{1}{\omega _{h1}'} \bigg (1+\dfrac{\omega _{r2}'}{\omega _p'}\bigg )\bigg ]P_{1}\end{aligned}$$

(33)

$$\begin{aligned} P_{3}'= & {} B \bigg [\dfrac{1}{\omega _{p}'}\bigg ] P_{1}\end{aligned}$$

(34)

$$\begin{aligned} P_{2}''= & {} C \bigg [\dfrac{1}{\omega _{h1}''} \bigg (1+\dfrac{\omega _{r2}''}{\Omega _p}\bigg )\bigg ] P_{1}\end{aligned}$$

(35)

$$\begin{aligned} P_{3}''= & {} C \bigg [\dfrac{1}{\Omega _{p}}\bigg ] P_{1} \end{aligned}$$

(36)

$$\begin{aligned} P_{2}'''= & {} D \bigg [\dfrac{1}{\omega _{h1}'''} \bigg (1+\dfrac{\omega _{r2}'''}{\Omega _p'}\bigg )\bigg ] P_{1}\end{aligned}$$

(37)

$$\begin{aligned} P_{3}'''= & {} D \bigg [\dfrac{1}{\Omega _{p}'}\bigg ] P_{1}\end{aligned}$$

(38)

$$\begin{aligned} P^{*}_{4}= & {} (C+D) \bigg [\dfrac{1}{\Omega _{bf}} \bigg (1+\dfrac{\Omega _{br}}{\Omega _{h2}}\bigg )\bigg ] P_{1}\end{aligned}$$

(39)

$$\begin{aligned} P^{*}_{5}= & {} (C+D) \bigg [\dfrac{1}{\Omega _{h2}}\bigg ] P_{1} \end{aligned}$$

(40)

Appendix B: Intuitive Derivation of the Expression for Average Rate of Translation

Following Cleland’s approach Cleland (1975) for replacing complex network of biochemical pathways by a simpler equivalent network and deriving the effective rates of the transitions of that network, we derive the expression for the average velocity of the ribosome in our model. To illustrate the method, we consider a simpler reaction

$$\begin{aligned} X \mathop {\rightleftharpoons }^{k_{1}}_{k_{-1}} Y \mathop {\rightarrow }^{k_{2}} Z \end{aligned}$$

The effective rate constant, $k_{1}'$, for $X \xrightarrow {k_{1}'} Y,$ is given by

$$\begin{aligned} k_{1}'=\dfrac{k_{1}k_{2}}{k_{-1}+k_{2}} \end{aligned}$$

The same treatment can be applied to our model.

Let us first assume that only correctly charged cognate tRNAs are present (i.e., assuming that mis-charged cognate, near-cognate and non-cognate tRNAs are absent in the surrounding). For the five consecutive steps of the cycle, we denote the transit times by $T_{1}$, $T_{2}$, $T_{3}$, $T_{4}$ and $T_{5}$, respectively. It is straightforward to see that

$$\begin{aligned} T_{1}= & {} \dfrac{1}{\omega _{a}}\bigg (1+\dfrac{\omega _{r1}}{\omega _{h1}}\bigg )\bigg (1+\dfrac{\omega _{r2}}{\omega _p}\bigg ) = \frac{1}{A} \end{aligned}$$

(41)

$$\begin{aligned} T_{2}= & {} \dfrac{1}{\omega _{h1}} \bigg (1+\dfrac{\omega _{r2}}{\omega _p}\bigg )\end{aligned}$$

(42)

$$\begin{aligned} T_{3}= & {} \dfrac{1}{\omega _{p}}\end{aligned}$$

(43)

$$\begin{aligned} T_{4}= & {} \dfrac{1}{\omega _{bf}} \bigg (1+\dfrac{\omega _{br}}{\omega _{h2}}\bigg )\end{aligned}$$

(44)

$$\begin{aligned} T_{5}= & {} \dfrac{1}{\omega _{h2}} \end{aligned}$$

(45)

Therefore, for the above cycle, i.e., when only correctly charged cognate tRNA molecules are present in the surrounding, the average velocity of the ribosome would be

$$\begin{aligned} \dfrac{1}{V_{c1}}= & {} T_{c1}= T_{1}+T_{2}+T_{3}+T_{4}+T_{5} \end{aligned}$$

(46)

Similarly, for the other three cycles we can specify the transit times in a similar manner. For mis-charged cognate tRNA, the corresponding symbols are $T'_{1},T'_{2},T'_{3},T'_{4},T'_{5}$, respectively, while for near-cognate tRNA, ths symbols are $T''_{1},T''_{2},T''_{3},T''_{4},T''_{5}$, respectively. For non-cognate tRNA, we have $T'''_{1},T'''_{2},T'''_{3},T'''_{4},T'''_{5}$, respectively.

Next, let us consider the general case when all the four different substrates are present in the surrounding; the kinetics of the system is described by full model shown in Fig. 3. The transit times are analogous to resistances in electrical circuits, which means that for a series of reaction, the transit times are additive and for parallel reaction pathways, the reciprocals of the transit times are additive. Hence, the average velocity for the complete model is

$$\begin{aligned} \dfrac{1}{V_\mathrm{tot}}= & {} T_\mathrm{tot}=\dfrac{A}{A+B+C+D} \Bigg (T_{1,\mathrm{eff}}+T_{2}+T_{3}+T_{4}+T_{5} \Bigg )\end{aligned}$$

(47)

$$\begin{aligned}&+\dfrac{B}{A+B+C+D}\Bigg (T_{1,\mathrm{eff}}+T'_{2}+T'_{3}+T'_{4}+T'_{5} \Bigg )\end{aligned}$$

(48)

$$\begin{aligned}&+ \dfrac{C}{A+B+C+D}\Bigg (T_{1,\mathrm{eff}}+T''_{2}+T''_{3}+T''_{4}+T''_{5} \Bigg )\end{aligned}$$

(49)

$$\begin{aligned}&+ \dfrac{D}{A+B+C+D}\Bigg (T_{1,\mathrm{eff}}+T'''_{2}+T'''_{3}+T'''_{4}+T'''_{5} \Bigg ) \end{aligned}$$

(50)

where

$$\begin{aligned} \dfrac{1}{T_{1,\mathrm{eff}}}= \dfrac{1}{T_{1}}+\dfrac{1}{T_{1}'}+\dfrac{1}{T_{1}''}+\dfrac{1}{T_{1}'''} \equiv A+B+C+D \end{aligned}$$

(51)

Appendix C: Master Equations and Derivation of Dwell Time Distribution

The master equations governing the time evolution of the probabilities are identical to those given in Appendix A, except for the following:

$$\begin{aligned} \dfrac{\mathrm{d}P_{1}(t)}{\mathrm{d}t}= & {} -\left( \omega _{a}+\omega ^{\prime }_{a} +\omega ^{\prime \prime }_{a}+\omega ^{\prime \prime \prime }_{a}\right) P_{1}(t)\nonumber \\&+\, \omega _{r1} P_{2}(t) + \omega ^{\prime }_{r1}P^{\prime }_{2}(t) + \omega ^{\prime \prime }_{r1}P^{\prime \prime }_{2}(t) \nonumber \\&+\, \omega ^{\prime \prime \prime }_{r1}P^{\prime \prime \prime }_{2}(t) + \omega _{r2}P_{3}(t) + \omega ^{\prime }_{r2}P^{\prime }_{3}(t) \nonumber \\&+\, \omega ^{\prime \prime }_{r2}P^{\prime \prime }_{3}(t) + \omega ^{\prime \prime \prime }_{r2}P^{\prime \prime \prime }_{3}(t) \nonumber \\ \dfrac{\mathrm{d}\widetilde{P_{1}}(t)}{\mathrm{d}t}= & {} \omega _{h2}P_{5}(t) + \Omega _{h2}P^{*}_{5}(t) \end{aligned}$$

(52)

and the normalization condition becomes

$$\begin{aligned}&P_{1}(t)+P_{2}(t)+P_{3}(t)+P_{4}(t)+P_{5}(t) +P'_{2}(t)+P'_{3}(t)+P''_{2}(t)+P''_{3}(t)\nonumber \\&\quad +P'''_{2}(t)+P'''_{3}(t)+P^{*}_{4}(t) +P^{*}_{5}(t)+\widetilde{P_{1}}(t)=1. \end{aligned}$$

(53)

Here, we take the initial conditions to be $P_{1}(0)=1$, and $P_{2}(0)=P_{3}(0)=P_{4}(0)=P_{5}(0)=P'_{2}(0) =P'_{3}(0)=P''_{2}(0)=P''_{3}(0)=P'''_{2}(0) =P'''_{3}(0)=P^{*}_{4}(0)=P^{*}_{5}(0)= \widetilde{P_{1}}(0)=0$.