1 Introduction

The objective of this paper is to propose new numerical methods for the bifurcation analysis of a large number of physiologically structured population models (PSPM) formulated with delay equations. The methods allow the computation of equilibrium branches and the detection of bifurcation points under one-parameter variation and the continuation of bifurcation curves in two-parameter planes.

In de Roos et al. (2010), numerical methods are developed for a size-structured (consumer) population competing for an unstructured (resource) population. The methods are used by Zhang et al. (2012) to analyse the size-dependent mechanism of energy allocation. The consumer–resource model is a generalization of a well-established biological model of Daphnia consuming algae (see e.g. McCauley et al. 1999; Chapter 9 of de Roos and Persson 2013).

In various models, the structured population interacts with several dynamic unstructured populations: in de Roos and Persson (2002), a top predator is incorporated additionally to the resource; in Getto et al. (2005), two resource populations, one for juveniles one for adults, are considered. In the formulation of the well-established fish cannibalism model in Claessen et al. (2004), the natural density dependence of vital rates can be cut by introducing so-called environmental interaction variables describing ingestion and predation pressure, see Diekmann et al. (2001) and Getto et al. (2005), see also Alarcón et al. (2014) for environmental interaction variables in a cell population model. We here define the environment via two components: the unstructured populations and the environmental interaction variables. Then, on the basis of the discussed points, we generalize the environment corresponding to de Roos et al. (2010) in two ways:

  • transition from one to several unstructured populations,

  • additional incorporation of environmental interaction variables.

The model under study in de Roos et al. (2010) was formulated as a Volterra functional equation (VFE) for the structured population, coupled to a delay differential equation (DDE) with distributed delay for the dynamics of the resource (the intrinsic resource dynamics given by an ordinary differential equation (ODE) minus a consumption term that gives rise to the delay) in Diekmann et al. (2010). Well-posedness and the principle of linearized stability for VFE/DDE is shown in Diekmann et al. (2007) and Diekmann and Gyllenberg (2012). For the analysis of sufficient conditions for consumer resource models, we refer to the works done by Diekmann et al. (2010) and by Diekmann and Korvasova (2016). By defining an interaction variable corresponding to the consumption term, we reformulate the model in de Roos et al. (2010) as a coupled system of two VFE and one ODE. We show that this formulation is suitable for both, the application of the numerical method that we elaborate and the discussed generalization. Moreover, we explain how also the generalized VFE/ODE fits into the discussed analytical framework.

After the formulation of the time-dependent system for the remainder of the paper, we focus on equilibria and time-independent systems. Hence, the time-independent system serves to derive the time-independent system and provides a formulation for future aims like linearization, stability and Hopf bifurcation analysis.

Our formulation of equilibrium conditions builds up on two older ideas:

  • the introduction of the basic reproduction number facilitates the biological interpretation of steady state conditions, see Diekmann et al. (2003),

  • the formulation as VFE/DDE (and also as VFE/ODE) allows the exploitation of linearities (in the population birth rate) that are consequences of mass action laws, see Boldin (2006) and Diekmann et al. (2010).

We here carry the second idea a step further by incorporating linearities in the unstructured populations defining similar decompositions as in Boldin (2006).

For models formulated with autonomous ODE, the numerical equilibrium and bifurcation analysis can easily be carried out using packages such as MATCONT (see e.g. Dhooge et al. 2006), COCO or AUTO. These packages use continuation methods (see e.g. Allgower and Georg 2003) to compute points that approximate an implicitly defined curve. Assuming that an initial point of the curve is known, the methods predict the next point of the curve by computing its tangent and then correct the predicted point by applying a modified Newton method (see e.g. Chapter 7 in Kelley 1995). The above-mentioned continuation packages permit the approximation of equilibrium curves, the continuation of limit cycles, the detection and computation of bifurcation points, and their continuation in parameter planes. For delay equation, the above-discussed software cannot be used. For DDE, the numerical equilibrium and bifurcation analysis can be done with the established package DDE-BIFTOOL (see Engelborghs et al. 2001), in particular continuation of equilibria and periodic orbits, computation of saddle-node and Hopf bifurcations and stability analysis. These routines are typically applied to equations with discrete delays but cannot be used if distributed delays appear. For linear autonomous DDE with discrete or distributed delays, stability analysis can be done with the package TRACE-DDE (see Breda et al. 2009).

The dynamics of the class of models presented in this paper is formulated at the population level with a nonlinear system of VFE/ODE. In the right-hand side of the VFE, the delay is distributed and the limits of integration are state dependent. Moreover, the kernels of the integrals are implicitly given by the solution of a nonlinear system of ODE. Due to these complexities, the existing software cannot be used to analyse equilibria and linearized stability of the class of models presented in this work.

In Kirkilionis et al. (2001), a numerical method for the computation of equilibrium branches is proposed for models formulated with VFE. The technique combines curve continuation with ODE solvers. The latter are used to compute the individual state given by the solution of nonlinear ODE and to approximate in parallel the integrals that appear in the map that defines the curve and that depend on the individual state. At the end of the paper, the authors suggest the detection and computation of transcritical, saddle-node and Hopf bifurcations as open problems. In de Roos et al. (2010), the method is extended to a bifurcation analysis of VFE/DDE systems that allows the division of parameter planes into regions of stability and, e.g. oscillation induced, instability of equilibria.

We here first extend the technique in Kirkilionis et al. (2001) to compute equilibrium branches of the presented class of models. Then, we adapt the established notions of test functions for finding bifurcation points to the context of PSPM. Next, we use these points as initial values for the continuation of bifurcations in parameter planes that, in contrast to one-parameter variation, can provide increased biological insight. In summary, we present methods for the computation of equilibria, transcritical and saddle-node bifurcations. Moreover, for the detection of transcritical bifurcations we propose new test functions that use discussed linear structures of the model to save computational cost, while for saddle-node we adapt those established for ODE systems.

We have tested and validated the developed methods with models of size-structured consumer–resource (Calsina and Saldaña 1995; Diekmann et al. 2010), trophic models describing invasion dynamics (de Roos and Persson 2002) and cannibalistic fish populations (Getto et al. 2005). For the validation, we have considered several examples for which ODE and integrals can be solved analytically. With the resulting functions, we have obtained expressions that implicitly define equilibria and bifurcations, in which there are neither integrals nor implicitly defined functions anymore. In this way, we defined standard Newton problems, the solutions of which served to compute errors which we found to lie below the tolerances of the method. By reproducing various curves from the literature, we show consistency of the obtained results with the data. We have also computed new curves and explain how some of these may serve to support analytically derived results, such as existence conditions for equilibria in Calsina and Saldaña (1995). Others of the new curves provide new biological insight by presenting a more complete picture of interesting phenomena as the life boat mechanism of cannibalism (van den Bosch et al. 1988) and regions of equilibria in parameter planes in three trophic models.

The remainder of the paper is structured as follows: We develop the formulation of PSPM as VFE/ODE in Sect. 2 and in Sect. 3 define various types of equilibria. In Sect. 4, we define equilibrium branches and bifurcation points for one-parameter variation analysis and bifurcation curves for two-parameter variation analysis. In Sect. 5, we present numerical methods for the computation of equilibrium and bifurcation curves under one- and two-parameter variation, respectively. First we introduce the numerical continuation method and discuss ODE solvers. Then, we derive the systems of equations that implicitly define the equilibrium curves and present test functions for the detection of transcritical and saddle-node bifurcations. Finally, we develop the methods for computing bifurcation curves in parameter planes. Section 6 is devoted to the validation of our methods with models from the literature. In Sect. 7, we present the conclusions of our research. Finally, in Appendix we present our algorithms in an established pseudo-code language to facilitate their implementation.

2 Formulation of a Class of Structured Population Models

In this section, we construct the general PSPM. For the modelling at the individual (i-) level and the step from the i-level to the population (p-) level, we use an analogous formalism and reasoning as for the consumer resource models in Diekmann et al. (2010) and de Roos et al. (2010).

2.1 Individual Development and Environment

We use \({{\mathcal {E}}}:=(I,E)\in {{\mathbb {R}}}^{s+n}\) to denote the environment of a structured population and \({{\mathcal {E}}}(t)\) its value at time t, where \(I(t)\in {{\mathbb {R}}}^s\) is a time-dependent vector of s interaction variables and \(E(t)\in {{\mathbb {R}}}^n\) a vector of n unstructured populations with intrinsic dynamics.

We denote by m the number of variables that are used to describe the i-state in view of its p-dynamically relevant behaviour. Commonly used i-state variables are the age or body size of the individual or related quantities. We assume a unique state at birth denoted by \(x_0 \in {{\mathbb {R}}}^m\). Next we call a history a real-valued function defined on an interval \([-a,0]\), \(a>0\), where we have in mind in particular the history of the environment and of the (to be defined) p-birth rate.

Let \(\bar{x}(\tau ):=\bar{x}(\tau ;\alpha ,\psi )\in {{\mathbb {R}}}^m\), with \(0< \tau \le \alpha \), be the i-state at age \(\tau \) assuming that at age \(\alpha \) the individual is alive and has experienced a history \(\psi \). Then, \(\bar{x}(\tau )\) is defined as the solution of the ODE

$$\begin{aligned} \begin{aligned} \frac{\hbox {d}\bar{x}(\tau )}{\hbox {d}\tau }&=g(\bar{x}(\tau ),\psi (-\alpha +\tau )), \quad 0<\tau \le \alpha , \\ \bar{x}(0)&=x_0, \end{aligned} \end{aligned}$$
(1)

where we introduce \(g(x,y)\in {{\mathbb {R}}}^{m}\) as the i-development rate for an individual that has state x and environment y. In the commonly used examples, g is the growth rate if the i-state is size, or the function that is constant one if the i-state is age. In a similar way, we denote by \(\bar{{{\mathcal {F}}}}(\tau ):=\bar{{{\mathcal {F}}}}(\tau ;\alpha ,\psi )\), with \(0< \tau \le \alpha \) the survival probability determined as the solution of

$$\begin{aligned} \begin{aligned} \frac{\hbox {d}\bar{{{\mathcal {F}}}}(\tau )}{\hbox {d}\tau }&=-\mu (\bar{x}(\tau ),\psi (-\alpha +\tau ))\bar{{{\mathcal {F}}}}(\tau ), \quad 0<\tau \le \alpha , \\ \bar{{{\mathcal {F}}}}(0)&=1, \end{aligned} \end{aligned}$$
(2)

where \(\mu (x,y)\) denotes the scalar and positive i-mortality rate for state x and environment y. Then, we denote with \(x(\alpha ,\psi )\in {{\mathbb {R}}}^m\) the i-state of an individual that at age \(\alpha \) has experienced history \(\psi \) and similarly by \({{\mathcal {F}}}(\alpha ,\psi )\) its survival probability. The latter introduced quantities x and \({{\mathcal {F}}}\) can be computed via the definitions \(x(\alpha ,\psi ):=\bar{x}(\alpha ;\alpha ,\psi )\) and \({{\mathcal {F}}}(\alpha ,\psi ):=\bar{{{\mathcal {F}}}}(\alpha ;\alpha ,\psi )\). Let us recall now the notation for translations

$$\begin{aligned} y_t(\theta )=y(t+\theta ), \quad \theta \le 0, \end{aligned}$$
(3)

of functions y of time commonly used in functional differential equations (see, for instance, Hale and Verduyn Lunel 1993). By \(y_t\) a history is defined, the history of y at time t. Then, \(x(\alpha ,{{\mathcal {E}}}_t)\) and \({{\mathcal {F}}}(\alpha ,{{\mathcal {E}}}_t)\) are, respectively, the i-state and the survival probability of an individual that at time t has age \(\alpha \). Next we denote by \(\beta (x,y)\) the i-reproduction rate, which is scalar and nonnegative, and by \(\gamma (x,y)\in {{\mathbb {R}}}^s\) the i-rate of impact at state x and environment y. The impact rate, e.g. consumption rate of resource, will a bit further down be used to specify the interaction variables. Then, the respective rates of an individual that at time t has age \(\alpha \) are given as \(\beta (x(\alpha ,{{\mathcal {E}}}_t),{{\mathcal {E}}}(t))\) and \(\gamma (x(\alpha ,{{\mathcal {E}}}_t),{{\mathcal {E}}}(t))\).

During its life, an individual can experience periods, for instance juvenile and adult period, which are such that upon the transition the individual’s dynamically relevant behaviour changes abruptly (see e.g. Diekmann et al. 2010) and so the modeller may want to incorporate jump discontinuities in the rates. Hence, we here think of the rates g, \(\mu \), \(\beta \) and \(\gamma \) as piecewise smooth functions, meaning as smooth as necessary for numerical purposes. In this sense, we denote by k the number of different life stages; hence, we can expect at most \(k-1\) switches due to discontinuities in any of the rates. Here switch refers to the switching between different expressions to define a rate upon a transition. The transition of an individual from one stage to another may be triggered by changes in its i-state and/or on its environment. Thus, it is relevant to detect and compute when a discontinuity occurs while solving numerically the system (1–2). For this, we define switch functions in a similar way than in Kirkilionis et al. (2001): As further modelling ingredients let \(d_j:=d_j(x,y)\), \(1\le j \le k-1\) be continuous functionals, such that for any fixed environment y the \((m-1)\)-manifolds implicitly defined by \(d_j(x,y)=0\) define a partition in regions where the vital rates are smooth. Moreover, we assume that the discontinuities are crossed transversally, i.e. assuming that an individual that has state \(\bar{x}(\alpha )\) is in the kth stage of its life; then for any \(j=1,\ldots ,k-1\), there exists a unique \(\tau _j\), such that for any sufficiently small \(\epsilon \)

$$\begin{aligned} d_j(\bar{x}(\tau _j-\epsilon ),\psi (-\alpha +\tau _j-\epsilon ))<0,\quad d_j(\bar{x}(\tau _j+\epsilon ),\psi (-\alpha +\tau _j+\epsilon ))>0. \end{aligned}$$
(4)

2.2 Dynamics at the Population Level

Let \(B(t)\in {{\mathbb {R}}}\) be the p-birth rate at time t. The density of individuals that at time t have age \(\alpha \) can be expressed as \({{\mathcal {F}}}(\alpha ,{{\mathcal {E}}}_t)B(t-\alpha )\). We denote by h the (finite) maximum age of individuals. Then, B should satisfy the VFE or renewal equation

$$\begin{aligned} B(t)=\int _0^h \beta (x(\alpha ,{{\mathcal {E}}}_t),{{\mathcal {E}}}(t)){{\mathcal {F}}}(\alpha ,{{\mathcal {E}}}_t)B(t-\alpha )\hbox {d}\alpha . \end{aligned}$$
(5)

In a similar way, we obtain

$$\begin{aligned} I(t)=\int _0^h \gamma (x(\alpha ,{{\mathcal {E}}}_t),{{\mathcal {E}}}(t)){{\mathcal {F}}}(\alpha ,{{\mathcal {E}}}_t)B(t-\alpha )\hbox {d}\alpha \end{aligned}$$
(6)

for the interaction variables I. Finally, we denote by \(\bar{F}\) (the motivation for the bar will become clear a little further down) a function whose value gives the rate of change of E(t), i.e.

$$\begin{aligned} \frac{\hbox {d}E(t)}{\hbox {d}t}=\bar{F}({{\mathcal {E}}}(t)). \end{aligned}$$
(7)

In summary, the dynamics at the p-level can be formulated as (5–7), with \({{\mathcal {E}}}=(I,E)\), which is a closed system with state variables B, I and E.

We remark that to apply the analytical formalism (see below), one can rewrite (5–7) as a system of the form

$$\begin{aligned} (u,v')(t)={\mathcal {G}}(u_t,v_t), \end{aligned}$$
(8)

where \({\mathcal {G}}\) acts on a product of an \(L^1\)-space and a space of continuous functions corresponding to u- and v-component, respectively. Note that if the right-hand side of (5–7) has I(t) dependence, it cannot be reproduced by defining such an operator and letting it act on \((B_t, I_t,E_t)\) because pointwise evaluation in \(L^1\) is not defined. A transformation to a system of the form (8) is possible under a reasonable assumption that includes that there exist components of \(\gamma \) that are independent of the I-variable, more precisely that \(\gamma \) has a hierarchical structure in this respect as formalized in Diekmann et al. (2001). Such a transformation step is carried out in (3.56–3.59) in Diekmann et al. (2007). In all the models considered in this paper, \(\gamma \) has the hierarchical structure such that the transformation can be done. System (8) can be interpreted as a VFE (u-component) coupled to a DDE (v-component). For such systems, well-posedness and linear stability theory is established (see Diekmann et al. 2007; Diekmann and Gyllenberg 2012).

To derive equilibrium conditions, however, the formulation (5–7), with \({{\mathcal {E}}}=(I,E)\) is more convenient and so we will not use (8).

2.3 Linearities in the Dynamics of the Unstructured p-Variables

As we will see further down, in many models due to mass action assumptions one encounters linearities at the p-level. We would like to exploit these linearities to reduce dimensions. For this purpose, it is convenient to have a notation that isolates components of a vector that have index in a certain set. Then, suppose that

$$\begin{aligned} u:=(u_1,\ldots ,u_r)^T,\quad {\mathcal {J}}:=\{j_1,\ldots ,j_k\}\subseteq \{1,\ldots ,r\},\quad \mathrm{with}\quad j_1<\ldots <j_k, \end{aligned}$$

are given.

We introduce the notation

$$\begin{aligned} u_{\mathcal {J}}:=(u_{j_1},\ldots ,u_{j_k})^T. \end{aligned}$$
(9)

Now, recalling that \(E\in {{\mathbb {R}}}^n\), i.e. n unstructured populations, we denote by l with \(0\le l\le n\) the number of unstructured populations on which we have a linear dependence in \(\bar{F}\). This means we assume that

$$\begin{aligned} \bar{F}({{\mathcal {E}}})=\left( \begin{array}{c} D({{\mathcal {E}}})E_{{\mathcal {I}}}\\ F({{\mathcal {E}}}) \end{array} \right) , \quad \begin{array}{l} {{\mathcal {I}}}:=\{1,\ldots ,l\}, \\ D_{ij}({{\mathcal {E}}}):=\delta _{ij}G_i({{\mathcal {E}}}), \; 1\le i,j\le l, \end{array} \end{aligned}$$
(10)

where \(\delta _{ij}\) denotes the Kronecker symbol such that D is diagonal, and

$$\begin{aligned} G({{\mathcal {E}}})=(G_1({{\mathcal {E}}}),\ldots ,G_l({{\mathcal {E}}}))^T\in {{\mathbb {R}}}^l\;\mathrm{and}\; F({{\mathcal {E}}})\in {{\mathbb {R}}}^{n-l} \end{aligned}$$

are given model ingredients (and \(\bar{F}\) is defined in an obvious way if \(l=0\) or \(l=n\)). Note that the assumption that the linearities are in the first l components of \(\bar{F}\) is without loss of generality. From the notation defined in (9), we here only need that

$$\begin{aligned} E_{{\mathcal {I}}}=(E_1,\ldots ,E_l), \end{aligned}$$

but further down we will make a more in depth use of the notation.

3 Equilibrium Analysis

An equilibrium state is a time-independent vector (B, I, E) that solves (5–7), with \({{\mathcal {E}}}=(I,E)\). We accept negative values for B, I and E in order to define test functions for detecting bifurcations in Sect. 5.4, but from a biological point of view only the nonnegative values of B, I and E make sense, so later on we will only consider these. From now on, we use the notation (I, E) instead of \({{\mathcal {E}}}\). Then, we find that (B, I, E) is an equilibrium if and only if

$$\begin{aligned} B(1- R_0( I, E))&=0, \end{aligned}$$
(11a)
$$\begin{aligned} I- B \varTheta ( I, E)&=0, \end{aligned}$$
(11b)
$$\begin{aligned} D( I, E) E_{{\mathcal {I}}}&=0, \end{aligned}$$
(11c)
$$\begin{aligned} F( I, E)&=0, \end{aligned}$$
(11d)

hold, where \(R_0( I, E)\) is defined by

$$\begin{aligned} R_0( I, E):=\int _0^h \beta (x(\alpha , I, E), I, E){{\mathcal {F}}}(\alpha , I, E)\hbox {d}\alpha , \end{aligned}$$
(12)

and \(\varTheta ( I, E)\) by

$$\begin{aligned} \varTheta ( I, E):=\int _0^h \gamma (x(\alpha , I, E), I, E){{\mathcal {F}}}(\alpha , I,E)\hbox {d}\alpha . \end{aligned}$$
(13)

Note that, as usual in population dynamics, \(R_0\) denotes the i-reproduction number. We call \(\varTheta \) the p-interaction variable. As it is shown later in the examples in Sect. 6, in general it is not possible to derive explicit expressions that characterize equilibrium states.

The linearities in (11) motivate us to think about different types of equilibria, for \(B=0\) or \(B\ne 0\) in (11a), and for \(E_i=0\) or \(E_i\ne 0\) for \(i\in {{\mathcal {I}}}\) in (11c). In order to define types of equilibrium states, we first define

$$\begin{aligned} {\mathcal {N}}:=\{1, \ldots , n\} \end{aligned}$$

and then say that for a set \({{\mathcal {K}}}\subseteq {{\mathcal {I}}}\), with \(\emptyset \subsetneq {{\mathcal {K}}}\subsetneq {\mathcal {N}}\), a vector

$$\begin{aligned} E\;\mathrm{is}\;{{\mathcal {K}}}\hbox {-trivial}\;:\Leftrightarrow \; E_i{\left\{ \begin{array}{ll} =0, &{}\forall i \in {{\mathcal {K}}},\\ \ne 0, &{} \forall i \in {{\mathcal {I}}}\setminus {{\mathcal {K}}}. \end{array}\right. } \end{aligned}$$
(14)

The \({{\mathcal {K}}}\)-triviality is used in the definition of transcritical bifurcations in Sect. 4.1 and implemented in the numerical methods in Sect. 5, where we consider new test functions and reduce the dimension of the model. In this research, we focus our attention on six types of equilibrium states disregarding other possible types:

  • trivial defined by \(B=0\) and \(E=0\),

  • \((B,{{\mathcal {K}}})\)-trivial where \(B=0\) and E is \({{\mathcal {K}}}\)-trivial,

  • B-trivial satisfying \(B=0\) and \(E_i\ne 0\) for all \(i\in {{\mathcal {I}}}\),

  • E-trivial defined by \(B\ne 0\) and \(E=0\),

  • \({{\mathcal {K}}}\)-trivial where \(B\ne 0\) and E is \({{\mathcal {K}}}\)-trivial,

  • nontrivial such that \(B\ne 0\) and \(E_i\ne 0\) for all \(i \in {{\mathcal {I}}}\).

The reader should note here that the motivation for the definition of equilibrium types is computational rather than biological. It is convenient to define the triviality of an equilibrium in terms of vanishing and nonvanishing components of the vector (B, I, E).

4 Behaviour Under Parameter Variation

Here we present the ingredients for analysing the behaviour of equilibrium types under one- and two-parameter variation. We denote by p a scalar parameter and by \(q:=(q_1,q_2)\) a vector of parameters and allow the model ingredients depend on p or q. First of all, we recall that the change in the qualitative behaviour of the dynamics of a model under parameter variation is a bifurcation (see e.g. Perko 2001). The types of bifurcations considered in this work are transcritical and saddle-node, which have codimension 1 and so define points in the p-line and curves in the \((q_1,q_2)\)-parameter plane. The detection of bifurcations in a one-parameter variation analysis is easier than in a two-parameter variation analysis, with a considerable reduction of the computational cost. So a natural way to deal with bifurcations is to start with one-parameter variation and then switch to two parameters.

4.1 One-Parameter Variation: Equilibrium Branches and Bifurcation Points

An equilibrium branch is a tuple (B, I, E, p) such that for fixed p the vector (B, I, E) satisfies the equilibrium conditions (11). Under p-variation, assuming certain regularity conditions (see e.g. Chapter 1 of Allgower and Georg 2003), an equilibrium defines a curve in the equilibrium-parameter space. We consider particular equilibrium branches for the types defined in Sect. 3.

At a transcritical bifurcation point, two equilibrium branches, a trivial and a nontrivial, intersect transversally. For biological reasons, we do not consider negative branches (see Boldin 2006); then at the neighbourhood of a transcritical bifurcation to one side, there is locally a unique equilibrium and to the other side two equilibrium states. The idea now is to consider branches defined through equilibrium types, choose one component of (B, E), and define transcritical bifurcation points with respect to that component. We assume that the p-interaction variable is positive, then \(I=0\) if and only if \(B=0\) and so the triviality (or nontriviality) of I is determined by B. An additional assumption is that the qualitative behaviour, triviality or positivity with respect to other components does not change. We consider and define two types of transcritical bifurcation points in terms of the intersecting branches:

  • B-transcritical. A point where either a trivial and an E-trivial, or a \((B,{{\mathcal {K}}})\)-trivial and a \({{\mathcal {K}}}\)-trivial, or a B-trivial and a nontrivial branch intersect transversally. It corresponds to the existence boundary for the structured population,

  • \(E_i\)-transcritical. Assume a set \({{\mathcal {K}}}\subseteq {{\mathcal {I}}}\) such that \(i\in {{\mathcal {K}}}\), and let \({{\mathcal {K}}}':={{\mathcal {K}}}\setminus \{i\}\). An \(E_i\)-transcritical bifurcation point is a point where a \((B,{{\mathcal {K}}})\)-trivial and a \((B,{{\mathcal {K}}}')\)-trivial, or a \({{\mathcal {K}}}\)-trivial and a \({{\mathcal {K}}}'\)-trivial branch intersect transversally.

Now for a point \(u^*:=(B^*,I^*,E^*,p^*)\) of an equilibrium branch, we denote by

$$\begin{aligned} T(u^*):=(T_1(u^*),\ldots ,T_{s+n+2}(u^*)) \end{aligned}$$
(15)

the tangent vector to the branch at \(u^*\), and through its last component we define a function \(T_{s+n+2}:{\mathcal {D}}(T_{s+n+2})\subset {{\mathbb {R}}}^{s+n+2}\rightarrow {{\mathbb {R}}}\). A saddle-node bifurcation occurs at \(u^*\) if an equilibrium branch changes its orientation with respect to the parameter p at \(u^*\), i.e. if \(T_{s+n+2}(u)\) changes its sign at \(u=u^*\) (see e.g. Chapter 10.2 of Kuznetsov 2004). Then, for a saddle-node bifurcation necessarily (11) extended to p-dependence coupled to

$$\begin{aligned} T_{s+n+2}(B,I,E,p)=0 \end{aligned}$$
(16)

hold. Considering the hyperplane \({\mathbb {R}}^{s+n+1}\times \{p^*\}\) in the equilibrium-parameter space, to one side there are locally two equilibrium states, at the hyperplane only one which is the saddle-node bifurcation point, and to the other side there is no equilibrium.

4.2 Two-Parameter Variation: Bifurcation Curves

Under two-parameter variation, assuming certain regularity conditions (see again Chapter 1 of Allgower and Georg 2003), a codimension 1 bifurcation defines a curve in the \((q_1,q_2)\)-parameter plane that divides the plane into regions in which the qualitative behaviour of the dynamics of the model does not change. Moreover, for a path in the \((q_1,q_2)\)-parameter plane crossing the bifurcation curve transversally, the qualitative behaviour of the dynamics changes at the bifurcation.

For the computation of bifurcation curves, the idea is to extend the definitions of bifurcations to two-parameter variation, obtain curves in the equilibrium-parameter space, and project them to the \((q_1,q_2)\)-parameter plane. With this method, we obtain bifurcation charts that with respect to the one-parameter variation add a variety of possibilities for biological interpretation (see e.g. de Roos et al. 2010).

5 Numerical Methods

In this section, we first present a numerical curve continuation method and an ODE solver. Then, we show the techniques for the computation of the discussed equilibrium branches, bifurcation points and bifurcation curves.

5.1 Numerical Continuation

Let us first consider a curve implicitly defined by

$$\begin{aligned} f(u)=0, \;\;f:{\mathcal {D}}(f)\subset {{\mathbb {R}}}^{N+1}\rightarrow {{\mathbb {R}}}^{N} \;\;\mathrm{smooth,} \end{aligned}$$
(17)

and a point \(u_0\in {\mathcal {D}}(f)\) satisfying

$$\begin{aligned} \begin{array}{rl} f(u_0)=0,&\;rank(f'(u_0))=N. \end{array} \end{aligned}$$
(18)

Numerical continuation methods are techniques to compute the curve \(f^{-1}(0)\) by obtaining an oriented sequence of points \(u_i\) for \(i=1,2,\ldots \), such that for a given tolerance tol, \(\Vert f(u_i)\Vert <tol\) for all i (see e.g. Allgower and Georg 2003). We here use the pseudo-arclength continuation, which is a predictor–corrector method that computes the approximation \(u_{i+1}\) to the curve from the approximation \(u_i\) in two steps:

  • euler tangent prediction. Prediction \(v_{i+1}\) of the point \(u_{i+1}\), considering the ith point \(u_i\), a tangent vector \(t(f'(u_i))\), and a step size \(\epsilon >0\),

    $$\begin{aligned} v_{i+1}=u_i+\epsilon t(f'(u_i)), \end{aligned}$$
    (19)

  • correction of the predicted point. Assuming that \(v_{i+1}\) is close enough to the curve, we find \(u_{i+1}\) applying a modified Newton method (for instance Broyden see e.g. Chapter 7 of Kelley 1995) to the problem

    $$\begin{aligned} \begin{array}{rcl} f(u)&{}=0, \\ \langle u-v_{i+1},t(f'(u))\rangle &{}=0. \end{array} \end{aligned}$$
    (20)

Here \(t(f'(u))\) is the normalized tangent vector in the positive direction of the curve induced by the Jacobian matrix of f, defined as the unique vector \(t \in {\mathbb {R}}^{N+1}\) such that

$$\begin{aligned} f'(u)t&=0, \nonumber \\ \Vert t\Vert&=1, \nonumber \\ \det \left( \begin{array}{ccc}f'(u) \\ t^T\end{array}\right)&>0. \end{aligned}$$
(21)

Given an initial point \(u_0\), we first approximate the curve in the positive direction, using \(t(f'(u))\) defined through (21) for the Euler prediction. Then, we proceed similarly in the negative direction considering the tangent vector in (21) with negative determinant. For equilibrium branches and bifurcation curves, as we will see in Sects. 5.3 and 5.5, f(u) is derived from the equilibrium conditions (11) and usually contains the terms \(R_0(I,E,p)\) and \(\varTheta (I,E,p)\) (we use p-dependence notation, but for bifurcation curves the dependence is on q instead of on p) that for a fixed p are given by (12–13). We propose then to combine the numerical continuation method with an ODE solver to compute \(R_0(I,E,p)\) and \(\varTheta (I,E,p)\) at every evaluation of f(u).

5.2 ODE Solver

Considering p-dependence (for q-dependence we proceed similarly), let

$$\begin{aligned} R_0( I,E,p)=\int _0^h \beta (x(\alpha , I, E,p), I,E,p){\mathcal {F}}(\alpha , I, E,p)\hbox {d}\alpha , \end{aligned}$$
(22)

and

$$\begin{aligned} \varTheta ( I, E,p)=\int _0^h \gamma (x(\alpha , I, E,p), I, E,p){\mathcal {F}}(\alpha , I, E,p)\hbox {d}\alpha , \end{aligned}$$
(23)

where \(x(\alpha , I, E,p)\) and \({\mathcal {F}}(\alpha , I,E,p)\) are obtained by solving (1–2). The survival probability, defined via (2), is an exponential function, which results in a stiff system with a solution with rapid variation. Hence, its computation with explicit methods might generate large global errors and high computational costs (see e.g. Chapter 2.7 of Ascher et al. 1995). To avoid this, instead of (2) we propose to solve

$$\begin{aligned} \begin{aligned} \frac{\hbox {d}{\mathcal {\bar{M}}}(\tau )}{\hbox {d}\tau }&=-\mu (\bar{x}(\tau ), I, E,p), \quad 0<\tau \le \alpha , \\ {\mathcal {\bar{M}}}(0)&=0, \end{aligned} \end{aligned}$$
(24)

define \({\mathcal {M}}(\alpha ,I,E,p):={\mathcal {\bar{M}}}(\alpha )\) and obtain the survival probability by

$$\begin{aligned} {\mathcal {F}}(\alpha ,I, E,p)=e^{{\mathcal {M}}(\alpha , I, E, p)}. \end{aligned}$$
(25)

We now propose to differentiate the integral equations (22–23) to obtain a system of ODE that can be solved in parallel with (1) and (24). So, using the short notation \(x(\alpha ):=x(\alpha ,I,E,p)\), \({\mathcal {M}}(\alpha ):={\mathcal {M}}(\alpha ,I,E,p)\), \(r(\alpha ):=r(\alpha ,I,E,p)\) and \(\theta (\alpha ):=\theta (\alpha ,I,E,p)\), we compute \(R_0( I, E,p)\) and \(\varTheta ( I, E,p)\) by solving the system

$$\begin{aligned} \frac{\hbox {d} x(\alpha )}{\hbox {d}\alpha }&=g(x(\alpha ), I, E,p), \quad 0<\alpha \le h, \end{aligned}$$
(26a)
$$\begin{aligned} x(0)&=x_0, \nonumber \\ \frac{\hbox {d}{\mathcal {M}}(\alpha )}{\hbox {d}\alpha }&= -\mu (x(\alpha ), I, E,p), \quad 0<\alpha \le h, \end{aligned}$$
(26b)
$$\begin{aligned} {\mathcal {M}}(0)&=0, \nonumber \\ \frac{\hbox {d} r(\alpha )}{\hbox {d}\alpha }&=\beta (x(\alpha ), I, E,p)e^{{\mathcal {M}}(\alpha )},\quad 0<\alpha \le h, \end{aligned}$$
(26c)
$$\begin{aligned} r(0)&=0, \nonumber \\ \frac{\hbox {d}\theta (\alpha )}{\hbox {d}\alpha }&=\gamma (x(\alpha ), I, E,p)e^{{\mathcal {M}}(\alpha )}, \quad 0<\alpha \le h, \\ \theta (0)&=0, \nonumber \end{aligned}$$
(26d)

up to \(\alpha =h\), and define \(R_0( I, E,p):=r(h)\) and \(\varTheta ( I, E,p):=\theta (h)\) (see Algorithm 2 in Appendix).

While solving (26) at stage j, for \(j=1,\ldots ,k-1\), we evaluate \(d_j(x,I,E,p)\) at every step to detect whether a switch to stage \(j+1\) has occurred. If so, we compute \(\tau _j\) by applying a Newton method to

$$\begin{aligned} d_j(x(\tau _j,I,E,p),I,E,p)=0, \end{aligned}$$
(27)

for which a dense solution of (26) is desirable. Next, we continue solving (26) in the stage \(j+1\) with the initial condition given by the solution at \(\tau _j\). We propose then to use an ODE solver with event location, for instance the Dopri5 method, which is an explicit embedded Runge–Kutta with dense output given by polynomial interpolation (see e.g. Dormand and Prince 1980; Chapter 2 of Hairer et al. 1993).

5.3 Computation of Equilibrium Branches

Here an initial \(u_0:=(B_0,I_0,E_0,p_0)\) to start the continuation is assumed to be known. Such a point can be obtained by applying for instance a Newton, a modified Newton or a gradient method to find a solution of (11) (see e.g. Kelley 1995). By checking which components of \(u_0\) vanish, we determine the type of equilibrium. The next step is to elaborate equilibrium conditions taking into account parameter dependence, that some of the equilibrium components may vanish and exploiting the linear structures in (11). Looking at (11) and considering the equilibrium type, these conditions are straightforward, but depend strongly on the equilibrium type. We therefore define the map \(H:{\mathcal {D}}(H)\subset {\mathbb {R}}^{s+n+2}\rightarrow {\mathbb {R}}^{s+n+1}\) that induces the conditions for an equilibrium \(y=(B,I,E)\) under dependence of a parameter p via

$$\begin{aligned} H(y,p)=0, \end{aligned}$$
(28)

in form of a table, see Table 1. As is clear from this first column, the possible vanishing of equilibrium components leads to parameter independence of these components on the one hand but violations of maximum rank conditions that the curve continuation problem should satisfy on the other hand. A simple reduction of the dimension by disregarding these components leads to a well-defined curve continuation problem. Necessarily, this curve continuation problem, which we denote by

$$\begin{aligned} \hat{H} (\hat{y},p) =0 \end{aligned}$$
(29)

for \(\hat{H}:{\mathcal {D}}(\hat{H})\subset {\mathbb {R}}^{r+1}\rightarrow {\mathbb {R}}^{r}\), is also equilibrium type specific and we refer again to Table 1 for a precise definition. Note that with considerable but very convenient abuse of notation for several functions, we do not denote dependence on components that are zero. Considering the two sets of conditions (28) and (29) along with Table 1, we can summarize our method as follows:

  • given \(u_0\), determine H from the equilibrium type by simplifying (11),

  • reduce the dimension to obtain \(\hat{u}_0\) and \(\hat{H}\) satisfying \(rank(\hat{H}'(\hat{u}_0))=r\),

  • apply numerical continuation to find an approximate solution to \(\hat{H}(\hat{u})=0\),

  • extend the approximate solution to obtain points \(u_i\) for \(i=1,\ldots ,\) that approximate the curve \(H(u)=0\).

Table 1 Dimension reduction in one-parameter continuation
Full size table

In Appendix in Algorithm 1, the equilibrium type is determined from \(u_0\) and the dimension reduction to compute \(\hat{u}_0\) is performed. Algorithm 6 corresponds to the numerical continuation method, where \(\hat{H}\) is evaluated at every \(\hat{u}_i\) with Algorithm 3 and the tangent prediction \(\hat{v}_{i+1}\) is computed with Algorithm 4.

5.4 Detection and Computation of Bifurcation Points

A test function \(\phi :{\mathcal {D}}(\phi )\subset {\mathbb {R}}^{r+1}\rightarrow {\mathbb {R}}\) (see e.g. Chapter 10.2 of Kuznetsov 2004) here is a smooth scalar function that has regular zeros at bifurcation points. During the continuation of an equilibrium given by (29), we thus first check at each step whether \(\phi (\hat{u}_i) \phi (\hat{u}_{i+1})< 0\) to detect a bifurcation. If this is the case, we apply a modified Newton method to (29) coupled to

$$\begin{aligned} \phi (\hat{y},p)&=0 \end{aligned}$$
(30)

to compute it. Then, we start again the continuation from the bifurcation. The regularity condition of the zeros imposed in the definition is to avoid problems while applying the modified Newton method; in particular, we want to avoid a Jacobian which has not maximum rank and so cannot be invertible. The selection of test functions is problem dependent (for each equilibrium branch in Table 1 and each type of bifurcation), and it is possible in most of the cases to choose one that only has regular zeros. We here propose new test functions for detecting transcritical bifurcation points and methods for their computation. On the other hand, we extend to systems of VFE/ODE a classical test function for the detection of saddle-node points in ODE and a classical method for their computation (see e.g. Chapter 10.2 of Kuznetsov 2004). The test functions presented here are assumed to have only regular zeros.

5.4.1 Transcritical Bifurcations

In Chapter 10.2 of Kuznetsov (2004), a classical technique including a test function to detect and compute transcritical bifurcation points is proposed. This method applied to our model has two main disadvantages which increase the computational cost:

  • the test function contains derivatives and tangent vectors so the implementation of numerical differentiation is needed,

  • for \(f(u)=0\) given by (11) a transcritical bifurcation \(u^*\) is not a regular point of the curve, as \(rank(f'(u^*))<N\). Due to this, once \(u^*\) is detected and computed it is necessary to calculate high-order derivatives to predict the next point of the curve.

We first explain how to derive alternative test functions from the maps H introduced in Table 1. In Sect. 4, types of transcritical bifurcations were defined in terms of types of intersecting branches. The idea is that we continue a branch of a certain type and consider the type of branch with which it may intersect. For both branches, maps H are defined in Table 1. In these two maps, we delete the components 2 to \(s+1\), i.e. the components that are derived from (11b), as well as those components that are identical in both maps. The unique remaining component in the intersecting branch, i.e. not the one that we continue, defines the test function. Finally, for the detection of the bifurcation we evaluate the test function at the points of the branch that we continue. In this way, the resulting test functions are:

  • detection of B-transcritical bifurcations. If the branch that we continue is E-trivial, \({\mathcal {K}}\)-trivial or nontrivial

    $$\begin{aligned} \phi (\hat{y},p)= B, \end{aligned}$$
    (31)

    if the branch is trivial, \(( B,{{\mathcal {K}}})\)-trivial or B-trivial

    $$\begin{aligned} \phi (\hat{y},p)=1-R_0(E_{{\mathcal {N}}\setminus \mathcal{J}},p), \end{aligned}$$
    (32)

    where \(\mathcal J\) is \({{\mathcal {I}}}\) for trivial, \({{\mathcal {K}}}\) for \(( B,{{\mathcal {K}}})\)-trivial and \(\emptyset \) for B-trivial,

  • detection of \( E_i\)-transcritical bifurcations. If we continue a \({{\mathcal {K}}}\)-trivial branch

    $$\begin{aligned} \phi (\hat{y},p)=G_i( I, E_{{\mathcal {N}}\setminus {{\mathcal {K}}}},p), \end{aligned}$$
    (33)

    if it is a \((B,{{\mathcal {K}}})\)-trivial

    $$\begin{aligned} \phi (\hat{y},p)=G_i(E_{{\mathcal {N}}\setminus {{\mathcal {K}}}},p), \end{aligned}$$
    (34)

    and if we continue a \({\mathcal {K'}}\)-trivial or a \((B,{\mathcal {K'}})\)-trivial branch

    $$\begin{aligned} \phi (\hat{y},p)= E_i. \end{aligned}$$
    (35)

The two disadvantages mentioned above do not affect the new approach: it is not necessary to compute derivatives and tangent vectors, and the bifurcation point is regular in the equilibrium branch. See Algorithm 5 in Appendix, where the evaluation of the test functions is implemented.

5.4.2 Saddle-Node Bifurcations

A commonly used test function for detecting saddle-node bifurcation points in ODE systems is given by

$$\begin{aligned} \phi (\hat{y},p)=\det \left( \frac{\partial \hat{H}(\hat{y},p)}{\partial \hat{y}}\right) , \end{aligned}$$
(36)

see e.g. Kuznetsov (2004). The tangent vector to the curve (29) at \((\hat{y},p)\) is given by \(\hat{T}(\hat{y},p):= t(\hat{H}'(\hat{y},p))\) (note here that we obtain (15) by extending the dimension of \(\hat{T}(\hat{y},p)\) to the original dimension). At a saddle-node point, \(\hat{H}(\hat{y},p)\) has maximum rank, and \(\phi \) given by (36) vanishes; as a consequence, the last component of \(\hat{T}\), let us say \(\hat{T}_{r+1}\), vanishes as well. Moreover, from the definition of saddle-node bifurcation we know that \(\hat{T}_{r+1}=T_{s+n+2}\) not only vanishes, but also changes its sign at the bifurcation. We propose then in the case of systems of VFE/ODE to use \(\hat{T}_{r+1}\) for the detection, as at every prediction of the curve continuation it is necessary to compute the tangent vector anyway. Then, once the bifurcation is detected we compute it applying a modified Newton method to (29) coupled to (36). See Algorithm 6 in Appendix for the details in numerical implementation.

5.5 Computation of Bifurcation Curves

Here we adapt the ideas presented in Sect. 5.3 to compute bifurcation curves. First we assume that a bifurcation point \((y^*,p^*)\) was computed during the equilibrium continuation and that we know its type. Adding a second parameter, we obtain the starting point \(u_0=(y^*,q^*)\). In Sect. 4, we defined types of bifurcations in terms of the behaviour of equilibrium states; then by considering equilibrium types, it is reasonable to think about maps \(L:{\mathcal {D}}(L)\subset {\mathbb {R}}^{s+n+3}\rightarrow {\mathbb {R}}^{s+n+2}\), that induce the conditions for bifurcations under dependence of q via

$$\begin{aligned} L(y,q)=0, \end{aligned}$$
(37)

and that are derived from the expressions H in Table 1. Again a reduction of dimension helps to avoid the violation of maximum rank conditions and saves costs. Then, we consider curve continuation problems

$$\begin{aligned} \hat{L} (\hat{y},q) =0, \end{aligned}$$
(38)

for \(\hat{L}:{\mathcal {D}}(\hat{L})\subset {\mathbb {R}}^{r+2}\rightarrow {\mathbb {R}}^{r+1}\) with maximum rank. The idea of the method is to obtain a starting value for the continuation \(\hat{u}_0\) by reducing the dimension of \(u_0\), apply curve continuation to solve (38) and extend the dimension of the resulting sequence of points to approximate the solution of (37).

Transcritical bifurcations are defined in terms of intersecting branches. Then, we consider two equilibrium branches that under p-variation are defined through systems of the type (28). By extending the left side of both systems to q-dependence and couple them, we obtain (37). Next we obtain (38) by reducing (37). Expressions for L(y, q) and \(\hat{L}(y,q)\) are given in Table 2 for each type of transcritical bifurcation.

For saddle-node bifurcations, we consider an equilibrium branch given by (28), which associated reduced dimensional system for continuation is (29). Since for saddle-node bifurcations, other than for transcritical bifurcations, it is only one branch that matters, we can use the dimension reduction in Table 1. Hence we can extend (29) to q-dependence and define

$$\begin{aligned} \hat{L}(\hat{y},q):=\left( \begin{array}{c} \hat{H}(\hat{y},q) \\ \psi (\hat{y},q)\end{array} \right) \end{aligned}$$
(39)

for each equilibrium type in Table 1, and for \(\psi \) as defined below. We have that \(\hat{H}:{\mathcal {D}}(\hat{H})\subset {\mathbb {R}}^{r+2}\rightarrow {\mathbb {R}}^r\), and for \((\hat{y},q)\in {\mathcal {D}}(\hat{H})\) satisfying \(\hat{H}(\hat{y},q)=0\) the Jacobian of \(\hat{H}\) has maximum rank. Then, \(\psi \) has to be a scalar function \(\psi :{\mathcal {D}}(\psi )\subset {\mathbb {R}}^{r+2}\rightarrow {\mathbb {R}}\) such that \(D\hat{L}(\hat{y},q)\) has maximum rank for all \((\hat{y},q)\in {\mathcal {D}}(\hat{L})\) satisfying (38). We then define \(\psi \) with the bordering technique proposed in Chapter 10.3 of Kuznetsov (2004). We consider the normalized vectors \(v_1\) and \(v_2\) in \({\mathbb {R}}^{r}\) satisfying

$$\begin{aligned} \Vert v_1\Vert =\Vert v_2\Vert =1, \quad v_1\in Null\left( \frac{\partial \hat{H}(\hat{y},q)}{ \partial \hat{y}}^T\right) , \quad v_2 \in Null\left( \frac{\partial \hat{H}(\hat{y},q)}{\partial \hat{y}}\right) , \end{aligned}$$
(40)

where Null refers to the null space. Note that under one-parameter variation a saddle-node bifurcation point \((\hat{y}^*,p^*)\) satisfies

$$\begin{aligned} rank(D\hat{H}(\hat{y}^*,p^*))=r, \quad \det \left( \frac{\partial \hat{H}(\hat{y}^*,p^*)}{\partial \hat{y}}\right) =0, \end{aligned}$$

which implies that the null spaces in (40) are one-dimensional, and \(v_1\) and \(v_2\) are uniquely determined (see Chapter 10.2.2 of Kuznetsov 2004). Next we define \(\psi (\hat{y},q)\) as the last component of the vector \(w \in {\mathbb {R}}^{r+1}\) given as the solution of

$$\begin{aligned} \left( \begin{array}{ccc} \frac{\partial \hat{H}(\hat{y},q)}{\partial \hat{y}} &{} &{} v_1\\ {v_2}^T &{} &{} 0 \end{array} \right) \begin{array}{l}w \end{array} =\left( \begin{array}{c} 0 \\ 1 \end{array} \right) . \end{aligned}$$
(41)
Table 2 Dimension reduction in two-parameter continuation: B-transcritical bifurcations (first three) and \(E_i\)-transcritical (last two)
Full size table

In Appendix, the curve continuation corresponds to Algorithm 9, where \(\hat{L}(\hat{y},q)\) is obtained with Algorithm 7 for transcritical bifurcations, and with Algorithm 8 for saddle-nodes.

6 Validation and Applications

We have implemented the methods in the development of Python routines. Considering as a basis the C-code developed by Andre M. de Roos for computing bifurcation curves in parameter planes (see Section 5 of de Roos et al. 2010), we have used standard modules of SciPy and NumPy, and for the solution of the ODE systems with event location the Sundials cvode method with absolute and relative tolerances \(10^{-12}\) and \(10^{-6}\), respectively. We have tested the routines and validated the methods with several examples for which the solution of the ODE system (26) can be obtained analytically.

For E-trivial, \({{\mathcal {K}}}\)-trivial and nontrivial equilibria, it is in general not possible to give explicit expressions for the equilibrium states; for these cases, then the validation is carried out as follows:

  • we solve analytically (26) and obtain expressions for \(R_0(I,E,p)\) and \(\varTheta (I,E,p)\) in which there are no integrals,

  • we introduce the expressions for \(R_0(I,E,p)\) and \(\varTheta (I,E,p)\) into the equilibrium conditions and derive an expression \(\bar{H}(y,p)=0\) that implicitly defines an equilibrium curve, and in which there are no terms implicitly defined by external equations,

  • for each point \(u_i=(y_i,p_i)\) computed with the method proposed in Sect. 5.3, we fix \(p=p_i\) and apply a modified Newton method with a tolerance of \(10^{-14}\) to solve \(\bar{H}(y,p)=0\) taking \(u_i\) as initial value,

  • we compute the error \(\Vert y_i-y\Vert \), y being the solution of \(\bar{H}(y,p)=0\).

With this process, we compute the error obtained in the solution of the ODE (26), which also contains the error of computation of the switches defined by (27). The error obtained in the modified Newton method remains as the unique error source in the case of equilibrium states for which explicit expressions cannot be provided.

For validating the method in Sect. 5.4 for the computation of bifurcation points, again we solve analytically the ODE system (26) and derive expressions \(\bar{H}(y,p)=0\), \(\bar{\phi }(y,p)=0\) that implicitly define the bifurcations and that do not contain terms implicitly defined by external equations. Next, we compute them applying a Newton method with a tolerance of \(10^{-14}\). Finally, we compute the error by comparing both solutions.

For the method presented in Sect. 5.5 for continuing bifurcations, the process is similar to the one described for equilibria:

  • we solve analytically (26) and obtain expressions for \(R_0(I,E,q)\) and \(\varTheta (I,E,q)\) in which there are no integrals,

  • we introduce \(R_0(I,E,q)\) and \(\varTheta (I,E,q)\) into the bifurcation conditions and derive an expression \(\bar{L}(y,p)=0\) that implicitly defines a bifurcation curve, and in which there are no terms implicitly defined by external equations,

  • for each point \(u_i=(y_i,q_i)\) computed with the method proposed in Sect. 5.5, we fix one component of q and apply a modified Newton method with a tolerance of \(10^{-14}\) to solve \(\bar{L}(y,q)=0\),

  • we compute the error \(\Vert y_i-y\Vert \).

We have validated the methods with two consumer–resource (Calsina and Saldaña 1995; Diekmann et al. 2010) and a trophic model describing invasion dynamics (de Roos and Persson 2002). Additionally, we have applied the methods to a fish cannibalistic model (Getto et al. 2005). Here we present the obtained results.

Table 3 Model ingredients for trees competing for light
Full size table

6.1 Trees Competing for Light in a Forest

Our first example is a size-structured consumer population of trees in a forest that compete for light (see Calsina and Saldaña 1995). We have left all model ingredients as in the reference but have additionally incorporated age structure into the population’s dynamical bookkeeping in order to test the algorithms with a two-dimensional, i.e. age–size, i-state space with a unique life stage. In the model, the behaviour of each individual depends on the total population I (size of the forest). In this model, the dynamics of the resource (light) are not taken into account, so there are no E-environmental variables. Finally, we do not consider external inflow of newborns (no seeds carried by the wind). The ingredients of the model are presented in Table 3. We vary the parameter K, that is the fraction of assimilated light that goes to growth and maintenance, whereas \(1-K\) is the according fraction for reproduction. Under K-parameter variation, the model has a trivial branch (B, I, K) in which \(B=0\) and \(I=0\), and a nontrivial branch with \(B,\;I>0\) satisfying

$$\begin{aligned} 1-\beta _0(1-K)e^{-I} \left( \frac{1-e^{-\mu (1+I)h}}{\mu (1+I)}+\frac{e^{-\left( \frac{V_0 K e^{-I}}{L}+\mu (1+I)\right) h}-1}{\frac{V_0 K e^{-I}}{L}+\mu (1+I)} \right)&=0, \end{aligned}$$
(42a)
$$\begin{aligned} I+\frac{B}{\mu (1+I)}\left( e^{-\mu (1+I) h}-1 \right)&=0. \end{aligned}$$
(42b)

The expression for B-transcritical bifurcations is given by \(B=0\), \(I=0\) and (42a).

Fig. 1
figure 1

Equilibria and bifurcations under K-parameter variation for the model of trees competing for light (first two panels) trivial (dotted) equilibrium branch, positive (continuous) equilibrium branch, and two B-transcritical bifurcation points \(*\). Error of the positive equilibrium branch (last panel) for a maximum step size of 0.02 in the tangent prediction and a tolerance of \(10^{-8}\) for the modified Newton method

Full size image
Fig. 2
figure 2

\((K,V_0)\)-parameter plane (upper panel) B-transcritical bifurcation curve for the model of trees competing for light in a forest, the points \(*\) are the bifurcations in Fig. 1 for \(V_0=0.8\). Error (lower panel) for a maximum step size of 0.1 and a tolerance of \(10^{-8}\) for the modified Newton method

Full size image
Table 4 Model ingredients for Daphnia
Full size table

Figure 1 shows the equilibrium branches computed with the method proposed in Sect. 5.3, and the error obtained for the nontrivial branch. We have detected and computed two B-transcritical bifurcations at \(K=6.8338\times 10^{-2}\) and \(K=0.7317\) with the method proposed in Sect. 5.4, with an error of the order of \(10^{-7}\). Assuming \(h=\infty \) and \(L=1\), Calsina and Saldaña (1995) concluded that for this model a unique nontrivial equilibrium exists if and only if

$$\begin{aligned} \mu <V_0K\left( \frac{{\sqrt{1+\frac{4\beta _0}{V_0}\frac{(1-K)}{K}}-1}}{2} \right) , \end{aligned}$$
(43)

and that for given \(\beta _0\) and \(V_0\), the value of K that maximizes B and I is

$$\begin{aligned} K_m=\frac{1}{2+\sqrt{V_0/\beta _0}}. \end{aligned}$$
(44)

Figure 1 is consistent with (43) for \(K\in (6.8338\times 10^{-2}, 0.7317)\) in the way that the corresponding equality holds at the bifurcations with an error of the order of \(10^{-5}\) which decreases while increasing the age h. Moreover, the expression derived for transcritical bifurcations considering \(h=\infty \) and \(L=1\) is the equality derived from (43). The value \(K_m\) that maximizes B and I in Figure 1 satisfies (44) with an error of the order of \(10^{-3}\) which decreases while reducing the maximum step size. Finally, Figure 2 shows the B-transcritical bifurcation in the \((K,V_0)\)-parameter plane computed with the method proposed in Sect. 5.5 and the obtained error with respect to the expression derived from (42a).

In Figs. 1 and 2, we see that the variation of the fraction K of light scheduled to growth and maintenance, and thus also of the fraction \(1-K\) scheduled to reproduction, can control the presence and size of the positive equilibrium. If there is little light for growth, there is more for reproduction, but on the other hand the slow growth has a negative effect on reproduction. Note also that mortality is not affected by light. There are hence several effects on individual reproduction numbers, and by analysing these in more detail, which is beyond the scope of this paper, one could interpret presence and size of the positive equilibria by using reproduction numbers.

6.2 Daphnia Consuming Algae

We now consider a size-structured consumer–resource model (see e.g. de Roos et al. 1990, 2010; Diekmann et al. 2010) where the unstructured resource has logistic dynamics in absence of consumers. The consumer population has two different life stages corresponding to the juvenile and the adult period. The individuals are juveniles if their size \(x\in [X_b,X_a]\), for \(X_b\) and \(X_a\) the sizes at birth and at maturation, respectively, and adults if \(x\in (X_a,X_m]\), \(X_m\) being the maximum attainable size under infinite food availability. Juvenile individuals cannot reproduce, whereas adults give birth to new individuals. The ingredients of the model are presented in Table 4. The model has a trivial equilibrium \((B,I,E)=(0,0,0)\), a B-trivial equilibrium \((B,I,E)=(0,0,K)\) and a nontrivial equilibrium with \(B,\;I,\;E>0\) satisfying

$$\begin{aligned} 1-R_m f(E)\bigg [- \frac{e^{-\mu h}-e^{-\mu {\tau }_1}}{\mu } X_m^2 f(E)^2 - \frac{e^{-(2g_m+\mu ) h}-e^{-(2g_m+\mu ) {\tau }_1}}{2g_m+\mu } ( X_m f(E)&\nonumber \\ -X_b)^2 + \frac{e^{-(g_m+\mu ) h}-e^{-(g_m+\mu ) {\tau }_1}}{g_m+\mu } 2 X_m f(E) (X_m f(E)-X_b ) \bigg ] =0,&\end{aligned}$$
(45a)
$$\begin{aligned} I-B \nu _s f(E)\bigg [-\frac{e^{-\mu h}-1}{\mu }X_m^2 f(E)^2 -\frac{e^{-(2g_m+\mu ) h}-1}{2g_m+\mu } \left( X_m f(E) -X_b\right) ^2\nonumber&\\ +\frac{e^{-(g_m+\mu ) h}-1}{g_m+\mu }2 X_m f(E) \left( X_m f(E)-X_b\right) \bigg ] =0,&\end{aligned}$$
(45b)
$$\begin{aligned} a_1\left( 1-\frac{E}{K}\right) -I=0&, \end{aligned}$$
(45c)

where

$$\begin{aligned} f(E)=\frac{\xi E}{1+\xi E} \end{aligned}$$
(46)

is the functional response and

$$\begin{aligned} {\tau }_1=-\frac{1}{g_m}\log \bigg ( \frac{X_a-X_m f(E)}{X_b-X_m f(E)}\bigg ) \end{aligned}$$
(47)

the age at maturation. The B-transcritical bifurcation is defined by \(B=0\), \(I=0\) and E and K defined by (45a) and (45c).

Fig. 3
figure 3

Equilibria and bifurcation under K-parameter variation (first two panels) for the Daphnia model: trivial (dotted), B-trivial (discontinuous) and nontrivial (continuous) equilibrium branches. B-transcritical bifurcation \(*\) (intersection of B-trivial and nontrivial branch). Error of the positive equilibrium branch (last panel) for a maximum step size of 0.02 in the tangent prediction and a tolerance of \(10^{-8}\) for the modified Newton method

Full size image
Fig. 4
figure 4

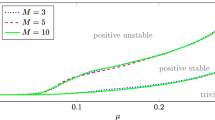
Equilibria and bifurcation under \(\mu \)-parameter variation (first two panels) for the Daphnia model: trivial (dotted), B-trivial (discontinuous) and positive (continuous) equilibrium branches. B-transcritical bifurcation \(*\) (intersection of B-trivial and nontrivial branch). Error of the positive equilibrium branch (last panel) for a maximum step size of 0.01 in the tangent prediction and a tolerance of \(10^{-8}\) for the modified Newton method

Full size image

Figure 3 shows the equilibrium branches under K-parameter variation, K being the carrying capacity, computed with the method proposed in Sect. 5.3 (first two panels). At \(K= 0.1268\), there is a B-transcritical bifurcation computed with the method proposed in Sect. 5.4. The error obtained for the nontrivial branch with respect to the curve defined by (45) is also shown in the figure (last panel). The error of the bifurcation is of the order of \(10^{-8}\). Similarly, Fig. 4 shows the equilibrium branches under \(\mu \)-parameter variation, with \(\mu \) the mortality rate parameter, and the error obtained for the nontrivial branch. The B-transcritical bifurcation occurs at \(\mu =0.2590\) and was computed with an error of the order of \(10^{-7}\). Under two-parameter variation, Fig. 5 shows the B-transcritical bifurcation curve in the \((\mu ,K)\)-parameter plane computed with the method proposed in Sect. 5.5. The figure also shows the error with respect to the expression derived from (45).

Fig. 5
figure 5

\((\mu ,K)\)-parameter plane (upper panel) B-transcritical bifurcation curve for the Daphnia model. Error (lower panel) for a maximum step size of \(5\times 10^{-3}\) and a tolerance of \(10^{-8}\) for the modified Newton method

Full size image

Looking at Fig. 3, we observe that if we increase the carrying capacity K, then the population birth rate B increases and the resource concentration E remains constant. Hence, the population consumption increases and so does the total population. In Fig. 4, we see that, as expected, if the mortality rate \(\mu \) is very high, then the population goes extinct. When decreasing \(\mu \), we see that B increases and the resource E decreases. The decrease in resource is due to an increasing consumption. If the mortality rate decreases further the p-birth starts decreasing due to competition for the resource E. The B-transcritical bifurcation curve in Fig. 5 is the existence boundary for the positive equilibrium and coincides with the one in Figure 7 in de Roos et al. (2010). Above the curve the model has a trivial, a B-trivial and a positive equilibrium, and below the curve only a trivial and a B-trivial. For in depth biological interpretation, we refer to the monograph de Roos and Persson (2013).

Table 5 Model ingredients for three trophic
Full size table
Fig. 6
figure 6

Equilibria and bifurcations under \(\rho \)-parameter variation for the 3-trophic model: \((B,\{2\})\)-trivial (dotted), \(\{2\}\)-trivial (dashed) and positive (continuous) equilibrium branches (the difference between B-components of the \((B, \{2\})\)-trivial and the \(\{2\}\)-trivial equilibrium is more visible in the scale of b and c). We see a saddle-node bifurcation at \(\rho =8.8489\times 10^{-6}\) in a, a B-transcritical bifurcation at \(\rho = 8.8569 \times 10^{-7}\) (intersection between \((B,\{2\})\)-trivial and \(\{2\}\)-trivial branch) in a and b and an \(E_2\)-transcritical bifurcation at \(\rho = 2.5360 \times 10^{-5}\) (intersection between \(\{2\}\)-trivial and positive branch) in a and c

Full size image

6.3 3-Trophic: Predator–Prey–Resource

This model for invasive populations is similar to the Daphnia consuming algae, but additionally incorporates an unstructured top predator. It is analysed in detail in de Roos and Persson (2002). The structured population has three stages where the individuals are, respectively, juveniles susceptible to predation, juveniles not susceptible to predation and adults. The individuals are juveniles susceptible to predation if their size \(x\in [X_b,X_v]\), for \(X_b\) and \(X_v\) the sizes at birth and at which individuals escape from predation, respectively, juveniles not susceptible to predation if their size \(x\in (X_v,X_a]\), \(X_a\) being the size at maturation, and adults if \(x\in (X_a,X_m]\), where \(X_m\) is the maximum attainable size under infinite food availability. The ingredients of the model are given in Table 5. Figure 6 shows in (a) the equilibrium branches and bifurcation points obtained by varying the productivity \(\rho \). For \({{\mathcal {K}}}=\{2\}\), the model has a \((B,{{\mathcal {K}}})\)-trivial equilibrium in which only the resource is positive (without consumers and predators) a \({{\mathcal {K}}}\)-trivial equilibrium with resource and consumers but not predators (the predator concentration \(E_2\) is zero), and two positive equilibria with resource, consumers and predators in a unique nontrivial branch. The population birth rate B for the \({{\mathcal {K}}}\)-trivial equilibrium is of the order of \(10^{-6}\) and has a positive slope that cannot be well appreciated in Fig. 6a; however, it can be appreciated in Fig. 6b and c, where the difference between the \((B,{{\mathcal {K}}})\)-trivial and the \({{\mathcal {K}}}\)-trivial equilibrium is much more visible by the change of scale in the vertical axis. In the \((B,{{\mathcal {K}}})\)-trivial equilibrium B, \(I_1\), \(I_2\), and \(E_2\) vanish while \(E_1=\rho /K\). The nontrivial equilibria satisfy

$$\begin{aligned} 1-R_m f(E) e^{-\mu _p {\tau }_1}\bigg [ - \frac{e^{-\mu h}-e^{-\mu {\tau }_2}}{\mu } X_m^2 f(E)^2 -\frac{e^{-(2g_m+\mu ) h} -e^{-(2g_m+\mu ) {\tau }_2}}{2g_m+\mu }&(X_b \nonumber \\ -X_m f(E))^2+\frac{e^{-(g_m+\mu ) h}-e^{-(g_m+\mu ) {\tau }_2}}{g_m+\mu } 2 X_m f(E)(X_m f(E)-X_b)\bigg ]=0,&\end{aligned}$$
(48a)
$$\begin{aligned} I_1-B I_m f(E) \bigg [ - \frac{e^{-(\mu + \mu _p) \tau _1}-1}{\mu + \mu _p} X_m^2 f(E)^2 -\frac{e^{-(2g_m+\mu + \mu _p) {\tau }_1}-1}{2g_m+\mu + \mu _p} (X_b&\nonumber \\ -X_m f(E))^2 +\frac{e^{-(g_m+\mu + \mu _p) {\tau }_1}-1}{g_m+\mu + \mu _p} 2 X_m f(E)(X_m f(E)-X_b)&\nonumber \\ +\, e^{-\mu _p {\tau }_1}\bigg ( - \frac{e^{-\mu h}-e^{-\mu {\tau }_1}}{\mu } X_m^2 f(E)^2 -\frac{e^{-(2g_m+\mu ) h}-e^{-(2g_m+\mu ){\tau }_1}}{2g_m+\mu } (X_b&\nonumber \\ -X_m f(E))^2 +\frac{e^{-(g_m+\mu ) h}-e^{-(g_m+\mu ) {\tau }_2}}{g_m+\mu } 2 X_m f(E)(X_m f(E)-X_b)\bigg )\bigg ]=0,&\end{aligned}$$
(48b)
$$\begin{aligned} I_2-B B_1 \bigg [ - \frac{e^{-(\mu + \mu _p) {\tau }_1}-1}{\mu + \mu _p} X_m^3 f(E)^3 -\frac{e^{-(g_m+\mu + \mu _p){\tau }_1}-1}{g_m+\mu + \mu _p} 3 X_m^2 f(E)^2 (X_b&\nonumber \\ -X_m f(E))-\frac{e^{-(2g_m+\mu + \mu _p){\tau }_1}-1}{2g_m+\mu + \mu _p} 3 X_m f(E) (X_m f(E)-X_b)^2&\nonumber \\ +\frac{e^{-(3g_m+\mu + \mu _p) {\tau }_1}-1}{3g_m+\mu + \mu _p} (X_m f(E)-Xb)^3\bigg ]=0,&\end{aligned}$$
(48c)
$$\begin{aligned} \rho -E_1 K-I_1=0,&\end{aligned}$$
(48d)
$$\begin{aligned} \frac{\epsilon a_1 I_2}{1+a_1 T_h I_2}-\delta =0,&\end{aligned}$$
(48e)

for \(B,I_1,I_2,E_1,E_2>0\), where

$$\begin{aligned} \mu _p:=\mu _p(I,E)=\frac{a_1 E_2}{1+a_1 T_h I_2} \end{aligned}$$

is the mortality due to predation,

$$\begin{aligned} f(E)=\frac{E_1}{R_h+ E_1} \end{aligned}$$
(49)

the functional response and

$$\begin{aligned}&{\tau }_1=-\frac{1}{g_m}\log \bigg ( \frac{X_v-X_m f(E)}{X_b-X_m f(E)}\bigg ),&{\tau }_2=-\frac{1}{g_m}\log \bigg ( \frac{X_a-X_m f(E)}{X_b-X_m f(E)}\bigg ), \end{aligned}$$
(50)

the ages at which the switches occur. Finally, the expression that the \({{\mathcal {K}}}\)-trivial equilibrium (in which \(E_2=0\)) satisfies is obtained by considering (48a–48d) with \(\mu _p=0\).

Fig. 7
figure 7

Errors of the \({{\mathcal {K}}}\)-trivial equilibrium branch (left panel) and of the positive branches (center and right panels) for a maximum step size of \(1.5\times 10^{-6}\) and a tolerance of \(10^{-8}\) for the modified Newton method

Full size image

The obtained errors for the \({{\mathcal {K}}}\)-trivial and for the nontrivial branches are of the order of \(10^{-13}\), \(10^{-10}\) and \(10^{-8}\), respectively (see Fig. 7). The expression for a B-transcritical bifurcation (intersection of the \((B,{{\mathcal {K}}})\)-trivial and the \({{\mathcal {K}}}\) trivial branches) is given by \(B=0\), \(I_1=0\), \(I_2=0\), \(E_2=0\), (48a) and (48d) with \(\mu _p=0\). At \(\rho =8.8569\times 10^{-7}\), a B-transcritical bifurcation was computed with an error of the order of \(10^{-15}\). The bifurcation is shown in detail in Fig. 6b. Saddle-node bifurcations in the nontrivial branch are given by (48) coupled to

$$\begin{aligned} \det \left( \frac{\partial \bar{H}(y,\rho )}{\partial y}\right) =0, \end{aligned}$$
(51)

where \(\bar{H}(y,\rho )\) is the left-hand side of (48). At \(\rho =8.8489\times 10^{-6}\), we have computed a saddle-node bifurcation with an error of the order of \(10^{-10}\). Finally at \(\rho =2.5360 \times 10^{-5}\), there is a \(E_2\)-transcritical bifurcation defined by (48) with \(E_2=0\) and \(\mu _p=0\). The bifurcation was computed with an error of the order of \(10^{-13}\) and is shown more in detail in Fig. 6c. Considering two-parameter variation, the \((\mu ,\rho )\)-parameter plane in Fig. 8 shows the B-transcritical bifurcation (dotted), the \(E_2\)-transcritical bifurcation (dashed), and the saddle-node bifurcation curve (continuous line), as well as the obtained errors for each curve. Figure 8 also shows the existing types of equilibria in each region of the parameter plane.

Fig. 8
figure 8

\((\mu ,\rho )\)-parameter plane and regions of existence of equilibria (upper panel). \({{\mathcal {K}}}=\{2\}\), B-transcritical (dotted), \(E_2\)-transcritical (dashed), and saddle-node (continuous) bifurcations for the three trophic model. Errors (rest of the panels) for a maximum step size of 0.002 for the tangent prediction and a tolerance of \(10^{-7}\) for the modified Newton method

Full size image

The obtained equilibria and bifurcations in the one-parameter variation analysis (i.e. Fig. 6) are the same as those presented in Figure 2 in de Roos and Persson (2002), which provides support for our method. In the reference, the authors provide a biological interpretation for them; in particular, based on stability considerations, they find that the \(E_2\)-transcritical bifurcation corresponds to the invasion threshold for the predator and the saddle-node to its persistence threshold. In the two-parameter variation analysis presented here, Fig. 8 shows that for low \(\mu \) values there is an \(E_2\)-transcritical and a saddle-node bifurcation corresponding to invasion and persistence as in the one-parameter variation analysis. Additionally, we see that for high \(\mu \) values the saddle-node bifurcation disappears and persistence and invasion boundaries coincide.

6.4 Cannibalism in Fish Populations

Our last example is based on the formulation of a size-structured fish cannibalistic model in Getto et al. (2005) that in turn was based on the rates and parameters in Claessen and de Roos (2003), see Claessen et al. (2004) for a detailed review on cannibalism modelling. A size-structured population with two stages corresponding to juveniles and adults is considered. Individuals are juveniles if their size \(x\in [X_b,X_a)\), where \(X_b\) and \(X_a\) are the lengths at birth and at maturation, respectively, and adults if \(x=X_a\). Juvenile individuals feed on a resource and grow, but do not reproduce, whereas adults feed on another resource, reproduce, but do not grow. Additionally, adults feed on juveniles, which generates in the mortality of juveniles a dependence on the density of adults and in the reproduction rate a dependence on the density of juveniles. The rates and parameters are presented in Table 6 in a similar formulation than the one used in Getto et al. (2005). The ingredients that govern the dynamics at the i-level are adapted from those in the more complex model presented in Claessen and de Roos (2003) in which adults also grow. \(B_1\) is the cannibalistic voracity; note that we obtain the noncannibalistic model if we set \(B_1=0\). The model has a B-trivial equilibrium in which \(B=0\), \(I_i=0\) for \(i=1,\ldots ,5\) and \(E_i=K_i\) for \(i=1,2\), and a nontrivial one. Note that (26a) cannot be solved analytically despite the growth rate being a rational function. Hence, we cannot present the error analysis as for the three other models.

Table 6 Model ingredients for analysing cannibalism effects
Full size table
Fig. 9
figure 9

Equilibria and bifurcations under \(K_2\)-parameter variation for the cannibalistic model: B-trivial (dotted), nontrivial for noncannibalistic (dashed) and nontrivial for cannibalistic (continuous) equilibrium branches. At \(K_2=1.5967\times 10^{-4}\), there is a B-transcritical bifurcation (intersection between B-trivial and nontrivial branches). At \(K_2=1.6501\times 10^{-4}\) and \(K_2=4.4056\times 10^{-5}\), there are saddle-node bifurcations for the nontrivial cannibalistic branch. In d, we show some details of c obtained by zooming in, where the projection of the equilibrium curve in the \((K,E_2)\)-plane result in a self-intersection, which does not occur in the equilibrium-parameter space

Full size image

In Fig. 9, we can see the equilibrium behaviour under variation of the carrying capacity \(K_2\) for the resource for adults. The effects of cannibalism become visible when comparing the nontrivial branch with the one of a model free of cannibalism. In particular, the figure shows the much studied lifeboat mechanism of cannibalism, see e.g. van den Bosch et al. (1988), which means that for a low carrying capacity \(K_2\) of the food source \(E_2\) of adults, the cannibalistic population can survive, whereas the noncannibalistic population goes extinct. However, Fig. 9 also suggests that adult individuals cannot feed only on juveniles, as for a very low value of \(K_2\) there is no positive equilibrium. Additionally, a bistability situation, i.e. two stable equilibria ’surrounding’ an unstable equilibrium, analogous to the one discussed in Claessen and de Roos (2003), can be suspected for \(K_2 \in (1.5967 \times 10^{-4}, 1.6501 \times 10^{-4})\) (note that in this work stability analysis is not presented). In the lowest of the three positive equilibria in Fig. 9a, the p-birth rate is small and the corresponding concentration of resource for juveniles \(E_1\) in Fig. 9b is large. This suggests a small population of juveniles, which grows fast and leads to a large population of adults. Assuming that the middle branch is unstable we do not interpret it. Finally in the highest of the three positive equilibria in Fig. 9a, the p-birth rate is large and the concentration of resource \(E_1\) for juveniles in Fig. 9b low. In this case, the population of juvenile individuals is large and grow slowly, which leads to a small population of adults.

7 Conclusions and Remarks

In this paper, we have developed a formulation for structured population models as a system of VFE/ODE. Such formulation describes many models studied in the literature and on the other hand can be easily transformed into a system to which analytical theory can be applied. For this general model, we have developed a detailed numerical method to compute equilibria, and to detect and continue transcritical and saddle-node bifurcations. We have implemented the method in the development of routines that we have tested with realistic models. The obtained results, which are consistent with those in the literature, validated successfully the presented method.

In the previous section, we have argued how the curves computed with our method reproduce biological effects analysed in detail for consumer–resource models in Calsina and Saldaña (1995) and Diekmann et al. (2010), for trophic chains in de Roos and Persson (2002), and for fish cannibalistic populations in Getto et al. (2005) and Claessen and de Roos (2003). Moreover, we have seen that the representation of the results in various types of bifurcation diagrams facilitates the biological interpretation. The method that we presented could thus be rather effortlessly adapted to reproduce biological conclusions for various types of established realistic models. We hence believe that is also a rather ready tool for new biological models and questions.

In a similar way as for the Daphnia model in Sect. 6.2, we have computed (but not presented) bifurcations for the model of fish stock dynamics proposed by Meng et al. (2013) and for metapopulation models as proposed in Section 5.2 of Diekmann et al. (2007).

We are currently developing a method for the computation of Hopf bifurcations that will also allow to determine stability properties of equilibria in parameter planes. The idea is to combine pseudo-spectral techniques established by Breda et al. (2015) for the computation of rightmost eigenvalues with curve continuation methods developed in the present paper.

The next step will then be to develop a user-friendly software with implemented analysis for both, the types of bifurcations considered here and Hopf bifurcations. Such a software can be a powerful tool to analyse bifurcations, as the achieved generality of the model formulation should make it unnecessary to develop new codes for particular case studies.