Abstract
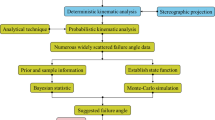
Discontinuity-controlled rock slope instability analysis is a difficult problem in the field of geotechnical engineering. Many random discontinuities existing in rock masses will negatively influence rock slope stabilities. This study is aimed to determine the failure angle (apparent angle of the sliding surface in the direction of the cut face) of potentially unstable blocks in discontinuity-controlled rock slopes in Dalian, China. For this purpose, a detailed discontinuity survey was conducted in seven exploratory trenches and two outcrops. Possible failure modes of the slope were predicted. Thus, according to theories of kinematics and probability statistics, it is possible to determine the failure angle of potentially unstable blocks with a new method that combines the results of Bayesian inference, probabilistic kinematic analysis and stereographic projection. Bayes’ formula was used to estimate the scientific value of the slope failure angle. A computer program called KINEMATIC was written to perform probabilistic kinematic analysis. Stereographic projection was used to verify the values obtained from the methods. Through the methodology proposed in the study, the failure angle of each excavation slope could be well calculated.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
Rock masses usually contain features such as bedding planes, faults, fissures, fractures, joints and other mechanical defects, which, although formed from a wide range of geological processes, possess the common characteristics of low shear strength, negligible tensile strength and high fluid conductivity compared with the surrounding rock material (Priest 1993). It has always been a problem to evaluate discontinuity-controlled rock slope instabilities in the field of geotechnical engineering. Complex discontinuities are widely distributed in rock masses, with uncertain distributions. Discontinuities make a rock mass have features of discontinuity, non-homogeneity and anisotropy and have an important influence on the mechanical and hydraulic behavior of the rock mass.
Kinematic analysis (Hoek and Bray 1981) can be used to identify potentially unstable blocks (i.e., plane, wedge and toppling failures), and it is vital for analyzing the stability of blocks in a rock mass and must precede any subsequent analysis (Lana and Gripp 2003). Probabilistic kinematic analysis (Chen et al. 1995) assumes that each discontinuity of each slope surface is randomly distributed, i.e., the position of each discontinuity and its scale in a particular rock mass can be found anywhere else in the rock mass. The procedures of probabilistic kinematic analysis are as follows (Zhang et al. 2013):
-
1.
Determine the orientation of each discontinuity collected from the rock outcrop.
-
2.
Determine the dip direction of the fractured rock slope.
-
3.
Consider that the critical slip surface extends along the discontinuity surfaces, and determine the dip angle range of the critical slip surface.
-
4.
Consider that the critical slip surface extends along the wedges (with each wedge composed of two discontinuities), and determine the dip angle range of the critical slip surface.
-
5.
Compare step 3 with step 4, and determine the dip angle of the final critical slip surface.
Kinematic analysis is the procedure for defining failure mechanisms through the use of stereographic projection methods. Since Panet (1969), the stereographic projection technique has been used to determine failure modes in numerous studies (Markland 1972; Goodman 1976; Hocking 1976; Cruden 1978; Lucas 1980; Hoek and Bray 1981; Matherson 1988; Kincal 2014). For discontinuities of well-developed rock slopes, there are several discontinuity sets that dominantly control the failure of the rock mass. In conventional stereographic projection, these discontinuity sets, dip direction of the slope and other geometrical features are used to plot on a stereographic projection net to evaluate the dip and dip direction of slope and discontinuities. However, there is a problem of the deterministic analysis: only representative orientation values (dip/dip direction) for identified discontinuity sets are considered when using stereographic projection or kinematic analysis (Admassu and Shakoor 2013). Thus, a new method, which combines the results of Bayesian inference, probabilistic kinematic analysis and stereographic projection, was proposed.
Bayesian statistics was introduced to analyze the data to obtain a more accurate calculation of the slope failure angle. The method of Bayesian inference is used to infer the slope failure angle based on prior information, sample information and posterior information. Prior information includes, but is not limited to, maps and surveys, local experience, visual observations, and published reports and studies. Sample information is from field investigation, sampling or tests. Posterior information is a result of comprehensive analysis of prior information and sample information. Through the Bayesian formula, the slope failure angle can be inferred from posterior information. A Bayesian approach is developed in this article that provides a probabilistic framework to integrate prior information and sample information and to provide a probabilistic characterization of slope failure angles using a limited number of discontinuities. It can be seen that prior information is fully utilized in Bayesian statistics, and this is different from classical statistics. In recent years, numerous studies (Ditlevsen et al. 2000; Christian 2004; Wang et al. 2010; Chiu et al. 2012; Papaioannou and Straub 2012; Cao and Wang 2014; Wang et al. 2014) have been performed using Bayesian statistics in the field of geotechnical engineering with good results.
In this study, a case study of discontinuity-controlled rock slopes at the Southeast Dalian Port, China, was used to illustrate the proposed approach. Through comprehensive comparison of Bayesian estimation, probabilistic kinematic analysis and stereographic projection, the failure angle of potentially unstable blocks of the planned excavation slopes can be calculated. Thus, the calculated values can provide some help for the final design, e.g., limit equilibrium analysis, etc.
Problem statement
Kinematic analysis has been used to analyze the structural condition of unfavorably oriented discontinuities using the stereographic projection method. In this analysis, the orientation of a discontinuity is compared with the slope orientation and friction angle by plotting the orientation of a discontinuity onto a stereonet or a Schmidt net. This stereonet-based kinematic analysis assumes that a tightly clustered orientation of the discontinuities exists. However, the orientation of discontinuities measured in the field is often scattered. Such variations cannot be included in traditional kinematic analysis, and the mean orientation of a discontinuity is used, which creates uncertainties. It is obvious that the discontinuity set represented by a mean value of the discontinuity orientation in a group could well reflect the general condition of the discontinuities. However, they could not well represent those discontinuities that deviate far from the mean value of all the discontinuities in a group, namely, some singular points on the stereonet. The singular points that might have an influence on the rock mass would be neglected. Thus, many combinations of these discontinuities are not shown in the final results. This is a problem of the deterministic analysis. Alternatively, probabilistic kinematic analysis considers all the discontinuities and their intersections. Recently, Admassu and Shakoor (2013) developed the computer program DIPANALYST for quantitative kinematic analysis; Zhang et al. (2013) determined the critical slip surface via probabilistic kinematic analysis, and Park et al. (2015) applied GIS-based probabilistic kinematic analysis to the spatially distributed steep rock slopes. The above-mentioned probabilistic kinematic analysis always requires many discontinuities surveyed in the field. However, actually, it is not easy to perform the survey of discontinuity for its time-consuming recording process, and sometimes the site environment is not suitable for the investigation of discontinuity. Thus, only a limited number of discontinuities can be obtained from field investigation, and on the other hand, a reasonable result is needed. To overcome this problem, a more effective and scientific method that combines the results of Bayesian inference, probabilistic kinematic analysis and stereographic projection was proposed. This method will be illustrated in the methodology section. Through this method, some meaningful results can be obtained. According to the authors’ opinion, these results offer a good complement to the problems mentioned above when using the stereographic projection technique and kinematic analysis.
Characteristics of the study area
The planned excavation slopes are located in the Southeast Dalian Port, Dalian City, China. The planned construction area is approximately 200 m in length from north to south and approximately 180 m in width from east to west, covering an area of approximately 36,000 m² (Fig. 1). The natural slope is gentle, with a gradient of 15° and a dip direction of approximately 0° N. The slope reaches elevations of 33 m on the southern slope and 17 m on the northern slope. It is approximately 1 km from the north slope to the seaside. According to the engineering requirements, the slope would be excavated steeply at an angle of 76° or more. The main lithological unit distributed in the studied area is Epiproterozoic Sinian, moderately highly weathered slate. Clay, gravel and miscellaneous fill are also found covering the slates. However, their thicknesses are uneven. The main colors of the slates are yellow-brown and gray-brown. The slates are predominated by clay minerals. Crystalloblastic fabric and slaty cleavage are characteristics of the slates. The thickness of the slate layer is approximately 2-5 mm, with a maximum thickness of 20 mm. The slope is cut by joints and fractures. These discontinuities are highly developed. Because the composition of the protolith is different, a phenomenon of soft and hard interbedded rock can be seen in Fig. 2. The weak interlayer has a poor weathering resistance. Its thickness is 4–10 cm, with a maximum of 20 cm. The hard interlayer has a strong weathering resistance, with a thickness of 2–25 cm.
In the field, bedrocks are exposed in the northeast and southwest of the study area, and discontinuities are very well developed in the rock mass. There are a few meters of fill soil at the surface in the northwest and southeast of the study area. The geological structure of the rock mass is complex with developed discontinuities. Thus, it is common to see some small-scale geological phenomena, such as joints, fissures, faults, folds, and so on (Fig. 3). As can be seen in Fig. 3a, the formation of the kink bands is early and beds are overturned; Fig. 3b shows that the fault cuts through soft and hard interbedded rock. The fault is about 10 cm wide and 2.5 m long. The faulted zone is broken and filled with mud. There are clear dislocations on both sides of the fault. The rock strata mainly steeply dip to the south, i.e., bedding surfaces steeply dip into slope face. The phenomena of folding are widespread. These phenomena could lead to a variety of orientations. Thus, the orientations of rock strata have high variability in the area. The dip direction of the bedding surface in the study area appears overturned and partly dips to the north.
Properties of the discontinuities
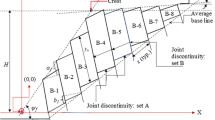
Properties of the discontinuities include the discontinuity dip/dip direction, discontinuity type, trace length, spacing, filling, weathering and so on to survey these properties; a total of nine outcrops were investigated in the study area in 2012 (Fig. 4). Seven of them were exploratory trenches excavated in the study area. The other two were natural outcrops near the northeast of the area. All the discontinuities were measured from these outcrops. Because the stratigraphic age in the study area is quite old and the strata have experienced several tectonic regimes, the discontinuities in the study area display the law of random distribution. Thus, each outcrop was regarded as a sampling window. Through the 9 sampling windows, a total of 1007 discontinuities were measured. For example, discontinuity information on the south exploratory trench, including the terminal point coordinate, the dip and dip direction, were collected using a rectangular sampling window with dimensions of 14.6 m in length and 1.8 m in height (Fig. 5). In addition to the orientation of the discontinuity, other properties, such as the type, spacing, persistency, aperture, filling, shape, weathering and water condition characteristics of the discontinuities, were described during the window sampling. Because probabilistic kinematic analysis is mainly concerned with discontinuity dip and dip direction, details relevant to other properties will not be given in the study. However, to illustrate the problem, the discontinuity properties of the south exploratory trench are summarized in Table 1.
The orientations of discontinuity were represented by a hybrid method discovered by Chen (1995). This method is a combination of the right-hand rule, traditional rose diagram of a strike and equal-area lower-hemisphere net. The so-called right-hand rule is a method used to determine the strike of a discontinuity. When a person faces one side of a strike line, the direction of his or her right hand is always the same as the dip direction of a discontinuity. Thus, the orientation of any discontinuity can be represented uniquely by the strike and dip angle. The right-hand rule can determine the strike of discontinuity in all quadrants, which complements the absent quadrants in the traditional rose diagram of the strike (usually NE and NW quadrants). The theory of the hybrid method used in Figs. 6 and 7 is that: (1) a lower hemisphere equal area projection is used for the analysis; (2) from the center of a circle to the edge, the dip angle of discontinuity ranges from 0° to 90°; (3) a modified traditional rose diagram of the strike determined by the right-hand rule is used. According to the authors’ opinion, the method is more convenient and useful in stress-field analysis of rock masses and more detailed in stability analyses of discontinuity-controlled rock masses (Chen et al. 2005). Through the investigation of nine outcrops, the measured discontinuity data were processed in rose and polar diagrams using the hybrid method (Fig. 6).
Rose and polar diagrams using the right hand rule: a south exploratory trench; b west exploratory trench; c west exploratory trench 2; d east exploratory trench; e supplementary exploratory trench 1; f supplementary exploratory trench 2; g north exploratory trench; h north outcrop 1; i north outcrop 2
Figure 6 shows that there is a common developmental characteristic of the random discontinuities existing in the study area. That is, the poles projected on the equal-area lower-hemisphere net have the characteristic of a random distribution. Many poles of discontinuities are distributed not only in the high dip angle area but also in the low dip angle area. Thus, it is difficult to conclude the developmental characteristic of these areas. However, the formation of most discontinuities is affected by tectogenesis. This suggests the discontinuities were influenced by some type of stress field, and they had grouping characteristics to some degree.
Through general representation of the discontinuity strike of the right-hand rule, a general characteristic and tendency result of random discontinuities could be achieved in the study area. However, the method could not clearly distinguish a representative attitude for a set of discontinuities. Thus, it is necessary to identify discontinuity sets in each sampling window. A method proposed by Shanley and Mahtab (1975, 1976) was employed in this study. The grouping result (Table 1; Fig. 7) of the orientation data of discontinuity in the south exploratory trench was processed using a program written by Chen (1995).
Methodology
With the structural geology conditions mentioned above, the failure modes of the discontinuity-controlled rock slope in the study are mainly plane, wedge and toppling failures. As explained by Hoek and Bray (1981), the kinematic conditions for discontinuity-controlled rock slope instabilities are shown in Fig. 8.
After determining failure modes, probabilistic kinematic analysis is used to determine the angle of the failure surface. Before this analysis, two assumptions should be made in the calculation: (1) Each discontinuity is randomly distributed in each excavation slope; (2) every discontinuity could have an influence on the stability of the excavation slopes.
Based on the above ideas, each discontinuity and combination of every two discontinuities must be analyzed in turn. This procedure was realized by the KINEMATIC computer program. The detailed procedures are shown as a flow chart in Fig. 9. The functions of the program are as follows: (1) The program can consider several parameters of the rock excavation slope (e.g., strike, dip direction and dip of the slope). (2) The program can consider mechanical parameters (e.g., c and ϕ) of the rock discontinuity. (3) For any single discontinuity, it can consider the influence of slope strike and discontinuity mechanical parameters simultaneously and automatically predetermine the potential of plane failure. Meanwhile, the dip and dip direction of the failure surface could be determined. (4) For all the discontinuities, the program can analyze potential wedge failure combined by every two discontinuities automatically. The trend and plunge of the intersections formed by the two discontinuities can be determined.
For the calculation mentioned above, design values, including the strike and dip angle, were used to represent the actual conditions of the excavation slope. The dip of the designed excavation slope is assumed to be 76°. Based on the results of the field work, the values of mechanical parameters of rock discontinuity are determined to be small. ϕ (internal friction angle) is defined as 27°, and c (cohesion) is temporarily defined as 0.
Through field investigation, a total of 88 discontinuities identified in the south exploratory trench were used to evaluate kinematic instabilities of the south excavation slope. By completing the KINEMATIC program, the statistical characteristics of the dip and dip direction of the potential unstable blocks analyzed by KINEMATIC are shown in Tables 2 and 3.
As shown in Tables 2 and 3, the data of potential unstable blocks caused by wedge and plane failure are quite limited in number. Thus, it is necessary to analyze these data for a better understanding of their statistical characteristics (Cao 2010; Yu 2011).
Bayes’ formula is used to estimate the slope failure angles analyzed by the probabilistic kinematic method. Bayesian statistics is a hierarchy with the most sophisticated model in statistical ideology. Any unknown parameter in an object function can be treated as a random variable. Previous experience is used as prior information. The unknown parameter is described by the prior distribution. Because prior information and sample information of the parameter are unified by Bayes’ formula, Bayesian estimation has greater precision (Zhang and Chen 1995; Li 1984). The most important feature of Bayesian statistics is that the concept of prior information is introduced during the process of statistical inference. Using Bayes’ formula, the slope failure angle can be estimated. The details of each step and its associated equations are summarized in what follows:
-
1.
Obtain the slope failure angle data of the south trench (sample information) and the slope failure angle data of two supplementary trenches (prior information) using KINEMATIC;
-
2.
Identify the optimum probability distribution functions (PDFs) (distribution forms) of slope failure angle data of the south trench and the supplementary trenches using GODFIT;
-
3.
Obtain correlation parameters such as μ and σ 2, and determine conditional probability distribution (CPD) (based on formula 1) such as formula 3 based on the optimum PDFs (take normal distribution as an example);
-
4.
Determine the posterior distribution (based on formula 2) such as formula 6, which was determined by formula 3, 4 and 5 (take normal distribution as an example);
-
5.
Determine evaluated value (expectation, i.e., slope failure angle) such as formula 7 (take normal distribution as an example).
This method makes the calculation result better reflect a prior understanding of the slope failure angle. Thus, it is more scientific and comprehensive for estimating slope stability.
The specific method is to treat the unknown parameter \( \theta \) in the general distribution density (or probability density) \( f\left( {x,\theta } \right) \) as a possible value of a random variable (or random vector) \( \varTheta \). In the field of the Bayesian method, the value of parameter \( \theta \) is usually used in the condition of \( \theta \) = \( \varTheta \). Thus, the usual probability density will be treated as the CPD (Box and Tiao 1973; Gong 2006), as shown in formula 1:
When the value of parameter \( \theta \) is set as \( \varTheta \), it has to show the distribution of \( \varTheta \). Before sampling, the distribution of the unknown parameter can be set based on simple initial prior knowledge. This refers to the prior distribution of \( \varTheta \). The distribution density (or probability function) of \( \varTheta \) is denoted as \( \pi \left( \theta \right) \). After sampling, based on the understanding of the probabilistic rule of the samples, through the calculation of Bayes’ formula, the prior distribution of the parameter is revised to the conditional distribution, which matches the samples. The conditional distribution is called a posterior distribution of \( \varTheta \), also known as the Bayesian distribution. From Bayes’ formula, the posterior distribution \( \pi \left( {\theta |x_{1} ,x_{2} , \ldots ,x_{n} } \right) \) can be calculated by formula 2:
Through the investigation of the discontinuities in the field and the probabilistic kinematic analyses by the program, a group of south-sloping failure angles is obtained. Bayesian estimation of the slope failure angle could be obtained using Bayes’ formula. As mentioned above, the advantage of Bayes’ formula is that it considers prior information. Thus, it is important to select prior information. In a certain area, the tectonism, components and environmental evolution of rock masses are similar. Because the rock lithology in the study area is slate, it is considered that the discontinuities investigated in each trench are integrally related. Meanwhile, the strike of each trench should be considered, i.e., using prior information concerning whether the trenches should have a similar strike. Thus, the prior information includes the failure angles of the two supplementary exploratory trenches excavated in the middle of the natural slope, and the sample information includes the failure angles of the south exploratory trench near the south slope. Therefore, the GODFIT computer program was written to study these data. The function of the program is to identify which PDF is optimal for analyzing the statistical characteristics of the data and calculate the correlation parameters. The optimum PDF is evaluated by the Kolmogorov-Smirnov goodness-of-fit test (Chen et al. 1996; Han et al. 2015). The K-S test is a nonparametric test whose statistical procedure does not rely on assumptions about the form of the distribution of populations. In this study, the K-S test was adopted to examine whether the difference between the mentioned distributions (normal or log-normal) of the measured trace length and sample data is significant. The K-S value was used to examine the distance between the distribution of the measured trace length and the sample data. The degree of freedom (DOF) is the number of values in the final calculation of a statistic that are free to vary. In the study, DOF refers to the number of sample groups divided by GODFIT automatically, and it has an influence on the K-S value.
Through the analysis of dip angles of 342 possible sliding wedges (sample information) in the south trench, a log-normal function is identified as the optimum PDF to fit the distribution characteristic of the dip angle data, as shown in Fig. 10a. In addition, through the analysis of the dip angles of a total of 3637 wedges (prior information) in the supplementary trench, a log-normal function is also the optimum PDF to fit the distribution characteristic of the dip angle data, as shown in Fig. 10b. For possible sliding planes, normal function is the optimum PDF to fit the distribution characteristic of the dip angle data in both the south trench (sample information) and the supplementary trench (prior information), as shown in Fig. 10c, d, respectively. The corresponding parameters are shown in Table 4.
Because the fit functions of prior information and sample information of the wedges are log-normal functions, the computational method is used to convert these functions from log-normal distributions to normal distributions. If x obeys a normal distribution, the CPD could be written as formula 3. According to Bayesian theory, the unknown parameter \( \theta \) in formula 3 is a possible value of the random variable \( \varTheta \), and the distribution of \( \varTheta \) is the prior distribution shown as formula 4. Thus, the joint density function can be written as formula 5:
In statistics, the process of adding samples is treated as the revised cognitive process of the distribution of \( \varTheta \). After sampling, N samples (\( x_{1} ,x_{2} , \ldots ,x_{n} \)) are obtained, and through mathematical deduction, the posterior distribution of \( \theta \) is shown as formula 6. The mathematical expectation of the posterior distribution is shown as formula 7.
Let y = lnx, y′ = lnθ, if x obeys a log-normal distribution, y obeys a normal distribution. In the form of a normal distribution, the mean value \( \mu^{\prime \prime } \) and variance \( \sigma^{\prime \prime 2} \) of the posterior distribution can be written as formula 8, respectively:
It should be noted that parameters \( \mu \), \( \sigma^{2} \) and \( \mu^{\prime } \), \( \sigma^{\prime 2} \) are the mean value and the variance of \( f\left( {y |\theta } \right) \) and \( \pi \left( {y^{\prime } } \right) \), respectively. Thus, when prior information and sample information are both in a log-normal distribution, the mathematical expectation (Xia and Ma 2008) is concluded as formula 9:
Therefore, when the failure mode is wedge sliding, because the slope failure angles of wedge sliding obey log-normal distribution (Table 4), the Bayesian estimation of the south-sloping failure angles can be calculated using formula 8 and 9 according to the parameters in Tables 3 and 4; the results are listed in Table 5. Similarly, when the failure mode of the south slope is plane sliding, 18 potential sliding planes of the south slope act as the sample information, and 119 potential sliding planes of the supplementary trenches act as the prior information. Through the calculation of the GODFIT program, a normal distribution is identified as the optimum PDF to fit the distribution characteristics of the prior and sample information. According to the parameters obtained from GODFIT (see Table 4), through formula 7, Bayesian estimations of plane failure angles can be obtained and are listed in Table 5. In the same way, the Bayesian estimation of the other trenches can be obtained.
According to the discontinuities and the grouping result of the discontinuity sets (Table 1; Fig. 7) in the south exploratory trench, the orientation of the slope face and the discontinuity sets are plotted in the stereonet (Fig. 11). Using the stereographic projection method, a potential sliding wedge formed by set 1 and set 2 is found. The dip direction of the intersection of the two sets is 45.36°, and the dip angle of the intersection is 70.16°. Thus, through the procedures to evaluate apparent dip from true dip (Admassu and Shakoor 2013; Park and West 2001), the failure angle of the excavation slope calculated by stereographic projection is 63.22°. Additionally, a group of potential sliding planes controlled by set 2 is found, with a failure angle of 69.17°.
Through comparative analyses of the results of the Bayesian estimation, the probabilistic kinematic method and stereographic projection, the failure angle of the south slope is eventually determined (see Table 5; Fig. 12). Similarly, the failure angles of the other slopes can be obtained.
As can be seen from Table 5 and Fig. 12, the values of the failure angles of the probabilistic kinematic method and Bayesian estimation are smaller than that of stereographic projection because the two methods consider each discontinuity plane and their intersections, especially certain planes in zones of lower concentrations. The values of the failure angles of Bayesian estimation are intermediate between the sample mean value and prior mean value of the probabilistic kinematic method because Bayesian estimation considers both sample information and prior information of the discontinuities.
Conclusion and discussion
The study is performed to apply Bayesian inference, the rules of kinematic analysis and stereographic projection to discontinuity-controlled rock slope instabilities with a different approach to including all measured discontinuities on the outcrops, testing all possible orientations and intersections of the planes with designed excavation slope geometry. Through the analyses of potential unstable blocks caused by plane failure, wedge failure and toppling failure, the failure angle of the south excavation slope is obtained. Because the three methods use different statistical methods, their results are also different.
The values of the failure angle of the probabilistic kinematic method and Bayesian estimation are smaller than that of stereographic projection (Fig. 12), because the probabilistic kinematic method and Bayesian estimation consider each discontinuity plane and their intersections, especially certain planes in zones of lower concentrations that can lead potential slides. The stereographic projection values calculated through three discontinuity sets that were represented by a mean value of the discontinuity orientation in each group could well reflect the general condition of the discontinuities. However, they could not represent those discontinuities that deviate far from the mean value of all the discontinuities in a group well, namely, some singular points on the stereonet. Those singular points that would lead to potential slides are neglected. Thus, many combinations of these discontinuities are not shown in the final results.
Bayesian inference is introduced to estimate the slope failure angle utilizing the results obtained from probabilistic kinematic analysis. Through the calculation with the GODFIT program, several types of PDFs could fit the data of failure angles in each exploratory trench. Thus, Bayes’ formula could be used for these data. The final result of this method considers both sample information and prior information. Thus, it is more scientific and economical than classical statistics. However, it should be noted that the selection of prior information is quite important. Proper prior information could give a precise value, but improper prior information would be misleading.
The probabilistic kinematic method requires analysis of each discontinuity plane and their intersections in a sample window. Thus, many meaningful analyses can be performed from this method through the KINEMATIC program, which considers the orientation and mechanical parameters of the discontinuities and the three failure modes. This method is more meticulous and complete than traditional stereographic projection.
Traditional stereographic projection analyzes each discontinuity set. This method offers a general guidance for kinematic analysis. However, a discontinuity set is usually a mean value of the discontinuities in a group and does not accurately represent discontinuities that deviate far from the mean values of a given group.
In the authors’ opinion, in the field of geotechnical engineering, especially for discontinuity-controlled rock with characteristics of randomicity and variability, the result of any single method cannot accurately represent actual conditions. Stereographic projection is reliable in general, probabilistic kinematic analysis is more meticulous, and Bayesian estimation is more scientific. The results of the three methods can be cross-referenced.
References
Admassu Y, Shakoor A (2013) DIPANALYST: a computer program for quantitative kinematic analysis of rock slope failures. Comput Geosci 54:196–202
Aksoy H, Ercanoglu M (2007) Fuzzified kinematic analysis of discontinuity-controlled rock slope instabilities. Eng Geol. doi:10.1016/j.enggeo.2006.10.007
Box GEP, Tiao GC (1973) Bayesian inference in statistical analysis. Addison-Wesley, Reading
Cao ZX (2010) The statistic analysis and reliability research of rock slope stability. M.S. Dissertation, Jilin University (in Chinese)
Cao ZJ, Wang Y (2014) Bayesian model comparison and characterization of undrained shear strength. J Geotech Geoenviron Eng 140:04014018
Chen JP, Xiao SF, Wang Q (1995) Three-dimensional network modeling of random fractures. Northeast Normal University Press, Changchun (in Chinese)
Chen JP, Shi BF, Wang Q (2005) Study on the dominant orientations of random fractures of fractured rock masses. Chin J Rock Mech Eng 02:241–245 (in Chinese)
Chiu CF, Yan WM, Yuen KV (2012) Reliability analysis of soil–water characteristics curve and its application to slope stability analysis. Eng Geol 135–136:83–91
Christian JT (2004) Geotechnical engineering reliability: how well do we know what we are doing? J Geotech Geoenviron Eng 130:985–1003
Cruden DM (1978) Discussion of G. Hocking’s paper ‘‘A method for distinguishing between single and double plane sliding of tetrahedral wedges’’. Int J Rock Mech Min Sci Geomech Abstr 15, 217
Ditlevsen O, Tarp-Johansen NJ, Denver H (2000) Bayesian soil assessments combining prior with posterior censored samples. Comput Geotech 26:187–198
Gong GL (2006) Probability and mathematical statistics. Tsinghua University Press, Beijing (in Chinese)
Goodman RE (1976) Methods of geological engineering in discontinuous rocks. West Publishing, San Francisco
Han XD, Chen JP, Wang Q, Li YY, Zhang W, Yu TW (2015) A 3D fracture network model for the undisturbed rock mass at the songta dam site based on small samples. Rock Mech Rock Eng. doi:10.1007/s00603-015-0747-5
Hocking G (1976) A method for distinguishing between single and double plane sliding of tetrahedral wedges. Int J Rock Mech Min Sci Geomech Abstr 13:225–226
Hoek E, Bray JW (1981) Rock slope engineering. The Institution of Mining and Metallurgy, London
Kincal C (2014) Application of two new stereographic projection techniques to slope stability problems. Int J Rock Mech Min Sci. doi:10.1016/j.ijrmms.2014.01.006
Lana M, Gripp M (2003) The use of inclined hemisphere projections for analyzing failure mechanisms in discontinuous rocks. Eng Geol 67:321–330
Li T (1984) Empirical bayes approach to reliability estimation for the exponential distribution. IEEE Trans Reliab 33:233–236
Lucas JM (1980) A general stereographic method for determining possible mode of failure of any tetrahedral rock wedge. Int J Rock Mech Min Sci Geomech Abstr 17:57–61
Markland JT (1972) A useful technique for estimating the stability of rock slopes when the rigid wedge sliding type of failure is expected. Imp Coll Rock Mech Res Rep 19:10
Matherson GD (1988) The collection and use of field discontinuity data in rock slope design. Q J Eng Geol 22:19–30
Panet M (1969) Discussion on “Graphical stability analysis of slopes in jointed rock”. By K.W. John. J Soil Mech Found DivProc ASCE 95:685–686
Papaioannou I, Straub D (2012) Reliability updating in geotechnical engineering including spatial variability of soil. Comput Geotech 42:44–51
Park H, West TR (2001) Development of a probabilistic approach for rock wedge failure. Eng Geol 59:223–251
Park HJ, Lee JH, Kim KM, Um JG (2015) Assessment of rock slope stability using GIS-based probabilistic kinematic analysis. Eng Geol. doi:10.1016/j.enggeo.2015.08.021
Priest SD (1993) Discontinuity analysis for rock engineering. Chapman and Hall, London
Shanley RJ, Mahtab MA (1975) FRACTAN: a computer code for analysis of clusters defined on the unit hemisphere: I.C. 8671, US Bureau of Mines, Washington, DC, p 49
Shanley RJ, Mahtab MA (1976) Delineation and analysis of clusters in orientation data. Math Geol 8:9–23
Wang Y, Au SK, Cao ZJ (2010) Bayesian approach for probabilistic characterization of sand friction angles. Eng Geol 114:354–363
Wang Y, Huang K, Cao Z, Standing JR, Calderhead B (2014) Bayesian identification of soil strata in London clay. Geotechnique 64:239–246
Xia YF, Ma SL (2008) Bayes inference of loss- and risk-function in logarithmic normal distribution parameter estimation. J Lanzhou Univ Technol 34:131–132 (in Chinese)
Yu L (2011) The stability assessment of fractured rock slope based on reliability. Ph.D Dissertation, Jilin University (in Chinese)
Zhang YT, Chen HF (1995) Bayesian inference. Science Press, Beijing (in Chinese)
Zhang W, Chen JP, Zhang W, Lu Y, Ma YF, Xiong H (2013) Determination of critical slip surface of fractured rock slopes based on fracture orientation data. Sci China Tech Sci 56:1248–1256. doi:10.1007/s11431-012-5129-6
Acknowledgements
This work was supported by the State Key Program of National Natural Science of China (grant nos. 41330636, 41402243) and the Graduate Innovation Fund of Jilin University (grant no. 2015013).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zhou, X., Chen, J., Chen, Y. et al. Bayesian-based probabilistic kinematic analysis of discontinuity-controlled rock slope instabilities. Bull Eng Geol Environ 76, 1249–1262 (2017). https://doi.org/10.1007/s10064-016-0972-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10064-016-0972-5