Effect of strength anisotropy on strain localization in natural clay

Abstract

Strain localization in soils causes the failure of slopes and foundations. Shear strength is an important factor that affects strain localization in soils. It is well known that the shear strength of natural clay is highly anisotropic due to the internal soil structure. An anisotropic failure criterion for natural clay is presented in which an anisotropic variable is used to describe the relative orientation between the stress directions and soil fabric. The failure criterion is employed in a Drucker–Prager model that considers the strain softening of natural clay. The effect of anisotropic strength on strain localization in clay is analyzed by two examples, including an undrained slope stability analysis and a simulation of a hollow cylinder test of Boom clay. It is found that the shear strength anisotropy affects both the strain localization pattern and factor of safety for the undrained slope. Simulation of the tests on Boom clay shows that the model with the anisotropic yield criterion yields an eye-shaped strain localization pattern that cannot be obtained by the model with the isotropic yield criterion.

1 Introduction

Strain localization, such as shear band development, causes the failure of slopes and foundations. Strain localization is affected by many factors [40, 51, 62]. Among them, the shear strength is one of the most important. Natural clays always have an anisotropic internal structure or fabric (e.g., particle orientation and void space distribution) that is caused by compaction or gravity [54, 61], which results in inherent anisotropy. This makes the shear strength of natural clay dependent on the loading direction [39] and the degree of saturation [30, 31]. Another kind of anisotropy is caused by loading history, called stress-induced anisotropy or induced anisotropy. The inherent anisotropy is addressed in this paper. Existing research has shown that the location of the slip surfaces and the factor of safety of a clay slope are significantly affected by strength anisotropy [55]. A significantly lower factor of safety will be obtained when strength anisotropy is considered. Furthermore, strain localization in Boom clay due to excavation is found to be influenced by strength anisotropy [20].

An anisotropic model is thus crucial for constitutive modeling in clays. The key feature of the anisotropic model is to use an anisotropic yield criterion for the modeling of inherent anisotropy and to incorporate a kinematic hardening law for the modeling of induced anisotropy [66]. Another attractive alternative to the kinematic hardening method is the micromechanics approach [66,67,68]. Rotated yield surfaces have been widely used in modeling the anisotropic behavior of clay [2, 12, 13, 35, 63, 64, 69]. This approach is effective for modeling the anisotropy caused by the previous loading history. The evolution of anisotropy can be easily considered in the modeling framework. However, when the initial effective stress state is isotropic, the soil fabric is typically assumed to be isotropic as well, which may not be reasonable for natural clay.

There have been several methods where inherent anisotropy was incorporated into the constitutive description [19, 53, 72]. One of the most important ways is to construct anisotropic models based on the existing isotropic criteria, such as the von Mises criterion [29], the Mohr–Coulomb criterion [48], the Cam-Clay model [45], and the modified Cam-Clay model [11].

To model the inherent anisotropy of natural clays, Casagrande and Carillo [8] presented an expression for the anisotropic undrained shear strength of clay, in which the direction of the major principal stress is needed. While this expression has been validated by the test results of some soils, such as Canadian Welland clay [43], it can only be used when the bedding plane is horizontal. Furthermore, Grimstad et al. [28] proposed an anisotropic Tresca model for describing the undrained response of clays, i.e., NGI-ADP. Krabbenhøft et al. [37] developed the AUS model following the works of Grimstad et al. [28]. This model includes three undrained shear strength parameters obtained by three sets of tests, including triaxial extension, triaxial compression, and simple shear. However, all these tests must be performed on a soil sample with a horizontal bedding plane. The model parameters will have to be adjusted when the bedding plane orientation is not horizontal in a real application. An anisotropic modified Cam-Clay model was proposed to describe the anisotropy of rock, which involves the microstructure tensor [6, 53, 72, 73]. It is denoted by a second-order tensor, which is the tensor product of the unit normal vector to the bedding plane and itself. Methods using fabric tensors have also been developed to model the strength anisotropy of soils. In these methods, joint invariants of the stress tensor and fabric tensor are needed in the formulations [14, 46, 49]. For instance, Gao et al. [22] developed an anisotropic model for soils based on the works of Yao et al. [65] and Dafalias et al. [14]. In this model, an anisotropic variable that describes the relative orientation between the loading direction and the material fabric is introduced. This model has been used for both soils and rocks.

Some of the models have been used in modeling strain localization in clay. The NGI-ADPSoft model based on NGI-ADP, which takes into account the strain-softening behavior of clays, has been used to analyze a full-scale railway embankment built on a soft clay deposit [15]. Based on the method of Pietruszczak and Mroz [49], Tang et al. [59] proposed a failure criterion in the form of Casagrande’s expression [8] to present an anisotropic DP model and conducted a simulation of strain localization in an undrained slope of clay. However, the failure criterion in this study lacks variety and is not applicable. In Belgium, Switzerland, and France, Boom clay, Opalinus clay, and Callovo-Oxfordian clay are candidate host rocks for the deep geological disposal of radioactive waste. Strain localization in these clays has been studied [5, 20, 44, 47]. In the study of Mánica et al. [44], a four-parameter complex anisotropic failure criterion proposed by Conesa et al. [10] using a curve-fitting approach was used. However, none of these studies attempts to construct a “complete” anisotropic constitutive model but dynamically updates the anisotropic cohesion and calculates the direction of the major principal stress in nonlinear incremental iterative calculations. In other words, the gradient of the yield function of the constitutive model does not include a component of anisotropic cohesion. Excessive load increments can affect the accuracy of describing cohesion [16].

In this study, an elastoplastic DP model is proposed that considers the anisotropic strength as well as strain-hardening/softening characteristics of clay. In the yield function, an anisotropic function of stress is used to describe the anisotropic strength of the clay. Since the shear strength is the focus of this study, the soil response is assumed to be purely elastic before failure. Under undrained conditions, the anisotropic DP model reduces to the anisotropic von Mises model. The model is implemented in the user subroutines of ABAQUS software [1]. The validation of the proposed anisotropic DP model is demonstrated by two typical examples, undrained slope stability analysis and simulation of the Boom clay hollow cylinder test, representing limit equilibrium and progressive failure problems, respectively. The effect of anisotropic strength on strain localization in clay is analyzed with emphasis.

2 Anisotropic plastic constitutive model

2.1 Anisotropic failure criterion

The cross-anisotropy of clays can be characterized by the symmetric second-order fabric tensor $F_{ij}$ [46].

$$ F_{ij} = \left[ {\begin{array}{*{20}c} {F_{x} } & 0 & 0 \\ 0 & {F_{y} } & 0 \\ 0 & 0 & {F_{z} } \\ \end{array} } \right] = \frac{1}{3 + \Delta }\left[ {\begin{array}{*{20}c} {1 + \Delta } & 0 & 0 \\ 0 & {1 - \Delta } & 0 \\ 0 & 0 & {1 + \Delta } \\ \end{array} } \right] $$

(1)

where $\Delta$ is a scalar and $0 < \Delta < 1$. It is assumed that the principal directions of the fabric tensor are consistent with the local coordinate system (x, y, z) and that the x–z plane is the isotropic plane, as shown in Fig. 1. The global coordinate axes are the x_i, y_i, and z_i axes. It is worth noting that the isotropic plane is not necessarily horizontal.

Fig. 1

Schematic diagram of the local coordinate system and the isotropic plane of the clay

The strength of clay depends on the soil structure in clay and the loading direction. Gao and Zhao [23] proposed an anisotropic function $g\left( A \right)$ (Eq. 2) to describe the anisotropic strength of geomaterials.

$$ g\left( A \right) = \exp \left[ {\mathop \sum \limits_{i = 1}^{n} e_{i} \left( {1 + A} \right)^{i} } \right] $$

(2)

where $e_{i}$ is a set of material parameters. For isotropic soil, $e_{i} = 0$. $A$ is the anisotropic state variable. Based on the deviatoric stress tensors $s_{ij}$ and the deviatoric part of the fabric tensor $d_{ij}$, the variable $A$ can be expressed as

$$ A = \frac{{s_{ij} d_{ij} }}{{\sqrt {s_{mn} s_{mn} } \sqrt {d_{mn} d_{mn} } }} = \frac{{s_{x} - 2s_{y} + s_{z} }}{2q} $$

(3)

where $d_{ij} = F_{ij} - F_{kk} \delta_{ij} /3$ and $q$ is the equivalent von Mises stress:

$$ q = \sqrt {\frac{3}{2}s_{ij} s_{ij} } $$

(4)

where ${s}_{ij}$ is the deviatoric stress tensor and ${s}_{x}$, ${s}_{y}$, and ${s}_{z}$ are deviatoric stresses in the three-axis directions of the local coordinate system. It is worth noting that the normalized deviatoric fabric tensor, i.e., Eq. (5), is just a constant diagonal matrix. Therefore, the microscopic parameter $\Delta$ is not required in the numerical simulation.

$$ \frac{{d_{ij} }}{{\sqrt {d_{mn} d_{mn} } }} = \frac{1}{\sqrt 6 }\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & { - 2} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right] $$

(5)

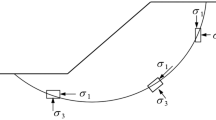
In the proposed model, the anisotropic function $g\left( A \right)$ is used to define the anisotropic strength of clays and $n = 3$. To illustrate how to determine the parameters ${e}_{1}$, ${e}_{2}$, and ${e}_{3}$, the hollow cylinder torsional shear test under undrained conditions on Gault clay in the UK [7] is taken as an example. In Fig. 2, $\alpha$ is the angle between the major principal stress and the axis of the isotropic plane. ${S}_{u}$ is the peak undrained shear strength of Gault clay for various $\alpha$ and ${S}_{u}=g(A){S}_{u0}$, where ${S}_{u0}$ is the undrained shear strength at $\alpha =0^\circ$.

Fig. 2

Comparison between the data of the torsional test on Gault clay [7] and the proposed anisotropic failure criterion

For the hollow cylinder torsional shear test, the formula $A^{\left( \alpha \right)}$ has been given [23]. $A^{\left( \alpha \right)}$ is used to determine the anisotropic parameters $e_{1}$, $e_{2}$, and $e_{3}$, and then, Eq. (3) with $e_{1}$, $e_{2}$, and $e_{3}$ is adopted in the numerical simulation.

$$ A^{\left( \alpha \right)} = \frac{{ - 3\cos^{2} \alpha + b + 1}}{{2\sqrt {b^{2} - b + 1} }} $$

(6)

where $b$ is the intermediate principal stress ratio expressed as

$$ b = \frac{{\sigma_{2} - \sigma_{3} }}{{\sigma_{1} - \sigma_{3} }} $$

(7)

$\sigma_{1}$, $\sigma_{2}$, and $\sigma_{3}$ are the major, intermediate, and minor principal stresses, respectively. The test results for Gault clay consist of five data points, of which the first ($\alpha = 0^\circ$), third ($\alpha_{p} = 39^\circ$), and fifth points ($\alpha = 90^\circ$) are chosen to determine $e_{1}$, $e_{2}$, and $e_{3}$ by solving Eqs. (3) with $b = 0.5$. Note that $b$ is a constant in all the tests.

$$ \left\{ {\begin{array}{*{20}c} {e_{1} \left( {1 + A^{\left( 0 \right)} } \right) + e_{2} \left( {1 + A^{\left( 0 \right)} } \right)^{2} + e_{3} \left( {1 + A^{\left( 0 \right)} } \right)^{3} = \ln K^{\left( 0 \right)} = 0} \\ {e_{1} \left( {1 + A^{{\left( {90^{ \circ } } \right)}} } \right) + e_{2} \left( {1 + A^{{\left( {90^{ \circ } } \right)}} } \right)^{2} + e_{3} \left( {1 + A^{{\left( {90^{ \circ } } \right)}} } \right)^{3} = \ln K^{{\left( {90^{ \circ } } \right)}} } \\ {e_{1} \left( {1 + A^{{\left( {\alpha_{p} } \right)}} } \right) + e_{2} \left( {1 + A^{{\left( {\alpha_{p} } \right)}} } \right)^{2} + e_{3} \left( {1 + A^{{\left( {\alpha_{p} } \right)}} } \right)^{3} = \ln K^{{\left( {\alpha_{p} } \right)}} } \\ \end{array} } \right. $$

(8)

where

$$ K^{\left( \alpha \right)} = g\left( {A^{\left( \alpha \right)} } \right) = \frac{{S_{u} }}{{S_{u0} }} $$

(9)

The prediction of the anisotropic failure criterion is shown in Fig. 2.

2.2 Anisotropic DP Yield Function and Potential Function

In Fig. 3, the isotropic linear DP yield criterion for clays in terms of effective stresses [17] is expressed as

$$ F\left( {p^{\prime}, q} \right) = q - m\left( {p^{\prime} + \frac{{c^{\prime}}}{{\tan \varphi^{\prime}}}} \right) = 0 $$

(10)

where

$$ m = \frac{{6{\text{sin}}\varphi^{\prime}}}{{3 - \sin \varphi^{\prime}}} $$

(11)

where $\varphi^{\prime}$ and $c^{\prime}$ are the effective internal friction angle and the effective cohesion, respectively. $p^{\prime}$ is the mean effective stress.

Fig. 3

Linear DP yield surface in (a) the meridional plane and (b) the deviatoric plane

There are two strength parameters in the DP yield criterion, i.e., internal friction angle and cohesion. Duncan and Seed [18] and Sergeyev et al. [54] concluded that the internal friction angle of clay shows only moderate anisotropy and is independent of the loading direction. However, the undrained shear strength and cohesion are highly anisotropic. Therefore, anisotropic DP yield criteria considering only cohesive anisotropy have been frequently used [20, 59, 60]. To describe the anisotropic shear strength of clays under drained conditions, the proposed anisotropic DP yield function is written as

$$ F\left( {p^{\prime}, q,A} \right) = q - m\left( {p^{\prime} + \frac{{g\left( A \right)c_{0}^{^{\prime}} }}{{\tan \varphi^{\prime}}}} \right) = 0 $$

(12)

where $c_{0}^{^{\prime}}$ is the effective cohesion measure in triaxial compression with the direction of the major principal stress parallel to the axis of the isotropic plane.

Under undrained conditions, $\varphi^{\prime} = 0$ and $S_{u0} = c_{0}^{^{\prime}}$ are assumed, and the DP yield function reduces to the von Mises yield function. Under plane strain conditions [1], the DP yield function is expressed as

$$ F\left( {q, A} \right) = q - \sqrt 3 S_{u0} g\left( A \right) = 0 $$

(13)

where $S_{u0}$ is the undrained shear strength when the direction of the major principal stress is parallel to the axis of the isotropic plane of the clay.

The plastic potential function $G$ of the proposed model is written as

$$ G = q - m^{\prime}p^{\prime} = 0 $$

(14)

where

$$ m^{\prime} = \frac{{6{\text{sin}}\psi }}{3 - \sin \psi } $$

(15)

where $\psi$ is the dilation angle. The gradient of the proposed anisotropic yield function is introduced in Appendix 1. Since the plastic potential function does not include the fabric tensor $F_{ij}$, the flow rule is noncoaxial [24, 71].

2.3 Hardening law and nonlocal strain softening

Strain localization is usually simulated by the plastic model with strength parameters that decrease linearly or nonlinearly with increasing equivalent plastic strain [32, 33, 36]. In the proposed model, the isotropic strain-hardening/softening law of clay is a function of the equivalent plastic strain $\varepsilon_{dp}$.

$$ \varepsilon_{dp} = \mathop \smallint \limits_{0}^{t} \sqrt {\frac{2}{3}\dot{\user2{e}}:\dot{\user2{e}}} dt $$

(16)

where $\dot{\user2{e}}$ is the rate tensor of the deviatoric plastic strain and $t$ is the time of the simulation.

The simplest softening law is a linear relationship between the shear strength and the equivalent plastic strain, e.g., the one proposed by Potts et al. [50], as shown in Fig. 4b. In the analysis in Sect. 4.2, a nonlinear hardening/softening relationship is used. Based on the anisotropic parameters of Gault clay, the method proposed by Gao and Zhao [23] is utilized to plot the yield surfaces in the deviatoric plane that change from a circle to an irregular ellipse due to the anisotropic function $g\left( A \right)$. The yield surface shape does not change but shrinks with increasing plastic strain (Fig. 4a).

Fig. 4

Isotropic strain-softening law and changes in (a) yield surface and (b) relation between undrained shear strength and the equivalent plastic strain

For simplicity, the anisotropy of undrained shear strength and the softening characteristics of cohesion are assumed to be independent. Therefore, in Fig. 5, the undrained shear strength can be illustrated as a function of the anisotropy parameters $e_{1}$, $e_{2}$, and $e_{3}$ and softening parameters $k_{r}$ and $\varepsilon_{dp}^{r}$.

Fig. 5

Undrained strength as a function of the equivalent plastic strain and major principal stress direction α

In finite element analysis (FEA), strain softening of the material results in mesh sensitivity. A partially nonlocal softening regularization approach proposed by Galavi and Schweiger [21] is employed to reduce the mesh sensitivity. In the approach, only the deviatoric strain is considered a nonlocal variable. A detailed introduction of the approach has been given [56, 57]. Following the implementation of the nonlocal approach proposed by Gao et al. [24], the nonlocal equivalent plastic strain at an integration point is expressed as

$$ \varepsilon_{dp}^{*} = \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {\varepsilon_{dp} } \right)_{i} \omega_{i} v_{i} }}{{\mathop \sum \nolimits_{i = 1}^{N} \omega_{i} v_{i} }} $$

(17)

where $N$ is the total number of integration points in the FEA. $\left( {\varepsilon_{dp} } \right)_{i}$, $v_{i}$, and $\omega_{i}$ are the local equivalent plastic strain, volume, and weight function at the ith integration point, respectively. The weight function expressed below is used.

$$ \omega_{i} = \frac{{r_{i} }}{{l^{2} }}\exp \left( { - \frac{{r_{i} }}{{l^{2} }}} \right) $$

(18)

where $l$ is the internal length parameter and $r_{i}$ is the distance between the current integration point and integration point $i$. Their units should be consistent with the units of the geometric dimensions of the model. To better describe the strain localization characteristics, the rate of the nonlocal equivalent plastic strain is given as

$$ \dot{\varepsilon }_{dp}^{*} = \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {\dot{\varepsilon }_{dp} } \right)_{i} \omega_{i} v_{i} }}{{\mathop \sum \nolimits_{i = 1}^{N} \omega_{i} v_{i} }} $$

(19)

3 Implementation of the model

The proposed anisotropic DP model is implemented in the user subroutines of ABAQUS software [1]. Figure 6 shows the flow chart of the user subroutines. The key parts of the code are the anisotropic yield criterion for clays and the nonlocal regularization approach. These two parts are implemented by the user subroutines to define a material’s mechanical behavior (UMAT) and to redefine field variables at an integration point (USDFLD). The stress integration algorithm for the constitutive model is the implicit backward Euler algorithm, which requires a Newton procedure to solve the nonlinear equations [3].

Fig. 6

Flow chart of the user subroutines for implementation of the proposed anisotropic DP model

4 Strain localization in anisotropic clay

To study the effect of anisotropic shear strength on the strain localization in natural clays, undrained slope stability analysis and simulation of the hollow cylinder test of Boom clay are chosen to represent the limit equilibrium problem and the progressive failure problem, respectively.

4.1 Stability analysis of undrained clay slope

There are two cases for stability analysis of undrained clay slopes. Case 1 is a stability analysis of an undrained clay slope with different anisotropic undrained shear strengths. Case 2 is a stability analysis of an undrained clay slope with different orientations of the bedding plane (i.e., isotropic plane), which might exist in naturally deposited clays owing to cross-bedding or post-depositional deformations. To better compare with the results in other literature, it is assumed that the potential function is consistent with the yield function in the proposed slope stability analysis.

4.1.1 Case 1: Slope with anisotropic undrained shear strengths

The cross-anisotropic shear strength relation for the undrained strength of clay proposed by Casagrande and Carillo [8] is expressed as

$$ S_{u} = S_{u0} \left[ {K + \left( {1 - K} \right)\cos^{2} \alpha } \right] $$

(20)

where $K$ is the ratio of the undrained shear strength at $\alpha = 90^\circ$ to $S_{u0}$. For isotropic clays, $K = 1.0$. Lo (1965) found that Casagrande’s expression is valid for the Welland clay in Canada. According to the cross-anisotropic strength relation, Chen et al. [9] proposed the upper bound (UB) method of limit analysis to evaluate the stability of anisotropic undrained slopes. Based on the proposed anisotropic DP model assuming ideal plasticity, the stability number $N_{s}$ of the slope is calculated by the finite element strength reduction method (FESRM) [27, 42, 58] and is compared with the UB solution.

$$ N_{s} = H_{c} \left( {\frac{\gamma }{{S_{u0} }}} \right) $$

(21)

where H_c is the critical height of the slope and $\gamma$ is the unit weight of the clay.

Normally, the FESRM is used to solve the safety factor for a slope with a given height rather than solving the critical height and corresponding stability number of the slope. There is a relation between the safety factor and the stability number. In the FESRM, $S_{u0}$ is used for the reduction, and the factor of safety $F_{s}$ is expressed as

$$ F_{s} = \frac{{S_{u0} }}{{S_{u0}^{f} }} $$

(22)

where $S_{u0}^{f}$ is the factored shear strength parameter. Therefore,

$$ N_{s} = H\left( {\frac{\gamma }{{S_{u0}^{f} }}} \right) = F_{s} H\left( {\frac{\gamma }{{S_{u0} }}} \right) $$

(23)

Taking the slope angle $\beta_{s} = 50^\circ$ as an example, Fig. 7 presents the geometry, finite element mesh, boundary conditions, and material parameters of the example, assuming that the clay has isotropic elasticity. The initial stress is caused by gravity. Figure 8 shows that there is little difference between the proposed anisotropic criterion and the Casagrande formula for $K = 1.5$ and $0.5$. Kimmeridge clay [7] is a natural clay with $K > 1$. Table 1 lists the stability number of the undrained slope obtained by the UB and the FESRM with various $K$. When $K = 1.0$, the finite element limit equilibrium method (FELEM) [41] is used to validate the FESRM. The results obtained by the two finite element methods are close with a percentage difference of only 3%. For $K < 1.0$, the stability number obtained by the FESRM is smaller than that obtained by the UB. This is because the UB result is an upper bound and the slip surface of the UB is a fixed logarithmic spiral. Moreover, the stability number obtained by the FESRM decreases with decreasing $K$. The percentage differences of the stability number obtained by the FESRM between $K = 0.5$ and $K$$=1.5$ and $K=0.5$ and $K=1.0$ are 42% and 17%, respectively.

Fig. 7

The geometry, finite element mesh, boundary condition, and material parameters of the anisotropic undrained slope

Fig. 8

Comparison between the criterion [8] and the proposed criterion for different $K$

Table 1 Comparison of stability number with slope angle ${\beta }_{s}=50^\circ$

In addition to the safety factor of the slope, the shape and location of the failure surface are also of great concern to geotechnical engineers or researchers. The equivalent plastic strain band (strain localization) across the slope is used as the criterion for the slope to reach the limit equilibrium state. In Fig. 9, a comparison of the slip surfaces obtained by the FELEM and FESRM with different $K$ is given. At $K = 1.0$, both slip surfaces are close. When $K \le 1.3$, the slip surface is a deep curved band. In contrast, when $K > 1.3$, the slip surface is a shallow curve band, which slides out from the toe of the slope.

Fig. 9

Comparison of the slip surfaces obtained by the FESRM (contour of equivalent plastic strain) and FELEM (solid line)

Figure 10 can be used to explain this difference. Figure 10a and b shows the contours of the angle $\alpha$ in the cases of $K = 0.5$ and $1.5$, and these two contours are similar. The angle $\alpha$ varies from zero to $90^\circ$ along the sliding direction of the slip surface, i.e., the solid line in Fig. 10a. The value of the undrained shear strength changes with $\alpha$. At $K = 0.5$, the strength increases with increasing angle $\alpha$, while at $K = 1.5$, the strength decreases, as shown in Fig. 10c and d. When $K = 1.5$, the clay on the right side of the foundation provides higher resistance, so the slip surface is shallow.

Fig. 10

Contours of the angle between the major principal stress and the axis of the isotropic plane at (a) $K = 0.5$ and (b) $K = 1.5$ and the comparison of the value of the anisotropic function g(A) at (c) $K = 0.5$ and (d) $K = 1.5$

4.1.2 Case 2: slope with inclined bedding planes

Conesa et al. [10] proposed a complex cross-anisotropic failure criterion for the undrained strength of clay and analyzed undrained clay slopes with various bedding plane orientations. An inclined bedding plane may exist in a soil slope due to the loading history [25]. Taking Boston blue clay in the USA [52] as an example, the ratio of undrained shear strength is plotted in Fig. 11. The slope angle $\beta_{s} = 30^\circ$ and other geometry, finite element mesh, boundary condition, and material parameters of the slope are the same as those in the last case. Figure 11 also shows that the proposed anisotropic strength criterion and that of Conesa et al. can both capture the test data.

Fig. 11

Comparison between the test data of Boston clay [52] and the anisotropic strength criteria

The orientation of the bedding plane is defined as the angle $\beta_{b}$ between the tangent of the isotropic plane and the x-axis. Figure 12 gives the stability numbers obtained by the proposed method and the method of Conesa et al. with different $\beta_{b}$. It shows that both results are close to each other. The angle $\beta_{b}$ related to the maximum and minimum stability numbers should occur at approximately 135° and 45°, respectively. The difference between the maximum stability number and the minimum stability number is approximately 27%.

Fig. 12

Comparison of stability numbers with different $\beta_{b}$

The slip surfaces obtained by the two methods are quite different, as shown in Fig. 13, although the stability numbers are consistent. Figure 13a shows the region consisting of all slip surfaces obtained by Conesa et al. with different $\beta_{b}$ and angles corresponding to the entry and exit points of the slip surfaces. This reveals that in the analysis of Conesa et al., the shape and location of the slip surface are hardly affected by the bedding plane orientations. However, our analysis yields a different result in which there is an obvious difference among the slip surfaces. The angle $\beta_{b}$ corresponding to the slip surface with lower curvature is 45° (Fig. 13c), while the angle corresponding to the slip surface with higher curvature is 135° (Fig. 13e). The slip surfaces are similar when $\beta_{s} = 0$ and $90^\circ$ (Fig. 13b and d). The essential difference between our undrained slope stability analysis and those from Conesa et al. is whether the gradient of the yield function involves the component of the anisotropic undrained strength.

Fig. 13

Comparison between (a) the results from Conesa et al. [10] and (b)–(e) the slip surfaces obtained by the proposed method

4.2 Simulation of the hollow cylinder test of Boom clay

In Belgium, Boom clay was selected as a candidate host formation for the disposal of high-level nuclear waste [4]. A set of Boom clay thick-walled hollow cylinder tests [38] reproduced the tunnel excavation in the host formation, approximated by reducing the internal confining pressure of the hollow cylinder specimen. Before and after unloading, the cross section of the specimen was scanned by X-ray tomography, and the displacement of the tracking points within the cross section was quantified. François et al. [20] established a hydromechanical constitutive model that can account for strain hardening/softening and elastic and plastic anisotropy to simulate the displacement of the tracking points in the hollow cylinder test. However, the major principal stress direction must be determined to obtain the drained shear strength.

Linear cross-anisotropic elastic Hooke’s law with five material parameters [26] is used to describe the elastic behavior of boom clay, i.e., the relation of effective stress ${\sigma }_{ij}^{^{\prime}}$ and strain ${\varepsilon }_{ij}$. ${E}^{^{\prime}}$, ${v}^{^{\prime}}$, and $G$ in Eq. (19) are Young’s modulus, Poisson’s ratio, and shear modulus. In the local Cartesian coordinate system (Fig. 1), the $x$-$z$ plane is assumed to be an isotropic plane. If the clay is elastic isotropic, the elastic stress–strain relation reduces to Hooke’s law with two material parameters, i.e., ${E}^{^{\prime}}$ and ${v}^{^{\prime}}$.

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\varepsilon_{z} } \\ {\gamma_{xy} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {E_{h}^{^{\prime}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{h}^{^{\prime}} }$}}} & {{\raise0.7ex\hbox{${ - v_{vh}^{^{\prime}} }$} \!\mathord{\left/ {\vphantom {{ - v_{vh}^{^{\prime}} } {E_{v}^{^{\prime}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{v}^{^{\prime}} }$}}} & {{\raise0.7ex\hbox{${ - v_{hh}^{^{\prime}} }$} \!\mathord{\left/ {\vphantom {{ - v_{hh}^{^{\prime}} } {E_{h}^{^{\prime}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{h}^{^{\prime}} }$}}} & 0 & 0 & 0 \\ {{\raise0.7ex\hbox{${ - v_{vh}^{^{\prime}} }$} \!\mathord{\left/ {\vphantom {{ - v_{vh}^{^{\prime}} } {E_{v}^{^{\prime}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{v}^{^{\prime}} }$}}} & {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {E_{v}^{^{\prime}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{v}^{^{\prime}} }$}}} & {{\raise0.7ex\hbox{${ - v_{vh}^{^{\prime}} }$} \!\mathord{\left/ {\vphantom {{ - v_{vh}^{^{\prime}} } {E_{v}^{^{\prime}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{v}^{^{\prime}} }$}}} & 0 & 0 & 0 \\ {{\raise0.7ex\hbox{${ - v_{hh}^{^{\prime}} }$} \!\mathord{\left/ {\vphantom {{ - v_{hh}^{^{\prime}} } {E_{h}^{^{\prime}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{h}^{^{\prime}} }$}}} & {{\raise0.7ex\hbox{${ - v_{vh}^{^{\prime}} }$} \!\mathord{\left/ {\vphantom {{ - v_{vh}^{^{\prime}} } {E_{v}^{^{\prime}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{v}^{^{\prime}} }$}}} & {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {E_{h}^{^{\prime}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{h}^{^{\prime}} }$}}} & 0 & 0 & 0 \\ 0 & 0 & 0 & {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {G_{v} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${G_{v} }$}}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {{\raise0.7ex\hbox{${2\left( {1 + v_{hh}^{^{\prime}} } \right)}$} \!\mathord{\left/ {\vphantom {{2\left( {1 + v_{hh}^{^{\prime}} } \right)} {E_{h}^{^{\prime}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{h}^{^{\prime}} }$}}} & 0 \\ 0 & 0 & 0 & 0 & 0 & {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {G_{v} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${G_{v} }$}}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\sigma_{x}^{^{\prime}} } \\ {\sigma_{y}^{^{\prime}} } \\ {\sigma_{z}^{^{\prime}} } \\ {\tau_{xy} } \\ {\tau_{xz} } \\ {\tau_{yz} } \\ \end{array} } \right\} $$

(24)

Figure 14 shows the geometry, mesh, and boundary conditions of the hollow cylinder test. Under plane strain conditions, the pore water pressure and total pressure at the inner boundary gradually decrease and remain stable after 4200 s. Table 2 lists the geomechanical, hydraulic, and physical parameters of Boom clay [20]. Compared with the original parameters of Boom clay, the parameter values have not changed, but the expression has changed. For example, the anisotropy parameter $K$ is used. The determination of $e_{1}$, $e_{2}$, and $e_{3}$ requires the results of a hollow cylinder torsional shear test, which increases the cost of parameter identification. Optimization-based parameter identification [34, 70] makes it possible to identify these parameters that come only from triaxial tests. For comparison with the same material parameters, $e_{1}$, $e_{2}$, and $e_{3}$ are determined by the test results of the triaxial tests. According to the original values of the anisotropic cohesion and Eqs. (1) and (3), the predicted shear strength of Boom clay is plotted in Fig. 15. The hardening behavior of the internal friction angle and softening behavior of cohesion are described by Eq. (25) [20] and plotted in Fig. 16.

$$ \left\{ {\begin{array}{*{20}c} {c^{\prime}\left( {\varepsilon_{dp} } \right) = c_{0}^{^{\prime}} + \frac{{\varepsilon_{dp} }}{{B_{S} + \varepsilon_{dp} }}c_{0}^{^{\prime}} \left( {k_{r} - 1} \right),{\text{ Softening}}} \\ {\varphi^{\prime}\left( {\varepsilon_{dp} } \right) = \varphi_{0}^{^{\prime}} + \frac{{\varepsilon_{dp} }}{{B_{H} + \varepsilon_{dp} }}\varphi_{0}^{^{\prime}} \left( {k_{p} - 1} \right),{\text{ Hardening}}} \\ \end{array} } \right. $$

(25)

Fig. 14

Geometry, finite element mesh, and boundary conditions of the hollow cylinder test

Table 2 Set of Boom clay geomechanical, hydraulic, and physical parameters in the cross-anisotropic DP model [20]

Fig. 15

The proposed anisotropic strength criterion of the cohesion for Boom clay

Fig. 16

Softening relation of the cohesion and hardening relation of the internal friction angle of Boom clay

A group of finite element simulations is performed in three types of meshes, i.e., 20 × 20, 40 × 40, and 60 × 60. With a 60 × 60 mesh, Fig. 17 shows the simulated radial displacements, the test results [38], and the simulated results [20] for horizontal, $45^\circ$, and vertical paths. The displacements of the horizontal and $45^\circ$ paths obtained by the FEA are close to the other two results. There is a certain deviation between the three displacement curves of the vertical path; however, their trends are the same. Overall, near the inner boundary, the proposed results are closer to the test data compared with those obtained by François et al. [20]. The deviation of the two numerical results may be due to whether the gradient of the yield function involves the component of anisotropic cohesion.

Fig. 17

Comparison of radial displacement in the horizontal ($0$), $45^\circ$, and vertical ($90^\circ$) directions between the FEA results with a mesh of 60 × 60, the test data [38] and the results obtained by François et al. [20]

Figure 18 shows the displacement curves for the three path endpoints located at the inner boundary of the cross section over the entire simulation time. The analysis process is roughly divided into three stages: unloading, consolidation, and stabilization. In the second half of the unloading stage, i.e., the plastic stage, the three curves of the displacement increase sharply. The displacements in the consolidation stage continue to increase and stabilize in the stabilization stage. Equivalent plastic strain rates of approximately 6500 s obtained by FEA using various meshes are plotted in Fig. 19. The contours of the equivalent plastic strain rate illustrate that the shape of the shear band is identical, although the mesh is coarse in Fig. 19a. The widths of the shear bands in Fig. 19b and c are close.

Fig. 18

The displacement curves of the three nodes at the intersection between the inner boundary and the three paths over the entire simulation time

Fig. 19

Rate of the equivalent plastic strain obtained by the finite element analyses with various meshes

Figure 19c is used to assemble the entire cross section of the sample, as shown in Fig. 20. The shape and boundary of the excavation damaged zone (EDZ) in the hollow cylindrical specimen are determined by the simulated shear band or displacement curve of the horizontal path.

Fig. 20

Predicted EDZ by FEA with the proposed anisotropic DP model

Four cases of anisotropic and isotropic elasticity and anisotropic and isotropic plasticity are analyzed. The results reveal that only anisotropic plasticity can yield eye-shaped strain localization (shear band), as shown in Fig. 21a and b. Moreover, Fig. 21c shows symmetric strain localization, while Fig. 21d shows axisymmetric strain localization. This analysis can reveal the necessity of the anisotropic strength of Boom clay in the simulation of strain localization.

Fig. 21

Rate of the equivalent plastic strain obtained by the finite element analyses with (a) anisotropic elasticity and anisotropic plasticity, (b) isotropic elasticity and anisotropic plasticity, (c) anisotropic elasticity and isotropic plasticity, and (d) isotropic elasticity and isotropic plasticity

Figure 22 shows the contour of the angle $\alpha$ with anisotropic elasticity and anisotropic plasticity. The angle $\alpha$ varies from zero in the horizontal direction to $90^\circ$ in the vertical direction. The value of the shear strength changes with $\alpha$. The clay in the vertical direction provides higher resistance, so the EDZ in the horizontal path is larger.

Fig. 22

Contour of the angle between the major principal stress direction and the axis of the isotropic plane

5 Conclusions

The shear strength of natural clay is highly anisotropic due to the internal structure. An anisotropic failure criterion is proposed for natural clays. An anisotropic variable is used to characterize the relative orientation between the soil fabric and principal stress directions. The model assumes that the cohesion of natural clay (or undrained shear strength) is anisotropic, while the friction angle is independent of the loading direction. A DP model with the anisotropic yield criterion has been used to model strain localization in natural clays.

The stability of an undrained clay slope has been analyzed. The results show that the anisotropic undrained strength affects the shape and location of the failure surface (strain localization) of the slope. In the first case, the percentage difference of the stability number obtained by the FESRM is 42% between $K = 0.5$ and $K = 1.5$. When $K > 1.3$, the shape of the slip surface is shallow. In the second case, with different bedding plane orientations, the percentage difference between the maximum and minimum stability numbers is approximately 27%. At $\beta_{b} = 45^\circ$, the range of the slip body is larger than that at other angles $\beta_{b}$. These results show that the influence of the strength anisotropy and bedding plane orientation on the undrained slope stability cannot be ignored. The influence on the strain localization leads to different slope reinforcement scheme designs.

The proposed model has been applied to simulate the hollow cylinder test on Boom clay. The displacement results are closer to the test data observed by the X-ray scan [38] than the results obtained by François et al. [20]. The nonlocal softening regularization method used reduces the mesh sensitivity. Furthermore, the rate of the equivalent plastic strain simulated by the nonlocal strain method can be taken to represent the EDZ in the sample. The range of the shear band (strain localization) in the test sample is affected by the anisotropic strength of Boom clay. Only anisotropic plasticity can yield eye-shaped strain localization.

Appendix 1: Gradient of the yield function

The gradient of the proposed anisotropic yield function is expressed as

$$ \frac{\partial F}{{\partial \sigma_{ij}^{^{\prime}} }} = \frac{\partial F}{{\partial p^{\prime}}}\frac{{\partial p^{\prime}}}{{\partial \sigma_{ij}^{^{\prime}} }} + \frac{\partial F}{{\partial q}}\frac{\partial q}{{\partial \sigma_{ij}^{^{\prime}} }} + \frac{\partial F}{{\partial A}}\frac{\partial A}{{\partial \sigma_{ij}^{^{\prime}} }} $$

(26)

where

$$ \frac{\partial F}{{\partial p^{\prime}}} = - m $$

(27)

$$ \frac{\partial F}{{\partial q}} = 1 $$

(28)

$$ \frac{\partial F}{{\partial A}} = - g\left( A \right)\left[ {e_{1} + 2e_{2} \left( {1 + A} \right) + 3e_{3} \left( {1 + A} \right)^{2} } \right]\frac{{mc_{0}^{^{\prime}} }}{{\tan \varphi^{\prime}}} $$

(29)

$$ \frac{{\partial p^{\prime}}}{{\partial \sigma_{ij}^{^{\prime}} }} = \frac{1}{3}\left\{ {\begin{array}{*{20}c} 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right\} $$

(30)

$$ \frac{\partial q}{{\partial \sigma_{ij}^{^{\prime}} }} = \frac{3}{2q}\left\{ {\begin{array}{*{20}c} {s_{x} } \\ {s_{y} } \\ {s_{z} } \\ {2\tau_{xy} } \\ {2\tau_{xz} } \\ {2\tau_{yz} } \\ \end{array} } \right\} $$

(31)

$$ \frac{\partial A}{{\partial \sigma_{ij}^{^{\prime}} }} = \frac{1}{2q}\left\{ {\begin{array}{*{20}c} 1 \\ { - 2} \\ 1 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right\} + \frac{A}{q}\frac{\partial q}{{\partial \sigma_{ij}^{^{\prime}} }} $$

(32)