Multi-step-ahead and interval carbon price forecasting using transformer-based hybrid model

Abstract

Accurate and stable carbon price forecasts serve as a reference for assessing the stability of the carbon market and play a vital role in enhancing investment and operational decisions. However, realizing this goal is still a significant challenge, and researchers usually ignore multi-step-ahead and interval forecasting due to the non-linear and non-stationary characteristics of carbon price series and its complex fluctuation features. In this study, a novel hybrid model for accurately predicting carbon prices is proposed. The proposed model combines multi-step-ahead and interval carbon price forecasting based on the Hampel identifier (HI), time-varying filtering-based empirical mode decomposition (TVFEMD), and transformer model. First, HI identifies and corrects outliers in carbon price. Second, TVFEMD decomposes carbon price into several intrinsic mode functions (imfs) to reduce the non-linear and non-stationarity of carbon price to obtain more regular features in series. Next, these imfs are reconstructed by sample entropy (SE). Subsequently, the orthogonal array tuning method is used to optimize the transformer model’s hyperparameters to obtain the optimal model structure. Finally, after hyperparameter optimization and quantile loss function, the transformer is used to perform multi-step-ahead and interval forecasting on each part of the reconstruction, and the final prediction result is obtained by summing them up. Five pilot carbon trading markets in China were selected as experimental objects to verify the proposed model’s prediction performance. Various benchmark models and evaluation indicators were selected for comparison and analysis. Experimental results show that the proposed HI-TVFEMD-transformer hybrid model achieves an average MAE of 0.6546, 1.3992, 1.6287, and 2.2601 for one-step, three-step, five-step, and ten-step-ahead forecasting, respectively, which significantly outperforms other models. Furthermore, interval forecasts almost always have a PICI above 0.95 at a confidence interval of 0.1, thereby indicating the effectiveness of the hybrid model in describing the uncertainty in the forecasts. Therefore, the proposed hybrid model is a reliable carbon price forecasting tool that can provide a dependable reference for policymakers and investors.

Introduction

Global warming stands as the greatest challenge confronting humanity in the twenty-first century, presenting a great threat to human survival and development. Greenhouse gas emissions (mainly carbon dioxide) from human industrialization activities are the direct cause of global warming. Many measures have been proposed to reduce emissions and control the trend of global warming. The emission trading system (ETS) was first proposed in the Kyoto Protocol, which assigns a price to carbon and is recognized as an effective policy tool to control emissions. In the 26th UN Climate Change Conference of the Parties (COP26), the importance of ETS for climate change was emphasized, and the global carbon trading system was initially finalized. Different from other financial markets, the carbon market emerged late and is characterized by an immature market system that is highly susceptible to other external factors, such as market regulation, energy, and environmental policies (Sun and Zhang 2018). These factors lead to dramatic fluctuations in carbon price. Therefore, building an accurate carbon price forecasting model that can help policymakers and enterprises understand the fluctuation pattern of carbon price and thus develop relevant policies and investment strategies is necessary (Hao et al. 2020). However, the non-linear, uncertain, and complex nature of carbon price fluctuations (Lutz et al. 2013) makes the accurate forecasting of carbon price series a significant challenge.

The importance of carbon prices has garnered substantial attention among researchers in recent years, thereby leading to a growing interest in the field of carbon price forecasting. Many scholars have proposed advanced carbon price forecasting models, and various models have been applied to carbon price forecasting. In general, these models can be divided into three main categories (Zhu et al. 2017), namely, (1) traditional time series models, (2) artificial intelligence models, and (3) hybrid models. Traditional time series models are primarily based on statistical methods. For example, autoregressive integrated moving average (ARIMA) (Zhu and Wei 2013), autoregressive conditional heteroscedasticity (GARCH) (Byun and Cho 2013); (Benz and Trück 2009), and other models. These statistical methods are based on the significance of constructing models that can capture certain statistical features of carbon price fluctuations, such as heteroscedasticity, fat-tailedness, and leverage effects. Although the construction of statistical models is simple, easy to implement, widely applied, and has achieved specific results, statistical models based on the assumption of linearity cannot effectively address these characteristics (Sun and Zhang 2018) because of the non-linear and non-stationarity characteristics of carbon prices (Tian and Hao 2020). Therefore, achieving satisfactory accuracy in carbon price forecasting using these traditional time series models is difficult.

In recent years, the rise of artificial intelligence (AI) has prompted the utilization of many AI models for carbon price forecasting. Compared with traditional time series models, these AI models exhibit better robustness and generalization ability and can effectively deal with non-linear and non-stationary time series (Han et al. 2019). The most commonly used models include support vector machines (SVMs), extreme learning machines (ELMs), and several types of artificial neural networks (ANNs). Yi et al. (2017) predicted carbon prices through back propagation neural network (BPNN). The experimental results proved that this model exhibited higher prediction accuracy than the statistical model. Du et al. (2022) employed a BPNN to predict prices in Fujian’s carbon market. They verified that BPNN could make effective carbon price predictions. These studies illustrate that AI models significantly improved prediction accuracy and could be adapted to various situations. Among these AI models, ANN-based models exhibit exceptional performance. Zhang and Wen (2022) predicted carbon price by using temporal convolutional neural network (TCN), and their experimental findings demonstrated the superior performance of TCN compared with traditional statistical models and some machine learning models, such as random forest (RF), XGBoost, and SVM. Therefore, ANN-based carbon price prediction models, such as LSTM, GRU, and TCN, have emerged as prominent contenders in the field. These sequential ANN models possess excellent ability for time series modeling. However, the failure to effectively handle long-term dependencies and interrelatedness in time series has left room for further improvement in carbon price forecasting accuracy. Transformer model based on attention mechanisms is more effective in the long-term dependence and interactions of time series data than other ANN structures (Wu et al. 2020), thereby appearing in time series modeling. Bommidi et al. (2023) utilized the transformer model for short-term wind speed prediction, and the experimental results proved that the prediction ability of the transformer model is higher than the commonly used sequential ANN structure. Wang et al. (2022) constructed a temporal fusion transform (TFT) to predict carbon prices in the Chinese pilot market, and experiments showed that TFT has superior prediction effects compared with LSTM and GRU. Therefore, the transformer model holds promising application prospects in carbon price forecasting.

Nevertheless, each single model has corresponding defects in the face of the current highly volatile and chaotic carbon price (Huang et al. 2021). The prediction accuracy of using single models is not the best and most ideal (Niu and Wang 2019). Many advanced hybrid models have been proposed and used. Hybrid models can be mainly classified into two categories, namely, by using decomposition techniques and integrated optimization algorithms. Many researchers employ signal decomposition techniques to decompose carbon price series, which reduces non-stationarity and extracts the different scale features of carbon prices (Zhu et al. 2018), thereby improving the predictive accuracy. Many decomposition methods that are used, commonly include empirical mode decomposition (EMD-Type), variational mode decomposition (VMD), and wavelet transformer. Yun et al. (2022) constructed a hybrid carbon price prediction model that included complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) and long short-term memory (LSTM). The experimental results show that the hybrid model exhibited better prediction performance than the single model. Sun et al. (2016) predicted the carbon price based on VMD and spiking neural networks (SNNs) and achieved good results. In experiments, VMD has demonstrated better feature extraction performance than EMD, which resulted in higher prediction accuracy. Liu and Shen (2019) combined the empirical wavelet transform (EWT) and gated recurrent unit (GRU) neural network to establish a hybrid model for carbon price prediction and verified through experiments that the model was superior to a single ARIMA, BPNN, and GRU. The decomposition algorithms, including EMD-type, VMD, and WT, offer effective ways to decompose the carbon price series. However, they possess certain drawbacks. VMD and WT require manual selection of decomposition level and wavelet basis function, respectively (Yang et al. 2021). EMD-type is an adaptive decomposition algorithm but is susceptible to mode aliasing phenomenon and be affected by end effects (Wu and Huang 2004). These issues can affect the quality of decomposition and thus lead to unstable forecasting outcomes. Time-varying filtering-based empirical mode decomposition (TVFEMD) was proposed by Li et al. 2017. TVFEMD is an adaptive method that can effectively overcome mode mixing aliasing and has high computational efficiency. Due to its superior performance, it has been applied in some time series forecasting, such as non-ferrous metal price forecast (Wang et al. 2021) and wind speed prediction (Xiong et al. 2021). Therefore, this study applies TVFEMD to decompose carbon price. Many researchers use optimization algorithms to optimize the model’s hyperparameters and thus improve its processing power. Considering that the performance of some AI models relies on the configuration of hyperparameters, especially ANN models (Zhang et al. 2017) and the accuracy of the model may fluctuate greatly with different hyperparameter settings, many scholars have employed intelligent optimization algorithms to optimize the configuration of model hyperparameters. Sun and Xu (2021) utilized linearly decreasing weight particle swarm optimization (LDWPSO) to optimize the hyperparameters of the wavelet least squares SVM (wLSSVM) and applied it to carbon price prediction. The optimized wLSSVM model demonstrated higher prediction accuracy than the non-optimized model. Sun and Zhang (2020) utilized an improved bat algorithm (IBA) to search for the optimal hyperparameters of extreme learning machine (ELM), which further enhanced ELM’s predictive performance. The selection of a proper optimization algorithm is crucial for model configuration. However, heuristic optimization algorithms often struggle to ensure the stability of their optimization results and can easily fall into local optima. In this study, an orthogonal array-based hyperparameter optimization technique was used to identify the optimal hyperparameter configuration of the model.

In previous discussions, the majority of forecasting methods primarily emphasize point forecast, thereby ignoring the importance of interval forecasting, which cannot be disregarded in forecasting. Interval forecasts quantify the uncertainty in carbon price forecasts and therefore contain more information than point forecasts (Zhang et al. 2016). Interval forecast is based on a certain level of significance of a set of upper and lower bounds. Compared with point forecast, it can reflect the possibility of result variation caused by uncertainty in the prediction. When time series exhibit high instability and non-linear trends, interval forecast is a powerful tool to help decision makers. Quantile regression (QR) is a regression analysis model in statistics that estimates the conditional quantile relationship between variables without knowing the type of variable distribution (He and Li 2018). QR can be well combined with ANN models to produce interval prediction results. Wang et al. (2020a, 2020b) combined LSTM with QR for short-term wind speed prediction, and the interval prediction results constructed by QR could cover the uncertainty of wind speed prediction well. Lim et al. (2021) integrated QR and transformer-based model and achieved remarkable interval forecasts. Therefore, this study combines the transformer model with QR for the interval forecasting of carbon prices. Furthermore, most models tend to overlook the presence of outliers in carbon price. In reality, carbon prices are commonly disturbed by non-controllable and unexpected non-repetitive information, such as the enactment of new market regulation policies, the upcoming date of carbon quota submission, or extreme weather. These factors can result in outliers within the carbon price series, potentially leading the model to learn erroneous information and leads to overfitting. Consequently, the generalization ability of the model is compromised. Sun et al. (2021) demonstrated that outliers in the carbon price series could negatively affect forecasts by using the box plot method to remove outliers from the carbon price. Hence, the identification and correction of outliers play a significant role in carbon price forecasting.

In summary, to fill the gap of the current research, this study constructs a hybrid carbon price forecasting method that combines Hampel identifier (HI), time-varying filtering for empirical mode decomposition (TVFEMD), transformer, and optimization with orthogonal array tuning (OATM) for multi-step-ahead and interval forecasting of carbon prices. First, HI is used to identify and correct outliers present in the original carbon price series to eliminate their negative impact on carbon price data. Subsequently, TVFEMD decomposes the processed carbon price series into multiple intrinsic mode functions (imfs), which are reconstructed through sample entropy (SE). Finally, based on the transformer model after the hyperparameters are optimized by OATM, each imfs is predicted, and the results are summed to obtain the deterministic prediction results. The quantile loss function is used to obtain the prediction intervals at various confidence levels. The main innovations and contributions of this study are outlined as follows:

• (1) Identification and correction of outliers. Carbon prices are irregular and fluctuate dramatically. By identifying and correcting the outliers in the original carbon price through HI, the basic information in the original data can be retained better, and the training of the model is not affected by the outliers, thus improving the prediction performance of the hybrid model.

• (2) An advanced data decomposition strategy is used. TVFEMD improves EMD. TVFEMD can eliminate the mode aliasing phenomenon in EMD and can adaptively decompose the original data into clearer and more detailed sub-sequences, thereby effectively reducing the non-linear and non-stationarity characteristics in carbon price series.

• (3) Advanced deep learning architecture is used. The deep learning (DL) model is widely used in carbon price forecasting. This study is the first to attempt to use the transformer model in carbon price forecasting, explore the potential of the transformer’s application in carbon pricing forecasting, and expand on related theoretical methods because this model has better modeling ability in terms of long-term dependence and interaction of series. Subsequently, because the performance of deep learning models is very sensitive to the configuration of hyperparameters, OATM is used in this study to optimize the hyperparameters in the transformer model. OATM makes a trade-off between time consumption and model accuracy to select the optimal hyperparameter configuration.

• (4) Multi-step-ahead and interval forecasts of carbon prices are constructed. Considering that the results of one-step-ahead forecasts are not sufficient to provide reliable information for investors and policymakers, the multi-step-ahead and interval of carbon price are predicted, which can better reflect the changing trend and fluctuation pattern of carbon price, based on the transformer’s excellent modeling ability of long-term dependence of series and quantile loss function. Multi-step-ahead prediction can represent the long-term trend of carbon price, whereas interval prediction can comprehensively reflect the fluctuation information of carbon price.

The remainder of this paper is presented as follows: “Methodology” presents the methodology used in this study. “Framework of the proposed forecasting system” describes the framework flow of the proposed hybrid model. “Data collection and preprocessing” contains the description of the data and the evaluation metrics. “Experimental analysis” presents the analysis and discussion of the experiments. Finally, “Conclusion” presents the conclusions.

Methodology

In this section, the main methods used in the proposed model of this study, including HI, TVFEMD, transformer, OATM, and quantile loss, are introduced.

Hampel identifier

HI is an effective outlier identification and correction technique that utilizes median deviation and absolute median deviation as the criteria for determining outliers with good robustness (Yao et al. 2019). For the data series: X={x₁,x₂,x₃,…,x_n}, k is the number of adjacent points on each side of x_i in a given window, the size of the moving window is 2k+1, the local median m_i, and the scale estimate of the median estimated deviation σ_i are calculated as follows:

$${m}_i=\textrm{median}\left({x}_{i-k},{x}_{i-k+1},\dots, {x}_i,\dots, {x}_{i+k-1},{x}_{i+k}\right),$$

(1)

$${\sigma}_i=k\cdot \textrm{median}\left(\left|{x}_{i-k}-{m}_i,\dots, \left|{x}_{i+k}-{m}_i\right|\right|\right),$$

(2)

where $k=\left(1/\left(\sqrt{2}{\operatorname{erfc}}^{-1}\left(1/2\right)\right)\right)\approx 1.4826$ is the unbiased estimate of the Gaussian distribution.

$$y_i=\left\{\begin{array}{lc}x_i,&\left|x_i-m_i\right|\leq n_\delta\sigma_i\\\mathrm{outlier},&\left|x_i-m_i\right|>n_\delta\sigma_i\end{array}.\right.$$

(3)

According to Eq. 3, if the absolute value of the difference between the evaluated data x_i and the local median m_i is greater than n_σ times σ_i, then the evaluated data x_i are considered an outlier, and the outlier is replaced by the local median m_i, and n_σ is usually set to 3 (Wang et al. 2020a, 2020b).

Time-varying filter empirical mode decomposition

TVFEMD, which is an improvement of the empirical modal decomposition (EMD), is proposed by Li et al. (2017).The decomposition of the imfs in EMD and EEMD cannot guarantee the existence of only one amplitude mode, and the local mean values determined by EMD through the third spline interpolation of the upper and lower envelopes are difficult to represent by a strict analytical expression, which may lead to meaningless imfs obtained by EMD and EEMD. TVFEMD improves the performance of frequency separation and stability at low sampling rates, solves the problem of modal aliasing, and preserves the time-varying characteristics of the time series. The meaning of the TVFEMD parameter is clear and simple to choose (Ma and Zhang 2020), which allows the imfs obtained by TVFEMD to represent the pattern features in the time series better.

The specific calculation steps of TVFEMD are presented as follows:

The instantaneous amplitude A(t) and frequency φ^‘(t) of the original sequence x(t) are obtained by Hibert transform; then, the local maximum value A(t_max) and the local minimum value A(t_min) of A(t) are solved. The interpolation of A(t_max) and A(t_min) yields β₁(t) and β₂(t); the instantaneous mean α₁(t)=(β₁(t)+β₂(t))/2 and the instantaneous envelope α₂(t)=(β₁(t)-β₂(t))/2 are calculated. η₁(t) and η₂(t) are obtained by the interpolation of φ^‘(t_max)A²(t_max) and φ^‘(t_min)A²(t_min).

$${\eta}_1(t)={\varphi}_1^{'}(t)\left[{\alpha}_1^2(t)-{\alpha}_1(t){\alpha}_2(t)\right]+{\varphi}_2^{'}(t)\left[{\alpha}_2^2(t)-{\alpha}_1(t){\alpha}_2(t)\right],$$

(4)

$${\eta}_2(t)={\varphi}_1^{'}(t)\left[{\alpha}_1^2(t)+{\alpha}_1(t){\alpha}_2(t)\right]+{\varphi}_2^{'}(t)\left[{\alpha}_2^2(t)+{\alpha}_1(t){\alpha}_2(t)\right].$$

(5)

Subsequently, ${\varphi}_1^{'}(t)$ and ${\varphi}_2^{'}(t)$ are calculated by Eqs. 6 and 7, respectively.

$${\varphi}_1^{'}(t)=\frac{\eta_1(t)}{2{\alpha}_1^2(t)-2{\alpha}_1(t){\alpha}_2(t)}+\frac{\eta_2(t)}{2{\alpha}_1^2(t)+2{\alpha}_1(t){\alpha}_2(t)},$$

(6)

$${\varphi}_2^{'}(t)=\frac{\eta_1(t)}{2{\alpha}_2^2(t)-2{\alpha}_1(t){\alpha}_2(t)}+\frac{\eta_2(t)}{2{\alpha}_2^2(t)+2{\alpha}_1(t){\alpha}_2(t)}.$$

(7)

Calculate the local cutoff probability ${\varphi}_{\textrm{bis}}^{'}(t)$.

$${\varphi}_{\textrm{bis}}^{'}(t)=\frac{\varphi_1^{'}(t)+{\varphi}_2^{'}(t)}{2}=\frac{\eta_2(t)-{\eta}_1(t)}{4{\alpha}_1(t){\alpha}_2(t)}.$$

(8)

The signal h(t) can be extracted by ${\varphi}_{\textrm{bis}}^{'}(t)$, and $h(t)=\cos \left[\int {\varphi}_{\textrm{bis}}^{'}(t) dt\right]$. The signal x(t) is approximated by B-sample interpolation of h(t) extreme points h(t_max) and h(t_max), and the result of the approximation is m(t).

Calculate the stopping criterion θ(t). When θ(t) is less than the threshold ξ, x(t) is treated as an imf, otherwise, set x(t) = x(t) − m(t), repeat the steps above until the stopping criterion is satisfied.

$$\theta (t)=\frac{B_{\textrm{Loughlim}}(t)}{\varphi_{avg}(t)},$$

(9)

$${B}_{\textrm{Loughlim}}(t)=\sqrt{\frac{\alpha_1^{\prime 2}(t)+{\alpha}_2^{\prime 2}(t)}{\alpha_1^2(t)+{\alpha}_2^2(t)}+\frac{\alpha_1^2(t){\alpha}_2^2(t)\left({\varphi}_1^{'}(t)-{\varphi}_2^{'}(t)\right)}{{\left({\alpha}_1^2(t)+{\alpha}_2^2(t)\right)}^2}},$$

(10)

$${\varphi}_{\textrm{avg}}(t)=\frac{\alpha_1^2(t){\varphi}_1^{'}(t)+{\alpha}_2^2(t){\varphi}_2^{'}(t)}{\alpha_1^2(t)+{\alpha}_2^2(t)}.$$

(11)

The original sequence x_raw(t) is finally decomposed into several imfs and a residual term，x_raw(t) =  ∑ IMF_k + Resid.

Transformer

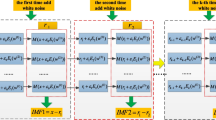
The transformer model has gained significant attention in time series modeling because of its ability to efficiently capture long-term dependencies in sequences and interactions between data. Unlike TCN or LSTM that rely on recursive and convolutional layers, transformer models the information in time series through the encoder–decoder structure (Wen et al. 2022), The encoder maps the input sequence X=[x₁,x₂,... ,x_n] into a continuous representation Z=[z₁,z₂,... ,z_n], and Z inputs the decoder to generate the output sequence Y=[y₁,y₂,... ,y_m]. The encoder and decoder are stacked with N identical modules, and each module mainly contains two parts: the multi-head self-attention layer and the feed-forward network (FFN). The structure of the Transformer model is shown in Fig. 1.

Fig. 1

Flow chart of the proposed hybrid forecasting system

The attention mechanism uses the query-key-value (QKV) ($Q=h{W}_m^Q$，$K=h{W}_m^K$，$V=h{W}_m^V$，h ∈ ℝ^N × d is the input，${W}_m^Q,{W}_m^K\in {\mathbb{R}}^{d\times {d}_k}$，and ${W}_m^V\in {\mathbb{R}}^{d\times {d}_v}$ is the trainable weight matrix model to generate the attention of the scaled dot product.

$$\textrm{Attention}\left(Q,K,V\right)=\textrm{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V.$$

(12)

To improve the learning ability of single attention, the transformer model applies multi-head attention (Vaswani et al. 2017). The QKV is linearly projected for m times. In each projection, the attention function is executed in parallel to generate the output results of dv dimension. The projected output results are spliced and projected again to obtain the final output results. The QKV is linearly projected for m times. In each projection, the attention function Eq. 13 is executed in parallel to generate the output results of d_v dimension. The projected output results are stacked and projected again to obtain the final output results.

$$\textrm{MultiHeadAtt}\left(Q,K,V\right)=\textrm{Concat}\left({\textrm{head}}_1,\dots, {\textrm{head}}_m\right){W}^O,$$

(13)

$${\textrm{head}}_i=\textrm{Attention}\left(Q{W}_i^Q,K{W}_i^K,V{W}_i^V\right),$$

(14)

where ${W}_i^Q,{W}_i^K\in {\mathbb{R}}^{d_{\textrm{model}}\times {d}_k}$，${W}_i^v\in {\mathbb{R}}^{d_{\textrm{model}}\times {d}_v}$，in multi-head attention d_k = d_v = d_model/m.

Carbon price series have long-term memory (Fan et al. 2019), and for better extraction of historical information, long time steps must be covered. However, not all time steps are relevant. In multi-head attention, the Softmax activation function is used to calculate the attention score equation (12), and Softmax cannot assign exactly zero scores because all scores sum to one, which reduces the attention allocation in the relevant time steps (Wiegreffe and Pinter 2019) and extracts information from the irrelevant time steps to add noise to the model, thereby affecting the performance of the transformer model. Therefore, this study uses the sparse mapping α-entmax (Peters et al. 2019) instead of Softmax, which is defined as follows:

$$\alpha -\textrm{entmax}(h)={\left[\left(\alpha -1\right)h-\tau \textbf{1}\right]}_{+}^{1/\alpha -1},$$

(15)

where []+ is the Relu activation function, 1 is a vector of all ones, and τ is the Lagrange multiplier. When α = 1 is equal to the Softmax function, when α > 1 can be sparse mapping, and α = 1.5 is a reasonable point (Martins and Fernandez Astudillo 2016). Therefore, this study set α = 1.5.

Orthogonal array tuning method

Zhang et al. (2019a) proposed OATM. Compared with the highly time-consuming and over-dependent configurations of grid search, random search, and Bayesian optimization, OATM uses an orthogonal list to extract the most representative and balanced experimental combinations from all possible combinations. Furthermore, the use of these experimental combinations to optimize hyperparameters can achieve a trade-off between optimization time and model performance. The specific steps of OATM are presented as follows:

• Step 1. An orthogonal array is constructed to optimize the hyperparameters. The orthogonal array consists of a finite number of factors, with each factor containing the same finite number of levels. The arrangement of factors in the array ensures that each pair of different factors appears together in the same number of ordered combinations. For example, Table 1 shows an orthogonal array with three factors and three levels each. The total number of combinations in the set of all factors and levels $\mathcal{S}$, $\textrm{Card}\left(\mathcal{S}\right)=3\times 3\times 3=27$, and the set of orthogonal array is$\mathcal{O}$，$\textrm{Card}\left(\mathcal{O}\right)=9$. The two sets are displayed in a cube, as shown in Fig. 1, where A1, A2, and A3 are the three levels of factor A, and B and C are also a set of factors. The 27 nodes on the surface of the cube are set $\mathcal{S}$, and the 9 red circles are set $\mathcal{O}$. In Fig. 1, each red circle is uniformly distributed, one exists on each edge, and three exist on each face. Thus, $\mathcal{O}$ can be used as a representative subset of the set $\mathcal{S}$, $\mathcal{O}\subseteq \mathcal{S}$. The different hyperparameters in optimization are the factors in the orthogonal array, and the levels correspond to the values that can be chosen in the hyperparameters.

Table 1 Orthogonal array with three factors and three levels

• Step 2. Experiments are performed for all combinations of hyperparameters in the orthogonal array.

• Step 3. Range analysis. Range analysis plays a pivotal role in OATM. The experimental results obtained from Step 2 are analyzed using arrange analysis to determine the optimal level and importance of each hyperparameter. The importance of a hyperparameter is calculated by its influence on the experimental results. Through range analysis, each hyperparameter is optimized, and the optimal levels are combined to create an optimized combination of hyperparameters, implying that the optimized hyperparameter combination may not be found among the existing orthogonal array.

• Step 4. Run the experiments on models with optimized hyperparameter combinations.

OATM utilizes a representative smaller subset of the hyperparameters for optimization, leading to higher efficiency, as depicted in Fig. 1. The grid search method requires 27 experiments, whereas OATM only requires 9 experiments, saving approximately 67% of time.

Quantile loss

In this study, quantile regression (QR) is used for forecasting the carbon price interval. QR uses the data to conduct regression analysis at different quantiles, which can show the relationship between variables more comprehensively (Zhang et al. 2019a, 2019b). By improving the loss function of deterministic forecasting to a quantile loss function (Wen et al. 2017), the model can be used for quantile regression, and its loss function is expressed as follows:

$$\mathcal{L}\left(\varOmega, \boldsymbol{W}\right)=\sum \nolimits_{y_t\in \varOmega}\sum \nolimits_{q\in \mathcal{Q}}\sum \nolimits_{\tau =1}^{\tau_{\textrm{max}}}\frac{\textrm{QL}\left({y}_t,\hat{y}\left(q,t-\tau, t\right),q\right)}{M{\tau}_{\textrm{max}}},$$

(16)

$$\textrm{QL}\left(y,\hat{y},q\right)=q{\left(y-\hat{y}\right)}_{+}+\left(1-q\right){\left(\hat{y}-y\right)}_{+},$$

(17)

where Ω is the training domain containing M samples; W is the weight of the model; Q is the set of quantile outputs $\mathcal{Q}=\left\{\upalpha /2,1-\upalpha /2\right\}$; 1 − α is the confidence interval if α=1, that is, the same loss as the point forecast is the MAE loss function; and (.)₊=max(0,.).

Evaluation indicators

This study selects several evaluation indicators to reflect the model’s performance in terms of precision and accuracy from various aspects. For deterministic forecasts, the evaluation indicators include mean absolute value error (MAE), root mean square error (RMSE), mean absolute percentage error (MAPE), goodness of fit (R²), and Taylor skill score (TSS). MAE represents the actual deviation; RMSE can represent the discrete degree of the sample; MAPE represents the overall level of error; R² represents the overall fit of the forecast; and TSS is a comprehensive index that reflects the correlation coefficient, standard deviation, and centered root-mean-square (CRMS) of the prediction results (Taylor 2001). The smaller MAE, RMSE, and, MAPE are, the smaller the prediction error is, and the closer R² and TSS are to 1, which indicates an accuracy of the model. For interval forecast, three indicators are selected: average width (AW), prediction interval coverage probability (PICP), and prediction interval normalized average width (PINAW), where AW reflects the interval width of the interval forecast, PICP represents the coverage of interval forecast, and PINAW represents the percentage of average width in the data range. Generally, the prediction interval constructed is expected to have a small interval width but a high coverage rate. Thus, AW, PICP, and PINAW must be integrated to measure the effects of interval prediction. The evaluation index is expressed as follows:

$$\textrm{MAE}=\frac{1}{n}{\sum}_{i=1}^n\left|{y}_i-{\hat{y}}_i\right|,$$

(18)

$$\textrm{RMSE}=\sqrt{\frac{1}{n}{\sum}_{i=1}^n{\left({y}_i-{\hat{y}}_i\right)}^2},$$

(19)

$$\textrm{MAPE}=\frac{1}{n}{\sum}_{i=1}^n\left|\frac{y_i-{\hat{y}}_i}{y_i}\right|,$$

(20)

$${R}^2=1-\frac{\sum_{i=1}^n{\left({y}_i-{\hat{y}}_i\right)}^2}{\sum_{i=1}^n{\left({y}_i-{\overline{y}}_i\right)}^2},$$

(21)

$$\textrm{TSS}=\frac{4{\left(1+r\right)}^4}{{\left(\textrm{SDR}+\frac{1}{\textrm{SDR}}\right)}^2{\left(1+{r}_0\right)}^4},$$

(22)

$$\textrm{AW}=\frac{1}{n}{\sum}_{i=1}^n\left({Ud}_i-{Ld}_i\right),$$

(23)

$$\textrm{PICP}=\frac{1}{n}{\sum}_{i=1}^n{C}_i,{C}_i=\left\{\begin{array}{c}1,{C}_i\in \left[{\textrm{Ld}}_i,{\textrm{Ud}}_i\right]\\ {}0,{C}_i\notin \left[{\textrm{Ld}}_i,{\textrm{Ud}}_i\right]\end{array}\right.,$$

(24)

$$\textrm{PINAW}=\frac{1}{n}{\sum}_{i=1}^n\left[\left({\textrm{Ud}}_i-{\textrm{Ld}}_i\right)/\left({y}_{\textrm{max}}-{y}_{\textrm{min}}\right)\right],$$

(25)

where y_i and ${\hat{y}}_i$ are the actual and predicted values, respectively; ${\hat{y}}_i$ represents the mean of the predicted values; n is the length of the sequence; r and SDR are the correlation coefficient and variance ratio between the predicted sequence and the actual sequence, respectively; and r₀ is set to one. Ud_i and Ld_i are the upper and lower boundaries of the interval prediction, respectively; y_max is the max value in the actual sequence; and y_min is the min value.

Framework of the proposed forecasting system

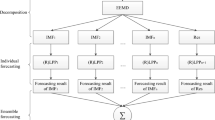
Figure 1 presents the framework flow of the designed hybrid carbon price forecasting system based on the methodology in the previous section. As seen in Fig. 1, the forecasting steps can be divided into the following parts:

• (1) Identification and correction of outliers. Owing to the complexity of carbon price, its fluctuation and fluctuation pattern become very drastic and irregular, respectively. Therefore, HI is used to process the original carbon price series to remove and correct outliers, thereby weakening the effects of outliers on model training.

• (2) Decomposition and reconstruction of carbon price. TVFEMD is applied to decompose the complex carbon price series to obtain several imfs, which contain the features with varying frequencies in series, thereby simplifying model learning. TVFEMD guarantees the existence of only one amplitude mode in the imfs. Thus, the imfs by TVFEMD are more detailed and greater in terms of quantity than those decomposed by EMD; however, more imfs extend computation time and increase accumulation of errors (Zhao et al. 2022). Hence, imfs need to be reconstructed, and the generally used method is to calculate the entropy value among different imfs (Sun et al. 2021); the complexity of imfs is classified according to the entropy value, and imfs that are classified into the same class are summed and merged (Wang and Qiu 2021). However, some studies (Sun and Huang 2020a, 2020b) suggest that high-frequency imfs contain complex fluctuations, and a secondary decomposition is implemented to further improve the prediction accuracy, thereby generating more imfs, which contradict the concept of reconstruction. TVFEMD can effectively solve this conflict because the imfs obtained by its decomposition are more detailed, especially in the high-frequency part. Hence, the use of TVFEMD for the secondary decomposition of the imfs in the high-frequency part is unknot necessary. Therefore, this study uses SE (Richman and Moorman 2000) to estimate the complexity of each imfs. On the one hand, SE is retained for the imfs with high complexity. On the other hand, imfs with low complexity and the imfs with similar sample SE values are summed and combined to reduce computational time consumption and error accumulation and to retain complex imf features. Normalization is performed to map the data to [0,1] before each component is inputted into the forecasting model.

• (3) Optimization of hyperparameters. The transformer model includes a large number of hyperparameters, and different hyperparameter settings can have a huge impact on the prediction performance. In this study, OATM is used to tune the hyperparameters of the model and determine the appropriate hyperparameter configurations to improve the performance of the model.

• (4) Forecasting of carbon price. First, the Transformer model is used to perform one-step-ahead and multi-step-ahead forecasting on the decomposed and reconstructed subsequents. In multi-step-ahead forecasting, the transformer model applies the autoregressive method to generate multi-step-ahead results (Graves 2013). Next, the model takes the previously generated prediction results as the input of the next prediction and then sums the prediction results of each subsequent. Finally, the final prediction results are obtained. Based on the deterministic prediction, the interval prediction of carbon price is made by using the quantile loss function to measure the uncertainty of the deterministic prediction.

• (5) Comparison and analysis. In this study, different single models, including machine learning models (SVM) and commonly used deep learning models (LSTM, GRU, and TCN) and decomposition methods (EMD, EEMD, and CEEMDAN) are selected for comprehensive comparison with the proposed hybrid model under a variety of evaluation indicators to prove the effectiveness of the proposed model.

Data collection and preprocessing

In this section, the original dataset of the carbon prices and its statistical features are described briefly. In addition, the results of the carbon price decomposition and reconstruction and hyperparameter optimization are presented.

Data collection

The closing price of the five pilot carbon trading markets in China, namely, Guangdong, Hubei, Beijing, Shanghai, and Shenzhen, were selected as experimental subjects to verify the effectiveness of the proposed model in this study. The annual carbon quota in the Shenzhen carbon market is separated from the previous carbon quota, such as SZ2013 and SZ2014. Hence, the Shenzhen carbon price is represented by weighting and averaging the closing prices of different carbon quotas. The date when the trading volume of the carbon market is 0 is excluded, and the selected period is from the establishment time of each market to September 2, 2022. The data are collected from http://www.tanpaifang.com/. The dataset of relevant statistical information (Table 2) selects several typical statistical indexes, including the max, min, mean, median, standard deviation, kurtosis and skewness, and ADFtest, to determine whether the Hubei carbon market is the most stable one among the aforementioned carbon markets. The standard deviation and the gap between the maximum and minimum values of all other carbon markets are relatively large, indicating that the carbon price series fluctuates dramatically. ADFtest shows that the P values of nearly all carbon markets, except Shenzhen carbon price, are much more significant than 0.05, indicating that the price data of these markets are non-stationary. The price series of these several carbon markets are shown in Fig. 2, where many sudden upward and downward fluctuations in price series are observed. For the convenience of comparison, the carbon price series after outlier identification and correction are shown in Fig. 2, and the comparison shows that the processed series eliminates some points of sharp fluctuations.

Table 2 Statistical description of the experimental data

Fig. 2

Original and corrected series of five carbon markets

In the experiment, the first 70%, the middle 10%, and the last 20% of the data are used as the training set, the validation set, and the test set, respectively. The training set is used to train the model, the validation set is used to optimize the model’s hyperparameters, and the test set is used to verify the model’s effectiveness.

Data decomposition and reconstruction

Guangdong carbon price is selected as an example to illustrate decomposition and reconstruction. According to the designed hybrid model, the carbon price series after removing outliers is decomposed into several imfs and a residual term through TVFEMD. Each imf represents different amplitude patterns in the original signal, as shown in Fig. 3. According to Fig. 3, 17 imfs significantly increase the calculation amount of the hybrid model. Therefore, SE is used to identify the complexity of different imfs. In other words, the higher the SE, the higher the complexity, and imfs with high complexity are retained one by one. This phenomenon retains the complex features in time series to avoid repetitive secondary decompositions while other imfs are reconstructed according to their SE values. Other imfs are also reconstructed according to their SE values, which not only reduces the calculation of the model to avoid overfitting but also retains the fluctuating features with higher complexity. SE division does not follow stringent rules and regulations, and it is divided by the overall distribution of SE (Zhou et al. 2022; Wang et al. 2022; Sun et al. 2021). According to Table 3 and Fig. 3, the complexity of imfs has a decreasing distribution, and imfs can be roughly divided into three parts. The SE values of imf1–imf4 are almost all over 1 and fluctuate sharply. Hence, these imfs are retained separately. In contrast, the SE values of imf5–imf8 are relatively small and concentrated between 0.3 and 0.5. Thus, these imfs are combined into a component, while the SE values of the remaining imfs are almost all below 0.2, combining these remaining imfs into another component. The reconstructed results are shown in Fig. 3. The rest of the carbon markets are also reconstructed based on similar division criteria for imfs, as shown in Fig. 4.

Fig. 3

Results of carbon price decomposition and reconstruction in Guangdong

Table 3 Sample entropy of each imf

Fig. 4

Sample entropy and reconstruction results for the rest of the carbon market

In this subsection, simple experiments are conducted to illustrate the effectiveness of the adopted decomposition–reconstruction method in terms of running time and forecasting accuracy. The optimized transformer model from “Interval forecasting” is used as the benchmark model. Running time and MAE are chosen as the criterion, and the results of the experiments are shown in Table 4. Table 4 demonstrates that a significant amount of running time is saved after reconstruction, without compromising its prediction accuracy. Thus, this decomposition–reconstruction method is used for all decomposition techniques in the following multi-step-ahead and interval prediction experiments.

Table 4 Comparison results before and after reconstruction

Hyperparameter optimization

In deep learning, the setting of hyperparameters plays a crucial role in determining the experimental results. In this study, OATM is used to optimize the model’s hyperparameters. OATM can effectively balance the optimization time and accuracy through a representative subset. In consideration of relevant studies (Meka et al. 2021; Vaswani et al. 2017; Zhang et al. 2019a), five hyperparameters in the transformer model, including the number of blocks (b_n), the number of neurons (n_n), the time step (t_s), the batch size (b_s), and the number of heads (h_n), are selected as factors for the OATM. Each factor contains four levels, as shown in Table 5. The carbon price in Guangdong is selected as the experimental data. All experiments are conducted using TensorFlow 2.7.0 under Python 3.8.8, and the number of cycles is set to 1000. To prevent overfitting, an adaptive reducing learning rate Adam optimizer is used, along with the early stop mechanism. The dropout rate is set to 0.2, and the activation function is Relu. The hyperparameter orthogonal array is constructed, and the experimental results are shown in Table 6. This table includes the validation set RMSE for 16 experiments. In comparison with the grid search method, which requires 1024 (4⁵) experiments, OATM can save 98.43% of the computational time.

Table 5 Factor-level table for the Transformer model

Table 6 Range analysis of the transformer model

The range analysis enables us to determine the optimal level and the most critical factor according to Table 6. R_leveli and M_leveli are the sum and mean of RMSE at different levels, respectively. The difference between the max M_leveli and the min M_leveli is used to calculate range, which is used to represent the importance of different factors. The greater the range is, the greater the importance of the factor will be. That is, the more sensitive the Transformer model is to this factor. The number of neurons is the most sensitive factor expressed in terms of RMSE, followed by the batch size, number of heads, number of blocks, and the time step. The optimal level under each factor is determined by the lowest M_leveli, from which the optimal hyperparameter combination of the Transformer model can be obtained (b_n = 3, n_n = 128, t_s = 25, b_s = 128, b_n = 4). Finally, the obtained optimal hyperparameter combinations are experimented, and the RMSE is obtained as 1.1075, which is better than the optimal result of 1.1160 in the orthogonal array, indicating that the OATM method can obtain the approximate global optimal solution of the hyperparameter to ensure the robustness of the model structure. All other models included in the comparison use OATM to determine their optimal structure. In other words, all models in the experiment are optimized by OATM.

Experimental analysis

Deterministic forecasting

The deterministic forecasts of carbon prices in the five carbon markets, including one-step, three-step, five-step, and ten-step-ahead forecasting, are analyzed. In addition, different graphs are used to compare the forecasting results more visually. For example, histograms are used to represent MAPE and R², radar chart is used to represent MAE and RMSE, and Taylor diagram is used to show the prediction results of these models. The forecasting results of each model are shown in Tables 7, 8, 9, and 10 (the optimal model is marked in bold, for presentation purposes, these tables only contain the results after using HI) and Figs. 5, 6, 7, 8, and 9 (containing the results of the model with and without HI). According to the results in Tables 7, 8, 9, and 10 and Figs. 5, 6, 7, 8, and 9, the fitted curves of the proposed HI-TVFEMD-transformer model are the closest to the actual values. More importantly, the RMSE, MAE, and MAPE of this model are significantly lower than those of other models, whereas their R² and TSS are almost always the highest, indicating that the forecasting performance of the proposed model is better than those of other benchmark models.

Table 7 Evaluation indicators of comparison models and the proposed model in one-step-ahead forecasting

Table 8 Evaluation indicators of comparison models and the proposed model in three-step-ahead forecasting

Table 9 Evaluation indicators of comparison models and the proposed model in five-step-ahead forecasting

Table 10 Evaluation indicators of comparison models and the proposed model in ten-step-ahead forecasting

Fig. 5

Deterministic forecasting results of the Guangdong market. The upper part corresponds to the histogram and radar plot; the middle part of the histogram is the starting value of MAPE and R²; M1, M2, M3, M4, M5, M6, M7, M8, and M9 represent SVM, LSTM, GRU, TCN, transformer, EMD-transformer, EEMD-transformer, CEEMDAN-transformer, and TVFEMD-transformer, respectively; the left side represents the plot without HI; and the right side represents the plot with HI. The middle part is the fitted curve. The part below it is the Taylor chart

Fig. 6

Deterministic forecasting results of the Hubei market

Fig. 7.

Deterministic forecasting results of the Beijing market

Fig. 8

Deterministic forecasting results of the Shanghai market

Fig. 9.

Deterministic forecasting results of the Shenzhen market

The following comparison was made according to Tables 7, 8, 9, and 10 and Figs. 5, 6, 7, 8, and 9.

Comparison I: the comparison of single model. Single model is the basis for hybrid models to achieve high accuracy. Therefore, this study selects several single models that are commonly used in the mainstream of carbon price forecasting. These models include a machine learning model (SVM) and three deep learning models (e.g., LSTM, GRU, and TCN) that can address the time sequence problem. A comprehensive comparison of Tables 6, 7, 8, and 9 and Figs. 5, 6, 7, 8, and 9 shows that the deep learning model outperforms the machine learning model in all five metrics (e.g., MAE, RMSE, MAPE, R², and TSS), suggesting that the deep learning model is more suitable for carbon price forecasting than the machine learning model. Among the deep learning models, the performance of LSTM, GRU, and TCN varies in different situations. Their respective strengths and weaknesses are shown in the histogram, radar chart, and Taylor diagram of each carbon market. For example, the MAPE of one-step-ahead prediction LSTM in Guangdong and Hubei are 0.0185 and 0.0237, respectively, which are better than GRU’s 0.0240 and 0.0238. Meanwhile, in Guangdong and Hubei, the MAPE of LSTM in the five-step prediction is 0.0776 and 0.0506, respectively, which is inferior to 0.0701 and 0.0500 of GRU. In the ten-step-ahead prediction in Shanghai, TCN is better than LSTM and GRU, and its MAPE is 0.0480, which is better than GRU’s 0.0584 and LSTM’s 0.0662. However, in most cases, the metrics for the transformer are the best among the single models, indicating that in the experiments, transformer’s learning ability is better than those of SVM, LSTM, GRU, and TCN for capturing the complexity and nonlinearity in the carbon price.

Comparison II: the comparison of the efficacy of HI. The validity of HI is evaluated by comparing the model’s predictive performance with and without the use of HI. According to Figs. 5, 6, 7, 8, and 9, the radar chart is in the inner circle without HI after using HI. Among the 180 (5 × 9 × 4) experiments, the number of experiments in which HI has improved all evaluation indicators is 113, and approximately 62.78% of the experiments have been improved while the remaining experiments have improved a few indicators. We calculated the average improvement rate of HI on MAE, RMSE, MAPE, R², and TSS in the Guangdong experiment (the value was obtained by averaging the improvement rates in each experiment), and HI improved by 20.56%, 11.95%, 19.77%, 1.54%, and 0.44%, respectively. The average improvement rate of HI at different steps in the Guangdong experiment was also calculated. HI improved the one-step-ahead forecast by 19.2959%, 1.2028%, 19.2068%, 0.1511%, and − 0.0558%, respectively; three-step-ahead forecast by 28.65%, 21.55%, 28.23%, 1.93%, and 0.90%, respectively; for the five-step ahead forecast by 12.40%, 9.52%, 11.53%, 1.01%, and 0.29%, respectively; and for the ten-step-ahead forecast by 21.89%, 15.55%, 20.13%, 3.06%, and 0.62%, respectively. HI improves MAE, RMSE, and MAPE more significantly. However, it does not improve R² and TSS significantly or even negatively. The reason is that the outliers in the series are identified and corrected by HI to eliminate the abnormal fluctuations, which make the fluctuation characteristics more obvious and reduce the model error. Meanwhile, MAE, RMSE, and MAPE are the metrics used to measure the error between the prediction and the actual models. R² and TSS are metrics that are based on the proportion of variance in the true values that can be explained by the model, the presence of outliers leads to increased variance in the series, and the model cannot learn this information after outliers are identified and corrected. Yet, by retaining these outliers, the model does not learn more useful information either. This instance prevents the model from fitting this part of the variance, which leads to no significant difference in R² and TSS before and after outlier processing. The above analysis demonstrates that outliers in carbon prices can negatively affect the training of the model, and, therefore, HI can improve the prediction ability of the model to some extent.

Comparison III: the comparison of different decomposition methods. According to Figs. 5, 6, 7, 8, and 9, the fitted curves for each carbon market demonstrate a closer fit to the actual values after incorporating the decomposition algorithm. Notably, EMD, EEMD, CEEMDAN, and TVFEMD all improve the prediction accuracy of the transformer model. However, the comparison of TVFEMD suggests that it has a more significant improvement than EMD, EEMD, and CEEMDAN. According to Table 7, HI-TVFEMD-transformer has an average MAPE of 0.0341 in one-step-ahead forecasting, whereas HI-EMD-transformer is 0.0818, HI-EEMD-transformer is 0.0775, and HI-CEEMDAN-transformer is 0.0802. The average MAPE of the transformer model is 0.1121. Comparing the different metrics in the predictions of various ahead steps, TVFEMD also exhibited the best performance, thereby proving the superiority of the TVFEMD method and improving the prediction accuracy of the proposed model.

Comparison IV: the comparison of different carbon markets. According to the Taylor diagram in Figs. 5, 6, 7, 8, and 9, the forecasting results of the Guangdong, Hubei, and, Shanghai carbon markets are more concentrated than those of Beijing and Shenzhen carbon markets, indicating that the carbon price fluctuations in these three carbon markets are more regular, thereby making the performance of various models less different. Consequently, the price series for the Beijing and Shenzhen carbon markets are more volatile, which better reflects the differences in the performance of various models. The HI-TVFEMD-transformer is closer to the actual point in the Taylor diagram in different carbon markets. Its performance is almost always optimal, indicating that it has strong robustness and can be adapted to different datasets.

Comparison V: the comparison of different step-ahead interval forecasting. The comparison results in Figs. 5, 6, 7, 8, and 9 and Tables 6, 7, 8, and 9 show that as the forecasting step increases, the forecasting accuracy of the model gradually decreases because of the lack of information required for forecasting. A single model often experiences varying degrees of forecasting lag. As the number of forecasting steps increases, a single model tends to consider the current price as the best forecast and learns only a simple mapping, thereby failing to capture the relevant features in the data. Conversely, the decomposition algorithm extracts the features of different carbon price time scales by decomposition. Thus, the model can learn smoother features, thereby effectively eliminating this phenomenon. As observed from the fitted curves in Figs. 5, 6, 7, 8, and 9, the prediction results of the hybrid forecasting model for the one-step and three-step-ahead forecasts will contain the fluctuation characteristics of the rapid oscillation in the sequence. In contrast, for the five-step and ten-step-ahead forecasts, the prediction results are smoother because learning the features in the high-frequency imfs for the larger span of steps is difficult for the model. These characteristics are almost unpredictable in large time step gaps because high-frequency imfs represent the characteristics of the short-term fluctuations of carbon price with strong volatility and sharp fluctuations. In this situation, the model can only learn the characteristics of medium- and low-frequency imfs, which represent the low frequency of the medium- and long-term trends in carbon prices. These imfs are more periodic and regular, which leads to smoother prediction results in one-step and three-step-ahead forecasts compared with five-step and ten-step-ahead forecasts.

Interval forecasting

Interval forecasts of carbon prices hold significant relevance in capturing carbon price uncertainty. They serve as valuable tools for assessing the future volatility of carbon prices, thus providing decision-makers insights that deterministic forecasts alone cannot provide. This study is based on the HI-TVFEMD-transformer and utilizes the quantile loss function for interval forecasting of carbon prices. The significance level α plays a crucial role in determining the width and coverage of the interval forecasting. To compare the performance of interval forecasting at various significance levels, this study considers different levels of α (α = 0.1,0.2,0.3) for conducting interval forecasting. Table 11 and Figs. 10, 11, 12, 13, and 14 show the results of the interval forecasting for each carbon market.

Table 11 Indicator results of interval forecasting

Fig. 10.

Interval forecasting results of the Guangdong market

Fig. 11

Interval forecasting results of the Hubei market

Fig. 12

Interval forecasting results of the Beijing market

Fig. 13

Interval forecasting results of the Shanghai market

Fig. 14

Interval forecasting results of the Shenzhen market

We can draw the following conclusions from Table 11 and Figs. 10, 11, 12, 13, and 14. The prediction results will change with α. Guangdong is taken as an example, α = 0.1, AW = 3.7517, PINAW = 0.0636, PICP = 0.9552; α = 0.2, AW = 2.9950, PINAW = 0.0508, PICP = 0.9356; and α = 0.3, AW = 1.3256, PINAW = 0.0225, PICP=0.8095. With the increase in significance level, the interval width and coverage of the interval prediction gradually decreases, indicating that the trade-off between width and coverage is needed during interval forecasting, wherein high coverage but large width or small width but low coverage result in less information contained in the prediction interval. Further comparison reveals that the AW of one-step-ahead interval forecast for the Beijing and Shenzhen carbon markets exceeds 15, whereas for other carbon markets, it hovers around 5. Additionally, when considering ten-step-ahead forecasts, the AW for the two aforementioned carbon markets exceeds 25, while for other carbon markets, it remains around 10. The interval forecast needs a larger width to cover the fluctuations of these two carbon markets, indicating that their volatility is significantly greater than those of other carbon markets. The AW of the Hubei carbon market is the smallest in almost all cases, thereby indicating a stable trend of low volatility. Moreover, the AW gradually increases with the same confidence interval as the forecasting step expands. For example, AW = 5.1689 for one-step-ahead and AW = 11.7828 for ten-step-ahead in Shanghai at α = 0.1. As the forecasting steps increase, the carbon price will have more significant fluctuations relative to the current price, thereby resulting in a larger estimation interval. The interval prediction based on HI-TVFEMD-transformer can explain the volatility of the carbon price well, indicating that the result is good and credible.

Conclusion

A hybrid forecasting model that combines HI, TVFEMD, and transformer is proposed to improve the accuracy of carbon price forecasting. First, HI is used to identify and correct any outliers present in the carbon price series. Then, the original carbon price series is decomposed into multiple imfs using TVFEMD to reduce non-stationarity, and the imfs are reconstructed by SE to reduce the time consumed by the model while retaining its complex features. Further, OATM optimized the hyperparameters of the transformer deep learning technique to select a reasonable hyperparameter configuration. Finally, Transformer and quantile loss functions are used for the multi-step-ahead and interval forecasting of carbon prices. To verify the validity of the proposed model from several aspects, five real carbon price data and four different forecasting steps were selected, and multiple models and decomposition methods were compared. Subsequently, interval forecasting was performed for each carbon market to measure carbon price uncertainty. The main conclusions drawn from this study are presented as follows:

• (1) On the one hand, the experimental results indicate that transformer outperforms SVM, LSTM, GRU, and TCN because of its excellent ability to extract long-term dependence and global features in sequences. On the other hand, TVFEMD exhibited better performance in characterizing the multiscale time–frequency features of carbon price sequences than EMD, EEMD, and CEEMDAN. Moreover, the prediction accuracy achieved by the proposed HI-TVFEMD-transformer hybrid forecasting model was better than most forecasting models, and its robustness and stability are demonstrated in multi-step-ahead forecasting. In most of the experiments, HI improves the prediction accuracy. In contrast, the effects of HI in a small proportion of the experiments are not evident, because although the outliers in the sequence can be eliminated to make the sequence more regular, they will make the sequence lose some fluctuation features.

• (2) The proposed hybrid model exhibits a high level of precision in forecasting carbon prices at multiple levels, encompassing deterministic and uncertain. Therefore, it can provide practical information for investors and policymakers. In the near future, investors can formulate investment strategies based on the results of multi-step-ahead forecasting and understand the possible risks through interval forecasting to avoid them. Meanwhile, policymakers can monitor the changes in carbon price fluctuations through the forecasting results in time and take corresponding measures to stabilize the prices when fluctuations are large.

Although the proposed hybrid forecasting model in this paper has shown excellent forecasting ability during the experiments, it still has room for improvement. First, the use of outlier identification and correction techniques can be considered. Also, more advanced outlier testing or denoising techniques can be used to process carbon prices in future research. Second, determining the SE threshold is based on the distribution and prior experience. However, it is considering whether a more scientific method can be used to determine the threshold of SE. Finally, carbon prices are affected by several factors, such as fossil fuel prices and economic development levels. Hence, studying how to model these factors is also worthwhile.