A Penalized Likelihood Method for Structural Equation Modeling

Abstract

A penalized likelihood (PL) method for structural equation modeling (SEM) was proposed as a methodology for exploring the underlying relations among both observed and latent variables. Compared to the usual likelihood method, PL includes a penalty term to control the complexity of the hypothesized model. When the penalty level is appropriately chosen, the PL can yield an SEM model that balances the model goodness-of-fit and model complexity. In addition, the PL results in a sparse estimate that enhances the interpretability of the final model. The proposed method is especially useful when limited substantive knowledge is available for model specifications. The PL method can be also understood as a methodology that links the traditional SEM to the exploratory SEM (Asparouhov & Muthén in Struct Equ Model Multidiscipl J 16:397–438, 2009). An expectation-conditional maximization algorithm was developed to maximize the PL criterion. The asymptotic properties of the proposed PL were also derived. The performance of PL was evaluated through a numerical experiment, and two real data illustrations were presented to demonstrate its utility in psychological research.

1 Introduction

Structural equation modeling (SEM) is a statistical method that is aimed toward explaining the moments among observable variables. The application of SEM involves a confirmatory testing of models proposed by researchers based on available theories. However, because of the complexity of human behavior, nearly all SEM models are subject to misspecification (Browne & Cudeck, 1993; MacCallum, 2003). Previous studies have shown that a misfit SEM model may lead to biased parameter estimates (Kaplan, 1988; Yuan, Marshall, & Bentler, 2003), incorrect standard errors (Arminger & Schoenberg, 1989; Yuan & Hayashi, 2006), and hence mistaken conclusions about psychological phenomena. Yet, in practice, an exploratory process seems to be an inevitable task for deriving a relatively plausible SEM model, especially when the development of the substantive theory is still in its infancy.

Exploratory structural equation modeling (ESEM; Asparouhov & Muthén, 2009) is now a major exploratory methodology for SEM. The ESEM replaces the confirmatory factor analysis (CFA; Jöreskog, 1969) measurement model in SEM with the exploratory factor analysis (EFA) model. Hence, the misfit caused by omitting nonzero loadings can be avoided. Several novel applications of the ESEM have been demonstrated (see Marsh, Morin, Parker, & Kaur, 2014 for a review). However, the ESEM cannot be utilized without drawbacks. Because the ESEM must freely estimate the entire loading matrix, prior knowledge of null relations among measurements and factors cannot be imposed, which attenuates the theory-driven nature of SEM methodology. In addition, compared to the usual SEM that assumes a sparse loading matrix (i.e., a loading matrix with many zero elements), the ESEM results in a dense loading matrix that generally includes unnecessary parameters. Previous studies have shown that SEM models with unnecessary model complexity yield less efficient estimators (Bentler & Mooijaart, 1989) and exhibit relatively low generalizability (Browne & Cudeck, 1989; Cudeck & Browne, 1983; Preacher, 2006). Also, a dense loading matrix is less interpretable than a sparse one (Trendafilov & Adachi, 2015).

Considering the potential limitations of ESEM, the current study proposes a penalized likelihood (PL) approach for SEM as a new methodology. Over the past 15 years, PL has become a popular method for statistical learning problems (see Bühlmann & van de Geer, 2011; Hastie, Tibshirani, & Friedman, 2009; Hastie, Tibshirani, & Wainwright, 2015 for reviews). Compared to the usual likelihood, the PL estimation criterion includes a penalty term to control the complexity of the hypothesized model. As the penalty level is chosen appropriately, PL can lead to a final model that balances the tradeoff between the model goodness-of-fit and model complexity (e.g., Hoerl & Kennard, 1970). Hence, the final model is relatively generalizable to other samples according to the rationale of a bias-variance tradeoff. By implementing sparsity-inducing penalties, PL can yield sparse estimates (i.e., estimates with elements that are exactly zero), which not only reduces the model complexity but also enhances the interpretability of estimation results. Furthermore, under the family of generalized linear models (GLM), theoretical results indicate that PL has the capacity to consistently identify all relevant and irrelevant covariates (Fan & Li, 2001). The resulting estimator possesses the so-called oracle property, i.e., it performs as well as if the researcher has known the true sparsity pattern of the parameters in advance. Finally, the PL estimation is proven to be an effective method for handling the problem of $P>N$, where P is the number of variables, and N is the sample size (e.g., Fan & Lv, 2011; Fan & Peng, 2004; Kwon & Kim, 2012).

Under the proposed PL, an SEM model is formulated with a confirmatory part and an exploratory part. The confirmatory part includes the functional form of the specified model and the theory-derived free and fixed parameters. The exploratory part, wherein a set of penalized parameters are specified to represent the ambiguous relations, is data-driven yet with model complexity controlled by the penalty term. Hence, the proposed PL is not a pure exploratory method. We call it a semi-confirmatory approach because the PL for SEM can embrace both existing theories and ambiguous relations that await further exploration. The PL then yields relatively efficient and interpretable sparse parameter estimates (e.g., loadings and path coefficients). A final SEM model with possibly high generalizability can be achieved through the choice of penalty level. As we shall see in Sect. 5, under suitable conditions the PL for SEM could result in an oracle estimator, i.e., an estimator that possesses the oracle property.

Several works have applied the idea of penalization to SEM or related latent variable modeling. Jung (2012) applied the ${\ell }_{2}$ penalty to SEM to improve the small sample performance of two-stage least squares estimation. Ning and Georgiou (2011) and Choi, Zou, and Oehlert (2011) implemented the ${\ell }_{1}$ penalty in an orthogonal EFA to obtain a sparse loading matrix. Subsequently, Hirose and Yamamoto (2014, 2015) considered more general concave penalties in an EFA, also for the purpose of obtaining a sparse loadings matrix. Under the generalized linear mixed model (GLMM) framework, several works have proposed PL methods for selecting nonzero fixed effects (Fan & Li, 2012, Groll & Tutz, 2014; Schelldorfer, Bühlmann, & van de Geer, 2011) or both fixed and random effects (Ibrahim, Zhu, Garcia, & Guo, 2011). Although the GLMM is quite flexible, and SEM can be formulated within it (e.g., Ibrahim et al., 2011), these PL methods cannot be used to explore the directional relations among latent variables. PL has also been applied to many other psychometric models, including principal component analysis (Zou, Hastie, & Tibshirani, 2006; Trendafilov & Adachi, 2015), the Rasch model (Tutz & Schauberger, 2015), and the cognitive diagnostic model (Chen, Liu, Xu, & Ying, 2015). However, none of these studies developed a general PL method for SEM. Our work concerns a PL method with several state-of-the-art penalties for a wide class of SEM models. The proposed PL can be used to simultaneously identify the sparsity patterns of many parameter matrices under an SEM framework, including the factor loading matrix, path coefficient matrix, and covariance matrices of latent variables and measurement errors.

This article is organized as follows: Sect. 2 presents the proposed PL for SEM. In Sect. 3, an algorithm for optimizing the PL criterion is described. Section 4 discusses several practical issues when implementing the PL. In Sect. 5, the asymptotic properties of the PL are derived. Section 6 presents two real data illustrations. A numerical experiment is presented in Sect. 7. Finally, merits, limitations, and further directions concerning this study are discussed.

2 A PL Method for SEM

Let Y denote a P-dimensional observable random vector with element $Y_{p} (p=1,2,\ldots ,P)$. The measurement part of SEM describes the relationships between the manifest variables and the latent variables

$$\begin{aligned} Y=\nu +\Lambda \eta +\epsilon , \end{aligned}$$

(1)

where $\nu$ is a P-dimensional intercept vector with element $\nu _{p}; \eta$ is an M-dimensional latent variable vector with element $\eta _{m} (m=1,2,\ldots ,M); \Lambda$ is a $P\times M$ factor loading matrix with element $\lambda _{pm}$, and $\epsilon$ is a P-dimensional measurement error vector with element $\epsilon _{p}$. The structural part of SEM describes the hypothesized relationships among latent variables

$$\begin{aligned} \eta =\alpha +\mathrm {B}\eta +\zeta , \end{aligned}$$

(2)

where $\alpha$ is an M-dimensional intercept vector with element $\alpha _{m}; \mathrm {B}$ is an $M\times M$ path coefficient matrix with element $\beta _{mk} (\beta _{mm}=0)$, and $\zeta$ is an M-dimensional residual vector with element $\zeta _{m}$. It is assumed that

• 1. $\epsilon$ has a zero mean and positive definite covariance matrix $\Psi$.

• 2. $\zeta$ has a zero mean and positive definite covariance matrix $\Phi$.

• 3. $\epsilon$ and $\zeta$ are uncorrelated.

Under these assumptions, the model-implied mean and covariance of Y are

$$\begin{aligned} \mu (\theta )= & {} \nu +\Lambda (I_{M}-\mathrm {B})^{-1}\alpha ,\end{aligned}$$

(3)

$$\begin{aligned} \Sigma (\theta )= & {} \Lambda (I_{M}-\mathrm {B})^{-1}\Phi {(I_{M}-\mathrm {B})^{-1}}^\mathrm{T}\Lambda ^\mathrm{T}+\Psi , \end{aligned}$$

(4)

respectively, where $\theta \in \Theta$ is a Q-dimensional parameter vector with element $\theta _{q}, \Theta \subset \mathfrak {R}^{Q}$ being a parameter space, and $I_{M}$ is the $M\times M$ identity matrix. The parameter vector $\theta$ only contains the unknown parameters in $\nu , \Lambda , \Psi , \alpha , \mathrm {B}$, and $\Phi$.

Consider a random sample $\mathcal {Y}_{N}=\left\{ Y_{n} \right\} _{n=1}^{N}$, the maximum likelihood (ML) estimation finds an estimate $\hat{\theta }$ that maximizes the log-likelihood function

$$\begin{aligned} \mathcal {L}(\theta )=\frac{1}{N}\sum \limits _{n=1}^N \log {\varphi _{\theta }\left( Y_{n} \right) }, \end{aligned}$$

(5)

where $\varphi _{\theta }(y)$ is the normal density, with mean and covariance as parameterized by $\theta$ in Eqs. (3) and (4), i.e., $\log {\varphi _{\theta }(y)}=-\frac{1}{2}\log \left| \Sigma (\theta ) \right| -\frac{1}{2}(y-\mu (\theta ))^\mathrm{T}{\Sigma (\theta )}^{-1}(y-\mu (\theta ))$. The log-likelihood function is established under the working assumption that the response variable Y has a multivariate normal distribution with the specified moment structure. In the current study, we consider the PL criterion

$$\begin{aligned} \mathcal {U}(\theta ,\gamma )=\mathcal {L}(\theta )-\mathcal {R}(\theta ,\gamma ), \end{aligned}$$

(6)

where $\mathcal {R}(\theta ,\gamma )=\sum _{q=1}^Q {c_{q}\rho \left( \left| \theta _{q} \right| ,\gamma \right) }$ is a penalty term with a penalty function $\rho (t,\gamma )$, a set of penalization indicators $\left\{ c_{q} \right\} _{q=1}^{Q}$, and a regularization parameter $\gamma$. A parameter with $c_{q}=0$ is freely estimated, and $c_{q}=1$ allows $\theta _{q}$ to be explored. The confirmatory part of the hypothesized model includes the functional forms of moment structures, freely estimated parameters, and fixed parameters. The exploratory part is formed by the parameters being penalized. By implementing sparsity-inducing penalties, non-null relationships in the exploratory part can be selected. Because the variance of an exogenous variable should be larger than zero, the proposed method requires $c_{q}$ to be zero if $\theta _{q}$ is a diagonal element of $\Psi$ or $\Phi$. Each component in $\mathcal {U}(\theta ,\gamma )$ plays a different role: $\mathcal {L}(\theta )$ measures the goodness-of-fit; $\mathcal {R}(\theta ,\gamma )$ measures the complexity, and $\gamma$ controls the tradeoff between the previous two components. A PL estimator $\hat{\theta }=\hat{\theta }(\gamma )$ is defined as a local maximizer of $\mathcal {U}(\theta ,\gamma )$. Note that different values of $\gamma$ yield different estimates even under the same data. An optimal value of $\gamma$ can be determined based on model selection criteria (see Sect. 4).

Fig. 1

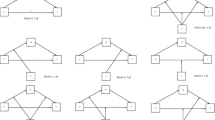
Path diagrams for two possible model specifications under the proposed penalized likelihood method. Left A specification for a factor analysis model with three latent factors and nine indicators. Right A specification for a full SEM model with five exogenous latent variables and two endogenous latent variables. Arrows with solid and broken lines represent freely estimated and penalized parameters, respectively.

Figure 1 illustrates two possible model specifications under the PL framework. Example 1 is an oblique three factor model with nine observed variables (left side of Fig. 1). Each variable is assumed to be mainly a measure of some latent factor (see the arrows with solid lines in Fig. 1). However, the PL specification does not exclude the possibility of cross loadings. All other loadings are estimated with penalization (see the arrows with broken lines in Fig. 1). The resulting penalty term is $\mathcal {R}(\theta ,\gamma )=\sum _{(p,m)\in \mathcal {C}} {\rho \left( \left| \lambda _{pm} \right| ,\gamma \right) }$, where $\mathcal {C}$ is a two-dimensional index set that indicates which loadings are to be penalized.

Example 2 is a full SEM model (right side of Fig. 1). Five exogenous $(\eta _{1}, \eta _{2}, \ldots , \eta _{5})$ and two endogenous $(\eta _{5}$ and $\eta _{6})$ latent variables are considered. For simplicity, the observed variables are omitted. The measurement part is assumed to be a seven-factor model without cross loadings. For the structural part, prior knowledge states that the exogenous factors are all correlated and that $\eta _{6}$ is influenced by $\eta _{1}, \eta _{2}$, and $\eta _{4}$ but not $\eta _{3}$ and $\eta _{5}$. No theory is available to specify the exact relationships among $\eta _{1}, \eta _{2}, \ldots , \eta _{5}$ and $\eta _{7}$. Hence, these effects were set as penalized parameters. The corresponding penalty term is simply $\mathcal {R}(\theta ,\gamma )=\sum \nolimits _{m=1}^5 {\rho \left( \left| \beta _{7m} \right| ,\gamma \right) }$.

Many penalty functions have been proposed in the literature (see Hastie, Tibshirani, & Wainwright, 2015). ${\ell }_{2}$ is the most well-known penalty function with the form

$$\begin{aligned} \rho _{{\ell }_{2}}(t,\gamma )=\gamma t^{2}. \end{aligned}$$

(7)

In linear regression, ${\ell }_{2}$ can be used to handle the problem of not full rank design matrix (Hoerl & Kennard, 1970). Another important penalty function is the ${\ell }_{1}$ penalty,

$$\begin{aligned} \rho _{{\ell }_{1}}(t,\gamma )=\gamma t. \end{aligned}$$

(8)

A linear regression with ${\ell }_{1}$, also called the lasso (least absolute shrinkage and selection operator; Tibshirani, 1996), is now a popular method due to its ability to produce sparse estimates. It can be shown that maximizing the PL criterion with ${\ell }_{1}$ is equivalent to solving the problem of maximizing $\mathcal {L}(\theta )$ subject to $\sum \nolimits _{q=1}^Q \left| \theta _{q} \right| \le K$, where K is a positive number depending on $\gamma$. Geometrically, $\sum \nolimits _{q=1}^Q \left| \theta _{q} \right| \le K$ forms a rhomboid in a Q-dimensional space. The maximizer of $\mathcal {U}(\theta ,\gamma )$ is the first place where the contours of $\mathcal {L}(\theta )$ touch the rhomboid. Because the rhomboid has corners on the axes, a sparse estimate arises when the maximizer is located at a corner (Tibshirani, 1996).

Under the ${\ell }_{1}$ penalty, the tasks of parameter estimation and variable selection can be simultaneously achieved. However, ${\ell }_{1}$ is only consistent for variable selection under certain restricted conditions (see Zhao & Yu, 2006; Zou, 2006). To overcome this problem, several nonconvex penalties have been proposed. Of these, SCAD (smoothly clipped absolute deviation; Fan & Li, 2001) and MCP (minimax concave penalty; Zhang, 2010) are the two most well known. The functional forms of SCAD and MCP are

$$\begin{aligned} \rho _{SCAD}(t,\gamma )= & {} \left\{ {\begin{array}{ll} \gamma t &{}\quad \hbox {if }\, t\le \gamma \\ -\frac{t^{2}+\gamma ^{2}-2\gamma \delta t}{2\left( \delta -1 \right) } &{} \quad \hbox {if }\, \gamma<t\le \gamma \delta \\ \frac{\gamma ^{2}\left( \delta ^{2}-1 \right) }{2\left( \delta -1 \right) } &{}\quad \hbox {if }\, \gamma \delta <t \\ \end{array}} \right. ,\end{aligned}$$

(9)

$$\begin{aligned} \rho _{MCP}(t,\gamma )= & {} \left\{ {\begin{array}{ll} \gamma t-\frac{t^{2}}{2\delta } &{} \quad \hbox {if }\, t\le \gamma \delta \\ \frac{1}{2}\gamma ^{2}\delta &{} \quad \hbox {if }\, \gamma \delta <t \\ \end{array}} \right. , \end{aligned}$$

(10)

respectively. Here, $\delta$ is a parameter that controls the convexity of either SCAD or MCP ($\delta >2$ for SCAD and $\delta >1$ for MCP). As $\delta \rightarrow \infty$ both SCAD and MCP become ${\ell }_{1}$. On the other hand, a small $\delta$ makes them behave similarly to the best subset selection method. In the GLM family, the theoretical results indicate that SCAD and MCP can both yield oracle estimators, even under the case of $P>N$ (Fan & Li, 2001; Kwon & Kim, 2012; Zhang, 2010).

It is worth noting that the PL estimation can be understood as a Bayesian maximum of a posteriori (MAP) method. ${\ell }_{2}$ and ${\ell }_{1}$ represent Gaussian and Laplace priors, respectively, and both SCAD and MCP comprise some improper priors (for further discussion, see Meng, 2008; Strawderman, Wells, & Schifano, 2013).

Because a PL with the ${\ell }_{2}$ penalty cannot select nonzero parameters though sparse estimation, the proposed PL method emphasizes ${\ell }_{1}$, SCAD, and MCP. In the latter paragraph, “PL-A” is used to indicate a PL method that uses A as a penalty function.

Remark 1

We have mentioned that the exploratory part contains all the ambiguous relations that await further exploration. Although the term “ambiguous relations” is used, in both Examples 1 and 2, the directionality of these relations is clearly specified. When the PL is implemented as an exploratory method, we recommend formulating all the relationships as clearly as possible. PL users should determine whether a relationship between two variables is directional or simply correlated. If the relation is directional, it should be determined which direction is sensible according to the available substantive theories. Blindly using PL is dangerous because it could result in many equivalent models. Under such cases, no theory is available to justify the use of PL, and the resulting model might be nonsense. PL users should avoid such practices.

Remark 2

It is worth noting that for any SEM model, if we replace all the zero loadings with penalized parameters, the PL with a small $\gamma$ can yield an ESEM-like estimate (see Hirose & Yamamoto, 2015 for such a result in an EFA case). On the other hand, a very large $\gamma$ results in an exactly traditional SEM result. Therefore, the proposed PL can be seen as a methodology that links the traditional SEM to the ESEM. In theory, through choosing $\gamma$, the PL has the capacity to obtain an optimal model on the continuum from the traditional SEM to the ESEM.

3 An ECM Algorithm for Optimizing the PL Criterion

In this section, an expectation-conditional maximization (ECM) algorithm (Meng & Rubin, 1993) for maximizing the PL criterion is proposed. The expectation–maximization (EM) algorithm (Dempster, Laird, & Rubin, 1977) is a popular method by which to obtain estimates in many PL applications with latent variables (e.g., Choi, Zou, & Oehlert, 2011; Garcia, Ibrahim, & Zhu, 2010; Hirose & Yamamoto, 2014; 2015; Ibrahim, Zhu, Garcia, & Guo, 2011). The EM algorithm includes two steps: the E-step calculates the conditional expectation of the complete data likelihood given the observed data, and the M-step maximizes the derived conditional expectation. ECM extends EM by replacing the M-step with several conditional maximizations, called CM-steps. As shown below, each CM-step in the proposed algorithm involves only a maximizer with a closed form expression.

Before introducing the proposed algorithm, some notations must be defined. Let A denote a $P\times M$ matrix with $a_{pm}$ being its (p, m) element. We use A[p, ], A[, m], and A[p, m] to denote the pth row, the mth column, and the (p, m) element of matrix A, respectively. Similarly, $A[ -p,], A[,-m]$, and $A[-p,-m]$ denote the submatrices of A with its pth row, mth column, and both deleted. If $A^{-1}$ exists, $a^{pm}$ is defined as the (p, m) element of $A^{-1}$. Also, b[p] is used to denote the pth element in vector b.

Instead of maximizing the PL criterion directly, the proposed ECM alternatively considers the complete data PL criterion

$$\begin{aligned} \mathcal {U}^{C}(\theta ,\gamma )\propto -\frac{1}{2}\mathrm {log}\left| \Psi \right| -\frac{1}{2N}\sum \limits _{n=1}^N {\epsilon _{n}^\mathrm{T}\Psi ^{-1}\epsilon _{n}} -\frac{1}{2}\mathrm {log}\left| \Phi \right| -\frac{1}{2N}\sum \limits _{n=1}^N {\zeta _{n}^\mathrm{T}\Phi ^{-1}\zeta _{n}} -\mathcal {R}(\theta ,\gamma ),\nonumber \\ \end{aligned}$$

(11)

where $\epsilon _{n}=Y_{n}-\nu -\Lambda \eta _{n}$ and $\zeta _{n}=\eta _{n}-\alpha -{\mathrm{B}}\eta _{n}$. Compared to the PL criterion in Eq. (6), which is constructed only based on the marginal normality of Y, the complete data PL treats the latent factor $\eta$ as observable and is established under the joint normality assumption of Y and $\eta$ with the relationships defined in Eqs. (1) and (2) (see Appendix A). Note that the normality of Y and $\eta$ is merely a working assumption. The ECM algorithm can still find a local maximizer when this assumption fails.

The E-step of ECM calculates the conditional expectation of $\mathcal {U}^{C}(\theta ,\gamma )$

$$\begin{aligned} \mathcal {M}(\theta |\hat{\theta }^{(t)})=\mathbb {E}[\mathcal {U}^{C}(\theta ,\gamma ) |\mathcal {Y}_{N},\hat{\theta }^{(t)}], \end{aligned}$$

(12)

where $\hat{\theta }^{(t)}=\hat{\theta }^{(t)}(\gamma )$ is the estimate at iteration t under the penalty level $\gamma$. Define $e_{V}^{(t+1)}=\mathbb {E}\left[ \left. \frac{1}{N}\sum \nolimits _{n=1}^N V_{n} \right| \mathcal {Y}_{N},\hat{\theta }^{(t)} \right]$ and $C_{VW}^{(t+1)}=\mathbb {E}\left[ \left. \frac{1}{N}\sum \nolimits _{n=1}^N {V_{n}W_{n}^\mathrm{T}} \right| \mathcal {Y}_{N},\hat{\theta }^{(t)} \right]$ for any random vectors $V_{n}$ and $W_{n}$. By the functional form of $\mathcal {U}^{C}(\theta ,\gamma )$, it suffices to calculate $e_{Y}, e_{\eta }^{(t+1)}, C_{YY}, C_{Y\eta }^{(t+1)}$, and $C_{\eta \eta }^{(t+1)}$ to obtain $\mathcal {M}\left( \left. \theta \right| \hat{\theta }^{(t)} \right)$ (see Appendix A).

After obtaining $\mathcal {M}\left( \left. \theta \right| \hat{\theta }^{(t)} \right)$, the qth CM-step increases the value of $\mathcal {M}\left( \left. \theta \right| \hat{\theta }^{(t)} \right)$ through maximizing $\mathcal {M}\left( \left. \theta \right| \hat{\theta }^{(t)} \right)$ under the restriction $g_{q}(\theta )=g_{q}\left( \hat{\theta }^{\left( t+\frac{q-1}{Q} \right) } \right)$, where $g_{q}(\theta )=\left( \theta _{1},\ldots ,\theta _{q-1},\theta _{q+1},\ldots ,\theta _{Q} \right)$ and $\hat{\theta }^{\left( t+\frac{q-1}{Q} \right) }$ is a maximizer of $\mathcal {M}\left( \left. \theta \right| \hat{\theta }^{(t)} \right)$ at the $(q-1)$th CM-step. Hence, each CM-step increases the value of $\mathcal {M}\left( \left. \theta \right| \hat{\theta }^{(t)} \right)$ in each coordinate. The main idea here is similar to that of the coordinate descent method, which is now the major method for maximizing PL in regressions (e.g., Breheny, & Huang, 2011; Friedman, Hastie, Höfling, & Tibshirani, 2007; Mazumder & Friedman, 2011).

SEM considers two types of parameters: regression-type coefficients and variance and covariance parameters. Regression-type coefficients include the parameters in $\Lambda , {\mathrm{B}}, \nu$, and $\alpha$, and the variance and covariance parameters include the parameters in $\Psi$ and $\Phi$. For the regression-type coefficients, the estimates under $\gamma =0$ can be updated through

$$\begin{aligned} \hat{\lambda }_{pj}^{(t+1)}= & {} \frac{1}{C_{\eta \eta }^{(t+1)}[j,j]}\left[ \left( C_{Y\eta }^{(t+1)}[ p,j ]-\hat{\nu }_{p}^{(t*)}e_{\eta }^{(t)}[j]-\hat{\Lambda }^{(t*)}[p,-j]C_{\eta \eta }^{(t+1)}[-j,j] \right) \right. \nonumber \\&\left. +\sum \limits _{p'\ne p} {\frac{\hat{\psi }^{{pp'}^{(t*)}}}{\hat{\psi }^{{pp}^{(t*)}}}\left( C_{Y\eta }^{(t+1)}[ p',j]-\hat{\nu }_{p'}^{(t*)}e_{\eta }^{(t+1)}[j]-\hat{\Lambda }^{(t*)}[p',]C_{\eta \eta }^{(t+1)}[,j] \right) } \right] , \end{aligned}$$

(13)

$$\begin{aligned} \hat{\beta }_{mj}^{(t+1)}= & {} \frac{1}{C_{\eta \eta }^{(t+1)}[j,j]}\left[ \left( C_{\eta \eta }^{(t+1)}\left[ m,j \right] -\hat{\alpha }_{m}^{(t*)}e_{\eta }^{(t+1)}[j]-\hat{\mathrm{B}}^{(t*)}[m,-j]C_{\eta \eta }^{(t+1)}[-j,j] \right) \right. \nonumber \\&\left. +\sum \limits _{m'\ne m} {\frac{\hat{\phi }^{{mm'}^{(t*)}}}{\hat{\phi }^{{mm}^{(t*)}}}\left( C_{\eta \eta }^{(t+1)}[m',j]-\hat{\alpha }_{{m'}^{(t*)}}e_{\eta }^{(t+1)}[j]-\hat{\mathrm{B}}^{(t*)}[ m', ]C_{\eta \eta }^{(t+1)}[,j] \right) } \right] ,\end{aligned}$$

(14)

$$\begin{aligned} \hat{\nu }_{p}^{(t+1)}= & {} e_{Y}[p]-\hat{\Lambda }^{(t*)}[p,]e_{\eta }^{(t+1)}+\sum \limits _{p^{'}\ne p} {\frac{\hat{\psi }^{{pp'}^{(t*)}}}{\hat{\psi }^{{pp}^{(t*)}}}\left( e_{Y}[p^{'} ]-\hat{\nu }_{{p^{'}}}^{(t*)}-\hat{\Lambda }^{(t*)}[p',]e_{\eta }^{(t+1)} \right) },\end{aligned}$$

(15)

$$\begin{aligned} \hat{\alpha }_{m}^{(t+1)}= & {} e_{\eta }^{(t+1)}[m]-\hat{\mathrm{B}}^{(t*)}[m,]e_{\eta }^{(t+1)}\nonumber \\&+\sum \limits _{m'\ne m} {\frac{\hat{\phi }^{{mm'}^{(t*)}}}{\hat{\phi }^{{mm}^{(t*)}}}\left( e_{\eta }^{(t+1)}[ m' ]-\hat{\alpha }_{m^{'}}^{(t*)}-\hat{\mathrm{B}}^{(t*)}[ m', ]e_{\eta }^{(t+1)} \right) }, \end{aligned}$$

(16)

where $\hat{\theta }^{(t*)}=\hat{\theta }^{\left( t+\frac{q-1}{Q} \right) }$ stands for the newly updated estimate (see Appendix B for the derivation). When $\gamma >0$, the CM-steps for updating $\hat{\lambda }_{pj}^{(t+1)}(\gamma ), \hat{\beta }_{mj}^{(t+1)}(\gamma ), \hat{\nu }_{p}^{(t+1)}(\gamma )$, and $\hat{\alpha }_{m}^{(t+1)}(\gamma )$ involve shrinkage steps, and the shrinkage functions depend on the choice of penalties. These shrinkage formulae are given in Table 1. Any fixed coefficient is kept at the pre-specified value in each iteration. For the variance and covariance parameters, the CM-steps are derived based on the iterative conditional fitting method (ICF; Chaudhuri, Drton, & Richardson, 2007). Compared to Newton-type methods, the ICF can ensure the semi-positive definiteness of $\hat{\Psi }$ and $\hat{\Phi }$. We extend the original ICF method by allowing the covariance parameters to be penalized (see Appendix C for the details).

Table 1 Shrinkage formulae for $\hat{\lambda }_{pj}^{(t+1)}(\gamma ), \hat{\beta }_{mj}^{(t+1)}(\gamma ), \hat{\nu }_{p}^{(t+1)}(\gamma ), \hat{\alpha }_{m}^{(t+1)}(\gamma ), \hat{\psi }_{pj}^{(t+1)}(\gamma ),\,\hbox {and}\,\hat{\phi }_{mj}^{(t+1)}(\gamma )$ with selected penalty functions.

In summary, the proposed ECM algorithm can be briefly described as

• 1. Initialize $e_{Y}=\frac{1}{N}\sum \nolimits _{n=1}^N Y_{n}, C_{YY}=\frac{1}{N}\sum \nolimits _{n=1}^N {Y_{n}Y_{n}^\mathrm{T}}$, and $\hat{\theta }^{(t)}\in \Theta$ such that $\Sigma \left( \hat{\theta }^{(t)} \right)$ is positive definite with $t=0$.

• 2. Compute $e_{\eta }^{(t+1)}, C_{Y\eta }^{(t+1)}$, and $C_{\eta \eta }^{(t+1)}$ according to Appendix A.

• 3. For $q=1, 2,\ldots ,Q$

  • (a) If $\theta _{q}$ is a regression-type coefficient, compute $\hat{\theta }_{q}^{(t+1)}$ by Eqs. (13)–(16) and the shrinkage formulae in Table 1.

  • (b) Otherwise, compute $\hat{\theta }_{q}^{(t+1)}$ by the regularized ICF method described in Appendix C and the shrinkage formulae in Table 1.

• 4. Repeat 2 and 3 until $\sum \nolimits _{q=1}^Q \left( \hat{\theta }_{q}^{\left( t-1 \right) }-\hat{\theta }_{q}^{(t)} \right) ^{2} \big / \sum \nolimits _{q=1}^Q \left( \hat{\theta }_{q}^{(t)} \right) ^{2} <\varepsilon$ for some small $\varepsilon >0$.

4 Practical Considerations in Implementing PL

In this section, we discuss several practical considerations when implementing PL. The first issue is related to the scale setting of the latent variables. After adding a penalty, the invariance property of ML no longer holds (e.g., PL analysis results based on covariance and correlation are not equivalent). Moreover, the scale of variables affects the shrinkage level directly (see Table 1). In SEM, the scale of latent variables is often set by fixing the values of certain factor loadings or factor variances. We suggest fixing the scaling loadings deliberately such that all the latent variables have variances of around one. Approximate unit variance can be achieved using a two-step method by first running a measurement model restricting $\phi _{m}^{2}=1$ for every m and then conducting PL with scaling loadings fixed at the corresponding estimates obtained in step one.

The second consideration concerns model identifiability. If the specified model $\tau (\theta )=\left( {\mu (\theta )}^\mathrm{T},{\mathrm {vech}\left( \Sigma (\theta ) \right) }^\mathrm{T} \right) ^\mathrm{T}$ is locally identified around $\theta$, PL can yield a locally unique estimate in a neighborhood of $\theta$, where $\mathrm {vech}\left( \cdot \right)$ is an operator that stacks nonduplicated elements of a symmetric matrix. However, even when $\tau (\theta )$ is not identified, it is still possible to obtain a locally unique PL estimate because the penalty term introduces additional constraints. Motivated by the results of McDonald (1982) and Shapiro and Browne (1983), one possible way for checking the local identifiability of $\tau (\theta )$ under the restriction of the penalty term is to examine whether $\frac{\partial \tau (\hat{\theta })}{\partial \theta _{\hat{\mathcal {A}}(\gamma )}^\mathrm{T}}$ is of full column rank, where $\theta _{\hat{\mathcal {A}}(\gamma )}$ is the subvector of $\theta$ formed by $\left\{ \theta _{q} \right\} _{q\in \hat{\mathcal {A}}(\gamma )}$, and $\hat{\mathcal {A}}(\gamma )=\left\{ \left. q \right| \hat{\theta }_{q}\ne 0 \right\}$ is the support of $\hat{\theta }$.

The third practical consideration involves the selection of an optimal regularization parameter $\gamma$. Let $\mathcal {D}(\hat{\theta })$ denote the sample discrepancy evaluated at $\hat{\theta }$, i.e., $\mathcal {D}(\hat{\theta })=\mathcal {D}_{ML}\left( \tau (\hat{\theta }),t \right) =-\log \left| {\Sigma (\hat{\theta })}^{-1}S \right| +\mathrm {tr}\left( {\Sigma (\hat{\theta })}^{-1}S \right) -P+\left( \bar{Y}-\mu (\hat{\theta }) \right) ^\mathrm{T}{\Sigma (\theta )}^{-1}\left( \bar{Y}-\mu (\hat{\theta }) \right)$, where $t=\left( {\mathrm {vech}(S)}^\mathrm{T},\bar{Y}^\mathrm{T} \right) ^\mathrm{T}$ with $S=\frac{1}{N}\sum \nolimits _{n=1}^N {\left( Y_{n}-\bar{Y} \right) \left( Y_{n}-\bar{Y} \right) ^\mathrm{T}}$ and $\bar{Y}=\frac{1}{N}\sum \nolimits _{n=1}^N Y_{n}$. The Akaike information criterion (AIC; Akaike, 1974) and the Bayesian information criterion (BIC; Schwarz, 1978) are two commonly used selectors,¹ defined as

$$\begin{aligned} AIC(\gamma )= & {} \mathcal {D}(\hat{\theta })+\frac{2}{N}e(\gamma ),\end{aligned}$$

(17)

$$\begin{aligned} BIC(\gamma )= & {} \mathcal {D}(\hat{\theta })+\frac{\log N}{N}e(\gamma ), \end{aligned}$$

(18)

where $e(\gamma )$ is the number of nonzero estimated parameters in $\hat{\theta }=\hat{\theta }(\gamma )$. Given a candidate set $\Gamma =\left\{ \gamma _{l} \right\} _{l=0}^{L}$ with $0=\gamma _{0}<\gamma _{1}<\ldots <\gamma _{L}$, an optimal $\gamma$ can be determined through selecting a $\hat{\gamma }$ that minimizes AIC or BIC on $\Gamma$. A method to construct ${\Gamma }$ is to choose L and $\gamma _{L}$ first and then set $\gamma _{l}=\frac{l}{L}\gamma _{L}$. We may simply choose a $\gamma _{L}$ such that all penalized parameters are estimated as zero. According to the updating formula in Table 1, $\gamma _{L}=1$ is large enough if both manifest and latent variables are standardized. Using the continuity of PL criterion, both $\left\{ AIC(\gamma ) \right\} _{{\gamma \in \Gamma }}$ and $\left\{ BIC(\gamma ) \right\} _{{\gamma \in \Gamma }}$ can be computed efficiently if $\hat{\theta }\left( \gamma _{l} \right)$ is used as a warm start for calculating $\hat{\theta }\left( \gamma _{l-1} \right)$ (see Friedman et al., 2007). When there are multiple minima on ${\Gamma }$, the largest minimizer is selected according to the principle of Occam’s razor. If SCAD or MCP is used, an optimal pair of $\left( \gamma ,\delta \right)$ can be determined with a similar strategy.

Model evaluation is the forth issue of practical concern. We suggest using goodness-of-fit indices for such purposes. Let $df(\hat{\gamma })={P(P+3)} \big / 2-e(\hat{\gamma })$ be the degrees of freedom of the final model, respectively, for the SEM framework presented in Sect. 2. When appropriate, these quantities, $\mu \left( \hat{\theta }(\hat{\gamma }) \right) , \Sigma \left( \hat{\theta }(\hat{\gamma }) \right)$, and $df(\hat{\gamma })$, can be substituted into an existing formula to calculate fit indices for assessing model-data fit. Yet, the validity of this tentative approach calls for a thorough investigation.

The final consideration concerns statistical inference. Inference in PL is generally difficult because of the difficulty of post-model-selection inference (e.g., Leeb & Pötscher, 2006). The theorems derived in the next section show that a heuristic estimator for the covariance matrix of $\hat{\theta }_{\hat{\mathcal {A}}(\gamma )}$ is $\hat{\mathcal {V}}\left( \hat{\theta }_{\hat{\mathcal {A}}(\gamma )} \right) =\frac{1}{N}\hat{\mathcal {F}}_{\hat{\mathcal {A}}(\gamma )}^{-1}\hat{\mathcal {H}}_{\hat{\mathcal {A}}(\gamma )}\hat{\mathcal {F}}_{\hat{\mathcal {A}}(\gamma )}^{-1},$ where $\hat{\mathcal {H}}_{\hat{\mathcal {A}}(\gamma )}=\frac{1}{N}\sum \nolimits _{n=1}^N {\frac{\partial \log {\varphi _{\hat{\theta }}(y_n)}}{\partial \theta _{\hat{\mathcal {A}}(\gamma )}}\frac{\partial \log {\varphi _{\hat{\theta }}(y_n)}}{\partial \theta _{\hat{\mathcal {A}}(\gamma )}^\mathrm{T}}},$ and $\hat{\mathcal {F}}_{\hat{\mathcal {A}}(\gamma )}=-\frac{\partial ^{2}\mathcal {L}(\hat{\theta })}{\partial \theta _{\hat{\mathcal {A}}(\gamma )}\partial \theta _{\hat{\mathcal {A}}(\gamma )}^\mathrm{T}}$. The square root of the diagonal of $\hat{\mathcal {V}}\left( \hat{\theta }_{\hat{\mathcal {A}}(\gamma )} \right)$ provides a standard error estimate. However, the method does not give standard errors for parameters shrunk to zero. The empirical performance of the standard error formula thus requires further evaluation.

5 Asymptotic Properties of the PL Method

In this section, asymptotic properties of the PL method for SEM are derived. Three theorems are presented. Theorems 1 and 2 concern the oracle property of the PL estimator, and Theorem 3 describes the asymptotic behavior of AIC and BIC with regard to choosing the regularization parameter. The big picture here is that under suitable conditions, PL with SCAD/MCP and BIC selector could result in an oracle estimator asymptotically.

Before presenting the derived theorems, some notations are introduced. For a vector $x\in \mathfrak {R}^{P}, \left\| x \right\| _{0}$ is used to denote the ${\ell }_{0}$ norm of x, i.e., $\left\| x \right\| _{0}=\sum \nolimits _{p=1}^P {1\left\{ x_{p}\ne 0 \right\} }$, where $1\left\{ \cdot \right\}$ is an indicator function. For a square matrix $A\in \mathfrak {R}^{P\times P}, \omega _\mathrm{min}(A)$ is used to denote the smallest eigenvalue of A. Given an index set $\mathcal {J}\subset \left\{ 1,2,\ldots ,P \right\} , x_{\mathcal {J}}$ is defined as the $\left| \mathcal {J} \right|$-dimensional vector formed by $\left\{ x_{p} \right\} _{p\in \mathcal {J}}$, and $A_{\mathcal {J}}$ is the $\left| \mathcal {J} \right| \times \left| \mathcal {J} \right|$ matrix formed by $\left\{ a_{pp'} \right\} _{p,p'\in \mathcal {J}}$, where $\left| \mathcal {J} \right|$ is the number of elements in $\mathcal {J}$.

To derive the asymptotic properties of the PL method, the following regularity conditions are assumed:

Condition A

$\mathcal {Y}_{N}=\left\{ Y_{n} \right\} _{n=1}^{N}$ is a random sample from some distribution F that satisfies (1) $\mathbb {E}(Y)=\mu ^{*}$; (2) ${\mathbb {V}\hbox {ar}}(Y)=\Sigma ^{*}\succ 0;$ i.e., $\Sigma ^{*}$ is positive definite; (3) there exists an $\varepsilon >0$ such that $\mathbb {E}\left( \left| Y_{p} \right| ^{4+\varepsilon } \right) <\infty$ for all p.

Condition B

For each $\theta \in \Theta$ and any combination of $q, q'$, and $q'' (q,q',q''=1,2,\ldots ,Q), \frac{{\partial }^{3}\tau (\theta )}{{\partial }\theta _{q}{\partial }\theta _{q'}{\partial }\theta _{q''}}$ exists.

Condition C

There exists a quasi-true parameter $\theta ^{*}{\in \Theta }$ such that (1) $\theta ^{*}\in \hbox {argmax}_{\theta \in \Theta } {\mathbb {E}\left( \mathcal {L}(\theta ) \right) }$; (2) $\left\| \theta ^{*} \right\| _{0}<\left\| \theta \right\| _{0}$ for any $\theta \in \hbox {argmax}_{\theta \in \Theta }{\mathbb {E}\left( \mathcal {L}(\theta ) \right) }$, but $\theta \ne \theta ^{*}$; (3) $\theta ^{*}$ is the unique maximizer of $\mathbb {E}\left( \mathcal {L}(\theta ) \right)$ on $\Theta _{\mathcal {A}^{*}}$, where $\mathcal {A}^{*}=\left\{ \left. q \right| \theta _{q}^{*}\ne 0 \right\}$ is the support of $\theta ^{*}; \Theta _{\mathcal {A}^{*}}={\Theta \cap }\left( \prod \nolimits _{q=1}^Q \mathfrak {X}_{q} \right)$ is the restricted parameter space with $\mathfrak {X}_{q}=\mathfrak {R}$ if $q\in \mathcal {A}^{*}$, and $\mathfrak {X}_{q}=\left\{ 0 \right\}$ otherwise; (4) there exists a neighborhood of $\theta ^{*}$ on $\Theta _{\mathcal {A}^{*}}$, denoted by ${\Omega }_{\mathcal {A}^{*}}(\theta ^{*})$ and a constant $\kappa _{1}>0$ such that $\omega _{\min }\left( \mathcal {F}_{\mathcal {A}^{*}}(\theta ) \right) >\kappa _{1}$ for all $\theta \in \Omega _{\mathcal {A}^{*}}(\theta ^{*})$, where $\mathcal {F}_{\mathcal {A}^{*}}(\theta )=\mathbb {E}\left( -\frac{\partial ^{2}\mathcal {L}(\theta )}{\partial \theta _{\mathcal {A}^{*}}\partial \theta _{\mathcal {A}^{*}}^\mathrm{T}} \right)$.

Condition D

For each combination of $q, q'$, and $q''$, there exists an F-integrable random function $K_{qq'q''}(y)$ such that $\left| \frac{{\partial }^{3}\log {\varphi _{\theta }(y)}}{{\partial }\theta _{q}{\partial }\theta _{q'}{\partial }\theta _{q''}} \right| <K_{qq'q''}(y)$ for all y and $\theta$ in the neighborhood of $\theta ^{*}$.

Condition E

The penalty term $\mathcal {R}(\theta ,\gamma )=\sum \nolimits _{q=1}^Q {c_{q}\rho \left( \left| \theta _{q} \right| ,\gamma \right) }$ satisfies (1) $c_{q}=1$ if $\theta _{q}^{*}=0$; (2) $\rho (t,\gamma )$ is increasing and concave in $t>0$; (3) $\frac{{\partial }\rho (t,\gamma )}{{\partial }t}$ is continuous in both t and $\gamma$; (4) $\frac{{\partial }\rho \left( 0+,\gamma \right) }{{\partial }t}=\gamma$; (5) $\frac{{\partial }\rho (t,\gamma )}{{\partial }t}=0$ if $t>\delta \gamma$.

Condition F

$\theta ^{*}$ is the unique maximizer of $\mathbb {E}\left( \mathcal {L}(\theta ) \right)$ on $\Theta$, and there exists a neighborhood of $\theta ^{*}$ on $\Theta$, denoted by ${\Omega }(\theta ^{*})$, and a constant $\kappa _{2}>0$ such that $\omega _{\min }\left( \mathcal {F}(\theta ) \right) \ge \kappa _{2}$ for all $\theta \in {\Omega }(\theta ^{*})$, where $\mathcal {F}(\theta )=\mathbb {E}\left( -\frac{\partial ^{2}\mathcal {L}(\theta )}{\partial \theta \partial \theta ^\mathrm{T}} \right)$.

Conditions A, B, and D are standard (e.g., Browne, 1984). Condition C requires the existence and the uniqueness of a quasi-true parameter $\theta ^{*}$ on a restricted parameter space $\Theta _{\mathcal {A}^{*}}$ even when $\tau (\theta )$ is not identifiable on the entire parameter space $\Theta$. However, the positive definiteness of $\mathcal {F}_{\mathcal {A}^{*}}(\theta )$ on ${\Omega }_{\mathcal {A}^{*}}(\theta ^{*})$ implies that $\tau (\theta )$ should be at least locally identified on $\Theta _{\mathcal {A}^{*}}$. Condition E requires that the penalization indicators must be one for all estimated true-zero parameters. Condition E also restricts the shape of the penalty function. Both SCAD and MCP satisfy these properties, but ${\ell }_{1}$ does not. Finally, Condition F is a restricted version of Condition C and is required to establish a global theoretical result.

Theorem 1

(Local oracle property) If Conditions A–E are true, $\gamma$ satisfies $\gamma \rightarrow 0$, and $\sqrt{N} \gamma \rightarrow \infty$ as $N\rightarrow \infty$, then there exists a strictly local maximizer of $\mathcal {U}(\theta ,\gamma )$, denoted by $\hat{\theta }=\hat{\theta }(\gamma )$, such that

• (a) $\hbox {lim}_{N\rightarrow \infty }{\mathbb {P}\left( \hat{\mathcal {A}}(\gamma )=\mathcal {A}^{*} \right) }=1$;

• (b) $\sqrt{N} \left( \hat{\theta }_{\mathcal {A}^{*}}-\theta _{\mathcal {A}^{*}}^{*} \right) \longrightarrow _{\mathcal {D}}\mathcal {N}\left( 0,{\mathcal {F}_{\mathcal {A}^{*}}^{*}}^{-1}\mathcal {H}_{\mathcal {A}^{*}}^{*}{\mathcal {F}_{\mathcal {A}^{*}}^{*}}^{-1} \right)$, where $\mathcal {F}_{\mathcal {A}^{*}}^{*}=\mathbb {E}\left( -\frac{\partial ^{2}\mathcal {L}(\theta ^{*})}{\partial \theta _{\mathcal {A}^{*}}\partial \theta _{\mathcal {A}^{*}}^\mathrm{T}} \right)$ and $\mathcal {H}_{\mathcal {A}^{*}}^{*}=\mathbb {E}\left( \frac{1}{N}\sum \nolimits _{n=1}^N {\frac{\partial \log {\varphi _{\theta ^{*}}\left( Y_{n} \right) }}{\partial \theta _{\mathcal {A}^{*}}}\frac{\partial \log {\varphi _{\theta ^{*}}\left( Y_{n} \right) }}{\partial \theta _{\mathcal {A}^{*}}^\mathrm{T}}} \right)$.

All the proofs of derived theorems can be found in the online supplemental materials. Part (a) of Theorem 1 states that the PL method has the potential to correctly identify zero and nonzero model parameters. Hence, it is possible to obtain an estimation result that performs as well as if the sparsity pattern is known in advance, as part (b) shows. Because Theorem 1 does not require Condition F to hold, it could still be true when the specified model is not identifiable on the entire parameter space.

Theorem 1 only ensures that asymptotically, there exists a local maximizer $\hat{\theta }$ such that the oracle property is satisfied. In practice, choosing such a local maximizer is difficult. Hence, it is hoped that a global result can be derived so that the obtained PL estimator is assuredly an oracle estimator. To derive such a global result, Condition F, which ensures the uniqueness of the quasi-true parameter on the whole parameter space, is required.

Theorem 2

(Global oracle property) Under Conditions A–F, $\gamma$ satisfies $\gamma \rightarrow 0$ and $\sqrt{N} \gamma \rightarrow \infty$ as $N\rightarrow \infty$. Asymptotically, there exists a unique global maximizer of $\mathcal {U}(\theta ,\gamma )$, denoted by $\hat{\theta }$, such that

• (a) $\hbox {lim}_{N\rightarrow \infty }{\mathbb {P}\left( \hat{\mathcal {A}}(\gamma )=\mathcal {A}^{*} \right) }=1$;

• (b) $\sqrt{N} \left( \hat{\theta }_{\mathcal {A}^{*}}-\theta _{\mathcal {A}^{*}}^{*} \right) \longrightarrow _{\mathcal {D}}\mathcal {N}\left( 0,{\mathcal {F}_{\mathcal {A}^{*}}^{*}}^{-1}\mathcal {H}_{\mathcal {A}^{*}}^{*}{\mathcal {F}_{\mathcal {A}^{*}}^{*}}^{-1} \right)$.

If Y is normally distributed and $\tau (\theta )$ is correctly specified, the information equality holds (i.e., ${\mathcal {F}_{\mathcal {A}^{*}}^{*}}^{-1}=\mathcal {H}_{\mathcal {A}^{*}}^{*})$ and Theorem 2 reduces to Corollary 1 below. The main implication of Corollary 1 is that the PL estimator can achieve the Cramér–Rao lower bound, even when the true sparsity pattern is unknown beforehand. Furthermore, Corollary 1 implies that the test statistic $N\cdot \mathcal {D}(\hat{\theta })$ is asymptotically distributed as a Chi-square random variable. Therefore, it is easy to construct an asymptotic $1-\alpha$ level test for examining the null hypothesis $\tau =\tau (\theta )$ versus the alternative $\tau \ne \tau (\theta )$. The asymptotic $\chi ^{2}$ distribution of the test statistic can be also used to justify the application of the goodness-of-fit indices described in Sect. 4.

Corollary 1

Under Conditions A–F and $\gamma$ satisfies $\gamma \rightarrow 0$ and $\sqrt{N} \gamma \rightarrow \infty$ as $N\rightarrow \infty$. If the density of Y is actually $\varphi _{\theta }(y)$, then asymptotically, there exists a unique global maximizer of $\mathcal {U}(\theta ,\gamma )$, denoted by $\hat{\theta }$, such that

• (a) $\hbox {lim}_{N\rightarrow \infty }{\mathbb {P}\left( \hat{\mathcal {A}}(\gamma )=\mathcal {A}^{*} \right) }=1$;

• (b) $\sqrt{N} \left( \hat{\theta }_{\mathcal {A}^{*}}-\theta _{\mathcal {A}^{*}}^{*}\right) \longrightarrow _{\mathcal {D}}\mathcal {N}\left( 0,{\mathcal {F}_{\mathcal {A}^{*}}^{*}}^{-1} \right)$;

• (c) $N\cdot \mathcal {D}(\hat{\theta })\longrightarrow _{\mathcal {D}}\chi _{{df}^{*}}^{2}$, where ${df}^{*}={P(P+3)} \big / 2-\left| \mathcal {A}^{*} \right|$.

Next, the asymptotic properties of AIC and BIC are derived under the proposed PL. Given a model $\tau (\theta )$, for any index set $\mathcal {A}\subset \left\{ 1,2,\ldots ,Q \right\}$, the minimum discrepancy function (MDF) value of $\tau (\theta )$ on $\Theta _{\mathcal {A}}$ is defined as $\mathcal {D}_{\mathcal {A}}^{*}=\hbox {min}_{\theta \in \Theta _{\mathcal {A}}}{\mathcal {D}_{ML}\left( \tau (\theta ),\tau ^{*} \right) }$, where $\tau ^{*} =\left( {\mathrm {vech}\left( \Sigma ^{*} \right) }^\mathrm{T},\mu ^{{*}^\mathrm{T}} \right) ^\mathrm{T}$. Hence, by examining the values of $\mathcal {D}_{\mathcal {A}}^{*}$ and $\mathcal {D}_{\mathcal {A}'}^{*}$, the correctness of $\tau (\theta )$ restricted on $\Theta _{\mathcal {A}}$ and $\Theta _{\mathcal {A}\prime }$ can be compared. According to the definition of $\mathcal {A}^{*}, \mathcal {D}_{\mathcal {A}^{*}}^{*}{\le }\mathcal {D}_{\mathcal {A}}^{*}$ for any $\mathcal {A}\subset \left\{ 1,2,\ldots ,Q \right\}$. If some $\mathcal {A}$ satisfies $\mathcal {D}_{\mathcal {A}^{*}}^{*}=\mathcal {D}_{\mathcal {A}}^{*}$, Condition C indicates that $\mathcal {A}^{*}$ must be more parsimonious than $\mathcal {A}$, i.e., $\left| \mathcal {A}^{*} \right| <\left| \mathcal {A} \right|$. Given a random sample $\mathcal {Y}_{N}$, the set of regularization parameters is partitioned into three subsets

$$\begin{aligned} {\Gamma }^{*}= & {} \left\{ \left. \gamma \right| \mathcal {D}_{\hat{\mathcal {A}}(\gamma )}^{*}=\mathcal {D}_{\mathcal {A}^{*}}^{*},| \hat{\mathcal {A}}(\gamma ) |=\left| \mathcal {A}^{*} \right| \right\} ,\end{aligned}$$

(19)

$$\begin{aligned} {\Gamma }^{+}= & {} \left\{ \left. \gamma \right| \mathcal {D}_{\hat{\mathcal {A}}(\gamma )}^{*}=\mathcal {D}_{\mathcal {A}^{*}}^{*},| \hat{\mathcal {A}}(\gamma ) |>\left| \mathcal {A}^{*} \right| \right\} ,\end{aligned}$$

(20)

$$\begin{aligned} {\Gamma }^{-}= & {} \left\{ \left. \gamma \right| \mathcal {D}_{\hat{\mathcal {A}}(\gamma )}^{*}>\mathcal {D}_{\mathcal {A}^{*}}^{*} \right\} . \end{aligned}$$

(21)

The subset ${\Gamma }^{*}$ contains all the values of $\gamma$ where the optimal model $\mathcal {A}^{*}$ is attained. On the other hand, ${\Gamma }^{+}$ and ${\Gamma }^{-}$ are formed by $\gamma$ such that the corresponding models are overfitted and underfitted, respectively. Note that $\hat{\mathcal {A}}(\gamma )$ with $\gamma \in {\Gamma }^{+}$ may not be really “overfitting” in the usual sense. An overfitting model is generally used to refer to a model that explains the phenomenon perfectly but contains unnecessary parameters. However, “overfitting” here is merely used to emphasize that $\hat{\mathcal {A}}(\gamma )$ contains unnecessary parameters because it is possible that $\mathcal {D}_{\hat{\mathcal {A}}(\gamma )}^{*}>0$.

Theorem 3

Let $\hat{\gamma }^{AIC}$ and $\hat{\gamma }^{BIC}$ denote the selection results based on AIC and BIC, respectively. Under Conditions A–F, we have

• (a) $\hbox {lim}_{N\rightarrow \infty }{\mathbb {P}\left( \hat{\gamma }^{AIC}\in {\Gamma }^{-} \right) }=0$ and $\hbox {lim}_{N\rightarrow \infty }{\mathbb {P}\left( \hat{\gamma }^{AIC}\in {\Gamma }^{+} \right) }>0;$

• (b) $\hbox {lim}_{N\rightarrow \infty }{\mathbb {P}\left( \hat{\gamma }^{BIC}\in {\Gamma }^{*} \right) }=1$.

Theorems 3 shows that asymptotically, both AIC and BIC select a model that attains the smallest MDF value $\mathcal {D}_{\mathcal {A}^{*}}^{*}$. However, only BIC yields a consistent selection result with respect to $\mathcal {A}^{*}$. AIC may suffer from the problem of overfitting. Of course, if ${\Gamma }^{+}$ is empty, AIC can also select the quasi-true model with the probability one. The derived results are consistent with the typical behavior of AIC and BIC in parametric regression models (e.g., Zhang, Li, & Tsai, 2012; Shao, 1997).

6 Real Data Illustrations

6.1 Real Data Illustration 1: Nine Psychological Tests

The nine psychological tests adopted from Holzinger and Swineford (1939) are often used to demonstrate factor analysis methods (e.g., Jöreskog, 1969; Rosseel, 2012). This data set contains the responses of 301 seventh and eighth grade students on nine mental tests. These tests are thought of as measuring three correlated abilities: visualization (tests 1, 2, 3), verbal intelligence (tests 4, 5, 6), and speed (tests 7, 8, 9). Under the CFA framework, all of the tests are assumed to be pure measures, and the associated measurement errors are uncorrelated. The left part of Table 2 presents the corresponding ML estimation result. The overall pattern of parameter estimates is reasonable; however, the goodness-of-fit indices show that the model does not fit the data well $(\chi ^{2}=85.30; df=24; p<.001; \mathrm{RMSEA}=0.092; \mathrm{CFI}=0.930; \mathrm{NNFI}=0.896)$.

Table 2 Parameter estimates of nine psychological tests under confirmatory, semi-confirmatory (PL), and exploratory factor analysis.

One possible cause of this misfit is that some tests are not pure measures. Nevertheless, it is difficult to specify the correct sparsity pattern of a loading matrix a priori. In such circumstances, PL is a plausible method by which to explore the underlying loading pattern. When using PL, the model is specified according to Example 1 in Sect. 2. The SCAD is utilized. Based on the value of $BIC(\gamma ), \left( \hat{\gamma },\hat{\delta } \right) =\left( 0.1, 2.5 \right)$ is selected from ${\Gamma \times \Delta }=\left\{ .01, .02,\ldots , .20 \right\} {\times }\left\{ 2.5, 3.5, 4.5 \right\}$. The central part of Table 2 shows the final PL estimation result. Three penalized loadings are identified as nonzero $(\hat{\lambda }_{71}, \hat{\lambda }_{91}$, and $\hat{\lambda }_{12})$. By using the standard error formula described in Sect. 4, all of the nonzero estimates are significantly different from zero at the 0.05 level. The smallest singular value of $\frac{\partial \tau \left( \hat{\theta }({\hat{\gamma }}) \right) }{\partial \theta _{\hat{\mathcal {A}}(\hat{\gamma })}^\mathrm{T}}$ is 0.15, indicating that the final model is locally identified. Goodness-of-fit indices show that the final model fits the data relatively well compared to the CFA result $(\chi ^{2}=35.53; df(\hat{\gamma })=21; p=.006; \mathrm{RMSEA}=0.048; \mathrm{CFI}=0.984; \mathrm{NNFI}=0.972)$.

An oblique EFA model is also used to fit the data. The right part of Table 2 shows the ML estimation result with a promax rotation (power $=$ 4). The estimated loading matrix is quite similar to the PL solution. Goodness-of-fit measures show that the EFA model also performs better than the CFA model $(\chi ^{2}=22.41; df=12; p=.033; \mathrm{RMSEA}=0.055; \mathrm{CFI}=0.987; \mathrm{NNFI}=0.963)$. However, the EFA model contains many nearly zero factor loadings, which means that the model is unnecessarily complex. As a result, the EFA model performs slightly worse than the PL on RMSEA and NNFI. It shows that a complex model does not always outperform a simple one if the considered fit index takes into account the issue of model complexity.

6.2 Real Data Illustration 2: Five Facets of Mindfulness and the Negative/Positive Affect

Chang, Lin, and Huang (2010) collected responses from 231 undergraduate students on the Five Facets Mindfulness Questionnaire (FFMQ; Baer, Smith, Hopkins, Krietemeyer, & Toney, 2006) and Positive and Negative Affect Schedule (PANAS; Watson, Clark, & Tellegen, 1988). The FFMQ is designed to measure five facets of mindfulness: acting with awareness (AA), nonjudgment (NJ), describing (DE), non-reactivity (NR), and observing (OB). PANAS measures the levels of positive affect (PA) and negative affect (NA) of an individual, respectively. In this illustration, the question “how do the five facets of mindfulness predict an individual’s PA and NA?” is investigated. Because the main purpose of the data analysis is to understand the relationships among latent variables, 21 parcels from the original items are formed. The measurement model is specified according to the relationships between the parcels and the latent constructs. Each factor is measured using three indicators. The loading of the first indicator for each factor is fixed. The fixed values are .941, .890, .906, .803, .757, .857, and .832, respectively. For the structural model, based on the empirical results of Baer et al. (2006), NA is expected to be influenced by AA, NJ, and NR, forming the confirmatory part of the structural model. However, the relationships between the five facets of mindfulness and the PA are unclear. Hence, these effects are set as penalized parameters. The model specification of the structural part is the same as that of Example 2 in Sect. 2.

Fig. 2

Final path coefficient estimates for the structural model of real data illustration 2. AA acting with awareness, NJ nonjudgment, DE describing, NR non-reactivity, OB observing, NA negative affect, PA positive affect. $^{*}p<.05; ^{**}p<.01; ^{***}p<.001$.

Figure 2 shows the path coefficient estimates in the structural model of Illustration 2. MCP is used as the penalty function, and $\left( \hat{\gamma },\hat{\delta } \right) =(.1, 1.5)$ is chosen from ${\Gamma \times \Delta }=\left\{ .01, .02,\ldots , .20 \right\} {\times }\left\{ 1.5, 2.5, 3.5 \right\}$ according to the value of $BIC(\gamma )$. The final model is locally identified because the smallest singular value of $\frac{\partial \tau \left( \hat{\theta }(\hat{\gamma }) \right) }{\partial \theta _{\hat{\mathcal {A}}(\hat{\gamma })}^\mathrm{T}}$ is 0.34. Goodness-of-fit indices indicate that the final model fitted the data reasonably $(\chi ^{2}=289.09; df(\hat{\gamma })=173; \mathrm{RMSEA}(\hat{\gamma })=0.054; \mathrm{CFI}(\hat{\gamma })=0.961; \mathrm{NNFI}(\hat{\gamma })=0.953)$. For the confirmatory part, AA, NJ, and NR were shown to have negative effects on an individual’s negative affect, as expected. For the exploratory part, only DE, NR, and OB were shown to have positive effects on individual PA.

7 Numerical Experiment

In this section, a numerical experiment was conducted to evaluate the performance of the PL method. Two different types of models were considered: an oblique factor analysis model and a complete SEM model. The simulations were conducted in an exploratory manner to assess the effectiveness of PL in recovering the underlying structure. Two questions were to be addressed in the simulation. First, how well does the PL estimator perform compared to the non-oracle ML (NML) and the oracle ML (OML) estimators? Second, how often does the PL method select the true model? The NML treats all the penalized parameters in PL as free parameters, and the OML is the usual ML estimation under the true model. Because the NML tends to yield a relatively unstable estimator, comparing the PL estimator with the NML estimator shows how PL improves the quality of estimation by controlling model complexity. On the other hand, the OML yields an oracle estimator that can be taken as a golden standard. Based on the theory of PL in Sect. 5, we expected that (a) the PL estimators will generally outperform the NML estimator, (b) the estimators from PL with SCAD/MCP and BIC, the so-called oracle PL, will perform similarly to the OML under large samples, and (c) the oracle PL will select the true model with high probability asymptotically.

For each model, normally distributed data under the true covariance structure were generated with sample sizes being 100, 200, 400, 800, or 1600 and 500 converged replications that were included under each condition. All the simulations were conducted in R (R Core Team, 2016) with the lsl package used for PL analysis (Huang, 2015).

Fig. 3

Path diagram for the true model of model 1 in the numerical experiment: an oblique factor analysis model. For simplicity, only values of factor correlations and loadings associated with the first factor are presented. Values of other factor loadings are set in a similar way.

Model 1 is an oblique factor analysis model with 20 indicators and 4 common factors. The true relationship among the indicators and factors is given in Fig. 3. The measurement error covariance matrix was set as a diagonal matrix such that each indicator had unit variance. Each data set was analyzed through PL with ${\ell }_{1}$/SCAD/MCP, NML, and OML. The three methods estimated the loading matrix $\Lambda$ in different ways. For the PL method, loadings in the “independent cluster” part, including $\left\{ \left. \lambda _{pm} \right| p=5(m-1)+k, m=1, \ldots , 4, k=1, \ldots , 5 \right\}$, were freely estimated, but loadings in the “non-independent cluster” part were set as penalized parameters. An optimal pair $\left( \hat{\gamma },\hat{\delta } \right)$ was chosen from $\Gamma \times \Delta$ through the value of AIC and BIC, where $\Gamma =\left\{ .01, .02, \ldots , .30 \right\}$ and $\Delta =\left\{ 2.2, 2.6, 3.0 \right\}$ for SCAD, and $\Delta =\left\{ 1.2, 1.6, 2.0 \right\}$ for MCP. For the NML method, an initial loading matrix was freely estimated and was then obliquely rotated to a partially specified target (Browne, 1972) by assuming the “non-independent cluster” part should be as small as possible. Finally, the OML only estimated the true nonzero parameters.

Table 3 Performances of PL, NML, and OML in Model 1: a factor analysis model.

Table 4 Performances of PL, NML, and OML in Model 2: An SEM Model.

Model 2 is an SEM model with 27 manifest and 9 latent variables. The true measurement model was specified as

$$\begin{aligned} \Lambda =I_{9}\otimes \left[ {\begin{array}{c} 0.80\\ 0.75\\ 0.70\\ \end{array} } \right] ,\quad \Psi =I_{9}\otimes \left[ \begin{array}{ccc} .36 &{} 0 &{} 0\\ 0 &{} .4375 &{} 0\\ 0 &{} 0 &{} .51\\ \end{array} \right] . \end{aligned}$$

(22)

The nonzero parameters in the path coefficient matrix ${\mathrm{B}}$ were $\beta _{21}=\beta _{32}=\beta _{54}=\beta _{65}=\beta _{87}=\beta _{98}=0.35$ and $\beta _{41}=\beta _{74}=\beta _{52}=\beta _{85}=\beta _{63}=\beta _{96}=0.45$. The residual covariance matrix $\Phi$ was chosen such that all the latent variables had unit variances. When a data set is analyzed through a PL method, all coefficients in the lower triangular of ${\mathrm{B}}$ are estimated with ${\ell }_{1}$, SCAD, or MCP. An optimal pair $\left( \hat{\gamma },\hat{\delta } \right)$ was chosen from ${\Gamma \times \Delta }$ using AIC and BIC, where ${\Gamma } =\left\{ .01, .02, \ldots , .30 \right\}$ and ${\Delta =}\left\{ 2.2, 2.6, 3.0 \right\}$ for SCAD, and ${\Delta =}\left\{ 1.2, 1.6, 2.0 \right\}$ for MCP. NML freely estimates all the lower diagonal paths, and OML estimates the true nonzero parameters only.

The performance of the proposed PL was evaluated with five criteria. First, the overall estimation quality was assessed by the estimated mean squared error (MSE), defined as

$$\begin{aligned} \widehat{\mathrm{MSE}}(\hat{\theta })=\frac{1}{R}\sum \limits _{r=1}^R {\left( \hat{\theta }^{(r)}(\hat{\gamma })-\theta ^{*} \right) ^\mathrm{T}\left( \hat{\theta }^{(r)}(\hat{\gamma })-\theta ^{*} \right) }, \end{aligned}$$

(23)

where $\hat{\theta }^{(r)}(\hat{\gamma })=\left( \hat{\theta }_{1}^{(r)}(\hat{\gamma }),\ldots ,\hat{\theta }_{Q}^{(r)}(\hat{\gamma }) \right) ^\mathrm{T}$ denoted the final estimate in the rth replication; $\theta ^{*}$ was the true parameter, and $R=500$ was the number of replications. Second, the degree of bias of an estimator was evaluated by the estimated squared bias (SB)

$$\begin{aligned} \widehat{SB}(\hat{\theta })=\left( \bar{\hat{\theta }}-\theta ^{*} \right) ^\mathrm{T}\left( \bar{\hat{\theta }}-\theta ^{*} \right) , \end{aligned}$$

(24)

where $\bar{\hat{\theta }}=\frac{1}{R}\sum \nolimits _{r=1}^R {\hat{\theta }^{(r)}(\hat{\gamma })}$ represented the empirical mean of $\hat{\theta }(\hat{\gamma })$. The third criterion, the proportion choosing the true model (PCTM), assessed selection consistency via the proportion of the true model that was chosen over the replications. The chance of correctly identifying the true nonzero parameters was the fourth criterion as evaluated by the estimated true discovery rate (TDR),

$$\begin{aligned} \widehat{\mathrm{TDR}}(\hat{\theta })=\frac{1}{R}\sum \limits _{r=1}^R \frac{\sum _{q\in \mathrm {B}} {\mathrm {1}\left\{ \hat{\theta }_{q}^{(r)}(\hat{\gamma })\ne 0 \right\} } }{\left| \mathcal {B} \right| }, \end{aligned}$$

(25)

where $\mathcal {B}=\left\{ \left. q \right| \theta _{q}^{*}\ne 0,c_{q}=1 \right\}$, and $\left| \mathcal {B} \right|$ was the size of $\mathrm {B}$. Lastly, the degree to which the true-zero parameters were incorrectly identified as nonzero was examined by the estimated false discovery rate (FDR)

$$\begin{aligned} \widehat{\mathrm{FDR}}(\hat{\theta })=\frac{1}{R}\sum \limits _{r=1}^R \frac{\sum _{q\in \mathcal {B}^{c}} {\mathrm {1}\left\{ \hat{\theta }_{q}^{(r)}(\hat{\gamma })\ne 0 \right\} } }{\left| \mathcal {B}^{c} \right| }, \end{aligned}$$

(26)

where $\mathcal {B}^{c}=\left\{ \left. q \right| \theta _{q}^{*}=0,c_{q}=1 \right\}$.

Tables 3 and 4 show the simulation results for models 1 and 2, respectively. The relative performance of the different PL implementations, NML, and OML, were similar across the two models. The OML estimator performed the best, with the lowest MSE and SB, and the NML estimator performed the worst, with a relatively large MSE. The PL estimators uniformly outperformed the NML estimator, supporting our expectations (a). Within the class of PL estimators, the estimators under the oracle PL performed better than those under ${\ell }_{1}$ or AIC. Especially, under relatively large sample sizes $(N\ge 800)$, the oracle PL estimators performed similarly to those of the OML estimator, confirming our expectations (b). The PCTM showed that the oracle PL was more likely to select the true model than the PL using ${\ell }_{1}$ or AIC. The high PCTM of the oracle PL under large sample sizes supported our expectations (c). If the oracle PL did not select the true model, the TDR of nearly one showed that it tended to choose relatively complex models. However, the selected models were not very complex because most FDRs were still low. For example, FDRs were all less than 0.05 if the sample size was at least moderate ($N\ge 200)$. Therefore, the model selected by the oracle PL was usually close to the true model.

Remark 3

Note that the performance of NML can be improved by hard-thresholding small parameter estimates or using model modification indices. However, in contrast to the hard-threshold or the modification method, PL can result in a continuous estimator by continuous thresholding. Theoretically, a continuous estimation is expected to be relatively stable than a noncontinuous one (see Breiman, 1996; Fan & Li, 2001). We generally recommend using continuous methods whenever they are available.

8 Conclusion and Future Direction

A penalized likelihood method for structural equation modeling is proposed in the present study. The major advantage of the PL method lies in its capacity to incorporate the confirmatory and the exploratory elements in a model, allowing for a simultaneous consideration of existing theories and ambiguous inter-variable relations that await exploration. The proposed method can be applied to a wide class of SEM models to efficiently reach an optimal model. The derived theorems show that the PL can asymptotically yield an oracle estimator. The numerical experiment further confirms such theoretical results. The better performance of PL over NML across all the sample sizes also demonstrates the benefit of controlling model complexity in an exploratory analysis. This preliminary evidence suggests that when uncertainty in relationships among variables exists, the PL method provides an option for conducting SEM.

The present study develops an ECM algorithm for optimizing the PL criteria. The ECM extends the algorithms of Choi, Zou, and Oehlert (2011) and Hirose and Yamamoto (2014, 2015) for EFA in the sense that the current algorithm allows structural parameters and covariances to be penalized. Because SEM can be formulated under GLMM or a regression with incomplete data, the ECM can be also seen as a variant of the algorithms developed by Garcia, Ibrahim, Zhu (2010) and Ibrahim, Zhu, Garcia, and Guo (2011) by considering SEM-specific parameters to be penalized. Nevertheless, the algorithms of Ibrahim and his colleagues could be more general in the sense that they consider any type of response belonging to an exponential family. In the future, it would be worth to generalizing our algorithm to SEM with more flexible response variables.

The novel PL method for SEM presented in this study is not without limitations. Future research in several directions can further our understanding of PL and provide improvements over the current development. First, the standard errors and goodness-of-fit indices under PL are proposed without numerical evaluation. Although both of them were used in our real data illustrations, further studies are required to examine their empirical performances. Second, our numerical experiment only considers relatively standard conditions. Future simulations can be extended to evaluate the PL under more realistic settings, such as non-normal data (e.g., Micceri, 1989), candidate sets without containing the true model (e.g., Cudeck & Henly, 1991), the presence of small parameters (e.g., Vrieze, 2012), and the case of $P>N$. Third, the PL method was not compared with model modification methods (e.g., Chou & Bentler, 1990; MacCallum, 1986). Future studies can be designed to compare these methods in order to understand their relative advantages and disadvantages. Finally, the present PL considers only linear SEM. In reality, the relationships among observed variables and latent variables might be nonlinear (e.g., Lee & Zhu, 2002). Developing PL methods for more complex SEM situations could enhance the applicability of the framework proposed herein.

Appendices

Appendix A: The E-Step of the ECM Algorithm

Under the normal assumption of $\epsilon$ and $\zeta$ and the model defined in Eqs. (1) and (2), the joint distribution of Y and $\eta$ is

$$\begin{aligned} \left( {\begin{array}{c} Y\\ \eta \\ \end{array} } \right) \sim \mathcal {N}\left[ \left( {\begin{array}{c} \mu \\ \kappa \\ \end{array} } \right) ,\left( {\begin{array}{cc} \Sigma &{} {\Xi }\Lambda ^\mathrm{T}\\ {\Lambda \Xi } &{} {\Xi }\\ \end{array} } \right) \right] , \end{aligned}$$

where ${\Sigma =\Lambda \Xi }\Lambda ^\mathrm{T}+\Psi ; \Xi =(I_{M}-\mathrm {B})^{-1}\Phi (I_{M}-\mathrm {B})^{{-1}^\mathrm{T}}; \mu =\nu +\Lambda \kappa$, and $\kappa =(I_{M}-\mathrm {B})^{-1}\alpha$. Therefore, the complete data log-likelihood in Eq. (11) can be obtained using the distribution of Y given $\eta$ and the distribution of $\eta$, or equivalently, the distribution of $\zeta$.

To derive the expression for the E-step, the conditional moments of the latent factor given the data are necessary. The joint normality of Y and $\eta$ implies that the conditional mean and variance of $\eta$ given Y are

$$\begin{aligned} \mathbb {E}\left( \left. \eta \right| Y \right)= & {} \kappa +{\Xi }\Lambda ^\mathrm{T}{\Sigma ^{-1}(Y-\mu )},\\ \mathbb {V}\mathrm {ar}\left( \left. \eta \right| Y \right)= & {} {\Xi -\Xi }\Lambda ^\mathrm{T}\Sigma ^{-1}\Lambda \Xi . \end{aligned}$$

Hence, we have

$$\begin{aligned} e_{\eta }^{(t+1)}= & {} J^{(t)}+K^{(t)}e_{Y},\\ C_{Y\eta }^{(t+1)}= & {} e_{Y}J^{{(t)}^\mathrm{T}}+C_{YY}K^{{(t)}^\mathrm{T}},\\ C_{\eta \eta }^{(t+1)}= & {} \hat{\Xi }^{(t)}-\hat{\Xi }^{(t)}\hat{\Lambda }^{{(t)}^\mathrm{T}}\hat{\Sigma }^{{(t)}^{-1}}\hat{\Lambda }^{(t)}\hat{\Xi }^{(t)}+J^{(t)}J^{{(t)}^\mathrm{T}}+J^{(t)}e_{Y}^\mathrm{T}K^{{(t)}^\mathrm{T}}\\&+K^{(t)}e_{Y}J^{{(t)}^\mathrm{T}}+K^{(t)}C_{YY}K^{{(t)}^\mathrm{T}}, \end{aligned}$$

where $J^{(t)}=\hat{\kappa }^{(t)}-\hat{\Xi }^{(t)}\hat{\Lambda }^{{(t)}^\mathrm{T}}\hat{\Sigma }^{{(t)}^{-1}}\hat{\mu }^{(t)}$ and $K^{(t)}=\hat{\Xi }^{(t)}\hat{\Lambda }^{{(t)}^\mathrm{T}}\hat{\Sigma }^{{(t)}^{-1}}$. The derivation of $C_{\eta \eta }^{(t+1)}$ is based on the identity $Var\left( \left. \eta \right| Y \right) =E\left( \left. \eta \eta ^\mathrm{T} \right| Y \right) -E\left( \left. \eta \right| Y \right) E\left( \left. \eta ^\mathrm{T} \right| Y \right)$.

Appendix B: The CM-Steps for Regression-Type Coefficients

Consider the updating scheme for $\lambda _{pj}$. If $\left| \lambda _{pj} \right| >0$, the first partial derivative of $\mathcal {M}\left( \left. \theta \right| \hat{\theta }^{(t)} \right)$ with respect to $\lambda _{pj}$ is

$$\begin{aligned} \frac{\partial \mathcal {M}\left( \left. \theta \right| \hat{\theta }^{(t)} \right) }{\partial \lambda _{pj}}= & {} \psi ^{pp}\left( C_{Y\eta }^{(t+1)}\left[ p,j \right] -\nu _{p}e_{\eta }^{(t+1)}[j]-\lambda _{pj}C_{\eta \eta }^{(t+1)}[j,j]-\Lambda [p,-j]C_{\eta \eta }^{(t+1)}[-j,j] \right) \\&+\sum \limits _{p^{'}\ne p} {\psi ^{pp^{'}}\left( C_{Y\eta }^{(t+1)}[ p^{'},j ]-\nu _{p'}e_{\eta }^{(t+1)}[j]{-\Lambda }[ p^{'}, ]C_{\eta \eta }^{(t+1)}[,j] \right) } \\&-\,c_{q}\frac{\partial \rho \left( \left| \lambda _{pj} \right| ,\gamma \right) }{\partial t}\mathrm {sign}\left( \lambda _{pj} \right) , \end{aligned}$$

where $c_{q}$ is the penalization indicator for $\lambda _{pj}$, and $\mathrm {sign}(t)=1\left\{ t>0 \right\} -1\left\{ t<0 \right\}$. With other parameters fixed at their newly updated values, the maximizer $\hat{\lambda }_{pj}^{(t+1)}(\gamma )>0$ should satisfy

$$\begin{aligned} \hat{\lambda }_{pj}^{(t+1)}(\gamma )+w_{q}^{(t*)}\frac{\partial \rho (|\hat{\lambda }_{pj}^{(t+1)}|,\gamma )}{\partial t}\mathrm {sign}\left( \hat{\lambda }_{pj}^{(t+1)}(\gamma ) \right) =\hat{\lambda }_{pj}^{(t+1)}, \end{aligned}$$

where $w_{q}^{(t*)}=\frac{c_{q}}{\hat{\psi }^{{pp}^{(t*)}}C_{\eta \eta }^{(t)}[j,j]}$ and $\hat{\lambda }_{pj}^{(t+1)}=\hat{\lambda }_{pj}^{(t+1)}(0)$ with the expression

$$\begin{aligned} \hat{\lambda }_{pj}^{(t+1)}= & {} \frac{1}{C_{\eta \eta }^{(t)}[j,j]}\left[ \left( C_{Y\eta }^{(t+1)}\left[ p,j \right] -\hat{\nu }_{p}^{(t*)}e_{\eta }^{(t+1)}[j]-\hat{\Lambda }^{(t*)}[p,-j]C_{\eta \eta }^{(t+1)}[-j,j] \right) \right. \\&\left. +\sum \limits _{p'\ne p} {\frac{\hat{\psi }^{{pp'}^{(t*)}}}{\hat{\psi }^{{pp}^{(t*)}}}\left( C_{Y\eta }^{(t+1)}[ p',j ]-\hat{\nu }_{p'}^{(t*)}e_{\eta }^{(t+1)}[j]-\hat{\Lambda }^{(t*)}[p',]C_{\eta \eta }^{(t+1)}[,j] \right) } \right] . \end{aligned}$$

The ${\ell }_{1}$ penalty yields an updating scheme satisfying

$$\begin{aligned} \hat{\lambda }_{pj}^{(t+1)}(\gamma )=\hat{\lambda }_{pj}^{(t+1)}-w_{q}^{(t*)}\gamma \mathrm {sign}\left( \hat{\lambda }_{pj}^{(t+1)}(\gamma ) \right) . \end{aligned}$$

Hence, the solution is the soft-thresholding rule

$$\begin{aligned} \hat{\lambda }_{pj}^{(t+1)}(\gamma )=S\left( \hat{\lambda }_{pj}^{(t+1)},w_{q}^{(t*)}\gamma \right) , \end{aligned}$$

where $S(\theta ,\gamma )=\hbox {sign}(\theta )\max \left\{ \left| \theta \right| -\gamma ,0 \right\}$ (see Donoho & Johnstone, 1994). For the SCAD and the MCP, the updating schemes are relatively complex. The SCAD gives the updating rule

$$\begin{aligned} \hat{\lambda }_{pj}^{(t+1)}(\gamma )=\left\{ {\begin{array}{ll} S\left( \hat{\lambda }_{pj}^{(t+1)},w_{q}^{(t*)}\gamma \right) &{}\quad \hbox {if }\hat{\lambda }_{pj}^{(t+1)}\le \gamma \left( 1+w_{q}^{(t*)} \right) , \\ \frac{S\left( \hat{\lambda }_{pj}^{(t+1)},{w_{q}^{(t*)}\gamma \delta } \big / \left( \delta -1 \right) \right) }{1-w_{q}^{(t*)} \big / \left( \delta -1 \right) }&{}\quad \hbox {if } \gamma \left( 1+w_{q}^{(t*)} \right)<\hat{\lambda }_{pj}^{(t+1)}\le \gamma \delta ,\\ \hat{\lambda }_{pj}^{(t+1)} &{}\quad \hbox {if } \gamma \delta <\hat{\lambda }_{pj}^{(t+1)}.\\ \end{array}} \right. \end{aligned}$$

The solution form can be obtained by setting the first derivative to be zero. The domain for each solution form can be solved based on the continuity of the derivative. Similarly, the MCP yields

$$\begin{aligned} \hat{\lambda }_{pj}^{(t+1)}(\gamma )=\left\{ {\begin{array}{ll} \frac{S\left( \hat{\lambda }_{pj}^{(t+1)},w_{q}^{(t*)}\gamma \right) }{1-w_{q}^{(t*)} \big / \delta } &{} \quad \hbox {if }\hat{\lambda }_{pj}^{(t+1)}\le \gamma \delta , \\ \hat{\lambda }_{pj}^{(t+1)} &{}\quad \hbox {if } \gamma \delta <\hat{\lambda }_{pj}^{(t+1)}. \\ \end{array}} \right. \end{aligned}$$

The CM-step for $\beta _{mj}, \nu _{p}$, or $\alpha _{m}$ is almost the same as this for $\lambda _{pj}$ and can be found in Table 1.

Appendix C: The CM-Steps for Variance and Covariance Parameters

Consider the CM-steps for parameters in $\Psi$. Let $\mathrm {sp}(p)=\left\{ \left. k \right| \psi _{pk}\ne 0,k{\in }\left\{ 1,2,\ldots ,P \right\} \backslash p \right\}$ denote the set of spouses of p and $\epsilon _{-p}=\left( \epsilon _{1},\ldots ,\epsilon _{p-1},\epsilon _{p+1},\ldots ,\epsilon _{P} \right) ^\mathrm{T}$. Given p and $j\in \mathrm {sp}(p)$, the factorization $\mathbb {P}\left( \epsilon \right) =\mathbb {P}\left( \left. \epsilon _{p} \right| \epsilon _{-p}\right) \mathbb {P}\left( \epsilon _{-p} \right)$ shows that the conditional maximization of $\psi _{pj}$ only involves the conditional distribution of $\epsilon _{p}$, a normal distribution with mean $\sum _{k\in \mathrm {sp}(p)} {\psi _{pk}\tilde{\epsilon }_{l(k)}(p)}$ and variance $\tilde{\psi }_{p}^{2}$, where $\tilde{\epsilon }_{l(k)}(p)$ is the l(k)th element of ${\Psi \left[ -p,-p \right] }^{-1}\epsilon _{-p}, l(k)$ is the column index of $\psi _{pk}$ in $\Psi [p,-p]$, and $\tilde{\psi }_{p}^{2}=\psi _{p}^{2}-\Psi [p,-p]{\Psi \left[ -p,-p \right] }^{-1}\Psi \left[ -p,p \right]$. By taking a derivative, $\frac{\partial \mathcal {M}(\theta |\hat{\theta }^{(t)})}{\partial \psi _{pj}} =\frac{1}{\tilde{\psi }_{p}^{2}}\left( u_{l(j)}^{(t*)}(p)-\psi _{pj}v_{l(j)l(j)}^{(t*)}(p)-\sum _{k\in \mathrm {sp}(p)\backslash j} {\psi _{pk}v_{l(j)l(k)}^{(t*)}(p)} \right) -c_{q}\frac{\partial \rho \left( \left| \psi _{pj} \right| ,\gamma \right) }{\partial t}\mathrm {sign}\left( \psi _{pj} \right) ,$ where $u_{l(j)}^{(t*)}(p)$ is the l(j)th element of $\hat{\Psi }^{(t*)}\left[ -p,-p \right] ^{-1}C_{\epsilon \epsilon }^{(t+1)}\left[ -p,p \right] , v_{jk}^{(t*)}(p)$ is the $\left( l(j),l(k) \right)$ element of ${\hat{\Psi }^{(t*)}\left[ -p,-p \right] }^{-1}C_{\epsilon \epsilon }^{(t+1)}\left[ -p,-p \right] {\hat{\Psi }^{(t*)}\left[ -p,-p \right] }^{-1}$, and

$$\begin{aligned} C_{\epsilon \epsilon }^{(t+1)}= & {} C_{YY}-e_{Y}\hat{\nu }^{{(t*)}^\mathrm{T}}-C_{Y\eta }^{(t+1)}\hat{\Lambda }^{{(t*)}^\mathrm{T}}-\hat{\nu }^{(t*)}e_{Y}^\mathrm{T}+\hat{\nu }^{(t*)}\hat{\nu }^{{(t*)}^\mathrm{T}}+\hat{\nu }^{(t*)}e_{\eta }^{{(t+1)}^\mathrm{T}}\hat{\Lambda }^{{(t*)}^\mathrm{T}}\\&-\hat{\Lambda }^{(t*)}C_{Y\eta }^{{(t+1)}^\mathrm{T}}+\hat{\Lambda }^{(t*)}e_{\eta }^{(t+1)}\hat{\nu }^{{(t*)}^\mathrm{T}}+\hat{\Lambda }^{(t*)}C_{\eta \eta }^{(t+1)}\hat{\Lambda }^{{(t*)}^\mathrm{T}}. \end{aligned}$$

Hence, under $\gamma =0, \, \psi _{pj}$ can be updated by

$$\begin{aligned} \hat{\psi }_{pj}^{(t+1)}=\left( u_{l(j)}^{(t*)}(p)-\sum \limits _{k\in \mathrm {sp}(p)\backslash j} {\hat{\psi }_{pk}^{(t*)}v_{l(j)l(k)}^{(t*)}(p)} \right) \big / {v_{l(j)l(j)}^{(t*)}(p)}. \end{aligned}$$

If $\gamma >0, \hat{\psi }_{pj}^{(t+1)}(\gamma )$ can be obtained through the shrinkage formula in Table 1 with $w_{q}^{(t*)}=\frac{c_{q}}{\hat{\tilde{\psi }}_{p}^{{2}^{(t*)}}v_{l(j)l(j)}^{(t*)}(p)}$. Using a similar technique, we obtain

$$\begin{aligned} \hat{\tilde{\psi }}_{p}^{{2}^{(t+1)}}=\left( C_{\epsilon \epsilon }^{(t+1)}\left[ p,p \right] -2\sum \limits _{k\in \mathrm {sp}(p)} {\hat{\psi }_{pk}^{(t*)}u_{l(k)}^{(t*)}(p)} +\sum \limits _{k\in \mathrm {sp}(p)} {\sum \limits _{j\in \mathrm {sp}(p)} \hat{\psi }_{pk}^{(t*)} \hat{\psi }_{pj}^{(t*)}v_{l(k)l(j)}^{(t*)}(p)} \right) , \end{aligned}$$

and then

$$\begin{aligned} \hat{\psi }_{p}^{{2}^{(t+1)}}=\hat{\tilde{\psi }}_{p}^{{2}^{(t+1)}}+\hat{\Psi }^{(t*)}[p,-p]{\hat{\Psi }^{(t*)}\left[ -p,-p \right] }^{-1}\hat{\Psi }^{(t*)}\left[ -p,p \right] . \end{aligned}$$

The CM-steps for parameters in $\Phi$ can be derived similarly by replacing $\epsilon , \Psi$, and $C_{\epsilon \epsilon }^{(t+1)}$ with $\zeta , \Phi$, and $C_{\zeta \zeta }^{(t+1)}$ respectively, where

$$\begin{aligned} C_{\zeta \zeta }^{(t+1)}= & {} C_{\eta \eta }^{(t+1)}-e_{\eta }^{(t+1)}\hat{\alpha }^{{(t*)}^\mathrm{T}}-C_{\eta \eta }^{(t+1)}\hat{\mathrm{B}}^{{(t*)}^\mathrm{T}}-\hat{\alpha }^{(t*)}e_{\eta }^{{(t)}^\mathrm{T}}+\hat{\alpha }^{(t*)}\hat{\alpha }^{{(t*)}^\mathrm{T}}\\&+\,\hat{\alpha }^{(t*)}e_{\eta }^{{(t+1)}^\mathrm{T}}\hat{\mathrm{B}}^{{(t*)}^\mathrm{T}}-\hat{\mathrm{B}}^{(t*)}C_{\eta \eta }^{(t+1)}+\hat{\mathrm{B}}^{(t*)}e_{\eta }^{(t+1)}\hat{\alpha }^{{(t*)}^\mathrm{T}}+\hat{\mathrm{B}}^{(t*)}C_{\eta \eta }^{(t+1)}\hat{\mathrm{B}}^{{(t*)}^\mathrm{T}}. \end{aligned}$$