1 Introduction

Differential item functioning (DIF) is the well-known phenomenon that the probability of a correct response among equally able persons differs in subgroups. For example, the difficulty of an item may depend on the membership to a racial, ethnic or gender subgroup. Then the performance of a group can be lower because these items are related to specific knowledge that is less present in this group. The effect is measurement bias and possibly discrimination, see, for example, Millsap and Everson (1993), Zumbo (1999). Various forms of differential item functioning have been considered in the literature, see, for example, Holland and Wainer (1993), Osterlind and Everson (2009), Rogers (2005). Magis, Bèland, Tuerlinckx, and Boeck (2010) give an instructive overview of the existing DIF detection methods.

We will investigate DIF in item response models, focusing on the Rasch model. In item response models, DIF is considered to be uniform, that is, the probability of correctly answering is uniformly greater for specific subgroups. Test statistics for the identification of uniform DIF have been proposed, among others, by Thissen, Steinberg, and Wainer (1993), Lord (1980), Holland and Thayer (1988), Kim, Cohen, and Park (1995) and Raju (1988). More recently, DIF has been embedded into the framework of mixed models (Van den Noortgate & De Boeck, 2005) and Bayesian approaches have been developed (Soares, Gonçalves, & Gamerman, 2009). Also, the test concepts developed in Merkle and Zeileis (2013) could be helpful to investigate dependence of responses on subgroups.

A severe limitation of existing approaches is that they are typically limited to the consideration of few subgroups. Most often, just two subgroups have been considered with one group being fixed as the reference group. The objective of the present paper is to provide tools that allow for several groups but also for continuous variables like age to induce differential item functioning. We propose a model that lets the item difficulties to be modified by a set of variables that can potentially cause DIF. The model necessarily contains a large number of parameters which raises severe estimation problems. But estimation problems can be solved by regularized estimation procedures. Although alternative strategies could be used we focus on regularization by penalization, using penalized maximum likelihood (ML) estimates. The procedure allows to identify the items that suffer from DIF and investigate which variables are responsible.

More recently, Strobl, Kopf, and Zeileis (2013) proposed a new approach that is also able to handle several groups and continuous variables but uses quite different estimation procedures. The work stimulated our research and we will compare our method to this alternative approach.

In Section 2, we present the model, in Section 3, we show how the model can be estimated. Then we illustrate the fitting of the model by use of simulation studies and real data examples.

2 Differential Item Functioning Model

We will first consider the binary Rasch model and then introduce a general parametric model for differential item functioning.

2.1 The Binary Rasch Model

The most widespread item response model is the binary Rasch model (Rasch 1960). It assumes that the probability that a participant in a test scores on an item is determined by the difference between two latent parameters, one representing the person and one representing the item. In assessment tests, the person parameter refers to the ability of the person and the item parameter to the difficulty of the item. More generally, the person parameter refers to the latent trait the test is supposed to measure. With X pi ∈{0,1}, the probability that person p solves item i is given by

$$P(X_{pi}=1) =\frac{\exp(\theta_p -\beta_i)}{1+\exp(\theta_p -\beta _i)} \quad p=1,\dots,P,i=1,\dots,I, $$

where θ p is the person parameter (ability) and β i is the item parameter (difficulty). A more convenient form of the model is

$$ \log\biggl(\frac{P(X_{pi}=1)}{P(X_{pi}=0)} \biggr)=\theta_p - \beta_i, $$
(1)

where the left-hand side represents the so-called logits, \(\operatorname {Logit}(P(X_{pi}=1))=\log({P(X_{pi}=1)}/ {P(X_{pi}=0}))\). It should be noted that the parameters are not identifiable. Therefore, one has to fix one of the parameters. We choose θ P =0, which yields a simple representation of the models to be considered later.

Under the usual assumption of conditional independence given the latent traits, the maximum likelihood (ML) estimates can be obtained within the framework of generalized linear models (GLMs). GLMs for binary responses assume that the probability π pi =P(X pi =1) is given by \(g(\pi_{pi})= \boldsymbol {x}_{pi}^{T}\boldsymbol {\delta }\), where g(⋅) is the link function and x pi is a design vector linked to person p and item i. The link function is directly seen from model representation (1). The design vector, which codes the persons and items and the parameter vector are seen from

$$\log\biggl(\frac{P(X_{pi}=1)}{P(X_{pi}=0)} \biggr)=\theta_p - \beta_i=\boldsymbol{1}_{P(p)}^T \boldsymbol {\theta }- \boldsymbol{1}_{I(i)}^T {\boldsymbol {\beta }}, $$

where \(\boldsymbol{1}_{P(p)}^{T}=(0,\dots,0,1,0,\dots,0)\) has length P−1 with 1 at position p, \(\boldsymbol{1}_{I(i)}^{T} =(0,\dots,0,1, 0,\ldots,0)\) has length I with 1 at position i, and the parameter vectors are θ=(θ 1,…,θ P−1), β=(β 1,…,β I ) yielding the total vector δ T=(θ T,β T). The design vector linked to person p and item i is given by \(\boldsymbol {x}_{pi}^{T}=(\boldsymbol{1}_{P(p)}^{T},-\boldsymbol{1}_{I(i)}^{T})\).

GLMs are extensively investigated in McCullagh and Nelder (1989), short introductions with the focus on categorical data are found in Agresti (2002) and Tutz (2012). The embedding of the Rasch model into the framework of generalized linear models has the advantage that software that is able to fit GLMs and extensions can be used to fit models very easily.

2.2 A General Differential Item Functioning Model

In a general model that allows the item parameters to depend on covariates that characterize the person, we will replace the item parameter by a linear form that includes a vector of explanatory variables. Let x p be a person-specific parameter that contains, for example, gender, race, but potentially also metric covariates like age. If β i is replaced by \(\beta_{i}+\boldsymbol {x}^{T}_{p} \boldsymbol {\gamma }_{i}\) with item-specific parameter γ i , one obtains the model

$$ \log\biggl(\frac{P(X_{pi}=1)}{P(X_{pi}=0)} \biggr)= \theta_p - \bigl(\beta_i+\boldsymbol {x}^T_p \boldsymbol {\gamma }_i \bigr). $$
(2)

For illustration, let us consider the simple case where the explanatory variable codes a subgroup like gender, which has two possible values. Let x p =1 for males and x p =0 for females. If item i functions differently in the subgroups, one has the item parameters

$$\beta_i+\gamma_i\ \mathrm{for}\ \mathrm{males}\ \mathrm{and} \ \beta_i \text{ for females}. $$

Then γ i represents the difference of item difficulty between males and females. If one prefers a more symmetric representation, one can choose x p =1 for males and x p =−1 for females obtaining

$$\beta_i+\gamma_i \text{ for males and} \ \beta_i-\gamma_i \text{ for females}. $$

Then γ i represents the deviation of the subpopulations in item difficulty from the baseline difficulty β i . Of course, in an item that does not suffer from differential item functioning, one has γ i =0 and, therefore, items for males and females are equal.

The strength of the general model (2) is that also metric covariates like age can be included. Thinking of items that are related to knowledge on computers or modern communication devices the difficulty may well vary over age. One could try to build more or less artificial age groups, or, as we do, assume linear dependence of the logits. With x p denoting age in years the item parameter is \(\beta_{i}+\operatorname{age} \gamma_{i} \). If γ i =0, the item difficulty is the same for all ages.

The multigroup case is easily incorporated by using dummy-variables for the groups. Let R denote the group variable, for example, race with k categories, that is, R∈{1,…,k}. Then one builds a vector (x R(1),…,x R(k−1)), where components are defined by x R(j)=1 if R=j and x R(j)=0 otherwise. The corresponding parameter vector γ i has k−1 components \(\boldsymbol {\gamma }_{i}^{T}=(\gamma_{i1}, \dots,\gamma_{i,k-1})\). Then the parameters are

$$\beta_i+\gamma_{i1} \ \mathrm{in}\ \mathrm{group}\ 1, \quad\dots\quad\beta_i+\gamma_{i,k-1},\ \mathrm{in}\ \mathrm{group}\ k-1,\quad\beta_i \ \mathrm{in}\ \mathrm{group}\ k. $$

In this coding the last category, k, serves as reference category, and the parameters γ i1,…,γ i,k−1 represent the deviations of the subgroups with respect to the reference category.

One can also use symmetric coding where one assumes \(\sum_{j=1}^{k}\gamma_{ij}=0\) yielding parameters

$$\beta_i+\gamma_{i1} \ \mathrm{in}\ \mathrm{group}\ 1, \quad\dots\quad\beta_i+\gamma_{i,k-1},\ \mathrm{in}\ \mathrm{group}\ k-1,\quad\beta_i +\gamma_{ik}\ \mathrm{in}\ \mathrm{group}\ k. $$

In effect, one is just coding a categorical predictor in 0–1-coding or effect coding; see, for example, Tutz (2012).

The essential advantage of model (2) is that the person-specific parameter includes all the candidates that are under suspicion to induce differential item functioning. Thus, one has a vector that contains age, race, gender and all the other candidates. If one component in the vector γ i is unequal zero, the item is group-specific. The parameter shows which of the variables is responsible for the differential item functioning. The model includes not only several grouping variables, but also metric explanatory variables.

The challenge of the model is to estimate the large number of parameters and to determine which parameters have to be considered as unequal zero. The basic assumption is that most of the parameters do not depend on the group, but some can. One wants to detect these items and know which one of the explanatory variables is responsible. For the estimation, one has to use regularization techniques that are discussed in the Section 3.

2.2.1 Identifiability Issues

The general model uses the predictor \(\eta_{pi}=\theta_{p} -\beta_{i}-\boldsymbol {x}^{T}_{p} \boldsymbol {\gamma }_{i}\) when person p tries to solve item i. Even if one of the basic parameters is fixed, say, β I =0, the model can be reparameterized by use of a fixed vector c in the form

$$\begin{aligned} \eta_{pi}&=\theta_p -\beta_i- \boldsymbol {x}^T_p \boldsymbol {\gamma }_i= \theta_p - \beta_i-\boldsymbol {x}^T_p (\boldsymbol {\gamma }_i- \boldsymbol {c})-\boldsymbol {x}^T_p \boldsymbol {c}=\tilde{\theta}_p - \beta_i-\boldsymbol {x}^T_p \tilde{\boldsymbol {\gamma }}_i, \end{aligned}$$

where \(\tilde{\theta}_{p}=\theta_{p}-\boldsymbol {x}^{T}_{p} \boldsymbol {c}\) and \(\tilde{\boldsymbol {\gamma }}_{i}=\boldsymbol {\gamma }_{i}-\boldsymbol {c}\). The parameter sets {θ p ,β i ,γ i } and \(\{ \tilde{\theta}_{p}, \beta_{i},\tilde{\boldsymbol {\gamma }}_{i}\}\) describe the same model, the parameters are just shifted by \(\boldsymbol {x}^{T}_{p} \boldsymbol {c}\) in the case of θ-parameters and c in the case of γ-parameters. In other words, the model is overparameterized and parameters are not identifiable. Additional constraints are needed to make the parameters identifiable. However, the choice of the constraints determines which items are considered as DIF-inducing items. Let us consider a simple example with a binary variable x p , which codes, for example, gender. Then the parameters are identifiable if one sets one β-parameter and one γ-parameters to zero. With six items and the unconstrained parameters (γ 1,…,γ 6)=(5,5,5,3,3,3) the constraint γ 1=0 yields the identifiable parameters (γ 1,…,γ 6)=(0,0,0,−2,−2,−2), whereas the constraint γ 6=0 yields the identifiable parameters (γ 1,…,γ 6)=(2,2,2,0,0,0). In the first case, one uses the transformation constant c=5, in the second case the transformation constant c=3. When the θ-parameters are transformed accordingly, one obtains two equivalent parameterizations. But in the first parameterization, the second three items show DIF, and in the second parameterization the first three items show DIF. It cannot be decided which of the item sets shows DIF because both parameterizations are valid. The model builder fixes by the choice of the constraint which set of items shows DIF. But this basic identifiability problem seems worse than it is. When fitting a Rasch model, one wants to identify the items that deviate from the model but assumes that the model basically holds for the majority of items. Thus, one aims at identifying the maximal set of items for which the model holds. Thus, if, for example, the unconstrained items can be given by (γ 1,…,γ 6)=(5,5,3,3,3,2), the choice γ 3=0 makes the items 3,4,5 Rasch-compatible and the rest has DIF. In contrast, γ 6=0 makes item 6 Rasch-compatible but the rest has DIF. Therefore, a natural choice is γ 3=0, where it should be emphasized again that any choice is legitimate. The fitting procedure proposed in the following will automatically identify the maximal set of items that is Rasch-compatible. We will come back to that in the following, but give here general conditions for the identifiability of items.

In the general model with predictor \(\eta_{pi}=\theta_{p} -\beta_{i}-\boldsymbol {x}^{T}_{p} \boldsymbol {\gamma }_{i}\), a set of identifiability conditions is

  1. (1)

    Set β I =0, \(\boldsymbol {\gamma }_{I}^{T}=(0,\dots,0)\) (or for any other item).

  2. (2)

    The matrix X with rows \((1,\boldsymbol {x}^{T}_{1}),\dots,(1,\boldsymbol {x}^{T}_{P})\) has full rank.

(for a proof, see the Appendix). The first condition means that for one item the β and the γ-parameters have to be fixed. It serves as a reference item in all populations. The second condition is a general condition that postulates that the explanatory variables have to contain enough information to obtain identifiable parameters. It is a similar condition as is needed in common regression models. It should be noted that the condition is general; the explanatory variables can be continuous or categorical. In the latter case, the matrix X contains the dummy variables that code the categorical variable. As in regular regression, in particular, highly correlated continuous covariates affect the rank of the design matrix and might yield unstable estimates. In the extreme case, estimates are not unique because they are not identifiable. Then one might reduce the set of covariates. In the case where estimates still exist, but are unstable, nowadays regularization method are in common use. A specific form of regularization is also used in the following.

3 Estimation by Regularization

3.1 Maximum Likelihood Estimation

Let the data be given by (X pi ,x p ), p=1,…,P,i=1,…,I. Maximum likelihood estimation of the model is straightforward by embedding the model into the framework of generalized linear models. By using again the coding for persons and parameters in the parameter vectors 1 P(p) and 1 I(i), the model has the form

$$\begin{aligned} \log\biggl(\frac{P(X_{pi}=1)}{P(X_{pi}=0)} \biggr)&= \theta_p - \beta_i-\boldsymbol {x}^T_p \boldsymbol {\gamma }_i \\ &=\boldsymbol{1}_{P(p)}^T \boldsymbol {\theta }- \boldsymbol{1}_{I(i)}^T {\boldsymbol {\beta }}-\boldsymbol {x}^T_p \boldsymbol {\gamma }_i. \end{aligned}$$

With the total vector given by \((\boldsymbol {\theta }^{T},{\boldsymbol {\beta }}^{T},\boldsymbol {\gamma }_{1}^{T},\dots,\boldsymbol {\gamma }_{I}^{T})\), one obtains for observation X pi the design vector \((\boldsymbol{1}_{P(p)}^{T},-\boldsymbol{1}_{I(i)}^{T},0,0,,\dots,-\boldsymbol {x}_{p}^{T}\dots,0,0)\), where the component \(-\boldsymbol {x}_{p}^{T}\) corresponds to the parameter γ i .

Although ML estimation is straightforward, estimates will exist only in very simple cases, for example, if the explanatory variable codes just two subgroups. In higher dimensional cases, ML estimation will deteriorate and no estimates or selection of parameters are available.

3.2 Penalized Estimation

In the following, we will consider regularization methods that are based on penalty terms. The general principle is, not to maximize the log-likelihood function, but a penalized version. Let α denote the total vector of parameters, in our case \(\boldsymbol {\alpha }^{T}=(\boldsymbol {\theta }^{T},{\boldsymbol {\beta }}^{T},\boldsymbol {\gamma }_{1}^{T},\dots,\boldsymbol {\gamma }_{I}^{T})\). Then one maximizes the penalized log-likelihood

$$l_p(\boldsymbol {\alpha }) = l(\boldsymbol {\alpha }) - \lambda J(\boldsymbol {\alpha }), $$

where l(⋅) is the common log-likelihood of the model and J(α) is a penalty term that penalizes specific structures in the parameter vector. The parameter λ is a tuning parameter that specifies how serious the penalty term has to be taken. A widely used penalty term in regression problems is J(α)=α T α, that is, the squared length of the parameter vector. The resulting estimator is known under the name ridge estimate, see Hoerl and Kennard (1970) for linear models and Nyquist (1991), Segerstedt (1992), LeCessie (1992) for the use in GLMs. Of course, if λ=0 maximization yields the ML estimate. If λ>0, one obtains parameters that are shrunk toward zero. In the extreme case λ→∞, all parameters are set to zero. The ridge estimator with small λ>0 stabilizes estimates but does not select parameters, which is the main objective here. Penalty terms that are useful because they enforce selection are L 1-penalty terms.

Let us start with the simple case of a univariate explanatory variable, which, for example, codes gender. Then the proposed lasso penalty for differential item functioning (DIF-lasso) is given by

$$J \bigl(\boldsymbol {\theta }^T,{\boldsymbol {\beta }}^T,\boldsymbol {\gamma }_1^T, \dots,\boldsymbol {\gamma }_I^T \bigr) =\sum _{i=1}^I | \gamma_i |, $$

which is a version of the L 1-penalty or lasso (for least absolute shrinkage and selection operator). The lasso was propagated by Tibshirani (1996) for regression models, and has been studied intensively in the literature; see, for example, Fu (1998), Osborne, Presnell, and Turlach (2000), Knight and Fu (2000), Fan and Li (2001), and Park and Hastie (2007). It should be noted that the penalty term contains only the parameters that are responsible for differential item functioning, therefore, only the parameters that carry the information on DIF are penalized. Again, if λ=0 maximization yields the full ML estimate. For very large λ, all the γ-parameters are set to zero. Therefore, in the extreme case λ→∞, the Rasch model is fitted without allowing for differential item functioning. The interesting case is in between, when λ is finite and λ>0. Then the penalty enforces selection. Typically, for fixed λ, some of the parameters are set to zero while others take values unequal zero. With a carefully chosen tuning parameter λ, the parameters that yield estimates \(\hat{\gamma}_{i}>0\) are the ones that show DIF.

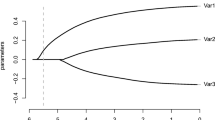
For illustration, we consider a Rasch model with 10 items and 70 persons. Among the 10 items, three suffer from DIF induced by a binary variable with parameters γ 1=2, γ 2=−1.5, γ 3=−2. Figure 1 shows the coefficient build-ups for the γ-parameters for one data set, that is, how the parameters evolve with decreasing tuning parameter λ. In this data set, ML estimates existed. We do not use λ itself on the x-axis but a transformation of λ that has better scaling properties. Instead of giving the λ-values on the x-axis, we scale it by \(\lVert \hat{\boldsymbol {\gamma }}\rVert /\max \|\hat{\boldsymbol {\gamma }}\|\), where \(\max \|\hat{\boldsymbol {\gamma }}\|\) corresponds to the L 2-norm of the maximal obtainable estimates, that is, the ML estimates. On the right side of Figure 1 one sees the estimates for λ=0 (\(\lVert \hat{\boldsymbol {\gamma }}\rVert /\max \|\hat{\boldsymbol {\gamma }}\|=1\)), which correspond to the ML estimates for the DIF model. At the left end, all parameters are shrunk to zero, corresponding to the value of λ, where the simple Rasch model without DIF is fitted. Thus, the figure shows how estimates evolve over diminishing strength of regularization. At the right end, no regularization is exerted, at the left side regularization is so strong that all γ-parameters are set to zero. The vertical line shows the tuning parameter selected by BIC (see below), which represents the best estimate for this selection criterion. If one uses this criterion, all items with DIF (dashed lines) are selected, obtaining estimates unequal zero. But for all items without DIF the estimates are zero. Therefore, in this data set, identification was perfect.

Figure 1.
figure 1

Coefficient build-up for Rasch model with DIF induced by binary variable, dashed lines are the items with DIF, solid lines are the items without DIF.

Full size image

In the general case with a vector of covariates that potentially induce DIF, a more appropriate penalty is a modification of the grouped lasso (Yuan & Lin, 2006), Meier, van de Geer, & Bühlmann, 2008. Let \(\boldsymbol {\gamma }_{i}^{T}=(\gamma_{i1},\dots,\gamma_{im})\) denote the vector of modifying parameters of item i, where m denotes the length of the person-specific covariates. Then the group lasso penalty for item differential functioning (DIF-lasso) is

$$J \bigl(\boldsymbol {\theta }^T,{\boldsymbol {\beta }}^T,\boldsymbol {\gamma }_1^T, \dots,\boldsymbol {\gamma }_I^T \bigr) =\sum _{i=1}^I \lVert \boldsymbol {\gamma }_i \rVert , $$

where \(\lVert \boldsymbol {\gamma }_{i}\rVert =(\gamma_{i1}^{2}+\dots+\gamma_{im}^{2})^{1/2}\) is the L 2-norm of the parameters of the ith item with m denoting the length of the covariate vector. The penalty encourages sparsity in the sense that either \(\hat{\boldsymbol {\gamma }}_{i}=\textbf{0}\) or γ is ≠0 for s=1,…,m. Thus, the whole group of parameters collected in γ i is shrunk simultaneously toward zero. For a geometrical interpretation of the penalty, see Yuan and Lin (2006). The effect is that in a typical application only some of the parameters get estimates \(\hat{\boldsymbol {\gamma }}_{i}\neq\textbf{0}\). These correspond to items that show DIF.

3.2.1 Choice of Penalty Parameter

An important issue in penalized estimation is the choice of the tuning parameter λ. In our case, it determines the numbers of items identified as inducing DIF. Therefore, it determines if all items with DIF are correctly identified and also if some are falsely diagnosed as DIF-items. To find the final estimate in the solution path, it is necessary to balance the complexity of the model and the data fit. However, one problem is to determine the complexity of the model, which in penalized estimation approaches is not automatically identical to the number of parameters in the model. We worked with several criteria for the selection of the tuning parameter, including cross-validation and AIC criteria with the number of parameters determined by the degrees of freedom for the lasso (Zou, Hastie, & Tibshirani, 2007). A criterion that yielded a satisfying balancing and which has been used in the simulations and applications is the BIC (Schwarz 1978) with the degrees of freedom for the group lasso penalty determined by a method proposed by Yuan and Lin (2006). Here, the degrees of freedom (of penalized parameters γ) are approximated by

$$ \tilde{df}_{\boldsymbol{\gamma}}(\lambda)=\sum\limits _{i=1}^II \bigl(\big\| \boldsymbol{\gamma}_i(\lambda)\big\| >0 \bigr)+ \sum \limits _{i=1}^I\frac{\lVert \boldsymbol{\gamma}_i(\lambda)\rVert }{\lVert \boldsymbol {\gamma}_i^{ML}\rVert }(m-1). $$

Since the person parameters and the item parameters are unpenalized, the total degrees of freedom are \(df(\lambda)=I+P+\tilde{df}_{\boldsymbol{\gamma}}(\lambda)-1\). The corresponding BIC is determined by

$$ \mathit{BIC}(\lambda)=-2\cdot l(\boldsymbol {\alpha }) + df(\lambda)\cdot\log(P \cdot I), $$

where l(α) is the log-likelihood of the current parameter vector α.

3.2.2 Identifiability and Estimation

As demonstrated at the end of Section 2, the model without constraints is not identifiable. Moreover, the identification of DIF-items depends on the constraints that are used. Because of the basic identifiability problem, one can define few or many items as DIF-items. The aim to find the maximal set of Rasch-compatible items with a small set of items characterized as DIF- items is strongly supported by the regularization approach. We first fit the full model without constraints. Because of the regularization term the parameters are estimable, although not identifiable, see Friedman, Hastie, and Tibshirani (2010), where this procedure has been used in multinomial regression models. With growing smoothing parameter more and more items are characterized as not being compatible with the Rasch model with the items that have the strongest deviation from the Rasch model being the first ones that show in the coefficient build-ups. In all cases that were considered, the value of the smoothing parameter chosen by our criterion was such that not all parameters showed DIF. Most often just few parameters had estimates \(\hat{\boldsymbol {\gamma }}_{i} \ne0\). Therefore, one of the items with \(\hat{\boldsymbol {\gamma }}_{i} = 0\) is chosen and used as reference. By rearranging items, one of these items is denoted by I and one sets β I =0, \(\boldsymbol {\gamma }_{I}^{T}=(0,\dots,0)\), which is obtained by computing \(\hat{\beta}_{i}-\hat{\beta}_{I}\) for the item difficulties and \(\hat{\boldsymbol {\gamma }}_{i}-\hat{\boldsymbol {\gamma }}_{I}\) for the γ-parameters, where \(\hat{\beta}_{i}\), \(\hat{\boldsymbol {\gamma }}_{i}\) denote the estimates for the full model. This yields the identifiable parameters that are considered in the following simulations and applications. Of course, in the simulations the true values are centered around the same item.

3.2.3 Further Remarks

We focus on penalized ML estimation. Regularized estimation with penalty terms has the advantage that the penalty term is given explicitly and, therefore, it is known how estimates are shrunk. An alternative procedure that could be used is boosting. It selects relevant variables by using weak learners and regularization is obtained by early stopping; see, for example, Bühlmann and Hothorn (2007), and for logistic models Tutz and Binder (2006). Although the form of regularization is not given in an explicit form it typically is as efficient as regularization with corresponding penalty terms. Also mixed model methodology as used by Soares, Gonçalves, and Gamerman (2009) to estimate DIF can be combined with penalty terms that enforce selection. However, methodology is in its infancy; see, for example, Ni, Zhang, and Zhang (2010), Bondell, Krishna, and Ghosh (2010).

4 The Fitting Procedure at Work

In the present section, it is investigated if the procedure is able to detect the items that show DIF. This is done in a simulation study where it is known which items are affected by DIF.

4.1 Illustration

For illustration, we will first consider several examples. In the first example, we have 70 persons, 10 items, three with DIF (\(\boldsymbol{\gamma}_{1}^{T}=(-1,0.8,1)\), \(\boldsymbol{\gamma}_{2}^{T}=(-1.1,0.5,0.9)\), \(\boldsymbol{\gamma}_{3}^{T}=(1,-1,-1)\), \(\boldsymbol{\gamma}_{4}^{T}=\cdots=\boldsymbol{\gamma}_{10}^{T}=(0,0,0)\)). The upper panel in Figure 2 shows the coefficient build-ups for an exemplary data set. Now one item is represented by three lines, one for each covariate. Again, items with DIF are given by nonsolid lines and items with DIF by solid lines. In this data set, the BIC criterion selects all the items with DIF and sets all items without DIF to zero.

Figure 2.
figure 2

Coefficient build-up for Rasch model with DIF induced by three variables, dashed lines are the items with DIF, solid lines are the items without DIF, upper panel shows perfect identification, in the lower panel identification is not perfect.

Full size image

In the lower panel, one sees a data set where identification is not perfect. It is seen that some items without DIF are falsely considered as inducing DIF. But also in this data set the items with DIF are the first ones to obtain estimates unequal zero when penalization is relaxed. The items without DIF obtain estimates unequal zero but estimates are very small.

An example without DIF is seen in Figure 3. The setting is the same as before (P=70, I=10), but all γ-parameters are set to zero. It is seen that the procedure also works well in the case of the Rasch model because all γ-parameters are estimated as zero.

Figure 3.
figure 3

Coefficient build-up for Rasch model without DIF .

Full size image

For further illustration, we show in the upper panel of Figure 4 the estimates of 100 simulated data sets for the same setting as in Figure 2. The box-plots show the variability of the estimates, the stars denote the underlying true values. The β-parameters in the left block represent the basic item parameter, which are estimated rather well. In the next block, the modifying parameters γ is are shown for items with DIF and in the last block the modifying parameters for items without DIF are shown. In this last block, the stars that denote true values are omitted since they are all zero. Overall, the estimates of the basic β-parameters (first block) and the items without DIF (third block) are quite close to their true values. In particular, the estimates of the parameters that correspond to items without DIF are zero or close to zero and are frequently diagnosed as not suffering from DIF. The γ-parameters in the middle block, which correspond to items with DIF, are distinctly unequal zero and, therefore, the DIF-items are identified. But the latter estimates are downward biased because of the exerted penalization, which shrinks the estimates.

Figure 4.
figure 4

Upper panel: Box plots of estimates for Rasch model with DIF induced by three variables, stars denote true values. Lower panel: the same model with a final ML step on selected items.

Full size image

The bias can be removed and estimators possibly improved by an additional refit. The fit of the model in combination with the selection of the tuning parameter yields the set of items that are considered as suffering from DIF. To avoid shrinkage and bias, one can compute a final unpenalized ML fit of the reduced model that contains only the parameters that have been selected as being nonzero. In the lower panel of Figure 4, the estimates with a final refit step are given. While the estimation of the basic β-parameters has hardly changed, the downward bias in item parameters for items with DIF is removed. However, the estimates of parameters for items without DIF automatically suffers. If one of these items is diagnosed as DIF-item, the final ML-fit yields larger values than the penalized estimate. The reduction of bias comes with costs. As is seen from Figure 4 the variability for the procedure with an additional ML step is larger. Penalization methods like lasso typically have two effects, selection and shrinkage. By shrinking estimates extreme values are avoided and standard errors are smaller but bias is introduced. The final ML estimate aims at a new balance of variance and bias but keeps the selection effect.

4.2 Simulation Scenarios

In the following, we give results for selected simulation scenarios based on 100 simulations. The person parameters are drawn from a standard normal distribution and we consider scenarios with varying strength of DIF. The item parameters have the form \(\beta_{i}+\boldsymbol {x}^{T}_{p} \boldsymbol {\gamma }_{i}\). We always work with standardized person characteristics x p , that is, the components have variance 1. A measure for the strength of DIF in an item is the variance \(V_{i}=\operatorname {var}(\beta_{i}+\boldsymbol {x}^{T}_{p} \boldsymbol {\gamma }_{i})\), which for independent components has the simple form \(V_{i}=\sum_{j} \gamma_{ij}^{2}\). For standardization, it is divided by the number of covariates m. The average of \(\frac{1}{m}\sqrt{V_{i}}\) over the items with DIF gives a measure of the strength of DIF in these items. The implicitly used reference value is the standard deviation of the person parameters, which is 1. We use three different strengths of DIF: strong, medium, and weak. For the parameters of strong DIF, the DIF strength is 0.25. For medium and weak DIF, the parameters from the strong DIF setting are multiplied by 0.75 and 0.5, respectively. Accordingly, the DIF strengths for medium and weak are 0.1875 and 0.125. An overall measure of DIF in a setting is the average of \(\frac{1}{m}\sqrt{V_{i}}\) over all items. For the strong scenario with 20 items, one obtains 0.05, for the medium and weak 0.038 and 0.025, respectively.

When calculating mean squared errors, we distinguish between person and item parameters. For person parameters, it is the average over simulations of \(\sum_{p} (\hat{\theta}_{p}-\theta_{p})^{2}/P\). For items it is the squared difference between the estimated item difficulty and the actual difficulty \(\sum_{p}\sum_{i} [(\beta_{i}+\boldsymbol {x}^{T}_{p} \boldsymbol {\gamma }_{i})-(\hat{\beta}_{i}+\boldsymbol {x}^{T}_{p} \hat{\boldsymbol {\gamma }}_{i})]^{2}/(I\cdot P)\).

One of the main objectives of the method is the identification of items with DIF. The criteria by which the performance of the procedure can be judged are the hits or true positives (i.e., the number of correctly identified items with DIF) and the false positives (i.e., the number of items without DIF that are falsely diagnosed as items with DIF).

The settings considered in the following are:

  • Setting 1: 250 persons, 20 items, 4 with DIF on 5 variables, parameters (strong DIF): \(\boldsymbol{\gamma}_{1}^{T}=(-0.8,0.6,0,0,0.8)\), \(\boldsymbol{\gamma}_{2}^{T}=(0,0.8,-0.7,0,0.7)\), \(\boldsymbol{\gamma}_{3}^{T}=(0.6,0,0.8,-0.8,0)\), \(\boldsymbol{\gamma}_{4}^{T}=(0,0,0.8,0.7,-0.5)\), \(\boldsymbol{\gamma}_{5}^{T}=\cdots=\boldsymbol{\gamma}_{20}^{T}=(0,0,0,0,0)\), two variables binary, three standard normally distributed.

  • Setting 2: 500 persons, items as in setting 1.

  • Setting 3: 500 persons, 20 items, 8 with DIF on 5 variables, items 1–4 as in setting 1, items 5–8 same as items 1–4.

  • Setting 4: 500 persons, 40 items, 8 with DIF, items 1–8 same as in setting 3.

  • Setting 5: same as Setting 2, but the person abilities differ along with the first (binary) covariate (θ|x 1=1∼N(1,1), θ|x 1=0∼N(0,1)).

Settings 1–4 vary in the number of persons and the number of items with and without DIF. In all of them, the person parameters are not linked to the predictor. As one reviewer of the paper remarked, it can occur in practice that there is correlation between the abilities of persons and the grouping variable. Therefore, it is of interest if the performance of DIF-detection suffers from correlation. The last setting, setting 5, explicitly includes correlation between the abilities and the first, binary predictor. Persons with predictor value x 1=1 are assumed to have higher abilities.

In Table 1, the MSEs as well as the hits and false positive rates are given for the fit of the Rasch model (without allowing for DIF), the DIF-lasso and the DIF-lasso with refit. It is seen that the accuracy of the estimation of person parameters does not depend strongly on the strength of DIF. It is quite similar for strong and medium DIF and slightly worse for weak DIF. Also, the fitting of the Rasch model or DIF-lasso yields similar estimates of person parameters. The refit procedure, however, yields somewhat poorer estimates in terms of MSE. The estimation of item parameters shows a different picture. DIF-lasso distinctly outperforms the Rasch model, in particular if DIF is strong the MSE is much smaller. The refit is better than the normal DIF-lasso in all of the settings except one. Therefore, when the focus is on the estimation of item parameters, the refit can be recommended for a more precise and unbiased estimation.

Table 1. MSEs for the simulation scenarios (upper panel) and average rates of hits/false positives (lower panel).
Full size table

The effect of correlation between abilities and predictors is investigated separately. The settings 2 and 5 use the same number of persons and parameters, but in setting 5 a binary covariate is highly correlated with the person abilities. The MSEs can be seen from Table 1. In Figure 5, the MSEs for the two settings are compared to each other for strong DIF with setting 2 being depicted in the left box plot and setting 5 in the right box plot. The upper panel shows the box plots for the MSEs of the person parameters, the lower for the item parameters. Again, it can be seen that for the person parameters the refit performs a little worse than the regular DIF-lasso and the Rasch model. The correlation in setting 5 makes estimation harder for all three methods but the estimation of person parameters does not suffer strongly. From the lower panel, which shows the MSEs for the item difficulties, it is seen that the DIF-lasso strongly outperforms the Rasch model and that the refit improves the estimation of the item-specific parameters. As for person parameters, the correlation affects the accuracy of estimation but not very seriously. Estimation accuracy in terms of MSE does not suffer strongly from the presence of correlation.

Figure 5.
figure 5

Box plots of MSEs for setting 2 (left box plot) and setting 5 (right box plot) for strong DIF.

Full size image

Since our focus is on the identification of DIF-items the hits and false positive rates are of particular interest. It is seen from the lower panel of Table 1 that the procedure works well. If DIF is strong the hit rate is 1 or close to 1, for medium DIF one needs more persons in the setting to obtain a hit rate of 1. Of course, for weak DIF identification is harder and one will not always find all the items with DIF. For 250 persons and weak DIF, there is not enough information anymore to have an acceptable selection performance. But the hit rate increases strongly when the number of persons is increased to 500 persons (setting 2) instead of 250 persons (setting 1).

One nice result is that the false positive rate is negligible. Although not all items with DIF may be found, it hardly occurs that items without DIF are falsely diagnosed. Only in setting 3 the false positive rate is slightly increased. When comparing the settings 2 and 5, which only differ because in the latter correlation between abilities and predictors is present, it is seen that the hit rate suffers only for weak DIF. For strong and medium DIF, the performance is very similar. Together with the results for the MSEs, DIF-lasso seems to perform rather well also in the case where the performance of persons is linked to a binary covariate. Differences in abilities and DIF are well separated.

4.3 Comparison with Methods for Multiple Groups

The method proposed here works for vector-valued predictors, but can be compared to existing methods that are limited to the handling of groups. Most of the established methods for detection of uniform DIF use just two groups representing, for example, gender. Magis, Bèland, Tuerlinckx, and Boeck (2010) set up a nice framework and shortly introduce into the existing DIF methods. For the case of one binary covariate, they consider the Mantel–Haenszel (MH) method, developed by Mantel and Haenszel (1959) and applied to DIF by Holland and Thayer (1988), the method of logistic regression (Swaminathan & Rogers, 1990) and Lord’s χ 2-test (Lord 1980). MH is a χ 2-test where the performances of the groups are tested against each other separately for all items, conditional on the total test score. For the method of logistic regression, a logit model is fitted using the total test score, the group membership and an interaction of test score and group membership as covariates. The response is the probability of a person to score on an item. For detection of uniform DIF, the parameter for the group membership is tested by a likelihood ratio or a Wald test. Lord’s χ 2-test uses the null-hypothesis that the item parameters are equal within both groups. The parameters are estimated by the maximum likelihood principle separately for the groups, then they are tested against each other by a χ 2-test. The methods can be generalized to the case of multiple groups. This has been done by Somes (1986) and Penfield (2001) for MH, Magis et al. (2011) for logistic regression and Kim et al. (1995) for Lord’s χ 2 test. In R (R Core Team 2012), these methods are implemented in the package difR (Magis, Beland, & Raiche, 2013), which is also described in Magis et al. (2010).

Since we are interested in the performance in the case of more complex predictors, we give the results of a simulation study where DIF in more than two groups is investigated. For the comparison, we use the implementation in difR (Magis et al. 2013). In the simulation study, three different settings are considered. The definition of the DIF strengths strong, medium, and weak is equivalent to the previous simulations. Each setting is run 100 times. We use P=500 persons and I=20 items. The groups are defined by a factor with q categories, which is either q=5 or q=6. For the DIF-lasso approach, this factor is represented by q−1 binary dummy variables. For the reference methods, we have the case of a q-groups comparison. The number of DIF-items is either n DIF=4 or n DIF=8.

Table 2 shows the results for the selection performance of the single methods. It can be seen that DIF-lasso is competitive for strong and medium DIF. It achieves even lower false positive rates than the other methods. For weak DIF, however, the true positive rate is smaller than for the competing methods. It selects too few variables resulting in minimal false positive rates, but too small true positive rates. The effect is ameliorated if the number of groups and the number of DIF items increases. It should also be noted that in the simple case of binary predictors the MH method and the other procedures designed explicitly for this case outperform the general method proposed here. Thus, for few groups and in particular for weak DIF, the alternative methods are to be preferred. If the predictor structure is more complex, the proposed method works well and allows to investigate the effect of vector-valued predictors.

Table 2. Means of true positives and false positives for the simulations with multiple groups.
Full size table

4.4 Separating the Group Effects from the Abilities

Following the suggestion of the editor, we briefly discuss how real differences in the populations in addition to DIF could be explicitly incorporated in a model. The main problem is that one has to model the effect of a grouping variable or, more general, a covariate on the ability of persons and still have an identifiable model. For categorical covariates, which are considered in the following, the separation of the group effect from DIF can be obtained by using an ANOVA-type representation of the model. But because of nesting the design is not that of a simple ANOVA model. Let the covariate be a categorical variable or factor like gender. Then one has two groups of persons, males and females. Because individuals have its own effect, individuals themselves can be seen as a factor. The third factor is determined by the items. A useful representation of the model treats gender, or, more general, the categorical covariate as a blocking factor. The individuals are the elements within a block, where it is essential that there is no connection between the individuals in different levels of the blocking variable. For the representation, the index p for the individual is replaced by the index (g,j), where g represents the level of the grouping variable (g=1,…,G) and j the individuals within blocks (j=1,…,n g ). There is no connection between observations (g,j) and (g′,j), g≠g′, but between observations (g,j) and (g,j′) because the latter are from the same level of the blocking variable. For a general treatment of nesting, see, for example, McCullagh and Nelder (1989).

The Rasch model (without DIF) for individual (g,j) and item i can then be represented by the predictor

$$\eta_{gji}=\eta_{0} + \alpha_{g}+ \delta_{gj} -\beta_i $$

with the usual symmetric side constraints ∑ g α g =∑ j δ gj =∑ i β i =0. In the model, the person parameter θ p has been replaced by the parameter η 0+α g +δ gj , where (g,j) represents person p. The model contains the constant η 0 and three factors, the grouping variable, the persons, nested within groups, and the items. The parameter α g represents the effect of the categorical covariate, which is separated from the effect δ gj of person (g,j). The model with DIF has the representation

$$\eta_{gji}=\eta_{0} + \alpha_{g}+ \delta_{gj} -( \beta_i + \gamma_{gi}) $$

with the additional side constraints ∑ g γ gi =∑ i γ gi =0. The additional parameters γ gi represent the interaction between the grouping variable and the items. It should be noted that the factor item interacts only with the grouping variable, not with the persons. This makes the model a very specific ANOVA-type model. Of course, alternative side constraints can be used. For example, ∑ i β i =0 can be replaced by β I =0, or ∑ g α g =0 can be omitted if η 0 is fixed by η 0=0. Here, we used symmetric side constraints because they are most often used in ANOVA-type models.

By using the embedding into the ANOVA framework with nesting structure, one obtains an identifiable model that separates the effect of the grouping variable from the persons. It works also for more than one grouping variable by specifying main effects (and possibly interaction effects) of the grouping variables and nesting the persons within the blocks.

5 Examples

5.1 Exam Data

Our first data example deals with the solution of problems in an exam following a course on multivariate statistics. There were 18 problems to solve and 57 students. In this relatively small data set, two variables that could induce DIF were available, the binary variables level (bachelor student of statistics: 1, master student with a bachelor in an other area: 0) and gender (male: 0, female: 1). Figure 6 shows the coefficient build-ups. With BIC as selection criterion, no item showed DIF. So we were happy that the results did not indicate that the exam was preferring specific subgroups.

Figure 6.
figure 6

Coefficient build-ups for exam data.

Full size image

In this simple case, in which potential DIF is induced by binary variables, which indicate the subpopulations, one can also use test statistics to examine if DIF is present because ML estimates exist. The embedding into the framework of generalized linear models allows to use the likelihood ratio test to test the null hypothesis γ 1=⋯,γ I =0 (for the theory see, for example, Tutz 2012). We consider the effects of gender and level separately. The p-values are 0.28 for gender and 0.38 for level. The result supports that DIF is not present. Alternatively, we used model checks based on conditional estimates as Andersen’s likelihood ratio test (Andersen 1973), which is implemented in the R-package eRm, see Mair, Hatzinger, and Maier (2012) and Mair and Hatzinger (2007). These tests resulted in p-values of 0.315 for gender and 0.417 for level and also support that DIF is not an issue in this data set.

5.2 Knowledge Data

An example that has also been considered by Strobl et al. (2013) uses data from an online quiz for testing one’s general knowledge conducted by the weekly German news magazine SPIEGEL. The 45 test questions were from five topics, politics, history, economy, culture, and natural sciences. We use the same subsample as Strobl et al. (2013) consisting of 1,075 university students from Bavaria, who had all been assigned a particular set of questions. The covariates that we included as potentially inducing DIF are gender, age, semester of university enrollment, an indicator for whether the student’s university received elite status by the German excellence initiative (elite), and the frequency of accessing SPIEGEL’s online magazine (spon).

Figure 7 shows as an example the coefficient build-ups for the covariate gender. At the path point that was selected by the BIC criterion (dashed vertical line), 16 of the 45 items showed DIF, which is not surprising because it is not a carefully constructed test that really focusses on one latent dimension. In Figure 8, the estimated effects of the items containing DIF are visualized. The upper panel shows the profile plots of the parameters for the included covariates. For each item with DIF, one profile is given. The lower panel shows the strengths of the effects in terms of the absolute value of the coefficients. One boxplot refers to the absolute values of the 16 parameters for one covariate. It is seen that the strongest effects are found for the covariate gender; the weakest effects are in the variable elite, which measures the status of the university where the student is enrolled. It should be noted that the importance of the single covariates for the DIF can be measured by the absolute values of their coefficients since all covariates were standardized.

Figure 7.
figure 7

Coefficient build-ups for covariate gender in Quiz Data; dashed vertical line indicates BIC-optimal path point.

Full size image
Figure 8.
figure 8

Upper panel: profile plot for coefficient estimates of items with DIF, profiles of the four items with highest DIF are highlighted; lower panel: boxplots of absolute values of coefficient-estimates for items with DIF.

Full size image

In Figure 8 (upper panel), four items are represented by dashed lines. They showed the strongest DIF in terms of the L 2-norm of the estimated parameter vector. All of them refer to economics. For illustration, these four items are considered in more detail. They are

  • Zetsche: “Who is this?” (a picture of Dieter Zetsche, the CEO of the Daimler AG, maker of Mercedes cars, is shown).

  • AOL: “Which internet company took over the media group Time Warner?”

  • Organic: “What is the meaning of the hexagonal ‘organic’ logo?” (Synthetic pesticides are prohibited)

  • BMW: “Which German company took over the British automobile manufacturers Rolls-Royce?”

The profiles for the items Zetsche, AOL, and BMW are quite similar. They are distinctly easier for male participants and for frequent visitors of SPIEGELonline. The item Organic shows a quite different shape being definitely easier for females. It is also easier to solve for students that are not frequent visitors of SPIEGELonline. The item differs from the other three items because it refers more to a broad education than to current issues. Also, females might be more intersted in (healthy) food in general. In this respect, female students and students that do not follow the latest news seem to find the item easier, therefore, the different profile.

6 An Alternative Method

In contrast to most existing methods, the proposed procedure allows to include all variables that might lead to DIF and identify the items with DIF. Quite recently, Strobl et al. (2013) proposed a new procedure that is also able to investigate the effect of a set of variables. Therefore, it seems warranted to discuss the differences between our method and the recursive partitioning approach advocated by Strobl et al. (2013).

Recursive partitioning is similar to CARTs (Classification and Regression Trees), which were propagated by Breiman, Friedman, Olshen, and Stone (1984). For a more recent introduction, see Hastie, Tibshirani, and Friedman (2009), or from a psychological viewpoint Strobl, Malley, and Tutz (2009). The basic concept of recursive partitioning and tree methods in regression models is to recursively partition the covariate space such that the dependent variable is explained best. In the case of continuous predictors, partitioning of the covariate space means that one considers splits in single predictors, that is, a predictor X is split into X≤c and X>c where c is a fixed value. All values c are evaluated and the best split is retained. If a predictor is categorical, splits refer to all possible subsets of categories. Recursive partitioning means that one finds the predictor together with the cut-off value c that explains the dependent variable best. Then given X≤c (and the corresponding subsample) one repeats the procedure searching for the best predictor and cut-off value that works best for the subsample with X≤c. The same is done for the subsample with X>c. The procedure of consecutive splitting can be visualized in a tree. Of course, there are many details to consider, for example, one has to define what best explanation of the dependent variable means, when to stop the procedure and other issues. For details, see Breiman et al. (1984).

In item response models, the partitioning refers to the predictors that characterize the persons. That means when using the person-specific variable X, for example, age, it is split into X≤c and X>c. The Rasch model is fit in these subpopulations yielding different estimates of item parameters. Then one has to decide if the difference between item estimates before splitting and after splitting is systematic or random. If it is systematic, the split is warranted. For the decision, Strobl et al. (2013) use structural change tests, which have been used in econometrics (see also Zeileis, Hothorn, & Hornik, 2008). Although the basic concept is the same as in the partitioning in regression models, now a model is fitted and, therefore, the method is referred to as model based partitioning. For details, see Strobl et al. (2013).

For the knowledge data Strobl et al. (2013) identified gender, spon and age as variables that induce DIF. This is in accordance with our results (Figure 8), which also identified these variables as the relevant ones. By construction, the partitioning approach yields areas, in which the effect is estimated as constant. The partitioning yielded eight subpopulations, for example, {female,spon≤1,age≤21} and {male,spon≤2−3,age≤22}. Within these subspaces, all items have estimates that are nonzero. Items that have particularly large values are considered as showing DIF. It is not clear what criterion is used to identify the items that actually show DIF. Strobl et al. (2013) just describe 5 items that seem to have large values. Therefore, one cannot compare the two approaches in terms of the number of selected items.

Let us make some remarks on the principles of the recursive partitioning approach to DIF and the penalization method proposed here.

Recursive partitioning can be considered a nonparametric approach as far as the predictors are concerned. No specific form of the influence of predictors on items is assumed. But, in the case of continuous variables implicitly a model is fitted that assumes that the effects are constant over a wide range, that is, over X≤c and X>c given the previous splitting. In contrast, our penalization approach assumes a parametric model for DIF. Although it can be extended to a model with unspecified functional form, in the present version it is parametric. An advantage of parametric models is that the essential information is contained in a modest number of parameters that show which variables are influential for specific items. A disadvantage of any parametric model is that it can be misspecified. The partitioning approach, considered as a more exploratory tool, is less restrictive, although assuming a constant value over wide ranges is also a restriction.

An advantage of the parametric model, if it is a fair approximation to the underlying structure, is the use of familiar forms of the predictor, namely a linear predictor, which, of course, can include interactions. In contrast, partitioning methods strongly focus on interactions. Typically, in each consecutive layer of the tree, a different variable is used in splitting. The result is smaller and smaller subpopulations, which are characterized as a combination of predictors. The subpopulations {female,spon≤1,age≤21} and {male,spon≤2−3,age≤22}, found for the knowledge data seem rather specific.

A potential disadvantage of tree based methods is their instability. A small change of data might result in quite different splits. That is the reason why tree-based methods have been extended to random trees, which are a combination of several trees on the same data set; see Breiman (2001).

The penalty approach uses an explicit model for DIF, and the model is separated from the estimation procedure. In the partitioning approach, the model and the fitting are entwined. For practitioners, it is often helpful to have an explicit form of the model that shows how parameters determine the modeled structure. Moreover, in the penalty approach, an explicit criterion is used to determine how many and which items show DIF. The ability to identify the right items has been evaluated in the previous section.

Of course, none of the models is true. Neither is the effect constant within an interval of age as assumed in the partitioning approach nor is the effect linear as assumed in the suggested model. But, as attributed to Box, although all models are wrong, some can be useful. Since the models are not nested, a goodness-of-fit test could yield a decision. But goodness-of-fit as a measure for the adequacy of a model is a tricky business in partitioning models as well as in regularized estimation procedures, in particular, in the framework of item response models. Therefore, not much is available in terms of goodness-of-fit, although it might be an interesting topic of future research.

One basic difference seems to be that the penalty approach uses all covariates, with the variables that are of minor relevance obtaining small estimates, but selects items. The partitioning approach selects variables, or more concisely combinations of covariates, but then estimates all items as having an effect, that is, estimates are unequal zero. Thus, penalty approaches focus on the selection of items, partitioning methods on the selection of combinations of covariates.

7 Concluding Remarks

A general model for DIF that is induced by a set of variables is proposed and estimation procedures are given. It is shown that the method is well able to identify items with DIF. The concept is general, with modifications it can be extended to models that include items with more than two categories as, for example, the graded response model (Samejima 1997) or the partial credit model (Masters 1982). Also, the assumption that items are modified in the linear form \(\boldsymbol {x}^{T}_{p} \boldsymbol {\gamma }_{i}\) can be relaxed to allow for additive functions f 1(x p1)+⋯+f m (x pm ) by using, for example, P-spline methodology (Eilers & Marx, 1996).

The estimation used here is penalized unconditional ML estimation. Alternative regularized estimators could be investigated, for example, estimators based on mixed models methodology. Also, the regularization technique can be modified by using boosting techniques instead of penalization.

The results shown here were obtained by an R program that is available from the authors. It uses the coordinate ascent algorithm proposed in Meier et al. (2008) and the corresponding R package grplasso (Meier 2009). Currently, we are developing a faster program that is based on more recently developed optimization techniques, namely the fast iterative shrinkage thresholding algorithm (Beck & Teboulle, 2009).