1 Introduction

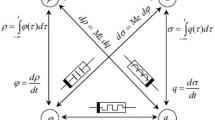
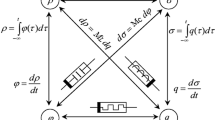
The theory of arbitrary order, real or complex, integrations, and derivatives is known as fractional calculus, and it generalizes the traditional notations for differentiation and integration. It's an extremely handy mathematical tool that was obscured and used very less, but, by the 1980s it was realized that fractional calculus translates the reality of nature better since it has more flexibility in differential order. This feature offers us a language through which we can communicate with nature. Recent years have seen the use of fractional calculus in a variety of disciplines, including engineering, material theory, biology, diffusion theory, economics, electromagnetic, control theory, robotics, signal, and image processing [1]. Fractional-order capacitors, also referred to as constant phase elements (CPEs), are becoming increasingly important in a wide range of applications where Cα stands for pseudo-capacitance and for order, also known as the dispersion coefficient. It offers an impedance of 1/Cαsα and a constant phase angle of -απ/2. The effective manufacturing of this device has recently been investigated by utilizing several materials. A few examples of the many methods used to create CPEs include the usage of graphene most recently in [7], fractal patterns on silicon [2], electrolytic process [3], submerging a polymer-coated capacitive type probe inside a polarizable solution [4,5,6], and electrolytic technique. All of these options, however, are commercially unavailable and lack the benefit of dynamic customization. Passive RC trees are now being used to simulate CPEs, for which the components may be produced using a variety of approaches, including continuing fraction expansion [8,9,10,11]. The Foster form is used to implement the circuit, which uses 5 resistors and 4 capacitors, and the fractional capacitor utilized in this study has been approximated by using continued fraction expansion (CFE) up to the fourth order [12]. The fractional element is halfway between a capacitor and a resistor, as we have a resistor at α = 0 and a capacitor at α = 1. The ideal CPE has a constant phase at all frequencies, but in practice, the phase is only constant over a small frequency range, which is referred to as the constant phase zone (CPZ). Because the phase oscillates somewhat even within the CPZ, actually realized CPEs are occasionally referred to as pseudo-CPEs. One of the key factors influencing interest in fractional calculus in applications is the nonlocality trait. Several intriguing physical phenomena have what are known as memory effects, which means that their current state depends not only on time and position but also on past states. For instance, in 1971, Professor Chua envisioned one such passive device. The circuit elements signify the relationship between pairs of the 4 electromagnetic entities of voltage, flux, charge, and current as shown in Fig. 1. The resistor relates voltage (v) with current (i) whereas the capacitor signifies the relationship between voltage (v) and charge (q). The inductor on the other hand relates the electromagnetic quantities of flux (ɸ) and current (i). However, the relationship between flux (ɸ) and charge (q) was not represented by any device. Therefore, in 1971, Professor Chua envisioned one such passive device. He postulated the existence of the memristor [13], a fourth essential circuit component that links flux and charge and whose resistance is determined by the total amount of charge that has travelled through it over a specific time period. He discussed the generalized concept of the memristor in 1976 [14]. But it was only after 2008, when, in HP-lab, Mr. Williams with his team realized the first memristor in physical form using TiO2, which drew the attention of many researchers towards this novel element [15]. It can be extremely difficult to describe and analyze systems with memory effects, such as the memristor, using conventional differential equations. Yet, nonlocality provides fractional derivatives with an inherent ability to include memory effects. Thus, fractional calculus may be a highly helpful technique for analysing this family of systems [16].

Fig. 1
figure 1

Relation between circuit elements [8]

Full size image

Following the successful implementation of the memristor, quick development occurred, and the concept was expanded to include inductors and capacitors having memories inside them, which resulted in two other components namely the meminductor and memcapacitor [17].

However, due to the unavailability of commercially available memelements, scholars began to realize various emulators in order to combat this issue. By extensive literature review, it was realized that there are two ways in which meminductance has been realized. Firstly, various emulators were designed to convert memristors into meminductors and memcapacitors using mutator circuits [17, 18]. In [19,20,21,22] memristors have been converted to memcapacitor and meminductors using operational amplifiers, current conveyors, resistors, and capacitors. Meminductors have also been made using memristors, trans-impedance op amps, multipliers, and a few resistors and capacitors [23,24,25]. The SPICE model to convert memristor into meminductor has been given in [26]. The disadvantage of this strategy is that the characteristics of the developed meminductor emulator are heavily reliant on the memristor emulator's features. The alternative method is to make meminductor emulators without using memristors. The meminductors using this method do not use memristors but various active and passive building blocks are employed instead. VDTAs, CDBAs, and capacitors have been used to create high-frequency memristor-less meminductor emulators [27, 28]. Multipliers, current conveyors, op-amps, and OTAs along with resistors and capacitors have been used to realize memristor-less meminductors [21, 29,30,31,32,33]. These meminductor emulators use a lot of active and passive components, which makes the circuit very complex and error prone.

The above-discussed meminductor and memcapacitor emulators realize integer-order emulators and provide less flexibility in terms of regulating various parameters when used in a variety of applications. As depicted in Fig. 2, the pinched hysteresis loops develop between current (i) and flux (ϕ) for the meminductor and between voltage (v) as well as charge (q) for the memcapacitor. To create varied applications and to better handle the numerous circuit parameters, fine control over the pinched hysteresis curves is required.

Fig. 2
figure 2

The relation between mem elements [17]

Full size image

The researchers faced this dilemma and therefore they turned to the field of fractional order devices in order to find a solution. A lot of research has been carried out over fractional-order memristors, which yielded some promising results in finely controlling the various parameters of the circuit [34,35,36,37,38,39,40,41] but since the concept of meminductors and memcapacitors is relatively new, therefore equal emphasis has not been given to fractional-order meminductor (FOMI) and memcapacitor (FOMC). Abdelouahab et al. in [42] presents the mathematical model of fractional-order mem elements. Few papers have been reported on the fractional-order meminductor and memcapacitor emulators. Four new fractional-order circuits have been proposed in [43] that contain fractional-order memristor, memcapacitor and meminductor. These fractional-order memristive, memcapacitive, and meminductive systems (FOMMMSs) exhibit a wide range of behaviours. In [44], the fractal-fractional-order domain of Caputo-Fabrizio is used to examine the dynamical properties of memcapacitor and meminductor. Fractional order memelements have been designed in [45] and their application in an analogue controller has been discussed. A general emulator circuit for fractional-order memelements has been realized in [46] using a multiplier, current conveyors, capacitors and resistors, and multiple pinched points have been obtained. Four universal fractional-order memelements emulators have been proposed in [47] using CCII, DVCC and analogue multiplier, DOTA + , BOCC. These emulators have been used to create a chaotic oscillator that demonstrates their capabilities. In [48], a fractional-order current-controlled meminductor model with a nonlinear window function is investigated, and the amplitude-frequency response properties of the meminductor under various excitation signals are analysed in depth. In [49], various arrangements of memristor, fractional-order capacitor, and resistor were employed to achieve fractional-order meminductor and memcapacitor. It has been demonstrated how the pinched point and the hysteresis loop area fluctuate with changes in α and frequency. The effect of change in α has been observed in [50] on floating fractional-order memelements realized using memristor and current conveyors. Different implementations of the emulator have been proposed using different active blocks and impedances. A current/voltage controlled universal emulator realized using two switches, a CCII block, a multiplier and a fractional order capacitor has been featured in [51]. In order to realize a fractional-order meminductor emulator circuit, a fractional-order capacitor that was constructed using the CFE method and Foster-I method is used. With the aid of two OTAs and a CDBA, the meminductor emulator has been realized. It is shown that the fractional-order meminductor emulator performs better than an integral-order meminductor emulator in terms of frequency responsiveness. In comparison to existing FOMI realisations described in the literature, the suggested fractional-order meminductor emulator has a lot simpler architecture and a much better frequency response.

The introduction is the first of this paper's seven sections. In Sect. 2, the characteristics of OTA and CDBA are described. In Sect. 3, the proposed grounded and floating fractional-order meminductor emulator's mathematical analysis is described. The simulation outcomes for grounded/floating configurations using the suggested fractional-order meminductor emulator are displayed in Sect. 4. In Sect. 5, the suggested fractional meminductor emulator is contrasted with current meminductor emulators. Section 6 discusses the use of the suggested meminductor emulators, and Sect. 7 provides the conclusions.

2 Characteristics of Voltage-Tunable OTA and CDBA

Figure 3 depicts the operational transconductance amplifier (OTA) symbol, which is voltage-tunable. It contains five terminals, including two input terminals (+ and −), two output terminals (+ and −), and a fifth terminal (VB) for regulating the OTA's transconductance gain (gm). Due to their extremely high input impedance, the two input terminals drain essentially no current as indicated by Eq. (1). When applied to the two high impedance input terminals of the OTA, " + " and "-," a differential voltage (Vin+—Vin-) results. This voltage is then converted to current (Ix+ and Ix-) at the output terminals "X", where the transconductance gain "gm" of the OTA depends on the bias voltage VB as given in Eq. 5. Figure 4 illustrates the CMOS implementation of an OTA [53].

$$I_{P} = I_{N} = 0$$
(1)
$$I_{X \pm } = \pm G_{m} \left( {V_{in + } - V_{in - } } \right)$$
(2)
$$G_{m} = \frac{K}{\sqrt 2 }\left( {V_{B} - V_{ss} - 2V_{th} } \right)$$
(3)

where,

$$K = \mu_{n} C_{ox} \left( \frac{w}{L} \right)$$
(4)
Fig. 3
figure 3

Symbol of OTA

Full size image
Fig. 4
figure 4

CMOS based Circuit diagram of OTA [53]

Full size image

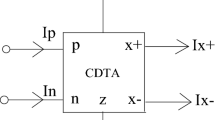
A current differencing buffered amplifier (CDBA), first described in [54], is represented by its symbol in Fig. 5. It is a 4-terminal analog building block having two output terminals (Z and W) and two input terminals (P and N). To apply the two currents IP and IN, two input terminals with low input impedance are used. It is possible to measure the difference between these currents at the ‘Z’ terminal. The ‘Z’ terminal is given an impedance to change IZ to VZ. To terminal W, an internal buffer replicates the voltage VZ. Equation 7 represents the terminal characteristics of a perfect CDBA. Figure 6 depicts CDBA's CMOS structure [55].

$$V_{N} = \, V_{P} = \, 0, \, I_{Z} = \, \left( {I_{P} {-}I_{N} } \right), \, V_{W} = \, V_{Z}$$
(5)
Fig. 5
figure 5

Symbol of CDBA

Full size image
Fig. 6
figure 6

Circuit diagram of CDBA [55]

Full size image

3 Design of the Proposed Fractional-Order Meminductor Emulator

In this section, the working principle of proposed fractional-order meminductor emulator along with realization of fractional-capacitor used in the design have been covered.

3.1 The Proposed circuit

Two OTAs and a CDBA are used in the proposed design of the incremental and decremental fractional-order meminductor emulator presented in Fig. 7. The " + " and "-" terminals of OTA1 accept the input voltage. The floating fractional-order meminductor emulator can be changed to a grounded fractional-order meminductor emulator by grounding the "-" terminal. The output of OTA1, “O1 + ”, is connected to the fractional capacitor C1. In the suggested design of the fractional meminductor emulator shown in Fig. 7a, the output terminals “O2-” and “O2+” of the second OTA (OTA2) are connected to the input terminals “ + ” and “-” of the first OTA (OTA1), respectively. The terminal “O2-” of OTA2 can be connected to terminal “P” or “N” of the CDBA in order to realize incremental or decremental meminductor emulators. By transferring the input current (IP = I02- + Iin or IN = IO2- + Iin) to the “Z” terminal, the capacitor C2 gets charged by CDBA. The transconductance (gm) of the OTAs is controlled to control the value of meminductance by transferring the voltage (VZ) to the CDBA's “W” terminal, which is connected to the OTA's VB terminal. A meminductor emulator is thus realized by adjusting the value of meminductance in accordance with the circuit's historical data (charge stored in C2).

Fig. 7
figure 7

a Proposed fractional meminductor emulator b RC realization of the fractional capacitor C1

Full size image

The mathematical analysis of proposed fractional-order incremental meminductor emulator is presented below.:

$$I_{01 + } = \, G_{m1} \left( {V_{in1} {-} \, V_{in2} } \right)$$
(6)
$$V_{01} = \frac{1}{{s^{\alpha } C_{1} }} \times I_{1}$$
(7)

where, \(\phi_{in}^{\alpha } = \frac{{V_{{\dot{i}n}} }}{{s^{\alpha } }} = \smallint V_{in} d^{\alpha } t\).

This is a fractional-order integral equation, which can be calculated by using the methods of [56] and [57]. Therefore, Eq. (7) can be written as:

$$V_{01} = \frac{1}{{s^{\alpha } C_{1} }} \times G_{m1} V_{in} = \frac{{G_{m1} }}{{C_{1} }} \times \phi_{in}^{\alpha } \left( t \right)$$
(8)
$$I_{02 - } = - G_{m2} V_{01}$$
(9)

As seen in Fig. 7, the terminal “O2-” is shorted to the CDBA's “P” terminal. The current Iz can therefore be expressed as,

$$I_{Z} = I_{P} = I_{in} + I_{O2 - }$$
(10)

The CDBA’s “Z” terminal will then have a voltage VZ,

$${\text{Vz}} = \frac{1}{{{\text{C}}_{2} }}\smallint {\text{Izdt}} = \frac{1}{{{\text{C}}_{2} }}\smallint \left( {{\text{I}}_{O2 - } + I_{in} } \right){\text{dt}}$$
(11)

Replacing the values of the current ‘V01-’ and ‘IO2’ from Eq. (8) and (9), respectively,

$$V_{z} = \frac{1}{{C_{2} }}\smallint \left( { - G_{m2} V_{01} + I_{in} } \right) {\text{d}}t = \frac{1}{{C_{2} }}\smallint \left( {\frac{{ - G_{m2} G_{m1} }}{{C_{1} }}\phi_{in}^{\alpha } + I_{in} } \right){\text{d}}t$$
(12)

Taking \(\smallint \phi_{in}^{\alpha } dt = \frac{{\phi_{in}^{\alpha } }}{{s^{\alpha + 1} }} = \rho^{\alpha }\) and \(\smallint I_{in} dt = q\left( t \right)\)

$$V_{z} = V_{w} = V_{B} = \frac{{ - G_{m1} G_{m2} }}{{C_{1} C_{2} }}\rho^{\alpha } + \frac{q\left( t \right)}{{C_{2} }}$$
(13)

The voltage VZ is transferred to CDBA's ‘W' terminal, which is coupled to the OTAs' ‘VB' terminal.

Since, \(G_{m1} = \frac{{K_{1} }}{\sqrt 2 }\left( {V_{B} - V_{ss} - 2V_{th} } \right)\), Therefore, replacing the value of ‘VB’ from Eq. 15 in Gm1

$$G_{m1} = \frac{K}{\sqrt 2 }\left( {\frac{{ - G_{m1} G_{m2} }}{{C_{1} C_{2} }}\rho^{\alpha } + \frac{q\left( t \right)}{{C_{2} }} - V_{ss} - 2V_{th} } \right)$$
(14)

With the help of Eq. (8) and (9), we get,

$$I_{02 - } = - G_{m2} V_{01} = \frac{{ - G_{m2} G_{m1} }}{{C_{1} }}\phi_{in}^{\alpha }$$
(15)

Using the value of Gm1 from Eq. (14) in Eq. (15), we have,

$$I_{02 - } = \frac{{ - G_{m2} }}{{C_{1} }}\frac{{K_{1} }}{\sqrt 2 }\left( {\frac{{ - G_{m1} G_{m2} }}{{C_{1} C_{2} }}\rho^{\alpha } + \frac{q\left( t \right)}{{C_{2} }} - V_{ss} - 2V_{th} } \right)\phi_{in}^{\alpha }$$
(16)

The relation among flux \(\phi_{in}^{\alpha }\), current I(t) and meminductance (ML) is given by.

$$\phi_{in}^{\alpha } = M_{L} I\left( t \right)$$
(17)

Equation 17 can be rearranged as,

$$I\left( t \right) = M_{L}^{ - 1} \phi_{in}^{\alpha }$$
(18)

Comparing Eq. (16) and (18), we get,

$$M_{L}^{ - 1} = \frac{{ - G_{m2} }}{{C_{1} }}\frac{{K_{1} }}{\sqrt 2 }\left( {\frac{{ - G_{m1} G_{m2} }}{{C_{1} C_{2} }}\rho^{\alpha } + \frac{q\left( t \right)}{{C_{2} }} - V_{ss} - 2V_{th} } \right)$$
(19)
$$M_{L}^{ - 1} = \frac{{G_{m2} K_{1} }}{{\sqrt {2 } C_{1} }}\left( {V_{ss} + 2V_{th} } \right) + \frac{{G_{m2} K_{1} }}{{\sqrt 2 C_{1} }}\left( {\frac{{G_{m1} G_{m2} }}{{C_{1} C_{2} }}\rho^{\alpha } - \frac{q\left( t \right)}{{C_{2} }}} \right)$$
(20)

Connecting the terminal ‘O2-’ with the ‘N’ terminal of the CDBA in Fig. 6, we obtain,

$$M_{L}^{ - 1} = \frac{{ - G_{m2} K_{1} }}{{\sqrt {2 } C_{1} }}\left( {V_{ss} + 2V_{th} } \right) - \frac{{G_{m2} K_{1} }}{{\sqrt 2 C_{1} }}\left( {\frac{{G_{m1} G_{m2} }}{{C_{1} C_{2} }}\rho^{\alpha } - \frac{q\left( t \right)}{{C_{2} }}} \right)$$
(21)

Therefore, the values of meminductance for decremental and incremental meminductance is obtained as,

$$M_{L} = \pm \frac{1}{{\frac{{ - G_{m2} K_{1} }}{{\sqrt {2 } C_{1} }}\left( {V_{ss} + 2V_{th} } \right)}} \pm \frac{1}{{\frac{{G_{m2} K_{1} }}{{\sqrt 2 C_{1} }}\left( {\frac{{G_{m1} G_{m2} }}{{C_{1} C_{2} }}\rho^{\alpha } - \frac{q\left( t \right)}{{C_{2} }}} \right)}}$$
(22)

According to Eq. (22), meminductance for incremental meminductor emulators tends to increase whereas meminductance for decremental meminductor emulators decreases.

By connecting the ‘-' terminal of ‘OTA1' to the ground or any other node, respectively, it can be demonstrated that the proposed fractional meminductor emulator may be used in both grounded and floating configurations without affecting its functionality.

3.2 The Fractional Capacitor

Although it is well known that there is no such thing as an ideal fractional capacitor, there have been several attempts to approximate them in order to use them in fractional order systems. In 1964, Carlson used the regular Newton process to derive the rational approximation of s1/n and applied it using the RC ladder network [52]. Similar to this, Matsuda sought to approximate the irrational function to a rational one in [58] fitting the original function in a group of points that were logarithmically separated from one another. In order to obtain a function and an approximation of the fractional order capacitor, additional approximation approaches and identification procedures are also provided in [58].

One of the most well-known and often employed methods for approximating a fractional order impedance is called continuous fraction expansion (CFE). According to [59], it is:

$$\left( {1 + x} \right)^{\delta } = \frac{1}{{1 - \frac{\delta x}{{1 + \frac{{\left( {1 + \delta } \right)x}}{{2 + \frac{{\left( {1 - \delta } \right)x}}{{3 + \frac{{\left( {2 + \delta } \right)x}}{{2 + \frac{{\left( {2 - \delta } \right)x}}{5 + \ldots }}}}}}}}}}}$$
(23)

in order to get a fractional capacitor's impedance function of the order of 0.5. We approximate till the fourth order in Eq. (23) by changing x and δ to (s-1) and -0.5, respectively, and to obtain the impedance function of the capacitor as

$$s^{ - 0.5} = \frac{{s^{4} + 36s^{3} + 126s^{2} + 84s + 9}}{{9s^{4} + 84s^{3} + 126s^{2} + 36s + 1}}$$
(24)

This gives us the impedance function for a fractional capacitor with 1F capacitance working best at an angular frequency (ω) of 1 rad/s.

By replacing ‘s’ by \(\frac{s}{{10^{6} }}\), and dividing Eq. (24) by the desired capacitance i.e., 10–6, we obtain the expression for a fractional capacitor (Eq. 25) with centre frequency as 106 and capacitance 1µF which has been used in the design of proposed fractional order meminductor.

$$\frac{1}{{10^{ - 6} \left( {\frac{s}{{10^{6} }}} \right)^{0.5} }} = \frac{1}{{10^{ - 6} }}.\frac{{\left( {\frac{s}{{10^{6} }}} \right)^{4} + 36\left( {\frac{s}{{10^{6} }}} \right)^{3} + 126\left( {\frac{s}{{10^{6} }}} \right)^{2} + 84\left( {\frac{s}{{10^{6} }}} \right) + 9}}{{9\left( {\frac{s}{{10^{6} }}} \right)^{4} + 84\left( {\frac{s}{{10^{6} }}} \right)^{3} + 126\left( {\frac{s}{{10^{6} }}} \right)^{2} + 36\left( {\frac{s}{{10^{6} }}} \right) + 1}}$$
(25)

Finding the roots and converting into partial fraction expansion form, we obtain:

$$10^{6} .\frac{{\left( {\frac{s}{{10^{6} }}} \right)^{4} + 36\left( {\frac{s}{{10^{6} }}} \right)^{3} + 126\left( {\frac{s}{{10^{6} }}} \right)^{2} + 84\left( {\frac{s}{{10^{6} }}} \right) + 9}}{{9\left( {\frac{s}{{10^{6} }}} \right)^{4} + 84\left( {\frac{s}{{10^{6} }}} \right)^{3} + 126\left( {\frac{s}{{10^{6} }}} \right)^{2} + 36\left( {\frac{s}{{10^{6} }}} \right) + 1}} = \frac{{10^{3} }}{9}\left( {1 + \frac{{A_{1} }}{x + 7.55} + \frac{{A_{2} }}{x + 1.42} + \frac{{A_{3} }}{x + 0.33} + \frac{{A_{4} }}{x + 0.31}} \right)$$
(26)

Now, by solving this partial fraction and using the foster analysis, we know that we need 5 resistors and 4 capacitors with values as given in Fig. 7b.

4 Simulation Results

Using 180 nm CMOS technology characteristics, the suggested meminductor emulator was simulated using the LTSpice simulator. A 0.9 V supply is used to power the suggested circuit. The bias voltage (VB) of the CDBA is set to -0.1 V, and the bias currents are IB1 = IB2 = 20µA. Capacitor C2 is calibrated to 40pF. In Table 1 below, the aspect ratios utilised to create the OTAs and CDBA are listed.

Table 1 Aspect ratios of OTA and CDBA
Full size table

4.1 Transient Analysis

An input sinusoidal signal with 100 mV amplitude and 100 kHz frequency was used to perform the transient analysis of the proposed decremental fractional-order meminductor emulator. Figure 8 depicts the transient waveforms for flux and current.

Fig. 8
figure 8

Transient analysis of the proposed fractional meminductor

Full size image

To produce the pinched hysteresis loop (PHL) for the proposed fractional-order meminductor emulator, a sinusoidal signal with amplitude 100 mV in a frequency range of 100 kHz to 3 MHz was used. The resultant PHL's area diminishes on increasing frequency, as illustrated in Fig. 9. Observing the values of flux (ɸ) on the x-axis of Fig. 9 can confirm this decrease in the hysteresis loop area. The hysteresis loop can last up to 3 MHz, but the pinched point shifts from the origin. As a result, for frequencies greater than 3 MHz, the loop deforms. The pinched hysteresis curves for integer-order decremental meminductor emulator have also been obtained in Fig. 10 but the pinched hysteresis loop deform much earlier as compared to fractional-order meminductor emulator.

Fig. 9
figure 9

PHLs of proposed decremental Fractional order meminductor at different frequencies a 100 kHz b 500 kHz c 1 MHz d 3 MHz

Full size image
Fig. 10
figure 10

PHLs of decremental integral order meminductor at different frequencies a 100 kHz b 500 kHz c 1 MHz d 3 MHz

Full size image

In Fig. 11, the PHLs of the proposed incremental fractional meminductor emulator are exhibited for frequencies between 100 kHz and 3 MHz. The pinched hysteresis loops for integer-order incremental meminductor emulator have also been obtained in Fig. 12 but the pinched hysteresis loop also deform much earlier as compared to fractional-order meminductor emulator.

Fig. 11
figure 11

PHLs of incremental fractional order meminductor emulator at different frequencies a 100 kHz b 500 kHz c 1 MHz d 3 MHz

Full size image
Fig. 12
figure 12

PHLs of incremental Integer-order meminductor emulator at different frequencies a 100 kHz b 500 kHz c 1 MHz d 3 MHz

Full size image

The temperature analysis was carried on a sinusoidal signal with 100 mV amplitude and frequency of 100 kHz, to assess the functioning of the proposed decremental/incremental fractional meminductor emulator. The temperature was adjusted between − 40 °C and + 40 °C. Figure 13 depicts the acquired results. The temperature study in Fig. 13 shows that the pinched hysteresis curves remain undistorted even when the temperature changes. As a result, the suggested decremental/incremental fractional meminductor emulator's temperature analysis is found to be satisfactory.

Fig. 13
figure 13

Temperature analysis of a decremental Fractional order meminductor and b incremental Fractional order meminductor

Full size image

4.2 Pinched Hysteresis Loops at High Frequency

The pinched point (V = I = 0) is found to move further from the origin at higher frequencies. By appropriately scaling the value of the capacitor (C2) utilised in the construction of the fractional meminductor emulator, this shifting can be avoided. The pinched hysteresis loops are displayed in Fig. 14, at various frequencies, when the capacitor value is adjusted correctly to keep the pinched point near the origin.

Fig. 14
figure 14

Pinched Hysteresis Loops for different values of capacitances a C2 = 11 pF b C2 = 6pF c C2 = 1pF d C2 = 1pF

Full size image

4.3 Non-Volatility Test

Using a square pulse with a 100 mV amplitude, a pulse width of 2 µs, and a time period of 5 µs as the input signal, the non-volatility test for the suggested fractional-order meminductor emulator was carried out. The incremental order non volatility test is depicted in Fig. 15a, and it can be seen that when the pulse is high, the meminductance increases while in the non-pulse period the meminductor retains its value. Similarly, in Fig. 15b, the non-volatility test for decremental fractional-order meminductor is shown, and clearly there is negligible change in the meminductance during the non-pulse period while it decreases when the pulse is high.

Fig. 15
figure 15

Non-volatility test for proposed fractional order meminductor a Incremental b Decremental

Full size image

5 Comparison of Proposed Fractional Order Meminductor Emulator with Other Meminductors in the Literature

The proposed fractional meminductor is contrasted with other meminductors in Table 2. The observations of Table 2 are given below,

  1. 1.

    Many of the reported meminductor emulators employ memristors alongside various passive and active components [19,20,21,22,23,24,25, 27], while the proposed circuit is memristor-less.

  2. 2.

    Many multipliers, current conveyors, operational amplifiers, as well as a significant amount of passive elements, are utilised by several meminductor;emulators; however, the proposed meminductor emulator is very simple in its design and makes use of minimal amount of components. [19, 22,23,24,25, 29,30,31,32,33, 46, 47, 49,50,51]

  3. 3.

    For the fractional-order inverse meminductor in [46] and the FOMI in [47,48,49,50,51], the highest frequency for which PHLs are valid is only in the order of kHz, but the maximum frequency for the suggested fractional meminductor emulator is 3 MHz.

  4. 4.

    The highest frequency for PHLs is limited to Hz and kHz for integral meminductor emulators reported in the literature [19, 20, 22,23,24,25, 29,30,31,32].

  5. 5.

    The proposed fractional meminductor can be used both as a floating and grounded fractional meminductor emulator while many of the emulators in the literature are of either only grounded type. [19, 20, 23, 30, 31, 46, 47, 51]

Table 2 Comparison of proposed circuit with other meminductor circuits in literature
Full size table

6 Application of the Proposed Fractional Meminductor Emulator

To test the proposed fractional meminductor emulator's functionality, we designed an adaptive learning circuit [60,61,62] that simulates an amoeba's behavioural reaction. The amoeba mechanism is based on the current and previous states of the system, and it describes the associative learning process. The following statements reflect an amoeba's associative learning process:

  1. 1.

    Remembering past events,

  2. 2.

    Predicting the future based on the past, and

  3. 3.

    To be able to recognise periodic event’s timing patterns.

This circuit, consisting of a capacitor, a resistor, and the fractional meminductor emulator (Fig. 16), represents the behaviour of the amoeba learning process.

Fig. 16
figure 16

Meminductor basedlAdaptive Learning Circuit

Full size image

The inductance of a meminductor fluctuates depending on the current that has flowed through it in the past, hence the meminductor adapts to the frequency of the temperature swings corresponding to the input voltage (Vin). It regulates the amoeba's movement, where the output voltage Vout, over the meminductor, indicates the amoeba's movement speed according to the temperature changes. The values of the components used in the adaptive learning circuit are R = 500Ω, C = 50nF and the fractional meminductor emulator.

From Fig. 17, we can clearly see that the output learns from the periodic behaviour of the input. After the low-temperature spike, it stays at low movement for some time in order to adapt quickly to the any other cold temperature spike. Only after sufficient time has passed, that it starts returning to the normal amount of activity, as can be seen after the first spike and between the 2nd and 3rd spike. This has shown that the designed adaptive learning circuit perfectly copies the behaviour of the amoeba learning.

Fig. 17
figure 17

Response of the adaptive learning circuit

Full size image

7 Conclusion

A new design for an implementation of a grounded and floating incremental/decremental fractional meminductor emulator has been developed using two OTAs, a CDBA, a grounded capacitor, and a fractional capacitor. This emulator operates across a wide frequency range because the pinched hysteresis loops are not distorted up to 3-MHz frequency. The emulator's performance has also been confirmed to be satisfactory throughout a broad temperature range. There are several benefits to the proposed fractional meminductor emulator, including the absence of memristors, straightforward circuit design, and strong frequency response. By putting the suggested fractional meminductor emulator to use in an adaptive learning circuit, its performance was also verified.