Optimization Analysis of Cooperative Spectrum Sensing System over Generalized $\kappa -\mu$ and $\eta -\mu$ Fading Channels

Abstract

This paper presents, optimization analysis of energy detection based cooperative spectrum sensing system (CSSS) with hard-decision combining. Several system parameters are optimized to evaluate an optimal performance theoretically over noisy and generalized fading channels. In particular, wireless environments with noise plus $\kappa -\mu$ and $\eta -\mu$ fading are considered in the sensing channels. More precisely, each secondary user (SU, also called as cognitive radio user) depend on an energy detector (ED). The SU collects the signal from the primary user (PU), is given as input to the ED, and the energy of the signal is calculated for making a binary decision locally. The locally obtained decisions are combined using hard-decision combining and a final decision about position of the PU is made. In this work, the novel mathematical expressions for detection probability of a single SU is derived first, subject to noise plus fading and validated by using Monte Carlo simulations. Next, we develop theoretical frame works for optimization analysis of CSSS using derived mathematical expressions. The channel error probability is considered in both sensing and reporting channels. Further, we derive closed-form optimal expressions of number of SUs and detection threshold subject to generalized fading and optimal values are calculated. Through receiver operating characteristics (ROC), complementary ROC and total error rate, system performance is evaluated for the significant influence of channel and network parameters. Finally, the influence of the generalized fading severity parameters, the signal-to-noise ratio (SNR), the number of SUs, the detection threshold, and the channel error probability on the performance of CSSS is also investigated.

1 Introduction

Cognitive radio (CR) technology has advanced to growth the spectrum efficiency. It sidesteps the conflicts between unused frequency bands (i.e, spectrum holes) of licensed users, also called as primary users (PUs) and spectrum scarcity of unlicensed users, also called as CR users [1]. The CR technology is one of the most helpful technologies in the field of wireless communications. At present, using the inbuilt global positioning system (GPS) app, minimum 2 billion number of smart mobile users can connect with satellites straightly. By 2020, the number of smart mobile users can be touched to 20 or 50 billion when satellites interface with internet of things (IoT) devices. The first step towards this is seamless integration of terrestrial mobile and satellites networks. Cognitive radio (CR) techniques play an important role to utilize the same spectrum in the both the networks achieve SatCom legacy. In the area of wireless communications, detection of unused frequency bands accurately and efficiently are compulsory for the implementation of protocols of a CR [2]. The reliable decision about PU status (presence or absence) can be obtained using energy detection (ED) technique when PU signal information is not known [3]. In a practical scenario, a single CR user (also called as secondary user, SU) can not take reliable decision when sensing channel is influenced by heavily fading along with noise. In such situations, cooperative multiple CRs based spectrum sensing (CSS) is helpful to take precise and global decision about PU by canceling the severity of noise and fading. In CSS, decisions of all SUs are combined by using several combining methods [4]. There are two important combining methods developed such as hard-data or soft-data combining methods. The performance of soft and hard data combining methods over generalized fading channels are discussed in [5]. These methods are processed at the control center, also called as fusion center (FC) [6, 7]. For minimizing the cost and complexity of the wireless networks, optimization of cognitive radio network is required without loosing the same performance level.

1.1 Related Work

In [8], performance of hard-data fusions for energy detection based CSS system is investigated subject to noise as well as different fading environments. However, studies on the optimization analysis is not discussed. In [9] and [10], optimization of cognitive radio network (CRN) is studied and discussion is limited to Rayleigh faded environment only. However, studies on the optimal system performance subject to both erroneous sensing and reporting channels are not investigated in [9] and the values of the optimal detection thresholds are not calculated in [10]. The optimization of generalized majority rule for heterogeneous cognitive radio network is studied in [11]. For a given fusion method, maximization of throughput at FC subject to erroneous reporting channels is analyzed in [12]. Analysis of optimized cooperative spectrum sensing network in presence of non-fading and fading environments is investigated in [13]. Generalized fading distributions are recently developed distributions to avoid several individual fading distributions. These distributions also provide several individual fading distributions for a specific fading severity parameter values. The $\alpha -\mu$, $\kappa -\mu$ and $\eta -\mu$ are the generalized distributions, $\alpha -\mu$, $\kappa -\mu$ and $\eta -\mu$ reduces to Weibull fading, Rician fading and Hoyt fading, respectively [14]. More precisely, when slow variations in amplitude of PU signal along with line-of-sight (LOS) component are received, the $\kappa -\mu$ fading can be used as the multipath fading [15]. For a specific values of $\kappa$ and $\mu$, the $\kappa -\mu$ fading provides one-sided Gaussian, Rayleigh, Rician and Nakagami-m fading. Also, when slow variations in amplitude of PU signal along with non-LOS component are received, the $\eta -\mu$ fading can be used as the multipath fading [15]. For a specific values of $\eta$ and $\mu$, the $\eta -\mu$ fading provides one-sided Gaussian, Rayleigh, Hoyt, and Nakagami-m fading. This provoked several researchers to investigate performance of ED-CSS over generalized fading environments. In [16], the investigation over $\kappa -\mu$ environment is discussed. A complex analytical model as a function of contour integrals was developed in [17]. The performances of Bayesian energy detector for spectrum sensing (single SU) in $\kappa -\mu$ and $\eta -\mu$ environments are discussed in [18, 19]. The studies on ED-CR spectrum sensing (single SU) in $\alpha -\eta -\mu$ and $\alpha -\kappa -\mu$ environments, following a Bayesian approach have been discussed recently in [20, 21]. The end expressions consist of integrals that can be decomposed to expressions in closed-form for a given specific values of the parameters. In instant, the efforts for finding new analytical expressions in generalized fading environments and optimization of cooperative spectrum sensing system (CSSS) cancels the essential analysis of several individual fading distributions in the field of wireless communications.

1.2 Overview and Contributions

In the present work, the number of SUs in the system and detection threshold are chosen as the optimizing parameters. The ROC and CROC, and total error rate (sum of missed detection and false alarm) are selected as the performance metrics. Total error rate minimization where an optimal point can be obtained at which any one of the traditional metrics is punished with respect to the other. The studies stated above reveal that the optimization analysis of CSSS in a generalized $\kappa -\mu$ and $\eta -\mu$ fading situations could be significant research area. The major works in this paper are presented below.

• 1. We derive novel-mathematical expression for probability of detection in a single SU subject to noise plus $\kappa -\mu$ and $\eta -\mu$ fading environments. The performance features (ROC) subject to noisy-generalized fading are novel.

• 2. We develop novel-analytical frameworks for optimization of CSSS using derived expression for detection probability of a single SU. Also, performance of CSSS is evaluated through CROC curves and total error rate using hard-decision fusion rules.

• 3. The expressions for optimal number of SUs and optimal detection threshold are derived subject to generalized fading. Optimal values are determined subject to fading.

• 4. The influences of the error probability of the channel (denoted as q), fading severity parameters, and system parameters on the optimal performance of CSSS are evaluated.

The works studied here are generic and can be prolonged to any other generalized fading environments.

1.3 Splitting of the Paper

The next sections of this paper are: In Sect. 2, the considered system with formal descriptions of signal and channel models is discussed. The mathematical expressions for detection probability are derived in generalized fading environments. In Sect. 3, theoretical frameworks for analysis of optimization under hard decision methods. In Sect. 4, the MATLAB based simulation and analytical results are given and discussed. Finally, whole paper is concluded in Sect. 5.

2 Considered System Model and Assumptions

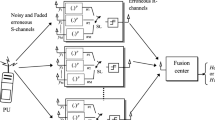
In this work, CSS system is proposed and it consists of a PU, number of SUs (N) and one FC. Each SU contains one ED. The proposed system is shown in Fig. 1 where PU, SUs and FC blocks are shown. The links connected from PU to SUs are the sensing channels and links connected from SUs to FC are the reporting channels. The PU is sensed, and each SU receives the information from PU subject to noise and fading. Also each SU transmits its information to a FC. The FC combines sensing information and performs hard-decision operations (e.g., OR rule, AND rule, and MAJORITY rule). Finally, a global decision is taken by the FC on the status of a PU. Figure 2 shows the functional diagram of energy detector. The sensing channel is influenced by a generalized fading. As stated in the previous Sect. 1 that two generalized models such as $\kappa -\mu$ and $\eta -\mu$ are considered individually. These models provides different statistical distributions for a specific values of parameters. One-sided Gaussian is obtained for $\kappa =0$ or $\eta =0$ and $\mu =0.5$. Rayleigh is obtained for $\kappa =0$ or $\eta =1$, $\mu =1$. Rician fading is obtained for $\kappa \ge 0$ and $\mu =1$. Nakagami-m (m is the Nakagami-m parameter) is obtained for $\kappa =0$, $\mu \ge 1$; or $\eta =1$, $\mu =m$. Hoyt or Nakagami-q (q is the parameter) is obtained for $\eta =q^2$ and $\mu =0.5$.

Fig. 1

The proposed cooperative spectrum sensing system (CSSS) with hard-decision fusion

Fig. 2

Various functional blocks of energy detector

Each SU obtains sensing data from PU in the form of local binary-decision. The obtained signal in jth SU, ${y_j}(t)(j \in \{ 1 \ldots N\} )$, can be expressed as

$$\begin{aligned} {y_j}(t) = \left\{ {\begin{array}{*{20}{l}} {{n_j}(t)}& \quad {{\mathcal {H}_0}}\\ {{h_j}s(t) + {n_j}(t)}&\quad {{\mathcal {H}_1}} \end{array}} \right. \end{aligned}$$

(1)

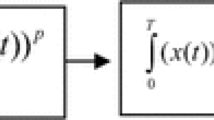
where s(t) indicates unknown primary signal and its energy is $E_s$, $n_j(t)$ indicates additive white Gaussian noise (AWGN), ${h_j}$ denotes coefficient of S-channel fading, ${\mathcal {H}_0}$ denotes presence and ${\mathcal {H}_1}$ denotes absence of a PU. The energy $E_j$ obtained under ${\mathcal {H}_0}$ over observation time (0, T) is

$$\begin{aligned} E_j=\int _0^T n_j^2(t) dt = \sum _{i=1}^{2u} n_{j_i}'^2. \end{aligned}$$

(2)

where $n_{j_i}'=n_{j_i}/\sqrt{N_{01}W}$ [3]; $n_{j_i}=n(i/(2W))$; $n_{j_i} \sim \mathcal {N}(0,N_{01}W); \forall i$, $u=TW$ is the time (T) bandwidth (W) product, and $N_{01}$ indicates noise power spectral (PSD) density (one-sided). Similar steps are used to estimate energy under hypothesis $\mathcal {H}_1$. The SU takes a decision locally by comparing energy with a predetermined threshold. In each SUs, same threshold is set.

2.1 Non-fading Channel (AWGN)

When S-channel is influenced by AWGN, the mathematical expressions of local false alarm and detection probabilities at jth SU are written as [3]

$$\begin{aligned} P_{f,j}&= \mathrm {Pr}[E_j > \lambda | \mathcal {H}_0] = {\varGamma }(u,\lambda /2)/{\varGamma (u)}, \end{aligned}$$

(3)

$$\begin{aligned} P_{d,j}&= \mathrm {Pr}[E_j > \lambda | \mathcal {H}_1] = Q_u \left( \sqrt{2\gamma _{s,j}},\sqrt{\lambda }\right) . \end{aligned}$$

(4)

where $\lambda$ is threshold, $\gamma _{s,j}$ is SNR, $Q_u(\cdot ,\cdot )$ is the Marcum Q-function of order u [22], $\varGamma (\cdot )$ and $\varGamma (\cdot ,\cdot )$ are the gamma and the incomplete gamma functions [23], respectively. In each SU the same average SNRs (${{\bar{\gamma }}_{s,j}} = {{\bar{\gamma }}_s};\,\forall j$) and the same false alarm probability (${P_{f,j}} = {P_f};\,\forall j$) are assumed. In the following subsequent subsections, the derivation of mathematical expression of a probability of detection in a SU over noisy-fading is presented.

2.2 The $\kappa -\mu$ Fading Channel

Assume that sensing channel is influenced by $\kappa -\mu$ fading, the $h_j$ differs and Eq. (3) contains $\gamma _{s}$ term, in jth SU, the average probability of detection, ${\bar{P}}_{d,j}$ is obtained as

$$\begin{aligned} {\bar{P}}_{d,j} = \int _0^\infty Q_m \left( \sqrt{2x},\sqrt{\lambda }\right) f_\gamma (x) dx \end{aligned}$$

(5)

where the probability density function (PDF), $f_\gamma (x)$ is shown as a function of $\gamma _{s}$. Under $\mathcal {H}_0$ (i.e., case with no primary user signal is received), it is observed from (4) that $P_f$ does not depend on $\gamma _{s,j}$ for any value of j. Hence, the mathematical expression for an average probability of false alarm (${\bar{P}}_{f,j}$) in $\kappa -\mu$ fading is same as the mathematical expression of $P_f$ over non-fading AWGN environment i.e., Eq. (4).

Assume that r is the envelop of $\kappa -\mu$ distribution. The r consists of two components (in-phase and quadrature) is given as [15]

$$\begin{aligned} {r^2} = \sum \limits _{i = 1}^p {{{({U_i} + {e_i})}^2}} + \sum \limits _{i = 1}^p {{{({W_i} + {g_i})}^2}} \end{aligned}$$

(6)

where $U_i$ and $W_i$ are Gaussian processes and not mutually dependent with mean ${\mathbb {E}}({U_i}) = {\mathbb {E}}({W_i}) = 0$, variance ${\mathbb {V}}({U_i}) = {\mathbb {V}}({W_i}) = {\sigma ^2}$, $e_i$ mean of the in-phase and $g_i$ is mean of the quadrature components of a ith cluster. Also, $\kappa$ and $\mu$ are the severity parameters of fading for defining the shape of the fading distribution. In detail, $\kappa$ is the ratio of total power of dominant component and total power of scattered waves, $\mu$ is the real extension of the p number of clusters, $\kappa$ and $\mu$ are given as [15]

$$\begin{aligned} \kappa = \frac{{\sum \nolimits _{i = 1}^p {(e_i^2 + g_i^2)} }}{{2p \sigma ^2 }},\,\mu = \frac{{{{\mathbb {E}}^2}[{r^2}]}}{{{\mathbb {V}}[{r^2}]}}\times \frac{{1 + 2\kappa }}{{(1 + \kappa )}^2} \end{aligned}$$

(7)

The PDF and the cumulative distribution function (CDF) in terms of $\gamma _{s}$ are given from [15] and [24]

$$\begin{aligned} \displaystyle {f_\gamma }(\gamma _{s} )& = \frac{\mu }{{\exp (\mu \kappa )}}{\left( {\frac{{1 + \kappa }}{{{\bar{\gamma }}_{s} }}} \right) ^{\frac{{\mu + 1}}{2}}}{\left( {\frac{\gamma _{s} }{\kappa }} \right) ^{\frac{{\mu - 1}}{2}}} \nonumber \\ \displaystyle& \quad \times \exp \left( { - \frac{{\mu (1 + \kappa )\gamma _{s} }}{{{\bar{\gamma }}_{s} }}} \right) {\mathcal {I}_{\mu - 1}}\left( {2\mu \sqrt{\frac{{\kappa (1 + \kappa )\gamma _{s} }}{{{\bar{\gamma }}_{s} }}} } \right) , \end{aligned}$$

(8)

$$\begin{aligned} {F_\gamma }(\gamma _{s} )& = 1 - {Q_u}\left( {\sqrt{2\kappa \mu } ,\sqrt{\frac{{2(1 + \kappa )\mu \gamma _{s} }}{{{\bar{\gamma }}_{s} }}} } \right) . \end{aligned}$$

(9)

where $\mathcal {I}_{z}(.)$ is the modified Bessel function of zth order and first kind [23]. The mathematical expression for average $P_d$ i.e., ${\bar{P}}_d^{\kappa - \mu }$ are derived by inserting (14) in (5) and infinite series form of Marcum Q-function [8]

$$\begin{aligned} \displaystyle {{\bar{P}}_d^{\kappa -\mu }}& = \mathcal {A}\sum \limits _{v = 0}^\infty {\frac{{\varGamma (u + v,\lambda /2)}}{{\varGamma (u + v)v!}}} \int _0^\infty {{\gamma _{s}}^{v + \frac{{\mu - 1}}{2}}} \nonumber \\ \displaystyle& \quad \times \exp \left( { - \frac{\left[ \mu (1 + \kappa ) + {\bar{\gamma }}_{s} \right] \gamma _{s} }{{\bar{\gamma }}_{s}}} \right) {\mathcal {I}_{\mu - 1}}\left( {2\mu \sqrt{\frac{\kappa (1 + \kappa )\gamma _{s} }{{\bar{\gamma }}_{s} }} } \right) d\gamma _{s}, \end{aligned}$$

(10)

where $\mathcal {A} = (\mu /\exp (\mu \kappa )){[(1 + \kappa )/{{\bar{\gamma }}_{s}}]}^{(\mu + 1)/2}{\kappa }^{(1-\mu )/2}$. The integral part in (16) is solved with help of [8]. Finally, we get

$$\begin{aligned} \displaystyle {{\bar{P}}_{d,j}^{\kappa - \mu }}& = {\left[ {\frac{{\mu (1 + k)}}{{{\bar{\gamma }}_{s} }}} \right] ^\mu }\frac{{\exp ( - \mu k)}}{{\varGamma (\mu )}} \nonumber \\ \displaystyle& \quad \times \sum \limits _{v = 0}^\infty {\frac{{\varGamma (u + v,\lambda /2)}}{{\varGamma (u + v)}}\frac{{\varGamma (v + \mu )}}{{v!}}} {\left( {\frac{{{\bar{\gamma }}_{s} }}{{\mu (1 + \kappa ) + {\bar{\gamma }}_{s} }}} \right) ^{\mu + v}}\nonumber \\ \displaystyle& \quad \times {}_1{\mathcal {F}_1}\left( {v + \mu ;\mu ;\frac{{{\mu ^2}\kappa (1 + \kappa )}}{{\mu (1 + \kappa ) + {\bar{\gamma }}_{s} }}} \right) . \end{aligned}$$

(11)

where ${}_1{\mathcal {F}_1}(.;.;.)$ is a confluent hypergeometric function [23]. Equation (11) reduces to one-sided Gaussian for $\kappa =0$, $\mu =0.5$; Rayleigh for $\kappa =0$, $\mu =1$; Rician for $\kappa =K$, $\mu =1$ (where $K\ge 0$); and Nakagami-m for $\kappa =0$, $\mu =m$ ($m\ge 1$).

2.3 The $\eta -\mu$ Fading Channel

The $\eta -\mu$ fading model is developed in two formats. However, one format is derived from another using ${\eta _{\mathrm{format2}}} = \frac{(1 - {\eta _{\mathrm{{format1}}}})}{(1 + {\eta _{\mathrm{{format1}}}}}$, where ${\eta _{{\mathrm{format1}}}}=\eta$ varies from 0 to $\infty$ and ${\eta _{\mathrm{format2}}}=\eta$ varies from $-$ 1 to 1. In the current work, format1 is applied in derivation. Assume that r is the envelop of $\eta -\mu$ distribution. The r consists of two components (in-phase and quadrature) is given as [15]

$$\begin{aligned} {r^2} = \sum \limits _{i = 1}^p {({X_i^2} + {Y_i^2})}, \end{aligned}$$

(12)

where $X_i$ and $Y_i$ are Gaussian processes and not mutually dependent Gaussian processes with mean ${\mathbb {E}}(X_i)={\mathbb {E}}(Y_i)=0$, variance ${\mathbb {V}}(X_i)=\sigma _X^2$, ${\mathbb {V}}(Y_i)=\sigma _Y^2$, the symbol p gives the number of clusters. $\eta$ and $\mu$ are the severity parameters of fading for defining the shape of the fading distribution. In detail, $\eta$ is the scattered power ratio of both in-phase and quadrature components, $\mu$ is the real extension of p/2 clusters. Analytically, $\eta$ and $\mu$ are given as [15]

$$\begin{aligned} \eta =\frac{{\sigma _X^2}}{{\sigma _Y^2}}, \quad \mu =\frac{{{{\mathbb {E}}^2}({r^2})}}{{2{\mathbb {V}}({r^2})}} \times \left[ {1 + {{\left( {\frac{H}{h}} \right) }^2}} \right] , \end{aligned}$$

(13)

where $h = (2 + {\eta ^{ - 1}} + \eta )/4$ and $H = ({\eta ^{ - 1}} - \eta )/4$. The PDF and CDF in terms $\gamma _{s}$ are expressed as [15]

$$\begin{aligned} \displaystyle {f_\gamma }(\gamma _s )& = \frac{{2\sqrt{\pi }h^{\mu }}}{{\varGamma (\mu )}}{\left[ {\frac{\mu }{{{\bar{\gamma }}_s }}} \right] ^{\mu + {\textstyle {1 \over 2}}}}{\left[ {\frac{\gamma _s }{H}} \right] ^{\mu - {\textstyle {1 \over 2}}}} \nonumber \\ \displaystyle& \quad \times \exp \left( { - \frac{{2\mu h\gamma _s }}{{{\bar{\gamma }}_s }}} \right) {\mathcal {I}_{\mu - {\textstyle {1 \over 2}}}}\left( {\frac{{2\mu H\gamma _s }}{{{\bar{\gamma }}_s }}} \right) \end{aligned}$$

(14)

$$\begin{aligned} {F_\gamma }(\gamma _s )& = \frac{{\sqrt{\pi }}}{{\varGamma (\mu )}}\sum \limits _{j = 0}^\infty {\frac{{{H^{2j}}g\left( {2\mu + 2j,\frac{{2\mu h\gamma _s }}{{{\bar{\gamma }}_s }}} \right) }}{{j!\varGamma (\mu + j + {\textstyle {1 \over 2}}){2^{2\mu + 2j - 1}}{h^{\mu + 2j}}}}} \end{aligned}$$

(15)

where $g(a,y) = \int _0^y {{t^{a - 1}}\exp ( - t)dt}$ denotes lower incomplete gamma function [23]. The average $P_d$, ${\bar{P}}_{d,j}^{\eta - \mu }$, is obtained by inserting (14) in (5) and infinite series form of the Marcum Q-function [23]

$$\begin{aligned} \displaystyle {{\bar{P}}_{d,j}^{\eta -\mu }}& = \mathcal {A}\sum \limits _{v = 0}^\infty {\frac{{\varGamma (u + v,\lambda /2)}}{{\varGamma (u + v)v!}}} \int _0^\infty {{\gamma _{s}}^{v + \mu -{\textstyle {1 \over 2}}}} \nonumber \\ \displaystyle& \quad \times \exp \left( { - \left[ 1+ \frac{{2\mu h}}{{{\bar{\gamma }}_{s} }} \right] {\gamma _{s}}} \right) {\mathcal {I}_{\mu - {\textstyle {1 \over 2}}}}\left( {\frac{{2\mu H\gamma _s }}{{{\bar{\gamma }}_s }}} \right) d\gamma _{s}, \end{aligned}$$

(16)

where $\mathcal {A} = \frac{{2\sqrt{\pi }h^{\mu }}}{{\varGamma (\mu )}}{\left[ {\frac{\mu }{{{\bar{\gamma }} }}} \right] ^{\mu + {\textstyle {1 \over 2}}}}{\left[ {\frac{1}{H}} \right] ^{\mu - {\textstyle {1 \over 2}}}}$. Using [25], the solution to the integral part in (16) is obtained and finally, we get

$$\begin{aligned} \displaystyle {{\bar{P}}_{d,j}^{\eta - \mu }}& = \frac{{2\sqrt{\pi }h^{\mu }}}{{\varGamma (\mu )}}{\left[ {\frac{\mu }{{{\bar{\gamma }}_s }}} \right] ^{2\mu }}\sum \limits _{v = 0}^\infty {\frac{{\varGamma (u + v,\lambda /2)}}{{\varGamma (u + v)v!}}} \nonumber \\ \displaystyle& \quad \times {\left( {1 + \frac{{2\mu h}}{{{\bar{\gamma }}_s }}} \right) ^{ - (v + 2\mu )}}\frac{{\varGamma (v + 2\mu )}}{{\varGamma (\mu + {\textstyle {1 \over 2}})}}\nonumber \\ \displaystyle& \quad \times {}_2{\mathcal {F}_1}\left( {\frac{{v + 2\mu + 1}}{2},\frac{{v + 2\mu }}{2};\mu + \frac{1}{2};{{\left( {\frac{{2\mu H}}{{{\bar{\gamma }}_s + 2\mu h}}} \right) }^2}} \right) . \end{aligned}$$

(17)

where ${}_2{\mathcal {F}_1}(.;.;.)$ is hypergeometric Gaussian function [23]. Equation (17) reduces to one-sided Gaussian for $\eta \rightarrow 0|\infty$, $\mu =0.5$; Hoyt for $\eta =q^2$ ($q\ge 0$), $\mu =0.5$; Rayleigh for $\eta =1$, $\mu =0.5$; and Nakagami-m for $\eta =1|0$, $\mu ={\textstyle {m \over 2}}|m$ (where $m\ge 0$). Under $\mathcal {H}_0$ (i.e., case with no primary signal is received), it is observed from (4) that $P_f$ is not depending on $\gamma _{s,j}$, for any value of j. Hence, the mathematical expression for an average probability of false alarm (${\bar{P}}_{f,j}$) in $\eta$ and $\mu$ fading is same as the mathematical expression of $P_f$ over non-fading AWGN environment i.e., Eq. (4).

At a single SU, the metric, total error rate is written as

$$\begin{aligned} {{\bar{P}}}=p(\mathcal {H}_1){\bar{P}_m}+p(\mathcal {H}_0){\bar{P}_f}. \end{aligned}$$

(18)

where $\bar{P}_m=1-{\bar{P}}_{d,j}$ is the local missed detection probability, $p(\mathcal {H}_1)$ shows the prior probability when the PU is present, and $p(\mathcal {H}_0)$ shows the prior probability when PU is absent. In the current work, $p(\mathcal {H}_1)=p(\mathcal {H}_0)=0.5$ is considered as the special case, however, the considered process is general.

3 Theoretical Framework of Optimization Analysis

The currents section studies the operations of various hard-decision combining methods at FC such as OR rule, AND rule and MAJORITY rule. Allowing cooperative sharing of sensing information among the multiple SUs (N) improves the overall performance. In cooperative approach, every SU performs ED operation, takes a local decision (binary ‘1’ means PU is present i.e. $\mathcal {H}_1$ or ‘0’ means PU is absent i.e. $\mathcal {H}_0$), and sends that decision to the FC for fusing operations. In all SUs, identical operations are assumed i.e.,

$$\begin{aligned} {\bar{P}}_{f,j}&= \Pr \{ {d_j} = 1|{\mathcal {H}_0}\}; {\bar{P}}_{f,j} = {{\bar{P}}_f}, \forall j, \end{aligned}$$

(19)

$$\begin{aligned} {\bar{P}}_{m,j}&= \Pr \{ {d_j} = 0|{\mathcal {H}_1}\}, {\bar{P}}_{m,j} = {{\bar{P}}_m}, \forall j \end{aligned}$$

(20)

$$\begin{aligned} {\bar{P}}_{d,j}&= \Pr \{ {d_j} = 1|{\mathcal {H}_1}\}, {\bar{P}}_{d,j} = {{\bar{P}}_d}. \forall j \end{aligned}$$

(21)

where $d_j$ is denoted for local decision in jth SU. Channel error, q is assumed in both channels (S and R). Under the influence of channel error in S-channel, mathematical expressions for false alarm and missed detections in a SU can be written as [10]

$$\begin{aligned} P_{fe}&= {{\bar{P}}_{f}}(1 - q) + (1 - {{\bar{P}}_{f}})q, \end{aligned}$$

(22)

$$\begin{aligned} P_{me}&= {{\bar{P}}_{m}}(1 - q) + (1 - {{\bar{P}}_{m}})q, \end{aligned}$$

(23)

$$\begin{aligned} P_{de}&= {{\bar{P}}_{d}}(1 - q) + (1 - {{\bar{P}}_{d}})q. \end{aligned}$$

(24)

where ${\bar{P}}_{f}$, ${\bar{P}}_{m}$, and ${\bar{P}}_{d}$ are already shown in (19), (20), and (21), respectively. Under the influence of channel error, the total error rate expression is

$$\begin{aligned} {{\bar{P}}_e}=P(\mathcal {H}_1){{P}_{me}}+P(\mathcal {H}_0){{P}_{fe}}. \end{aligned}$$

(25)

Now, under the influence of channel error in R-channel, cooperative probabilities at FC can be shown as

$$\begin{aligned} Q_{fe}&= \sum _{\ell =k}^N \left( {\begin{array}{c}N\\ \ell \end{array}}\right) (P_{fe})^\ell (1-{P_{fe}})^{N-\ell }, \end{aligned}$$

(26)

$$\begin{aligned} Q_{me}&= 1-\sum _{\ell =k}^N \left( {\begin{array}{c}N\\ \ell \end{array}}\right) (1-P_{me})^\ell (P_{me})^{N-\ell }, \end{aligned}$$

(27)

$$\begin{aligned} Q_{de}&= \sum _{\ell =k}^N \left( {\begin{array}{c}N\\ \ell \end{array}}\right) (P_{de})^\ell (1-{P_{de}})^{N-\ell }. \end{aligned}$$

(28)

From (26) and (27), the expressions of $Q_{me}$ and $Q_{fe}$ under OR rule are obtained for $k=1$, AND rule for $k=N$, and MAJORITY rule for $k = \left\lfloor {N/2} \right\rfloor$, where $\left\lfloor {.}\right\rfloor$ shows ceiling function which means the largest integer not greater than the argument. Then, the total error rate as a function of channel error is

$$\begin{aligned} {Q_{e}} =p(\mathcal {H}_1){Q_{me}} + p(\mathcal {H}_0){Q_{fe}}. \end{aligned}$$

(29)

It is observed that when set $q=0$ in (27), (26), and (29), expressions for error free CSSS can be derived. The analysis of optimization is studied in the next section.

3.1 Optimization of Number of SUs Over $\kappa -\mu$ and $\eta -\mu$ Fading

In this section, the exact optimal n solution under optimum voting rule is studied. An optimal voting rule that optimizes the Bayes risk function is shown in [9]. The total error rate instead of the Bayes risk function is not included here. The optimal value of n is derived when $\frac{{\partial {Q_{e}}}}{{\partial n}} = 0$.

$$\begin{aligned} \displaystyle&\Rightarrow \sum _{\ell =n+1}^N \left( {\begin{array}{c}N\\ \ell \end{array}}\right) \left[ (P_{fe})^\ell (1-P_{me})^{N-\ell }- (1-P_{me})^\ell (P_{me})^{N-\ell }\right] \nonumber \\ \displaystyle&\quad - \sum _{\ell =n}^N \left( {\begin{array}{c}N\\ \ell \end{array}}\right) \left[ (P_{fe})^\ell (1-{P_{fe}})^{N-\ell }-(1-P_{me})^\ell (P_{me})^{N-\ell }\right] =0 \nonumber \\ \displaystyle&\Rightarrow (P_{fe})^n{(1 - {P_{fe}})^{N - n}} - {(1 - {P_{me}})^n}(P_{me})^{N - n} = 0\nonumber \\&\displaystyle \Rightarrow n\ln \left( {\frac{{1 - {P_{me}}}}{{{P_{fe}}}}} \right) + n\ln \left( {\frac{{1 - {P_{fe}}}}{{{P_{me}}}}} \right) = N\ln \left( {\frac{{1 - {P_{fe}}}}{{{P_{me}}}}} \right) \nonumber \\&{n_{opt}} = \frac{{N\ln \left( {\frac{{1 - {P_{fe}}}}{{{P_{me}}}}} \right) }}{{\ln \left( {\frac{{1 - {P_{me}}}}{{{P_{fe}}}}} \right) + \ln \left( {\frac{{1 - {P_{fe}}}}{{{P_{me}}}}} \right) }}. \end{aligned}$$

(30)

Let $\beta ={\ln \left( {\frac{{1 - {P_{me}}}}{{{P_{fe}}}}} \right) / \ln \left( {\frac{{1 - {P_{fe}}}}{{{P_{me}}}}} \right) }$, then, we get ${n_{opt}}\approx \left\lceil {\frac{N}{{\beta + 1}}} \right\rceil$, where $\left\lceil {.}\right\rceil$ indicates the largest integer greater than the argument. When $P_{fe}$ and $P_{me}$ have same value, i.e., $\beta =1$, optimal choice of n is N/2, the OR rule and the AND rule are optimal when $\beta =N-1$, and $\beta =0$, respectively.

3.2 Optimization of Detection Threshold Over $\kappa -\mu$ and $\eta -\mu$ Fading

The exact solution of the optimal $\lambda$, considering optimum voting rule is presented in this section. The optimal value of $\lambda$ is obtained when $\frac{{\partial {Q_{e}}}}{{\partial \lambda }} = 0$.

$$\begin{aligned} \displaystyle&\frac{\partial {Q_{fe}}}{\partial \lambda } = \sum _{\ell =n}^N \left( {\begin{array}{c}N\\ \ell \end{array}}\right) \ell (P_{fe})^{\ell - 1}\frac{{\partial {P_{fe}}}}{{\partial \lambda }}{{(1 - {P_{fe}})}^{N - \ell }} \nonumber \\&\quad \displaystyle - \sum _{\ell =n}^N \left( {\begin{array}{c}N\\ \ell \end{array}}\right) (P_{fe})^{\ell }(N - \ell ){{(1 - {P_{fe}})}^{N - \ell - 1}}\frac{{\partial {P_{fe}}}}{{\partial \lambda }}, \end{aligned}$$

(31)

The Eq. (31) can be simplified further as

$$\begin{aligned} \frac{{\partial {Q_{fe}}}}{{\partial \lambda }}& = \frac{{\partial {P_{fe}}}}{{\partial \lambda }}\sum \limits _{\ell = n}^N {\left( {\begin{array}{c}N\\ \ell \end{array}}\right) (P_{fe})^{\ell - 1}{{(1 - {P_{fe}})}^{N - \ell }}}\nonumber \\&\displaystyle \times \left[ {\ell - (N - \ell )\frac{{{P_{fe}}}}{{1 - {P_{fe}}}}} \right] , \end{aligned}$$

(32)

where

$$\begin{aligned} \frac{{\partial {P_{fe}}}}{{\partial \lambda }} = - (1 - 2q)\frac{{{\lambda ^{u - 1}}\exp ( - \lambda /2)}}{{{2^u}(u - 1)!}}. \end{aligned}$$

(33)

Similarly,

$$\begin{aligned} \frac{{\partial {Q_{me}}}}{{\partial \lambda }}& = - \sum _{\ell =n}^N \left( {\begin{array}{c}N\\ \ell \end{array}}\right) \ell (P_{de})^{\ell - 1}\frac{{\partial {P_{de}}}}{{\partial \lambda }}{{(1 - {P_{de}})}^{N - \ell }}\nonumber \\&+ \sum _{\ell =n}^N \left( {\begin{array}{c}N\\ \ell \end{array}}\right) (P_{de})^\ell (N - \ell ){{(1 - {P_{de}})}^{N - \ell - 1}}\frac{{\partial {P_{de}}}}{{\partial \lambda }}, \end{aligned}$$

(34)

The Eq. (34) can be reduced to

$$\begin{aligned} \frac{{\partial {Q_{me}}}}{{\partial \lambda }}& = - \frac{{\partial {P_{de}}}}{{\partial \lambda }}\sum \limits _{\ell = n}^N {\left( {\begin{array}{c}N\\ \ell \end{array}}\right) (P_{de})^{\ell - 1}{{(1 - {P_{de}})}^{N - \ell }}}\nonumber \\& \quad \times \left[ {\ell - (N - \ell )\frac{{{P_{de}}}}{{1 - {P_{de}}}}} \right] , \end{aligned}$$

(35)

In the case of $\kappa -\mu$ fading, $P_{de}={\bar{P}}_{de}^{\kappa -\mu }$, we get

$$\begin{aligned} \frac{\partial {P_{de}}}{\partial \lambda }& = - \mathcal {A}(1 - 2q)\sum \limits _{v = 0}^\infty {\frac{\varGamma (v + \mu )}{v!(u + v - 1)!}} \frac{{\lambda ^{u + v - 1}}\exp ( - \frac{\lambda }{2})}{2^{u + v}}\nonumber \\& \quad \times {\left( {\frac{{{\bar{\gamma }}_{s} }}{{\mu (1 + \kappa ) + {\bar{\gamma }}_{s} }}} \right) ^{\mu + v}}{}_1{\mathcal {F}_1}\left( {v + \mu ;\mu ;\frac{{{\mu ^2}\kappa (1 + \kappa )}}{{\mu (1 + \kappa ) + {\bar{\gamma }}_{s} }}} \right) . \end{aligned}$$

(36)

Using (32) and (35), the solution to $\frac{{\partial {Q_{e}}}}{{\partial \lambda }} =0$ for $\lambda$ can be estimated numerically. The estimated value is the optimal threshold value in $\kappa -\mu$ environment. Similarly, in $\eta -\mu$ fading, $P_{de}={\bar{P}}_{de}^{\eta -\mu }$, then

$$\begin{aligned} \frac{\partial {P_{de}}}{\partial \lambda }& = - (1 - 2q)\frac{{\sqrt{\pi }h^{\mu }}}{{\varGamma (\mu )}}{\left[ {\frac{\mu }{{{\bar{\gamma }}_s }}} \right] ^{2\mu }}\sum \limits _{v = 0}^\infty {\frac{\varGamma (v + \mu )}{v!(u + v - 1)!}}\nonumber \\& \quad \times {(\lambda /2) ^{u + v - 1}}\exp (-\lambda /2) {\left( {1 + \frac{{2\mu h}}{{{\bar{\gamma }}_s }}} \right) ^{ - (v + 2\mu )}}\frac{{\varGamma (v + 2\mu )}}{{\varGamma (\mu + {\textstyle {1 \over 2}})}}\nonumber \\& \quad \times {}_2{\mathcal {F}_1}\left( {\frac{{v + 2\mu + 1}}{2},\frac{{v + 2\mu }}{2};\mu + \frac{1}{2};{{\left( {\frac{{2\mu H}}{{{\bar{\gamma }}_s + 2\mu h}}} \right) }^2}} \right) . \end{aligned}$$

(37)

Using (32) and (35), the solution to ${\partial Q_{e}}/{\partial \lambda } = 0$ for $\lambda _{opt}$ can be estimated numerically. The estimated value is the optimal threshold value in $\eta -\mu$ environment.

4 Discussions on Analytical Results

Current section presents proposed system performance with the help of MATLAB based results. The derived mathematical expressions (11) and (17) contains infinite series (terms) that should be truncated without decreasing accuracy. The terms required, indicated as $T_N$, can be calculated using MATLAB to get at least 5th place of decimal digit. Table 1 shows $T_N$ values for different ${\bar{\gamma }}_{s}$, $\kappa$ and $\mu$ values in the numerical evaluation of (11). For a fixed target of $T_N$, it is observed that accuracy increases as any one of the system parameters increases. Table 2 also presents $T_N$ required for the evaluation of (17). It is seen that when SNR fading parameter are high local performance increases.

Table 1 Evaluation of (11) to get required $T_N$ and 5th digit accuracy for $u=5$ and ${\bar{P}}_f=0.05$

Table 2 Evaluation of (17) to get required $T_N$ and 5th digit accuracy for $u=5$ and ${\bar{P}}_f=0.05$

Fig. 3

Performance of a single SU through ROC curves in the presence of noise plus $\kappa -\mu$ fading channel ($q=0$ and ${\bar{\gamma }}_{s}=10$ dB)

Fig. 4

Performance of a single SU through ROC curves ($\bar{P}_d$ versus $\bar{P}_f$) in the presence of noise plus $\eta -\mu$ ($q=0$ and ${\bar{\gamma }}_{s}=10$ dB)

Fig. 5

The total error rate performance comparison of a single SU ($N=1$) and multiple SUs ($N=5$, OR rule) for various $\eta$ and $\mu$ values ($q=0$, $u=5$ and ${\bar{\gamma }}_{s}=10$ dB, here $Q=Q_e$)

In Figs. 3 and 4, the receiver operating characteristics (ROC) curves under the influence of $\kappa -\mu$ and $\eta -\mu$ fading, respectively have been shown. The performance in terms detection probability increases when ${\bar{\gamma }}_{s}$ increases for fixed values of $\bar{P}_f$, $\kappa$, $\eta$, and $\mu$. as already mentioned in the introduction section that $\kappa -\mu$ model is quiet good for communication with LOS. The $\eta -\mu$ fading is also quiet good for communications with non-LOS. Hence, the performance in terms of detection probability is improved when $\kappa$ or $\eta$ increases for a specific value of $\bar{P}_f$, ${\bar{\gamma }}_{s}$, and $\mu$. Also, when $\mu$ increases detection performance is improved. The derived mathematical expressions are validated through computer based simulations. In Fig. 5, $Q_e$ is shown in terms of $\lambda$ for different $\eta$ and $\mu$ values. Minimum $Q_e$ is obtained for higher values of $\mu$ (number of clusters in fading increases as $\mu$ increases). For any set of $\eta$ and $\mu$ values, an optimal $\lambda$ at which $Q_e$ is minimum can be determined. It is seen that minimum $Q_e$ is achieved for the Nakagami-m fading case as compared to all other fading cases. It can also be seen that the network suffers more error rate with a single SU without cooperation ($N=1$) when compare to cooperative scheme ($N=5$).

Fig. 6

A comparative performance of different hard-decision schemes in terms of ${\bar{\gamma }}_{s}$ ($Q_{fe}=0.05$, $q=0$, $\eta =0.3$, $\mu =0.5$, $u=5$, and $N=5$)

In Fig. 6, $Q_{de}$ versus ${\bar{\gamma }}_{s}$, the comparative performance of hard-decision (OR rule, AND rule, and MAJORITY rule) schemes has been shown. In Fig. 6, it is seen that there is a significant improvement in detection performance with increase in ${\bar{\gamma }}_{s}$. This is due to the fact that for the huge value of ${\bar{\gamma }}_{s}$, noise in the S-channel decreases so that ${\bar{P}}_d$ increases at SU level. The $Q_{de}$ is maximum for OR rule as compared to all other schemes. The curve for non-cooperative sensing is also shown for comparison purposes. Also, less complexities can be involved while implementing the hard-decision schemes at FC.

Fig. 7

The total error rate performance of CSSS with erroneous sensing and reporting channels in $\kappa -\mu$ fading channel for different values of q ($N=5$, ${\bar{\gamma }}_{s}=10$ dB, and OR rule)

Fig. 8

Performance of CSSS with erroneous sensing and reporting channels through CROC under hard-decision fusion and for different q values ($\kappa =2$, $\mu =1$ (Rician fading), $N=5$, and ${\bar{\gamma }}_{s}=10$ dB)

Fig. 9

Optimal number of SUs ($n_{opt}$) for different values of $\lambda$, q, $\kappa$, and $\mu$ (${\bar{\gamma }}_{s}=10$ dB)

The impact of an error probability (q) of the both channels (sensing and reporting) on the total error and miss detection performance is shown in Figs. 7, and 8, respectively. In these figures, $q=0$ represents the CSSS without error i.e. error free CSSS. It can be observed that an error with q in the both sensing and reporting channels degrades the total error and miss detection performances of CSSS. It is an important to find out the optimum number of SUs, ${n_{opt}}$ which exactly used to make the final decision about the PU. In Fig. 9, ${n_{opt}}$ is shown as a function of $\lambda$ for different values of $\kappa$, $\mu$, and q. The ${n_{opt}}$ is also indicated for CSSS without error (i.e., $q=0$). It is seen in the figure that as q value increases, ${n_{opt}}$ value decreases. This is due to the fact that when the higher values of q are present in the channels, FC receives less number of binary decisions out of N number of decisions. Tables 3 and 4 describe the optimum values of N, and $\lambda$, respectively, for different $\kappa$, $\mu$, q, and N values. It can be noted that there is a significant impact on the optimum values of N and $\lambda$ for each of the parameter values. Table 5 describes the optimum values of $\lambda$ for different values of $\eta$, $\mu$, q, and N subject to each hard-decision scheme. It can also be noted that there is a significant impact on the optimum values of $\lambda$ for each of the parameter values. In Fig. 10, ${n_{opt}}$ is shown as a function of $\lambda$ for different values of $\eta$, $\mu$, and q. The ${n_{opt}}$ is also indicated for error free CSSS (when $q=0$ is set). It is seen in the figure that as q value increases, ${n_{opt}}$ value decreases. This is due to the fact that when the higher values of q are present in the channels, FC receives less number of binary decisions out of N number of decisions. Figure 11 depicts an influence of channel error (q) on the performance of total error rate. It is noted performance is degraded due to more error in both the channels.

Table 3 Optimal number of SUs ($n_{opt}$) for various values of ${\bar{\gamma }}_{s}$, $\lambda$, $\kappa$, and $\mu$ ($N=25$)

Table 4 Optimal values of $\lambda$ ($\lambda _{opt}$) for various values of $\kappa$, $\mu$, q, and N under different hard decision fusions (${\bar{\gamma }}_{s}=10$ dB)

Table 5 Optimal values of $\lambda$ ($\lambda _{opt}$) for various values of $\eta$, $\mu$, q, and N under different hard decision fusions (${\bar{\gamma }}_{s}=10$ dB)

Fig. 10

Optimal number of SUs ($n_{opt}$) for different values of $\lambda$, q, $\eta$, $\mu$, and N ($u=5$ and ${\bar{\gamma }}_{s}=10$ dB)

Fig. 11

The total error rate performance of CSSS with erroneous sensing and reporting channels in $\eta -\mu$ fading for various values of q ($N=5$, $u=5$, ${\bar{\gamma }}_{s}=10$ dB, and OR rule)

5 Conclusions

The optimization of ED-based CSSS has been studied subject to noise as well as generalized $\kappa -\mu$ or $\eta -\mu$ fading. Using systematic approach many novel and closed-form expressions at SU level and at CSSS level in fading have been developed. The analytical frameworks for optimization of CSSS have been developed. An optimal threshold value has been estimated where minimum total error rate value is obtained for all channel and network parameters values: fading parameters, the channel error, the average SNRs and number of SUs. As q value increases, optimal number of SUs decreases. This is due to fact that when the higher values of q are present in the channels, FC receives less number of binary decisions out of N number of decisions. High values of ${\bar{\gamma }}_{s}$, and N increases the overall detection probability significantly. It has been noted that for higher values of $\kappa$, $\eta$ and $\mu$ total error performance has been improved. The performance has been degraded at SUs and at FC due to more error in both the channels of sensing and reporting. When any one of $\kappa$, $\eta$ and $\mu$ increases performance has been improved for a fixed values of q and $\lambda$. The generated results are useful for developing a CSS system for terrestrial-satellite network in the filed of wireless communications. Cellular base station can be treated as licensed PU network and ground station or satellites can be treated as SUs on the same orbit in the case of terrestrial-satellite network.