1 Introduction

In present days, the uses of radio spectrum have become crowded due to increase in the number of communication networks and services. Various reports on spectrum utilization have shown an inefficient usage of spectrum statistics [1]. Hence, new method of allocation policy has to be introduced for the proper usage of radio spectrum. The cognitive radio (CR) concept is a better solution for an efficient utilization of available radio spectrum. The CR users called secondary users (SUs) [2] can utilize the available radio spectrum without interfering primary user’s (PU) operation. Spectrum sensing (SS) [3] is an important task to monitor the radio frequencies continuously. Notably, vacant bands present in the spectrum can be identified with the help of detection techniques. Conventional energy detection (CED) technique [4] is frequently used detection technique to identify the existence of PU by calculating the energy of the received signal. CED is the simplest one, non-coherent in nature, and also adds less complexity to CR network [5]. When a single CR based CED technique employed in the system, it might be facing a hidden terminal problem and thereby limiting its performance due to shadowing and fading effects. These drawbacks can be overcome by the cooperative spectrum sensing (CSS) [6] technique which introduces multiple CRs in the network to sense the spectrum and identify the existence of PU. The CSS network gives better detection probability values though shadowing and fading effects are present in the nature [7]. The performance of spectrum-sensing-based energy detection (ED) in cognitive radio networks (CRNs) over generalized fading channels and the fading channel is modelled by the extended generalized-K (EGK) distribution [8]. The average probability of detection of the energy detector (ED) over \(\upalpha -\upmu \) generalized fading channels with selection combining (SC) diversity reception using CSS network is discussed in [9]. An improved energy detection (IED) scheme [10] is introduced to improve the detection probability and to overcome the limitations present in the CED scheme. More precisely, the detection performance can be further improved significantly by replacing CED with an IED at each CR in CSS network [11]. The IED measures the received signal amplitude (i.e. PU’s transmitted signal) with an arbitrary positive power (p). In [12], an experimental approach of IED based spectrum sensing for CR network is proposed.

Sometimes, it is required to optimize the CSS network parameters to achieve the better performance and to minimize the complexity of the network. Optimization of CSS network using CED technique in CR network is discussed in [13]. In [14], optimized performance of CSS network is achieved by using a single antenna at each CR with an IED scheme over Rayleigh fading channel. In [15], performance is analyzed in CSS network using multiple antennas at each CR with an IED scheme over Rayleigh fading channel. The CSS network with an IED scheme is considered in [16] which uses optimization techniques to minimize the total error rate (It is the sum of missed detection and false alarm probabilities). The performance of CSS network with a single antennas at each CR with CED scheme over Rician fading channel is analyzed in [17]. Optimization of CSS network parameters with an IED scheme using the multiple antennas at each CR is investigated over AWGN and Rayleigh fading channels [18]. Similar analysis is carried out in Nakagami-m and Weibull fading channel with an IED scheme in [19,20,21].

It is also important to maximize the average channel throughput and network utility function to improve the detection performance of PUs. Due to fading effect in the environment sometimes PUs are not detected correctly, this may cause sever interference problem. This issue can be overcome, and PUs are exactly identified if the sensing time of each SU user is increases, this reduces the throughput value of the network. Hence, there is a trade-off between sensing time and throughput value of the network [22]. Throughput value can be increased if the sensing time decreases but it degrades the accurate detection of PUs. Hence, average channel throughput value will be increased by performing sensing and transmission simultaneously [23]. In [24], throughput maximization is considered over erroneous control channel using CED scheme. Similarly, network utility function should be maximized to improve the detection performance of PUs and to improve the spectral efficiency. The network utility function is maximized using an optimal number of SUs is addressed in [25]. Maximization of average channel throughput and network utility function performance analysis is evaluated using multiple antennas at each CR with an IED scheme over AWGN channel in [26].

It is an important to study optimal detection performance of IED based CSS network in Weibull fading environment because this channel has been developed in modelling multi-path waves propagating in non-homogeneous communication environments [27]. Weibull distribution is very flexible in both indoor and outdoor communication environments. Rayleigh and exponential distributions are considered as special cases of Weibull fading distribution for a certain fading parameter values. In urban communication environments, the distributions have the capability of accounting for propagation if the Rayleigh distribution fails e.g., digital enhanced cordless telecommunications (DECT) system. However, in spite of the usefulness of this distribution, the work related to CSS network with an IED scheme using multiple antennas at each CR over Weibull fading is not reported in the literature.

These above-stated literature papers are driven us to evaluate the performance of CROC curves, total error rate, average channel throughput and network utility function using the multiple antennas at each CR with an IED scheme over Weibull faded channel in this paper. Finally, with this paper, our contributions to an existing literature are as follows:

  • We have derived the novel closed-form of expression for missed detection probability \(\left( {P_m } \right) \), probability of false alarm \(\left( {P_f } \right) \) using the multiple antennas at each CR in Weibull fading channel.

  • The novel analysis of complementary receiver operating characteristics (CROC) is discussed with the firm support of analytical expressions and support of MATLAB simulations.

  • Selection combining (SC) diversity scheme is used at each CR to select the maximum value of decision statistics obtained from an IED at all antennas. The closed form of expressions for a threshold value using a single and multiple antennas at each CR for the CSS network are derived.

  • The novel closed-form of expressions are derived for optimized network parameters such as an optimum number of CR users \(\left( {N_{opt} } \right) \), the optimum value of threshold \(\left( {\lambda _{opt} } \right) \), and the optimum value of arbitrary power of received signal \(\left( {p_{opt} } \right) \) for a single and multiple antennas case.

  • The optimized expressions of network parameters are derived using hard decision fusion rules (OR-Rule and AND-Rule) at FC. The total error rate (\(Q_m +Q_f )\) analysis also discussed using these fusion rules.

  • Average channel throughput and maximization of network utility function analysis are evaluated using \(k=1+n\) and \(k=N-n\) fusion rules at FC over Weibull fading channel.

  • The impact of several network parameters such as fading parameter (V), multiple antennas at each CR (M), number of CR users (N), threshold value (\(\uplambda )\), and average S-channel SNR \(({\bar{\gamma }})\) on the proposed CSS network are investigated.

  • Comparison between CED and IED with (\(M>1\)) and without (\(M=1\)) diversity antenna case is also evaluated.

2 System model

The system model for an IED scheme is shown in Fig. 1. The functioning of IED is similar to CED. In [5], functioning of CED is described, it calculates the energy of the received signal. In case of IED [19], it measures the received signal strength with an arbitrary power (p) rather than squaring device. This extra feature in IED block diagram improves the detection performance about the PU.

Fig. 1
figure 1

System model of an improved energy detector

Full size image
Fig. 2
figure 2

Proposed model of cooperative spectrum sensing network

Full size image

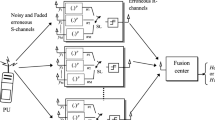
The proposed model of CSS network is shown in Fig. 2, it consist of multiple number of CR users (N), each CR is equipped with multiple antennas (M), a fusion center (FC), and a primary user (PU). In sensing channel (S-channel), each CR senses and stores the information about the PU. The sensing information available with each CR is reported to the FC through reporting channel (R-channel). The complete information is collected at FC, and final decision about the PU is taken at FC using fusion rules such as hard decision rules (OR-Rule and AND-Rule), k-out of N rules (\(k=1+n\) and \(k=N-n)\), where k represents the selected number of CRs, N is total number of available CRs, and n is a positive integer (\(n=2\)).

Based on received signal at j-th CR, the existence of PU (absence of PU:\(H_0 \) and presence of PU:\(H_1\)) can be decided using [5]:

$$\begin{aligned} y(\hbox {t})=\left\{ {\begin{array}{ll} n_j (t):&{} \quad H_0 \\ h_j *s(t)+n_j (t):&{} \quad H_1 \\ \end{array}} \right. \end{aligned}$$
(1)

In above expression s(t) represent the received signal at the input of IED, \(n_j (t)\) is the noise value at j-th CR and \(h_i \) is fading coefficient. In the proposed CSS network each CR equipped with multiple antennas (M), an IED scheme is used to detect the spectrum hole. Finally, expression at i-th antenna to make a local decision about the PU is given by [11]:

$$\begin{aligned} W_i =\left| {y_i} \right| ^{p}\quad p>0 \end{aligned}$$
(2)

For IED, p value should be more than 2, i.e., (\(p>\) 2) to achieve better detection probability than CED.

Each CR uses an IED technique to get the decision statistics from all (\(i = 1{\ldots }.M\)) antennas. With the help of selection combining, the largest value of \(w_i \) can be selected from all available \(w_i \) values and it is denoted as Z. Finally, to make decision about the PU, the value of Z is compared with detection threshold (\(\lambda \)) as given in [15],

$$ \begin{aligned} Z>\lambda :H_1 \& \,Z<\lambda :H_0 \end{aligned}$$
(3)

where \(\lambda \) can be obtained from the expression:

$$\begin{aligned} \lambda =\lambda _n \sigma _n^p . \end{aligned}$$
(4)

where \(\lambda _n \) represents the fixed normalized detection threshold value and \(\sigma _n^2 \) represents the noise power for \(p=2\).

The missed detection probability \((P_m )\) expression for Weibull fading channel is calculated with the help of pdf given in [26]:

$$\begin{aligned}&f_{w_i |H_1 } (\hbox {y})=\frac{2y^{\left( {2\big /p} \right) -1}C}{p}\left[ {\frac{\Gamma (\mathrm {P})}{(E_s \sigma _h^2 +\sigma _n^2 )}} \right] \left( {\hbox {y}^{2\big /p}} \right) ^{\mathrm{C}-1}\nonumber \\&\quad \quad \quad \quad \exp \left( {-\left\{ {\frac{y^{2\big /p}\Gamma (\mathrm {P})}{(E_s \sigma _h^2 +\sigma _n^2 )}} \right\} ^{C}} \right) \end{aligned}$$
(5)

where \(C=V/2\), \(P=1+1/C\), and V—is the Weibull fading parameter.

The missed detection probability expression for Weibull fading channel can be calculated as follows [14]:

$$\begin{aligned} P_m= & {} pr(\hbox {y}<\lambda |\hbox {H}_1 )=\int _0^\lambda {f_{w_i |\mathrm{H}_1 } } (\hbox {y})\hbox {dy} \end{aligned}$$
(6)
$$\begin{aligned}= & {} \int _0^\lambda \frac{2y^{\left( {2\big /p} \right) -1}C}{p}\left[ {\frac{\Gamma (\mathrm {P})}{(E_s \sigma _h^2 +\sigma _n^2 )}} \right] \left( {\hbox {y}^{2\big /p}} \right) ^{\mathrm{C}-1}\nonumber \\&\quad \exp \left( {-\left\{ {\frac{y^{2\big /p}\Gamma (P)}{(E_s \sigma _h^2 +\sigma _n^2 )}} \right\} ^{C}} \right) dy \end{aligned}$$
(7)
$$\begin{aligned}= & {} \int _0^{\left( {\frac{\Gamma (\mathrm {P})\lambda ^{2\big /p}}{(E_s \sigma _h^2 +\sigma _n^2 )}} \right) } {\exp (-\hbox {t})\hbox {dt}} \end{aligned}$$
(8)
$$\begin{aligned} P_m= & {} \left[ {1-\exp \left( {-\left\{ {\frac{\lambda ^{2\big /P}\Gamma (\mathrm {P})}{\sigma _n^2 (1+{\bar{\gamma }} )}} \right\} ^{C}} \right) } \right] \end{aligned}$$
(9)

where \({\bar{\gamma }}={E_s \sigma _h^2 }\big /p{\sigma _n^2 }\) is S-channel SNR, \(E_s \) is the signal energy, \(\sigma _h^2 \) is the fading channel coefficient variance.

We have considered that each CR is having multiple antennas and selection combining (SC) scheme is used to select the maximum value of antenna among all antennas (M).

Using the SC diversity scheme maximum value from all branches can be calculated as described in [15]

$$\begin{aligned} P_m =\Pr [\max (W_1 ,W_2 ,W_3 ...W_M )] \end{aligned}$$
(10)

Using the SC diversity under the hypothesis \(H_1\), the missed detection probability can be calculated as:

$$\begin{aligned} P_m =\Pr [\max (W_1 ,W_2 ,W_3 ...W_M )\le \;\lambda |H_1 ] \end{aligned}$$
(11)

The closed form of \(P_m \) expression for Weibull fading channel using an IED scheme with multiple antennas (M) at each CR is given in [20]:

$$\begin{aligned} P_m =\left[ {1-\exp \left( {-\left\{ {\frac{\lambda ^{2\big /P}\Gamma (\mathrm {P})}{\sigma _n^2 (1+\overline{\gamma })}} \right\} ^{C}} \right) } \right] ^{M} \end{aligned}$$
(12)

The \(P_m \) expression is different for different fading channels because it depends upon S-channel SNR. Similarly, expression for probability false alarm \((P_f )\) with a single antenna at each CR can be calculated using the pdf given in [26]:

$$\begin{aligned}&f_{w_i |\hbox {H}_0 } (\hbox {y})=\frac{2y^{\left( {2\big /p} \right) -1}C}{p}\left[ {\frac{\Gamma (\mathrm {P})}{(\sigma _n^2 )}} \right] \left( {\hbox {y}^{2\big /p}} \right) ^{\mathrm{C}-1}\nonumber \\&\quad \qquad \qquad \exp \left( {-\left\{ {\frac{\hbox {y}^{2\big /p}\Gamma (\mathrm {P})}{(\sigma _n^2 )}} \right\} ^{C}} \right) \end{aligned}$$
(13)

where \(C=V\big /2\), \(P=1+1\big /C\), and V – is the Weibull fading parameter.

The probability of false alarm expression for Weibull fading channel can be calculated as [14]:

$$\begin{aligned} P_f= & {} pr(y>\lambda |\hbox {H}_0 )=1-\int _0^\lambda {f_{w_i |\mathrm{H}_0 } } (\hbox {y})\hbox {dy} \end{aligned}$$
(14)
$$\begin{aligned}= & {} 1-\int _0^\lambda \frac{2y^{\left( {2\big /p} \right) -1}C}{p}\left[ {\frac{\Gamma (\mathrm {P})}{(\sigma _n^2 )}} \right] \left( {\hbox {y}^{2\big /p}} \right) ^{\mathrm{C}-1}\nonumber \\&\quad \qquad \qquad \exp \left( {-\left\{ {\frac{\hbox {y}^{2\big /p}\Gamma (\mathrm {P})}{(\sigma _n^2 )}} \right\} ^{C}} \right) dy \end{aligned}$$
(15)
$$\begin{aligned}= & {} 1-\int _0^{\left( {\frac{\Gamma (\mathrm {P})\lambda ^{2\big /p}}{(\sigma _n^2 )}} \right) } {\exp (-\hbox {t})\hbox {dt}} \end{aligned}$$
(16)
$$\begin{aligned} P_f= & {} \left[ {\exp \left( {-\left\{ {\frac{\lambda ^{2\big /P}\Gamma (\mathrm {P})}{\sigma _n^2 }} \right\} ^{C}} \right) } \right] \end{aligned}$$
(17)

If we consider multiple antennas (M) at each CR using selection combining (SC) diversity scheme, then expression for \((P_f )\) will be:

$$\begin{aligned} P_f =1-\left[ {1-\exp \left( {-\left\{ {\frac{\lambda ^{2\big /P}\Gamma (\mathrm {P})}{\sigma _n^2 }} \right\} ^{C}} \right) } \right] ^{M} \end{aligned}$$
(18)

2.1 Threshold calculation

Threshold value is more important to decide the presence or absence of primary user. It is also important to draw the complementary receiver operating characteristics (CROC) in the presence of Weibull fading channel. The closed form of expression for threshold value with a single antenna at each CR can be calculated using the \(P_f \) expression given by Eq. (17). Applying logarithm on both sides to Eq. (17), then it reduces to:

$$\begin{aligned} \ln (P_f )=-\left\{ {{\lambda ^{2\big /P}\Gamma (\mathrm {P})}/{\sigma _n^2 }} \right\} ^{C} \end{aligned}$$
(19)
$$\begin{aligned} \lambda =\left( {\frac{\sigma _n^2 }{\Gamma (\mathrm {P})}\left( {\ln \left( {1\big /{P_f }} \right) } \right) ^{1\big /C}} \right) ^{p\big /2} \end{aligned}$$
(20)

The above expression is useful to set the threshold value for the identification of PU in case of single antenna at each CR.

Similarly, the closed form of expression for threshold value using the multiple antennas at each CR can be calculated with the help of Eq. (18). Applying logarithm on both sides to Eq. (18) then it reduces to:

$$\begin{aligned} {\Longrightarrow }M\ln \left( {1-\exp \left( {-\left\{ {\frac{\lambda ^{2\big /P}\Gamma (\mathrm {P})}{\sigma _n^2 }} \right\} ^{C}} \right) } \right) =\ln \left( {1-P_f } \right) \nonumber \\ \end{aligned}$$
(21)

after simplification and step by step analysis is provided in “Appendix” section. Finally, the expression for threshold value is:

$$\begin{aligned} \lambda =\left( {\frac{\sigma _n^2 }{\Gamma (\mathrm {P})}\left( {\ln \left( {1\big /{\left( {1-\exp \left( {{\ln (1-P_f )}\big /M} \right) } \right) }} \right) } \right) ^{1\big /C}} \right) ^{p\big /2}\nonumber \\ \end{aligned}$$
(22)

With the help of above expression, the threshold can be set for the identification of PU when the multiple antennas are used at each CR.

3 Optimization of CSS network parameters

3.1 Optimization of threshold value using \(P_f \) and \(P_m \) expressions

An optimum value of threshold (\(\lambda _{opt} )\) is required to decide the existance of PU with minimum value of threshold. The closed form of expression for \(\lambda _{opt} \) for a single antenna case can be calculated by differentiate Eqs. (9 and 17) w.r.t to \(\uplambda \):

$$\begin{aligned}&\frac{\partial P_f }{\partial \lambda }+\frac{\partial P_m }{\partial \lambda }=0 \end{aligned}$$
(23)
$$\begin{aligned}&{\Longrightarrow }-\exp \left( {-\left\{ {\frac{\lambda ^{2\big /p}\Gamma (\mathrm {P})}{\sigma _n^2 }} \right\} ^{C}} \right) C\left\{ {\frac{\lambda ^{2\big /p}\Gamma (\mathrm {P})}{\sigma _n^2 }} \right\} ^{C-1}\frac{2\lambda ^{\left( {2\big /p} \right) -1}\Gamma (\mathrm {P})}{p\sigma _n^2 }\nonumber \\&\quad +\exp \left( {-\left\{ {\frac{\lambda ^{2\big /p}\Gamma (\mathrm {P})}{\sigma _n^2 \left( {1+\gamma } \right) }} \right\} ^{C}} \right) C\left\{ {\frac{\lambda ^{2\big /p}\Gamma (\mathrm {P})}{\left( {1+\gamma } \right) \sigma _n^2 }} \right\} ^{C-1}\frac{2\lambda ^{\left( {2\big /p} \right) -1}\Gamma (\mathrm {P})}{p\sigma _n^2 \left( {1+\gamma } \right) }\!=\!0\nonumber \\ \end{aligned}$$
(24)

after simplification and step by step analysis is provided in Appendix. Finally, expression for \(\lambda _{opt} \) is:

$$\begin{aligned} \lambda _{opt} =\left( {\frac{\sigma _n^2 }{\Gamma (\mathrm {P})}\left( {{C\ln \left( {1+\gamma } \right) }\Bigg /{\left( {1-\left\{ {\frac{1}{\left( {1+\gamma } \right) }} \right\} ^{C}} \right) }} \right) ^{1\big /C}} \right) ^{P\big /2}\nonumber \\ \end{aligned}$$
(25)

Similarly, the closed form of expression for \(\lambda _{opt} \) with the multiple antennas (\(M=3\)) at each CR case can be calculated using the above procedure and final expression for \(\lambda _{opt} \) is:

$$\begin{aligned} \lambda _{opt} =\left( {\frac{\sigma _n^2 }{\Gamma (\mathrm {P})}\left( {{C\ln \left( {1+\gamma } \right) }\Bigg /{\left( {2\left\{ {\frac{\gamma }{\left( {1+\gamma } \right) }} \right\} ^{C}} \right) }} \right) ^{1\big /C}} \right) ^{P\big /2}\nonumber \\ \end{aligned}$$
(26)

3.2 Optimization of arbitrary power of received signal (p) using \(P_f \) and \(P_m \) expressions

It is also necessary to optimize the arbitrary power of the received signal. The optimum value of p (\(p_{opt} \)) can be calculated by differentiating Eqs. (9) and (17) w.r.t p for a single antenna case:

$$\begin{aligned} \frac{\partial P_f }{\partial p}+\frac{\partial P_m }{\partial p}= & {} 0 \end{aligned}$$
(27)
$$\begin{aligned} \frac{\partial P_m }{\partial p}= & {} -M\left[ {1-\hbox {exp} \left( {-\left\{ {\frac{\lambda ^{2\big /p}\Gamma (\mathrm {P})}{\sigma _n^2 (1+\gamma )}} \right\} ^{C}} \right) } \right] ^{M-1}\nonumber \\&\quad \hbox {exp} \left( {-\left\{ {\frac{\lambda ^{2\big /p}\Gamma (\mathrm {P})}{\sigma _n^2 (1+\gamma )}} \right\} ^{C}} \right) C\left\{ {\frac{\lambda ^{2\big /p}\Gamma (\mathrm {P})}{\sigma _n^2 (1+\gamma )}} \right\} ^{C-1}\nonumber \\&\quad \quad \frac{2}{p^{2}}\frac{\lambda ^{\left( {2\big /p} \right) }\log \lambda \Gamma (\mathrm {P})}{\sigma _n^2 (1+\gamma )} \end{aligned}$$
(28)
$$\begin{aligned} \frac{\partial P_f }{\partial p}= & {} M\left[ {1-\exp \left( {-\left\{ {\frac{\lambda ^{2\big /p}\Gamma (\mathrm {P})}{\sigma _n^2 }} \right\} ^{C}} \right) } \right] ^{M-1}\nonumber \\&\quad \quad \hbox {exp} \left( {-\left\{ {\frac{\lambda ^{2\big /p}\Gamma (\mathrm {P})}{\sigma _n^2 }} \right\} ^{C}} \right) C\left\{ {\frac{\lambda ^{2\big /p}\Gamma (\mathrm {P})}{\sigma _n^2 }} \right\} ^{C-1}\nonumber \\&\quad \quad \frac{2}{p^{2}}\frac{\lambda ^{\left( {2\big /p} \right) }\log \lambda \Gamma (\mathrm {P})}{\sigma _n^2 } \end{aligned}$$
(29)

after simplification and step by step analysis is provided in “Appendix”. Finally, expression for \(p_{opt} \) is:

$$\begin{aligned} p_{opt} =\frac{2\ln \lambda }{\ln \left( {\left\{ {\frac{C\ln \left( {1+\gamma } \right) }{\left[ {1-\left( {\frac{1}{1+\gamma }} \right) ^{C}} \right] }} \right\} ^{1\big /C}\left( {\frac{\sigma _n^2 }{\Gamma (\mathrm {P})}} \right) } \right) } \end{aligned}$$
(30)

Similarly, the closed form of expression for \(p_{opt} \) with the multiple antennas (\(M=3\)) at each CR case can be calculated using the above procedure and final expression is:

$$\begin{aligned} p_{opt} =\frac{2\ln \lambda }{\ln \left( {\left\{ {\frac{C\ln \left( {1+\gamma } \right) }{(0.5)\left[ {1-\left( {\frac{1}{1+\gamma }} \right) ^{C}} \right] }} \right\} ^{1\big /C}\left( {\frac{\sigma _n^2 }{\Gamma (\mathrm {P})}} \right) } \right) } \end{aligned}$$
(31)

4 Total error calculations using hard decision rules

We have assumed that R-channel is perfect channel (i.e. error free R-channel) to calculate total error probability \((Q_m +Q_f )\) in different fading channels. Firstly, we require probability of false alarm \((P_f )\) and probability of missed detection \((P_m )\) expressions for each CR. Secondly, we can calculate \(Q_m \) and \(Q_f \) values using the below expressions, which are missed detection and false alarm probabilities of all CRs. The \(Q_m \) and \(Q_f \) expressions with an error rate \((p_e )\) in R-channel are given as [14]:

$$\begin{aligned} Q_f= & {} 1-[(1-P_f )(1-p_e )+p_e P_f ]^{N} \nonumber \\ Q_m= & {} [P_m (1-p_e )+p_e (1-P_m )]^{N} \end{aligned}$$
(32)

Finally, total error rate Z(N) is calculated by taking the sum of \(Q_f \) and \(Q_m \) as [14]:

$$\begin{aligned} Z(p,\lambda ,N)\cong Q_f +Q_m \end{aligned}$$
(33)

Expressions for \(Q_m \) and \(Q_f \) with perfect R-channel (\(p_e =0\)) when OR-logic is used at FC:

$$\begin{aligned} Q_f= & {} 1-[(1-P_f )]^{N} \nonumber \\ Q_m= & {} [P_m ]^{N} \end{aligned}$$
(34)

Similarly, expressions for \(Q_m \) and \(Q_f \) when AND-logic is used at FC:

$$\begin{aligned} Q_m= & {} 1-[(1-P_m )]^{N} \nonumber \\ Q_f= & {} [P_f ]^{N} \end{aligned}$$
(35)

4.1 Optimization of network parameters using ‘OR-Rule’ at FC

4.1.1 Optimization of number of CRs \((N_{opt} )\):

Optimization of number of CRs is required to achieve better performance with minimum number of CR numbers. Here we are calculating \(N_{opt} \) value for perfect channel. The closed form of expression for \(N_{opt} \) value for OR-Rule can be calculated using Eq. (33) as follows:

$$\begin{aligned}&\hbox {Total error rate}: \hbox {Z}(\hbox {N})=Q_m +Q_f \nonumber \\&\Delta \hbox {Z}(\hbox {N})=\hbox {Z}(\hbox {N}+1)-Z(\hbox {N})\nonumber \\&\Longrightarrow 1-[(1-P_f )]^{N+1}-1+[(1-P_f )]^{N}\nonumber \\&\quad +\, [P_m ]^{N+1}-[P_m ]^{N}=0, \end{aligned}$$
(36)

step by step analysis is provided in “Appendix” section. Finally, the expression for \(N_{opt} \) using OR-Rule at FC is

$$\begin{aligned} N_{opt} \quad = \quad \left\lceil {\frac{\ln \left( {\frac{1-P_m }{P_f }} \right) }{\ln \left( {\frac{1-P_f }{P_m }} \right) }} \right\rceil \end{aligned}$$
(37)

4.1.2 Optimization of threshold value \(\left( {\lambda _{opt} } \right) \)

The closed form of expression for \(\lambda _{opt} \) value can be calculated by differentiating Eq. (33) w.r.t to \(\uplambda \), and equating to zero.

$$\begin{aligned}&\frac{\partial Q_m }{\partial \lambda }+\frac{\partial Q_f }{\partial \lambda }=0 \end{aligned}$$
(38)
$$\begin{aligned}&\Longrightarrow {N}\left( {1-P_f } \right) ^{N-1}\frac{\partial P_f }{\partial \lambda }+N\left( {P_m } \right) ^{N-1}\frac{\partial P_m }{\partial \lambda }=0 \end{aligned}$$
(39)

For a single antenna case (\(M=1\)), \({\partial P_f }\big /{\partial \lambda }\) and \({\partial P_m }\big /{\partial \lambda }\) expressions are given in Eq. (24), substituting Eqs. (24) in (39), applying logarithm on both sides and solving algebric expressions, the above expression reduces to

$$\begin{aligned} \lambda _{opt}= & {} \left( \frac{\sigma _n^2 }{\Gamma (\mathrm {P})}\left( \left( {N-1} \right) \left( {\ln \left( {\frac{1-P_f }{P_m }} \right) } \right) \right. \right. \nonumber \\&\left. \left. \,+\,C\ln \left( {1+\gamma } \right) \Bigg /{\left( {1-\left\{ {\frac{1}{\left( {1+\gamma } \right) }} \right\} ^{C}} \right) } \right) ^{1\big /C} \right) ^{P\big /2}\nonumber \\ \end{aligned}$$
(40)

The above expression represents the optimum value of \(\uplambda \) with a single antenna at each SU, multiple number of SUs (N), and using OR-Rule at FC in the proposed CSS network.

Similarly, using the multiple antennas (\(M=3\)) at each CR and multiple number of SUs (N) in the proposed CSS network, the closed form of expression for \(\lambda _{opt} \) is:

$$\begin{aligned} \lambda _{opt}= & {} \left( \frac{\sigma _n^2 }{\Gamma (\mathrm {P})}\left( \left( {N-1} \right) \left( {\ln \left( {\frac{1-P_f }{P_m }} \right) } \right) \right. \right. \nonumber \\&\left. \left. \,+\,C\ln \left( {1+\gamma } \right) \Bigg /\left( {2\left\{ {\frac{\gamma }{\left( {1+\gamma } \right) }} \right\} ^{C}} \right) \right) ^{1\big /C} \right) ^{P/2}\nonumber \\ \end{aligned}$$
(41)

4.1.3 Optimization of arbitrary power of the received siganl \(\left( {p_{opt} } \right) \)

The closed form of expression for \(p_{opt} \) can be calculated by differentiating Eq. (33) w.r.t to p,

$$\begin{aligned}&\frac{\partial Q_m }{\partial p}+\frac{\partial Q_f }{\partial p}=0 \end{aligned}$$
(42)
$$\begin{aligned}&\Longrightarrow {N}\left( {1-P_f } \right) ^{N-1}\frac{\partial P_f }{\partial p}+\left( {P_m } \right) ^{N-1}\frac{\partial P_m }{\partial p}=0 \end{aligned}$$
(43)

For a single antenna case (\(M=1\)), \({\partial P_f }/{\partial p}\) and \({\partial P_m }\big /{\partial p}\) expressions are given in Eqs. (28) and  (29), substituting these equations in Eq. (42), apply logarithm on both sides, after simplification, the closed form of expression for \(p_{opt} \) is:

$$\begin{aligned} p_{opt} =\frac{2\ln \lambda }{\ln \left( {\left( {\frac{\left( {N-1} \right) \left( {\ln \left( {\frac{1-P_f }{P_m }} \right) } \right) \,+\,C\ln \left( {1+\gamma } \right) }{\left( {1-\left( {\frac{1}{1+\gamma }} \right) ^{C}} \right) }} \right) ^{1\big /C}\frac{\sigma _n^2 }{\Gamma (\mathrm {P})}} \right) }\nonumber \\ \end{aligned}$$
(44)

The above expression represents an optimum value of p with a single antenna at each SU, multiple number of SUs (N), and using OR-Rule at FC in the proposed CSS network.

Similarly, using the multiple antennas (\(M=3\)) at each CR and multiple number of SUs (N) in the proposed CSS network, the closed form of expression for \(p_{opt} \) is:

$$\begin{aligned} p_{opt} =\frac{2\ln \lambda }{\ln \left( {\left( {\frac{\left( {N-1} \right) \left( {\ln \left( {\frac{1-P_f }{P_m }} \right) } \right) \,+\,C\ln \left( {1+\gamma } \right) }{\left( {(0.5)\left( {\frac{\gamma }{1+\gamma }} \right) ^{C}} \right) }} \right) ^{1\big /C}\frac{\sigma _n^2 }{\Gamma (\mathrm {P})}} \right) }\nonumber \\ \end{aligned}$$
(45)

4.2 Optimization of network parameters using ‘AND-Rule’ at FC

4.2.1 Optimization of number of CRs \((N_{opt} )\)

The closed form of expression for \(N_{opt} \) value using AND-logic at FC can be calculated using Eqs. (35) and (36) as follows:

$$\begin{aligned}&\Longrightarrow 1-[(1-P_m )]^{N+1}-1+[(1-P_m )]^{N}\nonumber \\&+\, [P_f ]^{N+1}-[P_f ]^{N}=0 \end{aligned}$$
(46)

after simplification, above expression reduces to

$$\begin{aligned} \Longrightarrow \left( {{\left( {1-P_f } \right) }\Bigg /{P_m }} \right) =\left( {{\left( {1-P_m } \right) }\Bigg /{P_f }} \right) ^{N}, \end{aligned}$$

applying logarithm on both sides, the final expression for \(N_{opt} \) is:

$$\begin{aligned} N_{opt} \quad = \quad \left\lceil {\frac{\ln \left( {\frac{1-P_f }{P_m }} \right) }{\ln \left( {\frac{1-P_m }{P_f }} \right) }} \right\rceil \end{aligned}$$
(47)

4.2.2 Optimization of threshold value \(\left( {\lambda _{opt} } \right) \)

The closed form of expression for \(\lambda _{opt} \) value can be calculated using Eqs. (24), (35), (38), and (39) and, applying logarithm on both sides and solving algebric expressions, the expression for \(\lambda _{opt} \) is:

$$\begin{aligned} \lambda _{opt}= & {} \left( \frac{\sigma _n^2 }{\Gamma (\mathrm {P})}\left( \left( {N-1} \right) \left( {\ln \left( {\frac{P_f }{1-P_m }} \right) } \right) \right. \right. \nonumber \\&\left. \left. +\,C\ln \left( {1+\gamma } \right) \Bigg / \left( {1-\left\{ \frac{1}{\left( {1+\gamma } \right) } \right\} ^{C}} \right) \right) ^{1\big /C} \right) ^{P\big /2} \end{aligned}$$
(48)

The above expression represents an optimum value of \(\uplambda \) with single antenna at each SU, multiple number of SUs (N), and using AND-Rule at FC in the proposed CSS network.

Similarly, using the multiple antennas (\(M=3\)) at each CR and multiple number of SUs (N) in the proposed CSS network, the expression for \(\lambda _{opt} \) is:

$$\begin{aligned} \lambda _{opt}= & {} \left( \frac{\sigma _n^2 }{\Gamma (\mathrm {P})}\left( \left( {N-1} \right) \left( {\ln \left( {\frac{P_f }{1-P_m }} \right) } \right) \right. \right. \nonumber \\&\left. \left. +\,C\ln \left( {1+\gamma } \right) \Bigg /{\left( {2\left\{ {\frac{\gamma }{\left( {1+\gamma } \right) }} \right\} ^{C}} \right) } \right) ^{1\big /C} \right) ^{P\big /2} \end{aligned}$$
(49)

4.2.3 Optimization of arbitrary power of the received siganl \(\left( {p_{opt} } \right) \)

The closed form of expression for \(p_{opt} \) value can be calculated using Eqs. (28), (29), (35), (42), and (43), applying logarithm on both sides and solving algebric expressions, the expression for \(\lambda _{opt} \) is:

$$\begin{aligned} p_{opt} =\frac{2\ln \lambda }{\ln \left( {\left( {\frac{\left( {N-1} \right) \left( {\ln \left( {\frac{P_f }{1-P_m }} \right) } \right) \,+\,C\ln \left( {1+\gamma } \right) }{\left( {1-\left( {\frac{1}{1+\gamma }} \right) ^{C}} \right) }} \right) ^{1\big /C}\frac{\sigma _n^2 }{\Gamma (\mathrm {P})}} \right) } \end{aligned}$$
(50)

The above expression represents an optimum value of p with a single antenna at each SU, multiple number of SUs (N), and using AND-Rule at FC in the proposed CSS network.

Similarly, using the multiple antennas (\(M=3\)) at each CR and multiple number of SUs (N) in the proposed CSS network, the expression for \(p_{opt} \) is:

$$\begin{aligned} p_{opt} =\frac{2\ln \lambda }{\ln \left( {\left( {\frac{\left( {N-1} \right) \left( {\ln \left( {\frac{P_f }{1-P_m }} \right) } \right) \,+\,C\ln \left( {1+\gamma } \right) }{\left( {(0.5)\left( {\frac{\gamma }{1+\gamma }} \right) ^{C}} \right) }} \right) ^{1\big /C}\frac{\sigma _n^2 }{\Gamma (\mathrm {P})}} \right) }\nonumber \\ \end{aligned}$$
(51)

5 Throughput and network utility function analysis

The effective probability expressions for the proposed CSS network are calculated by considering an error rate \(\left( {p_e } \right) \) in R-channel. The expressions for effective false alarm and detection probabilities are given in [25] as:

$$\begin{aligned} p_{fe}= & {} P_f \left( {1-p_e } \right) +p_e \left( {1-P_f } \right) \end{aligned}$$
(52)
$$\begin{aligned} p_{de}= & {} P_d \left( {1-p_e } \right) +p_e \left( {1-P_d } \right) \end{aligned}$$
(53)

The information associated with CRs are transferred to FC through R-channel in the form of binary decisions (either 0 or 1). The final decision about the PU is taken at FC using the fusion rules (\(k=1+n\) and \(k=N-n\)) with the help of following expressions given in [25]:

$$\begin{aligned} P_{F,k}= & {} \sum _{l=k}^N {\left( {\begin{array}{c} N \\ l \\ \end{array}} \right) p_{fe} ^{l}\left( {1-p_{fe} } \right) ^{N-l}} \end{aligned}$$
(54)
$$\begin{aligned} P_\mathrm{{D},k}= & {} \sum _{l=k}^N {\left( {\begin{array}{c} N \\ l \\ \end{array}} \right) p_{de} ^{l}\left( {1-p_{de} } \right) ^{N-l}} \end{aligned}$$
(55)

where k represent the number of selected SUs, N is the total number of SUs, and n is the positive arbitrary integer (we have assumed \(n=2\) in our simulations).

5.1 Average channel throughput analysis

The average channel throughput (\(C_{avg} \)) for a given CSS network is calculated by an expression given in [28]:

$$\begin{aligned} C_{avg,k} (N)=\varphi _0 +\varphi _1 P_{D,k} (N)-\varphi _2 P_{F,k} (N) \end{aligned}$$
(56)

where

$$\begin{aligned} \varphi _0= & {} P_1 \left( {\mathop {C_p }\limits ^\sim +\mathop {C_s }\limits ^\sim } \right) +P_0 C_s \end{aligned}$$
(57)
$$\begin{aligned} \varphi _1= & {} P_1 \left( {C_p -\mathop {C_p }\limits ^\sim +\mathop {C_s }\limits ^\sim } \right) \end{aligned}$$
(58)
$$\begin{aligned} \varphi _2= & {} P_0 C_s \end{aligned}$$
(59)

\(\mathop {C_s}\limits ^\smallsmile \), \(C_s \) are the throughput of the secondary system in the presence and absence of PU respectively. Similarly, \(\mathop {C_p }\limits ^\smallsmile \), \(C_p \) represents the throughput of the primary system in the presence and absence of SU.

With the help of above expressions, the average channel throughput expressions for fusion rules (\(k=1+n \,\hbox {and}\, k=N-n\)) can be written as [25]:

$$\begin{aligned}&C_{avg,1+\mathrm{n}} (N)=\varphi _0 +\varphi _1 P_{D,1+\mathrm{n}} (N)-\varphi _2 P_{F,1+\mathrm{n}} (N) \end{aligned}$$
(60)
$$\begin{aligned}&C_{avg,N-n} (N)=\varphi _0 +\varphi _1 P_{D,M-n} (N)-\varphi _2 P_{F,M-n} (N)\nonumber \\ \end{aligned}$$
(61)

5.2 Network utility function analysis

The closed form of expression for maximizing the network utility function (NUF) of CSS network is given in [26]:

$$\begin{aligned} J(N)= & {} u_1 \left( {\left( {1-P_{F,k} (N)} \right) p(H_0 )+P_{m,k} (N)p(H_1 )} \right) \nonumber \\&-\,u_2 P_{m,k} (N)p(H_1 )-u_3 N \end{aligned}$$
(62)

The above mentioned closed form of NUF expression is a combination of three parts, in which first part gives the information regarding the amount of usage of spectrum. Sometimes, PUs are not detected accurately this may cause interference problem (PUs with SUs), this interference information is given by the second part of above expression. Finally, third part represents the utilization of resources in the network. \(\mu _1 \), \(\mu _2 \) and \(\mu _3 \) are the cost functions for the three sections. The network utility function increases with the cooperation SUs.

6 Results and discussions

The simulation results and their discussions are presented in this section. The effect on performance for different values of network parameters such as \(\lambda _n \), p, \({\bar{\gamma }} \), M, N, and V are discussed when the proposed system is effected by Weibull fading environment. The performance is evaluated using total error rate \(\left( {Q_m +Q_f } \right) \), complementory receiver operating characteristics (CROC), probability of detection \(\left( {Q_d } \right) \), average channel throughput \(\left( {C_{avg} } \right) \), and maximization of network utility function.

Figure 3 is drawn between probability of false alarm \(\left( {P_f } \right) \) and missed detection probability \(\left( {P_m } \right) \) values for Weibull fading channel. This MATLAB simulation is evaluated for various values of \({\bar{\gamma }}\) namely (10 and 5 dB), V namely (\(V=2, 3,\) and 4), \(M=1\), and \(p=3\). From the simulation it can be observed that \(P_m \) value decreases, as \(P_f \) value increases. Similar nature also observed other simulation parameters \({\bar{\gamma }} \) and V. As the fading parameter increases, fading effect present between transmitter and receiver is decreases, and there by \(P_m \) value decreases.

Fig. 3
figure 3

CROC curves for Weibull fading channel with a single antenna at each CR

Full size image
Fig. 4
figure 4

Methodology of simulation process

Full size image

When V value increases in Fig. 3 from \(V=3\) to \(V=4\), \(P_m\) value decreases by 68.5%, at \(P_f =0.01\), \({\bar{\gamma }} =10\,\hbox {dB}\), \(M=1\), and \(p=3\). Similarly, as the S-channel SNR value increases, noise value decreases in S-channel and it improves the detection probability of PU. As \({\bar{\gamma }} \) value increases from 5 to 10 dB, \(P_m\) value decreases by 71.6% at \(P_f =0.01\), \(M=1\), \(V=3\), and \(p=3\). Finally, our simulation results are exactly matches with Rayleigh fading channel when the Weibull fading channel parameter value chosen as \(V=2\) (Fig. 4).

Similar analysis (CROC analysis) is carried out in Fig. 5 also, considering multiple antennas at each CR in proposed CSS network over Weibull fading channel. Various values of M namely (\(M=1,2\) and 3), V namely (\(V=2\) and 3), \({\bar{\gamma }} =10\,\hbox {dB}\), and \(p=3\) are used in the simulation. The effect of multiple antennas on missed detection probability is shown using CROC curves in Fig. 5. As the multiple antennas at each CR increases, it improves the diversity order, hence, detection probability of PU is increases. The \(P_m \) value decreases by 87.7%, as M value increases from \(M=1\) to \(M=3\) at \(P_f =0.01\), \({\bar{\gamma }} =7\,\hbox {dB}\), \(p=3\), and \(V=3\). When \({\bar{\gamma }} \) value increases from 4 to 7 dB, \(P_m \) value decreases by 83.1% at \(P_f =0.01\), \(p=3\), \(M=3\), and \(V=3\). Finally, when V value increases from \(V=2\) (Rayleigh) to \(V=3\) (Weibull), \(P_m \) value decreases 62.4% at \(P_f =0.01\), \(p=3\), \(M=3\), and \(V=3\). All the simulation results are drawn with strong support of theoretical expressions and the simulation results are in perfect accordance with theoretical results.

Figure 6 shows the performance evaluation of a single CR user-based spectrum sensing as function of p for different values of M (namely \(M=1\) and 3). The performance is evaluated using \(P_m \) versus p curves when S-channel is effected by Weibull fading effect. In Fig. 6, \(P_m \) value decreases and \(P_f \) value increases, as p value increases.

As we know that the CED operations would be obtained for \(p=2\), the \(P_m \) value is almost equal to 1 for \(p=2\) and it reduces significantly for \(p>2\) (i.e. CR with IED). In other words, when CED is replaced with IED, there is a significant improvement in the missed detection performance. It can be observed from the simulation that for a particular value of p (\(p=3\)) when M value increases from 1 to 3, \(P_m \) value reduces from 0.5060 to 0.1296 (decreases by 74.3%) at \({\bar{\gamma }} =10\,\hbox {dB}\), and \(\uplambda =30\). Similarly, the curves for \(P_f \) versus p are also shown in Weibull fading channel. When M value increases from \(M=1\) to \(M=3\), \(P_f \) value increases from 0.02963 to 0.08628 (increases by 65.6%) at \(p=5\), \({\bar{\gamma }} =10\,\hbox {dB}\), and \(\lambda =30\). It can be observed that there is a trade-off between \(P_f \) and \(P_m \) with respect to parameter p. From the simulation, it can be concluded that higher and lower values of p cannot be considered due to the rise in \(P_f \) and fall in \(P_m \) values, respectively. As p value increases, an optimum value of p should be considered in order to maintain both \(P_m \) and \(P_f \) at a particular level and this optimum value can be obtained when both \(P_m \) and \(P_f \) are minimum.

Figure 7 is drawn between optimum value of threshold (\(\lambda _{opt} )\) versus S-channel SNR (\({\bar{\gamma }})\) values. This graph is simulated for various values of V namely (\(V=2\) and 3) and p namely (\(p=2\), 3 and 4). It can be observed from simulation that \(\lambda _{opt} \) value increases with the increment of \({\bar{\gamma }}\) value. As S-channel SNR value increases, noise variance value decreases, the reduced value of noise variance, improves the signal strength. When p value decreases from \(p=4\) (IED) to \(p=2\) (CED), \(\lambda _{opt} \) value decreases by 52.8% at \({\bar{\gamma }} =6\,\hbox {dB}\) and \(V=3\), it decreases by 49.2% at \({\bar{\gamma } } =6\,\hbox {dB}\) and \(V=2\). Similarly, \(\lambda _{opt} \) value also depends upon fading environment present in S-channel. When V value decreases from \(V=3\) to \(V=2\), \(\lambda _{opt} \) value decreases by 10.1% at \({\bar{\gamma }} =6\,\hbox {dB}\), and \(p=4\). This simulation is evaluated with strong support of theoretical expression analysis and is in perfect accordance with the theoretical results.

Fig. 5
figure 5

CROC curves for Weibull fading channel with the multiple antenna at each CR

Full size image
Fig. 6
figure 6

\(P_f \) and \(P_m \) versus p curves for Weibull fading channel

Full size image
Fig. 7
figure 7

\(\lambda _{opt} \) versus \({\bar{\gamma }} \) curves for Weibull fading channel with a single antenna at each CR

Full size image

Figure 8 is drawn between optimum value of arbitrary power of received signal (\(p_{opt} )\) versus \({\bar{\gamma }} \) values. The graph is simulated for various values of V namely (\(V=2\) and 3) and \(\uplambda \) namely (\(\uplambda =5\), 10 and 15). It can be observed from the simulation that \(p_{opt} \) value decreases with the increment of S-channel SNR. As \({\bar{\gamma }} \) value increases, noise variance value decreases which improves the signal strength. When \(\uplambda \) value decreases from \(\uplambda =15\) to \(\uplambda =5\), \(p_{opt} \) value decreases by 40.5% at \({\bar{\gamma }}=5\,\hbox {dB}\) and \(V=2\), it decreases by 43.2% at \({\bar{\gamma }}=6\,\hbox {dB}\) and V \(=\) 3. Similarly, \(p_{opt} \) value also depends upon fading environment present in S-channel i.e., \(p_{opt} \) value decreases as fading effect is increases in S-channel. When V value increases from \(V=2\) to \(V=3\), \(p_{opt} \) value decreases by 11.2% at \({\bar{\gamma }} =4\,\hbox {dB}\) and \(\uplambda =15\). This simulation is evaluated with strong support of theoretical expression analysis and it is exactly matches with theoretical results. In the proposed CSS network, if the number of CR users increases, there is a chance to occur larger delays while making a decision about the PU. Hence, it is necessary to find out the number of CR users that are exactly contributing in the process of making a decision about the PU, these CRs are known as the optimal number of CR users.

Fig. 8
figure 8

\(p_{opt} \) versus \({\bar{\gamma }} \) curves for Weibull fading channel with a single antenna at each CR

Full size image

An optimum number of CR users \(\left( {N_{opt} } \right) \) are calculated as a function of \(\uplambda \) using hard decision logic called (OR-Rule) at FC in Fig. 9. The \(N_{opt} \) value calculated for error free R-channel, various values of M, p, \({\bar{\gamma }}\), and V. From Fig. 9, it is clear that \(N_{opt} \) value increases with \(\uplambda \) and for a given \({\bar{\gamma }} \), p, and V values. Since we are using OR-Rule at FC, when \(\uplambda \) value increases, FC needs binary decisions from more SUs to reduce the missed detection probability. For a particular case, when \({\bar{\gamma }} \) value increases from 5 to 7 dB, \(N_{opt} \) value decreases by 50.0% at \(\uplambda =6\), \(M=2\), \(p=3\), and \(V=3\). The fading effect present in S-channel also influence in deciding the optimum number of CR users. As V value increases from \(V=2\) to \(V=3\), \(N_{opt} \) value decreases by 28.5% at \(\uplambda =8\), \(M=1\), \(p=3\), and \({\bar{\gamma }}=5\,\mathrm{dB}\).

It can also observe from simulation that \(N_{opt} \) value is less for lower threshold values and it also depends upon p value. If the detection scheme changes from CED (\(p=2\)) to IED (\(p=3\)), \(N_{opt} \) value decreases by 80.0% at \(\uplambda =8\), \(M=2\), \(V=3\), and \({\bar{\gamma }}=5\) dB. Finally, number of antennas at each CR also effect the \(N_{opt} \) value, as M value increases from \(M=1\) to \(M=2\), \(N_{opt} \) value decreases by 50% at \(\uplambda =7\), \(p=3\), \(V=3\), and \({\bar{\gamma }}=5\) dB.

Fig. 9
figure 9

\(N_{opt} \) versus \(\uplambda \) using OR-Rule at FC

Full size image

Figure 10 is drawn between \(Q_d \) and \({\bar{\gamma }} \) in Weibull fading channel for various values of p, N, and M namely (\(p=2\) and 3), (\(N=1,2,\) and 3) and (\(M=1\) and 2) using OR-Rule at FC. As \({\bar{\gamma }} \) value increases, \(Q_d \) value increases for any type of fading and for any values of p, N, and M. This is due to the fact that when S-channel SNR value increases, noise effect decreases in the S-channel connected to each CR, which leads to improvement in detection performance. For \(M=2\), \(N=3\), and \({\bar{\gamma }}=6\,\hbox {dB}\), as p value decreases from \(p=3\) (IED) to \(p=2\) (CED), \(Q_d \) value decreases by 72.5% in Weibull fading channel. This is due to increases in the received signal strength by an arbitrary power parameter (p). Similarly, \(Q_d\) value also increases by increasing the M value at each CR, this is because of increase in the diversity order of the antenna at each CR. For a particular case, \(p=3\), \({\bar{\gamma }}=4\) dB, and \(N=3\), when M value decreases from 2 to 1, \(Q_d \) value decreases by 19.6% using OR-Rule at FC. The detection probability also depends upon number of cooperative CR users in the network. When N value decreases from \(N=3\) to \(N=1\), \(Q_d \) value decreases by 50.4% for a single antenna case, \({\bar{\gamma }}=4\) dB, and p=3. Similarly, \(Q_d \) value decreases by 9.9% for multiple antenna case, when N value decreases from \(N=3\) to \(N=2\), \({\bar{\gamma }} =4\,\hbox {dB}\), and \(p=3\).

Fig. 10
figure 10

\(Q_d \) versus \({\bar{\gamma }} \) using OR-rule at FC

Full size image

In Fig. 11, total error probability \(\left( {Q_m +Q_f } \right) \) performance is analyzed as a function of p. Simulation results are in exact accordance with derived theoretical expressions. Three values of N (namely 1, 2, and 3), two values of M (namely 1 and 2), and two values of \(\lambda \) (namely 30 and 20) are considered as simulation parameters.

Fig. 11
figure 11

\(Q_m +Q_f \) versus p using OR-Rule at FC

Full size image

The performance is evaluated when S-channel effected by Weibull fading and OR-Rule is used at FC. It is evident from simulation that, as p value increases, the \(\left( {Q_m +Q_f } \right) \) value initially decreases, reaches to a minimum value, and then it increases. Similar variation is observed with all other simulation parameters. This nature of the curve is due to the decrease in \(\uplambda \) value for increasing p value according to (\(\uplambda =\uplambda _n \sigma _n^p \)). The increase in the \(P_f \) value at each CR and increase in \(Q_f \) value at FC are the reasons for improvement in the \((Q_m +Q_f )\) value. Not only total error performance is calculated from Fig. 11, but also an optimum value of p (\(p_{opt} )\) can be calculated. The p value at which total error rate is minimum can be treated as \(p_{opt} \). The optimum value of p also depends upon various network parameters. For a particular case, \((Q_m +Q_f )\) value decreases by 26.8%, as N value increases from \(N=1\) to \(N=3\) at \(p=2.3\), \(M=1\), \(\uplambda =30\), and \({\bar{\gamma }} =10\,\hbox {dB}\). The \(p_{opt} \) value decreases and also shifts towards left (moves towards origin) as N value increases. Similarly, the performance of CSS can be improved further by increasing the number of antennas at each CR user. As M value increases from \(M=1\) to \(M=2\), \(\left( {Q_m +Q_f } \right) \) value decreases by 55.9% at \(p=1.9\), \(\uplambda =30\), \(N=2\), and \({\bar{\gamma }}=10\,\hbox {dB}\). It can be clearly observed from the graph that as the \(\lambda \) value increases, the total error rate curve shifts towards right i.e., moves away from the origin.

Fig. 12
figure 12

\(Q_m +Q_f \) versus \(\uplambda \) using OR-Rule at FC

Full size image

In Fig. 12, \((Q_m +Q_f )\) performance is shown as a function of \(\lambda \) for various values of N, p, and M. The performance is evaluated for fixed values of \({\bar{\gamma }} \), V, and using OR-rule at FC. From the simulation we can justify the nature of the curve as follows; as \(\uplambda \) value increases, initially the total error rate value decreases to a minimum value, and later it increases. The nature of the curve remains same with other simulation parameters also. Along with the total error rate, optimum value of \(\uplambda \) (\(\uplambda _{opt} )\) also calculated using this simulation. The \(\uplambda \) value at which total error is minimum can be treated as optimum value of \(\uplambda \). The \(\left( {Q_m +Q_f } \right) \) value decreases by 95.3%, when N value increases from \(N=1\) to \(N=3\) at \(\uplambda =10\), \(M=1\), \(V=3\), \({\bar{\gamma }}=10\,\mathrm{dB}\), and \(p=3\). As Nvalue increases, \(\lambda _{opt} \) value also increases and the curve moves away from the origin i.e. shift towards right. The proposed CSS network performance with SC diversity (M > 1) outperforms the CSS system performance without diversity (M = 1) under the similar values of network and channel parameters. When M value increases from \(M=1\) to \(M=2\), \((Q_m +Q_f )\) value decreases by 87.5% at \(\uplambda =10\), \(N=3\), \(p=3\), \(V=3\) and \({\bar{\gamma }}=10\,\hbox {dB}\). It can be clearly observed from simulation that for fixed values of M and N, as p value decreases, total error rate curve shifts towards the origin.

Fig. 13
figure 13

\(N_{opt} \) versus \(\uplambda \) using AND-Rule at FC

Full size image

In Fig. 13, \(N_{opt} \) value is calculated as a function of \(\lambda \). The performance is evaluated using AND-Rule at FC for different values of p namely (\(p=2\) and \(p=3\)), V namely (\(V=2\) and \(V=3\)), M namely (\(M=1\) and \(M=2\)), and \({\bar{\gamma }}\) namely (\({\bar{\gamma }}=5\,\hbox {dB}\) and \({\bar{\gamma }}=7\,\hbox {dB}\)). The \(N_{opt} \) value is calculated when S-channel is effected by Weibull fading and R-channel is considered as error free channel. From the simulation, it is clear that \(N_{opt} \) value decreases with the increment of \(\uplambda \) value using AND-Rule at FC and similar nature is observed with other simulation parameters also. As \({\bar{\gamma }}\) value decreases from 7 to 5 dB, \(N_{opt} \) value decreases from 29 to 23 at \(\uplambda =0.6\), \(p=3\), \(M=2\), and \(V=3\), this is due to the decrease in signal strength in S-channel reduces the \(N_{opt} \) value. Similarly, as V value increases, \(N_{opt} \) value increases due to the increase in fading value which causes a decrease in fading effect in S-channel. As the fading factor value increases from \(V=2\) to \(V=3\), \(N_{opt} \) value increases from 11 to 31 at \(\lambda =0.5\), \({\bar{\gamma }}=5\,\hbox {dB}\), \(p=3\), and \(M=2\). Using the diversity scheme (SC) in our proposed IED-based CSS network improves the \(N_{opt} \) value compared to non-diversity scheme. When the number of antennas at each CR is increased from \(M=1\) to \(M=2\), there is a significant improvement in \(N_{opt} \) value from 6 to 31 at \(\lambda =0.5\), \({\bar{\gamma }}=5\) dB, \(p=3\), and \(V=3\) which implies that the system performance can be improved using the diversity technique in the network.

Two different fusion rules are operated individually at FC, namely OR-Rule and AND-Rule. The \(N_{opt} \) value is high at lower values of \(\uplambda \) using AND-Rule at FC. Similarly, \(N_{opt} \) value is high at higher values of \(\uplambda \) using OR-Rule at FC.

Figure 14 shows the performance analysis of probability of detection (\(Q_d )\) at FC versus \({\bar{\gamma }}\) using AND-Rule at FC. This performance is analysed when S-channel is affected by Weibull fading and R-channel is considered as the ideal (noiseless) channel. Various simulation parameters p, N, and M namely (\(p=2\) and \(p=3\)), (\(N=1\), \(N=2\), and \(N=3\)), and (\(M=1\) and \(M=2\)) are used in the simulation. The \(Q_d \) value increases with increase in the \({\bar{\gamma }}\) value. Similar nature is observed with the other simulation parameters also, this is due to increase in \({\bar{\gamma }}\) value reduces the noise value which improves the \(P_d \) value, consequently \(Q_d \) value increases. For \(M=2\), \(N=3\), and \({\bar{\gamma }}=7\,\hbox {dB}\), when p value decreases from \(p=3\) (IED) to \(p=2\) (CED), \(Q_d \) value decreases by 67.8% in Weibull fading channel. The \(Q_d \) value increases using the diversity scheme (M > 1) in the proposed CSS network compared to non-diversity scheme (\(M=1\)) and performance comparison between them is also shown in this simulation. For a particular case, \(p=3\), \({\bar{\gamma }}=6\) dB, and \(N=3\), when M value decreases from \(M=2\) to \(M=1\), \(Q_d \) value decreases by 49.1% using AND-Rule at FC. It is also observed that \(Q_d \) value decreases with the increment of N value. This is due to the fact that the FC makes a final decision about the PU positively only when all CRs responds positively (i.e. PU is present), according to AND-Rule. If any one of the SU responds negatively (i.e. PU is absent), then FC declares that PU is absent. Hence, in case of AND-Rule, \(Q_d \) value decreases with the increment in number of CRs. For the fixed values of \(\uplambda =30\) and \(V=3\), as Nvalue increases from \(N=1\) to \(N=3\), \(Q_d \) value decreases by 44.1% at \(M=1\), \({\bar{\gamma }}=6\) dB, and \(p=3\). Similarly, \(Q_d \) value decreases by 6.9% for multiple antenna case, when N value decreases from \(N=2\) to \(N=3\) at \({\bar{\gamma }}=6\,\hbox {dB}\), and \(p=3\).

Fig. 14
figure 14

\(Q_d \) versus \({\bar{\gamma }}\) using AND-Rule at FC

Full size image

Figure 15 is drawn between \((Q_m +Q_f )\) and p using AND-Rule at FC. This simulation is drawn with strong support of theoretical expressions and our simulation results are in perfect accordance with theoretical results. Three values of N (namely 1, 2, and 3), two values of M (namely 1 and 2), and two values of \(\uplambda \) (namely 30 and 20) are used to simulate Fig. 14 using MATLAB, with constant \(V=3\) and \({\bar{\gamma }}=10\) dB values. It is clear from the simulation that, as p value increases, \((Q_m +Q_f )\) value initially decreases to minimum and it then increases. Similar variations also observed with all other simulation parameters. This nature of the curve is due to the decrease in \(\lambda \) value for increasing pvalue according to (\(\lambda =\lambda _n \sigma _n^p )\). Hence, there is a scope for increment of \(P_f \) value at each CR and \(Q_f \) value at FC, which results in the improvement of \(\left( {Q_m +Q_f } \right) \) value. For a particular case, when N value increases from \(N=1\) to \(N=3\), \(\left( {Q_m +Q_f } \right) \) value decreases by 68.1% at \(p=4\), \(M=1\), \(\uplambda =30\), and \({\bar{\gamma }}=10\,\hbox {dB}\). The optimum value of p also increases and shifts towards right as N value increases. Similarly, when M value at each CR increases from \(M=1\) to \(M=2\), the \((Q_m +Q_f )\) value decreases by 60.8% at \(p=2.5\), \(\lambda =30\), \(N=3\), and \({\bar{\gamma }}=10\) dB. It can be observed from simulation that as the \(\uplambda \) value increases, the total error rate curve shifts towards left i.e. moves towards the origin.

Fig. 15
figure 15

\(Q_m +Q_f \) versus p using AND-Rule at FC

Full size image

Figure 16 is drawn between average channel throughput (\(C_{avg} )\) versus detection threshold (\(\uplambda )\) using \(k=1+n\) fusion rule at FC. The performance is evaluated using an IED scheme in proposed CSS network over Weibull fading channel for different values of N, M and error rate (\(p_e )\) in R-channel. Comparison between perfect R-channel and imperfect R-channel (i.e. error rate present in R-channel) also provided to show the effect of an error rate on \(C_{avg} \). It can be observed from Fig. 16 that the throughput value is maximum with error free R-channel and performance decreases as the error rate increases in R-channel.

Fig. 16
figure 16

\(C_{avg} \) versus \(\uplambda \) using \(k=1+n\) rule at FC

Full size image

As \(p_e \) value increases from \(p_e =0\) to \(p_e =0.2\), \(C_{avg} \) value decreases by 6.1% at \(M=2\) (multiple antennas case), \(N=3\), \({\bar{\gamma }}=10\,\hbox {dB}\), and \(\uplambda =8\). It is also observed that initially throughput value increases for lower values of detection threshold and it reaches to the maximum point after that it decreases for higher values of detection thresholds. The \(C_{avg} \) value increases with the cooperation of multiple numbers of SUs using the \(k=1+n\) fusion rule at FC. As N value increases from \(N=3\) to \(N=5\), \(C_{avg} \) value increases by 2.6% for a single antenna case, using \(k=1+n\) fusion rule, at \(\lambda =6\), \(p_e =0.2\), and \({\bar{\gamma }}=10\) dB. Finally, throughput value also depends upon the multiple antennas that are used at each CR. As the number of antennas at each CR increases from \(M=1\) to \(M=2\), \(C_{avg} \) value increases by 2.4% at \(\lambda =6\), \(N=4\), \(p_e =0.2\), and \({\bar{\gamma }}=10\,\hbox {dB}\). The above graph is simulated for following network parameters \({\bar{\gamma }}=10\,\hbox {dB}\), \(p_e =0\,\mathrm{and}\,0.2, k=1+n\) (\(n=2\)) fusion rule, \(C_s =10\), \({\breve{C}} _s =5\), \(C_p =20\), \({\breve{C}}p =10\), \(M=1\) and 2 and \(N=3\), 4, and 5.

Fig. 17
figure 17

\(C_{avg} \) versus \(\uplambda \) using \(k=N-n\) rule at FC

Full size image

Figure 17 is drawn between \(C_{avg} \) versus \(\uplambda \) using \(k=N-n\) fusion rule at FC. The performance comparison between perfect (i.e. error free) R-channel and imperfect R-channel is provided. It can be observed from Fig. 17 that the throughput value is maximum with error free R-channel and performance decreases as the error rate increases in R-channel. As \(p_e \) value increases from \(p_e =0\) to \(p_e =0.2\), \(C_{avg} \) value decreases by 5.7% at \(M=2\) (multiple antennas case), \(N=3\), \({\bar{\gamma }}=10\,\hbox {dB}\), and \(\uplambda =6\). \(C_{avg} \) value decreases with the cooperation of multiple numbers of SUs using \(k=N-n\) fusion rule. As N value increases from \(N=3\) to \(N=5\), \(C_{avg} \) value decreases by 1.6% for single antenna case, using \(k=N-n\) fusion rule at FC, at \(\uplambda =10\), \(p_e =0.2\), \({\bar{\gamma }}=10\,\hbox {dB}\). Finally, as the number of antennas at each CR decreases from \(M=2\) to \(M=1\), \(C_{avg} \) value decreases by 1.7% at \(N=4\), \(p_e =0.2\), \(\uplambda =8.25\), and \({\bar{\gamma }}=10\,\hbox {dB}\). The above mentioned simulation parameters (in Fig. 16) are used in this simulations also except \(k=N-n\) fusion rule at FC.

The effect on \(C_{avg} \) performance using \(k=1+n\) rule and \(k=N-n\) fusion rules at FC is that, \(C_{avg} \) value increases with the cooperation of CR users using \(k=1+n\) rule and it decreases using \(k=N-n\) fusion rule at FC.

Fig. 18
figure 18

NUF versus \(\lambda \) using \(k=1+n\) rule at FC

Full size image

Figure 18 is drawn between network utility function (NUF) and detection threshold (\(\uplambda )\) using \(k=1+n\) fusion rules at FC. NUF performance is evaluated using an IED scheme in the proposed CSS network over Weibull fading channel with an error rate (\(p_e )\) in R-channel. Network utility factor decreases as the error rate increases in the R-channel and this value is maximum with error free channel. As \(p_e \) value increases from \(p_e =0\) to \(p_e =0.05\), NUF value decreases by 16.3% at \(\uplambda =4\), \(M=2\), \(N=4\), \(p=3\), and \({\bar{\gamma }}=10\) dB. Using \(k=1+n\) fusion rule at FC, as the cooperation among the CR users are increases, NUF value increases. If the number of SUs are increases from \(N=3\) to \(N=5\), NUF value increases by 159.4% at \(M=1\), \(p_e =0.05\), \(\lambda =4\), and \({\bar{\gamma }}=10\,\hbox {dB}\). Similarly, as the number of antennas at each CR increases, NUF value increases. As M value increases from \(M=1\) to \(M=2\), NUF value decreases by 167.2% at \(N=4\), \(p_e =0.05\), \(\uplambda =4\), and \({\bar{\gamma }}=10\) dB. Simulation parameters \(P\left( {H_1 } \right) =0.3\), \(P\left( {H_0 } \right) =0.7\), \(\mu _1 =0.2\), \(\mu _2 =0.8\), \(\mu _3 =0.005\), \(M=1\) and 2, \(N=3\), 4 and 5, \(p_e =0\) and 0.05, and \({\bar{\gamma }}=10\,\hbox {dB}\) are used to evaluate these MATLAB simulations (Figs. 18 and 19).

Figure 19 is drawn between NUF and \(\uplambda \) using \(k=N-n\) fusion rules at FC. The performance comparison between error free and error rate present in R-channel is provided using the simulation. As \(p_e \) value increases from \(p_e =0\) to \(p_e =0.05\), NUF value decreases by 28.1% at \(\uplambda =1\), \(M=2\), \(N=4\), \(p=3\), and \({\bar{\gamma }}=10\) dB. Using \(k=N-n\) fusion rule at FC, as the cooperation among the CR users are increases, NUF value decreases. If the number of SUs are increases from \(N=3\) to \(N=5\), NUF value decreases by 51.0% at \(M=1\), \(p_e =0.05\), \(\uplambda =3\), and \({\bar{\gamma }}=10\) dB. Similarly, the number of multiple antennas at each CR increases, it improves the NUF value. As M value increases from \(M=1\) to \(M=2\), NUF value decreases by 51.4% at \(N=3\), \(p_e =0.05\), \(\uplambda =4\), and \({\bar{\gamma }}=10\,\hbox {dB}\). Finally, NUF value also depends upon arbitrary power of the received signal (p). From the graph we can able to say that NUF value improves with an IED scheme (\(p=3\)) compared to CED scheme (\(p=2\)), NUF value reduces with the reduction of p value.

Fig. 19
figure 19

NUF versus \(\uplambda \) using \(k=N-n\) rule at FC

Full size image

7 Conclusion

In this paper, we have proposed the cooperative spectrum sensing (CSS) network which is equipped with multiple antennas at each cognitive radio (CR). An improved energy detector (IED) scheme is used as detection scheme and performance is accessed over Weibull fading channel. Selection combining (SC) scheme is used at each CR, it receives the binary decisions about the primary user (PU) from an IED technique using the multiple antennas and selects better detection value of PU. The sensing information about the PU is passed to the fusion center (FC) through reporting channel (R-channel). Final decision made at FC using different fusion rules (OR-Rule, AND-Rule, \(k=1+n\), and \(k=N-n\) rules). We have derived novel expressions for missed detection and probability of false alaram using the multiple antennas at each CR in the presence of Weibull fading channel. The performance is anlyzed using complementary receiver operating characteristics (CROC) curves, total error rate, throughput analysis, and network utility function using the proposed CSS network. Finally, we have derived closed form of expressions for network parameters such as optimum number of CRs, optimum arbitrary power of received signal, and optimum detection threshold at each CR to obtain the optimal performance of CSS network. Our simulation results are perfectly inaccordance with the analytical results. The simulation results are depends upon various values of network parameters such as average sensing channel SNR (\({\bar{\gamma }})\), multiple antennas (M) at each CR, detection threshold value (\(\lambda \)), arbitrary power of the received siganl (p), Weibull fading parameter (V), and number of CR users (N). The performance is evaluated considering single and multiple antennas at each CR in Weibull fading channel. Comparison between CED and IED schemes are also provided. Finally, we can conclude that detection performance is improved by considering multiple antennas at each CR using an IED scheme.