Throughput performance of cooperative spectrum sensing network with improved energy detectors and SC diversity over fading channels

Abstract

This paper proposes a novel cooperative spectrum sensing network (CSSN) with improved energy detector (IED) based cognitive radio (CR) users. Every CR user is furnished with multiple antennas (M) and performs itself selection combining (SC) operation. All the CRs sense a primary user (PU) via erroneous sensing channels (S) and send the data to a fusion center (FC) via erroneous reporting channels (R). At FC, decision about PU is evaluated with the assistance of k-out-of-N rule. Detection probability expressions for a CR and FC subject to noise plus Rayleigh/Rician fading are developed. Also both simulation and analytical frameworks for throughput analysis are presented. The analytical performance results are also validated using simulation performance results. Performance comparisons between IED and conventional energy detectors (CED) are presented in terms of throughput and total error rate for several parameter values. Further, overall performance of throughput and total error rate in Rayleigh/Rician fading channels is investigated. The joint effects of diversity and fading on the CSSN throughput is also additionally discussed. Channel error (r) impact on the throughput and total error performances for each proposed and traditional networks is studied. Optimization of several parameters for maximizing the throughput and minimizing the total error is also studied. Throughput overall performance of proposed CSSN is plenty better than the conventional network in each fading channel. For several values of M and r, $p_{\mathrm{{opt}}}$, $\lambda _{\mathrm{{n, opt}}}$ and $N_{\mathrm{{opt}}}$ values are calculated subject to each fading environment. Both analytical and MATLAB simulation results are matched. Under imperfect channel conditions, performances in terms of throughput and total error are not up to the mark but significant performance improvement has been obtained with diversity at each CR level.

1 Introduction

Cognitive radio (CR) is a wireless device that is intelligently acts according to changes in real-time environment. It is also capable of monitoring, detecting and identifying licensed users (called primary users, PUs). The CRs also known as secondary users (SUs), or CR users/nodes. The SUs are allowed to use the empty frequency slots of PUs opportunistically as long as the PU is not used its frequency bands [1]. For 5G/6G based wireless networks, precise observation, detecting and gathering of data about utilization of PU’s radio frequency range as the function of time, frequency, and area are needed [2]. A few procedures for detecting the authorized frequency bands are designed, to be specific, energy detection (ED), matched filter, cyclo-stationary, and wavelet detection strategies. Among every one of these strategies, ED strategy is the least difficult one that can be utilized to identify and get the data about utilization of PU’s radio range since this procedure doesn’t need any priori data identified with PU [3]. Due to time varying nature of the environment, decision of a SU about PU is not exact and reliable if channel from CR to PU is seriously affected by noise plus fading [3, 4]. If this is the situation, many CR users can be allowed for spectrum sensing with cooperation among them (called as cooperative spectrum sensing, CSS) for taking exact decision on the PU’s status. In CSS scheme, in detection process, each CR user has its own information about spectrum usage of PU that should be passed and informed to each other CR user. Sharing of information about spectrum usage of PU among all CR users is compulsory because it is already discussed that few CR users may undergo more noise or fading in their links [5]. Information of every CR user is sent to a typical control place called as fusion center (FC) for fusing operation to get an ultimate choice on PU. Various fusing operations that are implemented at FC for finding a final decision of the PU status, to be specific, hard and soft data fusing operations [6, 7].

1.1 Related work

In [8, 9], the analysis of optimal sensing time and trade-off between sensing time and throughput for cognitive radio network (CRN) with conventional energy detectors (CEDs) are investigated. The CED can be replaced with IED in any CR node to increase CSS performance even further. The squaring procedure at the obtained signal amplitude is used to calculate the decision statistic in CED. In IED, power operation (p) within the amplitude of the received signal is considered for measuring the decision statistic [10, 11]. In wireless communications era, channels are having time-varying nature and hence the system performance is not up to the mark. Depending upon the type of applications, several channels like non-fading additive white Gaussian process (AWGN) and fading models like Rayleigh, Rician, Hoyt, and Weibull are developed. In [11, 12], the CSS including IEDs output is evaluated in faded sensing channels and ideal reporting channels, however, throughput performance and effect of imperfect reporting channel situations are not examined in [11, 12]. For sensing channels modeling, AWGN, Rayleigh, and Rician fading are used. Imperfect reporting channels, or erroneous reporting channels, are taken into account. The throughput of CSS with CEDs in $\kappa -\mu$ and $\eta -\mu$ generalized faded channels is investigated in [13]. [14, 15] investigates CSS’s throughput with IEDs in AWGN and Rayleigh fading environments. The throughput performance of secondary network under security threats with IEDs is investigated in [16]. Studies on throughput maximization for CRNs are presented in [17] and trade-off between energy and throughput under optimal sensing order in CRNs is discussed in [18]. We have been motivated and encouraged by the ongoing work on developing both theoretical and simulation models for the analysis of throughput and total error rate of considered CSSN network over Rayleigh and Rician fading channels. As compared to the throughput of Rayleigh fading, Rician fading, also known as Nakagami-n, shows better throughput. For Rician parameter $K=0$, the Rayleigh fading curves can be obtained. Satellite channels employ Rician fading when string dominant component is present in the received signal at the receiver [19, 20]. The efficiency of CSS with CEDs in terms of analytical throughput is addressed in [21]. Energy efficiency analysis of CSS with IEDs over Nakagami-q/n channels is discussed in [22]. The k-out-of-N fusion rule at FC is performed for taking the final decision about PU. This fusion rule is more effective and generalized which encompasses several sub fusion rules. In [26], the authors presented throughput framework and performance of CEDs based CRN over AWGN channel. The present paper considers the same throughput framework and analysis is extended to evaluate throughput and total error rate of IEDs based CCSN over Rayleigh and Rician Fading channels. Throughput maximization is significantly achieved with our proposed network when compare to conventional CR networks. This has motivated us again and according to the literature review, throughput and total error rate of CSSN with IEDs in AWGN, Rayleigh, and Rician fading channels could be a large and interesting research work. The following are the major and novel contributions:

• 1. The probability of detection over AWGN noise with Rayleigh and Rician fading channels has been established and the mathematical foundations for the proposed CSSN’s throughput analysis are also given. In [26], the authors investigated throughput performance of CEDs based CR network over AWGN channel only, but the present paper evaluates throughput of IEDs based CR networks over Rayleigh and Rician Fading channels. Throughput maximization is significantly achieved with our proposed network when compare to conventional CR networks.

• 2. The investigation of comparison between IEDs and CEDs for various sub fusion rules is addressed for several network parameter values. Furthermore, findings for throughput over noise plus either Rayleigh or Rician fading channels are analytically demonstrated.

• 3. The effects of SC diversity technique and fading on total error rate and throughput performances are also studied.

• 4. For both proposed and traditional networks, the impact of channel error on total error and throughput is investigated.

In this paper, the mathematical outlines are developed in a systematic manner; however, the current work may be extended to include further investigation on the proposed network performance in other fading environments.

1.2 Splitting of the paper

The remainder of the work is planned into several sections. A brief overview of the considered network is given in Sect. 2, along with comprehensive outline of theoretical frameworks for fusion strategies and network throughput. The simulation model for the proposed network is presented in Sect. 3. Performance comparisons of energy detectors are seen in Sect. 4, and finally conclusions are provided in Sect. 5.

2 System model

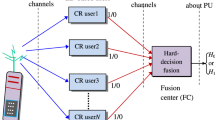
As shown in Fig. 1, a PU, N CR nodes, and one FC make up the proposed CSSN network. Every PU and FC node has a single transmit/receive antenna, while each CR node has a single transmit antenna and an IED with M receiving antennas. The SC diversity is a strategy used by all CR nodes. Via erroneous channels (S), each CR node detects a PU and sends its sensing data using erroneous channels (R) to FC. In detail, each CR node receives data from all of its antennas (M) and processes it using its IED. SC selects the largest value and compares it to a precisely chosen threshold, expressed by $\lambda$ (each CR node has the same $\lambda$); additionally, each CR makes a binary decision (local) about the existence or absence of PU. At FC, the k-out-of-N fusion rule is used to make the final or global decision. Finally, the probabilities of cooperative missed detection and false alarm are calculated for the overall error rate and throughput of the considered CSSN with CEDs and IEDs.

Fig. 1

The block diagram of a considered CSSN

Consider the received signal in j-th antenna ($j=1, 2,\ldots , M$) at each CR node, $y_j(n)$ (n denotes sample index)

$$\begin{aligned} {y_j}(n) = \left\{ {\begin{array}{ll} {{w_j}(n)}&{}{{{\mathcal {H}}_0}}\\ {{h_j}s(n) + {w_j}(n)}&{}{{{\mathcal {H}}_1}}, \end{array}} \right. \end{aligned}$$

(1)

where s(n) represents the primary signal to be detected (with energy $E_s$) [10]; $\{{w_j}(n)\} _{j = 1}^M$ is AWGN with zero-mean and variance $\sigma _n^2$, $h_j$ is the fading channel (S) coefficient. Here, ${w_j}(n)$ and $\{h_j\}$ are unrelated. At each CR node, assume that decision variable, represented as $W_j$, for determining whether the PU is present or not, as shown below [10,11,12]:

$$\begin{aligned} {W_j} = \mathrm{{ }}|{y_j}{|^p}. \end{aligned}$$

(2)

where p ($>0$) denotes an IED parameter. When $p=2$ is set in (2), an alternative decision variable of a conventional energy detection method [3] is obtained. The general expressions for false and miss detections are given from [23, eq. (41), chapter 2]:

$$\begin{aligned} P_f&= \int _\lambda ^\infty f_{U|{\mathcal {H}}_0}(u)du = 1 - F_{U|{\mathcal {H}}_0}(\lambda ) ; \quad U\ge 0, \end{aligned}$$

(3)

$$\begin{aligned} P_m&= \int _0^\lambda f_{U|{\mathcal {H}}_1}(u)du = F_{U|{\mathcal {H}}_1}(\lambda ) ; \quad U\ge 0. \end{aligned}$$

(4)

where $f_{U|{\mathcal {H}}_0}(u)$ and $f_{U|{\mathcal {H}}_1}(u)$ are the conditional probability density functions (PDFs) of U, respectively, for hypotheses ${\mathcal {H}}_0$ and ${\mathcal {H}}_1$. The cumulative distribution function (CDF) for IED is provided by [10,11,12]

$$\begin{aligned} {F_{W_j|{{\mathcal {H}}_i}}}(x) = \Pr \left[ |y_j|^p\,|_{{{\mathcal {H}}_i}} \le x\right] _{i=0,1}, \end{aligned}$$

(5)

where $\Pr [\cdot ]$ represents probability. Individual decision variables are calculated at every CR node in each antenna (i.e., $\left\{ {{W_j}} \right\} _{j = 1}^M$). Using the SC technique, the largest value of M decision variables is chosen i.e. $U=\max \{W_1,W_2,\ldots ,W_M\}$. The conditional CDF with SC for hypothesis ${\mathcal {H}}_0$, is written by [10,11,12]:

$$\begin{aligned} {F_{U|{{\mathcal {H}}_0}}}(u) = {\left[ {1 - \exp \left( { - \frac{{{u^{2/p}}}}{{\sigma _n^2}}} \right) } \right] ^M}\mathrm{{ }}. \end{aligned}$$

(6)

The output of SC is sent to an IED, which makes a local decision about the existence or non-exitance of PUs as follows: [10,11,12]:

$$\begin{aligned} U \underset{0}{\overset{1}{\gtrless }}\lambda , \end{aligned}$$

(7)

where $\lambda$ in a CR node is expressed as $\lambda = {\lambda _n}\sigma _n^p$, where the normalized threshold to be determined is represented by $\lambda _n$ and the standard deviation of a noise is denoted by $\sigma _n$. Every CR node is assumed to have the same threshold value and performs the same IED operation (power p). For a fixed value of $\lambda _n$, a factor involving p is used to normalize $\lambda$ [9]. In a CR node, the false alarm probability, $P_f$, is expressed as [12]:

$$\begin{aligned} {P_{f}} = 1 - {\left[ {1 - \exp \left( { - \frac{{{\lambda ^{2/p}}}}{{\sigma _n^2}}} \right) } \right] ^M}\mathrm{{ }}. \end{aligned}$$

(8)

It should be noted that $P_f$ is the same in any fading environment (i.e. ${{\bar{P}}_{f}}={P_{f}}$), since there is no PU signal for ${\mathcal {H}}_0$. As a result, no further discussion of $P_f$ is needed.

2.1 Non-fading (AWGN) environment

It is known that the fixed channel coefficient is $h_j=1, \forall j \in \{ 1,..M\}$ in this case. Using [24, eq. (9)], the expression of missed detection probability is obtained as follows:

$$\begin{aligned} {{\bar{P}}_{{m}}^{\mathrm{{AWG}}}} = {\left[ {1 - Q\left( {\sqrt{\frac{{2{E_s}}}{{\sigma _n^2}}} ,\mathrm{{ }}{\lambda ^{1/p}}\sqrt{\frac{2}{{\sigma _n^2}}} } \right) \mathrm{{ }}} \right] ^M}\mathrm{{ }}, \end{aligned}$$

(9)

where $Q(a,b) \buildrel \Delta \over = \int \limits _b^\infty {v\exp \left( { - \frac{{{v^2} + {a^2}}}{2}} \right) } {I_0}(av)\mathrm{d}v$ denotes the first-order Marcum Q-function [25].

2.2 Rayleigh fading environment

Fading channel coefficient $h_j$ represents a complex Gaussian random variable (RV) with zero mean and variance $\sigma _h^2$ in this case, i.e., ${h_j}\sim \mathcal {CN}(0,\sigma _h^2)$. The missed detection probability is expressed as:

$$\begin{aligned} {{\bar{P}}_{{m}}^{\mathrm{{Ral}}}} = {\left[ {1 - \exp \left( - \frac{{{\lambda ^{2/p}}}}{{\sigma _n^2(1 + {{\bar{\gamma }}_s})}}\right) } \right] ^M}. \end{aligned}$$

(10)

where ${\bar{\gamma }_s} = {E_s}\sigma _h^{\mathrm{{2}}}/\sigma _n^{\mathrm{{2}}}$ denotes the sensing channel’s average SNR.

From (8) and (10), an optimal sensing threshold, represented as ${\lambda _{\mathrm{{opt}}}}$, can be obtained if the result is $\partial ({P_{{m}}^{\mathrm{{Ral}}}} + {P_f})/\partial \lambda = 0$. At this ${\lambda _{\mathrm{{opt}}}}$, the total error rate of a single CR is minimized. More precisely, to get optimal threshold, partial derivative of ${P_{{m}}^{\mathrm{{Ral}}}}$+$P_f$ with respect to ${\lambda }$ should be performed where p and ${\bar{\gamma }}_s$ are fixed parameters and then set the result equal to zero.

Please be noted that it is difficult to get analytical expression for ${\lambda _{\mathrm{{opt}}}}$ for M number of antennas i.e general case. However, the expressions in closed-form are derived for $M =1$ and $M=3$ as follows:

$$\begin{aligned} {\lambda _{\mathrm{{opt}}}}^{M=1}= & {} {\left[ {\frac{{(\sigma _n^2 + E_s )\ln (1 + E_s/\sigma _n^2 )}}{{(E_s/\sigma _n^2)}}} \right] ^{p/2}} \end{aligned}$$

(11)

$$\begin{aligned} {\lambda _{\mathrm{{opt}}}}^{M=3}= & {} {\left[ {\frac{{(\sigma _n^2 + E_s )\ln (1 + E_s/\sigma _n^2 )}}{{(2E_s/\sigma _n^2)}}} \right] ^{p/2}} \end{aligned}$$

(12)

2.3 Nakagami-n (or Rician) fading environment

The PDF of Rician coefficient $|h_j|$ at j-th antenna is considered [19]. Coefficient represents the complex Gaussian distribution i.e., $\mathcal {CN} (s, \sigma ^2_{h})$, where s represents the average value that is to be considered as real. The $K>0$ represents the real fading parameter which is the powers of direct and the scattered paths signals ratio, i.e.,

$$\begin{aligned} K = s^2 / \sigma ^2_{h}. \end{aligned}$$

(13)

The ${\mathbb {E}}\{|h_j|^2\}=s^2+\sigma ^2_{h} \forall j \in \{ 1,..M\}$ represents the total fading power of both direct and scattered signal powers. Normalized fading power is assumed, i.e., ${\mathbb {E}}\{|h_j|^2\}=\Omega =1$, we obtain:

$$\begin{aligned} \sigma _{h}^2 = 1/(1+K) \quad s^2 = {K/(1+K)}. \end{aligned}$$

(14)

The envelop of obtained signal, $y_j$, has Rician distribution for hypothesis ${\mathcal {H}}_1$ and $y_j \sim \mathcal {CN} (s\sqrt{E_s},E_s \sigma _h^2+\sigma _n^2)$. The RV transformation is used to build the conditional PDF of $W_j=|y_j|^p$ as:

$$\begin{aligned} \begin{array}{l} \displaystyle f_{W_j|{{\mathcal {H}}_1}}^{\mathrm{{Ric}}}(y) = \frac{2 y^{(2/p)-1}}{p(E_s \sigma _h^2 + \sigma _n^2)} \exp \left( - \frac{y^{2/p}+s^2E_s}{E_s \sigma _h^2 + \sigma _n^2} \right) \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \displaystyle \times I_0\left( \frac{2s\sqrt{E_s}y^{1/p}}{E_s \sigma _h^2 + \sigma _n^2} \right) . \end{array} \end{aligned}$$

(15)

Then, the conditional CDF with SC is

$$\begin{aligned} F_{Z|{{\mathcal {H}}_1}}^{\mathrm{{Ric}}}(z) = \left[ 1 - Q \left( \sqrt{\frac{2E_s}{E_s \sigma _h^2 + \sigma _n^2}}, z^{1/p} \sqrt{\frac{2}{E_s \sigma _h^2 + \sigma _n^2}} \right) \right] ^M. \end{aligned}$$

(16)

Finally, using (4), (7), and (16 as inputs, the miss detection probability is obtained as:

$$\begin{aligned} {{\bar{P}}_{{m}}^{\mathrm{{Ric}}}} = \left[ 1 - Q \left( \sqrt{{2E_s}/{B}}, \lambda ^{1/p} \sqrt{{2}/{B}} \right) \right] ^M. \end{aligned}$$

(17)

where $B=\sigma _n^2(1+\bar{\gamma _s})$. The analytical expression for optimal $\lambda$ subject to Rician fading channel is not presented here due to complexity involved while deriving an expression for optimal $\lambda$.

2.4 The k-out-of-N fusion rule

The IED is performed in every CR node to make a final decision in the form of binary bits, either ‘1’ (present) or ‘0’ (absent), and sends this information to the FC for the fusing operation. Following that, the k-out-of-N fusion process is used. The OR rule for $k=1$, the AND rule for $k=N$, and the Majority rule for $k=\frac{N}{2}+1$ are all derived as sub rules. Every CR node’s output is presumed to be the same, i.e.

$$\begin{aligned} \Pr \{ {d_i} = 1|{{\mathcal {H}}_0}\}&= {\bar{P}}_{f,i}; {\bar{P}}_{f,i} = {{\bar{P}}_f}, \forall i (\in \{ 1,..N\}), \end{aligned}$$

(18)

$$\begin{aligned} \Pr \{ {d_i} = 0|{{\mathcal {H}}_1}\}&= {\bar{P}}_{m,i}; {\bar{P}}_{m,i} = {{\bar{P}}_m}, \forall i \end{aligned}$$

(19)

where ${\bar{P}}_{m,i}=1-{\bar{P}}_{d,i}$; $d_i$ denotes the decision made at the $i^{th}$ CR node. With the assumption of error probability, r, the new ${{\bar{P}}_f}$ and ${{\bar{P}}_m}$ in each CR are expressed as:

$$\begin{aligned} P_{fe}&= { {\bar{P}}_{f}}(1 - r) + (1 - {{\bar{P}}_{f}})r, \end{aligned}$$

(20)

$$\begin{aligned} P_{me}&= {{\bar{P}}_{m}}(1 - r) + (1 - {{\bar{P}}_{m}})r. \end{aligned}$$

(21)

In terms of channel error, the expressions at FC are as follows:

$$\begin{aligned} Q_{fe}(N)&= \sum _{\ell =k}^N \left( {\begin{array}{c}N\\ \ell \end{array}}\right) (P_{fe})^\ell (1-{P_{fe}})^{N-\ell }, \end{aligned}$$

(22)

$$\begin{aligned} Q_{me}(N)&= 1-\sum _{\ell =k}^N \left( {\begin{array}{c}N\\ \ell \end{array}}\right) (1-P_{me})^\ell (P_{me})^{N-\ell }. \end{aligned}$$

(23)

And $Q_{me}(N)=1-Q_{de}(N)$ and $P_{me}=1-P_{de}$. Every CR node and FC’s total error rate expressions are written as:

$$\begin{aligned} {{\bar{P}}_e}&=P({\mathcal {H}}_1){{P}_{me}}+P({\mathcal {H}}_0){{P}_{fe}}, \end{aligned}$$

(24)

$$\begin{aligned} {Q_{e}}(N)&= p({\mathcal {H}}_1){Q_{me}(N)} + p({\mathcal {H}}_0){Q_{fe}(N)}. \end{aligned}$$

(25)

where $P({\mathcal {H}}_0)$ denotes probability of the PU being absent and $P({\mathcal {H}}_1)$ denotes the prior probability of the PU being present, and $P({\mathcal {H}}_0)+P({\mathcal {H}}_1)=1$.

2.5 Framework for calculation of throughput

The CSSN’s throughput framework is presented here. For the k-out-of-N rule, the average channel throughput (denoted as $C_{avg}$) is written as [26]:

$$\begin{aligned} {C_{avg}}(N) = {r_0} + {r_1}[1-{Q_{me}}(N)] - {r_2}{Q_{fe}}(N). \end{aligned}$$

(26)

where

$$\begin{aligned} {r_0}&= p({{\mathcal {H}}_1})\left[ {{{ \mathcal {{\tilde{C}}}}_p} + {{ \mathcal {{\tilde{C}}}}_s}} \right] + p({{\mathcal {H}}_0}){{\mathcal {C}}_s}, \end{aligned}$$

(27)

$$\begin{aligned} {r_1}&= p({{\mathcal {H}}_1})\left[ {{{\mathcal {C}}_p} - {{ \mathcal {{\tilde{C}}}}_p} + {{ \mathcal {{\tilde{C}}}}_s}} \right] , \end{aligned}$$

(28)

$$\begin{aligned} {r_2}&= p({{\mathcal {H}}_0}){{\mathcal {C}}_s}. \end{aligned}$$

(29)

where ${\mathcal {C}}_s$ and ${\mathcal {C}}_p$ denote CSSN and PU networks throughput under ${\mathcal {H}}_0$, respectively. Under ${\mathcal {H}}_1$, ${ \mathcal {{\tilde{C}}}_s}$ and ${\mathcal {{\tilde{C}}}_p}$ denote CSSN and PU networks throughput, respectively.

The optimal number of CRUs in the proposed scheme that maximizes the $C_{avg}(N)$ is denoted as $N_{opt}$ written from [26]:

$$\begin{aligned} N_{\mathrm{{opt}}}= \left\lceil {\frac{{\ln ({r_1}/{r_2}) + k\mu }}{\eta } + (k - 1)} \right\rceil . \end{aligned}$$

(30)

where $\mu$ and $\eta$ are given by

$$\begin{aligned} \mu = \ln \left( {\frac{{1 - {P_{me}}}}{{{P_{fe}}}}} \right) ,\quad \eta = \ln \left( {\frac{{1 - {P_{fe}}}}{{{P_{me}}}}} \right) \end{aligned}$$

(31)

From (30), the optimum N expressions under OR rule and AND rule are derived i.e.,

$$\begin{aligned} N_{\mathrm{{opt}}}^{OR}&= \left\lceil {\frac{{\ln ({r_1}/{r_2}) + \mu }}{\eta }} \right\rceil . \end{aligned}$$

(32)

$$\begin{aligned} N_{\mathrm{{opt}}}^{AND}&= \left\lceil {\frac{{\eta - \ln ({r_1}/{r_2})}}{\mu }} \right\rceil . \end{aligned}$$

(33)

3 Simulation framework

The simulation framework for the proposed network is presented in this section. MATLAB/Mathematica is used to construct the simulation model. To validate the analytical frameworks established in the previous sections, the simulation is run using the following step-by-step method. The proposed simulation flow chart of proposed CSSN is shown in Fig. 2. The steps for calculating the cooperative false alarm probability, missed detection probability, total error rate (at single CR and FC levels) and throughput of the considered network are discussed below:

Fig. 2

Proposed CSSN simulation flow chart

• 1. Generate PU signal s(t) and equally likely hypothesis ${{\mathcal {H}}_0}$ and ${{\mathcal {H}}_1}$ using uniform random variable generator.

• 2. Generate AWGN signal at $j^{th}$ antenna $w_j(t)$ and sensing channel fading (Rayleigh or Rician) coefficient $h_j$ ($j=1\,\mathrm {to}$ M) are generated using Gaussian RVs.

• 3. Estimate the obtained signal at $j^{th}$ antenna, $y_j(t)$, at the input of each CR node is $y_j(t) = h_js(t)+w_j(t)$ for true hypothesis ${{\mathcal {H}}_1}$ and $y_j(t) = w_j(t)$ for true hypothesis ${{\mathcal {H}}_0}$.

• 4. Calculate $W_j$ at $j^{th}$ antenna using (2) for a given value of the IED parameter p.

• 5. Repeat the steps from 2 to 4 for M number of antennas and apply SC technique to select the maximum value of W i.e. $U=\mathrm {max}{(W_j)}$.

• 6. Estimate $\lambda$ from $\lambda = {\lambda _n}\sigma _n^p$ for fixed values of p, $\sigma _n$ and $\lambda _n$. For all CR nodes, we presume that $\lambda$ is the same.

• 7. Compare U obtained from step 6 with $\lambda$. If $U>\lambda$, the CR node then makes a hard binary choice of either 1 or 0.

• 8. The steps from 1 to 7 for N number of CR nodes are repeated and N number of decisions (1’s and 0’s) can be found. The binary decision of each CR node ‘1’ or ‘0’ will be sent to the FC for combining operations (k-out-of-N fusion rule) via erroneous reporting channel with channel error probability ‘r’.

• 9. For a huge number of simulations, steps from 1 to 8 are repeated.

• 10. Using (22) false alarm, using (23) missed detection, using (25) total error rate and using (26) throughput can be estimated.

• 11. Draw the simulation results for k-out-of-N (i.e. for various values k) subject to various parameter values of the channel and network namely, p, M, r, K, $\bar{\gamma }_s$, $\lambda _n$ and N.

3.1 Complexity analysis of the flow chart

The throughput maximization and total error minimization have significant complexities due to requirement of calculations of $Q_{me}$ and $Q_{fe}$ over erroneous sensing and reporting channels for all cooperating CRs (at FC). Majority logic fusion is a simple hard decision scheme and it reduces the burden of complexity for the calculation of optimal parameters of the network like $p_{\mathrm{{opt}}}$, $\lambda _{\mathrm{{n, opt}}}$, and $N_{\mathrm{{opt}}}$. Furthermore, when comparing performance over fading channels under Majority logic fusion (sub optimal rule) to performance over non-fading channels under the same Majority logic fusion, it is worth noting that performance over fading channels does not significantly increase the complexity at an individual CR level. However, decisions from IED based CRs increase complexity when compare to CED based CRs while evaluating the total error and throughput performances of the network.

4 Simulation and numerical results

This segment discusses the numerical and simulation results. MATLAB/Mathematica is used to plot all of the data. The proposed network’s throughput and total error rate is calculated using a variety of fading channel and network parameters. For drawing of plots, ${\mathcal {C}}_p=20$, ${ \mathcal {{\tilde{C}}}_p}=10$, ${\mathcal {C}}_s=10$, ${\mathcal {{\tilde{C}}}_s}=5$, $\bar{\gamma }_s=10$ dB, $N=5$, $\lambda _n=20$, $K=1$, 2 and 3 are the parameters used. The channel error probability of $r>0$ means that the channel is imperfect. The CED is represented by $p = 2$ in all statistics, while IED is represented by $p > 2$. In addition, $M=1$ indicates an IED without diversity, while $M>1$ indicates an IED with diversity.

Fig. 3

The $P_m$ versus p (single CR) over Rayleigh and Rician ($K=2$) fading for different M values ($\bar{\gamma }_s=10$ dB and $\lambda _n=30$)

In Rayleigh and Rician fading conditions, Fig. 3 demonstrates a single CR user output for many M and p values. Results in both operating environments show that $P_m$ decreases when p increases. It is noted that for $p=2$, $M=2$, and Rayleigh fading, $P_m$ is 0.9, and is 0.17 for $p=4$. It is seen that for any values of $\lambda _n$ and M CED performance is not significantly good when compare to IEDs. The performance is improved further with increasing in diversity. The impacts of Rayleigh and Rician fading severity on a single CR user are also shown in this figure. It is observed that Rayleigh fading degrades the performance of CR, but Rician fading impact is less on the performance characteristics of a CR. For example, performance is more significant when K from 0 to 2 increases (i.e., the fading severity decreases). The results with $K=0$ (Rician) also an alternative results with Rayleigh fading. The results based on MATLAB simulation match analytical expressions based results over two fading environments.

Fig. 4

The ${\bar{P}}_e$ performance in single CR node (${\bar{P}}_e$ versus $\lambda _n$) in Rayleigh fading for various values of M and r for both CED and IED based CR ($\bar{\gamma }_s=10$ dB)

Figure 4 shows a single CR user performance as function of total error for several M and r values over Rayleigh fading environment. Results show that ${\bar{P}}_e$ decreases when $\lambda _n$ increases up to certain value. The ${\bar{P}}_e$ increases for further increasing values of $\lambda _n$. There exists an optimal $\lambda _n$ where minimum total error is obtained. The optimal $\lambda _n$ depends on the type of detector and it varies with respect to the different values of M and r. The optimal values are noted for both simulation and analytically as shown in Table 1.

Fig. 5

The $C_{avg}$ versus p for various r and M values ($N=10$, $\bar{\gamma }_{s}=10$ dB, $\lambda _n=20$, Majority rule and Rayleigh fading channel)

Fig. 6

The $C_{avg}$ versus p for various r and M values ($N=10$, $\bar{\gamma }_{s}=10$ dB, $\lambda _n=20$, Majority rule and Rician fading channel)

Figures 5 and 6 show throughput versus p for various r and M values. Performance is evaluated in Rayleigh (Fig. 5) and Rician (Fig. 6) fading environments. From both the figures, there exists an optimal value of p where throughput is maximized. This optimal value changes with respect to r and M values. It is found that for $r=0.01$, $M=5$, and Rayleigh fading, the optimal p value is 3, and is 3.25 for $r=0.1$. Similarly, it is found that for $r=0.01$, $M=5$, and Rician fading, the optimal p value is 4, and is 3.5 for $r=0.1$. A significant performance improvement is obtained as M rises from 1 to 5 (i.e., the diversity increases) in both the figures. From both the figures, it is also possible to investigate the effects of Rayleigh and Rician fading intensity on throughput performance. It has been noted that Rayleigh fading degrades the throughput performance, but Rician fading impact is less on throughput performance.

Fig. 7

The $C_{avg}$ versus $\bar{\gamma }_{s}$ for various p and M values ($K=2$, $r=0.01$, $N=10$, $\lambda _n=20$, Majority rule and Rician fading channel)

The throughput is shown in Fig. 7 as a function of $\bar{\gamma }_{s}$ for various p and M values over Rician fading channel. IEDs and CEDs are considered under a Rician fading scenario for Majority rule to see the results. CSSN with CED ($M=1$) requires $\bar{\gamma }_{s}= 10$ dB for $C_{avg}$ = 14.1, but IED ($M=1$) requires only $\bar{\gamma }_{s}=3$ dB for each CR user, i.e., 7 dB gain on SNR is achieved when IEDs are used in the cooperative system instead of CEDs. For increasing M values, the throughput increases significantly, i.e. throughput is very high when diversity increases for both CEDs and IEDs.

Fig. 8

The $C_{avg}$ versus ${\bar{\gamma }}_{s}$ for various M values ($r=0.01$, $N=10$, $\lambda _n=20$, Majority rule and Rayleigh fading channel)

The throughput is shown as a function of $\bar{\gamma }_{s}$ for various M values over Rayleigh fading channel in Fig. 8. The findings are demonstrated using IEDs and CEDs under Majority rule in Rayleigh fading scenario. The CSSN with CED ($M=4$) requires $\bar{\gamma }_{s}= 10$ dB for $C_{avg}$ = 13.5, but IED ($M=4$) requires only $\bar{\gamma }_{s}=2$ dB for each CR user, i.e., 8 dB on gain in SNR is achieved when IEDs are used instead of CEDs. As the value of M is increased, the throughput increases dramatically, and the throughput is very high for both CEDs and IEDs.

Fig. 9

The $C_{avg}$ versus $\lambda _n$ for various p and M values ($K=1$, $r=0.01$, $\bar{\gamma }_{s}=10$ dB, $N=10$, $\lambda _n=20$, Majority rule and Rician fading channel)

The effects of p and M values on throughput for different values of $\lambda _n$ over Rician fading channel are shown in Fig. 9. It is noted that as diversity grows the throughput increases. For example, at $\lambda _n=30$ and CED case, the throughput values 12.5 and 13.8 are obtained for $M=1$ and $M=3$, respectively. Similarly, at $\lambda _n=30$ and IED case, the throughput values 14.8 and 15.0 are obtained for $M=1$ and $M=3$, respectively. As M increases, the magnitude of fading at the CR user level decreases, and the CR user’s individual output improves. For a large value of $\lambda _n$ (say $\lambda _n=50$), IEDs guarantee the better throughput performance than CEDs.

Fig. 10

The $C_{avg}$ versus $\lambda _n$ for various fusion rules ($K=2$, $p=4$, $M=2$, $r=0.01$, $\bar{\gamma }_{s}=10$ dB, $N=10$, $\lambda _n=20$, Majority rule and Rician fading channel)

Figure 10 shows the throughput performance for various fusion rules as function of $\lambda _n$ over Rician fading channel. It is noted from the figure that throughput performance with majority fusion rule is better when compare to other fusion rules. This is due to the fact that FC with majority rule exhibits very low errors (missed and false) and hence average number of transmission of correct decisions from all CRs to FC very high. False detections at FC level with OR rule are more, that is why, throughput performance is degraded with OR rule. Initially, when k value increases from 1 to 6 throughput increases but throughput decreases from $k=6$ to $k=10$, it is observed that majority rule is an optimal sub fusion where maximum throughput is obtained.

Fig. 11

The $C_{avg}$ versus $\lambda _n$ for various fusion rules ($r=0.01$, $\bar{\gamma }_{s}=10$ dB, $N=10$, $\lambda _n=20$, Majority rule and Rayleigh fading channel)

Figure 11 shows the throughput performance for various fusion rules as function of $\lambda _n$ over Rayleigh fading channel. It is noted from the figure that throughput performance with Majority fusion rule is better when compare to other fusion rules. As in Fig. 10, initially, when k value increases from 1 to 6 throughput increases but throughput decreases from $k=6$ to $k=10$, it is observed in this figure also that majority rule can be an optimal fusion where maximum throughput is obtained.

Fig. 12

The $N_{\mathrm{{opt}}}^{OR}$ versus $\lambda _n$ for both CED and IED over Rayleigh and Rician fading channels ($r=0.01$, $M=2$, $\bar{\gamma }_{s}=10$ dB and $N=10$)

For a given rule, the optimal N calculation is needed. For OR rule, the optimal N denoted as $N_{\mathrm{{opt}}}^{OR}$, as a function of $\lambda _n$ for erroneous ($r=0.01$) and Rayleigh and Rician fading channels is shown in Fig. 12. As compared to an IED-based system, the optimum N for the CED-based system is higher in both channels. It is also observed that as $\lambda _n$ increases, $N_{\mathrm{{opt}}}^{OR}$ increases for a given form of detector and fading. IEDs, once again, outperform CEDs in terms of the optimal number of CR nodes required.

Table 1 The ${\bar{P}}_e$ for various values of M and r over Rayleigh fading channel ($\lambda _n=1$ to 100 and $\bar{\gamma }_{s}=10$ dB)

Table 1 shows both simulation and analytical values of total error rate of a single CR. It is noted that as diversity increases the total error decreases for both CED and IED. High value of r degrades the total error performance. It is noted that for any r and M values, IED shows an excellent performance when compare to CEDs. The results of the MATLAB simulation are compared to the results of the theoretical expressions.

Table 2 Optimal $\lambda$ values in a single CR (${\bar{P}}_e$) for various $\bar{\gamma }_{s}$ values

Table 2 shows $\lambda _{\mathrm{{opt}}}$ values in a single CR under Rayleigh and Rician fading channels. The $\lambda _{\mathrm{{opt}}}$ values based on MATLAB simulation is validated though the results based on the analytical expressions given in (11) and (12) for Rayleigh case only. It is also noted that $\lambda _{\mathrm{{opt}}}$ values based on simulation subject to Rician case are also shown. It is observed that as $\bar{\gamma }_{s}$ or diversity increases the $\lambda _{\mathrm{{opt}}}$ decreases.

Table 3 The $Q_{e}$ for various r values over fading channels ($M=3$, $\lambda _n=50$, $\bar{\gamma }_{s}=10$ dB, and $N=10$)

Table 4 The $Q_{e}$ for various M values over fading channels ($r=0.01$, $\lambda _n=50$, $\bar{\gamma }_{s}=10$ dB, and $N=10$)

The output of CEDs and IEDs in fading channels is compared in Tables 3 and 4. At FC, the Majority fusion rule is taken into account. Table 3 compares the output of both CEDs and IEDs in terms of $Q_{e}$ under imperfect channel conditions. It is worth noting that when r rises, the overall error rate rises as well. Because, channel error probability decreases the number of correct receptions at FC. In Table 4, both CEDs and IEDs performances are compared under different diversity conditions. It is noted that total error rate decreases when diversity increases. Because, diversity increases the number of correct receptions at FC.

Table 5 $C_{avg}$ for various r values over various fading channels ($M=3$, $\lambda _n=50$, $\bar{\gamma }_{s}=10$ dB, and $N=10$)

Table 6 $C_{avg}$ for various M values over various fading channels ($r=0.01$, $\lambda _n=50$, $\bar{\gamma }_{s}=10$ dB, and $N=10$)

Tables 5 and 6 display throughput values over different fading channels for different r and M values, respectively. It can be shown that under imperfect channel conditions, throughput suffers, but throughput improves dramatically when diversity is increased. When compared to Rayleigh fading channel considered in the present work, if the network is run in a Rician fading environment, significant performance improvement is seen (from Tables 3, 4, 5, 6). Furthermore, the network performance with IEDs is much superior to a network with traditional detectors (from Table 3, 4, 5, 6).

5 Conclusions

We have looked at how well CSSN is performed in noisy environments with Rayleigh or Rician fading. We have developed frameworks for various performance metrics for both single CR node and the proposed CSSN. The theoretical results have been matched to MATLAB simulation based results. Throughput increases initially for increasing values of p and $\lambda _n$, then decreases for more increasing values of p and $\lambda _n$, indicating that the throughput has a maximum value. For all values of M and r, the optimal p, $\lambda _n$, and N values have been found, corresponding to which the throughput is maximized. With imperfect channel conditions, throughput and total error suffer, but both improve dramatically when diversity is increased. Finally, in both fading conditions, the proposed network with IEDs outperforms the network with traditional detectors in terms of throughput. This work is extremely beneficial to the advancement of next-generation wireless networks. The mathematical outlines developed in the present paper are established in a systematic manner; however, the current work could be expanded to include further investigation of the proposed network’s output in other fading environments.