1 Introduction

Active and passive methods of limiting sound emission are two methods in noise control system to control noise. Passive noise control (PNC) reduces noise by changing the architectural properties of the building or by including sound-dampening materials. PNC are usually very efficient for signals who’s frequency ranges from 500 Hz and higher [1]. PNC system is efficient in noise control only for certain noise frequencies and also increase the structural cost of the system. In addition, passive methods are incapable of handling noise in some application where the power source changes.

To reduce the shortcomings of PNC system, especially low-frequency noise, ANC methods were developed by researchers [2,3,4] for noise suppression. ANC method suppresses the noise by super-positioning secondary sound that are designed to cancel the primary noise. Anti-noise or the secondary sound is usually generated with equivalent amplitude and contradictory phase as that of the primary noise signal. ANC is an electro acoustic noise reducing system. The primary noise signal is combined with anti-noise signal which results in the cancellation of noise signal. PNC system becomes either expensive or bulky when controlling low-frequency noises and hence active noise control system are used to limit the low-frequency noises where passive noise control system becomes inefficient. ANC methods are beneficial in terms of volume, size, cost, weight and is developing rapidly to be the most efficient means of noise control system [5, 6].

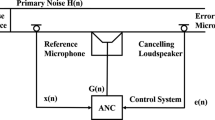
The ANC system uses FxLMS algorithm which is robust, less complex and is easy to implement [7, 8]. Figure 1 represents single-channel feedforward ANC system which uses FxLMS algorithm consisting of one reference noise microphone to obtain the primary noise x(n), 1-cancellation loudspeaker to propagate the anti-noise signal and one error microphone to deduct the residual error e(n) between the noise signal and the cancelling noise. Primary acoustic path is represented as P(z) and secondary path is represented as S(z). Offline or online system identification approach is used to identify the secondary path S(z) [9, 10]. Adaptive filter W(z) produces y(n) which is passed through secondary path S(z) to produce the anti-noise signal \(y^{\prime}(n)\). This signal is then fed to the cancellation loud speaker. A region of silence is created near the error microphone by super-positioning the anti-noise signal \(y^{\prime}(n)\) from the cancellation loudspeaker over the noise signal d(n) from the noise source. The remaining error e(n) from the error microphone is used by the adaptive filter W(z) which in turn minimises the noise residue at error microphone.

Fig. 1
figure 1

Block diagram of the single—channel FxLMS algorithm

Full size image

Since the anti-noise signal from the adaptive filter is modelled through S(z), the reference signal x(n) is passed through \(\hat{s}(z)\). The error e(n) is represented in (1)

$${\text{e}}({\text{n}}) = {\text{d}}({\text{n}}) - {\text{y}}^{{\prime }} ({\text{n}})$$
(1)

where \(y^{\prime}(n)\) is the anti-noisesignal. The expression to compute \(y^{\prime}(n)\) and y(n) are given in (2) and (3)

$$y^{\prime}(n) = s^{T} (n)\,y(n)$$
(2)
$$y(n) = w^{T} (n)\,x(n)$$
(3)

The FxLMS equation for ANC system is given in (4) is based on the assumption that reference microphone does not receive any acoustic feedback from cancellation loudspeaker.

$$w\left( {n + 1} \right) = w\left( n \right) + \mu e\left( n \right)\,[\hat{s}(n) * x^{\prime}\left( n \right)]$$
(4)

where μ represents the step size of the algorithm and \(\hat{s}(n)\) is the impulse response of \(\hat{s}(z)\). However, FxLMS algorithm becomes unstable if impulse noise with large amplitude exists in reference signal.

In this paper, will discuss the ANC method to control impulse noise. Instantaneous sharp noises are categorized as impulse noise. Impulsive noise can be mathematically modelled using symmetric α-stable (SαS) distribution function f(x). SαS distribution has the characteristic function of the form given in Eq. (5) [11,12,13].

$$\phi \,(t) = e^{{ - \gamma \left| t \right|^{\alpha } }}$$
(5)

where 0 < α < 2 is called the characteristics exponent which controls the heaviness of its tail and it is the shape parameter. When the values of α are close to 0 the distribution indicates high impulsive noise. For α = 2 the distribution becomes Gaussian. The heavy tail of the PDF of α-stable distribution is the key difference between the SαS distribution and the Gaussian distribution function. In (5), γ > 0 is called as dispersion parameter. Figure 2 shows the symmetric α-stable (SαS) distribution function variation with respect to varying α.

Fig. 2
figure 2

The PDFs of standard symmetric α-stable (SαS) process

Full size image

In this paper, a new noise and error signal with a soft threshold is introduced to improve the stability of FxLMS system. It further improves the robustness of the system by introducing variable step size based on the harmonic mean of input noise signal. The convergence rate of the system towards the desired output is improved in this system by varying step size according to the input noise signal and error signal. The proposed method has better noise reducing capacity than the already existing methods.

2 Relation to Prior Work

FxLMS algorithm used in ANC system is based on mean square error criterion. In case of impulsive noise which is non-Gaussian process, the mean square error is apoor optimization criterion which makes the FxLMS algorithm unstable. To overcome this Filtered-x least mean p-power algorithm (FxLMP) has been introduced [14]. FxLMP algorithm improves the performance of ANC system for impulsive noise but increases the computational complexity at each iteration. Sun’s algorithm and Akhtar’s algorithm were discussed to bring down the mathematical complexity of FxLMS algorithm for impulsive noise.

2.1 Filtered-x-Least Mean p-Power (FxLMP) Algorithm

Leahy et al. [14] designed FxLMP algorithm to overcome the limitations of FxLMSalgorithm. In case of impulsive noise where the variance is not finite, the mean square error criterion used in adaptive filtering in FxLMS algorithm is not an optimum objective so minimum dispersion is used as a measure. Minimising dispersion is equivalent to minimising a fractional lower order moment of the residual error, E{|e(n)|p}., for p < α. For some 0 < p < α, minimizing the pth moment E{|e(n)|p} ≈ |e(n)|p, the stochastic gradient method to update W(z) is given in Eq. (6) [11].

$$w(n + 1) = w(n) + \mu p\left| {e(n)} \right|^{p - 1} \text{sgn} (e(n))[\hat{s}(n) * x(n)]$$
(6)

where

$$\text{sgn} (e\,(n)) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {e\,(n) > 0} \hfill \\ 0 \hfill & {e\,(n) = 0} \hfill \\ { - 1} \hfill & {e\,(n) < 0} \hfill \\ \end{array} } \right.$$
(7)

The FxLMP algorithm reduces to FxLMS when p = 2. In conclusion, the convergence rate is fast when p is as close as possible to α, where the natural upper bound is p < α [14], since the moments do not exist for the larger values.

2.2 Sun’s Algorithm

To improve the convergence rate and the stability of ANC system for impulsive noises Sun et al. devised an algorithm [15]. In this algorithm, the noise signal is altered by threshold to overcome the difficulty of analytically expressing the noise in practice and to reduce the mathematical complexity and is given in Eq. (8)

$$\hat{x}(n) = \left\{ {\begin{array}{*{20}l} {x(n)} \hfill & {if\,x(n) \in [c1,c2]} \hfill \\ 0 \hfill & {otherwise} \hfill \\ \end{array} } \right.$$
(8)

Using eq 8 Sun’s algorithm is given in (9)

$$w\left( {n + 1} \right) = w\left( n \right) + \mu e\left( n \right)\,[\hat{s}(n) * \hat{x}\left( n \right)]$$
(9)

It is based on the following two approximations [15]

  1. 1.

    When the noise value moves towards 7 N, the PDF for practical noise always leans to 0 hence the probability of the sample signal having value greater than c1 or below c2 is presumed to be 0. Statistical method can be used in practice to estimate c1 and c2.

  2. 2.

    The distribution of noise within the range [c1, c2] is uniform.

The algorithmbecomes unstable for α < 1.5 but reduces the mathematical complication of FxLMS algorithm.

2.3 Akhtar’s Algorithm

Akthar’s algorithm clipps the reference noise signal and error signal e(n) which has large amplitude by threshold value [16, 17] and is given in Eqs. (10) and (11) as

$$x^{\prime\prime}(n) = \left\{ {\begin{array}{*{20}l} {c1} \hfill & {x(n) \le c1} \hfill \\ {c2} \hfill & {x(n) \ge c2} \hfill \\ {x(n)} \hfill & {otherwise} \hfill \\ \end{array} } \right.$$
(10)
$$e^{\prime\prime}(n) = \left\{ {\begin{array}{*{20}l} {c1} \hfill & {e(n) \le c1} \hfill \\ {c2} \hfill & {e(n) \ge c2} \hfill \\ {e(n)} \hfill & {otherwise} \hfill \\ \end{array} } \right.$$
(11)

Using (10) and (11), Akhtar algorithm is given as

$$w\left( {n + 1} \right) = w\left( n \right) + \mu e^{\prime\prime}\left( n \right)\,[\hat{s}(n)\, * x^{\prime\prime}\left( n \right)]$$
(12)

Akhtar’s method improves the convergence rate and stability of the system. This algorithm has the similar mathematical complication as FxLMS algorithm.

3 Proposed Method

Akthar’s algorithm [17] is further improved in the proposed algorithm to implemented single-channel feedforward ANC system using FxLMS algorithm with soft threshold. Soft threshold decreases the detail coefficients of high frequency or high magnitude components and reside low frequencies since low frequencies contain important signal information [18] based on the assumption that in high frequency or high magnitude the signal has less significance than noise. The magnitude of the resulting signalis decreased by the threshold value in the proposed technique. This technique slightly reduces the magnitude of the signal but eliminates the discontinuity existing in the signal resulting in smoother reconstructed signals. Aktahr’s algorithm is further improved by modifying the error signal as given in

$$e^{\prime\prime}(n) = \left\{ {\begin{array}{*{20}l} {sign\,(e\,(n))(\left| {e\,(n)} \right| - \lambda )} \hfill & {if\,\,\left| {e(n)} \right| > \gamma } \hfill \\ 0 \hfill & {if\,\left| {e(n)} \right| \le \gamma } \hfill \\ \end{array} } \right.$$
(13)

The modified reference signal x(n) is given in (14)

$$x^{\prime\prime}(n) = \left\{ {\begin{array}{*{20}l} {sign\,(x\,(n))(\left| {x(n)} \right| - \lambda )} \hfill & {if\,\,\left| {x(n)} \right| > \gamma } \hfill \\ 0 \hfill & {if\,\left| {x(n)} \right| \le \gamma } \hfill \\ \end{array} } \right.$$
(14)

Here \(x^{\prime\prime}\left( n \right)\) represents the reference signal clipped by adaptive threshold value γ which can be estimated using SURE [19]. The risk of the impulsive noise x(n) is given in (15)

$$R(n) = N + ||x(n)||^{2} + 2\sum\limits_{i = 0}^{N - 1} {\frac{{\partial x_{i} }}{\partial n}}$$
(15)

and the adaptive soft threshold is calculated in (16)

$$\gamma = \arg \hbox{min} \,\,R(n),\,\,\,\,n \in \,\{ x_{o} ,x_{1} ,x_{2} , \ldots ,x_{N - 1} \}$$
(16)

In this algorithm, the step size \(\mu\) is determined by the convergence rate and the ability to remove excess mean-square error in FxLMS algorithm. In the beginning, when the filter coefficient \(w\) is far from the ideal solution, the step-size \(\mu\) must be big to transfer the weight vector quickly toward the desired result. The step-size is decreased when the system starts to converge from mean to steady-state.

Impulsive noises are considered as noise disturbance with large amplitude and low probability. Hence the step size \(\mu\) should be chosen accordingly to make the system converge in the presence of large amplitude. Let \(x_{1} (n),x_{2} (n) \ldots x_{N} (n)\) be considered as impulsive noises of large amplitude with finite mean \(m\), when the system converges, \(\frac{1}{n}\sum\nolimits_{i = 1}^{N} {x_{i} }\) converges to \(m\) as \(n \to \infty\). By using this concept, harmonic mean H for the positive number of input noise signals \(x_{1} (n),x_{2} (n) \ldots x_{N} (n)\) is consider for defining the new variable step size \(\mu\), which can converge the system in the presence of noise with large positive amplitude. The harmonic mean for \(x_{1} (n),x_{2} (n) \ldots x_{N} (n)\) is given in Eq. (17)

$$H = \frac{N}{{\frac{1}{{x_{1} }} + \frac{1}{{x_{2} }} + \cdots + \frac{1}{{x_{N} }}}} = \frac{N}{{\sum\nolimits_{i = 1}^{N} {\frac{1}{{x_{i} }}} }}$$
(17)

The proposed variable step size \(\hat{\mu }(n)\) using H to improve the noise reduction in ANC system is given in equation

$$\hat{\mu }(n) = \mu \,\left[ {\frac{N}{{\sum\nolimits_{i = 1}^{N} {\frac{1}{{x_{i} (n)}}} }}} \right]$$
(18)

Using (13), (14), (17) and (18), the proposed FxLMS algorithm for ANC of impulse noise is given as (19)

$$w\left( {n + 1} \right) = w\left( n \right) + \hat{\mu }\left( n \right)e^{\prime \prime } ({\text{n}})[{\hat{\text{s}}}({\text{n}})*{\text{x}}^{\prime \prime } \left( {\text{n}} \right)]$$
(19)

The Eq. (19) represents FxLMS algorithm based on soft threshold. To further improve the robustness of the system “Harmonic Mean Step Size” is introduced in soft threshold FxLMS algorithm (STFxLMS).

3.1 Convergence Analysis

Let \(\alpha^{2} (n)\) be the power of the tracking error signal which is used to cancel the noise in the system due to step size. The \(\alpha^{2} (n)\) is calculated as

$$\alpha^{2} (n) = \frac{{E[e^{2} (n)]}}{{E[x^{2} (n)]}} = \frac{{\sigma^{2}_{e} (n)}}{{\sigma^{2}_{x} (n)}}$$
(20)

Here \(E[.]\) denotes the mathematical expectation whereas \(\sigma^{2}_{e} (n)\) and \(\sigma^{2}_{x} (n)\) denotes the power of error signal and input signal respectively. In some case, the input signal \(x(n)\) excitation may not happen. In such case \(\sigma^{2}_{x} (n) = 0\), which intern makes \(\alpha^{2} (n) \to \infty\). To avoid this condition, a small positive number \(\beta\) is added in (20) and it is rewritten as

$$\alpha^{2} (n) = \frac{{\sigma^{2}_{e} (n)}}{{\beta + \sigma^{2}_{x} (n)}}$$
(21)

Let us assume that the initial stage for unknown filter coefficient of the adaptive filter, the value of the \(\alpha^{2} (n)\) is large because of the mismatch in the system. Therefore, the harmonic mean H is large which will utilise maximum step size \(\hat{\mu }(n) = \mu_{\rm max }\), which will increase the convergence rate of the ANC system. As the number of iteration progresses, the value of \(\alpha^{2} (n)\) and harmonic mean H decreases \(\hat{\mu }(n)\) reduce. As the algorithm convergesto the steady state condition, \(\alpha^{2} (n) \approx 0\). At this moment, the system uses \(\mu^{\prime\prime}(n) \approx \mu_{\rm min } \approx \mu\) for lowering the steady-state error.

4 Results and Discussion

4.1 Computer Simulations

The performance of the STFxLMS algorithm with variable step size (VSS) using harmonic mean is analyzed with fixed step size and Akhtar’s method. Here both the acoustic path \(P(z)\) and secondary path \(S(z)\) is modelled as finite impulse response (FIR) filter. The length of the FIR filter for the primary path \(P(z)\) and secondary path \(S(z)\) are 256 and 128 respectively. The measure of FIR filter for estimated secondary path \(\hat{S}(z)\) is same as \(S(z)\). The length of FIR for adaptive controller filter \(W(z)\) is 192. For computer simulation, the impulsive noise is generated with \(\alpha = 1.2\), \(\alpha = 1.4\) and \(\alpha = 1.8\) respectively. There is no significance of mean square error in \(S\alpha S\) processes the second order moments do not exist. To overcome this, Average Noise Reduction (ANR) method [12] is used for noise reduction given in

$$ANR(n) = \frac{Ae\,(n)}{Ad\,(n)}$$
(22)

Here the \(Ae\,(n)\) is the estimated absolute values of residual error signal e(n) and \(Ad\,(n)\) is the estimated absolute values of disturbance signal d(n) given in (23) and (24), with forgetting factor λ = 0.99

$$Ae(n) = \lambda \,Ae(n - 1) + (1 - \lambda )|e(n)|$$
(23)
$$Ad\left( n \right) = \lambda Ad\left( {n - 1} \right) + \left( {1 - \lambda } \right)\left| {d\left( n \right)} \right|$$
(24)

4.1.1 Noise Reduction Characteristics for \(\alpha = 1.2\)

The simulation results for high impulse noise for case 1 (where \(\alpha = 1.2\)) is given in Figs. 3 and 4. The value of the two thresholds c1 and c2 are estimated experimentally through Akthar’s algorithm as 0.1 and 99.9 percentile of the impulse noise signal x(n) respectively. Figure 4 shows the ANR curves for STFxLMS algorithm with variable step size compared with fixed step size and Akthar’s method.

Fig. 3
figure 3

Impulsive noise generation for α = 1.2

Full size image
Fig. 4
figure 4

ANR curve for impulsive noise with α = 1.2

Full size image

It is noticed that the proposed method using STFxLMS and harmonic mean based step size has significantly increased the efficiency of the ANC system by reducing the noise level and converging to steady state condition with minimum noise level. Whereas, in STFxLMS with fixed step size the noise level is high initially and the system converges to a steady state where the noise level is still high than STFxLMS with variable step size. In Akhtar’s algorithm, the starting as well as steady state noise level remains high as compared with other two algorithms.

4.1.2 Noise Reduction Characteristics for α = 1.4 & 1.8

Figures 5 and 6 shows the impulsive noise generated for case2 (for α = 1.4) and case 3 (for α = 1.8) respectively. For case 2 the value of the two thresholds c1 and c2 are estimated experimentally through Akthar’s algorithm as 0.05 and 99.5 percentile of the impulse noise signal x(n). For case 3 the value of the two thresholds c1 and c2 are estimated experimentally through Akthar’s algorithm as 0.1 and 99.9 percentile of the impulse noise signal x(n).

Fig. 5
figure 5

Impulsive noise generation for α = 1.4

Full size image
Fig. 6
figure 6

Impulsive noise generation for α = 1.8

Full size image

The Figs. 7 and 8 represents the ANR curves for case 2 and case 3 respectively for the proposed STFxLMS algorithm with variable step size compared with fixed step size STFxLMS and Akthar’s method. In Figs. 7 and 8 the proposed algorithm STFxLMS with variable step size has significantly maintained low noise level instable state as compared to other algorithms. In case 2 and 3STFxLMSalgorithms with fixed step size acts almost similar to Akhtar’s algorithm.

Fig. 7
figure 7

ANR curve for impulsive noise with α = 1.4

Full size image
Fig. 8
figure 8

ANR curve for impulsive noise with α = 1.8

Full size image

4.2 Experimental Setup

In this experiment, the noise chamber consists of noise source (here a mixer grinder of 750 W power is used), primary microphone to measure the noise signal, loud speaker to produce the anti-noise signal corresponding to the noise signal measured by the primary microphone and an error microphone to fine tune the anti-noise signal to effectively control the noise signal.

The system uses Texas Instruments Mixed Signal Processor (MSP) 430G2x73 series, which is an ultra-low power consuming device with 16-bit RISC architecture and inbuilt Analog–to–Digital Converter (A/D) and Digital-to-Analog (DAC) converter. The Mixed Signal Microcontroller (MSP) 430G2x73 also has versatile comparator with built-in communication for universal serial communication interface and is capable of capturing analog signals, even with low cost sensors.

For testing purposes, the noise generated by the mixer grinder is converted into electrical signal using primary microphone, which is then converted into digital signal \(x(n)\) with 200 ksps. This system uses signal conditioning units such as pre-amplifier for conditioning the amplitude of the signal \(x(n)\) in accordance with the processor requirement and power amplifier to amplify the anti-noise signal from DAC to drive the loud speaker shown in Fig. 9. The control filter generates the anti-bits \(y(n)\) corresponding to the signal \(x(n)\) which gets amplified to produce anti-noise signal. The anti-noise signal is then coupled to the noise chamber using loud speaker.

Fig. 9
figure 9

Experimental Setup diagram

Full size image

The error microphone is used to fine tune the anti-noise using \(e^{\prime\prime}(n)\), \(x^{\prime\prime}(n)\), \(\hat{\mu }(n)\) and \(\alpha^{2} (n)\) given in (13), (14), (18) and (21) respectively. The results shown in Fig. 10 are tested for impulsive noise with α = 1.8, using RIGOL make Digital Storage Oscilloscope (DSO). The upper waveform represents the anti-noise signal corresponding to the noise signal which is represented by the lower waveform. It is noticed that the proposed algorithm generates the anti-noise signal with minimal residual noise, represented as strip lines in the anti-noise cure. The noise signal is measured from the output of the pre-amplifier and anti-noise signal is measured from output of DAC.

Fig. 10
figure 10

Experimental output of noise output versus anti-noise output

Full size image

4.3 Step by Step Analysis

Figures 11 and 12, represents the micro analysis of the how the proposed method converges towards the noise generated. The first signal is the noise measured, and the second signal is anti-noise generated, which is converging towards the noise signal. It is noticed that the anti-noise signal in this stage is noisy, due to influence of the remaining error deducted by the error microphone.

Fig. 11
figure 11

Experimental output of initial stage

Full size image
Fig. 12
figure 12

Experimental output of initial stage

Full size image

In Fig. 13, representing the observation taked during the intremediate stage where the residual noise due to DAC process starts to minimise, since the proposed algorithm is implemented in hardware.

Fig. 13
figure 13

Experimental output of intermediate stage noise output versus anti-noise output

Full size image

5 Conclusions

In this paper, investigated the effect of introducing harmonic mean based step-size over impulsive noise in active noise control system. Soft threshold is introduced to the FxLMS algorithm along with harmonic mean based variable step size (HMVSS) to overcome the issues caused by impulsive noise [Eqs. (13)–(19)]. Computer simulations and real-time experiment are used to explain the capability of the proposed algorithm in improving the performance of ANC system for impulsive noise.