1 Introduction

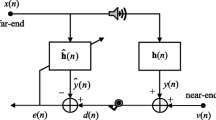
Over the course of the previous few years, there have been a great deal of enhancements made to the FxLMS algorithm for active noise cancellation. The feedforward FxLMS method [20, 21] is one of the most prominent one. In this technique, the adaptive filter is utilized as a controller to create an "anti-noise" signal. In other words, one uses a microphone to locate the reference noise, which is then used in the correlation process in order to cancel out the primary noise. On the other hand, the feedback FxLMS method [7, 9] takes advantage of the error signal but does not require any sensors to function properly. Because of the throughput limitations of the system, this method is mostly utilized for applications on headphones. However, it does not efficiently decrease the noise throughout the whole frequency spectrum since bandwidth is constrained. Narrowband disruptions, on the other hand, are effectively managed by this method. In the feedforward system, an additional path is created between the adaptive filter and the microphone before the ’anti-noise’ signal is allowed to reach the error microphones. This primary path leads to the adaptive filter. Therefore, in order to acquire an accurate weight update for the adaptive filter, we need to adjust for the secondary path impact that travels from to the error microphone. This is necessary in order to obtain an accurate weight update. Before the input signal is utilized for the adaptive filter, it first goes through an approximated version of the transfer function. Take note that decreasing the instantaneous squared error is our primary emphasis at the moment. There is no requirement for the use of a microphone within the feedback system. In this situation, the adaptive filter performs the function of a synthesizer by producing the reference signal based on the output of the adaptive filter as well as the error signal. That is to say, the reference signal for this situation is created internally. Despite the fact that, this technique makes the algorithm more likely to converge, it is not possible for it to eliminate the influence of the uncorrelated disturbance that would be present, as shown in [7]. Adaptive techniques on active noise control employing a hybrid strategy have been discussed in [1,2,3,4,5,6,7, 9,10,11]. In addition stochastic analysis of a filtered-x weighted accumulated LMS algorithm in case of narrowband ANC can be found in [3]. Recently active noise control methodologies utilizing frequency domain approach based on penalty factor [15], selective fixed filter [16] and multichannel arrangement for mitigating noise arriving from multiple directions have been introduced [6].

We add a supporting adaptive filter that is provided by the Least Mean Square Algorithm [17, 23] in order to guarantee that the control of uncorrelated noise v(n) is maintained. This is done in order to update the adaptive filter in the feed-forward FxLMS system by making use of an estimate of a desired error signal. This is done rather than the error signal, which would be distorted by the uncorrelated noise. Because of this, the convergence of the system is improved as a result of the fact that the error signal that is being used is unaffected by any external disturbances. In addition, recently variable step size has been discussed for handling impulsive noise with Gaussian noise and noisy inputs as well [8, 13,14,15,16,17,18,19,20,21,22,23,24,25]. The variable step size was included in this system in order to strike a compromise between the speed of convergence and its stability [2, 4]. While the filter would converge rapidly when the step size is too big, the filter would not be stable throughout this process. If it is set too low, the filter will be more stable, but it will take an excessive amount of time to converge. Therefore, in order to keep a balance between the speed of convergence and the stability of the system, we employ an adaptive variable step size that varies depending on the error that is created by the algorithm. This allows us to maintain a balance between the speed of convergence and the stability of the system. In this study, we will investigate several strategies that may be utilized in order to realize the following qualities of an Active Noise Control System. In this study, we will investigate several strategies that may be utilized in order to realize the following qualities of an active noise cancellation system.

  • Accomplish an optimal level of noise reduction despite the presence of wideband as well as narrowband disturbances.

  • Utilising the external adaptive filter that is part of Sun’s Method helps to increase the convergence of the weight vector as well.

  • A variable step size LMS block to the system will be employed in an attempt to dramatically cut down on the amount of noise.

Fig. 1
figure 1

Feed forward FxLMS algorithm

Full size image

2 Active Noise Cancellation Methods

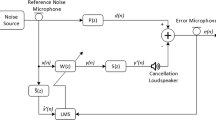
Figure 1 depicts the structure of a Feedforward FxLMS based ANC algorithm. A reference noise is produced by the use of sensors to collect information about the noise that is already there. This helps the feed-forward algorithm, which is used to minimize broadband noise. In this case, the adaptive filter \(\mathbf{{W}}\left( z \right) \) is put to use as a controller in order to produce an anti-noise signal denoted by y(n). A secondary route, denoted by the notation \(\mathbf{{S}}\left( z \right) \), connects the filter and the sensor prior to the anti-noise’s arrival to the sensor referred to as the secondary path. represented as.

$$\begin{aligned} y(n)={\textbf {w}}^{T}(n){\textbf {x}}(n), \end{aligned}$$
(1)

and

$$\begin{aligned} y'(n)=y(n)*s(n), \end{aligned}$$
(2)

with * standing for linear convolution and x(n) serving as the reference signal vector of \(\mathbf{{w}}\left( z \right) \), respectively. The desired signal, d(n), may be obtained by following the major acoustic route, which is denoted by P(z) . After that, the signal that is wanted is contrasted with the signal that is filtered by the adaptive filter, which is denoted as \(y'(n) \), to get the error signal, e(n) . That is,

$$\begin{aligned} d(n)={\textbf {x}}(n)*p(n), \end{aligned}$$
(3)

and

$$\begin{aligned} e(n)=d(n)-y'(n). \end{aligned}$$
(4)

In (3), the term p(n) denotes the impulse response of the primary path P(z). The weights are then updated as

$$\begin{aligned} {\textbf {w}}(n+1)={\textbf {w}}(n)+\mu {\textbf {x}}'(n)e(n), \end{aligned}$$
(5)

with \(\displaystyle {{\textbf {w}}}(n)=\text {[}{w_{0}(n),w_{1}(n),...w_{L-1}(n)}]\) being the coefficient vector of \({\displaystyle \text {W(z)}}\) of length L and \({{\textbf {x}}'(n)}\) is the filter reference signal through the secondary path estimate Ŝ(z), and \({\displaystyle \mu }\) is the step size. Figure 2 depicts the structure of a Feedback FxLMS based ANC algorithm. This method is more effective than others when applied to narrow band noise as it is dependent only on the output of the adaptive filter output and the error signal, the signal x(n) in this approach is one that is produced on the fly by the method itself

$$\begin{aligned} \begin{aligned} \textbf{x}(n)\approx d(n)&= e(n)-y'(n) \\&= e(n)-y(n)* \hat{s}(n). \end{aligned} \end{aligned}$$
(6)

The weight updating here follows the same equations as that in the feed forward algorithm.

Fig. 2
figure 2

Feedback FxLMS algorithm

Full size image

3 Methods to Improve the System

In this part of the article, we are going to investigate the many strategies that we may implement to enhance the performance of the noise cancelling system. These enhancements will be implemented in the next part, as well as the flow of the system being outlined. Although the Sun’s technique is highly helpful for convergence, there is a possibility that it is not as successful when it comes to removing the uncorrelated noise from the residual disturbance signal. Note that even while the combination of feedforward and feedback algorithms may be effective at limiting the amount of uncorrelated noise, it has poor convergence. As a result, we will be implementing a configurable step size as well as an external adaptive filter because these two features have the potential to dramatically increase convergence.

3.1 Sun’s Method

The uncorrelated noise that cannot be suppressed more effectively by utilizing the FxLMS algorithm is targeted for reduction with the aid of this technique. As described in the aforementioned publication [17, 19], Sun’s technique for updating the adaptive filter employs an estimate of the intended error signal rather than the actual error signal itself in order to perform the update. It is proposed to implement an adaptive filter denoted by the symbol H(z), whose input is the reference signal. The signal that is wanted is regarded as the error signal.

Additionally, the variable step size is a popular technique used to ensure faster convergence of the filter without compromising the stability of the system [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. There are many different strategies for variable step size. The step size \({\displaystyle \mu }\) is found using [5] as follows

$$\begin{aligned} \mu (n+1)=\alpha \mu (n)+\gamma e^{2}(n), \end{aligned}$$
(7)

with \({\displaystyle \alpha }\) and \({\displaystyle \beta }\) as constants that can be set by the user, and \({\displaystyle \textit{e(n)}}\) is the error signal. The step size must also satisfy the following conditions:

$$\begin{aligned} \mu (n+1) = {\left\{ \begin{array}{ll} \mu _{upper bound} & \text {if } \mu (n+1)> \mu _{upper bound}, \\ \mu _{lower bound} & \text {if } \mu (n+1)< \mu _{lower bound}, \\ \mu (n+1) & \text {otherwise}, \end{array}\right. } \end{aligned}$$
(8)

for all \({\displaystyle \textit{i}}\) such that weight \({\displaystyle {\varvec{{w}(i)}}}\) and signal \({\displaystyle {\varvec{{x}(i)}}}\) exists and \({\displaystyle \mu _{upper bound}}\) and \({\displaystyle \mu _{lower bound}}\) defining the window of possible step size values (Table 1).

Table 1 Proposed variable step-size combined Fx-LMS algorithm summary
Full size table

3.1.1 Online Identification of Secondary Path Function

There have been a lot of different online identification methods investigated in the past, and the most of them involve the addition of some additional white noise. The Simultaneous Equation Method (SEM), on the other hand, does not call for the injection of any extra white noise. In this section, the filter \(H_o(z)\) is presented as a means of modeling the overall model, which consists of the combination of the primary path and the secondary path. In this case, the modeling approach is largely independent of the ANC system. This indicates that it does not contribute any noise that is not desirable to the system as a whole.

Fig. 3
figure 3

Proposed variable step-size combined Fx-LMS algorithm

Full size image

4 Proposed Variable Step-Size Combined Fx-LMS Algorithm

In this setup, we use the combination of the feedforward and feedback algorithms with an introduction of an external filter, and use variable step size and online identification of secondary path to improve the performance of the Active Noise Control system. Figure 3 shows the block diagram of the proposed algorithm. In this method, the filter outputs of both \({\displaystyle \text {W}_{1}(z)}\) and \({\displaystyle \text {W}_{2}(z)}\) are added up to produce the cancelling signal \({\displaystyle \text {y}(n)}\). That is,

$$\begin{aligned} y(n)=y_{1}(n)*y_{2}(n), \end{aligned}$$
(9)

with \({\displaystyle \textit{y}_{1} \textit{(n)}}\) and \({\displaystyle \textit{y}_{2} \textit{(n)}}\) defined as,

$$\begin{aligned} y_{i}(n)={\textbf {w}}_{i}^\text {T}(n){\textbf {x}}_{i}(n), \end{aligned}$$
(10)

wherein \({\displaystyle {{\textbf {w}}}_{i}(n)=\text{[ }{w_{i,0}(n),w_{i,1}(n),...w_{i,L-1}(n)}]}\), as the coefficient vector of the filter \({\displaystyle \text {W}_{i}(z)}\), \({\displaystyle {{\textbf {x}}}_{i}(n)=\text{[ }{x_{i}(n),x_{i}(n-1),...x_{i}(n-L+1)}]}\), is the reference vector of the filter \({\displaystyle \text {W}_{i}(z)}\), with \({\displaystyle \text {i=1,2}}\) and \({\displaystyle \text {L}}\) being the order of the filter. When the cancelling signal \(\text {y}(n)\) is sent through the secondary path, we get

$$\begin{aligned} y'(n) = e(n)-y(n)*\hat{s}(n). \end{aligned}$$
(11)

Looking at the third adaptive filter \({\displaystyle \text {H(z)}}\), we get the cancelling signal \({\displaystyle \text {y}_{h}(n)}\) from the signal \({\displaystyle {{\textbf {x}}}_{1}(n)}\) as,

$$\begin{aligned} y_{h}(n)={\textbf {h}}^\text {T}(n){\textbf {x}}_{1}(n), \end{aligned}$$
(12)

where, \({\displaystyle \textit{e}_{h}(n)=\text {e}(n)-\text {y}_{h}(n)}\). So, the error signal here will be \({\displaystyle \text {e}(n)=\text {d}(n)-\text {y}'(n)}\)

$$\begin{aligned} {\textbf {w}}_{1}(n+1)={\textbf {w}}_{1}(n)+\mu (n) y_{h}(n){\textbf {x}}_{1}'(n), \end{aligned}$$
(13)

and

$$\begin{aligned} {\textbf {w}}_{2}(n+1)={\textbf {w}}_{2}(n)+\mu _{vss}(n) e_{h}(n){\textbf {x}}_{2}'(n), \end{aligned}$$
(14)

because the output of the filter \({\displaystyle \text {H(z)}}\) would converge to \({\displaystyle \text {d}(n)-\text {y}_{1}'(n)}\), and the error \({\displaystyle \text {e}_{h}(n)}\) converges to \({\displaystyle \text {v}(n)-\text {y}_{2}'(n)}\). This is because \({\displaystyle \text {H(z)}}\) depends on \({\displaystyle {{\textbf {x}}}_{1}(n)}\). Next, we implement a variable step-size that is integrated to adaptively adjust its values of the step size for the filter [10]. This allows us to regulate how quickly the algorithm converges on its solution. However, the variable step size approach was used for the other two filters as the first filter, \(W_1(z)\), already depends on the output of the second filter, H(z). In this case, the step size is treated as a variable, and we make use of (4), which is discussed in further detail in the work [7]. A further improvement to the system would be the introduction of online identification of secondary paths. The majority of the techniques for achieving this augmentation depend on the addition of white noise. The Simultaneous Equation Method (SEM) does not demand that it be done. For the purpose of modeling the overall path, we make use of an FIR filter with the coefficients h(n), which is introduced. H(z) represents the superposition of the primary and secondary pathways. Introducing online identification of secondary paths would improve the system more. We use an FIR filter \({\displaystyle {{\textbf {h}}(n)}}\) which is introduced for modeling the overall path with \({\displaystyle \text {H(z)}}\) being the superposition of the primary and secondary paths. The technique of computing the LMS blocks utilizes a variable step size, and the block that allows for the online identification of the secondary path has been introduced to the system. These recent adjustments should make it possible for the system to function more effectively in the face of a variety of disturbances while also lowering the noise ratio. The computational complexity of the algorithms was depicted in Table 2.

Table 2 Computational complexity
Full size table
Fig. 4
figure 4

MNR comparison between feedforward and feedback FxLMS, and the proposed algorithm with and without variable step size algorithm in the presence of uncorrelated noise

Full size image
Fig. 5
figure 5

a Secondary path modelling feedforward FxLMS method, b noise recognition feedforward FxLMS method, c secondary path modelling feedback FxLMS method, and d noise recognition feedback FxLMS method

Full size image
Fig. 6
figure 6

a Secondary path modelling feedforward FxLMS method, b secondary path and noise outputs obtained for Akhtar’s method, c secondary path modelling proposed method, and d noise recognition proposed method

Full size image

5 Simulation

To verify the feasibility of the proposed algorithm, a dummy primary and secondary path was initialized. The primary path was set to be the array, [0.9 \(-\)0.7 0.8 \(-\)0.48 0.5 \(-\)0.35 0.36 \(-\)0.32 0.3 \(-\)0.22 0.28 \(-\)0.2 0.22 \(-\)0.15 0.2 \(-\)0.14 0.14 \(-\)0.08 0.1 \(-\)0.05 0.05 \(-\)0.03 0.02 \(-\)0.01], and the secondary path was set at six-tenth of the last 12 elements of the primary path which yields in an increase in an computational complexity by a factor of 1.5 times compared to the Akhtar’s algorithm. The values \({\displaystyle \alpha }\) and \({\displaystyle \gamma }\) for variable step size was set to be 0.97 and \(4.8e^{-5}\) respectively, from [2]. We will see in the following sections that the optimum noise floor was found to be at 50dB and the filter order was ideal at a value of 16.

5.1 Mean Noise Ratio

The Mean Noise Ratio (MNR) measures the amount of noise present in the system and we plot the value through time. It is the average of the Signal to Noise Ratio (SNR) of multiple runs of the system. We took the MNR for 500 simulations and compared the output to the MNR of other ANC methods. Simulations and compared the output to the MNR of other ANC methods. Following [19] the SNR is computed as

$$\begin{aligned} \text {SNR}=20log \frac{E[e^2 (n)]}{E[d^2 (n)+v^2 (n)]}, \end{aligned}$$
(15)

with \({\displaystyle \text {e}(n)}\) being the error signal and \({\displaystyle \text {d(n)}}\), the desired signal. MNR is the average of the SNR values of multiple simulations and can be represented by the equation 16. Improvement in MNR is observed in case of the proposed approach in Fig. 4 compared to the counterparts suggesting the enhancement in performance.

$$\begin{aligned} \text {MNR}=\frac{\sum _{i=1}^{n} SNR_{i}}{n}, \end{aligned}$$
(16)

Figures 5a, c and 6a, c shows the noise plots of the feed forward algorithm, the feedback algorithm, Akhtar’s algorithm, and the proposed method, respectively, with Figs. 5b, d and 6b, d show the secondary path identification of the algorithms. It is clear from looking at Fig. 6c, d that the proposed method achieves a significantly superior performance with regard to the noise residual. The noise parameter plots clearly demonstrate that the proposed approach provides significantly more accurate results than either the feed-forward or the feedback methods concluding that the proposed approach in Fig. 3 outperforms its counterparts.

Fig. 7
figure 7

a MNR comparison of Proposed method with different Noise Floor values in decibels, and b MNR comparison between the proposed algorithm with different values of filter order, L

Full size image

5.2 Noise Floor

The noise floor was the variable that was employed in this case for the purpose of establishing the SNR value of the added additive white Gaussian noise. In order to find the result that corresponds most closely to reality, the simulation was run multiple times using each of the four possible SNR settings. The simulation was carried out in the time domain, and the noise floor of the disturbance was modified. The results of these changes are visible in the outputs of the simulation. In Fig. 7a, we can see that a rise in the noise floor of the active white Gaussian noise results in a reduction in the noise residual. It is important to take note that the difference is most pronounced between the values of 10 and 20 dB, and that the effect seems to become less pronounced as the value is increased beyond 50 dB. Therefore, a value of fifty decibels (dB) would be ideal for the noise floor.

Fig. 8
figure 8

MNR comparison between the different types of noise in classical and proposed algorithms

Full size image

5.3 Filter Order

The proposed algorithm’s performance was evaluated using a variety of filter orders, and the signal-to-noise ratio was analyzed and compared. In order to determine the order at which the MNR drops to its lowest possible value, a simulation was run with several different values of filter order, and the goal was to find the order at which this drop occurred. As shown in Fig. 7b, the performance does not significantly shift after it reaches an order value of 16.

5.4 Noise Type

The proposed algorithm was tested with both wideband and narrowband noise and the MNR produced can be seen in Fig. 8. It was simulated with both AWGN and Narrowband noise, and its performance in both cases was compared with Akhtar’s algorithm in [19], which is already superior to the traditional FxLMS method. The method that was presented in this paper was compared with its performance in both cases. The results of our analysis show that even though there is a difference in performance between the two noise conditions, the noise reduction achieved by the method under consideration is still noticeably superior to that achieved by the system described in Akthar’s work.

6 Conclusion

In this paper, enhancements were performed on a combination of FxLMS algorithms. An external adaptive filter was added to provide the feed-forward section of the system. Akhtar’s algorithm was used as the base to achieve optimal control of both correlated and uncorrelated noise. This was accomplished by using the base as a foundation. It was decided to implement an online identification of secondary Path block to improve the system’s performance in real-time. To improve the system’s ability to converge, a variable step size was also implemented in both the feedback filter and the external LMS filter. After running the simulation, it was discovered that the SNR had been raised to a higher level.