1 Introduction

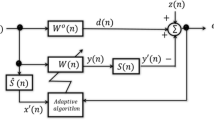
As per literature, researchers have been extensively using Active noise control (ANC) as it tends to perform well when low-frequency noise needs to be cancelled. The performance is better than the passive methods such as enclosures and silencers [1]. ANC under acoustic environment is based on the superposition property of sound waves causing destructive interference between the noise signal and its anti-phase (identical amplitude but opposite in phase) signal. This anti-phase noise is generated by an adaptive algorithm based controller [2]. The basic working of a single channel feed-forward adaptive algorithm-based ANC system is depicted in Fig. 1. Later, the samples of the reference signal \(\varvec{x}\left( \varvec{n} \right)\) and the instantaneous residual error \(\varvec{e}\left( \varvec{n} \right)\) are being used by the adaptive algorithm to update filter coefficients of an FIR filter and generate the anti-phase signal \(\varvec{h}\left( \varvec{n} \right)\). Thus, for giving \(\varvec{x}\left( \varvec{n} \right)\) and \(\varvec{e}\left( \varvec{n} \right)\) as input to the adaptive algorithms, two microphones are deployed, which produces the anti-noise signal \(\varvec{H}\left( \varvec{n} \right)\) and descends the cancelling loudspeaker.

Fig. 1
figure 1

Basic principle of broadband feedforward ANC system

Full size image

Impulsive noise cancellation achieved significant importance in the past decade and its solutions are being explored in a variety of fields such as acoustic impulse noise generated in industrial systems, impulse noise affecting vehicular travel, impulsive noise in wireless and power line communications [3,4,5]. To model the statistics of impulsive noise [6], symmetric alpha stable (SαS) distributions are used. The closed form expression does not exist for stable distributions, but the powerful computer processors have made it possible to compute stable distributions despite the lack of closed-form expressions. Therefore, for modelling impulsive noise, the characteristic equation is used which is given as

$$\varvec{\varphi }\left( \varvec{t} \right) = \varvec{e}^{{ -\varvec{\gamma}\left| \varvec{t} \right|^{\varvec{\alpha}} }}$$
(1)

The SαS distributions have a characteristic exponent parameter \(\alpha (0 < \alpha < 2)\), which controls the spread of the PDF, i.e., a smaller value of \(\alpha\) indicates that noise will be more impulsive with a heavier tail. The dispersion parameter \(\gamma\) is set to 1, to make the \(S\alpha S\) distribution as standard \(S\alpha S\) distribution. It is categorized as a normal distribution for \(\alpha = 2\), while the distribution is Cauchy for \(\alpha = 1\). Figure 2 represents the relationship between pdfs of \(S\alpha S\) with varying \(\alpha\). For \(\alpha < 2\), the second order moment is infinite. The performance of most widely used filtered-x least mean square (FxLMS) algorithm for ANC, which is considered to lessen the second order moment of the error signal, is severely degraded as it becomes unstable in the impulsive environment.

Fig. 2
figure 2

Probability density functions of the generic \(S\alpha S\) process

Full size image

Investigation of this performance challenge in literature has led to various solutions. Sun et al. [7] suggested an alteration in the already existing FxLMS algorithm that aimed towards the stability of the system. The modification limits the reference signal using a fixed threshold which tends to eliminate adverse effects of large amplitude of impulse. In [8], Akhtar and Mitsuhashi proposed an improvement in the algorithm [7], which involved replacement of impulses by new threshold values of the reference as well as error signal for enhanced stability and faster convergence. The requirement of runtime update of threshold parameters is a cause of the increase in computational complexity of algorithms proposed in [7, 8]. Normalized step-size FxLMS (NSSFxLMS), which excluded modification of reference or error signal, was proposed in [9]. Thus, selection of threshold parameters was not required, and complexity was reduced for NSSFxLMS. Another technique FxlogLMS by Wu et al. [10] was designed to reduce squared logarithmic transformations of error signal, which led to better results as far as the robustness was concerned but its tendency to reach a dead zone during the update of filter coefficients posed a drawback. Algorithm proposed by Bergamasco et al. [11] for ANC application estimate secondary path. A reformed filtered x least mean M-estimator (FxLMM) method based on two-part skewed triangular M-estimate has been proposed in [12], to ensure stability for high peak impulses. Authors in [13] proposed a step size normalized filtered reference least-mean-square (FxGSNLMS) method which generalizes the threshold based impulse noise cancelation by simulating cost function/error ratio using a Gaussian pdf. Huang et al. [14] proposed a variable step size approach for FxLMS algorithm, which was modified by using self-adjustable tap length by Chang and Chu [15] for improvement in convergence rate and mean error performance. Akhtar et al. [16] proposed an improvement in FxLMS algorithm using normalized step size to enhance its stability and reuse of data for improving its convergence rate. The algorithms in [12,13,14,15] are all robust to interference to the error microphone.

In [17], a robust modified gain filtered-x recursive least square (MGFxRLS) algorithm was presented that gives fast convergence than that of NSSFxLMS algorithm at the expenditure of high computational complexity. It is well known that convergence for all the LMS based impulsive noise control algorithms is relatively slow and have larger steady state error if compared with RLS based algorithms for non-stationary environment [18]. Therefore, there is need for exploring less complicated solutions which can ensure good convergence, reduced steady-state error, and enhanced robustness. A less complex robust adaptive algorithm is successfully presented [19, 20] for impulsive noise. This new Robust algorithm renders good noise cancellation capability due to its convex combination of cost functions and has low complexity but that hasn’t been validated in the ANC domain. Therefore, in this paper, Robust algorithm has been tested for the first time in ANC domain. As the Robust algorithm has been combined with filtered reference input, therefore it has been termed as the filtered-x least cosine hyperbolic algorithm. It can be assured from simulation results that proposed FxLCH algorithm is best suitable for the less rigorous impulsive environment but lacks robustness if the environment is more impulsive. In order to tackle this issue, further few alterations are suggested in the FxLCH algorithm for improving its convergence and robustness. The first alteration is clipped based FxLCH (CFxLCH) algorithm which clips the reference and error signals above some threshold parameters and then these modified signals are used for updating the weight equation of FxLCH algorithm. In the second alteration, the energy of the reference and error signals in the step size of the FxLCH algorithm is well incorporated by the modified FxLCH (MFxLCH).

The remainder of the paper is organized as follow: The proposed algorithm will be discussed in the Sect. 2 and further its two modifications are presented in Sects. 2.1 and 2.2. The complexity analysis of all the proposed algorithms is followed in Sect. 3. All the simulations following with their results are explained and presented in Sect. 4. Finally, Sect. 5 has the conclusion discussed in it.

2 Proposed solution based on FxLCH algorithm

The basic principle of adaptive filters is minimization of a certain cost function. The cost function of FxLMS algorithm is mean square error which assumes that the produced error is Gaussian in nature i.e. the second order moment (variance) is finite. However, whenever the signal becomes impulsive, variance of the signal is finite. Hence the FxLMS algorithm becomes unstable and for impulsive noise reduction it is not an ideal option. Considering impulsive noise, a new Robust algorithm with cost function based on the convex combination of cost functions is reported in literature [19]. The reported cost function is:

$$J\left( n \right) = \frac{{\log \left[ {\cosh \left( {\rho e\left( n \right)} \right)} \right]}}{\rho }$$
(2)

where \(\rho\) controls the sensitivity to large outliers in the error signal and also controls concavity in the cost function about the origin. It can be estimated by the standard deviation of error or its square. By using this cost function, the reported [19] weight update equation is:

$$v(n + 1) = v(n) + \mu \tanh [\rho e(n)][x(n)]$$
(3)

Noise robustness is achievable by the reported algorithm as the tangent hyperbolic saturates to ± 1 for large impulses. It is evident from the literature that this Robust algorithm has never been tested in the ANC domain. Therefore, the performance of the proposed method has been tested for impulsive noise suppression in the ANC domain and filtered-x version of the robust algorithm named as FxLCH algorithm is presented. The elementary schematic of a proposed algorithm dealing with impulsive noise control is shown in Fig. 3.

Fig. 3
figure 3

Schematic of proposed FxLCH algorithm-based ANC system

Full size image

The overall principle of the ANC system remains the same except that instead of a conventional adaptive filter, filtered-x version of the robust algorithm named as FxLCH algorithm is used. In this proposed algorithm, the weight update equation is as follows:

$$\begin{aligned} v(n + 1) = v(n) + \mu \tanh [\rho e(n)][x_{f} (n)] \hfill \\ \hfill \\ \end{aligned}$$
(4)
$$\begin{aligned} \tanh [\rho e(n)] = \left\{ {\begin{array}{*{20}l} {sign(e(n)),} \hfill & {\quad \left| {e(n)} \right| \ge {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \rho }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\rho $}}} \hfill \\ { - e(n)\left| {e(n)} \right|\rho^{2} + 2\rho e(n)} \hfill & {\quad otherwise} \hfill \\ \end{array} } \right\} \hfill \\ \hfill \\ \end{aligned}$$
(5)

where the reference noise signal vector is x\(\left( n \right) = \left[ {x\left( n \right),x\left( {n - 1} \right), \ldots ,x\left( {n - L + 1} \right)} \right]^{{\prime }}\) and estimated secondary path filter \(SS^{{\prime }} \left( z \right)\) filters the reference noise signal \(x_{f} \left( n \right)\).

For the convergence of the algorithm, it is very important to select an optimum value of the step size (µ) in the proposed FxLCH algorithm. The selection of value is critical as the convergence depends on the controlling parameters. This critical value can be determined by repetitive simulations for the best convergence.

The factor that needs to be considered here is, if the reference signal \(x_{f} \left( n \right)\) or the error signal \(e(n\)) from Eq. (4) are encountered by large amplitude pulses, then the proposed algorithm is likely to get unstable. Therefore, there is a need of few solutions that can cope up with the concern of stability. In the next section, two modifications in the proposed FxLCH algorithm have been suggested so robustness and stability can be achieved even while encountering high impulses. The modifications are as follows:

  1. (i)

    Clipped filtered-x LCH algorithm (CFxLCH algorithm).

  2. (ii)

    Modified step size filtered-x LCH algorithm (MFxLCH algorithm).

2.1 Clipped filtered-x LCH (CFxLCH) algorithm

In standard FxLCH algorithm, all samples of the reference noise vector are equally treated. A high impulse can make FxLCH algorithm unstable. The main aim is to boost the robustness of FxLCH algorithm while maintaining the same computational complexity as of FxLMS algorithm. Based on extensive simulations, a modified form of the FxLCH algorithm is proposed. In the FxLCH algorithm, the initial modification is founded on the thresholding technique. The reference and the error samples would be cropped if the selected thresholds are exceeded by the magnitude of samples of reference and error signals. This cropping would be done above the threshold values set by the signal statistics. In actual, an offline estimation of signal statistics is carried out. Figure 4 depicts the schematics of the modified form of the proposed FxLCH algorithm. The alteration in the reference and error signals of proposed CFxLCH algorithm is as follow:

$$x{\prime }\left( n \right) = \left\{ {\begin{array}{*{20}l} {l_{1} , } \hfill & { if\;\; x\left( n \right) \le l_{1} } \hfill \\ {l_{2 } , } \hfill & {if\;\; x\left( n \right) \ge l_{2} } \hfill \\ {x\left( n \right), } \hfill & {otherwise} \hfill \\ \end{array} } \right.$$
(6)
$$e^{\prime}\left( n \right) = \left\{ {\begin{array}{*{20}l} {l_{1} , } \hfill & {if\;\; e\left( n \right) \le l_{1} } \hfill \\ {l_{2 } , } \hfill & { if\;\; e\left( n \right) \ge l_{2} } \hfill \\ {e\left( n \right),} \hfill & {otherwise} \hfill \\ \end{array} } \right.$$
(7)

where \(l_{1}\) and \(l_{2}\) are lower and upper thresholds that have been reported in the literature [9], and these are calculated by the 1st (for \(l_{1}\)) and 99th (for \(l_{2}\)) percentile value of reference and error signals, respectively. The weight update equation with altered reference and error signals of proposed CFxLCH algorithm is

$$\begin{aligned} v(n + 1) = v(n) + \mu \tanh [\rho e^{'} (n)][ss(n)*x^{'} (n)] \hfill \\ \hfill \\ \end{aligned}$$
(8)
Fig. 4
figure 4

Schematic of proposed Clipped FxLCH algorithm-based ANC system

Full size image

The ANC system stability is ensured by cropping the high impulses to the threshold values. The enhanced robustness of proposed CFxLCH is validated by simulation results. Improved performance of the proposed CFxLCH algorithm is totally achieved by careful selection of thresholds. Moreover, the performance of different investigated variants of FxLMS algorithm i.e. Sun’s [7], modified Sun’s [8], Akhtar [9] and proposed CFxLCH algorithm, depends mainly on selecting a suitable threshold parameter [\(l_{1}\), \(l_{2}\)]. It is the main limitation of these threshold-based algorithms that if noise statistics change during runtime application then these threshold parameters need to be re-estimated. Therefore, another modification which is self-governing and also independent of threshold parameters [\(l_{1}\), \(l_{2}\)] is suggested in the next section of this paper.

2.2 Modified Filtered x LCH (MFxLCH) algorithm

In [9], a modified normalized step size is used with the standard FxLMS algorithm (NSSFxLMS) that enhanced its stability and robustness. Motivated by the performance of the modified normalized step size used in [9], we have modified the step size of FxLCH algorithm on the same lines. Thus, the second modification in the proposed FxLCH algorithm is named as Modified FxLCH (MFxLCH) algorithm. Here, the step size varies after each iteration depending upon the magnitude of the input sample as well as the energy of the error signal

$$\mu (n) = \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\mu } }}{{\left\| {x_{f} (n)} \right\|^{2} + K_{e} (n) + \beta }}$$
(9)

where \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\mu }\) is the optimum step size of the FxLCH algorithm, \(\mu \left( n \right)\) is the time-varying normalized step size, \(K_{e} \left( n \right)\) is the energy of error signal \(e\left( n \right)\) that is estimated online using a low pass estimator by the subsequent equation.

$$K_{e} \left( n \right) = \lambda K_{e} \left( {n - 1} \right) + \left( {1 - \lambda } \right)\left| {e^{2} \left( n \right)} \right|$$
(10)

where \(\lambda\), called as forgetting factor, has value \(0.9 < \lambda < 1\). When the excitation signal is impulsive in nature, there are much more variations in the error signal which can cause gradient noise amplifications in the FxLCH algorithm. For tacking the effect of such variations in the reference and the error signal, the power of the excitation signal \(||x_{f} \left( n \right)||^{2}\) and error signal \(K_{e} \left( n \right)\) is incorporated in the denominator of modified step size. By modifying this, the step size of the FxLCH algorithm will lessen and will freeze the adaptation of the algorithm transitorily for large impulses. As an outcome, the FxLCH algorithm will achieve robustness and stability to an extent while catering impulsive noise. Division by zero can be avoided by adding any small positive number beta \(\beta\) in the denominator of Eq. (9)

The weight update equation of the proposed method with above mentioned modifications is as follows:

$$\begin{aligned} v(n + 1) = v(n) + \mu (n)\tanh [\rho e(n)][x_{f} (n)] \hfill \\ \hfill \\ \end{aligned}$$
(11)

It is important to note that improved performance of the proposed MFxLCH algorithm does not involve threshold parameters [\(l_{1} ,l_{2}\)] calculations. Although it is based on an intuition-based modification, the results prove that there is an improvement in the robustness, if compared with other suggested alterations i.e. CFxLCH algorithm. Moreover, MFxLCH algorithm has shown better stability and robustness in comparison to the FxLCH algorithm. The MFxLCH algorithm also attains better convergence and almost same computational complexity as of NSSFxLMS [9], the best variant of FxLMS family as verified by simulation results.

3 Complexity analysis

In most of the cases, the computational complexity of any algorithm has an utmost significance. For this reason, equation wise analysis of the computational complexity of proposed FxLCH and MFxLCH algorithms is conducted and the results are presented in Tables 1 and 2. Analysis of other considered algorithms are tabulated in Tables 3, 4 and 5. The computational complexity is calculated by finding number of multiplications and additions required to compute solution for single iteration of the algorithm. The complexity of the investigated algorithms is calculated using the method given in [22].

Table 1 Complexity analysis of proposed FxLCH algorithm
Full size table
Table 2 Complexity analysis of proposed modified FxLCH algorithm
Full size table
Table 3 Complexity analysis of FxLMS algorithm
Full size table
Table 4 Complexity analysis of NSSFxLMS algorithm
Full size table
Table 5 Complexity analysis of proposed MGFxRLS algorithm
Full size table

Figure 5 shows the plots for computational complexities of the investigated algorithms. The proposed FxLCH and MFxLCH algorithm have almost same computational complexity as that of FxLMS and NSSFxLMS algorithm respectively, which makes it suitable for many applications (Table 6). The computational complexities of the newly proposed algorithms along with inspected algorithms [7,8,9, 17] are summarized in Table 6.

Fig. 5
figure 5

Complexity analysis of the investigated algorithms. a Number of additions, b number of multiplications

Full size image
Table 6 Summary of computational complexity of inspected algorithms
Full size table

4 Simulation results

In the simulation phase, modeling of statistical parameters of impulsive noise [6] is done by symmetric α-stable (SαS) distributions Distribution functions for some SαS distributions are depicted in Fig. 2. In this paper, two cases of impulsive noise environments using standard SαS process are considered in the simulation. All parameters have been tabulated in Table 7 that are being involved in the simulation phase of impulsive noise and the ANC environment. Matlab software is used to implement the ANC system. The comparison has been made between the performances of proposed algorithms with that of already discussed adaptive algorithms in the literature [7,8,9, 17]. Furthermore, it is assumed throughout the simulations that secondary path model \(SS\left( z \right)\) is kept same as estimated secondary path \(\widehat{ss}\left( z \right)\) [7,8,9,10,11,12,13,14,15,16,17]. The values of primary \(PP\left( z \right)\) and secondary \(SS\left( z \right)\) acoustic path coefficients are taken from data set given in [1]. The magnitude and phase of the primary and secondary path coefficients are depicted in Fig. 6.

Table 7 Parameter set for simulation of proposed algorithms
Full size table
Fig. 6
figure 6

Frequency response of acoustic primary and secondary path

Full size image

Mean noise reduction (MNR) is the performance metric for validating the performance of inspected algorithms in this paper. Calculations are as follows:

$$MNR\left( n \right) = E\left\{ {\frac{{Q_{e} \left( n \right)}}{{Q_{H} \left( n \right)}}} \right\}$$
(12)
$$Q_{e} \left( n \right) = \lambda Q_{e} \left( {n - 1} \right) + \left( {1 - \lambda } \right)\left| {e\left( n \right)} \right|$$
(13)
$$Q_{H} \left( n \right) = \lambda Q_{H} \left( {n - 1} \right) + \left( {1 - \lambda } \right)\left| {H\left( n \right)} \right|$$
(14)

where \(Q_{e} \left( n \right)\) and \(Q_{H} \left( n \right)\) are taken as the estimates of absolute value of error and disturbance signal. Here, the symmetric alpha stable model has generated two cases of impulsive noise environments by setting α = 1.65 and α = 1.45 respectively, which relates to less and more impulsiveness respectively.

Case 1

The impulsive noise generated by selecting α = 1.65 correspond to the less impulsive environment. The primary noise \(x(n\)) picked by reference microphone for α = 1.65 is depicted in Fig. 7.

Fig. 7
figure 7

Butterfly plots for the primary noise

Full size image

To validate the performance of proposed algorithms and to fetch the ideal values controlling parameters of discussed algorithms, multiple number of simulations are carried out. All the comprehensive simulation results are shown in Fig. 8(a–e) for the controlling parameters.

Fig. 8
figure 8

MNR curves for a Sun’s algorithm, b modified algorithm, c Akhtar algorithm, d NSSFxLMS algorithm, e MGFxRLS algorithm for case 1

Full size image

From the MNR curves of inspected algorithms in Fig. 8, optimum values of the controlling parameters are cited in Table 8.

Table 8 Selected values of controlling parameter
Full size table

The MNR curves for variants of FxLMS family are depicted in Fig. 9 using the best controlling parameters as listed in afore cited Table 8. It can be clearly seen from Fig. 8 that amongst the FxLMS family investigated algorithms, NSSFxLMS gives good convergence, low steady-state error and better stability.

Fig. 9
figure 9

MNR curves comparison of FxLMS and its variants with α = 1.65

Full size image

In Fig. 10, the MNR curve for proposed FxLCH algorithm is compared with standard FxLMS algorithm. It can be seen that the well celebrated FxLMS algorithm diverges for case 1, whereas the proposed FxLCH algorithm doesn’t diverge. The proposed FxLCH algorithm lacks robustness, therefore, its two suggested modifications i.e. CFxLCH and MFxLCH algorithms are simulated in Fig. 11. The optimum step size value of proposed FxLCH algorithm and its two modifications are determined by extensive simulations in Fig. 11 for α = 1.65. From simulation results of Fig. 11(d), we can see that the convergence and robustness of proposed MFxLCH algorithm is better among the other proposed algorithms. Whereas all the proposed algorithms achieve almost same steady state error.

Fig. 10
figure 10

Comparative results of MNR of proposed FxLCH and FxLMS algorithm for α = 1.65

Full size image
Fig. 11
figure 11

MNR comparison of proposed FxLCH and its variants for α = 1.65

Full size image

Figure 12 compares MNR curves of NSSFxLMS and MGFxRLS algorithms with the proposed MFxLCH algorithm for α = 1.65. From Fig. 9 it’s obvious that NSSFxLMS algorithm outclasses all other algorithms among FxLMS family when convergence speed is considered. According to [17], MGFxRLS algorithm performs better than the FxLMS family in terms of fast convergence speed and low steady-state error Therefore, comparison of the performance of proposed MFxLCH algorithm with that of NSSFxLMS and MGFxRLS algorithms for α = 1.65 is carried out. As shown in the Fig. 12 the proposed MFxLCH algorithm performs better, when convergence is considered, than NSSFxLMS algorithm with the steady state error approaching to that of the MGFxRLS algorithm and computational complexity almost same as of NSSFxLMS algorithm.

Fig. 12
figure 12

Comparison of MNR of proposed MFxLCH algorithm with various algorithms α = 1.65

Full size image

Case 2

The impulsive noise generated by selecting α = 1.45 correspond to more impulsive environment. In Fig. 13, the MNR curve for standard FxLMS algorithm is compared with proposed FxLCH algorithm for more impulsive case. It is evident that the proposed FxLCH algorithm depicts better convergence and enhanced stability as compared to standard FxLMS algorithm.

Fig. 13
figure 13

Evaluation of MNR of proposed FxLCH and FxLMS algorithm for α = 1.45

Full size image

The detailed simulations for the best controlling parameters presented in Table 8 for all the investigated algorithms i.e. Sun’s, Modified Sun’s, Akhtar, NSSFxLMS and MGFxRLS algorithm for α = 1.45 are depicted in Fig. 14(a–e). The best variant of FxLMS family is determined by rigorous simulations for α = 1.45 and the result is shown in Fig. 15.

Fig. 14
figure 14

MNR curves for a Sun’s algorithm, b modified algorithm, c Akhtar algorithm, d NSSFxLMS algorithm, e MGFxRLS algorithm for case 2

Full size image
Fig. 15
figure 15

MNR curves comparison of FxLMS and its variants with α = 1.45

Full size image

It can be seen from MNR curves of Fig. 15 that among the inspected algorithm of FxLMS family, NSSFxLMS algorithm exhibits good convergence and better stability. Further, the optimum values of step size parameter of proposed FxLCH algorithm and its two modifications i.e CFxLCH and MFxLCH algorithm are simulated in Fig. 16 for case 2 (α = 1.45). The fastest convergence, lowest steady state error and good robustness of proposed MFxLCH algorithm can be seen among the other proposed algorithms in this research.

Fig. 16
figure 16

Evaluation of MNR of proposed FxLCH algorithm and its variants for α = 1.45

Full size image

Figure 17 illustrates the MNR curves comparison of proposed MFxLCH algorithm with the best variants of FxLMS family and FxRLS family [21] in ANC domain for α = 1.45. It is clearly shown in Fig. 17 that proposed MFxLCH algorithm can be considered as a compromise between FxLMS and FxRLS family algorithms since proposed MFxLCH algorithm yields improved convergence than NSSFxLMS algorithm and almost achieves the same steady state error as that of the MGFxRLS algorithm with computational complexity of almost NSSFxLMS algorithm.

Fig. 17
figure 17

Evaluation of MNR of various algorithms with proposed MFxLCH algorithm α = 1.45

Full size image

5 Conclusions

In this paper, the already existing robust algorithm has been tested for the first time in the ANC domain for impulsive noise. Therefore, a new ANC algorithm based on filtered-x least cosine hyperbolic (FxLCH) adaptive algorithm is suggested to improve convergence and stability when there is impulsive noise. Illustrative simulations depicted that proposed FxLCH algorithm exhibits better stability than filtered-x least mean square family (FxLMS) algorithm but lacks robustness in presence of high impulsive noise. Therefore, to boost robustness of the algorithm, further two modifications are proposed. First proposed modification is clipped FxLCH (CFxLCH) which clips the reference and error signals, while, the second modification i.e. modified FxLCH (MFxLCH) algorithm combines modified normalized step size of the NSSFxLMS algorithm with the FxLCH algorithm. With regards to stability and robustness, both of the modifications performed better than the standard FxLCH algorithm. Furthermore, the results verified that proposed MFxLCH algorithm is a compromise between FxLMS and FxRLS family as the proposed MFxLCH algorithm, having computational complexity almost same as of NSSFxLMS algorithm gives better convergence than it, also can approach steady-state error of FxRLS family.