Abstract
In this paper, we propose three secrecy cooperative transmission protocols for a two-way energy-constrained relaying network in which two sources wish to exchange information with the help of multiple intermediate relays being subjected to wiretapping by multiple eavesdroppers. In the secure two-way communication (STW protocol), an energy-constrained relay is preselected via one of three investigated relay-selection strategies, which harvest the energy from the radio-frequency signals of one source and decode-and-forward the signals to another source. In secure two-way communication with network coding (STWNC protocol), the network coding technique is applied at a relay preselected via one of two investigated relay-selection strategies. In secure two-way communication with cooperative jamming and network coding (STWJNC protocol), under cooperative jamming, the network coding technique is applied at two sources and a preselected relay where a jammer-relay pair is preselected via one of two investigated selection strategies. The power-splitting receiver is applied at the energy-constrained relay for all proposed protocols. To evaluate performance, we derive new closed-form expressions for the secrecy outage probability and the throughput performance of the three protocols with the different relay and jammer-selection strategies. Our analysis is verified using Monte Carlo simulations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Energy harvesting is a promising solution to increase the life cycles of wireless devices and maintain network connectivity [1,2,3,4]. Conventionally, wireless devices harvest energy from external natural resources, such as wind, solar, or vibration, which is random and unsteady. Consequently, reliable communication is not ensured [5]. To cope with this limitation, energy harvesting from radio frequency (RF; or wireless power transfer) is an interesting approach [6,7,8,9,10]. The authors in [10] worked on an ideal receiver that can simultaneously decode the information and harvest the energy from a signal. In [5, 9], two practical receiver architectures were proposed: power splitting (PS), where the receiver splits the received signal into two parts (one for energy harvesting and one for information decoding), and time switching, where the receiver switches the received signal between information-decoding and energy-harvesting processes. Many researchers have subsequently investigated PS and TS in different system models and aspects [4, 11,12,13,14]. The authors in [4] investigated the symbol error rate of RF energy harvesting in a cooperative relaying network, where an energy-limited relay harvested the energy to assist in relaying the source information to the destination. In [11], co-channel interference was shown to be a potential energy source for a relay node in an opportunistic EH network. The authors in [12, 13] studied the throughput performance using both PS and TS in an amplify-and-forward (AF) relaying network [12], and they analyzed adaptive time-switching [13]. In [13], the power allocation strategy for a decode-and-forward (DF) relaying network was studied. In [15], the authors studied the throughput of three proposed wireless power transfer policies using a TS structure in an AF two-way relaying network. The authors in [16] study three different relay selection schemes of the DF energy-harvesting base power splitting relaying network.
Because the wireless medium has broadcasting nature, security issues for wireless communication has received considerable attention from researchers. Conventionally, security is addressed at higher layers using cryptographic methods [17]. However, due to the greater number of potential attacks when security is implemented at higher layers, many studies have been conducted on physical layer security (PLS). Security is evaluated in terms of the achievable secrecy rate (ASR), first defined by Aaron Wyner as the maximum rate of reliable information sent from the source to the desired destination in the presence of eavesdroppers [18]. Wyner showed that communication between the source and the destination is secure if the ASR of the source-eavesdropper link is smaller than that of the source-destination link. Following this finding, the authors in [19] studied physical layer security in wire-tap channels, and extended it to broadcast channels [20] and fading channels [21]. The application of PLS in cooperative communication to improve the secrecy performance of a wireless relaying network was investigated in [22]. In [23], the authors investigated physical layer security in a two-way relay network with friendly jammers under attack by an unauthenticated relay. In [24], the ergodic secrecy capacity metric was studied in distrusted AF relay networks. In [25], cooperative single-carrier systems affected by multiple eavesdroppers were evaluated in terms of the exact and asymptotic ergodic secrecy rate. Some relay-selection schemes [26] as well as assistance from a cooperative friendly jammer [27] have been shown to enhance the secrecy outage performance in cooperative cognitive radio networks. In [28], the authors analyze achievable secrecy rates with total and individual relay power constraints as well as design relay beamforming weights to enhance the secrecy rate for the cooperative multiple DF relay networks. The eavesdroppers are interfered with by jamming signals sent from a node acting as a jammer, which is selected from a number of relays [29]. In [30], while the source transmits an encoded signal, relays transmit a jamming signal to confound eavesdroppers.
The source message can be encrypted using network coding for two binary jamming messages, i.e., XOR the original binary stream of the source and the binary jamming stream. The attack of the eavesdropper can be perfectly avoided when the jamming message is securely transmitted in the cooperative jamming phase. Thus, to increase the secrecy obtained by transmitting the jamming message, the jamming message should be transmitted by the best jammer, which is selected from multiple available ones.
To the best of our knowledge, no published literature has investigated a cooperative jammer combined with network coding to improve the secrecy performance of the energy-constrained two-way DF relaying network in the presence of multiple eavesdroppers. In the current work, we propose three transmission protocols with various relay/jammer-selection strategies. These strategies each select a cooperative relay before the source transmits the signal [31]. The STW protocol does not use network coding or cooperative jamming, so the secrecy in the two-way transmission of this protocol is achieved via conventional operation with four time slots (TSs). The STWJNC protocol applies network coding at a preselected relay, which reduces the number of TSs to three. Finally, the STWJNC protocol employs cooperative jamming and uses network coding at both the source node and the selected relay. We compare these three protocols as follows. We analyze three relay-selection strategies for the STW protocol, two relay-selection strategies for the STWNC protocol, and two jammerrelay-selection strategies for the STWJNC protocol. The preselected relay harvests the energy from the two source nodes in the STW and STWNC protocols, whereas it harvests energy from the preselected jammer in the STWJNC protocol. For performance evaluation, the secrecy outage probability (SOP) and secrecy throughput performance (STP) are derived as closed-form expressions with high SNR regions for the STW and STWNC protocols, and as exact closed-form expressions for the STWJNC protocol. Our derivations are validated using Monte Carlo Simulation.
The rest of this paper is organized as follows. Section 2 describes three transmission protocols for a two-way energy-constrained DF relaying network. The transmission operation and performance analysis of the STW, STWNC, and STWJNC protocols are given in Sects. 3, 4, and 5, respectively. Section 6 presents the numerical results, and various design insights are discussed. Finally, Sect. 7 summarizes our conclusions.
Notation The notation \(\mathcal {CN}\left( {0,{N_0}} \right)\) denotes a circularly symmetric complex Gaussian random variable (RV) with zero mean and variance \({N_0}\). \(\mathcal {E}\left\{ . \right\}\) denotes mathematical expectation. The functions \({f_X}\left( . \right)\) and \({F_X}\left( . \right)\) present the probability density function (PDF) and cumulative distribution function (CDF) of RV X. The function \({K_1}\left( x \right)\) denotes a first-order modified Bessel function of the second kind [32], and \(\varGamma \left( {x,y} \right)\) is an incomplete Gamma function [32, Eq. (8.310.1)] . \(C_b^a = \frac{{b!}}{{a!\left( {b - a} \right) !}}\). Notation \(\Pr [.]\) returns the probability. Notation \({\left[ x \right] ^ + }\) returns x if \(x \ge 0\) and 0 if \(x < 0\). The sign \(\oplus\) indicates the XOR operator. The function \(_2{F_1}\left( . \right)\) represents Gausss hypergeometric function [32].
2 System Model
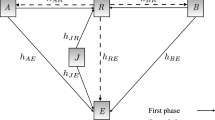
As shown in Fig. 1, we consider three transmission protocols for a wireless network consisting of two source nodes S1 and S2 (that want to exchange data), M energy-constrained relay nodes \({R_m}\), \(m \in \left\{ {1,2,\ldots ,M} \right\}\), N jammer nodes \({J_n}\), \(n \in \left\{ {1,2,\ldots ,N} \right\}\), and L malicious eavesdroppers \({E_l}\), \(l \in \left\{ {1,2,\ldots ,L} \right\}\). It is assumed that the direct link between the two source nodes is omitted due to deep shadowing [31]. Thus, communication between the two sources can be carried out through the best proactive DF relay, denoted \({R_s}\), that is selected from M available relay nodes by a particular selection strategy. It is worth noting that all L eavesdropper nodes can capture the information transmitted in the network. To enhance the secrecy of the communication, a jammer node \({J_s}\) is selected to broadcast a random binary jamming message to the two source nodes S1 and S2 in the presence of L eavesdropper nodes. We assume each node is equipped with a single antenna operating in half-duplex mode, and the global channel state information (CSI) is available [22] at each node. Therefore, \({R_s}\) and \({J_s}\) can be selected before transmitting the jamming and data. The selection schemes used in this paper for each protocol are described in the next sections.
We use \(\left( {{h_{AB}},{d_{AB}}} \right)\) to denote the Rayleigh channel coefficient over the distance for the link between two nodes A and B, where \(A \in \left\{ {S1,S2,{J_n},{R_s}} \right\}\), \(B \in \left\{ {S1,S2,{R_s},{E_l}} \right\}\), \(A \ne B\) and where \({R_s}\), \({J_s}\), and \({E_l}\) denote the \({m\mathrm{th}}\) relay node in cluster-R, the \({n\mathrm{th}}\) jammer node in cluster-J, and the \({l\mathrm{th}}\) eavesdropper node in cluster-E, respectively. Thus, the corresponding channel gain \({g_{AB}} \buildrel \varDelta \over = {\left| {{h_{AB}}} \right| ^2}\) is an exponential RV with parameters \({\lambda _{AB}} = {\left( {{d_{AB}}} \right) ^\beta }\), where \(\beta\) denotes the path-loss exponent.
In this paper, M relay nodes, N jammer nodes, and L eavesdropper nodes are located in cluster-R, cluster-J, and cluster-E, respectively [16]. Thus, the distance between two nodes in a cluster is insignificant compared to the distance between a node inside and a node outside a cluster, and the data links are independent and identically distributed (i.i.d) [31]. We obtain the corresponding cumulative distribution function (CDF) and probability density function (PDF) as \({F_{{g_{AB}}}}\left( x \right) = 1 - {e^{ - {\lambda _{AB}}x}}\) and \({f_{{g_{A,B}}}}\left( x \right) = {\lambda _{AB}}{e^{ - {\lambda _{AB}}x}}\), respectively.
We consider the energy harvesting technique as a power-splitting architecture with a power splitting ratio \(\rho \in \left( {0,1} \right)\) for energy harvesting and \((1 - \rho )\) for decoding the source signal [12, Fig. 3]. We assume that the fading coefficient \({h_{AB}}\) does not vary during one block time of completing the exchange of one packet between two source nodes, and that it is independent of and identical to the next block time [16]. For convenient demonstration, let P denote the transmit power of all transmitters, i.e., the two sources, the selected relay \({R_s}\), and the selected jammer \({J_s}\); let \({n_B}(t) \sim CN\left( {0,{N_0}} \right)\) indicate the zero-mean and variance \({N_0}\) of the additive white Gaussian noise (AWGN) at the receiver B, \(B \in \left\{ {S1,S2,{R_s},{E_l}} \right\}\); and let \({n_{B,c}}(k) \sim CN\left( {0,\mu {N_0}} \right)\) denote the zero-mean and variance of the noise that arises from converting a signal from the RF band to a baseband signal at all the receivers [16].
The next three sections present the operation and performance analysis of the three investigated transmission protocols. The performance of each protocol with the various relay/jammer selection strategies is evaluated using two performance metrics: SOP and STP.
3 Secure Two-Way Energy-Constrained Relaying Communication (STW)
3.1 Transmission Operation
The STW protocol takes four time slots (TSs) for the complete exchange of data between two source nodes S1 and S2 (see Fig. 1a) during a block time. In the first TS, S1 sends its signal \({x_{S1}}\), \(\mathcal {E}\left\{ {{{\left| {{x_{S1}}} \right| }^2} = 1} \right\}\), to the preselected energy-constrained relay \({R_s}\) in the presence of L eavesdropper nodes \({E_l}\), \(l \in \left\{ {1,2,\ldots ,L} \right\}\). The received signals at \({R_s}\) and \({E_l}\) are expressed respectively by
The received RF signal at the selected relay \({R_s}\), \({y_{S1{R_s}}}(t)\), is processed for energy harvesting (3) and information decoding (4), as follows:
The sampled baseband signals at \({E_l}\) and \({R_s}\), e.g., \({y_{S1{E_l}}}(k)\) and \({y_{S1{R_s},d}}(k)\), are obtained by down conversion of the signals \({y_{S1{R_s},d}}(t)\) and \({y_{S1{E_l}}}(t)\) in (2) and (4), respectively [12, 16], as follows
The received SNRs of the links \(S1 \rightarrow {E_l}\) and \(S1 \rightarrow {R_s}\) and the achievable secrecy rate (ASR) from S1 to \({R_s}\) can be attained from (5) and (6), respectively, as follows:
where \(\psi \buildrel \varDelta \over = \frac{P}{{{N_0}}}\), \({\omega _1} \buildrel \varDelta \over = \frac{1}{{1 + \mu }}\), \({\omega _2} \buildrel \varDelta \over = \frac{{1 - \rho }}{{1 - \rho + \mu }}\), \({g_{S1E\max }} \buildrel \varDelta \over = \mathop {\max }\nolimits _{l = 1,2,\ldots ,L} {g_{S1{E_l}}}\); the pre-log 1 / 4 indicates that there are four TSs for completing the transmission of the STW protocol.
From (3), the harvested energy at \({R_s}\) is given by
where \(0 \le \eta \le 1\) is the harvesting efficiency, and T is the transmission time of one TS.
\({R_s}\) uses the power \({P_{S1{R_s}}}\) in (11) to forward the data of S1 to S2 under eavesdropping by \({E_l}\) in the second TS during the time interval T. The transmitted power from \({R_s}\) and the received sampled baseband signals at S2 and \({E_l}\) are expressed respectively by
The received SNRs of the links \({R_s} \rightarrow S2\) and \({R_s} \rightarrow {E_l}\), and the ASR from \({R_s}\) to S2, are respectively given by
where \({\omega _3} \buildrel \varDelta \over = \frac{{\eta \rho }}{{1 + \mu }}\).
In the third and fourth TSs, the transmission of the links \(S2 \rightarrow {R_s}\) and \({R_s} \rightarrow S1\) under eavesdropping by \({E_l}\) are the same as those of links \(S1 \rightarrow {R_s}\) and \({R_s} \rightarrow S2\), respectively, due to the symmetric particularity. Thus, similarly to (9) and (16), we obtain the ASRs from S2 to \({R_s}\) and from \({R_s}\) to S1, respectively, as follows:
For this protocol, we consider three relay-selection schemes for choosing the relay \({R_s}\). In the first, we note that any eavesdropping of the selected relay \({R_s}\) occurs in the second and fourth TSs, so \({R_s}\) is selected based on the minimum eavesdropping channel (called MIRE), as represented in (19a). In the second, \({R_s}\) is selected based on the maximum channel gain of the link \(S1 - R\) (MAS1R), as formulated in (19b). In the third scheme, \({R_s}\) is selected randomly from the M available nodes (RAN) (19c).
3.2 Performance Analysis
3.2.1 Secrecy Outage Probability
The probability of a successful exchange of data between two source nodes is the probability that all four ASRs are above the target, \({C_t} > 0\). This can be formulated as follows:
The system experiences an outage if at least one of the four ASRs is less than \({C_t}\). In other words, the SOP of the STW protocol can be given by
By substituting the expressions of \(C_{S1{R_s}}^{{\mathrm{STW}}}\), \(C_{{R_s}S2}^{{\mathrm{STW}}}\), \(C_{S2{R_s}}^{{\mathrm{STW}}}\), and \(C_{{R_s}S1}^{{\mathrm{STW}}}\) from Eqs. (9), (16), (17), and (18), respectively, into (21), we obtain
where \(\varphi \buildrel \varDelta \over = {2^{4{C_t}}}\).
Depending on which of the three relay selection strategies is used, from (19a), (19b), and (19c), we obtain three expressions of SOP, \(P_{out,\mathrm{MIRE}}^{{\mathrm{STW}}}\), \(P_{out,\mathrm{MAS1R}}^{{\mathrm{STW}}}\), and \(P_{out,\mathrm{RAN}}^{{\mathrm{STW}}}\), respectively, as follows
where (23a) is obtained from (22) by applying the PDFs of RVs \({g_{S1E\max }}\), \({g_{S2E\max }}\), \({g_{S1{R_s}}}\), \({g_{S2{R_s}}}\), \({g_{{R_s}E\max }}\), \({g_{{R_s}S1}}\), and \({g_{{R_s}S2}}\) as follows: \({f_{{g_{S1E\max }}}}\left( {{x_1}} \right) = L{\lambda _{S1E}}\sum \nolimits _{t = 0}^{L - 1} {C_{L - 1}^t} {\left( { - 1} \right) ^t}{e^{ - \left( {1 + t} \right) {\lambda _{S1E}}{x_1}}}\) (see Appendix 1), \({f_{{g_{S2E\max }}}}\left( {{x_2}} \right) = L{\lambda _{S2E}} \sum \nolimits _{w = 0}^{L - 1} {C_{L - 1}^w} {\left( { - 1} \right) ^w}{e^{ - \left( {1 + w} \right) {\lambda _{S2E}}{x_2}}}\) (see Appendix 1), \({f_{{g_{S1{R_s}}}}}\left( {{x_3}} \right) = {\lambda _{S1R}}{e^{ - {\lambda _{S1R}}{x_3}}}\), \({f_{{g_{S2{R_s}}}}} \left( {{x_4}} \right) = {\lambda _{S2R}}{e^{ - {\lambda _{S2R}}{x_4}}}\), \({f_{{g_{{R_s}E\max }}}} \left( {{x_5}} \right) = ML{\lambda _{RE}}\sum \nolimits _{k = 0}^{L - 1} {C_{L - 1}^k} {\left( { - 1} \right) ^k}\sum \nolimits _{u = 0}^{M - 1} {C_{M - 1}^u} {\left( { - 1} \right) ^u} \sum \nolimits _{v = 0}^{Lu} {C_{Lu}^v} {\left( { - 1} \right) ^v}{e^{ - \left( {1 + k + v} \right) {\lambda _{RE}}{x_5}}}\) (see Appendix 1), \({f_{{g_{{R_s}S1}}}}\left( {{x_6}} \right) = {\lambda _{RS1}}{e^{ - {\lambda _{RS1}}{x_6}}}\), and \({f_{{g_{{R_s}S2}}}}\left( {{x_7}} \right) = {\lambda _{RS2}}{e^{ - {\lambda _{RS2}}{x_7}}}\), respectively, and denoted \({\varOmega _1}\left( {L,M,\varphi ,{\lambda _{RS1}},{\lambda _{RS2}},{\lambda _{RE}}} \right) \buildrel \varDelta \over = LM{\lambda _{E}}\sum \nolimits _{k = 0}^{L - 1} {C_{L - 1}^k} {\left( { - 1} \right) ^k}\sum \nolimits _{u = 0}^{M - 1} {C_{M - 1}^u} {\left( { - 1} \right) ^u}\sum \nolimits _{v = 0}^{Lu} {\frac{{C_{Lu}^v{{\left( { - 1} \right) }^v}}}{{\left( {1 + k + v} \right) {\lambda _{RE}} + \varphi \left( {{\lambda _{RS1}} + {\lambda _{RS2}}} \right) }}}\); (23b) is obtained from (22) by applying \({f_{{g_{S1E\max }}}}\left( {{x_1}} \right) = L{\lambda _{S1E}}\sum \nolimits _{t = 0}^{L - 1} {C_{L - 1}^t} {\left( { - 1} \right) ^t}{e^{ - \left( {1 + t} \right) {\lambda _{S1E}}{x_1}}}\), \({f_{{g_{S2E\max }}}}\left( {{x_2}} \right) = L{\lambda _{S2E}}\sum \nolimits _{w = 0}^{L - 1} {C_{L - 1}^w} {\left( { - 1} \right) ^w}{e^{ - \left( {1 + w} \right) {\lambda _{S2E}}{x_2}}}\), \({f_{{g_{S1{R_s}}}}}\left( {{x_3}} \right) = M{\lambda _{S1R}}\sum \nolimits _{k = 0}^{M - 1} {C_{M - 1}^k} {\left( { - 1} \right) ^k}{e^{ - \left( {1 + k} \right) {\lambda _{S1R}}{x_3}}}\), \({f_{{g_{S2{R_s}}}}} \left( {{x_4}} \right) = {\lambda _{S2R}}{e^{ - {\lambda _{S2R}}{x_4}}}\), \({f_{{g_{{R_s}E\max }}}} \left( {{x_5}} \right) = L{\lambda _{RE}}\sum \nolimits _{u = 0}^{L - 1} {C_{L - 1}^u} {\left( { - 1} \right) ^u}{e^{ - \left( {1 + u} \right) {\lambda _{RE}}{x_5}}}\), \({f_{{g_{{R_s}S1}}}}\left( {{x_6}} \right) = {\lambda _{RS1}}{e^{ - {\lambda _{RS1}}{x_6}}}\), \({f_{{g_{{R_s}S2}}}}\left( {{x_7}} \right) = {\lambda _{RS2}}{e^{ - {\lambda _{RS2}}{x_7}}}\), and denoted \({\varOmega _2}\left( {L,\varphi ,{\lambda _{RS1}},{\lambda _{RS2}},{\lambda _{RE}}} \right) \buildrel \varDelta \over = L{\lambda _{RE}}\sum \nolimits _{u = 0}^{L - 1} {\frac{{C_{L - 1}^u{{\left( { - 1} \right) }^u}}}{{\left( {1 + u} \right) {\lambda _{RE}} + \varphi \left( {{\lambda _{RS1}} + {\lambda _{RS2}}} \right) }}}\); (23c) is obtained in the same way as (23b) with \(M = 1\). We have the asymptotic expansion of the exponential function as follows
Note that \(\frac{{ - \left( {\varphi - 1} \right) {\lambda _{RS1}}}}{{{\omega _3}\psi {x_4}}} \rightarrow 0\) when \(\psi\) is high. We obtain the following approximate expression:
Then, the SOP of the STW protocol with each of the three relay-selection strategies can be expressed when \(\psi\) is high, as follows:
where
Lemma 1
The following expression is valid for the integral \({I_{1,\mathrm{MAS1R}}}\)
where \({\varOmega _3}\left( {L,\varphi ,{\omega _1},{\omega _2},{\lambda _{S2R}},{\lambda _{S2E}}} \right) \buildrel \varDelta \over = L{\lambda _{S2E}}\sum \nolimits _{w = 0}^{L - 1} {\frac{{C_{L - 1}^w{{\left( { - 1} \right) }^w}{\omega _2}}}{{\left( {1 + w} \right) {\omega _2}{\lambda _{S2E}} + \varphi {\omega _1}{\lambda _{S2R}}}}},\) \({\varOmega _4}\left( {L,M,\varphi ,{\omega _1},{\omega _2},\psi ,{\lambda _{S1R}},{\lambda _{S1E}}} \right) \buildrel \varDelta \over = LM{\lambda _{S1E}}\sum \nolimits _{t = 0}^{L - 1} {C_{L - 1}^t} {( { - 1} ) ^t}\sum \nolimits _{k = 0}^{M - 1} {\frac{{C_{M - 1}^k{{( { - 1} ) }^k}{\omega _2}{e^{\frac{{ - ( {1 + k} ) \left( {\varphi - 1} \right) {\lambda _{S1R}}}}{{{\omega _2}\psi }}}}}}{{( {1 + k}) \left[ ( {1 + t} ) {\omega _2}{\lambda _{S1E}} + ( {1 + k} ) {\varphi {\omega _1}{\lambda _{S1R}}} \right] }}},\) \({\varOmega _5}\left( {L,M,\varphi ,{\omega _1},{\omega _2},{\lambda _{S1R}},{\lambda _{S1E}}} \right) \buildrel \varDelta \over = L M {\lambda _{S1 E}}{\lambda _{S1 R}} \sum \nolimits _{t = 0}^{L - 1} {C_{L - 1}^t{{\left( { - 1} \right) }^t} \sum \nolimits _{k = 0}^{M - 1} {C_{M - 1}^k} {{\left( { - 1} \right) }^k}} \frac{{{\omega _2}}}{{\left( {1 + t} \right) {\omega _2}{\lambda _{S1E}} + \left( {1 + k} \right) \varphi {\omega _1}{\lambda _{S1R}}}}_2{F_1}\left( {1,1;2;\frac{{\left( {1 + t} \right) {\omega _2}{\lambda _{S1E}}}}{{\left( {1 + t} \right) {\omega _2}{\lambda _{S1E}} + \left( {1 + k} \right) \varphi {\omega _1}{\lambda _{S1R}}}}} \right) .\)
Proof
Given in Appendix 2. \(\square\)
From that, the integrals \({I_{1,\mathrm{MIRE}}}\) and \({I_{1,\mathrm{RAN}}}\) can be obtained as
Lemma 2
The following expression is valid for the integral \({I_{2,\mathrm{MAS1R}}}\)
Proof
Given in Appendix 3. \(\square\)
The integrals \({I_{2,\mathrm{MIRE}}}\) and \({I_{2,\mathrm{RAN}}}\) are then given by
Finally, we can obtain expressions for \(P_{out,\mathrm{MIRE}}^{{\mathrm{STW}}}\), \(P_{out,\mathrm{MAS1R}}^{{\mathrm{STW}}}\), and \(P_{out,\mathrm{RAN}}^{{\mathrm{STW}}}\) by substituting (27–30) into (26a–26c).
3.2.2 Secrecy Throughput Performance
In this subsection, we derive the STP of the STW protocol, which is defined as the effective time for the transmissions by the two sources S1 and S2 at the secrecy target rate \({C_t}\) bits/sec/Hz. In the STW protocol, the total number of time slots is 4T, and the effective communication time for a transmission from S1 to \({R_s}\) and from S2 to \({R_s}\) is 2T (the first and third TSs). The throughput of the STW protocol with one of the three relay-selection strategies is given by
where \(\tau _{{\mathrm{MIRE/MAS1R/RAN}}}^{{\mathrm{STW}}}\) and \(P_{out,{\mathrm{MIRE/MAS1R/RAN}}}^{{\mathrm{STW}}}\) are STP and SOP, respectively.
4 Secure Two-Way Energy-Constrained Relaying Communication with Network Coding (STWNC)
4.1 Transmission Operation
In the STWNC protocol, to reduce transmission time, we shorten the transmission period to 3T by applying the digital network coding technique at the preselected relay \({R_s}\). Thus, the STWNC protocol uses three time slots for a complete data-exchange period, as shown in Fig. 1b. In the first TS, the binary message \({m_{S1}}\) of the source S1 is presented by the signal \({x_{S1}}\), \(\mathcal {E}\left\{ {{{\left| {{x_{S1}}} \right| }^2} = 1} \right\}\), which is transmitted to the preselected energy-constrained relay \({R_s}\) in the presence of L eavesdropper nodes \({E_l}\), \(l \in \left\{ {1,2,\ldots ,L} \right\}\). The ASR from S1 to \({R_s}\) with this protocol is similar to that with the STW protocol, replacing the pre-log 1 / 4 with 1 / 3, as follows:
In this protocol, the preselected relay \({R_s}\) only harvested the energy from the received signal transmitted by S1 in the first TS. The harvested energy is the same as in (10):
The source S2 sends its message \({m_{S2}}\), presented as signal \({x_{S2}}\), to \({R_s}\) under eavesdropping by \({E_l}\); thus, the ASR from S2 to \({R_s}\) is expressed as
After successfully and safely decoding the two binary messages, \({m_{S1}}\) and \({m_{S2}}\), during the first two TSs, \({R_s}\) combines them by applying the digital network coding and generates a new message, \({m_{S1 \oplus S2}}\), where \({m_{S1 \oplus S2}} = {m_{S1}} \oplus {m_{S2}}\). The message \({m_{S1 \oplus S2}}\) is presented by the signal \({x_{S1 \oplus S2}}\), and it is broadcasted back to both source nodes S1 and S2 by \({R_s}\) during the third TS with the transmitted power \({P_{S1{R_s}}} = {E_{S1{R_s}}}/T = \eta \rho P{g_{S1{R_s}}}\). The received baseband signals at S1, S2, and \({E_l}\) can be respectively given by
Note that, during the third TS, the transmitted message \({m_{S1 \oplus S2}}\) is coded; thus, the eavesdroppers \({E_l}\) cannot obtain the messages from the two sources, \({m_{S1}}\) and \({m_{S2}}\). In other words, the eavesdroppers \({E_l}\), \(l \in \left\{ {1,2,\ldots ,L} \right\}\), do not impact the ASRs of the two links \({R_s} \rightarrow S1\) and \({R_s} \rightarrow S2\). Consequently, the achievable secrecy capacities of the links \({R_s} - S1\) and \({R_s} - S2\) are respectively expressed as
In the STWNC protocol, we do not consider the relay-selection scheme based on the minimum channel gain from the selected relay \({R_s}\) to eavesdroppers because there is no impact of eavesdroppers on the transmission of \({R_s}\) in the third TS. Thus, we analyze the performance with the two other considered relay-selection strategies, in (19b) and (19c), for this protocol.
4.2 Performance Analysis
4.2.1 Secrecy Outage Probability
The SOP with the STWNC protocol is expressed the same way as that with the STW protocol:
By substituting the expressions for \(C_{S1{R_s}}^{{\mathrm{STWNC}}}\), \(C_{S2{R_s}}^{{\mathrm{STWNC}}}\), \(C_{{R_s}S1}^{{\mathrm{STWNC}}}\), and \(C_{{R_s}S2}^{{\mathrm{STWNC}}}\) from Eqs. (32), (34), (38), and (39), respectively, into (40), we obtain
where \(\phi \buildrel \varDelta \over = {2^{3{C_t}}}\). By applying the relay selection strategy in (19b) (MAS1R) to this protocol, and approximating \({e^{\frac{{ - \left( {\phi - 1} \right) \left( {{\lambda _{RS1}} + {\lambda _{RS2}}} \right) }}{{{\omega _3}\psi {x_3}}}}} \approx 1 + \frac{{ - \left( {\phi - 1} \right) \left( {{\lambda _{RS1}} + {\lambda _{RS2}}} \right) }}{{{\omega _3}\psi {x_3}}}\), we attain the SOP for \(P_{out,\mathrm{MAS1R}}^{{\mathrm{STWNC}}}\) as follows:
where
With the relay selection strategy in (19c) (RAN), the SOP can be obtained as
4.2.2 Secrecy Throughput Performance
With the STWNC protocol, the effective transmission time of the two sources S1 and S2 at the secrecy target rate \({C_t}\) bits/sec/Hz is 2T / 3T. The throughput of this protocol with one of the two relay-selection strategies MAS1R or RAN is
5 Secure Two-Way Energy-Constrained Relaying Communication with Cooperative Jamming and Network Coding (STWJNC)
5.1 Transmission Operation
In the STWJNC protocol, there are four TSs for completing the exchange of data between two source nodes, as shown in Fig. 1c. In this protocol, the preselected jammer node \({J_s}\) has two functions that (1) help the two sources code their messages by XORing them with the jamming message, and (2) transmit the energy to the \({R_s}\). In the first TS, \({J_s}\) broadcasts the jamming message \({m_J}\) (presented by signal \({x_J}\)) to the two sources and the preselected relay \({R_s}\) in the presence of L eavesdroppers. The ASRs from \({J_s}\) to the two sources S1 and S1 are respectively given as
In this protocol, \({R_s}\) uses the received RF signal transmitted from \({J_s}\) for only harvesting the energy. Thus, the harvested power at \({R_s}\) is given by
We consider whether S1 and S2 can successfully and safely decode the jamming message in the first time slot, that is, S1 and S2 can successfully decode the jamming message, but the eavesdroppers cannot.
5.1.1 Consider the Case When the Two Source Nodes Can Successfully and Safely Decode the Jamming Message During the First Time Slot; i.e., \(C_{{J_s}S1}^{{\mathrm{STWJNC}}} \ge {C_t}\) and \(C_{{J_s}S2}^{{\mathrm{STWJNC}}} \ge {C_t}\)
We propose the optimal jammer-relay pair \(\left( {{J_s},{R_s}} \right)\) (called OPT) selection strategy (48a), described as follows: among the K jammers \(\left( {1 \le K \le N} \right)\) that can successfully and safely transmit the jamming message, an optimal jammer-relay pair is selected for which \({J_s}\) has the highest channel gain with \({R_s}\). For comparison, we analyze one more jammerrelay pair using a random (RAN) selection strategy, as formulated in (48b) below.
During the second TS, the source node S1 generates the coded message \({m_{S1 \oplus {J_s}}}\) (by \({m_{S1 \oplus {J_s}}} \buildrel \varDelta \over = {m_{S1}} \oplus {m_{{J_s}}}\)), and sends it to \({R_s}\). Note that the eavesdroppers cannot obtain the source message \({m_{S1}}\) in this case. The ASR of the link \(S1 - {R_s}\) is expressed as
where the index 1 in \(C_{S1{R_s}}^{{\mathrm{STWJNC,1}}}\) indicates that we are analyzing the STWJNC protocol of this case, e.g., \(C_{{J_s}S1}^{{\mathrm{STWJNC}}} \ge {C_t}\) and \(C_{{J_s}S2}^{{\mathrm{STWJNC}}} \ge {C_t}\).
Similarly, S2 transmits the coded message \({m_{S2 \oplus {J_s}}}\) (presented by the signal \({x_{S2 \oplus {J_s}}}\)) to \({R_s}\) during the third TS, and the ASR is obtained as follows
After successfully decoding the received messages \({m_{S1 \oplus {J_s}}}\) and \({m_{S2 \oplus {J_s}}}\) during the second and third TSs, the relay \({R_s}\) uses digital network coding to create a new message \({m_{S1 \oplus S2}}\) by XORing \({m_{S1 \oplus {J_s}}}\) and \({m_{S2 \oplus {J_s}}}\); i.e., \({m_{S1 \oplus {J_s}}} \oplus {m_{S2 \oplus {J_s}}} = {m_{S1}} \oplus {m_{{J_s}}} \oplus {m_{S2}} \oplus {m_{{J_s}}} = {m_{S1}} \oplus {m_{S2}} \buildrel \varDelta \over = {m_{S1 \oplus S2}}\). It then broadcasts the new message to the two source nodes during the fourth TS. If the two sources successfully decode the message \({m_{S1 \oplus S2}}\), they can safely extract the desired message by XORing it with their own messages. The ASRs of the two links \({R_s} - S1\) and \({R_s} - S2\) during the fourth TS are given respectively by
where \({\omega _4} \buildrel \varDelta \over = \frac{\eta }{{1 + \mu }}\).
5.1.2 Consider the Case When the Two Source Nodes do not Successfully and Safely Decode the Jamming Message During the First Time Slot; i.e., One of Source Nodes S1 and S2 does not Successfully Decode the Jamming Message or Atleast One Eavesdropper Gets the Jamming Message: \(C_{{J_s}S1}^{{\mathrm{STWJNC}}} < 0\) and/or \(C_{{J_s}S2}^{{\mathrm{STWJNC}}} < 0\)
In this case, there is no jammer that can successfully and safely transmit the jamming message to the two sources (\(K = 0\)). In other words, the jammers are unhelpful for coding the two sources messages; thus, the jammer \({J_s}\) is selected from the N jammer nodes to transmit the energy to \({R_s}\). The two jammer-relay pair selection strategies (48a) and (48b) can be rewritten as follows:
The eavesdroppers can impact the transmission of the two links \(S1 \leftrightarrow {R_s}\) and \(S2 \leftrightarrow {R_s}\); therefore, the ASRs from S1 to \({R_s}\) during the second TS, from S2 to \({R_s}\) during the third TS, and from \({R_s}\) to S1 and S2 during the fourth TS can be given respectively by
5.2 Performance Analysis
5.2.1 Secrecy Outage Probability of the STWJNC Protocol
Addressing the optimal jammerrelay-pair-selection strategy first, the SOP of the STWJNC protocol, \(P_{out{\mathrm{,OPT}}}^{{\mathrm{STWJNC}}}\), can be expressed as
where \(\Pr \left[ {K,N} \right]\) denotes the probability that there are K jammers and \(\Pr \left[ {0,N} \right]\) denotes the probability that there is no jammer that can successfully and safely transmit the jamming message to the two sources. These probabilities can be expressed as (59) and (60) as follows. We note that (59.2) is obtained from (59.1) by applying the result in Appendix 4
\(P_{out{\mathrm{,OPT}}}^{{\mathrm{STWJNC,1}}}\) and \(P_{out{\mathrm{,OPT}}}^{{\mathrm{STWJNC,2}}}\) are expressed by (61) and (62), respectively, below:
Lemma 3
The following expression is valid for \(P_{out{\mathrm{,OPT}}}^{{\mathrm{STWJNC,1}}}\)
where
Proof
See Appendix 5. \(\square\)
Lemma 4
The following expression is valid for \(P_{out{\mathrm{,OPT}}}^{{\mathrm{STWJNC,2}}}\)
Proof
See Appendix 6. \(\square\)
Combining (58), (59), (60), (63), and (64), we obtain the SOP for the STWJNC protocol with the optimal jammerrelay-pair-selection strategy. And when the random jammerrelay-pair-selection strategy is applied, the SOP of the STWJNC protocol can be derived by \(P_{out{\mathrm{,RAN}}}^{{\mathrm{STWJNC}}} = {\left. {P_{out{\mathrm{,OPT}}}^{{\mathrm{STWJNC}}}} \right| _{N = K = M = 1}}\).
5.2.2 Secrecy Throughput Performance of the STWNC Protocol
In the STWJNC protocol, the rate of the effective transmission time of the two sources S1 and S2 with respect to the total time is 2T / 4T. Thus, the throughput of this protocol with each of the two relay-selection strategies can be expressed as follows:
6 Numerical Results and Discussion
This section discusses the theoretical derivations and the Monte-Carlo simulations conducted to validate the analysis for the STW, STWNC, and STWJNC protocols described in the previous three sections. The simulations were conducted to verify the theoretical derivations as well as to determine the performance of the three proposed protocols. In a two-dimensional plan, the coordinates are \(\left( {0,0} \right)\), \(\left( {1,1} \right)\), \(\left( {{x_R},0} \right)\), \(\left( {{x_E},{y_E}} \right)\), and \(\left( {{x_J},{y_J}} \right)\), respectively, for the two source nodes S1 and S2, the relay-nodes-cluster-based \({R_m}\) with \(m \in \left\{ {1,2,\ldots ,M} \right\}\), the eavesdropper-nodes-cluster-based \({E_l}\) with \(l \in \left\{ {1,2,\ldots ,L} \right\}\), and (appearing only in the STWJNC protocol) the jammer-nodes-cluster-based \({J_n}\) with \(n \in \left\{ {1,2,\ldots ,N} \right\}\). Thus, the distances of the links \(S1 - {R_m}\), \(S2 - {R_m}\), \(S1 - {E_l}\), \(S2 - {E_l}\), \({R_m} - {E_l}\), \({J_n} - S1\), \({J_n} - S2\), \({J_n} - {R_m}\), and \({J_n} - {E_l}\) are \({d_{S1R}} = \left| {{x_R}} \right|\), \({d_{S2R}} = \left| {1 - {x_R}} \right|\), \({d_{S1E}} = \sqrt{{{\left( {{x_E}} \right) }^2} + {{\left( {{y_E}} \right) }^2}}\), \({d_{S2E}} = \sqrt{{{\left( {1 - {x_E}} \right) }^2} + {{\left( {1 - {y_E}} \right) }^2}}\), \({d_{RE}} = \sqrt{{{\left( {{x_R} - {x_E}} \right) }^2} + {{\left( {{y_E}} \right) }^2}}\), \({d_{JS1}} = \sqrt{{{\left( {{x_J}} \right) }^2} + {{\left( {{y_J}} \right) }^2}}\), \({d_{JS2}} = \sqrt{{{\left( {1 - {x_J}} \right) }^2} + {{\left( {1 - {y_J}} \right) }^2}}\), \({d_{JR}} = \sqrt{{{\left( {{x_R} - {x_J}} \right) }^2} + {{\left( {{y_J}} \right) }^2}}\), and \({d_{JE}} = \sqrt{{{\left( {{x_J} - {x_E}} \right) }^2} + {{\left( {{y_J} - {y_E}} \right) }^2}}\), respectively. In all the simulation scenarios, the following parameters were used: \(\mu = 1\), \(\beta = 3\), and \({C_t} = 0.5\). For simple presentation, the acronym \(\mathrm{U-V}\) indicates that we are considering the protocol U (\({\mathrm{U}} \in \left\{ {{\mathrm{STW,STWNC,STWJNC}}} \right\}\)) with the relay- or jammerrelay-pair-selection strategy V (\({\mathrm{V}} \in \left\{ {{\mathrm{MIRE,MAS1R,RAN,OPT}}} \right\}\)). In addition, we set \(\rho = 0.5\) and \(\eta = 0.8\) for the cases shown in Figs. 2, 3, 4 and 5.
Figure 2 shows an evaluation and comparison of the performance of the three protocols with their different relay selection strategies. The performance is based on the secrecy outage probability as a function of \(\psi\), M, L, or N, as shown in Fig. 2a–d. The positions of the cluster-based relays, eavesdroppers, and jammers are set at \(\left( {0.5,0} \right)\), \(\left( {0.5, - 1} \right)\), and \(\left( {0.5,0.5} \right)\), respectively. The SOPs of STW-MIRE, STW-MAS1R, STW-RAN, STWNC-MAS1R, and STWNC-RAN are approximately derived when is high, in Eqs. (26a), (26b), (26c), (43) and (44), respectively. Thus, the theoretical results curves are not exactly the same as the simulation curves (however, their differences are very small) when \(\psi\) is low, e.g., \(\psi < 10\) dB, as shown in Fig. 2a. In contrast, STWJNC-OPT and STWJNC-RAN are exactly derived, so the theoretical results match very well with the simulation results for all values of \(\psi\) , as shown in Fig. 2a. When \(\psi\) is fixed at a high value, e.g., \(\psi = 15\) dB, the simulation and theoretical results are in excellent agreement for STW-MIRE, STW-MAS1R, STW-RAN, STWNC-MAS1R and STWNC-RAN, as shown in Fig. 2b–d.
We can observe in Fig. 2a that all the protocols improve the secrecy outage performance for high values of \(\psi\). The SOPs of the STW protocol with its three relay-selection strategies (STW-MIRE, STW-MAS1R, and STW-RAN) are not decreased much because, when \(\psi\) increases, the eavesdropping channel gain also increases. Motivated to reduce the impact of eavesdroppers on the transmissions from the two source nodes by using a selected relay, we additionally use network coding with the STWNC protocol, and a combination of network coding and cooperative jamming with the STWJNC protocol. The results show that STWNC-MAS1R, STWNC-RAN, STWJNC-OPT, and STWJNC-RAN achieve higher performance than the STW protocol.
Next, we compare the performance between the STWNC and STWJNC protocols. Using the random selection scheme, STWJNC-RAN attains lower performance than STWCN-RAN because, when the jammer is chosen randomly, it is difficult for the STWJNC-RAN protocol to transmit the jamming message successfully and safely to the two source nodes during the first TS. Second, comparing the MAS1R strategy with the STWCN protocol and the OPT strategy with the STWJNC protocol, for low \(\psi\) (below about 12 dB), STWNC again outperforms STWJNC. This occurs because the two sources nodes may be unable to decode the jamming message transmitted from the selected jammer \({J_s}\) and because the relay may not harvest enough energy from the selected jammer to forward the information during the fourth TS. However, STWJNC-OPT achieves much higher performance than STWNC-MAS1R when \(\psi\) is high. The reason is that, with STWJNC-OPT, the selected relay \({R_s}\) uses the energy harvested from \({J_s}\) for transmission, whereas with STWNC-MAS1R, \({R_s}\) has to harvest the energy from the received RF signal transmitted from S1, which causes the decoding performance for the link \(S1 - {R_s}\) to be less with STWNC-MAS1R than with STWJNC-OPT.
STW-RAN, STWNC-RAN, and STWJNC-RAN maintain their SOPs as the number of relay nodes (M) increases, as shown in Fig. 2b, because a random relay is selected with each protocol. STW-MAS1R and STWNC-MAS1R have improved performance when the number of relays increases. This is because more energy can be harvested from S1, which improves the decoding process for the two links \(S1 - {R_s}\) and \({R_s} - S2\). In contrast, the performance of STWJNC-OPT is improved lightly when M increases. The performance of all protocols is reduced when the number of eavesdroppers (L) increases, as shown in Fig. 2c. This is because, when L increases, the impact of eavesdroppers on the system is greater. When the number of jammer nodes (N) increases, only the STWJNC-OPT protocol improves the performance because a change of N value only affects this protocol (Fig. 2d). Moreover, STWJNC-OPT still has lower performance than STWNC-MAS1R when \(N = 1,2\) because, with small values of N, STWJNC-OPT is unable to select a \({J_s}\) that can transmit successfully and safely to the two sources during the first TS. Finally, as shown in Fig. 2a–d, the performances of the STW-MIRE and STW- MAS1R protocols are very similar. With its lack of network coding, the STW protocol has the lowest performance with all relay-selection strategies and parameters. STWNC-RAN outperforms STWJNC-RAN in all Fig. 2a–d because, in this scenario, (1) network coding helps to improve performance by reducing the impact of eavesdroppers, and (2) STWNC-RAN uses three TSs, which is more effective than the four TSs of STWJNC-RAN. However, when the values of \(\psi\) and N are large enough, e.g., \(\psi \ge 15\) dB and \(N \ge 3\), with the optimal jammer-relay selection strategy (\({J_s}\) is preselected), the impact of eavesdroppers can be greatly reduced, and thus, STWJNC-OPT outperforms STWNC-MAS1R.
Figure 3 shows the impact of the position of the relay cluster on the secrecy performance of the protocols, as \({x_R}\) is shifted from 0.1 to 0.99. This figure shows that each protocol achieves its best performance when the relay is located around the midpoint between the two source nodes, i.e., \({x_R} \in \left( {0.45,0.55} \right)\) because a relay at this position can balance the efficiency of the decoding processes between the two links \(S1 \leftrightarrow R\) and \(S12 \leftrightarrow R\). The performance of STWJNC-RAN is higher than that of STWNC-RAN when the relays are located near S1, e.g., \({x_R} \in \left( {0.1,0.22} \right)\), or near S2, e.g., \({x_R} \in \left( {0.6,1} \right)\). This is because, for relays near S1, the distance between S2 and R is long, making it difficult in the STWNC-RAN protocol for the relay to harvest the energy and still achieve a high decoding performance for the received signal transmitted by S2. In contrast, the relay in STWJNC-RAN harvests the energy from the jammer, so the decoding efficiency of the link \(S2 \rightarrow R\) is improved.
The impact of the position of the eavesdroppers with respect to the relays and jammers is presented in Fig. 4. When the eavesdroppers are very far from the relays and jammers (\({y_E} = - 1\)), all protocols achieve their best performance because the eavesdroppers have the lowest impact. When the eavesdroppers are near the relays and far from the jammers (\({y_E} \in ( { - 0.6,0} )\)), STWJNC-RAN achieves higher performance than STWNC-RAN. This is because, when \({y_E} \in \left( { - 0.6,0} \right)\), the eavesdroppers have a strong impact on the data transmitted by the two sources and relays, which reduces the performance of STWNC-RAN. In contrast, with STWJNC-RAN, this impact is reduced by coding the jamming message transmitted by the jammer. STWNC-RAN outperforms STWJNC-RAN in the other regions of \({y_E}\), i.e., \({y_E} \in ( { - 1, - 0.6} )\) and \({y_E} \in ( {0,1} )\). This is because, (1) when \({y_E} \in ( { - 1, - 0.6} )\), the eavesdroppers have little impact, and STWNC-RAN is more effective because it uses fewer time slots than STWJNC-RAN, and (2) when \({y_E} \in ( {0,1} )\), the jammers unable to transmit successfully and safely the jamming message to two source nodes during the first TS of STWJNC-RAN because the eavesdroppers are very near the jammers. Moreover, STWJNC-OPT also has very bad performance (similar to the performances of the STWJNC-RAN and STW protocols) when the eavesdroppers are near the jammers, i.e., \({y_E} \in ( {0,1} )\).
In Fig. 5, we present the SOP as a function of \({y_J}\). As expected, only STWJNC-RANs and STWJNC-OPTs performances change, achieving their highest levels when \({y_J} \approx 0.2\). This can be explained by the fact that the position \(J( {{x_J} = 0.5,{y_J} \simeq 0.2} )\) is the optimal point such that (1) the two source nodes can receive the jamming message successfully and safely, and (2) the relay \({R_s}\) receives high energy from the RF signal transmitted by \({J_s}\).
In Fig. 6, we investigate the effect of \(\rho\) on the STP of the protocols. We can observe in Fig. 6 that the throughput performances of the STW and STWNC protocols are reduced when \(\rho\) increases because, at high \(\rho\) values, the quality of the decoding process at the relay is degraded. In contrast, when \(\rho\) is low, the decoding processes for the links \(S1 \rightarrow {R_s}\) and \(S2 \rightarrow {R_s}\) are guaranteed because \({R_s}\) does not harvest much energy from the RF signals transmitted from S1 and S2. In addition, the STW protocol with any of its relay selection schemes (MIRE, MAS1R, and RAN) has the lowest throughput performance. Finally, the STWNC protocol obtains higher secrecy throughput performance than the STWJNC protocol when \(\rho\) is not too large \(( {\rho \le 0.7} )\).
Figure 7 illustrates the secrecy throughput performance (STP) as a function of the energy harvesting efficiency \(\eta\). For very small values of \(\eta\) (\(0< \eta < 0.2\)), the STP of each protocol is low due to insufficient energy for the relay \({R_s}\) to transmit the data. When \(\eta\) increases, \({R_s}\) can harvest more energy, which improves the forwarding performance of \({R_s}\); however, the eavesdroppers can also more easily overhear the data. Thus, the STP keeps increasing very slightly as \(\eta\) increases, \(0.1< \eta < 0.9\). STWNC-MAS1R obtains the best STP among the seven considered schemes (Table 1).
7 Conclusions
In this paper, we first considered the conventional secured two-way energy-constrained relaying network along with three different relay selection strategies. Second, to improve performance, we applied a digital network coding technique at a preselected relay \({R_s}\) to reduce the number of time slots used as well as the impact of eavesdroppers on the forwarding process of \({R_s}\) during the third time slot. Third, we proposed another protocol that employs jammer nodes and combines cooperative jamming and network coding along with two different jammerrelay-pair-selection strategies. We derived closed-form expressions for secrecy outage probability and throughput performance for each scheme. We used Monte Carlo simulations to verify our analysis. The simulation and theoretical results showed the following. (1) The performances of all protocols improve with increasing \(\psi\), \(\eta\) or decreasing L, \(\rho\). (2) The outage performance of STWJNC-OPT is higher than that of STWNC-MAS1R when \(\psi\) and N are high enough; however, STWNC-MAS1R achieves better throughput performance than STWJNC-OPT. (3) The outage performance of STWJNC-RAN is only higher than that of STWNC-RAN when the relays are located near one of the two source nodes or eavesdroppers, but STWNC-RAN has higher throughput performance at all values, compared to STWJNC-RAN. (4) In all the scenarios, the outage and throughput performances of the STW protocol are the lowest. (5) The performances of STW-MIRE and STW-MAS1R are nearly the same. (6) The theoretical results match the simulation results well.
References
Raghunathan, V., Ganeriwal, S., & Srivastava, M. (2006). Emerging techniques for long lived wireless sensor networks. IEEE Communications Magazine, 44(4), 108–114.
Paradiso, J. A., & Starner, T. (2005). Energy scavenging for mobile and wireless electronics. IEEE Pervasive Computing, 4(1), 18–27.
Ulukus, S., Yener, A., Erkip, E., Simeone, O., Zorzi, M., Grover, P., et al. (2015). Energy harvesting wireless communications: A review of recent advances. IEEE Journal on Selected Areas in Communications, 33(3), 360–381.
Medepally, B., & Mehta, N. B. (2010). Voluntary energy harvesting relays and selection in cooperative wireless networks. IEEE Transactions on Wireless Communications, 8(11), 3543–3553.
Zhou, X., Zhang, R., & Ho, C. K. (2013). Wireless information and power transfer: Architecture design and rate-energy tradeoff. IEEE Transactions on communications, 61(11), 4754–4767.
Lumpkins, W. (2014). Nikola Teslas dream realized: Wireless power energy harvesting. IEEE Consumer Electronics Magazine, 3(1), 39–42.
Pinuela, M., Mitcheson, P. D., & Lucyszyn, S. (2013). Ambient RF energy harvesting in urban and semi-urban environments. IEEE Transactions on Microwave Theory and Techniques, 61(7), 2715–2726.
Grover, P., & Sahai, A. (2010). Shannon meet Tesla: Wireless information and power transfer. In IEEE international symposium on information theory proceedings (ISIT), pp. 2363–2367.
Zhang, R., & Ho, C. K. (2013). MIMO broadcasting for simultaneous wireless information and power transfer. IEEE Transactions on Wireless Communications, 12(5), 1989–2001.
Varshney, L. R. (2008). Transporting information and energy simultaneously. In IEEE international symposium on information theory (ISIT), pp. 1612–1616.
Liu, L., Zhang, R., & Chua, K. C. (2013). Wireless information transfer with opportunistic energy harvesting. IEEE Transactions on Wireless Communications, 12(1), 288–300.
Nasir, A. A., Xiangyun, Z., Durrani, S., & Kennedy, R. A. (2013). Relaying protocols for wireless energy harvesting and information processing. IEEE Transactions on Wireless Communications, 12(7), 3622–3636.
Nasir, A. A., Zhou, X., Durrani, S., & Kennedy, R. A. (2015). Wireless-powered relays in cooperative communications: Time-switching relaying protocols and throughput analysis. IEEE Transactions on Communications, 63(5), 1607–1622.
Ding, Z., Perlaza, S. M., Esnaola, I., & Poor, H. V. (2014). Power allocation strategies in energy harvesting wireless cooperative networks. IEEE Transactions on Wireless Communications, 13(2), 846–860.
Liu, Y., Wang, L., Elkashlan, M., & Duong, T. Q. (2014). Two-way relaying networks with wireless power transfer: Policies design and throughput analysis. In IEEE global communications conference (GLOBECOM), pp. 4030–4035.
Son, P. N., & Kong, H. Y. (2015). Energy-harvesting relay selection schemes for decode-and-forward dual-hop networks. IEICE Transactions on Communications, E98-B(4), 661–672.
Stallings, W. (2003). Cryptography and network security principles and practices (3rd ed.). Upper Saddle River, NJ: Prentice Hall.
Wyner, A. D. (1975). The wire-tap channel. The Bell System Technical Journal, 54(8), 1355–1387.
Leung-Yan-Cheong, S., & Hellman, M. E. (1978). The Gaussian wire-tap channel. IEEE Transaction on Information Theory, 24(4), 451–456.
Csiszar, I., & Korner, J. (1978). Broadcast channels with confidential messages. IEEE Transactions on Information Theory, 24(3), 339–348.
Liang, Y., Poor, H. V., & Shamai, S. (2008). Secure communication over fading channels. IEEE Transactions on Information Theory, 54(6), 2470–2492.
Dong, L., Han, Z., Petropulu, A. P., & Poor, H. V. (2010). Improving wireless physical layer security via cooperating relays. IEEE Transactions on Signal Processing, 58(3), 1875–1888.
Zang, R., Song, L., Han, Z., Jiao, B., & Debbah, M. (2010). Physical layer security for for two way relay communications with friendly jammers. In: IEEE global telecommunications conference (GLOBECOM), pp. 1–6.
Wang, L., Elkashlan, M., Huang, J., Tran, N. H., & Duong, T. Q. (2014). Secure transmission with optimal power allocation in untrusted relay networks. IEEE Wireless Communications Letters, 3(3), 289–292.
Wang, L., Kim, K. J., Duong, T. Q., Elkashlan, M., & Poor, H. V. (2014). On the security of cooperative single carrier systems. In IEEE global telecommunications conference (GLOBECOM), Austin, TX, pp. 1596–1601.
Duong, T. Q., Duy, T. T., Elkashlan, M., Tran, N. H., & Dobre, O. A. (2014). Secured cooperative cognitive radio networks with relay selection. In IEEE global telecommunications conference (GLOBECOM), Austin, TX, pp. 3074–3079.
Liu, Y., Wang, L., Duy, T. T., Elkashlan, M., & Duong, T. Q. (2015). Relay selection for security enhancement in cognitive relay networks. IEEE Wireless Communication Letters, 4(1), 46–49.
Jong-Ho, L. (2015). Cooperative relaying protocol for improving physical layer security in wireless decode-and-forward relaying networks. Wireless Personal Communications, 83(4), 3033–3044.
Krikidis, I., Thompson, J. S., & Mclaughlin, S. (2009). Relay selection for secure cooperative networks with jamming. IEEE Transactions on Wireless Communications, 8(10), 50035011.
Long, H., Xiang, W., Wang, J., Zhang, Y., & Wang, W. (2014). Cooperative jamming and power allocation with untrusty two-way relay nodes. IET Communications, 8(13), 2290–2297.
Duy, T. T., Duong, T. Q., Benevides da Costa, D., Bao, V. N. Q., & Elkashlan, M. (2015). Proactive relay selection with joint impact of hardware impairment and co-channel interference. IEEE Transaction on Communications, 64(5), 1594–1606.
Gradshteyn, I. S., Ryzhik, I. M., Jeffrey, A., & Zwillinger, D. (2007). Table of integral, series and products (7th ed.). London: Academic Press.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: The PDF of RVs \({\varvec{g_{{R_s}E\max }}}\), \({\varvec{g_{S2E\max }}}\), and \({\varvec{g_{S1E\max }}}\) When Using the Relay Selection Strategy in (19a)
The CDFs of RVs \({g_{{R_s}E\max }}\), \({g_{S2E\max }}\), and \({g_{S1E\max }}\) can be given respectively as
Then, by differentiating (66), (67), and (68), we obtain the PDFs of RVs \({g_{{R_s}E\max }}\), \({g_{S2E\max }}\), and \({g_{S1E\max }}\), respectively, as follows:
Appendix 2: Proof of Lemma 1
At first, the integral \({I_{{\mathrm{1,MAS1R}}}}\) can be expressed as
where (72.2) is obtained by approximating \({e^{\frac{{ - \left( {\varphi - 1} \right) {\lambda _{RS2}}}}{{{\omega _3}\psi {x_3}}}}} \approx 1 + \frac{{ - \left( {\varphi - 1} \right) {\lambda _{RS2}}}}{{{\omega _3}\psi {x_3}}}\).
The term \({I_3}\) and \({I_4}\) in (72) are denoted and derived as in (73) and (74) as follows
where (74.1) is obtained from by using \(\int _0^\infty {L{\lambda _{S2 E}} \sum \limits _{w = 0}^{L - 1} {C_{L - 1}^w} {{\left( { - 1} \right) }^w}{e^{ - \left[ {\frac{{\left( {1 + w} \right) {\omega _2}{\lambda _{S2E}} + \varphi {\omega _1}{\lambda _{S2R}}}}{{{\omega _2}}}} \right] {x_2}}}} = {\varOmega _3} \left( { L, \varphi , {\omega _1}, {\omega _2},{\lambda _{S2 R}}, {\lambda _{S2 E}}} \right)\) and \(\int _{\frac{{\varphi - 1}}{{{\omega _2}\psi }} + \frac{{\varphi {\omega _1}{x_1}}}{{{\omega _2}}}}^\infty {\frac{{{e^{ - \left( {1 + k} \right) {\lambda _{S1R}}{x_3}}}}}{{{x_3}}}} d{x_3} = \varGamma \left[ {0,\left( {1 + k} \right) {\lambda _{S1R}}\left( {\frac{{\varphi - 1}}{{{\omega _2}\psi }} + \frac{{\varphi {\omega _1}{x_1}}}{{{\omega _2}}}} \right) } \right]\) (see [32, Eq. (3.381.3)]); (74.2) is obtained from (74.1) by approximating \(\frac{{\varphi - 1}}{{{\omega _2}\psi }}\mathop \approx \limits ^{{\mathrm{high}}\,\,\psi \,} 0\); (73.3) is obtained from (74.2) by using the Eq. (6.455.1) of [32] in the case of \(\mu = 1\) and \(v = 0\), as \(\int _0^\infty {{e^{ - \beta x}}} \varGamma \left( {0,\alpha x} \right) dx = \frac{1}{{\alpha + \beta }}_2{F_1}\left( {1,\,1\,;\,2\,;\frac{\beta }{{\alpha + \beta }}} \right).\)
We finish the proof by combining (72), (73), and (74).
Appendix 3: Proof of Lemma 2
The integral \({I_{2,\mathrm{MAS1R}}}\) can be obtained after some steps with using [32, Eq. (3.381.3)] and approximating \(\frac{{\varphi - 1}}{{{\omega _2}\psi }} \approx 0\), and \(\frac{{ - \left( {\varphi - 1} \right) {\lambda _{RS2}}}}{{{\omega _3}\psi {x_3}}} \approx 0\) when \(\psi\) is high, as follows
where \({I_5}\) and \({I_6}\) are denoted and derived as in (76) and (77), respectively
We finish the proof by combining (75), (76), and (77).
Appendix 4: Proof of Equation (59.2)
The expression for the probability term \(\Pr \left[ {\min \left( {{C_{{J_1}S1}},{C_{{J_1}S2}}} \right) \ge {C_t}} \right]\) can be obtained as follows:
By substituting (78) into (59.1), we finish the proof.
Appendix 5: Proof of Lemma 3
By substituting (49), (50), (51), and (5) into (61), we obtain
From the optimal jammer and relay selection strategy, in (48a), the CDF of RV \({g_{{J_s}{R_s}}}\) is expressed as
By substituting (80), \({f_{{g_{S1{R_s}}}}}( {{x_1}} ) = {\lambda _{S1R}}{e^{ - {\lambda _{S1R}}{x_1}}}\), \({f_{{g_{S2{R_s}}}}}\left( {{x_2}} \right) = {\lambda _{S2R}}{e^{ - {\lambda _{S2R}}{x_2}}}\), \({f_{{g_{{J_s}{R_s}}}}}\left( {{x_3}} \right) = KM{\lambda _{JR}}\sum \nolimits _{k = 0}^{KM - 1} {C_{KM - 1}^k{{\left( { - 1} \right) }^k}{e^{ - \left( {1 + k} \right) {\lambda _{JR}}{x_3}}}}\), \({f_{{g_{{R_s}S1}}}}\left( {{x_4}} \right) = {\lambda _{RS1}}{e^{ - {\lambda _{RS1}}{x_4}}}\), and \({f_{{g_{{R_s}S2}}}}\left( {{x_5}} \right) = {\lambda _{RS2}}{e^{ - {\lambda _{RS2}}{x_5}}}\) into (79), we can obtain
From [32, Eq. (3.381.1)], \(\int _0^\infty {{e^{ - \beta /4x - \gamma x}}dx} = \sqrt{\beta /\gamma } {K_1}\left( {\sqrt{\beta \gamma } } \right)\), we obtain
By substituting (82) into (81), we complete the proof.
Appendix 6: Proof of Lemma 4
By substituting (54), (55), (56), and (57) into (62), we obtain
By substituting the PDFs of the eight RVs \({{g_{S1E\max }}}\), \({S2E\max }\), \({S1{R_s}}\), \({S2{R_s}}\), \({{g_{{J_s}{R_s}}}}\), \({{g_{{R_s}E\max }}}\), \({{g_{{R_s}S1}}}\), and \({{g_{{R_s}S2}}}\), into (83) and after some manipulations of (83), the Eq. (64) in Lemma 4 is obtained. This completes the proof.
Rights and permissions
About this article
Cite this article
Nguyen, S.Q., Kong, H.Y. Improving Secrecy Outage and Throughput Performance in Two-Way Energy-Constraint Relaying Networks Under Physical Layer Security. Wireless Pers Commun 96, 6425–6457 (2017). https://doi.org/10.1007/s11277-017-4485-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11277-017-4485-8