1 Introduction

Multi-layer Perceptron Neural Networks (MLP NNs) are widely used as soft computing instruments. These networks can help to solve non-linear problems. The MLP NNs are generally used to categorize the model, predict the data and approximate the functions [1–7]. Despite the applications, the distinguished capability to MLP NNs is that they learn [3]. Learning means that these networks can learn from an experience or an experiment just as human brain. This property (learning) is the essential part of NNs which may be divided into two types: supervised learning [8] and unsupervised learning [9]. For training the multi-layer artificial NNs (in most cases), optimized Back-Propagation (BP) [10] or standard algorithms [11] which are categorized under supervised learning methods are used. The BP algorithm is based on gradient and has drawbacks such as slow convergence [12] and application in small areas [13]. Therefore, it cannot be confidently used for practical purposes.

The final aim of learning in NNs is to find the best combination of their bias or weighed connections in such manner that we have minimum error in training the network and the test samples. Most of the errors of the MLP NN remain great for a long time in the training process and the learning algorithm directs it towards decreasing. This is common among gradient based learning processes such as the BP algorithm. Moreover the contingency of the BP algorithm is to a great extent dependent on the initial values of the learning rate and momentum. Improper values of these variables can even lead to the divergence of the algorithm. Numerous studies have been carried out to solve this problem with the BP algorithm [14]. However, sufficient optimization has not been obtained and each method has only had its side effects. Prior researches show that the heuristic algorithms can replace the gradient based learning algorithms [15], since the stochastic nature of these methods reduces the error percentage and possibility of trapping in local minimum compared to gradient based methods. But the problems of slow convergence speed and getting stuck in the local minimums still remain. We will try to solve these problems in the following section through using the chaotic maps.

Different evolutionary methods such as: gray wolf optimization [16], Particle Swarm Optimization (PSO) [17], Genetic Algorithm (GA) [18], Ant Colony Algorithm (ACO) [19], evolutionary strategies [20], and Biogeography-Based Optimizer (BBO) [1] have been used to train NNs. It has been proven through using the “no free lunch theorem” that the heuristic algorithms will not necessarily generate the best answers for the optimization problems [14, 21, 22]. On the one hand, this theorem and on the other hand the problems of the gradient based methods made researchers study the effects of different Evolutionary Algorithms (EAs) on the learning of MLP NNs and other different fields [23–27].

Regardless of the differences between the various meta-heuristic methods, they share a common feature of dividing the search process into “exploration” and “exploitation” stages [28, 29]. The exploration phase occurs when the algorithm tries to explore the reliable areas of the search space. The population undergoes sudden changes in this phase. Selection and recombination operators are executed in this phase. The exploitation phase is a phase in which the algorithms become contingent towards confident answers. The population undergoes small changes in this phase. The mutation operator occurs in this phase and in many cases there is no clear border between these two phases due to the random nature of the EAs. In other words, imbalance between these two phases leads to the algorithm getting stuck in the local minimum. A lot of studies have been carried out in order to improve the performance of the EAs through increasing the exploration and exploitation power. In this paper, BBO with Chaos (CBBO) will be used to train the MLP NN for classifying Sonar and other data sets.

This paper has been organized in a manner that the second section will introduce the MLP NNs. The third section discusses the overview of the BBO algorithm. Section 4 introduces the chaotic maps and applies them to the BBO algorithm. The method of applying the obtained CBBO method (as an evolutionary training algorithm) in MLP NN has been described in Sect. 5. The results will be discussed in Sect. 6 and finally the conclusion will be expressed in Sect. 7.

2 Multi-layer Perceptron Neural Network

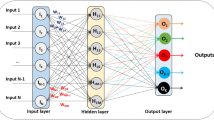
Figure 1 shows a MLP NN with two layers. R is the number of input nodes, S 1 is the hidden neurons and S 2 is the number of output neurons. As can be seen, there exist one-way connection between nodes in a MLP NN which is categorized under the feed-forward NNs family. The MLP NN outputs are calculated using the following equation:

$${\mathbf{n}}_{1} = {\mathbf{IW}} \times {\mathbf{P}} + {\mathbf{b}}_{1}$$
(1)

where \({\mathbf{IW}}\) is the connection weight matrix from the input nodes to the neurons of hidden layer, \({\mathbf{b}}_{1}\) is the neuron’s bias matrix (in hidden layer) and \({\mathbf{P}}\) is the node’s input matrix. Each hidden layer neuron’s output is calculated using a sigmoid function as given in Eq. (2):

Fig. 1
figure 1

A MLP NN with one hidden layer

Full size image
$${\mathbf{a}}_{1} = Sigmoid({\mathbf{n}}_{1} ) = \frac{1}{{1 + \exp ( - {\mathbf{n}}_{1} )}}$$
(2)

Final outputs after calculating the hidden nodes output can be defined as:

$${\mathbf{n}}_{2} = {\mathbf{LW}} \times a_{1} + {\mathbf{b}}_{2}$$
(3)
$${\mathbf{y}} = Sigmoid({\mathbf{n}}_{2} ) = \frac{1}{{1 + \exp ( - {\mathbf{n}}_{2} )}}$$
(4)

where \({\mathbf{LW}}\) is the connection weight matrix from the hidden layer to the output layer and \({\mathbf{b}}_{2}\) is the neuron’s bias matrix in the output layer. The most important parts of the MLP NNs are the connection weights and neuron’s biases. As one can see from above equations, the final output of the network is defined by connection weights and neuron’s biases. Training the MLP NN includes finding the best values for connection weights and neuron’s biases, so that the specific inputs result in desired outputs.

3 Biogeography-Based Optimizer Algorithm

The BBO algorithm was first proposed in 2008 by Simon and then developed by Seyedali Mirjalili in 2014 for optimization and classification task [1]. The main idea of this algorithm has been inspired by biology which discusses the spreading manner of animals and plants (in time and space). Different ecosystems (habitat or territories) will be examined based on emigration, immigration and mutation regarding this field of the paper. The evolution of ecosystems is the foundation of BBO algorithm with regard to different types of species and the effect of migration and mutation for obtaining a stable condition.

Like the GA, the BBO uses a number of search factors named “habitats”. These habitats are similar to chromosomes in the GA. The BBO algorithm considers each habitat as vector of habitants (like genes in the GA) which show the variables of the problem. Moreover the Habitat Suitability Index (HSI) is also defined for each habitat. High value of this index indicates having better conditions. The habitats are determined based on three main laws explained below at any given time [1]:

  1. I.

    Habitants residing at high-index habitats have a tendency to migrate to habitats with lower value of index.

  2. II.

    Habitants residing at low-index habitats have a tendency to attract migrants from habitats with high-index value.

  3. III.

    The habitats must change their habitants randomly without considering the value of their indexes.

This phenomenon creates a balance among different ecosystems in nature. In other words, nature has a tendency to improve the suitability of different environments. The BBO algorithm uses these concepts to improve the index of all the environments the results are used in exploiting a primary random solution for a specific problem.

The BBO starts through randomly selecting a series of habitats. Each habitat has n different habitants who are determined based on the variables of a specific problem. Moreover, each habitat has its own specific emigration, immigration and mutation rates which have been modeled from the places which are distinguished with regard to biology of the nature. Emigrating (\(\mu_{k}\)) and immigrating (\(\lambda_{k}\)) are defined as functions of the number of their habitants as below:

$$\mu_{k} = \frac{E \times n}{N}$$
(5)
$$\lambda_{k} = I \times \frac{1 - n}{N}$$
(6)

where n presents the number of the current habitants, N is the maximum permitted habitants which increases through the habitant suitability index (more suitable habitats, more habitants), E is the emigration maximum rate and I indicates the maximum rate of immigration [30]. Mutation is the third index of the BBO algorithm. It improves the exploitation capability of the BBO algorithm and preserves the variety of the habitats. This index is defined as Eq. (7):

$$m_{n} = M \times \left( {1 - \frac{{p_{n} }}{{p_{\hbox{max} } }}} \right)$$
(7)

In which M is the initial value of mutation which is defined by the user, p n is the probability of the n-th habitat undergoing mutation and p max is the maximum p n and is defined as Eq. (8):

$$p_{\hbox{max} } = \arg \hbox{max} \left( {p_{n} } \right)$$
(8)

We will introduce the chaotic maps in the following section and the manner of their application in improving the performance of the BBO algorithm.

4 Chaotic Maps for Improving the Biogeography-Based Optimizer Operator

The chaotic maps which have been used to improve the performance of BBO are explained in this section. Six chaotic maps have been used in this paper in accordance with Table 1 and Fig. 2. These chaotic maps are deterministic systems which have random behavior. In this paper, value 0.7 has been considered as the primary point of all the maps in accordance with Ref. [31]. As mentioned previously, three operators namely selection, migration and mutation operators are affected by the chaotic maps. We will explain them in the following section.

Table 1 Chaotic maps
Full size table
Fig. 2
figure 2figure 2

The chaotic maps and their pseudo-phase trajectories used in the paper

Full size image

4.1 Chaotic Maps for Selection

As it could be seen in Fig. 3, the habitats are selected for migration with probability equal to \(\lambda\). The chaotic maps are used to define this probability as shown in Fig. 4 [31].

Fig. 3
figure 3

Flowchart of the CBBO algorithm

Full size image
Fig. 4
figure 4

Chaotic selection

Full size image

4.2 Chaotic Maps for Migration

As shown in Fig. 3, migration after selecting the habitat will occur with probability equal to μ. We will use the chaotic maps as Fig. 5 in order to calculate this probability.

Fig. 5
figure 5

Chaotic migration

Full size image

Where C(t) is the value derivate from the chaotic map in the t-th iteration and x i shows the i-th habitant. Figure 5 indicates that the chaotic maps allow us to regulate the migration probability and consequently have migration with chaotic behavior.

4.3 Chaotic Maps for Mutation

The mutation probability is defined directly through chaotic maps as shown in Fig. 6.

Fig. 6
figure 6

Chaotic mutation

Full size image

In the following section, the CBBO will be first applied to a MLP NN and then it will be compared with PSO, GA, ACO, DE and BBO in the first stage. Different CBBO algorithms which use different chaotic maps are compared with each other in the following stage.

5 Training a Multi-layer Neural Network Using the CBBO Algorithm

CBBO algorithm will be applied to a MLP NN in this section for the purposes of finding the best combination of weighed connections and bias nodes in order to have the least amount of error. The general stages of training MLP by CBBO algorithm are shown in Fig. 7.

Fig. 7
figure 7

The general stages of CBBO algorithm for training the MLP NN

Full size image

5.1 Proposed Multi-layer Neural Network Structure

The vector method has been used to show the values of the weighed connections and bias nodes since we are not dealing with complex MLP NNs in this paper [32]. The Matlab toolbox will not be used in order to decrease the running time of the MLP NNs program. As an example of this coding method, the final vector of the MLP NN has been shown in Fig. 8 are brought into Eq. (9)

Fig. 8
figure 8

MLP NN with (N, 2N + 1, 1) structure

Full size image
$$habitat = \left[ {w_{11} w_{21} w_{31} \cdots w_{(2N + 1) \cdot N} W_{O1} W_{O2} W_{O3} \cdots W_{O(2N + 1)} b_{1} b_{2} b_{3} \cdots b_{2N + 1} } \right]$$
(9)

After displaying the MLP NN as habitat vector, it is essential to write an equation for computing the HSI (a suitable function) in order to evaluate each of them (the habitats).

5.2 Habitat Suitability Index (Fitness Function)

As mentioned previously the final aim of the learning methods is to train the NNs. The most important section of learning is the training process. Each training sample must include calculating the suitability index of all the habitats. In this paper, the HSI will be calculated through the Mean Squared Error method (MSE) and as Eq. (10).

$$E = \sum\limits_{k = 1}^{q} {\frac{{\sum\nolimits_{i = 1}^{m} {\left( {o_{i}^{k} - d_{i}^{k} } \right)^{2} } }}{q}}$$
(10)

In which q is the number of the training samples, m is the number of outputs, \(d_{i}^{k}\) is the desirable output from the i-th input when the k-th learning sample is applied to the input. For instance the HSI for the i-th habitat is calculated as Eq. (11):

$$HSI(Habitat_{i} ) = E\left( {Habitat_{i} } \right)$$
(11)

Learning in MLP NN can be formulated in two stages through using CBBO algorithm. The proposed diagram block has been shown in Fig. 7. As it could be seen in this figure, the suggested method starts with generating random sets from MLP NNs based on the number of the defined habitats. Each MLP NN corresponds to one habitat and each weight or bias corresponds to the habitants of that habitat. After the first step the MSE of each MLP NN is calculated through Eq. (10). Equations (5), (6), (9), (10) and (11) are used in the following step to update the emigrating, immigrating and mutation through the use of the chaotic maps. Then, the MLP NNs are combined based on emigrating and immigrating of the habitat. Afterwards each MLP NN undergoes change based on the mutation rate of its habitat. Selecting the elites is the last step of the proposed method in such manner that the best MLP NNs are protected in order to prevent destructions caused by the migration and mutation operators in the succeeding generation. These stages (from computing the MSE to selecting the elite) continue until the finishing conditions are met.

In order to see how the suggested algorithm works a conceptual image is shown in Fig. 9 regarding the migration occurring among the habitats in order for a MLP NN to learn through using the CBBO algorithm. Habitat 3 is more suitable (has the minimum value of HSI which indicates that the MSE is minimum for all the test samples) that habitats 1 and 2 in this image.

Fig. 9
figure 9

Migration between the habitats for learning of an MLP NN

Full size image

As it could be seen habitat 1 has the maximum amount of emigration while habitat 3 has the maximum immigration and so it accepts more habitants (weights and biases) in comparison with the other habitats.

Table 2 The set of data used in the test
Full size table

6 Explaining the Material and the Results

In this section, the CBBO algorithm will be measured through four data sets of available data in Table 2. In order for the evaluation to be comprehensive, these data have different dimensions and a number of examples. In each test, the efficiency of the CBBO algorithm will be compared with that of the other EAs regarding classification accuracy, convergence speed, and the probability of getting stuck in the local minimums. The comparing algorithms include: BBO, PSO, GA, ACO, DE. The CBBO algorithms will be divided and named with regard to the type of the used chaotic map and to which selection, migration, and mutation operators have these maps been applied to. For instance if the circle map has been used to correct the selection operator we will name that algorithm CBBO1. This naming style has been thoroughly shown in Table 3.

Table 3 Dividing the CBBO algorithms with regard to chaotic maps and the corrected operator
Full size table

6.1 Regulating the Parameters and Conducting the Experiment

The essential parameters and the primary values have been presented in Table 4. Each network was tested 10 times. The average result of trained NN will be computed and used for comparison. The classification rate and the test error percentage are two criteria used for comparing the mentioned algorithm. All the algorithms stop when the maximum iteration reaches 250 in order to compare relatively well. The convergence of the results will be eventually examined to carry out a comprehensive comparison. Since there is no standard for selecting the number of the hidden nodes, the suggestion proposed in [1] and Eq. (12) will be used based on the structure of the MLP NN in order to classify the sets of data.

Table 4 The primary parameters of the algorithms
Full size table
$$H = 2 \times N + 1$$
(12)

In this equation, N is the number of inputs and H shows the number of the hidden nodes. It is worth mentioning that the simulations were done with a personal computer with a 2.3 GHz CPU, 4 GB RAM and in Matlab software space. The results of the simulations have been shown in Fig. 10.

Fig. 10
figure 10figure 10figure 10

a Comparing the accuracy of classifying and convergence speed of the CBBO algorithm and criterion algorithms on Iris data set. b Comparing the classification accuracy and the convergence speed of different CBBO algorithms on the Iris data set. c Comparing the classification accuracy and convergence speed of the CBBO algorithm with criterion algorithms on Lenses data set. d Comparing the classification accuracy and convergence speed of different CBBO algorithms on Lenses data set. e Comparing the classification accuracy and convergence speed of CBBO algorithm with criteria algorithms on breast-cancer data set. f Comparing the classification accuracy and convergence speed of different CBBO algorithms on breast-cancer data set. g Comparing the classification accuracy and convergence speed of CBBO algorithm with criteria algorithms on Sonar data set. h Comparing the classification accuracy and convergence speed of different CBBO algorithms on Sonar data set

Full size image

As it could be seen in Fig. 10 that CBBO algorithm shows much better results in comparison with classic algorithms regarding classification accuracy and convergence speed in all cases. The weak results of the DE, ACO and PSO are also caused by the natural nature of these algorithms. These algorithms have no operator to suddenly change the solution of the problem and as a result they get stuck in the local minimums. Moreover, the ACO algorithm uses the pheromone matrix which increases the exploitation and learning ability of the algorithm this is considered an advantage in integrated problems, but it also increases the chances of getting stuck in local minimums. PSO are to a large extent dependent on the manner of the initial distribution of the particles and their primary stimuli based on the attraction between them. In case a large number of particles get stuck in the local minimums, the algorithm will slightly prevent the other particles from getting stuck.

The reason why the CBBO algorithm is more efficient in comparison with the GA in most cases is the different rate of emigration and immigration in each of habitats. The CBBO algorithm has two rates (emigration and immigration) for each of its habitat while the GA has one total regeneration rate for all the habitats of its population. This causes evolutionary behavior and a different recognition power. We could state in short that the ability to explore is very important in the issue of training a MLP NN. Therefore the random and sudden search steps are essential for the purposes of preventing getting stuck in the local minimums, when solving complex problems through using MLP NNs. Regarding the effect of the chaotic maps on the performance of CBBO algorithm, with regard to Fig. 10, it could be concluded that applying chaotic maps to the selection and migration operators dramatically improves the convergence speed of the algorithm in most cases in comparison with the other methods. This is because using these maps improves the exploration power of the algorithm and the search space is better explored. This better exploration of the search space makes the convergence speed much better and prevents the algorithm from getting stuck in the local minimums. In other words, using the chaotic migration in selection operators improves the performance of the CBBO algorithm. Of course, using the chaotic migration operators and the mutation operator also improve the results in comparison with the classic BBO algorithm, but their influence is not as much as that of the chaotic migration and selection operators.

7 Conclusion

A MLP NN is trained through the use of CBBO algorithm in this paper. Four data sets with different sizes were used to examine the effect of the CBBO algorithm on training MLP NNs. The obtained statistical results were compared with the results obtained from the PSO, GA, ACO, DE and BBO to stabilize the performance. The results indicate that with regard to the chaotic operators used in the CBBO algorithm and the exploration ability increasing in these operators, this algorithm is sufficiently capable of preventing from getting stuck in the local minimums in comparison with the criterion algorithm. Moreover, the superior efficiency of the CBBO algorithm in training the MLP NN can be seen based on the accuracy of the objectives classification results and the convergence speed from the obtained results.