1 Introduction

The genuine innovation of simulating the neurons in the human brain is represented in the intelligent mathematical model of artificial neural networks (ANN). The connection between neurons empowers the biological system to manage the body’s behavior through signal communication [1]. The artificial intelligence research community utilizes the neurons’ biological behavior as an essential part of solving machine learning problems such as classifications, clustering, feature extractions, regressions, and predictions. The base ANN has been categorized into different types due to their learning process such as convolutional neural network [2], feedforward neural network (FNN) [3], spiking neural networks (SNN) [4], recurrent neural network (RNN) [5], and radial basis function (RBF) network [6]. Learning is the capability of gaining knowledge from experience and training. There are two types of learning: supervised where the ANN work is assisted by outdoor feedback and unsupervised where ANNs depend totally on indoor feedback.

The learning process in each type of ANN is different. The following is a brief explanation of this process in the most common ANN structures [7, 8]. The FNN obtains the information using the input layer. Then, the hidden layer processes the inputs and produces the desired result in the output layer. Each layer attempt to learn certain weights to map the input into the output. This type of network does not have feedback connections to be returned to the model. The modification of FNN to have a loop on each hidden layer would develop the RNN. This loop restriction guarantees the capturing of sequential information in the input data. Additionally, the RNN shares the parameters across different time steps. Lastly, the CNN utilizes filters (i.e., kernels) to obtain from the input the relevant features by applying the convolution operation. The CNN automatically learns the filters which assist in wresting relevant features from the input data. As a result, a feature map is produced.

One of the most popular FNN is multi-layer perceptron (MLP). It is widely used to solve several types of optimization problems such as feature selection [9], classification [10, 11], predictions [12, 13], regressions [14], etc. The success of the learning process in MLP depends on the initial value of its parameters (i.e., weights and biases). These two parameters are optimized during the learning process using gradient decent optimization algorithm. However, this type of optimizer has two main shortcomings [15]: slow convergence and local optima. Therefore, several metaheuristic-based algorithms are adapted for MLP such as artificial bee colony [16], cuckoo search algorithm [17], gravitational search algorithm [18], grey wolf optimizer [19, 20], butterfly optimization algorithm [21], fish swarm algorithm [22], salp swarm algorithm [23, 24], glowworm swarm optimisation [25], genetic algorithm [26], grasshopper optimization algorithm [27, 28], dragonfly algorithm [16], krill herd algorithm [29], monarch butterfly optimization [30], social spider optimization algorithm [31], ant colony optimization [32], bat algorithm [33], biogeography based optimization [34], lightning search algorithm [35], ant lion optimizer [36], organisms search algorithm [37], and whale optimization algorithm [15].

Generally speaking, metaheuristic-based algorithms are general optimization frameworks which can be used to minimize/maximize an optimization problem using smart operators with the ability to navigate several niches in the search space [38]. The behavior of its smart operators is controlled by tuning or adapting parameters that affect the balance between exploration and exploitation processes. It is conventionally agreed that the metaheuristic-based algorithms can be classified into either population-based or local search algorithms due to their number of initial solution(s) [39]. The local search algorithms begin with a single solution. Iteratively, that solution is locally improved using the neighboring move strategy until the local minima is obtained. Local search algorithms are very efficient in navigating the niche of the initial solution, but it cannot explore several niches at the same time.

Oppositely, the population-based algorithms, such as evolutionary algorithms (EAs) and swarm intelligence, are initiated with several solutions stored in the population. Iteratively, these solutions are recombined and mutated until the population is maturely or prematurely converged. These types of algorithms can explore several search space niches because of their operators, but they cannot dig deeply in each converged niche as they can stuck in local optima [38]. Therefore, a new type of algorithm has recently proved its efficiency in tackling the optimization problem which is hybrid metaheuristic (or memetic algorithm (MA)) [40, 41].

Memetic Algorithm (MA) is the recent growing trend in evolutionary computation fields. In MA, the local search algorithm is hybridized as an operator in the iterative loop of the population-based algorithm. The main motivation behind this hybridization is to complement the advantages of both exploration and exploitation capabilities. The local search operator speeds up the convergence by concentrating on good solutions than mutating the solutions [42, 43]. The behaviour of the population-based algorithm in MA is inspired by Darwinian principles of natural selection as a gene notation. The meme notation in MA is introduced by Dawkins [44] which reflects the cultural behavior of the local search algorithm. Gene and meme units play a vital role in biological and cultural transmission. It is noted that the majority of the previous work in the training process of MLP relies on using the original version of the metaheuristic-based algorithm. Since the MLP performance substantially depends on the optimal value of its initial parameters which is refined in the later training stages. The original metaheuristic algorithms can be boosted by MA concepts.

This paper studies the effect of different MA versions as an efficient trainer to the MLP. The MLP is chosen as an efficient version of NN where this model applies feedforward to the NN. The structure of MLP is simple, easy to design, and its speed allows its fast evaluation using the proposed optimizer. Furthermore, this framework can be generalized to other NN structures. In this case, the MA algorithm enables finding the optimal configuration of the MLP to boost its performance by producing more accurate results. The following are the main contributions of the current work:

  • Six MA versions were introduced which are Hybrid Flower Pollination Algorithm (HFPA), Hybrid Salp Swarm Algorithm (HSSA), Hybrid Crow Search Algorithm (HCSA), Hybrid Grey Wolf Optimizer (HGWO), Hybrid Particle Swarm Optimization (HPSO), and Hybrid JAYA algorithm (HJAYA).

  • The original versions of the six population-based algorithms are used as a gene unit to refine the global search while the Adaptive \(\beta\)-hill climbing (A\(\beta\)HC) [45] is used as a meme unit for the local search process.

  • The A\(\beta\)HC is invoked in the iterative loop of any MA version with \(B_r\) probability where \(B_r \in [0,1]\). The higher value of \(B_r\) probability leads to higher usage of local improvement (A\(\beta\)HC).

  • The mean square error (MSE) is utilized to measure the results of the proposed MA versions where the MLP is used for classification purposes.

For evaluation purposes, fifteen classification datasets with different levels of complexity are used. Initially, the effect of \(B_r\) on the behavior of the proposed MA versions is studied. The comparative analysis is also conducted between the results of MA versions as well as those of their base algorithms. Interestingly for any MA version, the results produced are mostly better than those produced by the original algorithms. Furthermore, HGWO was able to produce the best overall results for almost all datasets used in comparison with the other proposed MA versions. In conclusion, the MA is a better choice to train MLP to produce results with high accuracy.

The remaining sections of this paper are arranged in the following order: the background about MLP and A\(\beta\)HC is given in Sect. 2. The proposed MA versions are thoroughly discussed in Sect. 3. The dataset description and the results discussions are given in Sect. 4. Finally, the conclusion and possible future expansions are described in Sect. 5.

2 Research background

The background section includes the basic knowledge about FNNs with a special concern for its variant used in this research (i.e., Multilayer perceptron (MLP)). Thereafter, the fundamentals of the adaptive \(\beta\)-hill climbing optimizer which is the local search algorithm used in the proposed MA versions are discussed.

2.1 Feedforward neural networks

Feedforward neural networks (FNN) are supervised learning algorithms that simulate the fact that the human brain is organized into a form of network architecture in which neurons are located in the layers, where there is a direct connection between each layer and the next one. In FNN structure design, the neurons are interconnected and grouped in three layers. The first layer, namely the input layer, comprises a set of neurons where it is equal to the number of input features in training data. The middle layer is known hidden layer and the last layer is known as the output layer that maps the predicted class labels in a form of output neurons in the FNN network [46].

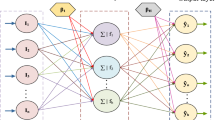
Multilayer perceptron (MLP) is a variant of the FNN model, where its network architecture is organized by interconnected neurons distributed in the layers. The information is transferred through these connections in one way. An example of MLP network structure embeds of the single hidden layer is shown in Fig. 1. MLPs mathematical model is constructed from three parameters: input data, weights, and biases. These parameters are fed into three equation steps to compute the output of MLPs as follows:

Fig. 1
figure 1

Network structure of MLPs with only single one hidden layer

Full size image
  1. (1)

    Initially, for each input in MLPs network structure, a weighted sum score is linked with them, where it is computed by using Eq. 1.

    $$\begin{aligned} S_{j} = \sum _{i=1}^{n} (w_{ij}.X_{i}) - \beta _{j} , j= 1,2, ... , h \end{aligned}$$
    (1)

    where n refers to the number of input nodes in the network, \(w_{ij}\) refers to the weight vector that connects the input node i with hidden node j, \(X_{i}\) is the ith input, and \(\beta _{j}\) is the bias of the jth hidden node.

  2. (2)

    In this step, the weighted vector output is fed into the activation function, called Sigmoid, and then the new output vector is transferred to the next layer as follows.

    $$\begin{aligned} S_{j} = Sigmoid (S_{j}) = \frac{ 1 }{ 1+ exp(-S_{j})}, j=1,2, ... h \end{aligned}$$
    (2)

    where \(S_{j}\) is the weighted sum score is the node j while h is the number of neurons in the hidden layer.

  3. (3)

    Eventually, the final output of the network is calculated as follows:

    $$\begin{aligned} \hat{y}_{k}= \sum _{i=1}^{m} w_{kj}f_{i} + b_{k} \end{aligned}$$
    (3)

where \(w_{jk}\) refers to the connection weight from hidden node j to the output node k, and \(b_{k}\) refers to the bias of the output node k.

It should be noted that the most significant factors in the estimation of the final output in MLPs are weight and bias vectors as demonstrated in Eqs. 1 and 3. Finding the proper values of weights and biases vectors play a vital role in generating a robust and accurate MLPs model [20].

2.2 Adaptive \(\beta\)-hill climbing optimizer

The \(\beta\)-hill climbing (\(\beta\)HC) optimizer is a recent local search-based algorithm proposed by Al-Betar [47]. Since its establishments, \(\beta\)HC has been successfully tailored to tackle several optimization algorithms such as feature selection [48, 49], classification problems [50], economic dispatch problems [51], examination timetabling problems [52], multiple-reservoir scheduling [53], generating substitution-Boxes [54], and sudoku game [55]. In specific, the \(\beta\)HC is hybridized with other population-based algorithms to improve their exploitation power. For example, the \(\beta\)HC is hybridized with bat algorithm for gene selection in [56], while it hybridized with cuckoo search for test optimization function in [57], and hybridized with polynomial harmony search algorithm [58]. Similarly, the \(\beta\)HC is hybridized with salp swarm optimization for text documents clustering problem [59]. The \(\beta\)HC is integrated within the flower pollination algorithm for person identification using EEG channel selection [60]. The \(\beta\)HC is hybridized with the artificial bee colony algorithm for test optimization functions in [61]. In another study, the adaptive \(\beta\)HC is combined within the grey wolf optimization for solving the non-convex economic load dispatch problem in [62]. The adaptive \(\beta\)HC is integrated within slime mould algorithm for solving numerical optimization problems [63], Finally, adaptive \(\beta\)HC is hybridized with salp swarm optimization for stock market prediction [64].

The main reasons behind using \(\beta\)HC optimizer are their features in which it is simple in concepts, easy-to-use, powerful in local refinement, speedy in convergence, and powerfully avoiding local optima. \(\beta\)HC optimizer has three main operators to improve the solution \(\mathcal {N}\)-operator, \(\beta\)-operator, and \(\mathcal {S}\)-operator. The first operator is responsible for neighbouring search controlled by \(\mathcal {N}\) parameter where \(\mathcal {N} \in [0,1]\). The second operator is responsible for the random search which is controlled by \(\beta\) parameter where \(\beta \in [0,1]\) (i.e., similar to a uniform mutation in Genetic Algorithm). The last operator is the greedy selection process to replace the current solution with the new one, if better. Recently, An adaptive version of \(\beta\)HC optimizer is proposed to yield a parameter-free \(\beta\)HC [45]. In Adaptive \(\beta\)HC (i.e., A\(\beta\)HC), the two parameters of \(\beta\)HC optimizer (i.e., \(\mathcal {N}\) and \(\beta\)) are updated during the search. Algorithm 1 shows the pseudo-code of A\(\beta\)HC.

As illustrated in the Algorithm 1 in the initialization step of A\(\beta\)HC, the values of \(\beta _{min}=0.001\), \(\beta _{max}=0.6\), and \(K=20\) parameters are assigned as suggested in [45] to determine how the parameters will be updated during the search. The initial solution \({{\varvec{x}}}=(x_1,x_2,\ldots , x_d)\) is generated randomly such as \(x_{i}=lb_i+(ub_i-lb_i)\times U(0,1)\), \(\forall i=1,2, \ldots , d\) where \(ub_i\) and \(lb_i\) are the upper and lower bound of variable \(x_i\), respectively and U(0, 1) generates a random uniform value between 0 and 1. The ultimate objective is to minimize \(f({{\varvec{x}}})\) such that \({{\varvec{x}}} \in {{\varvec{X}}}\) where \(X \in [{{\varvec{lb}}},{{\varvec{ub}}}]\). The three operators of improvement step in A\(\beta\)HC can be thoroughly discussed as follows:

  • \(\mathcal {N}\)-operator: The values of the current solutions \({{\varvec{x}}}\) is modified by moving to its neighbouring solution \({{\varvec{x}}}'\) as follows: \(x'_i = x_i \pm U(0,1) \times \mathcal {N}(t)\) where \(\mathcal {N}(t)\) is the distance bandwidth in iteration t. In A\(\beta\)HC, \(\mathcal {N}(t)\) is adapted during searching as provided in Eq. (4).

    $$\begin{aligned} \mathcal {N}(t) = 1 - C(t) \end{aligned}$$
    (4)

    Note that C(t) is calculated at time t as shown in Eq. (5).

    $$\begin{aligned} C(t) = \frac{t^{\frac{1}{K}}}{\text {Max\_t}^{\frac{1}{K}}} \end{aligned}$$
    (5)

    where K has a constant value reduced gradually to a value close to 0. \(\text {Max\_t}\) is the maximum iterations.

  • \(\beta\)-operator: The value of the decision variable \(x_i\) is randomly regenerated such as \(x_{i}''=lb_i+(ub_i-lb_i)\times U(0,1)\) with a probability of \(\beta\) where \(\beta \in [0,1]\). In A\(\beta\)HC, this parameter is automatically adapted during the improvement step as formulated in Eq. (6).

    $$\begin{aligned} \beta (t) = \beta _{min} + t \times \frac{\beta _{max}-\beta _{min}}{\text {Max\_t}} \end{aligned}$$
    (6)

    where \(\beta (t)\) represents the \(\beta\) value at iteration t. \(\beta _{min}\), \(\beta _{max}\) are the minimum and maximum value of \(\beta\) set in advance, respectively.

  • \(\mathcal {S}\)-operator: The selection operator works in a greedy strategy where the neighbouring solution \({{\varvec{x}}}''\) replaces the current one \({{\varvec{x}}}\), if fitter (i.e., (\(f({{\varvec{x}}}'')\le f({{\varvec{x}}})\))).

figure h

3 MA versions for MLP training

As aforementioned, the MLP has two main dilemmas affect its performance: slow convergence and local optima. The is occurred due to the stochastic configuration of its parameters (i.e., weight and biases). In order to find the proper values of its initial parameters, the MA versions for MLP are proposed in this section.

In general, the population-based algorithms have a sequence of commonly known steps: the first step is the initialization step where the optimization problem shall be defined in a Genotype form. The objective function to evaluate the solution, as well as the value range for each variable, shall be defined. Furthermore, the population initialization where a set of solutions are randomly generated, and their evaluation functions are computed. The second step is the improvement step where iteratively, the population undergoes refinements using different operators controlled by tuned or adapted parameters until a stopping criterion is met. The final step is collecting and filtering the final results where the genotype representation of the best-obtained solution is transformed to phenotype representation. These steps, as visualized in Fig. 2, are thoroughly discussed for each MA version proposed with the application as a trainer for MLP as follows:

Fig. 2
figure 2

The Steps of the proposed MA versions

Full size image

3.1 Initialization step

The MLP as a version of FNN is mostly used to tackle the classification problems. Each classification solution is normally represented as a vector of weights and biases such as \({{\varvec{x}}}=(x_1,x_2,\ldots ,x_d)\) where the variables in the classification solution \({{\varvec{x}}}\) is divided into two consecutive groups: weights \({{\varvec{w}}}=(w_1,\ldots ,w_n)\) of n weights and biases \({{\varvec{b}}}=(b_1,\ldots ,b_m)\) of m biases in which \(d=n+m\). There is no direct formula for calculating the number of hidden layers in MLP [65]. As a result, the MA-MLP applied a fixed structure MLP [15, 66] based on the classification data, the value of n and m can be calculated as in Eq. (7):

$$\begin{aligned} \begin{aligned} h = 2 \times K + 1 \\ n = K \times h + h \times o \\ m = h + o \end{aligned} \end{aligned}$$
(7)

Where the number of neurons h in MLP should be calculated based on the number of features K in the classification data. The number of output o resulting from MLP should be determined.

The objective function used to evaluate the classification solution is the mean square error (MSE) function. The MSE computes the distance between the actual classification value (i.e., y) and the predicted classification value (i.e., \(\hat{y}\)) found by MA-based MLP algorithm of all training instances. MA-based MLP will iteratively minimize the MSE based on the optimized weight-biases vector represented by the classification solution. In Eq. (8).

$$\begin{aligned} MSE = \sum _{t=1}^{T} \frac{\sum _{i=1}^{o}{(y^t_i- {\hat{y}}^t_i)^2}}{T} \end{aligned}$$
(8)

where T refers to the total number of used instances in the training dataset. The small t is the training instance. The ultimate objective function is formulated in Eq. (9).

$$\begin{aligned} \min f({{\varvec{x}}}) = MSE \end{aligned}$$
(9)

3.1.1 Initialize parameters of MA versions

In the initial step of the population-based algorithm, there are common algorithmic parameters which are population size (N) and the maximum number of iterations \(M_{t}\). The control parameters are normally different from one algorithm to another. The population-based algorithm used are FPA, SSA, CSA, GWO, PSO, and JAYA. Note that most of the control parameters of the population-based algorithms used in the proposed MA versions are adaptively updated during runs such as FPA, SSA, GWO, and JAYA where no control parameter shall be initialized. There are two population-based algorithms used in MA versions that should tune their parameters such as Awareness probability (AP) and Flight length (fl) in the CSA and intra-weight (w), acceleration coefficients (\(c_1\) and \(c_2\)) in PSO. For all MA versions, there is a control parameter called \(B_r\) where \(B_r \in [0,1]\) determines the volume of invoking the A\(\beta\)HC in the improvement loop of the population-based algorithm used.

3.1.2 Initialize the population

The population-based algorithms are normally initiated with a population of random solutions. These solutions are stored in a matrix of size \(d \times N\) as shown in Eq. (10). In MAP matrix, Each row represents a solution while each column represents a decision variable. The value range of each decision variable \(x_i \in [lb_i,ub_i]\) where \(lb_i\) is the lower bound and \(ub_i\) is the upper bounds of variable \(x_i\) (i.e., MLP weights and biases acceptable range).

$$\begin{aligned} {{{{\varvec{MAP}}}}}=&\left[ \begin{matrix} x^{1}_{1} &{} x^{1}_{2} &{} \cdots &{} x^{1}_{d} \\ x^{2}_{1} &{} x^{2}_{2} &{} \cdots &{} x^{2}_{d} \\ \vdots &{} \vdots &{} \cdots &{} \vdots \\ x^{N}_{1} &{} x^{N}_{2} &{} \cdots &{} x^{N}_{d}\\ \end{matrix} \right] . \end{aligned}$$
(10)

The objective function values of the whole populations are calculated using Eq. (9). Among the solutions stored in MAP, the best solution (i.e., \({{\varvec{x}}}^{b}\)), the worst solution (i.e., \({{\varvec{x}}}^{w}\)) are usually defined and updated during the improvement step. In PSO, the local best (i.e., \({{\varvec{x}}}^{lb}\)) and global best (i.e., \({{\varvec{x}}}^{gb}\)) are distinguished in which \({{\varvec{x}}}^{lb}\) is defined every iteration while \({{\varvec{x}}}^{gb}\) is the overall best solution found in the whole iterations. In GWO, the three best solutions are defined where the best solution is \({{\varvec{x}}}^{\alpha }\), second-bast is \({{\varvec{x}}}^{\beta }\), and third-best is \({{\varvec{x}}}^{\delta }\).

3.2 Improvement step

In general, each population-based algorithm has an improvement loop based on intelligence operators guided by control parameters. This is an iterative process where the current population is updated. The main difference between the population-based algorithms is the behaviour of the operators during their exploration and exploitation processes. Therefore, the operators in the improvement loop of population-based algorithms used in the proposed MA versions and the A\(\beta\)HC as a new operator are discussed in the following subsection.

3.2.1 The improvement step in hybrid flower pollination algorithm (HFPA)

Yang [67] proposed a new algorithm inspired by the plants blooming behavior which is called flower pollination algorithm (FPA). In FPA, there are three essential operators to update each solution. In the proposed HFPA, each generated solution is passed to A\(\beta\)HC algorithm as a new local refinement operator with a probability of \(B_r\). The flowchart of HFPA is given in Fig. 3. The operators of HFPA are discussed as follows:

Fig. 3
figure 3

Flowchart of the proposed HFPA

Full size image

  • Operator#1: Global Search (biotic)

    In each iteration (say t), any solution \({{\varvec{x}}}^i (t)\) in the population will be updated using biotic operator with probability of p as formulated in Eq. (11)

    $$\begin{aligned} {{\varvec{x}}}^i(t+1)= {{\varvec{x}}}^i(t) + L({{\varvec{x}}}^{gb}-{{\varvec{x}}}^i(t)) \end{aligned}$$
    (11)

    Note that the \({{\varvec{x}}}^i(t)\) represents the solution vector \({{\varvec{x}}}^i\) at iteration t. The best solution in the current iteration is \(x^{gb}\). The L parameter identify the step size. In order to mimic the step size, the Levy distribution is modelled in Eq. (12).

    $$\begin{aligned} L\sim \frac{\lambda \Gamma (\lambda )sin(\pi \lambda /2)}{\pi }\frac{1}{s^{1+\lambda }}, (s>> s_0 > 0) \end{aligned}$$
    (12)

    where L >0, and \(\Gamma (\lambda )\) is the standard gamma function, and \(s>0\) is the big steps that help in reaching the desired distribution. Note that the commonly used \(\lambda\) value is 1.5 [68].

  • Operator#2: Local Search of FPA (abiotic)

    With probability range of \(1-p\), each solution \({{\varvec{x}}}^i(t)\) is updated using abiotic operator as shown in Eq. (13).

    $$\begin{aligned} {{\varvec{x}}}^i(t+1)={{\varvec{x}}}^i(t) + \epsilon ({{\varvec{x}}}^j(t) - {{\varvec{x}}}^k(t)) \end{aligned}$$
    (13)

    where \({{\varvec{x}}}^j(t)\) and \({{\varvec{x}}}^k(t)\) are two selected randomly neighbouring solutions to the current solution. The main motivation behind abiotic operator is to emulate the restricted neighborhood of the flower constancy. \(\epsilon\) is randomly selected from the range [0,1].

  • Operator#3: A\(\beta\)HC local search

    To boost the exploitation capability of HFPA, each solution generated by the original operator of FPA is passed with a probability of \(B_r\). The discussion of A\(\beta\)HC is mentioned in Sect. 2.

  • Operator#4: Update population

    Each updated solution \({{\varvec{x}}}^{i}(t+1)\) is evaluated to confirm if it is fitter than its current solution \({{\varvec{x}}}^{i}(t)\) to be replaced such as \({{\varvec{x}}}^{i}(t)= {{\varvec{x}}}^{i}(t+1)\) where \(f({{\varvec{x}}}^{i}(t+1))\le f({{\varvec{x}}}^{i}(t))\).

3.2.2 The improvement step in hybrid salp swarm algorithm (HSSA)

The salp swarm algorithm (SSA) is a population-based technique introduced to simulate the salp swarming as a unique fish behaviour in which the salps move in the sea in form of a transparent barrel-shaped body [69]. In the original version of SSA, there are three essential operators to reconstruct each solution in the population (i.e., leader rule, follower rules, and Update population). In the proposed HSSA, each reconstructed solution is passed to A\(\beta\)HC algorithm as a new local refinement operator. The flowchart of HSSA is given in Fig. 4. These four operators are discussed as follows:

Fig. 4
figure 4

Flowchart of the proposed HSSA

Full size image

  • Operator#1: Leader rule

    The global best solution (i.e., \({{\varvec{x}}}^{gb}\)) is used to generate the decision variables of the group leader solution (i.e., \({{\varvec{x}}}^{1}\)) in which each decision variable ( \(x_i^1\) ) is generated as shown in Eq. (14)

    $$\begin{aligned} x_i^1 \leftarrow {\left\{ \begin{array}{ll} x^{gb}_i+r_1((ub_i-lb_i) r_2+lb_i) &{}r_3\ge 0.5 \\ x^{gb}_i-r_1((ub_i-lb_i) r_2+lb_i) &{}r_3< 0.5 \end{array}\right. } \end{aligned}$$
    (14)

    where \(x^{gb}_i\) is the decision variable i value in the global best solution. \(r_2\) and \(r_3\) values are two random values within the range [0,1]. The value of \(r_1\) is calculated using Eq. (15) which used to find the suitable trade-off between exploration and exploitation.

    $$\begin{aligned} r_1=2e^{-\left( \frac{4t}{M_{t}}\right) ^2} \end{aligned}$$
    (15)

    Recall that in Eq. (15), t is the current iteration while \(M_{t}\) is the maximum number of iteration.

  • Operator#2: Follower rules

    In this operator, the other solutions in the population are called followers. The decision variable values of the follower solutions are updated based on updated Newton’s law of motion as shown in Eq. (16).

    $$\begin{aligned} x^i_j (t+1)=\frac{1}{2} \left( x^i_j(t)+x^{i-1}_{j}(t)\right) \end{aligned}$$
    (16)

    where \(i \ge 2\) and \(x^i_j(t)\) shows the solution \({{\varvec{x}}}^i\) follower in jth dimension.

  • Operator#3: A\(\beta\)HC local search

    In order to boost the exploitation capability of HSSA, each solution generated by the original operator of SSA is passed with a probability of \(B_r\). The discussion of A\(\beta\)HC is given in Sect. 2.

  • Operator#4: Update population

    Each solution \({{\varvec{x}}}^{i} (t)\) is replaced by updated solution \({{\varvec{x}}}^{i}(t+1)\), if better (i.e., \(f({{\varvec{x}}}^{i}(t+1))\le f({{\varvec{x}}}^{i}(t))\)).

3.2.3 The improvement step in hybrid crow search algorithm (HCSA)

Crow Search Algorithm (CSA) is a population-based algorithm that imitates the natural phenomenon where the crows keep their excess food in hiding places in which the food is retrieved when needed [70]. In the original version of CSA, there are two essential operators to reconstruct each solution in the population (i.e., generate a new position and update the population). In the proposed HCSA, each reconstructed solution is passed to A\(\beta\)HC algorithm as a new local refinement operator. The flowchart of HCSA is given in Fig. 5. The HCSA operators will be discussed as follows:

Fig. 5
figure 5

Flowchart of the proposed HCSA

Full size image

  • Operator#1: Generate new positions

    In order to update the position of the solutions in the current population, the Eq. (17) is utilized. Two parameters are used to control the CSA (i.e., AP and fl). The parameter AP is used to control the updating positions of the current solution based on either neighbouring solution or generating a random solution (i.e., \({{\varvec{x}}}_r\)). The parameter AP is normally initialized with a set of values as many as population size (N) which takes very small values between 0 and 1. In most cases, \(AP=0.05\). The parameter fl determines the effect of local search or global search. large values of fl leads more to exploration while small value of fl leads to exploitation. As shown in Eq. (17), for any solution \({{\varvec{x}}}^{i}\), a random solution \({{\varvec{x}}}^{k}\) from the population is selected. The updated positions are affected by the different between the current solution \({{\varvec{x}}}^{i}\) and the random solution \({{\varvec{x}}}^{k}\).

    $$\begin{aligned} {{\varvec{x}}}^{i}(t+1) = {\left\{ \begin{array}{ll} {{\varvec{x}}}^{i}(t) +r_1 \times fl^{i}(t) \times ({{\varvec{x}}}^{k}(t) - {{\varvec{x}}}^{i}(t)) &{} r_2 \ge AP^{i}(t) \\ {{\varvec{x}}}_r &{} r_2 < AP^{i}(t) \end{array}\right. } \end{aligned}$$
    (17)

    Note that \(r_1\) and \(r_2\) are two values generated from a uniform random distribution between 0 and 1.

  • Operator#2:A\(\beta\)HC local search

    In order to boost the exploitation capability of HSSA, each solution generated by the original operator of SSA is passed with a probability of \(B_r\). The discussion of A\(\beta\)HC is given in Sect. 2.

  • Operator#3:update the population

    Each solution \({{\varvec{x}}}^{i} (t)\) is replaced by updated solution \({{\varvec{x}}}^{i}(t+1)\), if better (i.e., \(f({{\varvec{x}}}^{i}(t+1))\le f({{\varvec{x}}}^{i}(t))\)).

3.2.4 The improvement step in hybrid grey wolf optimizer (HGWO)

Grey Wolf Optimizer (GWO) is a population-based algorithm stimulated by how grey wolf packs lead and hunt [71]. In the proposed HGWO there are four essential operators to update each solution and the updated solution will be passed to A\(\beta\)HC algorithm as a new local refinement operator with a probability of \(B_r\). The flowchart of HGWO is presented in Fig. 6. These four operators will be discussed as follows:

Fig. 6
figure 6

Flowchart of the proposed HGWO

Full size image

  • Operator#1: Social hierarchy

    The grey wolf packs have a social hierarchy in which the three wolves with the highest fitness in x are choosed in the hope of obtaining the global optimal solution. The best, second best, and third best solutions are \({{\varvec{x}}}_\alpha\), \({{\varvec{x}}}_\beta\), \({{\varvec{x}}}_\delta\), respectively. Note that other solutions are symbolized as \({{\varvec{x}}}_\omega\). In each iteration the group of wolves in \({{\varvec{x}}}_\omega\) are pulled to \({{\varvec{x}}}_\alpha\), \({{\varvec{x}}}_\beta\), \({{\varvec{x}}}_\delta\) location.

  • Operator#2: Encircling prey

    The intelligent hunting behaviour will be observed after settling the social hierarchy of the grey wolf packs. It includes three steps: (1) The packs track, chase and approach the prey; (2) They encircle and harass the prey to exhaust it; (3) The packs attack the prey. These steps are symbolized mathematically as follows:

    $$\begin{aligned} {{\varvec{x}}}^i(t+1)={{\varvec{x}}}^i(t)-{{\varvec{A}}}\times {{\varvec{D}}} \end{aligned}$$
    (18)

    Note that the wolf next position is denoted by \({{\varvec{x}}}^i(t+1)\) , the current position is \({{\varvec{x}}}^i(t)\), the coefficient matrix is \({{\varvec{A}}}\) and the vector \({{\varvec{D}}}\) depends on the prey position (\({{\varvec{x}}}_{p}\)) which is calculated as follows:

    $$\begin{aligned}&{{\varvec{D}}}=\left| {{\varvec{C}}}\times {{\varvec{x}}}_{p}(t)-{{\varvec{x}}}^i(t)\right| \end{aligned}$$
    (19)
    $$\begin{aligned}&{{\varvec{C}}}=2\times {{\varvec{r}}}_{2} \end{aligned}$$
    (20)

    where \({{\varvec{r}}}_{2}\) is a vector that is generated randomly in the range [0,1].

  • Operator#3: Attacking prey

    As mentioned before, the fittest three solutions are denoted as \({{\varvec{x}}}_\alpha\), \({{\varvec{x}}}_\beta\), \({{\varvec{x}}}_\delta\). These solutions will be guiding other wolves to update their locations as follows:

    $$\begin{aligned} {{\varvec{x}}}^i(t+1)=\frac{1}{3} {{\varvec{x}}}_{1} +\frac{1}{3} {{\varvec{x}}}_{2} +\frac{1}{3} {{\varvec{x}}}_{3} \end{aligned}$$
    (21)

    where \({{\varvec{x}}}_{1}\) and \({{\varvec{x}}}_{2}\) and \({{\varvec{x}}}_{3}\) are computed using Eq. (22).

    $$\begin{aligned} \begin{aligned} {{\varvec{x}}}_{1}={{\varvec{x}}}_{\alpha }^i(t)-{{\varvec{A}}}_{1}\times {{\varvec{D}}}_{\alpha }\\ {{\varvec{x}}}_{2}={{\varvec{x}}}_{\beta }^i(t)-{{\varvec{A}}}_{2}\times {{\varvec{D}}}_{\beta }\\ {{\varvec{x}}}_{3}={{\varvec{x}}}_{\delta }^i(t)-{{\varvec{A}}}_{3}\times {{\varvec{D}}}_{\delta } \end{aligned} \end{aligned}$$
    (22)

    \({{\varvec{D}}}_{\alpha }\), \({{\varvec{D}}}_{\beta }\) and \({{\varvec{D}}}_{\delta }\) are computed by applying Eq. (23).

    $$\begin{aligned} \begin{aligned} {{\varvec{D}}}_{\alpha }=\left| {{\varvec{C}}}_{1}\times {{\varvec{x}}}_{\alpha }-{{\varvec{x}}}\right| \\ {{\varvec{D}}}_{\beta }=\left| {{\varvec{C}}}_{2}\times {{\varvec{x}}}_{\beta }-{{\varvec{x}}}\right| \\ {{\varvec{D}}}_{\delta }=\left| {{\varvec{C}}}_{3}\times {{\varvec{x}}}_{\delta }-{{\varvec{x}}}\right| \end{aligned} \end{aligned}$$
    (23)

  • Operator#4: A\(\beta\)HC local search

    The HGWO exploitation is enhanced by iterating through each developed solution of GWO with \(B_r\) probability. The discussion of A\(\beta\)HC is mentioned in Sect. 2.

3.2.5 The improvement step in hybrid particle swarm optimization (HPSO)

Particle swarm optimization (PSO) is inspired by the flocking birds’ behavior when they search for the source of adequate food [72]. In HPSO, there are three essential operators to update each solution and the generated solution will be passed to A\(\beta\)HC algorithm as a new local refinement operator to improve the generated solution. The flowchart of HPSO is illustrated in Fig. 7. These three operators are as follows:

Fig. 7
figure 7

Flowchart of the proposed HPSO

Full size image

  • Operator#1:update local best and global best solutions

    At each iteration, the local best solution (i.e., \({{\varvec{x}}}^{lb}\)) which is the best solution obtained in the current iteration must be determined. Furthermore, the global best solution (i.e., \({{\varvec{x}}}^{gb}\)) is updated.

  • Operator#2:update the positions

    Before each position in any solution is updated, the velocity vector \(v^i(t)\) is initially updated as shown in Eq. (25).

    $$\begin{aligned}&v^i(t+1)= w(t) \times v^i(t) + c_1 \times \left( r_1(t) \times \left( {{\varvec{x}}}^{lb} - {{\varvec{x}}}^{i}(t)\right) \right) \nonumber \\&\quad + c_2 \times \left( r_2 \times \left( {{\varvec{x}}}^{gb} - {{\varvec{x}}}^{i}(t)\right) \right) \end{aligned}$$
    (24)

    where \(w(t)=(w_{max}-t) \times (w_{max}-w_{min})/M_t\) represents the inertia weight parameter that decreases linearly within the range 0.9 to 0.4. Furthermore, the particles velocities are embedded in this parameter. Also, the acceleration coefficients \(c_1\) and \(c_2\) are user defined parameters that can be set as follows: \(0 \le c_1 \le 2\) and \(0 \le c_2 \le 2\). Finally, \(r_1\) and \(r_2\) are random values in the range [0,1] that are utilized to update the velocity.

    Thereafter, based on the updated velocity \(v^i(t+1)\), the positions of the new solution is updated as shown in Eq. (25):

    $$\begin{aligned} {{\varvec{x}}}^{i}(t+1) = {{\varvec{x}}}^{i}(t) + v^i(t+1) \end{aligned}$$
    (25)

  • Operator#3: A\(\beta\)HC local search

    The HPSO exploitation is enhanced by iterating through each developed solution of PSO with \(B_r\) probability. The discussion of A\(\beta\)HC is mentioned in Sect. 2.

3.2.6 The improvement step in hybrid JAYA algorithm (HJAYA)

JAYA is a Sanskrit term that means victory. The JAYA algorithm is a population-based optimization technique that applied the principle of “survival of the fittest” [73]. The solutions generated by JAYA are moving towards the global best solutions while moving away from the worst solutions. The algorithm is considered easy to utilize as it does not have specific parameters. The proposed HJAYA algorithm uses three essential operators to update each solution and the generated solution. The developed solutions are then passed to A\(\beta\)HC algorithm as a new local refinement operator to improve the generated solution with a probability of \(B_r\). The flowchart of HJAYA is presented in Fig. 8. These three operators will be discussed as follows:

Fig. 8
figure 8

Flowchart of the proposed HJAYA

Full size image

  • Operator#1: JAYA Evolution process

    The evolution process of JAYA is conducted using Eq. (26).

    $$\begin{aligned} {{\varvec{x}}}^{i}_{j}(t+1) = {{\varvec{x}}}^i_{j}(t) + r_1 \times ({{\varvec{x}}}^1_{j}(t) - |{{\varvec{x}}}^i_{j}(t)|) - r_2 \times ({{\varvec{x}}}^N_{j}(t) - |{{\varvec{x}}}^i_{j}(t)|) \end{aligned}$$
    (26)

    where the new updated solution is \({{\varvec{x}}}^{i}(t+1)\), and the current solution is \({{\varvec{x}}}^i(t)\). The random value in the range of [0,1] is denoted as \(r_1\) and \(r_2\). These values are used to obtain the equilibrium between exploration and exploitation. Also, the decision variable j in the best solution is symbolized as \({{\varvec{x}}}^i_{j}(t)\) and the decision variable j in the worst solution is symbolized as \({{\varvec{x}}}^N_{j}(t)\).

  • Operator#2: A\(\beta\)HC local search

    The HJAYA exploitation is enhanced by iterating through each developed solution of JAYA with \(B_r\) probability. The discussion of A\(\beta\)HC is mentioned in Sect. 2.

  • Operator#3:update population

    At each iteration the fitness value of the new solution \({{\varvec{x}}}^{i}(t+1)\) is computed. The new solution \({{\varvec{x}}}^{i}(t+1)\) will replace the current solution \({{\varvec{x}}}^i(t)\) if \(f( {{\varvec{x}}}^{i}(t+1))\le f({{\varvec{x}}}^i(t))\).

4 Experiments and results

In this section, the proposed hybridized adaptive \(\beta\)-hill climbing (A\(\beta\)HC) on the six MA versions for MLP is evaluated. The proposed MA versions are hybrid flower pollination algorithm (HFPA), hybrid salp swarm algorithm (HSSA), hybrid crow search algorithm (HCSA), hybrid grey wolf optimization (HGWO), hybrid particle swarm optimization (HPSO), and hybrid JAYA algorithm (HJA) by utilizing 15 datasets with different sizes and number of classes. The datasets details are presented in Sect. 4.1. The configuration of the experiments is portrayed in Sect 4.2. The performance of the different proposed MA versions on training MLP is explained Sect.4.3.

4.1 Test datasets

In this section, the performance of proposed hybrid methods, which are HCSA, HFPA, HSSA, HGWO, HJA, and HPSO, is investigated and evaluated using 15 benchmark classification optimization problems. Such optimization problems are provided by UCI Machine Learning Repository [74]. All datasets characteristics, including the number of classes, features, instances, hidden layers, and MLP structures are presented in Table 1. These datasets are selected due to their different class labels; i.e., two, three, four, six, and ten labels, to investigate the proposed methods efficiently.

This study utilises min-max normalization for all datasets to minimize the features’ effect with different difficulty levels. Features difficulty levels are mathematically formalized as follow:

$$\begin{aligned} x_{nor} = \frac{ x_{i} - F_{min}}{F_{max} - F_{min}} \end{aligned}$$
(27)

where \(x_{nor}\) denotes the normalized value of \(x_i\) in the range \([F_{min},F_{max}]\). \(F_{min}\) and \(F_{max}\) are the minimum and maximum values of the features, respectively.

Table 1 Benchmark datasets’ characteristics
Full size table

The number of hidden layers can be calculated on the basis of various methods. Accordingly, this study calculates neurons number in each hidden layer using the method utilized in [75, 76]. The utilized method is mathematically formulated as follow:

$$\begin{aligned} h=2 \times N +1; \end{aligned}$$
(28)

where h denotes the neurons number in the hidden layer and N is the number of features in the dataset. Accordingly, the input-hidden-output form is presenting the complete MLP structure of each dataset. For instance, the MLP structure is 8-17-10 for the Yeast dataset, 8, 17, and 10 denote the number of input features, hidden layers, and output class labels, respectively.

For testing and training, all datasets are divided into 30% and 70%, respectively. The stratified way is used to split each dataset [77]. This technique calculates each class’s ratio and then meets the train/test split rate based on the calculated ratio for each dataset. The use of this strategy helps preserve the share of every class in the data split and increases the representation of the classes of minorities. As a result, a balanced number of classes will be assigned for the train/test portions.

4.2 Experimental settings

The proposed six MA versions CSA, HFPA, HSSA, HGWO, HJA, and HPSO are compared using the same datasets. The specifications of the machine used for experimental results are presented in Table 2. The settings for the parameters of some MA versions are summarized in Table 3. Note that the \(B_r\) parameter values used are studied in the following section for all MA versions.

The algorithms are implemented for each data set over 30 independent runs. The number of epochs is a parameter that defines the total number of iterations the learning algorithm will run through the training dataset [78]. The number of epochs is 250. It is selected based on what was previously used in the literature [75, 76] which reduces the error from the model when used on similar datasets.

Table 2 Initial parameters of the comparative algorithms
Full size table
Table 3 Initial parameters of the comparative algorithms
Full size table

4.3 Comparison results

The performance of the different proposed MA versions (i.e., HCSA, HGWO, HSSA, HPSO, HFPA, and HJAYA) on training MLP are tested in this section. These algorithms are utilized to evolve the weights of networks as well as to select the optimal number of hidden neurons. Remarkably, each of the proposed MA versions is designed by hybridizing the original version of the population-based algorithm with an adaptive \(\beta\)-hill climbing optimizer (A\(\beta\)HC). Recall that the parameter settings of these algorithms are given in Sect. 4.2, while the characteristics of the datasets used for evaluation purposes are provided in Sect. 4.1.

Table 4 illustrates the results of running the proposed MA versions on 15 datasets using different settings of the \(B_r\) parameter. These results are summarized in terms of the mean, the standard deviation (STD), and the best-obtained classification accuracy. From Table 4, it can be seen that each of the proposed MA versions had four versions based on the value of the \(B_r\) parameter. The \(B_r\) parameter is studied using different settings (\(B_r\)= 0, \(B_r\)= 0.01, \(B_r\)= 0.1, and \(B_r\)= 0.3). The higher value of \(B_r\) parameter leads to a higher rate of calling the A\(\beta\)HC algorithm in the population-based algorithm, and thus a higher rate of exploitation during the search process. For instance, when the value of the \(B_r\) is equal to zero, this means that the A\(\beta\)HC is neglected, and thus the original versions of these algorithms (i.e., CSA, HWO, SSA, PSO, FPA, and JAYA). It should be noted that the best results are highlighted in bold font.

The experimental results shown in Table 4 are analyzed and discussed in two phases: I) comparing the results obtained by the different four versions of each MA, and II) comparing the best results obtained by all of the proposed MA versions. In general, it can be seen from the results recorded in Table 4 that the accuracy is gradually enhanced when the value of \(B_r\) is increased. Furthermore, the performance of the algorithm is worse than the other versions of the same algorithm (i.e., the hybrid version) when the value of \(B_r=0\) (i.e., using the original algorithm).

From Table 4, it can be seen that the performance of the HCSA with \(B_r=0.3\) outperforms three other versions of the same MA by obtaining the best results on 9 datasets in terms of the mean of the results, and in 10 datasets in terms of best results. On the other hand, the HCSA with \(B_r\)= 0.3 failed to obtain the best results for any of the datasets in the terms of mean results, while it got the best results on 2 datasets (i.e., Baloon, and Iris) in terms of best results. These two datasets are the easiest datasets where the Baloon dataset has 4 features, 9 samples, and 2 classes, while the Iris dataset has 4 features, 9 samples, and 3 classes. However, the HCSA with \(B_r\)= 0.01 achieved the best results on 2 datasets (i.e., Cancer, and Heart) in terms of the mean of the results, and 5 datasets in terms of best results. While the HCSA with \(B_r\)= 0.1 get the best results on 5 and 6 datasets in terms of mean and best results respectively.

Similarly, the results of studying the impact of the \(B_r\) parameter on the performance of the proposed HGWO algorithm are recorded in Table 4. Apparently, the performance of the HGWO is gradually enhanced, when the value of the \(B_r\) is increased based on the mean of the accuracy. Whereas, the HGWO with \(B_r\)= 0.3, HGWO with \(B_r\)= 0.1, HGWO with \(B_r\)= 0.01, and HGWO with \(B_r\)= 0.01 algorithms are got the best results in terms of the mean of accuracy on 7, 5, 4, and 2 datasets respectively. On the other hand, the effect of the \(B_r\) parameter on the performance of the HHWO algorithm in terms of best results is limited. This is because all versions of HGWO achieved almost the same number of the best results. The HGWO with \(B_r\)= 0.3, HGWO with \(B_r\)= 0.1, HGWO with \(B_r\)= 0.01, and HGWO with \(B_r\)= 0.01 algorithms are obtained the best results in terms of best accuracy on 5, 6, 7, and 5 datasets respectively. In addition, it can be observed from Table 4 that the HGWO with \(B_r\)= 0.3 is more robust than the three other versions of HGWO by getting the lowest STD values for all datasets.

The influence of the \(B_r\) parameter on the performance of the proposed HSSA is studied using four different values. The results of running the HSSA are recorded in Table 4. Clearly, the performance of the HSSA with \(B_r\)= 0.3 is better than the three other versions of HSSA by getting the best results on 8 datasets in terms of the mean of accuracy. Furthermore, the HSSA obtained the best results on 7 datasets in terms of the best accuracy. On the other hand, the performance of the HSSA with \(B_r\)= 0 performs better than the other three versions of HSSA by obtaining the best results on 4 datasets (i.e., Baloon, Cancer, Titanic, and Parkinson) in terms of the mean of the accuracy. While the HSSA with \(B_r\)= 0 is achieved the best results on 3 datasets (i.e., Baloon, Glass, and Vehicle) in terms of the best accuracy. The HSSA with \(B_r\)= 0.01 outperforms the three other versions of HSSA on 2 datasets (i.e., Heart, and Blood) and 4 datasets (i.e., Baloon, Iris, Cancer, and Blood) in terms of mean and best accuracy. While the results of the HSSA with \(B_r\)= 0.1 are better than those of the three other versions of the HSSA on 3 datasets (Baloon, Iris, and Seeds)and 5 datasets (i.e., Baloon, Iris, Heart, Seeds, and Parkinson) in terms of the mean and the best accuracy. Based on the above discussion, it can be observed that the proposed HSSA with \(B_r\)= 0.3 performs better than the three other versions of HSSA on the hardest datasets with the highest number of classes like Yeast, German, Ionosphere, Glass, Vertebral, and Monk datasets. This proves the efficiency of using the A\(\beta\)HC as a local search algorithm within the SSA algorithm to enhance the exploitation capability of the HSSA and thus guide the search process of the HSSA to achieve better results for the hardest datasets.

Table 4 illustrates the results of running the proposed HPSO with different configurations of \(B_r\) parameter. Remarkably, the proposed HPSO with \(B_r\)= 0.1 outperforms the three other versions of HPSO by obtaining the best results on 7 and 10 datasets in terms of the mean and the best accuracy respectively. While the HPSO with \(B_r\)= 0, HPSO with \(B_r\)= 0.01, and HPSO with \(B_r\)= 0.3 are achieved the best results in terms of the mean accuracy on 2, 4, and 3 datasets respectively. Furthermore, the HPSO with \(B_r\)= 0, HPSO with \(B_r\)= 0.01, and HPSO with \(B_r\)= 0.3 are got the best results in terms of the best accuracy on 5, 4, and 6 datasets respectively. Notably, all versions of HPSO achieved the same best results in terms of the best accuracy for Monk and Baloon datasets. From Table 4, it can be seen that the proposed HPSO with \(B_r\)= 0.3 can obtain the best results in terms of the mean of accuracy for the hardest datasets with a higher number of classes like German, Titanic, and Vehicle. While the HPSO with \(B_r\)= 0.3 fails to obtain the best results for any of the easiest datasets like Baloon. This leads us to conclude that the higher rate of the \(B_r\) parameter is useful for the hardest dataset, while the \(B_r\) parameter with considerable value is useful for solving the easiest datasets.

The results of studying the impact of the \(B_r\) parameter on the performance of the HFPA are also illustrated in Table 4. It can be seen from the results that the performance of the HFPA with \(B_r\)= 0.3 is better than the three other versions of HFPA by getting the best results in terms of accuracy mean on 8 datasets. In addition, it obtained the best results in terms of best accuracy on 7 datasets. The HFPA with \(B_r\)= 0 got the best results in terms of the mean of the accuracy for the Ionosphere dataset, while it obtained the best results in terms of the best accuracy on Baloon, and German datasets. Furthermore, the performance of the HFPA with \(B_r\)= 0 is worse than the three other versions of HFPA by getting the worst results for the remaining datasets. This is due to the fact that the value of the \(B_r\) parameter is equal to zero, and thus the calling the A\(\beta\)HC is neglected during the search. The HFPA with \(B_r\)= 0.01 obtained the best results in terms of the mean of the accuracy on 4 datasets (i.e., Heart, Blood, Titanic, and Parkinson), while it achieved the best results in terms of the best of the accuracy on 6 datasets. Finally, the HFPA with \(B_r\)= 0.1 got the best results in terms of the mean of the accuracy on Cancer and Seeds datasets. In addition, the HFPA with \(B_r\)= 0.1 obtained the best results in terms of the best accuracy on 6 datasets. From another perspective, it can be seen that the performance of the HFPA with \(B_r\)= 0.3 is more robust than the three other versions of HFPA by obtaining the smallest STD values for almost all datasets.

From Table 4, it can be shown that the proposed HJAYA with \(B_r\)= 0 is obtained the best results in terms of the mean of the accuracy on the Titanic dataset, and it is got the best results in terms of the best of the accuracy on 3 datasets. In contrast, the HJAYA with \(B_r\)= 0 performs worse than the three other versions of HJAYA for the remaining datasets. The HJAYA with \(B_r\)= 0.01, HJAYA with \(B_r\)= 0.1, and HJAYA with \(B_r\)= 0.3 achieved the best results in the terms of the mean of the accuracy on 4, 3, and 7 datasets respectively. in addition, the HJAYA with \(B_r\)= 0.01, HJAYA with \(B_r\)= 0.1, and HJAYA with \(B_r\)= 0.3 are got the best accuracy results on 6, 7, and 7 datasets. Clearly, no difference in the performance of the HJAYA algorithms when the value of the \(B_r\) parameter is bigger than zero in the terms of the best accuracy. Furthermore, the performance of the HJAYA \(B_r\)= 0.3 is better than the other versions of HJAYA, while the HJAYA \(B_r\)= 0.1 is more robust than the other versions of HJAYA in almost all datasets. This is because the higher value of the \(B_r\) parameter leads the HJAYA to converge quickly and thus get stuck in the problem of local optima in the early stages of the search process.

Table 4 The accuracy results of the HCSA, HGWO, HSSA, HPSO, HFPA, and HJAYA algorithms on 15 datasets (Bold is the best)
Full size table

Figure 9 illustrates the behavior of the proposed HCSA, HGWO, HSSA, HPSO, HFPA, and HJAYA algorithms using different settings of the \(B_r\) parameter on navigating the search space of the Monk and Vehicle datasets. It should be noted that these datasets are different in the number of features, samples, and classes to visualize the differences between the behavior of the different versions of each algorithm in solving these datasets. The x-axis and y-axis represents the correlation between the fitness values (MSE) and the iteration number. The slope of the curves represents convergence rates. Apparently, the convergence of the proposed MA versions when the value of the \(B_r\) \(> 0\) is faster than the convergence of them with \(B_r=0\). In addition, the convergence of hybrid-based algorithms with \(B_r\)= 0.3 is better than the other versions of each algorithm in almost all cases when it is used to solve Monk and Vehicle datasets. However, it can be seen that the behavior of the HJAYA with \(B_r\)= 0.01 is better than the three other versions of HJAYA in solving the Monk dataset. This is because the three other versions of the HJAYA algorithms converge fast and thus get stuck in local optima in the early stages of the search process. The convergence of the HCSA with \(B_r\)= 0.1 is gradually enhanced till the last stages of the search process when it is utilized to solve the Monk and Vehicle datasets. Finally, the convergence of the HPSO with \(B_r\)= 0.1 is better than the other versions of HPSO when it is applied to solving the Vehicle dataset.

Fig. 9
figure 9

Convergence results of HGWO, HSSA, HJAYA, HFPA, HPSO, and HCSA on Monk and Vehicle datasets

Full size image

In order to highlight which method has the best performance, the performance of the proposed MA versions (i.e., HCSA, HGWO, HSSA, HPSO, HFPA, and HJAYA) are compared against each other in Table 4. Firstly, the comparison in terms of the mean of the accuracy, it can be seen that the performance of the proposed HGWO performs better than the other comparative methods by obtaining the best results on 9 datasets. In addition, the performance of the HGWO is similar to some of the other comparative methods by obtaining the optimal results on Baloon datasets. The performance of the HSSA is better than the other algorithms on 3 datasets (i.e., Vertebral, German, and Yeast), while it is similar to other algorithms on the Baloon dataset. The HFPA obtains the best results on two datasets (i.e., Cancer, and Baloon). The HCSA performs similarly to or better than the other algorithms by obtaining the best results on Heart and Baloon datasets. The HPSO yields the best results on the Baloon dataset, while the HJAYA failed to obtain the best result for any of the datasets. The algorithms comparison in terms of the best accuracy shows that the proposed HGWO outperforms other algorithms on 4 datasets (i.e., Glass, Ionosphere, Vehicle, and Parkinson), while the performance of the HGWO is similar to some algorithms on 6 datasets (i.e., Titanic, Seeds, Vertebral, Iris, Baloon, and Monk). The HCSA performs better than other algorithms on Yeast datasets, while the performance of the HCSA is similar to some of the other algorithms on two datasets (i.e., Baloon, and Vertebral). The performance of the HPSO is similar to other algorithms by getting the same best results on four datasets (i.e., Monk, Baloon, Iris, and Cancer). The HSSA performs better than other algorithms on the German dataset, while its performance is similar to some of the other algorithms on 4 datasets (i.e., Monk, Baloon, Iris, and Cancer). The HJAYA yields the best results on the Heart dataset, while the performance of the HJAYA is similar to other algorithms on two datasets (i.e., Baloon, and Iris). The HFPA performs better than the other algorithms on the Blood dataset, while it obtains the same best results as the other algorithms on 5 datasets (i.e., Baloon, Iris, Cancer, Seeds, and Titanic). Based on the above discussions, we can conclude that the performance of the hybrid-based algorithms is better than the performance of the original versions of the algorithms. Furthermore, the performance of the proposed HGWO is better than the performance of the other hybrid-based algorithms on almost all of the datasets. This is since the GWO algorithm utilizes the three fittest solutions in the current population at each iteration to guide the search process. That leads to the solutions in the population following the fittest solutions and thus produces fast convergence.

Figure 10 illustrates the notched boxplot that is used to visualize the distributions of the MSE results for running the proposed MA versions, as well as the original versions of the algorithms on all datasets. It should be noted that the smallest distance between the best, median, and worst of the MSE results demonstrates the robustness of the algorithm.

Fig. 10
figure 10

Boxplot charts of MSE results of CSA, HCSA, GWO, HGWO, SSA, HSSA, PSO, HPSO, FPA, HFPA, JAYA, and HJAYA

Full size image

4.3.1 Friedman’s statistical test

This section provides a statistical study based on Friedman’s statistical test that shows the average rankings of all compared methods and their MA versions, including GWO, HGWO, SSA, HSSA, JAYA, HJAYA, FPA, HFPA, PSO, HPSO, CSA, and HCSA. Such average rankings are calculated using the results provided in Table 4. In Friedman’s statistical test, the null hypothesis (\(H_0\)) and alternative hypothesis (\(H_1\)) are used to investigate the behavior of the compared methods. \(H_0\) implies that the comparative methods’ behaviors are similar, whereas \(H_1\) indicates that the comparative methods’ behaviors are different. In addition, the p-value term is used to investigate whether a significant difference in the compared methods’ results, where a significant difference exists between the methods if p-value \(\le\) 0.05. Otherwise, no significant difference.

Figure 11 shows the average rankings of all compared methods. The figure proves the robust performance of HGWO in addressing the problem, where it obtained the lowest average rankings. However, JAYA and FPA achieved the worst results by obtaining the highest average rankings. In addition, significant differences between the comparative algorithms are proved, where the p-value obtained by Friedman’s test is less than 0.05. Accordingly, the \(H_0\) is rejected.

Fig. 11
figure 11

Average rankings of the comparative algorithms using Friedman’s statistical test

Full size image

The Holm and Hochberg procedures are then used as post-hoc techniques to demonstrate whether the controlled method’s results are significantly different from other methods’ results based on the adjusted \(\rho\)-value. Figure 11 shows that the controlled method is HGWO, as it achieves the lowest average rankings among all compared methods. Holm’s procedure rejects the null hypothesis \(H_0\) when the \(\rho\)-value \(\le 0.0125\), while Hochberg’s procedure rejects the null hypothesis \(H_0\) when the \(\rho\)-value \(\le 0.01\). The difference between the HGWO method and seven other methods (FPA, JAYA, CSA, HJAYA, PSO, SSA, and GWO) is significant, as shown in Table 5. Conversely, the difference between the HGWO method and four other methods (HFPA, HPSO, HCSA, and HSSA) is not significant. This section demonstrates that the HGWO algorithm is a new alternative that can solve such problems successfully.

Table 5 Holm/Hochberg results between the HGWO algorithm and other algorithms
Full size table

The proposed memetic computing framework can be used as a general structure for enhancing the performance of population-based optimization algorithms by distilling local search techniques. This improvement can empower the efficiency of MLP and thus produce more accurate results when utilized in different MLP-based applications. By means of hybridization of local search with the population-based optimization algorithm. The trade-off between local exploitation and global exploration can be achieved during the search.

5 Conclusion and future work

Using local-based search algorithms to hybridize population-based algorithms can boost their performance in terms of exploitation capability. This can help population-based search algorithms to have a balance between exploration and exploitation while examining the problem search space. In this paper, adaptive \(\beta\)-hill climbing (A\(\beta\)HC) is utilized as a local search refinement to hybridize six population-based metaheuristics for training MLP such as hybrid crow search algorithm (HCSA), hybrid flower pollination algorithm (HFPA), hybrid salp swarm algorithm (HSSA), hybrid grey wolf optimization (HGWO), hybrid JAYA algorithm (HJA), and hybrid particle swarm optimization (HPSO). The algorithms are exploring the search space to find the optimal values of MLP weights and biases.

The performance of the proposed six MA versions is evaluated using 15 datasets with different sizes and with a different number of classes. These datasets are normalized and then split into test and train sets 30% and 70% respectively. A stratified way is applied when splitting the dataset to ensure the presence of small classes when training MLPs. Each dataset is trained using MLP configured with a different number of inputs, hidden, and output neurons.

The tuning of the \(B_r\) parameter of A\(\beta\)HC shows that the accuracy results obtained by the proposed MA versions are gradually enhanced when this parameter value increases. This is because it empowers the exploitation capability of the algorithm. The obtained results show that all of the hybridized algorithms outperform the original version of the algorithms. In addition, the HGWO excels all other MA versions. Based on the statistical analysis results the following algorithms show competitive results as well for HFPA, HPSO, HCSA, and HSSA.

As a future direction, the proposed algorithm will be utilized to tackle real-world applications that have more complex search space. The proposed algorithms can be refined to have other local search techniques to improve their exploitation abilities. Several researchers investigated the sensitivity of the MLP to the number of added layers. For example, Zeng and Yeung [79] investigated ten MLPs with different layers starting with 2-1 and each time add a layer with two neurons into the previous MLP. In the future, the upper bounds for the number of layers in MLP can be investigated.