1 Introduction

Capacity analysis of multipath fading channels becomes an important and fundamental issue in the design and study of new generation wireless communication systems due to scarce radio spectrum available and due to the rapidly growing demand for wireless services. For applications such as wireless local area networks (WLANs), and satellite-based networks and cellular networks, the system consists of K users communicating with the base station (BS). The paths from different users to the BS are independent and time-varying channels which provide multiuser diversity in a multiuser wireless system.

This particular form of diversity could be exploited by tracking channel fluctuations between each user and the BS, and scheduling transmissions to users when their instantaneous channel quality is near maximum. Besides this, multiple antennas which separate the signals spatially from different users can also be used to provide multiple access gain; called space-division multiple access (SDMA). In this context, user scheduling solutions gain importance. Scheduling here refers to the problem of determining which users will be active in a given time-slot; resource allocation refers to the problem of allocating physical layer resources such as bandwidth and power among these active users. In modern wireless data systems, frequent channel quality feedback is available enabling both, the scheduled users and the allocation of physical layer resources to be dynamically adapted based on users’ channel conditions and quality of service (QoS) requirements. For point-to-point multiple input multiple output (MIMO) systems, the theoretical capacity is linearly proportional to min (N T , N R ) where N T is the number of transmit antennas and N R is the number of receive antennas [1]. These architectures provide spatial multiplexing by using MIMO multi-channel structure [1], or by space time codes that exploit coding and diversity gains [2], or through a combination of the two. For multiuser systems, the capacity becomes a K-dimensional region that defines the rates (R 1… R K ) simultaneously achievable by K users. The forward link from the BS to users is a broadcast channel, while the reverse link is a multiple access channel. Results on Shannon capacity [3] of single-user and multiuser MIMO channels were presented.

1.1 Literature Review

MIMO technology utilizes multiple antennas at the transmitter and/or receiver to improve transmission reliability, thereby providing diversity gain or to provide high raw data rates, thereby providing multiplexing gain. The pioneering work of Telatar [4] has shown that using multiple antennas offers remarkable spectral efficiency which leads to the extension of MIMO systems to multiuser scenarios.

Torabi et al. [5] derived mathematical expressions of average spectral efficiency (ASE), average bit error rate (BER) and outage probability considering Rayleigh fading channel for a MIMO OSFBC-OFDM system. Adaptive modulation schemes were employed. Both full-feedback and limited-feedback scenarios were considered. Numerical simulations and their advantages were studied and evaluated. An overview of scheduling algorithms was proposed for fourth generation multiuser wireless networks based on MIMO technology presented by Ajib and Haccoun [6]. The feedback load carrying instantaneous channel rates from all active subscribers to the base station is a drawback in a multiuser diversity scenario. This was shown to be unjustified by Gesbert and Alouini [7]. Goldsmith and Chua [8] proposed a variable-rate and variable-power M-quadrature amplitude modulation (MQAM) modulation scheme for high-speed data transmission over fading channels.

Tarokh et al. [9] introduced space-time block codes (STBC) for communication over Rayleigh fading channels using multiple transmit antennas. The selection combining transmission (SCT) scheme is the benchmark scheme with which all the proposed switched based access schemes are compared. Within each guard time interval, all K users are probed and the BS selects the user which reports the highest SNR [10]. With this mode of operation, the probability density function (PDF) of the output SNR [11] is taken as a base in analysing the performance of the multiuser system. Alouini et al. [12] proposed and analyzed an alternative form of switch and examine combining, namely one that waits for a channel coherence time if all the available diversity paths fail to meet a predetermined minimum quality requirement. An adaptive resource-allocation approach [13] which jointly adapts subcarrier allocation, power distribution, and bit distribution according to instantaneous channel conditions, was proposed for multiuser MIMO orthogonal frequency division multiplexing (OFDM) systems. Closed-form expressions for the bit error rate (BER) performance of space-frequency block coded OFDM (SFBC-OFDM) systems were derived [14] and evaluated for frequency-selective fading channels. A general model of gradient-based scheduling and resource allocation for orthogonal frequency division multiple access (OFDMA) systems [15] was considered. The optimal resource allocation for a multiuser MIMO-OFDMA downlink system using zero forcing space division multiple access (SDMA) with the objective of maximizing system capacity was considered [16]. The impact of multiuser diversity on spatial diversity gains for downlink transmission was evaluated [17]. Allocating power to the best set of users leads to the design of a scheduling scheme able to exploit both multiuser diversity and multiple access gain provided by SDMA [18].

Design rules exploiting correlations in transmit antennas in the MIMO case was presented. Rezki et al. [19] derived a closed-form expression for optimal capacity-achieving input distribution at low SNRs and the exact capacity of a non-coherent channel at low SNRs. The study of an Eigenvector-based artificial noise-based jamming technique was developed to provide increased wireless physical layer security in transmit-receive diversity systems [20] and the impact of channel estimation errors on system performance was analyzed. In earlier work [21], a complete view of adaptive modulation with MRC in different practical scenarios including the relation between the branches was presented. The effect of channel estimation error on the capacity and BER of a MIMO transmit maximal ratio transmission (MRT) and MRC receiver systems over uncorrelated Rayleigh fading channels was investigated in [22].

1.2 Organization of the Paper

The remainder of the paper is organized as follows: In Sect. 2, we describe the system and channel models for multiuser feedback system which are taken into consideration. In Sect. 3, spectral efficiencies of a fading channel with MRC diversity with impairments due to combining errors under full feedback scenario is discussed. In Sect. 4, we derive spectral efficiencies of a fading channel with MRC diversity with impairments due to combining errors under limited feedback scenario. In Sect. 5, we present numerical results for both feedback cases. Finally, Sect. 6 presents the conclusions.

2 System and Channel Model

If a time division multiplexing (TDM) system is considered, only one user has channel access per time-slot (for uplink or downlink). A single time-slot is divided into a guard time and an information transmission time. During guard-time, the base-station selects the user which gains access to the channel in the subsequent transmission time. The guard time is assumed to be fixed and equal to the amount of time necessary to probe all users. The time-duration of a single time-slot is assumed roughly equal to the channel coherence time, and the data burst is assumed to experience the same fading conditions as the preceding guard period (block fading). If an OFDM system is considered, the frequency selective fading channel is converted into several flat fading sub-channels and sub-channel fading can be considered as Rayleigh flat fading. The index [k, n] in γ is omitted for simplicity.

When a pilot signal is transmitted adjacent to the message band, the phase and amplitude of the pilot signal sensed are used to adjust the complex weighting factors of the individual branches. This results in true MRC combining [23]. In such cases, the fading of the pilot may not be completely correlated with that of the message, possibly because the pilot frequency is too far removed from the message. In this case, the complex weighting factors would be in error and degrades performance results. These effects can be completely described in terms of correlation coefficient, ρ, defined as the magnitude of complex cross-correlation between the transmission coefficients of the medium associated with the pilot and message frequencies [23]. Note that if ρ = 0, the pilot and message signals are uncorrelated (worst case), and if ρ = 1, the pilot and message signals are perfectly correlated and their correlation is represented as

$$ \rho = \left| {\frac{{\left\langle {p_{k} g_{k}^{ * } } \right\rangle }}{{\left\langle {p_{k} p_{k}^{ * } } \right\rangle }}} \right|^{2} $$
(1)

where pk(t) is the pilot and gk(t) is the message signal.

The cumulative density function (CDF) and PDF of the received SNR for each slot/sub-channel of each user at low SNR regime with combining errors is given [24] as

$$ \mathop F\nolimits_{\text{M}}^{{({\text{CE}})}} (\gamma ) = 1 - \left( {1 - \left( {1 - \rho^{2} } \right)^{M - 1} } \right)\exp \left( {\frac{ - \gamma }{{\bar{\gamma }}}} \right), $$
(2)
$$ \mathop f\nolimits_{\text{M}}^{{({\text{CE}})}} (\gamma ) = \frac{{\left( {1 - \left( {1 - \rho^{2} } \right)^{M - 1} } \right)}}{{\bar{\gamma }}}\exp \left( {\frac{ - \gamma }{{\bar{\gamma }}}} \right), $$
(3)

where M is the diversity order equal to Nt × Nr antennas, and CE stands for combining errors.

In the following section, we express PDF and the CDF for the SNR-based user scheduling scheme for the multiuser system which will enable us to establish a mathematical analysis and formulation for average spectral efficiency of the system with combining errors due to maximal ratio combining (MRC) for the Rayleigh fading case under study. For the feedback channel, we consider two scenarios: full feedback and limited-feedback of channel information to the transmitter. For both scenarios, we also express PDF and CDF for the SNR of the best and scheduled user.

3 User Scheduling with Full Feedback Scenario

Consider K users, and assume that full channel information is sent to the base station. If all K users are probed within each guard-time interval, and BS selects the user which reports the highest SNR, this type of feedback is called the full feedback or selection combining transmission (SCT). Assuming that users’ SNR are i.i.d, using the theory of order statistics [25], the PDF of the output SNR given in [26] as

$$ \mathop F\nolimits_{{\gamma_{\text{m}} }}^{{({\text{CE}})}} (\gamma ) = \left( {F_{M}^{(CE)} (\gamma )} \right). $$
(4)

Substituting (1) into (4), we have the CDF for the best user (with SNR γm) selected from K available users as

$$ \mathop F\nolimits_{{\gamma_{\text{m}} }}^{{({\text{CE}})}} (\gamma ) = \left( {1 - \left( {1 - \left( {1 - \rho^{2} } \right)^{M - 1} } \right)\exp \left( {\frac{ - \gamma }{\varGamma }} \right)} \right)^{K} . $$
(5)

By using the binomial expansion defined by\( \left( {1 - x} \right)^{K} = \sum\nolimits_{i = 0}^{K} {\left( {\begin{array}{*{20}c} K \\ i \\ \end{array} } \right)\left( { - 1} \right)^{i} x^{i} } \) in (5) and \( {\text{A}} = \left( {1 - \left( {1 - \rho^{2} } \right)^{M - 1} } \right) \), the CDF of the best user is obtained as

$$ F_{{\gamma_{m} }}^{(CE)} \left( \gamma \right) = \sum\limits_{n = 0}^{K - 1} {\left( \begin{gathered} K \hfill \\ n \hfill \\ \end{gathered} \right)} A^{n} ( - 1)^{n} \left( {\exp \left( {\frac{ - \gamma }{{\bar{\gamma }}}} \right)} \right)^{n} , $$
(6)

where γm is the SNR of the mth user which has the highest SNR. The PDF of γm is obtained by taking the derivative of the corresponding CDF in (6) with respect to γ as follows:

$$ f_{{\gamma_{m} }}^{(CE)} \left( \gamma \right) = Kf_{M}^{(CE)} (\gamma )\left( {F_{M}^{(CE)} (\gamma )} \right)^{K - 1} , $$
(7)

where \( f_{M}^{(CE)} (\gamma ) \) and \( F_{M}^{(CE)} (\gamma ) \) are defined in (1) and (2), respectively. Substituting (1) and (2) into (7), we have the PDF of γm as follows:

$$ f_{{\gamma_{m} }}^{(CE)} \left( \gamma \right) = K\left( {\frac{{\left( {1 - \left( {1 - \rho^{2} } \right)^{M - 1} } \right)}}{{\bar{\gamma }}}\exp \left( {\frac{ - \gamma }{{\bar{\gamma }}}} \right)} \right)\left( {1 - \left( {1 - \left( {1 - \rho^{2} } \right)^{M - 1} } \right)\exp \left( {\frac{ - \gamma }{{\bar{\gamma }}}} \right)} \right)^{K - 1} . $$
(8)

By using the binomial expansion defined by \( \left( {1 - x} \right)^{K} = \sum\nolimits_{i = 0}^{K} {\left( {\begin{array}{*{20}c} K \\ i \\ \end{array} } \right)\left( { - 1} \right)^{i} x^{i} } \) in (8) and after certain simplification, we have

$$ f_{{\gamma_{m} }}^{(CE)} \left( \gamma \right) = \frac{K}{{\bar{\gamma }}}\sum\limits_{n = 0}^{K - 1} {\left( {\begin{array}{*{20}c} {K - 1} \\ n \\ \end{array} } \right)} A^{n + 1} ( - 1)^{n} \left( {\exp \left( {\frac{ - \gamma }{{\bar{\gamma }}}} \right)} \right)^{n + 1} , $$
(9)

where \( A = 1 - \left( {1 - \rho^{2} } \right)^{M - 1} \).

Adaptation policies along with MRC scheme are employed at each user to enhance system capacity. Accordingly, there are four adaptation policies applied to improve system performance, namely (1) Optimal power and rate adaptation policy (OPRA), (2) Optimal rate adaptation policy (ORA), (3) Channel inversion with fixed rate policy (CIFR), and (4) Truncated channel inversion with fixed rate policy (TIFR) policies.

3.1 Optimal Simultaneous Power and Rate Adaptation Policy

Given an average transmit power constraint, the spectrum efficiency of a fading channel with received SNR PDF, \( f_{{\gamma_{m} }}^{{({\text{CE}})}} (\gamma ) \) for the best user, m, selected from all available K users and with optimal power and rate adaptation (OPRA) policy, \( \frac{{\left\langle {\text{C}} \right\rangle_{\text{OPRA}}^{{({\text{CE}})}} }}{B} \) [bits/s/Hz], is given as [27]

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{OPRA}}^{{({\text{CE}})}} }}{B} = \int\limits_{{\gamma_{0} }}^{\infty } {\log_{2} \left( {\frac{\gamma }{{\gamma_{0} }}} \right)} f_{{\gamma_{{_{m} }} }}^{{(\text{CE})}} (\gamma )d\gamma . $$
(10)

Substituting (9) into (10), we have

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{OPRA}}^{{({\text{CE}})}} }}{B} = \frac{K}{{\bar{\gamma }\ln 2}}\sum\limits_{n = 0}^{K - 1} {\left( {\begin{array}{*{20}c} {K - 1} \\ n \\ \end{array} } \right)A^{n + 1} ( - 1)^{n} \int\limits_{{\gamma_{0} }}^{\infty } {\ln \left( {\frac{\gamma }{{\gamma_{0} }}} \right)_{1} \left( {\exp \left( {\frac{ - \gamma }{{\bar{\gamma }}}} \right)} \right)^{n + 1} d\gamma } } . $$
(11)

Simplifying the integral in (11) using Eq. (2) of section 4.331 of [28], we obtain

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{OPRA}}^{{({\text{CE}})}} }}{B} = \frac{{K\gamma_{0} }}{\ln 2}\sum\limits_{n = 0}^{K - 1} {\left( {\begin{array}{*{20}c} {K - 1} \\ n \\ \end{array} } \right)A^{n + 1} } \left[ {\frac{1}{{(n + 1)\gamma_{0} }}E_{1} \left( {\frac{{(n + 1)\gamma_{0} }}{\varGamma }} \right)} \right], $$
(12)

where \( E_{1} (x) = \int_{x}^{\infty } {\frac{{e^{ - t} dt}}{t}} \) is the exponential integral function defined in p. xxxv [28], and B [Hz] is the channel bandwidth and γ 0 is the optimal cut-off SNR level below which data transmission is suspended. This optimal cut-off SNR, γ 0 must satisfy [27]

$$ \int\limits_{{\gamma_{0} }}^{\infty } {\left( {\frac{1}{{\gamma_{0} }} - \frac{1}{\gamma }} \right)\mathop f\nolimits_{{\gamma_{m} }}^{(CE)} (\gamma )d\gamma = 1} . $$
(13)

To achieve the capacity in (12), the channel fade level must be tracked both at the receiver and the transmitter, and the transmitter has to adapt its power and rate accordingly, allocating higher power levels and rates for good channel conditions (γ large), and lower power levels and rates for unfavourable channel conditions (γ small). Since no data is sent when γ < γ 0, the optimal policy suffers a probability of outage, \( {\text{P}}_{\text{out}}^{{({\text{CE}})}} \), equal to the probability of no transmission, given by

$$ {\text{P}}_{\text{out}}^{{({\text{CE}})}} = P\left( {\gamma < \gamma_{0} } \right) = 1 - \int\limits_{{\gamma_{0} }}^{\infty } {f_{{\gamma_{m} }}^{{(\text{CE})}} (\gamma )d\gamma } = \int\limits_{0}^{{\gamma_{0} }} {f_{{\gamma_{m} }}^{(CE)} } (\gamma )d\gamma . $$
(14)

Substituting (9) into (14) and simplifying the outage probability expression, we have

$$ \mathop {\text{P}}\nolimits_{\text{out}}^{{ ( {\text{CE)}}}} = K\sum\limits_{n = 0}^{K - 1} {\left( {\begin{array}{*{20}c} {K - 1} \\ n \\ \end{array} } \right)\frac{{A^{n + 1} }}{\varGamma }\left( { - 1} \right)^{n} } \,\left( {1 - \exp \;\left( {\frac{{ - \gamma_{o} (n + 1)}}{\varGamma }} \right)} \right). $$
(15)

3.2 Optimal Rate Adaptation with Constant Transmit Power Policy

With optimal rate adaptation to channel fading with a constant transmit power, the spectrum efficiency, \( \frac{{\left\langle {\text{C}} \right\rangle_{\text{ORA}}^{{({\text{CE}})}} }}{B} \) [bits/s/Hz], becomes [27]

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{ORA}}^{{({\text{CE}})}} }}{B} = \int\limits_{0}^{\infty } {\log_{2} (1 + \gamma )f_{{\gamma_{m} }}^{{(\text{CE})}} (\gamma )d\gamma } . $$
(16)

Substituting (9) into (16), we have

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{ORA}}^{{({\text{CE}})}} }}{B} = \frac{K}{{\bar{\gamma }}}\sum\limits_{n = 0}^{K - 1} {\left( {\begin{array}{*{20}c} {K - 1} \\ n \\ \end{array} } \right)} A^{n + 1} ( - 1)^{n} \int\limits_{0}^{\infty } {\log_{2} } (1 + \gamma )\left( {\exp \left( {\frac{ - \gamma }{{\bar{\gamma }}}} \right)} \right)^{n + 1} d\gamma . $$
(17)

Solving for the integral using Eq. (2) of section 4.337 of [28], we have

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{ORA}}^{{({\text{CE}})}} }}{B} = \frac{K}{\ln 2}\sum\limits_{n = 0}^{K - 1} {\left( {\begin{array}{*{20}c} {K - 1} \\ n \\ \end{array} } \right)} A^{n + 1} ( - 1)^{n} \frac{1}{n + 1}\left( {\exp \left( {\frac{n + 1}{{\bar{\gamma }}}} \right)E_{1} \left( {\frac{n + 1}{{\bar{\gamma }}}} \right)} \right). $$
(18)

3.3 Channel Inversion with Fixed Rate Policy

Channel capacity when the transmitter adapts its power to maintain a constant CNR at the receiver (i.e., inverts the channel fading) is also investigated in [27]. This technique uses a fixed-rate modulation and a fixed-code design since the channel after channel inversion appears as a time-invariant AWGN channel. As a result, channel inversion with fixed rate is the least complex technique to implement, assuming good channel estimates are available at the transmitter and receiver. The spectrum efficiency with this technique, \( \frac{{\left\langle {\text{C}} \right\rangle_{\text{CIFR}}^{{({\text{CE}})}} }}{B} \) [bits/s/Hz], is derived from the capacity of an AWGN channel, and is given as [27]

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{CIFR}}^{{ ( {\text{CE)}}}} }}{\text{B}} = \log_{2} \left( {1 + \frac{1}{{\int\limits_{0}^{\infty } {\frac{{f_{{\gamma_{\text{m}} }}^{{ ( {\text{CE)}}}} (\gamma )}}{\gamma }d\gamma } }}} \right). $$
(19)

Substituting (9) into (19) and solving using Eq. (3) in section 3.352 of [28], we obtain

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{CIFR}}^{{ ( {\text{CE)}}}} }}{\text{B}} = \log_{2} \left( {1 + \frac{1}{{\frac{K}{{\bar{\gamma }}}\sum\limits_{n = 0}^{K - 1} {\left( {\begin{array}{*{20}c} {K - 1} \\ n \\ \end{array} } \right)} A^{n + 1} ( - 1)^{n} E_{1} \left( {\frac{{(n + 1)\gamma_{\hbox{min} } }}{{\bar{\gamma }}}} \right) - E_{1} \left( {\frac{{(n + 1)\gamma_{\hbox{max} } }}{{\bar{\gamma }}}} \right)}}} \right). $$
(20)

3.4 Truncated Channel Inversion with Fixed Rate Policy

Channel inversion with fixed rate policy suffers a large capacity penalty relative to other techniques since a large amount of transmit power is required to compensate for deep channel fades. Another approach is to use a modified inversion policy which inverts channel fading only above a fixed cut-off fade depth, γ0. The spectrum efficiency with truncated channel inversion and fixed rate policy \( \frac{{\left\langle {\text{C}} \right\rangle_{\text{TIFR}}^{{({\text{CE}})}} }}{B} \) [bits/s/Hz] is derived in [27] as

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{TIFR}}^{{ ( {\text{CE)}}}} }}{\text{B}} = \log_{2} \left( {1 + \frac{1}{{\int\limits_{{\gamma_{0} }}^{\infty } {\frac{{\mathop f\nolimits_{{\gamma_{m} }}^{(CE)} (\gamma )}}{\gamma }d\gamma } }}} \right)\left( {1 - {\text{P}}_{\text{out}}^{{({\text{CE}})}} } \right). $$
(21)

Substituting (9) and (15) into (21) and solving using Eq. (2) in section 3.352 of [28], we obtain

$$ \begin{aligned}\frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{TIFR}}^{{ ( {\text{CE)}}}} }}{\text{B}} = \log_{2} \left( {1 + \frac{1}{{\frac{K}{\varGamma }\sum\limits_{n = 0}^{K - 1} {\left( {\begin{array}{*{20}c} {K - 1} \\ n \\ \end{array} } \right)A^{n + 1} ( - 1)^{n} E_{1} \left( {\frac{{(n + 1)\gamma_{0} }}{\varGamma }} \right)} }}} \right)\\ \left( {1 - K\sum\limits_{n = 0}^{K - 1} {\left( {\begin{array}{*{20}c} {K - 1} \\ n \\ \end{array} } \right)\frac{{A^{n + 1} }}{\varGamma }\left( { - 1} \right)^{n} } \,\left( {1 - \exp \;\left( {\frac{{ - \gamma_{o} (n + 1)}}{\varGamma }} \right)} \right)} \right). \end{aligned}$$
(22)

4 User Scheduling with Limited Feedback Scenario

In full-feedback communication, we assume that all users send their channel SNR information to the base station. Although the base station only requires a feedback from the user with the best channel quality, the users are not aware of the channel conditions of other users. Therefore, for the purpose of objective scheduling and resource allocation, the base station needs a feedback from all active users. In order to reduce the feedback load, in each frequency-slot only a set of active users whose channel SNR is greater than a pre-defined threshold (γ > γth) should feedback their channel information to the base station, and the other users remain silent. If none of the users have a SNR above the threshold (γ ≤ γth), the scheduler in the base station selects a random user. Assuming that the users’ SNRs are i.i.d, we can express the CDF of the selected user’s SNR as [26]

$$ \mathop F\nolimits_{{\gamma_{\text{m}} }}^{{({\text{CE}})}} (\gamma ) = \left\{ {\begin{array}{*{20}l} {\left( {F_{M}^{(CE)} \left( {\gamma_{th} } \right)} \right)^{K - 1} F_{M}^{(CE)} (\gamma )} \hfill & {\gamma \le \gamma_{th} } \hfill \\ {\sum\limits_{k = 1}^{K} {\left( \begin{gathered} K \hfill \\ k \hfill \\ \end{gathered} \right)\left[ {F_{M}^{(CE)} \left( {\gamma_{th} } \right)} \right]^{K - k} .} } \hfill & , \hfill \\ {{\text{x}}\left[ {F_{M}^{(CE)} \left( \gamma \right) - F_{M}^{(CE)} \left( {\gamma_{th} } \right)} \right]^{k} } \hfill & {\gamma > \gamma_{th} } \hfill \\ \end{array} } \right. $$
(23)

Therefore, the PDF can be obtained by taking the derivative of the above CDF in (23) with respect to γ. The PDF is written as [26]

$$ \mathop f\nolimits_{{\gamma_{\text{m}} }}^{{({\text{CE}})}} (\gamma ) = \left\{ {\begin{array}{*{20}l} {\left( {F_{M}^{(CE)} \left( {\gamma_{th} } \right)} \right)^{K - 1} f_{M}^{(CE)} \left( \gamma \right).} \hfill & {\gamma \le \gamma_{th} } \hfill \\ {\sum\limits_{k = 1}^{K} {\left( \begin{gathered} K \hfill \\ k \hfill \\ \end{gathered} \right)kf_{M}^{(CE)} \left( \gamma \right)\left[ {F_{M}^{(CE)} \left( {\gamma_{th} } \right)} \right]^{K - k} .} } \hfill & {} \hfill \\ {{\text{x}}\left[ {F_{M}^{(CE)} \left( \gamma \right) - F_{M}^{(CE)} \left( {\gamma_{th} } \right)} \right]^{k - 1} .} \hfill & {\gamma > \gamma_{th} } \hfill \\ \end{array} } \right. $$
(24)

By substituting the expressions for \( F_{M}^{{({\text{CE}})}} (\gamma ) \) and \( f_{M}^{{({\text{CE}})}} (\gamma ) \) from (2) and (3) into (23) and (24), and after simplification, we obtain new closed-form expressions for the CDF and PDF of the selected users’ SNR with combining errors under the limited feedback scenario as

$$ \mathop F\nolimits_{{\gamma_{\text{m}} }}^{{({\text{CE}})}} (\gamma ) = \left\{ {\begin{array}{*{20}l} {\left( {\sum\limits_{k = 0}^{K - 1} {\left( {\begin{array}{*{20}c} {K - 1} \\ k \\ \end{array} } \right)( - 1)^{k} A^{k} \exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)^{k} } } \right)\left( {1 - A\exp \left( {\frac{ - \gamma }{{\bar{\gamma }}}} \right)} \right).} \hfill & {\gamma \le \gamma_{th} } \hfill \\ {\sum\limits_{k = 1}^{K} {\left( \begin{gathered} K \hfill \\ k \hfill \\ \end{gathered} \right)\left[ {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right]^{K - k} .} } \hfill & {} \hfill \\ {{\text{x}}\left[ {A\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right) - A\exp \left( {\frac{ - \gamma }{{\bar{\gamma }}}} \right)} \right]^{k} } \hfill & {\gamma > \gamma_{th} ,} \hfill \\ \end{array} } \right. $$
(25)
$$ \mathop f\nolimits_{{\gamma_{\text{m}} }}^{{({\text{CE}})}} (\gamma ) = \left\{ {\begin{array}{*{20}l} {\left( {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{\varGamma }} \right)} \right)^{K - 1} \frac{A}{\varGamma }\exp \left( {\frac{ - \gamma }{\varGamma }} \right).} \hfill & {\gamma \le \gamma_{th}} \hfill \\ {\sum\limits_{k = 1}^{K} {\left( \begin{gathered} K \hfill \\ k \hfill \\ \end{gathered} \right)k\frac{A}{\varGamma }\exp \left( {\frac{ - \gamma }{\varGamma }} \right)\left[ {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{\varGamma }} \right)} \right]^{K - k} .} } \hfill & {} \hfill \\ {{\text{x}}\left[ {A\exp \left( {\frac{{ - \gamma_{th} }}{\varGamma }} \right) - A\exp \left( {\frac{ - \gamma }{\varGamma }} \right)} \right]^{k - 1} .} \hfill & {\gamma > \gamma_{th} ,} \hfill \\ \end{array} } \right. $$
(26)

respectively. The user scheduling with limited feedback scenario has two cases to be considered namely (1) Users whose SNRs are greater than the predetermined threshold are allowed to feedback their information to the base station (γ > γ th ). (2) If none of the users’ SNR is above the predetermined threshold, the scheduler selects a random user (γ ≤ γ th ). In the following section, we will discuss the adaptation policies for both the above cases separately.

4.1 Determining the SNR Threshold for Reduced-Feedback Load Scenario

The normalized average feedback load, \( \bar{F} \), is defined as the ratio of the average load per time-slot over the total number of active users K. It is equivalent to the probability of γ > γth. Therefore, it can be expressed in terms of the CDF as \( \bar{F} = Pr(\gamma > \gamma_{th} ) = 1 - F_{\gamma } \left( {\gamma_{th} } \right) \), i.e.,

$$ \mathop {1 - F}\nolimits_{\text{M}}^{{({\text{CE}})}} (\gamma ) = \left( {\left( {1 - \rho^{2} } \right)^{M - 1} } \right)\exp \left( {\frac{ - \gamma }{{\bar{\gamma }}}} \right) $$

where \( 0 \le \bar{F} \le 1 \) and \( \bar{F} = 1 \) corresponds to a full feedback load. Therefore, for a given feedback load, the corresponding SNR threshold, γth, depends on the multiuser system settings such as the number of transmit and receive antennas. This threshold can be obtained from \( \gamma_{th} = F_{\gamma }^{ - 1} (1 - \bar{F}) \) where \( F_{\gamma }^{ - 1} \) (CDF) is the inverse function of the given CDF in (2) and it can be calculated numerically [26] as

$$ \gamma_{th} = \varGamma \log \left( {\frac{1}{{\left( {1 - \rho^{2} } \right)^{M - 1} }}} \right). $$

4.2 Users’ SNRs Which are Greater than the Predetermined Threshold (γ > γ th)

The CDF and PDF of the selected user’s SNR with combining errors under limited feedback scenario with users SNRs which are greater than the predetermined threshold (γ > γ th) is rewritten from (25) and (26) as

$$ \mathop F\nolimits_{{\gamma_{\text{m}} }}^{{({\text{CE}})}} (\gamma ) = \sum\limits_{k = 1}^{K} {\left( \begin{gathered} K \hfill \\ k \hfill \\ \end{gathered} \right)\left[ {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right]}^{K - k} \left[ {A\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right) - A\exp \left( {\frac{ - \gamma }{{\bar{\gamma }}}} \right)} \right]^{k} , $$
(27)
$$ \mathop f\nolimits_{{\gamma_{\text{m}} }}^{{({\text{CE}})}} (\gamma ) = \sum\limits_{k = 1}^{K} {\left( \begin{gathered} K \hfill \\ k \hfill \\ \end{gathered} \right)k\frac{A}{{\bar{\gamma }}}\exp \left( {\frac{ - \gamma }{{\bar{\gamma }}}} \right)\left[ {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right]}^{K - k} \left[ {A\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right) - A\exp \left( {\frac{ - \gamma }{{\bar{\gamma }}}} \right)} \right]^{k - 1} , $$
(28)

respectively. Further simplification by applying binomial expansion yields

$$\begin{aligned} \mathop f\nolimits_{{\gamma_{\text{m}} }}^{{({\text{CE}})}} (\gamma ) &= \sum\limits_{k = 1}^{K} {\left( \begin{aligned} K \hfill \\ k \hfill \\ \end{aligned} \right)\,k\frac{{A^{k} }}{\varGamma }\left[ {1 - A\exp \;\left( {\frac{{ - \gamma_{th} }}{\varGamma }} \right)} \right]^{K - k} } \left[ {\exp \;\left( {\frac{{ - \gamma_{th} }}{\varGamma }} \right)} \right]^{k - 1}\\&\quad\times \exp \;\left( {\frac{ - \gamma }{\varGamma }} \right)\sum\limits_{l = 0}^{k - 1} {( - 1)^{l} \left( {\begin{array}{*{20}c} {k - 1} \\ l \\ \end{array} } \right) \frac{{\exp \;\left( {\frac{ - (l + 1)\gamma }{\varGamma }} \right)}}{{\exp \;\left( {\frac{{ - (l + 1)\gamma_{th} }}{\varGamma }} \right)}}} .\end{aligned} $$
(29)

By applying the four adaptation policies using the above PDF, we obtain expressions for capacity of limited feedback scenario with users SNRs which are greater than the predetermined threshold (γ > γ th) as follows:

4.2.1 Optimal Simultaneous Power and Rate Adaptation Policy

Substituting (29) into (10), we obtain the expression for \( \frac{{\left\langle {\text{C}} \right\rangle_{\text{OPRA}}^{{({\text{CE}})}} }}{\text{B}} \) [bits/s/Hz] from [27] as

$$ \begin{aligned} \frac{{\mathop {\left\langle C \right\rangle }\nolimits_{OPRA}^{(CE)} }}{B} & = \sum\limits_{k = 1}^{K} {\left( \begin{gathered} K \hfill \\ k \hfill \\ \end{gathered} \right)k\frac{{A^{k} }}{{\bar{\gamma }}}\left[ {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right]^{K - k} } \left[ {\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right]^{k - 1} \\ & \quad \times \sum\limits_{l = 0}^{k - 1} {( - 1)^{l} \left( {\begin{array}{*{20}c} {k - 1} \\ l \\ \end{array} } \right)} \int\limits_{{\gamma_{0} }}^{\infty } {\log_{2} \left( {\frac{\gamma }{{\gamma_{0} }}} \right)} \left( {\frac{{\exp \left( {\frac{ - (l + 1)\gamma }{{\bar{\gamma }}}} \right)}}{{\exp \left( {\frac{{ - (l + 1)\gamma_{th} }}{{\bar{\gamma }}}} \right)}}} \right)d\gamma . \\ \end{aligned} $$
(30)

Simplifying the integral in (30) using Eq. (2) of section 4.331 of [28], we obtain

$$ \begin{aligned} \frac{{\mathop {\left\langle C \right\rangle }\nolimits_{OPRA}^{(CE)} }}{B} & = \sum\limits_{k = 1}^{K} {\left( \begin{gathered} K \hfill \\ k \hfill \\ \end{gathered} \right)kA^{k} \left[ {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{\varGamma }} \right)} \right]^{K - k} } \left[ {\exp \left( {\frac{{ - \gamma_{th} }}{\varGamma }} \right)} \right]^{k - 1} \\ &\quad \times \sum\limits_{l = 0}^{k - 1} {\frac{{( - 1)^{l} }}{l + 1}\left( {\begin{array}{*{20}c} {k - 1} \\ l \\ \end{array} } \right)} \exp \left( {\frac{{l\gamma_{th} }}{\varGamma }} \right)E_{1} \left( {\frac{{(l + 1)\gamma_{0} }}{\varGamma }} \right). \\ \end{aligned} $$
(31)

The optimal policy suffers a probability of outage, \( {\text{P}}_{\text{OPRA}}^{{({\text{CE}})}} \), equal to the probability of no transmission. Substituting (29) into (14) and simplifying the outage probability expression, we have

$$ \begin{aligned} \mathop P\nolimits_{\text{out}}^{(CE)} & = \sum\limits_{k = 1}^{K} {\left( \begin{gathered} K \hfill \\ k \hfill \\ \end{gathered} \right)kA^{k} \left[ {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{\varGamma }} \right)} \right]^{K - k} } \left[ {\exp \left( {\frac{{ - \gamma_{th} }}{\varGamma }} \right)} \right]^{k - 1} \\ &\quad \times \sum\limits_{l = 0}^{k - 1} {\frac{{( - 1)^{l} }}{l + 1}\left( {\begin{array}{*{20}c} {k - 1} \\ l \\ \end{array} } \right)} \exp \left( {\frac{{ - l\gamma_{th} }}{\varGamma }} \right)\left[ {1 - \exp \left( {\frac{{ - (l + 1)\gamma_{0} }}{\varGamma }} \right)} \right]. \\ \end{aligned} $$
(32)

4.2.2 Optimal Rate Adaptation with Constant Transmit Power Policy

Substituting (29) into (16), we obtain the expression for [bits/s/Hz] as [27]

$$ \begin{aligned} \frac{{\mathop {\left\langle C \right\rangle }\nolimits_{ORA}^{(CE)} }}{B} & = \sum\limits_{k = 1}^{K} {\left( \begin{gathered} K \hfill \\ k \hfill \\ \end{gathered} \right)k\frac{{A^{k} }}{{\bar{\gamma }}}\left[ {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right]^{K - k} } \left[ {\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right]^{k - 1} \\ &\quad \times \sum\limits_{l = 0}^{k - 1} {( - 1)^{l} \left( {\begin{array}{*{20}c} {k - 1} \\ l \\ \end{array} } \right)} \int\limits_{0}^{\infty } {\log_{2} \left( {1 + \gamma } \right)} \left( {\frac{{\exp \left( {\frac{ - (l + 1)\gamma }{{\bar{\gamma }}}} \right)}}{{\exp \left( {\frac{{ - (l + 1)\gamma_{th} }}{{\bar{\gamma }}}} \right)}}} \right)d\gamma . \\ \end{aligned} $$
(33)

Solving (32) using Eq. (2) of section 4.337 of [28], we have

$$ \begin{aligned} \frac{{\mathop {\left\langle C \right\rangle }\nolimits_{ORA}^{(CE)} }}{B} & = \sum\limits_{k = 1}^{K} {\left( \begin{gathered} K \hfill \\ k \hfill \\ \end{gathered} \right)k\frac{{A^{k} }}{\varGamma }\left[ {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{\varGamma }} \right)} \right]^{K - k} } \left[ {\exp \left( {\frac{{ - \gamma_{th} }}{\varGamma }} \right)} \right]^{k - 1} \\ &\quad \times \sum\limits_{l = 0}^{k - 1} {\frac{{( - 1)^{l} }}{l + 1}\left( {\begin{array}{*{20}c} {K - 1} \\ l \\ \end{array} } \right)} \exp \left( {\frac{{l\gamma_{th} }}{\varGamma }} \right)\exp \left( {\frac{l + 1}{\varGamma }} \right)E_{1} \left( {\frac{l + 1}{\varGamma }} \right). \\ \end{aligned} $$
(34)

4.2.3 Channel Inversion with Fixed Rate Policy

The spectrum efficiency with this technique,\( \frac{{\left\langle {\text{C}} \right\rangle_{\text{CIFR}}^{{({\text{CE}})}} }}{\text{B}} \) [bits/s/Hz], is obtained by substituting (29) into (19) (given in [27]) as

$$ \frac{{\mathop {\left\langle C \right\rangle }\nolimits_{CIFR}^{(CE)} }}{B} = \log_{2} \left( {1 + \frac{1}{{\sum\limits_{k = 1}^{K} {\left( \begin{gathered} K \hfill \\ k \hfill \\ \end{gathered} \right)k\frac{{A^{k} }}{{\bar{\gamma }}}\left[ {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right]^{K - k} } \left[ {\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right]^{k - 1} \sum\limits_{l = 0}^{k - 1} {( - 1)^{l} \left( {\begin{array}{*{20}c} {k - 1} \\ l \\ \end{array} } \right)} \int\limits_{0}^{\infty } {\left( {\frac{{\exp \left( {\frac{ - (l + 1)\gamma }{{\bar{\gamma }}}} \right)}}{{\exp \left( {\frac{{ - (l + 1)\gamma_{th} }}{{\bar{\gamma }}}} \right)}}} \right)} d\gamma }}} \right). $$
(35)

Solving (34) using Eq. (3) in section 3.352 of [28], we obtain

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{CIFR}}^{{ ( {\text{CE)}}}} }}{\text{B}} = \log_{2} \left( {1 + \frac{1}{{\sum\limits_{k = 1}^{K} {\left( \begin{gathered} K \hfill \\ k \hfill \\ \end{gathered} \right)k\frac{{A^{k} }}{\varGamma }\left[ {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{\varGamma }} \right)} \right]^{K - k} } \left[ {\exp \left( {\frac{{ - \gamma_{th} }}{\varGamma }} \right)} \right]^{k - 1} \sum\limits_{l = 0}^{k - 1} {( - 1)^{l} \left( {\begin{array}{*{20}c} {k - 1} \\ l \\ \end{array} } \right)} \exp \left( {\frac{{l\gamma_{th} }}{\varGamma }} \right)\left[ {E_{1} \left( {\frac{{(l + 1)\gamma_{\hbox{min} } }}{\varGamma }} \right) - E_{1} \left( {\frac{{(l + 1)\gamma_{\hbox{max} } }}{\varGamma }} \right)} \right]}}} \right). $$
(36)

4.2.4 Truncated Channel Inversion with Fixed Rate Policy

The spectrum efficiency with truncated channel inversion and fixed rate policy \( \frac{{\left\langle {\text{C}} \right\rangle_{\text{TIFR}}^{{({\text{CE}})}} }}{\text{B}} \) [bits/s/Hz], for limited feedback scenario is derived by substituting (29) into (21) (given in [27]) as

$$ \frac{{\mathop {\left\langle C \right\rangle }\nolimits_{TIFR}^{(CE)} }}{B} = \log_{2} \left( {1 + \frac{1}{{\sum\limits_{k = 1}^{K} {\left( \begin{gathered} K \hfill \\ k \hfill \\ \end{gathered} \right)k\frac{{A^{k} }}{{\bar{\gamma }}}\left[ {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right]^{K - k} } \left[ {\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right]^{k - 1} \sum\limits_{l = 0}^{k - 1} {( - 1)^{l} \left( {\begin{array}{*{20}c} {k - 1} \\ l \\ \end{array} } \right)} \int\limits_{{\gamma_{0} }}^{\infty } {\left( {\frac{{\exp \left( {\frac{ - (l + 1)\gamma }{{\bar{\gamma }}}} \right)}}{{\exp \left( {\frac{{ - (l + 1)\gamma_{th} }}{{\bar{\gamma }}}} \right)}}} \right)} d\gamma }}} \right) \times \left( {1 - {\text{P}}_{\text{out}}^{{({\text{CE}})}} } \right) $$
(37)

Substituting (29) into (21) and solving using Eq. (2) in section 3.352 of [28], we have

$$ \begin{aligned} \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{TIFR}}^{{ ( {\text{CE)}}}} }}{\text{B}} & = \log_{2} \left( {1 + \frac{1}{{\sum\limits_{k = 1}^{K} {\left( \begin{gathered} K \hfill \\ k \hfill \\ \end{gathered} \right)k\frac{{A^{k} }}{\varGamma }\left[ {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{\varGamma }} \right)} \right]^{K - k} } \left[ {\exp \left( {\frac{{ - \gamma_{th} }}{\varGamma }} \right)} \right]^{k - 1} \sum\limits_{l = 0}^{k - 1} {( - 1)^{l} \left( {\begin{array}{*{20}c} {k - 1} \\ l \\ \end{array} } \right)E_{1} \left( {\frac{{(l + 1)\gamma_{0} }}{\varGamma }} \right)} }}} \right) \\ & \quad \times \left( {1 - \sum\limits_{k = 1}^{K} {\,\left( \begin{gathered} K \hfill \\ k \hfill \\ \end{gathered} \right)\,kA^{k} \left[ {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{\varGamma }} \right)} \right]^{K - k} } \left[ {\exp \left( {\frac{{ - \gamma_{th} }}{\varGamma }} \right)} \right]^{k - 1} \sum\limits_{l = 0}^{k - 1} {\frac{{( - 1)^{l} }}{l + 1}\left( {\begin{array}{*{20}c} {k - 1} \\ l \\ \end{array} } \right)} \exp \left( {\frac{{ - l\gamma_{th} }}{\varGamma }} \right)\left[ {1 - \exp \left( {\frac{{ - (l + 1)\gamma_{0} }}{\varGamma }} \right)} \right]} \right)\,. \\ \end{aligned} $$
(38)

4.3 All Users SNRs Lower than the Predetermined Threshold (γ ≤ γth)

The CDF and PDF in the case of all users’ SNRs are lower than the predetermined threshold with combining errors under limited feedback scenario with users’ SNRs which are greater than the predetermined threshold (γ ≤ γth), and is rewritten from (25) and (26) as

$$ \mathop F\nolimits_{{\gamma_{\text{m}} }}^{{({\text{CE}})}} (\gamma ) = \left( {\sum\limits_{k = 0}^{K - 1} {\left( {\begin{array}{*{20}c} {k - 1} \\ l \\ \end{array} } \right)( - 1)^{k} A^{k} \exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)^{k} } } \right)\left( {1 - A\exp \left( {\frac{ - \gamma }{{\bar{\gamma }}}} \right)} \right), $$
(39)
$$ \mathop f\nolimits_{{\gamma_{\text{m}} }}^{{({\text{CE}})}} (\gamma ) = \left( {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right)^{K - 1} \frac{A}{{\bar{\gamma }}}\exp \left( {\frac{ - \gamma }{{\bar{\gamma }}}} \right), $$
(40)

respectively. By applying the four adaptation policies using the above PDF, we get expressions for capacity of limited feedback scenario with all user SNRs lesser than the predetermined threshold as follows:

4.3.1 Optimal Simultaneous Power and Rate Adaptation Policy

Substituting (39) into (10), we obtain the expression for \( \frac{{\left\langle {\text{C}} \right\rangle_{\text{OPRA}}^{{({\text{CE}})}} }}{B} \) [bits/s/Hz] from [27] as

$$ \frac{{\mathop {\left\langle C \right\rangle }\nolimits_{OPRA}^{(CE)} }}{B} = \left( {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right)^{K - 1} \frac{A}{{\bar{\gamma }}}\int\limits_{{\gamma_{0} }}^{\infty } {\log_{2} } \left( {\frac{{\gamma_{0} }}{{\bar{\gamma }}}} \right)\exp \left( {\frac{ - \gamma }{{\bar{\gamma }}}} \right)d\gamma . $$
(41)

Simplifying the integral in (41) using Eq. (2) of section 4.331 of [28], we obtain

$$ \frac{{\mathop {\left\langle C \right\rangle }\nolimits_{OPRA}^{(CE)} }}{B} = \left( {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right)^{K - 1} \frac{A}{\ln 2}E_{1} \left( {\frac{{\gamma_{0} }}{{\bar{\gamma }}}} \right). $$
(42)

The optimal policy suffers a probability of outage, \( {\text{P}}_{\text{out}}^{{({\text{CE}})}} \), equal to the probability of no transmission. Substituting (39) into (14) and simplifying the outage probability expression, we have

$$ \mathop P\nolimits_{\text{out}}^{(CE)} = \left( {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right)^{K - 1} A\left[ {1 - \exp \left( {\frac{{ - \gamma_{0} }}{{\bar{\gamma }}}} \right)} \right]. $$
(43)

4.3.2 Optimal Rate Adaptation with Constant Transmit Power Policy

Substituting (39) into (16), we have the expression for \( \frac{{\left\langle {\text{C}} \right\rangle_{\text{ORA}}^{{({\text{CE}})}} }}{\text{B}} \) [bits/s/Hz] as

$$ \frac{{\mathop {\left\langle C \right\rangle }\nolimits_{ORA}^{(CE)} }}{B} = \left( {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right)^{K - 1} \frac{A}{{\bar{\gamma }}}\int\limits_{0}^{\infty } {\log_{2} } \left( {1 + \gamma } \right)\exp \left( {\frac{ - \gamma }{{\bar{\gamma }}}} \right)d\gamma . $$
(44)

Solving (44) using Eq. (2) of section 4.337 of [28], we have

$$ \frac{{\mathop {\left\langle C \right\rangle }\nolimits_{ORA}^{(CE)} }}{B} = \left( {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right)^{K - 1} \frac{A}{\ln 2}\exp \left( {\frac{1}{{\bar{\gamma }}}} \right)E_{1} \left( {\frac{1}{{\bar{\gamma }}}} \right) . $$
(45)

4.3.3 Channel Inversion with Fixed Rate Policy

The spectrum efficiency with this technique, \( \frac{{\left\langle {\text{C}} \right\rangle_{\text{CIFR}}^{{({\text{CE}})}} }}{B} \) [bits/s/Hz], is obtained by substituting (39) into (19) (given in [27]) as

$$ \frac{{\mathop {\left\langle C \right\rangle }\nolimits_{CIFR}^{(CE)} }}{B} = \log_{2} \left( {1 + \frac{1}{{\left( {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right)^{K - 1} \frac{A}{{\bar{\gamma }}}\int\limits_{0}^{\infty } {\frac{{\exp \left( {\frac{ - \gamma }{{\bar{\gamma }}}} \right)}}{\gamma }} d\gamma }}} \right). $$
(46)

Solving (46) using Eq. (3) in section 3.352 of [28], we obtain

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{CIFR}}^{{ ( {\text{CE)}}}} }}{\text{B}} = \log_{2} \left( {1 + \frac{1}{{\left( {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right)^{K - 1} \frac{A}{{\bar{\gamma }}}\left[ {E_{1} \left( {\frac{{\gamma_{\hbox{min} } }}{{\bar{\gamma }}}} \right) - E_{1} \left( {\frac{{\gamma_{\hbox{max} } }}{{\bar{\gamma }}}} \right)} \right]}}} \right). $$
(47)

4.3.4 Truncated Channel Inversion with Fixed Rate Policy

The spectrum efficiency with truncated channel inversion and fixed rate policy \( \frac{{\left\langle {\text{C}} \right\rangle_{\text{TIFR}}^{{({\text{CE}})}} }}{B} \) [bits/s/Hz] for limited feedback scenario is derived by substituting (39) into (21) (given in [27]) as

$$ \frac{{\mathop {\left\langle C \right\rangle }\nolimits_{TIFR}^{(CE)} }}{B} = \log_{2} \left( {1 + \frac{1}{{\left( {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right)^{K - 1} \frac{A}{{\bar{\gamma }}}\int\limits_{{\gamma_{0} }}^{\infty } {\frac{{\exp \left( {\frac{ - \gamma }{{\bar{\gamma }}}} \right)}}{\gamma }} d\gamma }}} \right)\left( {1 - {\text{P}}_{\text{out}}^{{({\text{CE}})}} } \right). $$
(48)

Solving (48) using Eq. (2) in section 3.352 of [28], we have

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{TIFR}}^{{ ( {\text{CE)}}}} }}{\text{B}} = \log_{2} \left( {1 + \frac{1}{{\left( {1 - A\exp \;\left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right)^{K - 1} \frac{A}{{\bar{\gamma }}}\left[ {E_{1} \left( {\frac{{\gamma_{0} }}{{\bar{\gamma }}}} \right)} \right]}}} \right) \times 1 - \left( {\left( {1 - A\exp \left( {\frac{{ - \gamma_{th} }}{{\bar{\gamma }}}} \right)} \right)^{K - 1} A\left[ {1 - \exp \left( {\frac{{ - \gamma_{0} }}{{\bar{\gamma }}}} \right)} \right]} \right). $$
(49)

5 Numerical Results

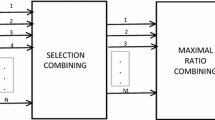
Figure 1 shows the block diagram of the multiuser system model for downlink transmission. Figure 2 shows the average spectral efficiency of the MIMO system with MRC diversity with combining errors versus number of users, with Nt transmit and Nr antennas for K users. Multiuser scheduler simply assigns the channel to a user with the highest instantaneous SNR that satisfies the target BER. In other words, the user having the highest SNR is scheduled for transmission, based on its SNR and the corresponding level, a suitable modulation mode is selected and power scheduled accordingly using the OPRA policy. As can be observed, increasing the number of active users improves the ASE. It is also observed from the graph that as the average SNR per branch increases the Spectral efficiency also increases. This is because increasing the average SNR, a higher level modulation mode can be selected and as the number of users increases, ASE reaches to its maximum achievable value even in the low SNR region. From Fig. 2, it is also inferred that for full feedback with F = 1 gives maximum spectral efficiency for the low SNR case. But if there are more users with SNR feedback greater than the threshold, then even F = 0.7 achieves the targeted spectral efficiency. Also, the spectral efficiency increases as the number of users increases as the spatial multiplexing gain increases.

Fig. 1
figure 1

Block diagram of the multiuser system model for downlink transmission

Full size image
Fig. 2
figure 2

Spectral efficiency for OPRA policy versus number of users (K) for different feedback loads (F)

Full size image

Figure 3 shows the average spectral efficiency of the MIMO system with MRC diversity with combining errors versus number of users K, for the ORA policy. Here, the rate of the information alone is changed in accordance to the channel statistics. The power is distributed equally among all Nt antennas. So, the spectral efficiency obtained is less compared to OPRA policy which follows water-filling policy to distribute power among the transmit antennas. It is also observed from the graph that as the average SNR per branch increases the Spectral efficiency also increases. From Fig. 3, it is clear that F = 1 provides the maximum spectral efficiency in the case of ORA policy also but less compared to OPRA policy. Also, the spectral efficiency increases as the number of users increases because transmitting to users with strong channel at all time, the overall spectral efficiency of the system is made higher.

Fig. 3
figure 3

Spectral efficiency for ORA policy versus number of users (K) for different feedback loads (F)

Full size image

Figures 4 and 5 show the average spectral efficiency of the MIMO system with MRC diversity with combining errors versus number of users K, for the CIFR and TIFR policy. Here, the channel characteristics are inverted in accordance to the channel statistics. This policy is very simple to implement but the improvement in spectral efficiency obtained is very less compared to OPRA and ORA policies. But F = 1 provides the maximum spectral efficiency. The increase in spectral efficiency is more pronounced at low branch SNRs for the full feedback case than feedback loads F < 1. Also, the spectral efficiency increases as the number of users increases as the spatial multiplexing gain increases. Comparing Figs. 4 and 5, it is inferred that TIFR policy provides a better performance than CIFR policy as the transmission is permitted beyond the optimal cut off SNR.

Fig. 4
figure 4

Spectral efficiency for CIFR policy versus number of users (K) for different feedback loads (F)

Full size image
Fig. 5
figure 5

Spectral efficiency for TIFR policy versus number of users (K) for different feedback loads (F)

Full size image

Figures 6 and 7 show the average spectral efficiency of the MIMO system with MRC diversity with combining errors versus number of users, with each user having increased number of receive antennas, for the OPRA and ORA policy for the full-feedback case (F = 1). From the graph, it is inferred that increasing the number of receive antennas improves the average spectral efficiency even in a single user scenario. This is due to the increased receiver antenna diversity. Again, OPRA policy yields best results at high average SNRs.

Fig. 6
figure 6

Spectral efficiency for OPRA policy versus number of users (K) for various receive antenna diversities (M)

Full size image
Fig. 7
figure 7

Spectral efficiency for ORA policy versus number of users (K) for various receive antenna diversities (M)

Full size image

6 Conclusions

The channel capacity per unit bandwidth for different adaptation policies over fading channels with impairments due to combining errors for low SNR regime for full-feedback and limited feedback case have been computed in this paper. Closed-form expressions for spectral efficiencies for four adaptation policies for Full-feedback case and two different limited feedback cases are derived for the MRC diversity reception case and for multiuser scenario. Optimal power and rate adaptation policy provides highest capacity over other adaptation policies with MRC diversity combining and for limited feedback case with \( \gamma > \gamma_{th} \). The numerical results are presented for the same. For the second case of limited feedback with \( \gamma \le \gamma_{th} \), closed-form expressions for spectral efficiencies for the four adaptation policies are also derived. In summary, this paper provides a deep insight on the spectrum efficiency for Rayleigh fading channels with feedback using multiuser scheduling over some of the earlier analytical work done [29–34] for spectrum efficiency for fading channels without feedback or scheduling.