1 Introduction

Cooperative communication is a form of distributed spatial diversity that intensifies cooperation between wireless terminals. There are several types of relaying which the two major types are non-regenerative [E.x. Amplify-and-Forward (AF)] and regenerative [1–9] [E.x. Decode-and-Forward (DF)]. The non-regenerative relaying is appealing most of the times due to its simplicity, as the relays just perform light linear processing on the received signal and forward the signal to the destination [10–14]. Creating several signal paths is one of the most important ways for increasing the diversity in wireless channels. Coping with the fading effects is important in wireless networks. Relay selection (RS) is one of the most important ways for decreasing the fading effects and achieving the diversity [15]. The relay selection problem is based on selecting an appropriate cooperative relay node in the network for a given pair of sources. Relay node selection for one way relay networks was investigated in [16], [17] and for two-way relay networks was investigated in [18]. Bit and symbol error rates are parameters that can help to measure the communication performance. BER is an effective parameter that specialize the information effectiveness. One of the most objective of the relay selection is to decrease the BER between the sources.

Physical layer network coding (PNC) is a subfield of network coding that increases the throughput more than network coding that was introduced in [19]. The PNC is based on the fact that when several electromagnetic waves come together within the same physical space, they add [20]. In [21] the problem of best suited relay selection in network coded wireless networks is discussed and it is shown that the performance of cooperative wireless communication in terms of throughput is better than the direct transmission scheme.

Power allocation (PA) is one of the most important factors for improving the system performance. An optimal power allocation for networks with multi relays was studied in [22]. In [23], the symbol error rate of single relay selection in cooperative networks was studied under Rayleigh fading channels and optimal power allocation among sources and relay was considered.

The combining of Alamouti space time coding (ASTC) and physical layer network coding schemes can provide the highest performance. In [24], the dual relay selection was based on the channels from relays to first source for second source and to second source for first source. In [25], a relay selection scheme was proposed which was based on the minimizing the maximum symbol error rate (SER) of two source nodes.

In this paper, we consider the bi-directional communication system with \(N\) relays. The single relay selection (SRS) scheme is proposed with considering the effect of both transmitters, then we derive the upper and lower bounds for signal to noise ratio (SNR) and by using the derived bounds we can derive lower and upper bounds for the end-to-end bit error rate. Subsequently, the dual relay selection (DRS) scheme is considered and the BER is derived for this scheme, too. For SRS and DRS, the PA is considered among the sources and the selected relay node(s). For SRS, considering the selection scheme, the higher performance is achieved while, for DRS, considering the combination of RS, ASTC and PNC lower bit error rates is obtained.

The diversity orders of various relay selection schemes, including the best-relay selection, best-worse channel selection, and maximum harmonic-mean selection were analyzed in [26]. The most important differences between our work and [26] are: (1) Our derived upper and lower bounds are more tighter than the proposed bounds in [26]. (2) We consider the power allocation between sources and the selected relay node but in [26], the equal power allocation is considered between the source nodes and the selected relay. The result is showed that with optimal power allocation, the performance improves significantly.

The remainder of this paper is organized as follows. Section 2 introduces the model of system and Sect. 3 gives the performance analysis of SRS scheme, while Sect. 4 presents performance of DRS scheme. Section 5 evaluates the power allocation for SRS and DRS. Finally, Sects. 6 and 7 provide the simulation results and conclusions.

2 System Model

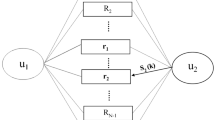
The network model is a two-way relay network consists of \(N\) relay nodes and two source nodes with single antenna (Fig. 1). In the first phase, the source nodes send their information to all of the relay nodes and then one of the relay nodes is selected by the source nodes. The channel coefficients are constant over one frame transmission and change from one frame to another.

Fig. 1
figure 1

System model of SRS

Full size image

Moreover, \(x_1\), \(x_2\) are transmitted signals by \(T_1\) and \(T_2\), respectively. The received signal in each of the relay nodes is equal to

$$\begin{aligned} x_{r_{k}}=\sqrt{P_{t}}h_{1,r_{k}}x_{1}+\sqrt{P_{t}}h_{2,r_{k}}x_{2}+n_{r_{k}}\qquad \forall k=1,\ldots ,N \end{aligned}$$
(1)

where \(P_t\) is the transmission power of the source nodes, while \(h_{1,r_{k}}\) and \(h_{2,r_{k}}\) are the fading coefficients between \(T_1\) , \(T_2 \) and \(r_{k}\), respectively. Furthermore, \(n_{r_{k}}\) is a zero-mean complex Gaussian random variable. The relays amplify the received signals and then send them to each of the source nodes. Therefore, the received signal in \(T_1\) is equal to

$$\begin{aligned} x_{T_{1},r_{k}}={\sqrt{P_{t}}\sqrt{P_{r}}{\beta _k}h_{1,r_{k}}h_{1,r_{k}}x_{1}+\sqrt{P_{t}}\sqrt{P_{r}}}{\beta _k}h_{2,r_{k}}h_{1,r_{k}}x_{2} +n_{T_{1},{r_{k}}}\qquad \forall k=1,\ldots ,N \end{aligned}$$
(2)

where \(\beta _k\) is the amplification gain defined as

$$\begin{aligned} \beta _k=\frac{\sqrt{P_r}}{\sqrt{P_t|h_{1,r_k}|^2+P_t|h_{2,r_k}|^2+N_0}} \qquad \qquad \forall k=1,\ldots , N \end{aligned}$$
(3)

And at high SNRs, \(\beta _k\) is defined as

$$\begin{aligned} \beta _k=\frac{\sqrt{P_r}}{\sqrt{P_t|h_{1,r_k}|^2+P_t|h_{2,r_k}|^2}} \qquad \qquad \forall k=1,\ldots , N \end{aligned}$$
(4)

where \(P_r\) is the transmitted power at relay nodes. Since each of the source nodes knows its own information, the source node can eliminate the self-interference term.

3 Performance Analysis of SRS

In the SRS scheme, both transmitters have an important role in selecting the best relay and select one of the relays that can maximize the average received SNR of the network. The selection is based on the following:

$$\begin{aligned} {R}=\max _{\begin{array}{c} k=1,\ldots ,N \end{array}} \left\{ \frac{1}{2}({\gamma _{T_1,r_{k}} +\gamma _{T_2,r_{k}}) }\right\} \end{aligned}$$
(5)

where \(\gamma _{T_1,r_{k}}\) ,\(\gamma _{T_2,r_{k}}\) are the signal to noise ratios of the \({T_1}\) and \({T_2}\), respectively. The BER is given by (6) that can be written as [27],

$$\begin{aligned} p_{b}=\mathrm {E}\left[ Q{\sqrt{2.\gamma }}\right] ={\frac{1}{2\sqrt{\pi }}} \int _{0}^{\infty }\frac{e^{-x}F_{\gamma }(x)}{\sqrt{x}}dx \end{aligned}$$
(6)

where \(Q(.)\) is the Gaussian Q-function and \(F_{\gamma}(x)\) is the cumulative density function (CDF) of random variable \(\gamma\). In this section the aim is to derive the BER of the SRS scheme with the objective in (5). We should first derive the CDF of (5). Since there are dependent variables in (5) finding an exact expression for the probability density function in all SNRs is difficult. Therefore, we attempt to find new upper and lower bounds. The SNR in each of the source nodes can be expressed by (7).

$$\begin{aligned} \gamma _{T_i,r_{k}}=\frac{{{P_{t}}{P_{r}} \beta _{k}}^2|h_{1,r_k}|^2|h_{2,r_k}|^2}{{N_0}(1+{P_{r}}|h_{i,r_k}|^2 \beta _{k}^2)}\qquad \quad \forall i=1,2 \end{aligned}$$
(7)

Then by defining \(p_t=\frac{P_t}{N_0}$ and $p_r=\frac{P_r}{N_0},\) the average received SNR is obtained as

$$\begin{aligned} \gamma&= \frac{1}{2}\left\{ \gamma _{T_1,r_{k}} +\gamma _{T_2,r_{k}}\right\} \nonumber \\&= \frac{1}{2}\left\{ \frac{{p_r}{p_t}|h_{1,r_k}|^2|h_{2,r_k}|^2}{(p_r+p_t) {|h_{1,r_k}|^2}+p_t{|h_2,r_k|^2}} +\frac{{p_r}{p_t}|h_{1,r_k}|^2|h_{2,r_k}|^2}{(p_r+p_t){|h_{2,r_k}|^2}+p_t{|h_1,r_k|^2}}\right\} \end{aligned}$$
(8)

The following proposition gives the bounds of (8).

Proposition 1

The average received SNR of both terminals is bounded as

$$\begin{aligned}&\frac{1}{2}\frac{4}{(\frac{p_t+p_r}{p_t}+1)^2} \frac{p_r(2p_t+p_r)}{p_t}\frac{|h_{1,r_k}|^2|h_{2,r_k}|^2}{|h_{1,r_k}|^2|+h_{2,r_k}|^2}\le {\gamma }\nonumber \\&\quad \le \frac{1}{2}{\frac{(2p_t+p_r)p_r}{p_t+p_r}} \frac{|h_{1,r_k}|^2|h_{2,r_k}|^2}{|h_{1,r_k}|^2|+h_{2,r_k}|^2} \end{aligned}$$
(9)

Proof

Let define \(Q\) as

$$\begin{aligned} Q=\frac{(|h_{1,r_k}|^2+|h_{2,r_k}|^2)^2}{\left( {\frac{p_t+p_r}{p_t}}|h_{1,r_k}|^2+|h_{2,r_k}|^2\right) \left( {\frac{p_t+p_r}{p_t}}|h_{2,r_k}|^2+|h_{1,r_k}|^2\right) } \end{aligned}$$
(10)

and define \(a=\frac{p_t+p_r}{p_t}\), \(x_1=|h_{1,r_k}|^2\), \(y_1= |h_{2,r_k}|^2\) and \(t = (ax_1+y_1)(ay_1+x_1)\), then the lower bound for t is equal to

$$\begin{aligned} t =(ax_1+y_1)(ay_1+x_1)=a(x_1^2+y_1^2)+(a^2+1)x_1y_1 \ge a(x_1+y_1)^2 \end{aligned}$$
(11)

Also the upper bound for \(t\) is equal to

$$\begin{aligned} t&= a(x_1^2+y_1^2)+(a^2+1)x_1y_1 \le a(x_1^2+y_1^2+2x_1y_1)\nonumber \\&\quad +(a^2+1-2a) \frac{(x_1+y_1)^2}{4}=\frac{(a+1)^2}{4}{(x_1+y_1)^2} \end{aligned}$$
(12)

From the above derived inequalities, the upper and lower bounds are derived for \(Q\) as the following:

$$\begin{aligned} \frac{4}{\left( \frac{p_t+p_r}{p_t}+1\right) ^2}\le Q \le \frac{1}{\frac{p_t+p_r}{p_t}} \end{aligned}$$
(13)

\(\square \)

Then by using proposition 1, the following equation for end-to-end CDF is obtained.

$$\begin{aligned} 1-e^{\left( -2\frac{p_t+p_r}{p_r(2p_t+p_r)} {(\lambda _{x_1}+{\lambda _{y_1}})x}\right) } \le F_{\gamma }(x) \le 1-e^{\left( -\frac{2p_t\left( \frac{p_r+p_t}{p_t}+1\right) ^2}{4p_r(2p_t+p_r)}{(\lambda _{x_1}+{\lambda _{y_1}})x}\right) }\qquad \quad \end{aligned}$$
(14)

where \(|h_{1,r_k}|^2\) and \(|h_{2,r_k}|^2\) are distributed according to exponential distribution with \(\lambda _{x_1}\) and \(\lambda _{y_1}\) parameters, respectively for all \(k=1,\ldots ,N\). By considering (5), the CDF of R can be written as

$$\begin{aligned} F_R(x)=(F_{\gamma }(x))^N \end{aligned}$$
(15)

Using (6), the BER is bound as:

$$\begin{aligned}&\frac{1}{2\sqrt{\pi }}\int _{0}^{\infty }{\frac{e^{-x}}{\sqrt{x}}}{\left( 1-e^{\left( -2\frac{p_t+p_r}{p_r(2p_t+p_r)} {(\lambda _{y_1}+{\lambda _{x_1}})x}\right) }\right) ^N}dx\nonumber \\&\quad \le \bar{P_e}\le \frac{1}{2\sqrt{\pi }}\int _{0}^{\infty } {\frac{e^{-x}}{\sqrt{x}}} {\left( 1-e^{\left( -\frac{2p_t\left( \frac{p_r+p_t}{p_t}+1\right) ^2}{4p_r(2p_t+p_r)} {(\lambda _{y_1}+{\lambda _{x_1}})x}\right) }\right) ^N}dx \end{aligned}$$
(16)

Then by using the binomial coefficients, (16) can be further simplified as in (17).

$$\begin{aligned}&\frac{1}{2\sqrt{\pi }}\sum _{i=0}^{i=N}\left(\begin{array}{l} N\\ i \end{array} \right) {(-1)^i}\int _{0}^{\infty } \frac{e^{-x}}{\sqrt{x}} \left( e^{\left( {-{2\frac{p_t+p_r}{p_r(2p_t+p_r)}(\lambda _{y_1} +{\lambda _{x_1}})x}}\right) }\right) ^i dx \le \bar{P_e}\nonumber \\& \quad\le \frac{1}{2\sqrt{\pi }}\sum _{i=0}^{i=N}\left(\begin{array}{l} N\\ i \end{array} \right){(-1)^i} \int _{0}^{\infty }\frac{e^{-x}}{\sqrt{x}} {\left( e^{\left( -2\frac{p_t\left( \frac{p_r+p_t}{p_t}+1\right) ^2}{4p_r(2p_t+p_r)} (\lambda _{y_1}+{\lambda _{x_1}})x\right) }\right) ^i}dx \end{aligned}$$
(17)

Using [28, Eq.(3.361)], (17) can be written as in (18).

$$\begin{aligned}&\frac{1}{2}\sum _{i=0}^{i=N}\left(\begin{array}{l} N\\ i \end{array} \right) {(-1)^i}\frac{1}{\sqrt{\left( 1+2i\frac{\lambda _{y_1} +{\lambda _{x_1}}}{p_r}\frac{p_t+p_r}{2p_t+p_r}\right) }} \le \bar{P_e}\nonumber \\&\quad \le \frac{1}{2}\sum _{i=0}^{i=N}\left(\begin{array}{l} N\\ i \end{array} \right){(-1)^i} \frac{1}{\sqrt{\left( 1+2ip_t\left( \frac{p_r+p_t}{p_t}+1\right) ^2 \frac{(\lambda _{y_1}+{\lambda _{x_1}})}{4p_r(2p_t+p_r)}\right) }} \end{aligned}$$
(18)

With using the fact that \( \lim _{x \rightarrow 0}1-e^{-x}=x\), the CDF of \(\gamma \) for high SNRs can be expressed as in (19).

$$\begin{aligned}&\left( 2\frac{p_t+p_r}{p_r(2p_t+p_r)} {(\lambda _{y_1}+{\lambda _{x_1}})x}\right) \le F_{\gamma }(x)\nonumber \\&\quad \le \left( 2\frac{p_t\left( \frac{p_r+p_t}{p_t}+1\right) ^2}{4p_r(2p_t+p_r)} {(\lambda _{y_1}+{\lambda _{x_1}})x}\right) \end{aligned}$$
(19)

By using (5), the BER at high SNRs can be written as in (20).

$$\begin{aligned}&\frac{1}{2\sqrt{\pi }}\left( 2\frac{p_t+p_r}{p_r(2p_t+p_r)} {(\lambda _{y_1}+{\lambda _{x_1}})}\right) ^N \Gamma \left( N+\frac{1}{2}\right) \le \bar{P_e}\nonumber \\&\quad \le \frac{1}{2\sqrt{\pi }} \left( 2\frac{p_t\left( \frac{p_r+p_t}{p_t}+1\right) ^2}{4p_r(2p_t+p_r)}{(\lambda _{y_1}+{\lambda _{x_1}})}\right) ^N \Gamma \left( N+\frac{1}{2}\right) \end{aligned}$$
(20)

where gamma function \(\Gamma (x)\), defined by the Euler integral \(\Gamma (x)=\int _{0}^{\infty }{t^{x-1}{e^{-t}}}dt\). The diversity order as defined in [29] is equal to \(N\). This result shows that the full diversity order is achieved.

4 Dual Relay Selection

The aim of dual relay selection (Fig. 2) is improving the BER in the network where two nodes are selected as relay nodes. In the first phase, \(T_1\) and \(T_2\) transmit simultaneously their signals to all the relays where the two channels from the source nodes to the same relay create a multiple access channel (MAC), then the transmitted signals are equal with \(x_{T_1}=\left(\begin{array}{l} {x^{1}_1}\\ {x^{2}_1} \end{array} \right)\) and \(x_{T_2}=\left(\begin{array}{l} {x^{1}_2}\\ {x^{2}_2} \end{array} \right)\) in the first phase. In order to guarantee the orthogonality of space-time coding, the transmitted signals are processed as \(x_{T_1}=\left(\begin{array}{l} {x^{1}_1}\\ {x^{2*}_1} \end{array} \right)\) and \(x_{T_2}=\left(\begin{array}{l} {x^{1}_2}\\ {x^{2*}_2} \end{array} \right) \). Then the received signal at the relay \(r_k\) is given by (21).

$$\begin{aligned} x_{r_{k}}=\sqrt{P_{t}}h_{1,r_{k}}x_{1}+ \sqrt{P_{t}}h_{2,r_{k}}x_{2}+n_{r_{k}}\qquad \forall k=1,\ldots ,N \end{aligned}$$
(21)

where \(P_t\) denotes the transmitted power at \( T_1\) and \(T_2\).

Fig. 2
figure 2

System model of DRS

Full size image

After receiving the signals in the relays, they amplify the received signals and then transmit those signals to the receivers. Then in the second phase, the signals transmitted by relays \(r_k\) and \(r_{k^{\prime}}\) can be expressed as \({{x_{r_{k}}^{\prime}}}=\left(\begin{array}{l}{x^{1}_{r_{k}}} \\ {-x^{2*}_{r_{k}}} \end{array} \right)\) and \({{x_{r_{k^{\prime}}}^{\prime}}}=\left(\begin{array}{l}{x^{1*}_{r_{k^{\prime}}}}\\ {x^{2*}_{r_{k^{\prime}}}}\end{array}\right)\). The received signal in transmitter \(T_1\) is hence given by (22).

$$\begin{aligned} X_{T_{1}}={\beta _{k}}h_{1,r_{k}}{{x_{r_{k}}^{\prime}}} +{\beta _{k^{\prime}}}h_{1,r_{k^{\prime}}}{{x_{r_{k^{\prime}}}^{\prime}}} +n_{{T_{1}}}{k}\ne {k^{\prime}} \end{aligned}$$
(22)

where \(k\) and \(k^{\prime}\) are the index of the selected relays. Also, the SNR in \(T_{1}\) is equal to (23).

$$\begin{aligned} \gamma _{T_{1}}=\frac{{{\beta _{k}}^2|h_{1,r_k}|^2{P_{t}}|h_{2,r_k}|^2 +{\beta _{k^{\prime}}}^2|h_{1,r_k^{\prime}}|^2{P_{t}}|h_{2,r_k^{\prime}}|^2}}{N_0({{{\beta _{k}}^2|h_{1,r_k}|^2 +{\beta _{k^{\prime}}}^2|h_{1,r_k^{\prime}}|^2}})} \end{aligned}$$
(23)

By considering \({\beta _{k}}\) and \({\beta _{k^{\prime}}}\) in equation (4), \(p_{t}=\frac{P_{t}}{N_{0}}\) and \(p_{r}=\frac{P_{r}}{N_{0}}\), then (23) can be written as

$$\begin{aligned} \gamma _{T_1}=\frac{{p_{r}}{p_{t}}|h_{1,r_k}|^2|h_{2,r_k}|^2}{{(2p_{r}+p_{t})}|h_{1,r_k}|^2+{p_{t}}|h_{2,r_k}|^2} +\frac{{p_{r}}{p_{t}}|h_{1,r_{k^{\prime}}}|^2|h_{2,r_{k^{\prime}}}|^2}{{(2p_{r}+p_{t})}|h_{1,r_{k^{\prime}}}|^2+{p_{t}}|h_{2,r_{k^{\prime}}}|^2} \end{aligned}$$
(24)

The SNR in \(T_{1}\) can be written as:

$$\begin{aligned} \gamma _{T_1}=\gamma _{T_1,r_{k}}+\gamma _{T_1,r_{k^{\prime}}} \end{aligned}$$
(25)

It is considered that the exponential parameters are equal to \(\lambda _{x_{1}}\), \(\lambda _{y_{1}}\), \(\lambda _{x_{2}}\) and \(\lambda _{y_{2}}\) for \(|h_{1,r_k}|^2\) , \(|h_{2,r_k}|^2\), \(|h_{1,r_{k^{\prime}}}|^2\) and \(|h_{2,r_{k^{\prime}}}|^2\) distributions, respectively, For all \(k=1,\ldots ,N\). Then the PDF of \(\gamma _{T_1}\) can be derived as the following

$$\begin{aligned} f_{\gamma _{T_1,r_{k}}}(x)={\frac{2p_{r}+p_{t}}{p_{r}}} \left( \frac{\lambda _{x_1}}{2p_r+p_t}+\frac{\lambda _{y_1}}{p_t}\right) \exp \left( -{\frac{2p_{r}+p_{t}}{p_{r}}} \left( \frac{\lambda _{x_1}}{2p_r+p_t}+\frac{\lambda _{y_1}}{p_t}\right) x\right) \end{aligned}$$
(26)

And for the PDF of \({\gamma _{T_1,r_{k^{\prime}}}}\), we will have

$$\begin{aligned} f_{\gamma _{T_1,r_{k^{\prime}}}}(x)={\frac{2p_{r}+p_{t}}{p_{r}}} \left( \frac{\lambda _{x_2}}{2p_r+p_t}+\frac{\lambda _{y_2}}{p_t}\right) \exp \left( -{\frac{2p_{r}+p_{t}}{p_{r}}}\left( \frac{\lambda _{x_2}}{2p_r+p_t}+\frac{\lambda _{y_2}}{p_t}\right) x\right) \end{aligned}$$
(27)

The CDF of \(\gamma _{T_1}\) can be expressed as

$$\begin{aligned} F_{\gamma _{T_{1}}}(x)=\frac{\alpha _{3}}{\alpha _{1}} (1-\exp (-\alpha _{1}x))-\frac{\alpha _{3}}{\alpha _{2}} \left( 1-\exp (-\alpha _{2}x)\right) \end{aligned}$$
(28)

where \({\alpha _1={\frac{2p_{r}+p_{r}}{p_{r}}} (\frac{\lambda _{x_1}}{2p_r+p_t}+\frac{\lambda _{y_1}}{p_t})}\), \({\alpha _2={\frac{2p_{r}+p_{t}}{p_{r}}}(\frac{\lambda _{x_2}}{2p_r+p_t} +\frac{\lambda _{y_2}}{p_t}})\) and \(\alpha _{3}=\frac{\alpha _{1}\alpha _{2}}{\alpha _{2}-\alpha _{1}}\) . Due to the selection of two relays, the maximizing of SNR is performing on \(N^{\prime}\) received signals that \(N^{\prime}\) is equal to \(\frac{N(N-1)}{2}\), as the following equation

$$\begin{aligned} R=\max _{\begin{array}{c} i=1,\ldots ,N^{\prime} \end{array}} \gamma _{T_{1},{i}} \end{aligned}$$
(29)

The CDF of \(R\) is equal to

$$\begin{aligned} F_R(x)=(F_{\gamma _{T_1}}(x))^{N^{\prime}} \end{aligned}$$
(30)

Then BER with considering (6) and using the derived CDF in (28) can be written as

$$\begin{aligned} \bar{P_e}=\frac{1}{2}\sum _{\begin{array}{c} i,j,k \end{array}} \left(\begin{array}{l}{N^{\prime}}\\ {i,j,k}\end{array}\right){\left( \frac{-\alpha _2}{\alpha _2-\alpha _1}\right) ^j} {\left( \frac{\alpha _1}{\alpha _2-\alpha _1}\right) ^k}\sqrt{\frac{1}{1+\alpha _1j+\alpha _2k}} \end{aligned}$$
(31)

And the CDF at high SNRs can directly obtained as

$$\begin{aligned} F_R(x)=\left( \frac{1}{2}{\alpha _1}{\alpha _2}{x^2}\right) ^{N^{\prime}} \end{aligned}$$
(32)

With considering (32), the BER at high SNRs can be expressed as

$$\begin{aligned} {\bar{P_e}}=\frac{1}{2\sqrt{\pi }} \int _{0}^{\infty }{\frac{e^{-x}}{\sqrt{x}}}{\left( \frac{1}{2} {\alpha _1}{\alpha _2}{x^2}\right) ^{N^{\prime}}}dx=\frac{1}{2\sqrt{\pi }} \left( \frac{1}{2}{\alpha _1}{\alpha _2}\right) ^{N^{\prime}}\Gamma \left( 2N^{\prime}+\frac{1}{2}\right) \end{aligned}$$
(33)

5 Power Allocation

In this section, we discuss about the optimum transmission power of the relay node in the single and dual relay selection schemes. The evaluating of power allocation for minimizing the BER is considered. our assumption is that the \(\lambda _{x_{1}}\), \(\lambda _{y_{1}}\), \(\lambda _{x_{2}}\) and \(\lambda _{y_{2}}\) are equal to 1.

5.1 Single Relay Selection

With considering the upper and lower bounds for \({\bar{P_{e}}}\), we can define the optimization problem for the lower bound as:

$$\begin{aligned} \left\{ \begin{array}{ll} \min &{} \bar{P}_ {{eL}}\\ s.t. &{}2P_t+P_r = P\\ &{}0 \le P_t \le P\\ &{}0 \le P_r \le P \end{array} \right. \end{aligned}$$
(34)

By setting the derivatives of Lagrangian in (34) versus \(P_t\) and \(P_r\) , we will have the following equations

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial {L( \bar{P}_ {{eL}})}}{\partial {P_t}} =\frac{\partial {\bar{P}_ {{eL}}}}{\partial {P_t}}+2\lambda =0\\ \frac{\partial {L(\bar{P}_ {{eL}})}}{\partial {P_r}} =\frac{\partial {\bar{P}_ {{eL}}}}{\partial {P_r}}+\lambda =0 \end{array} \right. \end{aligned}$$
(35)

where \(\lambda \) is a positive Lagrange multiplier. For the upper bound, we will have

$$\begin{aligned} \left\{ \begin{array}{ll} \min &{} \bar{P}_ {{eH}}\\ s.t. &{}2P_t+P_r = P\\ &{}0 \le P_t \le P\\ &{}0 \le P_r \le P \end{array} \right. \end{aligned}$$
(36)

We can rewrite the optimization problem as the following:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial {L(\bar{P}_ {{eH}})}}{\partial {P_t}} =\frac{\partial { \bar{P}_ {{eH}}}}{\partial {P_t}}+2\lambda =0\\ \frac{\partial {L (\bar{P}_ {{eH}})}}{\partial {P_r}} =\frac{\partial {\bar{P}_ {{eH}}}}{\partial {P_r}}+\lambda =0 \end{array} \right. \end{aligned}$$
(37)

With considering of (35), (37) and \(2P_t+P_r = P\), we can obtain

$$\begin{aligned} { \frac{P_r}{P_t}=2 } \end{aligned}$$
(38)

We can directly conclude that, in order to have the minimum \(\bar{P_ {e}}\) in the system with single relay selection, the relay power should be twice the sources’ power.

5.2 Dual Relay Selection

In view of the limited power available in the nodes, optimizing the allocated power for nodes is considered necessary, then the optimization problem for DRS is defined as

$$\begin{aligned} \left\{ \begin{array}{ll} \min &{} \bar{P_{e}}\\ s.t. &{}2P_t+2P_r=P\\ &{}0 \le P_t \le P\\ &{}0 \le P_r \le P \end{array} \right. \end{aligned}$$
(39)

By setting the derivatives of lagrangian of (39) with respect to \(P_t\) and \(P_r\) equal to zero, we have

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial {L(\bar{P_{e}})}}{\partial {P_t}} =\frac{\partial {\bar{{P}_{e}}}}{\partial {P_t}}+2\lambda =0\\ \frac{\partial {L(\bar{P_{e}})}}{\partial {P_r}} =\frac{\partial {\bar{{P}_{e}}}}{\partial {P_r}}+2\lambda =0 \end{array} \right. \end{aligned}$$
(40)

With considering of (40) and \(2P_t+2P_r = P\), we can get

$$\begin{aligned} \left\{ \begin{array}{ll} P_t=\frac{P}{4}\\ P_r=\frac{P}{4} \end{array} \right. \end{aligned}$$
(41)

For having the best result, it is necessary that \(\frac{P_r}{P_t}=1\) for DRS.

6 Simulation Result

The simulation results are considered in two cases, (1) single relay selection, (2) dual relay selection.

6.1 Single Relay Selection

In this section, we present some simulation results for the proposed schemes. In single relay selection, the effect of both sources is considered. The simulations are based on BPSK modulation and the Rayleigh fading has been considered for the channels. It is assumed that the noise statistics for all of the relays and source nodes are the same.

Figure 3 depicts the simulated and analytical BER performance of the presented scheme. This figure shows that the analytical and simulated results are converged to each other for high SNRs, then this simulation result verifies the correctness of the analytical results. The other result of this figure is that increasing the relay numbers has an important effect on the BER improvement.

Fig. 3
figure 3

Simulated BER performance for SRS, with \(P_r=P_t\)

Full size image
Fig. 4
figure 4

Comparison of the proposed with min-max scheme performance, with \(P_r=P_t\)

Full size image

In Fig. 4, the comparison of the proposed scheme and the reported scheme of [11] is presented. In [11], selection is based on the min max criterion, this figure shows that the proposed scheme has more than 1 dB performance gain versus the reported scheme in [11].

Figure 5 shows the effect of power allocation on the BER performance. In this figure, the comparison of equal power allocation (EPA) \((P_r=P_t)\) and optimal power allocation (OPA) \((P_t=2P_r)\) subject to the total power constraint for \(N=2,\)3, 4 is presented. This figure shows that OPA has better performance than EPA.

Figure 6 illustrates that the BER performances over \(a=\frac{P_r}{P_t}\) has its minimum amount for \(a=2\), which verifies our analytical results of power allocation. In this figure, the number of relays is equal to 3. Moreover, the difference between the simulated BER with the OPA and EPA is depicted. Figure shows that with the OPA, the system has more than 1 dB performance gain.

Fig. 5
figure 5

Simulated BER performance with EPA and OPA

Full size image
Fig. 6
figure 6

Simulated BER performance in terms of \(a=\frac{P_t}{P_r},\; N=3\)

Full size image

6.2 Dual Relay Selection

Figure 7 depicts the correctness of the analytical results, this figure shows that the analytical and simulated results are converged to each other for high SNRs.

Fig. 7
figure 7

Simulated BER performance for DRS, with \(P_r=P_t\)

Full size image

In Fig. 8, we consider the optimization problem for minimizing the BER. This figure demonstrates that the BER performance over \(a=\frac{p_r}{p_t}\) has the minimum amount for \(a=1\), that verifies the analytical results of power allocation.

Fig. 8
figure 8

Simulated BER performance in terms of \(a=\frac{P_r}{P_t}\)

Full size image

The comparison of the SRS and DRS schemes is also interesting. Improving the BER is necessary then DRS were proposed for achieving this aim, that Fig. 9 depicts the improvement in BER performance. Figure shows that with the DRS, the system has more that 1 dB performance gain.

7 Conclusion

Analysis of network coding and relay selection among the \(N\) relay nodes was presented. For single relay selection, closed-form expressions for the upper and lower bound of BER were obtained, then closed-form expressions for BER of DRS were obtained. For minimizing the BER, power allocation was considered among the sources and the selected relays. Results show that the number of relays has an important role in improving the BER and dual relay selection has better performance rather than single relay selection and the power allocation have a high effect on the BER performance.

Fig. 9
figure 9

Comparison of single and dual relay selection schemes

Full size image