Performance analysis of joint dual relay selection and physical layer network coding in two-way relay channels

Abstract

In this paper, we study joint dual relay- selection (RS) and physical network coding (PNC) schemes for wireless two-way relay channels. We propose four schemes in which the sources transmit information to the relays and two “best” relays are selected based on minimum bit-error-rate (BER) criterion. Then, the selected relays combine the received information from sources and broadcast it towards each other. The BER of the proposed schemes are obtained analytically and also verified through Monte Carlo simulations. The results indicate that the schemes have superior performance compared to an existing work which uses Alamouti space-time block codes (STBC).

1 Introduction

Cooperative relaying is one of the most attractive topics in wireless communications. The concept of physical-layer network coding (PNC) was proposed previously in wireless cooperative networks. In a long-range communication, due to obstacles such as buildings, trees, hills, mountains, and, in some cases, high voltage electric power lines the there is no direct link between a source and a destination. This makes non line of sight (NLOS) communication between users. Because of low power users or NLOS communications between the users, one of the most system models in cooperative communication is bidirectional relaying which is widely studied in the literature. Some of these obstructions reflect certain radio frequencies, while some simply absorb or garble the signals; but, in either case, they limit the use of many types of radio transmissions, especially when low on power budget. For example, cellular networks with a base station and some end users are the most common applications of two way relay networks, where a base station can serve as a relay to exchange the information of two end users. To improve the performance of such systems, we can use network coding or other signal combination methods. Another application of two-way relay communications is in Wireless Sensor Networks (WSNs). For example, in the case that data from two applications in two sensors are forwarded in opposite directions, two way relaying has to be involved.

In a simple two-way relay system, physical-layer network coding is an effective scheme for relay to map the simultaneously transmitted symbols from the sources into the network coded symbol using some simple algebraic operations. In traditional wireless two-way relay channels, the transmissions occur over four time slots. It is obvious that this scheme is not throughput efficient, hence, several PNC schemes have been introduced to improve the performance by reducing the number of transmission phases [1, 2, 5,6,7,8,9,10]. In these schemes, the relay may combine the information from the sources, received in two different transmission phases, and broadcasts the combined information to the sources in the next phase. Therefore, network coding save one time slot/transmission phase in two-way relaying. Now, if the sources transmit their information simultaneously, transmissions can occurs in only two time-slots [8]. Hence, two-way relay system provides higher spectral efficiency against the conventional one-way relay system [1]. However, the latter technique involves some complications for decoding of combined information in the multiple access phase [2].

Most of the existing studies on two-way relay channels, consider a communication system with only one relay [10,11,12,13,14]. Recently, multirelay two-way relaying systems with opportunistic PNC has been considered in the literature [1, 3, 4]. In multirelay channels, two sources exchange their information via one or more number of relays. Proper relay selection and signal combining at the selected relays can improve the performance of two-way relaying, significantly. On the other hand, utilizing all relays for transmissions will increase the complexity of communication system. Although to solve this problem, some researchers assume that the relays transmit their signals on orthogonal channels [15, 16], some relay selection techniques are required in these relaying systems. For instance, single-relay selection technique selects a relay in one-way relaying, which has the maximum end-to-end performance among all relays [14, 17, 18], or the relay which has the highest Signal to Noise Ratio (SNR) on its received signals [19]. If a proper strategy is employed for selecting the relays, the communication system will achieve the highest diversity order, and will have a BER near to the optimal schemes that utilizes all the relays.

In two-way relay channel, relay selection (RS) and network coding (NC) would be combined in various fashions. For example, [2] uses Double-Max criterion for relay selection and minimizes the instantaneous average sum BER of each source. In this scheme, the sources transmit their information to the relays in the first two time-slots. Next, the best relays that are selected by Double-Max criterion transmit their received information to the sources. The selected relays use Alamouti space-time block codes (STBC) to manage interference. Note that in space-time coding technique the relays need to have the other relay’s information, i.e., they should exchange their information with each other. Also, note that two selected relays could be the same; which in that case, one relay is used by the scheme [2]. In this paper, we study four schemes for two-way relay channel with two selected relays. In all schemes, at the first and the second time-slot, the sources transmit their information to the relays. Next, two “best” relays are selected based on Double-Max criterion. In the third time-slot, the selected relays exchange and combine their received information in various fashions and transmit simultaneously towards the sources. Throughout this paper, we assume that the relays have a reliable link for exchanging information with each other before transmission. In practice, the relays can be located closely and employ wireless link with high SNR for communicating with each other. This assumption is used in many works in relay communication networks [20,21,22,23,24,25].

In the first scheme, based on Amplify and Forward (AF) technique, the selected relays exchange the received signals with each other, and then each one broadcasts the signal of the other relay towards the sources. In the second and the third schemes, the relays decode the received signals, exchange decoded information with each other, and then each relay broadcasts the corresponding signals of the detected information by the other relay. There is a minor difference between these schemes for the cases where the selected relays are the same. In the fourth scheme, the relays decode the received signals, exchange information with each other to perform network coding and transmit the same network coded information.

We analyze the performance of the proposed schemes, derive a closed form expressions for BER of each scheme. Also, the analytical results are verified by Monte Carlo simulations. The results indicate that the schemes achieve the highest diversity order and outperform the scheme of [2] while not applying any complex space-time coding technique. Our simulation results indicate that the third and fourth schemes, which use network coding, have significantly higher performance than the first scheme.

The rest of this paper is organized as follows. The system model is described in Sect. 2. In Sect. 3, the proposed schemes for two-way relay channels are described and analyzed. In Sect. 4, the simulation results are presented. Finally, the conclusion is summarized in Sect. 5.

2 System model

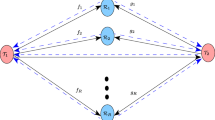
We consider a two-way relay channel with two sources and N relays. Without loss of generality, we have assumed that $b_1$ and $b_2$ are the information bits, transmitted by the sources $u_1$ and $u_2$ in an arbitrary time slot, respectively. Also, assume that $s_1$ and $s_2$ represent the binary phase-shift keying (BPSK) modulated symbols for $b_1$ and $b_2$.

We consider slow-fading channels with fading coefficient $h_{u_jR_i}$ between source $u_j$ and relay $R_i$ for $j=1,2$ and $i=1,\ldots ,N$. The channel fading coefficients are modeled as zero-mean unit variance independent circular symmetric complex Gaussian random variable. All of the noises, $n_{u_j R_i}$ for $j=1,2$ and $i=1,2,\ldots ,N$, are zero-mean complex Gaussian random variables with variance of $\sigma _n^2$.

The proposed schemes use three time-slots for communication in two-way relay channels. In the first time-slot, $u_1$ sends $s_1$ and in the second time-slot $u_2$ sends $s_2$ to the relays. Then, the relays $r_1$ and $r_2$ are selected based on Double-Max criterion [2] for the sources $u_1$ and $u_2$, respectively, i.e.,

$$\begin{aligned} \begin{aligned} r_1&=\underset{{i=1,2,\ldots ,N} \text {}}{\arg }\max {\;|h_{u_1 R_i}|^2\;}\\ r_2&=\underset{{i=1,2,\ldots ,N} \text {}}{\arg }\max {\;|h_{u_2 R_i}|^2\;} \end{aligned} \end{aligned}$$

(1)

Let’s denote the received signals by $r_1$ and $r_2$ by $y_{r_1}$ and $y_{r_2}$. These signals are expressed as

$$\begin{aligned} y_{r_{i}}=\sqrt{P_{u_i}}\;s_i\;h_{u_ir_i}+ n_{u_i,r_i} \end{aligned}$$

(2)

where $P_{u_i}$ is the transmission power of $u_i \;,\;i=1,2$, which we assume to be equal to $P_u$ for both sources.

In all the proposed schemes these relays are selected based on (1), but each scheme uses a different technique for combing the received signals and broadcasting information in the third time-slots. In our proposed schemes, the amount of information exchanged between the sources will be 2 symbols for 3 channel uses/time slots. So, the information exchange rate between the sources is $\frac{2}{3}$. The three phases of the proposed schemes are depicted in Fig. 1.

Fig. 1

Three phases of the proposed schemes

3 The proposed schemes

In this section, we describe the proposed joint relay selection and network coding schemes for wireless two-way channels.

3.1 First scheme

In the first scheme, the relays $r_1$ and $r_2$ are selected based on (1) and the selected relays exchange their signals (without decoding). In the third time-slot each relay transmits the received signal from the other relay such that the total transmission power of relays to be equal to $P_r$. If two selected relays are the same, the superposition of their raw signals will be transmitted by the relay.

Note that the transmission power for each relay must be normalized by $\beta _1$ and $\beta _2$ where

$$\begin{aligned} \beta _1= & {} \frac{1}{\sqrt{P_u| h_{u_1r_1}|^2+\sigma _n^2}}, \end{aligned}$$

(3)

$$\begin{aligned} \beta _2= & {} \frac{1}{\sqrt{P_u| h_{u_2r_2}|^2+\sigma _n^2}}. \end{aligned}$$

(4)

To calculate $\beta _1$ and $\beta _2$, the relays must obtain $h_{u_1r_1}$,$\sigma _n$, and $P_u$. As we know, the channel gains and the noise variance can be estimated using some training sequences. Also, we assume that the relays are informed from $P_u$ using feedback links.

After receiving the transmitted signals from the relays, each source omits its self-interference signal from the received signal, and then detects the information based on the received signal of the other source.

We will shows in Sect. 4 that the BER of this scheme is lower than the Alamouti space-time block codes technique presented in [2] and also it achieves a diversity order of N. Note that in this scheme, the relays broadcast their received signals to the sources without decoding, hence, the noises of the relays are transmitted along with the information signals of the sources, i.e., the power of the noise is amplified in the third time-slot. Therefore, when the noise power is high, BER worsens significantly. In the next schemes, we apply decoding process in the relays to improve the performance.

In the following, we derive an analytical expression for BER of the first scheme. The error probability of BPSK modulation for a given channel fading coefficient is:

$$\begin{aligned} p_{e_i|h_{u_ir_j}}=Q(\sqrt{2~\mathrm{SNR}_{u_i}}),\;i=1,2,\,\,\,\, j=1,2 \end{aligned}$$

(5)

where Q(.) is Gaussian Q-function. Note that $\mathrm{SNR}_{u_i}$ is a function of $|{h_{u_ir_j}}|^2$, thus, the error probability of source $u_i$ will be

$$\begin{aligned} p_{e_i}=E_{|{h_{r_ju_i}}|^2}[Q(\sqrt{2~\mathrm{SNR}_{u_i}}]. \end{aligned}$$

(6)

The following formula is used to simplify (6),

$$\begin{aligned} E_X[Q(\sqrt{bx})]=\frac{\sqrt{b}}{2\sqrt{2\pi }}\int _{0}^{\infty } \frac{e^{-bx/2}\; F_x(x)}{\sqrt{x}} \,dx \end{aligned}$$

(7)

where $F_x(.)$ is the cumulative distribution function (CDF) of random variable X. Now, if we use the first-order expansion of the probability density function (PDF), we have [2],

$$\begin{aligned} f_x(x)=\frac{a\;x^N}{\gamma ^{N+1}}+o(x^{N+\epsilon })\quad ,\; \epsilon >0 \end{aligned}$$

(8)

where $\gamma$ is SNR, N is the diversity order and a is a constant number. Note that we write a function g(x) of x as o(x) if $\lim _{x \rightarrow 0}\frac{g(x)}{x}=0$. Also, the value of a is determined by the probability density function. This value is not important in our diversity analysis. At high SNR, (7) can be approximated as

$$\begin{aligned} E_x[Q(\sqrt{bx})]= & {} \frac{a2^N\varGamma (N+3/2)}{(N+1)\;\sqrt{\pi }} (b\gamma )^{-(N+1)}\nonumber \\&+o(\gamma ^{-(N+1)}) \end{aligned}$$

(9)

As it is said in Sect. 3.1, in the third time slot each relay transmits the received signal from the other relay with transmission power equal to $\frac{P_r}{2}$. So, for source $u_i$, the received signal in the third phase can be expressed as

$$\begin{aligned} \begin{aligned} y_{u_i}=&{\sqrt{P_r/2}( \underset{y_{r_2u_i} \text {}}{\underbrace{\; (\sqrt{P_u}s_1h_{u_1r_1}+ n_{u_1r_1}\;) \beta _1\;}}h_{r_2u_i}} \\&+ \underset{y_{r_1u_i} \text {}}{\underbrace{{\; (\sqrt{P_u}s_2h_{u_2r_2}+ n_{u_2r_2}\;) \beta _2\;}}h_{r_1u_i}})+n_{u_i} \end{aligned} \end{aligned}$$

(10)

where, $y_{r_1u_i}$ and $y_{r_2u_i}$ are the transmitted signals from relays $r_1$ and $r_2$ to source $u_i,\,\,i=1,2$, respectively. At the end of the transmission process, each source omits its self-interference from $y_{u_i}$ and detects the other source’s information. In the other words, for $\;i,\,i^\prime =1,2$ and $i^\prime \ne i$, source $u_{i}$ calculates $y_{i}$ which contains the information of the source $u_{i^\prime }$ as following

$$\begin{aligned} \begin{aligned} y_{i}=&\sqrt{P_r/2}\;(\sqrt{P_u}\;s_{i^\prime }\;h_{u_{i^\prime }r_{i^\prime }}+n_{u_{i^\prime }r_{i^\prime }})\;h_{r_iu_i} \;\beta _{i^\prime }\\&+\sqrt{P_r/2}\; n_{u_{i}r_{i}}\;h_{u_{i}r_{i^\prime }}\;\beta _{i}+n_{u_i},\,\,\,i,\,i^\prime =1,2,\,\,i \ne i^\prime . \end{aligned} \end{aligned}$$

(11)

For the simplicity of BER derivations, we assume that $P_u \gg P_r$. The SNR expression for signal $y_{i}$ can be obtained as

$$\begin{aligned} \mathrm{SNR}_{u_i}&=\frac{P_u\;{P_r/2}\;\beta _{i^\prime }^{2} \;|h_{r_1u_1}|^2\;|h_{r_2u_2}|^2}{\sigma _n^2\;({P_r/2} \;|h_{r_iu_i}|^2\;\beta _{i^\prime }^{2}+{P_r/2} \;|h_{r_{i^\prime }u_{i}}|^2\beta _i^{2}+1)}\nonumber \\&\quad = \frac{P_r}{\sigma _n^2}\cdot \frac{P_u/2\;|h_{r_1u_1}|^2\;|h_{r_2u_2}|^2}{A} \end{aligned}$$

(12)

With some changes on the parameters, we obtain a formula for A as follows

$$\begin{aligned} \begin{aligned} A=&\big (P_u\;|h_{r_{i^{\prime }}u_{i^{\prime }}}|^2+\sigma _n^2\big )\\&\times \Bigg (1+\underbrace{\frac{\frac{\gamma _r}{2}|h_{r_{i^{\prime }}u_i}|^2}{\gamma _u \;|h_{r_iu_i}|^2+1}}_{B}+\underbrace{\frac{\frac{\gamma _r}{2} |h_{r_iu_i}|^2}{\gamma _u \;|h_{r_{i^{\prime }}u_{i^{\prime }}}|^2+1}}_{C}\Bigg ) \end{aligned} \end{aligned}$$

(13)

where $\gamma _{r}=P_r/\sigma _n^2$ and $\gamma _{u}=P_u/\sigma _n^2$.

For the tractability of mathematical analysis, we should simplify $SNR_{u_i}$ in (12). To this end, at first, we approximate A expression in (13). Specially, at large SNR, i.e, $\gamma _u>>1$, and for $P_u \gg P_r$, random variables B and C in (13) have small means with small variances. In fact, we can assume that these random variables are nearly zero with high probability. To justify this, we have plotted the PDF of terms B and C for large SNR’s in Fig. 2. The results show these random variables have values near zero with a negligible variance. In the other words, it can be inferred that $B<<1$ and $C<<1$ with high probability, i.e., they can ignored against the value 1 in (13). In addition, at high SNR, $\sigma _n^2$ can be ignored against $P_u$, therefore, (12) can be simplified as

$$\begin{aligned} \mathrm{SNR}_{u_i}\simeq \frac{1}{2}\;\gamma _{r}\;|h_{r_iu_i}|^2 \end{aligned}$$

(14)

Note that, if the selected relays are the same, (14) is still valid.

Fig. 2

The probability density function (PDF) of random variable B (C)

We know that $p_{u_i|h_{r_iu_i}}=Q(\sqrt{2\;\mathrm{SNR}_{u_i}})$. The PDF of $\mathrm{SNR}_{u_i}$ can be calculated based on (5)–(9) and (14), where $|h_{r_iu_i}|^2= \max \{|h_{r_iu_1}|^2,\, |h_{r_iu_2}|^2\}$. Thus, from [2], we have

$$\begin{aligned} \begin{aligned} f({ \mathrm{SNR}_{u_i}})=&N\;\gamma _{r}^{-1}(1-\exp (-2\gamma _{r}^{-1}\; \mathrm{SNR}_{u_i}))^{N-1} \\&\exp (-2\gamma _{r}^{-1}\; \mathrm{SNR}_{u_i}) \end{aligned} \end{aligned}$$

(15)

Now, by using (15) and (9), $p_{u_i}$ can be approximated at high SNR as

$$\begin{aligned} p_{{e_i}}=\frac{\varGamma (N+0.5)2^{N}}{2\sqrt{\pi }}\;(\gamma _{r})^{- N} \end{aligned}$$

(16)

where $\gamma _{r}=P_r/\sigma _n^2$ and N is the system diversity order. This equation shows the first scheme achieves the full diversity order same as the Alamouti space-time block codes technique in [2].

3.2 Second scheme

In the second scheme, the selected relays detect their received signals before broadcasting the information to the sources in the third time-slot. Using this technique, the effect of noise on BER will be reduced.

We denote the received signals of in the first and second relays $r_1$ and $r_2$ by $y_{r_1}$ and $y_{r_2}$ which are expressed in (2). In the third time-slot, at first, relay $r_i$ detects the information of source $u_i$ from the signals $y_{r_i},\; i=1,2$, by Maximum-Likelihood (ML) detection. Then the relays exchange their information with each other and similar to the first scheme, the each relay broadcasts the decoded information by the other relay (${\hat{s}}_1$ and ${\hat{s}}_2$) to the sources.

In the cases where the selected relays are the same, the relay broadcasts the summation of its detected values to the sources. Note that the transmission power of the relays must be normalized in the third time-slot. Finally, source $u_i$ detects the information of the other source after subtracting the signal its own information from the received signal.

Next, we analyze the performance of the second proposed scheme. At the end of the third time-slot, when the selected relays are different, source $u_i$ receives

$$\begin{aligned} y_{u_i} = \sqrt{P_r/2}(\underset{y_{r_2u_i} \text {}}{\underbrace{\;{\hat{s}}_1}} h_{r_{2} u_i}+ \underset{y_{r_1u_i} \text {}}{\underbrace{{\hat{s}}_{2}}} h_{r_1u_i})+n \end{aligned}$$

(17)

Note that, relay sends its information with total power of $P_r$, i.e, each relay broadcasts information with power of $P_r/2$. Then, each source detects the other source’s information after subtracting its own information from $y_{u_i}$. For this purpose, source $u_{i}$, $\;i=1,2$ and $i^\prime \ne i$, calculates a term $y_{i}$ containing the information of the source $u_{i^\prime }$ from (17), as

$$\begin{aligned} y_{i} = \sqrt{P_r/2}\; {\hat{s}}_{i^\prime } h_{r_{i} u_i}+n \end{aligned}$$

(18)

When the selected relays are the same, source $u_i$ receives

$$\begin{aligned} y_{u_i} = \sqrt{P_r}\; \left[ \sqrt{\frac{1}{2}}\;({\hat{s}}_1 + {\hat{s}}_2)\right] \;h_{r_iu_i}+n \end{aligned}$$

(19)

Note that in this case the relay must transmit $\sqrt{\frac{1}{2}}({\hat{s}}_1 + {\hat{s}}_2)$ instead of $({\hat{s}}_1 + {\hat{s}}_2)$ with a normalized power. Then, each source omits its self-interference to obtain $y_{i}$,

$$\begin{aligned} y_{i} = \sqrt{P_r/2}\; {\hat{s}}_{i^\prime } h_{r_{i} u_i}+n \end{aligned}$$

(20)

By comparing (18) and (20), we observe that in both situations, BER probability will be the same. The SNR expression for signal $y_{i}$ will be

$$\begin{aligned} \mathrm{SNR}_{u_i}=\frac{1}{2}\;\gamma _{r}\;|h_{r_iu_i}|^2 \end{aligned}$$

(21)

Then, similar to derivation of (15), we can find probability density function of $\mathrm{SNR}_{u_i}$ as

$$\begin{aligned} \begin{aligned} f_{ \mathrm{SNR}_{u_i}}=&N\;\gamma _{r}^{-1}(1-\exp (-2\gamma _{r}^{-1}\cdot \mathrm{SNR}_{u_i}))^{N-1} \\&\exp (-2\gamma _{r}^{-1}\cdot \mathrm{SNR}_{u_i}) \end{aligned} \end{aligned}$$

(22)

Finally, from (15) and (9), $p_{e_{u_i}}$ can be further approximated at high SNR as

$$\begin{aligned} p_{e_{u_i}}\approx \frac{(2)^{N}\varGamma \left( N+0.5\right) }{2\sqrt{\pi }}\left( \gamma _{r}\right) ^{-N},\;\;\;\;\;\;\forall i=1,2 \end{aligned}$$

(23)

In this scheme, the relays decode the transmitted information from the sources. If the relays detect information with error and it will affect BER of two-way channel. Therefore, we need to calculate BER expression for detecting bits by the relays. From (2), the SNR of the relays can be expressed as,

$$\begin{aligned} \mathrm{SNR}_{r_i} =\frac{P_u\ h_{u_ir_i}}{\sigma _{n}^{2}}\quad ,\;i=1,2 \end{aligned}$$

(24)

From (15), we have

$$\begin{aligned} f_{ \mathrm{SNR}_{r_i}}&\!=\!\left( \!\frac{P_r}{P_u}\!\right) N\gamma _{r}^{-1} \left( \!1\!-\!\exp \left( \!-\left( \!\frac{P_r}{P_u}\!\right) \gamma _{r}^{-1}\cdot \mathrm{SNR}_{r_i}\!\right) \!\right) ^{N-1}\nonumber \\&\quad \exp \left( -\left( \frac{P_r}{P_u}\right) \gamma _{r}^{-1}\cdot \mathrm{SNR}_{r_i}\right) \end{aligned}$$

(25)

Now, using (15) and (9), $p_{r_i}$ can be obtained approximately for high SNR as

$$\begin{aligned} p_{e_{r_i}}\approx \frac{\left( \frac{P_r}{P_u}\right) ^{N} \varGamma \left( N+0.5\right) }{2\sqrt{\pi }}\left( \gamma _{r}\right) ^{-N},\;\;\;\;\;\;\forall i=1,2 \end{aligned}$$

(26)

Note that various errors would affect the BER. Next, we describe a method to obtain the total BER for source $u_1$ (similarly $u_2$). Suppose that $r_1$ detects its received information correctly. In this case, if relay $r_2$ detects its information correctly but, $u_1$ detects its information received from the relays with error, $u_1$ will receive incorrect information. Similarly, if relay $r_2$ detects its information with error and $u_1$ detects its information received from the relays correctly, $u_1$ will receive incorrect information again. In other case, suppose that $r_1$ detects its received information with error. In this case, two another conditions can occur which affect the total BER. Relay $r_2$ detects correct information and $u_1$ detects its received information with error or relay $r_2$ detects its information with error and $u_1$ detects its information received from the relays correctly. Thus, the total BER can be expressed as

$$\begin{aligned} p_{e_i}&=[p_{c_{r_i^\prime }}p_{e_{u_i}}\!+\!p_{e_{r_{i^\prime }}}p_{c_{u_i}}] p_{c_{r_{i}}}\!+\!\underset{D}{\underbrace{[p_{c_{r_{i^\prime }}}p_{e_{u_i}} \!+\!p_{e_{r_{i^\prime }}}p_{c_{u_i}}]p_{e_{r_{i}}}}},\nonumber \\&\quad \forall \; i=1,2 \;\;and\;\; i\ne i^\prime \end{aligned}$$

(27)

where $p_{c_{r_i}}=1-p_{e_{r_i}}$ and $p_{c_{u_i}}=1-p_{e_{u_i}}$. Based on (26), at high SNR, we have $p_{c_{r_i}}\approx 1$. In addition, $p_{e_{r_i}}$ can be ignored against $p_{c_{r_i}}$. So, we can neglect term D in (27) and simplify it as

$$\begin{aligned} \begin{aligned} p_{e_i}\approx&\ p_{e_{r_i}}+p_{e_{u_i}}-\underset{\approx 0}{\underbrace{2p_{e_{r_i}}p_{e_{u_i}}}} \approx p_{e_{r_i}}+p_{e_{u_i}},&\;\forall \; i=1,2 \end{aligned} \end{aligned}$$

(28)

Therefore, according to (23), (26), and (28), $p_{e_i}$ can be further approximated at high SNR as

$$\begin{aligned} p_{e_{i}}\approx \frac{\left( \left( \frac{P_r}{P_u}\right) ^{N}+2^{N}\right) \varGamma \left( N+0.5\right) }{2\sqrt{\pi }}\left( \gamma _{r}\right) ^{-N},\quad \forall i=1,2\nonumber \\ \end{aligned}$$

(29)

This verifies that the scheme achieves the highest diversity order (N).

3.3 Third scheme

In the third scheme, we apply network coding (NC) to improve the BER in two-way relay channel. Note that NC would correct the detection error in some situations. For example for BPSK modulation as it can be seen in Table 1, if both relays detect the information with error, NC can cause the relays receive correct information from the sources. Hence, we expect to have a better BER in this scheme compared to the previously proposed schemes.

Table 1 NC capability on correcting the bit detection errors

This scheme is similar to the second scheme, except, when selected relays are the same in the third phase, the selected relay applies network coding. It sends the XOR of the information that is received in the first two time-slots. In this state, the sources first detect ${\hat{s}}_1\oplus {\hat{s}}_2$ and then source computes the other source’s information.

Note that in this scheme, we apply NC in the situation where the selected relays are the same. Nonetheless its performance is better than the first scheme and the second scheme. In the sequel, in our proposed fourth scheme, we apply always NC in order to improve the system average BER further.

The third scheme performs the same as the second scheme in the state in which the selected relays are different. Hence, it is obvious that in this state the BER of the scheme is exactly the same as the BER expression given in (29). Let $p_2$ denote the error probability when two different nodes are selected as relays, i.e,

$$\begin{aligned} \begin{aligned} p_{2}\approx&\frac{\left( \left( \frac{P_r}{P_u}\right) ^{N}+2^{N}\right) \varGamma \left( N+0.5\right) }{2\sqrt{\pi }}\left( \gamma _{r}\right) ^{-N},\\&\;\;\;\;\;\;\forall i=1,2 \end{aligned} \end{aligned}$$

When the selected relays are the same, source $u_i$ receives

$$\begin{aligned} y_{u_i} = \sqrt{P_r}({\hat{s}}_1 \oplus {\hat{s}}_2)h_{r_iu_i}+n \end{aligned}$$

(30)

In this case, the sources detect ${\hat{s}}_1\oplus {\hat{s}}_2$. If there is no detection error $({\hat{s}}_i = s_i)$, source $u_i$ finds the other source’s information as below

$$\begin{aligned} {\hat{s}}_{i^\prime }=({\hat{s}}_1 \oplus {\hat{s}}_2) \oplus s_i,\quad i=1,2 \; \text {and}\; i^\prime \ne i \end{aligned}$$

(31)

Now if the sources detect ${\hat{s}}_1 \oplus {\hat{s}}_2$ with error, the sources will not be able to detect the other source information correctly. Therefore, we must find the BER probability for detecting ${\hat{s}}_1 \oplus {\hat{s}}_2$. The SNR of $y_{u_i}$ can be expressed as,

$$\begin{aligned} \mathrm{SNR}_{u_i}=\gamma _{r}\;|h_{r_iu_i}|^2 \end{aligned}$$

(32)

Similar to the derivation of (15), we must find probability density function of $\mathrm{SNR}_{u_i}$. Thus,

$$\begin{aligned} \begin{aligned} f_{ \mathrm{SNR}_{u_i}}=&N\;\gamma _{r}^{-1}(1-\exp (-\gamma _{r}^{-1} \cdot \mathrm{SNR}_{u_i}))^{N-1} \\&\exp (-\gamma _{r}^{-1} \cdot \mathrm{SNR}_{u_i}) \end{aligned} \end{aligned}$$

(33)

Let $p_{e_{u_i}}$ be the error probability of the sources when same nodes are selected as relay. From (15) and (9), $p_{e_{u_i}}$ can be approximated at high SNR as

$$\begin{aligned} p_{e_{u_i}}\approx \frac{\varGamma \left( N+0.5\right) }{2\sqrt{\pi }} \left( \gamma _{r}\right) ^{-N},\;\;\;\;\;\;\forall i=1,2 \end{aligned}$$

(34)

According to performance analysis of the second scheme, the relays may detect their received bits incorrectly and this affects the total BER of the system. We denote the total error probability when the selected relays are the same by $p_1$ which is obtained as following,

$$\begin{aligned} \begin{aligned} p_{1}=&p_{c_{r_{i^\prime }}}p_{c_{r_i}}p_{e_{u_i}}+p_{c_{r_{i^\prime }}} p_{e_{r_i}}p_{c_{u_i}}+p_{e_{r_{i^\prime }}}p_{c_{r_i}}p_{c_{u_i}}\\&+p_{e_{r_{i^\prime }}}p_{e_{r_i}}p_{e_{u_i}}, \quad \forall \; i=1,2 \;\;\text {and}\;\; i\ne i^\prime \end{aligned} \end{aligned}$$

(35)

Using the same way in simplifying (27) and by having $p_{c_{r_i}}=1-p_{e_{r_i}}$ and $p_{c_{u_i}}=1-p_{e_{u_i}}$, at high SNR, $p_1$ can be approximated as

$$\begin{aligned} \begin{aligned} p_{1}&\approx p_{e_{r_{i^\prime }}}+p_{e_{r_i}}+p_{e_{u_i}}\\&=\frac{\left( 2\left( \frac{P_r}{P_u}\right) ^{N}+1\right) \varGamma \left( N+0.5\right) }{2\sqrt{\pi }}\left( \gamma _{r}\right) ^{-N},\\&\quad \forall \; i=1,2 \;\;\text {and}\;\; i\ne i^\prime \end{aligned} \end{aligned}$$

(36)

Finally, for BER expression at high SNR, we have

$$\begin{aligned} \begin{aligned} p_{e_{i}} \simeq&\frac{1}{N}\;p_{1}+ \frac{N-1}{N}\;p_{2} \\ =&\left[ \left( \frac{N+1}{N}\right) \left( \frac{P_r}{P_u}\right) ^N+\frac{1}{N}\right] \frac{\varGamma (N+0.5)}{2\sqrt{\pi }}\gamma _{r}^{-N} \end{aligned} \end{aligned}$$

(37)

This shows that by applying NC the SNR in this scheme becomes larger than the SNR of the second scheme, which results improvement on BER.

3.4 Fourth scheme

In this scheme, the selected relays apply network coding in all situations. In the third time slot the selected relays exchange their detected symbols and then they simultaneously broadcast $x_r = {\hat{s}}_1 \oplus {\hat{s}}_2$ to the sources with the total transmission power of $P_r$. Then each source detects the symbol of other source by decoding the received signal and omitting its own information.

Note that the links between $u_i$ and the selected relays, $h_{r_1u_i}$, $h_{r_2u_i}$, may have different phases; hence, the transmitted signals from two relays may weaken each other due to the phase difference. To alleviate this issue, the second relay must change the phase of its signal properly, i.e., it transmits $\alpha _\mathrm{opt} x_r$ instead of $x_r$, where $\alpha _\mathrm{opt}$ is a phase beam-forming coefficient. This parameter is chosen based on Max-Min criterion by following formula,

$$\begin{aligned} \alpha _\mathrm{opt}\!=\!\underset{|\alpha |=1 \text {}}{\arg }\max \big (\min \left\{ |h_{r_1u_1}\!+\!\alpha h_{r_2u_1}|, |h_{r_1u_2}\!+\!\alpha h_{r_2u_2}|\right\} \big )\nonumber \\ \end{aligned}$$

(38)

Here, $\alpha _\mathrm{opt}$ cannot be obtained in a closed-form. However, we can find it approximately by searching among $m>>1$ points on the complex unit circle. In other words, we assume that the phase of $\alpha$ is chosen from $\{0, 2\pi /m, 4\pi /m, \ldots , (m-1)2\pi /m\}$.

The received signals by the sources in the third time-slot is

$$\begin{aligned} y_{u_i} = \sqrt{\frac{P_r}{2}}(h_{r_1u_i}+\alpha _\mathrm{opt} h_{r_2u_i})({\hat{s}}_1 \oplus {\hat{s}}_2) +n_{u_i} \end{aligned}$$

(39)

Here, each relay transmits its information with power $P_r/2$.

Note that in practice the phases of $h_{r_1u_i}$ and $\alpha _\mathrm{opt}h_{r_2u_i}$ are close to each other. Therefore, (39) can be approximated as

$$\begin{aligned} y_{u_i} \simeq \sqrt{\frac{P_r}{2}}(|h_{r_1u_i}|+|h_{r_2u_i}|)\underset{y_{r_2u_i},y_{r_1u_i} \text {}}{\underbrace{({\hat{s}}_1 \oplus {\hat{s}}_2)}} +n_{u_i} \end{aligned}$$

(40)

In fact, the above approximation shows an ideal case, i.e., it is an upper bound for SNR, and it can be used as a benchmark in our analysis.

In the next, we analyze the BER at high SNR. When the selected relays are two different nodes, SNR can be written as

$$\begin{aligned} \begin{aligned} \mathrm{SNR} =&\frac{P_r}{2\sigma _n^2}\;\cdot ({|h_{r_1u_i}|}+{|h_{r_2u_i}|})^2 \end{aligned} \end{aligned}$$

The above term can be approximated as following,

$$\begin{aligned} \mathrm{SNR}\simeq \frac{P_r}{\sigma _n^2}\;\cdot ({|h_{r_1u_i}|}^2+{|h_{r_2u_i}|}^2) \end{aligned}$$

(41)

Let $p_{e_{u_i}}$ denote the error probability when two different nodes are selected as relays. From (9), we have

$$\begin{aligned} p_{e_{u_i}} \simeq \frac{\left[ 1-2^{-N+1}\right] \varGamma (N+0.5)}{2\sqrt{\pi }}\gamma _{r}^{-N} \end{aligned}$$

(42)

where $\gamma _{r}=P_r/\sigma _n^2$.

According to the performance analysis of the second scheme, the relays may detect their received bits with error and it affects the total BER of the system. So, total error probability when the selected relays are different is denoted by $p_2$, and it can be obtained as,

$$\begin{aligned} \begin{aligned} p_{2}=&p_{c_{r_{i^\prime }}}p_{c_{r_i}}p_{e_{u_i}} +p_{c_{r_{i^\prime }}}p_{e_{r_i}}p_{c_{u_i}}+p_{e_{r_{i^\prime }}}p_{c_{r_i}}p_{c_{u_i}}\\&+p_{e_{r_{i^\prime }}}p_{e_{r_i}}p_{e_{u_i}}, \quad \forall \; i=1,2 \;\;\text {and}\;\; i\ne i^\prime \end{aligned} \end{aligned}$$

(43)

Similar to simplifying (27), using $p_{c_{r_i}}=1-p_{e_{r_i}}$, and $p_{c_{u_i}}=1-p_{e_{u_i}}$, at high SNR, $p_2$ can be approximated as

$$\begin{aligned} p_{2}&\approx p_{e_{r_{i^\prime }}}+p_{e_{r_i}}+p_{e_{u_i}}\nonumber \\&\quad =\frac{\left( 2\left( \frac{P_r}{P_u}\right) ^{N}+[1-2^{-N+1}]\right) \varGamma \left( N+0.5\right) }{2\sqrt{\pi }}\left( \gamma _{r}\right) ^{-N},\nonumber \\&\qquad \forall \; i=1,2 \;\;\text {and}\;\; i\ne i^\prime \end{aligned}$$

(44)

If the selected relays by two sources are the same, the relay must forward its signal with power of $P_r$. It this case,

$$\begin{aligned} \begin{aligned} \mathrm{SNR} =&P_r/{\sigma _n^2}\;\cdot |h_{r_iu_i}|^2 \end{aligned} \end{aligned}$$

(45)

Let $p_{e_{u_i}}$ denote the error probability when a node is selected as relay. Then, from (9), we have

$$\begin{aligned} p_{e_{u_i}} \simeq \frac{\varGamma (N+0.5)}{2\sqrt{\pi }}\gamma _{r}^{-N} \end{aligned}$$

(46)

Similar to the performance analysis of the second scheme, the BER of the relays must be considered. So, total error probability when the selected relays are different is denoted by $p_1$, and it will be

$$\begin{aligned} \begin{aligned} p_{1}=&p_{c_{r_{i^\prime }}}p_{c_{r_i}}p_{e_{u_i}}+p_{c_{r_{i^\prime }}} p_{e_{r_i}}p_{c_{u_i}}+p_{e_{r_{i^\prime }}}p_{c_{r_i}}p_{c_{u_i}}\\&+p_{e_{r_{i^\prime }}}p_{e_{r_i}}p_{e_{u_i}}, \quad \forall \; i=1,2 \;\;\text {and}\;\; i\ne i^\prime \end{aligned} \end{aligned}$$

(47)

Using $p_{c_{r_i}}=1-p_{e_{r_i}}$, $p_{c_{u_i}}=1-p_{e_{u_i}}$, and after simplifying (35), at high SNR, $p_1$ can be approximated as

$$\begin{aligned} \begin{aligned} p_{1}\approx&\ p_{e_{r_{i^\prime }}}+p_{e_{r_i}}+p_{e_{u_i}}\\ =&\frac{\left( 2\left( \frac{P_r}{P_u}\right) ^{N}+1 \right) \varGamma \left( N+0.5\right) }{2\sqrt{\pi }}\left( \gamma _{r}\right) ^{-N},\\&\quad \forall \; i=1,2 \;\;\text {and}\;\; i\ne i^\prime \end{aligned} \end{aligned}$$

(48)

Using (47) and (48), and considering the probability of being the same for two selected relays, $p_{u_i}$ of source $u_i$ can be computed as following

$$\begin{aligned} p_{e_{u_i}}=\left( \frac{N-1}{N}\;p_{2}+\frac{1}{N}\;p_{1}\right) \end{aligned}$$

(49)

Finally, the asymptotic BER expression will be

$$\begin{aligned} \begin{aligned} p_{e_{i}} \simeq&\ \left[ \frac{2N\left( \frac{P_r}{P_u})^N(N-1)(1-2^{-N+1}\right) +1}{N}\right] \\&.\ \frac{\varGamma (N+0.5)}{2\sqrt{\pi }}\gamma _{r}^{-N} \end{aligned} \end{aligned}$$

(50)

where $\gamma _{r}=P_r/\sigma _n^2$ and N is the system diversity order.

4 Simulation results

In this section, we conduct various simulations to evaluate the performance of the proposed schemes. We assume that the average SNR of the link between any source $u_i$ and relay $r_j$ is $\gamma _{r}=P_r/\sigma ^2$.

The transmission power of the sources is set to be $P_u=34\;dBm$ and the transmission power of the relays is equal to $P_r=0\; dBm$. This means that the transmission power of the sources are much greater than the relays. BPSK modulation is used in the simulations, unless it is stated clearly. Also, information exchange among the relays assumed to be error free.

Figure 3 the BER of two sources are depicted in terms of SNR for $N=2, 4, 6$, where N is the number of relays. Since the communication system is symmetrical, the BER curves of two sources will be the same.

Fig. 3

BER comparison between source $u_1$ and source $u_2$ for various number of relays

In Fig. 4 the BER of all the proposed schemes are depicted versus SNR for different number of relays. The results indicate that as the number of relays grows the BER is improved significantly for all schemes.

Fig. 4

BER comparison among the proposed schemes for various number of relays

The simulation results indicate that the first and second scheme have almost similar performance. The second scheme outperforms the first scheme, because, the relays decode their received signals before retransmitting them. At high SNR the noise effect is negligible, thus, the first and second scheme perform similarly. In third scheme, network coding is used in some situations, hence, it outperforms the first and second schemes. Since the fourth scheme uses network coding always, it outperforms other proposed schemes.

The simulation and analytical results of the proposed schemes are compared in Figs. 5, 6, 7 and 8. Note that the analytical curves match with the simulation results only at high SNR, because BER expressions were derived for high SNR in (16), (29), (37) and (50). As we can see from these results, the simulations verify our analytical results given in III-A to III-D.

Fig. 5

The comparison of analytical expression and simulation results of scheme 1 for various number of relays

Fig. 6

The comparison of analytical expression and simulation results of scheme 2 for various number of relays

Fig. 7

The comparison of analytical expression and simulation results of scheme 3 for various number of relays

Fig. 8

The comparison of analytical expression and simulation results of scheme 4 for various number of relays

In Fig. 9, we compare the BER of Alamouti space-time codes [2] with our proposed schemes. Note that Alamouti space-time block codes scheme occurs in four time-slots but our schemes require three time-slots for a complete information exchange. To have a fair comparison on BER the bit-rate of these schemes must be the same. Hence, in Fig. 9, the performance of our schemes with 8-PSK modulation and Alamouti space-time block codes with 16-PSK modulation are compared. Our proposed schemes outperform the scheme of [2] at the same SNR. Also, the figure shows that all schemes achieve full diversity order.

Fig. 9

BER of the proposed schemes and Alamouti space-time block codes scheme [2] for number of relays equal to $N=2$

5 Conclusion

In this paper, we proposed four joint relay selection and network coding schemes for two-way relay channels. For relay selection, Double-Max criteria is used, which selects the best relay for each source. In these schemes the transmissions occur in three time-slots. We showed both analytically and by simulations that the proposed scheme are less complicated, more energy efficient, with superior BER performance compared to the existing work that uses Alamouti space-time block codes. Our future work concerns extending the proposed relay selection technique for other wireless networking scenarios.