Performance evaluation of joint relay selection and network coding for multi-source and multi-destination relay network

Abstract

Network coding and relay selection have attracted significant attention due to their performance improvement and spectral efficiency in wireless networks. In this work, we study joint relay selection and network coding cooperation schemes for M source-destination pairs assisted with N relays. We propose a new smart decode-and-forward max-min relay selection scheme based on the source-destination links’ outage status and L selected relays to enhance the communication system diversity. Our objective is realize joint network coding and relay selection strategies for maximizing the expected number of recovered packets by the intended destinations in various situations. We analyze the performance of the proposed scheme and prove that the maximum diversity order of $N+1$ is achieved when the number of active relays is at least $\lceil {\frac{N+1}{3}}\rceil$. Also, we show that the scheme can achieve a diversity order of 3L when $L<\lceil {\frac{N+1}{3}}\rceil$. Our analytical and simulation results indicate that the proposed scheme provides higher performance than the existing network coded cooperation schemes.

1 Introduction

Cooperative communication (CC) is an effective and powerful technique to alleviate channel fading effects by involving relay nodes. In particular, cooperative communication based on relay assistance can significantly improve end-to-end error probability by providing multiple replicas of the source messages to the destination. Various relaying protocols have been suggested for cooperative relay communications such as amplify-and-forward (AF), decode-and-forward (DF), compress-and-forward (CF), and so on [1,2,3]. Note that in CC the performance is improved at the expense of the spectral efficiency.

In order to overcome the performance degradation in terms of the spectral efficiency, network coded cooperation (NCC) techniques have been proposed [4,5,6,7]. In [6], network coding (NC) was introduced by Ahlswede et al. and implemented to achieve the max-flow rate for a single-source multicast. The basic idea is that each relay calculates a weighted sum of the received packets from different sources and forward the combination toward the destinations. In NCC the spectral efficiency can be improved by reducing the number of channel uses of the relays [8].

Taking a different approach, relay selection (RS) methods intend to reduce the transmission overhead in cooperative communication systems [9,10,11]. In [12], the diversity-multiplexing tradeoff (DMT) of a non-NC-based cooperative relaying scheme with relay selection for a cooperative communication setup with multiple source-destination pairs under the unicast scenario is studied. The paper shows that the scheme can achieve full diversity by selecting the best relay for each source-destination pair (i.e., totally M relays are selected for a network with M source-destination pairs).

Recently, RS protocols have garnered significant attention in order to further improve the spectral efficiency of NCC systems [8]. In particular, single relay selection (SRS) and multiple relay selection (MRS) protocols are proposed in [7]. It is shown that RS offers significant performance improvement on NCC systems in terms of throughput [8] and capacity [13] in comparison with the conventional all-participating relay schemes. In [14], a decode-and-forward based opportunistic single RS is proposed in two-way relay networks (TWRN). Some papers propose various techniques for combining RS and NC in TWRN [15,16,17,18,19].

The analysis of NCC with RS in multi-source multi-relay networks with a single destination has garnered significant attention in recent years. In [20] the performance of RS-based NCC for multiple-input multiple-output (MIMO) system is analyzed. In this system, the relays and the destination are equipped with multiple antennas and relay selection process is implemented based on max-min end-to-end criterion [20]. The closed-form expression for the outage probability (OP) under two different strategies are derived. In [21] the performance of generalized user-relay selection in a multiple-user multiple-relay NCC system is investigated. OP expression is derived and the achievable diversity order and coding gain are quantified [21]. Furthermore, the impact of outdated channel state information (CSI) on the outage probability and diversity gain of RS-based NCC is studied in [22]. In [23], a combination of NC and smart relay selection algorithm is proposed to improve the performance in terms of the outage probability and throughput.

In [24], the performance of NCC with RS is studied in terms of diversity-multiplexing tradeoff in a relay-aided network composed of multiple source-destination pairs in the unicast scenario. It is shown that full diversity order is achieved using the best relay selection strategy. However, the paper assumes that each destination can reliably (without error) overhear the packets that are not intended for it from the other sources. By removing this optimistic assumption, it is shown that the NCC scheme can only achieve the diversity order of 2.

In [12], the DMT of a wireless network with multiple source-destination pairs assisted with a number of relays is analyzed for multicast and unicast scenarios. The proposed scheme allows the relays to apply network coding on their received information. The scheme can achieve the full diversity order by employing all of the relays and at the expense of a slightly reduced multiplexing rate. Also, a relay selection algorithm is proposed in the paper with L selected relays. Under the proposed relay selection strategy, only the diversity order of $L+1$ can be achieved when the number of the selected relays is less than the number of sources. In other words, when the number of sources exceeds L, the full diversity order cannot be achieved under the proposed relay selection strategy.

The analysis of NCC with RS in the networks with multiple source-destination pairs has received less attention. Motivated by these considerations, we propose a joint relay selection and network coding scheme for M source-destination pairs assisted with N relays that exploits relay selection to improve the performance of the network in terms of outage probability and diversity gain.

Our objective is to determine an adaptive network coding and a relay selection strategy to maximize the expected number of recovered packets by the destinations and minimize the outage probability of unicast sessions. Considering the number of unsuccessful destinations in decoding their intended packets, the number of selected relays, and the number of packets that unsuccessful destinations have not decoded, we define various cases for relay selection and network coding strategies. Next, we confront 5 cases for the network and define the proper strategy for each case. In most cases, the selected relays apply linear network coding to perform transmissions, and in some cases, a subset of the selected relays are allocated to unsuccessful source-destination pair in order to forward the messages without network coding. The proposed scheme shows superior performance in comparison with the existing RS-based NCC and CC schemes.

The main contributions of this paper are as follows:

• We find upper and lower bounds for the outage event probability and derive the closed-form analytical expression for the bounds. The outage event is the event that the packet sent by one source (i.e., $S_i$) cannot be decoded by its destination (i.e., $D_i$) at the end of transmission phases.

• Based on the asymptotic expression of the outage probability, we have the following results on the diversity order:

  • (1) The maximum diversity order of $N+1$ is achieved when the number of active relays is at least $\lceil {(\frac{N+1}{3})}\rceil$.

  • (2) The scheme can achieve a diversity order of 3L when $L<\lceil {(\frac{N+1}{3})}\rceil$.

The rest of this paper is organized as follows. Section 2 describes the system model and an overview of the proposed scheme. Section 3 presents the performance analysis of the proposed scheme in terms of outage probability and diversity gain. In Sect. 4 the numerical results are presented and the performance of the proposed scheme is compared in terms of the outage probability and the achievable diversity order with the existing schemes in the literature. Finally, Section 5 concludes the paper.

2 System model

In this section we describe communication system model and relaying strategy.

2.1 General system description

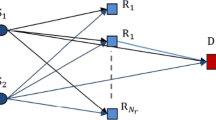
We assume a relay network consisting of M source-destination pairs denoted by $(S_1,D_1), \ldots , (S_M,D_M)$ and N relays denoted by $R_1, \ldots , R_N$, as shown in Fig. 1. Each source, $S_m$, intends to transmit a packet to its corresponding destination $D_m$ for $m=1,\ldots , M$. This scenario is called unicast scenario in the literature [12].

All nodes are assumed to be equipped with single antennas and operate in half-duplex mode. The channel between any pair of nodes is assumed to experience flat Rayleigh fading with Additive White Gaussian Noise (AWGN). In particular, the channel coefficient $h_{t_ir_j}$ between any two communication nodes ${t_i\longrightarrow r_j}$, $t_i \in \{S_1,\ldots ,S_M,R_1,\ldots ,R_N\} ,\; r_j \in \{R_1,\ldots ,R_N,D_1,\ldots ,D_M\}$, is modeled as independent identically distributed (i.i.d.) complex Gaussian random variable with zero mean and unit variance. We assume that $h_{t_ir_j}$ remains constant during the transmission time of a packet.

Further, we assume that the transmission power is equal to P and the additive noise at each link is an i.i.d. random variable that is modeled as ${\mathcal {CN} } (0,\sigma ^2)$. Let $x_{t_{i}} \in \mathbb {{C}}$ denotes the transmitted symbol from node $t_{i}$. The corresponding received signal at node ${r_{j}}$ is given by

$$\begin{aligned} y_{r_{j}}=\sqrt{P}\;\ h_{{t_{i}}{r_{j}}} x_{t_{i}}+N_{{t_{i}}{r_{j}}} \end{aligned}$$

(1)

where $N_{{t_{i}}{r_{j}}}$ is AWGN term and ${\mathbf {E}}[|x_{t_{i}}|^2]=1$. Clearly, the instantaneous signal to noise ratio (SNR) of link ${t_{i}}-{r_{j}}$ is

$$\begin{aligned} \gamma _{{t_{i}}{r_{j}}}=\frac{P|h_{{t_{i}}{r_{j}}}|^2}{\sigma ^2} \end{aligned}$$

(2)

and the instantaneous mutual information of the channel described in (1) with instantaneous SNR, ${\gamma _{{t_{i}}{r_{j}}}}$, is equal to

$$\begin{aligned} I\left( x_{t_{i}},y_{r_{j}}\right) =\log _2\left( 1+\gamma _{{t_{i}}{r_{j}}}\right) \end{aligned}$$

(3)

where $x_{t_{i}}$ and $y_{r_{j}}$ denote the transmitted symbol by node ${t_{i}}$ and the received symbol by node ${r_{j}}$.

In this NCC system, the outage of an intermediate link may lead to the outage of the overall system [8]. To analyze the outage probability, it is assumed an ideal communication system is employed, i.e., the information rate of R (in bits per channel use) is achieved over the link from $t_i$ to $r_{j}$ if and only if $I(x_{t_{i}},y_{r_{j}})>R$ [12]. Otherwise, the link ${{t_{i}}\longrightarrow {r_{j}}}$ will be in outage, and ${r_{j}}$ fails to decode $x_{t_{i}}$. The probability of this event can be expressed as

$$\begin{aligned} P_o &= {\mathrm{Pr}}\left( I(x_{t_{i}},y_{r_{j}})<R\right) ={\mathrm{Pr}}\left( \gamma _{{t_{i}}{r_{j}}}< \underbrace{2^R-1}_{\gamma _{th}}\right) \\&= {\mathrm{Pr}}\left( \gamma _{ij}<\gamma _{th}\right) ={\mathrm{Pr}}\left( |h_{{t_{i}}{r_{j}}}|^2<B\right) \end{aligned}$$

(4)

where $\gamma _{th}=2^R-1$, $B=\frac{(2^{R}-1)\sigma ^2}{P}=\frac{\gamma _{th}}{\bar{\gamma }_{{t_{i}}{r_{j}}}}$, and $\bar{\gamma }_{{t_{i}}{r_{j}}}=\frac{P}{\sigma ^2}$ denotes the average SNR of the link ${{t_{i}}\longrightarrow {r_{j}}}$.

Since the channels experience Rayleigh flat fading, $|h_{{t_{i}}{r_{j}}}|^2$ is exponentially distributed and $P_o=1-e^{-B}$ [12]. At the high-SNR regime, as $\bar{\gamma }_{{t_{i}}{r_{j}}} \rightarrow \infty$, we have ${\lim \nolimits _{\bar{\gamma }_{{t_{i}}{r_{j}}} \rightarrow \infty } B \rightarrow 0}$. Now, from Taylor series expansion of the exponential function ($e^{-B}=\sum _{\ell =1}^\infty \frac{(-B)^\ell }{\ell !}$), it is straightforward to show that $P_o\approx B$ when $\bar{\gamma }_{{t_{i}}{r_{j}}}$ is large.

Fig. 1

NCC communication system model

2.2 Transmission scheme

The proposed NCC scheme operates in two phases, namely, broadcasting and relaying phases. During the broadcasting phase, the sources transmit their packets (each packet consists of $\chi$ bits) in orthogonal time slots. During the relaying phase, sources remain silent and the selected relay(s) apply(s) NC in ${\mathcal {GF}}(2^\chi )$ and forward the network coded packets to the destinations. Note that, in some of our defined cases the selected relays forward the data received without applying NC. More details will be provided in Sect. 3.

• Broadcasting phase: Direct transmissions from sources to the destinations take place in M orthogonal time slots, i.e., their packets are transmitted in M non-overlapping time-slots. The destinations and relays will overhear these transmissions due to the broadcast nature of wireless medium.

• Relaying phase: The L selected relays transmit their information symbols toward the destinations in orthogonal time slots. The selection is based on the RS policy which maximizes the worst end-to-end SNR (max-min criterion described in Sect. 2.5).

2.3 Relay selection algorithm and network coding strategies

Let $M_o$ be the number of unsuccessful sources that their direct links with their destinations are in outage, and ${\mathbb {S}}$ denotes the set of unsuccessful sources and ${\mathbb {D}}$ to be the set of their corresponding destinations. Also, let $q_i$ to be the number of unsuccessful receptions by $D_i$ from all of ($M_o$) unsuccessful sources in the broadcasting phase, except $S_i$. In the next section, by considering the values of $M_o$, L and $q_i$, we will define five cases to analyze the outage probability of $D_i$. In most cases, the selected relays apply linear network coding to perform transmissions. For this purpose, the selected relays employ non-binary network coding based on maximum distance separable (MDS) codes [25]. In each case, different network coding strategy is applied and the selected relays linearly combine all or some of the $M_o$ packets that sent by unsuccessful sources to form network coded packets. The weighting coefficients are drawn from a set of MDS codes. It means that the generator matrix of MDS code could be exploited to generate network coding matrix i.e, the encoding vectors are constructed independently [23]. But, in some cases, a few selected relays are allocated to forward the decoded message toward destinations without employing network codes.

Next, we define some parameters which play a key role in our algorithm and analysis. By an abuse of notation, we denote the set of unsuccessful source-destination pairs as

$$\begin{aligned} {\mathbb {S}}=\left\{ S_1,\ldots ,S_{M_o}\right\} ,\;\;\; {\mathbb {D}}=\left\{ D_1,\ldots ,D_{M_o}\right\} \end{aligned}$$

(5)

Without loss of generality, we suppose $q_1 \ge q_2\ge \cdots \ge q_{M_o}$. Let $N_1$ to be the number of $q_k$’s which are larger than $L-1$, i.e.

$$\begin{aligned} \left\{ \begin{array}{ll} L \le q_{k} \le M_o-1 &{}\quad {{\mathrm{for}}}\; 1\le k \le N_1\\ 0 \le q_{k} \le L-1, &{}\quad {\mathrm{for}}\; N_1+1\le k \le M_o \end{array}\right. \end{aligned}$$

(6)

Let ${\mathbb {S}}'$ and ${\mathbb {D}}'$ to be the set of sources and their corresponding destinations for which the number of unsuccessful receptions does not exceed L, i.e.

$$\begin{aligned} {\mathbb {S}}'&=\left\{ S_{N_1+1},\ldots ,S_{M_o}\right\} , \quad {\mathbb {D}}'=\left\{ D_{N_1+1},\ldots ,D_{M_o}\right\} \end{aligned}$$

(7)

Also, $q'_i$ is the number of undecoded packets by $D_{i}\in \mathbb {D}'$ among the $M_o-N_{1}-1$ packets sent by ${\mathbb {S}}' \setminus \{S_i\}$ in the broadcasting phase.

We define five different cases for the outage event and use different relay selection strategies for those cases. In Case 1, the maximum number of unsuccessful source-destination pairs is equal to L (i.e., $1\le M_o\le L$). In Case 2, the number of unsuccessful source-destination pairs is greater than L (i.e., $M_o>L$), and the number of undecoded packets by each unsuccessful destination does not exceed L. (i.e., $0\le q_{k}\le L-1$, for all $1\le k \le M_o$). In this case, $N_1=0$, that means each destination can decode its intended packet by decoding all or some of the packets sent by L selected relays. In Case 3, $M_o>L$, but, unlike Case 2, $L\le N_1\le M_o$ and $q_k\ge L$ for all $1\le k \le N_1$. Hence, $N_1$ destinations require more than L transmissions to recover their intended packets. In this case, L random source-destination pairs are chosen to be supported in the relaying phase. Next, the best relay is selected for each of chosen source-destination pair in order to forward the received packet from the source to its destination without applying network coding. In Case 4, $M_o>L$, but, unlike Case 3, $1\le N_1<L$. In addition, $0\le q'_k \le L-N_1-1, \;\; {\mathrm{for}}\;\; N_1+1\le k\le M_o$. So, $N_1$ destinations require more than L transmissions to recover their intended packets. Therefore, one relay is selected for each pair of $N_1$ pairs $S_1-D_1, \ldots ,S_{N_1}-D_{N_1}$, to forward the message without applying network coding and $L-N_1$ relays are selected to support the other $M_o-N_1$ pairs by applying network coding. In Case 5, $M_o>L$ and $1\le N_1<L$, but unlike Case 4, $\exists k: \;\; N_1+1\le k\le M_o , \;\ q'_k\ge L-N_1$. Here, similar to Case 3, L random source-destination pairs from $M_o$ pairs are chosen to be supported in the relaying phase. The best relay for each chosen pair is selected to forward the message of each source to its destination without applying network coding.

For more clarity, in Fig. 2 the conditions under which each case occurs are presented in a flowchart. Obviously, these five cases are mutually exclusive.

Fig. 2

A flowchart to depict how different cases are defined

2.4 Implementation of the proposed scheme

Here we discuss how our scheme can be implemented in practice. We assume that after the broadcasting phase, each destination sends an acknowledgment (ACK)/negative-acknowledgment (NACK) regarding all its received/ not-received packets from various sources to a central controller. The ACK packet contains M bits where $k^{th}$ bit shows whether the packet of source $S_k$ has been successfully received or not. The central controller gathers totally $M^2$ bits from the destinations and to be informed about all successful/unsuccessful receptions of the destinations. Then, the central controller can figure out which one of 5 defined cases of our scheme has occurred.

Next, the central controller determines (depending on the case) which source-destination pairs must be supported by the relays in the relaying phase. The center also determines whether the packet of each source-destination pair must be network coded or the packet is forwarded without network coding. For this purpose, the central controller broadcast a packet to the relays which contain 2M bits. The first M bits show which source-destination pairs must be supported, where its $k^{th}$ bit determines whether the packet of $S_k$ need to be somehow relayed to $D_k$. The second M bits show which packets require network coding, i.e., its $k^{th}$ bits determines whether the of $S_k$ must be combined with the packets of other supported source via network coding or it is simply forwarded toward $D_k$.

We use the idea of distributed relay selection algorithm of [9]. We assume that the relays can evaluate the quality of their channels toward different sources and destinations by overhearing the request-to-send (RTS) and clear-to-send (CTS) packets sent by the sources and destinations in the broadcast phase. Note that here it is assumed from the reciprocity theorem [26] that the forward and backward channels are the same. In order to prioritize the relays, each relay uses a timer that is inversely proportional to its equivalent SNR with respect to intended source-destination pairs. To determine the order of transmissions and avoid unnecessary/lost transmissions or missing by the relays, we define a default ordering for the packets which are going to supported. For example, first the packets without network coding are transmitted by the order of indexes of their source-destination pairs. Next, the packets which require network coding are transmitted; the number of such packets is known from the central controller broadcast. Note that in this scheme the central controller does not need to gather channel state information (CSI) of the relays, it only determines which source-destination pairs must be supported in the relaying phase.

2.5 Notations and basic analysis

Here, we present the notations to describe the proposed scheme and provide the basic analysis. Note that RS is implemented based on the max-min selection criterion. The equivalent SNR for a relay in cooperative networks is defined as the weakest link associated with the relay [8]. In some situations, one relay is allocated to a pair of unsuccessful source-destination in order to forward the received packet from the source to its destination without applying network coding. Note that a relay can participate in communication between $S_i$ and $D_i$, only when it successfully receives the packet of $S_i$ in the broadcasting phase. We define, the equivalent SNR of relay $R_j$ as

$$\begin{aligned} {{\gamma }^{eq}_j(S_i,D_i)}=\min \left\{ \gamma _{S_iR_j},\gamma _{R_jD_i} \right\} \end{aligned}$$

(8)

In some cases, the selected relays apply NC to all of the received packets sent by the sources in ${\mathbb {S}}$ or ${\mathbb {S}}'$. In these situations, a relay would participate in the communication only if it receives the packets of all intended sources. Hence, the equivalent SNR of relay $R_j$ is defined as

$$\begin{aligned}&{{\gamma }^{eq}_j({\mathbb {S}},{\mathbb {D}})} \\& \quad= \min \left\{ \gamma _{S_1R_j},\ldots ,\gamma _{S_{M_o}R_j},\gamma _{R_jD_{1}},\ldots ,\gamma _{R_jD_{M_o}} \right\} \end{aligned}$$

(9)

$$\begin{aligned} \\&{{\gamma }^{eq}_j({\mathbb {S}}',{\mathbb {D}}')} \\&\quad =\min \left\{ \gamma _{S_{N_1+1}R_j},\ldots ,\gamma _{S_{M_o}R_j},\gamma _{R_jD_{N_1+1}},\ldots ,\gamma _{R_jD_{M_o}}\right\} \end{aligned}$$

(10)

Similarly, the equivalent SNR of relay $R_j$ for a given destination $D_i$ can be expressed as

$$\begin{aligned} {{\gamma }^{eq}_j\left( {\mathbb {S}},D_i\right) }&=\min \left\{ \gamma _{S_1R_j},\ldots ,\gamma _{S_{M_o}R_j},\gamma _{R_jD_{i}}\right\} \end{aligned}$$

(11)

$$\begin{aligned} {{\gamma }^{eq}_j\left( {\mathbb {S}}',D_i\right) }&=\min \left\{ \gamma _{S_{N_1+1}R_j},\ldots ,\gamma _{S_{M_o}R_j},\gamma _{R_jD_{i}}\right\} \end{aligned}$$

(12)

Since the SNR of the links are independent and exponentially distributed, the corresponding Cumulative Distribution Function (CDF) can be formulated as follows [7]

$$\begin{aligned} F_{{\gamma }^{eq}_j\left( {\mathbb {S}},{\mathbb {D}}\right) }(x)=1-e^{-\frac{x}{\bar{{\gamma }}^{eq}_j\left( {\mathbb {S}},{\mathbb {D}}\right) }} \end{aligned}$$

(13)

where

$$\begin{aligned} \bar{{\gamma }}^{eq}_j\left( {\mathbb {S}},{\mathbb {D}}\right)&=\left( {\frac{1}{\bar{\gamma }_{S_1R_j}}+\cdots +\frac{1}{\bar{\gamma }_{S_{M_o}R_j}} + \frac{1}{\bar{\gamma }_{R_jD_1}}+\cdots +\frac{1}{\bar{\gamma }_{R_jD_{M_o}}}}\right) ^{-1} \end{aligned}$$

The CDF of ${{\gamma }^{eq}_j}({\mathbb {S}}',{\mathbb {D}}'), {{\gamma }^{eq}_j}(S_i,D_i), {{\gamma }^{eq}_j}({\mathbb {S}},D_i),{{\gamma }^{eq}_j}({\mathbb {S}}',D_i)$ are defined similarly. Since the channels are i.i.d., we have

$$\begin{aligned} \bar{\gamma }_{S_iR_j}=\bar{\gamma }_{R_jD_i}=\bar{\gamma }\;\;\; \text {for all}\quad 1\le i \le M ,\quad 1\le j \le N \end{aligned}$$

(14)

Thus

$$\begin{aligned} F_{{{\gamma }^{eq}_j}\left( {\mathbb {S}},{\mathbb {D}}\right) }\left( \gamma _{th}\right)&=1-e^{-\frac{2M_o\gamma _{th}}{\bar{\gamma }}}=1-e^{-2M_oB} \end{aligned}$$

(15)

$$\begin{aligned} F_{{{\gamma }^{eq}_j}\left( {\mathbb {S}}',{\mathbb {D}}'\right) }\left( \gamma _{th}\right)&=1-e^{-\frac{2(M_o-N_1)\gamma _{th}}{\bar{\gamma }}}=1-e^{-2(M_o-N_1)B} \end{aligned}$$

(16)

$$\begin{aligned} F_{{{\gamma }^{eq}_j}\left( S_i,D_i\right) }\left( \gamma _{th}\right)&=1-e^{-\frac{2\gamma _{th}}{\bar{\gamma }}}=1-e^{-2B} \end{aligned}$$

(17)

$$\begin{aligned} F_{{{\gamma }^{eq}_j}\left( {\mathbb {S}},D_i\right) }\left( \gamma _{th}\right)&=1-e^{-\frac{\left( M_o+1\right) \gamma _{th}}{ \bar{\gamma }}}=1-e^{-\left( M_o+1\right) B} \end{aligned}$$

(18)

$$\begin{aligned} F_{{{\gamma }^{eq}_j}\left( {\mathbb {S}}',D_i\right) }\left( \gamma _{th}\right)&=1-e^{-\frac{\left( M_o-N_1+1\right) \gamma _{th}}{\bar{\gamma }}}=1-e^{-\left( M_o-N_1+1\right) B} \end{aligned}$$

(19)

where $B=\frac{\gamma _{th}}{\bar{\gamma }}$.

At the high-SNR regime, the following approximations can be derived using Taylor expansion

$$\begin{aligned}&F_{{{\gamma }^{eq}_j}\left( {\mathbb {S}},{\mathbb {D}}\right) }\left( \gamma _{th}\right) \approx 2M_oB \end{aligned}$$

(20)

$$\begin{aligned}&F_{{{\gamma }^{eq}_j}\left( {\mathbb {S}}',{\mathbb {D}}'\right) }\left( \gamma _{th}\right) \approx 2\left( M_o-N_1\right) B \end{aligned}$$

(21)

$$\begin{aligned}&F_{{{\gamma }^{eq}_j}\left( S_i,D_i\right) }\left( \gamma _{th}\right) \approx {2B} \end{aligned}$$

(22)

$$\begin{aligned}&F_{{{\gamma }^{eq}_j}\left( {\mathbb {S}},D_i\right) }\left( \gamma _{th}\right) \approx {\left( M_o+1\right) B} \end{aligned}$$

(23)

$$\begin{aligned}&F_{{{\gamma }^{eq}_j}\left( {\mathbb {S}}',D_i\right) }\left( \gamma _{th}\right) \approx {\left( M_o-N_1+1\right) B} \end{aligned}$$

(24)

We denote the $l^{th}$ largest value of the equivalent SNRs as

$$\begin{aligned}&\phi ^l\left( {\mathbb {S}},{\mathbb {D}}\right) ={\max }^{l}\left\{ {{\gamma }^{eq}_1}\left( {\mathbb {S}},{\mathbb {D}}\right) ,\ldots ,{{\gamma }^{eq}_N}\left( {\mathbb {S}},{\mathbb {D}}\right) \right\} \end{aligned}$$

(25)

$$\begin{aligned}&\phi ^l\left( {\mathbb {S}}',{\mathbb {D}}'\right) ={\max }^{l}\left\{ {{\gamma }^{eq}_1}\left( {\mathbb {S}}',{\mathbb {D}}'\right) ,\ldots ,{{\gamma }^{eq}_N}\left( {\mathbb {S}}',{\mathbb {D}}'\right) \right\} \end{aligned}$$

(26)

$$\begin{aligned}&\phi ^l\left( S_i,D_i\right) ={\max }^{l}\left\{ {{\gamma }^{eq}_1}\left( S_i,D_i\right) ,\ldots ,{{\gamma }^{eq}_N}\left( S_i,D_i\right) \right\} \end{aligned}$$

(27)

$$\begin{aligned}&\phi ^l\left( {\mathbb {S}},D_i\right) ={\max }^{l}\left\{ {{\gamma }^{eq}_1}\left( {\mathbb {S}},D_i\right) ,\ldots ,{{\gamma }^{eq}_N}\left( {\mathbb {S}},D_i\right) \right\} \end{aligned}$$

(28)

$$\begin{aligned}&\phi ^l\left( {\mathbb {S}}',D_i\right) ={\max }^{l}\left\{ {{\gamma }^{eq}_1}({\mathbb {S}}',D_i),\ldots ,{{\gamma }^{eq}_N}\left( {\mathbb {S}}',D_i\right) \right\} \end{aligned}$$

(29)

where ${\max }^{l}$ denotes the $l^{th}$ maximum of the set.

The probability that $l-1$ relays are operational (i.e., not in outage) can be written as

$$\begin{aligned}&F_{\phi ^l\left( {\mathbb {S}},{\mathbb {D}}\right) }\left( \gamma _{th}\right) ={\mathrm{Pr}}\left[ \; \left( N-l+1 \text { values of } \;\; {{\gamma }^{eq}_j}\left( {\mathbb {S}},{\mathbb {D}}\right) \le \gamma _{th}\right) \right. \\&\quad \left. \;\; \cap \left( l-1 \;\; \text {values of}\;\; {{\gamma }^{eq}_j}\left( {\mathbb {S}},{\mathbb {D}}\right) > \gamma _{th}\right) \;\right] \end{aligned}$$

(30)

This probability can be formulated as follows [7]

$$\begin{aligned} F_{\phi ^l\left( {\mathbb {S}},{\mathbb {D}}\right) }(\gamma _{th})&=\sum _{u=1}^l(-1)^{u-1} \left( {\begin{array}{*{20}c} {N - l + u} \\ {N - l + 1} \\ \end{array} } \right) {\varGamma }_l\left( u,\gamma _{th}\right) \end{aligned}$$

(31)

where

$$\begin{aligned} {\varGamma }_l\left( u,\gamma _{th}\right) =\sum _{\begin{array}{c} j_1=1,\ldots ,j_{N-l+u}=1 \\ j_1\ne \cdots\ne j_{N-l+u} \end{array}}^N \prod _{j=j_1}^{j_{N-l+u}}F_{{{\gamma }^{eq}_j}\left( {\mathbb {S}},{\mathbb {D}}\right) } \left( \gamma _{th}\right) \end{aligned}$$

(32)

and

$$\begin{aligned} \sum _{\begin{array}{c} j_1=1,\ldots ,j_t=1 \\ j_1\ne \cdots \ne j_t \end{array}}^n \prod _{m=j_1}^{j_t} x_m=\sum _{j_1=1}^{n-t+1}\ldots \sum _{j_t=j_{t-1}+1}^{n}(x_{j_1}\ldots x_{j_t}) \end{aligned}$$

(33)

Similarly, formulas can be derived for $F_{\phi ^l({\mathbb {S}}',{\mathbb {D}}')}(\gamma _{th})$, $F_{\phi ^l(S_i,D_i)}(\gamma _{th})$,$F_{\phi ^l({\mathbb {S}},D_i)}(\gamma _{th})$, $F_{\phi ^l({\mathbb {S}}',D_i)}(\gamma _{th})$.

Proposition 1

The asymptotic orders of $F_{\phi ^l({\mathbb {S}},{\mathbb {D}})}(\gamma _{th})$, $F_{\phi ^l({\mathbb {S}}',{\mathbb {D}}')}(\gamma _{th})$, $F_{\phi ^l(S_i,D_i)}(\gamma _{th})$, $F_{\phi ^l({\mathbb {S}},D_i)}(\gamma _{th})$, and $F_{\phi ^l({\mathbb {S}}',D_i)}(\gamma _{th})$ in terms of $\bar{\gamma }$ are asymptotically $\mathcal {O}(\bar{\gamma }^{-(N-l+1)})$.

Proof

For high-SNR, using the results of (20)–(24) and retaining the smallest exponent of B, we have

$$\begin{aligned}& F_{\phi ^l\left( {\mathbb {S}},{\mathbb {D}}\right) }\left( \gamma _{th}\right) \approx \left( {\begin{array}{*{20}c} N \\ {N - l + 1} \\ \end{array} } \right) {\left( 2M_oB\right) }^{(N-l+1)} \end{aligned}$$

(34)

$$\begin{aligned}& F_{\phi ^l\left( {\mathbb {S}}',{\mathbb {D}}'\right) }\left( \gamma _{th}\right) \approx \left( {\begin{array}{*{20}c} N \\ {N - l + 1} \\ \end{array} } \right) {\left( 2\left( M_o-N_1\right) B\right) }^{(N-l+1)} \end{aligned}$$

(35)

$$\begin{aligned}& F_{\phi ^l\left( S_i,D_i\right) }\left( \gamma _{th}\right) \approx \left( {\begin{array}{*{20}c} N \\ {N - l + 1} \\ \end{array} } \right) {(2B)}^{(N-l+1)} \end{aligned}$$

(36)

$$\begin{aligned}&F_{\phi ^l\left( {\mathbb {S}},D_i\right) }\left( \gamma _{th}\right) \approx \left( {\begin{array}{*{20}c} N \\ {N - l + 1} \\ \end{array} } \right) {\left( \left( M_o+1\right) B\right) }^{(N-l+1)} \end{aligned}$$

(37)

$$\begin{aligned}&F_{\phi ^l\left( {\mathbb {S}}',D_i\right) }\left( \gamma _{th}\right) \approx \left( {\begin{array}{*{20}c} N \\ {N - l + 1} \\ \end{array} } \right) {\left( \left( M_o-N_1+1\right) B\right) }^{(N-l+1)} \end{aligned}$$

(38)

where $B=\frac{\gamma _{th}}{\bar{\gamma }}$. Assuming N, M, and R to be constant, the asymptotic orders of above terms will be $\mathcal {O}(\bar{\gamma }^{-(N-l+1)})$.

For convenience, the main parameters and sets in analyzing the proposed strategy have been summarized in Table 1.

Table 1 List of main parameters

3 Performance analysis

In this section we analyze the outage probability and diversity order of the proposed scheme.

3.1 Outage probability

In this subsection, we obtain some closed-form expressions or derive the lower and the upper bounds for the outage probability of the system in various defined cases. Note that the probability of occurrence of each case is considered in the derivation of the bounds and closed-form expressions.

By considering a source-destination pair $(S_i,D_i)$ and the values of $M_o$, $N_1$ ($q_{k}$’s), and $q'_{k}$’s, we analyze each case separately in the following.

Case 1

In this case, $1\le M_o\le L$. The probability of occurrence of Case 1 will be used for obtaining lower and upper bounds on the outage probability. Since in this case all of L selected relays apply linear network coding on the all of $M_o$ packets sent by $S_1,\ldots ,S_{M_o}$, a selected relay can participate in the relaying phase only by decoding all of $M_o$ packets successfully. The relay selection algorithm is implemented based on max-min criterion, where the relays with the highest end-to-end SNRs are used. Hence, the $l^{th} (l=1,\ldots ,L)$ selected relay (denoted by $R^l_{S_{\text {case 1}}}$) is determined as following,

$$\begin{aligned} l=\arg {\max }^{l^{th}}_{j=1,\ldots ,N}\left\{ {{\gamma }^{eq}_j}\left( {\mathbb {S}},{\mathbb {D}}\right) \right\} \end{aligned}$$

(39)

It is assumed that $D_i$ is unsuccessful in the broadcasting phase (i.e., $D_i\in {\mathbb {D}}$), and the probability of this assumption is considered in our analysis. Hence, $D_i$ will be able to recover the packet sent by $S_i$ after receiving at least $q_i+1$ error-free packets, where $q_i+1$ is the number of undecoded packets by $D_i$ among those $M_o$ packets in the broadcasting phase.

Note that in this case, L relays with the highest end-to-end SNRs are used. The end-to-end SNR of each relay $R_j$ is dominated by the weakest link among the links associated with $R_j$ (i.e., $S_k \rightarrow R_j \rightarrow D_k , (k=1,2,\ldots ,M_o))$. So the SNR of the weakest link determines the equivalent SNR for each relay.

For deriving the upper bound, we suppose that a selected relay (i.e., $R^l_{S_{\mathrm{Case 1}}}$) is operational if the instantaneous SNR of all the links associated with $R^l_{S_{\mathrm{Case 1}}}$ (i.e., $S_k \rightarrow R^l_{S_{\mathrm{Case 1}}} \rightarrow D_k , (k=1,2,\ldots ,M_o)$) are above the reliability threshold $\gamma _{th}$.

To obtain the lower bound, we consider the best situation in which the selected relays are L best relays with the highest equivalent SNRs given in (11) (i.e., the links between $R_j$ and the other destinations except $D_i$ are ignored in determining the equivalent SNR of $R_j$). It means that $R^l_{S_{\text {case 1}}}$ is operational if the instantaneous SNR of all the links between $S_k \rightarrow R^l_{S_{\text {case 1}}} \rightarrow D_i, (k=1,2,\ldots ,M_o)$ are above the $\gamma _{th}$.

Let $E_i (\mathrm{Case 1})$ represents the outage event where Case 1 occurs and $D_i$ is not able to decode the packet sent by $S_i$. Now, we derive lower and upper bounds for the probability of $E_i\text{( }\mathrm Case 1)$ which denoted by ${\mathrm{Pr}}(E_i^{low}\text{( }\mathrm Case 1))$ and ${\mathrm{Pr}}(E_i^{up}\text{( }\mathrm Case 1))$ respectively. As mentioned before, the probability of occurrence of Case 1 is considered in the derivation of these bounds.

$$\begin{aligned} {\mathrm{Pr}}(E_i^{low}\left( \mathrm{{Case 1}}\right) )=&\sum _{M_o=1}^L \left( {\begin{array}{c}M-1\\ M_o-1\end{array}}\right) P_o^{M_o}\left( 1-P_o\right) ^{M-M_o} \\&\times \sum _{q_i=0}^{M_o-1} \left( {\begin{array}{c}M_o-1\\ q_i\end{array}}\right) P_o^{q_i}\left( 1-P_o\right) ^{M_o-q_i-1} \\&\sum _{l=1}^{q_i+1} F_{\phi ^l\left( {\mathbb {S}},D_i\right) }\left( \gamma _{th}\right) \end{aligned}$$

(40)

$$\begin{aligned} {\mathrm{Pr}}\left( E_i^{up}\left( \mathrm{{Case 1}}\right) \right) =&\sum _{M_o=1}^L \left( {\begin{array}{c}M-1\\ M_o-1\end{array}}\right) P_o^{M_o}\left( 1-P_o\right) ^{M-M_o} \\&\times \sum _{q_i=0}^{M_o-1} \left( {\begin{array}{c}M_o-1\\ q_i\end{array}}\right) P_o^{q_i}\left( 1-P_o\right) ^{M_o-q_i-1} \\&\sum _{l=1}^{q_i+1} F_{\phi ^l\left( {\mathbb {S}},{\mathbb {D}}\right) }\left( \gamma _{th}\right) \end{aligned}$$

(41)

where $P_o$ denotes the outage probability of each individual channel.

The first summation in (40) and (41) represents the probability that the link $S_i \rightarrow D_i$ and the other $M_o-1$ links between source-destination pairs are in outage in the broadcasting phase (i.e, $M_o$ sources, that $S_i$ is one of them, are unsuccessful in direct transmissions). The second summation stands for the probability that $q_i+1$ packets among the $M_o$ packets are not decoded by $D_i$ in the broadcasting phase. Note that $D_i$ requires to receive at least $q_i+1$ error-free packets from the selected relays to recover its own packet. The third summation is the probability that at most $q_i$ relays are operational, where $F_{\phi ^l({\mathbb {S}},{\mathbb {D}})}(x)$ and $F_{\phi ^l({\mathbb {S}},D_i)}(x)$ are the upper and lower bounds for the probability of existence $l-1$ operational relays, respectively.

The diversity order indicates the slope of the outage probability at high SNR [27], thus,

$$\begin{aligned}&\lim _{\bar{\gamma }\rightarrow \infty }\frac{-\log {\mathrm{Pr}}\left( E_i^{up}\left( \mathrm{Case 1}\right) \right) }{\log \bar{\gamma }} \\&\quad = \lim _{\bar{\gamma }\rightarrow \infty }\frac{-\log {\mathrm{Pr}}\left( E_i^{low}\left( \mathrm{Case 1}\right) \right) }{\log \bar{\gamma }} \\&\quad =\lim _{\bar{\gamma }\rightarrow \infty }\frac{-\log {\mathrm{Pr}}\left( E_i\left( \mathrm{Case 1}\right) \right) }{\log \bar{\gamma }}=N+1 \end{aligned}$$

(42)

Therefore, the diversity order achieved in Case 1 will be equal to $N+1$.

Proof

From Proposition 1, we know that

$$\begin{aligned}&{\lim _{\bar{\gamma }\rightarrow \infty }\frac{-\log F_{\phi ^l\left( {\mathbb {S}},{\mathbb {D}}\right) }\left( \gamma _{th}\right) }{\log \bar{\gamma }}} \\&\quad ={\lim _{\bar{\gamma }\rightarrow \infty }\frac{-\log F_{\phi ^l\left( {\mathbb {S}},D_i\right) }\left( \gamma _{th}\right) }{\log \bar{\gamma }}} \\&\quad =N-l+1. \end{aligned}$$

(43)

The dominant terms of the third summation is achieved at $l=q_i+1$ that gives the diversity order of $N-q_i$. Also, at high SNRs, ${\lim \nolimits _{\bar{\gamma }_{{t_{i}}{r_{j}}} \rightarrow \infty } P_o\approx B}$. By retaining the dominant terms in (40) and (41), when $M_o=1$ in the first summation and $l=q_i+1$ in the third one, the asymptotic results of (42) is derived.

Case 2

In this case, $M_o\ge L+1$, and $0\le q_{k}\le L-1$, for all $1\le k \le M_o$ (i.e., $N_1=0$). By the definition, $q_{k}+1$ represents the number of undecoded packets by $D_{k}\in {\mathbb {D}}$ among the packets sent by $S_1,\ldots ,S_{M_o}$ in the broadcasting phase. Hence, $D_{k}$ can decode the packet sent by $S_k$ successfully after receiving at least $q_{k}+1$ error-free packets in the relaying phase. Since, $q_{k}+1\le L$ for all $1\le k \le M_o$, we can select L relays apply linear network coding on the all of $M_o$ packets sent by $S_1,\ldots ,S_{M_o}$. It is necessary to mention that, if the selected relays decode all of $M_o$ packets successfully, they can participate in the relaying phase. The relay selection algorithm in this case is similar to Case 1 and l is given in (39).

Since $D_i\in {\mathbb {D}}$ (the probability of this event is considered in our derivations), it requires to receive at least $q_i+1$ error-free packets in the relying phase for recovering its own packet, otherwise, it will be in outage ($E_i(\mathrm Case 2)$). The steps of deriving upper and lower bounds for this outage probability are similar to the Case 1, except that for this case $M_o\ge L+1$ and $0\le q_{k}\le L-1$ for all $1\le k \le M_o$. Similar to Case 1, the lower and upper bounds can be formulated as follows

$$\begin{aligned}&\mathrm{{Pr}}\left( E_i^{low}\left( \mathrm{{Case 2}}\right) \right) \\&\quad =\sum _{M_o=L+1}^M {P_o}^{M_o}\left( 1-P_o\right) ^{M-M_o}\left( {\begin{array}{c}M-1\\ M_o-1\end{array}}\right) \\&\qquad \times \prod _{k=1,k\ne i}^{M_o}\sum _{q_k=0}^{L-1} \left( {\begin{array}{c}M_o-1\\ q_k\end{array}}\right) P_o^{q_k}\left( 1-P_o\right) ^{M_o-q_k-1} \\&\qquad \times \sum _{q_i=0}^{L-1} \left( {\begin{array}{c}M_o-1\\ q_i\end{array}}\right) {P_o}^{q_i}\left( 1-P_o\right) ^{M_o-q_i-1}\sum _{l=1}^{q_i+1} F_{\phi ^l_{\left( {\mathbb {S}},D_i\right) }} \left( \gamma _{th}\right) \end{aligned}$$

(44)

$$\begin{aligned}&{\mathrm{Pr}}\left( E_i^{up}\left( \mathrm{Case 2}\right) \right) \\&\quad =\sum _{M_o=L+1}^M {P_o}^{M_o}\left( 1-P_o\right) ^{M-M_o}\left( {\begin{array}{c}M-1\\ M_o-1\end{array}}\right) \\&\qquad \times \prod _{k=1,k\ne i}^{M_o}\sum _{q_k=0}^{L-1} \left( {\begin{array}{c}M_o-1\\ q_k\end{array}}\right) P_o^{q_k}\left( 1-P_o\right) ^{M_o-q_k-1} \\&\qquad \times \sum _{q_i=0}^{L-1} \left( {\begin{array}{c}M_o-1\\ q_i\end{array}}\right) {P_o}^{q_i}(1-P_o)^{M_o-q_i-1}\sum _{l=1}^{q_i+1} F_{\phi ^l_{\left( {\mathbb {S}},{\mathbb {D}}\right) }}\left( \gamma _{th}\right) \end{aligned}$$

(45)

Thus, the asymptotic behavior of the outage probability will be

$$\begin{aligned}&\lim _{\bar{\gamma }\rightarrow \infty }\frac{-\log {\mathrm{Pr}}\left( E_i^{up}\left( \mathrm{Case 2}\right) \right) }{\log \bar{\gamma }} \\&\quad = \lim _{\bar{\gamma }\rightarrow \infty }\frac{-\log {\mathrm{Pr}}\left( E_i^{low}\left( \mathrm{Case 2}\right) \right) }{\log \bar{\gamma }} \\&\quad =\lim _{\bar{\gamma }\rightarrow \infty }\frac{-\log {\mathrm{Pr}}\left( E_i\left( \mathrm{Case 2}\right) \right) }{\log \bar{\gamma }}=L+N+1 \end{aligned}$$

(46)

Proof

Similar to the proof of Case 1, the multiplication of third and fourth summations gives the diversity order of N. In addition, the dominant terms of (44) and (45) can be obtained by setting $M_o=L+1$ and $q_{k}=0$ from the first and second summations. Hence, the diversity order of $L+N+1$ is achieved for this case.

Case 3

For this case, let ${\mathcal {A}}{} \textit{1}$ the event that $M_o>L$ sources including $S_i$ to be in outage in the broadcasting phase. Obviously,

$$\begin{aligned} {\mathrm{Pr}}\left( {\mathcal {A}}{} \textit{1}\right) =\sum _{M_o=L+1}^M\left( {\begin{array}{c}M-1\\ M_o-1\end{array}}\right) P_o^{M_o}\left( 1-P_o\right) ^{M-M_o} \end{aligned}$$

(47)

Further, the probability of the event $L\le N_1\le M_o$ will be

$$\begin{aligned}&{\mathrm{Pr}}\left( {\mathcal {A}}{} \textit{2}\right) \\&\quad =\sum _{N_1=L}^{M_o} \left( {\begin{array}{c}M_o\\ N_1\end{array}}\right) \left( \prod _{k=1}^{N_1}\;\sum _{q_k=L}^{M_o-1}\left( {\begin{array}{c}M_o-1\\ q_k\end{array}}\right) P_o^{q_k}\left( 1-P_o\right) ^{M_o-q_{k}-1}\right) \\&\qquad \times \left( U\left( N_1-M_o\right) +\left( U\left( M_o-N_1-1\right) \right. \right. \\&\qquad \left. \left. \times \left( \prod _{k=N_1+1}^{M_o}\;\sum _{q_{k}=0}^{L-1}\left( {\begin{array}{c}M_o-1\\ q_{k}\end{array}}\right) P_o^{q_{k}}\left( 1-P_o\right) ^{M_o-q_{k}-1}\right) \right) \right) \end{aligned}$$

(48)

where $U(\cdot )$ represents the unit-step function whose value is equal to 0 for negative arguments and 1 for non-negative arguments [28].

Note that in this case, there is no guarantee that $N_1$ destinations are able to recover their intended packets even after receiving L error-free packets in the relaying phase, because, even with perfect links between source-relay and relay-destination, each $D_{k}\in {\mathbb {D}} \;(1\le k\le N_1)$ cannot recover $q_{k}+1>L$ packets after receiving L packets from the relays. Therefore, in this case, we randomly choose L source-destination among $M_o$ pairs to be supported in L relays. We denote the set of chosen sources and destinations by ${\mathbb {S}}^{ch}$ and ${\mathbb {D}}^{ch}$ respectively.

$$\begin{aligned} {\mathbb {S}}^{ch}=\left\{ S_1^{ch},\ldots ,S_L^{ch}\right\} ,\quad {\mathbb {D}}^{ch}=\left\{ D_1^{ch},\ldots ,D_L^{ch}\right\} \end{aligned}$$

(49)

Next, for each pair of chosen source-destination, a selected relay is allocated to forward the message of source to the destination without applying network coding. Here, the $l^{th}$ selected relay, $R^l_{S_{\text {case 3}}}$, is selected by the following formula,

$$\begin{aligned} l =\arg \max _{j=1,\ldots ,N} \left( \min \left\{ \gamma _{S_l^{ch}{R_j}} , \gamma _{R_j D_l^{ch}} \right\} \right) \end{aligned}$$

(50)

In this case, the outage event occurs if $S_i$ is not among randomly chosen sources with probability $\frac{M_o-L}{M_o}$. Also, this event occurs if $S_i-D_i$ is chosen to support in the relaying phase, but no relay can successfully decode and forward the message of $S_i$ to $D_i$ i.e., $\phi ^1(S_i,D_i)<\gamma _{th}$. Based on the explanations provided, ${\mathrm{Pr}}(E_i(\mathrm Case 3))$ can be obtained as follows

$$\begin{aligned} {\mathrm{Pr}}\left( E_i\left( \mathrm{{Case 3}}\right) \right)&={\mathrm{Pr}}\left( {\mathcal {A}}{} \textit{1}\right) {\mathrm{Pr}}\left( {\mathcal {A}}{} \textit{2}\right) \\&\quad \times \left( \frac{L}{M_o}F_{\phi ^1_{(S_i,D_i)}}(\gamma _{th})+\frac{M_o-L}{M_o}\right) \end{aligned}$$

(51)

In addition, by setting $M_o=L+1 ,\; N_1=L$, $\;q_1=\cdots =q_{L}=L$ and $q_{L+1}=\cdots =q_{M_o}=0$ in (51) and keeping the dominant term, we have

$$\begin{aligned} \lim _{\bar{\gamma }\rightarrow \infty }\frac{-\log {\mathrm{Pr}}\left( E_i\left( \mathrm{Case 3}\right) \right) }{\log \bar{\gamma }}=L^2+L+1 \end{aligned}$$

(52)

Case 4

In this case, we have $L\ge 2$, $M_o>L$, $1\le N_1<L$, and

$$\begin{aligned} 0\le q'_k \le L-N_1-1, \;\;\;\;\; {\mathrm{for}}\;\; N_1+1\le k\le M_o \end{aligned}$$

(53)

where $q'_k$ is the number of undecoded packets by $D_{k}\in \mathbb {D'}$ among the $M_o-N_{1}-1$ packets sent by ${\mathbb {S}}' \setminus \{S_k\}$ in the broadcasting phase.

To analyze the outage probability, we define the event: ${\mathcal {A}}{} \textit{3}\triangleq$ {$L \le q_{k} \le M_o-1, \; {\mathrm{for}}\;\; 1\le k \le N_1, \; {\mathrm{and}} \;\;0\le q'_k \le L-N_1-1, \;\;{\mathrm{for}}\;\; N_1+1\le k\le M_o$ }. Note that when $0\le q'_k \le L-N_1-1$, then $0 \le q_{k} \le L-1$, because we have, $q'_k \le q_{k} \le q'_k+N_1$.

The probability of occurrence of event $({\mathcal {A}}{} \textit{3})$ can be expressed as,

$$\begin{aligned}&{\mathrm{Pr}}\left( {\mathcal {A}}{} \textit{3}\right) \\&\quad =\left( \prod _{k=1}^{N_1}\;\sum _{q_k=L}^{M_o-1}\left( {\begin{array}{c}M_o-1\\ q_k\end{array}}\right) P_o^{q_k}(1-P_o)^{M_o-q_{k}-1}\right) \\&\qquad \times \left( \prod _{k=N_1+1}^{M_o}\;\sum _{q'_k=0}^{L-N_1-1}\left( {\begin{array}{c}M_o-N_1-1\\ q'_k\end{array}}\right) P_o^{q'_k}\left( 1-P_o\right) ^{M_o-N_1-q'_k-1}\right) \end{aligned}$$

(54)

In this case, a relay is allocated to each pair of $N_1$ pairs $S_1-D_1, \ldots ,S_{N_1}-D_{N_1}$, to forward the message of each source to its destination. Thus, in the first step, $N_1$ relays are selected to support all of these $N_1$ pairs. The relay selection criterion for selecting the $l^{th} (1\le l \le N_1)$ best selected relay, $R^l_{S_{\text {case 4}}}$ is given by

$$\begin{aligned} l= \arg \max _{j=1,\ldots ,N}\left( \min \left\{ \gamma _{S_{l}R_j}, \gamma _{R_jD_{l}}\right\} \right) , \;\;\; 1\le l \le N_1 \end{aligned}$$

(55)

Next, $L-N_1$ relays are selected to support the other $M_o-N_1$ pairs. Each selected relay which decode all of $M_o-N_1$ packets sent by $S_{N_1+1},\ldots , S_{M_o}$ successfully, can participate in the second phase by transmitting the linear combination of those packets. These relays are selected as follows

$$\begin{aligned}&l= \arg {\max }^{\left( l-{N_1}\right) ^{th}}_{j=1,\ldots ,N}\left( {\xi }_j\left( {\mathbb {S}}',{\mathbb {D}}'\right) \right) \;\;\;\;\;\; N_1+1 \le l \le L \end{aligned}$$

(56)

In order to derive the outage probability, the probabilities of occurrence of both states $(q_i>L-1$ or $0\le q'_i \le L-N_1-1)$ must be considered. The lower and upper bounds for ${\mathrm{Pr}}(E_i(\mathrm{Case 4}))$ will be,

$$\begin{aligned}&{\mathrm{Pr}}\left( E_i^{low}\left( \mathrm{{Case 4}}\right) \right) \\&\quad =U(L-2)\times \left( \left( {\mathrm{Pr}}\left( {\mathcal {A}}{} \textit{1}\right) \times \sum _{N_1=1}^{L-1}\left( {\begin{array}{c}M_o-1\\ N_1-1\end{array}}\right) {\mathrm{Pr}}\left( {\mathcal {A}}{} \textit{3}\right) \right. \right. \\&\qquad \left. \times F_{\phi ^1\left( S_i,D_i\right) }\left( \gamma _{th}\right) \right) +\left( {\mathrm{Pr}}\left( {\mathcal {A}}{} \textit{1}\right) \times \sum _{N_1=1}^{L-1}\left( {\begin{array}{c}M_o-1\\ N_1\end{array}}\right) \right. \\&\qquad \times \left( \prod _{k=1}^{N_1}\;\sum _{q_k=L}^{M_o-1}\left( {\begin{array}{c}M_o-1\\ q_k\end{array}}\right) P_o^{q_k}\left( 1-P_o\right) ^{M_o-q_{k}-1}\right) \\&\qquad \times \left( \prod _{k=N_1+1 ,k \ne i}^{M_o}\;\sum _{q'_k=0}^{L-N_1-1}\left( {\begin{array}{c}M_o-N_1-1\\ q'_k\end{array}}\right) P_o^{q'_k}\right. \\&\qquad \times \left. \left( 1-P_o\right) ^{M_o-N_1-q'_k-1}\right) \left( \sum _{q'_i=0}^{L-N_1-1}\left( {\begin{array}{c}M_o-N_1-1\\ q'_i\end{array}}\right) P_o^{q'_i}\right. \\&\qquad \times \left. \left. \left. \left( 1-P_o\right) ^{M_o-N_1-q'_i-1}\right) \sum _{l=1}^{q'_i+1}F_{\phi _{\left( {\mathbb {S}}',D_i\right) }^{l}}\left( \gamma _{th}\right) \right) \right) \end{aligned}$$

(57)

and

$$\begin{aligned}&{\mathrm{Pr}}\left( E_i^{low}\left( \mathrm{{Case 4}}\right) \right) \\&\quad =U(L-2)\times \left( \left( {\mathrm{Pr}}({\mathcal {A}}{} \textit{1})\times \sum _{N_1=1}^{L-1}\left( {\begin{array}{c}M_o-1\\ N_1-1\end{array}}\right) {\mathrm{Pr}}\left( {\mathcal {A}}{} \textit{3}\right) \right. \right. \\&\qquad \left. \times F_{\phi ^1\left( S_i,D_i\right) }\left( \gamma _{th}\right) \right) +\left( {\mathrm{Pr}}\left( {\mathcal {A}}{} \textit{1}\right) \times \sum _{N_1=1}^{L-1}\left( {\begin{array}{c}M_o-1\\ N_1\end{array}}\right) \right. \\&\qquad \times \left( \prod _{k=1}^{N_1}\;\sum _{q_k=L}^{M_o-1}\left( {\begin{array}{c}M_o-1\\ q_k\end{array}}\right) P_o^{q_k}\left( 1-P_o\right) ^{M_o-q_{k}-1}\right) \\&\qquad \times \left( \prod _{k=N_1+1 ,k \ne i}^{M_o}\;\sum _{q'_k=0}^{L-N_1-1}\left( {\begin{array}{c}M_o-N_1-1\\ q'_k\end{array}}\right) P_o^{q'_k}\right. \\&\qquad \left. \times (1-P_o)^{M_o-N_1-q'_k-1}\right) \left( \sum _{q'_i=0}^{L-N_1-1}\left( {\begin{array}{c}M_o-N_1-1\\ q'_i\end{array}}\right) P_o^{q'_i}\right. \\&\qquad \left. \left. \left. \times \left( 1-P_o\right) ^{M_o-N_1-q'_i-1}\right) \sum _{l=1}^{q'_i+1}F_{\phi _{\left( {\mathbb {S}}',{\mathbb {D}}'\right) }^{l}}\left( \gamma _{th}\right) \right) \right) \end{aligned}$$

(58)

Since at high SNRs, the last summation of (57), (58) is dominated by $l=q'_i+1$, its diversity order is equal to $N-q'_i$. Furthermore, at the high-SNR regime, the dominant terms of (57), (58) can be obtained when $M_o=L+1$, $N_1=1, \;q_1=L$, $q'_k=0 \;\;{\mathrm{for}}\;\; N_1+1\le k\le M_o,\;k\ne i$ and by setting $l=q'_i+1$ in the last summation. Thus, the asymptotic expressions will be,

$$\begin{aligned}&\lim _{\bar{\gamma }\rightarrow \infty }\frac{-\log {\mathrm{Pr}}\left( E_i^{up}\left( \mathrm{Case 4}\right) \right) }{\log \bar{\gamma }} \\&\quad =\lim _{\bar{\gamma }\rightarrow \infty }\frac{-\log {\mathrm{Pr}}\left( E_i^{low}\left( \mathrm{Case 4}\right) \right) }{\log \bar{\gamma }} \\&\quad =\lim _{\bar{\gamma }\rightarrow \infty }\frac{-\log {{\mathrm{Pr}}}\left( E_i\left( \mathrm{Case 4}\right) \right) }{\log \bar{\gamma }}=N+2L+1 \end{aligned}$$

(59)

Case 5

In this case $L\ge 2$, $M_o>L$, $N_1<L$, and $q_{k}$ is given in (6). Unlike Case 4, here, $\exists \;\; N_1+1\le k\le M_o :\;\ q'_k\ge L-N_1$. In order to analyze the outage probability, we define this event: ${\mathcal {A}}{} \textit{4}\triangleq$ {$1\le N_1<L, \; L \le q_{k} \le M_o-1 \;\; {\mathrm{for}}\;\; 1\le k \le N_1, \;\;0 \le q_{k} \le L-1 \;\; {\mathrm{for}}\;\; N_1+1\le k \le M_o,\;\;\exists k: \;\; N_1+1\le k\le M_o , \;\ q'_k\ge L-N_1$ }. The probability of the event ${\mathcal {A}}{} \textit{4}$ can be expressed as

$$\begin{aligned}&{\mathrm{Pr}}\left( {\mathcal {A}}{} \textit{4}\right) \\&\quad =\sum _{N_1=1}^L \left( {\begin{array}{c}M_o\\ N_1\end{array}}\right) \left( \prod _{k=1}^{N_1}\sum _{q_k=L}^{M_o-1}\left( {\begin{array}{c}M_o-1\\ q_k\end{array}}\right) P_o^{q_k}\left( 1-P_o\right) ^{M_o-q_{k}-1}\right) \\&\qquad \times \left( \left( \prod _{k=N_1+1}^{M_o}\sum _{q_{k}=0}^{L-1}\left( {\begin{array}{c}M_o-1\\ q_{k}\end{array}}\right) P_o^{q_{k}}\left( 1-P_o\right) ^{M_o-q_{k}-1}\right) \right. \\&\qquad \left. -\left( \prod _{k=N_1+1}^{M_o}\sum _{q'_k=0}^{L-N_1-1}\left( {\begin{array}{c}M_o-N_1-1\\ q'_k\end{array}}\right) P_o^{q'_k}\left( 1-P_o\right) ^{M_o-N_1-q'_k-1}\right) \right) \\ \end{aligned}$$

(60)

Thus, at least $N_1$ destinations are not able to recover the packets sent by their sources after receiving L linear combinations of data packets of $M_o$ sources. Similar to Case 4, we can allocate $N_1$ relays to these set of source-destination pairs and $L-N_1$ relays to the other unsuccessful pairs. But unlike Case 4, some of these $M_o-N_1$ destinations cannot recover their intended packets because in this case, $\exists \;\; N_1+1\le k\le M_o :\;\ q'_k\ge L-N_1$. Therefore, we choose L random source-destination pairs from $M_o$ pairs to support them in the relaying phase. Similar to Case 3, the set of chosen sources and destinations denote by ${\mathbb {S}}^{ch}$ and ${\mathbb {D}}^{ch}$ respectively that are given in (49).

A selected relay is allocated to each chosen pair to forward the message of source to its destination without applying network coding. Thus, L relays are selected for all L chosen pairs based on (50).

In this case, the outage event occurs in two situations. In the first one, $S_i$ is not among the L chosen sources, i.e., $S_i\notin {\mathbb {S}}^{ch}$. In the second situation, $S_i\in {\mathbb {S}}^{ch}$, but, there is not a successful relay in decode and forward the message of $S_i$ to $D_i$. Thus, ${\mathrm{Pr}}(E_i(\mathrm{Case 5}))$ will be

$$\begin{aligned}&{\mathrm{Pr}}\left( E_i\left( \mathrm{Case 5}\right) \right) =U(L-2)\times {\mathrm{Pr}}\left( {\mathcal {A}}{} \textit{1}\right) {{\mathrm{Pr}}}\left( {\mathcal {A}}{} \textit{4}\right) \\&\quad \times \left( \left( \frac{M_o-L}{M_o}\right) +\frac{L}{M_o}F_{\phi ^1\left( S_i,D_i\right) }\left( \gamma _{th}\right) \right) \end{aligned}$$

(61)

At high-SNR values by setting $M_o=L+1$ in ${\mathrm{Pr}}({\mathcal {A}}{} \textit{1})$, $N_1=1, \;q_1=L$ in ${\mathrm{Pr}}({\mathcal {A}}{} \textit{4})$ and collecting the dominant terms of (61), the asymptotic behavior of the outage probability can be obtained as follows

$$\begin{aligned} \lim _{\bar{\gamma }\rightarrow \infty }{\frac{-\log \left( {\mathrm{Pr}}\left( E_i\left( \mathrm{Case\,5}\right) \right) \right) }{\log \left( \bar{\gamma }\right) }}=3L \end{aligned}$$

(62)

Finally, we extract the overall outage probability of the system. Let ${\mathrm{Pr}}(E_i)$ denotes the probability that the information of $S_i$ cannot be decoded by the destination $D_i$ at the end of broadcasting and relaying phase. We obtain the probability of this event by considering all defined cases which represent some disjoint events:

$$\begin{aligned} {\mathrm{Pr}}\left( E_i\right) &={\mathrm{Pr}}\left( E_i\left( {\mathrm{Case 1}}\right) \right) +{\mathrm{Pr}}\left( E_i\left( \mathrm{{Case 2}}\right) \right) +{\mathrm{Pr}}\left( E_i\left( {\mathrm{Case 3}}\right) \right) \\&\quad +{\mathrm{Pr}}\left( E_i\left( {\mathrm{Case 4}}\right) \right) +{\mathrm{Pr}}\left( E_i\left( {\mathrm{Case 5}}\right) \right) \end{aligned}$$

(63)

3.2 Diversity order analysis

Here, we investigate the performance of the communication system in terms of achievable diversity order.

By keeping the dominant terms at high-SNR values in (63) and using the results of (42), (46), (52), (59) and (62), we have

$$\begin{aligned} \lim _{\bar{\gamma }\rightarrow \infty }\frac{-\log \left( {\mathrm{Pr}}\left( E_i\right) \right) }{\log (\bar{\gamma })}=\min (3L,N+1) \end{aligned}$$

(64)

For quasi static fading channels, the diversity order D is defined as [29]:

$$\begin{aligned} D \triangleq \lim _{\bar{\gamma }\rightarrow \infty }\frac{-\log \left( {\mathrm{Pr}}\left( E_i\right) \right) }{\log \left( \bar{\gamma }\right) } \end{aligned}$$

(65)

Hence, the maximum achievable diversity order will be $\min (3L,N+1)$. Therefore, our proposed scheme is capable of achieving full diversity order if $L\geqslant \lceil {(\frac{N+1}{3})}\rceil$. Note that full diversity is achieved using only L from N relays in the communication system. Moreover, this is achieved by allocating $M+L$ time-slots instead of $M+N$ time-slots which means utilizing fewer time-slots and a better spectral efficiency. Therefore, the proposed scheme provides better spectral efficiency compared to the network coded cooperation schemes without applying relay selection protocols.

Further, our scheme achieves the diversity order of 3L when $L<\lceil {(\frac{N+1}{3})}\rceil$. Note that the scheme of [12], namely DNCC achieves a fixed diversity order of $L+1$ by employing L relays without applying relay selection algorithm. Furthermore, by applying relay selection mechanism proposed in [12] (i.e., DNCC with RS scheme), only the diversity order of $L+1$ is achieved if $L<M$. In DNCC with RS, L best relays are selected to participate cooperation by applying NC. Also, the RS is implemented based on max-min criterion. Hence, in the situation that $N<M$, the full diversity order cannot provided by applying relay selection mechanism proposed in [12]. Also, the proposed scheme of [24] can only achieve the diversity order of 2 after removing the unrealistic assumption of the paper. These results show that our proposed schemes can provide higher diversity order in comparison with the existing network coded cooperation schemes with relay selection.

In addition, the performance of RS-based CC (without applying NC) has been studied in [12]. It was shown CC can provide the maximum diversity order of $N+1$ by selecting the best relay for each source-destination pair (i.e., totally M relays are selected for a network with M source-destination pairs). Hence, the scheme cannot provided the full diversity gain if the number of participant relays is less than M. However, in our scheme full diversity order can be achieved by employing only $\lceil {(\frac{N+1}{3})}\rceil$ relays. Also, when $M>\lceil {(\frac{N+1}{3})}\rceil$, by utilizing $M+\lceil {(\frac{N+1}{3})}\rceil$ time slots instead of 2M time slots full diversity can be achieved. This shows that our proposed scheme has a better spectral efficiency compared to CC scheme.

4 Numerical results

In this section, we provide some simulation results for supporting the theoretical expressions derived in the previous sections. For simulations, we consider i.i.d. frequency flat fading for the communication channels, i.e., we set $h_{t_{i}r_j}\sim \mathcal {CN} (0,\sigma ^2)$, $\gamma _{th}=0$ dB, and $\bar{\gamma }_{S_iR_j}=\bar{\gamma }_{R_jD_i}=\bar{\gamma }_{S_iD_i}=\bar{\gamma }$ for all i, j. We consider a network with $M=3$ source-destination pairs, $N=5$ relays. The number of selected relays is $L=1,2$ and the rate is $R=1$.

In order to simulate the communication system, we construct an $M\times M$ matrix with $\{0,1\}$ entries which models various links between the sources and destinations after broadcasting phase by considering the outage probability of each link. After selecting L relays, this matrix is extended to an $(M+L)\times M$ matrix by appending the state of the links between the selected relays and the destinations. Next, by considering the entries of the extended matrix we determine whether the destination $D_i$ is able to recover the packet sent by $S_i$ or not.

In all simulations the probability of outage event (${\mathrm{Pr}}(E_i)$) in terms of SNR ($\bar{\gamma }$) is depicted. The simulation results indicate that the asymptotic and the analytical curves have the same slopes at high SNRs. As expected, the simulation results match with the analytical results in Case 1 ($L=1$), Case 3 and Case 5. For Case 1 ($L=2$), Case 2 and Case 4, the obtained curves are bounded with the derived analytical upper and lower bounds with the same slope at high SNRs that validates our theoretical formulas.

Figure 3a shows when $L=1$ upper and lower bounds of ${\mathrm{Pr}}(E_i\text{( }\mathrm Case 1))$ are identical and match with the analytical results. Also, the asymptotic slopes of the curves in Fig. 3a, b are equal to $N+1=6$ as expected.

The slopes of the curves in Fig. 4a, b show the diversity orders of 7 and 8 for $L=1$ and $L=2$, respectively. The results in fact imply that the achievable diversity in Case 2 is equal to $N+L+1$.

In Fig. 5a, b, we investigate the outage performance of Case 3 for $L=1, 2$. The results indicate that the derived analytical outage formula (51) agrees with the simulation result. Furthermore, at high SNRs, the slopes of the curves in Fig. 5a, b reveal that the achievable diversity orders of Case 3 are equal to 3 and 7 when $L=1$ and $L=2$, respectively. Hence, they validate the accuracy of our formula in (52) that the diversity order of $L^2+L+1$ is achieved in Case 3.

Figure 6a, b, illustrate the outage probability for Case 4 and Case 5 when $L=2$. As mentioned in Sect. 3, Case 4 and Case 5 do not occur when $L=1$. As can be seen, the asymptotic slope of the curves are equal to $N+2L+1=10$ and $3L=6$ for Case 4 and, Case 5, respectively.

Figure 7 compares our proposed scheme and the schemes of [12] which employs L selected relays. Note that in CC scheme [12], the best relay for each source-destination pair is selected to cooperate in the relaying phase. Therefore, if the number of unsuccessful source-destination pairs is greater than L, L unsuccessful source-destination pairs are randomly chosen and the best relay for each pair is selected in CC scheme. The simulation results in Fig. 7a indicate that our scheme outperforms the other schemes in terms of outage probability. We observe that CC and DNCC with RS only provide the diversity order of $L+1=2$ when $L=1$. However, our scheme achieves the diversity order of $3L=3$.

Figure 7b compares the outage probability of our scheme with DNCC with RS and CC schemes. The results show that CC and DNCC with RS schemes can provide the diversity order of $L+1=3$, while the proposed scheme achieves the maximum diversity order of $N+1=6$. Although CC outperforms the proposed scheme in terms of outage probability at low SNRs, but its outage probability worsens for $\bar{\gamma }\ge 9$ dB, because, it achieves a lower diversity order ($L+1$ instead of $N+1$). These results also validate that our proposed scheme can provide the diversity order of $\min (3L,N+1)$ which matches with our analytical formula (64). Also, the results confirm that full diversity is obtained when $L\geqslant \lceil {(\frac{N+1}{3})}\rceil$.

Fig. 3

Average outage probability per source versus $\bar{\gamma }_{SD}$ in Case 1

Fig. 4

Average outage probability per source versus $\bar{\gamma }_{SD}$ in Case 2

Fig. 5

Average outage probability per source versus $\bar{\gamma }_{SD}$ in Case 3

Fig. 6

Average outage probability per source versus $\bar{\gamma }_{SD}$ in Case 4, Case 5

Fig. 7

Average outage probability per source versus $\bar{\gamma }_{SD}$ in our proposed scheme, CC, DNCC with RS

5 Conclusion

In this paper, we studied the network coded cooperation schemes for unicast communication system with M source-destination pairs assisted with N relays that exploits relay selection. We determined an adaptive network coding strategy for the selected relays improve the expected number of recovered packets by the destinations. We derived upper and lower bounds for the outage probability showing that the diversity orders of $N+1$ is achieved when the number of active relays is at least $\lceil {(\frac{N+1}{3})}\rceil$. Moreover, we proved that the proposed scheme achieves a diversity order of 3L when $L<\lceil {(\frac{N+1}{3})}\rceil$. Our scheme leads to a better spectral efficiency in comparison with the existing network coded cooperation schemes. In addition, the scheme provides a higher diversity order in comparison with the existing schemes when $L<\lceil {(\frac{N+1}{3})}\rceil$.

The future work concerns improving the proposed scheme in various ways. Note that in some cases of our proposed scheme, the selected relays apply NC to all of the received packets sent by the sources in ${\mathbb {S}}$ or $\mathbb {S'}$. The performance of the system can be improved by partitioning unsuccessful source-destination pairs into different groups, and select a few relays for each group based on max-min algorithm such that totally L relays are selected. In this situation the number of associated links for each relay decrease and the best relays for each group can be selected more properly, i.e., with higher equivalent SNR. Furthermore, note that in this paper we assumed that the number of selected relays is fixed, but in some situation (e.g., case 1) it is possible to allocate less than L relays to improve the spectral efficiency while keeping the same diversity order. Finally considering multiple-input multiple-output (MIMO) NCC systems with relay selection can be another extension to our work which can provide much higher diversity orders.