Multi-cluster MIMO non-orthogonal multiple access for multi-cell systems

Abstract

In this paper, we present a multi-cluster multiple-input multiple-output non-orthogonal multiple access technique to improve spectral efficiency by simultaneously transmitting multiple data streams to multiple clusters in multi-cell systems. This technique employs receive beamforming matrices for cell-edge users that minimize the multi-cell interference power, irrespective of the number of interfering cells. Based on the receive beamforming matrices, the technique designs transmit beamforming matrices for a serving base station (BS) that eliminate inter-cluster interference (ICI) between cell-edge users and maximize the lower bounds of the received SNRs at the cell-edge users. Then, the technique uses the transmit beamforming matrices to find receive beamforming matrices for cell-center users that eliminate ICI between the cell-center users and maximize the lower bounds of the received SNRs at the cell-center users. This technique does not require channel feedback from the users to the serving BS in order to find all the receive beamforming matrices, thereby reducing system overhead. In addition, based on the transmit and receive beamforming matrices, the proposed technique allocates the transmit power to clusters and users of each cluster in a manner that maximizes the sum rate performance under power constraints supporting fairness between clusters and between users in each cluster. We demonstrate through simulations that the proposed technique achieves better sum rate and outage performances than the existing techniques and can provide a good balance between the performances and the number of clusters simultaneously supported by the serving BS.

1 Introduction

Wireless data traffic is explosively increasing due to a rapidly growing number of wireless access devices and the increase in demand for various high-quality wireless services [1]. In order to cope with this soaring wireless data traffic, next-generation wireless communication systems are actively discussed [2,3,4,5]. Since those systems should offer high transmission capacity with limited spectrum resources, techniques improving spectral efficiency receive a lot of attention [6,7,8,9,10,11,12]. Specifically, non-orthogonal multiple access (NOMA) may provide higher spectral efficiency than orthogonal multiple access, which has been widely employed in existing wireless communication systems, by simultaneously serving multiple users utilizing the same time and frequency resource [13, 14]. Therefore, NOMA is considered a promising technique for next-generation wireless communication systems [15, 16].

To enhance spectral efficiency in single-input single-output (SISO) and multiple-input multiple-output (MIMO) cellular systems, the NOMA techniques using successive interference cancellation (SIC) are proposed in [17]. In the MIMO-NOMA scheme in [18], a base station (BS) employs random beamforming and intra-cluster superposition coding and a receiver exploits SIC. Although the techniques decrease system overhead, they cannot remove inter-cluster interference (ICI) and cannot transmit multiple data streams to each cluster. In addition, the techniques treat multi-cell interference (MCI) as noise and do not attempt to mitigate it. The multiple-input single-output NOMA technique in [19] combines zero-forcing beamforming (ZFBF) with the hybrid NOMA precoding in [20] to minimize inter- and intra-cluster interference. However, this technique cannot be extended to MIMO systems straightforwardly and does not consider MCI.

The MIMO-NOMA technique in [21] provides low-complexity beamforming using singular value decomposition based on multiple-user channel state information (CSI). Although this technique is applicable for NOMA transmission to a single cluster with multiple users, it cannot be used to simultaneously transmit data streams to multiple clusters. To cancel ICI, the NOMA scheme in [22] employs ZFBF at a transmitter in a system with a single antenna at each receiver. However, this scheme requires a large number of transmit antennas for ICI cancellation and cannot be simply extended to a system with multiple antennas at each receiver. To eliminate ICI by using a small number of transmit antennas in a system with multiple antennas at each receiver, the MIMO-NOMA technique in [23] utilizes receive beamforming vectors orthogonal to ICI at each receiver. The MIMO-NOMA technique in [24] uses signal alignment to decrease the number of receive antennas necessary for ICI elimination.

However, the techniques in [21,22,23,24] cannot transmit multiple data streams to each cluster and do not deal with interference from adjacent cells. To simultaneously eliminate ICI and interference from one adjacent cell experienced by cell-edge users, the MIMO-NOMA techniques in [25] utilize interference alignment to design coordinated beamforming vectors. The techniques employ a practical user clustering where NOMA may provide a significant performance gain. However, they cannot transmit multiple data streams to each cluster and cannot deal with interference from more than one adjacent cell. To transmit multiple data streams to a cluster, the MIMO-NOMA technique in [26, 27] exploits the generalized singular value decomposition (GSVD) [28] to convert a MIMO-NOMA system into multiple SISO-NOMA systems. The technique in [29] uses the layered transmission schemes in [30, 31] for MIMO-NOMA transmissions and effectively allocates the transmit power to data streams for the layered transmissions.

Although the techniques in [26, 27, 29] may transmit multiple data streams to a single cluster, they are unable to transmit multiple data streams to multiple clusters simultaneously. Furthermore, they cannot handle interference from adjacent cells. The MIMO-NOMA technique in [32] considers a two-cell MIMO-NOMA interference channel and designs transmit beamforming matrices that maximize a weighted sum rate of two users, each with the largest channel gain in its own cell. However, this technique cannot support simultaneous transmission to multiple clusters in a cell and cannot be extended to deal with interference from more than one adjacent cell.

To improve spectral efficiency by simultaneously transmitting multiple data streams to multiple clusters in multi-cell systems, we propose a multi-cluster (MC) MIMO-NOMA beamforming technique and a power allocation scheme for beamformed data streams. This beamforming technique employs receive beamforming matrices for cell-edge users that minimize the MCI power, irrespective of the number of interfering cells. By utilizing the receive beamforming matrices, the technique finds transmit beamforming matrices for a serving BS that eliminate ICI between cell-edge users and maximize the lower bounds of the received SNRs at the cell-edge users. Then, the technique uses the transmit beamforming matrices to design receive beamforming matrices for cell-center users that eliminate ICI between the cell-center users and maximize the lower bounds of the received SNRs at the cell-center users.

Since this technique does not require channel feedback from the users to the serving BS in order to design all the receive beamforming matrices, it reduces system overhead. Furthermore, based on the transmit and receive beamforming matrices, the proposed scheme allocates the transmit power to clusters and users of each cluster in a manner that maximizes the sum rate performance under power constraints supporting fairness between clusters and between users in each cluster. It is demonstrated through simulations that the proposed MC-MIMO-NOMA method obtains better sum rate and outage performances than the existing techniques and can offer a good balance between the performances and the number of clusters simultaneously supported by the serving BS.

We note that the proposed MIMO-NOMA technique is distinguished from the existing techniques in the following points:

• It can transmit multiple data streams to multiple clusters simultaneously.

• It deals with interference from multiple neighboring cells and effectively mitigates the interference.

• It is applicable regardless of the number of interfering cells.

• It offers a trade-off between the number of clusters to serve simultaneously and the number of data streams to be transmitted to each cluster, thereby providing a good balance between the sum rate and outage performances and the number of clusters served simultaneously.

• It allocates the transmit power to clusters and users of each cluster to maximize the sum rate performance under power constraints that support fairness between clusters and between users in each cluster.

The rest of the paper is organized as follows. In Sect. 2, we describe the MC-MIMO-NOMA system model experiencing MCI. In Sect. 3, we state the proposed transmit and receive beamforming technique for the MC-MIMO-NOMA system and the proposed power allocation scheme for beamformed data streams. Section 4 provides the simulation results demonstrating the sum rate and outage performances of the proposed MC-MIMO-NOMA method. Finally, some concluding remarks are presented in Sect. 5. The notations used in this paper are as follows. Matrices and vectors are denoted by symbols in boldface. $\text{tr}\{\cdot \}$ indicates the trace of a square matrix. $\text{det}(\cdot )$ means the determinant of a square matrix. $\text{diag}\{\cdot \}$ represents the diagonal matrix with the given elements as entries in the main diagonal. ${\textbf{A}}(:,i)$ and ${\textbf{A}}(i,i)$ mean the ith column and the ith main diagonal element of the matrix ${\textbf{A}}$, respectively. ${\textbf{I}}_m$ and ${\textbf{0}}$ represent the identity matrix with dimension m and a zero matrix or vector of appropriate dimensions, respectively. $(\cdot )^H$, $E\{\cdot \}$, and $\Vert \cdot \Vert$ represent Hermitian, statistical expectation, and $l_2$-norm, respectively. Table 1 details the abbreviations used in this paper.

Table 1 List of abbreviations

2 Multi-cell MC-MIMO-NOMA system model

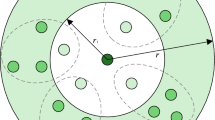
In this paper, we consider a MC-MIMO-NOMA system experiencing MCI from L adjacent cells as shown in Fig. 1. The serving cell BS simultaneously transmits data streams to K clusters with M transmit antennas. Two users, which are a cell-center user and a cell-edge user, exist in each cluster and NOMA is applied for data transmission to the users. Since this user pairing for NOMA provides high spectral efficiency [14, 17], the user pairing is widely adopted in NOMA systems. Each user receives $J(\le N)$ data streams with N receive antennas. In addition, the BSs of the L interfering cells are also equipped with M transmit antennas.

Fig. 1

MC-MIMO-NOMA system suffering from multi-cell interference

Denoting the channel from the serving cell BS to the cell-edge user in the kth cluster of the cell and the interfering channel from the lth adjacent cell BS to the cell-edge user as ${\textbf{H}}_{k,\text{e}}$ and ${\textbf{G}}_{k,l}$, respectively, we can express the received signal ${\textbf{y}}_{k,\text{e}}$ at the cell-edge user as

$$\begin{aligned} {\textbf{y}}_{k,\text{e}} = {\textbf{H}}_{k,\text{e}}{\textbf{s}}_k + \underbrace{{\textbf{H}}_{k,\text{e}} \sum ^{K}_{i=1,i\ne k} {\textbf{s}}_{i}}_{\text {ICI}} + \underbrace{\sum ^{L}_{l=1} {\textbf{G}}_{k,l} {\textbf{x}}_l}_{\text {MCI}} + {\textbf{n}}_{k,\text{e}}, \end{aligned}$$

(1)

where ${\textbf{x}}_l$ represents the data vector transmitted by the lth adjacent cell BS and ${\textbf{n}}_{k,\text{e}}$ indicates an AWGN vector with a mean zero vector and a covariance matrix $\sigma ^2_n{\textbf{I}}_N$. The data vector ${\textbf{s}}_{k}$ is given by superimposing data streams for the users in the kth cluster according to the NOMA principle in the power domain and then transforming them by the transmit beamforming matrix ${\textbf{P}}_k$ with size $M \times J$, which is expressed as

$$\begin{aligned} {\textbf{s}}_k&= {\textbf{P}}_k {\textbf{d}}_k\nonumber \\ {\textbf{d}}_k&= {\textbf{D}}_{k,\text{c}} {\textbf{d}}_{k,\text{c}} + {\textbf{D}}_{k,\text{e}} {\textbf{d}}_{k,\text{e}}. \end{aligned}$$

(2)

${\textbf{d}}_{k,\text{c}}$ and ${\textbf{d}}_{k,\text{e}}$ are the data symbol vectors for the cell-center and cell-edge users in the kth cluster, respectively. The power of each element in the data symbol vectors is normalized to unity. The $J \times J$ diagonal matrices ${\textbf{D}}_{k,\text{c}}$ and ${\textbf{D}}_{k,\text{e}}$ are the power allocation matrices for the cell-center and cell-edge users in the kth cluster, respectively, and $\sum _{k=1}^K \text{tr}\left\{ {\textbf{D}}_{k,\text{c}}^2 + {\textbf{D}}_{k,\text{e}}^2 \right\} =P_T$, where $P_T$ is the total transmit power.

The cell-edge user applies the receive beamforming matrix ${\textbf{W}}_{k,\text{e}}$ with size $N \times J$ to the received signal ${\textbf{y}}_{k,\text{e}}$ in (1) in order to recover J desired data streams, as given in

$$\begin{aligned} {\textbf{W}}_{k,\text{e}}^H {\textbf{y}}_{k,\text{e}}&= {\textbf{W}}_{k,\text{e}}^H {\textbf{H}}_{k,\text{e}}{\textbf{s}}_{k} +{\textbf{W}}_{k,\text{e}}^H {\textbf{H}}_{k,\text{e}} \sum ^{K}_{i=1,i \ne k} {\textbf{s}}_{i}\nonumber \\&\quad + {\textbf{W}}_{k,\text{e}}^H \sum ^{L}_{l=1} {\textbf{G}}_{k,l} {\textbf{x}}_{l} + {\textbf{W}}_{k,\text{e}}^H {\textbf{n}}_{k,\text{e}}. \end{aligned}$$

(3)

Since the MCI is negligible at cell-center users, the MCI is treated as merged into the AWGN at the users. Denoting the channel from the serving cell BS to the cell-center user in the kth cluster of the cell as ${\textbf{H}}_{k,\text{c}}$, we can express the received signal ${\textbf{y}}_{k,\text{c}}$ at the cell-center user as

$$\begin{aligned} {\textbf{y}}_{k,\text{c}} = {\textbf{H}}_{k,\text{c}} {\textbf{s}}_{k} + \underbrace{{\textbf{H}}_{k,\text{c}} \sum ^{K}_{i=1,i \ne k} {\textbf{s}}_{i}}_{\text {ICI}} + {\textbf{n}}_{k,\text{c}}, \end{aligned}$$

(4)

where ${\textbf{n}}_{k,\text{c}}$ is an AWGN vector having the same attributes as ${\textbf{n}}_{k,\text{e}}$. The cell-center user also applies the receive beamforming matrix ${\textbf{W}}_{k,\text{c}}$ with size $N \times J$ to the received signal ${\textbf{y}}_{k,\text{c}}$ in (4) in order to recover J desired data streams, as given in

$$\begin{aligned} {\textbf{W}}_{k,\text{c}}^H {\textbf{y}}_{k,\text{c}}&= {\textbf{W}}_{k,\text{c}}^H {\textbf{H}}_{k,\text{c}}{\textbf{s}}_{k} \nonumber \\&\quad + {\textbf{W}}_{k,\text{c}}^H {\textbf{H}}_{k,\text{c}} \sum ^{K}_{i=1,i \ne k} {\textbf{s}}_{i} + {\textbf{W}}_{k,\text{c}}^H {\textbf{n}}_{k,\text{c}}. \end{aligned}$$

(5)

3 Proposed MC-MIMO-NOMA technique for multi-cell systems

Figure 2 shows the transmitter structure of the BS for the proposed multi-cell MC-MIMO-NOMA technique and Fig. 3 shows the receiver structure of the cell-center and cell-edge users for the proposed technique. The transmitter sequentially performs power allocation $\left( {\textbf{D}}_{k,\text{c}},\; {\textbf{D}}_{k,\text{e}}\right)$, NOMA modulation, pre-processing $\left( {\textbf{Z}}_k^{-H}\right)$, and transmit beamforming $\left( {\textbf{P}}_k\right)$. The receiver of the cell-center user sequentially performs receive beamforming $\left( {\textbf{W}}_{k,\text{c}}\right)$, post-processing $\left( {\textbf{U}}_{k,\text{c}}\right)$, SIC, and symbol detection, whereas the receiver of the cell-edge user sequentially performs receive beamforming $\left( {\textbf{W}}_{k,\text{e}}\right)$, post-processing $\left( {\textbf{U}}_{k,\text{e}}\right)$, and symbol detection.

Fig. 2

Transmitter structure for a serving BS in the proposed multi-cell MC-MIMO-NOMA technique

Fig. 3

Receiver structure for cell-center and cell-edge users in the proposed multi-cell MC-MIMO-NOMA technique

The transmit and receive beamforming in this system is designed to mitigate the MCI and to eliminate the ICI at the cell-center and cell-edge users in order to improve spectral efficiency. In addition, this system performs the inter-cluster and inter-stream power allocation along with the pre-processing at the BS and the post-processing at the users to enhance spectral efficiency further. In what follows, we present how to design the transmit and receive beamforming and how to determine the power allocation including the pre-processing at the BS and the post-processing at the users.

3.1 Design of transmit and receive beamforming matrices

The proposed transmit and receive beamforming matrices are designed in three steps. The first step is to find the receive beamforming matrices ${\textbf{W}}_{1,\text{e}},{\textbf{W}}_{2,\text{e}}, \ldots ,{\textbf{W}}_{K,\text{e}}$ for K cell-edge users to mitigate the MCI effectively. That is, ${\textbf{W}}_{k,\text{e}}$ is designed to minimize the MCI power and whiten the MCI plus noise as follows. First, the $N \times J$ matrix ${\bar{\textbf{W}}}_{k,\text{e}}$ minimizing the MCI power is obtained from

$$\begin{aligned} {\bar{\textbf{W}}}_{k,\text{e}} =\arg \min _{{\bar{\textbf{W}}}_{k,\text{e}}^H {\bar{\textbf{W}}}_{k,\text{e}} = {\textbf{I}}_J} \text{tr} \left\{ {\bar{\textbf{W}}}_{k,\text{e}}^H {\textbf{R}}_{k,\text{MCI}} {\bar{\textbf{W}}}_{k,\text{e}}\right\} , \end{aligned}$$

(6)

where ${\textbf{R}}_{k,\text{MCI}}$ is the MCI covariance matrix given as ${\textbf{R}}_{k,\text{MCI}} = \sum ^{L}_{l=1} {\textbf{G}}_{k,l} E\left\{ {\textbf{x}}_{l} {{\textbf{x}}_{l}}^H \right\}$ ${{\textbf{G}}_{k,l}}^H$. Solving (6), we find ${\bar{\textbf{W}}}_{k,\text{e}}$ whose columns are composed of the eigenvectors of ${\textbf{R}}_{k,\text{MCI}}$ corresponding to the J smallest eigenvalues $\lambda _{k,1}.$ $\lambda _{k,2},\ldots ,\lambda _{k,J}$. Then, the matrix ${\textbf{W}}_{k,\text{e}}$ whitening the MCI plus noise is given as

$$\begin{aligned} {\textbf{W}}_{k,\text{e}} &= {\bar{\textbf{W}}}_{k,\text{e}} \\ &\quad \cdot \text{diag}\left\{ \frac{1}{\sqrt{\lambda _{k,1} + \sigma _n^2}},\; \frac{1}{\sqrt{\lambda _{k,2} + \sigma _n^2}}, \ldots , \frac{1}{\sqrt{\lambda _{k,J} + \sigma _n^2}} \right\} . \end{aligned}$$

(7)

We note that the cell-edge users can find their own receive beamforming matrices without channel feedback. This reduces system overhead.

The second step is to use ${\textbf{W}}_{1,\text{e}}, {\textbf{W}}_{2,\text{e}}, \ldots , {\textbf{W}}_{K,\text{e}}$ to find the transmit beamforming matrices ${\textbf{P}}_1, {\textbf{P}}_2, \ldots , {\textbf{P}}_K$ that eliminate the ICI between the cell-edge users. In detail, by utilizing the effective channels ${\textbf{W}}_{1,\text{e}}^H {\textbf{H}}_{1,\text{e}}, {\textbf{W}}_{2,\text{e}}^H {\textbf{H}}_{2,\text{e}}, \ldots , {\textbf{W}}_{K,\text{e}}^H {\textbf{H}}_{K,\text{e}}$ to K cell-edge users in all the clusters, the $(K-1)J \times M$ matrices ${{\boldsymbol{\mathcal{H}}}}_k$ for $1 \le k \le K$ are formed as

$$\begin{aligned} {{\boldsymbol{\mathcal{H}}}}_{k,\text{e}}&=\big [{\textbf{H}}_{1,\text{e}}^H{\textbf{W}}_{1,\text{e}} \;{\textbf{H}}_{2,\text{e}}^H {\textbf{W}}_{2,\text{e}} \;\cdots \;{\textbf{H}}_{{k-1},\text{e}}^H{\textbf{W}}_{{k-1},\text{e}}\nonumber \\&\quad {\textbf{H}}_{{k+1},\text{e}}^H{\textbf{W}}_{{{k+1},\text{e}}} \; {\textbf{H}}_{{k+2},\text{e}}^H{\textbf{W}}_{{k+2},\text{e}} \;\cdots \;{\textbf{H}}_{K,\text{e}}^H {\textbf{W}}_{K,\text{e}} \big ]^H. \end{aligned}$$

(8)

To eliminate the ICI, the following condition is required for $1 \le k \le K$.

$$\begin{aligned} {{\boldsymbol{\mathcal{H}}}}_{k,\text{e}} {\textbf{P}}_k = {\textbf{0}}. \end{aligned}$$

(9)

If the condition $M \ge KJ$ is satisfied, a nonzero matrix ${\textbf{P}}_k$ satisfying (9) is given as

$$\begin{aligned} {\textbf{P}}_k = {\bar{\textbf{V}}}_k {\boldsymbol{\Omega }}_k. \end{aligned}$$

(10)

Here, ${\bar{\textbf{V}}}_k$ is the $M \times (M-KJ+J)$ matrix whose columns are composed of $(M-KJ+J)$ right singular vectors of ${{\boldsymbol{\mathcal{H}}}}_{k,\text{e}}$ corresponding to zero singular values and the $(M-KJ+J) \times J$ matrix ${\boldsymbol{\Omega }}_k$ is an arbitrary full rank matrix.

The matrix ${\boldsymbol{\Omega }}_k$ can be optimized to maximize the lower bound for the received SNR at the cell-edge user with the constraint $\Vert {\boldsymbol{\Omega }}_k(:,j)\Vert =1$ for $1\le j \le J$. Representing ${\textbf{W}}_{k,\text{e}}^H {\textbf{y}}_{k,\text{e}}$ in (3) using ${\textbf{W}}_{k,\text{e}}$ in (7) and ${\textbf{P}}_k$ in (10) as

$$\begin{aligned} {\textbf{W}}_{k,\text{e}}^H {\textbf{y}}_{k,\text{e}} = {\textbf{W}}_{k,\text{e}}^H {\textbf{H}}_{k,\text{e}}{\bar{\textbf{V}}}_k {\boldsymbol{\Omega }}_k{\textbf{d}}_k + {\textbf{W}}_{k,\text{e}}^H \left( \sum ^{L}_{l=1} {\textbf{G}}_{k,l} {\textbf{x}}_{l} + {\textbf{n}}_{k,\text{e}}\right) , \end{aligned}$$

(11)

we can write the received SNR at the cell-edge user, which is denoted by $\text{SNR}_{k,\text{e}}$, as

$$\begin{aligned}{} & {} \text{SNR}_{k,\text{e}} =J^{-1}\;\text{tr}\left\{ {\textbf{W}}_{k,\text{e}}^H {\textbf{H}}_{k,\text{e}}{\bar{\textbf{V}}}_k {\boldsymbol{\Omega }}_k{{\textbf{R}}_{{\textbf{d}}_k}{\boldsymbol{\Omega }}}_k^H {\bar{\textbf{V}}}_k^H {\textbf{H}}_{k,\text{e}}^H {\textbf{W}}_{k,\text{e}} \right\} , \end{aligned}$$

(12)

where ${\textbf{R}}_{{\textbf{d}}_k} = E\left\{ {\textbf{d}}_k {\textbf{d}}_k^H\right\}$. When we express ${\textbf{W}}_{k,\text{e}}^H {\textbf{H}}_{k,\text{e}}{\bar{\textbf{V}}}_k$ by SVD with a $J \times J$ unitary matrix ${{\boldsymbol{\mathcal{U}}}}_{k,\text{e}}$, a $J \times J$ diagonal matrix ${\boldsymbol{\Lambda }}_{k,\text{e}}$ and a $(M-KJ+J) \times J$ matrix ${{\boldsymbol{\mathcal{V}}}}_{k,\text{e}}$ as

$$\begin{aligned} {\textbf{W}}_{k,\text{e}}^H {\textbf{H}}_{k,\text{e}}{\bar{\textbf{V}}}_k={{\boldsymbol{\mathcal{U}}}}_{k,\text{e}} {\boldsymbol{\Lambda }}_{k,\text{e}} {{\boldsymbol{\mathcal{V}}}}_{k,\text{e}}^H, \end{aligned}$$

(13)

$\text{SNR}_{k,\text{e}}$ is lower-bounded as

$$\begin{aligned} \text{SNR}_{k,\text{e}}&= J^{-1}\;\text{tr}\left\{ {\boldsymbol{\Lambda }}_{k,\text{e}}^2 {{\boldsymbol{\mathcal{V}}}}_{k,\text{e}}^H {\boldsymbol{\Omega }}_k{\textbf{R}}_{{\textbf{d}}_k}{\boldsymbol{\Omega }}_k^H {{\boldsymbol{\mathcal{V}}}}_{k,\text{e}}\right\} \nonumber \\&\ge {\det \left( {\boldsymbol{\Lambda }}_{k,\text{e}}^2 {{\boldsymbol{\mathcal{V}}}}_{k,\text{e}}^H {\boldsymbol{\Omega }}_k{\textbf{R}}_{{\textbf{d}}_k}{\boldsymbol{\Omega }}_k^H {{\boldsymbol{\mathcal{V}}}}_{k,\text{e}}\right) }^{\frac{1}{J}}\nonumber \\&= \left( \left| \det \left( {{\boldsymbol{\mathcal{V}}}}_{k,\text{e}}^H {\boldsymbol{\Omega }}_k\right) \right| ^2 \det \left( {\boldsymbol{\Lambda }}_{k,\text{e}}^2 {\textbf{R}}_{{\textbf{d}}_k} \right) \right) ^{\frac{1}{J}}. \end{aligned}$$

(14)

From Hadamard’s inequality that states that $\left| \det ({\textbf{A}})\right| \le \prod _{j=1}^J \left\| {\textbf{A}}(:,j)\right\|$, we obtain

$$\begin{aligned} \left| \det \left( {{\boldsymbol{\mathcal{V}}}}_{k, \text{e}}^H {\boldsymbol{\Omega }}_k \right) \right| \le \prod _{j=1}^J \left\| {{\boldsymbol{\mathcal{V}}}}_{k,\text{e}}^H {\boldsymbol{\Omega }}_k(:,j)\right\| . \end{aligned}$$

(15)

It is found that to achieve the equality in (15) while maximizing $\prod _{j=1}^J \left\| {{\boldsymbol{\mathcal{V}}}}_{k,\text{e}}^H {\boldsymbol{\Omega }}_k(:,j)\right\|$, ${\boldsymbol{\Omega }}_k$ should be given as

$$\begin{aligned} {\boldsymbol{\Omega }}_k = {{\boldsymbol{\mathcal{V}}}}_{k,\text{e}}{\textbf{V}}_{\Omega }, \end{aligned}$$

(16)

where ${\textbf{V}}_{\Omega }$ is an arbitrary unitary matrix with size $J \times J$. Thus, the transmit beamformaing matrix ${\textbf{P}}_k$ is obtained with ${\textbf{V}}_{\Omega } = {\textbf{I}}_J$ as

$$\begin{aligned} {\textbf{P}}_k = {\bar{\textbf{V}}}_k {{\boldsymbol{\mathcal{V}}}}_{k,\text{e}}. \end{aligned}$$

(17)

The third step is to find the receive beamforming matrices ${\textbf{W}}_{1,\text{c}},{\textbf{W}}_{2,\text{c}}, \ldots ,{\textbf{W}}_{K,\text{c}}$ for K cell-center users to eliminate the ICI between the cell-center users. When we define the $N \times (K-1)J$ matrix ${{\boldsymbol{\mathcal{H}}}}_{k,\text{c}}$ as

$$\begin{aligned} {{\boldsymbol{\mathcal{H}}}}_{k,\text{c}}:= \big [ {\textbf{H}}_{k,\text{c}}{\textbf{P}}_1 \;{\textbf{H}}_{k,\text{c}}{\textbf{P}}_2 \; \cdots \; {\textbf{H}}_{k,\text{c}}{\textbf{P}}_{(k-1)} \; {\textbf{H}}_{k,\text{c}}{\textbf{P}}_{(k+1)} \; {\textbf{H}}_{k,\text{c}}{\textbf{P}}_{(k+2)} \; \cdots \; {\textbf{H}}_{k,\text{c},}{\textbf{P}}_K \big ], \end{aligned}$$

(18)

the ICI elimination requires

$$\begin{aligned} {\textbf{W}}_{k,\text{c}}^H {{\boldsymbol{\mathcal{H}}}}_{k,\text{c}} = {\textbf{0}},\quad k=1, 2, \ldots ,K. \end{aligned}$$

(19)

If the condition $N \ge KJ$ is satisfied, a nonzero matrix ${\textbf{W}}_{k,\text{c}}$ satisfying (19) is given as

$$\begin{aligned} {\textbf{W}}_{k,\text{c}} = {\bar{\textbf{U}}}_{k,\text{c}} {\boldsymbol{\Psi }}_k. \end{aligned}$$

(20)

Here, ${\bar{\textbf{U}}}_{k,\text{c}}$ is the $N \times (N-KJ+J)$ matrix whose columns are composed of $(N-KJ+J)$ left singular vectors of the matrix ${{\boldsymbol{\mathcal{H}}}}_{k,\text{c}}$ corresponding to zero singular values and the $(N-KJ+J) \times J$ matrix ${\boldsymbol{\Psi }}_k$ is an arbitrary full rank matrix.

The matrix ${\boldsymbol{\Psi }}_{k,\text{c}}$ can be also optimized to maximize the lower bound for the received SNR at the cell-center user with the constraint $\Vert {\boldsymbol{\Psi }}_k(:,j)\Vert =1$ for $1\le j \le J$. Representing ${\textbf{W}}_{k,\text{c}}^H {\textbf{y}}_{k,\text{c}}$ in (5) using ${\textbf{W}}_{k,\text{c}}$ in (20) as

$$\begin{aligned} {\textbf{W}}_{k,\text{c}}^H{\textbf{y}}_{k,\text{c}} = {\boldsymbol{\Psi }}_k^H {\bar{\textbf{U}}}_{k,\text{c}}^H{\textbf{H}}_{k,\text{c}} {\textbf{P}}_k {\textbf{d}}_k + {\boldsymbol{\Psi }}_k^H {\bar{\textbf{U}}}_{k,\text{c}}^H {\textbf{n}}_{k,\text{c}}, \end{aligned}$$

(21)

we can write the received SNR at the cell-center user, which is denoted by $\text{SNR}_{k,\text{c}}$, as

$$\begin{aligned} \text{SNR}_{k,\text{c}} = J^{-1}\sigma _n^{-2}\;\text{tr}\left\{ {\boldsymbol{\Psi }}_k^H {\bar{\textbf{U}}}_{k,\text{c}}^H {\textbf{H}}_{k,\text{c}} {\textbf{P}}_k {\textbf{R}}_{{\textbf{d}}_k} {\textbf{P}}_k^H {\textbf{H}}_{k,\text{c}}^H {\bar{\textbf{U}}}_{k,\text{c}}{\boldsymbol{\Psi }}_k\right\} . \end{aligned}$$

(22)

When we express ${\bar{\textbf{U}}}_{k,\text{c}}^H{\textbf{H}}_{k,\text{c}} {\textbf{P}}_k$ by SVD with a $(N-KJ+J)\times J$ matrix ${{\boldsymbol{\mathcal{U}}}}_{k,\text{c}}$, a $J \times J$ diagonal matrix ${{\boldsymbol{\Lambda }}_{k,\text{c}}}$ and a $J \times J$ unitary matrix ${{\boldsymbol{\mathcal{V}}}}_{k,\text{c}}$ as

$$\begin{aligned} {\bar{\textbf{U}}}_{k,\text{c}}^H{\textbf{H}}_{k,\text{c}} {\textbf{P}}_k = {{\boldsymbol{\mathcal{U}}}}_{k,\text{c}} {\boldsymbol{\Lambda }}_{k,\text{c}} {{\boldsymbol{\mathcal{V}}}}_{k,\text{c}}^H, \end{aligned}$$

(23)

$\text{SNR}_{k,\text{c}}$ is lower-bounded as

$$\begin{aligned} \text{SNR}_{k,\text{c}}&= J^{-1}\sigma _n^{-2}\;\text{tr}\left\{ {\boldsymbol{\Psi }}_k^H {{\boldsymbol{\mathcal{U}}}}_{k,\text{c}} {\boldsymbol{\Lambda }}_{k,\text{c}} {{\boldsymbol{\mathcal{V}}}}_{k,\text{c}}^H{\textbf{R}}_{{\textbf{d}}_k} {{\boldsymbol{\mathcal{V}}}}_{k,\text{c}} {\boldsymbol{\Lambda }}_{k,\text{c}} {{\boldsymbol{\mathcal{U}}}}_{k,\text{c}}^H {\boldsymbol{\Psi }}_k\right\} \nonumber \\&\ge \sigma _n^{-2}{\det \left( {\boldsymbol{\Psi }}_k^H {{\boldsymbol{\mathcal{U}}}}_{k,\text{c}} {\boldsymbol{\Lambda }}_{k,\text{c}} {{\boldsymbol{\mathcal{V}}}}_{k,\text{c}}^H{\textbf{R}}_{{\textbf{d}}_k} {{\boldsymbol{\mathcal{V}}}}_{k,\text{c}} {\boldsymbol{\Lambda }}_{k,\text{c}} {{\boldsymbol{\mathcal{U}}}}_{k,\text{c}}^H {\boldsymbol{\Psi }}_k\right) }^{\frac{1}{J}}\nonumber \\&= \sigma _n^{-2}\left( \left| \det \left( {{\boldsymbol{\mathcal{U}}}}_{k,\text{c}}^H{\boldsymbol{\Psi }}_k\right) \right| ^2 \det \left( {\boldsymbol{\Lambda }}_{k,\text{c}}^2 {\textbf{R}}_{{\textbf{d}}_k} \right) \right) ^{\frac{1}{J}}. \end{aligned}$$

(24)

From Hadamard’s inequality, we obtain

$$\begin{aligned} \left| \det \left( {{\boldsymbol{\mathcal{U}}}}_{k,\text{c}}^H{\boldsymbol{\Psi }}_k\right) \right| \le \prod _{j=1}^J \left\| {{\boldsymbol{\mathcal{U}}}}_{k,\text{c}}^H {\boldsymbol{\Psi }}_k(:,j)\right\| . \end{aligned}$$

(25)

Like in (15), it is found that to achieve the equality in (25) while maximizing $\prod _{j=1}^J\left\| {{\boldsymbol{\mathcal{U}}}}_{k,\text{c}}^H {\boldsymbol{\Psi }}_k(:,j)\right\|$, ${\boldsymbol{\Psi }}_k$ should be given as

$$\begin{aligned} {\boldsymbol{\Psi }}_k = {{\boldsymbol{\mathcal{U}}}}_{k,\text{c}}{\textbf{U}}_{\Psi }, \end{aligned}$$

(26)

where ${\textbf{U}}_{\Psi }$ is an arbitrary unitary matrix with size $J \times J$. Thus, the receive beamforming matrix ${\textbf{W}}_{k,\text{c}}$ is obtained with ${\textbf{U}}_{\Psi } = {\textbf{I}}_J$ as

$$\begin{aligned} {\textbf{W}}_{k,\text{c}} = {\bar{\textbf{U}}}_{k,\text{c}} {{\boldsymbol{\mathcal{U}}}}_{k,\text{c}}. \end{aligned}$$

(27)

The cell-center users can also find their own receive beamforming matrices without channel feedback, thereby reducing system overhead.

In summary, the proposed technique finds the receive beamforming matrices for the cell-center and cell-edge users and the transmit beamforming matrices for the serving BS as follows.

• Step 1: The cell-edge user in the kth cluster obtains the MCI covariance matrix ${\textbf{R}}_{k,\text{MCI}}$ and finds its own receive beamforming matrix ${\textbf{W}}_{k,\text{e}}$ in (7) using ${\bar{\textbf{W}}}_{k,\text{e}}$ whose columns are composed of the eigenvectors of ${\textbf{R}}_{k,\text{MCI}}$ corresponding to the J smallest eigenvalues.

• Step 2: The serving BS obtains the effective CSI ${\textbf{W}}_{k,\text{e}}^H {\textbf{H}}_{k,\text{e}}$ for $1 \le k \le K$ with channel feedback from the K cell-edge users and finds the transmit beamforming matrices ${\textbf{P}}_k$ for $1 \le k \le K$ as given in (17).

• Step 3: The cell-center user in the kth cluster obtains the precoded CSI ${\textbf{H}}_{k,\text{c}}{\textbf{P}}_i$ for $1\le i \le K$ through channel estimation and finds its own receive beamforming matrix ${\textbf{W}}_{k,\text{c}}$ as given in (27).

Accurate CSI feedback from the cell-edge users is required to design effective transmit beamforming matrices. In consideration of the system overhead caused by the channel feedback, this technique may be beneficially employed in slow fading channel environments where frequent channel feedback is unnecessary. When imperfect CSI due to delayed feedback of quantized CSI is used to design the transmit beamforming matrices, the ICI between the cell-edge users cannot be eliminated perfectly, thereby causing performance degradation. In the future, this technique will be extended to be robust against imperfect CSI.

3.2 Determination of power allocation

By using the transmit and receive beamforming matrices designed in Sect. 3.1, we can rewrite the received signals at the cell-center and cell-edge users in the k cluster as

$$\begin{aligned} {\textbf{W}}_{k,\text{c}}^H{\textbf{y}}_{k,\text{c}} = {\textbf{W}}_{k,\text{c}}^H{\textbf{H}}_{k,\text{c}} {\textbf{P}}_k {\textbf{d}}_k + {\textbf{W}}_{k,\text{c}}^H {\textbf{n}}_{k,\text{c}} \end{aligned}$$

(28)

$$\begin{aligned} {\textbf{W}}_{k,\text{e}}^H{\textbf{y}}_{k,\text{e}} = {\textbf{W}}_{k,\text{e}}^H {\textbf{H}}_{k,\text{e}}{\textbf{P}}_k {\textbf{d}}_k + {\textbf{W}}_{k,\text{e}}^H {\boldsymbol{\epsilon }}_{k,\text{e}}, \end{aligned}$$

(29)

where ${\boldsymbol{\epsilon }}_{k,\text{e}} = \sum ^{L}_{l=1} {\textbf{G}}_{k,l} {\textbf{x}}_{l} + {\textbf{n}}_{k,\text{e}}$. Then, we can express ${\textbf{W}}_{k,\text{c}}^H{\textbf{H}}_{k,\text{c}}{\textbf{P}}_k$ and ${\textbf{W}}_{k,\text{e}}^H{\textbf{H}}_{k,\text{e}}{\textbf{P}}_k$ by GSVD as, respectively,

$$\begin{aligned} {\textbf{W}}_{k,\text{c}}^H{\textbf{H}}_{k,\text{c}}{\textbf{P}}_k = {\textbf{U}}_{k,\text{c}}{\boldsymbol{\Sigma }}_{k,\text{c}}{\bar{\textbf{Z}}}_k^H \end{aligned}$$

(30)

$$\begin{aligned} {\textbf{W}}_{k,\text{e}}^H{\textbf{H}}_{k,\text{e}}{\textbf{P}}_k = {\textbf{U}}_{k,\text{e}}{\boldsymbol{\Sigma }}_{k,\text{e}}{\bar{\textbf{Z}}}_k^H, \end{aligned}$$

(31)

where ${\textbf{U}}_{k,\text{c}}$ and ${\textbf{U}}_{k,\text{e}}$ are $J \times J$ unitary matrices, ${\boldsymbol{\Sigma }}_{k,\text{c}}$ and ${\boldsymbol{\Sigma }}_{k,\text{e}}$ are $J \times J$ diagonal matrices, and ${\bar{\textbf{Z}}}_k$ is a $J \times J$ nonsingular matrix.

When we define the column-normalizing matrix ${\boldsymbol{\Xi }}_k$ as

$$\begin{aligned} {\boldsymbol{\Xi }}_k:= \text{diag}\left\{ \left\| {\bar{\textbf{Z}}}_k^{-H}(:,1)\right\| ^{-1}, \left\| {\bar{\textbf{Z}}}_k^{-H}(:,2)\right\| ^{-1}, \ldots , \left\| {\bar{\textbf{Z}}}_k^{-H}(:,J)\right\| ^{-1}\right\} , \end{aligned}$$

(32)

the BS applies the pre-processing matrix ${\textbf{Z}}_k^{-H} = {\bar{\textbf{Z}}}_k^{-H} {\boldsymbol{\Xi }}_k$ to the data symbol vector ${\textbf{d}}_k$ prior to the transmit beamforming ${\textbf{P}}_k$ as shown in Fig. 2. The cell-center and cell-edge users apply the post-processing matrices ${\textbf{U}}_{k,\text{c}}^H$ and ${\textbf{U}}_{k,\text{e}}^H$ to their receive beamformed signals ${\textbf{W}}_{k,\text{c}}^H{\textbf{y}}_{k,\text{c}}$ and ${\textbf{W}}_{k,\text{e}}^H {\textbf{y}}_{k,\text{e}}$, respectively, which is shown in Fig. 3. Then, the received signals ${\bar{\textbf{y}}}_{k,\text{c}} = {\textbf{U}}_{k,\text{c}}^H{\textbf{W}}_{k,\text{c}}^H{\textbf{y}}_{k,\text{c}}$ and ${\bar{\textbf{y}}}_{k,\text{e}} = {\textbf{U}}_{k,\text{e}}^H{\textbf{W}}_{k,\text{e}}^H {\textbf{y}}_{k,\text{e}}$ are expressed as

$$\begin{aligned} {\bar{\textbf{y}}}_{k,\text{c}}&= {\textbf{U}}_{k,\text{c}}^H{\textbf{W}}_{k,\text{c}}^H{\textbf{y}}_{k,\text{c}} = {\boldsymbol{\Sigma }}_{k,\text{c}} {\boldsymbol{\Xi }}_k {\textbf{d}}_k + {\textbf{U}}_{k,\text{c}}^H {\textbf{W}}_{k,\text{c}}^H {\textbf{n}}_{k,\text{c}} \nonumber \\&= {\bar{\boldsymbol{\Sigma }}}_{k,\text{c}} {\textbf{d}}_k + {\bar{\textbf{n}}}_{k,\text{c}} \end{aligned}$$

(33)

$$\begin{aligned} {\bar{\textbf{y}}}_{k,\text{e}}&= {\textbf{U}}_{k,\text{e}}^H{\textbf{W}}_{k,\text{e}}^H{\textbf{y}}_{k,\text{e}} = {\boldsymbol{\Sigma }}_{k,\text{e}} {\boldsymbol{\Xi }}_k {\textbf{d}}_k + {\textbf{U}}_{k,\text{e}}^H {\textbf{W}}_{k,\text{e}}^H {\boldsymbol{\epsilon }}_{k,\text{e}} \nonumber \\&= {\bar{\boldsymbol{\Sigma }}}_{k,\text{e}} {\textbf{d}}_k + {\bar{\boldsymbol{\epsilon }}}_{k,\text{e}}, \end{aligned}$$

(34)

where ${\bar{\boldsymbol{\Sigma }}}_{k,\text{c}} = {\boldsymbol{\Sigma }}_{k,\text{c}} {\boldsymbol{\Xi }}_k$, ${\bar{\boldsymbol{\Sigma }}}_{k,\text{e}} = {\boldsymbol{\Sigma }}_{k,\text{e}} {\boldsymbol{\Xi }}_k$, ${\bar{\textbf{n}}}_{k,\text{c}} = {\textbf{U}}_{k,\text{c}}^H {\textbf{W}}_{k,\text{c}}^H {\textbf{n}}_{k,\text{c}}$, and ${\bar{\boldsymbol{\epsilon }}}_{k,\text{e}} = {\textbf{U}}_{k,\text{e}}^H {\textbf{W}}_{k,\text{e}}^H {\boldsymbol{\epsilon }}_{k,\text{e}}$. Thus, the MIMO-NOMA system in each cluster is decomposed into J parallel SISO-NOMA systems, which enables the application of existing techniques for SISO-NOMA systems.

Next, we discuss power allocation maximizing the sum rate of this system. Denoting the rate at the cell-center user and the rate at the cell-edge user in the kth cluster as ${{\mathcal{R}}}_{k,\text{c}}$ and ${{\mathcal{R}}}_{k,\text{e}}$, respectively, we can express ${{\mathcal{R}}}_{k,\text{c}}$ and ${{\mathcal{R}}}_{k,\text{e}}$ achievable by the system with perfect SIC at the cell-center user as

$$\begin{aligned} {{\mathcal{R}}}_{k,\text{c}}&= \sum _{j=1}^{J} \log _2 \left( 1 + h_{k,j}p_{k,j}\right) , \nonumber \\ {{\mathcal{R}}}_{k,\text{e}}&= \sum _{j=1}^{J} \log _2 \left( 1 + \frac{f_{k,j} q_{k,j}}{f_{k,j} p_{k,j}+1}\right) , \end{aligned}$$

(35)

where $h_{k,j} = \frac{\left| {\bar{\boldsymbol{\Sigma }}}_{k,\text{c}}(j,j)\right| ^2}{\sigma _n^2}$, $f_{k,j} = \min \left\{ \left| {\bar{\boldsymbol{\Sigma }}}_{k,\text{e}}(j,j)\right| ^2,\; \frac{\left| {\bar{\boldsymbol{\Sigma }}}_{k,\text{c}}(j,j)\right| ^2}{\sigma _n^2}\right\}$, $p_{k,j} = {\textbf{D}}_{k,\text{c}}^2(j,j)$ and $q_{k,j} = {\textbf{D}}_{k,\text{e}}^2(j,j)$. To maximize the sum rate ${{\mathcal{R}}}_{\text{sum}}$, which is given as ${\mathcal{R}}_{\text{sum}} = \sum _{k=1}^{K}\left( {{\mathcal{R}}}_{k,\text{c}} + {{\mathcal{R}}}_{k,\text{e}}\right)$, with a fair power allocation between clusters as well as between users in each cluster, the power allocation for $p_{k,j}$ and $q_{k,j}$ is optimized as follows:

$$\begin{aligned}&\left\{ {\textbf{p}}^{\star },\; {\textbf{q}}^{\star }\right\} = \arg \max _{{\textbf{p}},\; {\textbf{q}}} {{\mathcal{R}}}_{\text{sum}}\nonumber \\&{\text {subject to:}}\nonumber \\&\sum _{k=1}^{K} {{\bar{P}}}_k \le P_T, \; {{\bar{P}}}_k \ge \nu _k \frac{P_T}{K}, \nonumber \\&\sum _{j=1}^{J} p_{k,j} \le \delta _k {{\bar{P}}}_k,\quad \text{and} \quad \sum _{j=1}^{J} q_{k,j} \le \left( 1-\delta _k\right) {{\bar{P}}}_k, \end{aligned}$$

(36)

where ${\textbf{p}} =[p_{1,1}, p_{1,2},\ldots , p_{1,J},\ldots , p_{K,1}, p_{K,2},\ldots , p_{K,J}]$, ${\textbf{q}} =[q_{1,1}, q_{1,2},\ldots , q_{1,J},\ldots , q_{K,1}, q_{K,2},\ldots , q_{K,J}]$, and ${{\bar{P}}}_k$ is the power to be allocated to the kth cluster. The parameters $\nu _k$ and $\delta _k$ are all set to values between 0 and 1 for fairness between users in each cluster as well as clusters. This optimization is performed by alternately employing two processes described below. In the first process, the optimal power allocation for clusters is initially estimated. In the second process, the optimal powers to be allocated to the cell-center and cell-edge users in each cluster are determined using the power allocated to the cluster in the first process. These processes are iteratively performed until ${{\bar{P}}}_k$, $p_{k,j}$ and $q_{k,j}$ are all obtained with the required accuracy.

In detail, to estimate the power allocation for clusters maximizing the sum rate in the first process, we express $p_{k,j}$ and $q_{k,j}$ to  $a_{k,j}{{\bar{P}}}_k$ and  $b_{k,j}{{\bar{P}}}_k$, respectively. $a_{k,j}$ and $b_{k,j}$ indicate the ratios of ${\bar{P}}_k$ allocated to the cell-center and cell-edge users in the kth cluster, respectively. In the first process, we find ${\bar{P}}^{(m)}_k$, which is the power allocated to the kth cluster at the mth iteration, by maximizing the function ${{\mathcal{L}}}^{(m)}$ as

$$\begin{aligned} {\mathcal{L}}^{(m)}\left( {\bar{\textbf{P}}}^{(m)},\; \mu ^{(m)}\right)&= \sum _{k=1}^{K} \sum _{j=1}^{J} \left\{ \log _2 \left( 1 + h_{k,j} a^{(m)}_{k,j}{{\bar{P}}}^{(m)}_k\right) + \log _2 \left( 1 + \frac{f_{k,j}b^{(m)}_{k,j}{{\bar{P}}}^{(m)}_k }{f_{k,j} a^{(m)}_{k,j}{{\bar{P}}}^{(m)}_k +1}\right) \right\} \nonumber \\&\quad + \mu ^{(m)}\left( P_T - \sum _{k=1}^{K} {{\bar{P}}}^{(m)}_k\right) \end{aligned}$$

(37)

$$\begin{aligned} \frac{\partial {{\mathcal{L}}}^{(m)}}{\partial {{\bar{P}}}^{(m)}_k}&= \sum _{j=1}^J \left\{ \frac{\alpha ^{(m)}_{k,j}}{\alpha ^{(m)}_{k,j}{\bar{P}}^{(m)}_k + 1} + \frac{\beta ^{(m)}_{k,j}}{{\beta ^{(m)}_{k,j}\bar{P}}^{(m)}_k + 1} - \frac{\gamma ^{(m)}_{k,j}}{{\gamma ^{(m)}_{k,j}\bar{P}}^{(m)}_k + 1} \right\} \nonumber \\&\quad - \mu ^{(m)} = 0 \end{aligned}$$

(38)

$$\begin{aligned} {{\bar{P}}}^{(m)}_k&= \max \left\{ {{\tilde{P}}}^{(m)}_k,\; \nu _k \frac{P_T}{K} \right\} , \end{aligned}$$

(39)

where ${\bar{\textbf{P}}}^{(m)}=\left[ {{\bar{P}}}^{(m)}_1, {\bar{P}}^{(m)}_2, \ldots , {{\bar{P}}}^{(m)}_K \right]$, $\alpha ^{(m)}_{k,j} = h_{k,j} a^{(m)}_{k,j}$, $\beta ^{(m)}_{k,j} = f_{k,j}\left( a^{(m)}_{k,j} + b^{(m)}_{k,j}\right)$ and $\gamma ^{(m)}_{k,j} = f_{k,j} a^{(m)}_{k,j}$. $\mu ^{(m)}$ is a Lagrange multiplier in the mth iteration. $a^{(m)}_{k,j}$ and $b^{(m)}_{k,j}$ indicate the ratios of ${{\bar{P}}}^{(m)}_k$ allocated to the cell-center and cell-edge users in the kth cluster at the mth iteration, respectively. Furthermore, $a^{(m)}_{k,j}$ and $b^{(m)}_{k,j}$ are refined in the second process and transferred to the first process for the next iteration, which will be described later. ${{\tilde{P}}}^{(m)}_k$ in (39) indicates the value of ${{\bar{P}}}^{(m)}_k$ obtained from (38) for a given value of $\mu ^{(m)}$. Equations (38) and (39) are repeatedly solved for ${{\bar{P}}}^{(m)}_k$ by adjusting the value of $\mu ^{(m)}$ until the sum power $\sum _{k=1}^K{{\bar{P}}}^{(m)}_k$ is sufficiently close to $P_T$.

In the second process, we find $p^{(m)}_{k,j}$ and $q^{(m)}_{k,j}$, which are the estimates of $p_{k,j}$ and $q_{k,j}$ at the mth iteration, maximizing the function $l^{(m)}_k$ with ${\bar{P}}^{(m)}_k$ obtained from the first process as follows:

$$\begin{aligned}&l_k^{(m)} \left( {\textbf{p}}^{(m)}_k,\;{\textbf{q}}^{(m)}_k,\;\mu ^{(m)}_{k,\text{c}},\; \mu ^{(m)}_{k,\text{e}} \right) \nonumber \\&\quad = \sum _{j=1}^J \left\{ \log _2 \left( 1 + h_{k,j}p^{(m)}_{k,j}\right) + \log _2 \left( 1 + \frac{f_{k,j} q^{(m)}_{k,j}}{f_{k,j} p^{(m)}_{k,j}+1}\right) \right\} \nonumber \\&\qquad + \mu ^{(m)}_{k,\text{c}}\left( \delta _k {{\bar{P}}}_k^{(m)} - \sum _{j=1}^{J} p^{(m)}_{k,j} \right) \nonumber \\&\qquad + \mu ^{(m)}_{k,\text{e}}\left( \left( 1-\delta _k\right) {\bar{P}}_k^{(m)} - \sum _{j=1}^{J} q^{(m)}_{k,j} \right) \end{aligned}$$

(40)

$$\begin{aligned} \frac{\partial l_k^{(m)}}{\partial q^{(m)}_{k,j}}&= \frac{f_{k,j}}{f_{k,j}q^{(m)}_{k,j}+f_{k,j}p^{(m)}_{k,j}+1} - \mu ^{(m)}_{k,\text{e}} = 0 \end{aligned}$$

(41)

$$\begin{aligned} \frac{\partial l_k^{(m)}}{\partial p^{(m)}_{k,j}}&= \frac{h_{k,j}}{ h_{k,j}p^{(m)}_{k,j}+1} + \frac{f_{k,j}}{f_{k,j}p^{(m)}_{k,j}+f_{k,j}q^{(m)}_{k,j}+1} \nonumber \\&\quad -\frac{f_{k,j}}{f_{k,j}p^{(m)}_{k,j}+1} - \mu ^{(m)}_{k,\text{c}} = 0, \end{aligned}$$

(42)

where ${\textbf{p}}^{(m)}_k =\left[ p^{(m)}_{k,1}, p^{(m)}_{k,2},\ldots , p^{(m)}_{k,J}\right]$ and ${\textbf{q}}^{(m)}_k =\left[ q^{(m)}_{k,1}, q^{(m)}_{k,2},\ldots , q^{(m)}_{k,J}\right]$. $\mu ^{(m)}_{k,\text{c}}$ and $\mu ^{(m)}_{k,\text{e}}$ are Lagrange multipliers in the mth iteration. The optimal $p^{(m)}_{k,j}$ and $q^{(m)}_{k,j}$ in (41) and (42) are obtained using the alternating maximization in [29]. When we denote the values of $p^{(m)}_{k,j}$ and $q^{(m)}_{k,j}$ at the ith alternation of the mth iteration as $p_{k,j}^{(m(i))}$ and $q_{k,j}^{(m(i))}$, respectively, the maximization is performed as

$$\begin{aligned} q_{k,j}^{(m(i))} = \max \left\{ \frac{1}{{\mu ^{(m)}_{k,\text{e}}}} - p_{k,j}^{(m(i-1))} - \frac{1}{f_{k,j}},\; 0 \right\} \end{aligned}$$

(43)

$$\begin{aligned} \frac{h_{k,j}}{ h_{k,j}p_{k,j}^{(m(i))}+1}&+ \frac{f_{k,j}}{f_{k,j}p_{k,j}^{(m(i))}+f_{k,j}q_{k,j}^{(m(i))}+1}\nonumber \\&- \frac{f_{k,j}}{f_{k,j}p_{k,j}^{(m(i))}+1} - \mu ^{(m)}_{k,\text{c}} = 0 \end{aligned}$$

(44)

$$\begin{aligned} p_{k,j}^{(m(i))} = \max \left\{ {{\tilde{p}}}_{k,j}^{(m(i))},\; 0 \right\} , \end{aligned}$$

(45)

where ${{\tilde{p}}}^{(m(i))}_{k,j}$ in (45) represents the value of $p^{(m(i))}_{k,j}$ obtained from (44) for a given value of $\mu ^{(m)}_{k,\text{c}}$. Since $p_{k,j}^{(m(i))}$ is not available until the ith alternation is completed, $p_{k,j}^{(m(i-1))}$ instead of $p_{k,j}^{(m(i))}$ is used to find $q_{k,j}^{(m(i))}$ in (43). The alternating maximization in (43)–(45) is continued until the sum powers $\sum _{j=1}^J p^{(m(i))}_{k,j}$ and $\sum _{j=1}^J q^{(m(i))}_{k,j}$ are sufficiently close to $\delta _k {\bar{P}}^{(m)}_k$ and $\left( 1-\delta _k \right) {{\bar{P}}}^{(m)}_k$ by adjusting the values of $\mu ^{(m)}_{k,\text{c}}$ and $\mu ^{(m)}_{k,\text{e}}$, respectively.

When the alternating maximization in the mth iteration is completed at the Ith alternation, $p^{(m(I))}_{k,j}$ and $q^{(m(I))}_{k,j}$ are assigned to $p^{(m)}_{k,j}$ and $q^{(m)}_{k,j}$, respectively. Then, the power ratios $a^{(m+1)}_{k,j}$ and $b^{(m+1)}_{k,j}$ for the $(m+1)$th iteration in the first process are refined as

$$\begin{aligned} a^{(m+1)}_{k,j}&= \frac{p^{(m)}_{k,j}}{\sum _{j=1}^J \left( p^{(m)}_{k,j} + q^{(m)}_{k,j}\right) },\nonumber \\ b^{(m+1)}_{k,j}&= \frac{q^{(m)}_{k,j}}{\sum _{j=1}^J \left( p^{(m)}_{k,j} + q^{(m)}_{k,j}\right) }. \end{aligned}$$

(46)

$a^{(m+1)}_{k,j}$ and $b^{(m+1)}_{k,j}$ are returned to the first process in order to find ${{\bar{P}}}_k^{(m+1)}$, which is in turn used to find $p^{(m+1)}_{k,j}$ and $q^{(m+1)}_{k,j}$ in the second process. These processes are alternately performed until ${\bar{P}}_k$, $p_{k,j}$ and $q_{k,j}$ are all obtained with the required accuracy. Finally, the power allocation matrices ${\textbf{D}}_{k,\text{c}}$ and ${\textbf{D}}_{k,\text{e}}$ for the kth cluster are given using $p_{k,j}$ and $q_{k,j}$ obtained from this optimization as

$$\begin{aligned} {\textbf{D}}_{k,\text{c}}&= \text{diag}\left\{ \sqrt{p_{k,1}},\; \sqrt{p_{k,2}}, \ldots , \sqrt{p_{k,J}}\right\} \nonumber \\ {\textbf{D}}_{k,\text{e}}&= \text{diag}\left\{ \sqrt{q_{k,1}},\; \sqrt{q_{k,2}}, \ldots ,\sqrt{q_{k,J}}\right\} . \end{aligned}$$

(47)

In summary, the proposed procedure optimizing the power allocation is as follows:

• Step 1: The index m is initialized to 1 and the power ratios $a^{(m)}_{k,j}$ and $b^{(m)}_{k,j}$ are set to initial values.

• Step 2: The power ${{\bar{P}}}^{(m)}_k$ allocated to the kth cluster at the mth iteration is obtained using (38) and (39).

• Step 3: The powers $p^{(m)}_{k,j}$ and $q^{(m)}_{k,j}$, which are allocated to the cell-center and cell-edge users in the kth cluster at the mth iteration, respectively, are obtained using (43)–(45) with the power constraint ${{\bar{P}}}^{(m)}_k$.

• Step 4: If ${{\bar{P}}}_k$, $p_{k,j}$ and $q_{k,j}$ are all obtained with the required accuracy, this procedure is terminated and the power allocation matrices ${\textbf{D}}_{k,\text{c}}$ and ${\textbf{D}}_{k,\text{e}}$ are obtained as given in (47). Otherwise, Step 5 is performed.

• Step 5: The power ratios $a^{(m+1)}_{k,j}$ and $b^{(m+1)}_{k,j}$ are refined using (46) and the index m is increased by 1. Then, Steps 2, 3, and 4 are re-performed sequentially.

Steps 1 and 2 represent the first process, while Steps 3, 4, and 5 represent the second process.

This power allocation is executed at BSs and may require high computational complexity because it iteratively finds roots of nonlinear equations. Thus, it is suitable for use in BSs with high computational capabilities. In this power allocation, as the number of clusters (K) increases, the complexity of the first process allocating power to K clusters increases. And as the number of data streams transmitted to each cluster (2J) increases, the number of alternations in the second process tends to become larger to allocate power to the data streams with the required accuracy, thereby increasing computational complexity. When the value of KJ is fixed, the complexity of this power allocation becomes higher for a moderate number of clusters. In the future, it would be worth exploring non-iterative power allocation methods that achieve the performance close to the proposed power allocation to reduce computational complexity for use in low-cost BSs.

4 Simulation results

In this section, we evaluate the sum rate and outage performances of the proposed MC-MIMO-NOMA technique through simulations. In the simulations, the serving cell is considered to be interfered from three adjacent cells, which means $L=3$. For the kth cluster, the distances between the serving BS and the cell-center user, between the serving BS and the cell-edge user, and between the lth adjacent cell BS and the cell-edge user are denoted as $r_{k,\text{c}}$, $r_{k,\text{e}}$, and $r_{k,l}$, respectively. We consider that while $r_{k,\text{c}}$ is uniformly distributed between $2\text{m}$ and $3\text{m}$, $r_{k,\text{e}}$ and $r_{k,l}$ are uniformly distributed between $9\text{m}$ and $10\text{m}$. BSs employ the number of transmit antennas (M) equal to the number of receive antennas (N) equipped at the users.

The channel matrices ${\textbf{H}}_{k,\text{c}}$, ${\textbf{H}}_{k,\text{e}}$, and ${\textbf{G}}_{k,l}$ are given as ${r_{k,\text{c}}}^{-\frac{\alpha }{2}}{\bar{\textbf{H}}}_{k,\text{c}}$, ${r_{k,\text{e}}}^{-\frac{\alpha }{2}}{\bar{\textbf{H}}}_{k,\text{e}}$, and ${r_{k,l}}^{-\frac{\alpha }{2}}{\bar{\textbf{G}}}_{k,l}$, respectively, where the elements of ${\bar{\textbf{H}}}_{k,\text{c}}$, ${\bar{\textbf{H}}}_{k,\text{e}}$, and ${\bar{\textbf{G}}}_{k,l}$ are randomly generated from circular symmetric complex Gaussian distributions with zero mean and unit variance, and the path loss exponent $\alpha$ is set to 3. The serving BS transmits $\frac{M}{K}$ NOMA-modulated data streams to each cluster, where K indicates the number of clusters simultaneously supported by the serving BS. The parameter $\nu _k$ is set to 0.2. This means that the serving BS allocates at least $0.2\frac{P_T}{K}$ of power to each cluster, where $P_T$ indicates the total transmit power of the serving BS. The parameter $\delta _k$ is set to 0.1. This means that the serving BS may allocate up to $0.1{{\bar{P}}}_k$ of power to the cell-center user in the kth cluster, where ${{\bar{P}}}_k$ indicates the transmit power allocated to the kth cluster. The SNR $\eta$ is given as $\eta = \frac{P_T}{\sigma _n^2}$. Each sum rate performance is found by averaging the instantaneous sum rates obtained from 2000 random channel realizations.

To show the impact of power allocation on the proposed transmit and receive beamforming technique for MC-MIMO-NOMA systems, Figs. 4 and 5 compare the sum rate performances obtained from three power allocation schemes. The schemes are the proposed power allocation, equal cluster power allocation, and equal stream power allocation. Equal power allocation associated with the equal cluster power allocation and the equal stream power allocation is widely used as a baseline scheme for performance comparison [29, 33]. The equal cluster power allocation is the same as the proposed power allocation, except that the serving BS allocates $\frac{P_T}{K}$ of power to each cluster. The equal stream power allocation scheme evenly distributes the total transmit power $P_T$ to M data streams. The MC-MIMO-NOMA systems with $M=N=4$ and $M=N=8$ are considered in Figs. 4 and 5, respectively.

Fig. 4

Comparison of the sum rate performances according to different power allocation schemes applied to the proposed transmit and receive beamforming technique in the MC-MIMO-NOMA system with $M=N=4$

Fig. 5

Comparison of the sum rate performances according to different power allocation schemes applied to the proposed transmit and receive beamforming technique in the MC-MIMO-NOMA system with $M=N=8$

As we can see from those figures, the propose power allocation scheme achieves the best performances of them. This is because the proposed scheme effectively allocates the transmit power for each cluster and the transmit power for each data stream in consideration of channel states in all clusters. In detail, as the number of clusters simultaneously supported by the serving BS decreases, the sum rate performances of the proposed scheme are improved further. When the number of clusters decreases, the transmit power to be allocated to each cluster increases on average and the number of data streams for each cluster increases as well. By effectively allocating more transmit power to data streams to be transmitted through good quality channels in each cluster, the proposed scheme improves the sum rate performances. In addition, as the number of clusters increases, the performance gaps between the proposed scheme and the others become larger. This is because the proposed scheme exploits the increased cluster diversity to allocate the transmit power to each cluster efficaciously. When the serving BS simultaneously supports as many clusters as the number of transmit antennas, only a single NOMA modulated data stream is transmitted to each cluster. Since the equal stream power allocation is identical to the equal cluster power allocation in this case, the performances of both schemes are identical in those figures.

Figure 6 demonstrates the sum rate performances of the proposed MC-MIMO-NOMA technique, which employs both the proposed transmit and receive beamforming and the proposed power allocation, with the increasing number of interfering cells. In this simulation, we consider two systems with $M=N=4$ and $M=N=8$ and the serving BS simultaneously supports 2 clusters in each system. It is shown in all the systems that regardless of the number of interfering cells, the proposed technique consistently improves the performances as the SNR $\eta$ increases. This confirms the effectiveness of the proposed technique. However, the performances gradually deteriorate with the increasing number of interfering cells. This is because the residual MCI power after MCI mitigation also increases as the number of interfering cells increases.

Fig. 6

Comparison of the sum rate performances of the proposed technique in the MC-MIMO-NOMA systems with $M=N=4$ and $M=N=8$ as the number of interfering cells increases from 1 to 3

In Figs. 7 and 8, the sum rate performances of the proposed technique are compared with those of the existing MC-MIMO-NOMA techniques that are the MIMO-NOMA technique in [23] and the signal-alignment based MIMO-NOMA technique in [24]. The existing techniques utilize time sharing among multiple BSs to avoid MCI. Figures 7 and 8 show the performance comparisons for the MC-MIMO-NOMA systems with $M=N=4$ and $M=N=8$, respectively. We can see that regardless of the number of clusters simultaneously supported by the serving BS in all the systems, the proposed technique achieves better performances than the existing techniques. Since the existing techniques transmit only a single NOMA modulated data stream to each cluster, they may simultaneously support as many clusters as the number of transmit antennas. However, the existing techniques cannot be extend to transmit multiple data streams to each cluster even though they simultaneously support fewer clusters than the number of transmit antennas. In contrast, the proposed technique can transmit multiple data streams to each cluster at the expense of simultaneously supporting fewer clusters than the number of transmit antennas, thereby improving the sum rate performances. Thus, the proposed technique may provide a good balance between the number of clusters to be simultaneously supported by the serving BS and the sum rate performance by adjusting the number of data streams to be transmitted to each cluster as needed.

Fig. 7

Comparison of the sum rate performances between the proposed technique and the existing techniques in the MC-MIMO-NOMA system with $M=N=4$

Fig. 8

Comparison of the sum rate performances between the proposed technique and the existing techniques in the MC-MIMO-NOMA system with $M=N=8$

Figures 9 and 10 demonstrate the outage probability for a cell-center user, which is given as $\text{Pr}({{\mathcal{R}}}_{k,\text{c}} < 1\,\mathrm{bps/Hz})$ and that for a cell-edge user, which is given as $\text{Pr}({{\mathcal{R}}}_{k,\text{e}} < 0.02\,\mathrm{bps/Hz})$, in the kth cluster. The MC-MIMO-NOMA systems with $M=N=4$ and $M=N=8$ are considered in Figs. 9 and 10, respectively. It can be seen from both figures that regardless of the number of clusters, the proposed technique achieves lower outage probabilities for the cell-center user than the existing techniques. In addition, as the number of clusters simultaneously supported by the serving BS decreases, the outage performance for the cell-center user is further improved in the proposed technique. This is because the number of data streams transmitted to each cluster increases with the decreasing number of the clusters.

Fig. 9

Comparison of the outage performances for cell-center and cell-edge users between the proposed technique and the existing techniques in the MC-MIMO-NOMA system with $M=N=4$

Fig. 10

Comparison of the outage performances for cell-center and cell-edge users between the proposed technique and the existing techniques in the MC-MIMO-NOMA system with $M=N=8$

As we can see from Fig. 9, the outage probabilities for the cell-edge user in the proposed technique are lower than those in the existing techniques at SNRs less than 24 dB. Furthermore, the proposed technique with 2 clusters achieves better outage performance than the existing techniques at SNRs less than 30 dB. Figure 10 shows similar performance trends to Fig. 9. In detail, the outage probabilities for the cell-edge user in the proposed technique are lower than those in the existing techniques at SNRs less than 25 dB. While the proposed technique with 4 clusters achieves better outage performance than the existing techniques at SNRs less than 29 dB, the proposed technique with 2 clusters achieves better outage performance than the existing techniques at SNRs less than 33 dB. Since the number of data streams transmitted to each cluster increases with the decreasing number of the clusters in the proposed technique, the outage performance for the cell-edge user in the proposed technique is improved with the decreasing number of the clusters. In contrast, the existing techniques employing MCI avoidance achieve better outage performance for the cell-edge user than the proposed technique at SNRs greater than 30 or 33 dB as shown in Figs. 9 and 10. This is because the performance for the cell-edge user in the proposed technique is affected by the residual MCI power after MCI mitigation.

We see from this performance evaluation that the proposed technique can improve the outage performances for all the users by transmitting multiple data streams to each cluster at the expense of simultaneously supporting fewer clusters than the number of transmit antennas. Thus, the proposed technique may provide a good balance between the number of clusters to be simultaneously supported by the serving BS and the outage performances by adjusting the number of data streams to be transmitted to each cluster as needed. Considering comprehensively the sum rate, the outage probabilities for all the users, and the flexibility for balancing between the performances and the number of clusters simultaneously supported by the serving BS, we confirm that the proposed technique is more beneficial than the existing techniques.

To investigate the sum rate and outage performances of the proposed technique for SC-MIMO-NOMA systems, we compare the performances of the proposed technique transmitting data streams to only a single cluster with those of the existing SC-MIMO-NOMA techniques. The existing techniques are the SC-MIMO-NOMA technique exploiting GSVD and equal stream power allocation in [26, 27] and the SC-MIMO-NOMA technique employing layered transmissions and an effective power allocation scheme for the layered transmissions in [29]. Figure 11 shows the sum rate performances of the proposed technique and the existing techniques for the SC-MIMO-NOMA systems with $M=N=4$ and $M=N=8$. Figures 12 and 13 show the outage performances of the proposed technique and the existing techniques for the SC-MIMO-NOMA systems with $M=N=4$ and $M=N=8$, respectively. The definitions of outage probabilities for cell-center and cell-edge users in the figures are the same as those in Figs. 9 and 10. The existing techniques use time sharing among multiple BSs to avoid MCI.

Fig. 11

Comparison of the sum rate performances between the proposed technique and the existing techniques in the SC-MIMO-NOMA systems with $M=N=4$ and $M=N=8$

Fig. 12

Comparison of the outage performances for cell-center and cell-edge users between the proposed technique and the existing techniques in the SC-MIMO-NOMA system with $M=N=4$

Fig. 13

Comparison of the outage performances for cell-center and cell-edge users between the proposed technique and the existing techniques in the SC-MIMO-NOMA system with $M=N=8$

It can be seen from Fig. 11 that the proposed technique still achieves better sum rate performances than the existing techniques in all the systems. This is because the proposed technique effectively mitigates MCI and optimally allocates the transmit power to data streams to maximize the sum rates. In addition, the proposed technique for the SC-MIMO-NOMA systems obtains higher sum rates than the proposed technique for the MC-MIMO-NOMA systems in Figs. 7 and 8 at the expense of fewer clusters simultaneously supported by the serving BS. This is because the CSI combined with the precoder and receive beamformers for ICI elimination tends to be degraded in the MC-MIMO-NOMA systems and the total transmit power is allocated to multiple data streams more effectively in the SC-MIMO-NOMA systems than in the MC-MIMO-NOMA systems. Figures 12 and 13 demonstrate that the proposed technique has lower outage probabilities than the exiting techniques over the entire SNR range. This confirms that the proposed technique can provide the required data rates more reliably than the existing techniques by using effective MCI mitigation and optimal power allocation. Furthermore, the proposed technique for the SC-MIMO-NOMA systems achieves better outage performances than the proposed technique for the MC-MIMO-NOMA systems in Figs. 9 and 10 at the expense of fewer clusters simultaneously supported by the serving BS.

Figures 14 and 15 show the sum rate performances of the proposed technique compared with those of the existing techniques in [23, 24, 26, 27, 29] when the serving cell is interfered from two adjacent cells. The SC-MIMO-NOMA and MC-MIMO-NOMA systems with $M=N=2$ are considered in Fig. 14, while the systems with $M=N=4$ are considered in Fig. 15. As expected, the proposed technique achieves better performance than the existing techniques for both SC-MIMO-NOMA and MC-MIMO-NOMA systems, which demonstrates the superiority of the proposed technique. In addition, it is reaffirmed that the proposed technique for the SC-MIMO-NOMA systems achieves higher sum rates than the one for the MC-MIMO-NOMA systems at the expense of fewer clusters served simultaneously. This is because the combined CSI tends to be degraded in the MC-MIMO-NOMA systems, while the transmit power is allocated more effectively to multiple data streams in the SC-MIMO-NOMA systems. Compared with the proposed technique in Figs. 7 and 11 for the systems with $M=N=4$, the proposed technique in Fig. 15 obtains higher sum rates. This is because the number of interfering adjacent cells is reduced from three to two, thereby decreasing MCI.

Fig. 14

Comparison of the sum rate performances between the proposed technique and the existing techniques in the SC-MIMO-NOMA and MC-MIMO-NOMA systems with $M=N=2$ when the serving cell is interfered from two adjacent cells

Fig. 15

Comparison of the sum rate performances between the proposed technique and the existing techniques in the SC-MIMO-NOMA and MC-MIMO-NOMA systems with $M=N=4$ when the serving cell is interfered from two adjacent cells

5 Conclusion

To improve spectral efficiency by transmitting multiple NOMA modulated data streams to each cluster in multi-cell systems, we proposed the MC-MIMO-NOMA technique to design transmit and receive beamforming matrices and perform power allocation between clusters and between data streams in each cluster. In detail, cell-edge users design their own receive beamforming matrices to minimize the MCI power, irrespective of the number of interfering cells. By using the receive beamforming matrices, the serving BS constructs its own transmit beamforming matrices to eliminate ICI between cell-edge users and maximize the lower bounds of the received SNRs at the cell-edge users. Cell-center users then use the transmit beamforming matrices to find their own receive beamforming matrices that eliminate ICI between them and maximize the lower bounds of their received SNRs. Since all users can directly find their own receive beamforming matrices without channel feedback to the serving BS, the proposed technique decreases system overhead. Furthermore, based on the transmit and receive beamforming matrices, the proposed technique allocates the transmit power to clusters and users of each cluster in a manner that maximizes the sum rate performance under power constraints supporting fairness between clusters and between users in each cluster. The simulation results demonstrated that the proposed technique achieves better sum rate and outage performances than the existing techniques and may provide a good balance between the performances and the number of clusters simultaneously supported by the serving BS. This confirms that the proposed technique is more beneficial than the existing techniques. Despite these advantages, the proposed technique has some limitations. Imperfect CSI feedback from cell-edge users may cause performance degradation. The proposed iterative power allocation imposes a computational burden. Addressing these technical issues will be a future research topic.