Coordinated Multicell Beamforming Based on Power Minimization in an Uplink–Downlink Configured Massive MIMO Network

Abstract

In this paper, the coordinated beamforming problem is investigated to minimize the sum transmit power of the system in a two-cell network, downlink transmission in one cell and uplink transmission in the other cell. It is assumed that the base stations (BSs) and the users are equipped with multiple input multiple output (MIMO) antennas, and the coordinated beamforming vectors are designed for the BS in the downlink cell and the users in the uplink cell under the signal-to-interference plus noise ratio (SINR) constraints. Then, the problem is extended for a scenario where the BSs and users have massive MIMO antennas, and using the random matrix theory, an algorithm is proposed to design the coordinated beamforming vectors. Simulation results show that this coordinated beamforming algorithm for the massive MIMO scenario accurately tracks the optimal sum transmit power minimization beamforming approach, while it reduces the computational complexity of the coordinated beamforming.

1 Introduction

We investigate the problem of coordinated beamforming in an uplink–downlink configuration of a two-cell dynamic time division duplexing (TDD) network to minimize the sum power of beamforming vectors with the signal-to-interference plus noise ratio (SINR) constraints. The coordinated beamforming problem has been investigated extensively in the downlink transmission of multicell multiple input multiple output (MIMO) networks (Venturino et al. 2010; Garzas et al. 2014; Utschick and Brehmer 2012; Huang et al. 2014; Li et al. 2015; He et al. 2015; Tervo et al. 2018; Boukhedimi et al. 2017; Patcharamaneepakorn et al. 2015; Dahrouj and Yu 2010; Lakshminarayana et al. 2015; Zakhour and Hanly 2012; Huang et al. 2013; Belschner et al. 2019; Barman Roy et al. 2019; Kazi and Wainer 2019; Asgharimoghaddam et al. 2019; Kwon and Park 2020; Khamidullina et al. 2020; Bai et al. 2020). This scheme addresses involving both the intracell and intercell interference in beamforming problems.

For instance, in Venturino et al. (2010), Garzas et al. (2014), Utschick and Brehmer (2012) the authors taking both the intracell and intercell interference into account investigated the weighted sum rate maximization problem subject to power consumption constraints. Also, the authors of Kwon and Park (2020) presented a non-iterative algorithm for coordinated beamforming to maximize the SINR of the users, which improves the overall sum rate of the system. The energy efficiency of the system is another objective function which could be maximized by designing the coordinated beamforming vectors (Huang et al. 2014; Li et al. 2015; He et al. 2015; Tervo et al. 2018). Moreover, the problems of signal-to-leakage plus noise ratio (SLNR) maximization and modified SLNR (mSLNR) maximization have been investigated for coordinated beamforming in Boukhedimi et al. (2017) and Patcharamaneepakorn et al. (2015). Besides, a generalized singular value decomposition (SVD) scheme is presented in Khamidullina et al. (2020) to be employed for coordinated beamforming in multicell MIMO systems. Another target for designing the coordinated beamforming vectors is sum power minimization subject to SINR constraints for each user (Dahrouj and Yu 2010; Lakshminarayana et al. 2015; Zakhour and Hanly 2012; Huang et al. 2013; Asgharimoghaddam et al. 2019). Furthermore, the authors in Bai et al. (2020) leveraged the coordinated beamforming to enhance the secrecy of the multicell MIMO systems.

The coordinated beamforming problem is also examined in massive MIMO (mMIMO) systems, in which the number of antennas is much more than the number of Users. In order to implement the coordinated beamforming in such systems, it is required to exchange lots of channel information between the base stations (BSs). Therefore, the researchers employed the random matrix theory to design the beamforming vectors which only depend on the statistics of the channels. These schemes have been investigated in the downlink transmission of multicell mMIMO networks. In He et al. (2015), the authors extended the energy efficiency maximization problem for multicell mMIMO networks and used the random matrix theory to propose a reduced overhead algorithm for coordinated beamforming. Also, the SLNR maximization problem has been proposed in Boukhedimi et al. (2017) for a two-tier mMIMO scenario including macro and small cells. Furthermore, the authors in Lakshminarayana et al. (2015) and Zakhour and Hanly (2012) used the random matrix theory to form the coordinated beams for minimizing the sum power of the beamforming vectors in a multicell mMIMO network.

The above researches discussed multicell TDD networks in which, at each time, all cells have downlink or uplink transmission. However, in the recent years by increasing the demands such as video downloading and video sharing, the requests for both the downlink and uplink transmissions are growing and highly time variable (Agustin et al. 2017). Therefore, the dynamic TDD networks have been proposed, in which, based on the demands of the users, the cells could have downlink or uplink transmission (Shen et al. 2012). Under the influence of this possibility, such a scenario could happen that at the same time some cells have downlink transmission and the other cells have uplink transmission. Thus, the users would experience new types of intercell interference such as BS to BS (downlink to uplink) and user to user (uplink to downlink) interference (Kim et al. 2020). In order to overcome this problem in MIMO networks, different coordinated beamforming approaches are proposed, which could be divided into two general categories. In the first category, only the downlink to uplink intercell interference is considered, i.e., the downlink BSs are equipped with MIMO antennas and form their beams considering the intercell and intracell interference, but the uplink users have single antennas and transmit without considering the intercell interference (Ko et al. 2018; Guimaraes et al. 2018; Cavalcante et al. 2018). For instance, the authors in Ko et al. (2018) used the interference alignment concept to form the coordinated beams for the downlink BSs. A priced-based beamforming approach is proposed in Guimaraes et al. (2018), for coordinated beamforming in the downlink cells. Also, in Cavalcante et al. (2018) the authors minimized the transmit power of the base stations subject to SINR constraints for each of the users in the downlink cells and keeping the BS to BS interference below a threshold. In the other category of the proposed schemes, both the uplink to downlink and downlink to uplink interferences are considered. In fact the downlink BSs form their beams with respect to intracell and downlink to uplink interference and the uplink users form the beam or allocate the power, considering the uplink to downlink interference (Yoon and Cho 2015; Aghashahi et al. 2019; Jayasinghe et al. 2015; Lagen et al. 2017; Aghashahi et al. 2018; Yoon et al. 2019; Cavalcante et al. 2019; Lee et al. 2020). A scenario is studied in Yoon and Cho (2015), where the BSs have MIMO antennas and the users have single antennas, and both the uplink to downlink and downlink to uplink interferences are considered. The authors of this research designed the coordinated beamforming vectors for the downlink BSs and allocated power to the uplink users to maximize the energy efficiency of the system. Also, in a similar scenario the authors of Aghashahi et al. (2019) investigated the energy efficiency maximization problem to allocate the coordinated transmit power for both the uplink users and downlink BSs. Moreover, the weighted sum rate maximization problem is considered in Jayasinghe et al. (2015) and Lagen et al. (2017) and the coordinated beamforming vectors for the BSs in the downlink cells and the users in the uplink cells are designed. In particular, in Lagen et al. (2017) the sum rate of the users is maximized by jointly considering the scheduling, transmission direction selection and beamforming problems. The SLNR maximization is another problem investigated in a dynamic TDD scenario with MIMO BSs and user, in which both the downlink BSs and uplink users attempt to reduce the intercell interference leakage (Aghashahi et al. 2018).

Moreover, in Yoon et al. (2019) the authors considered mean squared error minimization problem and jointly designed the beamforming vectors for downlink and uplink users in a dynamic TDD network. Also, some other researches focused on the sum power minimization problem in a dynamic TDD system with multiple antenna BSs (Cavalcante et al. 2019; Lee et al. 2020). In Lee et al. (2020), power allocation is performed for the uplink single antenna users, whereas in Cavalcante et al. (2019) the users are equipped with MIMO antennas.

Contribution: Taking the above considerations into account, in this paper, we consider the problem of coordinated beamforming in a two-cell network, where one cell has downlink transmission and the other cell has uplink transmission. We assume that the BSs and the users are equipped with MIMO antennas, and we design the coordinated beamforming vectors for the BS in the downlink cell and the users in the uplink cell. Based on the demanded rates, we assume that the network has some constraints on the minimum rate of each user. On the other hand, an important parameter is the amount of transmit power by the BSs and the users. Therefore, we consider the sum transmit power of the network as the criteria and minimize it under the SINR constraints to ensure a minimum rate for each user. In addition, we employ the random matrix theory to propose an algorithm to solve the problem for the scenario where the BSs and the users have mMIMO antennas. Such scenario could happen when each of the users in our model is a small BS or an access point connected to a macro BS through a wireless backhaul. It must be noted that the sum power minimization problem would be so complicated for the mMIMO scenario; therefore, we propose a method to leverage the computational complexity. We find equations for the Lagrangian multipliers of the sum power minimization problem, which only depend on the channel statistics and the norm of the receive filters. Then, employing the independence of the Lagrangian multipliers from the instantaneous channel information, we propose a less complicated iterative algorithm to solve the power minimization problem for the dynamic TDD mMIMO scenario. Actually, in the first algorithm proposed for MIMO systems, we require the coefficients of the receive filters to obtain the Lagrangian multipliers, and therefore, it should be performed in each iteration, while in the second algorithm, since we only require the norm of the receive filters, it could be performed once, out of the iteration loop. This is the reason that the computational complexity is reduced in the second algorithm. Moreover, since the Lagrangian multipliers in the second algorithm are independent of instantaneous CSI, we could even more reduce the computational complexity by obtaining the Lagrangian multipliers only with the change of the statistics of the channel. Simulation results show that yet our mMIMO coordinated beamforming algorithm tracks the results of the optimum sum power minimization approach.

Organization.The rest of the paper is organized as follows: In Sect. 2, the system model is introduced. In Sect. 3, the coordinated beamforming vectors are designed for MIMO systems. The proposed coordinated beamforming approach is extended for mMIMO systems in Sect. 4. The computational complexity of the algorithms is compared in Sect. 5, and some simulation results are provided in Sect. 6. Section 7 concludes the paper.

Notations. The vectors and the matrices are denoted with boldface letters and boldface capital letters, respectively. For matrix $\mathbf{A}$, $tr\{{\mathbf {A}}\}$ denotes the trace of this matrix , i.e., $tr\{{\mathbf {A}}\}=\sum _{i} A_{i,i}$, $\mathrm {diag}({\mathbf {A}})$ shows the diagonal matrix with the elements ${\mathbf {A}}_{i,i}$ and ${\mathbf {A}}^{T}$and ${\mathbf {A}}^{H}$ are the transpose and the Hermitian of matrix $\mathbf{A}$, respectively. The $N \times N$ identity matrices are represented with ${\mathbf {I}}_{N}$. Notation $\mathop {\longrightarrow }\limits ^{a.s.}$ denotes the almost sure convergence.

2 System Model

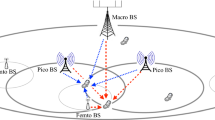
In this paper, a two-cell network is considered in which the first cell has downlink transmission and the second one has uplink transmission (Fig. 1). In each cell, there is one BS with N antennas which serves K users each equipped with M antennas. In this scenario, we design the beamforming vectors for the BS in the downlink cell and users in the uplink cell in a coordinated manner. Let the $i^{\mathrm{th}}$ BS and the $k^{\mathrm{th}}$ user terminal (UT) in the $j^{\mathrm{th}}$ cell be represented with BS(i) and UT(j,k), respectively. The notations of the channel matrices and the beamforming vectors are as shown in Table 1. Also, it is assumed that the elements of the channel matrices are i.i.d. complex Gaussian random variables. Then, the received signal at UT(1,k) after the receive filter is Heath and Lozano (2018),

$$\begin{aligned} \begin{aligned}&y_{1,\textit{k}} ^ {DL}={\mathbf {v}}_{1,k} ^{DL}\bigg (\underbrace{ {\mathbf {H}} _{1,1,k} ^{H} {\mathbf {w}}_{1,k} ^{DL} x_{1,k}^{DL}}_{\text { Signal}}+\underbrace{\sum _{m\ne k} {\mathbf {H}} _{1,1,k} ^{H} {\mathbf {w}}_{1,m} ^{DL} x_{1,m}^{DL} }_{\text {Intracell\, Interference}}+\\&\quad \underbrace{\sum _{n=1} ^{K} {\mathbf {H}} _{2,n} ^{1,k} {\mathbf {v}}_{2,n} ^{UL} x_{2,n} ^{UL}}_{ \text {Intercell\, Interference}}+\underbrace{ {\mathbf {z}}_{1,k} }_{\text {AWGN}}\bigg ), \end{aligned} \end{aligned}$$

(1)

where $x_{1,m}^{DL}$ is the information signal sent for UT(1,m), $x_{2,n} ^{UL}$ is the information signal transmitted by UT(2,n) and ${\mathbf {z}}_{1,k}\sim {\mathcal {N}}(0,N_0 {\mathbf {I}}_{M\times M})$ is the corresponding additive white Gaussian noise. The first term in (1) is the desired signal sent for UT (1,k), the second term is sum of the intracell interference, the third term is sum of the intercell (uplink to downlink) interference, and the last term is the corresponding additive white Gaussian noise.

Fig. 1

The system model of a two-cell dynamic TDD network, where cell 1 has downlink transmission and simultaneously cell 2 has uplink transmission (uplink–downlink scenario)

Furthermore, the received signal at BS(2) after the receive filter corresponding to UT(2,k) is Heath and Lozano (2018),

$$\begin{aligned} \begin{aligned}&y_{2,k} ^{UL}={\mathbf {w}}_{2,k} ^{UL}\bigg (\underbrace{ {\mathbf {H}} _{2,2,k}{\mathbf {v}}_{2,k} ^{UL} x_{2,k}^{UL}}_{\text { Signal}}+\underbrace{\sum _{m\ne k} {\mathbf {H}} _{2,2,m}{\mathbf {v}}_{2,m} ^{UL} x_{2,m}^{UL}}_{\text {Intracell\, Interference}}+\\&\quad \underbrace{ \sum _{n=1} ^{K} {\mathbf {H}} _{1,2} {\mathbf {w}}_{1,n} ^{DL} x_{1,n} ^{DL}}_{ \text {Intercell\, Interference}}+\underbrace{ {\mathbf {z}}_{2,k}}_{\text {AWGN}}\bigg ), \end{aligned} \end{aligned}$$

(2)

where the first term is the desired signal sent for UT(2,k), the second term is sum of the intracell interference, the third term is sum of the intercell (downlink to uplink) interference, and ${\mathbf {z}}_{2,k}\sim {\mathcal {N}}(0, N_0 {\mathbf {I}}_{N\times N})$ is the corresponding AWGN vector. Then, the SINR at UT(1,k) would be Heath and Lozano (2018),

$$\begin{aligned} \begin{aligned}&\mathrm {SINR}_{1,k} ^{DL}=\\&\quad \dfrac{\vert {\mathbf {v}}_{1,k} ^{DL} {\mathbf {H}} _{1,1,k} ^{H} {\mathbf {w}}_{1,k} ^{DL} \vert ^2}{\sum \nolimits _{m\ne k} \vert {\mathbf {v}}_{1,k} ^{DL} {\mathbf {H}} _{1,1,k} ^{H} {\mathbf {w}}_{1,m} ^{DL} \vert ^2+\sum \nolimits _{n=1} ^{K} \vert {\mathbf {v}}_{1,k} ^{DL} {\mathbf {H}} _{2,n} ^{1,k} {\mathbf {v}}_{2,n} ^{UL} \vert ^2+ \Vert {\mathbf {v}}_{1,k} ^{DL} \Vert ^2 N_{0} }, \end{aligned} \end{aligned}$$

(3)

where the numerator is the power of the desired signal received by UT(1,k) and the denominator is the sum of the power of the intracell and intercell interference and the power of the corresponding AWGN, respectively. Moreover, the SINR corresponding to UT(2,k) is Heath and Lozano (2018),

$$\begin{aligned} \begin{aligned}&\mathrm {SINR}_{2,k} ^{UL}\\&\quad =\dfrac{\vert {\mathbf {w}}_{2,k} ^{UL} {\mathbf {H}} _{2,2,k}{\mathbf {v}}_{2,k} ^{UL} \vert ^2}{\sum \limits _{m\ne k} \vert {\mathbf {w}}_{2,k} ^{UL} {\mathbf {H}} _{2,2,m}{\mathbf {v}}_{2,m} ^{UL} \vert ^2+\sum \limits _{n=1} ^{k} \vert {\mathbf {w}}_{2,k} ^{UL} {\mathbf {H}} _{1,2} {\mathbf {w}}_{1,n} ^{DL} \vert ^2+\Vert {\mathbf {w}}_{2,k} ^{UL}\Vert ^2 N_{0}}, \end{aligned} \end{aligned}$$

(4)

where the numerator is the power of the desired signal corresponding to $\mathrm {UT}(2,k)$ received by $\mathrm {BS}(2)$ and the denominator is the sum of the power of the interference caused by other users in cell-2 and the interference caused by BS(1) and corresponding AWGN, respectively.

Table 1 The notations of the channel matrices and the beamforming vectors

In this paper, various receivers such as MRC, local MMSE and MMSE are considered for the BS in the uplink cell and the users in the downlink cell, to evaluate the performance of the proposed coordinated beamforming approaches. Employing the formulas for these receivers Chockalingam and Rajan (2014); Jayasinghe et al. (2015), the expressions for the receive filters would be as follows,

$$\begin{aligned}&{\mathbf {v}}_{1,k}^{\textit{DL},\mathrm {MRC}}=({\mathbf {H}}_{1,1,k}^{\textit{H}}{\mathbf {w}}_{1,k}^{DL})^{\textit{H}} \ \forall k, \end{aligned}$$

(5)

$$\begin{aligned}&{\mathbf {w}}_{2,k}^{\textit{UL},\mathrm {MRC}}=({\mathbf {H}}_{2,2,k}{\mathbf {v}}_{2,k}^{\textit{UL}})^{H} \ \forall k. \end{aligned}$$

(6)

$$\begin{aligned}&{\mathbf {v}}_{1,k}^{\textit{DL},\mathrm {LMMSE}}\nonumber \\&=({\mathbf {H}}_{1,1,k}^{\textit{H}}{\mathbf {w}}_{1,k}^{DL})^{\textit{H}}\left( \sum _{m=1}^{K} ({\mathbf {H}}_{1,1,k}^{\textit{H}}{\mathbf {w}}_{1,m}^{DL})({\mathbf {H}}_{1,1,k}^{\textit{H}}{\mathbf {w}}_{1,m}^{DL})^{\textit{H}}+N_{0}{\mathbf {I}}_{M}\right) ^{-1}, \end{aligned}$$

(7)

$$\begin{aligned}&{\mathbf {w}}_{2,k}^{\textit{UL},\mathrm {LMMSE}}\nonumber \\&= \quad ({\mathbf {H}}_{2,2,k}{\mathbf {v}}_{2,k}^{\textit{UL}})^{H}\left( \sum _{m=1}^{K}({\mathbf {H}}_{2,2,m}{\mathbf {v}}_{2,m}^{\textit{UL}})({\mathbf {H}}_{2,2,m}{\mathbf {v}}_{2,m}^{\textit{UL}})^{H}+N_{0}\mathrm {I_{N}}\right) ^{-1}. \end{aligned}$$

(8)

$$\begin{aligned}&{\mathbf {v}}_{1,k}^{\textit{DL},\mathrm {MMSE}}=({\mathbf {H}}_{1,1,k}^{\textit{H}}{\mathbf {w}}_{1,k}^{DL})^{\textit{H}}\Bigg (\sum _{m=1}^{K} ({\mathbf {H}}_{1,1,k}^{\textit{H}}{\mathbf {w}}_{1,m}^{DL})({\mathbf {H}}_{1,1,k}^{\textit{H}}{\mathbf {w}}_{1,m}^{DL})^{\textit{H}}+ \nonumber \\&\sum _{n=1}^{K}({\mathbf {H}}_{2,n}^{1,k}{\mathbf {v}}_{2,n}^{UL})({\mathbf {H}}_{2,n}^{1,k}{\mathbf {v}}_{2,n}^{UL})^{\textit{H}}+N_{0}{\mathbf {I}}_{M}\Bigg )^{-1}, \end{aligned}$$

(9)

$$\begin{aligned}&{\mathbf {w}}_{2,k}^{\textit{UL},\mathrm {MMSE}}=({\mathbf {H}}_{2,2,k}{\mathbf {v}}_{2,k}^{\textit{UL}})^{H}\Bigg (\sum _{m=1}^{K}({\mathbf {H}}_{2,2,m}{\mathbf {v}}_{2,m}^{\textit{UL}})({\mathbf {H}}_{2,2,m}{\mathbf {v}}_{2,m}^{\textit{UL}})^{H}\nonumber \\&\quad+ \sum _{n=1}^{K}({\mathbf {H}}_{1,2}{\mathbf {w}}_{1,n}^{\textit{DL}})({\mathbf {H}}_{1,2}{\mathbf {w}}_{1,n}^{\textit{DL}})^{H}+N_{0}\mathrm {I_{N}}\Bigg )^{-1}. \end{aligned}$$

(10)

3 Sum Power Minimization Problem in MIMO Systems

In this Section, we formulate the sum power minimization problem to design the coordinated beamforming vectors. The criteria of the problem is the sum power of the beamforming vectors, and as the constraints of the optimization problem, the SINR of each of the users is considered to be more than a specified threshold; then, the optimization problem would be,

$$\begin{aligned} \begin{array}{cl} \underset{{\mathbf {w}}_{\mathrm {1},k} ^{DL},{\mathbf {v}}_{2,k} ^{UL}\forall k }{\min } & \sum \limits_{k=1}^{K}\left( \Vert {\mathbf {w}}_{1,k} ^{DL} \Vert ^{2}+ \Vert {\mathbf {v}}_{2,k} ^{UL}\Vert ^{2} \right) \\ \mathrm {s.t.} &\mathrm {SINR}_{1,k}^{DL} \ge \gamma _{1,k} \quad k=1,\dots ,K , \\ &\mathrm {SINR}_{2,k}^{UL} \ge \gamma _{2,k} \quad k=1,\dots ,K, \end{array} \end{aligned}$$

(11)

where $\gamma _{1,k}$ and $\gamma _{2,k}$ are thresholds of SINRs corresponding to $\mathrm {UT(1,k)}$ and $\mathrm {UT}(2,k)$, respectively. Replacing the SINR definitions from (3) and (4), and after some mathematical calculations, problem (11) would be,

$$\begin{aligned}&\underset{{\mathbf {w}_{1,k} ^{DL},\mathbf {v}_{2,k} ^{UL} \forall k}}{\min } {\sum _{k=1}^{K}\left( \mathbf {w}_{1,k} ^{DL,H} \mathbf {w}_{1,k } ^{DL}+\mathbf {v}_{2,k} ^{UL,H}\mathbf {v}_{2,k} ^{UL}\right) } \nonumber \\&\qquad -\frac{1}{\gamma _{1,k}}\mathbf {w}_{1,k} ^{DL,H}\mathbf {H} _{1,1,k} \mathbf {v}_{1,k} ^{DL,H} \mathbf {v}_{1,k} ^{DL} \mathbf {H} _{1,1,k} ^{H} \mathbf {w}_{1,k} ^{DL}+ \nonumber \\&\qquad +\sum _{m\ne k} \mathbf {w}_{1,m} ^{DL,H}\mathbf {H} _{1,1,k} \mathbf {v}_{1,k} ^{DL,H} \mathbf {v}_{1,k} ^{DL} \mathbf {H} _{1,1,k} ^{H} \mathbf {w}_{1,m} ^{DL}+ \nonumber \\&\qquad +\sum _{n=1} ^{K} \mathbf {v}_{2,n} ^{UL,H}\mathbf {H} _{2,n} ^{1,k,H}\mathbf {v}_{1,k}^{DL,H} \mathbf {v}_{1,k} ^{DL} \mathbf {H} _{2,n} ^{1,k} \mathbf {v}_{2,n} ^{UL} +\nonumber \\&\qquad + \Vert \mathbf {v}_{1,k} ^{DL} \Vert ^2 N_{0} {\le 0 \quad k=1,\dots ,K }\nonumber \\&\qquad -\frac{1}{ \gamma _{2,k}}\mathbf {v}_{2,k} ^{UL,H}\mathbf {H} _{2,2,k}^{H} \mathbf {w}_{2,k} ^{UL,H} \mathbf {w}_{2,k} ^{UL} \mathbf {H} _{2,2,k}\mathbf {v}_{2,k} ^{UL} + \nonumber \\&\qquad +\sum _{m\ne k} \mathbf {v}_{2,m} ^{UL,H}\mathbf {H} _{2,2,m}^{H} \mathbf {w}_{2,k} ^{UL,H} \mathbf {w}_{2,k} ^{UL} \mathbf {H} _{2,2,m}\mathbf {v}_{2,m} ^{UL}+ \nonumber \\&\quad +\sum _{n=1} ^{K}\mathbf {w}_{1,n} ^{DL,H}\mathbf {H} _{1,2}^{H} \mathbf {w}_{2,k} ^{UL,H} \mathbf {w}_{2,k} ^{UL} \mathbf {H} _{1,2} \mathbf {w}_{1,n} ^{DL} +\nonumber \\&\quad +\Vert \mathbf {w}_{2,k} ^{UL}\Vert ^2 N_{0}{\le 0 \quad k=1,\dots ,K. } \end{aligned}$$

(12)

It must be noted that the problem in (12) is nonconvex; however, it could be rewritten as a second order cone problem; then, the strong duality holds (Wiesel et al. 2006), and Karush-Kuhn-Tucker (KKT) conditions are sufficient (Boyd and Vandenberghe 2004). Hence, in order to solve the problem in (12), we evaluate the Lagrangian function and investigate the KKT conditions.

Based on the definition of the Lagrangian of the optimization problem in Boyd and Vandenberghe (2004), the Lagrangian of the problem (12) would be,

$$\begin{aligned}&L\big (\mathbf{w }_{\mathrm{1}},\mathbf{v }_{\mathrm{2}},{{\varvec{\lambda }}}_{\mathrm{1}},{{\varvec{\lambda }}}_{\mathrm{2}}\big )=\sum _{k=1}^{K}\bigg (\mathbf{w }_{1,k} ^{DL,H} \mathbf{w }_{1,k } ^{DL}+ \mathbf{v }_{2,k} ^{UL,H}\mathbf{v }_{2,k} ^{UL}\nonumber \\&\qquad +\frac{\lambda _{\mathrm{1},k}}{N}\big (-(\mathrm{1}+\frac{\mathrm{1}}{\gamma _{\mathrm{1},k}})\mathbf{w }_{1,k} ^{DL,H}\mathbf{H } _{1,1,k} \mathbf{v }_{1,k} ^{DL,H} \mathbf{v }_{1,k} ^{DL} \mathbf{H } _{1,1,k} ^{H} \mathbf{w }_{1,k} ^{DL}\nonumber \\&\qquad +\sum _{m=1}^{K} \mathbf{w }_{1,m} ^{DL,H}\mathbf{H } _{1,1,k} \mathbf{v }_{1,k} ^{DL,H} \mathbf{v }_{1,k} ^{DL} \mathbf{H } _{1,1,k} ^{H} \mathbf{w }_{1,m} ^{DL}\nonumber \\&\qquad +\sum _{n=1} ^{K} \mathbf{v }_{2,n} ^{UL,H}\mathbf{H } _{2,n} ^{1,k,H}\mathbf{v }_{1,k}^{DL,H} \mathbf{v }_{1,k} ^{DL} \mathbf{H } _{2,n} ^{1,k} \mathbf{v }_{2,n} ^{UL} + \Vert \mathbf{v }_{1,k} ^{DL} \Vert ^2 N_{\mathrm{0}}\big )\nonumber \\&\qquad +\frac{\lambda _{\mathrm{2},k}}{M}\big (-(\mathrm{1}+\frac{\mathrm{1}}{ \gamma _{\mathrm{2},k}})\mathbf{v }_{2,k} ^{UL,H}\mathbf{H } _{2,2,k}^{H} \mathbf{w }_{2,k} ^{UL,H} \mathbf{w }_{2,k} ^{UL} \mathbf{H } _{2,2,k}\mathbf{v }_{2,k} ^{UL} \nonumber \\&\qquad +\sum _{m=1}^{K} \mathbf{v }_{2,m} ^{UL,H}\mathbf{H } _{2,2,m}^{H} \mathbf{w }_{2,k} ^{UL,H} \mathbf{w }_{2,k} ^{UL} \mathbf{H } _{2,2,m}\mathbf{v }_{2,m} ^{UL}\nonumber \\&\qquad +\sum _{n=1} ^{K}\mathbf{w }_{1,n} ^{DL,H}\mathbf{H } _{1,2}^{H} \mathbf{w }_{2,k} ^{UL,H} \mathbf{w }_{2,k} ^{UL} \mathbf{H } _{1,2} \mathbf{w }_{1,n} ^{DL} +\Vert \mathbf{w }_{2,k} ^{UL}\Vert ^2 N_{\mathrm{0}}\big )\bigg ), \end{aligned}$$

(13)

where ${\mathbf {w}}_{\mathrm{1}}=\left[ {\mathbf {w}}_{\mathrm{1},\mathrm{1}}^{DL},\dots ,{\mathbf {w}}_{\mathrm{1},K}^{DL}\right] ^{T}$, ${\mathbf {v}}_{\mathrm{2}}=\left[ {\mathbf {v}}_{\mathrm{2},\mathrm{1}}^{UL},\dots ,{\mathbf {v}}_{\mathrm{2},K}^{UL}\right] ^{T}$, ${\varvec{\lambda }}_{\mathrm{1}}=\left[ \lambda _{\mathrm{1},\mathrm{1}},\dots ,\lambda _{\mathrm{1},K}\right] ^{T}$ and ${\varvec{\lambda }}_{\mathrm{2}}=\left[ \lambda _{\mathrm{2},\mathrm{1}},\dots ,\lambda _{\mathrm{2},K}\right] ^{T}$, and the coefficients $\frac{1}{N}$ and $\frac{1}{M}$ before the Lagrangian multipliers are lied to simplify the formulations in the following, especially in mMIMO scenario in Sect. 4 (See Appendix 8.3).

Based on the KKT conditions, the gradient of the Lagrangian with respect to main variables in optimal point is equal to zero, then the following conditions are resulted in the problem,

$$\begin{aligned}&\dfrac{\partial L\big ({\mathbf {w}}_{\mathrm{1}},{\mathbf {v}}_{\mathrm{2}},\mathbf {{\varvec{\lambda }}}_{\mathrm{1}},\mathbf {{\varvec{\lambda }}}_{\mathrm{2}}\big )}{\partial {\mathbf {w}}_{1,k} ^{DL} }=\mathrm{0} \quad k=1,\dots ,K, \end{aligned}$$

(14)

$$\begin{aligned}&\dfrac{\partial L\big ({\mathbf {w}}_{\mathrm{1}},{\mathbf {v}}_{\mathrm{2}},\mathbf {{\varvec{\lambda }}}_{\mathrm{1}},\mathbf {{\varvec{\lambda }}}_{\mathrm{2}}\big )}{\partial {\mathbf {v}}_{2,k} ^{UL} }=0, \quad k=1,\dots ,K, \end{aligned}$$

(15)

which leads to,

$$\begin{aligned}&\bigg (\mathbf{I}_{N}-\frac{\lambda _{\mathrm{1},k}}{N}\big (1+\frac{1}{\gamma _{1,k}}\big ){\mathbf {H}} _{1,1,k} {\mathbf {v}}_{1,k} ^{DL,H} {\mathbf {v}}_{1,k} ^{DL}{\mathbf {H}} _{1,1,k} ^{H}\nonumber \\&\qquad +\sum _{m=1}^{K}\big (\frac{\lambda _{\mathrm{1},m}}{N}{\mathbf {H}} _{1,1,m} {\mathbf {v}}_{1,m} ^{DL,H} {\mathbf {v}}_{1,m} ^{DL} {\mathbf {H}} _{1,1,m} ^{H} \nonumber \\&\qquad +\frac{\lambda _{\mathrm{2},m}}{M} {\mathbf {H}} _{1,2}^{H} {\mathbf {w}}_{2,m} ^{UL,H} {\mathbf {w}}_{2,m} ^{UL} {\mathbf {H}} _{1,2}\big )\bigg ){\mathbf {w}}_{1,k} ^{DL}=\mathrm{0} \quad k=1,\dots ,K, \end{aligned}$$

(16)

$$\begin{aligned}&\bigg (\mathbf{I}_{M}-\frac{ \lambda _{2,k}}{M}\big (1+\frac{1}{ \gamma _{2,k}}\big ){\mathbf {H}} _{\mathrm{{2,2}},k}^{H} {\mathbf {w}}_{\mathrm{{2}},k} ^{UL,H} {\mathbf {w}}_{\mathrm{{2}},k} ^{UL} {\mathbf {H}} _{\mathrm{{2,2}},k}\nonumber \\&\qquad +\sum _{n=1}^{K}\big ( \frac{ \lambda _{2,n}}{M}{\mathbf {H}} _{\mathrm{{2,2}},k}^{H} {\mathbf {w}}_{\mathrm{{2}},n} ^{UL,H} {\mathbf {w}}_{\mathrm{{2}},n} ^{UL} {\mathbf {H}} _{\mathrm{{2,2}},k}\nonumber \\&\qquad +\frac{ \lambda _{1,n}}{N}{\mathbf {H}} _{\mathrm{{2}},k} ^{\mathrm{{1}},n,H}{\mathbf {v}}_{\mathrm{{1}},n}^{DL,H} {\mathbf {v}}_{\mathrm{{1}},n} ^{DL} {\mathbf {H}} _{\mathrm{{2}},k} ^{\mathrm{{1}},n}\big )\bigg ){\mathbf {v}}_{\mathrm{{2}},k} ^{UL}=0, \quad k=1,\dots ,K. \end{aligned}$$

(17)

Then, by some calculation and simplification on (16), we obtain the optimal beamforming vector corresponding to $\mathrm {UT}(1,k)$ as follows,

$$\begin{aligned} \begin{aligned}&{\mathbf {w}}_{\mathrm{{1}},k} ^{DL}=\dfrac{\sqrt{p_{1,k}}\frac{\lambda _{1,k}}{N}\big (1+\frac{1}{\gamma _{1,k}}\big )\bigg ( \mathbf{I}_{N}+{\varvec{\Sigma }}_{1}\bigg )^{-1} {\mathbf {H}} _{\mathrm{{1,1}},k} {\mathbf {v}}_{\mathrm{{1}},k} ^{DL,H}}{\Vert \frac{\lambda _{1,k}}{N}\big (1+\frac{1}{\gamma _{1,k}}\big )\big (\mathbf{I}_{N}+{\varvec{\Sigma }}_{1}\big )^{-1} {\mathbf {H}} _{\mathrm{{1,1}},k} {\mathbf {v}}_{\mathrm{{1}},k} ^{DL,H}\Vert }. \\&\quad k=1,\dots ,K, \end{aligned} \end{aligned}$$

(18)

where,

$$\begin{aligned} \begin{aligned} {\varvec{\Sigma }}_{1}=&\sum _{m=1}^{K}\bigg (\frac{\lambda _{\mathrm{1},m}}{N}{\mathbf {H}} _{\mathrm{{1,1}},m} {\mathbf {v}}_{\mathrm{{1}},m} ^{DL,H} {\mathbf {v}}_{\mathrm{{1}},m} ^{DL} {\mathbf {H}} _{\mathrm{{1,1}},m} ^{H}+ \\&+\frac{\lambda _{\mathrm{2},m}}{M} {\mathbf {H}} _{\mathrm{{1,2}}}^{H} {\mathbf {w}}_{\mathrm{{2}},m} ^{UL,H} {\mathbf {w}}_{\mathrm{{2}},m} ^{UL} {\mathbf {H}} _{\mathrm{{1,2}}}\bigg ), \end{aligned} \end{aligned}$$

(19)

and $p_{1,k}$ is,

$$\begin{aligned} \begin{aligned}&p_{1,k}=({\mathbf {v}}_{\mathrm{{1}},k} ^{DL}{\mathbf {H}} _{\mathrm{{1,1}},k} ^{H}{\mathbf {w}}_{\mathrm{{1}},k} ^{DL})^2\\&\quad {\big \Vert \frac{\lambda _{1,k}}{N}\big (1+\frac{1}{\gamma _{1,k}}\big )\big (\mathbf{I}_{N}+{\varvec{\Sigma }}_{1}\big )^{-1} {\mathbf {H}} _{\mathrm{{1,1}},k} {\mathbf {v}}_{\mathrm{{1}},k} ^{DL,H}\big \Vert ^2 }, \quad k=1,\dots ,K. \end{aligned} \end{aligned}$$

(20)

Moreover, simplifying (17) we find the optimal ${\mathbf {v}}_{\mathrm{{2}},k} ^{UL}$ as,

$$\begin{aligned} \begin{aligned}&{\mathbf {v}}_{\mathrm{{2}},k} ^{UL}=\dfrac{\sqrt{p_{2,k}}\frac{\lambda _{2,k}}{M}\big (1+\frac{1}{ \gamma _{2,k}}\big )\bigg ( \mathbf{I}_{M}+{\varvec{\Sigma }}_{2,k}\bigg )^{-1}{\mathbf {H}} _{\mathrm{{2,2}},k}^{H} {\mathbf {w}}_{\mathrm{{2}},k} ^{UL,H}}{\Vert \frac{\lambda _{2,k}}{M}\big (1+\frac{1}{ \gamma _{2,k}}\big )\big ( \mathbf{I}_{M}+{\varvec{\Sigma }}_{2,k}\big )^{-1}{\mathbf {H}} _{\mathrm{{2,2}},k}^{H} {\mathbf {w}}_{\mathrm{{2}},k} ^{UL,H} \Vert }, \\&\quad k=1,\dots ,K, \end{aligned} \end{aligned}$$

(21)

where

$$\begin{aligned} \begin{aligned} {\varvec{\Sigma }}_{2,k}=&\sum _{n=1}^{K}\bigg ( \frac{\lambda _{2,n}}{M}{\mathbf {H}} _{\mathrm{{2,2}},k}^{H} {\mathbf {w}}_{\mathrm{{2}},n} ^{UL,H} {\mathbf {w}}_{\mathrm{{2}},n} ^{UL} {\mathbf {H}} _{\mathrm{{2,2}},k}\\&+\frac{\lambda _{1,n}}{N}{\mathbf {H}} _{\mathrm{{2}},k} ^{\mathrm{{1}},n,H}{\mathbf {v}}_{\mathrm{{1}},n}^{DL,H} {\mathbf {v}}_{\mathrm{{1}},n} ^{DL} {\mathbf {H}} _{\mathrm{{2}},k} ^{\mathrm{{1}},n}\bigg ), \\&k=1,\dots ,K, \end{aligned} \end{aligned}$$

(22)

and

$$\begin{aligned} \begin{aligned} p_{2,k}=&({\mathbf {w}}_{\mathrm{{2}},k} ^{UL} {\mathbf {H}} _{\mathrm{{2,2}},k}{\mathbf {v}}_{\mathrm{{2}},k} ^{UL})^{2}\\&{\big \Vert \frac{\lambda _{2,k}}{M}\big (1+\frac{1}{ \gamma _{2,k}}\big )\bigg (\mathbf{I}_{M}+{\varvec{\Sigma }}_{2,k}\bigg )^{-1}{\mathbf {H}} _{\mathrm{{2,2}},k}^{H} {\mathbf {w}}_{\mathrm{{2}},k} ^{UL,H} \big \Vert ^{2}},\\&k=1,\dots ,K. \end{aligned} \end{aligned}$$

(23)

In addition, we use (16) and (17) to find the Lagrangian multipliers and consequently the following equation system is obtained for them,

$$\begin{aligned} \begin{aligned} \lambda _{1,k}&=\dfrac{1}{\frac{1}{N}\big (1+\frac{1}{\gamma _{1,k}}\big ){\mathbf {v}}_{\mathrm{{1}},k} ^{DL} {\mathbf {H}} _{\mathrm{{1,1}},k}^{H}\big (\mathbf{I}_{N}+{\varvec{\Sigma }}_{1}\big )^{-1} {\mathbf {H}} _{\mathrm{{1,1}},k} {\mathbf {v}}_{\mathrm{{1}},k} ^{DL,H}}, \\&\quad k=1,\dots ,K, \\ \lambda _{2,k}&=\dfrac{1}{\frac{1}{M}\big (1+\frac{1}{ \gamma _{2,k}}\big ){\mathbf {w}}_{\mathrm{{2}},k} ^{UL}{\mathbf {H}} _{\mathrm{{2,2}},k}\big (\mathbf{I}_{M}+{\varvec{\Sigma }}_{2,k}\big )^{-1}{\mathbf {H}} _{\mathrm{{2,2}},k}^{H} {\mathbf {w}}_{\mathrm{{2}},k} ^{UL,H}},\\&k=1,\dots ,K. \end{aligned} \end{aligned}$$

(24)

Since the Lagrangian multipliers, i.e., $\lambda _{1,k}$ and $\lambda _{2,k}$ are appeared in the equations of ${\varvec{\Sigma }}_{1}$ and ${\varvec{\Sigma }}_{2,k}$, Eq. (24) is a system of simultaneous equations with two unknown variables. In order to solve this equation system, we state the following theorem.

Theorem 1

Assume that function $f: {\mathbb {R}}^{2K}\rightarrow {\mathbb {R}}^{2K}$ be defined as $f({\varvec{\lambda }}_1,{\varvec{\lambda }}_2)=[f_{1,1},\dots ,f_{1,K},f_{2,1},\dots ,f_{2,K}]^{T}$, where for all k,

$$\begin{aligned} \begin{aligned}&f_{1,k}({\varvec{\lambda }}_1,{\varvec{\lambda }}_2)\\&\qquad = \dfrac{1}{\frac{1}{N}\big (1+\frac{1}{\gamma _{1,k}}\big ){\mathbf {v}}_{\mathrm{{1}},k} ^{DL} {\mathbf {H}} _{\mathrm{{1,1}},k}^{H}\big (\mathbf{I}_{N}+{\varvec{\Sigma }}_{1}\big )^{-1} {\mathbf {H}} _{\mathrm{{1,1}},k} {\mathbf {v}}_{\mathrm{{1}},k} ^{DL,H}}, \\&\qquad k=1,\dots ,K,\\&\qquad f_{2,k}({\varvec{\lambda }}_1,{\varvec{\lambda }}_2)\\&\quad =\dfrac{1}{\frac{1}{M}\big (1+\frac{1}{ \gamma _{2,k}}\big ){\mathbf {w}}_{\mathrm{{2}},k} ^{UL}{\mathbf {H}} _{\mathrm{{2,2}},k}\big (\mathbf{I}_{M}+{\varvec{\Sigma }}_{2,k}\big )^{-1}{\mathbf {H}} _{\mathrm{{2,2}},k}^{H} {\mathbf {w}}_{\mathrm{{2}},k} ^{UL,H}},\\&\qquad k=1,\dots ,K, \end{aligned} \end{aligned}$$

then the fixed point iteration algorithm (See Algorithm 2.2 in Burden and Faires (2010)) for finding the fixed point of function f converges to a unique solution.

Proof

See Appendix 8.1. $\square$

Equation (24) is actually the equation for finding the fixed point of the defined function in Theorem 1 and therefore could be solved using the fixed point iteration algorithm.

It must be noted that variables $p_{1,k}$ and $p_{2,k}$ defined in (20) and (23) are the power of the beamforming vectors ${\mathbf {w}}_{\mathrm{{1}},k} ^{DL}$ and ${\mathbf {v}}_{\mathrm{{2}},k} ^{UL}$, respectively, and in order to find them, we take attention to the other KKT condition, which is,

$$\begin{aligned} \begin{aligned} \lambda _{1,k}(\gamma _{1,k}-\mathrm {SINR}_{1,k}^{DL} )&=0, k=1,\dots ,K, \\ \lambda _{2,k}(\gamma _{2,k}-\mathrm {SINR}_{2,k}^{UL} )&=0, k=1,\dots ,K. \end{aligned} \end{aligned}$$

(25)

Moreover, based on (18) and (21) each of the beamforming vectors is proportional to one of the Lagrangian multipliers; then, none of the Lagrangian multipliers could be equal to zero. Hence, all the inequality constraints would be forced to equality. Therefore, if the normalized beamforming vectors be denoted by ${\hat{\mathbf{w}}}_{1,k}^{DL}$ and ${\hat{\mathbf{v}}}_{2,k}^{UL}$, the following equations would be satisfied,

$$\begin{aligned} \begin{aligned}&\frac{p_{\mathrm{{1}},k}}{\gamma _{1,k}} \vert {\hat{\mathbf{v}}}_{\mathrm{{1}},k} ^{DL} {\mathbf {H}} _{\mathrm{{1,1}},k} ^{H} {\hat{\mathbf{w}}}_{\mathrm{{1}},k} ^{DL} \vert ^2-\sum _{m\ne k}p_{\mathrm{{1}},m} \vert {\hat{\mathbf{v}}}_{\mathrm{{1}},k} ^{DL} {\mathbf {H}} _{\mathrm{{1,1}},k} ^{H} {\hat{\mathbf{w}}}_{\mathrm{{1}},m} ^{DL} \vert ^2-\\&\quad \sum _{n=\mathrm {1}} ^{K}p_{\mathrm{{2}},n} \vert {\hat{\mathbf{v}}}_{\mathrm{{1}},k} ^{DL} {\mathbf {H}} _{\mathrm{{2}},n} ^{\mathrm{{1}},k} {\hat{\mathbf{v}}}_{\mathrm{{2}},n} ^{UL} \vert ^2= \Vert {\hat{\mathbf{v}}}_{\mathrm{{1}},k} ^{DL} \Vert ^2 N_{0} \quad k=1,\dots ,K,\\&\quad \frac{p_{\mathrm{{2}},k}}{\gamma _{2,k}}\vert {\hat{\mathbf{w}}}_{\mathrm{{2}},k} ^{UL} {\mathbf {H}} _{\mathrm{{2,2}},k}{\hat{\mathbf{v}}}_{\mathrm{{2}},k} ^{UL} \vert ^2-\sum _{m\ne k}p_{\mathrm{{2}},m} \vert {\hat{\mathbf{w}}}_{\mathrm{{2}},k} ^{UL} {\mathbf {H}} _{\mathrm{{2,2}},m}{\hat{\mathbf{v}}}_{\mathrm{{2}},m} ^{UL} \vert ^2-\\&\quad \sum _{n=\mathrm {1}} ^{k}p_{\mathrm{{1}},n} \vert {\hat{\mathbf{w}}}_{\mathrm{{2}},k} ^{UL} {\mathbf {H}} _{\mathrm{{1,2}}} {\hat{\mathbf{w}}}_{\mathrm{{1}},n} ^{DL} \vert ^2= \Vert {\hat{\mathbf{w}}}_{\mathrm{{2}},k} ^{UL}\Vert ^2 N_{0} \quad k=1,\dots ,K, \end{aligned} \end{aligned}$$

(26)

which form a system of 2K linear equations with 2K unknowns of $p_{i,k}$s, where $i=1,2$ and $\quad k=1,\dots ,K$. In order to solve the equation system (26), we write it as follows,

$$\begin{aligned} {\mathbf {F}}\begin{bmatrix} p_{1,1}\\ \vdots \\ p_{1,K}\\ p_{2,1}\\ \vdots \\ p_{2,K} \end{bmatrix}=\begin{bmatrix} \Vert {\hat{\mathbf{v}}}_{\mathrm{{1}},1} ^{DL} \Vert ^2 N_{0}\\ \vdots \\ \Vert {\hat{\mathbf{v}}}_{\mathrm{{1}},K} ^{DL} \Vert ^2 N_{0}\\ \Vert {\hat{\mathbf{w}}}_{\mathrm{{2}},1} ^{UL}\Vert ^2 N_{0}\\ \vdots \\ \Vert {\hat{\mathbf{w}}}_{\mathrm{{2}},K} ^{UL}\Vert ^2 N_{0} \end{bmatrix}, \end{aligned}$$

(27)

where matrix ${\mathbf {F}}$ is,

$$\begin{aligned} {\mathbf {F}}= \begin{bmatrix} F^{1,1} & F^{1,2} \\ F^{2,1} & F^{2,2} \end{bmatrix}, \end{aligned}$$

(28)

and its components satisfy the following conditions,

$$\begin{aligned}&F_{k,m}^{1,1}={\left\{ \begin{array}{ll} \frac{1}{\gamma _{1,k}}\vert {\hat{\mathbf{v}}}_{\mathrm{{1}},k} ^{DL} {\mathbf {H}} _{\mathrm{{1,1}},k} ^{H} {\hat{\mathbf{w}}}_{\mathrm{{1}},k} ^{DL} \vert ^2 & m=k \\ -\vert {\mathbf {v}}_{\mathrm{{1}},k} ^{DL} {\mathbf {H}} _{\mathrm{{1,1}},k} ^{H} {\hat{\mathbf{w}}}_{\mathrm{{1}},m} ^{DL} \vert ^2 & m\ne k \end{array}\right. }, \end{aligned}$$

(29)

$$\begin{aligned}&F_{k,m}^{1,2}=-\vert {\hat{\mathbf{v}}}_{\mathrm{{1}},k} ^{DL} {\mathbf {H}} _{\mathrm{{2}},m} ^{\mathrm{{1}},k} {\hat{\mathbf{v}}}_{\mathrm{{2}},m} ^{UL} \vert ^2 , \end{aligned}$$

(30)

$$\begin{aligned}&F_{k,m}^{2,1}=-\vert {\hat{\mathbf{w}}}_{\mathrm{{2}},k} ^{UL} {\mathbf {H}} _{\mathrm{{1,2}}} {\hat{\mathbf{w}}}_{\mathrm{{1}},m} ^{DL} \vert ^2, \end{aligned}$$

(31)

$$\begin{aligned}&F_{k,m}^{2,2}= {\left\{ \begin{array}{ll} \frac{1}{\gamma _{2,k}}\vert {\hat{\mathbf{w}}}_{\mathrm{{2}},k} ^{UL} {\mathbf {H}} _{\mathrm{{2,2}},k}{\hat{\mathbf{v}}}_{\mathrm{{2}},k} ^{UL} \vert ^2 & m=k \\ -\vert {\hat{\mathbf{w}}}_{\mathrm{{2}},k} ^{UL} {\mathbf {H}} _{\mathrm{{2,2}},m}{\hat{\mathbf{v}}}_{\mathrm{{2}},m} ^{UL} \vert ^2 & m\ne k \end{array}\right. }, \end{aligned}$$

(32)

then,

$$\begin{aligned} \begin{bmatrix} p_{1,1}\\ \vdots \\ p_{1,K}\\ p_{2,1}\\ \vdots \\ p_{2,K} \end{bmatrix}={\mathbf {F}}^{-1}\begin{bmatrix} \Vert {\hat{\mathbf{v}}}_{\mathrm{{1}},1} ^{DL} \Vert ^2 N_{0}\\ \vdots \\ \Vert {\hat{\mathbf{v}}}_{\mathrm{{1}},K} ^{DL} \Vert ^2 N_{0}\\ \Vert {\hat{\mathbf{w}}}_{\mathrm{{2}},1} ^{UL}\Vert ^2 N_{0}\\ \vdots \\ \Vert {\hat{\mathbf{w}}}_{\mathrm{{2}},K} ^{UL}\Vert ^2 N_{0} \end{bmatrix}. \end{aligned}$$

(33)

So far the equations are found for the receive filters, the beamforming vectors, the Lagrangian multipliers and the power of the beamforming vectors, which form a system of equations with multiple unknowns. Now, we propose an iterative algorithm (Algorithm 1) to solve this equation system. In this algorithm, first the initial values are set for the receive filters, then the evaluation of the Lagrangian multipliers, beamforming vectors and receive filters are iterated, respectively, until the sum transmit power of the beamforming vectors converges to a constant value. Finally, the computation of the power of the beamforming vectors happens out of the iteration process, and regarding the equivalence of Eqs. (25) and (33), the values of the SINRs would become the target values, i.e., $\gamma _{1,k}$ and $\gamma _{2,k}$ $k=1,\dots , K$. We must note that the process of obtaining the Lagrangian multipliers solves the equation system (24) using the fixed point iteration algorithm.

4 Sum Power Minimization Problem in mMIMO Networks

In this section, it is assumed that the BSs and the users are equipped with mMIMO antennas. Increasing the number of antennas naturally increases the computational complexity of Algorithm 1, and the algorithm would become inappropriate for coordinated beamforming in the mMIMO scenario. Accordingly, the aim is to propose a simplified coordinated beamforming algorithm for such system. Obviously, the complexity of the fixed point iteration used to find the Lagrangian multipliers is sensitive to the number of antennas, and regarding (24), it could be observed that the Lagrangian multipliers depend on the instantaneous channel state information; therefore, when this information changes, a complex process to find the Lagrangian multipliers should be repeated in the main iteration part of the Algorithm. Accordingly, we find a new equation system for the Lagrangian multipliers, which only depends on the channel statistics and thus should not be necessarily solved in each run, and even in the main iteration, of the algorithm. In addition, in Sect. 6, we will show that the new equation system could be solved with lower complexity than the fixed point iteration in Algorithm 1. As a prerequisite, the variances of the elements of the channel matrices are denoted as shown in Table 2.

Table 2 The variances of the channels

First, in the following theorem, we use the linear algebra to find equivalent terms for the denominator terms of the Lagrangian multiplies in Eq. (24), and therefore, we obtain a new equation for the Lagrangian multipliers.

Theorem 2

Let for $k=1,\dots , K$:

$$\begin{aligned} \begin{aligned} {\varvec{\Sigma }}_{1,k}^{\prime }&\triangleq {\varvec{\Sigma }}_{1}-\frac{\lambda _{\mathrm{1},k}}{N}{\mathbf {H}} _{\mathrm{{1,1}},k} {\mathbf {v}}_{\mathrm{{1}},k} ^{DL,H} {\mathbf {v}}_{\mathrm{{1}},k} ^{DL} {\mathbf {H}} _{\mathrm{{1,1}},k} ^{H}, \\ {\varvec{\Sigma }}_{2,k}^{\prime }&\triangleq {\varvec{\Sigma }}_{2,k}-\frac{\lambda _{2,k}}{M}{\mathbf {H}} _{\mathrm{{2,2}},k}^{H} {\mathbf {w}}_{\mathrm{{2}},k} ^{UL,H} {\mathbf {w}}_{\mathrm{{2}},k} ^{UL} {\mathbf {H}} _{\mathrm{{2,2}},k}, \end{aligned} \end{aligned}$$

(34)

then if $N,M\longrightarrow \infty$ the following equation for the Lagrangian multipliers $\lambda _{1,k}$, $k=1,\dots ,K$ is resulted from (24),

$$\begin{aligned} \lambda _{1,k}=\dfrac{\gamma _{1,k}}{m_{{\varvec{\Sigma }}_{1,k}^{\prime }}(-1)\Vert {\mathbf {v}}_{1,k}^{DL}\Vert ^{2}\sigma _{1,1,k}^{2}}, \end{aligned}$$

(35)

where $m_{{\varvec{\Sigma }}_{1,k}^{\prime }}(-1)=\frac{1}{N}tr\{\big ({\varvec{\Sigma }}_{1,k}^{\prime }+\mathbf{I}_{N}\big )^{-1}\}$. We could also approximate $\lambda _{2,k}$, $k=1,\dots ,K$ by some mild assumptions (explained in the proof of the theorem) as follows,

$$\begin{aligned} \lambda _{2,k} \simeq \dfrac{\gamma _{2,k}}{m_{{\varvec{\Sigma }}_{2,k}^{\prime }}(-1)\Vert {\mathbf {w}}_{2,k}^{UL}\Vert ^{2}\sigma _{2,2,k}^{2}}, \end{aligned}$$

(36)

where $m_{{\varvec{\Sigma }}_{2,k}^{\prime }}(-1)=\frac{1}{M}tr\{\big ({\varvec{\Sigma }}_{2,k}^{\prime }+\mathbf{I}_{M}\big )^{-1}\}$.

Proof

See Appendix 8.2. $\square$

We must note that $m_{{\varvec{\Sigma }}_{1,k}^{\prime }}(-1)$ and $m_{{\varvec{\Sigma }}_{2,k}^{\prime }}(-1)$ appeared in Eqs. (35) and (36), depend on the channel coefficients; Therefore, we use the following theorem to obtain an equation system to derive $m_{{\varvec{\Sigma }}_{1,k}^{\prime }}(-1)$ and $m_{{\varvec{\Sigma }}_{2,k}^{\prime }}(-1)$, which only depends on the variances of the channel coefficients.

Theorem 3

Assume that for $k=1,\dots ,K$, Eq. (34) is valid and $m_{{\varvec{\Sigma }}_{1,k}^{\prime }}(-1)=\frac{1}{N}tr\{\big ({\varvec{\Sigma }}_{1,k}^{\prime }+\mathbf{I}_{N}\big )^{-1}\}$ and $m_{{\varvec{\Sigma }}_{2,k}^{\prime }}(-1)=\frac{1}{M}tr\{\big ({\varvec{\Sigma }}_{2,k}^{\prime }+\mathbf{I}_{M}\big )^{-1}\}$, then when $N,M,K\longrightarrow \infty$ and $M=N$, we have the following,

$$\begin{aligned} m_{{\varvec{\Sigma }}_{1,k}^{\prime }}(-1)&\mathop {\longrightarrow }\limits _{N,K\longrightarrow \infty }^{a.s.}{\bar{m}}_{{\varvec{\Sigma }}_{1,k}^{\prime }}(-1), \\ m_{{\varvec{\Sigma }}_{2,k}^{\prime }}(-1)&\mathop {\longrightarrow }\limits _{N,K\longrightarrow \infty }^{a.s.}{\bar{m}}_{{\varvec{\Sigma }}_{2,k}^{\prime }}(-1), \end{aligned}$$

where ${\bar{m}}_{{\varvec{\Sigma }}_{1,k}^{\prime }}(-1)$ and ${\bar{m}}_{{\varvec{\Sigma }}_{2,k}^{\prime }}(-1)$ satisfy the following fixed point equations,

$$\begin{aligned}&{{\bar{m}}}_{{\varvec{\Sigma }}_{1,k}^{\prime } } ( -1) = \left( {\frac{1}{N}\sum \limits _{i \ne k}^K {\frac{{\lambda _{1,i} \left\| {\mathbf{v}_{1,i}^{DL} } \right\| ^2 \sigma _{1,1,i}^2 }}{{1 + \lambda _{1,i} \left\| {\mathbf{v}_{1,i}^{DL} } \right\| ^2 \sigma _{1,1,i}^2 {{\bar{m}}}_{{\varvec{\Sigma }}_{1,k}^{\prime } } (-1)}}} } \right. \nonumber \\&\qquad \left. { + \frac{1}{M}\sum \limits _{j = 1}^K {\frac{{\lambda _{2,j} \left\| {\mathbf{w}_{2,j}^{UL} } \right\| ^2 \sigma _{1,2}^2 }}{{1 + \lambda _{2,j} \left\| {\mathbf{w}_{2,j}^{UL} } \right\| ^2 \sigma _{1,2}^2 \bar{m}_{{\varvec{\Sigma }}_{1,k}^{\prime } } ( -1)}} + 1} } \right) ^{ - 1}, \end{aligned}$$

(37)

$$\begin{aligned}&{{\bar{m}}}_{{\varvec{\Sigma }}_{2,k}^{\prime } } ( -1) = \left( {\frac{1}{N}\sum \limits _{i = 1}^K {\frac{{\lambda _{1,i} \left\| {\mathbf{v}_{1,i}^{DL} } \right\| ^2 (\sigma _{2,k}^{1,i} )^2 }}{{1 + \lambda _{1,i} \left\| {\mathbf{v}_{1,i}^{DL} } \right\| ^2 (\sigma _{2,k}^{1,i} )^2 {{\bar{m}}}_{{\varvec{\Sigma }}_{2,k}^{\prime } } ( -1)}} + } } \right. \nonumber \\&\qquad \left. {\frac{1}{M}\sum \limits _{j \ne k}^K {\frac{{\lambda _{2,j} \left\| {\mathbf{w}_{2,j}^{UL} } \right\| ^2 \sigma _{2,2,j}^2 }}{{1 + \lambda _{2,j} \left\| {\mathbf{w}_{2,j}^{UL} } \right\| ^2 \sigma _{2,2,j}^2 {{\bar{m}}}_{{\varvec{\Sigma }}_{2,k}^{\prime } } (-1)}} + 1} } \right) ^{ - 1}. \end{aligned}$$

(38)

Proof

See Appendix 8.3. $\square$

From Theorems 2 and 3, it could be concluded that when $N,M,K\longrightarrow \infty$ and $M=N$, the system of 2K equations with 2K unknowns (24) is equivalent to a system consisting Eqs. (35), (36), (37) and (38). We must note that this equation depends on the power of the receive filters, which fortunately could be specified arbitrarily independent of the receive filter vectors.¹ Therefore, for coordinated beamforming, we should first solve the above equation system and then the equation system involving the beamforming vectors and the receive filters could be solved. Accordingly, we propose Algorithm 2 to design the coordinated beamforming vectors in the mMIMO scenario. In this algorithm, the steps of finding the Lagrangian multipliers depend on the channel statistics, which change very slower than the instantaneous of the channel coefficients (Viering et al. 2002). Thus, we could use the long-term time constant of the channels² and obtain the Lagrangian multipliers only after expiration of this time. Moreover, it must be noted that in Algorithm 2, as well as Algorithm 1, the power of the beamforming vectors is obtained at the final step and consequently the actual amounts of the target SINRs are achieved for all users.

Corollary 1

Although, the problem discussed above is for two cells (one has downlink transmission and the other has uplink transmission), one could generalize the scenario to the case of multicell, i.e., some cells with downlink transmission and others with uplink transmission. The problem is formulized as in the following,

$$\begin{aligned} \begin{array}{cl} \underset{{\mathbf {w}}_{i,k} ^{DL},{\mathbf {v}}_{j,k} ^{UL}\forall k }{\min } &\sum _{k=1}^{K}\left( \sum _{i=1}^{L_1}\Vert {\mathbf {w}}_{i,k} ^{DL} \Vert ^{2}+\sum _{j=1}^{L_2} \Vert {\mathbf {v}}_{j,k} ^{UL}\Vert ^{2} \right) \\ \mathrm {s.t.} & \mathrm {SINR}_{i,k}^{DL} \ge \gamma _{i,k}^{DL} \quad k=1,\dots ,K, \quad i=1,\dots ,L_1, \\ & \mathrm {SINR}_{j,k}^{UL} \ge \gamma _{j,k}^{UL} \quad k=1,\dots ,K, \quad j=1,\dots ,L_2, \end{array} \end{aligned}$$

where $L_1$ is the number of downlink cells, $L_2$ is the number of uplink cells, and K is the number of users per cell. Moreover, ${\mathbf {w}}_{i,k} ^{DL}$, $\mathrm {SINR}_{i,k}^{DL}$ and $\gamma _{i,k}^{DL}$ denote the beamforming vector, the SINR and the threshold of the SINR corresponding to the $k^{\mathrm{th}}$ user in the $i^{\mathrm{th}}$ downlink cell, respectively. Similarly, ${\mathbf {v}}_{j,k} ^{UL}$, $\mathrm {SINR}_{j,k}^{UL}$ and $\gamma _{j,k}^{UL}$ represent the beamforming vector, the SINR and the threshold of the SINR for the $k^{\mathrm{th}}$ user in the $j^{\mathrm{th}}$ uplink cell, respectively. It must be noted that this problem could be the subject of the future research.

Table 3 The computational complexity of the proposed algorithms, using MRC receivers

5 Computational Complexity

In this section, we compare the computational complexity of the proposed algorithms. As an example, it is assumed that the users in the downlink cell and the BS in the uplink cell are equipped with MRC receivers. We consider that the iteration number of each of the algorithms is 15 times to make sure both the algorithms are converged (Fig. 3). Moreover, $t_1$ is the iteration number of each of the inner loops in the process of finding the Lagrangian multipliers in Algorithm 2, $t_2$ is the iteration number of outer loop in the process of finding the Lagrangian multipliers in Algorithm 2 and $t_3$ is the iteration number in process of finding the Lagrangian multipliers in Algorithm 1. By this assumptions, we count the number of multipliers performed in each algorithm as the computational complexity. Then, the computational complexity of beamforming in the downlink and uplink cells would be as shown in Table 3.

It could be observed that the complexity of the beamforming in downlink and uplink cells in Algorithm 1 is of the order of ${\mathcal {O}}(K(N^3+M^3)+K^2(M^2+MN))$ and the complexity of Algorithm 2 is of the order of ${\mathcal {O}}(K^2(M^2+MN))$. Thus, with respect to the number of antennas M and N, Algorithm 2 is computationally simpler than Algorithm 1. Moreover, it must be noted that since in algorithm 2, the Lagrangian multipliers are obtained using the statistics of the channels, it is not necessary to recalculate them until the channel statistics change.

6 Simulation Results

In order to evaluate and compare the proposed beamforming schemes, some simulation examples are provided. A two-cell system is considered, in which the distance between the BSs of different cells is $\mathrm {D}$ meters, and K users are uniformly distributed in each cell in the coordination region (Fig. 2), where the users are more affected by the intercell interference compared to the remaining area of the cells. The simulation parameters are set as shown in Table 4.

First, the convergence of the proposed beamforming algorithms is investigated. In Fig. 3, the sum transmit power of the beamforming vectors in the downlink and uplink cells are plotted versus the number of iterations of the algorithms for MRC, local MMSE and MMSE receivers, individually. In this simulation, $M=N=32$,$K=2$ and the desired SINR for all the users is equal to $\gamma =3dB$. It could be observed that for all the receivers both the algorithms converge from sum transmit power point of view. Moreover, for evaluation of the algorithms we calculate the mean and standard deviation of the achieved SINRs over the variations of the channel coefficients, for various number of antennas by setting $\gamma =3$dB. We observe that the mean of the achieved SINRs of two algorithms is equal to 3dB and the standard deviations of them are in the order of $10^{-16}$ dBm, which is negligible.

Fig. 2

The coordination region of the cells, where the users experience more intercell interference compared to the remaining area of the cell. In this region, the minimum distance of the users from their corresponding BS is equal to $0.25 \mathrm {D}$

Table 4 The simulation settings

For the performance evaluation of Algorithm 2, the sum transmit power variation is illustrated versus the desired SINR $\gamma$ in Fig. 4. In this example, $K=2$ and $M=N=32$ are set. It could be observed that for all the receivers, the consumed power in both the downlink and uplink cells for Algorithm 2 is close to that of Algorithm 1. This subject confirms the performance of Algorithm 2 and shows the near optimality of the algorithm in this scenario.

In order to investigate the performance of Algorithm 2 for various number of antennas, the sum transmit power of the algorithms is plotted versus the number of antennas at each BS and user (which are assumed to be equal) in Fig. 5 by setting $K=2$ and $\gamma =3$dB. It could be observed that by increasing the number of antennas, the sum transmit power decreases, which is expected, since more antennas focus the power more accurately on the desired receiver. Moreover, as the number of antennas increases, the sum transmit power of Algorithm 2 more accurately tracks the performance of Algorithm 1.

Fig. 3

Sum transmit power versus the number of iterations of Algorithms 1 and 2, $K=2$, $M=N=32$, $\gamma =3$dB a Using MRC receiver. b Using local MMSE receiver. c Using MMSE receiver

Fig. 4

Sum transmit power versus desired SINR $\gamma$, $K=2$ $M=N=32$ a Using MRC receiver. b Using local MMSE receiver. c Using MMSE receiver

Fig. 5

Sum transmit power versus the number of antennas, $K=2$, $\gamma =3$ dB a Using MRC receiver. b Using local MMSE receiver. c Using MMSE receiver

For investigation of the performance of Algorithm 2 for various number of UTs, the sum transmit power in the cells versus the number of UTs in each cell (K) is depicted in Fig. 6. In this figure each BS and UT has $N=M=64$ antennas and the desired SINR is equal to $\gamma =3$dB. It could be observed that the performance of algorithm 2 is affected by the number of UTs per cell, so that by increasing the value of K we have a small gap between the sum transmit power of two algorithms. This is because the number of approximations in Algorithm 2 is equal to K (for more details see the proof of Theorem 2 in Sect. 8.2) and increasing the number of approximations can affect the performance of the algorithm.

Now, we compare the performance of the algorithms from the energy efficiency (EE) point of view. The EE of a communication system could be defined as the ratio of the sum rate to the total power consumption of the system (Li et al. 2015; He et al. 2015; Tervo et al. 2018). Thus, in our scenario it could be expressed as,

$$\begin{aligned} \mathrm {EE}=\dfrac{\sum _{i=1}^{2}\sum _{k=1}^{K}\log (1+\mathrm {SINR}_{i,k})}{\sum _{k=1}^{K}\left( \Vert {\mathbf {w}}_{1,k} ^{DL} \Vert ^{2}+ \Vert {\mathbf {v}}_{2,k} ^{UL}\Vert ^{2} \right) +NP_{C}^{BS}+P_{0}^{BS}+KMP_{C}^{UT}+P_{0}^{UT}}, \end{aligned}$$

(40)

where $\mathrm {SINR}_{i,k}$ is the SINR of the UT(i, k), and $P_{C}^{BS}$ and $P_{C}^{UT}$ are the constant power consumption per antenna at each BS and user, respectively. Moreover, $P_{0}^{BS}$ and $P_{0}^{UT}$ are, respectively, the basic power consumption at each BS and user and are independent of the number of transmit antennas (Ng et al. 2012). In Fig. 7, the EE of the algorithms versus the number of UTs per cell is illustrated. In this example, the number of Antennas at each BS and UT and the desired SINR are, respectively, set to $N=M=64$ and $\gamma =3$dB. It could be observed that, as expected, by increasing the number of UTs the EE of the algorithms increases. Moreover, for the various number of UTs per cell the EE of Algorithm 2 is close to that of Algorithm 1. This subject shows that the small gap between the sum transmit power of two algorithms could not affect the performance of Algorithm 2 from the EE point of view. In Fig. 8, the EE of the algorithms versus the number of antennas (N) at each BS and UT is depicted. As it is expected that more antennas bring us a higher rate, in this example, the desired SINR in dB is chosen to be proportional to N, i.e., $\gamma =0.25 N$ dB. It could be observed that although, by increasing the number of antennas, the system have more total power consumption, the EE of the system is growing. Furthermore, it could be noted that the EEs of the algorithms versus N closely track each other.

Fig. 6

Sum transmit power versus the number of UTs per cell, $M=N=64$, $\gamma =3$ dB a Using MRC receiver. b Using local MMSE receiver. c Using MMSE receiver

Fig. 7

Energy efficiency versus the number of UTs per cell, $M=N=64$, $\gamma =3$ dB a Using MRC receiver. b Using local MMSE receiver. c Using MMSE receiver

Fig. 8

Energy efficiency versus the number of Antennas, $K=2$, $\gamma =0.25 N$ dB a Using MRC receiver. b Using local MMSE receiver. c Using MMSE receiver

7 Conclusion

In this paper, the problem of coordinated multicell beamforming was investigated in a two-cell MIMO network, where there are downlink transmission in one cell and uplink transmission in the other cell. The coordinated beamforming vectors were designed for the downlink BS and the uplink users to minimize the sum transmit power of the beamforming vectors subject to per user SINR constraints. Next, the sum power minimization problem was extended to a mMIMO network, and using random matrix theory, an algorithm was proposed for coordinated beamforming, in which the number of computations is reduced. Using simulation examples, it was shown that the mMIMO algorithm achieves nearly optimal results in terms of the amount of power consumption. Also, the energy efficiency of the algorithms were compared and it was observed that the energy efficiency of the mmMIMO algorithm is comparable to the optimal coordinated beamforming algorithm.

Appendix

1.1 The proof of Theorem 1

In order to prove Theorem 1, we use the concept of standard function defined in Yates (1995) and Lemma 1.

Definition 1

A function $f: \mathrm {R}^{n}\rightarrow \mathrm {R}^{n}$, where for ${\mathbf {x}}=[x_1,\dots ,x_n]$, $f(x_{1},\dots ,x_{n})=[f_1({\mathbf {x}}),\dots ,f_n({\mathbf {x}})]^{T}$ is said to be a standard function if it satisfies the following conditions,

• 1. Positivity: If ${\mathbf {x}}=[x_{1},\dots ,x_{n}]^{T}$ and $\forall i\ x_{i}\ge 0$ then $\forall i$ $\ f_{i}({\mathbf {x}})\ge 0$.

• 2. Monotonicity: If ${\mathbf {x}}=[x_{1},\dots ,x_{n}]^{T}$ , ${\mathbf {y}}=[y_{1},\dots ,y_{n}]^{T}$ and for all i, $x_i \ge y_i$ then $\forall i \ f_i({\mathbf {x}})\ge f_i({\mathbf {y}})$.

• 3. Scalability: For all $\rho \ge 0$, and ${\mathbf {x}}$, $\forall i$ $\rho f_i({\mathbf {x}})\ge f_i(\rho {\mathbf {x}})$.

Lemma 1

If f be a standard function, then the fixed point iteration algorithm converges to a unique solution.

Proof

The proof could be found in Yates (1995). $\square$

Now, we prove that the function defined in Theorem 1 is standard and then its fixed point could be found using the fixed point iteration algorithm. Accordingly, we investigate the conditions of the standard function,

• 1. Positivity: It must be shown that for $i=1,2$, $\forall k$, $f_{i,k}( {\varvec{\lambda }}_{i},{\varvec{\lambda }}_{2})>0$

  $$\begin{aligned}&\forall k \lambda _{1,k}, \lambda _{2,k}>0\Longrightarrow {\varvec{\Sigma }}_{1}\succ 0\Longrightarrow \big ({\varvec{\Sigma }}_{1}+\mathbf{I}_{N}\big )\succ 0 \Longrightarrow \big ({\varvec{\Sigma }}_{1}+\mathbf{I}_{N}\big )^{-1}\succ 0 \Longrightarrow \\&\quad \forall k \ f_{1,k}( {\varvec{\lambda }}_{1},{\varvec{\lambda }}_{2})>0. \\&\quad \forall k \lambda _{1,k}, \lambda _{2,k}>0\Longrightarrow {\varvec{\Sigma }}_{2,k}\succ 0\Longrightarrow \big ({\varvec{\Sigma }}_{2,k}+\mathbf{I}_{M}\big )\succ 0 \Longrightarrow \\&\quad \big ({\varvec{\Sigma }}_{2,k}+\mathbf{I}_{M}\big )^{-1}\succ 0 \Longrightarrow \forall k\ f_{2,k}( {\varvec{\lambda }}_{1},{\varvec{\lambda }}_{2})>0. \end{aligned}$$

• 2. Monotonicity: It must be confirmed that,

  $$\begin{aligned}&\forall i,k \ \lambda _{i,k}>\lambda _{i,k}^{\prime } \Longrightarrow f_{i,k}( {\varvec{\lambda }}_{1},{\varvec{\lambda }}_{2}) >f_{i,k}( {\varvec{\lambda }}_{1}^{\prime },{\varvec{\lambda }}_{2}^{\prime }). \\&\quad {\varvec{\Sigma }}_{1}={\varvec{\Sigma }}_{1}^{\prime }+\big ({\varvec{\Sigma }}_{1}-{\varvec{\Sigma }}_{1}^{\prime }\big ) \Longrightarrow {\varvec{\Sigma }}_{1}=\\&\quad \sum _{m=1}^{K}\bigg (\frac{\lambda _{\mathrm{1},m}^{\prime }}{N}{\mathbf {H}} _{\mathrm{{1,1}},m} {\mathbf {v}}_{\mathrm{{1}},m} ^{DL,H} {\mathbf {v}}_{\mathrm{{1}},m} ^{DL} {\mathbf {H}} _{\mathrm{{1,1}},m} ^{H}+\frac{\lambda _{\mathrm{2},m}^{\prime }}{M} {\mathbf {H}} _{\mathrm{{1,2}}}^{H} {\mathbf {w}}_{\mathrm{{2}},m} ^{UL,H} {\mathbf {w}}_{\mathrm{{2}},m} ^{UL} {\mathbf {H}} _{\mathrm{{1,2}}}\bigg )+\\&\quad \sum _{m=1}^{K}\bigg (\frac{(\lambda _{\mathrm{1},m}-\lambda _{\mathrm{1},m}^{\prime })}{N}{\mathbf {H}} _{\mathrm{{1,1}},m} {\mathbf {v}}_{\mathrm{{1}},m} ^{DL,H} {\mathbf {v}}_{\mathrm{{1}},m} ^{DL} {\mathbf {H}} _{\mathrm{{1,1}},m} ^{H}+\frac{(\lambda _{\mathrm{2},m}-\lambda _{\mathrm{2},m}^{\prime })}{M} {\mathbf {H}} _{\mathrm{{1,2}}}^{H} {\mathbf {w}}_{\mathrm{{2}},m} ^{UL,H} {\mathbf {w}}_{\mathrm{{2}},m} ^{UL} {\mathbf {H}} _{\mathrm{{1,2}}}\bigg ). \end{aligned}$$

  As mentioned, $\lambda _{i,k}>\lambda _{i,k}^{\prime }$ and then ${\varvec{\Sigma }}_{1}-{\varvec{\Sigma }}_{1}^{\prime }\succ 0$; on the other hand, based on the Proposition 4 in Wiesel et al. (2006), for nonnegative matrices $\mathbf{C}$ and $\mathbf{D}$ and vector $\mathbf{x}$ in the range of $\mathbf{C}$, the following equation is satisfied,

  $$\begin{aligned} \dfrac{1}{{\mathbf {x}}^{H} \big ({\mathbf {C}}+{\mathbf {D}}\big )^{-1}{\mathbf {x}}}\ge \dfrac{1}{{\mathbf {x}}^{H} {\mathbf {C}}^{-1}{\mathbf {x}}}, \end{aligned}$$

  (41)

  then with defining ${\mathbf {x}}={\mathbf {H}}_{1,1,k} {\mathbf {v}}_{1,k}^{DL,H}$, ${\mathbf {C}}=\mathbf{I}_{N}+{\varvec{\Sigma }}_{1}^{\prime }$ and ${\mathbf {D}}={\varvec{\Sigma }}_{1}-{\varvec{\Sigma }}_{1}^{\prime }$, the result would be,

  $$\begin{aligned}&\dfrac{1}{\frac{1}{N}\big (1+\frac{1}{\gamma _{1,k}}\big ){\mathbf {v}}_{1,k} ^{DL} {\mathbf {H}} _{1,1,k}^{H}\big (\mathbf{I}_{N}+{\varvec{\Sigma }}_{1}\big )^{-1} {\mathbf {H}} _{1,1,k} {\mathbf {v}}_{1,k} ^{DL,H}} \ge \\&\quad \dfrac{1}{\frac{1}{N}\big (1+\frac{1}{\gamma _{1,k}}\big ){\mathbf {v}}_{1,k} ^{DL} {\mathbf {H}} _{1,1,k}^{H}\big (\mathbf{I}_{N}+{\varvec{\Sigma }}_{1}^{\prime }\big )^{-1} {\mathbf {H}} _{1,1,k} {\mathbf {v}}_{1,k} ^{DL,H}}; \end{aligned}$$

  then, $f_{1,k}( {\varvec{\lambda }}_{1},{\varvec{\lambda }}_{2}) >f_{1,k}( {\varvec{\lambda }}_{1}^{\prime },{\varvec{\lambda }}_{2}^{\prime })$. This equation could be similarly proved for $f_{2,k}$.

• 3. Scalability: It should be proved that for $\rho > 1$,

  $$\begin{aligned} \forall i,k \ \rho f_{i,k}( {\varvec{\lambda }}_{1},{\varvec{\lambda }}_{2}) > f_{i,k}(\rho {\varvec{\lambda }}_{1},\rho {\varvec{\lambda }}_{2}). \end{aligned}$$

Assume that $\rho > 1$ be arbitrary, then,

$$\begin{aligned} \rho f_{1,k}( {\varvec{\lambda }}_{1},{\varvec{\lambda }}_{2})=\dfrac{1}{\frac{1}{N}\big (1+\frac{1}{\gamma _{1,k}}\big ){\mathbf {v}}_{1,k} ^{DL} {\mathbf {H}} _{1,1,k}^{H}\big (\rho \mathbf{I}_{N}+\rho {\varvec{\Sigma }}_{1}\big )^{-1} {\mathbf {H}} _{1,1,k} {\mathbf {v}}_{1,k} ^{DL,H}}, \end{aligned}$$

where

$$\begin{aligned}&\rho \mathbf{I}_{N}+\rho {\varvec{\Sigma }}_{1}=\rho \mathbf{I}_{N}+\rho \sum _{m=1}^{K}\bigg (\frac{\lambda _{\mathrm{1},m}}{N}{\mathbf {H}} _{1,1,m} {\mathbf {v}}_{1,m} ^{DL,H} {\mathbf {v}}_{1,m} ^{DL} {\mathbf {H}} _{1,1,m} ^{H}+\\&\quad \frac{\lambda _{\mathrm{2},m}}{M} {\mathbf {H}} _{1,2}^{H} {\mathbf {w}}_{2,m} ^{UL,H} {\mathbf {w}}_{2,m} ^{UL} {\mathbf {H}} _{1,2}\bigg )=(\rho -1)\mathbf{I}_{N}+\mathbf{I}_{N} \\&\quad +\rho \sum _{m=1}^{K}\bigg (\frac{\lambda _{\mathrm{1},m}}{N}{\mathbf {H}} _{1,1,m} {\mathbf {v}}_{1,m} ^{DL,H} {\mathbf {v}}_{1,m} ^{DL} {\mathbf {H}} _{1,1,m} ^{H}\\&\quad +\frac{\lambda _{\mathrm{2},m}}{M} {\mathbf {H}} _{1,2}^{H} {\mathbf {w}}_{2,m} ^{UL,H} {\mathbf {w}}_{2,m} ^{UL} {\mathbf {H}} _{1,2}\bigg ). \end{aligned}$$

As mentioned, $\rho >1$ and then, $(\rho -1)\mathbf{I}_{N}\succeq 0$; hence, defining ${\mathbf {C}}=\mathbf{I}_{N}+\rho {\varvec{\Sigma }}_{1}$ and ${\mathbf {D}}=(\rho -1)\mathbf{I}_{N}$, based on (41), the following equation is resulted,

$$\begin{aligned}&\rho f_{1,k}( {\varvec{\lambda }}_{1},{\varvec{\lambda }}_{2}) = \dfrac{1}{\frac{1}{N}\big (1+\frac{1}{\gamma _{1,k}}\big ){\mathbf {v}}_{1,k} ^{DL} {\mathbf {H}} _{1,1,k}^{H}\big (\rho \mathbf{I}_{N}+\rho {\varvec{\Sigma }}_{1}\big )^{-1} {\mathbf {H}} _{1,1,k} {\mathbf {v}}_{1,k} ^{DL,H}}\ge \\&\quad \dfrac{1}{\frac{1}{N}\big (1+\frac{1}{\gamma _{1,k}}\big ){\mathbf {v}}_{1,k} ^{DL} {\mathbf {H}} _{1,1,k}^{H}\big (\mathbf{I}_{N}+\rho {\varvec{\Sigma }}_{1}\big )^{-1} {\mathbf {H}} _{1,1,k} {\mathbf {v}}_{1,k} ^{DL,H}}\\&\quad = f_{1,k}(\rho {\varvec{\lambda }}_{1},\rho {\varvec{\lambda }}_{2}). \end{aligned}$$

This equation could be similarly confirmed for $f_{2,k}$.

Accordingly, f is a standard function, and based on Lemma 1, the fixed point of this function could be found using the fixed point iteration algorithm.

1.2 The Proof of Theorem 2

In order to prove Theorem 2, we first state the following Lemmas.

Lemma 2

(Silverstein and Bai (1995)) Assume that ${\mathbf {A}} \in {\mathbb {C}}^{N\times N}$ be a hermity and invertible matrix. Then, for any vector ${\mathbf {x}} \in {\mathbb {C}}^{N\times 1}$ and $\tau \in {\mathbb {C}}$, if ${\mathbf {A}}+\tau {\mathbf {x}}{\mathbf {x}}^{H}$ is an invertible matrix, then the following equations are held

$$\begin{aligned} ({\mathbf {A}}+\tau {\mathbf {x}}{\mathbf {x}}^{H})^{-1}&={\mathbf {A}}^{-1}-\dfrac{{\mathbf {A}}^{-1}\tau {\mathbf {x}}{\mathbf {x}}^{H}{\mathbf {A}}^{-1}}{1+\tau {\mathbf {x}}^{H}{\mathbf {A}}^{-1} {\mathbf {x}}}, \end{aligned}$$

(42)

$$\begin{aligned} {\mathbf {x}}^{H}({\mathbf {A}}+\tau {\mathbf {x}}{\mathbf {x}}^{H})^{-1}&=\dfrac{{\mathbf {x}}^{H}{\mathbf {A}}^{-1}}{1+\tau {\mathbf {x}}^{H}{\mathbf {A}}^{-1} {\mathbf {x}}}. \end{aligned}$$

(43)

Lemma 3

(Bai and Silverstein (1998)) Assume that ${\mathbf {x}},{\mathbf {y}}\sim {{\mathcal {C}}}{{\mathcal {N}}}(\mathrm{0},\frac{1}{N} \mathbf{I}_{N}) \in {\mathbb {C}}^{N }$ be independent and $\mathbf{A}$ be a hermity matrix independent of ${\mathbf {x}}$ and ${\mathbf {y}}$, then ${\mathbf {x}}^{H}{\mathbf {A}}{\mathbf {x}} \mathop {\longrightarrow }\limits _{N\rightarrow \infty }^{a.s.} \frac{1}{N} tr\{{\mathbf {A}}\}$ and ${\mathbf {x}}^{H}{\mathbf {A}}{\mathbf {y}}\mathop {\longrightarrow }\limits _{N\rightarrow \infty }^{a.s.} 0.$

Lemma 4

For $k=1,\dots ,K$,

$$\begin{aligned} {\mathbf {H}}_{1,1,k}{\mathbf {v}}_{1,k}^{DL,H}&\sim {{\mathcal {C}}}{{\mathcal {N}}}(0,\Vert {\mathbf {v}}_{1,k}^{DL}\Vert ^{2}\sigma _{1,1,k}^{2}\mathbf{I}_{N}),\\ {\mathbf {H}}_{2,2,k}^{H}{\mathbf {w}}_{2,k}^{UL,H}&\sim {{\mathcal {C}}}{{\mathcal {N}}}(0,\Vert {\mathbf {w}}_{2,k}^{UL}\Vert ^{2}\sigma _{2,2,k}^{2}\mathbf{I}_{M}). \end{aligned}$$

Proof

The proof is straightforward. $\square$

Now, considering (24) we have,

$$\begin{aligned} \lambda _{1,k}=\dfrac{1}{\frac{1}{N}\big (1+\frac{1}{\gamma _{1,k}}\big ){\mathbf {v}}_{1,k} ^{DL} {\mathbf {H}} _{1,1,k}^{H}\big (\mathbf{I}_{N}+{\varvec{\Sigma }}_{1}\big )^{-1} {\mathbf {H}} _{1,1,k} {\mathbf {v}}_{1,k} ^{DL,H}} , \end{aligned}$$

and on the other hand based on Lemma 2,

$$\begin{aligned} \begin{aligned}&{\mathbf {v}}_{1,k} ^{DL} {\mathbf {H}} _{1,1,k}^{H}\big (\mathbf{I}_{N}+{\varvec{\Sigma }}_{1}\big )^{-1} {\mathbf {H}} _{1,1,k} {\mathbf {v}}_{1,k} ^{DL,H}\\&\quad =\dfrac{{\mathbf {v}}_{1,k} ^{DL} {\mathbf {H}} _{1,1,k}^{H}\big (\mathbf{I}_{N}+{\varvec{\Sigma }}_{1}^{\prime }\big )^{-1} {\mathbf {H}} _{1,1,k} {\mathbf {v}}_{1,k} ^{DL,H}}{1+\frac{\lambda _{1,k}}{N}{\mathbf {v}}_{1,k} ^{DL} {\mathbf {H}} _{1,1,k}^{H}\big (\mathbf{I}_{N}+{\varvec{\Sigma }}_{1}^{\prime }\big )^{-1} {\mathbf {H}} _{1,1,k} {\mathbf {v}}_{1,k} ^{DL,H}} , \end{aligned} \end{aligned}$$

then,

$$\begin{aligned} \lambda _{1,k}=\dfrac{1+\frac{\lambda _{1,k}}{N}{\mathbf {v}}_{1,k} ^{DL} {\mathbf {H}} _{1,1,k}^{H}\big (\mathbf{I}_{N}+{\varvec{\Sigma }}_{1}^{\prime }\big )^{-1} {\mathbf {H}} _{1,1,k} {\mathbf {v}}_{1,k} ^{DL,H}}{\frac{1}{N}\big (1+\frac{1}{\gamma _{1,k}}\big ){\mathbf {v}}_{1,k} ^{DL} {\mathbf {H}} _{1,1,k}^{H}\big (\mathbf{I}_{N}+{\varvec{\Sigma }}_{1}^{\prime }\big )^{-1} {\mathbf {H}} _{1,1,k} {\mathbf {v}}_{1,k} ^{DL,H}}, \end{aligned}$$

hence,

$$\begin{aligned} \lambda _{1,k}=\dfrac{\gamma _{1,k}}{\frac{1}{N}{\mathbf {v}}_{1,k} ^{DL} {\mathbf {H}} _{1,1,k}^{H}\big (\mathbf{I}_{N}+{\varvec{\Sigma }}_{1}^{\prime }\big )^{-1} {\mathbf {H}} _{1,1,k} {\mathbf {v}}_{1,k} ^{DL,H}}. \end{aligned}$$

(44)

Also, based on Lemma 4, ${\mathbf {H}}_{1,1,k}{\mathbf {v}}_{1,k}^{DL,H}\sim {{\mathcal {C}}}{{\mathcal {N}}}(0,\Vert {\mathbf {v}}_{1,k}^{DL}\Vert ^{2}\sigma _{1,1,k}^{2}\mathbf{I}_{N})$ and it is clear that the matrix ${\varvec{\Sigma }}_{1,k}^{\prime }$ and vector ${\mathbf {H}} _{1,1,k} {\mathbf {v}}_{1,k} ^{DL,H}$ are independent, then based on Lemma 3,

$$\begin{aligned} \begin{aligned}&\frac{1}{N}{\mathbf {v}}_{1,k} ^{DL} {\mathbf {H}} _{1,1,k}^{H}\big (\mathbf{I}_{N}+{\varvec{\Sigma }}_{1}^{\prime }\big )^{-1} {\mathbf {H}} _{1,1,k} {\mathbf {v}}_{1,k} ^{DL,H}\\&\quad \mathop {\longrightarrow }\limits _{N\rightarrow \infty }^{a.s.} \frac{1}{N} \Vert {\mathbf {v}}_{1,k}^{DL}\Vert ^{2}\sigma _{1,1,k}^{2} tr\{\big (\mathbf{I}_{N}+{\varvec{\Sigma }}_{1}^{\prime }\big )^{-1}\}. \end{aligned} \end{aligned}$$

On the other hand, according to the assumption of the theorem, $m_{{\varvec{\Sigma }}_{1,k}^{\prime }}(-1)=\frac{1}{N}tr\{\big (\Sigma _{1,k}^{\prime }+\mathbf{I}_{N}\big )^{-1}\}$, hence,

$$\begin{aligned} \begin{aligned}&\frac{1}{N}{\mathbf {v}}_{1,k} ^{DL} {\mathbf {H}} _{1,1,k}^{H}\big (\mathbf{I}_{N}+{\varvec{\Sigma }}_{1}^{\prime }\big )^{-1} {\mathbf {H}} _{1,1,k} {\mathbf {v}}_{1,k} ^{DL,H}\\&\quad \mathop {\longrightarrow }\limits _{N\rightarrow \infty }^{a.s.} \Vert {\mathbf {v}}_{1,k}^{DL}\Vert ^{2}\sigma _{1,1,k}^{2} m_{{\varvec{\Sigma }}_{1,k}^{\prime }}(-1), \end{aligned} \end{aligned}$$

(45)

then considering (44), we result the following equation for the Lagrangian multipliers,

$$\begin{aligned} \lambda _{1,k}=\dfrac{\gamma _{1,k}}{ \Vert {\mathbf {v}}_{1,k}^{DL}\Vert ^{2}\sigma _{1,1,k}^{2} m_{{\varvec{\Sigma }}_{1,k}^{\prime }}(-1)}. \end{aligned}$$

Now, we prove the second equation of Theorem 2; considering (24), we have,

$$\begin{aligned} \lambda _{2,k}=\dfrac{1}{\frac{1}{M}\big (1+\frac{1}{ \gamma _{2,k}}\big ){\mathbf {w}}_{2,k} ^{UL}{\mathbf {H}} _{2,2,k}\big (\mathbf{I}_{M}+{\varvec{\Sigma }}_{2,k}\big )^{-1}{\mathbf {H}} _{2,2,k}^{H} {\mathbf {w}}_{2,k} ^{UL,H}}, \end{aligned}$$

also based on Lemma 2,

$$\begin{aligned} \begin{aligned}&{\mathbf {w}}_{2,k} ^{UL}{\mathbf {H}} _{2,2,k}\big (\mathbf{I}_{M}+{\varvec{\Sigma }}_{2,k}\big )^{-1}{\mathbf {H}} _{2,2,k}^{H} {\mathbf {w}}_{2,k} ^{UL,H}=\\ &\quad =\dfrac{{\mathbf {w}}_{2,k} ^{UL}{\mathbf {H}} _{2,2,k}\big (\mathbf{I}_{M}+{\varvec{\Sigma }}_{2,k}^{\prime }\big )^{-1}{\mathbf {H}} _{2,2,k}^{H} {\mathbf {w}}_{2,k} ^{UL,H}}{1+\frac{\lambda _{2,k}}{M}{\mathbf {w}}_{2,k} ^{UL}{\mathbf {H}} _{2,2,k}\big (\mathbf{I}_{M}+{\varvec{\Sigma }}_{2,k}^{\prime }\big )^{-1}{\mathbf {H}} _{2,2,k}^{H} {\mathbf {w}}_{2,k} ^{UL,H}}, \end{aligned} \end{aligned}$$

then,

$$\begin{aligned} \lambda _{2,k}=\dfrac{1+\frac{\lambda _{2,k}}{M}{\mathbf {w}}_{2,k} ^{UL}{\mathbf {H}} _{2,2,k}\big (\mathbf{I}_{M}+{\varvec{\Sigma }}_{2,k}^{\prime }\big )^{-1}{\mathbf {H}} _{2,2,k}^{H} {\mathbf {w}}_{2,k} ^{UL,H}}{\frac{1}{M}\big (1+\frac{1}{ \gamma _{2,k}}\big ){\mathbf {w}}_{2,k} ^{UL}{\mathbf {H}} _{2,2,k}\big (\mathbf{I}_{M}+{\varvec{\Sigma }}_{2,k}^{\prime }\big )^{-1}{\mathbf {H}} _{2,2,k}^{H} {\mathbf {w}}_{2,k} ^{UL,H}}, \end{aligned}$$

hence,

$$\begin{aligned} \lambda _{2,k}=\dfrac{\gamma _{2,k}}{\frac{1}{M}{\mathbf {w}}_{2,k} ^{UL}{\mathbf {H}} _{2,2,k}\big (\mathbf{I}_{M}+{\varvec{\Sigma }}_{2,k}^{\prime }\big )^{-1}{\mathbf {H}} _{2,2,k}^{H} {\mathbf {w}}_{2,k} ^{UL,H}}. \end{aligned}$$

(46)

But based on (22), the matrix ${\varvec{\Sigma }}_{2,k}^{\prime }$ is not independent of the vector ${\mathbf {H}} _{2,2,k}^{H} {\mathbf {w}}_{2,k} ^{UL,H}$ then the term $\frac{1}{M}{\mathbf {w}}_{2,k} ^{UL}{\mathbf {H}} _{2,2,k}\big (\mathbf{I}_{M}+{\varvec{\Sigma }}_{2,k}^{\prime }\big )^{-1}{\mathbf {H}} _{2,2,k}^{H} {\mathbf {w}}_{2,k} ^{UL,H}$ could not be accurately approximated. However, if it be assumed that the eliminated term of matrix ${\varvec{\Sigma }}_{2,k}$, $\frac{\lambda _{2,k}}{M}{\mathbf {H}} _{2,2,k}^{H} {\mathbf {w}}_{2,k} ^{UL,H} {\mathbf {w}}_{2,k} ^{UL} {\mathbf {H}} _{2,2,k}$ is the dominant term among the terms containing the random matrix ${\mathbf {H}} _{2,2,k}^{H}$,

then ${\varvec{\Sigma }}_{2,k}^{\prime }$ and ${\mathbf {H}} _{2,2,k}^{H} {\mathbf {w}}_{2,k} ^{UL,H}$ could be considered independent, then based on Lemma 3 and Lemma 4,

$$\begin{aligned} \begin{aligned}&\frac{1}{M}{\mathbf {w}}_{2,k} ^{UL}{\mathbf {H}} _{2,2,k}\big (\mathbf{I}_{M}+{\varvec{\Sigma }}_{2,k}^{\prime }\big )^{-1}{\mathbf {H}} _{2,2,k}^{H} {\mathbf {w}}_{2,k} ^{UL,H} \\&\quad \mathop {\longrightarrow }\limits _{M\rightarrow \infty }^{a.s.}\frac{1}{M}\Vert {\mathbf {w}}_{2,k}^{UL}\Vert ^{2}\sigma _{2,2,k}^{2}tr\{\big (\mathbf{I}_{M}+{\varvec{\Sigma }}_{2,k}^{\prime }\big )^{-1} \}, \end{aligned} \end{aligned}$$

hence, based on the assumption of the theorem we have,

$$\begin{aligned}&\frac{1}{M}{\mathbf {w}}_{2,k} ^{UL}{\mathbf {H}} _{2,2,k}\big (\mathbf{I}_{M}+{\varvec{\Sigma }}_{2,k}^{\prime }\big )^{-1}{\mathbf {H}} _{2,2,k}^{H} {\mathbf {w}}_{2,k} ^{UL,H} \\&\quad \mathop {\longrightarrow }\limits _{M\rightarrow \infty }^{a.s.} \Vert {\mathbf {w}}_{2,k}^{UL}\Vert ^{2}\sigma _{2,2,k}^{2}m_{{\varvec{\Sigma }}_{2,k}^{\prime }}(-1), \end{aligned}$$

then based on (45), the result would be,

$$\begin{aligned} \lambda _{2,k}\simeq \dfrac{\gamma _{2,k}}{m_{{\varvec{\Sigma }}_{2,k}^{\prime }}(-1)\Vert {\mathbf {w}}_{2,k}^{UL}\Vert ^{2}\sigma _{2,2,k}^{2}}, \end{aligned}$$

where using $\simeq$ is because of that it was connived to consider ${\varvec{\Sigma }}_{2,k}^{\prime }$ and ${\mathbf {H}} _{2,2,k}^{H} {\mathbf {w}}_{2,k} ^{UL,H}$ independent.

1.3 The proof of Theorem 3

In order to prove Theorem 3, we first state the following theorem from the random matrix theory,

Theorem 4

(See Theorem 5 in Lakshminarayana et al. (2015)) Consider matrix $\mathbf{B}=XTX^{ H}$, where $\mathbf{X}=\frac{ 1}{\sqrt{ N}}\mathbf{Y}\in {\mathbb {C}}^{ N\times LK}$ with components $Y(p,q)\sim {{\mathcal {C}}}{{\mathcal {N}}}(0,1)$ and ${\mathbf {T}}=\mathrm {diag}\big (t_{1},\dots ,t_{LK}\big )\in {\mathbb {R}}^{LK\times LK}$ be a non-random diagonal matrix. Assume that $m_{{\mathbf {B}}}(z)=\frac{1}{N}tr\{\big ({\mathbf {B}}-z\mathbf{I}_{N}\big )^{-1}\}$, $z \in {\mathbb {R}}$ then,

$$\begin{aligned} m_{{\mathbf {B}}}(z)\mathop {\longrightarrow }\limits _{N,K\rightarrow \infty }^{a.s.}{\bar{m}}_{{\mathbf {B}}}(z), \end{aligned}$$

where ${\bar{m}}_{{\mathbf {B}}}(z)$ is the unique solution of following fixed point equation,

$$\begin{aligned} {\bar{m}}_{{\mathbf {B}}}(z)=\bigg (\frac{1}{N}\sum \limits _{i=1}^{LK}\dfrac{t_{i}}{1+t_{i}{\bar{m}}_{{\mathbf {B}}}(z)}-z\bigg )^{-1}. \end{aligned}$$

(47)

Now, we rewrite matrix ${\varvec{\Sigma }}_{1,k}^{\prime }$ as,

$$\begin{aligned} {\varvec{\Sigma }}_{1}^{\prime }&=\sum _{m\ne k}^{K}\frac{\lambda _{\mathrm{1},m}}{N}{\mathbf {H}} _{1,1,m} {\mathbf {v}}_{1,m} ^{DL,H} {\mathbf {v}}_{1,m} ^{DL} {\mathbf {H}} _{1,1,m} ^{H}\\&\qquad +\sum _{m=1}^{K}\frac{\lambda _{\mathrm{2},m}}{M} {\mathbf {H}} _{1,2}^{H} {\mathbf {w}}_{2,m} ^{UL,H} {\mathbf {w}}_{2,m} ^{UL} {\mathbf {H}} _{1,2}\\ &\quad =\bigg [\frac{{\mathbf {H}} _{1,1,1} {\mathbf {v}}_{1,1} ^{DL,H} }{\sqrt{N}\sigma _{1,1,1}},\dots ,\frac{{\mathbf {H}} _{1,1,k-1} {\mathbf {v}}_{1,k-1} ^{DL,H} }{\sqrt{N}\sigma _{1,1,k-1}},\frac{{\mathbf {H}} _{1,1,k+1} {\mathbf {v}}_{1,k+1} ^{DL,H} }{\sqrt{N}\sigma _{1,1,k+1}},\\&\qquad \dots ,\frac{{\mathbf {H}} _{1,1,K} {\mathbf {v}}_{1,K} ^{DL,H} }{\sqrt{N}\sigma _{1,1,K}},\frac{{\mathbf {H}}_{1,2}^{H} {\mathbf {w}}_{2,1} ^{UL,H}}{\sqrt{M}\sigma _{1,2}},\dots ,\frac{{\mathbf {H}} _{1,2}^{H} {\mathbf {w}}_{2,K} ^{UL,H}}{\sqrt{M}\sigma _{1,2}}\bigg ] \\&\quad \mathrm {diag}\bigg (\lambda _{1,1}\sigma _{1,1,1}^{2}\Vert {\mathbf {v}}_{1,1}^{DL}\Vert ^{2},\dots ,\lambda _{1,k-1}\sigma _{1,1,k-1}^{2}\Vert {\mathbf {v}}_{1,k-1}^{DL}\Vert ^{2},\\&\lambda _{1,k+1}\sigma _{1,1,k+1}^{2}\Vert {\mathbf {v}}_{1,k+1}^{DL}\Vert ^{2},\dots ,\lambda _{1,K}\sigma _{1,1,K}^{2}\Vert {\mathbf {v}}_{1,K}^{DL}\Vert ^{2}\bigg )\\&\bigg [\frac{{\mathbf {H}} _{1,1,1} {\mathbf {v}}_{1,1} ^{DL,H} }{\sqrt{N}\sigma _{1,1,1}},\dots ,\frac{{\mathbf {H}}_{1,1,k-1} {\mathbf {v}}_{1,k-1} ^{DL,H} }{\sqrt{N}\sigma _{1,1,k-1}},\frac{{\mathbf {H}}_{1,1,k+1} {\mathbf {v}}_{1,k+1} ^{DL,H} }{\sqrt{N}\sigma _{1,1,k+1}},\\&\dots ,\frac{{\mathbf {H}} _{1,1,K} {\mathbf {v}}_{1,K} ^{DL,H} }{\sqrt{N}\sigma _{1,1,K}},\frac{{\mathbf {H}}_{1,2}^{H} {\mathbf {w}}_{2,1} ^{UL,H}}{\sqrt{M}\sigma _{1,2}},\dots ,\frac{{\mathbf {H}}_{1,2}^{H} {\mathbf {w}}_{2,K} ^{UL,H}}{\sqrt{M}\sigma _{1,2}}\bigg ]^{H}\\&={\mathbf {X}}_{1}{\mathbf {T}}_{1}{\mathbf {X}}_{1}^{H}, \end{aligned}$$

where

$$\begin{aligned}&{\mathbf {X}}_{1}=\bigg [\frac{{\mathbf {H}} _{1,1,1} {\mathbf {v}}_{1,1} ^{DL,H} }{\sqrt{N}\sigma _{1,1,1}},\dots ,\frac{{\mathbf {H}} _{1,1,k-1} {\mathbf {v}}_{1,k-1} ^{DL,H} }{\sqrt{N}\sigma _{1,1,k-1}},\frac{{\mathbf {H}} _{1,1,k+1} {\mathbf {v}}_{1,k+1} ^{DL,H} }{\sqrt{N}\sigma _{1,1,k+1}},\\&\quad \dots ,\frac{{\mathbf {H}} _{1,1,K} {\mathbf {v}}_{1,K} ^{DL,H} }{\sqrt{N}\sigma _{1,1,K}},\frac{{\mathbf {H}}_{1,2}^{H} {\mathbf {w}}_{2,1} ^{UL,H}}{\sqrt{M}\sigma _{1,2}},\dots ,\frac{{\mathbf {H}} _{1,2}^{H} {\mathbf {w}}_{2,K} ^{UL,H}}{\sqrt{M}\sigma _{1,2}}\bigg ], \end{aligned}$$

and matrix $\mathbf{T}$ is,

$$\begin{aligned}&\mathrm {diag}\bigg (\lambda _{1,1}\sigma _{1,1,1}^{2}\Vert {\mathbf {v}}_{1,1}^{DL}\Vert ^{2},\dots ,\lambda _{1,k-1}\sigma _{1,1,k-1}^{2}\Vert {\mathbf {v}}_{1,k-1}^{DL}\Vert ^{2},\\&\quad \lambda _{1,k+1}\sigma _{1,1,k+1}^{2}\Vert {\mathbf {v}}_{1,k+1}^{DL}\Vert ^{2},\dots ,\lambda _{1,K}\sigma _{1,1,K}^{2}\Vert {\mathbf {v}}_{1,K}^{DL}\Vert ^{2}\bigg ). \end{aligned}$$

The vector ${\mathbf {Y}}_{1}=\sqrt{ N}{\mathbf {X}}_{1}$ is a zero mean normal random vector with variance one, then based on Theorem 4 when N and K limit to infinity, the following would be resulted,

$$\begin{aligned}m_{{\varvec{\Sigma }}_{1,k}^{\prime }}(-1)=\frac{1}{N}tr\{\big (\Sigma _{1,k}^{\prime }+\mathbf{I}_{N}\big )^{-1}\}\mathop {\longrightarrow }\limits _{N,K\longrightarrow \infty }^{a.s.}{\bar{m}}_{{\varvec{\Sigma }}_{1,k}^{\prime }}(-1),\end{aligned}$$

where ${\bar{m}}_{{\varvec{\Sigma }}_{1,k}^{\prime }}(-1)$ is the unique solution of Eq. (37).

Equation (38) could be similarly proved by rewriting matrix ${\varvec{\Sigma }}_{2,k}^{\prime }$.