1 Introduction

In contrast to the conventional orthogonal multiple access (OMA), the non-orthogonal multiple access (NOMA) can reasonably accommodate more than one user via non-orthogonal resource allocation, via power-domain user multiplexing, with the exploitation of the channel gain differences among users. Recently, these features have been exploited the B5G wireless systems. The significant power differences in dealing with cell-center and cell-edge users facilitates the successful decoding of the power-domain NOMA signals designated for each user, enabling the use of relatively low-complexity receivers at the receiver side [1, 2].

Due to the exponential increase in the number of device connections, effective utilization of energy and spectrum efficiency (EE and SE, respectively) has become ever more crucial in the design of mobile wireless systems. NOMA is a suitable technology for 5G and B5G networks that can improve EE and SE, outperforming existing orthogonal frequency multiple access techniques (OFDMA), while can accommodate a vast count of machine-to-machine (M2M) communication devices.

The NOMA schemes increase the system throughput. Beyond that, system and user SE can be significantly improved under NOMA schemes since the users served by different power levels can transmit at the same frequency and at the same time slot [1]. Since MIMO technology exploits the spatial domain and NOMA exploits the power domain, the two technologies can be combined to improve the system spectrum efficiency [2]. A possibility for improving the system SE with NOMA is also exploiting the spatial degrees of freedom enabled by MIMO technologies, which is paramount for complying the performance requirements of 5G networks [3].

Multiple-antenna-aided NOMA design can use directional beamforming or spatial multiplexing to provide array gains or increase the system’s throughput. Also, adopting appropriate strategies for the transmit precoding matrix enables the creation of user-specific channels. Exploring such configurations leads to a generalized NOMA design for satisfying the heterogeneous user QoS requirements [4].

1.1 Resource Efficiency (RE): EE\(\times\)SE Trade-off

The fast growth of data traffic in recent systems has been accompanied by an increase in energy consumption. This situation, combined with limitations in the battery capacity occasioned by a reduction in the terminal size limits, makes the EE one dominant concern in the design of 5G and B5G wireless communication systems. As a consequence, in recent years numerous works focusing on analyzing and enhancing not only the SE, but also the EE of wireless communication systems. E.g., authors in [5] present a more general and flexible measure called Resource Efficiency (RE). The RE concept has also been explored in [6] for massive MIMO (M-MIMO) applications, where the RE is defined as a weighted combination of EE and power-normalized SE. This new performance measure has more flexibility in striking a tradeoff between SE and EE, despite difficulties in solving the resulting optimization problem. Hence, the authors in [6] first investigate an uplink (UL)/downlink (DL) duality for the RE maximization purpose. Moreover, they demonstrate that UL/DL duality has a more general form that can be directly used to tackle either the EE or RE beamforming design problem.

In [7], the EE improvement for DL NOMA systems is formulated as a non-convex optimization subject to a minimum satisfying SE while guaranteeing the quality of service (QoS) for each user. The authors show that optimization problem’s solution is achieved when an optimal power allocation is obtained. In [8], the EE-SE trade-offs in power domain NOMA and OFDMA systems are compared with respect to variation of system bandwidth. Simulation results demonstrate that the NOMA technique outperforms the prevailing OFDMA technique concerning EE and SE; thus, NOMA can be seen as a promising technology for 5G and B5G networks, especially in order to support the functionality of the Internet of things (IoT) and the massive machine-type communications (mMTC) scenarios.

Another strategy to improve the SE-EE tradeoff in B5G networks is combining NOMA with simultaneous wireless information and power transfer (SWIPT) technique. In [9], the authors investigate joint power allocation and time switching (TS) control for EE optimization in TS-SWIPT NOMA systems. The goal is to optimize the system EE while satisfying the constraints on maximum transmit power budget, minimum data rate, and minimum harvested energy per terminal. The proposed EE optimization method in [9] is neither linear nor convex, involving joint optimization of power allocation and time-switching factors. The dual-layer algorithm is proposed to solve the problem iteratively. The Dinkelbach method (DKM) is employed in the inner layer to optimize the power allocation and in the outer layer to control the time-switching assignment. Numerical results demonstrate a significant performance gain of the SWIPT-enabled NOMA system over OMA scheme in terms of EE. Moreover, [10] investigates the EE resource allocation in the wireless power transfer (WPT)-based massive MIMO-NOMA networks. The joint transmit power, WPT time, antenna selection, and subcarrier allocation scheme has been proposed to solve the system EE maximization problem. The authors deploy the non-linear fraction programming approach to convert the original non-convex problem to be convex and solve the optimization problem by developing a novel distributed alternating direction method of multipliers (ADMM)-based EE resource allocation algorithm under perfect and imperfect CSI.

The power proportion allocation for each user in the DL MIMO-NOMA systems is analyzed in [11]. The successive interference cancellation (SIC) is deployed to recover users’ signals with the higher differences between channel gains. In the proposed optimization design, initially, the minimum total power and the power proportion factor for each active user are obtained. After that, the maximum system EE, the equal data rate, total power, and power-proportion distribution along the users and clusters are determined. Both optimization procedures deployed the same constraints and all users were subjected to an equal data rate. The numerical results reveal the total number of users reaches the maximum EE in each analyzed cluster-user configuration. The number of total users in the cell for a specific number of users-per-cluster (2, 3 or 4) that simultaneously maximize EE and the equal data rate per user (maximum fairness) depends on the path-loss channel coefficients, the number of users-per-cluster and the cell coverage (radius).

A comparative resource allocation analysis in terms of received bits-per-antenna SE and EE metrics in the DL single-cell M-MIMO-NOMA systems is carried out in [12], considering single-antenna devices, and the devices’ loadingFootnote 1 ranging \(0<\frac{K}{M} \leqslant 2\) operating under three different PA strategies: (a) the inverse of the channel power allocation; (b) water-filling (WF)-based allocation method, and (c) the naive equal power allocation method. Under the adopted configuration power-domain NOMA with two devices per cluster, and ZF precoding, NOMA operating under many antennas can favor a group of devices with higher array gain. Authors adopt a useful performance metric by evaluating the area under SE and EE curves, measuring the bit-per-antenna and bit-per-antenna-per-watt efficiency, respectively, corroborating the superiority of NOMA w.r.t. M-MIMO about 300% for the SE-area and 200% for the EE-area metric.

In the context of maximizing the rate while using minimum transmit power, the NOMA design in [13] provides a multi-objective optimization (MOO) to efficiently allocate resources in the multi-user NOMA systems supporting DL transmission. The suggested optimization technique jointly improves spectrum and energy efficiency while satisfying the constraints on users’ quality of services (QoS) requirements, transmit power budget, and successive interference cancellation. The authors employ dual decomposition techniques to obtain an efficient solution for the joint spectrum and energy optimization problem. The proposed joint approach significantly outperforms its counterpart OMA schemes in terms of both energy and spectral efficiency. Furthermore, [14] considers a relaxation of the joint (intractable) optimization of resource allocation problem for the DL MU-MIMO-NOMA. Users are organized in clusters of strong/weak pairs, with the aim of optimizing three resources: clustering, beamforming, and power allocation scheme to attain transmitted power minimization subject to a rate constraint for each user. The joint problem is split into three sub-problems: clustering, which is formulated as a mixed integer linear programming problem, beamforming, and power allocation.

DL MIMO-NOMA and DL M-MIMO-NOMA transmission schemes can be broadly classified into two categories: the beamformer-based structure, in which one beamformer is used for each user, and the cluster-based structure, where one beamformer serves multiple users; e.g., as in [4]. In this work, we focus on the cluster-based MIMO NOMA structure, which is based on separating the users and grouping them into several clusters while each beamformer serves all the users of a specific cluster. Then, by applying an appropriate detector design, the intercluster interference (ICI) can be reduced substantially or even totally suppressed, depending on which beamformer is used.

A cluster-based MIMO-NOMA design is proposed by [15]. In contrast to the ones mentioned before, this design allows the existence of ICI, applying specific user grouping and power allocation schemes in order to reduce this kind of interference. Besides, it was assumed a configuration with N transmit antennas at the BS and N clusters, with the assumption that each cluster has two users for the sake of simplicity. It was also assumed each user has a single antenna. Among the users in a specific cluster, the user who has a larger (smaller) channel gain is defined as a strong (weak) user. As a simple and practical alternative, zero-forcing beamforming (ZF-BF) is used under perfect channel state information at the transmitter (CSIT), and the precoding is performed by considering the channel gain of a particular user of each cluster. The user using the BF vector based on its own channel does not receive any interference from the other beams, i.e., ICI is virtually zero. On the other hand, the other users belonging to the same cluster suffer intracluster interference (IaCI), which negatively affects the decoding of the received signal. Since it is unhelpful when the strong users perform successive interference cancelation (SIC), the authors consider the generation of the BF vectors based on the channels of the strong users of each cluster. To minimize the IaCI of the weaker channel users and maximize the sum capacity while guaranteeing the capacity requirement of the weak user, the authors respectively propose a clustering algorithm and a suitable power allocation scheme.

Another cluster-based MIMO-NOMA design is proposed in [16]. This design also allows the existence of ICI, applying a technique for reducing the interference and increasing the strength of the desired signals. The authors of [16] also utilize a ZF-BF technique, but in this approach, the precoding is performed by considering the equivalent channel gain of each cluster, instead of any particular user channel gain.

In this work, we deal with a kind of user-clustering approach based on making the channel gains of users more distinctive and sorting the users in a specific cluster according to their equivalent normalized channel gains. This strategy enables the user with the highest channel gain, namely cluster head, to have its gain very similar to the cluster equivalent channel gain, and thus to be able to almost completely cancel both the ICI and IaCI by invoking ideal SIC. Hence, each of the other users in the cluster efficiently suppresses the ICI by estimating their own cluster’s equivalent channel gain, by multiplying their received signal by a user-specific decoding scaling weight factor sent by the base station (BS) prior to the data transmission process.

The main advantage of this custer interference-tolerant designs is that they do not impose any number of antennas constraints at the BS or at the users, which implies that the number of antennas in each user is not somehow attached to the number of antennas at the BS and, thus, these design can be applied to scenarios where the BS is equipped with a large antenna array, such as in massive MIMO and extra large MIMO (SL-MIMO) based NOMA systems or NOMA millimeter-wave communication scenarios.

1.2 Contributions

In this paper, we consider the multiuser power allocation for a cluster-based DL MIMO-NOMA system, aiming at achieving a fair balance between the SE and the EE through the use of the RE as a more general and flexible figure-of-merit measure. An improved clustering-based NOMA M-MIMO structure is proposed under the RE perspective. Users of Power-domain NOMA M-MIMO are grouped into several clusters with each beamforming (BF) serving the users from a specific cluster. The RE figure of merit in downlink (DL) NOMA M-MIMO is evaluated by applying power allocation (PA) strategies. Based on two different channel cluster-head selection strategies (Type I – equivalent channel vectors; Type II – channel matrix singular value decomposition), the cluster-head is able to effectively mitigate intra-cluster interference. The main contributions of this work are threefold:

(a):

A full analysis and evaluation of a clustering-based NOMA structure in massive MIMO under the resource efficiency (EE-SE tradeoff) perspective by combining the EE and SE performance metrics;

(b):

The proposed methodology indicated a preferable grouping strategy for achieving the RE optimality;

(c):

Extensive numerical evaluation of two types of grouping-based NOMA-MIMO schemes corroborating the resource efficiency performance gains.

1.3 Notation

In the following, boldface lowercase and uppercase characters denote vectors and matrices, respectively. The operators \((\cdot )^H\), \({\textrm{tr}}\left( {\cdot } \right)\) and \({\mathbb {E}}\left[ {\cdot } \right]\) denote conjugate transpose, trace, and expectation, respectively. The \(M \times M\) identity matrix is denoted by \(\mathbf {{I}}_M\). A random vector \(\mathbf {{x}} \sim {\mathcal {C}}{\mathcal {N}}\{\mathbf {{m}},{\varvec{\Theta }}\}\) is complex Gaussian distributed with mean vector \(\mathbf {{m}}\) and covariance matrix \({\varvec{\Theta }}\).

The remainder of this paper is divided as follows. The system model is described in Sect. 2. NOMA precoding designs and user grouping are discussed in Sect. 3. Power allocation schemes under the RE criterion are discussed in Sect. 4. In Sect. 5, numerical results are provided, and the work is concluded in Sect. 6.

2 System Model

Let’s consider a DL multi-user (MU) MIMO-NOMA system with a single cell and one BS equipped with M transmit antennas for beamforming formation. The total number of user equipment (UE) in a cell is K, where \(K\geqslant M\), and each UE is considered to have one receive antenna. Also, the receive antennas are grouped into N clusters, and the n-th cluster consists of \(K_n\) receive antennas such that \(\sum _{n=1}^{N}K_n = K\). The users in each cluster are scheduled according to the NOMA principles. The NOMA features include: (a) the exploitation of the power difference of users and the asymmetric application of SIC in the power and rate allocation, mainly in DL NOMA; (b) a user close to BS and a user far away from the BS form a group or cluster; the former and latter users are called strong and weak users, respectively (channel gains); (c) it is expected to transmit a higher power to the weak user than the strong user due to path loss; (d) SIC principle: assuming the same radio resource block (RB), the signal to the weak user received by the strong user results in a higher SINR than that at the weak user, which implies that the strong user is able to decode the signal to the weak user and remove it using SIC to decode the desired signal without multiple access interference (MAI). On the other hand, at the weak user, the signal to the strong user is negligible as its transmission power is lower than that of the weak user. Thus, the weak user decodes the desired signal without using SIC; (e) Power difference exploitation is crucial in NOMA: there are different power allocation schemes for NOMA, considering fairness (equal rate allocation), EE, and RE concepts.

In the assumed conditions, each BF vector serves an individual cluster, which means all clusters use the same spectrum resources. For simplicity, in this analysis, we assume each UE equipped with a single antenna and a fixed number \({\mathcal {K}}\) of users in each cluster, i.e., \(K = {\mathcal {K}}\times N\).

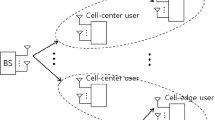
The users are considered randomly distributed in a hexagonal cell, and the BS is assumed to be located at its center. Figure 1 illustrates a generic system cell following the described assumptions. The most significant distance from the center to the edge of the cell is denoted by r. We also consider a minimum distance from the BS where the users are located, represented as a disk with a radius \(r_1~~ (r_1 \ll r)\), and with the BS situated at its center.

Fig. 1
figure 1

Generic clusterized MU-MIMO NOMA system model. K is the # user; \({\mathcal {K}}\) is the # users per cluster. Cluster-heads are assumed to be distributed within the specific distance \(r_1\) from BS. The BS is considered to have \(M\in [4; \,\, 128]\) antennas

Full size image

The data stream for the n-th cluster, corresponding to the n-th element of the transmitted data vector is defined as:

$$\begin{aligned} \textrm{s}_n = \sum _{k=1}^{{\mathcal {K}}}\sqrt{p_{n,k}}{\bar{s}}_{n,k}, \end{aligned}$$
(1)

where \(p_{n,k}\) and \({\bar{s}}_{n,k} \sim {\mathcal {C}}{\mathcal {N}}\{0,1\}\) are the transmit power and symbol of the k-th user from the n-th cluster, and \(\sum _{k=1}^{{\mathcal {K}}}p_{n,k} = 1\).

The transmitted data vector \({\textbf{s}} \in {\mathbb {C}}^{M\times 1}\) is then defined as:

$$\begin{aligned} {\textbf{s}} = \begin{bmatrix} \textrm{s}_{1}&\textrm{s}_{2}&\ldots&\textrm{s}_{n}&\ldots&\textrm{s}_{N} \end{bmatrix}^{\intercal }. \end{aligned}$$
(2)

Also, the data vector \({\textbf{s}}\) is multiplied by a power matrix \(\mathbf {{P}} \in {\mathbb {R}}^{N \times N}\) and a precoding matrix \({\textbf{G}} \in {\mathbb {C}}^{M\times N}\) and, then, transmitted over a radio channel \({\textbf{H}} \in {\mathbb {C}}^{K\times M}\). Each \({\textbf{H}}_n \in {\mathbb {C}}^{{\mathcal {K}}\times M}\) represents the radio channel of all \({\mathcal {K}}\) users in the n-th cluster, and can be expressed as:

$$\begin{aligned} {\textbf{H}}_n = \begin{bmatrix} {\textbf{h}}_{n,1}&{\textbf{h}}_{n,2}&\ldots&{\textbf{h}}_{n,{\mathcal {K}}} \end{bmatrix}^{\textsc {t}}, \end{aligned}$$
(3)

with \({\textbf{h}}_{n,k} \in {\mathbb {C}}^{1 \times M}\) as the radio channel gain vector of the k-th user in the n-th cluster, composed by the product of pathloss (long term) \(\beta _{n,k}\) and the short-term (small scale) fading term.

Thus, the radio channel matrix \({\textbf{H}} \in {\mathbb {C}}^{K\times M}\) is expressed as:

$$\begin{aligned} {\textbf{H}} = \begin{bmatrix} {\textbf{H}}_1&{\textbf{H}}_2&\ldots&{\textbf{H}}_n&\ldots&{\textbf{H}}_N \end{bmatrix}^{\intercal }. \end{aligned}$$
(4)

The power matrix corresponding to the power allocated to each cluster is defined as \(\mathbf {{P}} = \textrm{diag}(p_1,\cdots ,p_N) \in {\mathbb {R}}^{N \times N}\), with \(\sum _{n=1}^{N}p_n = P_{\textsc {t}}\), where \(P_{\textsc {t}} \geqslant 0\) is the total available transmit power at the BS.

The transmitted signal \({\textbf{x}} \in {\mathbb {C}}^{M\times 1}\) obtained after the power and precoding vector \(\mathbf {{g}}_n \in {\mathbb {C}}^{M\times 1}\) for each cluster \(n=1,\ldots ,N\) can be written as:

$$\begin{aligned} {\textbf{x}} = {\textbf{G}} \mathbf {{P}}^{1/2}{\textbf{s}} = \sum _{n=1}^{N}\sqrt{p_n}\mathbf {{g}}_ns_n. \end{aligned}$$
(5)

Also, the precoding vectors are normalized to satisfy the average power constraint thus:

$$\begin{aligned} {\mathbb {E}}\left[ {\parallel \mathbf {{x}} \parallel ^2} \right] = {\textrm{tr}}\left( {\mathbf {{P}}\mathbf {{G}}^H\mathbf {{G}}} \right) \leqslant P_{\textsc {t}}, \end{aligned}$$
(6)

Hence, the SNR at the transmitter side is denoted as \(\gamma = \frac{P_{\textsc {t}}}{\sigma ^2}\).

The received signal \({\textbf{y}} \in {\mathbb {C}}^{K \times 1}\) can be expressed as:

$$\begin{aligned} {\textbf{y}} = \begin{bmatrix} {\textbf{y}}_{1}&{\textbf{y}}_{2}&\ldots&{\textbf{y}}_{n}&\ldots&{\textbf{y}}_{N} \end{bmatrix}^{\intercal }, \end{aligned}$$
(7)

where each \({\textbf{y}}_{n} \in {\mathbb {C}}^{{\mathcal {K}} \times 1}\) is constituted by the signals received for each of the \({\mathcal {K}}\) users in the n-th cluster, such as:

$$\begin{aligned} {\textbf{y}}_{n} = \begin{bmatrix} \textrm{y}_{n,1}&\textrm{y}_{n,2}&\ldots&\textrm{y}_{n,k}&\ldots&\textrm{y}_{n,{\mathcal {K}}} \end{bmatrix}^{\intercal }, \end{aligned}$$
(8)

where \(\textrm{y}_{n,k} \in {\mathbb {C}}\) corresponds to the signal received by the k-th user of the n-th cluster.

The array \({\textbf{y}} \in {\mathbb {C}}^{K \times 1}\) can be written in terms of its components as:

$$\begin{aligned} {\textbf{y}} = {\textbf{H}} {\textbf{G}} {\textbf{P}}^{1/2} {\textbf{s}} + {\textbf{z}}, \end{aligned}$$
(9)

where \({\textbf{z}} \sim {\mathcal {C}}{\mathcal {N}}\{{\textbf{0}}_{K\times 1},\sigma ^2{{\textbf{I}}_K}\}\) represents the complex Gaussian noise vector with variance \(\sigma ^2\), whose elements are represented as \(\textrm{z}_{n,k} \sim {\mathcal {C}}{\mathcal {N}}\{0,\sigma ^2\}\). The received signal for the k-th user in the n-th cluster can then be expressed as:

$$\begin{aligned} \textrm{y}_{n,k} = {\textbf{h}}_{n,k}{\textbf{G}}\mathbf {{P}}^{1/2}\mathbf {{s}}+\textrm{z}_{n,k}. \end{aligned}$$
(10)

3 Precoding Design and Grouping Strategy

In the MIMO-NOMA model under consideration, with \(K>M\), and thus we utilize a precoding technique suggested by [16], which is based on [17], where the actual channel matrix \({\textbf{H}}_n \in {\mathbb {C}}^{{\mathcal {K}}\times M}\), defined in (11), corresponding to the \({\mathcal {K}}\) users of the n-th cluster is transformed into an equivalent channel vector \(\bar{{\textbf{h}}}_n \in {\mathbb {C}}^{1\times M}\), defined as either the channel of the user closer to the BS in each cluster (Type I) or as SVD of the \({\textbf{H}}\) (Type II). This manipulation then leads to a total channel matrix \(\bar{{\textbf{H}}} \in {\mathbb {C}}^{N\times M}\) as an equivalent to \({\textbf{H}}\), which provides compatible dimension for precoding application. The radio channel matrix corresponding to the n-th cluster can be expressed as:

$$\begin{aligned} {\textbf{H}}_n = \begin{bmatrix} {\textbf{h}}_{n,1}&{\textbf{h}}_{n,2}&\ldots&{\textbf{h}}_{n,k}&\ldots&{\textbf{h}}_{n,{\mathcal {K}}} \end{bmatrix}^{\intercal }. \end{aligned}$$
(11)

3.1 Cluster-Head Selection Strategies

In the context of this work, the channel cluster-heads are obtained in two ways: (a) as the equivalent channel vectors in Eq. (12), namely MIMO-NOMA Type I; (b) applying singular value decomposition (SVD) on the channel matrix \({\textbf{H}}_n\) in Eq. (14), and referred herein as MIMO-NOMA Type II.

Type I—Channel matrix based on equivalent channel vectors For calculating the equivalent channel matrix let’s assume the channel of the user closer to the BS in each cluster as the cluster equivalent channel vector, such as adopted in [15]. According to this approach, the equivalent radio channel matrix \(\bar{{\textbf{H}}} \in {\mathbb {C}}^{N\times M}\) formed by the equivalent channels of all the N clusters can be expressed as:

$$\begin{aligned} {\bar{{\textbf{H}}}} = \begin{bmatrix} \bar{{\textbf{h}}}_1&\bar{{\textbf{h}}}_2&\ldots&\bar{{\textbf{h}}}_n&\ldots&\bar{{\textbf{h}}}_N \end{bmatrix}^{\intercal }. \end{aligned}$$
(12)

Type II—Channel matrix based on singular value decomposition (SVD). Taking the SVD of \({\textbf{H}}_n\) we obtain:

$$\begin{aligned} {\textbf{H}}_{n_{[{\mathcal {K}}\times M]}} = {\textbf{U}}_{n_{[{\mathcal {K}}\times {\mathcal {K}}]}} {\varvec{{\Sigma }}}_{n_{[{\mathcal {K}}\times M]}}{\textbf{V}}_{n_{[M\times M]}}^H. \end{aligned}$$
(13)

In the considered system, each beamforming vector is utilized by one cluster. According to this configuration, the equivalent radio channel matrix \(\bar{{\textbf{H}}}_n \in {\mathbb {C}}^{1\times M}\) representing the equivalent channel of the n-th cluster can be obtained as:

$$\begin{aligned} {\bar{{\textbf{H}}}}_{n_{[1\times M]}} = {\textbf{u}}_{{n,1}_{[1\times {\mathcal {K}}]}}^{H}{\textbf{U}}_{n_{[{\mathcal {K}}\times {\mathcal {K}}]}} {\varvec{{\Sigma }}}_{n_{[{\mathcal {K}}\times M]}} {\textbf{V}}_{n_{[M\times M]}}^H, \end{aligned}$$
(14)

where \({\textbf{u}}_{n,1}^{H}\) is the Hermitian transpose of the first column of \({\textbf{U}}_n\) in (13).

3.2 RZF Precoding

In this work, we considered the regularized zero-forcing (RZF) precoding, which can be faced as a generalization of the Zero-Forcing (ZF) precoding, in which a regularization parameter is added to the pseudo-inverse matrix. Considering a system equipped with the RZF precoder and the equivalent channel matrix \(\bar{\mathbf {{H}}}\), the precoding matrix solution is given by [18,19,20]:

$$\begin{aligned} \mathbf {{G}}_{{\textsc {zf}}} = \alpha \bar{\mathbf {{H}}}^H\left( {\bar{\mathbf {{H}}}\bar{\mathbf {{H}}}^H + \xi {\textbf{I}}_M} \right) ^{-1}, \end{aligned}$$
(15)

or equivalently as

$$\begin{aligned} \mathbf {{G}}_{{\textsc {zf}}} = \alpha \left( {\bar{\mathbf {{H}}}^H\bar{\mathbf {{H}}} + \xi {\textbf{I}}_M} \right) ^{-1}\bar{\mathbf {{H}}}^H, \end{aligned}$$
(16)

where the normalizing constant \(\alpha\) is chosen to satisfy the power constraint (6), and \(\xi > 0\) is the regularization parameter.

As stated in [21], by assuming independence between the data symbols, the normalization constant for the RCI precoding is expressed as

$$\begin{aligned} \alpha = \sqrt{\dfrac{P_{{\textsc {{t}}}}}{{\textrm{tr}}\left( {{\mathbf {{P}}}\bar{\mathbf {{H}}}\left( {\bar{\mathbf {{H}}}^H\bar{\mathbf {{H}}} + \xi {\textbf{I}}_M} \right) ^{-2}\bar{\mathbf {{H}}}^H } \right) }}, \end{aligned}$$
(17)

where now the normalization factor \(\alpha\) depends on the channel realization \({\textbf{H}}\), as well as the regularization factor \(\xi\).

3.3 System Throughput

Using the RZF precoder (16), the received vector \(\mathbf {{y}}\) and signal \(y_{n,k}\) for each user can be respectively expressed as

$$\begin{aligned} \mathbf {{y}} = \alpha \mathbf {{H}}\left( {\bar{\mathbf {{H}}}^H\bar{\mathbf {{H}}} + \xi \mathbf {{I}}_M} \right) ^{-1}\bar{\mathbf {{H}}}^H\mathbf {{P}}^{1/2}\mathbf {{s}} + \mathbf {{n}} \end{aligned}$$
(18)

Since SIC is performed within each MIMO-NOMA cluster, the dynamic power allocation in each of them is performed in a way a user can decode and then supress the intra-cluster interference from users with channel gains lower then its own. Thus, the signal received for the k-th user of the n-th cluster is denoted by:

$$\begin{aligned} y_{n,k}&= \alpha \sqrt{p_n}{\textbf{h}}_{n,k}\left( {\bar{\mathbf {{H}}}^H\bar{\mathbf {{H}}} + \xi \mathbf {{I}}_M} \right) ^{-1}\bar{\mathbf {{h}}}_{n}^H\sqrt{p_{n,k}}{\bar{s}}_{n,k} + \nonumber \\&\quad + \underbrace{\alpha \sqrt{p_n}{\textbf{h}}_{n,k}\left( {\bar{\mathbf {{H}}}^H\bar{\mathbf {{H}}} + \xi \mathbf {{I}}_M} \right) ^{-1}\bar{\mathbf {{h}}}_{n}^H\sum _{j=1}^{k-1}\sqrt{p_{n,j}}{\bar{s}}_{n,j}}_{\text {intra-cluster interference}} + \nonumber \\&\quad + \underbrace{\sum _{i=1,i\ne n}^{N} \alpha \sqrt{p_i}{\textbf{h}}_{n,k}\left( {\bar{\mathbf {{H}}}^H\bar{\mathbf {{H}}} + \xi \mathbf {{I}}_M} \right) ^{-1}\bar{\mathbf {{h}}}_{i}^H\textrm{s}_i}_{\text {inter-cluster interference}} + \textrm{z}_{n,k}, \end{aligned}$$
(19)

where the first term in the right side of (19) is the desired signal for the k-th user from the n-th cluster, while the other terms are the interference introduced by the other users in the same cluster and in other clusters plus the received thermal noise. In order to avoid excessive complexity, we advocate the use of single-user detection at the DL receiver side (UE)Footnote 2. Hence, the SINR in each user is expressed as in Eq. (20) [18, 22].

$$\begin{aligned} \text {SINR}_{n,k} = \frac{\alpha ^2|{\textbf{h}}_{n,k}\left( {\bar{\mathbf {{H}}}^H\bar{\mathbf {{H}}} + \xi \mathbf {{I}}_M} \right) ^{-1}\bar{\mathbf {{h}}}_{n}^H|^2 {p_{n,k}}}{\underbrace{\alpha ^2|{\textbf{h}}_{n,k}\left( {\bar{\mathbf {{H}}}^H\bar{\mathbf {{H}}} + \xi \mathbf {{I}}_M} \right) ^{-1}\bar{\mathbf {{h}}}_{n}^H|^2 p_n\sum _{j=1}^{k-1}p_{n,j}}_{\text {intra-cluster interference}} + \underbrace{\sum _{i=1,i\ne n}^{N} \alpha ^2|{\textbf{h}}_{n,k}\left( {\bar{\mathbf {{H}}}^H\bar{\mathbf {{H}}} + \xi \mathbf {{I}}_M} \right) ^{-1}\bar{\mathbf {{h}}}_{i}^H|^2 p_i}_{\text {inter-cluster interference}} + \underbrace{\sigma ^2}_{\text {Noise}} }. \end{aligned}$$
(20)

The achievable throughput for the k-th user of the n-th cluster can then be bounded as:

$$\begin{aligned} R_{n,k} = \log _2 \left( 1 + \text {SINR}_{n,k} \right) \qquad \text {[bits]}, \end{aligned}$$
(21)

where \(\text {SINR}_{n,k}\) is given by Eq. (20), where the IaCI and ICI are explicity indicated. Finally, the overall achievable cell system throughput for this clustering based system is given by:

$$\begin{aligned} R_{\textrm{cell}} = \sum _{m=1}^{M}\sum _{k=1}^{{\mathcal {K}}} \log _2 \left( 1 + \text {SINR}_{m,k} \right) \qquad \text {[bits]}. \end{aligned}$$
(22)

3.4 User Grouping Strategy

The optimal user grouping for conventional NOMA and MIMO NOMA systems requires an exhaustive search among all the users in a cell, in order to consider all possible combinations of user grouping for each particular user [16, 23]. This requirement leads to an extremely high computational complexity for optimal user clustering in MIMO NOMA systems, and thus can not be used in practical systems.

In M-MIMO system, each device is served by a single beamforming vector. The ZF technique is a popular interference suppressing beamforming since it eliminates all inter-user interference using individual beamforming for each device, while such interference suppressing is facilitated by the favorable propagation in massive MIMO configurations. To perform ZF precoding in NOMA system, it is essential to understand the NOMA user-pairing concept.

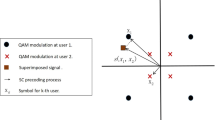
Inherent to the power-domain NOMA system, user clustering can be performed in several ways after the user-sorting and the user classification in center-users and edge-users subsets. Because we know that the SE of NOMA is directly proportional to the difference between the pathloss of the users, a natural choice consists in pairing users with as higher as possible pathloss differences [24]. For the case of \({\mathcal {K}}=2\):

$$\begin{aligned} \Delta \beta _k = \beta _k - \beta _{K+1-k}, \end{aligned}$$
(23)

forming the cluster for \(n = 1,...,N\). With the pair formed, carefully beamforming vector selection is required. Hence, in NOMA we assume that the beamforming vector for paired users is the same.

Assumption 1: In user-pairing procedure, we assume that the paired users are aligned with the BS so that the same beamforming can serve all paired users simultaneously. Hence, by admitting that each pair of devices is spatially aligned with the BS, and using localizing tools described, for instance, in [25, 26], one should assume a priori user-pairing step in NOMA systems. In assuming user-pairing step available, the (near) aligned users regarding the BS.Footnote 3 will be selected to form a specific cluster, as suggested in Fig. 1. The motivation for choosing aligned users as a cluster formation criterion lies in inter-cluster interference reduction, facilitating the precoding design while improving SE and RE.

Assumption 2: In NOMA system, beamforming serves more than one aligned device simultaneously; specifically, in this paper, two or more aligned devices per cluster are admitted according to the user-pairing step, while eliminating the inter-cluster interference completely (favourable propagation) under adopted perfect CSI conditions.

In a conventional NOMA system, it is preferable to pair users whose channel conditions are significantly different, what improves the sum-rate of the users belonging to the same cluster, and also its respective individual user’s rate [1]. In our work we utilize a sub-optimal user clustering scheme for DL MIMO NOMA systems, which exploits the channel gain differences among the users combined to a power allocation scheme targeting an enhancement in the sum-spectral efficiency in the cell.

According to the user-clustering scheme proposed in this work, the cluster head in each DL MIMO NOMA cluster can almost completely cancel the intra-cluster interference, thus, achieving maximum throughput gain in comparison to the other users in the cluster. Based on this consideration, one strategy to maximize the overall system capacity in each cluster consists in selecting the high channel gain users in the cell as the cluster-heads of different MIMO NOMA clusters. This consideration can also be used to determine the number of clusters in the cell, based on the number of high channel gain users available.

3.5 Resource Efficiency (RE)

Instead of focusing on the SE or the EE separately as in the traditional design, it is much more effective balance the attainable system SE and EE by adopting the resource efficiency (RE) metric, such as discussed in [5, 6].

Conventional system designs usually focus on the SE, defined for a single cell system with K single-antenna users and a BS equipped with M antennas as

$$\begin{aligned} \textrm{SE} = \sum _{i=1}^{K} R_i\,\, =\,\, \sum _{i=1}^{K} \log _2(1 + \textrm{SINR}_i)\qquad \text {[bits]}. \end{aligned}$$
(24)

On the other hand, the energy efficiency (EE) has became an important figure of merit in the wireless communication systems; the EE is defined as the ratio of the weighted sum-rate to the total power consumption. The EE in (bits/Hz/Joule) or (bits/W) for the same K user single-cell system can be expressed as:

$$\begin{aligned} \text {EE} = \frac{\text {SE}}{\varpi \sum _{i=1}^{K}p_i + MP_c + P_0} \qquad \left[ \frac{\textrm{bits}}{\textrm{W}}\right] , \end{aligned}$$
(25)

where \(P_c\) is assumed a constant circuit power consumption per BS antenna, including power dissipations in the transmit filter, the mixer, the frequency synthesizer, and the digital-to-analog converter; \(P_0\) is the basic power consumed at the BS which is independent of the number of transmit antennas and \(\varpi > 1\) is a constant accounting for the inefficiency of the RF power amplifier at the BS [6].

The resource efficiency is expressed as a weighted sum of the EE and the SE, and can be formulated as:

$$\begin{aligned} \text {RE} = \text {EE} + \mu \frac{ \text {SE}}{\varpi P_{\textsc {t}} + MP_c + P_0} \qquad \left[ \frac{\textrm{bits}}{\textrm{W}}\right] , \end{aligned}$$
(26)

where \(\mu \geqslant 0\) is the weighting factor, controlling the priority of EE and the SE on the design. When \(\mu = 0\), Eq. (26) reduces to the EE; on the other hand, it tends to the SE for \(\mu \gg 1\). Hence, the weight value choice should be defined by the system designer [6]. Notice that the denominator of the second term of (26) is a normalization used to unify the units of the two terms, expressing the maximum power consumption allowed (lower EE) when all M antennas at the BS are activated and the total RF power resource (\(P_{\textsc {t}}\)) has been fully allocated.

3.6 RE Applied to Cluster-Based MIMO-NOMA Design

In order to apply the RE concept and analyze the performance of the defined cluster-based MIMO-NOMA system model, one can define the spectral efficiency metric for NOMA system as:

$$\begin{aligned} \textrm{SE}_{\textrm{noma}} = \sum _{n=1}^{N}\sum _{k=1}^{{\mathcal {K}}} R_{n,k}. \end{aligned}$$
(27)

where N is the number of clusters; hence, the cluster loading is simply defined by \({\mathcal {C}} = \frac{{\mathcal {K}}}{K}\). Furthermore, based on (25) the EE in NOMA system can be expressed as:

$$\begin{aligned} \text {EE}_{\textrm{noma}} = \frac{\sum _{n=1}^{N}\sum _{k=1}^{{\mathcal {K}}} R_{n,k}}{\varpi \sum _{n=1}^{N}p_{n} + MP_c + P_0}. \end{aligned}$$
(28)

where \(p_{n}\) is the power consumption in the nth cluster.

Finally, the RE for MIMO-NOMA can be defined combining (27) and (28) into (26) as:

$$\begin{aligned} \text {RE} _{\textrm{noma}} = \text {EE}_{\textrm{noma}} + \mu \cdot \frac{ \text {SE}_{\textrm{noma}} }{\varpi P_{{\textsc {t}}} + MP_c + P_0} \,\, \quad \left[ \frac{\textrm{bits}}{\textrm{W}}\right] . \end{aligned}$$
(29)

with \(\mu \in \Re _{+}\). Notice that the RE for MIMO-NOMA depends on both the adopted power allocation policy, \(P_{n,k}\), as well as the cluster formation strategy, which impacts the n-th set \({\mathcal {K}}_n\) and respective power allocated to each user belonging to this subset, \(p_{n,k}\).

4 Adopted Power Allocation Strategy in NOMA

In this MIMO-NOMA system, the power allocation is performed in a two-step method [16]. First, the total BS transmit power is divided into the number of transmit beams, and the transmit power for a beam is proportional to the number of users served by that beam/cluster, i.e., \(p_n \,\, \propto \,\, {\mathcal {K}}_n\), where \({\mathcal {K}}_n\) is the number of users inside the cluster n.

Step 1.:

Power per Cluster: For simplicity of analysis, but without loss of generality, let’s consider all the clusters have the same number of users \({\mathcal {K}} \equiv {\mathcal {K}}_n, \forall n\), then all the transmit beams serve the same number of users and, thus, the BS transmit power \(P_{\textsc {t}}\) is equally divided among the beams.

$$\begin{aligned} p_n \,\, = \,\, \frac{P_{\textsc {t}}}{{\mathcal {K}}}, \qquad n=1, 2,\ldots , N \end{aligned}$$
(30)

where \(P_{\textsc {t}}\) is the BS transmit power budget.

Step 2.:

Power per User: The PA per user into each NOMA cluster method consists in allocating a fraction of available power per cluster \(p_n\) for individual user in each cluster. The PA for the \({\mathcal {K}}\) at the nth cluster is scheduled according to the power-domain NOMA principle, and thus the intra-cluster dynamic power allocation is essential. We adopt a PA procedure based on the inversion of channel state (ICS). In the sequel we describe the ICS procedure.

4.1 PA Based on CSI Inversion

In this strategy, the power coefficients are determined based on the CSI experienced by the n-th cluster of the k-th user. The relation between the power shared per user and its channel state is assumed to be inversely proportional:

$$\begin{aligned} p_{n,k} ~\propto ~ \frac{1}{{\mathbb {E}}[{\textbf{h}}_{n,k}]}, \end{aligned}$$
(31)

where \({\mathbb {E}}[{\textbf{h}}_{n,k}]\) is the average radio channel gain taken over M antennas, and updated at each channel coherence time. This PA strategy means that the BS assigns highest power fractions to users which experience weak channel conditions, while assigning less power to the users with strong channel gain conditions [27]. As a result, the power fraction assigned to the k-th user from the n-th cluster is:

$$\begin{aligned} p_{n,k} = \frac{{\mathbb {E}}[{\textbf{h}}_{n,i}]}{{\mathbb {E}}[{\textbf{h}}_{n,k}]} p_{n,i}, \quad ~~ i \ne k, \qquad i=1, 2, \ldots , {\mathcal {K}}_n. \end{aligned}$$
(32)

Considering the above equation and the fact that \(\sum _{k=1}^{{\mathcal {K}}_n}p_{n,k} = p_n\), one can write:

$$\begin{aligned} p_{n,k}\left( \sum _{i=1}^{{\mathcal {K}}_n}\frac{{\mathbb {E}}[{\textbf{h}}_{n,k}]}{{\mathbb {E}}[{\textbf{h}}_{n,i}]}\right) = p_n, \end{aligned}$$
(33)

which leads to following power allocation policy for user k belonging to the cluster n:

$$\begin{aligned} p_{n,k} = \left( {\mathbb {E}}[{\textbf{h}}_{n,k}] \sum _{i=1}^{{\mathcal {K}}_n} \frac{1}{{\mathbb {E}}[{\textbf{h}}_{n,i}]}\right) ^{-1}. \end{aligned}$$
(34)

5 Numerical Results

In this section, we investigate the performance of the proposed user-clustering and power allocation schemes via numerical simulations. The main parameters deployed in the numerical simulations are listed in Table 1.

Fig. 2
figure 2

Samples of users clusterization for \(K=128\) users: a \(N=2\); b \(N=4\), and c \(N=7\) clusters

Full size image
Table 1 MIMO-NOMA simulation parameters
Full size table

The radio channel was considered as the product of long-term (path-loss) and short-term (Rayleigh fading) described by a complex Gaussian distribution with zero mean and unit variance. The adopted path-loss model assumes that the transmitted signal power decays according to

$$\begin{aligned} {\mathcal {L}} = \frac{G_{0}}{(d_k)^{{\mathfrak {b}}}} \end{aligned}$$

where \(d_k\) is the distance between BS and the related user k, the term \({\mathfrak {b}}\) is the path-loss exponent, and \(G_{0}\) is the loss at a reference distance \(d_0\), considering Tx and Rx antenna gains. For analysis simplicity, a single cell has been considered, with the single BS located at the center of the cell area. The cell radius is set to \(r=500\) m while the distance between a user and the BS is confined to \(50<d_k< 500\) m. Hence, the average SNR at the receiver side is denoted as \(\bar{\gamma }_{\textrm{rx}} = {\mathcal {L}} \cdot \gamma = {\mathcal {L}}\cdot \frac{P_{\textsc {t}}}{\sigma ^2}\). The circuit power per antenna activation is assumed \(P_c =\) 30 dBm, and the necessary power consumed at the BS is defined as \(P_0 =\) 40 dBm. The inefficiency factor of the power amplifier is set to \(\varpi =1.5\). The cluster-heads are assumed to be distributed within a specific distance \(r_1\) from the BS, as sketched in Fig. 1. Figure 2 depicts examples of typical users’ spatial distribution inside the cell for different number of clusters and a fixed number of users \(K=128\).

In the following numerical results we discuss the MIMO-NOMA system performance in terms of system SE, EE and RE. For analysis simplicity, all the simulations are performed considering a single transmission time interval (TTI) with its instantaneous channel gains perfectly estimated, i.e., perfect CSI estimations. Besides, it is assumed the channel gains of the users in each cluster identically and independently distributed (i.i.d.), i.e., uncorrelated channel gains, aiming at evidencing the potential of each clustering and power allocation configurations subject to the spatial and power-domain diversity techniques.

Moreover, the channel cluster-heads is obtained as the equivalent channel vectors, denominated MIMO-NOMA Type I, while the channel cluster-heads obtained by applying singular value decomposition (SVD) on the channel matrix \({\textbf{H}}_n\) in eq. (14), is referred as MIMO-NOMA Type II. In the next two subsections, especially in Subsect. 5.2, both MIMO-NOMA clustering types are compared in terms of SE, EE, and RE performance.

5.1 SE, EE and RE for MIMO-NOMA Type I

Figure 3 depicts the SE, EE, and RE metrics for the MIMO-NOMA-I with \(M = 3\) antennas, \(K = 30\) users, considering different values of \(\mu \in [1; \, 20]\). As expected and predicted by Eq. (26), the RE reaches better performance for higher values of \(\mu\), emphasizing the importance of SE in the SE-EE tradeoff design.

Fig. 3
figure 3

MIMO-NOMA-I: SE, EE and RE vs weighting EE-SE factor (\(\mu\)) for \(M = 3\), \(K = 30\)

Full size image

Optimal number of BS antennas per user-cluster, \(\text {A}_{\text {optz}}\). Figure 4 depicts the SE, EE and RE of MIMO-NOMA I for different values of BS antennas \(M\in \{4;\, 128\}\), and fixed number of mobile terminals (\(K=128\)) and a cluster loading \({\mathcal {C}} = 0.25\); while a high weighting factor SE-EE (\(\mu =10\)) is considered since as predicted by Eq. (26), the RE reaches better performance for higher values of \(\mu\). However, the EE and RE values do not improve substantially when the number of BS antennas increases beyond \(M\approx 64\). Such a massive antenna array serves \(N=4\) clusters, each one with a fixed \({\mathcal {K}}=32\) [users/ cluster]. One can conclude that the RE and EE do not improve substantially beyond:

$$\begin{aligned} \text {A}_{\text {optz}} = \frac{M}{{\mathcal {K}}} \approx 2 \,\, \left[ \frac{\text {antennas}}{\text {users per cluster}}\right] . \end{aligned}$$

as a consequence of the favorable propagation effect.

Fig. 4
figure 4

SE, EE and RE for different number of antennas M, \(\mu =10\), cluster loading \({\mathcal {C}}=\frac{{\mathcal {K}}}{K} =\frac{1}{4}\), and fixed \(K=128\)

Full size image

Optimal number of users per cluster, \({\mathcal {K}}_{\text {optz}}\). Figure 5 presents the RE vs. SNR of the MIMO-NOMA Type I system for different numbers of antennas at the BS, setting \(M=N\) clusters, and different numbers of users per cluster \({\mathcal {K}}=\frac{K}{N}=\frac{30}{N}\) in the cell and with a fixed \(K=30\) number of users. By analyzing the RE system performance when the number of clusters N is changed, one can see the condition in which the higher RE is attained is:

$${\mathcal{K}}_{{{\text{optz}}}} = 2{\mkern 1mu} {\mkern 1mu} \left[ {\frac{{{\text{users}}}}{{{\text{cluster}}}}} \right],$$

which is achieved in Fig. 5 under \(M=15\) antennas and \(K=30\) users for all range of SNR values. This is an expected result since a higher number of antennas at the BS implies a higher directivity in the transmission to each cluster, reducing the ICI. Also, the resultant smaller number of users per cluster \({\mathcal {K}}\) leads to reduced intra-cluster interference (IaCI). Interestingly, we have found that instead of having the condition of three users per cluster as the second best performance condition in MIMO-NOMA Type I, however, we have obtained the condition \(M = 5\) antennas, which results in a total of \({\mathcal {K}}=6\) [users/cluster], corresponding to the second highest RE results.

Fig. 5
figure 5

RE for \(M \in [3; 5; 6; 10; 15]\), \(K = 30\) and \(\mu = 10\)

Full size image

5.1.1 Optimal Transmit Power

Figure 6 analyses the resource efficiency as a function of BS transmit power budget \(P_{\textsc {t}}\in [1;\, 31]\) [dBm], considering three SE-EE weighting factor: \(\mu =1, 5\) and 10, with \(M = 64\), and cluster loading \({\mathcal {C}} =0.25\). As one can see from Eq. (26), the RE reaches better performance for higher values of \(\mu\), while it is invariant with the weighting factor value. Indeed, there is an optimal value of transmit power budget \(P_{\textsc {t}}^*\) that maximizes the RE regardless the \(\mu\) value. In the adopted system configuration, this value results \(P_{\textsc {t}}^*=7\) [dBm], \(\forall \,\,\mu \in [1; 10]\).

Fig. 6
figure 6

RE as a function of BS transmit power budget \(P_{\textsc {t}}\) [dBm] for \(M = 64\) antenas, \(K=128\), and \({\mathcal {C}}=\frac{{\mathcal {K}}}{K} =\frac{1}{4}\)

Full size image
Fig. 7
figure 7

RE MIMO-NOMA I and II for \(M \in [3, 5]\), \(K \in [30, 60]\) and \(\mu = 10\)

Full size image

5.2 MIMO-NOMA Type I vs MIMO-NOMA Type II

A comparison of the two MIMO-NOMA channel equivalent calculations is presented in Fig. 7 for different system dimensions \(M\cdot K\). Remember that the equivalent channel calculation for MIMO-NOMA Type II is obtained by applying the singular value decomposition (SVD) on the \({\textbf{H}}_n\) in Eq. (14). As one can infer from these results, the MIMO-NOMA Type II approach is inferior to MIMO-NOMA Type I regarding RE, presenting a plateau in RE value when SNR increases, indicating that the singular value decomposition of the channel matrix is a sub-optimal and inefficient approach to attain high RE performance. Such RE difference regarding Type I and II appears to become more remarkable for an increase in the number of users in this MIMO system configuration. Among relevant information depicted in Fig. 7, one can highlight the reduction in the system performance for a larger number of users (\(K=60\)). This indicates there is a limit in the RE performance enhancement achieved by an increase in the value of K, after which the interference caused by the additional users per cluster implicates RE degradation. Besides, when the number of BS antennas is not enough to form suitable clusters with reduced ICI, which implies a high number of users per cluster, the RE degrades considerably under high SNR regime.

6 Conclusion

In this paper, we have analyzed the resource efficiency in a cluster-based MIMO NOMA system through the application of a simple two-step power allocation strategy for allocating transmit power per cluster and power per user. Following the proposed user-clustering scheme, the cluster head in each DL MIMO NOMA cluster can almost completely cancel the intra-cluster interference, and, thus, achieve enhanced throughput gains.

The analysis of the system performance in terms of RE demonstrated that the best performance occurs for two users per cluster. However, the second-highest RE values are not always attained for the subsequent higher numbers of users per cluster. Instead, there are conditions where a cluster configuration with a much higher number of users per cluster was shown to have the second-highest RE performance.

Another interesting finding reveals that, as a consequence of the favorable propagation effect, the RE and EE do not improve substantially beyond \(\text {A}_{\text {optz}} \geqslant 2 \, \left[ \frac{\text {antennas}}{\text {users per cluster}}\right]\), serving as a lower bound to the designer establish the minimum number of BS antennas in a massive MIMO system.

Comparing the RE performance attained by both MIMO-NOMA channel equivalent calculations (Type I vs. Type II) demonstrated that, for the assumed system conditions, the equivalent channel obtained through the SVD leads to inferior performance results, in comparison to the direct enumeration of the cluster head’s channel based on the higher channel gains.

Observing the system RE reveals that for an increase in the number of users also showed that an excessive number of users per cluster and when compared with the available number of BS antennas (M) can result in a remarkable degradation in the system RE performance.

In practice, it may not be realistic to schedule all the huge number of machine-type users in a few clusters using NOMA massive MIMO. An alternative is to build a hybrid system, in which NOMA is combined with OMA techniques such as OFDMA. In such a scheme, multiple clusters can utilize the same beamforming vector while using orthogonal spectrum resources to each other, with the users in each cluster scheduled according to the NOMA principles.