A novel game theoretic approach for market-driven dynamic spectrum access in cognitive radio networks

Abstract

Current cutting-edge solutions to the spectrum shortage problem are unable to meet the growing demand for a limited spectrum. A key dimension beyond state-of-the-art solutions is to exploit the free spectrum more effectively. Although various schemes have been proposed for trading spectrum, few studies have focused on optimal admission of spectrum requests for maximizing service providers' (SP’s) profit. Thus, this timely study presents a novel intelligent admission scheme for spectrum requests from the perspective of a non-cooperative game, in which the information of all participants (customers and providers) is incomplete to others, and each player wishes to maximize its benefit. The proposed control admission policy may evict clients in-service to release spectrum for serving certain, e.g., wealthy clients. Evicted clients are compensated using a dynamic strategy that adopts greedy game theory to capture the conflict of interest between SP and evicted users. Simulation experiment results validate and demonstrate the feasibility and efficiency of the proposed scheme, compared to a benchmark reinforcement learning approach and another widely used scheme for admission and eviction control of cognitive radio users.

1 Introduction

Dynamic spectrum allocation has been introduced to the spectrum market and has substantially increased SP's profit [1,2,3,4,5,6]. Implementation of advanced spectrum trading techniques has been thriving worldwide. Networks are characterized by a limited frequency spectrum, performance requirements, and high demand for service. In the spectrum market, an SP hires a spectrum for clients in the form of services. In this work, the key objective of an SP is maximizing its profit by evicting in-service users who generate the lowest profit. Each client can access the spectrum, so there is no client in a queue with a higher bid, in which a usage fee is paid under the SP's pricing guidelines. Based on their needs, clients choose their preferred bids. Making the most money is SPs' main goal. As a result, it's crucial to examine the economic issues that result from clients and SPs having competing goals. [7, 8].

To maximize its profit, an SP should consider serving the richest clients with a sufficient amount of spectrum, and the SP's trading policy admits spectrum requests based on generated profit. In this work, we propose a new game theory-based spectrum trading model where clients are allowed to access the spectrum only when the profit generated by serving them is higher than the profit of serving clients in waiting queues. The richest clients are given priority over other clients. Therefore, the clients must release a channel to which each new richest client joins the waiting queue, and the spectrum state changes from "occupied" to "free" for serving the richest newcomer. When a client no longer transmits on the channels, these channels can be used again by other clients. One purpose of this work is to extract an optimal control policy that maximizes a real-valued function of profit by optimizing the client's admission and eviction. Although the optimal user admission control problem has been tackled in many studies, these often neglect time-varying spectrum bid prices. Uncertain bid prices necessitate joint control of client admission and eviction to maximize the SP profit. However, in case the available spectrum is inadequate to serve a new richest client, the SP should determine which clients in-service to be evicted. The evicted users must receive some sort of compensation, which may vary depending on the spectrum needs of individual users and consequently have an impact on the SP's profitability.

Because the utility of an SP aims to minimize compensation for evicted clients and maximize SP's profit while users seek to maximize compensation amount, we consider the game between SP and clients using a novel multi-stage game model. In this model, the utility SP sets the amount of compensation, while the clients respond to the compensation by adjusting the spectrum they use (i.e., release the spectrum). The proposed utility functions consider the cost of eviction of clients and the satisfaction level of clients.

The contribution of this work is thus twofold:

• Firstly, it proposes a new game theory-based spectrum trading model, namely, a preemption game for profit maximization. In our model, an SP temporarily leases its free channels to clients and charges them for their opportunistic usage of the spectrum accordingly. To maximize its profit, SP negotiates with clients who paid the lowest spectrum price to release their spectrum in exchange for financial compensation. The objective is to utilize the released spectrum for serving new, more financially capable clients to maximize the SP’s profit.

• Secondly, a novel game theory-based policy for selecting a set of clients in-service that generates the maximum profit has been introduced. The proposed policy decides whether a newly arriving client should be served or added to a queue to achieve better profit. The policy seeks to sequentially select a sequence of clients to optimize the profit function from a waiting set of clients. The profit function to be optimized is not static but varies over time based on the offered spectrum prices by clients. In such cases, the performance of traditional policy for spectrum trading may deteriorate. This is because most of these algorithms continue to treat stale data of the spectrum market as being equally important as fresh data. Hence, proposing new algorithms for spectrum trading and theory to handle time variations in spectrum bids is crucial for profit maximization for SPs. SPs face a unique challenge with time-varying profit function due to offered prices for spectrum—that necessitates a trading policy that considers client's in-service and clients' in-waiting. The policy applies joint control of clients' admission and eviction. For-profit maximization, the spectrum that was hired to clients (called in-service clients) with lower profit should be relocated to the best offers. Upon the arrival of a profitable spectrum request, the SP should select the appropriate client to be evicted if the new request generates more profit. However, the evicted clients will be compensated with some form of reimbursement, where the agreements are reached in bargaining games that reveal the preferences of the clients and SP.

The remaining section of this paper is organized as follows. The associated work is shown in Sect. 2. Then, the system model and assumptions are described in Sect. 3. After that, Sect. 4 introduces our new game theory-based, the profit-driven business model for optimal admission of spectrum requests. Then, In Sect. 5, we evaluate the performance of the proposed model and evaluate the adoption capabilities of the proposed model for profit maximization in the spectrum market. Finally, the conclusion and remarks of this paper are presented in Sect. 6.

2 Related work

A vast amount of literature places great emphasis on utilizing spectrum trading in networks. In this literature, we will focus on the results of maximizing SP profit in the spectrum market. In [8], stochastic optimization techniques were used to handle the problem of channel availability uncertainty and to determine the appropriate collection of channels for each spectrum request at the lowest cost. Two distinct limitations on spectrum demand have been proposed. The throughput must surpass a particular percentage of the requested one. To address the demand deficit, the potential for channel subleasing among the SUs was also looked at. In [10], a new spectrum demand model was proposed to maximize SP's profit. Uncertainty for spectrum demand was considered in this model. To maximize its profit, SP chooses a more cost-effective spectrum and meets its clients' needs. The prospect theory was used in [10] to analyze SP’s optimal decision problem in a secondary spectrum market. The trade-off between an operator's expectation of profit and risk preference was investigated. Authors in [1] proposed a new algorithm for spectrum renting. The suggested algorithm does not depend on knowing market factors and has a finite competitive ratio and low time complexity. The proposed algorithm, which maintains a spectrum without knowledge of the characteristics of the related random processes, was designed by authors using resources from ski-rental literature. In [12], relaxation algorithms were used to model spectrum auctions as a valid spectrum trading policy. The proposed method’s main concern was maximizing the profit of the SPs while taking into account interference and market constraints.

In [13], The authors developed a game theoretical analysis of the interaction between the SP and clients before putting forth new algorithms for data pricing and channel allocation. The results showed that SP loses revenue when clients reject the SP's offer to underweight the service guarantee. As a result, a new pricing method was suggested to strengthen the system's capacity for making decisions and enhance spectrum management in the spectrum market. A new service provider was suggested in [14] to make it easier for customers to access spectrum and harvest an erratic spectrum supply. Using a three-dimensional (3D) conflict graph, the authors described the conflicts and competitions mathematically among candidates for the spectrum. Under several cross-layer constraints, the SP's revenue maximization problem was stated as the optimal spectrum trading problem. To search for workable answers, fresh heuristic methods were also suggested.

To maximize SP's profit, high-resolution pricing models were developed in [15] to facilitate price adaptation to the spectrum market state dynamically. SP’s profit was quantified by using the queuing theory. A wider variety of different traffic arrival and service rate distributions were modeled using the Markov model. In [16], authors proposed two optimization models using stochastic optimization algorithms for achieving either the target Grade of Service (GoS) of clients where the budget of SP is unrestricted or maximizing SP’s profit but with a restricted budget. Spectrum resources were assumed to be available for SP, and it can borrow spectrum under a merchant mode.

Two fundamental types of spectrum rental agreements were put out by the authors in [17]: short-term opportunistic-access agreements and long-term guaranteed bandwidth agreements. Through these agreements, SP can achieve the needed flexibility and trade-offs in terms of service quality, effective spectrum use, and pricing. Moreover, the authors proposed a new algorithm to help SP for adapting the spectrum contract portfolio dynamically subject to satisfy customer spectrum demands, to increase SP's profit in the spectrum market. The problem of spectrum trading was presented as a stochastic dynamic programming problem, with decision-making taking into consideration the market prices for the contracts and the demand for spectrum.

The main goal of the Size-Negotiable Auction Mechanism (SNAM) tool proposed in [18] is to enable clients to adopt a spectrum bidder's coverage to provide room for further negotiation while auctioning. The SNAM's bidder offers its bid to access spectrum per unit space and a group of coverage spans. The auctioneer manages the interference regions to prevent interference between bidders to increase the overall coverage region.

In [19], the service provider negotiates with the spectrum owner to pay less to access certain content. The service provider catches content to enable mobile subscribers/users to access this content. The interaction among spectrum owners, service providers, and clients was modeled using game theory. A sub-gradient-based iterative algorithm was proposed to guarantee convergence to the Stackelberg equilibrium.

In [20], the authors suggested a new spectrum trading scheme. The suggested scheme’s main concern was serving the most significant number of clients with the lowest overall spectrum cost while considering the time-varying achievable transmit rate and level of channel usage across different SPs. The problem was designed as an optimization problem to increase the total client number while increasing the SP's profit. To solve an optimization problem, one must initially conceptualize it, describe it, and then develop an equation for it to identify the least or highest value of the issue the derivatives or exit points to provide a solution. Authors in [1] proposed a new practical auction mechanism to solve the problem of spectrum redistribution for networks. The scheme achieved high spectrum utilization by exploiting channels’ spatial re-usability. In [2021 a new cycle auction mechanism was proposed to trade the users with the lowest energy efficiency among the base stations for heterogeneous networks.

A multi-priority non-cooperative power-control game was suggested by the authors in [22]. The proposed game's primary objective is to allow several small cell base stations to utilize available spectrum resources simultaneously without impairing the quality of service provided to the spectrum owner (QoS). Spectrum price was used as a control parameter in the proposed game to prioritize spectrum owners over clients for accessing the spectrum. In [23], The authors examined various potential strategies for multi-operator spectrum sharing based on 5G terrestrial networks' dynamic spectrum access. They identified the spectrum trading method to be practically the most appropriate candidate for efficient spectrum usage. A hybrid cooperative, competitive game was adopted for spectrum renting. Authors proposed a new admission and eviction control of cognitive radio users (AECCR) in [24]. For this scheme, clients can access the free spectrum only when their legacy users are temporarily unoccupied and pay usage to the SP, the SP evicts clients upon the return of the legacy users. An ideal control strategy for evicting clients was derived using a semi-Markov decision process.

The main concern of the proposed scheme in [25] was providing data transmissions with QoS requirements. In [26], SP leases the licensed channels temporarily from the spectrum owner through spectrum auction and rents to the client. Clients use rented spectrum opportunistically when the primary users are not using the channels. By enhancing admission and eviction controls for the dynamic spectrum market, the SP aims to boost profits. [27, 28], the authors proposed new reinforcement learning (RL) scheme for profit maximization in spectrum trading where a trading policy was extracted using an unsupervised learning paradigm. The extracted policy enables spectrum owners to increase profit by adjusting spectrum range in response to changes in spectrum market status and conditions. In [29, 30], While the primary receiver is used to decode information from both the primary transmitter and the backscatter device, the primary transmitter is designed to aid in both the primary and backscatter device broadcasts. The authors suggest a new method for getting temporary spectrum by keeping an eye out for "spectrum holes" in licensed bands and dynamically leasing from the SP [31]. This allows an SP to adapt its investment strategy and fee structure to the needs of its customers. When considering the cost and uncertainty trade-offs, the scheme extracts the optimum sensing and leasing spectrum amounts. The authors in [32] investigated how time-division multiple access (TDMA] is implemented in Wi-Fi and LTE-U networks. The networks' access protocol was designed using the fairness criterion so that everyone has an equal opportunity. The Nash bargaining method was used to decide which of several fair protocols was the fairest.

The above works discuss the profit maximization problem in the spectrum market. The main challenge of spectrum trading is the uncertainty of new arrival bids of the spectrum, as the SP does not know the customers’ bids beforehand. The majority of earlier studies have simply optimized the admission of current requests, ignoring the admission of future deserving spectrum requests that can further boost the SP’s profit. When facing the uncertainty of bids, most prior studies of spectrum trading compute the profit of SP based on the current system state. To maximize its anticipated profit, an SP optimizes the choices made in the suggested trading schemes. These models, however, fall short of accurately representing the very complex decision-making process found in actual spectrum markets. The suggested approach gives SP the ability to assess a choice based on anticipated gains or losses compared to the existing profit. Previous studies assumed the channels are always available in the spectrum market. Such ignorance of the limited spectrum of resources made them inapplicable to real-world problems.

3 System model

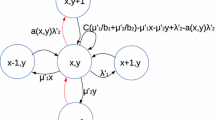
In the spectrum market, N clients (bidders) who compete for a total spectrum size of W are considered. All clients submit their requests simultaneously in a sealed bid manner. Each client knows its bidding quantity and price but does not know about other spectrum requests. Each client only rents spectrum from an SP. It is assumed that requests for spectrum arrive as a Poisson stream with an arrival rate of (i.e., number of requests per unit of time). It is believed that each request's service time will be dispersed exponentially. Poisson arrival processes are described as having exponential interarrival times. The quantity of arrivals per unit of time has a Poisson distribution in such a process. Request’s inter-arrival times are independent and uniformly distributed with exponential random variables. These assumptions have been chosen to reflect some of the reality of wireless applications, such as mobile call traffic. The exponential distribution frequently addresses the duration before a particular event. According to the exponential distribution, smaller values happen more frequently than large ones. Probability distributions with uniform distributions have outcomes that are all similarly predictable. Results are discrete and have the same probability in a discrete uniform distribution. Results are continuous and infinite in a continuous uniform distribution. Data that are closer to the mean are more common in a normal distribution. Figure 1 presents an overview of the system. As depicted in this Figure, all clients submit their requests simultaneously in a sealed bid manner.

Fig. 1

System overview

Let $C_{i}$ denote the unit marginal cost of renting the spectrum for ith request, $P_{i}$ denotes the unit rents price of the spectrum (i.e. a channel) for ith request, $t_{i}$ represents the rental period of spectrum for ith request, and $d_{i}$ indicates the demand (number of channels) for ith request in a constant price scenario, ${\acute{P}}$ is new spectrum price. The marginal cost is the slope of the total cost, or the rate at which it increases with production, and is expressed in dollars per unit while the total cost is expressed in dollars. The average cost, which is the overall cost divided by the number of units produced, is distinct from the marginal cost. A product's or service's utility is the functionality it provides to solve a certain requirement. The utility may explain "what the service performs" or determine if it is “fit for purpose”. A service must either support the customer's performance or liberate the user from limitations to be beneficial. The utility function of the SP is computed as:

$$U = \sum\limits_{{i = 0}}^{Q} \left({P_{i} d_{i} t_{i} - C_{i} d_{i} t_{i} }\right)-v ({\acute{P}}) - R$$

(1)

where $v\left( {{\acute{P}}} \right)$ is the cost of varying users' demand in response to time-varying prices, $Q$ represents the number of requests fulfilled, and $R$ is the amount of reimbursement for the evicted client in-service. The cost of raising spectrum price $v\left( {{\acute{P}}} \right)$ can be expressed as:

$$v\left( {{\acute{P}}} \right) = \sum\limits_{i = 0}^{E} {\left( {P_{i} d_{i} t_{i} - C_{i} d_{i} t_{i} } \right)}$$

(2)

where $E$ is the number of clients who switch to another service provider due to rising service prices. The cost of serving ith request includes the amount of money the client pays for renting spectrum and its service satisfaction and it is computed as follows:

$$C_{s} = P_{i} d_{i} t_{i} + S\left( W \right)$$

(3)

where $S\left( W \right)$ is the clients' satisfaction function with service. This function quantifies clients' satisfaction with the service level caused by the shortage of available spectrum. If the size of the free spectrum ($W$) is smaller than demand ($d$), the client is not satisfied, and the value of the function will be positive. Clients’ satisfaction increases faster as the spectrum shortage decreases. On the other hand, if the available spectrum size is greater than the demand for service, the clients will be satisfied, and the function value will be negative. In our work, we select $S\left( W \right)$ as follows:

$$S\left( W \right) = \rho B\left( W \right)$$

(4)

where $B\left( W \right)$ is the blocking probability [33], and $\rho$ is the weight of the client satisfaction, which models the nature and client behavior. The utility function for the ith client is the negative of its cost, which can be expressed as follows:

$$U_{i} = - C_{s} = - P_{i} d_{i} t_{i} - S\left( W \right) + R$$

(5)

The system state is defined as:

$$Z_{t} = \left( {W,D_{v} ,P_{v} } \right) = \left\{ {\begin{array}{*{20}l} W \hfill \\ {D_{v} = \left( {d_{1} , d_{2} , \ldots , d_{N} } \right)} \hfill \\ {P_{v} = \left( {p_{1} , p_{2} , \ldots , p_{N} } \right)} \hfill \\ \end{array} } \right.$$

(6)

SP should take action when the system state changes. System state changes upon customers’ arrival or departure. For a state $Z_{t}$, the action space can be represented as follows:

$$A(Z_{t} ) = \left\{ {\begin{array}{*{20}l} {0, \;reject\;new\;request} \hfill \\ {1, \;add\;new\;request\;to\;queue} \hfill \\ {2, \;serve\;request\;if\;W > d} \hfill \\ {3, \;serve\;request\;if\;{\acute{d}} < d} \hfill \\ {4, \;serve\;new\;request\; by\;evicting\;clients\; in - service } \hfill \\ \end{array} } \right.$$

(7)

SP may evict some clients to serve a new higher price request to maximize the profit. Moreover, SP may motivate the client to reduce the order size of the spectrum to utilize a small size spectrum. Table 1 summarizes the primary notations used throughout the problem description for clarity.

Table 1 List of relevant notations

4 Game theory based profit optimization

To maximize SP’s profit, a new scheduling scheme for serving clients based on the reported profit is proposed. Game theory is utilized in this scheme for spectrum allocation.

4.1 Game theory for profit maximization

Game theory is an area of applied mathematics that provides methods for studying situations in which parties, known as players, make interdependent decisions. A greedy algorithm is an algorithmic strategy that selects the best option at each simple step to eventually lead to a globally optimal solution. This dependency forces each player to take the other player's potential actions, or tactics, into consideration while constructing strategy. This indicates that the algorithm selects the best answer available at the time without considering the effects. SP attempts to evict some users' in-service to serve wealthy clients. This behavior of SP is modeled using game theory, where SP offers compensation for evicted users to motivate them to release all channels or parts of the spectrum. A game can be described by a set of players, which are the evicted users and SP. In this game, each player $i$ has the utility function $u_{i}$. The utility for each player for chosen strategy quantifies a player’s satisfaction with its decision (i.e., releasing spectrum). The game theory places a significant emphasis on utilities. They enable the use of real-valued functions in game theoretic analysis by representing the preferences that players have for various outcomes in terms of real numbers. The same formula that use to determine expected value is also used to calculate expected utility rather than adding probability and economic amounts.

Let $L$ be the number of players in the game and assume $Y$ is a non-empty set of $H^{L}$ representing the state of players’ strategies. A game in strategic form consists of a group of players, a set of strategies for each player, and an outcome for each vector of strategies. Generally, the outcome is determined by the vector of utilities that the players get from the result. The strategy of each client is a decision on releasing spectrum. The set $U$ denotes the set of performance metrics, and it can be defined as follows:

$$U = \left\{ {u \in H^{L} :\exists y \in Y} \right\}$$

(8)

Let $u_{l}$ be the minimum performance metrics for players to accept bargain (i.e. minimum requirements) with SP for releasing its channels.

Definition 1

The utility function $u_{l} \in H^{L}$, is said to be Pareto optimal if $\forall u_{j}$ $\in H^{L}$, $u_{j} \ge u_{i}$, then $u_{j} = u_{i} .$

From Definition 1, it is clear that there is no solution for the spectrum hiring problem which improves SP’s satisfaction without reducing the level of satisfaction for evicted clients. The hiring spectrum is Pareto optimal, where the number of solutions is infinite. In this work, the game theory will be applied to find the one-of-a-kind and fair Pareto optimal solution. Pareto efficiency indicates that resources are allocated in the most cost-effective way possible, but it does not imply equality or fairness. When no economic adjustment can benefit one person without harming at least one other, such a situation is referred to as the Pareto optimal condition of the economy. An outcome of a game is Pareto optimum if no other outcome gives every player at least as well off and at least one strictly better off. It follows that no change to a Pareto-optimal result can be made without harming at least one player.

Cooperative bargaining is the process through which two individuals agree on how to divide a surplus that they may generate together. The surplus produced by the two players may frequently be distributed in a variety of ways, enabling the players to bargain about how to divide rewards. Due to the potential for external enforcement of cooperative conduct, a cooperative game involves competition between groups of players in game theory. The cooperative bargaining game theory is summarized below.

Definition 2

The mapping policy G $\left( {U, u_{j} } \right)$ $H^{L}$ is said to be a cooperative game theory if:

• 1. G $\left( {U, u_{j} } \right) \in U$

• 2. G $\left( {U, u_{j} } \right)$ is Pareto optimal.

• 3. Independent for any linear transformation function: for any function $T: H^{L}$ $H^{L}$, $T\left( {u_{j} } \right)u_{i}$, then G $\left( {T\left( U \right), T(u_{j} )} \right)$ = $T\left( {{\text{G}}(U, u_{j} )} \right)$.

• 4. G $(U, u_{j} )$ satisfies independence of irrelevant alternatives if for all mapping situations $U$ and ${\acute{U}}$ with ${\acute{U}}$ $\subset U$ and G $({\acute{U}}, u_{j} ) \in U$ we have G $({\acute{U}}, u_{j} ) = {\text{G}}\left( {U, u_{j} } \right).$

• 5. G($U, u_{j} )$ is symmetric and it does not distinguish between the players. If $u_{j} = u_{i}$ then G $(U, u_{j} ) =$ G $(U, u_{i} )$.

In the eviction game theory (bargaining), each player reveals their preference over the available spectrum. The agreement was reached to reveal the preferences of bargainers. The rationality of customers is the underlying assumption of the revealed preference theory. In other words, they will have evaluated a variety of options before selecting the best investment selection for them. As a result, if a customer selects one choice from the available options, that option must be the preferred option. Clients’ in-service repetitively submit their prices to the SP, which selects the clients with minimum prices. A stable state that is a Nash equilibrium solution is reached after several price bidding iterations.

The following measures are used to stop clients from bargaining:

• Be very explicit about the asking price and the rationale behind it.

• Never suggest that they want their engagement more than they require your solution.

• Move the conversation away from the price and onto other points that are negotiable.

Definition 3

(Nash equilibrium). In game theory, Nash equilibrium is a key idea. According to this, each player chooses the payoff-maximizing strategy in an equilibrium given the tactics of the other players. However, it loses its benefits in games with numerous equilibria and requires substantial assumptions on the understanding of the strategies of the other players. The result of a noncooperative game for two or more players in which no player's predicted outcome can be modified by altering one's strategy is also its solution in game theory. The dominant strategy equilibrium is a more robust idea in the Nash equilibrium. If a player's payoff-maximizing approach is separate from the other players' tactics, it is considered to be a dominating strategy. Strategy-proof mechanisms exhibit the dominant strategy equilibrium. No considerations are made regarding the knowledge that the agents have access to about one another in a strategy-proof system, and each bidder determines their own best strategy without needing the others to operate rationally. Every player in a negotiating game is put in a position where they cannot alter their tactics to increase their utility.

Theorem 1

Assume that the utility function f(u i) for each player in the eviction game is concave, upper bounded, and defined on Y, which is a convex function and compact subset of HL. Assume that each player can improve the utility function by switching up their approach. Then, a special barging solution (u*) is negotiated. The best answer, f(u*), can be written as:

$$u^{*} = \mathop {\max }\limits_{{\forall i \in A_{G} }} f\left( {u^{*} } \right) - f\left( {u_{i} } \right),\;u^{*} \in U$$

(9)

where $A_{G}$ is the set of players in the game. Each player's weight $w_{i}$ depends on the number of bargaining units and the bid of a jth rich client. The weight is normalized by scaling its values to fall within the range of 0.0–1.0 as follows:

$$w_{i} = d_{j} \frac{{b_{j} }}{{\mathop {\max b_{k} }\limits_{{\forall k \in A_{G} }} }}$$

(10)

Proposition

Each ith player in the eviction game weighs $w_{i}$. For this game, a unique solution is existing, and it can be considered as an optimization problem solution as in the following equation:

$$u^{*} = \mathop {\max }\limits_{{\forall i \in A_{G} }} w_{i} \left( {f\left( {u^{*} } \right) - \mathop {\min }\limits_{{\forall f\left( {u_{i} } \right) \in Y}} f\left( {u_{i} } \right)} \right)$$

(11)

Proof

The set of utility functions $Y$ is a convex and compact subset of $H^{L}$. The power function $\left( {f\left( {u^{*} } \right) - \mathop {\min }\limits_{{\forall f\left( {u_{i} } \right) \in Y}} f\left( {u_{i} } \right)} \right)^{{w_{i} }}$ is adopted as a utility function for each player in the eviction game. Thus, the utility function defined on $Y$ is concave if 0 < $w_{i}$ < 1. The optimization problem in the bargaining game can be expressed as follows:

$$u^{*} = \mathop {\max }\limits_{{\forall i \in A_{G} }} \left( {f\left( {u^{*} } \right) - \mathop {\min }\limits_{{\forall f\left( {u_{i} } \right) \in Y}} f\left( {u_{i} } \right)} \right)^{{w_{i} }}$$

(12)

Note that the minimum performance metrics for ith player $u_{i}$ = 0 if $u_{i} = f\left( {u^{*} } \right) - \mathop {\min }\limits_{{\forall f\left( {u_{i} } \right) \in Y}} f\left( {u_{i} } \right) = 0$, so the optimal solution can be extracted for the bargaining game. Hence, it is reasonable to map the eviction game into an N-player multiple bargaining game because of the following reasons:

• 1. Each player requires a minimum number of channels ($d_{i}$). The initial agreement between SP and a client can be set as 0 where a request may be rejected.

• 2. The amount of reimbursement for the evicted client depends on the bid of rich clients. More amount of reimbursement is paid to a client with having higher weight. Therefore, a weight variable could be constructed with numerous parameters to represent the clients’ priority.

• 3. Clearly, the eviction game has the Pareto optimality properties and the optimal spectrum allocation should be a Pareto optimal solution. The Pareto optimality standard efficiently and more effectively is defined in terms of individuals as follows: If it is impossible to transfer resources in a way that benefits one person without affecting at least one other person, the allocation is considered efficient. Therefore, efficiency in consumption, efficiency in production, and efficiency in both consumption and production are requirements for achieving Pareto optimality.

Definition 4

A bargaining solution $u_{i}$ is Pareto optimal solution where $u_{i}$ ∈ $U$ if and only if $u_{j} = u_{i}$ for all $u_{j}$ satisfying $u_{j} \ge u_{i}$.

4.2 Optimal profit response to eviction policy

To find SP's optimal profit response to the eviction policy, we consider the bids of new clients and the expected profit of serving clients in-service. Expected profit for serving a new higher price request i is computed as follows:

$$E_{p} = P_{i} d_{i} t_{i} - C_{i} d_{i} t_{i} - C_{e}$$

(13)

where $C_{e}$ is the cost of eviction ith the client and it is calculated as:

$$C_{e} = R + P_{i} d_{i} t_{i} - t_{e}$$

(14)

where $t_{e}$ is the eviction time. SP selects a client in-service with the lowest reward and starts negotiating with the client to release its spectrum. The performance of each player depends on the number of channels allocated to it. Let $d_{i}^{min}$ denote the minimum spectrum for the ith client and $d_{i}$ is the rented spectrum for the ith client. The optimal allocation for the spectrum can be obtained by resolving this optimization problem:

$$\mathop {\max }\limits_{{\forall i \in A_{G} }} w_{i} \left( {f\left( {u^{*} } \right) - \mathop {\min }\limits_{{\forall f\left( {u_{i} } \right) \in Y}} f\left( {u_{i} } \right)} \right)$$

(15)

Subject to

$$0 \le d_{i} \le W$$

$$d_{i} \ge d_{i}^{min}$$

$$\sum\limits_{i = 1}^{N} {d_{i} \le W}$$

The solution vector for this game is a convex and non-empty set. For each player, the utility function can be presented in terms of the spectrum:

$$f\left( {u_{i} } \right) = w_{i} \ln \left( {d_{i} - d_{i}^{\min } } \right)$$

(16)

Utility function should satisfy the following constraints:

$$\frac{{\partial f\left( {u_{i} } \right)}}{{\partial d_{i} }} > 0$$

$$\frac{{\partial^{2} f\left( {u_{i} } \right)}}{{\partial^{2} d_{i} }} < 0$$

Thus, $f\left( {u_{i} } \right)$ is a concave function. SP rents spectrum for clients based on the bids. For SP, there is a population of $L$ clients who may release a spectrum. SP has the desire to grasp ith client spectrum described by the fowling condition:

$$D\left( R \right) = - R + w_{i} {\epsilon}_{i}$$

(17)

where I is the actualization of a randomly distributed random variable with a continuously differentiable density, and [a,b] of the extended real line as its support. SP must incur a bargaining cost $c_{b}$ to find clients who accept to release the spectrum. Hence, the grasping function of the spectrum can be expressed as follows:

$$D\left( R \right) = - R + w_{i} {\epsilon}_{i} - c_{b}$$

(18)

We consider the equilibria at which ith client accept $s R^{*}$ which is the minimum amount of reimbursement. Assume SP holds the best offer with ${\acute{R}}$, jth client, which differs from $R^{*}$. If SP tries with another client, ith client, expecting $R^{*}$ to release its spectrum, then SP will prefer ith client's spectrum if $R^{*} + w_{i} {\epsilon}_{i}$ exceeds ${\acute{R}} + w_{j} {\epsilon}_{j}$ and ${\epsilon}_{i}$ exceeds ${\epsilon}_{i} + \frac{{\left( { R^{*} - {\acute{R}}} \right)}}{{w_{i} }}$. Thus, the added utility for SP can be presented as:

$$\left( {{\acute{R}} - R^{*} } \right) + w_{i} \left( {{\epsilon}_{i} - {\epsilon}_{j} } \right) = w_{i} \left( {{\epsilon}_{i} - y} \right)$$

(19)

The expected increment in the utility of searching for one more client is computed as follows:

$$w_{i} h\left( y \right) = w_{i} \int\limits_{y}^{\infty } {\left( {{\epsilon} - y} \right)f\left( {\epsilon} \right)d{\epsilon} }$$

(20)

SP usually tends to search for clients who may accept less amount reimbursement. On the other hand, SP stops searching when the utility is not improving anymore. Since $w_{i} > 0$, the expected increment in utility from bargaining one more client exceeds the bargaining cost if only if $y < {\acute{y}}$ where ${\acute{y}}$ is computed as follows:

$$h\left( {{\acute{y}}} \right) = \frac{{c_{b} }}{{w_{i} }}$$

(21)

SP should stop bargaining if $y < {\acute{y}}$.

Theorem 2

Given the number of clients that SP does not bargain with them and this stopping rule is true for ${\acute{N}} = 1,$ After N clients are in service, the likelihood that SP will stop bargaining with more clients decreases as a function of both the negotiation cost and the client count.

Proof

For ${\acute{N}} + 1$, if $y > {\acute{y}}$ and SP does not bargain with one more client, then either a smaller value of $y$ is revealed or a larger one is. In any case, SP gets the best spectrum price (i.e. less amount of reimbursement) corresponding to $y > {\acute{y}}$. Since there is only ${\acute{y}}$ left to bargain and it was assumed the stopping rule is optimal, SP would then stop bargaining. Thus, when there are ${\acute{N}} + 1$ clients left and $y$ exceeds ${\acute{y}}$, SP would not search for more clients in-service since this will decrease SP's profit. Thus, the stopping criteria are valid for ${\acute{N}}$, it is valid for ${\acute{N}} + 1$ by induction. The reservation value ${\acute{y}}$ determines the probability that SP goes on bargaining more clients. The larger value of ${\acute{y}}$, the more likelihood of considering more clients for bargaining. ${\acute{y}}$ is a strictly decreasing function of ratio $\frac{{c_{b} }}{{w_{i} }}$ since the function $h\left( {{\acute{y}}} \right)$ is strictly decreasing. The value of ${\acute{y}}$ goes from $b$ to $- \infty$ as $\frac{{c_{b} }}{{w_{i} }}$ goes from zero to $- \infty .$ Thus, the probability that SP terminates bargaining more clients after ${\acute{N}}$ clients in-service is an increasing function of the bargaining cost and a decreasing function of the number of clients in-service. The value ${\acute{y}}$ cannot exceed the upper bound, $b,$ of the support of ${\mathcalligra{f}}$ The value ${\acute{y}}$ equals $b$ if $c_{b} = 0$ and if SP bargaining all clients in-service. However, the value of ${\acute{y}}$ can be less the than the lower bound, $a,$ of the support of ${\mathcalligra{f}}$. Therefore, we have:

$$\left( {w_{i} h\left( {{\acute{y}}} \right) = w_{i} \left( {{\epsilon}_{i} - {\acute{y}}} \right)} \right) > w_{i} \left( {{\epsilon}_{i} - a} \right)$$

(22)

this implies that:

$$c_{b} > w_{i} \left( {{\epsilon}_{i} - a} \right)$$

(23)

This means if SP expects all clients to seek the same amount of reimbursement, the expected incremental of SP's profit (i.e. SP's utility) from bargaining more clients is less than the search cost. Then, the only motive for bargaining for more clients would be the possibility of having the remaining clients seeking for less amount of reimbursement. The probability of bargaining ith the client is computed as follows:

$$\Pr \left( i \right) = \frac{1}{{{\acute{N}}}}$$

(24)

Given that the ith client accepts an amount of reimbursement ${ }R^{*}$. Then, it is optimal for SP to use the previous stopping bargaining rule for bargaining with an ith client. Hence, the probability that SP accepts ith client's offer is computed as:

$$\Pr \left( {y > {\acute{y}}} \right) = 1 - {\mathcal{F}}\left( {{\acute{y}} + \Delta } \right)$$

(25)

where $\Delta$ is the standardized reimbursement of ith client and it is computed as follows:

$$\Delta = \frac{{{\acute{R}} - R^{*} }}{{{\acute{N}}}}$$

(26)

where ${\acute{R}}$ denotes the new SP offer for compensating the client in-service. The probability of bargaining with an ith client first is $\frac{1}{{{\acute{N}}}}$, second with probability $\frac{{{\mathcal{F}}\left( {{\acute{y}}} \right)}}{{{\acute{N}}}}$, third with probability $\frac{{{\mathcal{F}}\left( {{\acute{y}}} \right)}}{alban}$, and so on. SP pays reimbursement for an ith client if it samples all clients and the ith client yields the highest profit. The demand of spectrum for SP to serve wealthy clients is the sum of the series that represents clients who accept the offer of SP. SP’s demand for spectrum is calculated as follows:

$$D\left( {{\acute{R}}, R^{*} } \right) = \frac{1}{{{\acute{N}}}}\left[ {1 - {\mathcal{F}}\left( {{\acute{y}} + \Delta } \right)} \right]\left[ {\frac{{1 - {\mathcal{F}}\left( {{\acute{y}}} \right)^{{{\acute{N}}}} }}{{1 - {\mathcal{F}}\left( {{\acute{y}}} \right)}}} \right] + \mathop \smallint \limits_{ - \infty }^{{{\acute{y}} + \Delta }} {\mathcal{F}}\left( {{\epsilon} - y} \right)^{n} {\mathcalligra{f}}\left( {\epsilon} \right)d{\epsilon}$$

(27)

The derivative of SP's demand concerning ${\acute{R}}$, evaluated at ${\acute{R}} = R^{*}$, is:

$$\frac{{\partial D\left( {{\acute{R}},R^{*} } \right)}}{{\partial {\acute{R}}}}\left( {{\acute{R}}, R^{*} } \right) = \frac{1}{{w_{i} }}\left[ { - \frac{{{\mathcalligra{f}}\left( {{\acute{y}}} \right)}}{{{\acute{N}}}}\frac{{1 - {\mathcal{F}}\left( {{\acute{y}}} \right)^{{{\acute{N}}}} }}{{1 - {\mathcal{F}}\left( {{\acute{y}}} \right)}} + f\left( {{\acute{y}}} \right) {\mathcal{F}}\left( {{\acute{y}}} \right)^{{{\acute{N}} - 1}} - \mathop \int \limits_{ - \infty }^{{{\acute{y}}}} \left( {{\acute{N}} - 1} \right) {\mathcalligra{f}}\left( {\epsilon} \right)^{2} {\mathcal{F}}\left( {\epsilon} \right)^{{{\acute{N}} - 2}} d{\epsilon} } \right]$$

(28)

The last two terms can be written together as $\int_{ - \infty }^{{{\acute{y}}}} {\acute{{\mathcalligra{f}}}\left( {\epsilon} \right) {\mathcal{F}}\left( {\epsilon} \right)^{{{\acute{N}} - 1}} d{\epsilon} }$. Hence, the symmetric equilibrium amount of reimbursement is:

$$R^{*} = \frac{{ - D\left( {{\acute{R}},R^{*} } \right) {\mathcalligra{f}}\left( {{\acute{y}}} \right)}}{{\frac{{\partial D\left( {{\acute{R}},R^{*} } \right)}}{{\partial {\acute{R}}}}}} = \frac{{w_{i} }}{{\frac{{1 - {\mathcal{F}}\left( {{\acute{y}}} \right)^{{{\acute{N}}}} }}{{1 - {\mathcal{F}}\left( {{\acute{y}}} \right)}} {\mathcalligra{f}}\left( {{\acute{y}}} \right) - {\acute{N}}\mathop \int \nolimits_{ - \infty }^{{{\acute{y}}}} {\mathcalligra{f}}\left( {\epsilon} \right) {\mathcal{F}}\left( {\epsilon} \right)^{{{\acute{N}} - 1}} d{\epsilon} }}$$

(29)

The first two terms in Eq. 28 in the bracket are negative and can be written as follows:

$$- \frac{{f\left( {{\acute{y}}} \right)}}{{{\acute{N}}}}\frac{{1 - {\mathcal{F}}\left( {{\acute{y}}} \right)^{{{\acute{N}}}} }}{{1 - {\mathcal{F}}\left( {{\acute{y}}} \right)}} + {\mathcalligra{f}}\left( {{\acute{y}}} \right){\mathcal{F}}\left( {{\acute{y}}} \right)^{{{\acute{N}} - 1}} = - \frac{{{\mathcalligra{f}}\left( {{\acute{y}}} \right)}}{{{\acute{N}}}}\mathop \sum \limits_{k = 0}^{{{\acute{N}} - 1}} \left[ {{\mathcal{F}}\left( {{\acute{y}}} \right)^{k} - {\mathcal{F}}\left( {{\acute{y}}} \right)^{{{\acute{N}} - 1}} } \right]$$

(30)

Thus, $\frac{{\partial D\left( {{\acute{R}},R^{*} } \right)}}{{\partial {\acute{R}}}}\left( {{\acute{R}}, R^{*} } \right)$ is negative and from (29), $R^{*}$ is nonnegative. We assume the function ${\mathcal{F}}$ is logarithmically concave which is an increasing hazard rate.

Proposition

The symmetric equilibrium amount of reimbursement $R^{*}$ is an increasing function of the bargaining cost if $c_{b} < w_{i} \left( {{\epsilon}_{i} - a} \right)$ and the function ${\mathcal{F}}$ is logarithmically concave, and a decreasing of the number of clients in-service ${\acute{N}}$. Hence,

$$\mathop {\lim }\limits_{{c_{b} \to 0}} R^{*} = \frac{{w_{i} }}{{{\acute{N}}\left( {{\acute{N}} - 1} \right)\mathop \int \nolimits_{ - \infty }^{\infty } {\mathcalligra{f}}\left( {\epsilon} \right)^{2} {\mathcal{F}}\left( {\epsilon} \right)^{2} d{\epsilon} }}$$

(31)

$$\mathop {\lim }\limits_{{{\acute{N}} \to 0}} R^{*} = \frac{{w_{i} {\mathcal{F}}\left( {{\acute{y}}} \right)}}{{{\mathcalligra{f}}\left( {{\acute{y}}} \right)}}$$

(32)

Higher bargaining cost reduces the profit of SP and if the bargaining cost is nearly zero, the bargaining game outcome will be close to optimal value if SP knows about clients’ information and matches corresponding values.

The proposition indicates what happens if their sufficient heterogeneity in weights ($w_{i}$) assigned to the clients. The limit in Eq. 31 is the equilibrium amount of reimbursement and it can be obtained when the bargaining cost goes to zero where clients in-service have the same weights. This does not happen in real life, but rather, for large cb enough where the threshold value of bargaining cost increases as the weight of client in-service increases. This situation never happens if the distribution of the amount of reimbursement is unbounded below (i.e. the amount of reimbursement is minus infinity). The proposition stresses that the amount of reimbursement falls with the number of clients in service. Furthermore, the amount of reimbursement is affected by the number of clients in-service.

5 Performance evaluation

To assess our proposed Greedy Game Theory scheme (GGT), Profit and network throughput are taken into account as performance measures to quantify the performance of the suggested solution. Quantifying the advantages and effects of the suggested GGT strategy on SP's profit is the goal of this investigation. In the simulation experiments, various scenarios are used to observe the performance metrics. Our proposed GGT scheme is compared against the benchmark RL [26], and AECCR schemes [23]. Comparative experiments were performed using the proposed GGT to analyze the following aspects of the system performance:

• The effect of optimal admission on SP’s profit by comparing the reported profit for the three schemes.

• The effect of our proposed scheme on network throughput.

In a city setting, nodes are dispersed at random over a (200,200) m2 area. Table 2. presents the simulation parameters used to evaluate the algorithms and our proposed approach for simulation.

Table 2 Simulation parameters

5.1 Impact of spectrum demand on the profit

This section looks into how spectrum demand affects SP's bottom line. Figure 2 demonstrates how profit grows as client demand for spectrum does. This figure shows that GGT significantly outperforms both the RL scheme and AECCR scheme, under various network conditions.

Fig. 2

Profit under different values of spectrum demand, where λ is the number of requests per second

Specifically, Fig. 2 reveals that under low-to-high spectrum demand, the proposed GGT scheme generates more profit compared to other schemes. This increment is mainly attributed to the dynamic selection of clients who pay more, and hence, increase the reported profit significantly. Figure 2 also shows that the profit enhancement is increased with higher spectrum demand. This is expected because the larger values of spectrum demand increase the likelihood of finding new and better clients to generate more profit. The benchmark RL scheme is only interested in selecting the best offers and completes executing these requests in-service regardless of the new arrival requests with more rewards.

To maximize the profit, the GGT scheme prioritizes the new richest clients by attempting to evict some clients in-service and compensating them. The licensed frequency band is reserved for the primary user (PU) use. Priority Access License is SAS's term for Licensed Shared Access (PAL). SAS introduces a third layer for unlicensed opportunistic spectrum access with General Authorized Access, replacing LSA's exclusion of opportunistic access if persistent protection is not given (GAA). Users of PAL are protected from GAA tier interference, but not from that of the incumbents. The main concern of the AECCR scheme is protecting primary users (PUs) so it enforces clients to release channels upon the Pu's return. The SP is not receiving any reward when SP starts accessing the spectrum. Clearly, with the increase in PU’s activities, the reported profit for SP gracefully degrades.

Our GGT scheme generated the highest profit because it adapts to the system state in terms of offered spectrum prices. Adaptation should occur while clients are served to maximize SP profit. To show the dynamic behavior of the GGT scheme in selecting wealthy clients, we compare the average leasing prices for three schemes in Fig. 3. Note that the GGT scheme had the highest collected average spectrum price among all remaining schemes. This is anticipated as this scheme leases spectrum for the richest clients as much as possible. Furthermore, Fig. 3 reveals that under high spectrum demand, the proposed GGT scheme increases spectrum prices by up to 60% compared to the AECCR scheme. Figure 4 illustrates the throughput performance under different loads (i.e. spectrum demand) for the three schemes. The result shows that both GGT and RL schemes significantly outperform the AECCR scheme, irrespective of the various network conditions. Specifically, Fig. 4 reveals that the throughput enhancement is larger under moderate-to-high spectrum demand than the low demand of spectrum for both GGT and RL schemes. However, the performance of AECCR is degraded significantly due to primary users (PUs) activities. PUs are served immediately and clients are evicted to release their spectrum for PUs. The performance of the AECCR scheme is the worst, due to the limited number of available channels that are used to serve clients.

Fig. 3

Average spectrum price under different values of spectrum demand

Fig. 4

Throughput performance under different values of spectrum demand

Figure 5 shows the acceptance rate for clients' requests under different values of spectrum demand for the three schemes. The acceptance rate decreases for all schemes as the traffic load becomes higher due to the limited size of the spectrum. Moreover, Fig. 5 shows that the proposed method met the demands for most spectrum requests and outperformed other schemes. This is anticipated as this scheme vacates some requests and compensates them. These requests are classified as served since they accessed the spectrum and received reimbursement. This proves the efficiency of our proposed scheme and highlights how important it is to make efficient management and resource-tuning decisions in the spectrum market.

Fig. 5

Requests acceptance rate under different values of spectrum demand, where λ is the number of requests per second

5.2 Impact of spectrum demand on eviction cost

In this part, we investigate the ability of our proposed scheme to exploit the status of service demand to select clients for eviction, an omitted issue in existing studies. Figure 6 reveals that under different service demands, moderate and high levels of spectrum demand, the proposed scheme selects clients who accept the lowest amount of reimbursement resulting in reducing the cost of eviction significantly. Furthermore, Fig. 6 indicates that as the spectrum demand increases the likelihood of finding clients with the lowest eviction cost increases. We investigate the impact of bargaining costs on the amount of reimbursement.

Fig. 6

Eviction cost under different values of spectrum demand, where λ is the number of requests per second

Figure 7 demonstrates that the amount of reimbursement is smaller at larger bargaining costs due to the increasing number of clients that the SP negotiates with. The more clients the SP needs to negotiate with, the more options the SP has to offer. In other words, the greater the options for SP to reduce the amount of reimbursement, the better chances of closing the deal with clients. We report in Fig. 8 the amount of reimbursement under different clients’ satisfaction levels. It is worth noting that reimbursement decreases at lower satisfaction levels. This is because as the satisfaction levels decrease, the QoS requirement becomes stricter so that more in-service clients may reject the release spectrum with a lower amount of reimbursement. Thus, the SP increases the amount of reimbursement to motivate them for vacating channels. By contrast, as the satisfaction level increases, the QoS requirement becomes less strict so that more clients accept a lower amount of reimbursement.

Fig. 7

Amount of reimbursement as a function of bargaining cost

Fig. 8

Client’s satisfaction level as a function of the amount of reimbursement

Finally, we report in Fig. 9 the amount of reimbursement under different values of clients' budgets. Note that if an SP does not offer a suitable amount of reimbursement, clients may not release the spectrum. The results show that owning more cash, makes clients stop their cravings for reimbursement. Hence, the SP should increase the amount of reimbursement to motivate wealthy clients to release the spectrum (as shown in Fig. 9).

Fig. 9

Client's budget as a function of the amount of reimbursement

6 Conclusion

A Novel GGT-based profit-driven online spectrum business model is proposed for the dynamic spectrum market in this work. Profit and network throughput are considered performance measures to quantify the performance of the suggested solution in our proposed Greedy Game Theory scheme (GGT). Further, our model exploits the varying charging prices among the submitted requests and decides where to place the spectrum and how to prioritize profitable clients. Besides, the proposed method shows increased SP profits significantly by optimal admission for clients' requests, considering the collected profits in its allocation decisions when compared with the existing RL and AECCR schemes, because the benchmark RL scheme is only interested in selecting the best offers and completes executing these requests in-service regardless of the new arrival requests with more rewards and the main concern of the AECCR scheme is protecting primary users (PUs) so it enforces clients to release channels upon PUs return. In future work, an interesting direction to pursue is cooperating with other SPs for optimal admission of spectrum requests. Managing the spectrum becomes more complex in this case as the SP needs to consider the interaction and relations among the different SPs. We will also use machine learning and integrate fuzzy-logic and game theory-based optimization [34] using deep, and reinforcement learning [35], as well as possible cognitive control-theoretic elasticity, approaches [36]. Finally, we intend to test our proposed schemes in real-time systems.