Profit-maximization spectrum sharing in opportunistic duopoly market under dynamic spectrum pricing and QoS constraints

Abstract

Cognitive radio (CR) technology is crucial for enabling dynamic spectrum management. CR allows opportunistic spectrum sharing with licensed primary radio (PR) users by allowing the so-called secondary users to dynamically access the under-utilized parts of the frequency bands that are allocated/licensed to the PR networks (PRNs). The CR system pays a utilization-dependent price to PRNs for utilizing the unused spectrum. An essential challenge in this domain is how to characterize the economic implications of spectrum sharing between the CR system and PRNs. Specifically, we consider a CR system with two competing CR service providers. This market model is known as the “duopoly model,” a market structure premise that consists of two companies providing the same type of service. For such a model, we investigate the problem of maximizing the overall achieved profit in the CR system. Specifically, we mathematically formulate the profit-maximization spectrum assignment problem for the two CR providers subject to spectrum sharing, power distribution, spectrum pricing, and quality of service constraints. We demonstrate that this optimization problem is an NP-hard binary nonlinear programming problem. Therefore, we adopt a meta-heuristic optimization method based on Antlion Optimization to solve the problem suboptimally. Simulation results revealed that our proposed profit-aware optimization significantly outperforms traditional CR-based spectrum access mechanisms.

1 Introduction

The proliferation of wireless mobile applications and services has substantially increased the need for additional radio spectrum. Future wireless networks (e.g., fifth generation (5 G) and beyond 5 G) will require massive spectrum opportunities, yet there are limited spectrum resources. Consequently, innovative, dynamic spectrum access solutions are needed. Cognitive radio (CR) technology was developed to facilitate such a dynamic spectrum access paradigm [1, 2]. CR technology provides opportunistic spectrum access to the underutilized portion of the licensed frequency bands allocated to the legacy primary radio networks (PRNs). In such an operating environment, the coexistence of unlicensed CR networks (CRNs) and licensed PRNs should be regulated [3,4,5]. Specifically, the CR system should encourage the PRNs to cooperate by paying utilization-dependent spectrum rent and serving the unlicensed CR users (secondary users) at a higher price than the primary radio (PR) users [6,7,8]. From a business perspective, telecommunications markets follow the so-called “oligopoly” market structure, in which a few firms compete in the market to provide similar services (typically, the licensed telecommunications service providers (PRNs) are few because of the limited resources of the spectrum). The phrase “oligopoly” stems from the Latin “olgoi,” meaning “few,” and ’pole-o,” meaning “to sell.” Thus, it translates as “few sellers” [9,10,11].

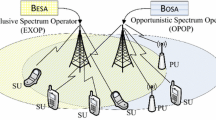
Accordingly, three main market structures can be defined for the coexistence between the CRNs and PRNs: a few PRNs with one CRN, a few PRNs with two CRNs, and a few PRNs with a few CRNs. It is important to highlight the fact that the market model of a few PRNs with two CRNs is known as a “duopoly model,” which is a particular scenario of the oligopoly model when there are only two CR service providers [12,13,14,15]. This paper investigates the profit-maximization problem in CR systems regarding spectrum allocation under the duopoly market model. Figure 1a illustrates the PR oligopoly market model (stage 1) and the CR duopoly market model as the competition in the CR market between only two firms (stage 2). The underutilized PR channels in the PRN market are available for the CRN market (CRN1 and CRN2). The CR users in each CRN compete to access the spectrum available to each CR firm. When allocating channels to the two operating CRNs, the following factors should be considered: (1) The price paid by the CR system to the PRNs for access to their idle channels increases as the PR activity (channel utilization) increases; and (2) The price charged by the CR system for each CR user, known as secondary users (SU), by the CR system should be greater than the price charged to each PR user by the PR systems to get the same service. Previous studies have addressed the spectrum pricing problem in CR systems to offer the best pricing plans for using the available spectrum. However, none of them investigated the impact of CR channel assignment on the overall achieved CR profit [4]. On the other hand, several CR-based channel assignment solutions have been proposed for enabling efficient CR systems, but without considering the achieved CR profit (i.e., the impact of the utilization-dependent price was not considered in the developed channel assignment solutions) [4]. Only some studies have looked into the profit-maximization channel assignment problem in a single CRN while accounting for the time-varying characteristics of PR channel quality and the utilization-dependent fees of utilizing the idle portions of the licensed spectrum. Therefore, this article investigates the channel assignment problem in a duopoly CR market to maximize the achieved CR profit by the two competing CRNs while meeting a set of quality of service (QoS) and design constraints. The constraints include the incurred utilization-dependent fees of utilizing the PR spectrum by the CR system, the admitted SUs’ subscription fees, the time-variant channel gain between the communicating SUs across the idle PR channels, the minimum rate demand requirement, and the exclusive channel occupancy. This problem is mathematically formulated, which turned out to constitute a non-linear binary programming problem, an NP-hard problem. Thus, we adopt the Antlion meta-heuristic optimization (ALO) algorithm to solve the channel assignment problem suboptimally. The effectiveness of the proposed profit-maximization channel assignment scheme is demonstrated using extensive simulation experiments. Compared to reference channel assignment algorithms, our proposed scheme significantly enhances the overall profit achieved by the CR system.

The rest of this paper is structured as follows. The network model is explained in Sect. 2. The channel assignment problem in a duopoly CR market model, with the goal of maximizing the CR system profit, is stated and formulated in Sect. 3. Section 4 proposes an ALO-based algorithm to solve the formulated profit-maximization problem. In Sect. 5, the performance evaluation and results are provided. The conclusion of the paper is provided in Sect. 6.

Fig. 1

Coexistence between Duopoly CR and Oligopoly PR markets in the telecommunication sector: market models and network architecture

2 Network and market model

We consider a CR system with two unlicensed service providers (CRN1 and CRN2). The competition between the two CRNs can be represented as a duopoly market. The two CRNs geographically coexist with a few licensed PRNs. Let ${\mathcal {N}}$ denote the set of all PRNs. The PRNs are authorized to utilize a specific set of frequency channels ${\mathcal {C}}$. The CR system can opportunistically utilize the idle portions of the PR spectrum. The status of a PR channel (idle or busy) and the level of PR activity over that channel can be determined by employing spectrum sensing or by continuously examining spectrum-data platforms (e.g., [16, 17]). This allows for real-time updates on the status of each PR channel at various locations within the service area of the CR system. The price paid by the CR system to the PRNs to utilize the channels depends on the level of PR activities. Let $\zeta _n\in [0,1]$ represent the activity level of PR users in PRN n. Higher PRN utilization results in a higher price for the idle spectrum. Specifically, the price that the CR system pays for utilizing an idle channel belonging to the PRN n is $f_i=(1+\zeta _n)\times Z$, where Z is the price paid by the CR system when $\zeta _n=0$ The PRN system sets the value of Z to ensure that the SU subscription fee per requested service (P) is greater than the PR user subscription fee (this is because the PRNs are the owners of the channels). Each CRN includes a base station that can serve a number of SU subscribers. Let ${\mathcal {U}}_1$ and ${\mathcal {U}}_2$ represent SU customers from CRN 1 and CRN 2, respectively. Figure 1b depicts a network with two CRNs that coexist with a few PRNs. The market structure that represents our network model is the duopoly market structure. In this context, the important problem is how to allocate channels to different SUs in the two CRNs such that the overall CR system profit is maximized. The CR profit is defined as the difference between the total CR revenue and the paid expenses to the PRNs (the total cost of utilizing the licensed spectrum) [18]. The total profit made by the CR system with two CRN firms can be written as follows:

$$\begin{aligned} \Pi _{CR}= & {} \Pi _{CR,1}+\Pi _{CR,2}\nonumber \\= & {} (TR_{1}+TR_{2})-(TC_{1}+TC_{2}) \end{aligned}$$

(1)

where $\Pi _{CR,1}$ and $\Pi _{CR,2}$ are the total profit made by CRN 1 and CRN 2, $TR_1$ and $TR_2$ are CRN 1 and CRN 2’s total revenues, and $TC_1$ and $TC_2$ are CRN 1 and CRN 2’s total prices (costs) paid to the PRNs.

3 Profit maximization problem under duopoly CR market model

3.1 Problem statement and design constraints

Given the set of available idle PR channels, the set of contending users in CRN1 (${\mathcal {U}}_1$), the set of contending users in CRN2 (${\mathcal {U}}_2$), the set of achieved data rates between CR Base-station 1 (2) and the contending users ${\mathcal {U}}1$ (${\mathcal {U}}2$) over each idle channel i (i.e., $r_{j,1}^{(i)},\forall j \in {\mathcal {U}}_1, i \in {\mathcal {C}}$, $r_{j,2}^{(i)}, \forall j\in {\mathcal {U}}_2, i \in {\mathcal {C}}$), the highest price a CR firm can pay to the PRN system to serve one SU, and the CR subscription fee P; our goal is to determine the appropriate channel assignment that can result in serving the greatest number of SUs in the two CRNs at the lowest overall cost (highest CR system profit), subject to:

• 1. Rate demand constraint A SU j can be served only if its total transmission rate over the assigned channels exceeds the rate demand requirement ($R_D$).

• 2. Cost constraint The highest price a CR firm can pay to the PR system to provide a service for a SU j should not exceed a predefined profit margin $\gamma$,

• 3. Exclusive channel occupancy constraint An available PR channel can be assigned to only a single SU at a given time.

• 4. Hardware constraint Because each SU device contains $L_x$ transceivers, the largest number of channels that can be provided to a single SU is limited to $L_x$.

• 5. SNR constraint If the received SNR over channel i for SU j is greater than a predefined threshold (SNR$_th$), the ith channel can be utilized by the SU j.

3.2 Problem formulation

To proceed in our formulation, we introduce the binary decision variables $\left\{ \alpha _{j, k}^{(i)}\right\} , k=1,2$ as follows:

$$\begin{aligned} \alpha _{j, k}^{(i)}= \left\{ \begin{array}{ll} 1, &{} \quad \text {if ch. }i\text { is assigned to SU }j\text { in CRN }k \\ 0, &{} \quad \text {Otherwise.} \end{array}\right. \end{aligned}$$

(2)

By using the defined variables, our objective function ($\Pi _{CR}$) can be expressed in terms of $\alpha _{j, k}^{(i)}$ as:

$$\begin{aligned} \Pi _{C R}=\sum _{k=1}^2 \sum _{j \in {\mathcal {U}}_{k}} P\times {{\textbf {1}}}\left[ \sum _{i \in {\mathcal {C}}} \alpha _{j, k}^{(i)}\right] - \sum _{k=1}^2 \sum _{j \in {\mathcal {U}}_{k}} \sum _{i \in {\mathcal {C}}} f_{i} \alpha _{j, k}^{(i)} \end{aligned}$$

(3)

where ${{\textbf {1}}} [.]$ stands for the indicator function, P is the price charged by the CRN k to serve the SU j and $f_i$ is the activity-dependent price paid by the CR system to the PRNs to access channel i. Setting the decision variable $\alpha _{j,k}^{(i)}$ to 0 ensures the SNR constraint for every SU j with SNR $\le$ $\hbox {SNR}_th$ over channel i. Using the expression in (3) and defining the design constraints in terms of $\alpha _{j,k}^{(i)}$, we can represent our optimization problem mathematically as follows:

$$\begin{aligned} \displaystyle \max _{\alpha _{j, k}^{(i)}}&\quad \sum _{k=1}^2 \sum _{j \in {\mathcal {U}}_{k}} P\times {{\textbf {1}}}\left[ \sum _{i \in {\mathcal {C}}} \alpha _{j, k}^{(i)}\right] - \sum _{k=1}^2 \sum _{j \in {\mathcal {U}}_{k}} \sum _{i \in {\mathcal {C}}} f_{i} \alpha _{j, k}^{(i)}\nonumber \\ \text {s.t.}&\quad \sum _{i\in {\mathcal {C}}} R_{j, k}^{(i)} \alpha _{j, k}^{(i)} \ge \{R_D \text{ or } 0\},~\forall _{j} \in {\mathcal {U}}_{k}, k=1,2 \nonumber \\&\quad \sum _{i\in {\mathcal {C}}} f_i\alpha _{j, k}^{(i)} \le \gamma ,~\forall _{j} \in {\mathcal {U}}_{k},~ k=1,2 \nonumber \\&\quad \sum _{k=1}^2 \sum _{j\in {\mathcal {U}}_k} \alpha _{j, k}^{(i)} \le 1,~\forall _{i} \in {\mathcal {C}} \nonumber \\&\quad \sum _{i \in {\mathcal {C}}} \alpha _{j, k}^{(i)} \le L_x,~\forall j \in {\mathcal {U}}_{k}, ~k=1,2. \end{aligned}$$

(4)

The maximization problem in (4) is a binary non-linear programming problem because of the non-linearity of the indicator function and the either/or data rate constraint. To make the problem more tractable, the indicator function and the and/or constraint can be expressed in linear forms. Specifically, the indicator function can be linearized by introducing auxiliary binary decision variables ($X_{j,k}={{\textbf {1}}}\left[ \sum _{i \in {\mathcal {C}}} \alpha _{j, k}^{(i)}\right]$) and introducing the two linear constraints below:

$$\begin{aligned}{} & {} X_{j, k} \le \sum _{i \in {\mathcal {C}}} \alpha _{j, k}^{(i)}\nonumber \\{} & {} \text{ and }\nonumber \\{} & {} X_{j, k} \ge \frac{\sum _{i\in {\mathcal {C}}} \alpha _{j, k}^{(i)}}{|{\mathcal {C}}|}, ~\forall j\in {\mathcal {U}}_k, ~k=1,2. \end{aligned}$$

(5)

The new constraints assure that $X_{j, k}=1$ if at least one $\alpha _{j, k}^{(i)}=1$, ensuring that the SU j can be served (that is, the SU j is allocated at least one channel when $X_{j, k}=1$).

The either/or data rate constraint for each SU j belonging to CRN k can be linearized by defining two new 0/1-auxiliary variables $y_{j, k}^{1}$ and $y_{j, k}^{2}$ and adding the following constraints:

$$\begin{aligned}{} & {} \sum _{i\in {\mathcal {C}}} r_{j, k}^{(i)} \alpha _{j, k}^{(i)} \le \Gamma y_{j, k}^{1}\nonumber \\{} & {} -\sum _{i \in {\mathcal {C}}} r_{j, k}^{i} \alpha _{j, k}^{(i)} \le -R_D+\Gamma y_{j, k}^{2} \nonumber \\{} & {} y_{j, k}^{1}+y_{j, k}^{2}=1. \end{aligned}$$

(6)

Substituting (5) and (6) into (4), the Duopoly-based CR profit maximization problem can be written as a binary linear programming (BLP) problem as follows:

$$\begin{aligned} \displaystyle \max&\quad \sum _{k=1}^2 \sum _{j \in {\mathcal {U}}_{k}} P\times X_{j, k} - \sum _{k=1}^2 \sum _{j \in {\mathcal {U}}_{k}} \sum _{i \in {\mathcal {C}}} f_{i} \alpha _{j, k}^{(i)}\nonumber \\ \text {s.t.}&\quad \sum _{i \in {\mathcal {C}}} r_{j, k}^{(i)} \alpha _{j, k}^{(i)} \le \Gamma y_{j, k}^{1}, \forall _{j} \in {\mathcal {U}}_{k},~ k=1,2 \nonumber \\&\quad -\sum _{i \in {\mathcal {C}}} r_{j, k}^{i} \alpha _{j, k}^{(i)} \le -R_D+\Gamma y_{j, k}^{2}, \forall {j} \in {\mathcal {U}}_{k},~ k=1,2 \nonumber \\&\quad y_{j, k}^{1}+y_{j, k}^{2}=1, \forall {j} \in {\mathcal {U}}_{k},~ k=1,2 \nonumber \\&\quad X_{j, k}-\sum _{i \in {\mathcal {C}}} \alpha _{j, k}^{(i)} \le 0, \forall _{j, k} \in {\mathcal {U}}_{k},~ k=1,2 \nonumber \\&\quad -X_{j, k}+\frac{\sum _{i \in {\mathcal {C}}} \alpha _{j, k}^{(i)}}{C} \le 0, \forall _{j} \in {\mathcal {U}}_{k},~ k=1,2\nonumber \\&\quad \sum _{i\in {\mathcal {C}}} f_i\alpha _{j, k}^{(i)} \le \gamma ,~\forall _{j} \in {\mathcal {U}}_{k},~ k=1,2 \nonumber \\&\quad \sum _{k=1}^2 \sum _{j\in {\mathcal {U}}_k} \alpha _{j, k}^{(i)} \le 1,~\forall _{i} \in {\mathcal {C}} \nonumber \\&\quad \sum _{i \in {\mathcal {C}}} \alpha _{j, k}^{(i)} \le L_x,~\forall j \in {\mathcal {U}}_{k}, ~k=1,2. \end{aligned}$$

(7)

4 The proposed Antlion (ALO)-based solution

The optimization problem presented in (7) is a BLP that has NP-hard complexity. Thus, meta-heuristic optimization can be used to solve this type of problem. Metaheuristics are algorithms that are driven by nature to discover approximations of answers to specific computationally challenging optimization problems. Metaheuristics are developed using swarming behaviors such as those of the Antlion, firefly, cuckoo, ant, fish, bee, and others [19,20,21]. Properties that support metaheuristic methods include adaptability, homogeneity, illation-free resources, and the capacity to avoid local optima [22]. One of the most colorblueeffective metaheuristic optimization algorithms is ALO. According to the ALO algorithm, ants in the ground are picked up and trapped by the antlion holes. In optimization theory, ants represent the potential candidate solutions to a specific optimization problem within the search space. The ability to catch ants is coded with information about how the objective function relates to the ants and the antlion. The antlion-generated holes and the ants’ random motion inside the search field are both relevant to the implementation of the ALO. The ALO optimization is executed in five steps to obtain approximate sub-optimal solutions: (1) random ant march (walk of ants), (2) antlion pit trapping, (3) ants moving toward the antlion (taking down the prey), (4) shifting the pit, and (5) elitism.

4.1 ALO optimization algorithm

The discussion of dynamic random hill-climbing in this paper focuses on problems where the ALO method can easily find the local optimum. Using hill-climbing methodologies, an ant lion’s ability to leap higher is improved. The algorithm’s global search capabilities can be enhanced by a dynamic hill-climbing mechanism that balances exploration and development. For executing the optimization, the following requirements are assumed:

• In the search area, ants move along a variety of random paths in all directions.

• Antlion traps have an effect on idly walking.

• Antlions can make holes that are appropriate for their size (more powerful fitness, bigger hole).

• Large holes yield higher chances of finding more ants.

• The most athletic antlion will repeatedly catch each ant.

• The subjective movement scale has been adaptively reduced to mimic sliding ants toward the antlion.

• An antlion may have caught and pulled an ant under the sand when the ant became more athletic than the antlion.

• To increase its chances of capturing new prey, the antlion digs a pit close to the most recent caught prey’s position.

4.1.1 Ant’s random walks

The ants randomly explore the search area to collect food, and the antlions construct traps in order to catch them. The ants’ movement is modeled as a random walk as follows:

$$\begin{aligned} X(t)= & {} [ 0,cusum(2r(t_1))-1, cusum(2r(t_2))-1, \nonumber \\{} & {} \quad \ldots cusum(2r(t_T))-1 ]. \end{aligned}$$

(8)

where cusum stands for calculated cumulative sum, T is the maximum number of iterations, X(t) is the motion of ants at iteration $t_i$, and r(t) is a stochastic function that can be expressed as [23]:

$$\begin{aligned} r(t)=\bigg \{ \begin{array}{ll} 0, &{}\quad \text {if rand} \le 0.5\\ 1, &{}\quad \text {if rand}>0.5. \end{array} \end{aligned}$$

(9)

The term rand presents a random number that has a uniform distribution in the range [0, 1]. According to the random motion mechanism, the ant locations change after each iteration. The spontaneous ants’ movement has to be normalized such that it is mapped into a location inside the actual search field based on the upper and lower values. The following formula can be applied for each iteration to find the location of the ants [23].

$$\begin{aligned} X_{i}^{t}=\frac{(X_{i}^{t}-x_{i})(d_{i}-c_{i}^{t})}{d_{i}^{t}-a_{i}}+c_{i} \end{aligned}$$

(10)

where $a_{i}$ and $d_{i}$ represent an ant’s minimum and maximum values for random motion, respectively. $d_{i}^{t}$ and$c_{i}^{t}$ stand for the antlion’s lowest and highest position values at the iteration of ith, respectively.

4.1.2 Trapping in Antlion’s pits

This represents the vicinity of the chosen antlion. When an ant enters the trap, the antlion immediately begins hunting it and drags it down into the pit, which has an effect on how the ants move. The mathematical model for this step is given as [23]:

$$\begin{aligned} c_{i}^{t}= & {} Antlion_{j}^{t}+c^{t} \end{aligned}$$

(11)

$$\begin{aligned} d_{i}^{t}= & {} Antlion_{j}^{t}+d^{t} \end{aligned}$$

(12)

where $Antlion_{j}^{t}$ is the location of each selected jth antlion at the ith iteration, and $d^{t}$ and $c^{t}$ are the maximum and minimum values for the variables related to ant i during the ith iteration.

4.1.3 Sliding ants towards antlion

A roulette wheel is utilized to mimic the antlion’s hunting abilities. Specifically, the ALO uses a roulette wheel operator during the optimization process to choose antlions according to their fitness. This mechanism increases the likelihood that fitter antlions can capture ants.

The techniques presented so far allow antlions to construct traps in proportion to their fitness, and ants should move at random. When an antlion finds an ant in the trap, it throws sand from the trap’s center to prevent colorbluethe ant’s escaping. The ants’ random walk hyper-sphere radius is dynamically reduced to mathematically present such behavior. The change in the trap range as the number of iterations evolves can be given as:

$$\begin{aligned} c^{t}= & {} \frac{c^{t}}{I}, \end{aligned}$$

(13)

$$\begin{aligned} d^{t}= & {} \frac{d^{t}}{I}. \end{aligned}$$

(14)

The term I is a constant that is computed in accordance with the iterative process (the current iteration t) as follows:

$$\begin{aligned} I=\left\{ \begin{array}{ll} 1+10^{2\frac{t}{T}}, &{}\quad \text{ if } 0.1T<t<0.5T \\ 1+10^{3\frac{t}{T}}, &{}\quad \text{ if } 0.5T<t<0.75T \\ 1+10^{4\frac{t}{T}}, &{}\quad \text{ if } 0.75T<t<0.9T \\ 1+10^{5\frac{t}{T}}, &{}\quad \text{ if } 0.9T<t<0.95T \\ 1+10^{6\frac{t}{T}}, &{}\quad \text{ if } 0.95T<t<T \\ 1,&{}\quad \text{ otherwise }. \end{array} \right\} \end{aligned}$$

(15)

4.1.4 Catching prey and rebuilding the trap

In this stage, an ant’s new position is evaluated for its fitness. If an ant is fitter than its associated antlion, it is captured by the antlion, which then reconstructs the trap for the next hunt. To maximize its chances of capturing new prey, the antlion must adapt its location to the most recently hunted ant’s location. This stage can be mathematically expressed as:

$$\begin{aligned} Antlion_{j}^{t}= Ant_{i}^{t}, \text{ if } f(Antlion_{j}^{t})>f(Ant_{i}^{t}) \end{aligned}$$

(16)

where $Antlion_{j}^{t}$ represents the location of the selected antlion j at iteration t, and $Ant_{i}^{t}$ symbolizes the position of ant i at the tth iteration.

4.1.5 Elitism

It is a key feature of evolutionary-based methods that enables maintaining the best-found solution at any optimization time. In ALO, the best antlion generated thus far during every iteration is stored and identified as elite. Because the elite antlion is the fittest, it is capable of influencing the behavior of all ants during the optimization process. Consequently, it is supposed that each ant moves around an antlion that is determined simultaneously using the roulette wheel as well as the elite. Accordingly, the location of the ith ant at the tth iteration can be determined as:

$$\begin{aligned} Ant_{i}^{t}= \frac{RA^{t} + RE^{t} }{2} \end{aligned}$$

(17)

where $RA^{t}$ and $RE^{t}$ respectively denote the arbitrary movements, selected based on the roulette wheel, near an antlion and near an elite at the tth iteration.

4.2 The ALO-based profit-maximization algorithm

Under the duopoly model, ALO can be effectively utilized to solve the profit maximization problem in (7). Each anthill entity in the algorithm represents the ants’ locations and maps them to a channel-user index. The lion’s position represents the ant’s elite location inside the search space (feasible channel-user assignment). The algorithm then evaluates the objective function trade to examine the fitness/objective value of the antlions and then chooses the best one based on the “survival of the fittest” principle. After completing the iterations, the elite antlion that has the best fitness value (highest CR profit) is considered the best sub-optimal solution (the best channel-user assignment in the CR system). The location of the elite lion represents the CR system’s maximum profit.

Specifically, the ALO-based channel assignment is executed as follows: the initial obtained solution (ant location) is mapped into a channel-user assignment and assessed to determine the objective function (the CR profit). Upon completion of the evaluation procedure, the best fitness (highest CR profit) is recorded as elite antlion-fitness and elite antlion-position. The ALO then repeats the same assessment procedure based on (9)–(17) until the maximum number of iterations is reached. The pseudo-code in Algorithm 1 summarizes the operation details of the proposed ALO-based CR-profit maximization algorithm.

4.3 Computational complexity analysis

Typically, the time complexity (i.e., the number of operations required to obtain the sub-optimal solution) is used to assess the efficacy of optimization algorithms [24]. The time complexity of metaheuristic algorithms heavily depends on the population size, number of iterations, number of loops, and number of function evaluations.

The following quantifies the time-complexity analysis of the proposed ALO-based algorithm in Algorithm 1. Line 1 represents the algorithm’s parameters’ initialization (number of population n, dimension $d=1$, the maximum number of iteration Itermax), which has a time complexity of O(n). In lines 2 and 3, the algorithm computes the objective function (CR profit) for each feasible channel-user assignment (the fitness of ants and antlions) and then determines the best-found solution so far (identifies the elite), which incurs a time complexity of O(n). The main loop (While) starts from line 4, and it stops when the iteration reaches the maximum number of iterations. The complexity of each line is multiplied by the maximum iteration (Itermax) in this while loop. In the for loop (for each antlion) in line 5, the steps in this loop are executed n times with time complexity ($O(Itermax \times n)$). Because the antlion’s random walk is independently generated for each dimension (d) in lines 6-8, the time complexity for these lines is $O(Itermax \times n \times d)$. The time complexity of calculating all ant positions in lines 5-10 is $O(Itermax \times n)$. The cost values of the ants with updated positions can be calculated with time complexity $O(Itermax \times n)$ in lines 11-19. Thus, the time complexity of the used ALO algorithm with $d=1$ is $O(Itermax\times n)$ as $d=1$.

Observation In our proposed ALO-based algorithm, the only two adjustable parameters that impact the algorithm’s performance and complexity are the maximum number of iterations and the population size n. In general, the performance of ALO algorithms improves as the population size increases, up to a sufficient size. After such a sufficiently large n, increasing n does not improve ALO performance, but rather adds unnecessary computational complexity. Therefore, an empirical investigation is necessary for determining the best parameters that optimize the performance of the proposed ALO-based optimization algorithm while incurring the least computational complexity.

5 Performance evaluation

We compare the performance of the proposed ALO-based profit-maximization channel assignment algorithm (MaXPCA) with that of two reference CRN channel assignment algorithms, the maximum-rate assignment (MaXRCA) and the minimum-channel assignment (MiNCCA), using MATLAB simulations. The MaXRCA algorithm seeks to increase the number of admitted SUs with the highest overall network throughput without considering the overall profit achieved in the CR system. On the other hand, MiNCCA attempts to maximize the number of served CR users using the least number of PR channels without awareness of the network’s overall profit. For a fair comparison, the channel-assignment optimization problems in MaXPCA, MaXRCA, and MiNCCA are computed using the ALO optimization algorithm and under the same QoS and design constraints.

5.1 Simulation setup

In a network area of $200 \,\hbox {m} \times 200 \,\hbox {m}$, we consider two CRN service providers to coexist geographically with four PRNs. Every PRN is authorized to utilize a set of $|{\mathcal {C}}|/4$ orthogonal channels, each with a bandwidth of 5 MHz. The number of CR users in each CRN is set to 50 SUs. The SUs in each CRN are uniformly distributed in the service area. The Rayleigh fading channel model characterizes the channel gain between any two communicating SUs [25]. The PR activity level (spectrum utilization) determines the cost of accessing channel i ($f_i$) at a specific time. Throughout the simulation time, the PR activity level $\zeta _n(t)$ for each PRN n is uniformly varied in the range $[\zeta _n^{min}, \zeta _n^{max}]$.The activity level ranges for the PRNs 1, 2, 3, 4 are [0.1, 0.4], [0.1, 0.5], [0.5, 0.9], and [0.4, 0.9], respectively. As a result, the cost of using a channel i in a PRN n at a given time t is given as $f_i = (1 + \zeta _n(t)) \times 10$ price units. We set the CR service subscription fee to $P = 30$ units of price. The maximum CRN cost paid to PRNs to serve a single SU is $\gamma =25$ price units. We note that a similar evaluation methodology that is based on the unit price was considered in [26, 27]. The number of PR channels varies from 20 to 80.

The rate demand is set to $R_D = Rd$ Mbps for all SUs. The main performance metric in our study is the achieved CR profit. The presented results are the average of 100 experiments, each lasting for 2000 optimization instances.

5.2 Simulation results

The achieved CR overall profit is depicted in Fig. 2 with the number of SUs per each CRN for different numbers of PR channels (20, 40, 60, and 80) and $R_d = 10$ Mbps. Figure 2 also indicate that as the number of available PR channels increases, the number of SUs that can be served increases for all algorithms, resulting in higher CR profit. In particular, Figs. 2a, b show that for $|{\mathcal {C}}|=80$ and 60, the CR system can serve up to 40 and 30 SUs, respectively. Furthermore, for $|{\mathcal {C}}|=40$ and 20, Figs. 2(c) and (d) indicate that up to 20 and 10 SUs can be served, respectively. Figure 2 shows that for $|{\mathcal {C}}|=80$, our MaXPCA algorithm can provide a profit of up to 727 per unit price, while the MaXRCA and MinCCA algorithms respectively provide 610 and 500 per unit price. Specifically, for the identical number of admitted SUs and regardless of the number of available PR channels, MaXPCA outperforms MaXRCA and MinCCA by up to $20\%$ and $45\%$, respectively. This is due to the fact that our proposed channel assignment takes into consideration the interdependence between the activity-dependent price for PR channel utilization by the CR system and the received data rates across the different idle channels. Therefore, MaXPCA chooses the channel-user assignment that meets the SU’s rate demand at the lowest cost, regardless of the amount of used spectrum (i.e., our proposed ALO-based MaXPCA algorithm prefers choosing 2 low-price PR channels with a combined transmission rate that exceeds $R_d$ over one high data-rate, high-price channel).

Fig. 2

CR profit vs. the number of SUs for the different numbers of PR channels

Fig. 3

CR profit vs. the rate requirements for different number of PR channels

Figure 3 investigates the profit performance versus the rate demand requirements under different numbers of PR channels and 50 SUs. Figures 3a–d demonstrate that our proposed ALO-based MaxPCA algorithm performs better than the other two algorithms, regardless of $R_D$ and ${{\mathcal {C}}}$. The proposed ALO-based profit-aware algorithm outperforms the Max-rate and minimum channel assignment by up to $20\%$ and $35\%$, respectively. The achieved profit of $R_d \le 14$ Mbps is clearly the highest of any algorithm. This is because the chances of serving the SUs with the required rate demand using one channel are high. Serving each SU will require more than one channel at $R_d \le 14$ Mbps, resulting in higher costs and lower profit. Figures 3a–d show how profit increases as $|{\mathcal {C}}|$ increases. This is expected because of the higher availability of PR channels and the resulting higher number of served SUs, which increases the achieved CR profit.

The performance of the various algorithms is examined in Table 1 under various rate demand ranges, where the transmission rate requirement $R_d$ for every SU is uniformly chosen from the range $[R_d^{min}, R_d^{max}]$. The results indicate that our proposed algorithm significantly outperforms the other algorithms, irrespective of the rate demand range. Finally, Fig. 4 depicts the convergence (iterative) curve of our ALO-based algorithm with $N=80$ channels. The average best objective values are plotted versus the number of iterations. It is clear that the proposed ALO profit-maximization algorithm converges after 300 iterations. This convergence behavior of the proposed ALO-based profit-maximization assignment algorithm indicates that the ALO algorithm has an effective global-search capability, which can eliminate the local optimum constraints that exist in other evolutionary algorithms (this results in line with that presented in [28]).

Table 1 Profit performance for variable rate demand for the different channel assignment algorithms

Fig. 4

The convergence performance of the ALO-based MaXPCA algorithm

6 Conclusion

In this paper, we investigated the channel assignment problem in a duopoly CR market model to enhance the profit achieved in the CR system while achieving a set of QoS and design constraints. The set of design constraints includes the utilization-dependent mandated price paid to the PRNs, the total paid subscription fees by all served SUs, the SU link-quality characteristics across the different channels, and the available transceivers at each SU. This aim was pursued by taking into account the time-varying characteristics of the various PR channels and the dependence between the spectrum utilization and cost paid by the CR system. The mathematical formulation of the channel assignment problem was shown to be a BLP problem that seeks to increase the CRNs’ profit by reducing the CR paid fees to the PRNs while simultaneously servicing the largest possible number of SUs. We adopted the well-known ALO technique, which can provide sub-optimal solutions in polynomial time since the optimum solution to this BLP could not be obtained in polynomial time. Simulation results revealed that the proposed profit-aware channel assignment depicts a significant CR profit improvement over previously proposed profit-unaware CR channel assignment algorithms. This improvement is attributed to the fact that our algorithm considers the interdependence between the price of PR channels and their utilization levels as well as the SU achieved rate over the various PR channels.