Analysis of secrecy outage performance for full duplex NOMA relay systems with appearance of multiple eavesdroppers

Abstract

Full-duplex (FD) relay systems including a transmit antenna selection and a non-orthogonal multiple access (NOMA) methods are analyzed under presence of multiple eavesdroppers. A channel state information of both the considered system and eavesdroppers is assumed to be outdated and eavesdroppers eavesdrop information signals independently. A closed-form of secure outage probability (SOP), secrecy throughput of every user is derived to evaluate the secrecy performance, and the mathematical analysis approach is verified by the Monte-Carlo simulation. Furthermore, the Golden-Section Search algorithm is proposed to find the maximum of the secrecy throughput of the considered FD-NOMA system. Numerical results indicate that there exists the SOP floor in the considered system and it is constrained by the channel gain of near user. Moreover, there is the optimal signal to interference plus noise ratio value which minimizes the SOP of the system regardless of the number of eavesdroppers. In comparison with half-duplex NOMA model, the SOP of FD-NOMA model is better.

1 Introduction

Nowadays, a non orthogonal multiple access (NOMA), as well known is a promising technique to improve significantly a spectral efficiency for the fifth generation (5G) and beyond (5GB) mobile networks [1,2,3]. It is to meet the requirement of connection for large multiple users systems and growing demand for the amount of data traffic. The number of devices and connections in wireless networks, as well as the spectrum demand continuously increase. To detect the signals of multiple users with different power levels or codes, a successive interference cancellation (SIC) method is applied to all users [4, 5].

Also, a full-duplex (FD) communication can improve the spectral efficiency by receiving and transmitting simultaneously via the same bandwidth [6,7,8], furthermore to mitigate the self-interference of the FD model, analog and digital domains cancellation methods are employed. According to a report in [9, 10], the capability mitigation of the self-interference cancellation (IC) can be up to 110 dB. On the other hand, the multi-antenna deployment has improved the system performance, while transmit antenna selection (TAS) can reduce the cost, power consumption and hardware complexity [11]. Combination of TAS and FD can improve the secure performance, because the TAS enhances a signal to noise ratio (SNR) in legitimate channels and the FD provides a higher data rate transmission.

Presently, some works evaluated the performance of FD cooperative NOMA systems as in  [12,13,14]. In these works, the authors derived a closed-form expression of outage probability (OP) and ergodic capacity (EC) of the proposed system. The hybrid half-duplex (HD)/FD cooperative NOMA system was carried out in [15], the optimal power allocation in the sense of maximum EC and minimum OP was derived. The above mentioned works considered simple models and without investigating the secure performance of the system. Meanwhile, wireless networks are especially vulnerable to eavesdrop due to broadcasting signals on wireless channels. Generally, traditional security approaches employ symmetric and asymmetric cryptographic algorithms to achieve secure communications.

Recently, physical layer security (PLS) has attracted attention as a simple method to guarantee secure communications in wireless networks. The basic idea of PLS is that it utilizes physical characteristics of wireless channels to protect the source message against eavesdroppers. The common metric used to evaluate the PLS of wireless communication networks is secrecy capacity, which is defined as the maximal achievable rate at which messages can be reliably sent from a source to a receiver without being decoded by any eavesdropper. In other words, communication data can be theoretically secured without using any traditional cryptographic mechanisms if the condition of legitimate propagation channel is better than that of eavesdroppers [16,17,18]. The history of PLS can be traced back to Shannon’s information theoretic secrecy analysis [16], and then was developed into the work of Wyner on the wiretap channel [17], where two legitimate users communicate over the main channel and an eavesdropper accesses to signals from the illegitimate channel. In [18], Csiszar and Kornor proved that there exist channel codes that guarantee the security of wireless communication networks. Since the 1949s, the PLS of wireless communication systems has been studied. It is studied continuously until now [19,20,21,22]. Presently, PLS is still a major problem in the overall structure of wireless networks. Especially, for multi-user systems, where intertwinements between legitimate users may have occurred, the PLS has attracted more attention.

The study on PLS for NOMA systems has been presented in many literatures [23,24,25,26], where each work considered a different aspect. The work in [23] investigated a secrecy outage probability (SOP) of far and near users, where signals are transmitted by a base station via the FD relay and the direct link. In this scenario, the authors considered the case of the presence of only one eavesdropper. To improve the secure performance of NOMA systems, the authors in [24] use a jammer to an eavesdropper appearance in the uplink channel, as such the configuration of the system consists of multi-user, one BS and one eavesdropper. This is the simplified scenario investigated with external eavesdropper in communication links from users to the BS. The impact of imperfect CSI on PLS of NOMA system is considered by the authors in [25], this word proposed an algorithm to optimize the power allocation for the transmitter in the sense of minimum OP and SOP. The work carried out in this scenario is that the authors only considered the secrecy of NOMA downlink signals with the appearance of one eavesdropper. Similar to investigation of SOP for the NOMA downlink in [25], the authors in [27] considered the secrecy performance of NOMA downlink with two users. The decoding capability of eavesdroppers is investigated in two case, i.e., perfect and imperfect received signals.

Based on the summarization mentioned above, we know that these works considered the system with an HD model and one eavesdropper, most of them refer to the case of point-to-point communication. Therefore, we are going to propose an idea that close to the work in [26]. In this model, the authors proposed a system, where the best relay with HD model forwards signals to two users by the NOMA scheme, and another relay is selected as a jammer to one eavesdropper. A major problem with this scheme is the interference between relays, cancellation of interference of each relay is very difficult and lets hardware complexity increase.

To the best of our knowledge, the system with the TAS algorithm at the source, the NOMA scheme at FD relay and multiple eavesdroppers, is not taken into consideration in any literature. Motivated by the general problem of securing propagation over wireless channels, in this paper, we mainly focus on the SOP of the TAS-FD-NOMA system with multiple eavesdroppers. The effect of channel state information (CSI) on the TAS scheme is discussed when the CSI between the desired devices is assumed to be outdated, whereas the CSI between the relay and eavesdroppers is unknown. Because the relay doesn’t know the CSI, several techniques to improve the secrecy performance such as artificial noise, beamforming and jamming are unsuitable to use in our work.

The contributions of this paper are summarized as follows:

• We propose and analyze the SOP of FD-NOMA system with multiple eavesdroppers overhearing the information of two users. To improve the secure performance, the source is equipped with multiple antennas and the TAS scheme. To investigate the proposed system in a practical scenario, the non-colluding multiple eavesdroppers are considered, it can be found in Internet of Things (IoT) and future wireless networks [28].

• We analyze the security of FD-NOMA relay system by deriving the closed-form expression of SOP, and provide insights of the SOP over Rayleigh fading channel propagation condition, the outdated CSI for TAS scheme and the imperfect CSI at eavesdroppers. The theoretical analysis is validated via simulations.

• Instead of consideration of the secrecy capacity, we investigate the secrecy throughput of the FD-NOMA system. We propose to utilize the Golden-Section Search algorithm to find the maximum of the secrecy throughput. Two lemmas are proved to explain the property of our work, and they also can be applied for investigating another work.

• We propose the FD model at the relay to improve the data rate of legitimate channel, and then the FD model is compared with the HD model based on the SOP performance of the proposed system.

• The performance of the proposed system is investigated based on the number of antennas of the source, the self interference cancellation coefficients at the full-duplex devices and the transmission power.

The rest of the paper is organized as follows. Section 2 describes the system model, and Sect. 3 presents the detailed analysis of the considered FD-NOMA relay system. The main results and their implications are discussed in detail in Sect. 5. Finally, Sect. 6 concludes the paper.

2 FD-NOMA relay systems with multiple non-colluding eavesdroppers

2.1 System model

Fig. 1

System model of the considered FD-NOMA relay system with multiple non-colluding eavesdroppers

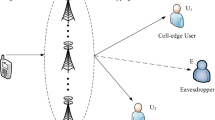
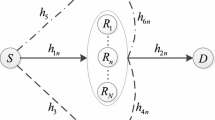
In this paper, the downlink FD-NOMA relay system as illustrated in Fig. 1 is investigated. The source ($\mathrm {S}$) is equipped with K antennas, and transmits its data to two legitimate end-users ($\mathrm{D}_i$) with the assistance of the relay $\mathrm{R}$ which utilizes the decode-and-forward (DF) scheme in the FD model. As the same with the work in [26], we assume that the direct link is unavailable due to long distance, blockage and shadowing. Furthermore, only two end-users are considered because the degradation of system performance is proportional to the number of users due to applying SIC [29]. The system also includes overhearing attacks of multi-malicious eavesdroppers, $\mathrm{E}_l, l \in \{1,2,\ldots ,L \}$.¹ The relay node is equipped with two antennas for the active FD mechanism. The advantage of this mechanism is self-interference cancellation at the antenna domain, because of natural isolation which arises from the sheer physical distance between transmit and receive antennas, and rational installation guarantee obstacles between transmit and receive antennas to block the line-of-sight signal. Whereas, due to the limitation of the size, users and eavesdroppers have only one antenna, which is the same configuration in [24,25,26].

All the channels are assumed to follow the Rayleigh fading block model. Let’s $h_{1,k}\sim \mathcal{CN}(0,\Omega _\mathrm{SR})$ and $h_{2,E_l}\sim \mathcal{CN}(0,\Omega _\mathrm{RE})$ denote the channel fading (including large-scale and small-scale) coefficient of propagation channel from antennas of the $\mathrm S$ to the relay and from the relay to eavesdroppers, respectively. Moreover, $\tilde{g}_i$ represents the channel fading coefficient of channel between the best relay and the $i^{th}$ user, i.e. $g_i=\tilde{g}_i\sqrt{d_i^{-\alpha }}$, then ${g_i} \sim \mathcal{CN}(0,\Omega _{\mathrm{RD}_{i}})$, where $i\in \{1,2\}$ and $\Omega _{\mathrm{RD}_{i}}={\mathbb E} \{|g_i|^2\}$, $d_i$ is the distance between the best relay and $\mathrm{D}_i$, and $\alpha$ is the path-loss coefficient. Without loss of generality, it is assumed that the channel gains are sorted according to an ascending order $|g_2|^2<|g_1|^2$.

On the other hand, we also denote $h_\mathrm{RR}\sim \mathcal{CN}(0,\Omega _\mathrm{RR})$ as the channel fading coefficient between the transmit antenna and the receiver antenna of the relay, thus $|h_\mathrm{RR}|^2$ is exponentially distributed with $\mathbb E \{|h_\mathrm{RR}|^2\}=\Omega _\mathrm{RR}$, which is closely related to the strength of the loop-back interference.

The additive white Gaussian noise (AWGN) at each receiver is represented by ${w}_\mathcal{A}\sim \mathcal{C}\mathcal{N}(0, \sigma ^2_\mathcal{A})$, $\mathcal{A}\in \{\mathrm{R,E, D}_i\}$, in which $\sigma ^2_\mathcal{A}$ is the noise variance. In this paper, we assume that the CSI is perfect at the receiver. In contrast, the feedback CSI from the R to the S is outdated, and channels estimation at eavesdroppers is imperfect due to the R doesn’t know the channel from itself to eavesdroppers.² Thus, the estimated channel of R-$\mathrm{E}_l$ can be represented via actual and estimation error channels as

$$\begin{aligned} h_{2,E_l} = \hat{h}_{2,E_l} + \epsilon _{E_l}, \end{aligned}$$

(1)

where, $\epsilon _{E_l}\sim \mathcal{CN}(0, \sigma _\mathrm{E_l}^2)$ and $\hat{h}_{2,E_l}\sim \mathcal{CN}(0,\hat{\Omega }_\mathrm{RE})$ denote the coefficient of the estimation error and actual channels between R-$\mathrm{E}_l$, respectively. According to [30, 31], $\hat{\Omega }_\mathrm{RE}= \Omega _\mathrm{RE}-\sigma _\mathrm{E_l}^2$ is the normalized channel gain of $\hat{h}_{2,E_l}$, which is statistically independent of $\epsilon _{E_l}$. On the other hand, we assumed that $\rho _{E_l}$, $0\le {\rho _{E_l}}\le 1$ is the correlation coefficient of channel estimation error, which indicates the difference between the actual and estimated channel. Moreover, the normalized variance of the estimation error is $\sigma _\mathrm{E_l}^2=\rho _{E_l}\Omega _\mathrm{RE}$, thus, we have $\hat{\Omega }_\mathrm{RE}= (1-\rho _{E_l})\Omega _\mathrm{RE}$.

The transmit antenna selection (TAS) scheme can reduce the power consumption and complexity of wireless systems because only one RF chain is used, hence the TAS is applied to the $\mathrm S$.³ The operation of the TAS scheme can be summarized as follows. First, the $\mathrm S$ sends the pilot sequence one-by-one to the $\mathrm R$ for the channel estimation. After that the $\mathrm R$ selects a transmit antenna associated with the best instantaneous SNR, and gives feedback with the index of the selected antenna to the $\mathrm S$. This feedback information can be presented by a binary vector with the number of bits $b=\log _2N$.

2.2 Calculation of transmission rate

Due to the time-varying characteristics of $\mathrm S$ – $\mathrm R$ channel, its coherent time may be altered when the feedback delay is larger than the transmission block period T. Consequently, the feedback information of CSI for the selected antenna is outdated at the S. Mathematically, we have signal to noise ratio (SNR) of TAS scheme as

$$\begin{aligned} \gamma _{\mathrm{SR}} = \mathrm{arg} \max _{k=1\div K}\gamma _{1,k}. \end{aligned}$$

(2)

Let’s denote $\rho _{1,k}$ as the correlation coefficients between the actual channel, $\hat{h}_{1,k}$, and the estimated channel, $h_{1,k}$. For simplicity, we assume that the correlation coefficients $\rho _{1,k}$, $k=1,\cdots ,K$ is the same, i.e., $\rho _{1,k} =\rho , \text {with}\,\,\,k = 1, 2, \cdots ,K$. By using Markov chain, the relationship of $h_{1,k}$ and $\hat{h}_{1,k}$ can be modeled by the correlation coefficient $\rho$ as

$$\begin{aligned} h_{1,k} = \rho \hat{h}_{1,k} + \sqrt{1 - \rho ^2} {e}_{1,k}, \end{aligned}$$

(3)

where ${e}_{1,k}$ is an error term due to outdated changes and is modeled by a circular symmetric complex Gaussian random variable, i.e., ${e}_{1,k} \sim \mathcal{CN}(\mu , \sigma ^2)$. The coefficient $\rho$, $0\le \rho \le 1$, depends only on the time delay and can be considered as the measurement of the channel fluctuation rate. To reduce the complexity of mathematical equations, we denote $X= \mathrm{arg} \max _{k=1\div K}|h_{1,k}|^2$ in the following analysis.

Remark 1

According to [32], a probability density function (PDF) of SNR of $\mathrm S- R$ link with the TAS scheme in the case of outdated CSI is given by

$$\begin{aligned} f_X(x) =&\sum \limits _{k = 1}^{K}\left( {\begin{array}{c}K\\ k\end{array}}\right) \frac{(-1)^{k-1}k}{\Omega _\mathrm{SR}\Delta (\rho )}\exp \left( -\frac{kx}{\Omega _\mathrm{SR}\Delta (\rho )}\right) , \end{aligned}$$

(4)

where $\Delta (\rho ) = 1+(k-1)(1-\rho ^2)$.

From (4), a cumulative distribution function (CDF) of X is expressed as follows.

$$\begin{aligned} F_X(x) \!=\!\sum \limits _{k = 1}^{K}\left( {\begin{array}{c}K\\ k\end{array}}\right) (\!-\!1)^{k-1}\Big [1\!-\! \exp \Big (\!-\!\frac{kx}{\Omega _\mathrm{SR}\Delta (\rho )}\Big )\Big ]. \end{aligned}$$

(5)

Based on the property of CDF, i.e., $F_X(\infty )=1$, then when $x\rightarrow \infty$ in (5), $\sum \nolimits _{k = 1}^{K}\left( {\begin{array}{c}K\\ k\end{array}}\right) (-1)^{k-1}=1$. Thus, we can rewrite (5) as

$$\begin{aligned} F_X(x) =1-&\sum \limits _{k = 1}^{K}\left( {\begin{array}{c}K\\ k\end{array}}\right) (-1)^{k-1}\exp \left( -\frac{kx}{\Omega _\mathrm{SR}\Delta (\rho )}\right) . \end{aligned}$$

(6)

Proof of Remark 1 is depicted in [32].

The PDF in (4) and the CDF in (6) are probability functions which model the statistical channel gain between S - $\mathrm R$ link with the outdated CSI. From these equations, we can recognize that when the CSI is outdated, the variance of channel fading amplitude increases, and then the received SINR is decreased.

We assume that the relay processes the received signal within one time slot, thus the signal which is transmitted at the relay is the received signal from the source in the previous slot. The signal of $\mathrm D_1$ and $\mathrm D_2$ is respectively denoted by $x_1$ and $x_2$, then the received signal at the relay in the FD model is represented by

$$\begin{aligned} y_\mathrm{R} \!\!=\! \!h_\mathrm{SR}(\sqrt{a_1 P_\mathrm{S}}x_1 \!\!+\!\! \sqrt{a_2 P_\mathrm{S}} x_2) \!\!+\!\! \sqrt{\eta P_\mathrm{R}} x_\mathrm{R}h_\mathrm{RR}\!\!+\!\! w_\mathrm{R}, \end{aligned}$$

(7)

where $h_\mathrm{SR}=\mathrm{arg} \max _{k=1\div K}h_{1,k}$ is the channel fading coefficient from the selected antenna of S to the R. $a_1$ and $a_2$ denote the power allocation coefficients for the $x_1$ and $x_2$ signals, respectively with $a_1+a_2=1$. Following the principle of NOMA, to achieve the boundary of the user capacity, let $a_2>a_1$.⁴

The coefficient of residual self interference cancellation (RSIC) is denoted by $\eta$, it represents the remaining self-interference after cancellation process, and depends on the quality of designing FD self interference mitigation. To notice that the component $\sqrt{\eta P_\mathrm{R}} x_\mathrm{R}h_\mathrm{RR}$ will be subtracted by the self-interference cancellation techniques such as antenna isolation, analog and digital domain suppression.

Furthermore, according to the NOMA principle, the relay R performs a successive interference cancellation (SIC) for the $x_2$, and then detect the $x_1$. That is, the R decodes the signal $x_2$ while treating the $x_1$ as interference, then removes the $x_2$ from the received signal and decodes the $x_1$. Thus SINR at the R of $x_1$ and $x_2$ in the case of perfect SIC⁵ is given as

$$\begin{aligned} \gamma _\mathrm{R}^{x_1}&=\frac{a_1 P_\mathrm{S}|h_\mathrm{SR}|^2}{\eta P_\mathrm{R}|h_\mathrm{RR}|^2 +\sigma _\mathrm{R}^2}, \end{aligned}$$

(8)

$$\begin{aligned} \gamma _\mathrm{R}^{x_2}&=\frac{a_2 P_\mathrm{S}|h_\mathrm{SR}|^2}{a_1 P_\mathrm{S}|h_\mathrm{SR}|^2+\eta P_\mathrm{R}|h_\mathrm{RR}|^2+\sigma _\mathrm{R}^2}. \end{aligned}$$

(9)

After successfully decoding, the R re-encodes the $x_1$ and $x_2$, $\sqrt{a_1 P_\mathrm{R}}x_1 + \sqrt{a_2 P_\mathrm{R}} x_2$, to transmit to the $\mathrm D_1$ and $\mathrm D_2$ in the next time slot. Thus, the received signal at the $\mathrm D_1$ and $\mathrm D_2$ is given as

$$\begin{aligned} y_\mathrm{D_1}&= g_1(\sqrt{a_1 P_\mathrm{R}}x_1 + \sqrt{a_2 P_\mathrm{R}} x_2)+w_\mathrm{D_1}, \end{aligned}$$

(10)

$$\begin{aligned} y_\mathrm{D_2}&= g_2(\sqrt{a_1 P_\mathrm{R}}x_1 + \sqrt{a_2 P_\mathrm{R}} x_2)+w_\mathrm{D_2}. \end{aligned}$$

(11)

Similar to the SIC method at the R, the $\mathrm D_1$ firstly detects and subtracts the $x_2$ based on the SIC structure, and then decodes the $x_1$, while the $\mathrm D_2$ decodes its own signal with considering the $x_1$ as interference. Thus, the SINR at the $\mathrm D_1$ and $\mathrm D_2$ is given as

$$\begin{aligned} \gamma _\mathrm{D_1}^{x_2}&=\frac{a_2 P_\mathrm{R}|g_1|^2}{a_1 P_\mathrm{R}|g_1|^2+\sigma _\mathrm{D_1}^2}, \end{aligned}$$

(12)

$$\begin{aligned} \gamma _\mathrm{D_1}^{x_1}&=\frac{a_1 P_\mathrm{R}|g_1|^2}{\sigma _\mathrm{D_1}^2}, \end{aligned}$$

(13)

$$\begin{aligned} \gamma _\mathrm{D_2}^{x_2}&=\frac{a_2 P_\mathrm{R}|g_2|^2}{a_1 P_\mathrm{R}|g_2|^2+\sigma _\mathrm{D_2}^2}. \end{aligned}$$

(14)

Due to the broadcast property of the signals in wireless environment, the received signal of the eavesdropper $\mathrm{E}_l$ is given as follows.

$$\begin{aligned} y_{\mathrm{E}_l} = h_{\mathrm{2, E}_l}(\sqrt{a_1 P_\mathrm{R}}x_1 + \sqrt{a_2 P_\mathrm{R}} x_2)+w_{\mathrm{E}_l}. \end{aligned}$$

(15)

In the case of non-colluding, every eavesdropper processes the received signal independently, overhearing is successful if one of them can detect the signal. Therefore, the channel of the best one in the set of eavesdroppers is taken into account, that means the channel gain between the R and eavesdroppers is the best one in all of eavesdroppers, $h_{\mathrm{2, E}} = \max _{l=1\div L} h_{2,E_l}$. Similar to [34,35,36], we consider the worst-case, i.e., the eavesdropper can detect the signal powerfully, it can detect the $x_1$ (or the $x_2$) without being interfered by the $x_2$ (or the $x_1$), and then the maximal SNR of received signals at eavesdroppers is given as

$$\begin{aligned} \gamma _{\mathrm{E}}^{x_i} =\frac{a_i P_\mathrm{R}}{\sigma _{\mathrm{E}_l}^2}| h_{\mathrm{2, E}}|^2, \quad i \in \{1, 2\}. \end{aligned}$$

(16)

Since the DF protocol is applied to the R, the end-to-end transmission rate of $x_1$ and $x_2$ over legitimate channels equals the lowest rate of all transmitted hops from the S to the end-user. Consequently, it can be calculated by the minimum SINR of all related nodes as follows.

$$\begin{aligned} \mathrm{C}^{x_1}&= \log _2\Big (1+ \min \{\gamma _\mathrm{R}^{x_1}, \gamma _\mathrm{D_1}^{x_1} \}\Big ), \end{aligned}$$

(17)

$$\begin{aligned} \mathrm{C}^{x_2}&= \log _2\Big (1+ \min \{\gamma _\mathrm{R}^{x_2}, \underbrace{\gamma _\mathrm{D_1}^{x_2}}_\mathrm{SIC}, \gamma _\mathrm{D_2}^{x_2} \}\Big ). \end{aligned}$$

(18)

On the other hands, the rate of $x_1$ and $x_2$ over wiretap channels is given as

$$\begin{aligned} \mathrm{C}_\mathrm{E}^{x_i}&= \log _2\Big (1+ \gamma _{\mathrm{E}}^{x_i}\Big ), i\in \{1,2\}. \end{aligned}$$

(19)

To notice that the secrecy capacity is denoted as the gap of capacity between legitimate and eavesdropping channels [19, 23], i.e., $\mathrm{C^{sec}}= [\mathrm{C}^{x_i}- \mathrm{C}_\mathrm{E}^{x_i}]^+$. In order to evaluate the secrecy capacity $\mathrm{C^{sec}}$, we estimate the instantaneous capacity of legitimate and eavesdropping channels, it is described in detail in Sect. 4.

3 Performance analysis of SOP

In this section, we provide the closed-form expressions of the SOP from the $\mathrm{S}$ to the $\mathrm{D}_i$ of the system. The SOP is defined by the probability that the end-to-end secrecy capacity is lower than the given positive secure transmission rate [26].

$$\begin{aligned} \mathrm{SOP}^{x_i}&= \Pr \Big ( [\mathrm{C}^{x_i}-\mathrm{C}_\mathrm{E}^{x_i}]^{+} <r_i\Big ), \end{aligned}$$

(20)

where $[x]^{+}= \max \{0,x\}$, where, $\mathrm{C}^{x_i}$ and $\mathrm{C}_\mathrm{E}^{x_i}$ given in (17), (18) and (19) are, respectively. $r_i = r_b-r_e$ is also called the transmission rate of confidential data, $r_b$ denotes the codeword rate of the legitimate channel while $r_e$ is the equivocation rate of the eavesdropping channel. It indicates that, smaller $r_i$ leads to smaller SOP, smaller $r_b$ and higher $r_e$.

As evaluation in [23, 37], the received signals $x_1$ and $x_2$ at eavesdroppers are different, thus we investigate the SOP of $x_1$ and $x_2$ separately.

3.1 Secrecy outage probability of $x_1$

The $\mathrm{SOP}$ of $x_1$ is defined as the probability that the instantaneous secrecy capacity of $x_1$, i.e. $[\mathrm{C}^{x_1}-\mathrm{C}_\mathrm{E}^{x_1}]^{+}$, is below the predefined threshold value of secure transmission rate, $r_1$. The SOP of $x_1$ is given as in Proposition 1.

Proposition 1

The SOP of $x_1$ in the TAS - FD - NOMA relay system under the condition of outdated CSI at the S and imperfect CSI at the eavesdropper is given as

$$\begin{aligned} {\text{SOP}}^{{x_{1} }} = & 1 - \sum\limits_{{k = 1}}^{K} {\sum\limits_{{l = 1}}^{L} {( - 1)^{{k + l - 2}} } } \left( {\begin{array}{*{20}c} K \\ k \\ \end{array} } \right)\left( {\begin{array}{*{20}c} L \\ l \\ \end{array} } \right)\frac{{lP_{{\text{S}}} \Omega _{{{\text{SR}}}} \Delta (\rho )}}{{\beta P_{{\text{R}}} \hat{\Omega }_{{{\text{RE}}}} }} \\ & \frac{{\exp (\frac{{(1 - \gamma _{{{\text{th}}}} )}}{{a_{1} \Omega _{{{\text{SR}}}} \Delta (\rho )P_{{\text{S}}} }} + \frac{{1 - \gamma _{{{\text{th}}}} }}{{a_{1} P_{{\text{R}}} \Omega _{{{\text{RD}}_{{\text{1}}} }} }})}}{{{\mathcal{A}}_{2} + {\mathcal{A}}_{3} + {\mathcal{A}}_{4} }}, \\ \end{aligned}$$

(21)

where

$$\begin{aligned} \quad \gamma _\mathrm{th}&= 2^{r_1}, beta = \Omega _\mathrm{RR}k\eta P_\mathrm{R}(\gamma _\mathrm{th}-1)\\&+a_1\Omega _\mathrm{SR} \Delta (\rho ) P_\mathrm{S},\\ \mathcal{A}_2&= \frac{\gamma _\mathrm{th} \Omega _\mathrm{RR}k \eta P_\mathrm{R}}{\beta }, \mathcal{A}_3 = \frac{k\gamma _\mathrm{th}}{a_1 P_\mathrm{S}\Omega _\mathrm{SR}\Delta (\rho )} + \frac{\gamma _\mathrm{th}}{a_1 P_\mathrm{R}\Omega _\mathrm{RD_1}},\\ \mathcal{A}_4&= \frac{l}{a_1 P_\mathrm{R}\hat{\Omega }_\mathrm{RE}}. \end{aligned}$$

From (21), we can recognize that the average channel gain between the R and eavesdroppers, $\hat{\Omega }_\mathrm{RE}$, the channel gain of self - interference, $\Omega _\mathrm{RR}$, and the outdated CSI, $\Delta (\rho )$, linearly influence the SOP of $x_1$. Moreover, the number of relay nodes, K, and the number of eavesdroppers, L, also impact on the secrecy performance. From (17) and (20) we can rewrite SOP of $x_1$ as

$$\begin{aligned} \mathrm{SOP}^{x_1}&=\Pr \Big ( [\mathrm{C}^{x_1}-\mathrm{C}_\mathrm{E}^{x_1}]^{+}<r_1\Big )\nonumber \\&= \Pr \Bigg (\log _2 \Big [\frac{1+\gamma _1}{1+\gamma _{\mathrm{E}_l}^{x_1}}\Big ]<r_1\Bigg )\nonumber \\&=\Pr \Big ( \frac{1+\gamma _1}{1+\gamma _{\mathrm{E}_l}^{x_1}}<2^{r_1}\Big )\nonumber \\&= \int _{0}^{\infty }\Pr \Big (\gamma _1<2^{r_1}(1+x)-1\Big )f_{\gamma _{\mathrm{E}_l}^{x_1}}(x)dx. \end{aligned}$$

(22)

To obtain the closed-form for (22), we derive the CDF and PDF of $\gamma _1$ and $\gamma _{\mathrm{E}}^{x_1}$ with respect to x variable. From (16), we have the PDF of $\gamma _{\mathrm{E}}^{x_i}$ as

$$\begin{aligned} f_{\gamma _{\mathrm{E}}^{x_i}}(x)=\sum _{l=1}^{L}\left( {\begin{array}{c}L\\ l\end{array}}\right) \frac{(-1)^{l-1}l}{a_i P_\mathrm{R}\hat{\Omega }_\mathrm{RE}}\exp \Big (-\frac{l x}{a_i P_\mathrm{R}\hat{\Omega }_\mathrm{RE}}\Big ), \end{aligned}$$

(23)

where $i\in \{1, 2\}$.

Let $\gamma _1=\min \{\gamma _\mathrm{R}^{x_1}, \gamma _\mathrm{D_1}^{x_1} \}$ and $y=2^{r_1}(1+x)-1$, and after some manipulations, the CDF of $\gamma _1$ can be given as

$$\begin{aligned} F_{{\gamma _{1} }} (x) = & 1 - \sum\limits_{{k = 1}}^{K} {( - 1)^{{k - 1}} } \left( {\begin{array}{*{20}c} K \\ k \\ \end{array} } \right)\exp ({\mathcal{A}}_{1} )\frac{{a_{1} P_{{\text{S}}} \Omega _{{{\text{SR}}}} \Delta (\rho )}}{\beta } \\ & \frac{1}{{1 + {\mathcal{A}}_{2} x}}\exp ( - {\mathcal{A}}_{3} x). \\ \end{aligned}$$

(24)

The detail of proof for (24) is presented in the Appendix A. Note that in the case of small $\mathcal{A}_2$, we can approximate by Taylor expansion as $\frac{1}{1+\mathcal{A}_2x}\rightarrow \exp (-\mathcal{A}_2x)$. Replace (24) and (23) into (22), the SOP of $x_1$ is rewritten as follows.

$$\begin{aligned} \mathrm{SOP}^{x_1}=&1-\sum _{k=1}^{K}(-1)^{k-1}\left( {\begin{array}{c}K\\ k\end{array}}\right) \sum _{l=1}^{L}(-1)^{l-1}\left( {\begin{array}{c}L\\ l\end{array}}\right) \nonumber \\&\frac{l a_1\Omega _\mathrm{SR} \Delta (\rho ) P_\mathrm{S}}{\beta a_1 P_\mathrm{R}\hat{\Omega }_\mathrm{RE}}\exp (\mathcal{A}_1)\nonumber \\ \times&\int \nolimits _{0}^{\infty }\exp [\!-\!x(\mathcal{A}_2 \!+\!\mathcal{A}_3 \!+\!\mathcal{A}_4 )]dx. \end{aligned}$$

(25)

Using [38, eq. (3.310. 11)], we have the closed-form expression of $\mathrm{SOP}^{x_1}$ as shown in (21).

3.2 Secrecy outage probability of $x_2$

The $\mathrm{SOP}$ of $x_2$ is defined as the probability that the instantaneous secrecy capacity of $x_2$ is below the predefined threshold value of secure transmission rate, $r_2$. In the NOMA scheme, the secrecy capacity of $x_2$ is different from that of $x_1$, because the signal detection in the NOMA technique must use the SIC operation. Thus, from (9), (12) and (14), the end-to-end SINR of $x_2$ can be modeled as an equivalent single hop whose output SINR is presented as $\gamma _2=\min \{\gamma _\mathrm{R}^{x_2}, \gamma _\mathrm{D_1}^{x_2}, \gamma _\mathrm{D_2}^{x_2} \}$, which is dominated by the weakest case. Thus we have Proposition 2 providing the SOP of $x_2$ as follows.

Proposition 2

With the outdated CSI at the S and error CSI at the eavesdroppers, the SOP of $x_2$ in the TAS-FD-NOMA relay system is given as

$$\begin{aligned} \mathrm{SOP}^{x_2} =&1-\sum _{k=1}^{K}(\!-\!1)^{k-\!1}\left( {\begin{array}{c}K\\ k\end{array}}\right) \sum _{l=1}^{L}(\!-\!1)^{l-\!1}\left( {\begin{array}{c}L\\ l\end{array}}\right) \nonumber \\&\times \frac{l}{a_2 P_\mathrm{R}\hat{\Omega }_\mathrm{RE}} \frac{\Delta \pi }{2N}\sum _{n=1}^{N}\frac{\Omega _\mathrm{SR}\Delta (\rho )P_\mathrm{S}(a_2\!-\!a_1\chi _u)}{\chi _u\xi +\Omega _\mathrm{SR}\Delta (\rho ) a_2 P_\mathrm{S}}\sqrt{1\!\!-\!\!\phi _n^2}\nonumber \\&\!\times \!\exp \left( {\!-\frac{k\chi _u}{\Omega _\mathrm{SR}\Delta (\rho )P_\mathrm{S}(a_2-a_1\chi _u)}\!-\!\frac{l\chi _u}{a_2P_\mathrm{R} \hat{\Omega }_\mathrm{RE}}}\right) \nonumber \\&\times \exp \left( \!-\!\frac{\chi _u}{\Omega _\mathrm{RD_1}P_\mathrm{R}(a_2\!\!-\!\!a_1\chi _u)}\!\!-\!\!\frac{\chi _u}{\Omega _\mathrm{RD_2}P_\mathrm{R}(a_2\!\!-\!\!a_1\chi _u)}\right) , \end{aligned}$$

(26)

where $\Delta = \frac{1-\gamma _\mathrm{th} a_1}{a_1\gamma _\mathrm{th}}$, $\gamma _\mathrm{th} = 2^{r_2}$, $\xi =(k\eta P_\mathrm{R}\Omega _\mathrm{RR}-\Omega _\mathrm{SR} \Delta (\rho )a_1P_\mathrm{S})$ and $u=\frac{\Delta }{2}\Big [\phi _n +1\Big ]$ with $\phi _n= \cos \Big (\frac{(2n-1)\pi }{2N} \Big )$.

As the same with conclusion for Proposition 1, we also recognize clearly that the power allocation coefficient, $a_1$ and $a_2$, significantly impacts on the secrecy performance. Thus, in the NOMA scheme, the suitable power allocation coefficient should be used to improve the rate of $\mathrm{D}_i$. From (18) and (20), we can rewrite the SOP of $x_2$ as follows.

$$\begin{aligned} \mathrm{SOP}^{x_2}&= \Pr \Big ( [\mathrm{C}^{x_2}-\mathrm{C}_\mathrm{E}^{x_2}]^{+}<r_2\Big )\nonumber \\&= \Pr \Big (\log _2 \Big [\frac{1+\gamma _2}{1+\gamma _{\mathrm{E}_l}^{x_2}}\Big ]<r_2\Big ) \nonumber \\&=\Pr \Big ( \frac{1+\gamma _2}{1+\gamma _{\mathrm{E}_l}^{x_2}}<2^{r_2}\Big )\nonumber \\&= \int _{0}^{\infty }\Pr \Big (\gamma _2<2^{r_2}(1+x)-1\Big )f_{\gamma _{\mathrm{E}_l}^{x_2}}(x)dx. \end{aligned}$$

(27)

In oder to derive the closed-form expression for (27), firstly the CDF of $\gamma _2$ and the PDF of $\gamma _{\mathrm{E}}^{x_2}$ is proposed. From (9), (12) and (14), we have $\gamma _2$ as in (28).

$$\begin{aligned}&\gamma _2=\min \Bigg \{\frac{a_2 P_\mathrm{S}|h_\mathrm{SR}|^2}{a_1 P_\mathrm{S}|h_\mathrm{SR}|^2+\eta P_\mathrm{R}|h_\mathrm{RR}|^2+\sigma _\mathrm{R}^2}, \frac{a_2 P_\mathrm{R}|g_1|^2}{a_1 P_\mathrm{R}|g_1|^2+\sigma _\mathrm{D_1}^2},\nonumber \\&\frac{a_2 P_\mathrm{R}|g_2|^2}{a_1 P_\mathrm{R}|g_2|^2+\sigma _\mathrm{D_2}^2} \Bigg \}, \end{aligned}$$

(28)

According to (28), we have the CDF of $\gamma _2$ as given in (29) and (30), and its derivation is provided in detail in Appendix B.

$$\begin{aligned}&{F_{\gamma _2}(y)=} 1- \sum _{k=1}^{K}(\nonumber \\&-1)^{k-1}\left( {\begin{array}{c}K\\ k\end{array}}\right) \frac{\Omega _\mathrm{SR}\Delta (\rho )P_\mathrm{S}(a_2-a_1y)}{y(k\eta P_\mathrm{R}\Omega _\mathrm{RR}-\Omega _\mathrm{SR}\Delta (\rho ) a_1P_\mathrm{S})+\Omega _\mathrm{SR} \Delta (\rho )a_2 P_\mathrm{S}}\nonumber \\&\times \exp \Big (-\frac{ky}{\Omega _\mathrm{SR}\Delta (\rho )P_\mathrm{S}(a_2-a_1y)}\Big ) \nonumber \\&\times \exp \Big (\!-\!\frac{y}{\Omega _\mathrm{RD_1}P_\mathrm{R}(a_2-a_1y)}\!-\! \frac{y}{\Omega _\mathrm{RD_2}P_\mathrm{R}(a_2-a_1y)}\Big ),\nonumber \\&\text {if } y < \frac{a_2}{a_1} \end{aligned}$$

(29)

$$\begin{aligned}&1, \quad \quad \text {if } y \ge \frac{a_2}{a_1}. \end{aligned}$$

(30)

Then, replace (29) and (23) into (27), we can rewrite the SOP of $x_2$ as follows.

$$\begin{aligned}&\mathrm{SOP}^{x_2}\!=\!1\!\!-\!\!\!\sum _{k=1}^{K}(\!-\!1)^{k\!-\!1}\left( {\begin{array}{c}K\\ k\end{array}}\right) \sum _{l=1}^{L}(\nonumber \\&-1)^{l\!-\!1}\left( {\begin{array}{c}L\\ l\end{array}}\right) \frac{l}{a_2 P_\mathrm{R}\hat{\Omega }_\mathrm{RE}} \underbrace{\int _{0}^{\Delta }\Psi (\chi _x)\exp (\!-\!\frac{lx}{a_2 P_\mathrm{R}\hat{\Omega }_\mathrm{RE}})dx}_{\mathcal{W}(u)}, \end{aligned}$$

(31)

where $\Delta = \frac{1-\gamma _\mathrm{th} a_1}{a_1\gamma _\mathrm{th}}$, $\chi _x=\gamma _\mathrm{th}+\gamma _\mathrm{th} x-1$ and $\gamma _\mathrm{th}=2^{r_2}$,

$$\begin{aligned} \Psi (\chi _x)&= \frac{\Omega _\mathrm{SR}\Delta (\rho )P_\mathrm{S}(a_2-a_1\chi _x)}{\chi _x \xi +\Omega _\mathrm{SR}\Delta (\rho ) a_2 P_\mathrm{S}} \exp \nonumber \\&\Big (-\frac{k\chi _x}{\Omega _\mathrm{SR}\Delta (\rho )P_\mathrm{S}(a_2-a_1\chi _x)}\Big ) \nonumber \\&\times \exp \!\left( {\!\!-\!\frac{\chi _x}{\Omega _\mathrm{RD_1}P_\mathrm{R}(a_2\!\!-\!a_1\chi _x)}\!-\!\frac{\chi _x}{\Omega _\mathrm{RD_2}P_\mathrm{R}(a_2\!\!-\!a_1\chi _x) }}\!\!\right) \!\!, \end{aligned}$$

(32)

with $\xi =k\eta P_\mathrm{R}\Omega _\mathrm{RR}-\Omega _\mathrm{SR}\Delta (\rho ) a_1P_\mathrm{S}$ and $f_{\gamma _{\mathrm{E}}^{x_2}}(x)$ is presented in (23).

The integral in (31) is very difficult to obtain the closed-form expression, therefore the approximation by using Gaussian–Chebyshev quadrature [39, eq: (25.4.30)] is applied to obtain the expression of $\mathcal{W}(u)$ as

$$\begin{aligned} \mathcal{W}(u)=&\frac{\Delta }{2}\sum _{n=1}^{N}\frac{\pi }{N}\frac{\Omega _\mathrm{SR}\Delta (\rho )P_\mathrm{S}(a_2\!-\!a_1\chi _u)}{\chi _u\xi +\Omega _\mathrm{SR}\Delta (\rho ) a_2 P_\mathrm{S}}\sqrt{1\!-\!\phi _n^2}\nonumber \\&\times \exp \Big ({-\frac{k\chi _u}{\Omega _\mathrm{SR}\Delta (\rho )P_\mathrm{S}(a_2-a_1\chi _u)}-\frac{l\chi _u}{a_2P_\mathrm{R} \hat{\Omega }_\mathrm{RE}}}\Big )\nonumber \\&\times \exp \!\!\left( \!\!{-\!\frac{\chi _u}{\Omega _\mathrm{RD_1}P_\mathrm{R}(a_2\!\!-\!a_1\chi _u)}\!-\!\frac{\chi _u}{\Omega _\mathrm{RD_2}P_\mathrm{R}(a_2\!\!-\!a_1\chi _u) }}\!\!\right) \!\!, \end{aligned}$$

(33)

where u and $\phi _n$ are provided in Proposition 2.

Remark 2

According to [40], we assume that the $\mathrm R$, $\mathrm D_1$ and $\mathrm D_2$ perform the SIC operation perfectly, the eavesdroppers have enough capability to detect multiuser data, the secrecy outage of $x_1$ is independent of $x_2$. This means that the SOP of $x_1$ has no effect on the SOP of $x_2$. Thus the SOP for which the eavesdroppers can detect at least one of $x_1$ and $x_2$ can be given as

$$\begin{aligned} \mathrm{SOP}&= \Pr \Big (\min \{[\mathrm{C}^{x_1}-\mathrm{C}_\mathrm{E}^{x_1}], [\mathrm{C}^{x_2}-\mathrm{C}_\mathrm{E}^{x_2}]\} \le r_i\Big )\nonumber \\&= 1-\Pr \Big ([\mathrm{C}^{x_1}-\mathrm{C}_\mathrm{E}^{x_1}]>r_i, [\mathrm{C}^{x_2}-\mathrm{C}_\mathrm{E}^{x_2}] >r_i\Big )\nonumber \\&= 1-(1- \mathrm{SOP}^{x_1})(1-\mathrm{SOP}^{x_2})\nonumber \\&= \mathrm{SOP}^{x_1}+ \mathrm{SOP}^{x_2} -\mathrm{SOP}^{x_1} \mathrm{SOP}^{x_2}. \end{aligned}$$

(34)

The $\mathrm SOP$ in (34) is the security outage probability of the system when eavesdroppers can overhear $x_1$ and/or $x_2$ successfully, it is represented by the SOP of $x_1$ and the SOP of $x_2$.

Remark 3

In case the eavesdropper can decode successfully the signals $x_1$ and $x_2$, they can detect both the $x_1$ and $x_2$. It means that the secure transmission rate of the strongest user is less than the certain threshold rate $r_i$. Thus, we have the mathematical form as follows.

$$\begin{aligned} \mathrm{SOP}&= \Pr \Big (\max \{[\mathrm{C}^{x_1}-\mathrm{C}_\mathrm{E}^{x_1}], [\mathrm{C}^{x_2}-\mathrm{C}_\mathrm{E}^{x_2}] \}<r_i \} \Big )\nonumber \\&= \Pr \Big ([\mathrm{C}^{x_1}-\mathrm{C}_\mathrm{E}^{x_1}]<r_i, [\mathrm{C}^{x_2}-\mathrm{C}_\mathrm{E}^{x_2}]<r_i \} \Big )\nonumber \\&= \Pr \Big (\frac{1+\gamma _1}{1+\gamma _{\mathrm{E}_l}^{x_1}}< r_i, \frac{1+\gamma _2}{1+\gamma _{\mathrm{E}_l}^{x_2}}<r_i\Big )\nonumber \\&= \Pr \Big (\frac{1+\gamma _1}{1+\gamma _{\mathrm{E}_l}^{x_1}}< r_i\Big ) \Pr \Big (\frac{1+\gamma _2}{1+\gamma _{\mathrm{E}_l}^{x_2}}<r_i\Big ). \end{aligned}$$

(35)

It is rewritten via $\mathrm{SOP}^{x_1}$ and $\mathrm{SOP}^{x_2}$ by

$$\begin{aligned} \mathrm{SOP}&= \mathrm{SOP}^{x_1}\mathrm{SOP}^{x_2}. \end{aligned}$$

(36)

The $\mathrm SOP$ in (36) is the security outage probability of the system when eavesdroppers can overhear both the $x_1$ and $x_2$ successfully, it is a special case of the $\mathrm SOP$ in (34).

4 Performance analysis of secrecy throughput

When the codeword is long enough (i.e., its duration is larger than the channel coherence time), the ergodic capacity should be used as a performance metric. In contrast, when the codeword is short (i.e., its duration is less than the channel coherence time), the throughput should be used instead of the ergodic capacity. Assuming that the signals $x_1$ and $x_2$ are transmitted with rates of $r_1$ and $r_2$, respectively. The secrecy throughput of FD-NOMA relay system can be determined as

$$\begin{aligned}&\tau (r)=\underbrace{\sum _{i=1}^{2}r_i\Pr (\log _2(1+\gamma _\mathrm{e2e}^{x_i})> r_i)}_{J_1}\nonumber \\&\quad-\underbrace{\sum _{i=1}^{2}r_i\Pr (\log _2(1+\gamma _\mathrm{E}^{x_i})> r_i)}_{J_2}, \,\, i\in \{1, 2\}, \end{aligned}$$

(37)

where $\gamma _\mathrm{e2e}^{x_1} = \min \{\gamma _\mathrm{R}^{x_1}, \gamma _\mathrm{D_1}^{x_1} \}$ and $\gamma _\mathrm{e2e}^{x_2}= \min \{\gamma _\mathrm{R}^{x_2}, \gamma _\mathrm{D_1}^{x_2}, \gamma _\mathrm{D_2}^{x_2} \}$.

Remark 4

Equation (37) indicates that a very high code rate $r_i$ lets the probability of successfully decoding signals and the secrecy throughput of system be lower. In contrast, low ${r}_i$ results in high probability of successfully decoding signals, however the throughput may not be high as expected because of the low ${r}_i$. According to the NOMA principle, the secrecy throughput of the considered NOMA-FD system can be rewritten as

$$\begin{aligned} \tau (r)&= r_1(1-\mathrm{SOP}^{x_1})+r_2(1-\mathrm{SOP}^{x_2}). \end{aligned}$$

(38)

It is noticed that, the secrecy throughput is a function of transmission rate. Thus, the optimal transmission rate that maximizes the secrecy throughput of each NOMA user needs to be found. From (37), for a given transmission power, $J_1$ can be calculated as

$$\begin{aligned} J_1&= \underbrace{r_1\Pr (\log _2(1+\gamma _\mathrm{e2e}^{x_1})> r_1)}_{Q_1}\\\nonumber&\quad+\underbrace{r_2\Pr (\log _2(1+\gamma _\mathrm{e2e}^{x_2})> r_2)}_{Q_2}. \end{aligned}$$

(39)

Replacing $\gamma _\mathrm{e2e}^{x_1}$ and $\gamma _\mathrm{e2e}^{x_2}$ into (39), we have

$$\begin{aligned} Q_1= r_1Pr\Big (\!\frac{a_1 P_\mathrm{S}|h_\mathrm{SR}|^2}{\eta P_\mathrm{R}|h_\mathrm{RR}|^2 +\sigma _\mathrm{R}^2}>\xi _1 \Big )\Pr \Big (\frac{a_1 P_\mathrm{R}|g_1|^2}{\sigma _\mathrm{D_1}^2}>\xi _1\Big ), \end{aligned}$$

(40)

and

$$\begin{aligned} Q_2=&r_2\Pr \Big (\frac{a_2 P_\mathrm{S}|h_\mathrm{SR}|^2}{a_1 P_\mathrm{S}|h_\mathrm{SR}|^2+\eta P_\mathrm{R}|h_\mathrm{RR}|^2+\sigma _\mathrm{R}^2}>\xi _2\Big ) \nonumber \\&\Pr \Big (\frac{a_2 P_\mathrm{R}|g_1|^2}{a_1 P_\mathrm{R}|g_1|^2+\sigma _\mathrm{D_1}^2}>\xi _2\Big )\nonumber \\&\times \Pr \Big (\frac{a_2 P_\mathrm{R}|g_2|^2}{a_1 P_\mathrm{R}|g_2|^2+\sigma _\mathrm{D_2}^2}>\xi _2\Big ). \end{aligned}$$

(41)

where $\xi _1=2^{r_1}-1$ and $\xi _2=2^{r_2}-1$.

From (40) and (41), we can find $\xi _i$ or $r_i$ that maximizes $Q_1(r_1)$ and $Q_1(r_2)$ with certain transmission power and average channel gain.

$$\begin{aligned} Q_1(\xi _1)&=\log _2(1+\xi _1)\sum _{k=1}^{K}(-1)^{k-1}\left( {\begin{array}{c}K\\ k\end{array}}\right) \nonumber \\&\frac{ a_1P_\mathrm{S}\Omega _\mathrm{SR}\Delta (\rho )}{\Omega _\mathrm{RR} k \xi _1 \eta P_\mathrm{R} + a_1 P_\mathrm{S}\Omega _\mathrm{SR}\Delta (\rho )}\nonumber \\&\times \exp \Big (-\frac{\xi _1}{\Omega _\mathrm{RD_1} a_1P_\mathrm{R}}-\frac{k\xi _1}{\Omega _\mathrm{SR} \Delta (\rho ) a_1P_\mathrm{S}}\Big ), \end{aligned}$$

(42)

$$\begin{aligned} Q_2(\xi _2)&=\log _2(1+\xi _2)\sum _{k=1}^{K}(-1)^{k-1}\left( {\begin{array}{c}K\\ k\end{array}}\right) \nonumber \\&\quad\frac{\Omega _\mathrm{SR}\Delta (\rho)P_\mathrm{S}(a_2-a_1\xi _2)}{\xi _2[k\eta P_\mathrm{R}\Omega _\mathrm{RR}-\Omega _\mathrm{SR}\Delta (\rho ) a_1P_\mathrm{S}]+\Omega _\mathrm{SR} \Delta (\rho )a_2 P_\mathrm{S}}\nonumber \\&\quad\times \exp \Big (-\frac{k\xi _2}{\Omega _\mathrm{SR}\Delta (\rho )P_\mathrm{S}(a_2-a_1\xi _2)}\nonumber \\&\quad-\frac{\xi _2}{\Omega _\mathrm{RD_1}P_\mathrm{R}(a_2-a_1\xi _2)}\nonumber \\&\quad-\frac{\xi _2}{\Omega _\mathrm{RD_2}P_\mathrm{R}(a_2-a_1\xi _2)}\Big ), \end{aligned}$$

(43)

These equations are rewritten as follows.

$$\begin{aligned}&Q_1(\xi _1)\ge \log _2(1+\xi _1)\frac{ a_1P_\mathrm{S}\Omega _\mathrm{SR}\Delta (\rho )\exp (-\mu _1 \xi _1)}{\xi _1 \Omega _\mathrm{RR} 1 \eta P_\mathrm{R} + a_1 P_\mathrm{S}\Omega _\mathrm{SR}\Delta (\rho )}, \end{aligned}$$

(44)

$$\begin{aligned}Q_2(\xi _2)&\ge \log _2(1+\xi _2)\frac{\Omega _\mathrm{SR}\Delta (\rho )P_\mathrm{S}(a_2-a_1\xi _2)}{\xi _2\beta _1+\Omega _\mathrm{SR} \Delta (\rho )a_2 P_\mathrm{S}}\exp \nonumber \\&\quad-\Big (\frac{\mu _2 \xi _2}{a_2-a_1\xi _2}\Big ), \end{aligned}$$

(45)

where $\mu _1 = \frac{1}{\Omega _\mathrm{RD_1} a_1P_\mathrm{R}}+\frac{1}{\Omega _\mathrm{SR} \Delta (\rho ) a_1P_\mathrm{S}}$, $\mu _2= \frac{1}{\Omega _\mathrm{SR}\Delta (\rho )P_\mathrm{S}}+\frac{1}{\Omega _\mathrm{RD_1}P_\mathrm{R}}+\frac{1}{\Omega _\mathrm{RD_2}P_\mathrm{R}}$ and $\beta _1 = \eta P_\mathrm{R}\Omega _\mathrm{RR}-\Omega _\mathrm{SR}\Delta (\rho ) a_1P_\mathrm{S}$. To notice that (44) and (45) are linear with (42) and (43), respectively.

The maximal $J_1$ for given transmission power and average channel gains can be determined via following optimization problem

$$\begin{aligned} \xi _i^*= \mathrm{arg} \max _{\begin{array}{c} 0<\xi _1<r_\mathrm{max}\\ 0<\xi _2 <a_2/a_1 \end{array}} Q_{i} (\xi _i). \end{aligned}$$

(46)

To find the feasible $\xi _i$ values, we have the Lemmas for the property unique root as follows.

Lemma 1

For $a,b, c>0$, the below function has one and only one maximum value in the interval $[0, r_\mathrm{max})$.

$$\begin{aligned} f(x)=\log _2(1+x)\frac{a }{bx+c}\exp (-\mu x), 0\le x<r_\mathrm{max}. \end{aligned}$$

(47)

If $x^*$ is the value that maximizes f(x), the function f(x) monotonically increases in the interval $[0, x^*)$ and then monotonically decreases in the interval $( x^*, r_\mathrm{max})$. This means that f(x) is an unimodal function in the interval $[0, r_\mathrm{max})$.

Lemma 2

For $a,b>0$, the below function has one and only one maximum value in the interval [0, a/b).

$$\begin{aligned} \psi (x)=\log _2(1+x)\frac{\mathcal{D}(a-bx) }{\beta _1 x+\mathcal{C}}\exp (-\frac{\mu x}{a-bx}), 0\le x< a/b. \end{aligned}$$

(48)

If $x^*$ is the value that maximizes $\psi (x)$, the function $\psi (x)$ monotonically increases in the interval $[0, x^*)$, and then monotonically decreases in the interval $( x^*, a/b)$. This means that $\psi (x)$ is an unimodal function in the interval [0, a/b).

The proof of Lemmas 1 and 2 is given in detail in Appendix C. Moreover, the throughput of eavesdroppers can be derived as

$$\begin{aligned} J_2= \underbrace{r_1\Pr (\log _2(1+\gamma _\mathrm{E}^{x_1})> r_1)}_{Q_3}+\underbrace{r_2\Pr (\log _2(1+\gamma _\mathrm{E}^{x_2})> r_2)}_{Q_4}. \end{aligned}$$

(49)

Similar to $Q_1(\xi _1)$ and $Q_2(\xi _2)$, $Q_3(\xi _1)$ and $Q_4(\xi _2)$ are calculated as

$$\begin{aligned} Q_3(\xi _1)=&\log _2(1+\xi _1)\sum _{l=1}^{L}\left( {\begin{array}{c}L\\ l\end{array}}\right) (-1)^{l-1}\exp \Big (-\frac{l \xi _1}{a_1 P_\mathrm{R}\hat{\Omega }_\mathrm{RE}}\Big ), \end{aligned}$$

(50)

$$\begin{aligned} Q_4(\xi _2)=&\log _2(1+\xi _2)\sum _{l=1}^{L}\left( {\begin{array}{c}L\\ l\end{array}}\right) (-1)^{l-1}\exp \Big (-\frac{l \xi _2}{a_2 P_\mathrm{R}\hat{\Omega }_\mathrm{RE}}\Big ). \end{aligned}$$

(51)

Once above two Lemmas are satisfied, the throughput $\xi _i^*$ is maximized by using the Golden-Section Search (GSS) method as shown in Algorithm 1, where $\tau (\xi _1) = Q_1(\xi _1)-Q_3(\xi _1)$ and $\tau (\xi _2)=Q_2(\xi _2)-Q_4(\xi _2)$.

5 Numerical results

In this section, the Monte-Carlo simulation is used to verify our derivations and evaluate the novel of the proposed model. In this system, the terminal is assumed to be stationary, thus, the path loss of the S - R and R - D links is characterized as average gain, i.e. $\Omega _\mathrm{SR}=\mathbb E\{|h_{1, k}|^2\}$, $\Omega _\mathrm{RR}=\mathbb E\{|h_\mathrm{RR}|^2\}$, $\Omega _\mathrm{RD_1}=\mathbb E\{|g_1|^2\}$, and $\Omega _\mathrm{RD_2}=\mathbb E\{|g_2|^2\}$. The average SNR is defined as the ratio of the transmit power to the variance of AWGN, i.e., $\mathrm{SNR} = P_\mathrm{S}/\sigma ^2$. Except some special cases, in other scenarios, we set $\hat{\Omega }_\mathrm{RE}$ = −5 dB, the noise variance $\sigma _\mathrm{R}^2=\sigma _\mathrm{D_1}^2=\sigma _\mathrm{D_2}^2=\sigma ^2=1$ and transmit power $P_\mathrm{S}=P_\mathrm{R}=P$. The Monte-Carlo simulation performs with $10\times 2^{14}$ independent trials. The other parameters are shown in Table 1, which are referred from [26].

Table 1 The parameters of the system using for simulation

In all figures, the Monte-Carlo simulation result is represented by marks, whereas the theoretical analysis result is plotted by a dark line. Firstly, we can observe that the simulation results match perfectly with the analysis results. It provides that our analysis is reasonable. The other notable result from all following figures is that the SOP of $\mathrm{D}_2$ is firstly improved and then return into worst with high transmit SNR, it is identified with results and conclusion in [23, 26]. It is explained that, $\mathrm D_2$ decodes its own signal by treating the signal of $\mathrm D_1$ as interference, while $\mathrm D_1$ performs the SIC operation to cancel the signal of $\mathrm D_2$, and then decodes its own signal. Furthermore, due to the residual self-interference cancellation of FD technique, the SOP of $\mathrm D_1$ is saturated in high SNR regime.

Fig. 2

The SOP for various number of L with $K=3$, $\Omega _\mathrm{RR}= -20$ dB, $\rho _E = 0.2$, $\rho = 0.9$

In Fig. 2, we illustrate the impact of a number of eavesdroppers on the SOP of the considered system versus SNR in dB. It can be observed from Fig. 2 that the security performance is degraded as the number of eavesdroppers increases. It’s easily explained that with more eavesdroppers, the capability overhearing the information of legitimate channels is increased, i.e., the chance for one of them to overhear the desired message becomes higher. On the other hand, the SOP of each user is improved in the low SNR region, and then the SOP of $\mathrm{D}_2$ is saturated, while the SOP of $\mathrm{D}_1$ becomes worse. In addition, the simulation curves overlap with the corresponding analytical curves, it confirms the correctness of our theoretical analysis.

Fig. 3

SOP for various the number of K with $L=3$, $\Omega _\mathrm{RR}= -20$ dB, $\rho _E = 0.2$, $\rho = 0.9$

Figure 3 demonstrates the SOP versus SNR with the correlation coefficient of channel estimation error at the eavesdropper, $\rho _E=0.2$ and correlation coefficient of the outdated CSI at the source, $\rho =0.9$. In this figure, we recognize that the SOP is improved in terms of increasing the number of antennas. However, observation is that the gap between the curves is difference with different number of antennas at the S, K, where K increases from 1 to 2, the gap is larger when K increases from 2 to 3. The reason is, the number of antennas at the FD relay is 2, therefore the performance is improved slowly when K is larger than 2. On the other hand, we also recognize that the shape of curves in Fig. 3 is the same as them in Fig. 2, the reason is explained as above.

Fig. 4

Impact of the loop-back interference channel gain, $\Omega _\mathrm{RR}$ on the SOP with $K=3$ and $L=3$, $\rho _E = 0.2$, $\rho = 0.9$

Figure 4 illustrates the SOP of $\mathrm{D}_1$ versus the average SNR with the various value of self-interference channel gain, $\Omega _\mathrm{RR}$. From this figure we know that intensifying $\Omega _\mathrm{RR}$ lets the SOP degrade. It is because the SOP is considered as the ratio of SNR between the legitimate channel and wiretapping channel. Meanwhile, the larger the $\Omega _\mathrm{RR}$ is, the smaller the SNR of the legitimate channel becomes. Thus, to guarantee the secrecy performance, the performance of SIC of $x_2$ at the relay and the $\mathrm{D}_1$ should ensure perfectly, as well as the residual self-interference at the relay node must be mitigated.

Fig. 5

The SOP for various $\rho _E$ with $L=3$, $K=3$, $\Omega _\mathrm{RR}= -20$ dB, $\rho = 0.9$

The eavesdropper is a passive system, it doesn’t train the CSI in the communication process. Therefore, the eavesdropper hardly obtains the perfect CSI. Figure 5 demonstrates the SOP of $\mathrm{D}_1$ with different values of correlation coefficient of channel estimation error at the eavesdropper, $\rho _E$. As shown in this figure, when $\rho _E$ increases, the error of CSI for signal detection at the eavesdropper increases, thus the SOP is improved.

Fig. 6

Comparison of SOPs with $L=3$, $K=3$ and $\Omega _\mathrm{RR}= - 20$ dB, $\rho = 0.9$, $\rho _E=0.2$

Figure 6 demonstrates the SOP of the system versus average SNR in dB. In this result, we investigated the secrecy performance of the NOMA system, i.e., the SOP of each user and the SOP of overall system following Remark 2 and Remark 3. Also, we consider the SOP for the case of OMA technique to compare the secrecy performances of them. Firstly, we see that the theoretical result of Remark 3 is matched with the simulation in all SNR region, while the theoretical result of Remark 2 is approximate with the simulation result, especially in high SNR region. Another observation is that, the secrecy performances of the system depends mostly on the SOP of $\mathrm{D}_2$. Intuitively, the user that mostly loses security dominates the overall secrecy performance of the system. Finally, we recognize that with the low SNR region, the SOP of NOMA outperforms the SOP of OMA scheme. In contrast, at the high SNR region, the SOP of the OMA scheme is better.

Fig. 7

Comparison of SOP of FD and HD techniques with the NOMA relay protocol with $L=3$ and $K=3$, $\Omega _\mathrm{RR}= - 20$ dB, $\rho _E=0.2$, $\rho =0.9$

Figure 7 present the SOP of each user in two cases, i.e., HD and FD techniques, versus SNR in dB. Similar to the other figures, when SNR increase, the SOP of both users firstly decreases, and then increases or reaches the saturation point. Moreover, the secrecy performance of FD-NOMA system always outperform the HD-NOMA system. The reason is that the communication phase of HD and FD is performed with one and two phases, respectively. Thus, the predefined threshold value of HD and FD is respectively $\gamma _\mathrm{th} = 2^{2r_1}$ and $\gamma _\mathrm{th} = 2^{r_1}$.

Fig. 8

System secrecy through versus the SNR $L=3$, $K=3$ and $\Omega _\mathrm{RR}= - 20$ dB, $\rho = 0.9$, $\rho _E=0.2$

The secrecy throughput of each user and sum of them are represented in Fig. 8 versus average SNR in dB. From this figure we can see that, the secrecy throughput of $\mathrm D_2$ firstly increases, reaches to the maximum value at SNR = 0 dB, and then decreases when the average SNR increases. In contrast, the secrecy throughput of $\mathrm D_1$ firstly increases, and then saturates at the high SNR regime. It is because that, the signal of $\mathrm D_1$ interferes with the $\mathrm D_2$, while the signal of $\mathrm D_2$ are removed (by SIC operation) at $\mathrm D_1$.

Fig. 9

Sum secrecy through versus the SNR with different transmission rates, $L=3$, $K=3$ and $\Omega _\mathrm{RR}= - 20$ dB, $\rho = 0.9$, $\rho _E=0.2$

Figure 9 demonstrates the sum secrecy throughput of the considered FD-NOMA relay system with different transmission rates (codeword rates). The secrecy throughput is increased when the average SNR increases. However, the secrecy throughput of low r is higher than that of larger r in the low average SNR regime. Whereas, in the high average SNR regime, the secrecy throughput is improved with increasing transmission rate, i.e. the secrecy throughput of high r is larger than that of low r.

Fig. 10

Sum secrecy through versus transmission rate, SNR = 10 dB, $\Omega _\mathrm{RR}= - 20$ dB, $\rho = 0.9$, $\rho _E=0.2$. The optimal $r^*$ and maximum $\tau$ derived by the Golden-Section Search

Figure 10 illustrated the secrecy throughput of the $\mathrm D_1$, $\mathrm D_2$ and sum of them versus the transmission rate, we set SNR = 10 dB and other parameters as shown in Fig. 10. From this figure, we can recognize that the secrecy throughput firstly increases and then decreases for any transmission rate, $r_i$. Moreover, the optimal value of $r^*$ derived by the Golden-Section Search method are the same as simulation result. On the other hand, the optimal value of $r^*$ for the maximum secrecy throughput of $\mathrm D_1$ is different from that for the maximum secrecy throughput of $\mathrm D_2$. The reason is similar to the result in Fig. 8.

6 Conclusion

In this paper, we have proposed and analyzed the TAS - FD - NOMA relay system with the assumption of the presentation of multiple eavesdroppers. The SOP of each user, as well as the SOP of the whole system are considered as a criterion to evaluate the secrecy performance of the system. The closed-form expressions of SOP of every user and the approximate SOP of overall system are derived under condition of outdated CSI for the TAS and channel estimation error at eavesdroppers. With the numerical and analytical results, this paper has provided valuable insight into the secure performance of FD-NOMA system, i.e. the SOP of a near user (User 1) is much higher than that of a far user (User 2), especially in high SNR region; the SOP is improved when the correlation coefficient of channel estimation error at the eavesdropper reduces and/or the correlation coefficient of the outdated CSI at the source increases. The calculation result indicates that the FD-NOMA system outperforms the HD-NOMA system in terms of the same transmission time slot. Furthermore, the secrecy throughput is investigated, and the Golden-Section Search method is applied to find the optimal value of transmission rate in order to maximize the secrecy throughput of every user and sum of them.

The TAS - FD - NOMA relay system was proposed and its SOP was evaluated, however, the number of hops as well as the number of users were restricted to two, moreover, the eavesdropper was assumed to be non-colluding. The system with more hops, more users and colluding eavesdropper will be considered in our future work.

Appendix

1.1 Appendix A

This appendix aim is to provide the proof of CDF of SINR end to end for User 1. As denoted in the previous section, $\gamma _1=\min \{\gamma _\mathrm{R}^{x_1}, \gamma _\mathrm{D_1}^{x_1}\}$, the CDF of $\gamma _1$ can be written as

$$\begin{aligned} F_{\gamma _1}(y)&=\Pr (\min \{\gamma _\mathrm{R}^{x_1}, \gamma _\mathrm{D_1}^{x_1} \}<y)\nonumber \\&=1-\Pr (\min \{\gamma _\mathrm{R}^{x_1}, \gamma _\mathrm{D_1}^{x_1} \}>y). \end{aligned}$$

(52)

From (8) and (13) we have

$$\begin{aligned} F_{\gamma _1}(y)&=\!1\!-\!\Pr \!\Big (\!\frac{a_1 P_\mathrm{S}|h_\mathrm{SR}|^2}{\eta P_\mathrm{R}|h_\mathrm{RR}|^2 \!+\!\sigma _\mathrm{R}^2}\!>\!y, \frac{a_1 P_\mathrm{R}|g_1|^2}{\sigma _\mathrm{D_1}^2}\!>\!y\!\Big )\nonumber \\&=1\!-\!\Pr \!\Big (\!\frac{a_1 P_\mathrm{S}|h_\mathrm{SR}|^2}{\eta P_\mathrm{R}|h_\mathrm{RR}|^2 \!+\!\sigma _\mathrm{R}^2}\!>\!y \!\Big )\Pr \!\Big (\!\frac{a_1 P_\mathrm{R}|g_1|^2}{\sigma _\mathrm{D_1}^2}\!>\!y\!\Big ). \end{aligned}$$

(53)

Without loss of generality, we assume that $\sigma _\mathrm{R}^2=\sigma _\mathrm{D_1}^2 =1$, and by using the probability condition, we can rewrite (53) as

$$\begin{aligned} F_{\gamma _1}(y) \!=\!1\!-\!&\int \limits _0^\infty \Bigg [1\!-\! F_{|h_\mathrm{SR}|^2}\Big (\frac{y(\eta P_\mathrm{R}z\!+\!1)}{a_1 P_\mathrm{S}} \Big ) \Bigg ]f_Z(z)dz \Bigg [1\nonumber \\&-F_{|g_1|^2} \Big ( \frac{y}{a_1P_\mathrm{R}}\Big )\Bigg ]. \end{aligned}$$

(54)

Because the CDF of $|g_1|^2$ follows the Rayleigh distribution, $F_{|g_1|^2}(x)= 1- \exp \Big (-\frac{x}{\Omega _3 a_1P_\mathrm{R}}\Big )$ and $Z=|h_\mathrm{RR}|^2$ are modeled by Rayleigh distribution, i.e., $f_Z(z)= \frac{1}{\Omega _\mathrm{RR}}\exp (-\frac{z}{\Omega _\mathrm{RR}})$. From (54), we can rewrite $F_{\gamma _1}(y)$ as follows.

$$\begin{aligned} F_{\gamma _1}(y)&=1- \sum _{k=1}^{K}(-1)^{k-1}\left( {\begin{array}{c}K\\ k\end{array}}\right) e^{-\frac{y}{\Omega _3 a_1P_\mathrm{R}}}\nonumber \\&-\frac{ky}{\Omega _\mathrm{SR}\Delta (\rho ) a_1P_\mathrm{S}} \frac{1}{\Omega _\mathrm{RR}}\int \limits _0^\infty e^{-\frac{ky\eta P_\mathrm{R}z}{\Omega _\mathrm{SR}\Delta (\rho ) a_1P_\mathrm{S}}- \frac{z}{\Omega _\mathrm{RR}}}dz. \end{aligned}$$

(55)

By using $\int \nolimits _0^\infty \exp (-ax)dx=1/a$ [38, eq. (3.310. 11)], we can obtain the closed-form expression of $F_{\gamma _1}(y)$.

$$\begin{aligned} F_{\gamma _1}(y)&=1- \sum _{k=1}^{K}(-1)^{k-1}\left( {\begin{array}{c}K\\ k\end{array}}\right) e^{-\frac{y}{\Omega _3 a_1P_\mathrm{R}}}\nonumber \\&-\frac{ky}{\Omega _\mathrm{SR} \Delta (\rho ) a_1P_\mathrm{S}} \frac{ a_1P_\mathrm{S}\Omega _\mathrm{SR}\Delta (\rho )}{\Omega _\mathrm{RR} k y \eta P_\mathrm{R} + a_1 P_\mathrm{S}\Omega _\mathrm{SR}\Delta (\rho ) }, \end{aligned}$$

(56)

where $y=2^{r_1}(1+x)-1$. After some manipulation we have

$$\begin{aligned} F_{\gamma _1}(x) & =1-\sum _{k=1}^{K}(\!-\!1\!)^{k-1}\left( {\begin{array}{c}K\\ k\end{array}}\right) \exp (\!\mathcal{A}_1\!)\frac{a_1P_\mathrm{S}\Omega _\mathrm{SR}\Delta (\rho )}{\beta \!+\!\gamma _\mathrm{th} \Omega _\mathrm{RR} k P_\mathrm{R}\eta x}\nonumber \\&\quad\times \exp \Big (\!-\!\frac{k\gamma _\mathrm{th} x}{a_1 P_\mathrm{S}\Omega _\mathrm{SR}\Delta (\rho )} - \frac{\gamma _\mathrm{th} x}{a_1 P_\mathrm{R}\Omega _\mathrm{RD_1}}\Big ),\nonumber \\&= 1- \sum _{k=1}^{K}(-1)^{k-1}\left( {\begin{array}{c}K\\ k\end{array}}\right) \exp (\mathcal{A}_1)\nonumber \\&\frac{a_1P_\mathrm{S}\Omega _\mathrm{SR}\Delta (\rho )}{\beta } \frac{1}{1+\mathcal{A}_2x}\exp (-\mathcal{A}_3x), \end{aligned}$$

(57)

where $\gamma _\mathrm{th} = 2^{r_1}$, $\beta = \Omega _\mathrm{RR}k\eta P_\mathrm{R}(\gamma _\mathrm{th}-1) +a_1\Omega _\mathrm{SR}\Delta (\rho ) P_\mathrm{S}$, $\mathcal{A}_1=\frac{k(1-\gamma _\mathrm{th})}{a_1 \Omega _\mathrm{SR}\Delta (\rho )k P_\mathrm{S}} + \frac{1-\gamma _\mathrm{th}}{a_1P_\mathrm{R}\Omega _\mathrm{RD_1}},$ $\mathcal{A}_2 = \frac{\gamma _\mathrm{th} \Omega _\mathrm{RR}k \eta P_\mathrm{R}}{\beta }$ and $\mathcal{A}_3 = \frac{k\gamma _\mathrm{th}}{a_1 P_\mathrm{S}\Omega _\mathrm{SR}\Delta (\rho )} + \frac{\gamma _\mathrm{th}}{a_1 P_\mathrm{R}\Omega _\mathrm{RD_1}}$. The CDF of $\gamma _1$ is obtained and the proof is completed.

1.2 Appendix B

From (28), we know that SNR of each link is independence, thus the CDF of $\gamma _2$, i.e., $F_{\gamma _2}(y)=\Pr (\gamma _2<y)$ is derived as

$$\begin{aligned} F_{\gamma _2}(y)\!&=\! 1\!-\!\underbrace{\Pr \Big (\frac{a_2 P_\mathrm{S}|h_\mathrm{SR}|^2}{a_1 P_\mathrm{S}|h_\mathrm{SR}|^2\!+\!\eta P_\mathrm{R}|h_\mathrm{RR}|^2\!+\!\sigma _\mathrm{R}^2}\!>\!y\Big )}_{\mathcal{O}_1 }\nonumber \\&\!\times \Pr \!\Big (\!\frac{a_2 P_\mathrm{R}|g_1|^2}{a_1 P_\mathrm{R}|g_1|^2\!+\!\sigma _\mathrm{D_1}^2}\!>\!y\!\Big ) \Pr \!\Big (\!\frac{a_2 P_\mathrm{R}|g_2|^2}{a_1 P_\mathrm{R}|g_2|^2\!+\!\sigma _\mathrm{D_2}^2}\!>\!y\!\Big ). \end{aligned}$$

(58)

Using the probability condition, the first part in (58) is rewritten as

$$\begin{aligned} \mathcal{O}_1= \int \limits _0^\infty \Pr \Big (|h_\mathrm{SR}|^2> \frac{y(\eta P_\mathrm{R}z+1)}{P_\mathrm{S}(a_2-a_1y)}\Big )f_{|h_\mathrm{RR}|^2}(z)dz. \end{aligned}$$

(59)

Using (6) and $f_{|h_\mathrm{RR}|^2}(z)$ in Appendix A, we can get the $\mathcal{O}_1$ as

$$\begin{aligned} \mathcal{O}_1 \!=\!&\sum _{k=1}^{K}(\!-\!1\!)^{k-1}\left( {\begin{array}{c}K\\ k\end{array}}\right) \exp \!\Big (\!\!\!-\!\frac{ky}{\Omega _\mathrm{SR}\Delta (\rho ) P_\mathrm{S}(\!a_2\!-\!a_1y\!)}\! \Big ) \nonumber \\&\!\times \!\frac{1}{\Omega _\mathrm{RR}}\int \limits _0^\infty \exp \!\Big (\!\!-\!\frac{ky\eta P_\mathrm{R}z}{\Omega _\mathrm{SR}\Delta (\rho ) P_\mathrm{S}(\!a_2\!-\!a_1y\!)}\!-\! \frac{z}{\Omega _\mathrm{RR}}\Big )dz. \end{aligned}$$

(60)

Applying [38, eq. (3.310. 11)] for integral component in (60) with respect to z variable, we obtain the closed-form of $\mathcal{O}_1$. On the other hand, the channel is modeled by Rayleigh distribution, thus $|g_1|^2$ and $|g_2|^2$ follows the exponential distribution. From the second and third probability parts in (58), and with some manipulation, we have the CDF of $\gamma _2$ as shown in (29).

1.3 Appendix C

This appendix provides the proof of Lemma 1 and Lemma 2. Firstly, we present the step-by-step to prove Lemma 1. Because the object problem is maximization and object function is convex, i.e., the problem of (46) is non convex with respect to $\xi _i$. Thus, we must prove the increase and decrease of function f(x) in (47) via the extremum problem. We take the first derivation of f(x) with respect to x as

$$\begin{aligned} \frac{d f(x)}{dx}=\frac{\exp (-\mu _1 x)}{(bx+c)\ln 2}\Big [\frac{a}{1+x} -\frac{ab \ln (1+x)}{bx+c}-a\ln (1+x) \Big ]. \end{aligned}$$

(61)

For $x>0$, we have $\frac{\exp (-\mu _1 x)}{(bx+c)\ln 2}>0$. Thus, we can find the solutions of f(x) through $g(x)=\frac{a}{1+x} -\frac{ab \ln (1+x)}{bx+c}-a\ln (1+x)$. To notice that, since there exists a neighborhood of $x^*$ in $(0, r_\mathrm{max})$ which lets g(x) change from positive to negative values, i.e., g(x) reaches the maximum value at $x^*$. For $x=0$, we have $g(x)=a >0$ and $x\rightarrow r_\mathrm{max}$, thus $g(x)=\frac{a}{1+r_\mathrm{max}} -\frac{ab \ln (1+r_\mathrm{max})}{br_\mathrm{max}+c}-a\ln (1+r_\mathrm{max}) <0$, $\forall a, b, c >0.$ On the other hand, the first derivation of g(x) with respect to x is $\frac{d g(x)}{dx}=-a \big (\frac{1}{(1+x)^2}+\frac{1}{(1+x)\ln 2} + \frac{b}{(1+x)(c+bx)\ln 2}-\frac{b\ln (1+x)}{(c+bx)^2\ln 2} \big )<0, \,\,\, 0\le x<r_\mathrm{max}$. Therefore, $\frac{d f(x)}{dx}>0$ in the interval $[0, x^*)$ and $\frac{d f(x)}{dx}<0$ in the interval $(x^*, r_\mathrm{max}).$ The proof of Lemma 1 is finished.

The proof of Lemma 2 is similar to that of Lemma 1, to notice that the first derivation of $\psi (x)$ with respect to x is represented as

$$\begin{aligned}&\frac{d \psi (x)}{dx}=\frac{exp\Big (-\frac{\mu _2 x}{a-bx} \Big )(a-bx)\mathcal{D}}{(\beta _1x +\mathcal{C} )\ln 2}\nonumber \\&\times \underbrace{\Big [\frac{1}{1+x} -\frac{\ln (1+x)}{\beta _1x+\mathcal{C}}-b\ln (1+x) + \Big (-\frac{b\mu _2 x}{a-bx} - \frac{\mu _2}{a-bx}\Big )\ln (1+x)\Big ]}_{G(x)}, \end{aligned}$$

(62)

and

$$\begin{aligned} \frac{d G(x)}{dx}=&-\Big (\frac{1}{(1+x)}+\frac{b}{1+x}+\frac{1}{(1+x)(\beta _1x+\mathcal{C})}\Big )\nonumber \\ {}&+\frac{\beta _1\ln (1+x)}{(\beta _1x+\mathcal{C})^2}\nonumber \\&- \Big ( \frac{b\mu _2}{(a-bx)^2} +\frac{b^2\mu _2x}{(a-bx)^2}+\frac{b\mu _2}{a-bx} \Big )\ln (1+x). \end{aligned}$$

(63)

In general, there is one and only one $x^*$ in the interval (0, a/b) that $\psi (x)$ obtains a maximum value. The proof of Lemma 2 is completed, i.e., there always exist a transmission rate that maximizes the secrecy throughput of the considered FD-NOMA relay system.