Secrecy Outage of Dual-Hop Amplify-and-Forward Relay System with Diversity Combining at the Eavesdropper

Abstract

In this paper, a dual-hop amplify-and-forward relay system is considered with an eavesdropper where each link undergoes independent, non-identical, flat Rayleigh fading. The eavesdropper is capable of diversity combining the direct and relayed communication from the source using maximal ratio combining (MRC) and selection combining (SC). Closed-form upper and lower bounds on secrecy outage probability are derived. Closed-form approximate secrecy outage probability and ergodic secrecy rate is also obtained when source–relay link average signal-to-noise ratio (SNR) is high. Asymptotic analysis is presented when dual-hop links have equal or unequal average SNR. It is found that SC has both the secrecy outage and ergodic secrecy rate performances are better than MRC. To achieve the same secrecy outage performance of SC, MRC requires relatively higher SNR at lower rate. MRC also requires relatively higher SNR to achieve same secrecy rate performance of SC when eavesdropper link quality degrades. It is observed that lower bound for secrecy outage is tight and tends towards secrecy outage as SNR increases. It is interesting to find that either one of the dual-hop link can limit the performances even if the other link average SNR is infinitely high.

1 Introduction

The broadcast nature of the wireless medium necessitates secure communication since any unintended receiver (eavesdroppers) can overhear signals emanating from a source [1, 2]. This has led researchers to extensively study physical layer techniques for information security [3,4,5,6,7,8], which can prevent eavesdropping without upper layer data encryption.

Recently relayed cooperation in physical layer security has got increased attention among researchers as it can overcome the wireless channel impairments and improve the performance of secure wireless communications [9,10,11,12,13,14,15,16,17,18]. In [9], the four-terminal relay–eavesdropper channel is introduced. Noise-forwarding, compress-and-forward, and amplify-and-forward (AF) cooperation strategies are discussed and the corresponding achievable rates are derived. In [10] and [11], AF and or decode-and-forward (DF) relays are used in dual-hop cooperative multi relay system to optimize the achievable secrecy rate or the total transmit power. Apart from AF and DF strategies they also introduce cooperative jamming in which the source transmits the encoded signal and relays transmit a weighted jamming signal to confuse the eavesdroppers. In [12], secrecy outage probability of various single relay selection schemes are derived for dual-hop multi-relay DF system. To simplify the analysis it assumes high signal-to-noise ratio (SNR) where all the relay nodes successfully decode the source transmission. Using the same system model and assumptions, [13], selects a relay and a jammer and finds secrecy outage probability of the same. Using both the DF and AF relays in dual-hop multi-relay system, [14], derives closed-form intercept probability or the probability of non zero secrecy capacity expressions for various relay selection schemes. Unlike [12] and [13, 14] does not use high SNR assumption. Using the DF relays in multi-hop system, [15] evaluates the probability of non-zero secrecy capacity, secrecy capacity and secure outage probability when eavesdropper intercepts signals from the source and all the relaying nodes. It does not consider any diversity combining at the eavesdropper.

Secrecy outage probability, which is defined as the probability that a targeted secure data rate cannot be achieved [8, 9], is an important criterion to measure whether users predefined quality of service can be met. Secrecy outage probability is obtained for dual-hop system in [12,13,14,15] using DF relays but not using AF relays. Though [14] also uses AF relay it does not obtain secrecy outage probability instead it evaluates probability of non zero secrecy capacity. In this paper we not only find secrecy outage probability we also find ergodic secrecy rate. Using AF relays, non zero secrecy capacity is easier to find than secrecy outage probability. Using AF relay in dual-hop scenario, [16] finds approximate secrecy outage probability when eavesdropper gets the relayed information. In the same scenario approximate secrecy outage probability is obtained when single relay is selected from multiple relays in [17]. Secrecy outage probability of a dual-hop system using AF relay containing multiple antennas is considered in [18].

Relays can not only improve the data transmission against direct transmission it can also provide diversity benefit to the eavesdropper. Direct link between source–eavesdropper or source–destination are absent in [12,13,14, 16,17,18]. As no direct link to eavesdropper is present in these papers, eavesdropper can not derive any diversity benefit. The assumption of direct link to the eavesdropper in our system makes our system different from these papers. Recently in [19], diversity combining at the eavesdropper is considered where direct and relayed signals from the source is combined to get the secure source message. Only maximal ratio combining (MRC) technique is considered for the diversity combining. In a dual-hop AF relay system, source–relay link is common between source–destination and source–eavesdropper links. As a result, SNRs at the eavesdropper and the destination are not independent rather correlated. This important fact is not taken into consideration in [19], rather it assumes independence of SNRs. It also assumes high SNR scenario. This two assumptions make secrecy outage analysis easier. Easier analysis allows to consider both the direct links from source to destination and eavesdropper in [19]. This makes our system different from [19] as we have considered only the direct link to eavesdropper for mathematical tractability after considering correlation between SNRs at eavesdropper and destination. Ergodic secrecy rate is also not evaluated in [19]. Though the fact of correlation is embedded in the derivation, [16,17,18] do not consider the direct link from source to eavesdropper. In a cognitive radio setup the diversity benefit is exploited in favour of eavesdropper in multiple eavesdroppers case in [20]. As no relays are used for data transmission in [20], no question of correlation in SNRs arises due to relaying. Neither of the papers in [12,13,14,15,16,17,18,19] evaluate ergodic secrecy rate for the system. We evaluate ergodic secrecy rate in our system considering diversity benefit at the eavesdropper.

In this paper, we concentrate on dual-hop system with AF relay for evaluating secrecy outage probability and ergodic secrecy rate performance. We consider that the eavesdropper is able to derive diversity benefit by tapping the signals from both the source and the relaying nodes. Both the MRC and selection combining (SC) diversity techniques are considered at the eavesdropper. By considering correlation between SNRs at the eavesdropper and the destination due to common source–relay link between them, we derive the secrecy outage probability. Assuming high SNR of the source–relay link we evaluate the ergodic secrecy rate. Though [18] does not mention specifically about correlation between SNRs at the eavesdropper and destination, the treatment is entirely different in our paper than in [18]. We also provide asymptotic analysis for secrecy outage and ergodic secrecy rate which is not present in [16,17,18,19]. This work generalizes [16]. Results in [16] can be derived from this paper by evaluating limiting case of source–eavesdropper average link SNR to zero.

The main contributions of this paper can be summarized as following.

• Taking more realistic assumption that the effective SNRs at the destination and eavesdropper are not independent but correlated we do the performance analysis of the MRC and SC diversity combining schemes at the eavesdropper.

• Derivation of exact secrecy outage probability is mathematically intractable hence we evaluate the upper and lower bounds of secrecy outage probability. Lower bound is found to be tight and tend to the actual secrecy outage probability as SNR increases.

• An approximate secrecy outage probability is derived when source–relay link has high SNR. We also find the ergodic secrecy rate with same source–relay link high SNR assumption.

• Asymptotic analysis for both the performances are presented when each hop in dual-hop system has same or different average SNR.

• As MRC is the best diversity combining technique for the eavesdropper, SC has better secrecy outage performance than MRC for a given parameter. To achieve same secrecy outage probability that of SC, MRC requires relatively higher SNR at lower rate. MRC also requires relatively higher average SNR to achieve same ergodic performance of SC when eavesdropper link quality degrades.

• We observe that either of the source–relay or relay–destination link quality can limit both secrecy outage and ergodic secrecy rate performance even if the other link quality is infinitely good.

The rest of the paper is organized as follows. System model is described in the Sect. 2. Some mathematical preliminaries needed are derived in the Sect. 3. Secrecy outage probability is presented in the Sect. 4. In Sect. 5, ergodic secrecy rate performance is obtained. Section 6 provides the asymptotic analysis of secrecy outage probability and ergodic secrecy rate. Results are shown in the Sect. 7 and finally conclusions are drawn in the Sect. 8.

Notation ${\mathcal {E} }\left( x\right)$ denotes exponential distribution with parameter $x, \mathbb {P}[\cdot ]$ is the probability of an event, $F_X(\cdot )$ denotes the cumulative distribution function (CDF) of a random variable (RV) X and $f_X(\cdot )$ is its probability distribution function (PDF), $\mathbb {E}_X[\cdot ]$ is the expectation operation over RV X. $\max \{\cdot \}$ denotes the maximum of its arguments whereas $\min \{\cdot \}$ denotes the minimum of its arguments, and $(x)^+\triangleq \max (0,x)$.

2 System Model

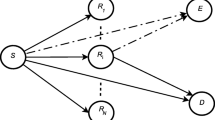
We consider a dual-hop communication system where a source node S is communicating with a destination node D with the help of a relay node R (Fig. 1). A direct communication path from S to D is not considered as there may be obstacles between them or they may be far apart. Communication is taking place in half-duplex manner via two orthogonal time slots. In the first time slot S is transmitting its information to the R and in the second time slot R is amplifying and forwarding the same information to the D. A channel state information (CSI) assisted AF relay R is considered. The relay gain is set according to the S to R instantaneous channel gain to fix certain output power from R. An eavesdropper E is considered to be present in the system which is capable of listening both the communication from S and R. It then diversity combines the information from two subsequent time slots to get the secure source message. The link gains between any two arbitrary node x and $y, h_{xy}$, is assumed to be independently flat Rayleigh faded but not identical among the links. Appropriate combination of x and y are to be taken from the set $\{s, r, e, d\}$. The set of small letters, $\{s, r, e, d\}$, directly corresponds to the set of nodes in capital letters, $\{S, R, E, D\}$. The instantaneous SNR between x and $y, \gamma _{xy}$, can be expressed as

$$\begin{aligned} \gamma _{xy} = \frac{P_{x} h_{xy}^2}{N_{0_{y}}}, \end{aligned}$$

(1)

where $P_{x}$ is the transmit power from node $x, N_{0_{y}}$ is the noise variance of the additive white Gaussian noise at y. As $h_{xy}$ is Rayleigh distributed, $\gamma _{xy}$ is exponentially distributed [21]. The parameter of exponential distribution is $\beta _{xy}, \gamma _{xy}\sim {\mathcal {E}}(\beta _{xy})$, such that average SNR of $\gamma _{xy}$ is

$$\begin{aligned} \mathbb {E}_{h_{xy}}[\gamma _{xy}] = \frac{P_{x} \mathbb {E}_{h_{xy}}[h_{xy}^2]}{N_{0_{y}}} =\frac{1}{\beta _{xy}}. \end{aligned}$$

(2)

When $y=e$, the parameter $\beta _{xy}=\alpha _{xy}$ is assumed. For example, S–R link parameter is $\beta _{sr}$ but S–E link parameter is $\alpha _{se}$. This is for easy follow up of the equations.

Fig. 1

System Model for analyzing secrecy outage probability of a dual-hop communication system using AF relay

The secrecy capacity of the system can be stated as [1, 5, 9, 14]

$$\begin{aligned} C_{S} = {\frac{1}{2}\left[\log _2\left(\frac{1+\gamma _{M} }{1+\gamma _{E} }\right)\right]}^+, \end{aligned}$$

(3)

where $\gamma _{M} , \gamma _{E}$ are the effective main channel and eavesdropper channel SNR at the D and E respectively. With appropriate AF relay gain [22,23,24], the effective SNRs of the S–R–D and S–R–E paths, $\gamma _{M}$ and $\gamma _{sre}$ respectively, can be written as

$$\begin{aligned} \gamma _{M} =\frac{\gamma _{sr} \gamma _{rd}}{\gamma _{sr}+ \gamma _{rd}}; ~~~ \gamma _{sre} =\frac{\gamma _{sr} \gamma _{re}}{\gamma _{sr}+ \gamma _{re}}, \end{aligned}$$

(4)

where $\gamma _{sr}, \gamma _{rd}$ and $\gamma _{re}$ are the instantaneous SNRs of the paths S–R, R-D and R–E respectively. SNRs in (4) is also the approximate SNR at relatively high SNR when relay gain is set differently [22,23,24]. $\gamma _{E}$ is the SNR after diversity combining the S–E and R–E paths at E. Ergodic secrecy rate of the system can be obtained by averaging $C_S$ over $\gamma _M$ and $\gamma _E$ as

$$\begin{aligned} \bar{C}_{S} = \frac{1}{2}\mathbb {E}_{\gamma _M} \mathbb {E}_{\gamma _E} \left[\log _2\left(1+\gamma _{M}\right)- \log _2\left(1+\gamma _{E}\right)\right], \end{aligned}$$

(5)

when $\gamma _M>\gamma _E$.

Secrecy outage probability is then defined for the system as [5]

$$\begin{aligned} P_o\left(R_s\right)&=\mathbb {P}\left[ C_{S}< R_s \right] = \mathbb {P}\left[ \frac{1+\gamma _{M} }{1+\gamma _{E} } < \rho \right] \end{aligned}$$

(6)

$$\begin{aligned}&= \mathbb {E}_{\gamma _{E} } \left[ F_{\gamma _{M} } \left[ \left(1+\gamma _{E} \right) \rho -1\right] \right], \end{aligned}$$

(7)

where $R_s$ is the desired threshold secrecy rate of the system and $\rho =2^{2R_s}$.

To improve secrecy performance by improving the diversity of the system, multi-relay system with relay selection can further be investigated.

3 Mathematical Preliminaries

In this section, some mathematical preliminaries are presented for the work. Two inequalities are presented and a proposition with corollary is derived, which will be used later in this paper.

If x, y are arbitrary positive real numbers then following bound holds

$$\begin{aligned} \frac{1}{2}\min \left(x,y \right) \le \frac{xy}{x+y}\le \min \left(x,y \right). \end{aligned}$$

(8)

This bound can easily be obtained from harmonic mean inequality of (x, y) [23, 25]. This is also typically used in CSI assisted multi hop AF relay networks at high SNR to approximate or bound the end-to-end equivalent SNR [26, 27]. There, x and y are the individual hop SNR in dual-hop case. By looking at (4) and (8), it can be understood that upper and lower bounds of $\gamma _M$ and $\gamma _{sre}$ can easily be found and will be used in subsequent sections.

Proposition 1

The moment generating function (MGF) of a RV $T \triangleq \min (X,Y)$ conditioned on X, where $X \sim {\mathcal {E}}(\beta _x)$ and $Y \sim {\mathcal {E}}(\beta _y)$ are independent exponentially distributed RVs is

$$\begin{aligned} M_{T|X}(s|x)=\frac{\left(1-e^{-(\beta _y -s)x} \right) }{1 -\frac{s}{\beta _y}}+ e^{-(\beta _y-s) x}. \end{aligned}$$

(9)

Proof

See Appendix 1 for proof.

Corollary 1

The MGF of a RV $T \triangleq \frac{1}{2}\min (X,Y)$ conditioned on X, where $X \sim {\mathcal {E}}(\beta _x)$ and $Y \sim {\mathcal {E}}(\beta _y)$ are independent exponentially distributed RVs respectively, is

$$\begin{aligned} M_{T|X}(s|x)=\frac{\left(1-e^{-(2\beta _y -s)\frac{x}{2}} \right) }{1 -\frac{s}{2\beta _y}}+ e^{-(\beta _y-s) \frac{x}{2}}. \end{aligned}$$

(10)

Proof

See Appendix 2 for proof.

4 Secrecy Outage Probability

In this section we evaluates upper bound, lower bound and approximate expressions of secrecy outage probability, $P_o(R_s)$. As the first hop link S–R is common between S–R–D as well as S–R–E, the effective SNR at D and E are not independent but correlated. So to evaluate $P_o(R_s)$, we will first evaluate the conditional $P_o(R_s)$, conditioned on the the first hop SNR, $\gamma _{sr}$, and then average it over $\gamma _{sr}$. Exact closed-form $P_o(R_s)$ is mathematically intractable when MRC and SC diversity combining is done at the E. Hence we find upper bound, lower bound and approximate expressions of $P_o(R_s)$ for each diversity combining techniques. Using the lower bound of $\gamma _{M}, \gamma _{M}^{ (LB)}$, and the upper bound of $\gamma _{E}, \gamma _{E}^{ (UB)}$, in (6) we find the upper bound of $P_o\left(R_s\right)$ as $P_o^{(UB)}\left(R_s\right)$. Using the upper bound of $\gamma _{M}, \gamma _{M}^{ (UB)}$, and the lower bound of $\gamma _{E}, \gamma _{E}^{ (LB)}$, in (6) we find the lower bound of $P_o\left(R_s\right)$ as $P_o^{(LB)}\left(R_s\right)$. We denote UB and LB as the upper bound and lower bound respectively and use (8) to find the same.

4.1 MRC at Eavesdropper

As SNR after MRC diversity combining is the summation of the individual SNRs [28], the MGF of the effective SNR $\gamma _{E}$ will be the multiplication of MGFs of $\gamma _{se}$ and $\gamma _{sre}$ [29].

4.1.1 Lower Bound

The MGF of $\gamma _{E}^{ (LB)}$ conditioned on $\gamma _{sr}$ can be written using MGF of $\gamma _{se}$ and lower bound of $\gamma _{sre}$. With the help of (8) and Corollary 1 the conditional MGF of $\gamma _{E}^{ (LB)}$ is

$$\begin{aligned} M_{\gamma _E^{ (LB)}|\gamma _{sr}}(s|x)=&\frac{1}{\left( 1-\frac{s}{\alpha _{se}}\right) \left( 1-\frac{s}{2\alpha _{re}}\right) }+ \frac{e^{-(2\alpha _{re}-s)\frac{x}{2}}}{\left( 1-\frac{s}{\alpha _{se}}\right) } -\frac{e^{-(2\alpha _{re}-s)\frac{x}{2}}}{\left( 1-\frac{s}{\alpha _{se}}\right) \left( 1-\frac{s}{2\alpha _{re}}\right) }. \end{aligned}$$

(11)

The corresponding PDF can be found from (11) for $\alpha _{se}\ne 2\alpha _{re}$ with the help of [30] as

$$\begin{aligned}&f_{\gamma _E^{ (LB)}|\gamma _{sr}}(t|x)=\frac{2\alpha _{se}\alpha _{re}}{\alpha _{se}-2\alpha _{re}}\left(e^{-2\alpha _{re} t}-e^{-\alpha _{se} t}\right) \nonumber \\&\quad +\,\left[\alpha _{se} e^{-\alpha _{se}t}e^{(\alpha _{se}-2\alpha _{re})\frac{x}{2}}-\frac{2\alpha _{se}\alpha _{re}}{\alpha _{se}-2\alpha _{re}} \left(e^{-2\alpha _{re}t}-e^{-\alpha _{se}t}e^{(\alpha _{se}-2\alpha _{re})\frac{x}{2}}\right)\right] u\left(t-\frac{x}{2}\right). \end{aligned}$$

(12)

The lower bound of secrecy outage probability for the given $\gamma _{sr}$ can then be found by using (7) as

$$\begin{aligned} P_{o|\gamma _{sr}}^{ (LB)}(R_s|x) = \mathbb {E}_{\gamma _{E}^{ (LB)}|\gamma _{sr}}\left[ F_{\gamma _{M}^{ (UB)}|\gamma _{sr}}\left[ \left(1+t\right) \rho -1|x\right] \right]. \end{aligned}$$

(13)

With the help of (8) and (59), the conditional CDF of the upper bound of $\gamma _{M}$ conditioned on the $\gamma _{sr}$ can be written as

$$\begin{aligned} F_{\gamma _{M}^{ (UB)}|\gamma _{sr}}\left[\left(1+t\right)\rho -1|x\right] = \left\{ \begin{array}{ll} 1-e^{-\beta _{rd}\left(\left(1+t\right)\rho -1\right)} &{} \quad t < \frac{x-(\rho -1)}{\rho }\\ 1 &{} \quad t \ge \frac{x-(\rho -1)}{\rho }\\ \end{array} \right. . \end{aligned}$$

(14)

Averaging in (13) has to be carried out after appropriately partitioning the integration region as PDF and CDF in (12) and (14) respectively are defined differently within different limits. It should be kept in mind that finally unconditional $P_o (R_s)$ has to be found out by averaging (13) over $\gamma _{sr}$. Dummy variable x in (14) is basically for $\gamma _{sr}$ to finally integrate (13) over RV $\gamma _{sr}$. Observing (14) we can see that if $x<(\rho -1)$ then $F_{\gamma _{M}^{ (UB)}|\gamma _{sr}}(\cdot )$ becomes unity irrespective of its argument. Now consider $x \ge (\rho -1)$. Observing (12) and (14), we need to find out that what is the relationship between $L_1$ and $L_2$ depending on $\rho$ and x, where $L_1=\frac{x-\left(\rho -1\right)}{\rho }$ and $L_2=\frac{x}{2}$. Whether $L_1 < L_2$ or vice versa. Following limits

$$\begin{aligned} 0<L_1<L_2<\infty , \end{aligned}$$

(15)

always hold if $\rho \ge 2$ for $x \ge (\rho -1)$. Now for $\rho \le 2$, following limits

$$\begin{aligned} 0<L_1<L_2<\infty , \end{aligned}$$

(16)

hold when $(\rho -1)\le x\le \frac{2(\rho -1)}{2-\rho }$. Following limits

$$\begin{aligned} 0<L_2<L_1<\infty , \end{aligned}$$

(17)

hold when $x\ge \frac{2(\rho -1)}{2-\rho }$ for $\rho \le 2$. Notice that (15) and (16) are identical. Depending on the $\rho$, whether it is greater or less than two, different lower bounds are obtained from (13). Let us call them $LB_1$ for $\rho >2$ and $LB_2$ for $\rho \le 2$. So the averaging in (13) can be evaluated using (12) and (14) when $\rho \ge 2$ and $x\ge (\rho -1)$ as

$$\begin{aligned} P_{o|\gamma _{sr}}^{ (LB_1)}(R_s|x)&=\int _0^{L_1} \left[1-e^{-\beta _{rd}\left((1+t)\rho -1\right)}\right] \frac{2\alpha _{se}\alpha _{re}}{\alpha _{se}-2\alpha _{re}} \left(e^{-2\alpha _{re} t}-e^{-\alpha _{se} t}\right)dt\nonumber \\&\quad +\,\int _{L_1}^{L_2} \frac{2\alpha _{se}\alpha _{re}}{\alpha _{se}-2\alpha _{re}} \left(e^{-2\alpha _{re} t}-e^{-\alpha _{se} t}\right)dt\nonumber \\&\quad +\,\int _{L_2}^{\infty }\left[\frac{2\alpha _{se}\alpha _{re}}{\alpha _{se}-2\alpha _{re}} \left(e^{-2\alpha _{re} t}-e^{-\alpha _{se} t}\right)\nonumber \right.\\&\quad +\,\left.\alpha _{se} e^{-\alpha _{se}t}e^{(\alpha _{se}-2\alpha _{re}) \frac{x}{2}}-\frac{2\alpha _{se}\alpha _{re}}{\alpha _{se}-2\alpha _{re}} \left(e^{-2\alpha _{re}t}-e^{-\alpha _{se}t}e^{(\alpha _{se}-2\alpha _{re}) \frac{x}{2}}\right)\right]dt. \end{aligned}$$

(18)

Result of (18) can again be used for $LB_2$ as (15) and (16) are identical. Finally the unconditional $P_{o}^{ (LB_1)}(R_s)$ for $\rho \ge 2$ can then be obtained following (15) as

$$\begin{aligned} P_{o}^{ (LB_1)}(R_s)&=\int _0^{(\rho -1)} f_{\gamma _{sr}}(x) dx +\int _{(\rho -1)}^\infty P_{o|\gamma _{sr}}^{ (LB_1)}(R_s|x)f_{\gamma _{sr}}(x)dx, \end{aligned}$$

(19)

where $f_{\gamma _{sr}}(x) =\beta _{sr}\exp (-\beta _{sr}x)$ is the exponential PDF of $\gamma _{sr}$. After solving (19), $P_{o}^{ (LB_1)}(R_s)$ is expressed in (28).

When $\rho \le 2$ and $\gamma _{sr }\ge \frac{2(\rho -1)}{2-\rho }$, (13) can be evaluated just as (18) to

$$\begin{aligned} P_{o|\gamma _{sr}}^{ (LB_2)}(R_s|x)&=\int _0^{L_2} \left[1-e^{-\beta _{rd}\left((1+t)\rho -1\right)}\right]\frac{2\alpha _{se}\alpha _{re}}{\alpha _{se}-2\alpha _{re}}\left(e^{-2\alpha _{re} t}-e^{-\alpha _{se} t}\right)dt\nonumber \\&\quad +\,\int _{L_2}^{L_1} \left[1-e^{-\beta _{rd}\left((1+t)\rho -1\right)}\right]\left[\frac{2\alpha _{se}\alpha _{re}}{\alpha _{se}-2\alpha _{re}}\left(e^{-2\alpha _{re} t}-e^{-\alpha _{se} t}\right)\right.\nonumber \\&\quad \left.+\,\alpha _{se} e^{-\alpha _{se}t}e^{(\alpha _{se}-2\alpha _{re})\frac{x}{2}}-\frac{2\alpha _{se} \alpha _{re}}{\alpha _{se}-2\alpha _{re}} \left(e^{-2\alpha _{re}t}-e^{-\alpha _{se}t}e^{(\alpha _{se}-2\alpha _{re})\frac{x}{2}}\right)\right]dt\nonumber \\&\quad +\,\int _{L_1}^{\infty } \left[ \frac{2\alpha _{se}\alpha _{re}}{\alpha _{se}-2\alpha _{re}}\left(e^{-2\alpha _{re} t}-e^{-\alpha _{se} t}\right)\right.\nonumber \\&\quad \left.+ \,\alpha _{se} e^{-\alpha _{se}t}e^{(\alpha _{se}-2\alpha _{re})\frac{x}{2}} -\frac{2\alpha _{se}\alpha _{re}}{\alpha _{se}-2\alpha _{re}} \left(e^{-2\alpha _{re}t}-e^{-\alpha _{se}t}e^{(\alpha _{se}-2\alpha _{re})\frac{x}{2}}\right)\right]dt. \end{aligned}$$

(20)

Reusing $P_{o|\gamma _{sr}}^{ (LB_1)}(R_s|x)$ from (18) as (15) and (16) are identical, the unconditional secrecy outage probability for $\rho \le 2$ can be evaluated to

$$\begin{aligned} P_{o}^{ (LB_2)}(R_s)=\int _0^{(\rho -1)} f_{\gamma _{sr}}(x) dx +\int _{(\rho -1)}^{\frac{2(\rho -1)}{(2-\rho )}} P_{o|\gamma _{sr}}^{ (LB_1)}(R_s|x)f_{\gamma _{sr}}(x)dx +\int _{\frac{2(\rho -1)}{(2-\rho )}}^\infty P_{o|\gamma _{sr}}^{ (LB_2)}(R_s|x)f_{\gamma _{sr}}(x)dx. \end{aligned}$$

(21)

The final solution of (21) is expressed in (29).

4.1.2 Upper Bound

We follow the similar method as followed while finding the lower bound of secrecy outage probability here as well. At first using MGF method, the PDF of $\gamma _{E}^{ (UB)}(\cdot )$ conditioned on $\gamma _{sr}, f_{\gamma _{E}^{ (UB)}|\gamma _{sr}} (\cdot )$, can be found. With the help of (8) and proposition 1, the PDF can be found for $\alpha _{se}\ne \alpha _{re}$ as

$$\begin{aligned} f_{\gamma _E^{ (UB)}|\gamma _{sr}}(t|x)&=\frac{\alpha _{se}\alpha _{re}}{\alpha _{se}-\alpha _{re}}\left(e^{-\alpha _{re} t}-e^{-\alpha _{se} t}\right) \nonumber \\&\quad + \,\left[\alpha _{se} e^{-\alpha _{se}t}e^{(\alpha _{se}-\alpha _{re})x}-\frac{\alpha _{se}\alpha _{re}}{\alpha _{se}-\alpha _{re}} \left(e^{-\alpha _{re}t}-e^{-\alpha _{se}t}e^{(\alpha _{se}-\alpha _{re})x}\right)\right] u(t-x). \end{aligned}$$

(22)

Then following the method of finding lower bound of secrecy outage probability in the previous section, the upper bound of the secrecy outage probability can also be found as

$$\begin{aligned} P_{o|\gamma _{sr}}^{ (UB)}(R_s|x) = \mathbb {E}_{\gamma _{E}^{ (UB)}|\gamma _{sr}}\left[ F_{\gamma _{M}^{ (LB)}|\gamma _{sr}}\left[ \left(1+t\right) \rho -1|x\right] \right]. \end{aligned}$$

(23)

The CDF $F_{\gamma _{M}^{ (LB)}|\gamma _{sr}}(\cdot )$ can be found by following (8) and (62) as

$$\begin{aligned} F_{\gamma _{M}^{ (LB)}|\gamma _{sr}}(\left(1+t\right) \rho -1|x)=\left\{ \begin{array}{ll} 1-e^{-2\beta _{rd}\left(\left(1+t\right)\rho -1\right)} &{} \quad t < \frac{x-2(\rho -1)}{2\rho }\\ 1 &{} \quad t \ge \frac{x-2(\rho -1)}{2\rho }\\ \end{array} \right. . \end{aligned}$$

(24)

For the integration of (23), the integration regions must be divided as is done for the lower bounds from (15) to (17). From (24) we can see that if $x<2(\rho -1), F_{\gamma _{M}^{ (LB)}|\gamma _{sr}}(\cdot )$ is unity for any argument. Now looking (22) and (24) together, when $x\ge 2(\rho -1)$ for any values of $\rho \ge 1$ (i.e. $R_s\ge 0$), we can see that following limit holds for the integration

$$\begin{aligned} 0<\frac{x-2\left(\rho -1\right)}{2\rho }<x<\infty . \end{aligned}$$

(25)

Rest is similar to the derivation of lower bound in previous section. The solution is directly written in (30).

4.1.3 Approximate Analysis

If SNR of either one hop in a dual-hop AF relay system is very high compared to other, the end-to-end SNR can be approximated by its upper bound given in (8) [26, 27]. This approximation works better and better when the difference between individual hop SNRs increases i.e. either of the hop channel quality gets better and better compared to other. Motivated by this fact, we find an approximate secrecy outage probability as $P_o^{(AP)}\left(R_s\right)$ assuming high SNR of S–R link i.e. $1/\beta _{sr}>>1/\beta _{rd}$ and $1/\beta _{sr}>>1/\beta _{re}$. AP is used to denote the approximation. $P_o^{(AP)}\left(R_s\right)$ is obtained using upper bound of $\gamma _{M}, \gamma _{M}^{ (UB)}$, and upper bound of $\gamma _{E}, \gamma _{E}^{ (UB)}$, in (6) following (8).

Finding approximate secrecy outage probability is similar to that of finding the upper bound. In this case we have to use $F_{\gamma _{M}^{ (UB)}|\gamma _{sr}}(\cdot )$ instead of $F_{\gamma _{M}^{ (LB)}|\gamma _{sr}}(\cdot )$. The approximate secrecy outage probability, $P_{o}^{ (AP)}(R_s)$, can be achieved after evaluating conditional approximate secrecy outage probability

$$\begin{aligned}&P_{o|\gamma _{sr}}^{ (AP)}(R_s|x) = \mathbb {E}_{\gamma _{E}^{ (UB)}|\gamma _{sr}}\left[ F_{\gamma _{M}^{ (UB)}|\gamma _{sr}}\left[ \left(1+t\right) \rho -1|x\right] \right]. \end{aligned}$$

(26)

Now we have to average (26) over $\gamma _{sr}$ to get the unconditional approximate secrecy outage probability. While evaluating (26) we use CDF $F_{\gamma _{M}^{ (UB)}|\gamma _{sr}}(\cdot )$ from (14), PDF $f_{\gamma _{E}^{ (UB)}|\gamma _{sr}}(\cdot )$ from (22). When $\gamma _{sr}< (\rho -1), F_{\gamma _{M}^{ (UB)}|\gamma _{sr}}(\cdot )$ is unity. When $\gamma _{sr}\ge (\rho -1)$ for any values of $\rho \ge 1$, integration limits must be

$$\begin{aligned} 0<\frac{x-\left(\rho -1\right)}{\rho }<x<\infty . \end{aligned}$$

(27)

The final expression of $P_{o}^{ (AP)}(R_s)$ is written in (31).

Bounds and approximate secrecy outage probability of MRC diversity combining at the eavesdropper where $P_o^{ (LB_1)}(R_s)$ is for $\rho > 2$ or $R_s > 0.5$ and $P_o^{ (LB_2)}(R_s)$ is for $\rho \le 2$ or $R_s \le 0.5$.

$$\begin{aligned} P_o^{ (LB_1)}(R_s)= & {} 1-\frac{2\alpha _{se}\alpha _{re}\exp \left(-\left(\rho -1\right)\left(\beta _{sr}+\beta _{rd}\right)\right)}{\left(\rho \beta _{rd}+\alpha _{se}\right)\left(\rho \beta _{rd}+2\alpha _{re}\right)} \left[ 1-\frac{\beta _{sr}\left(\frac{2\rho \beta _{rd}+\alpha _{se}+2\alpha _{re}}{\rho }+\beta _{sr}\right)}{\left(\beta _{sr}+\beta _{rd}+\frac{\alpha _{se}}{\rho }\right) \left(\beta _{sr}+\beta _{rd}+\frac{2\alpha _{re}}{\rho }\right)}\right]. \end{aligned}$$

(28)

$$\begin{aligned} P_o^{ (LB_2)}(R_s)= & {} P_o^{ (LB_1)}(R_s)-\frac{\alpha _{se}\beta _{sr}}{\left(\rho \beta _{rd}+\alpha _{se}\right)\left(\rho \beta _{rd}+2\alpha _{re}\right)} \left[\frac{\rho \beta _{rd}\exp {\left(\left(\rho -1\right)\left(\beta _{rd}+\frac{2(\rho \beta _{rd}/2+\alpha _{re}+\beta _{sr})}{(2-\rho )} \right)\right)}}{\rho \beta _{rd}/2+\alpha _{re}+\beta _{sr}} \right.\nonumber \\&\left.+\,\frac{\exp {\left(\frac{2\left(\rho -1\right)(\beta _{sr}+\beta _{rd}+2\alpha _{re})}{(2-\rho )}\right)}}{(\beta _{sr}+\beta _{rd}+\alpha _{se}(1/\rho -1/2)+\alpha _{re})(\beta _{sr}+\beta _{rd}+2\alpha _{re}/\rho )}\right]. \end{aligned}$$

(29)

$$\begin{aligned} P_o^{ (UB)}(R_s)= & {} 1-\frac{\alpha _{se}\alpha _{re}\exp \left(-2\left(\rho -1\right)\left(\beta _{sr}+\beta _{rd}\right)\right)}{\left(2\rho \beta _{rd}+\alpha _{se}\right)\left(2\rho \beta _{rd}+\alpha _{re}\right)} \left[ 1-\frac{\beta _{sr}\left(\frac{4\rho \beta _{rd}+\alpha _{se}+\alpha _{re}}{2\rho }+\beta _{sr}\right)}{\left(\beta _{sr}+\beta _{rd}+\frac{\alpha _{se}}{2\rho }\right) \left(\beta _{sr}+\beta _{rd}+\frac{\alpha _{re}}{2\rho }\right)}\right]. \end{aligned}$$

(30)

$$\begin{aligned} P_o^{ (AP)}(R_s)= & {} 1-\frac{\alpha _{se}\alpha _{re}\exp \left(-\left(\rho -1\right)\left(\beta _{sr}+\beta _{rd}\right)\right)}{\left(\rho \beta _{rd}+\alpha _{se}\right)\left(\rho \beta _{rd}+\alpha _{re}\right)} \left[ 1-\frac{\beta _{sr}\left(\frac{2\rho \beta _{rd}+\alpha _{se}+\alpha _{re}}{\rho }+\beta _{sr}\right)}{\left(\beta _{sr}+\beta _{rd}+\frac{\alpha _{se}}{\rho }\right) \left(\beta _{sr}+\beta _{rd}+\frac{\alpha _{re}}{\rho }\right)}\right]. \end{aligned}$$

(31)

4.2 SC at Eavesdropper

The SC diversity combiner selects the maximum SNR between S–E and S–R–E paths [28]. In this section also, the bounds and approximate expression of secrecy outage probability is obtained as in MRC diversity combining. Depending on the usage of upper or lower bound of $\gamma _M$ and $\gamma _E$ in (6) we can have upper, lower or approximate expression of secrecy outage probability.

4.2.1 Lower Bound

The CDF of the SNR at the output of SC diversity combiner with independent input SNRs is simply the product of the corresponding CDFs [28]. The conditional CDF of $\gamma _{E}^{ (LB)}$, conditioned on the $\gamma _{sr}$, can be evaluated using CDF of $\gamma _{se}$ and conditional CDF of $\gamma _{sre}^{ (LB)}$. With the help of (8) and (62) conditional CDF of $\gamma _{E}^{ (LB)}$ is

$$\begin{aligned} F_{\gamma _{E}^{ (LB)}|\gamma _{sr}}(t|x)=\left\{ \begin{array}{ll} \left(1-e^{-\alpha _{se} t}\right)\left(1-e^{-2\alpha _{re} t}\right) \quad t >\frac{x}{2}\\ 1-e^{-\alpha _{se} t} \quad t \geq \frac{x}{2}\\ \end{array} \right. . \end{aligned}$$

(32)

The corresponding PDF can be found by differentiating (32) with respect to t as

$$\begin{aligned} f_{\gamma _{E}^{ (LB)}|\gamma _{sr}}(t|x)= \left\{ \begin{array}{ll} \alpha _{se}e^{-\alpha _{se}t}(1-e^{-2\alpha _{re}t})+2\alpha _{re} e^{-2\alpha _{re}t}(1-e^{-\alpha _{se}t}) \quad t< \frac{x}{2}\\ \alpha _{se}e^{-\alpha _{se}t}+e^{-\alpha _{re}x}(1-e^{-\alpha _{se} \frac{x}{2}})\delta (t-\frac{x}{2}) \quad t \ge \frac{x}{2}\\ \end{array} \right. \end{aligned}$$

(33)

$F_{\gamma _{M}^{ (UB)}|\gamma _{sr}}(\cdot )$ can be found from (14). The secrecy outage probability lower bound then can be evaluated from (7). Here again, depending on whether $\rho >2$ or $\rho \le 2$ there will be two lower bounds $LB_1$ and $LB_2$ as in MRC. The three limits of MRC in (15), (16) and (17) are also applicable here. The derivation procedure is similar to that of MRC so final expressions of $P_o^{ (LB_1)}(R_s)$ and $P_o^{ (LB_2)}(R_s)$ are directly shown in (35) and (36) respectively.

4.2.2 Upper Bound

Here,

$$\begin{aligned} f_{\gamma _{E}^{ (UB)}|\gamma _{sr}}(t|x)= \left\{ \begin{array}{ll} \alpha _{se}e^{-\alpha _{se}t}(1-e^{-\alpha _{re}t})+\alpha _{re}e^{-\alpha _{re}t}(1-e^{-\alpha _{se}t}) &{} \quad t < x\\ \alpha _{se}e^{-\alpha _{se}t}+e^{-\alpha _{re}x}(1-e^{-\alpha _{se} x})\delta (t-x) &{} \quad t \ge x\\ \end{array} \right. , \end{aligned}$$

(34)

is obtained by similar method of lower bound with the help of (8), proposition 1. $F_{\gamma _{M}^{ (LB)}|\gamma _{sr}}(t|x)$ can be obtained from (24). The rest of the procedure is similar as described in the lower bound of SC diversity combining. The rest is identical to that of obtaining upper bound of MRC diversity combining because both of them use same integrations limits. The final result of $P_o^{ (UB)}(R_s)$ is expressed in (37).

4.2.3 Approximate Analysis

The approximate analysis of SC considers same high SNR assumption of $1/\beta _{sr}$ as in approximate analysis of MRC. First we find $f_{\gamma _{E}^{ (UB)}|\gamma _{sr}}(t|x)$ and $F_{\gamma _{M}^{ (UB)}|\gamma _{sr}}(t|x)$ from (34) and (14) respectively with the help of (8) and proposition 1. The procedure then follows the procedure of obtaining approximate analysis of MRC diversity combining technique. Both MRC and SC uses same integration partitioning limits for obtaining approximate analysis. Finally approximate secrecy outage expression of SC diversity combining, $P_o^{ (AP)}(R_s)$, is expressed in (38).

Bounds and approximate secrecy outage probability of SC diversity combining at the eavesdropper where $P_o^{ (LB_1)}(R_s)$ is for $\rho > 2$ or $R_s > 0.5$ and $P_o^{ (LB_2)}(R_s)$ is for $\rho \le 2$ or $R_s \le 0.5$.

$$\begin{aligned} P_o^{ (LB_1)}(R_s)= 1-\frac{\alpha _{se}\exp \left(-\left(\rho -1\right)\left(\beta _{sr}+\beta _{rd}\right)\right)}{\left(\rho \beta _{rd}+\alpha _{se}\right)} \left[ 1-\frac{\beta _{sr}}{\beta _{sr}+\beta _{rd}+\frac{\alpha _{se}}{\rho }}\right] -\frac{2\alpha _{re}\exp \left(-\left(\rho -1\right)\left(\beta _{sr}+\beta _{rd}\right)\right)}{\left(\rho \beta _{rd}+2\alpha _{re}\right)} \nonumber \\ \times \left[ 1-\frac{\beta _{sr}}{\beta _{sr}+\beta _{rd}+\frac{2\alpha _{re}}{\rho }}\right] +\frac{\left(\alpha _{se}+2\alpha _{re}\right)\exp \left(-\left(\rho -1\right)\left(\beta _{sr}+\beta _{rd}\right)\right)}{\left(\rho \beta _{rd}+\alpha _{se}+2\alpha _{re}\right)} \left[ 1-\frac{\beta _{sr}}{\beta _{sr}+\beta _{rd}+\frac{\alpha _{se}+2\alpha _{re}}{\rho }}\right]. \end{aligned}$$

(35)

$$\begin{aligned} P_o^{ (LB_2)}(R_s)= & {} P_o^{ (LB_1)}(R_s) +\frac{\beta _{sr}\exp \left(-\frac{2\left(\rho -1\right)}{2-\rho }\left(\beta _{sr}+\beta _{rd}+\frac{\alpha _{se}}{2}+\alpha _{re}\right)\right)}{\left(\rho \beta _{rd}+\alpha _{se}+2\alpha _{re}\right)}\left[\frac{\rho \beta _{rd}}{\beta _{sr}+\alpha _{re}+\frac{\alpha _{se}+\rho \beta _{rd}}{2}} +\frac{\alpha _{se}+2\alpha _{re}}{\beta _{sr}+\beta _{rd}+\frac{\alpha _{se}+2\alpha _{re}}{\rho }}\right] \nonumber \\&-\,\frac{\beta _{sr}\exp \left(-\frac{2\left(\rho -1\right)}{2-\rho }\left(\beta _{sr}+\beta _{rd}+\alpha _{re}\right)\right)}{\left(\rho \beta _{rd}+2\alpha _{re}\right)}\left[\frac{\rho \beta _{rd}}{\beta _{sr}+\alpha _{re}+\frac{\rho \beta _{rd}}{2}} +\frac{2\alpha _{re}}{\beta _{sr}+\beta _{rd}+\frac{2\alpha _{re}}{\rho }}\right]. \end{aligned}$$

(36)

$$\begin{aligned} P_o^{ (UB)}(R_s)= & {} 1-\frac{\alpha _{se}\exp \left(-2\left(\rho -1\right)\left(\beta _{sr}+\beta _{rd}\right)\right)}{\left(2\rho \beta _{rd}+\alpha _{se}\right)} \left[ 1-\frac{\beta _{sr}}{\beta _{sr}+\beta _{rd}+\frac{\alpha _{se}}{2\rho }}\right] -\frac{\alpha _{re}\exp \left(-2\left(\rho -1\right)\left(\beta _{sr}+\beta _{rd}\right)\right)}{\left(2\rho \beta _{rd}+\alpha _{re}\right)} \nonumber \\&\times \left[ 1-\frac{\beta _{sr}}{\beta _{sr}+\beta _{rd}+\frac{\alpha _{re}}{2\rho }}\right] +\frac{\left(\alpha _{se}+\alpha _{re}\right)\exp \left(-2\left(\rho -1\right)\left(\beta _{sr}+\beta _{rd}\right)\right)}{\left(2\rho \beta _{rd}+\alpha _{se}+\alpha _{re}\right)} \left[ 1-\frac{\beta _{sr}}{\beta _{sr}+\beta _{rd}+\frac{\alpha _{se}+\alpha _{re}}{2\rho }}\right]. \end{aligned}$$

(37)

$$\begin{aligned} P_o^{ (AP)}(R_s)= & {} 1-\frac{\alpha _{se}\exp \left(-\left(\rho -1\right)\left(\beta _{sr}+\beta _{rd}\right)\right)}{\left(\rho \beta _{rd}+\alpha _{se}\right)} \left[ 1-\frac{\beta _{sr}}{\beta _{sr}+\beta _{rd}+\frac{\alpha _{se}}{\rho }}\right] -\frac{\alpha _{re}\exp \left(-\left(\rho -1\right)\left(\beta _{sr}+\beta _{rd}\right)\right)}{\left(\rho \beta _{rd}+\alpha _{re}\right)} \nonumber \\&\times \left[ 1-\frac{\beta _{sr}}{\beta _{sr}+\beta _{rd}+\frac{\alpha _{re}}{\rho }}\right] +\frac{\left(\alpha _{se}+\alpha _{re}\right)\exp \left(-\left(\rho -1\right)\left(\beta _{sr}+\beta _{rd}\right)\right)}{\left(\rho \beta _{rd}+\alpha _{se}+\alpha _{re}\right)} \left[ 1-\frac{\beta _{sr}}{\beta _{sr}+\beta _{rd}+\frac{\alpha _{se}+\alpha _{re}}{\rho }}\right]. \end{aligned}$$

(38)

Remark 1

From (28) to (31), it can be observed that neither of the equations contain $(\alpha _{se}-2\alpha _{re})$ or $(\alpha _{se}-\alpha _{re})$ in the denominator. The term is canceled out with the same term in the numerator while deriving the equations. This says that the expressions might be evaluated when $(\alpha _{se}=2\alpha _{re})$ or $(\alpha _{se}=\alpha _{re})$, though (12) or (22) does not permit in those cases to proceed. This is verified by simulations in the numerical results.

Remark 2

This paper is the generalization of [16], as the performance of the dual-hop system without direct link between S and E can easily be obtained by tending S–E link average SNR to zero. The expressions in [16] can be achieved by tending $1/\alpha _{se}\rightarrow 0$ in the equations from (28) to (38). The derivation is not shown due to space constraint.

5 Ergodic Secrecy Rate

This section finds the ergodic secrecy rate of the system when eavesdropper performs MRC or SC diversity combining. When MRC and SC diversity combining is performed at the E the secrecy rate can be written from (3) as

$$\begin{aligned} C_{S}^{MRC} = {\frac{1}{2}\left[\log _2\left(\frac{1+\frac{\gamma _{sr}\gamma _{rd}}{1+\gamma _{sr}+\gamma _{rd}}}{1+\gamma _{se}+ \frac{\gamma _{sr}\gamma _{re}}{1+\gamma _{sr}+\gamma _{re}} }\right)\right]}^+, \end{aligned}$$

(39)

and

$$\begin{aligned} C_{S}^{SC} = {\frac{1}{2}\left[\log _2\left(\frac{1+\frac{\gamma _{sr}\gamma _{rd}}{1+\gamma _{sr}+\gamma _{rd}}}{1+\max \left\lbrace \gamma _{se}, \frac{\gamma _{sr}\gamma _{re}}{1+\gamma _{sr}+\gamma _{re}} \right\rbrace }\right)\right]}^+, \end{aligned}$$

(40)

respectively. Where superscripts MRC and SC in (39) and (40) respectively are to indicate MRC and SC combining. $\gamma _M$ is replaced by $\gamma _M=\frac{\gamma _{sr}\gamma _{rd}}{1+\gamma _{sr}+\gamma _{rd}}$ while $\gamma _E$ is replaced by $\gamma _E=\gamma _{se}+ \frac{\gamma _{sr}\gamma _{re}}{1+\gamma _{sr}+\gamma _{re}}$ for MRC combining and $\gamma _E=\max \lbrace \gamma _{se}, \gamma _{sre} \rbrace$ for SC combining.

Derivation of exact ergodic secrecy rate seems mathematically intractable assuming correlation of SNRs at the eavesdropper and destination. Even getting closed form upper, lower bounds or approximate secrecy rate as was obtained for secrecy outage probability in Section 4 is also mathematically intractable. The particular case when quality of the S–R link is very good i.e. $1/\beta _{sr}>>1/\beta _{rd}$ or $1/\beta _{sr}>>1/\beta _{re}$, we can assume that the SNR at the E and D are independent. Assuming further overall high SNR scenario the secrecy rate in (3) can be reduced to

$$\begin{aligned} C_{S} = {\frac{1}{2}\left[\log _2\left(\frac{\gamma _{M} }{\gamma _{E} }\right)\right]}^+. \end{aligned}$$

(41)

The ergodic secrecy rate can be evaluated by imposing positive secrecy, i.e. $\gamma _M>\gamma _E$, as

$$\begin{aligned} \bar{C}_S = \frac{1}{2\ln 2} \int _0^\infty \int _y^\infty \left[\ln \left(x\right)-\ln \left(y \right)\right] f_{\gamma _M}(x)f_{\gamma _E}(y)dxdy. \end{aligned}$$

(42)

To find the distribution $f_{\gamma _M}(x), f_{\gamma _E}(y)$ we use $\gamma _{sre} \approx \min {\left(\gamma _{sr},\gamma _{re}\right)}, \gamma _{M} \approx \min {\left(\gamma _{sr},\gamma _{rd}\right)}$ as is used in Section 4. The distribution of the minimum of the two independent exponentially distributed RV is exponential. The parameter of the resulting exponential RV is the addition of the parameters of the input exponentials. Hence $\gamma _{sre}$ and $\gamma _M$ are exponential RV with parameters $(\beta _{sr}+\alpha _{re})$ and $(\beta _{sr}+\beta _{rd})$ [29].

5.1 MRC at the Eavesdropper

In this section $\gamma _E$ is the SNR at the output of a MRC combiner. The distribution of $\gamma _E$ can then be obtained by finding the distribution of the addition of the two independent RVs $\gamma _{sre}$ and $\gamma _{se}$. The distribution of $\gamma _E$ can then be obtained by finding distribution of the addition of the two independent exponentially distributed RVs with different parameters following [30] as

$$\begin{aligned} f_{\gamma _E}(y)&=\frac{\alpha _{se}\left(\beta _{sr}+\alpha _{re}\right)}{\left(\beta _{sr}+\alpha _{re}\right)-\alpha _{se}} e^{-\alpha _{se} y} + \frac{\alpha _{se}\left(\beta _{sr}+\alpha _{re}\right)}{\alpha _{se}-\left(\beta _{sr}+\alpha _{re}\right)} e^{-\left(\beta _{sr}+\alpha _{re}\right)y}. \end{aligned}$$

(43)

The solution of (42) can be obtained in closed form as

$$\begin{aligned} \bar{C}_S^{MRC} = \frac{1}{2\ln 2}\left[\frac{\alpha _{se}\ln \left(1+\frac{\beta _{sr}+\alpha _{re}}{\beta _{sr}+\beta _{rd}}\right)}{\left(\beta _{sr}+\alpha _{re}\right)-\alpha _{se}} + \frac{\left(\beta _{sr}+\alpha _{re}\right)\ln \left(1+\frac{\alpha _{se}}{\beta _{sr}+\beta _{rd}}\right)}{\alpha _{se}-\left(\beta _{sr}+\alpha _{re}\right)}\right], \end{aligned}$$

(44)

While deriving (44), we use the solutions of integrals from 1.6.10.3, page 249 of [31] and 2.5.3.1, page 71 of [32]. The superscript MRC in (44) denotes the ergodic secrecy rate for MRC combiner at the eavesdropper.

5.2 SC at the Eavesdropper

In this section $\gamma _E$ is the SNR at the output of a SC combiner. The distribution is to be found by finding maximum of the two independent exponentially distributed RVs. The CDf can be obtained as

$$\begin{aligned} F_{\gamma _E}(y)&=\mathbb {P}\left[\max \left(\gamma _{se},\gamma _{sre}\right)\le y\right]=\mathbb {P}\left[(\gamma _{se}\le y\right]\mathbb {P}\left[\gamma _{sre}\le y\right)]\nonumber \\&=\left(1-\exp \left(-\alpha _{se}y\right)\right)\left(1-\exp \left(-(\beta _{sr}+\alpha _{se})y\right)\right). \end{aligned}$$

(45)

The PDF can be obtained by differentiating (45) as

$$\begin{aligned} f_{\gamma _E}(y)&= \alpha _{se}\exp (-\alpha _{se} y)+(\beta _{sr}+\alpha _{se}) \exp (-(\beta _{sr}+\alpha _{se})y) \nonumber \\&-\,(\alpha _{se}+\beta _{sr}+\alpha _{se}) \exp (-(\alpha _{se}+\beta _{sr}+\alpha _{se})y) \end{aligned}$$

(46)

The ergodic secrecy rate can be obtained by evaluating (42) as

$$\begin{aligned} \bar{C}_S^{SC} = \frac{1}{2\ln 2}\left[\ln \left(1+\frac{\alpha _{se}}{\beta _{sr}+\beta _{rd}}\right)+ \ln \left(1+\frac{\beta _{sr}+\alpha _{re}}{\beta _{sr}+\beta _{rd}}\right)-\ln \left(1+\frac{\alpha _{se}+\beta _{sr}+\alpha _{re} }{\beta _{sr}+\beta _{rd}}\right)\right] \end{aligned}$$

(47)

Same integral solutions from 1.6.10.3, page 249 of [31] and 2.5.3.1, page 71 of [32] are used. The superscript SC in (47) denotes the ergodic secrecy rate for SC combiner at the eavesdropper.

6 Asymptotic Analysis

In this section, asymptotic analysis of approximate secrecy outage probability and ergodic secrecy rate is provided for the analysis done in the sects. 4 and 5. Asymptotic analysis gives simpler expression as a function of constituent parameters. It helps easily predict the behaviour of the secrecy outage probability with the variation of the parameters at a very high SNR.

6.1 Secrecy Outage Probability

The behaviours of the equations from (28) to (38) are difficult to analyze in terms of its constituent parameters. The behaviour is important whether the average SNRs of S–R and R–D links are equal or not. When these two are equal, we call it as balanced case and when unequal we call as unbalanced case. Asymptotic analysis is achieved by tending the average SNR of both the S–R and R–D links to infinity keeping them equal in the balanced case. In the unbalanced case either of the S–R or R–D link’s average SNR tending to infinity keeping other fixed. For both the balanced and unbalanced cases average SNRs of S–E and R–E links are kept fixed. Balanced or unbalanced cases are important from the perspective of power allocation to the S and R. For example if average channel gains of S–R and R–D links and noise power at each nodes are identical then allocating different transmit powers to S and R will create unbalance. Unbalance can also occur if there are unequal distances between nodes with same transmit and noise powers.

Asymptotic analysis is shown for both the MRC and SC diversity combining techniques done in (31) and (38) respectively. Asymptotic analysis for upper and lower bounds are similar and skipped. For the balanced case, we evaluate asymptotic expression by tending $1/\beta _{sr}=1/\beta _{rd}=1/\beta \rightarrow \infty$ or ${\beta }\rightarrow 0$. This scenario can occur if S and D are getting closer to R by the same amount compared to the eavesdropper. This scenario can also occur with increased transmit power to S and R keeping other parameters fixed. While evaluating asymptotic analysis, we find constant terms in the numerator vanishes. Then our task reduces to collecting all coefficients of $\beta$ in the numerator and constant term not involving $\beta$ from the denominator. Here we have assumed that higher order terms of $\beta$ approaches zero much faster than $\beta$. All the asymptotic expressions are evaluated in this paper follow the same method described above. After some mathematical manipulations it can be shown that asymptotic expression of approximate secrecy outage in (31) when eavesdropper does the MRC diversity combining is

$$\begin{aligned} P_o^{(AS)}(R_s)\Big |_{\text {MRC}}^{\text {Balanced}}= \frac{2}{\frac{1}{\beta }}\left[\rho \left(\frac{1}{\alpha _{se}}+\frac{1}{\alpha _{re}}\right)+(\rho -1)\right]. \end{aligned}$$

(48)

AS is used for asymptotic expression and $(\cdot )|_{\text {MRC}}^{\text {Balanced}}$ is used to identify that the term is for balanced case in MRC combining. Asymptotic expression of approximate secrecy outage in (38) for SC diversity combining is

$$\begin{aligned}&P_o^{(AS)}(R_s)\Big |_{\text {SC}}^{\text {Balanced}} =\frac{2}{\frac{1}{\beta }}\left[\rho \left(\frac{1}{\alpha _{se}}+\frac{1}{\alpha _{re}}\right)+(\rho -1) -\frac{\rho }{\alpha _{se}+\alpha _{re}}\right]. \end{aligned}$$

(49)

Asymptotic analysis for unbalanced case is similar to balanced case. Contrary to balanced case, constant term does not vanishes in the numerator which gives a constant term in the asymptotic expression. For the unbalanced case we first consider $1/\beta _{rd}$ is fixed and $1/\beta _{sr}=1/\beta \rightarrow \infty$. This situation can arise if source is getting closer to the relay keeping other nodes fixed or with unequal power distribution. The asymptotic expression of approximate secrecy outage probability in (31) for MRC is

$$\begin{aligned}&P_o^{(AS)}(R_s)\Big |_{\text {MRC}}^{\text {Unbalanced}}= 1-\frac{\alpha _{se} \alpha _{re} e^{-(\rho -1)\beta _{rd}}}{\left(\beta _{rd} \rho +\alpha _{se}\right)\left(\beta _{rd} \rho +\alpha _{re}\right)} +\frac{1}{\frac{1}{\beta }}\left[\frac{\rho \left(2\rho \beta _{rd}+\alpha _{se}+\alpha _{re}\right)+\alpha _{se}\alpha _{re}\left(\rho -1\right) e^{-\left(\rho -1\right)\beta _{rd}}}{\left(\rho \beta _{rd}+\alpha _{se}\right)\left(\rho \beta _{rd}+\alpha _{re}\right)}\right]. \end{aligned}$$

(50)

When SC is done, approximate secrecy outage probability in (38) approaches a constant value of

$$\begin{aligned} P_o^{(AS)}(R_s)\Big |_{\text {SC}}^{\text {Unbalanced}}= 1&-\frac{\alpha _{se} e^{-(\rho -1)\beta _{rd}}}{\left(\beta _{rd} \rho +\alpha _{se}\right)} -\frac{\alpha _{re} e^{-(\rho -1)\beta _{rd}}}{\left(\beta _{rd} \rho +\alpha _{re}\right)} -\frac{\left(\alpha _{se} +\alpha _{re}\right) e^{-(\rho -1)\beta _{rd}}}{\left(\beta _{rd} \rho +\alpha _{se} +\alpha _{re}\right)}. \end{aligned}$$

(51)

The unbalanced case of $1/\beta _{sr}$ is fixed and $1/\beta _{rd}=1/\beta \rightarrow \infty$, can occur if destination is getting closer to the relay while other nodes are fixed. Asymptotic expression of approximate secrecy outage probability in this case for MRC in (31) is

$$\begin{aligned}&P_o^{(AS)}(R_s)\Big |_{\text {MRC}}^{\text {Unbalanced}}= 1-\frac{\alpha _{se} \alpha _{re} e^{-(\rho -1)\beta _{sr}}}{\left(\beta _{sr} \rho +\alpha _{se}\right)\left(\beta _{sr} \rho +\alpha _{re}\right)}\nonumber \\&\quad +\,\frac{1}{\frac{1}{\beta }}\left[\frac{\rho \left(2\rho \beta _{sr}+\alpha _{se}+\alpha _{re}\right) +\alpha _{se}\alpha _{re}\left(\rho -1\right)e^{-\left(\rho -1\right)\beta _{sr}}}{\left(\rho \beta _{sr}+\alpha _{se}\right)\left(\rho \beta _{sr}+\alpha _{re}\right)}\right.\nonumber \\&\quad \left. +\,\rho \left(\frac{1}{\alpha _{se}}+\frac{1}{\alpha _{re}}\right) \left( 1- \frac{\alpha _{se}\alpha _{re}e^{-\left(\rho -1\right)\beta _{sr}}}{\left(\rho \beta _{sr}+\alpha _{se}\right)\left(\rho \beta _{sr}+\alpha _{re}\right)}\right)\right]. \end{aligned}$$

(52)

For the unbalanced case, when $1/\beta _{sr}$ is fixed and $1/\beta _{rd}=1/\beta \rightarrow \infty$, the asymptotic expression for SC is same as in (51) but $\beta _{rd}$ has to be replaced by $\beta _{sr}$.

In unbalanced case, the asymptotic value reaches a constant. Asymptotic expression can be expressed as a summation of constant and a asymptotically varying term with $\beta$. The asymptotically varying term dominates at low SNR ($1/\beta$) and at high SNR it is insignificant compared to constant term. The asymptotically varying term is shown only for MRC diversity combining. We have skipped others due to space limitations, though asymptotically varying term can be achieved for all the diversity combining techniques.

Remark 3

By comparing (48) with (49) it can be seen that to achieve same secrecy outage probability, MRC requires higher main channel SNR than SC for a given parameter. This is because, MRC is the optimal diversity combining technique for E. By doing MRC, E achieves better performance than SC.

We now check how this relative SNR difference between MRC and SC behaves with required secrecy rate ($\rho =2^{2R_s}$). By taking the difference of SNRs in decibels (dB) of MRC and SC from (48) and (49) for $\rho _i$ where $i=1, 2$, we get,

$$\begin{aligned} G_i&= \frac{1}{\beta _{MRC}^i}\bigg| _\text {dB}-\frac{1}{\beta _{SC}^i}\bigg|_\text {dB} = -10 \log _{10}\left[1-\frac{\frac{\rho _i}{\alpha _1+\alpha _2}}{\rho _i\left(\frac{1}{\alpha _1}+\frac{1}{\alpha _2}\right)+\left(\rho _i-1\right)}\right]. \end{aligned}$$

(53)

Here $1/\beta _{MRC}^i|_\text {dB}$ and $1/\beta _{SC}^i|_\text {dB}$ are the average SNRs in dB corresponding to $\rho _i$ for MRC and SC respectively. $G_1$ will be greater than $G_2$ if following happens

$$\begin{aligned} \frac{\frac{\rho _1}{\alpha _1+\alpha _2}}{\rho _1\left(\frac{1}{\alpha _1}+\frac{1}{\alpha _2}\right)+\left(\rho _1-1\right)}&> \frac{\frac{\rho _2}{\alpha _1+\alpha _2}}{\rho _2\left(\frac{1}{\alpha _1} +\frac{1}{\alpha _2}\right)+\left(\rho _2-1\right)}\nonumber \\ \Rightarrow \frac{1}{1-\frac{1}{\rho _1\left( 1+\frac{1}{\alpha _1}+\frac{1}{\alpha _2}\right) }}&> \frac{1}{1-\frac{1}{\rho _2\left( 1+\frac{1}{\alpha _1}+\frac{1}{\alpha _2}\right) }}. \end{aligned}$$

(54)

From (54) it is very clear that $G_1>G_2$ only if $\rho _1< \rho _2$. This says that, in order to achieve the same secrecy outage probability of SC, MRC needs relatively higher main channel SNR when required secrecy rate is low than the case when required secrecy rate is high.

Remark 4

We compare (50) and (52) for MRC combining. The secrecy outage probability achieves the same constant value irrespective of unbalance caused due to fixed average SNR in S–R or R–D. The constants are the same function of $\beta _{sr}$ or $\beta _{rd}$. This shows that either of the S–R or R–D link quality can equally serve as a bottleneck for achievable secrecy even if we infinitely increase the SNR of the other link.

Remark 5

The reason of remark 4 is not quite obvious as the system is not symmetric with respect to variation in either of the S–R or R–D link. Variation in $\gamma _{rd}$ only affects $\gamma _M$ but variation in $\gamma _{sr}$ affects both the $\gamma _M$ and $\gamma _E$. It has to be noted that we provide an approximation to the secrecy outage probability as exact solution is intractable. The derivation approximated both the S–R–E and S–R–D link SNRs by the minimum of the constituent link SNRs. So, when the S–R link average SNR is higher than that of the R–E link (it has to be maintained to achieve reasonable secrecy outage), probability of getting R–E link increases. Similarly between S–R and R–D links, if S–R link average SNR is higher, then probability of R-D being selected is higher or vice versa. Depending on either of the unbalance cases whether S–R or R–D is selected, $\gamma _M$ is symmetric to both the cases but for the $\gamma _E$, it is only R–E for most of the cases. This makes $\gamma _E$ symmetric to the variations on $\gamma _{sr}$ or $\gamma _{rd}$. Hence makes the system symmetric for both the unbalanced cases.

Remark 6

The variable terms in (50) and (52) are not the same function of $\beta _{sr}$ or $\beta _{rd}$. At higher $1/\beta _{sr}$, the two equations are quite same as second summation term inside the brackets in (52) will vanish at higher $1/\beta _{sr}$. This verifies that the system is not actually symmetric but as $1/\beta _{sr}$ increases it tends to a symmetric system as pointed out in remark 5.

6.2 Ergodic Secrecy Rate

The ergodic secrecy rate in Section 5 approximates the actual ergodic secrecy rate when average SNR of the S–R link, $1/\beta _{sr}$, is high. In such a unbalance case when $1/\beta _{sr}$ is fixed and $1/\beta _{rd}$ tends to infinity the asymptotic values can be derived by simply putting $\beta _{rd} = 0$ in (44) and (47) as

$$\begin{aligned} \bar{C}_S^{MRC}= & {} \frac{1}{2\ln 2}\left[\frac{\alpha _{se}\ln \left(1+\frac{\beta _{sr}+\alpha _{re}}{\beta _{sr}}\right)}{\left(\beta _{sr}+\alpha _{re}\right)-\alpha _{se}} + \frac{\left(\beta _{sr}+\alpha _{re}\right)\ln \left(1+\frac{\alpha _{se}}{\beta _{sr}}\right)}{\alpha _{se}-\left(\beta _{sr}+\alpha _{re}\right)}\right], \end{aligned}$$

(55)

$$\begin{aligned} \bar{C}_S^{SC}= & {} \frac{1}{2\ln 2}\left[\ln \left(1+\frac{\alpha _{se}}{\beta _{sr}}\right)+ \ln \left(1+\frac{\beta _{sr}+\alpha _{re}}{\beta _{sr}}\right)-\ln \left(1+\frac{\alpha _{se}+\beta _{sr}+\alpha _{re} }{\beta _{sr}}\right)\right], \end{aligned}$$

(56)

respectively. The asymptotic expressions tend to constant quantities with respect to $1/\beta _{rd}$.

7 Results

This section compares the analytical results derived in this paper with the simulated ones. In the figures, A is denoted as the analysis, S is denoted as the simulation. LB and UB are the lower bound and upper bound respectively. Results are drawn assuming direct link and relayed link qualities to eavesdropper are same i.e. $1/\alpha _{se}=1/\alpha _{re}=1/\alpha$. This is reasonable to assume as eavesdropper may be equidistant from source and destination. The results with different eavesdropper channel qualities are similar. In all the figures secrecy outage probabilities, $P_o(R_s)$, are compared. The unit of required threshold secrecy rate, $R_s$, is assumed to be bits per channel use (bpcu). Required threshold secrecy rate, $R_s$, is assumed as low as 0.1 and as high as 2.0 to cover reasonable span of secrecy rate. In the figures we have dropped all the superscripts from $P_o(R_s)$ which was used to distinguish various schemes.

Fig. 2

Lower and upper bounds of secrecy outage probability for MRC diversity combining at the eavesdropper

Fig. 3

Lower and upper bounds of secrecy outage probability for SC diversity combining at the eavesdropper

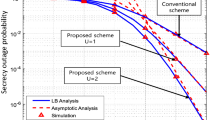
In Fig. 2, LB and UB of $P_o(R_s)$ for MRC diversity combining are plotted as a function of main channel SNR $1/\beta$, for the balanced case of $1/\beta _{sr}= 1/\beta _{rd}=1/\beta$. Results are drawn from (28), (29) and (30) respectively which are developed in the Section 4. The figures are plotted for low and high rate requirement of $R_s=0.1, 2.0$ respectively for two different eavesdropper channel qualities $1/\alpha =3, 9$ dB. Figure  3 shows bounds for SC diversity combining derived in (35), (36) and (37) for the same set up of Fig. 2. When $R_s>0.5$ or $\rho >2$ we plot $P_o(R_s)$ from (28) and (35) while from (29) and (36) when $R_s\le 0.5$ or $\rho \le 2$. These two figures depicts that the LB derived is tight for both the MRC and SC at all rates and all eavesdropper channel qualities. Lower bound tends towards simulation as SNR increases. It is also very intuitive to see from the figures that improvement in eavesdropper channel quality degrades the achievable $P_o(R_s)$ for a given rate requirement. Also, higher rate requirement requires higher SNR to achieve same $P_o(R_s)$ for a given eavesdropper channel quality.

Fig. 4

Comparison of secrecy outage probabilities of SC and MRC diversity combining for unbalanced case

Figure 4 compares the approximate $P_o(R_s)$ of the MRC and SC diversity combining techniques obtained from (31) and (38) for the unbalanced case. The unbalanced case of $1/\beta _{sr}$ is fixed is considered and results are obtained by varying $1/\beta _{rd}=1/\beta$ keeping $1/\alpha =3$ dB. The results are shown for required rate of $R_s=0.5, 2$, when $1/\beta _{sr}=40$ dB is relatively low and for required rate of $R_s=0.1, 1.5$, when $1/\beta _{sr}=60$ dB is relatively high. We find that both the MRC and SC curves saturates to a fixed value drawn by horizontal dashed line. This confirms the analysis in Section 6, that tells either of the two hop in main channel can limit the secrecy outage performance. This dashed lines are the constant value derived at (52) and (51) for MRC and SC respectively. For the sake of clarity dashed lines of MRC is only shown in the figure. The dashed line for $1/\beta _{sr}=60$ dB is not visible in the figure due to the limits in the vertical axis. The asymptotically varying term in (52) is shown by solid straight line. It interestingly meets the dashed line at the $1/\beta =40$ dB, which is exactly the same fixed $1/\beta _{sr}$ for which the curves are drawn. This signifies that the saturation starts as soon as SNR of the R–D link passes the fixed SNR of the S–R link. The saturation of curves can not be seen in Figs. 2 and 3 as neither of the main hop channel SNR is fixed in balanced case. As proposed in the Section 4, the curves obtained by approximate analysis exactly matches for all values of $R_s$ with the simulation, when S–R link quality is very good i.e. high average SNR of $1/\beta _{sr}=60$ dB.

Fig. 5

Comparison of secrecy outage probabilities of SC and MRC diversity combining for balanced case

Figure 4 depicts the scenario in which results are obtained assuming S–R link SNR is very high thus matches well with the simulation. Now the results obtained for $1/\beta _{sr}$ is high is applied when S–R and R–D link average SNR is balanced. The performance is plotted in Fig. 5. The figure is obtained for low and high rate of $R_s= 0.1, 2$ when $1/\alpha =3, 9$ dB. Those matches fairly well with the simulation but not as good as the case when plotted for $1/\beta _{sr}$ is high. The asymptotic expression for MRC and SC in (48) and (49) respectively are also plotted by solid straight line. Careful observation may reveal that for a given $1/\alpha$, the gap between MRC and SC asymptotes are more when $R_s$ is low than when $R_s$ is high. This confirms our derivation at (54) that $G_1>G_2$ i.e. MRC needs relatively higher SNR at low $R_s$ to achieve same secrecy outage of SC, than at high $R_s$.

Fig. 6

Comparison of ergodic secrecy rate for SC and MRC diversity combining in unbalanced case

In Fig. 6 we show the ergodic secrecy rate comparison for SC and MRC diversity combining techniques when unbalance is created by fixing $1/\beta _{sr}$ and increasing $1/\beta _{rd}=1/\beta$. Two cases are considered when $1/\beta _{sr}$ is very high i.e. $1/\beta _{sr}=60$ dB and relatively low i.e. $1/\beta _{sr}=40$ dB. As discussed in Section 5 when $1/\beta _{sr}$ is very high, the analysis with independent assumption matches very well with the simulation. This can be seen from the graph for $1/\beta _{sr}=60$ dB at both the $1/\alpha _{se} =3$ dB and $1/\alpha _{se} =12$ dB. When $1/\beta _{sr}$ is relatively low i.e. $1/\beta _{sr} =40$ dB conformation between analysis and simulation is fine, but not as good as it was for $1/\beta _{sr}=60$ dB. It can be seen from the figure that when unbalance is created by fixing $1/\beta _{sr}$ to a predefined value, curves saturate to a constant value as shown by the horizontal dashed line. Dashed lines are due to the constant derived in (55) and (56) for MRC and SC respectively. It can easily be verified from (44) and (47) that if unbalance is created by fixing $1/\beta _{rd}$ to a predefined value and increasing $1/\beta _{sr}$, the ergodic secrecy rate saturates to the same constant value. It can be verified by proceeding the similar way as is done in Section 6.2. This proves that by fixing a predefined average SNR value to any of the dual-hop link, ergodic secrecy rate can not be increased beyond a certain value by increasing the other hop link average SNR infinitely. This observation is similar to what is seen for secrecy outage probability in Fig. 4. It can also be seen that when quality of the link towards eavesdropper improves, the gap between SC and MRC curves decreases. This proves that the MRC requires more average SNR, $1/\beta _{rd}$, to achieve the same performance of SC when eavesdropper link quality gradually decreases.

8 Conclusions

A dual-hop AF relay system is considered in which an eavesdropper diversity combines both the direct and relayed communication from the source. Two diversity combining techniques, MRC and SC, is considered in this work for secrecy outage probability and ergodic secrecy rate analysis. Upper and lower bounds on secrecy outage probability are obtained. Approximate secrecy outage probability and ergodic secrecy rate is obtained assuming source–relay link average SNR is high. Asymptotic analysis of the approximate secrecy outage probability and ergodic secrecy rate is provided. It is observed that lower bound for secrecy outage is tight and tends towards simulated secrecy outage probability as SNR increases. It is found that for a given parameter, SC has better secrecy outage and ergodic secrecy rate performance than MRC. It is seen that, MRC requires relatively higher SNR to achieve same secrecy outage performance of SC at lower rate than at higher rate. MRC also requires relatively higher average SNR to achieve same ergodic secrecy rate when eavesdropper link quality is low. It is interesting to note that either of the source–relay or relay--destination link quality can serve as a bottleneck for both secrecy outage and ergodic secrecy rate, even if the other link average SNR is infinitely increased.

Appendices

Appendix 1: Proof of Proposition 1

Proof

CDF and the PDF of the random variable T can be found in [16, 17]. For the convenience of the reader we deduce the the CDF of the RV T conditioned on $X, F_{T|X}(t|x)$, here again. From the definition of CDF we get

$$\begin{aligned} F_{T|X}(t|x)&= \mathbb {P}[\min (x,y)\le t|x]\nonumber \\&=1-\mathbb {P}[\min (x,y)> t|x]\nonumber \\&=1-\mathbb {P}[x> t|x]\mathbb {P}[y> t|x]\nonumber \\&=\left\{ \begin{array}{ll} 1-\mathbb {P}[y> t|x]&{} \quad t < x\\ 1 &{} \quad t \ge x\\ \end{array} \right. . \end{aligned}$$

(57)

We can write (57) from the fact that

$$\begin{aligned} \mathbb {P}[x> t|x]=\left\{ \begin{array}{ll} 1 &{} \quad t < x\\ 0 &{} \quad t \ge x\\ \end{array} \right. . \end{aligned}$$

(58)

As X and Y are independent, by simply using CDF of RV Y i.e. CDF of exponential distribution in (57) we get the CDF of the a RV T as

$$\begin{aligned} F_{T|X}(t|x)=\left\{ \begin{array}{ll} 1-e^{-\beta _yt} &{} \quad t < x\\ 1 &{} \quad t \ge x\\ \end{array} \right. . \end{aligned}$$

(59)

By differentiating (59) with respect to t we get the PDF as

$$\begin{aligned} f_{T|X}(t|x)=\left\{ \begin{array}{ll} \beta _ye^{-\beta _yt} &{} \quad t<x\\ \delta (t-x)e^{-\beta _yx} &{}\quad t \ge x\\ \end{array} \right. . \end{aligned}$$

(60)

From the definition, MGF expressed in (9) can be found by simply evaluating the following integrals

$$\begin{aligned} M_{T|X}(s|x)&=\int _0^x \beta _y e^{-(\beta _y-s)t}dt + \int _ x^\infty e^{-\beta _y x} e^{st} \delta (t-x)dt. \end{aligned}$$

(61)

Appendix 2: Proof of Corollary 1

Proof

Directly following the proof of proposition 1, the CDF is obtained in [16, 17] as

$$\begin{aligned} F_T(t|x) =\left\{ \begin{array}{ll} 1-e^{-2\beta _{y}t} &{} \quad t < \frac{x}{2}\\ 1 &{} \quad t \ge \frac{x}{2}\\ \end{array} \right. . \end{aligned}$$

(62)

The corresponding PDF is derived in [16, 17] by differentiating (62) as

$$\begin{aligned} f_T(t|x) =\left\{ \begin{array}{ll} 2\beta _{y} e^{-2\beta _{y}t} &{} \quad t < \frac{x}{2}\\ \delta \left(t-\frac{x}{2}\right)e^{-\beta _{y}x} &{} \quad t \ge \frac{x}{2}\\ \end{array} \right. . \end{aligned}$$

(63)

Using standard derivation of MGF as in (61), we can find MGF of RV T in (10).