1 Introduction

The need of high data rate and continuous services is increasing day by day with the proliferation of wireless communication systems [1,2,3,4]. The quality of a wireless communication system is severely degraded by a physical phenomenon known as fading [5,6,7]. Multipath and shadowing are two detrimental effects on the quality of radio signals received during wireless propagation [8, 9]. Therefore, there is a requirement of precise modelling of the wireless system for faithful realization of the earlier services and to get improved and reliable performance. In recent years, numerous fading models were proposed by researchers across the globe to meticulously design the wireless systems [10,11,12,13,14,15,16]. The signals from various components or routes meet at the receiver with different gains and phases contribute in fading, is known as multipath fading [17,18,19]. On the other hand, the shadowing results in low speed changes of the mean signal power, which is attributed by the topographical obstacles such as trees, buildings along the path of the transmitter (Tx) and receiver (Rx) [20,21,22,23,24,25,26,27,28,29,30].

The short term (small scale) signal fluctuations also termed as multipath fading are modelled by the well-known models such as Rayleigh, Rice (Nakagami-n), Hoyt, Nakagami-m, and Weibull distributions. More specifically, these models are used for modelling of non-line-of-sight (NLOS) scenarios, whereas Rician is used for line-of-sight (LOS) components. In past years, researchers have proposed some new versatile and flexible models namely \({\kappa -\mu }\), \({\eta -\mu }\) and \({\alpha -\mu }\) to precisely analyze the effect of small scale fading on the wireless channel. Furthermore, these models can be modified to other convincing multipath distributions like Rayleigh, Rice (Nakagami-n), one-sided Gaussian distributions by simple remodelling the fading parameters [14, 17,18,19].

In the last few decades, the log-normal (LN) distribution was the high priority choice of the research community to model the effect of shadowing in the wireless propagation environment [6]. A great magnitude of research has been done so far in the domain of wireless system performance analysis such as bit error rate and channel capacity analysis over LN distribution [20,21,22,23,24,25,26,27]. The LN distribution also finds its usage in satellite communication, radar communication to analyze the effect of fading and also in the field of statistics [24, 25]. Despite of the wide popularity of the LN, it is not much used by the researchers in composite fading statistics due to its difficult mathematical representation which results in numerical intractability [20, 27, 28]. A substitute of LN known as Gamma distribution, used for modelling of shadowing effect in realistic environment such as \({\kappa -\mu /}\)Gamma, \({\eta -\mu /}\)Gamma have been proposed in [31,32,33,34,35,36]. In [37] and [38], authors have investigated the performance of communication system where shadowing is modelled with the use of gamma distribution. Although the Gamma distribution has well ordered mathematical structure, it does not match the long-tailed characteristics of LN distribution especially at the high standard deviations [6].

Another distribution which shows near harmony with the LN at high standard deviations is inverse gaussian (IG) distribution [28, 39]. Although IG is highly suitable with the LN distribution, but it fails in finding the exact closed-form module for the analysis of wireless channel such as optimum rate adaptation (ORA) capacity analysis and probability density function (PDF) with selection combining diversity scheme [28]. Most of the composite fading structures proposed by the research community with gamma and IG distributions are expressed in either finite/infinite series representations or sum of mixture of Gamma and IG distributions, respectively [6]. Recently, a new model which ensues the long-tailed characteristics of LN distribution and has a sound competency over the gamma and IG, known as inverse gamma (IGamma) distribution is discussed in [6, 40, 41]. Apart from the communication, the utility of the IGamma is also exploited in other fields such as statistics, mathematics, and science [42]. In [29], authors have justified the utility of inverse gamma in investigating the performance of wireless system where shadowing is predominant. Authors also used the empirical measurements for performing set of goodness-of-fit tests which supports the claim of inverse gamma distribution for characterizing the shadowing effect in wireless channel modelling. The research has been validated with the help of the Cramer-von Mises test. In [6], authors have performed the comparison of inverse gamma distribution with other shadowed fading distributions based on the moment matching methods together with the Kullback–Leibler divergence for different fading scenarios.

The joint effect of shadowing and multipath must be taken into consideration for the realistic modelling of the digital communication systems. In such practical scenarios, composite fading models are best fitted to analyze the outcomes of the communication system in a more realistic environment where multipath fading and shadowing co-exists [14]. O. S. Badarneh in [43] suggested \(\alpha\)–\(\eta\)–\(\mathcal {F}\) and \(\alpha\)–\(\kappa\)–\(\mathcal {F}\) composite fading distributions. In [44], authors have evaluated the capacity of the channel over the \(\mathcal {F}\) composite fading channel. The performance analysis of mobile receiver with random way point mobility in internet of thing network is examined over composite \(\mathcal {F}\) fading model by Badarneh et al. in [45]. In [46], authors have used Fisher-Snedecor \(\mathcal {F}\) composite fading models for analysing the performance of a Non-Orthogonal Multiple Access (NOMA) network. Bithas et al. in [47] have suggested a new composite fading model to describe the received signal characteristics in Unmanned Aerial Vehicle (UAV)-enabled communications scenario where shadowing co-exists with the single and double-scattering propagation.

Open literature is flooded with many composite fading models and every model has its merits and demerits. A single fading model cannot be justifiable for each fading scenario. The composite fading distributions available in the literature lag in rendering extensive modelling of the fading phenomenon. Moreover, there have been various composite fading models based on different shadowing and multipath fading distributions. However, these models lead to the ambiguity in various performance matrices of interest. In last few years some composite models using IGamma for characterizing shadowing such as the KMIG and EMIG have been proposed by the researchers [14, 15].

The fundamental statistics of KMIG and EMIG composite fading models are explored in [40, 41], where the authors have supported their work by the vast experimental measurements in terms of traditional and growing wireless applications. These applications includes vehicular and wearable communication systems. The tractable solutions of various analyses are also possible due to their straight mathematical structure. In [41, 48, 49], the analytical expressions for ergodic capacity and coherent bit error rate for multiple amplitude modulation format are discussed over aforementioned composite fading channels. The results are obtained in infinite summation terms, thus truncation error is also included.

To the best of our knowledge, the available literature has a huge scope in extensive performance investigation of the digital communication system with inverse gamma shadowing based composite fading models. Keeping in view of the above facts, the following performance investigation of the digital communication system are carried outs in this work:

  • Unified analytical expressions for the average SEP with coherent and non-coherent modulation schemes.

  • The earlier proposed formulations contain infinite series representation, thus truncation error is also provided.

  • Asymptotic analysis is also provided for previously discussed performance matrices along with coding and diversity gains.

  • Analytical expressions for the ORA, CIFR, and TIFR channel capacity are derived.

  • The expressions for ORA capacity contain single infinite summation term, whereas the expressions proposed in [41, 48] have multiple summation terms and valid for integer parameters of \(m_s\).

  • The closed-form results obtained under CIFR policy do not show any impact of shadowing as the mathematical notations are independent of shadowing parameter \(m_s\).

  • Channel capacity analysis is also done with low and high power to visualise and subsequently gain more physical insight to the system performance.

  • Further, ORA and CIFR results are simplified under different fading conditions.

The remaining part of work is organized as follows. The structure of KMIG and EMIG composite fading models are explained in the Sect. 2. Performance evaluation under average symbol error probability of composite fading distributions are given in Sect. 3. Asymptotic analysis is carried out in Sect. 4. Channel capacity analysis under various adaptive schemes like ORA, CIFR, and TIFR is given in Sect. 5. Section 6 deals with the result and discussion . Finally, the concluding remark has been made in Sect. 7.

2 Statistics of KPIG and EMIG composite fading models

For \(\kappa\), \(\mu\), \(m_s\), \(\gamma\), \(\bar{\gamma }\) \(\in ~ R^+\), the instantaneous signal-to-noise-ratio (SNR) PDF of KPIG composite distribution is given as [40]

$$\begin{aligned} \begin{aligned} f_{Y}(\gamma )=\dfrac{\exp \left( -\mu \kappa \right) ~\mu ^{\mu }~{\left( \kappa +1\right) }^{\mu }~{\left( m_{s}\bar{\gamma }\right) }^{m_{s}}~\gamma ^{\mu -1}}{B{\left( m_{s},\mu \right) }~\left[ \mu \left( \kappa +1\right) \gamma +m_{s}\bar{\gamma }\right] ^{m_{s}+\mu }}\\\times \, {_1}{F_1}\left[ m_{s}+\mu ;\mu ;\dfrac{\mu ^{2}\kappa {(\kappa +1)\gamma }}{\mu {(\kappa +1)\gamma +m_{s}\bar{\gamma }}}\right] \end{aligned} \end{aligned}$$
(1)

where B(.) signifies the Beta function [50, Eq. (8.384.1)] and \({{_1}{F_1}(.;.;.)}\) denotes the confluent hypergeometric function [50, Eq. (9.210.1)]. Invoking the identity [51, Eq. (07.20.02.0001.01)], (1) can be re-written as

$$\begin{aligned}&f_{Y}(\gamma )=\sum \limits _{r=0}^{\infty }\nonumber \\&\quad \dfrac{{(m_{s}+\mu )_{r}}~{(\mu \kappa )^{r}}~\exp \left( -\mu \kappa \right) ~\mu ^{\mu +r}~{\left( \kappa +1\right) }^{\mu +r}~{(m_{s}\bar{\gamma })^{m_{s}}}~{\gamma ^{\mu +r-1}}}{{{r}{!}}~{(\mu )_{r}}~{B(m_{s},\mu )}~\left[ \mu \left( \kappa +1\right) \gamma +m_{s}\bar{\gamma }\right] ^{m_{s}+\mu +r}} \end{aligned}$$
(2)

where \({(.)_r}\) represents the Pochhammer symbol [51, Eq. (06.10.02.0001.01)].

For \(\eta\), \(\mu\), \(m_s\), \(\gamma ,\bar{\gamma }\) \(\in ~ R^+\), the instantaneous SNR PDF of EMIG composite distribution is expressed as [40, Eq. (13)]

$$\begin{aligned} \begin{aligned}&f_{Y}(\gamma )=\dfrac{2^{2\mu }~\mu ^{2\mu }~h^{\mu }~{(m_s\bar{\gamma })}^{m_s}~{\gamma }^{2\mu -1}}{B(m_s,2\mu )~(2\mu h\gamma +m_s\bar{\gamma })^{m_s+2\mu }}~\\&\quad \times \,{_2}{F_1}\left( \frac{m_s+2\mu }{2},\frac{m_s+2\mu +1}{2};\frac{2\mu +1}{2};\frac{(2\mu H\gamma )^{2}}{(2\mu h\gamma +m_s\bar{\gamma })^{2}}\right) \end{aligned} \end{aligned}$$
(3)

By utilising [51, Eq. (07.20.02.0001.01)], the PDF given by (3) can be re-written as

$$\begin{aligned}&f_{Y}(\gamma )=\sum \limits _{r=0}^{\infty }\nonumber \\&\quad \dfrac{(\frac{m_s+2\mu }{2})_{r}~(\frac{m_s+2\mu +1}{2})_{r}~(2\mu H \gamma )^{2r}~2^{2\mu }~\mu ^{2\mu }~h^{\mu }~{(m_s\bar{\gamma })}^{m_s}~{\gamma }^{2\mu -1}}{{r}!~(\frac{2\mu +1}{2})_{r}~(2\mu h \gamma +m_s\bar{\gamma })^{2r}~B(m_s,2\mu )~(2\mu h\gamma +m_s\bar{\gamma })^{m_s+2\mu }}~~\dfrac{}{}~~ \end{aligned}$$
(4)

For both distributions, shadowing is associated with the scale parameter given by \(m_{s}\). On the other hand, \(\kappa\) (total dominant to scattered power ratio), \(\mu\) (number of multipath clusters arriving at the receivers), and \(\eta\) have two alternate formates, where in \(format-I\), \(\eta\) is given as the ratio of scattered wave power between the in-phase and quadrature components of each bunch of multipath with \(h={\left( 2+\eta ^{-1}+\eta \right) }/{4}\) and \(H={(\eta ^{-1}-\eta )}/{4}\). On the contrary, \(\eta\) is defined as the correlation coefficient between the in-phase and quadrature components in \(format-II\) [40] with \(h={1}/{(1-\eta ^{2})}\) and \(H={\eta }/{(1-\eta ^{2})}\)) are the multipath parameters. In the present paper, \(format-I\) is used while using the EMIG composite fading distribution for investigating the various performance matrices.

3 Average symbol error probability

The straightforward methodology to derive the average SEP of a fading channel, is to take ensemble average of the conditional SEP over fading SNR, \(\gamma\) [28]

$$\begin{aligned} \bar{P}_e=\int \limits _{0}^{\infty } P_e(\gamma )f_Y(\gamma )d\gamma \end{aligned}$$
(5)

where \(P_{e}(\gamma )\) is \(\gamma\)-dependent instantaneous symbol error rate (SER) of the modulation techniques [6, Eq. (17)].

3.1 ASEP of coherent modulation scheme

The generalised expression of the probability of error for the coherent modulation schemes over additive white Gaussian noise (AWGN) channel is given by [6, Eq. (18)]

$$\begin{aligned} P_{e}{(\gamma )}=A_{P}\,erfc{(\sqrt{B_{P}\gamma })} \end{aligned}$$
(6)

where erfc(.) is the complementary error function and the values of \(A_{P}\) and \(B_{P}\) for different modulation schemes are given in [52, Table I] .

3.1.1 ASEP of coherent modulation scheme for KMIG composite fading model

By putting the value of (2) and (6) into (5), one obtains

$$\begin{aligned} \begin{aligned}&\bar{P}_{e}^{coh}=\sum \limits _{r=0}^{\infty }\dfrac{{(m_{s}+\mu )_{r}}~{(\mu \kappa )^{r}}~\exp \left( -\mu \kappa \right) ~\mu ^{\mu +r}{\left( \kappa +1\right) }^{\mu +r}~{(m_{s}\bar{\gamma })^{m_{s}}}}{{{r}{!}}~{(\mu )_{r}}~{B(m_{s},\mu )}}\\&\quad \times \, {A_{P}}\int \limits _{0}^{\infty }\dfrac{\gamma ^{\mu +r-1}~erfc{(\sqrt{B_{P}\gamma })}}{\left[ \mu \left( \kappa +1\right) \gamma +m_{s}\bar{\gamma }\right] ^{m_{s}+\mu +r}}{d\gamma }~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned} \end{aligned}$$
(7)

Employing simple variable transformation along with the identity [53, Eq. (2.8.3.4)], (7) can be written as

$$\begin{aligned} \begin{aligned}&\bar{P}_{e}^{coh}=\sum \limits _{r=0}^{\infty }\dfrac{{(m_{s}+\mu )_{r}}~{(\mu \kappa )^{r}}~\exp \left( -\mu \kappa \right) {(\mu \left( \kappa +1\right) )}^{\mu +r}~{A_{P}}}{{{r}{!}}~{(\mu )_{r}}~{B(m_{s},\mu )}~{\sqrt{\pi }}~{(\mu +r)}~{(B_{P}m_{s}\bar{\gamma })^{\mu +r}}}~\\&\quad \times \,\varGamma {\left( \dfrac{2\mu +2r+1}{2}\right) }\\&\quad ~{_3}F_{1}\left( m_{s}+\mu +r,\mu +r,\mu +r +\,\frac{1}{2};\mu +r+1;\dfrac{-\mu {(\kappa +1)}}{B_{P}~m_{s}\bar{\gamma }}\right) \end{aligned} \end{aligned}$$
(8)

where \(_pF_q(.,.)\) is the generalised hypergeometric function [50]. The above expression is analytical solution of the average SEP of KMIG composite fading model for different coherent modulation schemes, where \({\varGamma (.)}\) denotes the Gamma function [50, Eq. (8.310.1)]. Truncating the infinite series given by (8) after \({p-1}\) terms, one obtains the following error metric

$$\begin{aligned} \begin{aligned}&T=\sum \limits _{r=p}^{\infty }\dfrac{{(m_{s}+\mu )_{r}}~{(\mu \kappa )^{r}}~\exp \left( -\mu \kappa \right) {(\mu \left( \kappa +1\right) )}^{\mu +r}~{A_{P}}}{{{r}{!}}~{(\mu )_{r}}~{B(m_{s},\mu )}~{\sqrt{\pi }}~{(\mu +r)}~{(B_{P}m_{s}\bar{\gamma })^{\mu +r}}}~\\&\quad \times \,\varGamma {\left( \dfrac{2\mu +2r+1}{2}\right) }\\&\quad ~{_3}F_{1}\left( m_{s}+\mu +r,\mu +r,\mu +r+\,\frac{1}{2};\mu +r+1;\dfrac{-\mu {(\kappa +1)}}{B_{P}~m_{s}\bar{\gamma }}\right) \end{aligned} \end{aligned}$$
(9)

Both Gauss hypergeometric and Gamma functions in (9) have monotonically decreasing nature with respect to r, then (9) can be upper bounded by the inequality as given below with the use of basic definitions of pochhammer symbol and gamma function [54, 55]

$$\begin{aligned} \begin{aligned}&T\le \dfrac{A_{P}~\exp {(-\mu \kappa )}(\mu (\kappa +1))^{\mu }~\varGamma {(\mu +\frac{1}{2})}}{\mu ~\sqrt{\pi }~{B(m_{s},\mu )}~{\left( B_{P}~m_{s}\bar{\gamma }\right) ^{\mu }}}\\&\quad \sum \limits _{r=0}^{\infty }\dfrac{{(m_{s}+\mu )_{r}}~{(\mu +\frac{1}{2})_{r}}}{r{!}~{(\mu +1)_{r}}}\\&\quad \left( \dfrac{{\mu }^{2}\kappa {(\kappa +1)}}{B_{P}~m_{s}\bar{\gamma }}\right) ^{r}\\&\quad \times \, ~{_3}F_{1}\left( m_{s}+\mu +p,\mu +p,\mu +p +\,\frac{1}{2};\mu +p+1;\dfrac{-\mu {(\kappa +1)}}{B_{P}~m_{s}\bar{\gamma }}\right) \end{aligned} \end{aligned}$$
(10)

The infinite series expression in the above equation(10) can be represented in closed-form upper bound with the use of generalized hypergeometric function [50] as follows

$$\begin{aligned} \begin{aligned}&T\le \dfrac{A_{P}~\exp {(-\mu \kappa )}(\mu (\kappa +1))^{\mu }~\varGamma {(\mu +\frac{1}{2})}}{\mu ~\sqrt{\pi }~{B(m_{s},\mu )} ~{\left( B_{P}~m_{s}\bar{\gamma }\right) ^{\mu }}}\\&\quad ~{_2}F_{1}\left( m_{s}+\mu ,\mu +\frac{1}{2};\mu +1,\dfrac{\mu ^{2}{(\kappa +1)}}{B_{P}~m_{s}\bar{\gamma }}\right) \\&\quad \times \, ~{_3}F_{1}\left( m_{s}+\mu +p,\mu +p,\mu +p +\,\frac{1}{2};\mu +p+1;\dfrac{-\mu {(\kappa +1)}}{B_{P}~m_{s}\bar{\gamma }}\right) \end{aligned} \end{aligned}$$
(11)

3.1.2 ASEP of coherent modulation scheme for EMIG composite fading model

By putting the value of (4) and (6) into (5) and after certain simple mathematical manipulations, one obtains

$$\begin{aligned} \begin{aligned}&\bar{P}_{e}^{coh}\\&\quad =\sum \limits _{r=0}^{\infty }\dfrac{A_{p}~(2\mu )^{2\mu +2r}~h^{\mu }~H^{2r}~(m_s\bar{\gamma })^{m_s}~(\frac{m_s+2\mu }{2})_{r}~(\frac{m_s+2\mu +1}{2})_{r}}{{r}!~B(m_s,2\mu )~(\frac{2\mu +1}{2})_{r}}\\&\quad \times \,\int \limits _{0}^{\infty }\dfrac{\gamma ^{2\mu +2r-1}~erfc(\sqrt{B_P\gamma })}{(2\mu h \gamma +m_s \bar{\gamma })^{m_s+2\mu +2r}}~d\gamma ~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned} \end{aligned}$$
(12)

After necessary change of variables in integral part of (12) and following the similar approach as in Sect. 3.1.1, it insinuates

$$\begin{aligned} \begin{aligned}&\bar{P}_{e}^{coh}\\&\quad =\sum \limits _{r=0}^{\infty }\dfrac{A_{p}~(2\mu )^{2\mu +2r}~h^{\mu }~H^{2r}~\varGamma (\mu +r)~\varGamma {(\frac{4\mu +4r+1}{2})}}{2 \sqrt{\pi }~{r}!~\varGamma (\mu )~B(m_s,2\mu +2r)~(\mu +r)~(B_P~m_s \bar{\gamma })^{2\mu +2r}}\\&\quad \times \,{_3}{F_1}\left( m_s+2\mu +2r,2\mu +2r,\frac{4\mu +4r+1}{2};2\mu +2r\right. \\&\quad \left. +\,1;\frac{-2\mu h}{B_P~m_s \bar{\gamma }}\right) \end{aligned} \end{aligned}$$
(13)

Truncating the infinite series given by (13) with p number of terms, results to the following error metric

$$\begin{aligned} \begin{aligned}&T=\dfrac{A_{p}~(2\mu )^{2\mu }~h^{\mu }}{2\sqrt{\pi }~\varGamma {(\mu )} ~(B_P~m_s \bar{\gamma })^{2\mu }}\sum \limits _{r=p}^{\infty }\\&\quad \dfrac{\varGamma (\mu +r)~\varGamma {(\frac{4\mu +4r+1}{2})}}{{r}!~B(m_s,2\mu +2r)~(\mu +r)~}{\left( \dfrac{2\mu H }{B_{P} m_{s} \bar{\gamma }}\right) ^{2r}}\\&\quad \times \,{_3}{F_1}\left( m_s+2\mu +2r,2\mu +2r,\frac{4\mu +4r+1}{2};2\mu \right. \\&\quad \left. +\,2r+1;\frac{-2\mu h}{B_P~m_s \bar{\gamma }}\right) \end{aligned} \end{aligned}$$
(14)

After following the similar approach as in the 3.1.1, the closed-form upper bound expression for the truncation error in (14) is given as follows

$$\begin{aligned} \begin{aligned}&T\le \dfrac{A_{p}~(2\mu )^{2\mu -1}~h^{\mu }}{\sqrt{\pi }~(B_P~m_s \bar{\gamma })^{2\mu }~B(m_s,2\mu )}~\\&\quad \times \,{_3}{F_1}\left( m_s+2\mu +2p,2\mu +2p, 2\mu +2p+\frac{1}{2};2\mu +2p+1;\frac{-2\mu h}{B_P~m_s \bar{\gamma }}\right) \\&\quad \times \,{_4}{F_2}\left( \mu +\frac{1}{4},\mu +\frac{3}{4},\frac{m_{s}+2\mu +1}{2},\mu ;\mu \right. \\&\quad \left. +\,\frac{1}{2},\mu +1;\left( \frac{4\mu h}{B_{P}m_{s}\bar{\gamma }}\right) ^{2}\right) \end{aligned} \end{aligned}$$
(15)

3.2 ASEP of non-coherent modulation scheme

Sometimes, it becomes tedious to trace the phase of the received signal while analysing the performance of a communication system. In such cases, non-coherent modulation schemes play a pivotal role in the faithful implementation of the system. In the past, a lot of research has been done in the field of non-coherent modulation schemes for different fading channels [27, 28, 56, 57]. In the following sections, we presents the analytical solutions for different non-coherent schemes over aforementioned composite fading models. The instantaneous SEP expression for non-coherent policies is defined as [6, Eq. (26)]

$$\begin{aligned} {P_e}(\gamma )=A_n~\exp (-B_n\gamma ) \end{aligned}$$
(16)

where the parameters \(A_{n}\) and \(B_{n}\) covering a wide range of non-coherent modulation formats are listed in [56, Table 2].

3.2.1 ASEP of non-coherent modulation scheme of KMIG

By using the PDF of KMIG given in (2) and (16) into (5), it results

$$\begin{aligned} \begin{aligned}&\bar{P}_{e}^{NCoh}\\&\quad =\sum \limits _{r=0}^{\infty }\dfrac{{(m_{s}+\mu )_{r}}~{(\mu \kappa )^{r}}~\exp \left( -\mu \kappa \right) ~\mu ^{\mu +r}~{\left( \kappa +1\right) }^{\mu +r}~{(m_{s}\bar{\gamma })^{m_{s}}}~{A_{n}}}{{{r}{!}}~{(\mu )_{r}}~{B(m_{s},\mu )}}\\&\quad \qquad \times \,\int \limits _{0}^{\infty }\dfrac{\gamma ^{\mu +r-1}~\exp {({-B_{n}\gamma })}}{\left[ \mu \left( \kappa +1\right) \gamma +m_{s}\bar{\gamma }\right] ^{m_{s}+\mu +r}}~{d\gamma }~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned} \end{aligned}$$
(17)

Now, employing the identity [55, Eq. (2.3.6.9)] and [50, Eq. (9.210.2)], (17) can be written in simplified form as

$$\begin{aligned} \begin{aligned}&\bar{P}_{e}^{NCoh}=\sum \limits _{r=0}^{\infty }\dfrac{(\mu \kappa )^{r}}{r!~\exp (\mu \kappa )}\\&\quad {\left\{ \begin{array}{ll} {_1}F_{1}\left( \mu +r;1-m_{s};\dfrac{B_{n}~m_{s}\bar{\gamma }}{\mu {(\kappa +1)}}\right) \\ + {\left\{ \begin{array}{ll}{\left[ {\dfrac{B_{n}~m_{s}\bar{\gamma }}{\mu {(\kappa +1)}}}\right] }^{m_{s}} \dfrac{\varGamma (-m_{s})}{B(m_{s},\mu +r)}\\ {_1}F_{1}\left( m_{s}+\mu +r;m_{s}+1;{\dfrac{B_{n}~m_{s}\bar{\gamma }}{\mu {(\kappa +1)}}}\right) \end{array}\right. } \end{array}\right. } \end{aligned} \end{aligned}$$
(18)

Truncating the infinite series given by (18) with p number of terms, will results in the following truncation error metric

$$\begin{aligned} \begin{aligned}&T=\sum \limits _{r=p}^{\infty }\dfrac{(\mu \kappa )^{r}}{r!~\exp (\mu \kappa )}\\&\quad {\left\{ \begin{array}{ll} {_1}F_{1}\left( \mu +r;1-m_{s};\dfrac{B_{n}~m_{s}\bar{\gamma }}{\mu {(\kappa +1)}}\right) \\ + {\left\{ \begin{array}{ll}{\left[ {\dfrac{B_{n}~m_{s}\bar{\gamma }}{\mu {(\kappa +1)}}}\right] }^{m_{s}} \dfrac{\varGamma (-m_{s})}{B(m_{s},\mu +r)}\\ {_1}F_{1}\left( m_{s}+\mu +r;m_{s}+1;{\dfrac{B_{n}~m_{s}\bar{\gamma }}{\mu {(\kappa +1)}}}\right) \end{array}\right. } \end{array}\right. } \end{aligned} \end{aligned}$$
(19)

Following the similar approach as in the Sect. 3.1.1 and with the use of generalized hypergeometric functions [50], the closed-form upper bound expression for the truncation error of (18) can be given by following inequality

$$\begin{aligned} \begin{aligned}&T\le \exp {(-\mu \kappa )}~{_1}{F_1}\left( \mu +p;1-m_{s};\frac{B_{n}m_{s}\bar{\gamma }}{\mu (\kappa +1)}\right) ~{_1}{F_1}\left( 1;1;\mu \kappa \right) \\&\quad +\, \dfrac{e^{-\mu \kappa } \varGamma {(-m_{s})}}{B{(m_{s},\mu )}}\\&\quad \times \,{\left( \dfrac{B_{n}m_{s}\bar{\gamma }}{\mu (\kappa +1)}\right) ^{m_{s}}}{_1}{F_1}\left( m_{s}+\mu +p;m_{s}+1;\frac{B_{n}m_{s}\bar{\gamma }}{\mu (\kappa +1)}\right) \\&\quad ~{_1}{F_1}\left( m_{s}+\mu ;\mu ;\mu \kappa \right) \end{aligned} \end{aligned}$$
(20)

3.2.2 ASEP of non-coherent modulation scheme of EMIG

Substituting the PDF of EMIG given by (4) and (16) into (5), with following the same approach as in Sect. 3.2.1, it follows

$$\begin{aligned} \begin{aligned}&\bar{P}_{e}^{NCoh}=\sum \limits _{r=0}^{\infty }\dfrac{A_n~\varGamma (\mu +r)~H^{2r}}{r!~\varGamma (\mu )~h^{\mu +2r}}\\&\quad {\left\{ \begin{array}{ll} {_1}F_{1}\left( 2\mu +2r;1-m_{s};\dfrac{B_{n}m_{s}\bar{\gamma }}{2\mu h}\right) \\ +\,{\left\{ \begin{array}{ll}{\left( {\dfrac{B_{n}m_{s}\bar{\gamma }}{2\mu h}}\right) }^{m_{s}} \dfrac{\varGamma (-m_{s})}{B(m_{s},2\mu +2r)}\\ ~{_1}F_{1}\left( m_{s}+2\mu +2r;1-m_{s};{\dfrac{B_{n}~m_{s}\bar{\gamma }}{2\mu h}}\right) \end{array}\right. } \end{array}\right. } \end{aligned} \end{aligned}$$
(21)

The truncation error for infinite series representation given by (21) is obtained while truncating it to p number of terms, it follows

$$\begin{aligned} \begin{aligned}&T=\sum \limits _{r=p}^{\infty }\dfrac{A_n~\varGamma (\mu +r)~H^{2r}}{r!~\varGamma (\mu )~h^{\mu +2r}}\\&\quad {\left\{ \begin{array}{ll} {_1}F_{1}\left( 2\mu +2r;1-m_{s};\dfrac{B_{n}m_{s}\bar{\gamma }}{2\mu h}\right) \\ +\,{\left\{ \begin{array}{ll}{\left( {\dfrac{B_{n}m_{s}\bar{\gamma }}{2\mu h}}\right) }^{m_{s}} \dfrac{\varGamma (-m_{s})}{B(m_{s},2\mu +2r)}\\ ~{_1}F_{1}\left( m_{s}+2\mu +2r;1-m_{s};{\dfrac{B_{n}~m_{s}\bar{\gamma }}{2\mu h}}\right) \end{array}\right. } \end{array}\right. } \end{aligned} \end{aligned}$$
(22)

With the same methodology as in the Sect. 3.1.1 and with the use of generalized hypergeometric functions [50], the closed-form upper bound expression for the truncation error of (21) can be given by following inequality

$$\begin{aligned} \begin{aligned}&T\le \frac{A_{n}}{h^{\mu }}{_1}{F_1}\left( 2\mu +2p;1-m_{s};\frac{B_{n}m_{s}\bar{\gamma }}{2\mu h} \right) \\&\quad {_2}{F_1}\left( \mu ,1;1;\frac{H^{2}}{h^{2}} \right) \\&\quad +\, \dfrac{A{n}~\varGamma {(-m_{s})}\varGamma {(m_{s}+2\mu )}}{h^{\mu }~\varGamma {(2\mu )}} {\left( \dfrac{B_{n}m_{s}\bar{\gamma }}{2\mu h}\right) ^{m_{s}}}\\&\quad {_1}{F_1}\left( m_{s}+2\mu +2p;1-m_{s};\frac{B_{n}m_{s}\bar{\gamma }}{2\mu h)}\right) \\&\quad \times \,{_2}{F_1}\left( \frac{m_{s}+2\mu }{2},\frac{m_{s}+2\mu +1}{2};\frac{2\mu +1}{2};\frac{H^{2}}{h^{2}}\right) \end{aligned} \end{aligned}$$
(23)

4 Asymptotic analysis

Asymptotic analysis is one of the vital analysis of the wireless communication system at high SNR. This helps in predicting the slope and shifting of the curve. It also assist in investigating the different performance metrics of the digital communication channel in the absence and presence of the diversity [58, 59] in a convenient way. In the following sections, we present the origin envelope as well as power PDFs of KMIG and EMIG composite fading models. Closed-form asymptotic solutions of BER for the aforementioned composite fading models is also presented.

4.1 Origin PDF of KMIG

The origin envelope PDF of \(\kappa -\mu\) distribution is well defined in [59] as

$$\begin{aligned} f_{X}(x)\approx \dfrac{2\mu ^{\mu }~(\kappa +1)^{\mu }~x^{2\mu -1}}{\varGamma (\mu )~\exp (\mu \kappa )~\bar{x}^{2\mu }}+\varphi \end{aligned}$$
(24)

where \(\varphi\) is the higher order terms. The IGamma random variable (RV) with shape parameter \(m_s\) and scale parameter \(\frac{m_s}{\varOmega _s}\), where \(\varOmega _s\) is set equal to unity (i.e. \(\varOmega _s=1\)) [14] is given as follows

$$\begin{aligned} f_{W}(w)=\dfrac{m_s^{m_s}}{\varGamma (m_s)}w^{-m_s-1}\exp \left( \frac{-m_s}{w}\right) \end{aligned}$$
(25)

The composite envelope PDF of KMIG channel at origin is calculated by averaging conditional PDF of \(\kappa -\mu\) fading distribution with respect to random variations of mean signal power of IGamma fading distribution [14] as follows

$$\begin{aligned} f_{X}(x)\approx \int \limits _{0}^{\infty }\dfrac{2\mu ^{\mu }~(1+\kappa )^{\mu }~x^{2\mu -1}~m_s^{m_s}~w^{-m_s-1}}{\varGamma (\mu )~\varGamma (m_s)~e^{\mu \kappa }~(\sqrt{w})^{2\mu }}\exp (\frac{-m_s}{w})~{dw}+\varphi \end{aligned}$$
(26)

Applying transformation of variables and with the inclusion of the identity [50, Eq. 2.3.3.1], the above expression is modified as

$$\begin{aligned} f_{X}(x)\approx \dfrac{2\mu ^{\mu }~(1+\kappa )^{\mu }~x^{2\mu -1}}{m_s^{\mu }~e^{\mu \kappa }~B(m_s,\mu )}+\varphi \end{aligned}$$
(27)

The expression for origin SNR density function of the KMIG distribution is obtained by the use of [60, Eq. (2.3)]

$$\begin{aligned} f_{Y}(\gamma )^{asym}\approx P\gamma ^{Q-1}+\varphi \end{aligned}$$
(28)

where \(P=\dfrac{\mu ^{\mu }~(1+\kappa )^\mu }{m_s^{\mu }~e^{\mu \kappa }~B(m_s,\mu )}\) and \(Q=\mu\).

4.2 Origin PDF of EMIG

The origin envelope PDF of \(\eta -\mu\) distribution is given in [59] as

$$\begin{aligned} f_{X}(x)\approx \dfrac{4\sqrt{\pi }~\mu ^{2\mu }~h^\mu ~x^{4\mu -1}}{\varGamma (\mu )~\varGamma (\mu +\frac{1}{2})~\bar{x}^{4\mu }}+\varphi \end{aligned}$$
(29)

with the use of similar method as in previous Sect. 4.1, the power PDF of EMIG in closed-form can be written as

$$\begin{aligned} f_{Y}(\gamma )^{asym}\approx A\gamma ^{B-1}+\varphi \end{aligned}$$
(30)

where \(A=\dfrac{2\sqrt{\pi }~\mu ^{2\mu }~h^{\mu }~\varGamma (m_s+2\mu )}{\varGamma (\mu )~\varGamma (m_s)~\varGamma (\mu +\frac{1}{2})~m_s^{2\mu }}\) and \(B=2\mu\).

4.3 Coherent ASEP

Substituting (28) and (6) into (5) and by utilising the identity [53, Eq. 2.8.2.1], one can find the closed-form asymptotic solution of the KMIG composite fading channel for coherent average SEP

$$\begin{aligned} \bar{P}_{e}^{coh,asym}\approx \dfrac{A_p~P~\varGamma (\frac{2\mu +1}{2})}{\sqrt{\pi }~{Q}~(B_p~\gamma _s)^Q} \end{aligned}$$
(31)

In the above expression (31), \(\gamma _s=\frac{E_s}{N_0}\) is the unfaded SNR, where \(E_s\) is the energy per symbol, \(N_0\) is the one-sided power spectral density of AWGN channel. Similarly, the closed-form asymptotic solution of EMIG fading channel is obtained by plugging (30) and (6) into (5) and by utilising the identity [53, Eq. 2.8.2.1] as

$$\begin{aligned} \bar{P}_{e}^{coh,asym}\approx \dfrac{A_p~A~\varGamma (\frac{4\mu +1}{2})}{\sqrt{\pi }~{B}~(B_p~\gamma _s)^{B}} \end{aligned}$$
(32)

In [61], Wang and Giannakis illustrated that diversity gain (DG) and coding gain (CG) can be employed for the characterization of average SEP. Authors has also suggested that these gains are influenced by the asymptotic power PDF around the origin. Furthermore, CG and DG can be calculated in the following manner

$$\begin{aligned} P_{e}= \left( G_{c}~\bar{\gamma }\right) ^{-G_{d}} \end{aligned}$$
(33)

where \(G_{c}\) is the CG and \(G_{d}\) is the DG [61]. So comparing (32) with (33), for the coherent modulation scheme over KMIG, the DG is given as \(G_{d}=\mu\), where the CG is given as follows

$$\begin{aligned} G_{c}= B_{p}\left( \dfrac{\sqrt{\pi }~\mu }{A_{p}~P~\varGamma (\frac{2\mu +1}{2})}\right) ^{\frac{1}{\mu }} \end{aligned}$$
(34)

Similarly for EMIG , the DG is given as \(G_{d}=2\mu\), where the CG is given as follows

$$\begin{aligned} G_{c}= B_{p}\left( \dfrac{\sqrt{\pi }~2\mu }{A_{p}~A~\varGamma (\frac{4\mu +1}{2})}\right) ^{\frac{1}{2\mu }} \end{aligned}$$
(35)

4.4 Non-coherent ASEP

By putting (28) and (16) into (5) and with the use of [50, Eq. 3.381.4], one can obtain the closed-form solution over KMIG as follows

$$\begin{aligned} \bar{P}_{e}^{Ncoh,asym}\approx \dfrac{A_n~P~\varGamma (Q)}{(B_n~\gamma _s)^{Q}} \end{aligned}$$
(36)

Similarly, the closed-form expression of EMIG composite fading channel for non-coherent average SEP can be obtained by putting (30) and (16) into (5) and by the use of identity [50, Eq. 3.381.4] as follows

$$\begin{aligned} \bar{P}_{e}^{Ncoh,asym}\approx \dfrac{A_n~A~\varGamma (B)}{(B_n~\gamma _s)^{B}} \end{aligned}$$
(37)

So with the use of (36) in (33), the DG over KMIG is given by \(G_{d}=\mu\), where the CG is given as follows

$$\begin{aligned} G_{c}= \dfrac{B_{n}}{\left( A_{p}~P~\varGamma (\mu )\right) ^{\frac{1}{\mu }}} \end{aligned}$$
(38)

Similarly for the EMIG the DG and CG are given by comparing (37) with (33), which gives \(G_{d}=2\mu\) and CG is given as follows

$$\begin{aligned} G_{c}= \dfrac{B_{n}}{\left( A_{p}~A~\varGamma (2\mu )\right) ^{\frac{1}{2\mu }}} \end{aligned}$$
(39)

5 Channel capacity

Shannon’s channel capacity describe the relation of capacity of a channel in the form of amount of data that a channel can supports with minimum probability of error [28, 30]. The amount of information that a channel can transmit/receive is a function of the fading state of the channel [12, 18]. Capacity of a fading channel reduces if the transmitter power does not changes. Adaptive transmission policies can help in minimizing the effect of fading on channel’s ability to carry the information. Channel state information(CSI) plays a vital role in improving the system efficiency as far as channel capacity is concerned [6, 28]. Different adaptive transmission policies which depends on CSI are given in the following Subsections with complete analysis.

5.1 Optimum rate adaptation

ORA transmission scheme is implemented in the scenario where receiver has the perfect information of the CSI. Transmitter power does not changes and the rate of transmission depends on the channel conditions in the case of ORA scheme. Thus, the ORA transmission policy over a fading SNR is obtained by the following relation [6, 26]

$$\begin{aligned} C_{ORA}=\int \limits _{0}^{\infty } ~W~C_{awgn}~f_{Y}(\gamma )d\gamma \end{aligned}$$
(40)

where \(C_{awgn}=\log _2(1+\gamma )\) and channel bandwidth in Hz is represented by W

5.1.1 ORA for KMIG fading model

With the use of (2) in (40) and applying some mathematical manipulations, we find that

$$\begin{aligned} \begin{aligned} C_{ORA}=\sum \limits _{r=0}^{\infty }\dfrac{{W}~{(m_{s}+\mu )_{r}}~{(\mu \kappa )^{r}}~\exp \left( -\mu \kappa \right) ~{(m_{s}\bar{\gamma })^{m_{s}}}}{{{r}{!}}~{(\mu )_{r}}~{B(m_{s},\mu )~\log (2)}~{\left[ \mu \left( \kappa +1\right) \right] }^{m_{s}}}\\ \int \limits _{0}^{\infty }\dfrac{\gamma ^{\mu +r-1}\log \left( \gamma +1\right) }{\left[ \gamma +\dfrac{\bar{\gamma }m_{s}}{\mu {(1+\kappa )}}\right] ^{r+m_{s}+\mu }}~{d\gamma } \end{aligned} \end{aligned}$$
(41)

By the help of the identity [55, Eq. (2.5.10.56)] in (41), the expression results into

$$\begin{aligned} \begin{aligned}&C_{ORA,}=\sum \limits _{r=0}^{\infty }\mathcal {A}\\&\quad {\left\{ \begin{array}{ll} \psi (m_{s}+\mu +r)-\psi (m_{s})\\ -\,{\left\{ \begin{array}{ll} \frac{(\mu +r)}{(m_{s}+\mu +r)} {\left( 1-\dfrac{m_{s}\bar{\gamma }}{\mu (\kappa +1)}\right) }\\ {{_3}F_{2}\left( \mu +r+1,1,1;2,m_{s}+\mu +r+1;1-\dfrac{m_{s}\bar{\gamma }}{\mu (\kappa +1)}\right) } \end{array}\right. } \end{array}\right. } \end{aligned} \end{aligned}$$
(42)

where \(\mathcal {A}=\dfrac{W{(m_{s}+\mu )_{r}}\exp \left( -\mu \kappa \right) ~{(\mu \kappa )^{r}}~B{(\mu +r,m_{s})}}{{{r}{!}}{(\mu )_{r}}{B(m_{s},\mu )\log \left( 2\right) }}\) and \(\psi (.)\) is the psi function [50].

The above expression can be further reduced with the help of basic mathematical simplifications [50], the final solution for the ORA can be re-written as

$$\begin{aligned} \begin{aligned} C_{ORA,}&=\sum \limits _{r=0}^{\infty }\dfrac{W~\exp {\left( \mu \kappa \right) }{\left( {\mu \kappa } \right) ^{r}}}{{r}{!}~{\log (2)}}\\&{\left\{ \begin{array}{ll} \psi (m_{s}+\mu +r)-\psi (m_{s})\\ -\,{\left\{ \begin{array}{ll} \frac{(\mu +r)}{(m_{s}+\mu +r)} {\left( 1-\dfrac{m_{s}\bar{\gamma }}{\mu (\kappa +1)}\right) }\\ {{_3}F_{2}\left( \mu +r+1,1,1;2,m_{s}+\mu +r+1;1-\dfrac{m_{s}\bar{\gamma }}{\mu (\kappa +1)}\right) } \end{array}\right. } \end{array}\right. } \end{aligned} \end{aligned}$$
(43)

The above mathematical notation can be further re-expressed under high SNR, deducing (41) at high values of SNR i.e. \({\gamma>>1}\) such that \({\log _{2}(1+\gamma )\approx \log _{2}(\gamma )}\), one obtains

$$\begin{aligned} \begin{aligned}&C_{ORA}^{{HP}}\approx \sum \limits _{r=0}^{\infty }\\&\quad \dfrac{{W}~{(m_{s}+\mu )_{r}}~{(\mu \kappa )^{r}}~\exp \left( -\mu \kappa \right) ~{(m_{s}\bar{\gamma })^{m_{s}}}}{{{r}{!}}~{(\mu )_{r}}~{B(m_{s},\mu )~\log (2)}~{\left[ \mu \left( \kappa +1\right) \right] }^{m_{s}}}\\&\quad \times \, \int \limits _{0}^{\infty }\dfrac{\gamma ^{\mu +r-1}\log \left( \gamma \right) }{\left[ \gamma +\dfrac{m_{s}\bar{\gamma }}{\mu {(\kappa +1)}}\right] ^{m_{s}+\mu +r}}~{d\gamma } \end{aligned} \end{aligned}$$
(44)

With the help of the identity [55, Eq. 2.6.4.7], (44) can be re-written as given below

$$\begin{aligned}&C_{ORA}^{{HP}}\approx \sum \limits _{r=0}^{\infty }\nonumber \\&\quad \dfrac{W~\exp (-\mu \kappa )~(\mu \kappa )^{r}}{r{!}~\log (2)}\nonumber \\&\quad \left( \log \left( \frac{m_s \bar{\gamma }}{\mu (\kappa +1)}\right) +\psi (\mu +r)-\psi (m_s)\right) \end{aligned}$$
(45)

Similarly, at the low values of SNR, i.e. \(\gamma<<1\), \(\log _{2}{(1+\gamma )}\approx ~\gamma \log _{2}{(e)}\), now with the use of previous relation in (41), the ORA capacity can be calculated by finding the \(1^{st}\) order moment of KMIG distribution by the use of \(n=1\) in [40, Eq. (8)]

$$\begin{aligned}&C_{ORA}^{{LP}}\nonumber \\&\quad \approx \dfrac{W~\log _{2}(e)~m_s\bar{\gamma }~\exp (-\mu \kappa )~B(m_s-1,\mu +1)}{\mu (\kappa +1)~B(m_s,\mu )}\nonumber \\&\quad {_1}F_{1}(\mu +1,\mu ,\mu \kappa ) \end{aligned}$$
(46)

With some basic mathematical manipulation, the above solution can be modified as given below

$$\begin{aligned}&C_{ORA}^{{LP}}\approx \dfrac{W~\log _{2}(e)~m_s\bar{\gamma }~\exp (-\mu \kappa )}{(\kappa +1)~(m_s-1)}\nonumber \\&\quad {_1}F_{1}(\mu +1,\mu ,\mu \kappa ) \end{aligned}$$
(47)

Further, at \(m_s\) \(>>1\) (47) reduced to

$$\begin{aligned} C_{ORA}^{{LP}}\simeq \dfrac{W~\log _{2}(e)\bar{\gamma }~\exp (-\mu \kappa )}{(\kappa +1)}~{_1}F_{1}(\mu +1,\mu ,\mu \kappa ) \end{aligned}$$
(48)

5.1.2 ORA for EMIG fading model

Substituting the PDF relation (4) into (40) and following similar step as in Sect. 5.1.1, one obtains

$$\begin{aligned} \begin{aligned} C_{ORA}=\sum \limits _{r=0}^{\infty }\dfrac{W(\frac{m_s+2\mu }{2})_{r}~(\frac{m_s+2\mu +1}{2})_{r}~H^{2r}~(m_s\bar{\gamma })^{m_s}}{r!~(\frac{2\mu +1}{2})_{r}~B(m_s,2\mu )~\log {(2)}~(2\mu )^{m_s}~h^{m_s+\mu +2r}}\\ \times \,\int \limits _{0}^{\infty }\dfrac{\gamma ^{2\mu +2r-1}~\log (\gamma +1)}{({\gamma +\frac{m_s\bar{\gamma }}{2\mu h}})^{2\mu +2r+m_s}}~d\gamma ~~~~~~~~~~~~~~~~ \end{aligned} \end{aligned}$$
(49)

By the help of the identity [55], the above expression can be re-written as

$$\begin{aligned} \begin{aligned} C_{ORA}=\sum \limits _{r=0}^{\infty }\hat{\mathcal {A}} {\left\{ \begin{array}{ll} \psi (m_{s}+2\mu +2r)-\psi (m_{s})\\ -\, {\left\{ \begin{array}{ll} \frac{(2\mu +2r)}{(m_{s}+2\mu +2r)}~{\left( 1-\dfrac{m_{s}\bar{\gamma }}{2\mu h}\right) }~\\ {{_3}F_{2}\left( 2\mu +2r+1,1,1;2,2\mu +2r+m_{s}+1;1-\dfrac{m_{s}\bar{\gamma }}{2\mu h}\right) } \end{array}\right. } \end{array}\right. } \end{aligned} \end{aligned}$$
(50)

where \(\hat{\mathcal {A}}=\dfrac{W~ \varGamma (\mu +r)~H^{2r}}{r!~\varGamma (\mu )~\log (2)~h^{\mu +2r}}\).

By following the same method as in the Sect. 5.1.1, the above expression at high values of SNR can be re-written as

$$\begin{aligned}&C_{ORA}^{{HP}}\approx \sum \limits _{r=0}^{\infty }\nonumber \\&\quad \dfrac{W\varGamma (\mu +r)~H^{2r}}{r!~\varGamma (\mu )~\log (2)~h^{\mu +2r}}\left[ \log \left( \frac{m_s\bar{\gamma }}{2\mu h}\right) +\psi (2\mu +2r)-\psi (m_s)\right] \end{aligned}$$
(51)

The solution to ORA capacity at low SNR is determined by evaluating the \(1^{st}\) order moment of the EMIG distribution [40, Eq. (19)]

$$\begin{aligned} C_{ORA}^{{LP}}\approx \dfrac{W~\log _{2}(e)~m_s \bar{\gamma }}{(m_s-1)~h^{\mu +1}}~{_2}F_{1}\left( \mu +\frac{1}{2},\mu +1;\mu +\frac{1}{2};\frac{H^2}{h^2}\right) \end{aligned}$$
(52)

Similar to KMIG, (52) at high value of shadowing parameters \(m_s\) takes the structure

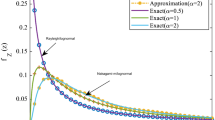
$$\begin{aligned} C_{ORA}^{{LP}}\approx \dfrac{W~\log _{2}(e) \bar{\gamma }}{h^{\mu +1}}~{_2}F_{1}\left( \mu +\frac{1}{2},\mu +1;\mu +\frac{1}{2};\frac{H^2}{h^2}\right) \end{aligned}$$
(53)

The approximate expressions given by (48) and (53) are evolved while considering \(m_s\) \(>>\)1, as quite prominent case seen in the practical urban scenarios. These results are independent of shadowing parameter and thus set the lower limit of the spectral efficiency (i.e. minimum achievable capacity) in terms of \(m_s\) under low-power regime and similar observation can be made from the Fig. 1. The above derived expressions have generic nature, thus can be transformed to the ergodic capacity analysis for variety of fading distributions by selecting suitable values of parameter as given in [40, Table I]. The suitability of the previous relations in different propagation environments have been examined through measurement data, such as wearable off-body communication (i.e., for car parking LOS environment where \(m_s\) is having the value 100 for both fading models [40, Table II]), device-to-device (D2D) communication (i.e., for indoor non-LOS environment where \(m_s\)=50 for EMIG fading model [40, Table IV]), and vehicle-to-vehicle (V2V) communication (i.e. for LOS environment where \(m_s\)=100 for aforementioned composite fading models [40, Table V]).

Fig. 1
figure 1

ORA capacity versus \(m_s\) under low-power regime

Full size image

5.2 Channel inversion with fixed rate

More power is given to the channel which having low SNR and vice versa. By following this approach the received power can be made constant. In other words we can say that power given by the transmitter is inversely proportional to the SNR of the fading channel. In this case fading channel is assumed as the time-invariant AWGN channel by the Tx and Rx, which further helps in reducing the dependency on the behaviour of fading channel [6, 28].

The channel capacity with CIFR adaptation scheme is defined as [26, Eq. (17)]

$$\begin{aligned} C_{CIFR}=W\log _2\bigg [1+\dfrac{1}{\underbrace{E[Y^{-1}]}_{I_0}}\bigg ] \end{aligned}$$
(54)

5.2.1 CIFR for KMIG fading model

Solution of \({I_0}\) in (54) is obtained by putting \(n=-1\) in [40, Eq. (8)]

$$\begin{aligned}&{I_0}={\bigg [\dfrac{\mu (1+\kappa )}{m_{s}\bar{\gamma }}\bigg ]}\nonumber \\&\quad \dfrac{\exp (-\mu \kappa )}{B(m_{s},\mu )}{B(1+m_{s},\mu -1)}~{_1}F_{1}(\mu -1,\mu ,\mu \kappa ) \end{aligned}$$
(55)

After incorporating the value of \({I_0}\) from (55) into (54) and with some basic mathematics yields

$$\begin{aligned}&C_{CIFR}=W\log _2\nonumber \\&\quad \bigg [1+\dfrac{m_{s}\bar{\gamma }~B(m_{s},\mu )~\exp (\mu \kappa )}{\mu (\kappa +1)~B(m_{s}+1,\mu -1)~{{_1}F_{1}(\mu -1,\mu ,\mu \kappa )}}\bigg ] \end{aligned}$$
(56)

with the use of identity, \(\exp (-x){_1}F_{1}(\hat{a};\hat{b};x)={_1}F_{1}(\hat{b}-\hat{a};\hat{a};-x)\) [51, Eq. (07.20.17.0013.01)] and basic definition of beta function i.e. \(B(a,b)=\dfrac{\varGamma (a)\varGamma (b)}{\varGamma (a+b)}\) [50], the Eq. (56) can be written as

$$\begin{aligned} C_{CIFR}=W\log _2\bigg [1+\dfrac{\bar{\gamma }(\mu -1)}{\mu (\kappa +1){_1}F_{1}(1;\mu ;-\mu \kappa )}\bigg ] \end{aligned}$$
(57)

The expression (57) can be re-written for high values of received SNR with some basic mathematical approximation as given below

$$\begin{aligned} C_{CIFR}^{HP}=W\log _2\bigg [\dfrac{\bar{\gamma }(\mu -1)}{\mu (\kappa +1){_1}F_{1}(1;\mu ;-\mu \kappa )}\bigg ] \end{aligned}$$
(58)

Similarly, at low SNR, the CIFR capacity can be written in closed-form with basic mathematical approximations

$$\begin{aligned} C_{CIFR}^{LP}=\dfrac{W~\bar{\gamma }~(\mu -1)\log _{2}(e)}{\mu (\kappa +1)~{_1}F_{1}(1;\mu ;-\mu \kappa )} \end{aligned}$$
(59)

For \(\mu\) \(>>\) \(1\), (57), (58), and (59) can be simplified as

$$\begin{aligned}&C_{CIFR}\approx W\log _2\bigg [1+\dfrac{\bar{\gamma }}{(\kappa +1){_1}F_{1}(1;\mu ;-\mu \kappa )}\bigg ] \end{aligned}$$
(60)
$$\begin{aligned}&C_{CIFR}^{HP}\approx W\log _2\bigg [\dfrac{\bar{\gamma }}{(\kappa +1){_1}F_{1}(1;\mu ;-\mu \kappa )}\bigg ] \end{aligned}$$
(61)
$$\begin{aligned}&C_{CIFR}^{LP}\approx \dfrac{W~\bar{\gamma }\log _{2}(e)}{(\kappa +1)~{_1}F_{1}(1;\mu ;-\mu \kappa )} \end{aligned}$$
(62)

The above results are derived under the case when \(\mu\) \(>>\)1 (i.e., number of multipath clusters are very high) which is often seen in dense urban environment where multipath components are dominant. It is observed form the Fig. 2(a–c) that the approximate results given by (60), (61), and (62) converge to (57), (58), and (59) at higher values of multipath parameter \(\mu\).

Fig. 2
figure 2

CIFR capacity versus multipath parameter \(\mu\)

Full size image

5.2.2 CIFR for EMIG fading model

Substituting n=\(-1\) into [40, Eq. (19)] and using basic definition of Beta and Gamma function [50], the solution to \(I_0\) for EMIG distribution is obtained as

$$\begin{aligned} \begin{aligned} I_0=\dfrac{2\mu h}{(2\mu -1)~\bar{\gamma }~h^{\mu }} ~{_2}F_{1}\left( \mu -\frac{1}{2},\mu ;\mu +\frac{1}{2};\frac{H^2}{h^2}\right) \end{aligned} \end{aligned}$$
(63)

Further, putting (63) into (54), it follows that

$$\begin{aligned} C_{CIFR}=W\log _2\bigg [1+\dfrac{(1-\frac{1}{2\mu })\bar{\gamma }~h^{\mu -1}}{{_2}F_{1}\left( \mu -\frac{1}{2},\mu ;\mu +\frac{1}{2};\frac{H^2}{h^2}\right) }\bigg ] \end{aligned}$$
(64)

Furthermore, CIFR under EMIG composite fading model at high and low SNR can be calculated with the similar approach as in Sect. 5.2.1 which results in the following expressions

$$\begin{aligned}&C_{CIFR}^{HP}\approx \log _2\bigg [\dfrac{(1-\frac{1}{2\mu })\bar{\gamma }~h^{\mu -1}}{{_2}F_{1}\left( \mu -\frac{1}{2},\mu ;\mu +\frac{1}{2};\frac{H^2}{h^2}\right) }\bigg ] \end{aligned}$$
(65)
$$\begin{aligned}&C_{CIFR}^{LP}\approx \dfrac{W~(2\mu -1)~\bar{\gamma }~\log _{2}(e)}{2\mu ~h^{1-\mu }~{_2}F_{1}\left( \mu -\frac{1}{2},\mu ;\mu +\frac{1}{2};\frac{H^2}{h^2}\right) } \end{aligned}$$
(66)

The closed-form expressions obtained in (57), (58), (59), (64), (65), and (66) do not contain shadowing parameter \(m_s\), thus CIFR policy is independent of shadowing.

5.3 Truncated CIFR

A large amount of transmitted power is consumed in the case of CIFR for recouping the critical fading in the wireless channel. TIFR is the improved version of CIFR scheme, such that it regress the fading only above a cut-off fading threshold (\(\gamma _0\)) [60]. The solution of the outage capacity is given as [26, Eq. (26)]

$$\begin{aligned} C_{out}=W\log _2\left[ 1+\dfrac{1}{\int \limits _{\gamma _{0}}^{\infty }\dfrac{f_{Y}(\gamma )}{\gamma }d\gamma }\right] \left( 1-P_{out}(\gamma _{0})\right) \end{aligned}$$
(67)

5.3.1 TIFR for KMIG fading model

By using (2) into integral part of (67) and employing the identity [50, Eq. (3.194.2)], the integral is simplified as

$$\begin{aligned} \begin{aligned}&{\int \limits _{\gamma _{0}}^{\infty }\dfrac{f_{Y}(\gamma )}{\gamma }d\gamma }=\xi \\&\quad =\sum \limits _{r=0}^{\infty }\dfrac{{(m_{s}+\mu )_{r}}~{(\mu \kappa )^{r}}~{\exp (-\mu \kappa )}}{{r}!~(\mu )_{r}~{B(m_{s},\mu )}~(m_s+1)~(\gamma _{0})^{m_s+1}}\left( \dfrac{~m_s\bar{\gamma }}{\mu (\kappa +1)}\right) ^{m_s}\\&\quad \times \,{_2}F_{1}\left( \mu +r+m_{s},1+m_{s};2+m_{s};\dfrac{-m_{s}\bar{\gamma }}{\gamma _{0}~\mu (\kappa +1)}\right) \end{aligned} \end{aligned}$$
(68)

Now, substituting the value of (68) into (67) and with some mathematical manipulations, reduced expression for outage capacity is given as follows

$$\begin{aligned} C_{out}=W\log _2\left[ 1+\frac{1}{\xi }\right] \left( 1-P_{out}(\gamma _{0})\right) \end{aligned}$$
(69)

where \(P_{out}\) is the outage probability of KMIG as given in [40, Eq. 5].

The TIFR capacity expression for KMIG fading channel is derived by considering the maximum value of outage capacity over range of \(\gamma _{0}\)

$$\begin{aligned} C_{TIFR}= max_{\gamma _{0}}C_{out} \end{aligned}$$
(70)

The high and low SNR solution for the outage capacity are obtained by basic mathematical approximation in (69). After following the same method as in the Sect. 5.2.1, results into

$$\begin{aligned}&C_{out}^{HP}\approx -W\log _2\left( \xi \right) ~\left( 1-P_{out}(\gamma _{0})\right) \end{aligned}$$
(71)
$$\begin{aligned}&C_{out}^{LP}\approx \left( \dfrac{1}{\xi }\right) ~\log _{2}(e)~\left( 1-P_{out}(\gamma _{0})\right) \end{aligned}$$
(72)

5.3.2 TIFR for EMIG fading model

By substituting (4) into (67), and with the help of similar methodology as given in the previous Sect. 5.3.1, one can obtain the final expression for outage capacity as

$$\begin{aligned} C_{out}=W\log _2\left[ 1+\frac{1}{\chi }\right] \left( 1-P_{out}(\gamma _{0})\right) \end{aligned}$$
(73)

where \(P_{out}\) is given by [40, Eq. 14] and \(\chi\) is defined as follows

$$\begin{aligned} \begin{aligned} \chi =\sum \limits _{r=0}^{\infty }\dfrac{\varGamma (\mu +r)~H^{2r}~{_2}F_{1}\left( m_{s}+2\mu +2r,m_{s}+2r+1;m_{s}+2r+2;\dfrac{-m_{s}\bar{\gamma }}{\gamma _{0}~2\mu h}\right) }{\varGamma (\mu )~r!~B(m_s,2\mu +2r)~(m_s+2r+1)~h^{\mu +2r}~(2\mu h)^{m_s}~(m_s\bar{\gamma })^{-m_s}} \end{aligned} \end{aligned}$$
(74)

The TIFR capacity expression for EMIG fading channel is derived by considering the maximum value of outage capacity over range of \(\gamma _{0}\) as given in (70). The high and low SNR solution for the outage capacity are obtained with the use of simple mathematical approximations in (73), with following the methodology stated in Sect. 5.2.1.

Fig. 3
figure 3

Average SEP of KMIG composite fading channel for MPSK with different constellation sizes

Full size image
Fig. 4
figure 4

Average SEP of EMIG composite fading channel for BPSK and DBPSK with different values of fading parameters (\(\mu\) =1.4, \(m_s\)= 1.1 and \(\eta\) = 0.1 & 0.9)

Full size image
Fig. 5
figure 5

Coding and diversity gain as a function of number of multipath clusters

Full size image

6 Results and discussion

In this section, the proposed analytical formulations of KMIG and EMIG composite fading channels are validated through numerical and simulated results. In addition, we present multiple plots of various performance matrices to visualize the impact of fading parameters. It is noted from the plots that Monte-Carlo simulation (generated by considering \(10^6\) number of random variables) and proposed analytical results perfectly coincide for wide range of the considered system parameters. It is also observed that the derived expressions are containing simplified mathematical functions which are directly available in MATLAB. For the simulation of the provided analytical results (expressions with infinite summation), we have considered 25 number of summation terms such that the relative error of \(10^{-6}\) is achieved.

Fig. 6
figure 6

Channel capacity of KMIG composite fading channel under ORA scheme with \(\kappa\) = 1,5 and \(m_s\) = 0.92,6

Full size image

The average SEP of KMIG and EMIG composite fading channels for different fading scenarios are depicted in Figs. 3 and 4. In Fig. 3, the average SEP of KMIG composite fading model is demonstrated for M-ary phase shift keying (MPSK) with constellation size M = 8, 16, and 32. The figure shows the exact result obtained by numerically solving (7), the analytical result (8), and the Monte-Carlo simulation are in perfect agreement. The asymptotic results obtained in (32) are also included in this figure. The fading parameters, such as \(\kappa\) = 1.2, \(\mu\) = 2, and \({m_s}\) = 4 are considered. It is clearly evident from the figure that average SEP degrades with constellation size which supports the theoretical concepts, as constellation size increases, the Euclidean distance between symbols decreases which further results in a higher probability of error. It is clearly visible that the asymptotic plots are in perfect agreement with the simulation results. Performance of the EMIG composite fading channel is evaluated under coherent binary phase shift keying (BPSK) and non-coherent differential binary phase shift keying (DBPSK) modulation scheme with \({m_s=1.1}\) and \({\mu =1.4}\) in Fig. 4. It is clearly visible that the numerical solutions are in agreement with the analytical results obtained through (13) and (21). As we know that coherent modulation schemes are superior to non-coherent modulation schemes and similar observation has been made from the figure. It is perceived from the figure that the channel conditions improve with the \({\eta }\) (0.1 to 0.9), as the average SEP plot shows a downward shift.

Fig. 7
figure 7

Channel capacity of KMIG composite fading channel under ORA and CIFR with low SNR approximations

Full size image
Fig. 8
figure 8

Channel capacity of EMIG composite fading channel under CIFR scheme with \(\eta =0.1,0.5, m_s=2.5\) and \(~\mu =1.5,5.5\)

Full size image

In Fig. 5, coding and diversity gain are given as a function of number of multipath clusters (\(\mu\)). It is visible from the plot that, the coding gain decreases gradually with the parameter \(\mu\) while the diversity gain improves. This also validate the previously obtained expression of the diversity gain as it is directly proportional to the parameter \(\mu\). On the other hand coding gain is dependent on all other fading parameters \((\kappa ,\mu ~\)and\(~m_{s})\) as clear from the figure as well as from the numerical expressions. Superiority of coherent modulation schemes over non-coherent is also validated form this figure which supports the theoretical concept.

Figures 6, 7, 8, 9 deal with the channel capacity analysis of KMIG and EMIG composite fading channels under different adaptation schemes. Figure 6 indicates the effect of fading on the channel capacity under ORA scheme over KMIG composite distribution. The analytical solutions are plotted with the help of (43) and validated with Monte Carlo simulations. The analysis of the results is done at the single value of \(\mu\) and different values of \(\kappa\) and \(m_s\). It is clearly detectable from the figure that channel capacity enhances by decreasing the value of \(m_s\) and increasing the values of \(\kappa\) from 1 to 5, satisfying the theoretical concepts. Furthermore, the high SNR approximation result (45) is included in this figure. The result perfectly coincide to the analytical result at high-power. Low SNR approximation of ORA (47) and CIFR (59) adaptation schemes are compared under different fading conditions over the KMIG composite fading model in Fig. 7. It is clearly evident from the plot that CIFR scheme has significant variation by increasing the value of shadowing parameter \(\kappa\) from 0.5 to 3.5 while no such variation is noticed in the case of ORA. It is also observed that low-power ORA analysis is independent of fading parameter \(\kappa\).

Figure 8 depicts the analytical result of CIFR capacity for EMIG composite fading model obtained through (64) at different values of multipath parameters, i.e. \(\eta\) and \(\mu\) while shadowing parameter \({m_s}\) is kept constant. An increase in the values of \(\eta\) and \(\mu\) must ensure the improvement in channel capacity, and it is perceived from the figure that increase in the values of \(\eta\) (0.1 to 0.5) and \(\mu\) (1.5 to 5.5), the capacity curve under CIFR shifts upwards. High SNR approximations with the help of derived analytical result of (58) are also shown in the figure. It is inferred from the figure that as the channel condition becomes more severe, the high-power solution converges toward much higher values of SNR, which in turn supported from the observations noticed in the Fig. 6.

Channel capacity under CIFR and TIFR for KMIG composite fading model is compared in Fig. 9 with different values of shadowing parameter \(m_s\). It is a well-known fact that the TIFR is superior to CIFR adaptation scheme, and similar observation is evident from the figure for same values of fading parameters, satisfying the theoretical concepts. It is also clear from the figure that increasing the value of shadowing parameter \(m_s\) from 2 to 30 shows a significant impact on TIFR schemes, whereas in the case of CIFR no such impact is visible (as can be verified from the derived result 57 that is independent of shadowing parameters). On the other hand, it is noted that CIFR converges to TIFR at high SNR showing a similar impact on the capacity of the system.

Fig. 9
figure 9

Channel capacity under CIFR and TIFR schemes for KMIG composite fading channel with \(m_s=2,30,~\kappa =2\) and \(~\mu =3\)

Full size image

7 Conclusion

In this paper, the performance analysis of wireless channels over composite KMIG and EMIG fading models has been carried out. First, the novel analytical expressions for average SEP under coherent and non-coherent modulation schemes, such as MPSK, BPSK, DBPSK, etc., was developed for the KMIG and EMIG composite fading models. Moreover, the effect of fading parameters on channel conditions were demonstrated with the help of asymptotic solutions with coding and diversity gain. A comparative analysis among various adaptation schemes of the channel capacity, such as ORA, CIFR, and TIFR has been carried out. While considering practical cases approximate results are obtained for ORA (under low-power regime) and CIFR (specifically for KMIG model). The significant effect of composite fading conditions on the performance of wireless channels has been identified for different values of SNR. All the results have been compared with Monte-Carlo simulations and with the exact results to authenticate the correctness of the proposed analytical solutions. Finally, the results of the current paper are of significant importance as these solutions can be utilized in the investigation of the traditional as well as modern wireless systems.