1 Introduction

Development of societies, ever-growing population and the result which is increasing demand for water in one hand, and the shortage of its resources shows the importance of efficient water resources management. A considerable portion of the water used by the countries is provided from surface reservoirs and dams. Therefore, it's crucial to find the optimal reservoir operation policies, to efficiently manage the distribution and reduce losses (Dahmani and Yebdri 2020). The use of various optimization methods of operation is one of the efficient approaches used so far. However, over time, novel and efficient methods are introduced to address the shortcomings of previous ones. The first studies on the optimal operation of reservoirs used linear programming methods, then dynamic planning and stochastic dynamic programming were used (Loucks 1968; Arunkumar and Jothiprakash 2012; Stedinger et al. 1984). Even though these methods grant optimal utilization policy, but it also has some limitations, like linear consideration and discretization of the problem. Also, as the number of variables increases, the computation time increases significantly (Ohadi and Jafari-Asl 2021; Rad et al. 2022). To overcome these shortcomings, researchers, inspired by the behavior of animals, humans, and natural phenomena, proposed a new method called meta-heuristic algorithms (Mirjalili et al. 2017; Jafari-Asl et al. 2021a). These methods are not dependent on the type of problem in terms of linearity and nonlinearity and do not need discretization. Those have good speed and accuracy compared to other available methods. The meta-heuristics methods have different types. The reason behind this diversity can be considered as improving the accuracy and increasing the speed of achieving the optimal solution (MiarNaeimi et al. 2021). So far, various meta-heuristics methods, such as simulated annealing (SA; Teegavarapu and Simonovic 2002; Mantawy et al. 2001), honey-bee mating optimization (HBMO; Afshar et al. 2007; Bozorg Haddad et al. 2008), particle swarm optimization (PSO; Ghimire and Reddy 2013; Reddy and Nagesh Kumar 2007), have been successfully used in reservoir operation management.

Anand et al. (2018) proposed a new simulation–optimization model based on the soil and water assessment tool (SWAT) and GA to determine the optimal operation policies for a two-reservoir system in the Ganges River Basin, India. In their study, the reducing of the monthly water deficit and the increasing the hydropower generation were considered as objective functions. Niu et al. (2018) developed a new optimization model for optimizing the operation program of water releasing of reservoirs. The parallel multi-objective particle swarm optimization (PMOPSO) was used, which is an enhanced version of multi-objective PSO.

Srinivasan and Kumar (2018) introduced an efficient simulation–optimization model to find the optimal program of reservoir operation. In their study, the non-dominated sorting genetic algorithm (NSGA-II) was used. Feng et al. (2018) Proposed a new model based on a parallel multi-objective genetic algorithm (PMOGA) for the ecological operation of hydropower generation. The results showed this parallel approach and the population decomposition strategy led to the increase of the convergence speed and algorithm accuracy in finding the optimal solution.

Inadequate operation of dam reservoirs will waste valuable water resources. It's also noteworthy that the construction of dams has many environmental effects. Considering the environmental aspects and costs of dam construction, it is clear that the efficient operation of reservoirs is necessary. But reservoir operation is a nonlinear and complex optimization problem, so it is not appropriate to use any optimization method to solve it. Meta-heuristic methods have often been successfully used to solve the problem of optimal reservoir operation, but one of the weaknesses of such methods is finding the approximate solution which is close to the global optimal solution, but they cannot find the global solution. A review of the literature of studies shows that the most of those researches focused on modifying and combining the meta-heuristics algorithms to achieve the desired solution and suitable operation policies for reservoir management.

It is noteworthy that uncertainty is an integral part of all systems that can invalidate deterministic optimization results. But in most studies, this issue is not taken into account. (Muronda et al. 2021; Rad et al. 2022; Kasiviswanathan et al. 2021; Jafari-Asl et al. 2021b; Bozorg-Haddad et al. 2021; Thomas et al. 2021) have carried studies on reservoir operation optimization by considering the uncertainty of parameters. However, the research on the influence of uncertainties on reservoir exploitation policy requires further studies. Therefore, the contribution of the present study are as follows:

  1. 1.

    Improving the MVO algorithm performance using GA to find the optimal solution and evaluating the performance of the hybrid algorithm in determining the optimal operation policy of the Amirkabir Dam reservoir.

  2. 2.

    Presenting a reliability-based design optimization (RBDO) approach to consider the uncertainty of the effective parameters in the issue of reservoir operation using Monte Carlo.

The remainder of the current paper is organized as follows: Sect. 2 describes the methodology. Section 3 shows the results of proposed simulation–optimization model. Section 4 presents the findings, contributions, and future work.

2 Materials and Methods

2.1 Optimization Techniques

2.1.1 Multi-verse Optimization Algorithm (MVO)

According to the Big Bang theory, the universe was created based on a big bang. Multi-verse is one of the new theories introduced by physicists. This theory believed that there is more than one big bang and that each big bang creates a universe. This theory holds that there are other worlds besides the world in which we live. Mirjalili et al. (2016) introduced MVO to solve optimization problems based on the three concepts of white holes, black holes, and wormholes in multi-world theory. Like many other population-based algorithms, MVO performs the search process in two stages: exploration and exploitation. The concepts of white holes and black holes are used to explore the search space, and wormholes are used to exploit search spaces. The MVO assumes that every solution is a universe and every variable of this solution is an object within this universe. In addition, an inflation rate is set for each solution, which is proportional to the value of the objective function.

In the process of optimization, the following rules apply to the universes of this algorithm (Mirjalili et al. 2017):

  • Higher inflation means it is more likely to have white holes

  • Higher inflation means it is less likely to have black holes.

  • Universes with higher inflation rates tend to send objects through white holes.

  • Universes with lower inflation rates tend to receive more objects through black holes.

  • Objects from all over the universe can be transported to the best universe by the random motion of wormholes, regardless of inflation.

The MVO begins the optimization process by creating a series of random universe. In each iteration, objects in high-inflation universe tend to move towards low-inflation universe. This transfer from one universe to another takes place through a black or white hole. At the same time, each universe randomly sends its objects towards the best world through wormholes. This process continues until the termination conditions of the algorithm are fulfilled. The MVO is mathematically modeled as follow (Hosseini et al. 2021):

Assume that:

$$U=\left[\begin{array}{ccccc}{x}_{1}^{1}& {x}_{1}^{2}& ...& ...& {x}_{1}^{d}\\ {x}_{2}^{1}& {x}_{2}^{2}& ...& ...& {x}_{2}^{d}\\ :& :& :& :& :\\ :& :& :& :& :\\ {x}_{n}^{1}& {x}_{n}^{2}& ...& ...& {x}_{n}^{d}\end{array}\right]$$
(1)

where d is the number of variables and n is the number of universes:

$${x}_{i}^{j}=\left\{\begin{array}{cc}{x}_{k}^{j}& r1<NI(Ui)\\ {x}_{i}^{j}& r1\ge NI(Ui)\end{array}\right.$$
(2)

where \({x}_{i}^{j}\) indicates the jth variable of ith universe, Ui denotes the ith universe, NI(Ui) is normalized inflation rate of the ith universe, r1 is a random number between 0 and 1, and \({x}_{k}^{j}\) shows the jth variable of kth universe selected by a roulette wheel selection mechanism.

To provide domestic change for each universe and to have a high probability of inflation using wormholes, we assume that wormhole tunnels always exist between any of the universes and the best universe ever created. This mechanism is shown in Eq. (3).

$${x}_{i}^{j}=\left\{\begin{array}{cc}\left\{\begin{array}{cc}{X}_{j}+TDR\times ((u{b}_{j}-l{b}_{j})\times r4+l{b}_{j})& r3<0.5\\ {X}_{j}-TDR\times ((u{b}_{j}-l{b}_{j})\times r4+l{b}_{j})& r3\ge 0.5\end{array}\right.& r2<WEP\\ {x}_{i}^{j}& r2\ge WEP\end{array}\right.$$
(3)

where \({X}_{j}\) is the jth variable of best universe formed so far, TDR is a coefficient, WEP is another coefficient, \(l{b}_{j}\) is the lower bound of jth variable, \(u{b}_{j}\) shows the upper bound of jth variable, \({x}_{i}^{j}\) is the jth variable of ith universe, and r2, r3, r4 are random numbers in [0, 1]. The formula of both coefficients are as follows:

$$WEP=\mathit{min}+l\times \left(\frac{\mathit{max}-min}{L}\right)$$
(4)

where min is the minimum probability of a wormhole is suggested as 0.2, max is the maximum of a wormhole (1 in this paper), \(l\) represents the current iteration, and L indicates the maximum iterations.

$$TDR=1-\frac{{l}^\frac{1}{p}}{{L}^\frac{1}{p}}$$
(5)

where p is the exploitation accuracy over the iterations (6 in this paper). The higher p, the faster and more accurate local search.

2.1.2 Genetic Algorithm (GA)

GA is an efficient technique to solve a variety of optimization problems inspired by genetic science. Genetics deals with how biological information is inherited and transmitted from one generation to the next among living things (Mai et al. 2020). According to genetics, the main factor in transferring biological information in living organisms are chromosomes and genes. In the process of generational transfer, superior stronger genes and chromosomes remain, and weaker genes get destroyed. In the implementation process of GA, first, an initial population of individuals is randomly generated without considering any specific criterion. For all zero-generation chromosomes, the fit-value is determined by the objective function; Then, with different mechanisms defined for the selection operator, a portion of the initial population will be selected as the parent and the others as the mutation candidates. These selected individuals will then be cut and mutated. Then, the competency of the solutions obtained for these individuals is compared with that of the initial population (zero generation) in terms of the fit-value (Seghier et al. 2021a, b). The population with the most numbers will be selected as the initial population for the next stage of the algorithm. Each step of the iteration of the algorithm creates a new generation that will move towards evolution according to the modifications made to it.

2.1.3 Hybrid Multi-verse-genetic Algorithm (HMVGA)

The proposed HMVGA consists of two parts: the first part uses MVO to generate the initial position of each universe and evaluate the fitness of objective function; the second part utilizes the GA operators (e.g., crossover and mutation) for converting the generated initial position to chromosome and improved their efficiency. In other words, in the first step, the initial position of each universe is generated, and then a copy of these initial solutions is created and inserted into the GA. The GA converts the initial solutions and their objective function values to chromosomes and genes, respectively. After that, the GA operators are applied to them, and the objective function value is calculated for each of them. Then the chromosomes are returned to the MVO and become universes again. Finally, the universes are sorted based on their fitness, thus completing the first iteration. These steps will continue until the termination conditions are satisfied. The pseudo-codes of the proposed MVGA is presented in Algorithm 1.

figure a

2.2 Reliability Analysis Method

For probabilistic modeling of systems and considering the effect of the uncertainty parameter on resistance (R) and the load (L), it is necessary to define one or more limit state functions (LSF). If \({\varvec{X}}=[{x}_{1},{x}_{2},\dots ,{x}_{n}]\) the parameter vector has uncertainty, the limit state function of the system is defined as follows (Jafari-Asl et al. 2021c, d):

$$g\left(x\right)=R-\mathrm{L}$$
(6)

The limit state function modeling estimates three states for the system:

$$\left\{\begin{array}{l}g\left(x\right)<0 \quad The\;system\;is\;fail\\ g\left(x\right)>0 \quad The\;system\;is\;safe\end{array}\right.$$
(7)

If g(x) = 0, the system is in between working and failed. Based on this, the failure probability of system is estimated as follows:

$${P}_{f}=Prob\left[g\left({\varvec{X}}\right)\le 0\right]=\int \dots {\int }_{g\left({\varvec{X}}\right)\le 0}{f}_{{\varvec{X}}}\left({x}_{1},{x}_{2},\dots ,{x}_{n}\right){dx}_{1}{dx}_{2}\dots {dx}_{n}$$
(8)

where \({f}_{{\varvec{X}}}\left({x}_{1},{x}_{2},\dots ,{x}_{n}\right)\) is the joint probability density function (PDF) of \({\varvec{X}}\).

Due to the complexity of the integral and the difficulty of a direct solution, in recent decades, researchers have proposed various solving methods. MCS is one of the most accurate methods available, which is utilized in this study.

2.2.1 Monte Carlo Simulation (MCS)

The basis of Monte Carlo Simulation methods for estimation of the probability of failure is the production of random samples in accordance with the joint probability density function of the random variables, where the response of the system is calculated for each set of random variables generated. In this method, random samples are produced based on the statistical distribution functions of the various random variables and then the LSF is assessed based on each set of samples, and the probability of system failure is calculated by dividing the number of states g(X) ≤ 0 by the total number of sample sets (Eq. (9) and (10)) (Jafari-Asl et al. 2021c).

$${P}_{f}=P\left[g\left({X}_{1},{X}_{2},\dots , {X}_{n}\right)\le 0\right]=\frac{1}{N}{\sum}_{i=1}^{N}I\left({X}_{1},{X}_{2},\dots , {X}_{n}\right)$$
(9)

where, N is the total number of simulations, \(I\left({X}_{1},{X}_{2},\dots , {X}_{n}\right)\) is a function defined by:

$$I\left({X}_{1},{X}_{2},\dots , {X}_{n}\right)=\left\{\begin{array}{c}1 if g\left({X}_{1},{X}_{2},\dots , {X}_{n}\right)<0 \\ 0 if g\left({X}_{1},{X}_{2},\dots , {X}_{n}\right)>0\end{array}\right.$$
(10)

2.3 Proposed Method

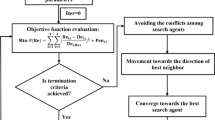
In the present study, a new optimization algorithm as a combination of MVO and GA was developed for optimal dam reservoir operation under uncertainties. For this purpose, the data of the study repository was initially inserted into Easy-Fit software, and the statistical distribution type of variables was determined. The MVGA was then combined with the MCS to provide an optimal schedule for operating the reservoirs in the event of parameter uncertainties. The general flowchart of the method is shown in Fig. 1:

Fig. 1
figure 1

Flowchart of MVGA-MCS

Full size image

2.4 Case Study of Benchmark Functions

Before using the new algorithm to solve the reservoir operation problem, we used six benchmark functions that have already been used in several types of research to evaluate the performance of the new algorithm in comparison with GA and MVO. Table 1 shows the benchmark functions and their characteristics (MiarNaeimi et al. 2018; Safaeian Hamzehkolaei and MiarNaeimi 2021).

Table 1 The Mathematical benchmark functions
Full size table

2.5 Case Study of Karaj Reservoir

Amir Kabir reservoir is located near the Karaj River in the north of Karaj (Iran) along the longitude of 51° 30′ 58'' and latitude of 35o 58′ 45''. The elevation is 1297 m above sea level. This reservoir is one of the most important resources for agricultural usage in Karaj and supplying drinking water for both Tehran and Karaj. Karaj reservoir basin area is about 864 km2, and its average annual yield is about 415 MCM. Figure 2 displays the location of Karaj reservoir.

Fig. 2
figure 2

The location of the study area in Iran

Full size image

The study period of the present study starts from March 2007 to February 2018 (132 months). Monthly data included are rainfall, entrance flowrate to reservoir, evaporation rate, seepage, overflow, drinking and agricultural demands. Table 2 indicates the demand values of drinking water of Tehran and Karaj as well as the amount of agricultural demand in Karaj.

Table 2 Monthly requirements for the study area (Mm3)
Full size table

2.6 Reservoir Optimization Model

2.6.1 Objective function

In the present study which emphasize to optimize the operation of the Amir Kabir reservoir, the objective function was defined as summation of the square difference between the agricultural demands and the release (\({D}_{t}-{R}_{t}\)) (Dahmani and Yebdri 2020):

$$F=\sum\limits_{t=1}^{NT}{\left(\frac{{D}_{t}-{R}_{t}}{{D}_{max}}\right)}^{2}$$
(11)

The purpose is minimizing. For its normalization, the difference between agricultural demands and the release were divided to the maximum demand (Dmax). In this equation, NT is the total period, Dt represents the rate of demand in the period t, Rt denotes the release rate, and Dmax shows the maximum absolute need in the total periods.

2.6.2 Problem Constraints

Constraints are one of the critical elements in optimization problems that define the range of possible solutions in these problems. Continuity equation is the most important constraints in this optimization problem, which is determined based on Eq. (12).

$${S}_{t}+\Delta {S}_{t}={S}_{t+1}$$
(12)

In this equation, the volume of storage at the beginning of the period is St and the volume at the end of the period is St+1.Also, the volume change during the period is computed \(\Delta {S}_{t}\), which is considered as Eq. (13).

$$\Delta {S}_{t}={I}_{t}+{P}_{t}-{O}_{1t}-{E}_{t}-{O}_{2t}-P{e}_{t}$$
(13)

where \({I}_{t}\) is the input to the reservoir at time t, \({P}_{t}\) denotes the amount of rainfall on the surface of the reservoir, \({O}_{1t}\) represents the output of the reservoir, which includes the output to agriculture and drinking water, \({E}_{t}\) is evaporation rate from the surface of reservoir water, \(P{e}_{t}\) indicates the overflow rate from the reservoir.

The release rate in each period should not be less or more than a specific limit. In other words, as shown in Eqs. (14) and (15), the release at each interval (Ri) must be between the minimum (Rmin) and maximum release rate (Rmax). Meanwhile, the volume of the reservoir at each period (Si) must be between the minimum (Smin) and the maximum volume of the reservoir (Smax).

$${{R}_{min}\le R}_{i}\le {R}_{max}$$
(14)
$${{S}_{min}\le S}_{i}\le {S}_{max}$$
(15)

Also, the resiliency, and vulnerability indices used by Bozorg-Haddad et al. (2021) are considered to evaluate the performance of developed models compared with together. The resiliency of the reservoir is defined by the time a system takes to recover from the failure state to normal state. The resiliency index can be expressed as:

$$\gamma =\frac{{f}_{s}}{f}$$
(16)

In which, γ represents the resiliency index, f is number of the states, and \({f}_{s}\) is the total number of failures occurring during the entire operation period. The vulnerability denotes to the extent of possible reservoir failures and can be expressed as:

$${M}_{f}={Max}_{NT}\frac{({D}_{t}-{R}_{t})}{{D}_{t}}$$
(17)

where \({M}_{f}\) represents the largest failure observed in a continuous series of failures.

3 Results and Discussion

3.1 Mathematical Functions

MVGA was compared with GA, and MVO by minimizing four benchmark functions. Finding the best values ​​of the setting parameters of algorithms has a significant effect on convergence and finding the optimal solution. These parameters are generally defined by sensitivity analysis. To solve the benchmark problems, the values ​​of these parameters are determined based on the reference articles. Also, the maximum number of iterations and the initial population of the algorithms were considered to be 500 and 30 (Table 3). In the optimization process, the WEP parameter increases linearly from 0.2 to 1, and the TDR parameter decreases linearly from 1 to 0.

Table 3 Parameter settings of counterparts
Full size table

Twenty runs were applied for each function provided in Table 4 to examine the effectiveness of MVGA. According to Table 4, the average of 20 MVGA performances is the lowest compared to GA and MVO for the six benchmark functions. Concerning the best solution obtained, MVGA was able to find the minimum value in all six benchmark functions. The Wilcoxon rank-sum test was performed to show the solution accuracy found by MVGA and their non-randomness. This test is non-parametric and statistical, used to evaluate the similarity of two dependent samples. In this test, if the p-value for each algorithm is more than 0.005, it indicates random answers. Since the result of the algorithm that has the best answer, cannot be compared with itself, the probability value of P for the best algorithm is shown with N / A (Not Applicable) (Miarnaeimi et al. 2018). As evident, MVGA has been able to overcome the shortcomings of both the MVO and GA algorithms. Also, according to Fig. 3, MVGA has good convergence in all six benchmark functions; This indicates high speed and accuracy in achieving optimal solution.

Table 4 MVGA, GA, and MVO statistical results of 20 runs for benchmark functions
Full size table
Fig. 3
figure 3

Comparison of convergence curves of MVGA, MVO and GA for benchmark functions

Full size image

3.2 Case of Amir Kabir Reservoir

3.2.1 Deterministic Approach

After evaluating the performance of MVGA to solve the benchmark problems, the setting parameters of Table 3 were used to solve the optimization reservoir operation issue. The decision variable of reservoir operation is finding the optimal monthly release rate from the reservoir. The during of operation in this study is 132 months for Amir Kabir reservoir, so MVGA in this system has 132 decision variables. The problem was solved using MVGA, MVO, and GA over 11-year time series, based on the available information. The solutions obtained from the ten implementations of the three algorithms MVGA, GA, and MVO are shown in Table 5. In terms of average optimal responses, MVGA, MVO, and GA models are in the first to third ranks, respectively, with values of 35.88, 227.76, and 448.87. In terms of coefficient of variation of optimal response, MVGA with 0.10 has the lowest value among the models, and MVO and GA models with 0.70 and 1.16 are in the following ranks, respectively.

Table 5 Ten random results for MVGA, MVO and GA
Full size table

The convergence curve for the studied algorithms in finding the optimal operation model of the Amir Kabir reservoir is shown in Fig. 4. MVGA's high capability in solving large and complex problems has been proved in benchmarks. Figure 4 also shows that MVGA converges faster than the GA and MVO in solving the complex problem of reservoir operation and is closer to the global optimum. The resiliency values and vulnerability indices for the models developed are also available in Table 6. In terms of resiliency, MVGA with a value of 0.536 has the highest value among the models, and MVO and GA are in the following ranks with a decrease of 6.7 and 14.4% compared to MVGA, respectively. In terms of vulnerability, MVGA with 0.55 has the lowest value, and MVO and GA with 8.4 and 33% increases compared to MVGA are in the following ranks, respectively.

Fig. 4
figure 4

Convergence curves of MVGA, MVO and GA Amir Kabir reservoir

Full size image
Table 6 Results of resiliency and vulnerability indices for the Amir Kabir reservoir
Full size table

3.2.2 Reliability-based Design Optimization (RBDO) Approach

To solve the RBDO issue of reservoir operation, the definite constraints of the problem are considered LSF in such a way that by violating any constraint, at any time, the optimal program fails. Demand, inflow, and evaporation are considered uncertain parameters. For this purpose, the statistical distribution of variables is first determined using EasyFit software by using the available databases (Fig. 5). Table 7 represents the statistical distribution of the variables and shows that evaporation and demand have the generalized extreme value (GEV) distribution and Inflow has a lognormal (LN) distribution. Based on Table 8 databases, 1,000,000 sample series are generated for each variable (Fig. 6). The MVGA adjustment parameters are selected according to Sect. 3.2.1 and only the population number and maximum iteration rate are determined according to the sensitivity analysis in this step as 80 and 2500. The probabilistic model developed based on MVGA and MCS was implemented ten times.

Fig. 5
figure 5

Monthly inflow, evaporation, and downstream demand of Amir Kabir reservoir (March 2007 to February 2018)

Full size image
Table 7 The statistical characterization of parameters
Full size table
Table 8 Ten results of MVGA-MCS
Full size table
Fig. 6
figure 6

Histograms of the uncertain variables used to develop the RBDO model

Full size image

The results of ten random run are presented in Table 8. The coefficient of variation resulting from random performances for MVGA-MCS equals 0. 0920. The values of the best and worst solutions are 26.0154 and 35.4957 respectively. Therefore, the difference between the minimum and maximum solutions is less than 8.4803, which is very small. In Fig. 7, the convergence curve of the objective function of the Amir Kabir reservoir operation model was plotted using the RBDO approach by the MVGA-MCS model. As evident, the RBDO approach was able to converge 2500 times.

Fig. 7
figure 7

minimum, maximum, and average solutions of MVGA-MCS for Amir Kabir reservoir

Full size image

The resiliency and vulnerability values for the solution obtained from the RBDO approach are 0.61 and 0.53, respectively, which shows that utilizing the RBDO approach to solve the problem of dam reservoirs operation was able to provide a robust release schedule. Also, considering the uncertainty of the parameters, the probability of failure of the optimal operation program is equal to 0.006% in this case. In the case of definite operation, all three algorithms have been able to minimize the objective function, but in case of uncertainty in the parameters of demand, inflow, and evaporation, it may violate the constraints, which leads to failure. The failure probability of the operation plan provided by the definite models MVGA, MVO, and GA in the presence of uncertainties is 77%, 75%, and 71%, respectively. Figures 8 and 9 show the monthly release and reservoir storage of Amir Kabir Dam based on deterministic approaches of MVGA, MVO, and GA models and RBDO approach. The optimal release of all developed models was almost in the same range, and for storage of the reservoir, all models observed the maximum and minimum range. In general, the findings of this study indicate that the use of MVGA to solve the problem of optimal reservoir operation has a very suitable performance. It is also clear that using the RBDO approach for this purpose leads to an optimal operation plan with higher reliability and resiliency and lower vulnerability.

Fig. 8
figure 8

Released water volume

Full size image
Fig. 9
figure 9

Storage volume evolution

Full size image

4 Conclusion

In the present study, the performance of MVO was evaluated alone and in combination with GA in optimizing the problem of dam reservoir operation in both deterministic and probabilistic states. The study area is Amir Kabir Dam, located in the center of Iran on the Aji Chay River. The during of operation includes 132 months. For performance evaluation of the developed algorithm, first, six benchmark functions were solved. The results of 20 performances for benchmark functions showed that MVGA has higher convergence and accuracy than both GA and MVO. Considering the problem of optimal dam reservoir operation, minimizing the deficit between downstream demand and release from reservoir during the operation period was considered the objective function, Monthly release volume from the reservoir as decision variables and reservoir continuity, reservoir storage volume, and release volume as constraints. In this phase, the results proved the superiority of MVGA over GA and MVO in terms of convergence, target function value, reversibility, and vulnerability. Then, by determining the statistical distribution of inflow, demand, and evaporation variables, a probabilistic model based on MCS and MVGA was developed to solve the problem of reservoir operation under conditions of uncertainty in the parameters. The results also indicate the success of the new hybrid algorithm developed at this phase in finding the optimal solution and determining a robust and reliable program for dam reservoir operation. The value of the resiliency index 61% which is the highest value and vulnerability index 51% was obtained among the MVGA-MCS, MVGA, MVO, and GA models. According to the optimal performance of the algorithm presented in this study, it is suggested to utilize MVGA and a surrogate reliability method for solving reliability-based multi-objective optimization of reservoir operation problem. The performance of this algorithm needs to be evaluated by solving multi-objective problems.