Hybrid Algorithm of Particle Swarm Optimization and Grey Wolf Optimizer for Reservoir Operation Management

Abstract

Metaheuristics are highly efficient optimization methods that are widely used today. However, the performance of one method cannot be generalized and must be examined in each class of problems. The hybrid algorithm of particle swarm optimization and grey wolf optimizer (HPSOGWO) is new swarm-based metaheuristic with several advantages, such as simple implementation and low memory consumption. This study uses HPSOGWO for reservoir operation optimization. Real-coded genetic algorithm (RGA) and gravitational search algorithm (GSA) have been used as efficient methods in reservoir optimization management for comparative analysis between algorithms through two case studies. In the first case study, four benchmark functions were minimized, in which results revealed that HPSOGWO was more competitive compared with other algorithms and can produce high-quality solutions. The second case study involved minimizing the deficit between downstream demand and release from the Hammam Boughrara reservoir located in Northwest Algeria. A constrained optimization model with non-linear objective function was applied. Based on the average solutions, HPSOGWO performed better compared with RGA and was highly competitive with GSA. In addition, the reliability, resiliency, and vulnerability indices of the reservoir operation, which was derived from the three algorithms, were nearly similar to one another, which justified the usability of HPSOGWO in this field.

1 Introduction

Optimization algorithms aim to determine values of decision variables that maximize or minimize an objective function with or without constraints. Several algorithms, such as linear programming (LP; Loucks 1968), non-linear programming (NLP; Arunkumar and Jothiprakash 2012), and stochastic dynamic programming (SDP; Stedinger et al. 1984), have been used to solve problems in reservoir optimization management for a single or a system of reservoirs. Despite the performance and wide usability of the classical methods, they suffer from several disadvantages, such as inability to solve problems with non-linear and non-convex objective functions (i.e., in the case of LP) and the curse of dimensionality (Sharif and Swamy 2014).

Evolutionary optimization algorithms (EOAs) are new methods for searching the approached solutions for optimization problems with reasonable computation time and acceptable accuracy. Several EOAs, such as genetic algorithm (GA; Chang and Chen 1998; Ahmed and Sarma 2005), particle swarm optimization (PSO; Kumar and Reddy 2007; Ghimire and Reddy 2013), gravitational search algorithm (GSA; Bozorg-Haddad et al. 2016), and weed optimization algorithm (WOA; Karami et al. 2019), have been successfully used and efficiently addressed critical issues in reservoir operation management.

EOAs have many drawbacks despite their advantages. First, no evidence demonstrates the generalizability of the performance and superiority of a metaheuristic method across applications (Wolpert et al. 1997). Second, a large part of EOAs can overlook the global optimal solution and become trapped in a local one. Third, several algorithms suffer from imbalance between exploration and exploitation capabilities during a search. Fourth, the majority of EOAs cannot detect the stochastic nature of certain variables (e.g., inflow, evaporation, and non-linear form of constraints; Karami et al. 2019). Finally, EOAs are sensitive to parameter setting. In this context, exploring other algorithms that can surpass these drawbacks is necessary.

Singh and Singh (2017) developed the hybrid algorithm of particle swarm optimization and grey wolf optimizer (HPSOGWO), which is a recent nature-inspired algorithm. It is a combination of PSO (Eberhart and Kennedy 1995) and grey wolf optimizer (GWO) (Mirjalili et al. 2014) that exploits the benefits of the two algorithms and outperform their drawbacks. During the optimization process, search agents in HPSOGWO mimic the hunting behavior of grey wolves (Canis lupus) via the GWO and update their positions by using the PSO approach. Similarities exist between GWO and HPSOGWO in the majority of the structure. However, HPSOGWO retains the main advantages of the GWO, such as the simple design, ease of coding, and low memory consumption (Faris et al. 2018). The authors of HPSOGWO compared it with PSO and GWO by minimizing 23 benchmark functions from the work of Yao et al. (1999). Based on statistical results, HPSOGWO displays better performance in terms of solution quality, stability, computational time, and capability to achieve the global optimum.

The water resource management field has yet to apply HPSOGWO, which may encourage researchers to explore its capabilities in this field. Thus, this study tests and compares HPSOGWO with RGA and GSA. Comparison was based on minimizing four benchmark functions and solving the reservoir operating optimization problem with a constrained non-linear objective function. The algorithms were evaluated based on the statistical results of analysis on the one hand and the reliability, vulnerability, and resiliency indices of reservoir operation on the other hand. Examining the performance of HPSOGWO in dealing with the aforementioned problems is the ultimate objective of this study.

2 Materials and Methods

2.1 Optimization Techniques

2.1.1 Hybrid PSOGWO

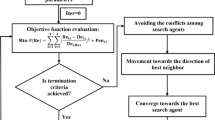
HPSOGWO is a novel hybrid metaheuristic algorithm, which merges the functionalities of PSO with GWO to improve the exploration and exploitation abilities of GWO and PSO, respectively (Singh and Singh 2017). HPSOGWO imitates the hunting behavior of grey wolves in nature in the form of GWO. Grey wolves live in groups of 5 to 12 members with a strict hierarchy organized from top to bottom in four categories, namely, alpha (α), beta (β), delta (δ), and omega (ω). The alpha is considered the dominant member of the group and is responsible for making decisions regarding the social behavior of the group especially during hunting. The beta and delta are subordinate to the alpha and can control the remainder of the group (omega). The hunting mechanism of grey wolves has specific steps as follows: (1) tracking, chasing, and approaching,(2) pursuing, encircling, and harassing the prey until it stops moving, and (3) attacking.

In the mathematical model, HPSOGWO runs in the following steps:

• 1. N grey wolves are defined and placed randomly in the search space as follows:

  $$ X_{i} = \{ {x_{i}^{1}}, {x_{i}^{2}}, ... {x_{i}^{l}}, ... , {x_{i}^{d}} \} {\kern15pt} i =1, {\dots} N $$

  (1)

  where ${x_{i}^{l}}$ denotes the position of the i th wolf at the l th dimension, and d refers to the search space dimension.

• 2. Fitness is computed for the search agents by using the objective function. Then, the agents are ranked in descending order according to fitness, and the first three best agents are provided with X_α, X_β, and X_δ attributes, respectively.

• 3. Coefficient vectors $\overrightarrow {a}$, $\overrightarrow {A}$, and $\overrightarrow {C}$ are updated to guide the search process by using the following equations:

  $$ \overrightarrow{a} = 2 (1- \frac{k}{K_{max}}) $$

  (2)
  $$ \overrightarrow{A}=2\overrightarrow{a}\cdot \overrightarrow{r}_{1} - \overrightarrow{a} $$

  (3)
  $$ \overrightarrow{C}=2 \cdot \overrightarrow{r}_{2} $$

  (4)

  where k is the current iteration, and K_max denotes the maximum number of iterations. r₁ and r₂ are random vectors in [0,1]. Coefficient $\overrightarrow {a}$ will decrease linearly from 2 to 0 at the end of the process.

• 4. Wolves α, β, and δ are considered closest to the prey because the position of the prey is unknown. The encircling and hunting behaviors can be performed as follows:

  $$ \begin{array}{c} \overrightarrow{D}_{\alpha} = |\overrightarrow{C}_{1} \cdot \overrightarrow{X}_{\alpha} - w * \overrightarrow{X}|, \\ \overrightarrow{D}_{\beta} = |\overrightarrow{C}_{2} \cdot \overrightarrow{X}_{\beta} - w * \overrightarrow{X}|, \\ \overrightarrow{D}_{\delta} = |\overrightarrow{C}_{3} \cdot \overrightarrow{X}_{\delta} - w * \overrightarrow{X}| \end{array} $$

  (5)
  $$ \begin{array}{c} \overrightarrow{X}_{1} = \overrightarrow{X}_{\alpha} - \overrightarrow{A}_{1} \cdot \overrightarrow{D}_{\alpha}, \\ \overrightarrow{X}_{2} = \overrightarrow{X}_{\beta} - \overrightarrow{A}_{2} \cdot \overrightarrow{D}_{\beta}, \\ \overrightarrow{X}_{3} = \overrightarrow{X}_{\delta} - \overrightarrow{A}_{3} \cdot \overrightarrow{D}_{\delta} \end{array} $$

  (6)

• 5. The velocities and positions of the wolves are updated by using the PSO approach as follows:

  $$ v_{i}^{k+1}= w*({v_{i}^{k}} + c_{1} r_{1} (x_{1}- {x_{i}^{k}}) + c_{2} r_{2} (x_{2} - {x_{i}^{k}}) + c_{3} r_{3}(x_{3}-{x_{i}^{k}})) $$

  (7)
  $$ x_{i}^{k+1} = {x_{i}^{k}} + v_{i}^{k+1} $$

  (8)

  where w represents the inertia constant generated randomly in [0,1], and r₃ is a random value in [0,1].

• 6. Repeat steps 2 to 5 until the maximum number of iterations is reached. Afterward, the search agents stop moving, and final position X_α is considered the best solution.

2.1.2 Real-coded Genetic Algorithm

Wright (1991) introduced the real-coded GA (RGA), which is another method of coding individuals using either real or binary values. In RGA, each gene represents a variable of the problem, and the size of genome is kept the same as the length of the solution. Wright (1991), Janikow and Michalewicz (1991), and Chang and Chen (1998) compared the two versions and concluded that RGA produces superior results compared with binary-coded GA.

In RGA and for a given optimization problem, a population of N possible solutions $X_{i} = ({x_{i}^{1}}, {x_{i}^{2}}, ... , {x_{i}^{d}})$ is commonly generated in a pseudo-random manner. During iterations, the population evolves by forming generations of solutions through three operations, namely, selection, crossover, and mutation.

In this version of RGA, the stochastic tournament technique is adopted to perform the selection step, where individuals or ”genomes” from the population are randomly selected for crossover. To perform the crossover operation, the random single-point technique is used. It consists of generating a random index l less than d. Therefore, genomes of the couple exchange genes from index l to d. For example, a pair of genomes $X_{1} = ({x_{1}^{1}},..., {x_{1}^{l}}, ..., {x_{1}^{d}})$ and $X_{2}=({x_{2}^{1}}, ..., {x_{2}^{l}}, ..., {x_{2}^{d}})$ becomes $X_{1}^{\prime } = ({x_{1}^{1}}, ..., {x_{2}^{l}}, ..., {x_{2}^{d}})$ and $X_{2}^{\prime } = ({x_{2}^{1}}, ..., {x_{1}^{l}}, ..., {x_{1}^{d}})$ after performing a crossover.

To operate mutation, a random single-point mutation is employed, where one gene ${x_{i}^{l}}$ is randomly chosen for a selected offspring $X_{i}^{\prime }$ and changed by a random feasible value ${y_{i}^{l}}$. Thus, a set of size 2N includes fathers, and an offspring is obtained. To guarantee convergence, N individuals with low performance are eliminated, and the process is repeated until the maximum number of iterations is reached.

2.1.3 Gravitational Search Algorithm

GSA is one of the novel population-based metaheuristic algorithms. The population in GSA pertains to a set of searcher agents, which are considered masses that interact with one another by the laws of gravity and movement (Rashedi et al. 2009). The GSA process starts with initializing a population by considering a set of N agents $X_{i} = ({x_{i}^{1}}, ..., {x_{i}^{d}})$ defined in the search space with dimension d. The i th position ${x_{i}^{l}}$ of agent X_i in the l th dimension is randomly defined with a feasible value. Then, the fitness of each agent is calculated by using the objective function. Therefore, gravitational and inertia masses are computed as follows:

$$ m_{i}(k)= \frac{fit_{i}(k)-worst(k)}{best(k)-worst(k)} $$

(9)

$$ M_{i}(k)= \frac{m_{i}(k)}{{\sum}_{j=1}^{N} m_{j}(k)} $$

(10)

$$ M_{ai}= M_{pi}=M_{ii}=M_{i} $$

(11)

where fit_i(k) is the fitness value of the i th agent, best(k) and worst(k) are the best and worst fitness, respectively, at iteration k. M_ai, M_pi, and M_ii are active, passive, and inertia masses respectively. The gravitational force acting on agent i by agent j is computed as follows:

$$ F_{ij}^{l}(k)=G(k) \frac{M_{pi}(k) \cdot M_{aj}(k)}{R_{ij}(k)+\epsilon_{g}} ({x_{j}^{l}}(k) - {x_{i}^{l}}(k)) $$

(12)

where R_ij(k) is the Euclidean distance between agents i and j. 𝜖_g is a small constant, and G(k) is the gravitational constant updated at each iteration as follows:

$$ G(k)= G_{0} e^{(\frac{-\alpha_{g} k}{K_{max}})} $$

(13)

where G₀ and α_g are initialized at the beginning, and K_max is the maximum number of iterations. G will be reduced with the increase in iterations. Therefore, the total force acting on agent i is calculated as follows:

$$ {F_{i}^{l}}(k)= \sum\limits_{j \in K_{best}, j\neq i}^{} rand_{j} \cdot F_{ij}(k) $$

(14)

where rand_j is a random number in [0,1], and K_best is the set of first K agents with the best fitness. K_best will decrease linearly, and only one agent will be applying force on the others by the end of the process.

Newton’s law of movement denotes that object acceleration a is dependent only on applied force F and object mass M. In GSA, the following equation is used to calculate acceleration.

$$ {a_{i}^{l}}(k) = \frac{{F_{i}^{l}}(k)}{M_{ii}(k)} $$

(15)

To move agents through the search space, velocities and positions are updated as follows:

$$ {v_{i}^{l}} (k+1) = rand_{i} \cdot {v_{i}^{l}}(k) + {a_{i}^{l}}(k) $$

(16)

$$ {x_{i}^{l}} (k+1) = {x_{i}^{l}} (k) + {v_{i}^{l}} (k+1) $$

(17)

where ${v_{i}^{l}}(k)$ and ${x_{i}^{l}}(k)$ denote the velocity and position, respectively, of agent i in dimension l at iteration k, whereas rand_i is a uniform random variable in [0,1]. The process is repeated until iterations reach their maximum limit, where the best fitness value is the global fitness, whereas the position of the corresponding agent is the global solution.

2.2 Case Study of Benchmark Functions

Before comparing HPSOGWO with RGA and GSA in reservoir operating optimization, four standard mathematical functions as reported by Yao et al. (1999) are used to evaluate the performance of algorithms. Table 1 shows the benchmark functions and their characteristics. Function F₁ is unimodal, which has one global minimum and no local minima. F₂, F₃, and F₄ are multimodal functions with one global minimum and many local minima. The algorithms are launched 20 times independently for each function minimization, where the population size is set to 30, and the maximum iteration number is set to 3,000.

Table 1 Mathematical benchmark functions

2.3 Case Study of Hammam Boughrara Reservoir

The Hammam Boughrara reservoir is the most important reservoir in Tlemcen Wilaya (far Northwest of Algeria). It is located on the confluence between Mouillah and Tafna Rivers at $1^{\circ }39^{\prime }61^{\prime \prime }$W longitude and $34^{\circ }52^{\prime }23^{\prime \prime }$N latitude, 13 km downstream from Maghnia Town. Figure 1 shows the geographic location of the study area. The reservoir is characterized by 177 million cubic meters (MCM) of capacity and 23.3 MCM of dead storage. It drains a basin shared between the Algerian and Moroccan territories with an area of 2,914 km², a perimeter of 241 km, and a main thalweg of 104.4 km. The climate of the basin is semi-arid and experiences a wet season from November to April and a dry season from May to October. Maximum precipitations are observed in December with an average of 64.2 mm, whereas the minimal precipitations occur in July with an average of 2.36 mm. The average annual temperature and wind speed are 18.5^∘C and 24 m/s, respectively. Monthly inflows are variable with a maximum average of 6.29 MCM recorded frequently in November, and a minimum of 0.88 MCM in June. The reservoir started operations in September 2000 for multiple purposes, such as (1) water supply for Maghnia at 17 MCM/year, (2) water supply reinforcement for Oran Town (located approximately 140 km Northeast of Maghnia) at 33 MCM/year, and (3) irrigation for the Maghnia perimeter (6,000 ha) at 9 MCM/year. The perimeter is supplied with 38 MCM/year of water by the Beni Bahdel reservoir, which is located approximately 30 km upstream from the Hammam Boughrara reservoir.

Fig. 1

Location of Hammam Boughrara reservoir

2.4 Reservoir Optimization Model

In general, the operation of the reservoir is governed by the following constraints:

2.4.1 Mass Balance Constraints

$$ S_{t+1} =S_{t} + Q_{t} - R_{t} - Ev_{t} - I_{t} - O_{t} \qquad t=1,{\dots} T $$

(18)

where S_t and S_t+ 1 are the starting and ending reservoir storage (in MCM), respectively, at time period t. Q_t, R_t, Ev_t, I_t, and O_t are inflow, release, evaporation, infiltration, and overflow (MCM), respectively, during time period t. T pertains to operating duration.

The evaporation loss is computed as follows:

$$ Ev_{t} = ev_{t} A_{t} $$

(19)

where ev_t and A_t are evaporation and reservoir area, respectively, at time period t.

2.4.2 Storage Constraints

$$ S_{min} \leq S_{t} \leq S_{max} {\kern30pt}t =1,{\dots} T $$

(20)

where S_min and S_max are the minimum and maximum storage volumes, respectively, of the reservoir (MCM).

2.4.3 Release Constraints

$$ 0 \leq R_{t} \leq D_{t} {\kern50pt}t =1,{\dots} T $$

(21)

where D_t is downstream demand (MCM) at time period t.

2.4.4 Overflow Constraints

During the operating period of the reservoir, overflow O_t is estimated as follows:

$$ O_{t}= Max((S_{t+1} - S_{max}),0){\kern30pt} t =1,{\dots} T $$

(22)

2.4.5 Constraints Application

If constraints (Equations [20] and [21]) are not satisfied, then the following penalties are applied (Karami et al. 2019):

$$ P_{1,t} = \begin{bmatrix} \frac{(S_{min}-S_{t+1})^{2}}{S_{min}} & \longleftarrow \ & \text {if} S_{t+1} < S_{min}\\ 0 & \longleftarrow & \text{otherwise} \end{bmatrix} $$

(23)

$$ P_{2,t} = \begin{bmatrix} (\frac{S_{t+1}-S_{max}}{S_{max}})^{2} & \longleftarrow \ & \text {if} S_{t+1} > S_{max}\\ 0 & \longleftarrow & \text{otherwise} \end{bmatrix} $$

(24)

$$ P_{3,t} = \begin{bmatrix} \frac{(R_{t}-D_{t})^{2}}{D_{max}} & \longleftarrow \ & \text {if} R_{t}> D_{t}\\ 0 & \longleftarrow & \text{otherwise} \end{bmatrix} $$

(25)

where D_max denotes the maximum downstream demand (MCM) over the considered operating duration T.

2.4.6 Objective Function

This study aims to minimize water supply deficits from the reservoir. As a result, volumes of release are considered decision variables. By applying penalties, the optimization function is expressed as follows:

$$ Minimize(Z) = \sum\limits_{t=1}^{T} ((\frac{R_{t}-D_{t}}{D_{max}})^{2} + P_{1,t} + P_{2,t} + P_{3,t}) $$

(26)

where T is considered 36 months. Figure 2 shows the monthly inflow, downstream demand, and evaporation loss curves from September 2009 to August 2012 (36 months). These data are used as input to the optimization model. In addition, the average of monthly infiltration loss (0.033 MCM) is considered. Notably, hydrological and water consumption data are provided by the water service office of Tlemcen.

Fig. 2

Monthly inflow, evaporation, and downstream demand of Hammam Boughrara reservoir (September 2009 to August 2012)

2.5 Evaluation Indices

The reliability, resiliency, and vulnerability indices proposed by Hashimoto et al. (1982) are considered to evaluate the performance of HPSOGWO compared with RGA and GSA.

2.5.1 Reliability

Volumetric reliability (a_v) reflects the relation between release and downstream demand for total operation period T:

$$ a_{v} = \frac{{\sum}_{t=1}^{T} {R_{t}}} {{\sum}_{t=1}^{T} D_{t}} $$

(27)

2.5.2 Resiliency

It is defined by the time a system takes to return to normal state following a failure state:

$$ \gamma = \frac{f_{s}}{f} $$

(28)

where γ represents the resiliency index, f is the number of failure periods, and f_s pertains to the number of failure series, which is a sequence of successive failure periods preceded and followed by non-failure periods.

2.5.3 Vulnerability

Vulnerability index (σ) measures the severity of failures:

$$ \sigma = \frac{{\sum}_{j=1}^{f_{s}} \max(Sh_{j})} {f_{s}} $$

(29)

where Sh_j is the maximum shortage during the j th failure series.

3 Results and Discussion

3.1 Mathematical Functions

HPSOGWO was compared with RGA and GSA by minimizing four benchmark functions. Twenty runs were applied for each function provided in Table 1 to examine the effectiveness of HPSOGWO. A population of 30 agents and 3,000 iterations were employed, which indicates that a 9.0E + 04 evaluation function was performed for each run. The parameters of HPSOGWO were set as follows: C₁ = C₂ = C₃ = 0.5 and w = 0.5(Rand() + 1). However, the mutation frequency was set to 0.2 for RGA, whereas those of GSA were set as follows: G₀ = 100 and α_g = 20.

Table 2 reports the statistical comparison of the solutions found over 20 runs. Clearly, HPSOGWO found the best solutions, which were closest to the global minimum of functions F₁, F₂, and F₃. However, the best solutions of the three algorithms were closer to one another for function F₄. In addition, the average and standard deviation of the HPSOGWO solutions were best for F₃ and second best for the remainder.

Table 2 HPSOGWO, RGA, and GSA statistical results of 20 runs for benchmark functions

According to the mean values of the F₂ solutions, the three algorithms failed to reach the global minimum of function F₂ over several runs, which indicates that they were trapped in the local minima. Results confirm those by Rashedi et al. (2009) and Singh and Singh (2017). Moreover, the results obtained by RGA largely differed from the overall minima of F₁, F₂, and F₃, which may be caused by the small population size (N = 30). Rashedi et al. (2009) and Bozorg-Haddad et al. (2016) revealed comparable findings when they used small population sizes in RGA.

Figure 3 displays the average values of the convergence trends. Clearly, HPSOGWO converged slower than RGA and GSA for F₁, F₂, and F₃, but converged simultaneously with RGA and was faster than GSA for F₄. However, a stagnation of the RGA convergence trend was observed far from the global minimum for F₁ and F₃, whereas it has progressed slowly for F₂. In addition, another stagnation was observed for F₂ and F₃ by GSA, which indicates the trapping of RGA and GSA in the local minima. On the contrary, the average convergence curve of HPSOGWO was improved with the progress in iterations in all cases, which indicates that it could escape from local minima trapping. Thus, the results demonstrate the effectiveness of HPSOGWO in solving similar problems.

Fig. 3

Average convergence trends of HPSOGWO, RGA, and GSA for mathematical functions

3.2 Case of Hammam Boughrara Reservoir

Table 3 reports the sensitivity analysis of HPSOGWO, RGA, and GSA. The test was carried out to determine the suitable values of algorithm parameters. For HPSOGWO, the best objective function value (3.05E − 08) was achieved by a population size of 30 and C₁ = C₂ = C₃ = 0.6. For RGA, a population size of 100 and a mutation frequency of 0.2 provided the best objective function value (8.57E − 05). Typically for GSA, a population size of 100, α_g = 10, and G₀ = 20 are necessary to obtain the best value of the objective function (1.31E − 07). Thus, the HPSOGWO found the best solution using the small search population size (N = 30). In addition, Table 3 highlights that the solutions achieved by RGA and GSA were improved by increasing the population size and, consequently, function evaluation. Notably, the maximum number of iterations equals 3,000 was applied.

Table 3 Sensitivity analysis of RGA, GSA, and HPSOGWO

Table 4 provides the results of 10 random runs of the three algorithms, where the tuning parameters values cited in Table 3 that gave the best solutions were used. Results in Table 4 also indicate that HPSOGWO found the best solution, whereas the worst, average, and standard deviation of HPSOGWO were worse than those of GSA, but better than those of RGA. The variation coefficient results of HPSOGWO was less than those of RGA and GSA, which indicate that HPSOGWO is less stable compared with the others. Despite the high value of variation coefficient, the average and standard deviation values prove the efficiency of HPSOGWO.

Table 4 Ten random results for HPSOGWO, RGA, and GSA

Figure 4 shows a comparison between the convergence trends of the algorithms and the minimum, maximum, and average solution curves for HPSOGWO. Results show that the convergence of HPSOGWO occurred earlier than RGA and GSA, and their minimum, maximum, and average solution curves were converged to one another.

Fig. 4

a convergence trends of HPSOGWO, RGA, and GSA for Hammam Boughrara reservoir and b minimum, maximum, and average solutions for HPSOGWO algorithm

Figure 5 presents the results of the root square mean error (RMSE) between monthly release and downstream demand. The RMSE of the HPSOGWO results were in the order of 2.5E − 04 and better than RGA for each month by 100%, which is also better than those of GSA in the majority of months by 75%.

Fig. 5

Monthly RMSE of algorithms during the operation period (MCM)

Figure 6 illustrates the optimal releases from the Hammam Boughrara reservoir as calculated by the three algorithms and storage evolution during the operating period. Results indicate the superposition of the release curves with downstream demand for the three algorithms. The derived curves for storage presented the same trend and found between the minimum and maximum storage volumes of the reservoir. In fact, they evidently show the algorithms’ consideration of the minimum and maximum storage constraints.

Fig. 6

a released water volume and b storage volume evolution

Table 5 presents high reliability and resiliency, and low vulnerability for all algorithms. The values of the indices were identical for HPSOGWO and GSA and better than RGA. These finding confirms the previous results and proves the capability of HPSOGWO to optimize reservoir operation.

Table 5 Results of reliability, resiliency, and vulnerability indices for the Hammam Boughrara reservoir

4 Conclusion

Evolutionary algorithms have recently been used to solve a wide range of optimization problems. This study evaluated a hybrid algorithm of PSO and GWO, which is collectively called HPSOGWO. The study used two case studies, namely, minimizing four benchmark functions and solving the single reservoir optimization problem using the non-linear objective function. In addition, HPSOGWO was compared with two efficient algorithms, namely, RGA and GSA, whose performances were verified in the literature.

In the first case study, the algorithms were independently run for 20 times, where HPSOGWO proved its competitive capability of minimizing unimodal and multimodal mathematical functions. It was ranked the most powerful among half of the studied benchmarks and second for the remainder.

Optimizing the Hammam Boughrara reservoir operation was selected as the second case study, where the three algorithms were independently run 10 times. Sensitivity analysis demonstrated that HPSOGWO required a small search population size and can achieve high-quality solutions. Moreover, the average monthly RMSE indicated the high precision of release computation by HPSOGWO compared with the other algorithms. However, the average and standard deviation of the results revealed that HPSOGWO ranked second to GSA. The reliability and resiliency indices for the algorithms were high, whereas the vulnerability index was low. Furthermore, the indices for HPSOGWO and GSA were identical and better than RGA. Hence, the previous results prove the usability of HPSOGWO for such problems.

Despite the capability of HPSOGWO to overcome trapping in the local minima, it suffers from drawbacks, such as low stability, which is indicated by the high value of variation coefficient compared with RGA and GSA. Thus, additional efforts are needed to improve its performance.