Sustainable Conjunctive Water Use Modeling Using Dual Fitness Particle Swarm Optimization Algorithm

Abstract

In any meta-heuristic algorithm, each search agent must move to the high-fitness areas in the search space while preserving its diversity. At first glance, there is no relationship between fitness and diversity, as two key factors to be considered in selecting a guide for the solutions. In other words, each of these factors must be evaluated in its specific and independent way. Since the independent ways to evaluate the fitness and diversity usually make any meta-heuristic consider these factors disproportionately to choose the guides, the solutions’ movements may be unbalanced. In this paper, we propose a novel version of the Particle Swarm Optimization (PSO) algorithm, named Dual Fitness PSO (DFPSO). In this algorithm, not only fitness and diversity of the particles are properly evaluated, but also the abilities to evaluate these features are integrated to avoid the abovementioned problem in determining the global guide particles. After verification of the DFPSO via applying them to several benchmark functions, it is applied to solve a real-world optimal conjunctive water use management problem. The objective is minimizing shortages in meeting irrigation water demands under several climatic conditions. The optimal results suggest that while the water demands are desirably met, the cumulative groundwater level (GWL) drawdown is highly decreased to help maintain the sustainability of the aquifer, demonstrating the high efficiency of the DFPSO to also handle the practical engineering problems.

1 Introduction

1.1 Particle Swarm Optimization

Particle Swarm Optimization (PSO) is a stochastic population-based meta-heuristic technique, first proposed by Kennedy and Eberhart (1995). The population of the PSO algorithm includes several particles which mimic animals’ social behavior such as insects, birds, and fishes in their movements in the space. Each particle attempts to find food cooperatively, while frequently changing the search pattern based on the experiences of itself and other particles in finding food (Wang et al. 2018). The population diversity at any step of the PSO algorithm is of great importance to improve the global search of the algorithm. In PSO, the easiest way to preserve diversity in the population is resetting or mutating some particles, whenever diversity is going to be lost (Wang et al. 2018). Wu et al. (2014) proposed a superior-guided PSO (SSG-PSO) with a novel solution-based mutation strategy. In this algorithm, a set of superior solutions are updated using the evolutionary operators and other solutions learn from these recorded solutions. Zhou et al. (2016) proposed a reverse learning competitive PSO algorithm utilizing competitive group optimization and reverse learning mechanism and chose the best-matching learning mechanisms concerning the fitness value of the particles. Chen et al. (2018) employed two different crossover operations to find promising exemplars. Then, through applying crossover on the personal historical best position of each particle, the effective exemplars were bred to better preserve the diversity. Rezaei and Safavi (2020) proposed the GuASPSO algorithm as a novel PSO variant. In this algorithm, the local guide particles are all divided into several clusters to endow every region in the search space with a chance to globally guide the particles. This chance is set to be gradually decreased as the iterations go on to balance the exploration and exploitation phases of the GuASPSO. Liu et al. (2021) utilized the Gaussian white noise with adjustable intensity to randomly perturb the acceleration coefficients of the PSO in order not to only keep the diversity of the swarm, but also to boost the chance of the particles not being trapped in local optima.

1.2 Conjunctive Water Use Management

Conjunctive water use was first conceptualized by Burt (1964). The use of both sources of surface water and groundwater brings about some advantages and disadvantages. Groundwater suffers no losses due to seepage, leakage, evaporation, and water transfer, and this fact bestows groundwater superiority to the surface water (Afshar et al. 2010). The groundwater is subject to low sedimentation. In addition, the groundwater vulnerability to be contaminated and climate change-resulting droughts are of low chance. The main disadvantage of the groundwater use may be hidden in its need for a high amount of energy for pumping, leading it to be costly to be extracted from the underlying water table. Soil subsidence due to groundwater over-extraction is another disadvantage of this source of water. The surface water also benefits from some unique advantages including the capability for generating electrical energy and providing a suitable bed for recreation and flood control. Among the disadvantages, the construction of the large surface water reservoirs is always breeding crucial environmental problems such as providing the possibility for the downstream of the river feeding the reservoir to be desiccated. The conjunctive use of both surface and groundwater use can hold a good balance between the advantages and disadvantages of these water resources (Hollander et al. 2009).

There are plenty of researches being carried out to investigate the different effects of conjunctive water use management on societies. Rezaei et al. (2017a) proposed a novel multi-objective PSO algorithm, named f-MOPSO, utilizing the transformation of the diversity to the extremity of the non-dominated solutions in the objective space. The algorithm was designed to solve a bi-objective conjunctive water use management problem. Rezaei et al. (2017b) developed the f-MOPSO to also handle a tri-objective optimal multi-crop pattern planning problem. Fazlali and Shourian (2018) applied a nested optimization procedure coupling the shuffled frog leaping algorithm (SFLA) and the network flow programming (NFP) algorithm to maximize the net benefit obtained from the crop production. Wei et al. (2020) developed an optimization model for water resource allocation based on interval-parameter two-stage stochastic programming. Kerebih and Keshari (2021) developed a coupled simulation–optimization-based conjunctive water use model. The simulator was the MODFLOW whose simulation results were introduced to the optimization model utilizing the response matrix method. Majedi et al. (2021) developed another simulation–optimization framework in which the water balance and the water resources reserves were simulated by the MODFLOW and WEAP models, respectively. The simulators were then linked to the NSGA-II to maximize the supply of water and hydropower demands while sustaining the aquifer.

1.3 The Proposed Algorithm and the Organization of the Paper

This paper aims to propose a novel improved variant of the PSO algorithm, named Dual Fitness Particle Swarm Optimizer (DFPSO). We found one of the special features of the fuzzy logic theory called fuzzy implication function very useful to enhance the capabilities of the PSO algorithm. The organization of this paper is as follows. Section 2 describes the methodology introducing the original PSO algorithm and the proposed DFPSO algorithm in detail. In Sect. 3, the proposal is validated through implementation on a set of benchmark functions. Section 4 first introduces the study area and the mathematical formulation of the optimal conjunctive water use management model. Thereafter, the proposed DFPSO algorithm is applied to solve this model and the results are presented and discussed in detail in Sect. 5. Finally, Sect. 6 concludes the paper.

2 Methods

2.1 Original Particle Swarm Optimization (PSO)

Suppose for a D-dimensional optimization problem, ${X}_{i}=({x}_{i1}, {x}_{i2}, \dots , {x}_{iD})$ and ${V}_{i}=\left({v}_{i1}, {v}_{i2}, \dots , {v}_{iD}\right)$ are the ith particle’s position vector and velocity vector, respectively. If ${Pbest}_{i}^{t}=\left({p}_{i1}, {p}_{i2}, \dots , {p}_{iD}\right)$ is the personal best (Pbest) position of the ith particle and ${Gbest}^{t}=\left({p}_{g1}, {p}_{g2}, \dots , {p}_{gD}\right)$ represents the global best (Gbest) position of the swarm at the tth iteration, the velocity and position of each particle are updated using Eqs. (1) and (2).

$$V_{i}^{t+1}=wV^{t}_{i}+c_{1}r_{1}(Pbest^{t}_{i}-X^{t}_{i})+c_{2}r_{2}(Gbest^{t}+X^{t}_{i})$$

(1)

$${X}_{i}^{t+1}={X}_{i}^{t}+{V}_{i}^{t+1}$$

(2)

where i Є{1, 2, …, N}, D is the number of dimensions and N is the swarm size; superscript t is the iteration number; w is the inertia weight; r₁ and r₂ are two random vectors and c₁ and c₂ are cognitive and social scaling parameters, respectively. An efficient form of Eq. (2) is the constriction coefficient model shown below (Rezaei et al. 2017a):

$${V}_{i}^{t+1}=\chi [{V}_{i}^{t}+{\varphi }_{1}\left({Pbest}_{i}^{t}-{X}_{i}^{t}\right)+{\varphi }_{2}\left({Gbest}^{t}-{X}_{i}^{t}\right)]$$

(3)

where $\chi$, ${\varphi }_{1}$, and ${\varphi }_{2}$ are introduced in Eq. (5).

$$\chi =\frac{2k}{|2-\varphi -\sqrt{\varphi (\varphi -4)}|}; \varphi ={\varphi }_{1}+{\varphi }_{2}; {\varphi }_{1}={c}_{1}{r}_{1}; {\varphi }_{2}={c}_{2}{r}_{2}$$

(4)

where χ is the constriction factor. The parameter k Є [0,1] in Eq. (5) controls the exploration and exploitation abilities of the swarm, which can be calculated as follows:

$$k= {k}_{max}-\frac{{k}_{max}-{k}_{min}}{{iter}_{max}}\times t$$

(5)

where k_max and k_min are constants that must be set properly; t is the number of iterations, and iter_max is the maximum number of iterations.

2.2 The Proposed Method: Dual Fitness Particle Swarm Optimization (DFPSO)

The major shortcoming the PSO algorithm suffers from is lacking a strategy to maintain the diversity of the particles in the search space while optimization is going on over the iterations. In this paper, a novel approach is proposed to simultaneously evaluate diversity of the particles along with their fitness by a single index. According to the fuzzy logic, the multiplication of the fuzzy membership degrees of several variables represents their similarity. This multiplication is named the product-based Larsen implication function. On the other hand, the multiplication of several fuzzy membership degrees, denoted by ${\mu }_{1}\times {\mu }_{2}\times \dots \times {\mu }_{n}$, can be regarded as the pseudo-geometric average of those membership degrees, i. e. the geometric average of all membership degrees denoted by $\sqrt[n]{{\mu }_{1}\times {\mu }_{2}\times \dots \times {\mu }_{n}}$ without defining the nth root for the product. When the root of the geometric average is the same for all products in comparisons such as the case study in this paper, the nth root could be neglected in calculations. Therefore, the product of the membership degrees assigned to several particles’ objective values can simultaneously reflect the average and the similarity existing among these particles. In DFPSO, the total fitness of a particle depends on the dual fitness of its opposite particles. When calculating the objective function values obtained for each particle at each iteration, the new Pbest particle is selected. Then, for all opposite Pbest particles of a certain Pbest particle, the pseudo-geometric average of the fuzzy membership degrees attributed to the Pbests is calculated. In a minimization problem, when the product of the membership degrees of the opposites of a focused particle is increased, firstly all the opposite objectives are of larger and thus, worse values, and secondly the similarity among these objectives increases, indicating that these particles are located at a more-densely populated region. Consequently, the focused particle has a smaller objective value and is, at the same time, more diversified in the search space, representing its suitability. With a similar inference, the less the pseudo-geometric average value for a given particle, the worse that particle will be. As a result, the pseudo-geometric average can be used as a weight for each particle, delineating its power to guide other particles. To accomplish this idea, an ascending sigmoidal fuzzy membership function for a given set of x values should be defined as follows:

$$f\left(x\right)=\frac{1}{1+ {e}^{a(x-c)}}$$

(6)

where a and c are the tunable parameters of the fuzzy membership function and a < 0. This function defines the membership degree of the variable x to the set of “high x values”. Rezaei et al. (2017a) proved that $c=\mu$ and $a=\frac{-4}{\sigma \sqrt{e}}$, where $\mu$ is the mean of the x values belonging to the x fuzzy set and $\sigma$ is the standard deviation of the x set. In addition, e is Napier’s constant. Replacing x with the objective function value of a given Pbest particle, the fuzzy membership degree of the jth Pbest particle can be calculated according to Eq. (8).

$${MF}_{j}^{t}=\frac{1}{1+\mathrm{exp}\left[-\frac{4}{{\sigma }^{t}\sqrt{e}}\times \left({Z}_{Pbest,j}^{t}-{\mu }^{t}\right)\right]};j=1, 2, \dots , N$$

(7)

where ${Z}_{Pbest,j}^{t}$ is the objective function value of the jth Pbest particle in the tth iteration, ${\sigma }^{t}$ is the standard deviation of the objective function values of all Pbest particles in the tth iteration, ${\mu }^{t}$ is the mean of the Pbest particles’ objective values in the tth iteration, ${MF}_{j}^{t}$ is the fuzzy membership function value of the jth Pbest particle and $N$ is the number of particles in the swarm. Then, the dual fitness index (DFI) of the ith Pbest particle can be calculated as follows.

$${DFI}_i^t={MF}_1^t\times\dots\times{MF}_{i-1}^t\times{MF}_{i+1}^t\times\dots\times{MF}_N^t={\textstyle\prod_{\begin{array}{c}j=1\\j\neq1\end{array}}^N}{MF}_j^t$$

(8)

where $N$ is the swarm size and ${DFI}_{i}^{t}$ is the dual fitness index assigned to the ith particle at the tth iteration. Therefore, a weighted average should be defined for all Pbest particles to yield the unique Gbest for each of them. Equation (10) indicates the mentioned relation:

$${Gbest}_{i}^{t}=\frac{\sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{N}{DFI}_{j}^{t}{\times Pbest}_{j}^{t}}{\sum_{j=1}^{N}{DFI}_{j}^{t}+\varepsilon }$$

(9)

where ${Gbest}_{i}^{t}$ is the global best particle calculated for the ith particle in the tth iteration and ${Pbest}_{j}^{t}$ is the personal best particle for the jth particle in the tth iteration. Moreover, the ε is a very small positive number applied to hinder the denominator of the fraction coming in Eq. (10) to get a zero value. Thus, the Eq. (4) applied in the standard PSO algorithm is turned into Eq. (11) in DFPSO as follows:

$${V}_{i}^{t+1}=\chi [{V}_{i}^{t}+{\varphi }_{1}\left({Pbest}_{i}^{t}-{X}_{i}^{t}\right)+{\varphi }_{2}\left({Gbest}_{i}^{t}-{X}_{i}^{t}\right)]$$

(10)

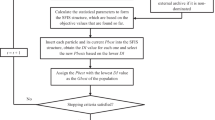
The rest of the steps of the proposed DFPSO algorithm are the same as typically pursued in the standard PSO algorithm. Figure 1 depicts the flowchart of the DFPSO algorithm.

Fig. 1

Flowchart of DFPSO

3 Results on the Benchmark Functions

To validate the performance of the DFPSO algorithm in solving optimization problems, at the first stage, it is compared with six other PSO variants including CLPSO (Liang et al. 2006), HPSO-TVAC (Ratnaweera et al. 2004), FIPSO (Mendes et al. 2004), LPSO (Kennedy and Mendes 2002), DMSPSO (Liang et al. 2005), and LFPSO (Hakli and Uguz 2014). At the second stage, the DFPSO is compared with four other independent meta-heuristic algorithms including GA (Holland 1992), GSA (Rashedi et al. 2009), GWO (Mirjalili et al. 2014), and the original PSO (Kennedy and Eberhart 1995).

All of the competitive algorithms are implemented on six high-dimensional benchmark functions spanning a variety of the difficulties for an optimization algorithm to search for the global optimum. The mathematical formulations of these benchmark functions are shown in (Tian et al. 2019). All of these functions are to be minimized. The optimal objective value of all these benchmark functions is zero. These problems include three uni-modal functions (F₁-F₃) and three multi-modal functions (F₄-F₆).

As the results of the PSO-based algorithms are all derived from (Tian et al. 2019), all of the settings are just the same as are in this research. In detail, the number of dimensions for all test functions is set to 30, the number of the iterations was set to 1000 and the population size of all the algorithms was set to 40. The results of running the proposed DFPSO and other PSO variants are shown in Table 1. The results of the implementation of the proposed DFPSO and other independent algorithms can also be seen in Table 2. The term “Std” means “standard deviation” in all these Tables.

Table 1 Minimization results of the benchmark functions solved by the PSO variants. (The performance criteria corresponding to the best-performing algorithms are bold-faced).

Table 2 Minimization results of the benchmark functions solved by the independent algorithms (The performance criteria corresponding to the best-performing algorithms are bold-faced)

As can be seen, the proposed DFPSO outperforms the other PSO-based competitors in all of the benchmark functions, except for F₃. The statistical results of the proposed DFPSO as compared to the other competitive independent algorithms can also suggest the superiority of the proposal in almost all criteria.

4 Conjunctive Surface-ground Water use Management

4.1 Study Area

The Gavkhouni river basin with an area of 41,547 km² is located at the Central Plateau river basin in Iran. The basin is including 21 sub-basins. The study area is Najafabad Plain located in west-central Iran as a part of the Zayandeh-Rud River Basin located in the greater Gavkhouni river basin. This plain is of 1712 km² area, with coordinates between 50° 33′ 32″ to 51° 40′ 00″ Eastern longitudes and 32° 19′ 14″ to 33° 00′ 32″ Northern latitudes (Fig. 2). It is worthwhile mentioning that the “RB” in the Iran map in Fig. 2 is the acronym of “River Basin”. The Najafabad aquifer occupies an area of 940.9 km² including 14,623 wells with an annual discharge of 852.7 million cubic meters (MCM) (Yekom Consulting Engineers 2013). Najafabad plain comprises two main sub-plains: (i) Nekouabad-Right, and (ii) Nekouabad-Left. As a result of coverage of a large amount of agricultural and horticultural production, the Najafabad sub-basin is identified as the most important sub-basin of the greater Gavkhouni basin. Thus, the agricultural sector is the most water-consuming in the region consuming 93.3% of the water supplied in the region (Yekom Consulting Engineers 2013).

Fig. 2

Najafabad Plain in the Gavkhouni River Basin, Iran (Rezaei et al. 2017b)

Lacking reliable surface water resources in the region poses challenges in surface water supply for this region, imposing much more pressure on groundwater resources to meet increasing agricultural demands in this region, such that the groundwater level in the Nekouabad-Right and Nekouabad-Left regions experiences a drastic 13 and 20 m drawdown in just a decade.

4.2 Simulation–optimization Model Mathematical Formulation

Here, a simulation–optimization model is used to solve the conjunctive use problem, as the optimization model formulation contains some decision variables such as the monthly surface water allocated and groundwater extracted volumes over a whole planning period (scenario), and also some state variables such as the monthly GWL variations which should be estimated through a simulation process.

$$Minimize Z=\sum_{j=1}^{12}{\left[\left({D}_{ij}-{Sup}_{ij}\right)/{D}_{ij}\right]}^{2}\times \left(1+{Z}_{pen1}+{Z}_{pen2}\right);i=1, 2, 3$$

(11)

$${Z}_{pen1}={m}_{1}\times \left\{1-Gaussian\left(\left|min\left[\left({GW}_{max}-\sum_{j=1}^{12}{GW}_{ij}\right),0\right]\right|\right)\right\};i=1, 2, 3$$

(12)

$${Z}_{pen2}={m}_{2}\times \left\{1-Gaussian\left(\left|min\left[\left(\sum_{j=1}^{12}{\Delta H}_{ij}-{\Delta H}_{i,min}\right),0\right]\right|\right)\right\};i=1, 2, 3$$

(13)

$$Gaussain\left(x\right)=\mathrm{exp}(-{x}^{2}/2)$$

(14)

Subject to:

$${D}_{ij}={\sum }_{c=1}^{Nc}{CD}_{ijc}\times {A}_{ic}\times {10}^{-5}$$

(15)

$${Sup}_{ij}={SW}_{ij,net}+{GW}_{ij,net}$$

(16)

$${SW}_{ij,net}=a\times b\times c\times {SW}_{ij}$$

(17)

$${GW}_{ij,net}=a\times {GW}_{ij}$$

(18)

$${SW}_{ij}={D}_{ij}/(a\times b\times c)\;and\;{GW}_{ij}=0;\;if\;{SW}_{ij,net}\ge {D}_{ij}$$

(19)

$${GW}_{ij}=\left({D}_{ij}-{SW}_{ij,net}\right)/a;\;if\;{SW}_{ij,net}<{D}_{ij}\;and\;{GW}_{ij,net}\ge {D}_{ij}-{SW}_{ij,net}$$

(20)

$${SW}_{j,min}^{avail}\le {SW}_{ij}\le {SW}_{j,max}^{avail}$$

(21)

$${GW}_{j,min}^{avail}\le {GW}_{ij}\le {GW}_{j,max}^{avail}$$

(22)

$${H}_{ij}={H}_{i,j-1}-{\Delta H}_{i,j-1};\;for\;j\ne 1$$

(23)

$${H}_{ij}={H}_{0}; for j=1$$

(24)

where the parameters are defined below.

$Z$ = Objective function.

${Z}_{pen1}$ = First penalty function applied to restrict the cumulative groundwater extraction over the whole planning period.

${Z}_{pen2}$ = Second penalty function applied to restrict the cumulative groundwater level (GWL) variations over the whole planning period.

${m}_{1}$ = Penalty coefficient of the first penalty function.

${m}_{2}$ = Penalty coefficient of the second penalty function.

${D}_{ij}$ = Net water demand of the jth month of a normal water year (MCM).

${Sup}_{ij}$ = Net surface and ground water supplied in the jth month of the ith year (scenario) (MCM).

${A}_{ic}$ = Cultivated area of the cth crop in a normal water year (ha).

${\Delta H}_{ij}$ = GWL variation in the jth month of the ith year (m). Note that the value of this parameter is positive when groundwater rises and is negative when groundwater withdraws.

${\Delta H}_{i,min}$ = Optimal cumulative GWL variations in the ith year (scenario) set depending on the climate conditions of each scenario (wet, normal, and dry) (m).

${H}_{ij}$ = initial GWL in the jth month of the ith year (scenario) (m).

${CD}_{ijc}$ = Net crop water requirement of the cth crop in the jth month of the ith year (scenario) (mm).

${GW}_{ij,net}$ = Net groundwater volume extracted from the aquifer in the jth month of the ith year (scenario) (MCM).

${GW}_{ij}$ = Gross groundwater volume extracted from the aquifer in the jth month of the ith year (scenario) (MCM).

${GW}_{max}$ = Maximum annual revivable groundwater extraction volume (MCM).

${SW}_{ij,net}$ = Net surface water volume allocated to the cultivated area in the jth month of the ith year (scenario) (MCM).

${SW}_{ij}$ = Gross surface water volume allocated to the cultivated area in the jth month of the ith year (scenario) (MCM).

$a$ = Coefficient of efficiency for the water use in the farm considering the water losses through evaporation and also the deep percolation to the aquifer set to 0.56.

$b$ = Coefficient of efficiency for the water transfer through the main channels set to 0.85.

$c$ = Coefficient of efficiency for the water transfer through the secondary channels set to 0.9

${SW}_{j,min}^{avail}$ = Minimum volume of the surface water allocated to the cultivated area in the historical data in the jth month (MCM).

${SW}_{j,max}^{avail}$ = Maximum volume of the surface water allocated to the cultivated area in the historical data in the jth month (MCM).

${GW}_{j,min}^{avail}$ = Minimum volume of the groundwater extracted from the aquifer in the historical data in the jth month (MCM).

${GW}_{j,max}^{avail}$ = Maximum volume of the groundwater extracted from the aquifer in the historical data in the jth month (MCM).

${H}_{0}$ = Initial depth to the groundwater table level (m).

$i$ = Indicator of the year (scenario), (i = 1, for a wet year, i = 2 for a normal year and i = 3 for a dry year).

$j$ = Indicator of the month of each year (scenario), (j = 1, 2, …, 12).

5 Preparing the Simulation–optimization Model

5.1 Artificial Neural Network

The simulation section is a multi-layer perceptron feed-forward neural network (MLPFNN) model which is well trained over the historical data. In the MLPFNN, each layer includes several neurons whose connections with the neurons located at the previous layer are called the weights of the network. The connections between the neurons in a layer and a special unit-sized neuron in the previous layer are called the biases of the network. Every MLPFNN model consists of the weights and biases as the effective parameters required to be optimized through a training process. The optimal number of these parameters depends on the number of neurons set at each layer of the multi-layer neural network. To have a plausible performance in the simulation, the number of the effective parameters of the network must not be more than the data series presented to the network in the training/optimizing stage. In this paper, the MLPFNN model utilizes 286 input data series each of which comprises 14 features for the Nekouabad-Right sub-area and 13 features for the Nekouabad-Left sub-area. Generally, the inputs involve precipitation with up to two lags, temperature with up to two lags, surface water allocation with up to two lags, groundwater extraction with up to one lag, the deep percolation of the water from the river with up to one lag and finally, the initial monthly GWL. It is worthwhile mentioning that from the 286 data series, 65% is utilized for training the network, 10% is for the validation and 25% is for the test round. The network is adopted as a single-hidden-layer network. The number of the hidden neurons of the MLPFNNs was calculated to be maximally 11 and 12 for the Nekouabad-Right and Nekouabad-Left Regions, respectively. Thereafter, a series of trials and errors were conducted to estimate the optimal number of the hidden neurons. The results show that the structure of the network of the Nekouabad-Right must be 14–7-1 and the structure of the network of the Nekouabad-Left must be 13–10-1, each of which yields the best performance of the MLPFNNs for the respective study sub-area. Afterward, the networks designed were run several times and the best overall results were given. Finally, the correlation coefficients of the training, validation, and test data with the target data of the best network designed for the Nekouabad-Right Region were obtained equal to 0.8406, 0.9171, and 0.8173, respectively. Furthermore, the correlation coefficients were attained equal to 0.7449, 0.8401, and 0.8607 for the training, validation, and test stages of the Nekouabad-Left Region best network designed, respectively.

5.2 DFPSO Algorithm

For solving the real-world conjunctive water use management problem, the DFPSO algorithm was used as the optimizer. The population size was set to 20 and the maximum number of iterations was set to 200 for the DFPSO algorithm. The other parameter settings of the DFPSO are just like those at the typical PSO algorithm.

6 Results and Discussion

In this paper, we aim at developing a management model for optimizing conjunctive surface-ground water use addressing a wide range of management aspects. This optimal management model aims at minimizing the shortages of irrigation water while controlling the cumulative groundwater level drawdown. In this study, three wet, normal, and dry water years representing different climatic conditions faced by the region are considered as the planning periods, to benchmark the capability of the management model to manage the effects these climatic conditions could impose on the study area when operating the water resources systems. The study area includes two sub-areas named Nekouabad-Right and Nekouabad-Left regions. The Nekouabad-Left is larger in area than the Nekouabad-Right while benefiting from more surface water transferred to which. Meanwhile, the groundwater reserved at the aquifer beneath the Nekouabad-Left region suffers much more decline, as a result of the larger area cultivated at this region which in turn, needs more groundwater volume to be discharged and feed the crops of this sub-area. Here, the conjunctive use of the water resources in these two regions is optimized and the results are presented at the next sub-sections as the optimal operating policies the decision-makers can consider and implement in the region to increase the efficiency of the water use and improve the agricultural activities carried out in the field.

6.1 Nekouabad-right

6.1.1 Scenario I: Wet Year (2006–2007)

While the water demands are fully met in this scenario, the GWL rises by 2.12 m. This amount of rising is more than 1.86 m GWL rise observed in the Nekouabad-Right Region in the actual operation. As the results suggest, the groundwater is extracted by 4% less than that in the actual operation, while the surface water is allocated by 52% more than what is observed in the region, contributing not only the water demands to be supplied, but also the GWL reaches a level above than that in the actual operation.

6.2 Scenario II: Normal Year (2004–2005)

In this scenario, except for the winter and spring months, the GWL is always higher than what is observed in the actual operation, such that the 1.14 m GWL drawdown observed in the region is turned into 28 cm GWL rise calculated by the model. In all over the planning period of this scenario except for July and August, the groundwater volume extracted from the aquifer is more than what is offered by the model.

6.3 Scenario III: Dry Year (2010–2011)

While in this scenario, the model supplies over 97% of the water demands, the cumulative GWL drawdown is calculated to be 1.4 m which is half of the cumulative drawdown observed in the study area. Furthermore, the ratio of the groundwater discharge to the groundwater recharge computed by the model is always less than what is observed in the study area, illustrating more surface water is allocated while nearly the same groundwater is extracted as offered by the model. Since this scenario occurs in a dry year, it is mandatory to somehow exploit the groundwater as the more abundant source of water to meet as much of the water demands as possible and to sustain the aquifer at the same time. Figure 3 displays the optimized GWL variations versus what is observed in the actual operation in the Nekouabad-Right region in three examined scenarios.

Fig. 3

Cumulative GWL variations in the Nekouabad-Right; (a) scenario I; (b) scenario II; (c) scenario III

It is noteworthy that the monthly water demands in all scenarios are averagely fully met and thus, reducing the GWL variations is the major problem the simulation–optimization model attempts to solve in this study sub-area.

6.4 Nekouabad-left

6.4.1 Scenario I: Wet Year (2006–2007)

The results of running the simulation–optimization model indicate 1.75 m rise in the cumulative GWL, while the GWL has risen by 3.72 m in the actual operation over the whole planning period of this scenario. The reason making the GWL less rise as computed by the model compared to what is observed in the region may be found in the structure of the MLPFNN simulator which is unable to precisely estimate the GWL variations in the extreme climatic conditions as it is known that in a water year, there are much more surface water resources including the abundant surface water available in the irrigation channels, high precipitation and high infiltration from the river, resulting in the high rise of the GWL. This problem was alleviated in the Nekouabad-Right Region due to a lower extremity of the climatic conditions contributing the GWL to more rise in a wet year representing scenario I.

6.5 Scenario II: Normal Year (2004–2005)

Due to the normal climatic conditions of this year, the model can achieve 1.45 m rise in the GWL over the whole period, while the cumulative rise is observed to be 25 cm in the actual operation. Also, the water demands are fully met in this scenario as the model results suggest. The surface water allocation is increased by 34% and the groundwater extraction is decreased by 9%, which in turn helps the GWL be higher at the end of the period as compared to that in the actual operation.

6.6 Scenario III: Dry Year (2010–2011)

In this critical scenario, the groundwater is withdrawn by 3.94 m in level as calculated by the model. This figure is versus 5.36 m GWL drawdown observed in action. The ratio of the aquifer discharge volume to the total surface-ground water volume interaction reaches from 56 to 48% in the model computations which in turn, causes a more desirable balance to be held in the groundwater exploitation which helps such a vital groundwater resource be sustained in such a dry year. Figure 4 displays the optimized GWL variations versus what is observed in the actual operation in the Nekouabad-Left region in three examined scenarios.

Fig. 4

 Cumulative GWL variations in the Nekouabad-Left; (a) scenario I; (b) scenario II; (c) scenario III  

It is noteworthy that the monthly water demands in all scenarios except for scenario III are averagely fully met. In scenario III the monthly demands are averagely met by 88%. Thus, reducing the GWL variations is the major problem the simulation–optimization model attempts to tackle in this study sub-area.

7 Conclusion

In this paper, a new variant of the Particle Swarm Optimization (PSO) algorithm, named Dual Fitness PSO (DFPSO) was proposed. In the meta-heuristic algorithms, the fitness and diversity of the solutions are the main factors to be addressed in selecting a guide causing the search particles’ movements in the search space; however, these movements could be unbalanced when the fitness and diversity are measured by two different and separate mechanisms. In this case, it is possible that achieving high fitness is of higher priority than preserving the diversity when the particles are gathered in a closed region in the search space. Applying separate mechanisms, it is also probable that maintaining the diversity is of higher priority than reaching the high fitness when the solutions are so far from the fitted region of the search space. In the latter case, the particles could be trapped in local optima. As a solution, we attempted to incorporate the capability of evaluating fitness and diversity and make it the mission of the global best (Gbest) particle. In DFPSO, there are also multiple Gbests to help better preserve the diversity. The proposed approach was validated through implementation on a set of benchmark functions.

The proposed algorithm was then employed to solve an optimal conjunctive use of surface and ground water problem under three different climatic conditions. The objectives were to minimize the shortages of water, while maximizing the groundwater table sustainability. The results showed that the optimization model can desirably satisfy the water demands while decreasing the cumulative groundwater level drawdown. As the future work, we aim at improving the DFPSO algorithm by investigating whether the personal best (Pbest) particles might be eliminated from the updating procedure of the particles in favor of local optima avoidance to further strengthen the exploration capability of this algorithm.