Introduction

Most of the rivers, located in the large-scale mountainous watersheds, are considered as the important sources of water availability that significantly affect the hydrologic regimes of the downstream areas (Srivastava et al. 2013). The integrative management of large-scale river basins needs a comprehensive hydrological modeling (Bilondi and Abbaspour 2013; Marhaento et al. 2017). Numerous number of physically based integrated distribution models have been developed for watershed analysis and management, such as Hydrologic Simulation Program-Fortran (HSPF) (Bicknell et al. 1996), Erosion Productivity Impact Calculator (EPIC) (Wang et al. 2012), Water Erosion Prediction Project (WEPP) (Flanagan et al. 2012), Hydrology Laboratory-Research Distributed Hydrologic Model (HL-RDHM) (Koren et al. 2004), and Soil and Water Assessment Tools (SWAT) (Arnold et al. 1998). Among them, the SWAT model as a semi-distributed model is widely used in many countries worldwide to evaluate hydrological processes (e.g., rainfall-runoff, sediment, climate change, land use, evapotranspiration, and water quality) at large-scale watersheds (Afshar and Hassanzadeh 2017; Afshar et al. 2017b; Arnold et al. 2011; Bilondi and Abbaspour 2013; Rostamian et al. 2008; Shi et al. 2014; Abbaspour et al. 2007; Lin et al. 2015).

The SWAT model is a physically based model; however, the correct values of the parameters cannot be directly measured due to measurement limitations and scale issues (Li et al. 2010). Therefore, the applicability of the model stems on the values of model parameters that should be computed through an inverse modeling (IM) approach via a calibration process (Schoups and Vrugt 2010; Laloy et al. 2010; Leta et al. 2015; Laloy and Vrugt 2012). The calibration process in a modeling scheme plays an important role to capture the optimal parameter values which reasonably accord with reality (Leta et al. 2016). Rigorous uncertainty due to some errors in the input (forcing) and output data, model structure, and algorithms significantly impacts the hydrological modeling results (Beven 2006). Thus, In order to formulate the inverse modeling (IM) problems for Uncertainty Analysis (UA) in various river basin models, informal and formal Bayesian frameworks have been developed. Informal Bayesian approaches, developed without rigorous statistical assumptions, attempt to regard all uncertainties by improved parameter uncertainty. Generalized Likelihood Uncertainty Estimation (GLUE) (Beven and Binley 1992), Sequential Uncertainty Fitting version 2 (SUFI-2) (Abbaspour et al. 2004), and Parameter Solution (ParaSol) (Van Griensven and Meixner 2006) are examples of informal approaches. The formal Bayesian approaches use appropriate statistical assumptions and apply reliable likelihood functions to estimate the posterior probability density (pdf) function of the model parameters and also the total predictive uncertainty (Vrugt et al. 2008; Schoups and Vrugt 2010; Kuczera and Parent 1998; Rivera et al. 2015). The Markov Chain Monte Carlo (MCMC) algorithms are examples of formal Bayesian approaches. One of the most commonly used MCMC algorithm is called DiffeRential Evolution Adaptive Metropolis (DREAM-ZS). This algorithm was originated from the DREAM (Vrugt et al. 2009a) and was applied as an effective and robust sampler (Vrugt et al. 2009b; Laloy and Vrugt 2012). In order to generate the candidate points for the individual chains, the DREAM-ZS uses samplings from the past states. The DREAM-ZS has several preferences over the DREAM algorithm: (i) only three parallel chains are needed for posterior sampling and therefore the time for burn-in is reduced, (ii) it needs fewer function evaluations than the DREAM to converge to the suitable limiting distribution, and (iii) it consisted of a snooker updater which produces jumps beyond the updates of parallel direction that increases the variety of the candidate points (Ter Braak and Vrugt 2008).

In this study, informal and formal Bayesian approaches including SUFI-2 and DREAM-ZS were employed for calibration, uncertainty analysis, and the estimation of model parameters. The SUFI-2 algorithm is a semi-automated procedure in the SWAT-Calibration and Uncertainty Program (SWAT-CUP; Abbaspour et al. 2007), which is widely used for optimizing the parameters of the SWAT model (Setegn et al. 2010; Abbaspour 2011; Wu and Chen 2015; Kumar et al. 2017; Parajuli et al. 2018). Some studies in different application areas show that this approach is of high computational efficiency for satisfactory uncertainty prediction, especially for time-consuming works within large-scale watersheds by the models like SWAT simulator in comparison with the other methods within the SWAT-CUP (Abbaspour et al. 2007; Rostamian et al. 2008; Yang et al. 2008; Setegn et al. 2010; Zhang et al. 2015). Thus far, many research works have been accomplished by means of the SUFI-2 for the uncertainty analysis of SWAT model parameters (Abbaspour et al. 2007; Singh et al. 2013; Memarian et al. 2014; Narsimlu et al. 2015; Li et al. 2017). The DREAM-ZS algorithm has been recently applied to calibrate and analyze the uncertainty of hydrological models (Kozelj et al. 2014; Leta et al. 2015; Nourali et al. 2016; Xu et al. 2017; Zeng et al. 2018), and due to the benefits of the DREAM algorithm (Ter Braak and Vrugt 2008), it was used in this research paper. Although many techniques exist to analyze uncertainty, only a few are available to be compared together (Mantovan and Todini 2006; Yang et al. 2008; Bilondi and Abbaspour 2013). According to the literature review, the comparison and integration of SUFI-2 and DREAM-ZS in multisite calibration has not been reported yet. Therefore, the current study was conducted to combine and compare the uncertainty prediction capabilities of two algorithms, i.e., SUFI-2 and DREAM-ZS, simultaneously by using new evaluation indices. This study tries to calibrate the SWAT model in a multisite mode for hydrological simulation of the Kashafrood River Catchment (KRC) as a large mountainous watershed in Iran with high spatial variability.

Materials and methods

Study area and data set

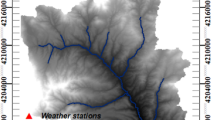
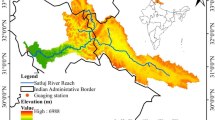
In this research paper, SWAT model with a daily time step was employed to model the hydrological conditions of the Kashafrood River Catchment (Iran). The KRC is located in the northeastern part of Iran in Khorasan Razavi Province (KRP), and is known as the biggest catchment in KRP with a drainage area of 16,870 km2. The total length of Kashafrood River, as the longest river in this catchment, is about 285 km. Geographically, KRC is situated between latitudes of 35° 35′N and 37° 07′N and longitudes of 58° 15′E and 61° 13′E (Fig. 1). The watershed altitude varies from 390 m (in the southeast part) to 3302 m (in the northwest part) above sea level, with a mean elevation of 1846 m and a mean slope of 4.7%. Mashhad, the second most populous city in Iran, is located within the KRC. The climate of KRC is classified within the semi-arid category with low annual precipitations and high evapotranspiration in summer (Afshar et al. 2017a; Sayari et al. 2013). In this catchment, most of the precipitation (50–77%) occurs from January to May (Afshar et al. 2017a) and the annual average precipitation of this area is about 340 mm, with high spatial variation. The average maximum and minimum temperature of KRC is 20.6 and 7.1 °C, respectively.

Fig. 1
figure 1

Location map of the study area

Full size image

In this research paper, a 35-m-resolution digital elevation model (DEM) was obtained from the National Cartographic Center (NCC) of Iran. The land use map based on field investigation was extracted from the classification of Indian Remote Sensing (IRS) satellite imagery. The soil map was obtained from the Range and Watershed Management Department (RWD) of Khorasan Razavi Province. Daily climatology data containing 34 precipitation stations and 12 temperature stations located inside the catchment were obtained from the Iran Meteorological Organization (IMO) during the period of 1992–2011 (see Fig. 1). Stream flow data including five monthly runoff gauges (Sar Asiab Shandiz (SARASSHA), Zire Band Golestan (ZIRBAGOL), Golestan Jaghargh (GOLHAGHR), Hesar Dehbar (HESDEHB), and Kartian (KARTIAN)) were acquired from the Water Resource Management Company (IWRMC) (see Fig. 1). General information on runoff gauges is presented in Table 1.

Table 1 General information of hydrometric stations in Kashafrood catchment
Full size table

Dominant land uses in KRC are pasture (50.9%), agricultural land-generic (28.6%), and winter wheat (15.6%), and the others are forest, urban, and water body (4.9%). Heterogeneous mix of silty, loamy, silty loam, and clay soils are the predominant soil types at the northern and center parts of the watershed, while dominant soil types of the middle line of catchment are silty clay loam and loamy sand. Location of study area, meteorological stations, and stream flow gauges are presented in Fig. 1.

The SWAT model

The SWAT model was developed by the United States Department of Agriculture–Agricultural Research Services (USDA-ARS) for assessing and forecasting the impact of different management scenarios on water quality, groundwater resources, soil erosion, and pollution loading (Arnold et al. 1998; Narsimlu et al. 2015; Leta et al. 2016; Afshar and Hassanzadeh 2017). It operates on a daily or sub-daily time step, as a semi-distributed conceptual model for large-scale watersheds. In this model, the catchment is delineated into a number of sub-basins which are further divided into hydrological response units (HRUs). The HRUs are unequaled mixes of soil type, land cover, and slope classes (Arnold et al. 2011). They are distributed non-spatially, and due to the lumping resemblance of soil and land use areas into a single unit, their computational cost using SWAT is decreased (Neitsch et al. 2011). In the SWAT model, the water balance is represented by the processes of snowmelt, infiltration, evaporation, plant uptake, lateral flow, percolation, groundwater flow, and the channel routing (Neitsch et al. 2011), as represented by Eq. (1):

$$ {\mathrm{Sw}}_{\mathrm{t}}={\mathrm{Sw}}_0+{\sum}_{\mathrm{i}=1}^{\mathrm{t}}\left({\mathrm{R}}_{\mathrm{day}}-{\mathrm{Q}}_{\mathrm{surf}}-{\mathrm{E}}_{\mathrm{a}}-{\mathrm{W}}_{\mathrm{seep}}-{\mathrm{Q}}_{\mathrm{qw}}\right) $$
(1)

where Swt and Sw0 are the final and initial water content on the day i (mm) and Rday, Qsurf, Ea, Wseep, and Qqw are, respectively, the amount of precipitation, surface runoff, evapotranspiration, return flow, and water entering the vadose zone from the soil profile on the day i in mm. In this study, surface runoff was predicted by means of the modified Soil Conservation Service Curve Number (SCS-CN) approach (USDA-SCS 1986) based on land use, soil type, and the antecedent moisture condition. Moreover, the Hargreaves method (Hargreaves and Samani 1985) was employed to calculate potential evapotanspiration (PET), and finally, the Muskingum approach (Chow et al. 1988) was utilized for the stream flow routing. More details on the SWAT model can be found in Arnold et al. (1998).

Informal Bayesian framework (SUFI-2)

SUFI-2 algorithm known as an informal Bayesian approach is an iterative process. It is implemented in the SWAT-CUP interface (Abbaspour et al. 2004, 2007) and is linked to SWAT model. SWAT-CUP interface is used for model calibration, validation, sensitivity, and uncertainty analysis and is able to analyze a large number of parameters and measured data from several multisite flow gauging stations simultaneously (Abbaspour et al. 2004, 2007). In order to find the optimal parameter uncertainties from prior ranges, the SUFI-2 (Abbaspour et al. 2004, 2007) combines calibration and uncertainty analysis with the minimum number of iterations and the smallest possible prediction uncertainty band (Abbaspour 2011; Wu and Chen 2015). Since this procedure is involved with parameter sets, it can explicitly take into account the interaction between the parameters. SUFI-2 algorithm attempts to bracket most of the measured data (more than 80%) within the 95 percent prediction uncertainty (95PPU) of the model with as narrow as possible uncertainty band. Similar to GLUE approach, in SUFI-2 all sources of uncertainty (parameter, conceptual model, forcing input, etc.) are mapped on the parameters (Abbaspour et al. 2004, 2007; Yang et al. 2008) because the likelihood measure value implicitly reflects all sources of errors and any effects of the co-variation of parameters’ values on model performance and is associated with a parameter set (Beven and Freer 2001). In SUFI-2, the parameter set is firstly sampled from a uniform distribution in a Latin Hypercube Sampling (LHS) framework disallowing 5% of the very bad simulations. For each parameter set the objective function is calculated. Then, the output uncertainty of the model is quantified within the 95% band of the prediction uncertainty (95PPU) and is calculated at the 2.5 and 97.5% levels of the cumulative distribution of the output variables (Yang et al. 2008). The parameter ranges are taken as the final parameter values. More details on SUFI-2 can be found in Abbaspour et al. (2004) and Yang et al. (2008).

Formal Bayesian framework (DREAM-ZS)

The DREAM algorithm exhibited high efficacy and merits in numerous studies which was employed (Surfleet and Tullos 2013; Joseph and Guillaume 2013; Zahmatkesh et al. 2015; Engeland et al. 2016). It represents excellent sampling efficiencies in calibration problems, such as multimodal target distributions and high-dimensional search problems. Furthermore, it is capable to be linked with a parallel computing through running multiple chains. This algorithm is originated from the Shuffled Complex Evolution Metropolis (SCEM) algorithm (Vrugt et al. 2003) and the Differential Evolution-Markov Chain (DE-MC) method (Ter Braak 2006). Using Bayesian updating, the DREAM algorithm, proposed by Vrugt et al. (2009a,b) is a MCMC sampler to search the posterior distributions related to the parameter values and to estimate the uncertainty of parameter in a high-dimensional sampling problems. In this algorithm, the impacts of input data, parameters, and the uncertainties of model structure are separated from the total uncertainty (Vrugt et al. 2008). The DREAM-ZS is an updated version of the DREAM algorithm which is developed to estimate the parameter posterior probability function (pdf). The letters “Z” and “S” in DREAM-ZS refer to sampling from the past state and a snooker updater, respectively (Laloy and Vrugt 2012). Checking the convergence of the chain to the posterior distribution, one can obtain this data from the R-statistic proposed by Gelman-Rubin (Gelman and Rubin 1992).

The posterior distribution becomes stationary when the values of this criterion are less than 1.2 for all of the parameters (Vrugt et al. 2009a,b). Finally, after convergence, when the number of parameter samples is sufficiently high, the last 20% of the samples are extracted to assess the uncertainty and an estimation of the statistical values of the posterior distribution can be made (i.e., the mean and variance values) (Gelman and Rubin 1992; Laloy and Vrugt 2012). More detailed description of DREAM-ZS is completely represents by Vrugt et al. (2009a) and will not be repeated herein.

Quantification of parameter and total prediction uncertainty

The runoff component simulated by the SWAT model can be illustrated by

$$ \widehat{\mathrm{Y}}=\mathrm{f}\ \left(\uptheta, \upvarphi, \widehat{\mathrm{X}}\right) $$
(2)

where Ŷ is the vector of model output or predictions (N × 1), θ is the vector of unknown model parameter sets with d dimension, φ represents the initial condition, and finally, \( \widehat{\mathrm{X}} \) is the matrix of the measured input data (e.g., precipitation, minimum and maximum temperature). In the Bayesian framework, parameter sets (θ) are optimized through minimizing the residual errors e (θ), which contains the difference between the model prediction Ŷ and the corresponding observed output Yt. The residual errors, as a statistical model explaining a prior expected behavior at time step t, are defined as

$$ \mathrm{e}\left(\uptheta \right)={\mathrm{Y}}_{\mathrm{t}}-\widehat{\mathrm{Y}} $$
(3)

The unknown parameters of model such as random variables, the posterior density function (pdf), and p(θ|Y) (the relationship between the model and the data) can be described under Bayes theorem (Box and Tiao 1992):

$$ \mathrm{p}\ \left(\uptheta |\mathrm{Y}\right)=\frac{\mathrm{p}\left(\uptheta \right)\times \mathrm{p}\left(\mathrm{Y}|\uptheta \right)}{\mathrm{p}\left(\mathrm{Y}\right)}\propto \mathrm{p}\left(\uptheta \right)\times \mathrm{L}\left(\uptheta |\mathrm{Y}\right) $$
(4)

where p(θ) is the prior distribution, p(Y|θ) ≡ L(θ|Y) signifies the likelihood function of θ, and the normalization factor (p(Y)) is obtained through the numerical integration over the parameter space. In some cases, the normalization factor can be neglected and p(θ|Y) is proportional to the p(θ) multiplied by L(θ|Y).

Likelihood function in formal and informal Bayesian framework

The identification of a range of plausible parameter sets along with the estimation of parameter and prediction uncertainty is simply extracted from mapped parameter space to likelihood space (Vrugt et al. 2013; Schoups and Vrugt 2010; Box and Tiao 1992). The probabilistic measure which is used to estimate the statistical distribution of the model residuals is called the likelihood function (Kozelj et al. 2014). In a hydrologic model, the parameters, uncertainties, and statistical analysis have to be computed through a proper likelihood function (He et al. 2010). Moreover, the results are unreliable if the likelihood function is applied without reasonably indicating the distribution of model errors. The residual error assumptions can be classified into error variance, error distribution, and error correlation structures at different parts of the model response (Dumont et al. 2014).

In recent years, to estimate parameter uncertainty, formal or informal likelihood functions in Bayesian approaches have been employed by several researchers (Nourali et al. 2016; Leta et al. 2016; Pourreza-Bilondi et al. 2016; Dumont et al. 2014; Hernandez-Lopez and Frances 2017; Yang et al. 2008; Mantovan and Todini 2006; Beven et al. 2008; Vrugt et al. 2009b). According to the formal approach, one begins from an assumed statistical model for the residual errors. In other words, the functional type of the joint pdf for the residual errors is identified as a priori (Box and Tiao 1992). This factual model is then used to determine the suitable shape of the likelihood function (Box and Tiao 1992). The benefit of the formal approach is that error model hypotheses are expressed unequivocally and their legitimacy can be confirmed as a posteriori (e.g., Schoups and Vrugt 2010). The formal approach, in any case, has been censured for depending too intensely on residual error presumptions that do not reflect reality in numerous applications (Beven et al. 2008). On the other hand, informal likelihood functions have been proposed as a sober minded way to deal with uncertainty approximation within the sight of complex residual error structures (Nash and Sutcliffe 1970; Beven and Binley 1992; Vrugt et al. 2009b; Schoups and Vrugt 2010).

The SUFI-2 algorithm as an informal parameter estimation technique enables testing various types of objective functions that are known as informal likelihood functions in calibration processes (Abbaspour 2011). In this study, Nash and Sutcliffe (NS) coefficient as an informal likelihood function was used to calibrate the SUFI-2 algorithm based on five discharge stations across the study catchment (Nash and Sutcliffe 1970):

$$ \mathrm{L}\left({\uptheta}_{\mathrm{i}}|\mathrm{Y}\right)=\mathrm{NS}=1-\frac{{\upsigma_{\mathrm{e}}}^2}{{\upsigma_{\mathrm{o}}}^2}=1-\frac{\sum \limits_{\mathrm{j}=1}^{\mathrm{N}}{\left({\widehat{\mathrm{Y}}}_{\mathrm{j}}\left({\uptheta}_{\mathrm{i}}\right)-{\mathrm{Y}}_{\mathrm{j}}\right)}^2}{\sum \limits_{\mathrm{j}=1}^{\mathrm{N}}{\left({\mathrm{Y}}_{\mathrm{j}}-\overline{\mathrm{Y}}\right)}^2} $$
(5)

where i = 1,2,…,K, θi is the ith set of parameters, Ŷj (θi) is the jth type of the model output (like the simulated runoff) under θi set of parameters, Y is the measured runoff, Yj is the jth observation of Y, Ῡ is the mean of the observations, K is the number of parameter sets, and N is the number of observations.

In this study, the DREAM-ZS as a sampling algorithm was set to sample from the Bayesian posterior and was combined with the standard least squares (SLS) as a common and simple formal likelihood function used by many researchers around the world. It was employed under the assumptions that the residual errors are independent (uncorrelated) and identically distributed (i.i.d.), following a normal or Gaussian distribution with zero mean and constant variance (homoscedastic errors) (Box and Tiao 1992; Yang et al. 2008; Vrugt et al. 2009b; Schoups and Vrugt 2010; Vrugt et al. 2013; Dumont et al. 2014; Pourreza-Bilondi et al. 2016; Nourali et al. 2016; Leta et al. 2016; Hernandez-Lopez and Frances 2017). This formal likelihood is known as the Gauss-Markov (GM) theorem:

$$ \mathrm{L}\left({\uptheta}_{\mathrm{i}}|\mathrm{Y}\right)={\prod}_{\mathrm{i}=1}^{\mathrm{N}}\frac{1}{\sqrt{2\uppi {\widehat{\upsigma}}_{\mathrm{i}}^2}}\exp \left[-\frac{1}{2{\widehat{\upsigma}}_{\mathrm{i}}^2}{\left({\mathrm{Y}}_{\mathrm{i}}-{\widehat{\mathrm{Y}}}_{\mathrm{i}}\left({\uptheta}_{\mathrm{i}}\right)\right)}^2\right] $$
(6)

where \( {{\widehat{\sigma}}_i}^2 \) is the standard deviation of the residuals.

The model setup and the uncertainty assessment strategies

In this study, the watershed was divided into 217 sub-basins and with a threshold area of 4852 ha. A total of 635 HRUs was defined in the model with threshold values of 20, 20, and 10% for land use, soil, and slope class, respectively. Then, for slope discretization, the multiple slope option was selected with four classes of 0–5, 5–10, 10–15, and > 15%. The flow was simulated based on the availability of data from 1992 to 2011. To make the hydrological cycle operational, and decrease the effect of the initial condition on the model output, the first 3 years (1992–1995) were used as the warm-up period of the model. Finally, the model was calibrated using monthly data sets over an 11-year time span, from 2001 to 2011.

The over-parameterization in the SWAT model during the model parameter optimization leads to a complex and time-consuming calibration process (Nossent and Bauwens 2012). Therefore, Sensitivity Analysis (SA) was carried out by SWAT-CUP tool to improve the understanding of the influential and non-influential parameters of the model on runoff discharge. Most sensitive parameters were recognized through the SA algorithm, i.e., Latin-Hypercube-One-At-a-Time (LH-OAT) incorporated in SWAT-CUP (Van Griensven et al. 2006; Leta et al. 2016). The LH-OAT was employed to depict a primary population of parameters (prior distributions), which leads to the calculation of the 95PPU for a given output variable. Twenty parameters were identified as sensitive parameters in this study (Table 2). Furthermore, initial ranges of these parameters were determined based on the SWAT manual (Arnold et al. 2011). These sensitive parameters are important to represent runoff, base flow, infiltration, and channel routing processes. The posterior distribution of the parameters, with uniform prior distributions, was derived according to preselected ranges (Table 2). The behavioral parameter sets were applied to generate model outputs. Therefore, the results were analyzed to achieve the 95% total prediction uncertainty (95PPU) bands by calculating 2.5 and 97.5% levels of the cumulative distribution related to the output variables.

Table 2 Sensitive parameters obtained from LH-OAT and their prior ranges
Full size table

The assessment of two parameter uncertainty analysis methods (SUFI-2 and DREAM-ZS algorithms) was conducted through two uncertainty assessment strategies, i.e., S1 and S2. These strategies were recognized by two different initial parameter ranges as shown in Table 3. The prior ranges of the S1 strategy were adopted from SWAT manual, and the prior ranges of the S2 strategy were selected using a compromising approach between the prior and posterior ranges extracted from S1 strategy. As it is depicted in Table 3, prior ranges of S2 were adopted mainly from S1 posterior ranges.

Table 3 The description of two considered strategies
Full size table

The flowchart of SWAT modeling with both SUFI-2 and the DREAM-ZS frameworks utilized in computing the parameter values and predictive uncertainty is illustrated in Fig. 2.

Fig. 2
figure 2

Computational framework of this study

Full size image

Performance assessment of the SUFI-2 and DREAM-ZS algorithms

Many indices have been applied and proposed to assess the simulation accuracy of hydrological models and the prediction bounds generated by the various uncertainty methods. These indices can also be represented as the criteria for comparing the prediction bounds acquired from different uncertainty assessment methods. Moreover, the high-quality simulations are obtained from parameter combinations within the parameter ranges based on two criteria, i.e., P-factor and d-factor. In other words, the SUFI-2 and DREAM-ZS algorithms, as an iterative process, attempt to bracket most of the measured data within the 95PPU of the model (P-factor) with as narrow as possible uncertainty band (d-factor). In this study, the model prediction uncertainty was evaluated in the SUFI-2 and the DREAM-ZS algorithms by means of two indices as well NS efficiency which illustrates the goodness of fit between the simulated and the observed data (Nash and Sutcliffe 1970). The formula is given as follows:

$$ \mathrm{NS}=1-\frac{\sum \limits_{\mathrm{i}=1}^{\mathrm{N}}{\left({\widehat{\mathrm{Y}}}_{\mathrm{i}}-{\mathrm{Y}}_{\mathrm{i}}\right)}^2}{\sum \limits_{\mathrm{i}=1}^{\mathrm{N}}{\left({\mathrm{Y}}_{\mathrm{i}}-\overline{\mathrm{Y}}\right)}^2} $$
(7)

where Yi is the observed runoff data in step i, Ŷi is the simulated runoff data, Ῡ is the mean of observed runoff data, and N is the number of observed data points.

P-, d-, and NS factors range from 0 to 100%, 0 to ∞, and − ∞ to 1, respectively. During the calibration process, a good fit between the simulated and the observed values is achieved when the P-factor is close to 100% (bracket all observed data by prediction uncertainty band) and d-factor close to 0 (to achieve relatively small uncertainty band) (Yang et al. 2008). Furthermore, the evaluation of model prediction based on Moriasi et al. (2007) is very fine when the NS values are between 0.75 and 1 and it may be satisfactory if NS is greater than 0.36. The parameter ranges and the posterior parameter distributions can be obtained when the acceptable values of P- and d-factor and NS efficiency are reached.

According to the previous sections, the SUFI-2 algorithm attempts to assess all sources of uncertainties (e.g., model structure and input data) based on the best parameters (Abbaspour et al. 2007), while the DREAM-ZS tries to separate them from the total uncertainty (Vrugt et al. 2009a). A high level of symmetry prompts an alluring forecast bound. In this way, other than that the prediction limits should cover the observed discharges, the mean difference between the lower and upper forecast limits ought to be roughly equivalent to the observed discharges. Besides, we expect that the modeled prediction limits would be asymmetrical with regard to the observed discharges because of the non-linearity of the hydrological forms and the model structure utilized. As indicated by the observed hydrograph, diminishing the asymmetry level of the prediction limits to the littlest conceivable degree is a sensible point and it would end up being a sensibly precise and vigorous estimator (Xiong et al. 2009).

In addition to three prior indices (P-factor, d-factor, and NS), two new indices of average degree of asymmetry, i.e., the index of average deviation amplitude and its dimensionless variant (S), and the average relative deviation amplitude (T), were employed in this paper to compare the results of two different uncertainty framework. The perfect case is acquired when the estimations of S and T are zero (for more information about S and T indices, refer to Xiong et al. 2009). The SWAT is considered as a calibrated model if the acceptable values of these criteria (P-factor, d-factor, NS, S, and T) are reached.

Results and discussion

In this study, two strategies related to the SUFI-2 and DREAM-ZS applications were implemented in SWAT to simulate stream flow in the KRC. It should be noted that the observed data in the study area are very restricted; therefore, all results from two strategies were only illustrated for the calibration data set.

S1 strategy

In SWAT-CUP, after running the first iteration, the goodness of fit between the observed and the simulated runoff data is computed. As this case study is involved with multiple-site calibration, it needs to assign weights for these sites and then weighted objective function values are calculated. Then, new parameter ranges are suggested for next iterations. All of the processes of calibration and uncertainty analysis were done with 20 parameters with NS as an objective function for each of the 5 gauging stations, separately. In addition, the minimum value of the objective function threshold of this strategy (S1) for the behavioral samples was chosen to be 0.5. The final upper and lower bounds of the posterior parameters as well as the fitted values of parameter (obtained from SUFI-2 uncertainty technique) are shown in Table 4.

Table 4 The optimum values of parameters in SWAT model obtained from the S1 strategy with prior ranges of parameters
Full size table

Results of marginal posterior distributions of the SWAT behavioral parameters derived from the SUFI-2 procedure are plotted in Fig. 3, and the best parameter values for all parameters is also depicted with a blue symbol (cross) (also see Table 4). The x axis in each histogram reveals the posterior ranges of each individual parameter. Although the shape of distributions demonstrates the degree of parameter uncertainty, the calibration of parameter estimates may be considered as model values. In general, the fine identifiable parameters are obtained from the sharp and peak distributions, while the flat distributions show more parameter uncertainty (Jin et al. 2010). As shown in Fig. 3, almost all of the parameters have entirely different posterior distributions than the prior in terms of both the parameter range and the shape of the distributions, except for the parameter ALPHA_BF which shows a uniform distribution with a narrower range. According to Fig. 3, it should be noted that some of the SWAT parameters (e.g., CN2, SHALLST, ESCO, SMFMN, and CH_N2) are well identified within their prior ranges and their distributions are approximately Gaussian. While, the other parameters reveal either negatively (e.g., SOL_AWC, SOL_K, GW_REVAP, RCHRG_DP, SLSUBBSN, CH_K2, SMTMP, TIMP, and PCPMM) or positively skewed (e.g., GW_DELAY, SOL_BD, EPCO, SFTMP, and SURLAG) distributions (may be not considered as easily identifiable parameters) and the mass of the posterior distribution is concentrated at their lower or upper bounds, respectively. On the other hand, some parameters (except GW_REVAP, ESCO, CH_N2, CH_K2, SMFMN, and TIMP) are better defined and the width of posterior distributions covers only a relatively narrow interior region compared to the prior range (the prior ranges of parameters are relatively wide). This indicates that the measured runoff data include enough information to approximate these parameters and those ones have less uncertainty, whereas the other parameters (e.g., GW_DELAY, ESCO, CH_N2, CH_K2, SMFMN, and TIMP) show considerably larger ranges and these parameters are more uncertain. Thus, the SUFI-2 procedure is capable of assessing the uncertainty parameters in the SWAT model.

Fig. 3
figure 3

Marginal posterior distributions of SWAT parameters under S1 strategy

Full size image

Correlation coefficient matrix of the posterior parameter samples for the SUFI-2 algorithm (S1 strategy) is shown in Table 5. Results show that the correlations between all of the sensitive parameters of the SWAT model are very low and there are no significant correlations (all coefficients less than 0.04). It should be expressed that, although a rigorous probabilistic formulation does not exist in the SUFI-2 algorithm, the parameter uncertainty may be propagated correctly through hypercube sampling. SUFI-2 does not consider parameter correlation; thus, some simulations with poor objective function values may be picked out as the non-behavioral ones.

Table 5 The parameter posterior correlation matrix for the strategy S1
Full size table

The 95PPU at five stations on monthly basis for the period 2001–2011 derived from the SUFI-2 algorithm are plotted in Fig. 4. The total uncertainty denotes the combined influences of parameter, model condition, and data calibration uncertainty. The model was calibrated for KRC with one upstream (SARASSHA), three midstream (ZIRBAGOL, GOLJAGHR, and HESDEHB), and one downstream (KARTIAN) gauging stations. Analysis of hydrographs indicates that the calibrated model relatively underestimates the peak runoff, while it is slightly overestimated in 2008, 2009, and 2010 at the lower and middle parts of the catchment (KARTIAN, HESDEHB, and GOLJAGHR) and in 2009 at the middle and upper parts of the catchment (ZIRBAGOL and SARASSHA), especially in the recession limb. This may be reasoned that in the SWAT simulation, SCS method was employed, which does not consider precipitation duration and intensity (Arnold et al. 2011). On the other hand, the accuracy of the model is good in peak discharge estimations, although not excellent. It should be expressed that rainfall gauge stations are not a very good representative of precipitation over the basin, because in the map show there are no rain gauges in some high-altitude parts of the study basin. Moreover, the KRC region is a mountainous watershed and is exposed to high spatial and temporal variability in rainfall distribution that cannot be captured exactly using these rain gauges in this basin. Therefore, such a limitation could have contributed to some degree of simulation uncertainty (Memarian et al. 2014; Cho et al. 2009). Furthermore, at all stations, the base flow was of high correspondence. As it can be seen in Fig. 4, most of the measured data were bracketed by the 95PPU (from 57% in SARASSHA to 74% in HESDEHB), which illustrates that the uncertainties in the SWAT model within the permissible limits were relatively decreased. Similar d-factor was achieved at all gauging stations (from 0.9 in KARTIAN to 1.29 in ZIRBAGOL).

Fig. 4
figure 4

The 95% prediction uncertainty ranges of five runoff stations in S1 strategy by the SUFI-2 algorithm: the light shaded area represents the total uncertainty, red dots show the observed data, and the black line depicts the best prediction runoff

Full size image

The results, based on the three evaluation criteria (NS, P-factor, and d-factor), are shown in Table 6. In this study, the sources of uncertainty, i.e., U1, U2, and U3, are reflected as the total uncertainty in S1, the total uncertainty in S2, and the parameter uncertainty in S2, respectively. According to Table 6, the NS coefficient during the calibration period was obtained as 0.6 in HESDEHB up to 0.71 in SARASSHA. Among three gauging stations, it seems that SWAT model in HESDEHB shows a good performance (NS = 0.6, P-factor = 0.74, and d-factor = 0.92). Generally, it can be revealed that in this study, the results of calibration in KRC can be qualified as “satisfactory” under the S1 strategy. Finally, it should be expressed that the uncertainty in the SUFI-2 procedure is relatively medium. Therefore, the results of the DREAM-ZS procedure must be analyzed to select the best algorithm and strategy, which is represented in the next section.

Table 6 Index values of NS, P-factor, and d-factor considered in both strategies of uncertainty for runoff simulation
Full size table

S2 strategy

The DREAM-ZS was applied as a sampler to separate the sources of error raised from the parameters of other uncertainty sources (e.g., model structure and input data) to estimate the total predictive uncertainty (Vrugt et al. 2008). In this study, all of the processes of calibration and uncertainty analysis were conducted with 20 parameters as the most sensitive parameters with SLS as a likelihood function for each of the 5 gauging stations (Box and Tiao 1992) under the S2 strategy. Hence, the sampling from the prior parameter distributions (Table 7) for a total number of 120,000 runs is the initial step for the DREAM-ZS. This algorithm was run with three parallel chains to estimate the posterior distributions. Convergence of the DREAM-ZS was monitored by using R statistic (Gelman and Rubin 1992) for each parameter. When the R statistic for all sampled parameters goes below the threshold value of 1.2, then the convergence of the algorithm can be achieved. In this study, the S2 strategy met the convergence criteria after performing about 99,800 runs for all sensitive parameters.

Table 7 The fitted value of posterior parameters in the SWAT model obtained from the S2 strategy with prior ranges of parameters
Full size table

After converging the chains, only the last 20% of the samples (i.e., 20,000 parameter set) generated by the DREAM-ZS was applied to plot the posterior parameter distributions. These plots are visually illustrated in Fig. 5. Moreover, the best values (maximum likelihood) for all of the parameters are depicted with a blue symbol (cross) (see Table 7). In this figure, the posterior distributions for all parameters reveal the existence of several distributions in both shapes and parameter ranges. In all of the parameters, the width of the prior ranges in the S2 strategy was smaller than S1 strategy. Furthermore, it was found that in some parameters (e.g., ALPHA_BF, RCHRG_DP, and SFTMP), the width of posterior ranges in the S2 strategy decreased compared to the S1 strategy. It should be noted that the S2 strategy employed the SLS likelihood function (Eq. (6)), which considers different sources of error such as input, output, or model structure errors, separately. Whereas the S1 strategy used the NS likelihood function (Eq. (5)), which delineates these errors only for parameter uncertainty. Consequently, the prior parameter ranges in the S2 strategy were smaller than the S1 strategy. These results exhibit that the DREAM-ZS procedure skillfully optimized some parameters for a complex model in comparison with the SUFI-2 procedure. Additionally, the DREAM-ZS procedure may easily recognize the identifiable parameters and maintains less uncertainty. Moreover, some parameters except for SOL_BD, SURLAG, PCPMM, SOL_K, SLSUBBSN, and EPCO are overlapping in terms of shape and range for both strategies (see Figs. 3 and 5). Furthermore, the TIMP for the S1 and S2 and EPCO and ALPHA_BF for the S2 strategy are the only parameters that retain a fixed distribution shape. It establishes that these parameters have less uncertainty in the SWAT model. The results demonstrated that the ranges of other parameters must be relaxed, as well. For instance, the distributions of GW_DELAY, ESCO, and CH_N2 remarkably deviate from normality in the S1 strategy and centralize to their upper or lower bounds in the S2 strategy. In addition, some parameters arrive to similar distributions or are very close to each other. For example, CN2, ALPHA_BF, SOL_AWC, SOL_BD, SLSUBBSN, and SURLAG showed almost the same values around 0.21, 0.04, 0.26, − 0.14, 99, and 11.2 for both strategies, respectively.

Fig. 5
figure 5

Marginal posterior parameters distributions of SWAT model under S2 strategy

Full size image

The correlation matrices of the posterior parameter samples for the DREAM-ZS algorithm (the S2 strategy) after convergence are given in Table 8. The results of S2 strategy, as illustrated in Table 8, have been modified in relation to the S1 strategy. As illustrated in Table 8 and referred to Table 5, the correlation matrix of the posterior parameter samples of the DREAM-ZS revealed that most correlation values of pairwise parameters in the S2 strategy increased and were significantly better than those in the S1 strategy. For example, in the S2 strategy, the significant positive correlations were shown between the pairwise parameters such as (SOL_AWC, ESCO), (ALPHA_BF, SOL_AWC), and (ESCO, SFTMP) with the values of 0.87, 0.78, and 0.75, respectively, and significant negative correlations were shown between the pairwise parameters such as (CH_N2, CH_K2), (SMTMP, TIMP), and (SURLAG, PCPMM) with the values of − 0.63, − 0.53, and − 0.50, respectively (see Table 8). The rest of parameters have no significant correlation and most of them are correlated with a coefficient of less than 0.5. Nevertheless, the high correlations between aforementioned parameters in the S2 strategy provide important information about the uncertainty of parameters and indicate powerful interactions among those parameters and their effect on model response. Therefore, these parameters may be fixed in KRC region, before calibrating the SWAT model.

Table 8 The parameter posterior correlation matrix for strategy S2
Full size table

After convergence is attained, the last 20% of the samples of the SWAT model that adequately fit the model to the observations were exerted to generate model outputs. Then, the 95% confidence interval was depicted by calculating 2.5 and 97.5%. The time series data of the total uncertainty, parameter uncertainty, and the best simulation according to the SLS likelihood function and the observed runoff discharge at the five stations on monthly basis for the calibration period (1992 to 2011) were derived by the DREAM-ZS algorithm in the S2 strategy and are plotted in Fig. 6.

Fig. 6
figure 6

The 95% prediction uncertainty ranges of five runoff stations in S2 strategy: the light and dark shaded area, respectively, represents the total and parameter uncertainty; the red dots show the observed data; and the black line depicts the best prediction of runoff

Full size image

As it can be seen in Fig. 6, the widths of the total uncertainty for S2 are a little higher than S1 (according to Table 6; e.g., in SARASSHA, d-factor for the total uncertainty in S1 and S2 are 1.1 and 1.77, respectively, and for the parameter uncertainty in S2 is 0.25). Therefore, most of the observed points (more than 89%) in the DREAM-ZS strategy fall inside the 95% prediction uncertainty bounds and the P-factor is larger than the SUFI-2, which indicates a high performance of the model. For the S2 strategy, the total uncertainty band brackets 89 to 98% of the observed data with a similar d-factor from 1.36 to 5. The results of S2 are almost similar to each other and differ from the S1 strategy (see Fig. 6 and also Table 6). For example, the maximum and minimum P-factor and d-factor correspond to GOLJAGHR (S2: P-factor = 98 and d-factor = 4.49) and ZIRBAGOL (S2: P-factor = 89 and d-factor = 1.36), respectively. By considering the SWAT parameter uncertainty alone for the S2 strategy, only 19 to 34% of the observed data are bracketed (difficulty illustrated in Fig. 6). The limits of the upper and lower parameter uncertainty in the S2 strategy cover most of the observed data in these bands, indicating significant improvement compared to the S1 strategy. Furthermore, the gap between 95% prediction due to model parameters and observed data may be reasoned by the input/output data or the inadequacy of the model structure (Laloy et al. 2010). Note that the bounds of parameters and the total uncertainty are quite narrow and wide, respectively. Therefore, this result demonstrates that there is remarkable uncertainty in input data or structure of the model utilized in this study. The comparison between the two strategies, using NS, illustrates that the S2 strategy exhibits better performance than the S1 strategy. Furthermore, on average at all stations, the NS value was found to be around 0.71 and 0.65 in S2 and S1, respectively (Table 6). Although the NS values in both strategies are similar, the S2 strategy shows a relatively stronger relationship between the simulated runoff and the observations, which is investigated further in the next section. Although in DREAM-ZS the simulated monthly high flows are slightly underestimated in some months and overestimated in other months (especially at the end part of the calibration time period), it reveals a more realistic model with its tendency to further reduce the difference between observed and simulated data. Some different results between the informal and formal Bayesian frameworks are due to different fundamentals in their philosophies and mathematical rigor. As an example, the DREAM-ZS uses formal mathematics and Monte Carlo Markov Chain simulation to derive prediction and parameter uncertainty, whereas the SUFI-2 has a weak statistical basic (Mantovan and Todini 2006). Furthermore, the SUFI-2 does not try to discrete the parameters, input data, and structural errors in the model from the total uncertainty.

Comparison between SUFI-2 and DREAM-ZS

The indices S and T were utilized to compare the 95% prediction uncertainty band (95PPU) and the performance of uncertainty analysis. As shown in Table 9, both S and T at multisite runoff stations under the U2 uncertainty source have decreased, as compared to the U1. Results indicated that a low S (or T) value (in the other words a high degree of symmetry) normally corresponded to a large average band width of the estimated prediction bounds. Both S and T indices at all runoff stations under the U3 were greater than U1 and U2. However, we cannot compare the results of U3 with the U1, because the values of U1 are resulted from a SUFI-2 algorithm that attempts to predict all sources of uncertainties (Abbaspour et al. 2007). The highest values of S and T resulted from U1 in SARASSHA with the values of 0.51 and 1.01, whereas the lowest values of these indices were obtained under U2 in GOLJAGHR with values of 0.07 and 0.39, respectively.

Table 9 Average asymmetry degree indices of S and T considered in both strategies of uncertainty for runoff simulation
Full size table

Consequently, compared to S1, the S2 strategy, which considers both SUFI-2 and DREAM-ZS algorithms, arguably presented better results and lower uncertainties by considering the S and T indices. As a result, the fitted values of parameters in S2 can be applied to estimate the hydrology cycle processes in KRC with the SWAT model.

Summary and conclusion

This paper investigated informal and formal Bayesian frameworks (i.e., SUFI-2 and DREAM-ZS) by defining two different strategies that simulate runoff discharge over a 16,870-km2 semi-arid catchment system in Iran using the SWAT model. Among the initial parameters, 20 parameters were identified as the sensitive parameters to survey the calibration and uncertainty processes at five runoff gauging stations. The optimization of parameters in the SUFI-2 and DREAM-ZS algorithms were conducted by considering NS and SLS as the likelihood functions. The best posterior parameters in the S1 strategy (the use of the SUFI-2 algorithm) were obtained after a total number of 3000 runs while the S2 strategy (the use of DREAM-ZS algorithm) met the convergence after performing 120,000 iterations. The source code of DREAM-ZS was also modified to predict the parameter uncertainty at two or more runoff stations in a large-catchment system. In this research study, another strategy, i.e., S2, was investigated, as well. Although it was run by the DREAM-ZS algorithm, the prior ranges of this strategy were similar to the prior ranges in S1. S2 strategy did not target the convergence threshold; therefore, it was eliminated from the list of studied strategies in this research.

The results of the marginal density showed that different posterior parameter distributions resulted from different techniques. For the S1 strategy, both shape and parameter ranges in all of the parameters had different posterior distributions than their prior ranges except for ALPHA_BF. While the distributions of CN2, SHALLST, ESCO, SMFMN, and CH_N2 were well defined and approximately Gaussian, the parameters were either negatively or positively skewed. The width of some parameters covered only a narrow region interior compared to the prior range. For the S2 strategy, several modes were seen in both shape and parameter ranges. In S2, the TIMP, EPCO, and ALPHA_BF parameters maintained a constant distribution and had less uncertainty in the SWAT model while the other parameter ranges need to be relaxed. The width of posterior ranges in S2 either increased or decreased compared to S1.

The results of the correlation matrix between the sensitive parameters showed that for the S1 there were very low significant correlations, whereas for S2, the correlations were modified and significantly better than the S1 strategy (positively and negatively significant correlations could be seen in most parameters). The highest correlation values were observed between SOL_AWC and ESCO.

The results of uncertainty and calibration analysis showed that in the both strategies, the calibrated model relatively underestimated the peak runoff in most months at all stations, whereas in some months of the year, the recession limb was overestimated. However, the base flow illustrated high correspondence. In S1, most of the measured data were bracketed by the 95PPU (from 57 to 74%) and similar d-factors (from 0.9 to 1.29) were seen at all stations. Additionally, the HESDEHB station was determined to have a good performance. Even though the uncertainty in the S1 strategy was deemed as relatively satisfying, the width of the total uncertainty in S2 was higher than S1. Most of the measured data (more than 89%) in S2 located inside the 95PPU and were higher than the S1 strategy and d-factor in S2 (from 1.36 to 5) was larger than S1. Similar to the S1, the peak runoff points in the S2 strategy of DREAM-ZS were slightly underestimated and in some months were overestimated compared to the observed data.

Finally, the results of the supplementary evaluation criteria as new indices of the average asymmetry degree (S and T) at all stations revealed that for the total uncertainty, the both indices were greater in S1 than S2.

The results further indicated that a combination method of two formal and informal Bayesian frameworks can provide a better approach for runoff simulation than either formal or informal methods, individually. The uncertainty analysis confirmed the higher efficiency of DREAM-ZS algorithm (S2 strategy) to predict simultaneous parameter uncertainty in KRC as a spatially heterogeneous catchment than the SUFI-2 algorithm.

For future studies, the researchers can modify the source of SWAT model to assimilate data between physical and simulation processes in the model for the better investigation of parameter uncertainty in different Bayesian methods.