Adaptive Metaheuristic Scheme for Generalized Multiple Abnormality Detection in a Reservoir Pipeline Valve System

Abstract

This paper presents mathematical and algorithmic developments related to general abnormality (multiple leakages and multiple partial blockages) detection in a simple pipeline system. Formulations for leakages and blockages were combined and reformulated to address general abnormalities efficiently in the frequency domain. Unsteady friction effects on laminar and turbulent flow conditions were considered during formulation development using 2D frequency-dependent and 1D acceleration-based models, respectively. The developed formula was tested in terms of model parsimony, computational accuracy, and flexibility for superposition in abnormality representation. Based on the proposed formulation, a novel multiple abnormality detection algorithm, called the adaptive metaheuristic scheme (AMS), was developed by integrating a stepwise genetic algorithm. The application of the developed method to a hypothetical pipeline system demonstrated the potential of the AMS for predicting general features of abnormality, even without access to prior information regarding the number and distribution of abnormalities. The developed method demonstrated robustness for the prediction of abnormality distributions and reliability, even in noise-contaminated signals. The adaptive predictability of the AMS can be characterized by not only its robustness for unknown multiple abnormality features but also its self-diagnostic capabilities during the calibration procedure.

1 Introduction

Leakages and blockages in pipeline systems can be generated by factors such as high-pressure fluctuations, corrosion, biofilm development, deterioration of pipe walls, and even failures in manufacturing processes. The detection of leakages is important for water distribution authorities not only in terms of preventing water loss, but also in terms of securing drinking water from intrusion by potential contaminants, including pathogens. As fluid passes through the reduced cross-sectional area near a blockage, the flow energy tends to dissipate and flow conveyance can be reduced, which can increase the costs of both the management (water quality) and operation (pumping) of pipeline systems.

Considering the serviceability of a continuous water supply and its cost, non-intrusive methods for detecting leakages and blockages have been explored using pressure wave analysis associated with abnormal boundary conditions. Many attempts have been made to detect leakages or blockages in pipeline systems using transient-based methods in either the time or frequency domains, or both (Duan et al. 2014; Nguyen et al. 2018; Ranginkaman et al. 2019; Marchis and Milici 2019; Capponi et al. 2020; Gong et al. 2020). Pressure waves can be generated using various methods, including conventional valve maneuvers, pressure generation tanks, and electrical sparks (Brunone et al. 2008; Gong et al. 2018). Most studies on leakage detection or blockage detection have been conducted for the diagnosis of a single defect boundary condition within a pipeline.

When a water distribution system has deteriorated, the spatial features of abnormalities are not necessarily pointwise, but are more likely to be distributed across multiple points (Verde 2001). Considering the strength of frequency-domain approaches for defining the locations of specific boundary conditions, transfer matrices have been widely used to represent leakages or blockages (Mohapatra et al. 2006). An efficient formulation for multiple leakage representation was proposed for a simple reservoir pipeline system and a linearized model for the identification of leak numbers through iterative beamforming has also been proposed (Wang and Ghodaui 2018). A detection scheme for one leakage and one blockage was proposed based on an analytical derivation for a branched pipeline system through the incorporation of a metaheuristic engine (Kim 2016). The generalization of multiple leakages and blockages is required to address general circumstances in field pipeline systems to improve the detectability of abnormalities.

The development of a multiple abnormality detection scheme is a critical landmark for the diagnosis of pipeline defects for several reasons. The conditions in field pipeline systems never provide an indication of either the number or distribution of problematic boundary conditions. The dimensions of a problem cannot be determined and its sequence and identity are unknown in the context of solution optimization. Therefore, a robust analysis framework is required to address the unknown characteristics associated with multiple leakages and blockages. Developing a comprehensive mathematical structure for any combination of leakages and blockages along a pipeline is useful for designing a robust detection scheme for multiple abnormalities. Existing mathematical expressions of leakages and blockages (Mohapatra et al. 2006), namely point matrices, must be further generalized to improve the efficiency of representation and implementation flexibility for detection algorithms. As the number of abnormalities increases (to more than a few), the complexity of existing formulations tends to increase exponentially, making the identification of a specific leakage or blockage among multiple abnormalities virtually impossible from either a mathematical or signal processing perspective.

The simultaneous detection of leakages and blockages is a challenging engineering problem because of the distinct wave reflection patterns between two different defect boundaries. If the distribution of leakages and blockages is repeated in either triangular or intermittent patterns, the flow velocity can increase or decrease along a pipeline under both steady and unsteady flow conditions. This means that the existing steady friction model (Wylie and Streeter 1993) may not sufficiently represent the flow regime of a pipeline system for the representation of multiple abnormalities. Therefore, the proper consideration of unsteady friction is important for developing a reliable formulation for multiple abnormality detection methods (Zielke 1968; Brunone et al. 1991).

To develop a robust abnormality detection method based on pressure signals, the response pattern of an abnormality must be distinguished from those of pipeline system components such as the pipeline, reservoir, and valves. A detection algorithm must be carefully designed based on an understanding of the combined pressure patterns of leakages and blockages.

Therefore, in this study, two main objectives representing important building blocks for multiple abnormality detection schemes for a simple pipeline system were defined as follows:

• First, a multiple abnormality function (MAF) was developed for the efficient expression and flexible evaluation of impedance, as well as the adaptable calibration of multiple abnormalities in a reservoir pipeline system. Unsteady friction models for laminar and turbulent flows are integrated into the MAF in terms of impedance.

• Second, a multiple abnormality detection algorithm was developed for an unknown number of leakage and blockage distributions. An adaptive metaheuristic scheme (AMS) is proposed for the proactive control of metaheuristic operations depending on the distribution and number of abnormalities.

To demonstrate the potential of the developed techniques in terms of the realization of a multiple abnormality detection algorithm, a hypothetical pipeline system is introduced. The test results for several multiple abnormality detection methods demonstrate the potential of the proposed AMS for different flows and abnormality distributions. The impact of noise on multiple abnormality detectability was also analyzed to highlight the applicability of the developed method.

2 Mathematical Development for Analysis

2.1 Governing Equations for Unsteady Flow

The mass and momentum balance equations for a one-dimensional transient flow in a pressurized pipeline are approximated under steady friction as follows (Wyile and Streeter 1993):

$$\frac{{a^{2} }}{gA}\frac{\partial Q}{{\partial x}} + \frac{\partial H}{{\partial t}} = 0,$$

(1)

$$\frac{\partial Q}{{\partial t}} + gA\frac{\partial H}{{\partial x}} + \frac{fQ\left| Q \right|}{{2DA}} = 0,$$

(2)

where x is the distance along the pipeline, t is time, a is the wave speed, g is the acceleration due to gravity, A is the cross-sectional area, Q is the discharge, H is the piezometric pressure head, and f is the Darcy-Weisbach friction factor.

The relationship between the upstream and downstream head and discharge $f\left( {H_{U} ,Q_{U} ,H_{D} ,Q_{D} } \right)$ can be expressed in the frequency domain as (Wylie and Streeter 1993; Chaudhry 2014)

$$H_{D} = H_{U} cosh\gamma x - Q_{U} Z_{c} sinh\gamma x,$$

(3)

$$Q_{D} = - \frac{{H_{U} }}{{Z_{c} }}sinh\gamma x + Q_{U} cosh\gamma x,$$

(4)

where the propagation constant is $\gamma = \sqrt {\frac{gA}{{a^{2} }}s(\frac{s}{gA} + \frac{fQ}{{gDA^{2} }}} )$, the characteristic impedance is $Z_{C} = \frac{{\gamma a^{2} }}{gAs}$, and s is the complex frequency.

2.2 Impedance of Multiple Abnormalities in a Simple Pipeline

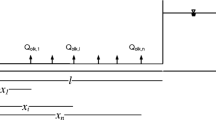
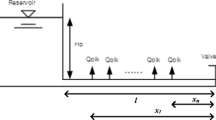
The relationships between the complex head and discharge between the upstream reservoir and downstream valve (Fig. 1) for multiple abnormality conditions can be expressed as a transfer matrix of leakages and blockages as follows:

$$\begin{aligned}\left[ {\begin{array}{*{20}c} {H_{DV} } \\ {Q_{DV} } \\ \end{array} } \right] &= \left[ {\begin{array}{*{20}c} {cosh\gamma x_{n} } & { - Z_{c} sinh\gamma x_{n} } \\ {\frac{{ - sinh\gamma x_{n} }}{{Z_{c} }}} & {cosh\gamma x_{n} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 \\ {\frac{{Q_{olk,i} }}{{2H_{o} }}} & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {cosh\gamma \left( {x_{n - 1} - x_{n} } \right)} & { - Z_{c} sinh\gamma (x_{n - 1} - x_{n} )} \\ {\frac{{ - sinh\gamma (x_{n - 1} - x_{n} )}}{{Z_{c} }}} & {cosh\gamma (x_{n - 1} - x_{n} )} \\ \end{array} } \right] \\&\ldots \left[ {\begin{array}{*{20}c} {cosh\gamma \left( {x_{1} - x_{2} } \right)} & { - Z_{c} sinh\gamma \left( {x_{1} - x_{2} } \right)} \\ {\frac{{ - sinh\gamma \left( {x_{1} - x_{2} } \right)}}{{Z_{c} }}} & {cosh\gamma \left( {x_{1} - x_{2} } \right)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & { - \frac{{2\Delta H_{j} }}{{Q_{0} }}} \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {cosh\gamma \left( {l - x_{1} } \right)} & { - Z_{c} sinh\gamma \left( {l - x_{1} } \right)} \\ {\frac{{ - sinh\gamma \left( {l - x_{1} } \right)}}{{Z_{c} }}} & {cosh\gamma \left( {l - x_{1} } \right)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {H_{UR} } \\ {Q_{UR} } \\ \end{array} } \right]\end{aligned}$$

(5)

Here, $H_{DV}$ and $Q_{DV}$ are the complex head and discharge at the downstream valve, respectively; $H_{UR}$ and $Q_{UR}$ are the complex head and discharge at the upstream reservoir, respectively; l is the length between the upstream and downstream; $x_{1} ,x_{2} , \ldots x_{n}$ are the distances between each abnormality and the downstream valve; $Q_{olk,i}$ is the leak quantity for the ith leakage; $\Delta H_{j}$ is the pressure head variation caused by the jth blockage; and $H_{0}$ and $Q_{0}$ are the mean pressure head and discharge, respectively.

Fig. 1

Schematic of a reservoir pipeline system with multiple abnormalities

Applications of hyperbolic trigonometry to extensions of pipeline components can significantly simplify the expression of hydraulic impedance ($Z = H_{DV} /Q_{DV} )$. Nonlinear terms with multiple abnormalities can be ignored for very low orders of mathematical terms with abnormalities. The hydraulic impedance at a downstream valve for multiple abnormality conditions can be expressed as:

$$Z_{DV} = ( {Z_{A} + \textstyle\sum_{i = 1}^{n1} Z_{B,i} + \textstyle\sum_{j = 1}^{n2} Z_{B,j} } )/( {1 + \textstyle\sum_{i = 1}^{n1} Z_{C,i} + \textstyle\sum_{j = 1}^{n2} Z_{C,j} })$$

(6)

where $Z_{A} = - Z_{c} \times \left( {e^{\gamma l} - e^{ - \gamma l} } \right)/\left( {e^{\gamma l} + e^{ - \gamma l} } \right)$.

If the number of leakages is $n1$, then the terms Z_B,i and Z_C,i terms in Eq. (6) can be expressed as

$$\textstyle\sum_{i = 1}^{n1} Z_{B,i} = \textstyle\sum_{i = 1}^{n1} \left\{ { - Z_{c}^{2} Q_{olk,i} /\left( {2H_{0} } \right)} \right\}/\{ {1 + \frac{{e^{\gamma l} + e^{ - \gamma l} + e^{{\gamma \left( {2x_{i} - l} \right)}} + e^{{\gamma \left( {l - 2x_{i} } \right)}} }}{{e^{\gamma l} + e^{ - \gamma l} - e^{{\gamma \left( {2x_{i} - l} \right)}} - e^{{\gamma \left( {l - 2x_{i} } \right)}} }}} \},$$

(7)

$$\textstyle\sum_{i = 1}^{n1} Z_{C,i} = \textstyle\sum_{i = 1}^{n1} \left\{ {Z_{c} Q_{olk,i} /\left( {2H_{0} } \right)} \right\}/\{ {\frac{{e^{{\gamma x_{i} }} - e^{{ - \gamma x_{i} }} }}{{e^{{\gamma x_{i} }} + e^{{ - \gamma x_{i} }} }} + \frac{{e^{{\gamma \left( {l - x_{i} } \right)}} + e^{{\gamma \left( {x_{i} - l} \right)}} }}{{e^{{\gamma \left( {l - x_{i} } \right)}} - e^{{\gamma \left( {x_{i} - l} \right)}} }}} \},$$

(8)

where $x_{i}$ is the distance from a downstream valve to any upstream ith leakage.

If the number of blockages is $n2$, then the terms Z_B,j and Z_C,j in Eq. (6) can be expressed as

$$\textstyle\sum_{j = 1}^{n2} Z_{B,j} = \textstyle\sum_{j = 1}^{n2} \left\{ { - 2\Delta H_{j} /\left( {Q_{0} } \right)} \right\}/\{ {1 + \frac{{e^{\gamma l} + e^{ - \gamma l} - e^{{\gamma \left( {2x_{j} - l} \right)}} - e^{{\gamma \left( {l - 2x_{j} } \right)}} }}{{e^{\gamma l} + e^{ - \gamma l} + e^{{\gamma \left( {2x_{j} - l} \right)}} + e^{{\gamma \left( {l - 2x_{j} } \right)}} }}} \},$$

(9)

$$\textstyle\sum_{j = 1}^{n2} Z_{C,j} = \textstyle\sum_{j = 1}^{n2} \left\{ {2\Delta H_{j} /\left( {Z_{c} Q_{0} } \right)} \right\}/\{ {\frac{{e^{{\gamma x_{j} }} + e^{{ - \gamma x_{j} }} }}{{e^{{\gamma x_{j} }} - e^{{ - \gamma x_{j} }} }} + \frac{{e^{{\gamma \left( {l - x_{j} } \right)}} - e^{{\gamma \left( {x_{j} - l} \right)}} }}{{e^{{\gamma \left( {l - x_{j} } \right)}} + e^{{\gamma \left( {x_{j} - l} \right)}} }}} \},$$

(10)

where $x_{j}$ is the distance from a downstream valve to any upstream jth blockage and $\Delta H_{j}$ is the jth pressure head reduction.

The term $Z_{A}$ in Eq. (6) represents the impact of pipeline extension. The structure of this equation also indicates that abnormality impacts on hydraulic impedance are nonlinear, but can be efficiently expressed by superimposing functions such as $\textstyle\sum_{i = 1}^{n1} Z_{B,i}$ + $\textstyle\sum_{j=1}^{n2}Z_{B,j}$ and $\textstyle\sum_{i = 1}^{n1} Z_{C,i}$ + $\textstyle\sum_{j = 1}^{n2} Z_{C,j}$, which allows each abnormality to be considered independently.

2.3 Impedance of Multiple Abnormalities Using an Unsteady Friction Model Under Laminar Flow

The impact of unsteady friction on laminar flow conditions can be considered by modeling the radial distribution of velocity, which can be expressed through 2D equations of motion and continuity as follows (Suo and Wylie 1989)

$$\frac{1}{\rho }\frac{\partial p}{{\partial x}} + \frac{\partial u}{{\partial t}} - \nu \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial u}{{\partial r}}} \right) = 0,$$

(11)

$${\rho a}^{2} \frac{\partial u}{{\partial x}} + \frac{\partial p}{{\partial t}} = 0.$$

(12)

Here, $\rho$ is the density of the fluid, and u and p are the velocity and pressure, respectively, as functions of time (t), axial distance (x), and radial distance (r). Equations (11) and (12) are collectively known as the frequency-dependent friction approach for laminar flow (Zielke 1968).

The hydraulic impedance of multiple abnormalities with frequency-dependent friction can be expressed as

$${Z_{DV}}^{\prime} = ( {{Z_{A}}^{\prime} + \textstyle\sum_{i = 1}^{n1} {Z_{B,i}}^{\prime} + \textstyle\sum_{j = 1}^{n2} {Z_{B,j}}^{\prime} } )/( {1 + \textstyle\sum_{i = 1}^{n1} {Z_{C,i}}^{\prime} + \textstyle\sum_{j = 1}^{n2} {Z_{C,j}}^{\prime}} )$$

(13)

where ${Z_{A}}^{\prime} = - Z_{s} \times \left( {e^{\Gamma \left( l \right)} - e^{{\Gamma \left( { - l} \right)}} } \right)/\left( {e^{\Gamma \left( l \right)} + e^{{\Gamma \left( { - l} \right)}} } \right)$.

The propagation constant is expressed as $\Gamma \left( x \right) = sx/( {a\sqrt {( {1 - 2J_{1} ( {iD\sqrt {s/\nu } })} )/( {{\text{iD}}/2\sqrt {s/\upsilon } J_{0} ( {iD\sqrt {s/\nu } } )} )} })$ and the characteristic impedance is expressed as $Z_{s} = a/( {gA\sqrt {( {1 - 2J_{1} ( {iD\sqrt {s/\nu } })} )/( {{\text{iD}}/2\sqrt {s/\upsilon } J_{0} ( {iD\sqrt {s/\nu } })})} })$, where i is an imaginary unit, and J₀ and J₁ are first-type Bessel functions of the zeroth and first orders, respectively.

The terms for multiple leakages, ${Z_{B,i}}^{\prime}$ and ${Z_{C,i}}^{\prime}$ in Eq. (13), can be expressed as

$$\textstyle\sum_{i = 1}^{n1} {Z_{B,i}}^{\prime} = \textstyle\sum_{i = 1}^{n1} \left\{ { - Z_{s}^{2} Q_{olk,i} /\left( {2H_{0} } \right)} \right\}/\{ {1 + \frac{{e^{\Gamma \left( l \right)} + e^{{\Gamma \left( { - l} \right)}} + e^{{\Gamma \left( {2x_{i} - l} \right)}} + e^{{\Gamma \left( {l - 2x_{i} } \right)}} }}{{e^{\Gamma \left( l \right)} + e^{{\Gamma \left( { - l} \right)}} - e^{{\Gamma \left( {2x_{i} - l} \right)}} - e^{{\Gamma \left( {l - 2x_{i} } \right)}} }}}\}$$

(14)

$$\textstyle\sum_{i = 1}^{n1} {Z_{C,i}}^{\prime} = \textstyle\sum_{i = 1}^{n1} \left\{ {Z_{s} Q_{olk,i} /\left( {2H_{0} } \right)} \right\}/\{ {\frac{{e^{{\Gamma \left( {x_{i} } \right)}} - e^{{\Gamma \left( { - x_{i} } \right)}} }}{{e^{{\Gamma \left( {x_{i} } \right)}} + e^{{\Gamma \left( { - x_{i} } \right)}} }} + \frac{{e^{{\Gamma \left( {l - x_{i} } \right)}} + e^{{\Gamma \left( {x_{i} - l} \right)}} }}{{e^{{\Gamma \left( {l - x_{i} } \right)}} - e^{{\Gamma \left( {x_{i} - l} \right)}} }}} \}$$

(15)

The terms for multiple blockages, namely ${Z_{B,j}}^{\prime}$ and ${Z_{C,j}}^{\prime}$ in Eq. (13), can be expressed as

$$\textstyle\sum_{j = 1}^{n2} {Z_{B,j}}^{\prime} = \textstyle\sum_{j = 1}^{n2} \left\{ { - 2\Delta H_{j} /\left( {Q_{0} } \right)} \right\}/\{ {1 + \frac{{e^{\Gamma \left( l \right)} + e^{{\Gamma \left( { - l} \right)}} - e^{{\Gamma \left( {2x_{j} - l} \right)}} - e^{{\Gamma \left( {l - 2x_{j} } \right)}} }}{{e^{\Gamma \left( l \right)} + e^{{\Gamma \left( { - l} \right)}} + e^{{\Gamma \left( {2x_{j} - l} \right)}} + e^{{\Gamma \left( {l - 2x_{j} } \right)}} }}} \},$$

(16)

$$\textstyle\sum_{j = 1}^{n2} {Z_{C,j}}^{\prime} = \textstyle\sum_{j = 1}^{n2} \left\{ {2\Delta H_{j} /\left( {Z_{s} Q_{0} } \right)} \right\}/\{ {\frac{{e^{{\Gamma \left( {x_{j} } \right)}} + e^{{\Gamma \left( { - x_{j} } \right)}} }}{{e^{{\Gamma \left( {x_{j} } \right)}} - e^{{\Gamma \left( { - x_{j} } \right)}} }} + \frac{{e^{{\Gamma \left( {l - x_{j} } \right)}} - e^{{\Gamma \left( {x_{j} - l} \right)}} }}{{e^{{\Gamma \left( {l - x_{j} } \right)}} + e^{{\Gamma \left( {x_{j} - l} \right)}} }}} \}.$$

(17)

2.4 Impedance of Multiple Abnormalities Using an Unsteady Friction Model Under Turbulent Flow

The impact of unsteady friction on turbulent flow conditions can be evaluated as the difference between the friction contributions from temporal and convective accelerations, and the momentum equation can be expressed as (Ramos et al. 2004)

$$\frac{1}{{\text{g}}}\frac{\partial V}{{\partial {\text{t}}}} + \frac{{\partial {\text{H}}}}{{\partial {\text{x}}}} + {\text{F}}_{{\text{s}}} + {\text{F}}_{{\text{u}}} = 0,$$

(18)

$$\frac{{a^{2} }}{g}\frac{\partial V}{{\partial x}} + \frac{\partial H}{{\partial t}} = 0,$$

(19)

where V is the one-dimensional velocity, F_s is a steady friction term expressed as $F_{s} = fV\left| V \right|/\left( {2gD} \right)$, F_u is an unsteady friction term expressed as $F_{u} = \frac{1}{g}\left( {k_{1} \frac{\partial V}{{\partial t}} + ak_{2} Sign\left( V \right)\left| {\frac{\partial V}{{\partial x}}} \right|} \right)$, k₁ is the unsteady friction coefficient for the temporal acceleration term, and k₂ is the unsteady friction coefficient for the convective acceleration term.

The impedance formulation for a reservoir pipeline valve (RPV) system with multiple abnormalities (MAF-1D) can be expressed as

$${Z_{DV}}^{\prime\prime} = ( {{Z_{A}}^{\prime} + \textstyle\sum_{i = 1}^{n1} {Z_{B,i}}^{\prime} + \textstyle\sum_{j = 1}^{n2} {Z_{B,j}}^{\prime}})/( {1 + \textstyle\sum_{i = 1}^{n1} {Z_{C,i}}^{\prime} + \textstyle \sum_{j = 1}^{n2} {Z_{C,j}}^{\prime}})$$

(20)

where ${Z_{A}}^{\prime} = \left( {e^{{ - \gamma_{2} l}} - e^{{\gamma_{1} l}} } \right)/\left( {e^{{\gamma_{1} l}} /Z_{c1} + e^{{ - \gamma_{2} l}} /Z_{c2} } \right)$, the propagation constants $\gamma_{1}$ and $\gamma_{2}$ can be defined as $\gamma_{1,2} = ( {\mu mCs \mp \sqrt {\left( {mCs} \right)^{2} + 4\left( {s^{2} CL + RCs} \right)} } )/2$, ${\text{m}} = \left( {ak_{2} } \right)/\left( {2gA} \right)$, ${\text{C}} = \left( {{\text{gA}}} \right)/a^{2}$, ${\text{L}} = \left( {1 + k_{1} } \right)/\left( {gA} \right)$, and the characteristic impedances are $Z_{c1} ,Z_{c2} = \frac{{\gamma_{1} }}{Cs},\frac{{\gamma_{2} }}{Cs}$.

The impact of the multiple leakage terms ${Z_{B,i}}^{\prime\prime}$ and ${Z_{C,j}}^{\prime\prime}$ is expressed as follows:

$$\begin{aligned}\mathop \sum \limits_{i = 1}^{n1} {Z_{B,i}}^{\prime\prime} &= \left\{ { - 1/\left( {2H_{0} } \right)\textstyle\sum_{i = 1}^{n1} Q_{olk,i} Z_{c1} Z_{c2} ( {e^{{\gamma_{1} l}} + e^{{ - \gamma_{2} l}} - e^{{\gamma_{1} x_{i} - \gamma_{2} \left( {l - x_{i} } \right)}} - e^{{ - \gamma_{2} x_{i} + \gamma_{1} \left( {l - x_{i} } \right)}} }) } \right\}\\&/\{ {\frac{{e^{{\gamma_{1} l}} \left( {Z_{c1} + Z_{c2} } \right)}}{{Z_{c1} }} + \frac{{e^{{ - \gamma_{2} l}} \left( {Z_{c1} + Z_{c2} } \right)}}{{Z_{c2} }} } \},\end{aligned}$$

(21)

$$\begin{aligned}\mathop \sum \limits_{i = 1}^{n} {Z_{C,i}}^{\prime\prime} &= \left\{ { - 1/\left( {2H_{0} } \right)\textstyle\sum_{i = 1}^{n1} Q_{olk,i} ( {Z_{c1} \left( {e^{{ - \gamma_{2} l}} - e^{{ - \gamma_{2} x_{i} + \gamma_{1} \left( {l - x_{i} } \right)}} } \right) + Z_{c2} \left( {e^{{\gamma_{1} x_{i} - \gamma_{2} \left( {l - x_{i} } \right)}} - e^{{\gamma_{1} l}} } \right)} ) } \right\}\\&/\{ {\frac{{e^{{\gamma_{1} l}} \left( {Z_{c1} + Z_{c2} } \right)}}{{Z_{c1} }} + \frac{{e^{{ - \gamma_{2} l}} \left( {Z_{c1} + Z_{c2} } \right)}}{{Z_{c2} }} }\}.\end{aligned}$$

(22)

The impact of the multiple blockage terms ${Z_{B,j}}^{\prime\prime}$ and ${Z_{C,j}}^{\prime\prime}$ is expressed as follows:

$$\begin{aligned}\mathop \sum \limits_{j = 1}^{n2} {Z_{B,j}}^{\prime\prime} &= \mathop \sum \limits_{j = 1}^{n2} \{ { - 2\Delta H_{0,j} /\left( {Q_{0} } \right)( {e^{{\gamma_{1} l}} + e^{{ - \gamma_{2} l}} + Z_{c1} /Z_{c2} e^{{\gamma_{1} x_{j} - \gamma_{2} \left( {l - x_{j} } \right)}} - Z_{c2} /Z_{c1} e^{{ - \gamma_{2} x_{j} + \gamma_{1} \left( {l - x_{j} } \right)}} }) } \}\\&/\{ {\frac{{e^{{\gamma_{1} l}} \left( {Z_{c1} + Z_{c2} } \right)}}{{Z_{c1} }} + \frac{{e^{{ - \gamma_{2} l}} \left( {Z_{c1} + Z_{c2} } \right)}}{{Z_{c2} }} } \},\end{aligned}$$

(23)

$$\begin{aligned}\mathop \sum \limits_{j = 1}^{n2} {Z_{C,j}}^{\prime\prime} &= \mathop \sum \limits_{i = 1}^{n} \{ { - 2\Delta H_{0,j} /\left( {Q_{0} } \right)( {Z_{c1} \left( {e^{{ - \gamma_{2} l}} - e^{{\gamma_{1} x_{j} - \gamma_{2} \left( {l - x_{j} } \right)}} } \right) + Z_{c2} \left( {e^{{ - \gamma_{2} x_{j} + \gamma_{1} \left( {l - x_{j} } \right)}} - e^{{\gamma_{1} l}} } \right)} )} \}\\&/\left\{ {Z_{c2} \left( {Z_{c1} + Z_{c2} } \right)e^{{\gamma_{1} l}} + Z_{c1} \left( {Z_{c1} + Z_{c2} } \right)e^{{ - \gamma_{2} l}} } \right\}.\end{aligned}$$

(24)

3 Adaptive Metaheuristic Scheme

If the number of abnormalities is unknown before optimization, then the dimensions of a problem for the application of a metaheuristic engine cannot be determined. In other words, the conventional scheme of inverse transient analysis cannot handle multiple abnormality problems. The other source of uncertainty in optimization is the distribution of abnormalities. Depending on the sequence of abnormality boundary conditions (either leakages or blockages), an appropriate calibration scheme should be adopted.

The AMS is introduced for the proactive control of metaheuristic operations depending on the number of abnormalities and their distribution. To relax the undetermined number of parameters, the conventional structure of a genetic algorithm (GA) was modified to implement a stepwise search structure for each abnormality. A GA is a powerful search tool that uses evolution-based principles to find optimal solutions (Goldberg 1989).

Depending on the sign of the local pressure head gradient $\left( {\Delta h/\Delta t} \right)_{i}$, where i is the time step, the feature of each abnormality can be determined (either a leakage or blockage). Once the calibration for a predetermined bound is completed, the stepwise abnormality detection procedure is repeated until a transient signal bounces back from an upstream reservoir to the pressure sensor, which is assumed to be located at the downstream valve. Figure 2 illustrates the flowchart of the proposed AMS for detecting multiple abnormalities. The bound of a potential abnormality is determined by considering that the time-domain reflectometry principle primarily stems from the reflection of a pressure wave in the case of an abnormality condition. Depending on the candidate solutions for abnormality locations and quantities, the pressure variation of the transient can be calculated to fit the objective function and the optimal parameters can be derived.

Fig. 2

Flowchart for the proposed AMS for the stepwise detection of multiple abnormalities

The identification of the pressure variation features for an abnormality is important, but other relatively low-frequency pressure responses can be considered redundant. The objective function for abnormality detection does not necessarily address all time series for the theoretical period of a pipeline system (Wylie and Streeter 1993). The proposed optimization scheme counts several pressure points for a specific abnormality calibration. To designate the search range for each abnormality, two arrays called ITT1(k) and ITT2(k) are introduced (k is the number of multiple abnormalities). A sequential comparison of adjacent pressure gradients to the tolerance of the pressure sensor error (TOL) is performed, and ITT1(k) and ITT2(k) can be determined as follows:

$$if\left( {DIFF1 > TOL. \& .DIFF2 < TOL} \right) then$$

$$ITT1\left( k \right) = i - 2; ITT2\left( k \right) = i + 2; k = k + 1,$$

(25)

where $DIFF1 = ABS\left[ {\left\{ {h\left( i \right) - h\left( {i - 1} \right)} \right\}/dt} \right]$, $DIFF2 = ABS\left[ {\left\{ {h\left( {i + 1} \right) - h\left( i \right)} \right\}/dt} \right]$, and $h\left( i \right)$ is the pressure head at time step i, which iterates between two and nf. The symbol nf is an integer representing 2 l / a, where l is the pipeline length and a is the wave speed. In this study, the normalized pressure head for a steady-state pressure head was used for h(i), and a value of one was adopted for the TOL.

Based on the identification of the calibration interval using Eq. (25), the objective function (OF) for the simultaneous detection of multiple leakages can be simply defined as

$$OF = {\text{min}}[\textstyle\sum_{k = 1}^{m} \{ \textstyle\sum_{i = ITT1\left( k \right)}^{ITT2\left( k \right)} \left( {h_{obs} \left( i \right) - h_{cal} \left( i \right)} \right)^{2} \} ],$$

(26)

where m is the number of multiple abnormalities, and $h_{obs} \left( i \right)$ and $h_{cal} \left( i \right)$ are the observed and calculated pressure heads at time step i, respectively.

To improve the predictability of abnormalities, three enhanced schemes were implemented to concentrate the calibration potential of the metaheuristic engine.

3.1 Enhanced Adaptive Scheme 1

To minimize the impact of pressure noise on the abnormality detection process, enhanced adaptive scheme 1 was implemented in the AMS. Noise can be generated by the error bounds associated with a measurement device such as a pressure transducer, one or more residuals of a preexisting transient impact, or signal contamination during the information transformation procedure. If noise statistics are unbiased and the distribution of a pressure signal is temporally uniform, then the presence of such noise is not always detrimental to the prediction of leakages (Lee et al. 2013). However, the residual transitional pressure head disturbances introduced by a water hammer can be an obstacle to the detection of leakages with small leakage discharges. Consequently, the impact of noise on the first abnormality detection procedure can affect the next search for additional abnormalities.

Therefore, a stepwise abnormality detection scheme must be refined to minimize the impact of disturbances from previous abnormalities. The objective function of the pressure signal from the first wave reflection ($OF_{1}$) is defined as

$$OF_{1} = {\text{min}}[ {\textstyle\sum_{i = ITT1\left( 1 \right)}^{ITT2\left( 1 \right)} \left( {h_{obs} \left( i \right) - h_{cal} \left( i \right)} \right)^{2} }].$$

(27)

The objective function for the pressure signal from the second to the mth wave reflection $(OF_{j})$ is defined as

$$OF_{j} = {\text{min}}[\textstyle\sum_{i = ITT1\left( j \right)}^{ITT2\left( j \right)} \{ ( {h_{obs} \left( i \right) - Cuth_{obs} } ) - (h_{cal} \left( i \right) - Cuth_{cal} )\}^{2} ],$$

(28)

where, $Cuth_{obs}$ and $Cuth_{cal}$ are equal to $h_{obs} \left( {ITT1\left( j \right)} \right)$ and $h_{cal} \left( {ITT1\left( j \right)} \right)$, respectively.

3.2 Enhanced Adaptive Scheme 2

The prediction of abnormality locations is the most important factor for the practical management of water distribution systems. The potential locations of multiple abnormalities are not necessarily defined according to the total length of a pipeline and the bounds for multiple abnormalities can be defined on much finer scales.

Defining different search ranges for each abnormality facilitates enhanced parameter convergence compared to the conventional case. Enhanced adaptive scheme 2 implements distinct bounds for abnormality locations through the sequential optimization of abnormalities.

The maximum and minimum bounds, $MaxB$ and $MinB$, for the location of the first abnormality and the other abnormality locations are defined as

$$MinB = 0, i = 1;\;MinB = a \times ITT2\left( {i - 1} \right)/2,\,i > 1;\;MaxB = a \times ITT2\left( i \right)/2,{ }i \ge 1,$$

(29)

where i = 1,.., m, and m is the total number of abnormalities. The bounds defined by Eq. (29) are the ranges of the leak location in m.

3.3 Enhanced Adaptive Scheme 3

Inverse transient analysis frequently uses pressure time series during multiples of the theoretical period of an RPV system (e.g.,$4l/a$, …). This can be useful for calibrating additional pipeline parameters (e.g., friction and system characteristics) over leakages. However, the ASM focuses on the prediction of abnormalities and the impact of other pipeline components such as the length and wave speed can be redundant. Therefore, it is more effective to exclude additional impacts such as the pipeline structure in the formulation of the multiple abnormality function. This means that the proposed method only considers the impact of abnormalities stemming from external valve actions and their associations with the frictional impact on the pipeline system. Enhanced adaptive scheme 3 implements exclusive hydraulic impedances for multiple abnormalities under unsteady friction conditions.

By using hydraulic impedances for the 2D unsteady friction models, the identified exclusive impedance for multiple abnormalities in an RPV system, namely the identical multiple abnormality function for laminar flow, can be expressed as

$${ZI_{DV}}^{\prime} = ( {\textstyle\sum_{i = 1}^{n1} {Z_{AC,i}}^{\prime} + \textstyle\sum_{j = 1}^{n2} {Z_{AC,j}}^{\prime} - \textstyle\sum_{i = 1}^{n1} {Z_{B,i}}^{\prime} - \textstyle \sum_{j = 1}^{n2} {Z_{B,j}}^{\prime}})/( {1 + \textstyle\sum_{i = 1}^{n1} {Z_{C,i}}^{\prime} + \textstyle\sum_{j = 1}^{n2} {Z_{C,j}}^{\prime}}),$$

(30)

$$\textstyle\sum_{i = 1}^{n1} {Z_{AC,i}}^{\prime} = \frac{{Z_{s}^{2} }}{{2H_{0} }} \times \frac{{e^{\Gamma \left( l \right)} - e^{{\Gamma \left( { - l} \right)}} }}{{e^{\Gamma \left( l \right)} + e^{{\Gamma \left( { - l} \right)}} }} \times \textstyle \sum_{i = 1}^{n1}[ {Q_{olk,i} /\{ {\frac{{e^{{\Gamma \left( {x_{i} } \right)}} - e^{{\Gamma \left( { - x_{i} } \right)}} }}{{e^{{\Gamma \left( {x_{i} } \right)}} + e^{{\Gamma \left( { - x_{i} } \right)}} }} + \frac{{e^{{\Gamma \left( {l - x_{i} } \right)}} + e^{{\Gamma \left( {x_{i} - l} \right)}} }}{{e^{{\Gamma \left( {l - x_{i} } \right)}} - e^{{\Gamma \left( {x_{i} - l} \right)}} }}}\}}]$$

(31)

$$\textstyle\sum_{j = 1}^{n2} {Z_{AC,j}}^{\prime} = - \frac{2}{{2H_{0} }} \times \frac{{e^{\Gamma \left( l \right)} - e^{{\Gamma \left( { - l} \right)}} }}{{e^{\Gamma \left( l \right)} + e^{{\Gamma \left( { - l} \right)}} }} \times \textstyle\sum_{j = 1}^{n2} [ {\Delta H_{j} /\{ {\frac{{e^{{\Gamma \left( {x_{j} } \right)}} + e^{{\Gamma \left( { - x_{j} } \right)}} }}{{e^{{\Gamma \left( {x_{j} } \right)}} - e^{{\Gamma \left( { - x_{j} } \right)}} }} + \frac{{e^{{\Gamma \left( {l - x_{j} } \right)}} - e^{{\Gamma \left( {x_{j} - l} \right)}} }}{{e^{{\Gamma \left( {l - j} \right)}} + e^{{\Gamma \left( {x_{j} - l} \right)}} }}}\}}].$$

(32)

The leakage number ($n1$) and blockage number ($n2$) can be varied as the calibration scheme identifies additional abnormalities.

Based on the 1D unsteady friction model, the identified multiple abnormality function for turbulent flow, which is the sole hydraulic impedance at a downstream valve for an RPV system, can be expressed as

$${ZI_{DV}}^{\prime\prime} = ( {\textstyle\sum_{i = 1}^{n1} Z^{\prime\prime}_{AC,i} + \textstyle\sum_{j = 1}^{n2} Z^{\prime\prime}_{AC,j} - \textstyle\sum_{i = 1}^{n1} Z^{\prime\prime}_{B,i} - \textstyle\sum_{j = 1}^{n2} Z^{\prime\prime}_{B,j} })/( {1 + \textstyle\sum_{i = 1}^{n1} {Z_{C,i}}^{\prime\prime} + \textstyle\sum_{j = 1}^{n2} {Z_{C,j}}^{\prime\prime}}),$$

(33)

$$\mathop \sum \limits_{i = 1}^{n1} {Z_{AC,i}}^{\prime\prime} = - \frac{1}{{2H_{0} }}\frac{{Z_{c1}^{2} Z_{c2}^{2} \left( {e^{{\gamma_{1} l}} - e^{{ - \gamma_{2} l}} } \right)}}{{\left( {Z_{c1} + Z_{c2} } \right)\left( {Z_{c2} e^{{\gamma_{1} l}} + Z_{c1} e^{{ - \gamma_{2} l}} } \right)^{2} }}$$

$$\textstyle\sum_{i = 1}^{n1} Q_{olk,i} \left\{ {Z_{c1} \left( {e^{{ - \gamma_{2} l}} - e^{{ - \gamma_{2} x_{i} + \gamma_{1} \left( {l - x_{i} } \right)}} } \right) + Z_{c2} \left( {e^{{\gamma_{1} x_{i} - \gamma_{2} \left( {l - x_{i} } \right)}} - e^{{\gamma_{1} l}} } \right)} \right\},$$

(34)

$$\mathop \sum \limits_{j = 1}^{n2} {Z_{AC,j}}^{\prime\prime} = \frac{2}{{Q_{0} }}\frac{{Z_{c1} Z_{c2} \left( {e^{{\gamma_{1} l}} - e^{{ - \gamma_{2} l}} } \right)}}{{\left( {Z_{c1} + Z_{c2} } \right)\left( {Z_{c2} e^{{\gamma_{1} l}} + Z_{c1} e^{{ - \gamma_{2} l}} } \right)^{2} }}$$

$$\textstyle\sum_{j = 1}^{n2} \Delta H_{o,j} \left\{ {Z_{c1} \left( {e^{{ - \gamma_{2} l}} - e^{{\gamma_{1} x_{j} - \gamma_{2} \left( {l - x_{j} } \right)}} } \right) + Z_{c2} \left( {e^{{ - \gamma_{2} x_{j} + \gamma_{1} \left( {l - x_{j} } \right)}} - e^{{\gamma_{1} l}} } \right)} \right\}.$$

(35)

4 Results

4.1 An RPV System with Multiple Abnormalities

Multiple abnormalities were considered in an RPV system to test the performance of the developed method for detecting multiple leakages and blockages. The target RPV system has been used in several experimental studies (Kim 2011, 2016). A distribution of 10 abnormalities was considered, as shown in Fig. 1. The length of the pipeline is 87.22 m, its internal diameter is 0.02 m, and the wave propagation speed is assumed to be 1395 m/s. The steady-state discharge is 4.71 × 10^–5 m³/s and the steady pressure head is 23.2 m. The leak quantity is 4.71 × 10⁻⁶ m³/s and the coefficient for blockage (Ck) is 225, which represents one-third of the areal ratio of the cross section. The distance between different abnormalities is 7.93 m. The unsteady friction coefficients for the 1D model k₁ and k₂ are 0.0345. This value was calibrated in an experimental study by Kim (2011, 2016). A water hammer is introduced by instant valve closure downstream. Considering a flow velocity of 0.15 m/s, the Joukowski pressure is 21.32 m, indicating pressure oscillation between 44.52 and 1.88 m during a water hammer event. To compute the pressure responses through frequency-domain formulations, the maximum and minimum frequencies of impedance-based analysis should be specified. In this study, the frequencies ranged from 0 to 325 rad/s. The number of samples for the fast Fourier transform was 32,768, meaning the interval of frequency analysis was 0.00014 rad/s. Fine-resolution analysis in the frequency domain indicated that the computational interval was 0.00105 s.

4.2 Comparisons Between a Conventional Transfer Matrix and MAF

4.2.1 Hydraulic Impedances in a Downstream Valve

Hydraulic impedances were computed using the conventional transfer matrix and the MAF under the assumption of steady friction for two distinct abnormality distributions, as shown in Fig. 1. Figure 3 presents the amplitude differences between the hydraulic impedances at a downstream valve for two different formulations of abnormalities using the conventional transfer matrix and MAF under the steady friction model. The impedance comparisons between the conventional transfer matrix and MAF under the two unsteady friction models are well matched. The maximum difference between the conventional transfer matrix and MAF is approximately 4% and the frequency distributions of the different friction models are similar. Hydraulic impedance calculations for another abnormality distribution (e.g., five leakages in a row next to five blockages) also exhibited small differences between the conventional transfer matrix and MAF for unsteady friction models (not presented). Therefore, the evaluation of hydraulic impedance using the MAF can be considered as an alternative to the conventional transfer matrix for multiple abnormality representation in RPV systems.

Fig. 3

Differences in hydraulic impedance as percentages [(Conventional Matrix−MAF)/(Conventional Matrix) × 100] under steady friction (SF), acceleration-based unsteady friction (AUSF), and frequency-dependent friction-based unsteady friction (FUS) for the abnormality distribution in Fig. 1 at the downstream valve

4.2.2 Model Parsimony and Flexibility

One distinctive strength of the MAF compared to the conventional matrix is the parsimony of the representation of multiple abnormalities in an RPV system. Two distinct wave propagation characteristics of the acceleration-based unsteady friction model introduce substantial complexity into formulations of pressure and discharge in the frequency domain (Kim 2011). This makes the consideration of multiple leakages and multiple blockages extremely complicated. For example, the numbers of terms for three abnormalities in an RPV system (within the traditional transfer function matrix) are 128 and 32 for the acceleration-based unsteady friction model and frequency-dependent unsteady friction model, respectively.

Figure 4 presents the number of mathematical terms required for hydraulic impedances for various numbers of abnormality conditions at a downstream valve in an RPV system using a traditional formulation (impedance method) and the MAF for the acceleration-based unsteady model. The traditional formulations exhibit substantial incremental patterns as the number of abnormalities increases and the complexity of the MAF is much smaller than that of the traditional impedance formulation. The improvement of model parsimony in the mathematical expressions for 11 abnormality conditions between the two different approaches is on the order of six for the acceleration-based unsteady friction model. The difference in the number of required mathematical terms between the conventional formulation and MAF for the frequency-dependent model is on the order of five under laminar flow conditions.

Fig. 4

Number of terms required for the impedances of the conventional formulation and MAF under a 1D unsteady friction model of turbulent flow

4.3 Multiple Abnormality Detection

To test the performance of the proposed AMS (Fig. 2), transients for the 10 abnormalities presented in Fig. 1 were considered for both laminar and turbulent flow conditions. The leakage quantities for leakages located at 79.24 m, 64.43 m, and 15.86 m from the downstream valve were 1.42 × 10^–6 m³/s (10% of the mean flowrate), and those for the leakages located at 47.57 m and 31.72 m were 2.82 × 10⁻⁶ m³/s (20% of the mean flow rate). The coefficients (Ck) for partial blockages located at 71.36 m, 55.5 m, 39.65 m, 23.79 m, and 7.93 m from the downstream valve were 225, representing flow through 33.3% of the cross-sectional area. The calibration bounds of the abnormality locations were between the upstream reservoir and downstream valve (0–87.22 m). The search ranges for leak quantities and the blockage coefficient (Ck) were defined to be between 1 × 10⁻⁶ m³/s and 1 × 10⁻⁵ m³/s, and between 25 and 250, respectively. The best parameters for either leakage or blockage were delineated through 1275 iterations of the GA. The crossover probability and creep mutation probability for the GA were set to 0.5 and 0.04, respectively. The TOL for DIFF1 and DIFF2 for the AMS was set to 1.0.

Table 1 presents the abnormality prediction results when using the AMS with a frequency-dependent friction model under laminar flow conditions for the abnormality distribution presented in Fig. 1. The predicted distribution, number, and locations of abnormalities are in good agreement with the correct values. The maximum error in location is 1.76 m for the ninth leakage, representing a prediction accuracy of greater than 97.9%. The predictions of the blockage coefficient (Ck) also generally match well with the correct values, but the values for leak quantity are low depending on the location. Generally, the sensitivity of the leak quantity value is lower than those of the other parameters (Lee et al. 2013). This is because the order of the leakage term, namely $Q_{olk} /2H_{0}$, is on the order of −7.

Table 1 Abnormality prediction results for the distribution presented Fig. 1 using the unsteady friction model for laminar flow

Table 2 presents the abnormality predictions when using the acceleration-based unsteady friction model for the same abnormality conditions represented in Table 1. Both the distribution and locations of the abnormalities exhibit good agreement with the correct locations. The predictability of the leakage quantity and relative opening of partial blockages is better than that in Table 1, which can be attributed with the greater number of unsteady friction parameters used in the acceleration-based model.

Table 2 Abnormality prediction results for the distribution presented Fig. 1 using the unsteady friction model for turbulent flow

5 Discussion

5.1 Parameters for the AMS

The predictive power of the AMS depends on the parameters used to identify abnormalities. The time interval $dt$ strongly affects the TOL (Eq. 25), which is one of the most important parameters for successful abnormality prediction. If the TOL is above an appropriate range, the AMS can miss relatively small leakages and blockages, resulting in fewer abnormalities being predicted compared to the actual number. If the TOL is lower than an appropriate range, excessive abnormalities may be predicted, which typically appear as multiple concentrated abnormalities near a specific defect boundary condition. The time interval between ITT1(k) and ITT2(k) can be adjusted based on $dt$. If $dt$ is too large or small, it can result in either missing abnormalities or a reduction in accuracy. The determination of appropriate values for the TOL and time interval between ITT1(k) and ITT2(k) can be performed using a heuristic method. Based on a preliminary visual inspection of the identified pressure values, the TOL parameters were determined to be one and nine for laminar and turbulent flow conditions, respectively. Several iterative tests using different TOLs between 5 and 11 provided almost identical results to those listed in Tables 1 and 2, indicating the robustness of the TOL as a parameter for different abnormalities.

The AMS enforces the reduction of residuals when an additional abnormality is identified. This means that the time series of residual pressure heads can demonstrate the performance of the AMS in terms of mean error skewness and accuracy for the particular abnormality conditions in Tables 1 and 2. In other words, the AMS facilitates the diagnostic evaluation of the accuracy of a specific abnormality parameter in the time scale of the corresponding response. This feature provides substantial support for predicting the degree of calibration for any specific parameter. The time series of residuals in the AMS can be useful for determining an appropriate TOL value. If an absolute residual pressure time series is not apparently reduced (compared to the identified pressure) for a specific defect boundary, then the TOL should be reduced to successfully identify the abnormality. The TOL should be increased if the AMS exhibits idle iterations with minimal improvement during the residual minimization process.

5.2 Impact of Noise in Pressure Signals

For the AMS, noise can affect abnormality predictability and can be generated from the error bound of a pressure transducer or oscillatory computational behavior in frequency-domain computations. Equations (30) and (33) deliberately exclude oscillatory features from the frequency-domain approach by removing abrupt variations in pressure, such as those caused by water hammer.

To address possible errors in the pressure transducer and its data acquisition process, two types of systematic errors and random noise were considered to test the robustness of the proposed multiple abnormality detection scheme. One type is a zero-offset error that shifts the entire scale up or down by a zero-offset value. Considering the error bound of the pressure sensor used, the zero offset was specified to 0.05% of the measurement. The other type is a span error, which indicates that the distance from the zero point to the full-scale value may be incorrect, which magnifies the error at the upper end of the scale. This study assumed a 0.1% span error. Additionally, white noise was added to the pressure signal with two systematic errors, resulting in an error bound of $\pm 0.05$% (from a commercially available pressure transducer).

The TOL parameters for DIFF1 and DIFF2 for the AMS were identical to those represented in Table 2. Table 3 presents the AMS predictions of the 10 intermittent abnormalities for noise-contaminated pressure values. Both the distribution of abnormalities and locations exhibit similar values to those listed in Table 2. The predictability for leakage quantities and the Ck values of blockages exhibits similar accuracy to the case without noise (Table 2). The robustness of multiple abnormality prediction in terms of various types of noise can be explained by the concentrated calibration approach of the AMS, including the objective functions in enhanced adaptive schemes 1 and 2 and the leak isolated impact function defined in enhanced adaptive scheme 3.

Table 3 Abnormality prediction results for the distribution presented Fig. 1 for a noise-contaminated pressure signal using the unsteady friction model for turbulent flow

5.3 Features of the AMS

The AMS has several distinctive features compared to previous transient-based leakage and blockage detection algorithms. First, the MAF comprehensively addresses both leakages and blockages under the conditions of unsteady friction and either laminar or turbulent flow, which facilitate the adaptable identification of abnormalities under the unknown circumstances of field pipeline systems. The proposed MAF plays an important role in the computation of transients in the AMS. Another notable strength of the AMS approach is that there is no limitation on the number of abnormalities if the time scale of the data is sufficiently small. As illustrated in Fig. 2, the loop for new abnormality searching in the AMS can be iterated as long as any meaningful residual is left, even if the number and distribution of abnormalities are unknown. The other distinct advantage over previous algorithms is the self-diagnosing feature of the AMS, which is associated with enhanced adaptive scheme 3. This provides robustness to the calibration parameter for converging the AMS to a global optimal solution. An additional iterative test for an important optimization parameter, namely the TOL, indicated that a wide range of TOL values yielded solutions identical to those listed in Tables 1 and 2, which significantly reduces the uncertainty of abnormality prediction. In particular, the AMS was designed to concentrate its calibration potential on the designated interval (enhanced adaptive scheme 2) and minimize noise from previous calibrations (enhanced adaptive scheme 1). This significantly improves its prediction capability for abnormality locations (Tables 1 and 2), even in the presence of different types of noise, as shown in Table 3.

6 Conclusion

Efficient and comprehensive formulations of multiple abnormalities (multiple leakages and multiple partial blockages) were proposed for a reservoir pipeline valve system. Unsteady friction impacts under laminar and turbulent flow conditions were considered using a 2D frequency-dependent model and 1D acceleration-based model. The validity of the proposed formula was verified by comparing its impedance distributions to those of existing approaches. The proposed formula exhibited significant improvements in terms of model parsimony and flexibility in the representation of abnormality distributions with almost identical accuracy compared to existing approaches.

The MAF was implemented and the AMS was developed to predict multiple abnormalities in RPV systems. Three enhanced schemes were proposed to improve the performance of the proposed algorithm. The performance of the developed algorithm was tested on several hypothetical examples (for laminar and turbulent models) with 10 abnormalities. The results demonstrated that it provides reliable prediction capabilities, even without prior information regarding the dimensions, identities, or distributions of abnormalities. The residual elimination procedure not only provides a unique opportunity to evaluate the performance of each abnormality prediction, but also adaptively identifies sensitive parameters for enhanced prediction. In future work, experimental validations of the proposed method will be required to prove its applicability for both laboratory and field pipeline systems.