1 Introduction

The leakage in water distribution systems is responsible water loss and deterioration of water quality for drinking water (Araujo et al. 2006; Ferrante et al. 2014; Haghighi and Ramos 2012). Detection of leakage and system parameters (e.g., friction) in pipe networks had been explored based on inverse transient analysis (ITA) (Liggett and Chen 1994). A reflection of a pressure wave from an unusual boundary condition has been widely used for the detection of leakage in pipeline systems (Colomb et al. 2009; Duan et al. 2014; Ferrante et al. 2014; Vítkovský et al. 2007). The impedance-based method yielded a simultaneous calibration of wave speed, pipeline length, leakage, unsteady friction, and valve action, for an experimental reservoir pipeline valve (RPV) system (Kim et al. 2014). Proper consideration of unsteady friction is critical for reliable calibration of various parameters that can be useful to address uncertainties in pipeline systems, such as the leakage rate, friction, and wave propagation speed along the pipeline system (Covas and Ramos 2010; Kim 2011). The unsteady friction impact on transients can be considered using two distinct modeling approaches; the two dimensional (2-D) model considers the radial velocity distribution (Suo and Wylie 1989; Zielke 1968), while the one dimensional (1-D) model is based on the instantaneous acceleration encountered in the momentum equation (Brunone et al. 1991; Ramos et al. 2004). Analytical pressure responses were derived for multiple leakages in the frequency domain (Duan et al. 2011).

Even though multiple leakages were frequently found in real life water distribution systems, most of existing leak detection approaches had only handled the detection of a single leakage. Calibration of multiple leakages was also restricted for leakage numbers less than three. This is largely because the dimension of problems under multiple leakage conditions cannot be known a priori. In addition, this was partially because of the potential issues owing to the multiple local optima for the large number of parameters in the metaheuristic approaches employed (e.g., genetic algorithm and particle swam optimization). Extremely complex analytical expressions of multiple leakages in the frequency domain is another serious problem especially if the number of leakages is greater than four.

In this paper, an innovative detection method is developed to predict multiple leakages in a reservoir pipeline valve (RPV) system. Based on a formulation of hydraulic impedance, an isolated multiple leakage function (IMLF) is derived and implemented into the multiple leakage scheme. Considering an unknown condition of a problem dimension for numerous multiple leakage situations, the iterative metaheuristic scheme (IMS) was developed to adaptively control the calibration process for the unknown number of leakages. Considering the various uncertainties and the challenging calibration environment for the large number of the multiple leakage problem, three advanced schemes were developed to improve leakage detectability under rigorous leakage conditions. Validity of each advanced scheme can be confirmed through serial tests using combinations of each missed scheme in association with a complete set of advanced schemes. Robustness of the proposed method can be shown through comparisons between applications of an extension of the conventional impedance approach and those of impedance responses. Application examples in this paper demonstrate a unique capability of the proposed method for the detection of large number of leakages in a pipeline system.

2 Transients Models for Pipeline Flow

The unsteady flow equations in a pipeline system consist of continuity and momentum equations in the forms of partial differential equations described as (Wylie and Streeter 1993):

$$ \frac{a^2}{g}\frac{\partial V}{\partial x}+\frac{\partial H}{\partial t}=0 $$
(1)
$$ \frac{1}{g}\frac{\partial V}{\partial t}+\frac{\partial H}{\partial x}+\frac{fV\left|V\right|}{2 gD}=0 $$
(2)

where, a is the wave propagation speed, g is the gravitational acceleration, V is the mean velocity, H is the pressure head, f is the Darcy−Weisbach friction factor, D is the diameter, and the independent variables x and t are distance and time, respectively.

Considering the impact of unsteady friction on turbulent flow in terms of local and convective accelerations, eq. (2) can be expressed as follows (Ramos et al. 2004):

$$ \frac{1}{g}\frac{\partial V}{\partial t}+\frac{\partial H}{\partial x}+\frac{fV\left|V\right|}{2 gD}+\frac{1}{g}\left({k}_1\frac{\partial V}{\partial t}+{ak}_2\frac{\partial V}{\partial x}\right)=0 $$
(3)

where, k 1 is the unsteady friction coefficient for the temporal acceleration term and k 2 is the unsteady friction coefficient for the convective acceleration term.

If the velocity is considered under a laminar flow, the radial distribution of the velocity can be expressed via the 2 − D continuity and momentum equations as (Zielke 1968):

$$ \uprho {a}^2\frac{\partial u}{\partial x}+\frac{\partial p}{\partial t}=0 $$
(4)
$$ \frac{1}{\rho}\frac{\partial p}{\partial x}+\frac{\partial u}{\partial t}-\nu \frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial u}{\partial r}\right)=0 $$
(5)

where u, p are the velocity and pressure depending on the x(axial distance) and r(radial distance) of the 2-D space, ν is the kinematic viscosity, and ρ is the density of the fluid.

3 Multiple Leakage Function

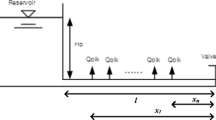
An RPV system is used for derivations of the pressure response under the conditions of multiple leakages, as shown in Fig. 1. The impedance, the ratio of head to discharge, can be derived in the frequency domain along the pipeline (Chaudhry 1987; Wylie and Streeter 1993).

Fig. 1
figure 1

A reservoir pipeline valve (RPV) system with multiple leakages

Full size image

Implementing a generalized leakage point matrix (Mpesha et al. 2001) into hydraulic impedance expression, a multiple leakage function (MLF) for the 1-D unsteady friction model was derived as follows,

$$ {\displaystyle \begin{array}{c}{Z}_V=\left({Z_A}^{\hbox{'}}+{\sum}_{i=1}^n{Z_{B,i}}^{\hbox{'}}\right)/\left(1+{\sum}_{i=1}^n{Z_{C,i}}^{\hbox{'}}\right)\\ {}{Z_A}^{\hbox{'}}=\left({e}^{-{\gamma}_2l}-{e}^{\gamma_1l}\right)/\left({e}^{\gamma_1l}/{Z}_{c1}+{e}^{-{\gamma}_2l}/{Z}_{c2}\right)\\ {}\sum \limits_{i=1}^n{Z}_{B,i}^{\hbox{'}}\\ {}=\left\{-{Q}_{olk,i}/\left(2{H}_0\right){\sum}_{i=1}^n{Z}_{c1}{Z}_{c2}\left({e}^{\gamma_1l}+{e}^{-{\gamma}_2l}-{e}^{\gamma_1{x}_i-{\gamma}_2\left(l-{x}_i\right)}-{e}^{-{\gamma}_2{x}_i+{\gamma}_1\left(l-{x}_i\right)}\right)\kern0.5em \right\}\\ {}/\left\{\frac{e^{\gamma_1l}\left({Z}_{c1}+{Z}_{c2}\right)}{Z_{c1}}+\frac{e^{-{\gamma}_2l}\left({Z}_{c1}+{Z}_{c2}\right)}{Z_{c2}}\ \right\}\\ {}\sum \limits_{i=1}^n{Z}_{C,i}^{\hbox{'}}\\ {}=\left\{-{Q}_{olk,i}/\left(2{H}_0\right){\sum}_{i=1}^n\left({Z}_{c1}\left({e}^{-{\gamma}_2l}-{e}^{-{\gamma}_2{x}_i+{\gamma}_1\left(l-{x}_i\right)}\right)+{Z}_{c2}\left({e}^{\gamma_1{x}_i-{\gamma}_2\left(l-{x}_i\right)}-{e}^{\gamma_1l}\right)\right)\kern0.5em \right\}\\ {}/\left\{\frac{e^{\gamma_1l}\left({Z}_{c1}+{Z}_{c2}\right)}{Z_{c1}}+\frac{e^{-{\gamma}_2l}\left({Z}_{c1}+{Z}_{c2}\right)}{Z_{c2}}\ \right\}\end{array}} $$
(6)

where, the propagation constants γ1 and γ2 can be defined as \( {\gamma}_{1,2}=\left(\mp mCs+\sqrt{(mCs)^2+4\left({s}^2 CL+ RCs\right)}\right)/2 \), m = (ak 2 )/(2gA), \( C=\frac{gA}{a^2} \), and L = (1 + k 1 )/(gA). In this case, k 1 and k 2 are the unsteady friction coefficients for the temporal and convective acceleration terms, respectively, and \( {Z}_{c1},{Z}_{c2}=\frac{\gamma_1}{Cs},\frac{\gamma_1}{Cs} \) are the characteristic impedances, Qolk, i a leak discharge for the ith point, H0 is the steady flow head, l is the length of the pipeline, and x n , xn − 1, …x1 are the distances from the downstream valve to any upstream nth, n-1th,..,1st leakages, respectively.

The MLF for the 2-D unsteady friction model was expressed as follows,

$$ {\displaystyle \begin{array}{c}{Z}_V=\left({Z_A}^{{{}^{\hbox{'}}}^{\hbox{'}}}+{\sum}_{i=1}^n{Z_{B,i}}^{{{}^{\hbox{'}}}^{\hbox{'}}}\right)/\left(1+{\sum}_{i=1}^n{Z_{C,i}}^{{{}^{\hbox{'}}}^{\hbox{'}}}\right)\\ {}{Z_A}^{{{}^{\hbox{'}}}^{\hbox{'}}}=-{Z}_s\cdot \left({e}^{\Gamma (l)}-{e}^{\Gamma \left(-l\right)}\right)/\left({e}^{\Gamma (l)}+{e}^{\Gamma \left(-l\right)}\right)\\ {}\sum \limits_{i=1}^n{Z_{B,i}}^{\hbox{'}\hbox{'}}=\sum \limits_{i=1}^n\left\{-{Z_s}^2{Q}_{olk,i}/\left(2{H}_0\right)\right\}/\left\{1+\frac{e^{\Gamma (l)}+{e}^{\Gamma \left(-l\right)}+{e}^{\Gamma \left(2{x}_i-l\right)}+{e}^{\Gamma \left(l-2{x}_i\right)}}{e^{\Gamma (l)}+{e}^{\Gamma \left(-l\right)}-{e}^{\Gamma \left(2{x}_i-l\right)}-{e}^{\Gamma \left(l-2{x}_i\right)}}\right\}\\ {}\sum \limits_{i=1}^n{Z_{C,i}}^{\hbox{'}\hbox{'}}=\sum \limits_{i=1}^n\left\{{Z}_s{Q}_{olk,i}/\left(2{H}_0\right)\right\}/\left\{\frac{e^{\Gamma \left({x}_i\right)}-{e}^{\Gamma \left(-{x}_i\right)}}{e^{\Gamma \left({x}_i\right)}+{e}^{\Gamma \left(-{x}_i\right)}}+\frac{e^{\Gamma \left(l-{x}_i\right)}+{e}^{\Gamma \left({x}_i-l\right)}}{e^{\Gamma \left(l-{x}_i\right)}-{e}^{\Gamma \left({x}_i-l\right)}}\right\}\end{array}} $$
(7)

where, \( {\Gamma}_x= sx/\Big(a\sqrt{1-2{J}_1\left( iD/2\sqrt{s/\nu}\right)/\left( iD/2\sqrt{s/\nu }{J}_0\left( iD/2\sqrt{s/\nu}\right)\right)} \); s is frequency, D is a diameter, and \( {Z}_S=a/\Big( gA\sqrt{1-2{J}_1\left( iD/2\sqrt{s/\nu}\right)/\left( iD/2\sqrt{s/\nu }{J}_0\left( iD/2\sqrt{s/\nu}\right)\right)} \). In this instance, i is the imaginary unit, J 0 and J 1 are Bessel functions of the first kind of the zero and first order, respectively.

4 Iterative Metaheuristic Scheme

The numbers of leakage determines the dimension of the metaheuristic optimization task. One critical issue in the detection of multiple leakages is the unknown number of leakages along pipeline systems. This means that the conventional structure of the inverse transient analysis cannot handle multiple leakage problems. The IMS is developed for an adaptive control of metaheuristic operations depending on any number of leakages. A stepwise abnormality detection procedure determines bounds for a possible leakage location and a genetic algorithm (GA) focuses in locating the leakage point and the leaked quantity for identifying predetermined bounds of a possible leakage. Once the leakage calibration for a predetermined bound is completed, the stepwise abnormality detection procedure is repeated until a transient signal is bounced back from an upstream reservoir to the pressure sensor that is assumed to be located at the downstream valve. Figure 2 illustrates the structure of the IMS.

Fig. 2
figure 2

Structure of the iterative metaheuristic scheme

Full size image

The bound for a possible leakage is determined by considering that the leak detection principle primarily originates as a results of the reflection of the pressure wave in case of an abnormality condition (Liggett and Chen 1994; Meniconi et al. 2011). The recognition of the pressure variation features for a leakage is critical and other relatively low frequency pressure signals seem redundant. The objective function for leakage detection does not necessarily consider the entire set of time steps for the theoretical period of a pipeline system (Wylie and Streeter 1993). This means that we can only count a few pressure points for the calibration of a leakage. Two arrays, namely ITT1(k) and ITT2(k), are introduced to identify abnormality, where k is the number of multiple leakages. A sequential comparison of the adjacent pressure variation to the tolerance of the pressure sensor error (TOL) is useful and ITT1(k) and ITT2(k) can be determined as follows;

$$ DIFF1= ABS\left[P(i)-P\left(i-1\right)\right] $$
(8)
$$ DIFF2= ABS\left[P\left(j+1\right)-P(j)\right] $$
(9)
$$ {\displaystyle \begin{array}{c} if\left( DIFF1> TOL.\&. DIFF2< TOL\right)\ then\\ {}\ ITT1(k)=i-2; ITT2(k)=j+1;k=k+1\end{array}} $$
(10)

where, P(i) and P(j) are the pressures at time steps i and j, and i and j iterate between 2 and n. The symbol n is an integer for 2 l/a, l is a pipeline length, and a is the wave speed. Depending on the sharpness of the transient signal, dummy variables i and j can be identical, or alternatively j = i + 1 or 2…n. If i is equal to j in eqs. (8) and (9), four adjacent pressure points are designated to each leakage calibration in terms of ITT1(k) and ITT2(k) in eq. (10). Determining TOL is important because if the TOL is changed, the leakage recognition potential of the proposed method can be different.

Based on the identification of calibration points from eqs. (8) to (10), the objective function (OF) for the simultaneous detection of multiple leakages can be simply defined as,

$$ OF={\sum}_{k=1}^m{\sum}_{i= ITT1(k)}^{ITT2(k)}{\left({P}_{obs}(i)-{P}_{cal}(i)\right)}^2 $$
(11)

where, m is the number of multiple leakages, and P obs (i) and P cal (i) are the observed and calculated pressures at the time step i, respectively.

The best parameters for eq. (11), leakage locations and quantities for all bounds, were recorded in each GA optimization and were printed out at the end of the IMS.

4.1 Advanced Scheme 1

Advanced Scheme 1 (AS1) is developed to minimize the impact of pressure noise in the leakage detection process. The noise can be generated from a rapid valve closure action, a residual or multiple residuals of a pre-existing transient impact, a regular oscillation of a pump system, and a signal contamination in the data acquisition procedure. If the statistical characteristics of noise are un-biased and the distribution of the pressure signal is temporally uniform, an existence of such noise is not always necessarily detrimental to the calibration of leakage (Kim et al. 2014). However, a transitional pressure oscillation introduced with an initiation of a water hammer can be an obstacle for the detection of a leakage having a small leakage discharge, and the disturbance impact to the first leakage detection procedure can be sequential in efforts to searching for other leakages.

A stepwise leakage detection scheme is implemented to minimize the impact of the disturbance from previous leakages. The objective function of the pressure signal from a first wave reflection (OF1) is defined as,

$$ {OF}_1={\sum}_{i= ITT1(1)}^{ITT2(1)}{\left({P}_{obs}(i)-{P}_{cal}(i)\right)}^2 $$
(12)

The objective function for the pressure signal from the second to the mth wave reflection (OF j ) can be defined as,

$$ {OF}_j={\sum}_{i= ITT1(j)}^{ITT2(j)}\left\{\left[{P}_{obs}(i)-{CutP}_{obs}\right]-{\left[{P}_{cal}(i)-{CutP}_{cal}\right]}^2\right\} $$
(13)

where, CutP obs and CutP cal are equal to P obs (ITT1(j)) and P cal (ITT1(j)).

Equation (13) provides a substantial relaxation to possible pressure differences associated with other leakage impacts that often expressed in terms of the undetectable pressure noise.

4.2 Advanced Scheme 2

One of the most important parameters in the multiple leakage detection algorithm is the location of each leakage. Unlike a single leakage detection case, in which the bounds for the leakage location are defined by the length of the pipeline, the bounds for the multiple leakage scheme can be designated at a much finer scale. Adjusted searching ranges for each leakage provide better parameter convergence conditions than the conventional case for the calibration using a metaheuristic engine, such as GA. The advanced Scheme 2 (AS2) implements different bounds for leakage location depending on the sequential order of leakage.

Using the stepwise leakage detection, the definition of the maximum and minimum bounds, (MaxBound, Minibound) for the distance to the leakage using a pressure signal from a first wave reflection are,

$$ MiniBound=0; MaxBound={a}^{\ast } ITT2(1)/2 $$
(14)

MaxBounds, MiniBounds for other leakage locations can be defined as,

$$ {\displaystyle \begin{array}{l} MiniBound={a}^{\ast } ITT2\left(j-1\right)/2;\\ {} MaxBound={a}^{\ast } ITT2(j)/2\end{array}} $$
(15)

where, j = 2,..,m, and m is the number of leakages. Depending upon the valve closure time, MaxBounds can be moderately relaxed subject to higher ranges in order to secure a convergence to a global optimum.

4.3 Advanced Scheme 3

Conventional ITA for leakage detection had used pressure time series during multiples of a theoretical period of a RPV system (e.g., 2 l/a, 4 l/a, 8 l/a, ..). This is not only for the calibration practice for leakage but also for redundant computational tasks for all other parameters (friction along the pipeline, system characteristics, and system operation) (Kim et al. 2014). The impact of the pipeline component can be effectively removed from the formulation of the dimensionless multiple leakage function. This means that we only consider the impact of leakages upon an external excitation and its association with the frictional impact of the pipeline system. Advanced Scheme 3 (AS3) introduces hydraulic impedances for multiple leakages with corresponding unsteady friction considerations.

Using hydraulic impedances for the 2-D models (eqs. (4) and (5)), the exclusive hydraulic impedance for multiple leakages for a RPV system, namely IMLF, can be expressed as,

$$ {\displaystyle \begin{array}{c}{Z}_{DV}=\left({\sum}_{i=1}^n{Z}_{A,i}-{\sum}_{i=1}^n{Z}_{B,i}\right)/\left(1+{\sum}_{i=1}^n{Z}_{C,i}\right)\\ {}\sum \limits_{i=1}^n{Z}_{A,i}=\frac{{Z_s}^2}{2{H}_0}\cdot \frac{e^{\Gamma (l)}-{e}^{\Gamma \left(-l\right)}}{e^{\Gamma (l)}+{e}^{\Gamma \left(-l\right)}}\cdot \\ {}{\sum}_{i=1}^n\left[{Q}_{olk,i}/\left\{\frac{e^{\Gamma \left({x}_i\right)}-{e}^{\Gamma \left(-{x}_i\right)}}{e^{\Gamma \left({x}_i\right)}+{e}^{\Gamma \left(-{x}_i\right)}}+\frac{e^{\Gamma \left(l-{x}_i\right)}+{e}^{\Gamma \left({x}_i-l\right)}}{e^{\Gamma \left(l-{x}_i\right)}-{e}^{\Gamma \left({x}_i-l\right)}}\right\}\right]\\ {}\sum \limits_{i=1}^n{Z}_{B,i}=\sum \limits_{i=1}^n\left\{-{Z_s}^2{Q}_{olk,i}/2{H}_0\right\}/\left\{1+\frac{e^{\Gamma (l)}+{e}^{\Gamma \left(-l\right)}+{e}^{\Gamma \left(2{x}_i-l\right)}+{e}^{\Gamma \left(l-2{x}_i\right)}}{e^{\Gamma (l)}+{e}^{\Gamma \left(-l\right)}-{e}^{\Gamma \left(2{x}_i-l\right)}-{e}^{\Gamma \left(l-2{x}_i\right)}}\right\}\\ {}\sum \limits_{i=1}^n{Z}_{C,i}=\sum \limits_{i=1}^n\left\{{Z}_s{Q}_{olk,i}/2{H}_0\right\}/\left\{\frac{e^{\Gamma \left({x}_i\right)}-{e}^{\Gamma \left(-{x}_i\right)}}{e^{\Gamma \left({x}_i\right)}+{e}^{\Gamma \left(-{x}_i\right)}}+\frac{e^{\Gamma \left(l-{x}_i\right)}+{e}^{\Gamma \left({x}_i-l\right)}}{e^{\Gamma \left(l-{x}_i\right)}-{e}^{\Gamma \left({x}_i-l\right)}}\right\}\end{array}} $$
(16)

The leakage number n can be varied as the calibration scheme proceeds to identify additional leakages. Based on eqs. (1) and (3) for the 1-D model, the IMLF, being an exclusive the hydraulic impedance at the downstream valve for multiple leakages for a RPV system can be expressed as

$$ {\displaystyle \begin{array}{c}{Z}_{DV}=\left({\sum}_{i=1}^n{Z_{A,i}}^{\hbox{'}}-{\sum}_{i=1}^n{Z_{B,i}}^{\hbox{'}}\right)/\left(1+{\sum}_{i=1}^n{Z_{C,i}}^{\hbox{'}}\right)\\ {}\sum \limits_{i=1}^n{Z}_{A,i}^{\hbox{'}}=\frac{1}{2{H}_0}\frac{{Z_{c1}}^2{Z_{c2}}^2\left({e}^{\gamma_1l}-{e}^{-{\gamma}_2l}\right)}{\left({Z}_{c1}+{Z}_{c2}\right)\left({Z}_{c2}{e}^{\gamma_1l}+{Z}_{c1}{e}^{-{\gamma}_2l}\right)\left({e}^{\gamma_1l}+{e}^{-{\gamma}_2l}\right)}\cdot \\ {}{\sum}_{i=1}^n{Q}_{olk,i}\left\{{Z}_{c1}\left({e}^{-{\gamma}_2l}-{e}^{-{\gamma}_2{x}_i+{\gamma}_1\left(l-{x}_i\right)}\right)+{Z}_{c2}\left({e}^{\gamma_1{x}_i-{\gamma}_2\left(l-{x}_i\right)}-{e}^{\gamma_1l}\right)\right\}\ \\ {}\sum \limits_{i=1}^n{Z}_{B,i}^{\hbox{'}}=\left\{-{Q}_{olk,i}/2{H}_0{\sum}_{i=1}^n{Z}_{c1}{Z}_{c2}\left({e}^{\gamma_1l}+{e}^{-{\gamma}_2l}-{e}^{\gamma_1{x}_i-{\gamma}_2\left(l-{x}_i\right)}-{e}^{-{\gamma}_2{x}_i+{\gamma}_1\left(l-{x}_i\right)}\right)\kern0.5em \right\}\\ {}/\left\{\frac{e^{\gamma_1l}\left({Z}_{c1}+{Z}_{c2}\right)}{Z_{c1}}+\frac{e^{-{\gamma}_2l}\left({Z}_{c1}+{Z}_{c2}\right)}{Z_{c2}}\ \right\}\\ {}\sum \limits_{i=1}^n{Z}_{C,i}^{\hbox{'}}=\left\{-{Q}_{olk,i}/2{H}_0{\sum}_{i=1}^n\left({Z}_{c1}\left({e}^{-{\gamma}_2l}-{e}^{-{\gamma}_2{x}_i+{\gamma}_1\left(l-{x}_i\right)}\right)+{Z}_{c2}\left({e}^{\gamma_1{x}_i-{\gamma}_2\left(l-{x}_i\right)}-{e}^{\gamma_1l}\right)\right)\kern0.5em \right\}\\ {}/\left\{\frac{e^{\gamma_1l}\left({Z}_{c1}+{Z}_{c2}\right)}{Z_{c1}}+\frac{e^{-{\gamma}_2l}\left({Z}_{c1}+{Z}_{c2}\right)}{Z_{c2}}\ \right\}\end{array}} $$
(17)

Equations (16) and (17) can be used under laminar and turbulent flow conditions, respectively.

5 Example Applications with Discussion

5.1 A Hypothetical RPV System with Multiple Leakages

A hypothetical RPV system with multiple leakages was assumed to test performances of a developed method for multiple leakage predictability (Fig. 1). The length of the pipeline was 110 m and the internal diameter was 0.02 m. The wave speed was assumed to be 1395 m/s and the steady flow rate was 4.71 × 10−5 m3/s. The steady pressure head was 23.2 m and the kinematic viscosity of water was 1.17 × 10−6 m2/s. The unsteady friction coefficients, k 1 and k 2 , for the 1-D model were assumed to be 0.0345, based on the experimental study by Kim (2011). The dimensions of a hypothetical RPV system were identical to those used for an experimental study of the comprehensive leakage calibration except for a pipeline length (Kim et al. 2014). Multiple leakages and leakage discharges were introduced at different locations depending on the example. A water hammer was introduced by an instant closure of the downstream valve. In order to compute the pressure responses through frequency domain formulations, the maximum and minimum frequencies for the impedance-based analysis should be specified. In this study, ranges of frequencies ranged between 0 rad/s and 3125 rad/s. The number of samples for the fast Fourier Transform was 16,384, which means that the interval of the frequency analysis was 0.00014 rad/s. Fine resolution analysis in the frequency domain provide time domain responses in time intervals of 0.00105 s.

5.2 Validation of AS1, AS2, and AS3

In order to show the distinct contribution of AS1, AS2 and AS3 for a better prediction of multiple leakages, three additional algorithms were fabricated through the merging of different combinations into IMS, which results one missing component out of three advanced schemes. Using a RPV system in Fig. 1, five leakages were introduced and the distances for leakage numbers 1, 2, 3, 4, and 5 were 20 m, 40 m, 60 m, 80 m, and 100 m from the downstream valve. Leak discharges for the five leakages were between 2 × 10−5 m3/s and 4 × 10−5 m3/s. Table 1 resulted multiple leakage calibrations for the four algorithms (e.g., 1 + 2, 2 + 3, 1 + 3 and 1 + 2 + 3) using a frequency dependent friction model for unsteady friction consideration. Identical parameters for GA and IMS (e.g. TOL) were used in four predictions. As presented in Table 1, three missing algorithms cannot predict five leakages but only three leakages with lower accuracies in terms of both the leakage locations and quantities. However, the complete integration of the three schemes (1 + 2 + 3) provides a successful calibration for five leakage locations and leakage discharges with a much better accuracy than those for the missing schemes. This is the compelling evidence that each of the advanced schemes independently plays a different role towards the improvement of the multiple leakage prediction in conjunction with IMS.

Table 1 Multiple leakage calibrations with a frequency dependent friction model for various combinations of advanced schemes
Full size table

5.3 Comparison of IMS to Traditional GA Calibration

One difference between the IMS and the existing methods for leakage calibration is the flexibility of the IMS for the dimension related to the multiple leakage number. While the structure of the existing approaches demands a predefined leakage number, IMS controls the optimization process since each abnormality signal is detected on the basis of eq. (10). An additional advantage of IMS is associated with the concentration of the calibration power into a designated interval defined through eqs. (10) and (11) and its combination with the three advanced schemes.

The performance of IMS can be compared with existing methods. The conventional multiple leakage expressions were implemented into GA based approaches (Kim et al. 2014). Considering the limitation in calibration parameters of the traditional GA method, only three leakages were assumed for the pipeline system in Fig. 1. Four different conditions were introduced to test the multiple leakage potential. The locations were 70 m, 50 m, and 30 m and leakage discharges were either 2% or 5% with respect to the mean flowrate for conditions 1 and 2, respectively. Conditions 3 and 4 assumed leakage locations closer to the downstream valve (e.g., 30 m, 20 m, and 10 m) or closer to the upstream reservoir (e.g., 80 m, 70 m, and 60 m). Assuming a laminar flow condition, frequency-dependent friction was implemented to consider the unsteady friction impact in the pressure variation. Table 2 shows the leakage calibration results using an extension of the traditional GA method with a predefined leakage parameter number set to value of six. The number of candidate solutions in each generation was 51 and the generation number was 54, thereby indicating that the total iteration was 2754 for the GA operation. Table 2 shows relatively good predictions under condition 3 (leakages closer to the pressure response position than those for other conditions), but the predictions of the other conditions were generally poor.

Table 2 Three leakage calibrations using a conventional GA with a frequency dependent friction model for the pressure series at the end of the RPV system
Full size table

Four identical leakage conditions were used for tests of leakage calibration with IMS, as indicated in Table 2. In order to provide a similar meta-heuristic optimization circumstance to those listed in Table 2, the number of total iterations for IMS was limited to 2700. Table 3 lists the leakage calibration results using IMS without a predefined parameter number (e.g. the value of six is listed in Table 2). Both leakage locations and discharges exhibit very good agreements in correcting leakage information under all conditions (see Table 3). This indicates that IMS provides better convergence for multiple leakage predictions that potentially suffered from multiple local optima compared to those of traditional approaches. Furthermore, it also has an additional handling capability for an unknown number of leakages.

Table 3 Three leakage calibrations using IMS with a frequency dependent friction model for the pressure series at the end of the RPV system
Full size table

Table 4 presents the calibrations of four leakage conditions using an extension of an acceleration based friction model (see Eq. (7)), thereby implementing a conventional GA method. Prediction of leakage locations and discharges in Table 4 are similar to those that appeared in Table 2. Table 5 shows multiple leakage calibrations using IMS with an acceleration based friction model without a predefined parameter number. Better agreements between actual leakage information and calibrations can be found in Table 5 compared to those that appeared in Table 4. The structure of IMS, the determination of stepwise abnormality bounds and the subsequent identification of each leakage location and quantity, are mainly responsible for the difference in the predictability between conventional GA based approaches (e.g., Tables 2 and 4) and IMS applications (e.g., Tables 3 and 5). Implementation of AS1, AS2, and AS3 also largely relaxes various issues in multiple leakage detection, such as the noise impact, focusing of the calibration power into a designated bound, and the evaluation of isolated responses for the leakage impact.

Table 4 Three leakage calibrations using a conventional GA with an acceleration based model for the pressure series at the end of the RPV system
Full size table
Table 5 Three leakage calibrations using IMS with an acceleration based friction model for the pressure series at the end of the RPV system
Full size table

5.4 Multiple Leakage Calibration and Tolerance

One of the notable strengths of the IMS approach is that there is no limitation in regard to the maximum number of leakages. However, the behavior of IMS can be sensitive to TOL because TOL is related to the leakage recognition window of the pressure signal. Additional examples were introduced to show other potential uses of IMS and the impact of TOL in calibration. Based on a hypothetical pipeline system shown in Fig. 1, 10 leakages were introduced. Leakage locations were equally distributed every 10 m with respect to each other along the pipeline system, and the leakage discharge varied between 1% and 6% with respect to the mean flowrate. Fig. 3 shows leakage calibrations of IMS with a frequency-dependent friction model for conditions of TOL = 0.2%, 0.1%, and 0.05%. If the TOL was 0.2%, only two leakages were found at 38.5 m and 79.8 m, and six leakages were predicted when TOL = 0.1%. All 10 leakages were successfully calibrated with a good agreements to the leakage locations under the condition of TOL = 0.05%. The predictions of leakage discharges were also in a good agreement except the last one, which is located 100 m apart from the downstream valve for TOL = 0.05%. Fig. 4 presents calibrations of an acceleration based model for leakage condition that is identical to that of Fig. 3 using three TOL conditions. While the prediction with TOL = 0.2% only yields three leakages at 19.9 m, 40.0 m, and 80.0 m, those for TOL = 0.1% and TOL = 0.05% correspondingly yield 7 and 10 leakages (all close to true leak locations), respectively (see Fig. 4). Leakage predictions shown in Fig. 3 and Fig. 4 indicate that the uncertainty of the pressure sensor is important regardless of laminar or turbulent flow conditions.

Fig. 3
figure 3

Multiple leakage calibrations of IMS with a frequency-dependent friction model with tolerances of the pressure sensor error of 0.2%, 0.1% and 0.05%

Full size image
Fig. 4
figure 4

Multiple leakage calibrations of IMS with an acceleration based friction model with tolerances of the pressure sensor error of 0.2%, 0.1% and 0.05%

Full size image

6 Conclusion

The prediction of multiple leakages in water distribution systems is an important and practical problem for many water authorities. Inverse transient analysis of multiple leakages is an extremely challenging task because of the unknown number of parameters, impact of disturbances through leakages both along the longitudinal and radial velocity profiles, uncertainty in abnormality boundary conditions, noise of pressure signal, and large number of calibrating parameters. In order to address the several issues for the solution of multiple leakage problems, this study proposes an iterative metaheuristic scheme that modifies a conventional GA to handle unknown dimensions of multiple leakages and concentrates the calibration scope on the pressure signals that exhibit abnormalities. Three additional advanced schemes were developed to improve detectability of leakages through the relaxation pre-existing pressure impacts, confining leakage searching bounds and implementing the IMLF in the proposed scheme. Both 1-D and 2-D unsteady friction models were implemented into the derivation of the pressure response function for a reservoir pipeline system that has multiple leakages.

Leakage calibration examples for missing combination schemes showed that each advanced scheme distinctively contributes to improve prediction. Comparisons of leakage prediction results between extensions of conventional methods and the proposed method highlight that the integration of the iterative metaheuristic scheme into three advanced schemes provides robustness in parameter optimization such as multiple local optima, and feasibility of the existence of an unknown number of parameters. Calibration examples for 10 leakages not only showed the potential of the developed method for a large number of unknown parameters but also indicated the importance in the tolerance of the pressure sensor uncertainty. Experimental verification of the proposed method and further development for more complex pipeline networks, or considerations of various hydraulic devices can constitute future research issues.