1 Introduction

Generally, the Middle East is characterized by two features of water scarcity and rapid population growth. Therefore, water is the main factor for future development in this region. The issue of water scarcity for all countries, with arid and semi-arid climates, has been a longstanding issue and access to water resources for agricultural and industrial purposes is particularly important. Groundwater resources are used in different parts of the world in various sectors such as agriculture, environment and industry and so on. In order to be responsive to these demands and needs of water, a desirable method should be done. With no pumping limit from an aquifer, groundwater can be permanently and irreversibly reduced (Scanlon et al. 2010, Famiglietti et al. 2011 and Gautam and Prajapati, 2014).

Due to the decrease in groundwater level and their negative balance, optimization of pumping will be of great help in the present situation. So the first step is recognition of groundwater flow and the second step is recognition of optimization method.

One of the ways to understand groundwater flows is to use numerical methods, including finite element and finite difference methods to solve the governing equations of groundwater flow. For the first time in 1933, a simple comparative model of conductive sheet was used to study the movement of the water front into the aquifer, as well as the effect of changing the wells spacing in the aquifer (Prickett, 1979). These methods usually solve the governing equations of groundwater flow in saturated zone by discretization of the problem. Due to the existence of these discrete solutions, many interpolation methods have been developed to calculate the flow velocity (Pokrajac and Lazic, 2002). An analytic element method is a numerical method for groundwater flow modeling (Craig and Rabideau, 2006). Strack et al. (1987) modeled the Dutch groundwater flow and concluded that the methodology of the analytic element model properly simulates the hydrological complexities at large scales. Steward and Allen (2013) used modeling of the Kansas high plain aquifer flow through an analytic element method. The results indicated these methods are capable of modeling local detail within a large-scale regional model of the high plains aquifer.

As mentioned, the second step is to know the optimization methods. Most of real-world optimization problems are often large-scale problems, and because of the high number of variables and constraints, simple optimization techniques such as linear and non-linear methods are no longer effective. For this reason, many meta-heuristic algorithms have recently been proposed, which though do not always ensure the global optimum solution, however give quite good results in an acceptable computation time (Pour and Zeynali, 2015).

Meta-heuristic algorithms such as genetic algorithm, annealing simulation, ant colony optimization, grasshopper optimization algorithm, etc. are among the researches to obtain near optimal solutions to large-scale optimization problems in water resource management. Genetic algorithm can be used to optimize groundwater surface water systems (Peralta et al. 2014), optimizing coefficients of sediment rating curve (Zeynali and Shahidi, 2018), groundwater monitoring (Babbar-Sebens and Minsker, 2012) and Coastal groundwater management problems (Ketabchi and Ataie-Ashtiani, 2015). The PSO is also a population-based random search algorithm whose applications in water resource engineering are: reservoir optimization (Saadatpour and Afshar 2013; Guo et al. 2013; Nagesh Kumar and Janga Reddy, 2007; Zhang et al. 2014), designing distribution systems, water and sewage (Izquierdo et al. 2008) and calibration of hydrological models (Gill et al., 2006; Zambrano-Bigiarini and Rojas 2013).

Ayvaz and Karahan (2008) used a simulator / optimizer model to investigate the proper locations for groundwater pumping and also the amount of pumping in a two-dimensional hypothetical aquifer. In the simulator / optimizer model, a finite difference method was used to estimate groundwater. In this study, optimization of the genetic algorithm was used to optimize the pumping value from each well. The simulator / optimizer model performance was tested on a hypothetical aquifer for both Steady-State and Transient-State flow. The results indicated that when the number of pumping wells is higher than the actual number of wells, the well-known configuration is well adapted to the optimal configuration. Also, the results indicated that optimal locations are detected whenever the search process begins. Finally, the performance of the proposed model is compared with a GA solution in which appropriate situations and pumping rates are considered as decision variables. The results show that the proposed model reduces the error rate by up to 14%.

Cyriac and Rastogi (2016) investigated the optimization of pumping policy using a finite element-particle optimization model in a confined heterogeneous anisotropic synthetic aquifer. In this research the objective was to find the optimum number of wells and pumping discharges of those such that their collective drawdown is minimized while meeting the demand at a reasonable cost. Constraints on the location of the wells and the maximum allowable pumping discharge are also imposed. After analyzing the aquifer behavior in the presence of 8, 9 and 10 pumping wells, the optimal number of wells is selected. The results of this research indicated the model employed is capable of solving the present problem.

Sadeghi-Tabas et al. (2017) used a multiple search algorithm for adaptive genetic algorithm (amalgam) developed by Vrugt and Robinson (2007) to optimize the location of wells and pumping rates. In this study, the pumping rate with three minimization objective, namely the minimum lack of supply, the change in the index of deficiency and minimization of discharge in designated areas, was chosen to determine an optimal solution for the discharge and recharge of groundwater. Hydraulic conductivity and specific performance parameters of the groundwater model have been optimized using an optimization algorithm by minimizing the total deviation between the observed and simulated water column depth. These parameters were then used in AMALGAM to optimize pumping variables. In general, the results revealed that the modeling-optimization-simulation method could compute a set of optimal solutions displayed on a Pareto front.

Patel and Rastogi (2019) investigated groundwater estimation using global strong form collocation-based meshfree method in a field like synthetic confined aquifer domain. The developed model is tested on a two dimensional confined aquifer synthetic flow problem and the results are compared with the analytical and numerical solutions. In this research different time steps and varied pumping schedules were also assessed for a performance check. The results of this research indicated the model employed is capable of solving the present problem.

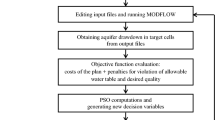
The purpose of this study is to combine finite element method and meta-heuristic algorithms and apply it to optimization of location of pumping wells. In many areas, well drilling licensing is issued in a limited number, so optimizing the location of harvesting from a hypothetical aquifer with a specified number of wells to minimize the level of aquifer drawdown is the main objective of this study. In fact, in this study, by combining finite element method with optimization methods such as genetic algorithm (GA), particle swarm optimization (PSO) and firefly Algorithm (FA), is will presented a simulation/optimization model for optimizing water harvesting from a hypothetical aquifer.

2 Material and Methods

2.1 Specification of Hypothetical Aquifer

In this study, a hypothetical heterogeneous anisotropic aquifer with a total area of 1.5 km2 is described in Fig. 1. It has a thickness of 100 m and is approximately 1.5 km long and 1 km wide. This hypothetical aquifer is divided into triangular elements, each side of that is 0.1 km long, and therefore the number of its triangular elements is 252 and the number of nodes is 150. The aquifer is defined in three different zone in terms of hydraulic conditions, with the number of 80 triangular elements (Zone 1) have a hydraulic conductivity of 11.5 m/day, 100 south triangular elements (Zone 2), have a hydraulic conductivity equal to 6.7 m/day and 72 eastern elements (Zone 3) have a hydraulic conductivity equal to 2.8 m/day. The hypothetical aquifer is considered no-flow boundary in south and north and along the eastern boundary, the known flow condition is specified (2 m3/day/m), and in the western part of the aquifer, there is a river that has created static head boundary conditions.

Fig. 1
figure 1

Schematic view of the hypothetical aquifer studied

Full size image

Considering the specificity of the aquifer, before solving the optimization problem and the use of meta-heuristic algorithms, the groundwater level should first be estimated in the hypothetical aquifer, which is done by using the finite element method. How the aquifer reacts to the defined conditions is presented in Fig. 2. This form of groundwater level is considered without taking any wells. In the next step, the meta-heuristic algorithms should find the optimal position of the four wells with different pumping discharges in order to minimize the groundwater drawdown compared to the initial level shown in Fig. 2. It should be noted that the algorithms used do not allow wells in the boundary nodes to be considered.

Fig. 2
figure 2

3D View of Groundwater Level in the studied area

Full size image

2.2 Finite Element

The finite element method has high flexibility in issues where the boundaries are irregular or in problems that are heterogeneous and anisotropic in the aquifer flow. Also, finite element methods can solve problems, such as transferring contaminants or moving frontiers. Finally, the choice of problem solving method depends on factors such as the complexity of the problem and the user-friendliness of each of the methods.

2.2.1 Governing Flow Equation

The governing equation describing the flow in a two-dimensional heterogeneous anisotropic confined aquifer is given by (Bear 1979):

$$ \frac{\partial }{\partial x}\left[{T}_x\frac{\partial h}{\partial x}\right]+\frac{\partial }{\partial y}\left[{T}_y\frac{\partial h}{\partial y}\right]=S\frac{\partial h}{\partial t}+{Q}_w\delta \left(x-{x}_i\right)\left(y-{y}_i\right)-q $$
(1)

Following initial condition is applicable

$$ h\left(x,y,0\right)={h}_0\left(x,y\right)x,y\in \varOmega $$
(2)

And the boundary conditions are given as:

Dirichlet boundary condition (fixed Head Boundary)

$$ h\left(x,y,t\right)={h}_1\left(x,y,t\right)x,y\in \partial {\varOmega}_1 $$
(3)

Known flow boundary

$$ T\frac{\partial h}{\partial n}=q\left(x,y,t\right)x,y\in \partial {\varOmega}_2 $$
(4)

where h(x, y, t) = Piezometric Head, T(x, y) = Transmissivity along the principal Cartesian axes (m2/day), S = Storage coefficient, x, y = Horizontal space variables (m), Qw = Source or sink function (−Qw = source, +Qw = sink) (m3/day), t = Time in days, Ω = Flow region, ∂Ω = Boundary region (∂S1 ∪ ∂Ω2 = ∂Ω), \( \frac{\partial }{\partial n}= \)Normal derivative, h0(x, y) = Initial head in the flow domain (m), h1(x, y, t) = Known head value of the boundary head (m), q(x, y, t) = Known inflow rate (m3/day/m) and δ is the Dirac delta function = 1 if x = xi, y = yi, = 0 if x ≠ xi, y ≠ yi.

2.2.2 Finite Element Formulation of Groundwater Flow

Finite element method (FEM) is a numerical technique to find the solution to first- and second-order partial differential governing equations. It develops a system of simultaneous equations through an integral formulation which when solved gives the value of the unknown field state variables at discrete locations in the domain. The system of equations generated by Galerkin FEM formulation can be represented as (Gray et al. 1977; Pinder and Gray, 2013):

For time-variant condition:

For two successive time intervals t and t + Δt where Δt is the time step

$$ \left[G\right]\left\{{h}_I^{t+\varDelta t}\right\}+\frac{1}{\varDelta t}\left[P\right]\left\{\left({h}_I^{t+\varDelta t}\right)-\left({h}_I^t\right)\right\}=\left\{F\right\} $$
(5)

[G] = Conductance matrix, [P] = Storativity matrix, {F} = Flux vector.

The initial groundwater head in the aquifer is known and the head at each subsequent time step is found by solving the above equations.

2.3 Boundary Conditions

2.3.1 Border with Current Flow

Suppose that L is a boundary node and is located at a boundary that has vertical and definite flow through its cross section (Fig. 3). The boundary integral is not only zero in the two pieces of the line iL and Lm, because the boundary of the nodes i and m, and the values of NL are zero.

Fig. 3
figure 3

Finite element in certain boundary flow conditions

Full size image

The interpolator function NL varies linearly between the nodes L and i, as well as L and m between two values from zero to one. Therefore, the integrals are calculated in such a way that the input L of the vector {f} is equal to the following expression:

$$ {f}_L=\frac{q_1}{K}\;\frac{\overline{iL}}{2}+\frac{q_2}{K}\frac{\overline{Lm}}{2} $$
(6)

Where \( \overline{iL} \) represents the distance between the nodes i, L, and \( \overline{Lm} \), showing the distance between the nodes L and m. The amount of flow through the sides of the sides of the side is distributed uniformly across the sides (Wang and Anderson, 1995).

In short, it can be stated that the boundary conditions are merged with the column vector {f}. For all internal nodes or nodes located on non-flow boundaries, fL = 0 . For nodes located on a boundary with a given flow, the value of fLis determined by Eq. (5).

2.3.2 The Boundary with the Hydraulic Load Is Known

Fixed boundary conditions reduce the number of unknowns. The value of fL for the boundary node L is negligible and can be assumed to be zero. Because the value of fL is zero for all internal nodes. In the problem where its boundary conditions are known, it can be accepted {f} = 0.

2.4 Genetics Algorithm

Genetic Algorithm is inspired from natural life of creatures. This algorithm is based on iteration and its principles have been adapted from genetics science. In the genetic algorithm, there is a major population, some of which are selected as parents, and the population that is produced is named as children after Crossover. Also, the number of population can also mutate. Eventually, from these three populations, the population is as large as the second generation, and the subsequent replication begins.

In this algorithm, a variety of methods can be used in how to code, parent selection, mutate, crossover and type of chromosomes, which will be briefly explained below.

Some types of coding methods include direct coding, indirect coding, binary coding and mutation coding (Zeynali and Shahidi, 2018). In this study, direct coding for each chromosome as a string of numbers is used. Thus, considering four wells, a chromosomal string will have four genes, each gene is equal to the number of one node.

There are several ways to select parents for action, roulette wheel selection is the most commonly used selection method. This method is used not only in this algorithm but also in many other algorithms. The probability of selecting each chromosome is calculated on the basis of its objective function. There is another phase in the genetic algorithm in which the chromosomal string cut and the pieces are swapped together. This phase is called crossover.

Mutation is another phase in the genetic algorithm that amplifies the search in a decision space. The methods for performing mutation operations are: reversing the bit, changing the sequence, inversion, and changing the value of a gene. (Zeynali and Shahidi, 2018). In issues like the present one, we can use changing the sequence and the value of a gene, because in a chromosome, the change the sequence of genes means the number of nodes, therefore, location of one well can be swapped with another well in the aquifer. The inversion of a chromosome can cause the first and fourth pumping wells and the second and third pumping wells to be swapped together. In changing the value of a gene, the node number one can also change, and thus the location of a pumping well changes. However, reverse of the gene in this study cannot be used because, assuming that the target gene has a value of 20, with its inversion, that gene value is 0.05, which is not an acceptable value for a gene.

On the other hand, if the discharge pump is equal to all the wells, changing the sequence of genes and the inversion of chromosomes will no longer be effective, since in general there is no change in the conditions of the problem. It is also necessary to mention that when the value of a single gene (number one node) is changed, the new value should be an integer value, meaning that the value of 20 is valid for a node (node number), while the value is 20.5 as the number. The node is not node or the value of 30 is the number 1 of the boundary node and therefore cannot be selected as a value for a gene. However, in this study, the methods of changing the sequence and inversion the chromosome with different probability percent were used.

The flow chart of genetic algorithm for this optimization problem shown in Fig. 4a.

Fig. 4
figure 4

Flow chart of algorithms

Full size image

2.5 Particle Swarm Algorithm

Particle swarm algorithms also known as the birds algorithm, as well as other meta-heuristic algorithms, create a random population of individuals and each person in the population has a set of variables that should be determined by their optimal value. When a particle with velocity vector V(t) has reached a new location from its previous location in decision space, it can be moved to the Personal Best, or Global Best or go straight to its path; in this case, none of the choices alone is appropriate. Therefore, the new velocity vector V(t + 1) is calculated according to the Eq. (7), (Eberhart and Kennedy, 1995):

$$ {V}_{\left(t+1\right)}=w.{V}_{(t)}+{C}_1.{r}_1.\left({P}_{(t)}-{X}_{(t)}\right)+{C}_2.{r}_2.\left({G}_{(t)}-{X}_{(t)}\right) $$
(7)

Where C1and C2are fixed numbers; r1C1 and r2random vectors are between zero and one; P(t)is the best position where the X particle has ever been, and G(t)is the best position where all the particles have been found so far. The new position is also calculated according to the Eq. (8):

$$ {X}_{\left(t+1\right)}={X}_{(t)}+{V}_{\left(t+1\right)} $$
(8)

In this case X(t)is the previous position and X(t + 1)is the current position of the particle.

The flow chart of particle swarm optimization for this optimization problem shown in Fig. 4b).

2.6 Firefly Algorithm

In the firefly algorithm the new position of the firefly, xi′, whose previous position was xi, and is being absorbed into the light intensity with more light intensity at position xj, is calculated as the Eq. (9) (Yang, 2010):

$$ {x_i}^{\prime }={x}_i+{\beta}_0{e}^{-\gamma {r}^m}\left({x}_j-{x}_i\right)+\alpha {\varepsilon}_i $$
(9)

In this regard, εiis a random vector with uniform distribution or Gaussian distribution, γ is the absorption coefficient of light, and α is a coefficient known as the mutation coefficient, and it can be changed in each iteration to converge to the algorithm (Yang, 2010). The flow chart of firefly algorithm for this optimization problem shown in Fig. 4c.

It should be noted that in this research, determination of the location of a well is considered to determine the groundwater level after the pumping well in a node. Then, this level of groundwater is compared with the initial groundwater level and their difference in each node is determined. For determinate the capture zone of pumping wells, we calculated difference in all nodes. Then in the each nodes that it’s this different was higher than 0.5 m, that node be in capture zone of pumping well.

2.7 The Objective Function

In this research, after determination location of wells at the surface of the aquifer, the groundwater level in all nodes is calculated. Before that we had an initial level of groundwater and now we can calculated difference between these two levels. In fact, the objective function in this study is to minimize the difference in groundwater level calculated with the initial level in the aquifer, which can be calculated objective function from Eq. (10):

$$ \mathit{\operatorname{Min}}\kern0.24em Z=\left|\sum \limits_{i=1}^{N\; Node}\left(H-\hat{H}\right)\right| $$
(10)

In this case, Z is the value of the objective function, N Node is equal to the number of nodes, H is equal to the groundwater level of the ground before applying the pumping wells, and \( \hat{H} \)is also equal to the secondary level of groundwater after applying the pumping wells.

3 Results and Discussion

The genetic algorithm has many parameters that can affect the performance of this algorithm. Some of these parameters are the number of the population, the number of parents, the type of crossover, the probability of mutation, the structure of chromosomes, and so on. In this research, a uniform crossover was used, and the method of coding chromosomes was direct coding (each gene = a node number). The values of the parameters of the genetic algorithm are given in Table 1.

Table 1 The value of parameters used in GA
Full size table

In the PSO algorithm, the sum of the parameters C1 and C2, must be less than or equal to four. Examination of different values for parameters C1 and C2 from one to 2.5 with a steps of 0.5 showed that the value of 1.5 for these two parameters gives the best value of the objective function which is equal to 42.9423. This result has been like Cyriac and Rastogi (2016). The W parameter, the weighted inertia, has changed in each iteration, but its value has always been between 0.4 and 0.7 and the population size is 10.

In the firefly algorithm, the value of β0 according to the Yang is usually equal to one.

The parameters of the firefly algorithm such as m, γ, α, and β0are obtained by trial and error and the most appropriate values of these parameters which together produce the best value for the objective function are shown in Table 2. This single run alone cannot determine the efficiency of an algorithm to solve an optimization problem; therefore, each of the algorithms with the best value of parameters obtained for it is run five times, and their average is also calculated. Because the decision is based on the average of iterations, it is more accurate than making decisions based on a single implementation.

Table 2 The value of parameters used in FA
Full size table

In Table 3, the results of five times run of GA, FA and PSO algorithms are presented. This table indicates that, GA give the best answers. Also, the firefly algorithm has never been able to find a solution that will reduce the value of the objective function to less than 50%, and therefore, generally, this algorithm is not able to solve this problem.

Table 3 The results of five runs of algorithms
Full size table

Table 4 shows the statistical characteristics of GA, FA and PSO. This indicates that, among these three algorithms, GA with the average value of the objective function (35.97) has the best performance, and then PSO with 47.87 and, FA with 51.27, they rank next.

Table 4 Statistical characteristics of the performance of GA, FA and PSO
Full size table

However, according to the results, the genetic algorithm has had the best performance. In the genetic algorithm, this performance can be attributed to the use of mutation and crossover operators for exploration and exploitation phases.

Generally, the FA is the weakest algorithm in this optimization problem. Because in the five-time running this algorithm, the value of the objective function is not lower than 50 at all. On the other hand, in this algorithm every fireflies should be compare to all other fireflies. So Comparison Pairwise of fireflies means nested loop and this mechanism increases algorithm run time. Changes in the objective function versus iteration shown in Fig. 5. As seen in this figure, in GA, the value of the objective function fixed in 20th iteration. Also, FA didn’t have a good performance because of entrapment in local optima. Also PSO needs more time to reach a suitable solution.

Fig. 5
figure 5

Performance of GA, PSO and FA algorithms

Full size image

In the following, several other outputs of the GA are presented. In Fig. 6a, shown the location of four pumping wells. Capture zone of tow pumping wells that located on the south side of the aquifer aren’t overlap together.

Fig. 6
figure 6

The hypothetical aquifer view and optimal location of wells

Full size image

In Fig. 6b, groundwater head contour after pumping is shown. In this figure, the western, northern and southern sides have a constant head equal to100 m, because in the western side, due to the existence of the river, the head is constant in this boundary, and also on the northern and southern borders is no-flow boundary, but on the east we have steady-state flow boundary.

The results of the interpolation of groundwater head for GA are also shown in Fig. 6c. In addition, the 3-D view of groundwater head when pumping wells applied in aquifer is shown in Fig. 6d. this figure show, the maximum of drawdown in the aquifer is about 2.5 m.

4 Conclusion

In this study, the performance of hybrid-finite element and meta-heuristic algorithms in minimizing groundwater drawdown was investigated. In this research defined a hypothetical aquifer with total area equal to 1.5 km2, there was in this aquifer 252 triangular elements and 150 nodes. Also, this aquifer had no-flow boundary in north and south and steady-state flow in east and static head in west. After specifying the characteristics of the aquifer, without considering any wells, groundwater level was estimated by finite element method. Subsequently, four pumping wells with different pumping rate were considered, therefore the meta-heuristic algorithms should optimize the location of these pumping wells to find the best value for objective function or near optimum. In this research, three meta-heuristic algorithms were used: GA, FA and PSO. The results indicated that all the algorithms have the ability to combine with finite element method. The results also indicated that the genetic algorithm has a high performance in solving this problem and the mean value of the objective function was 35.97. The results also show that the algorithms tend to choose the location of pumping wells located near the eastern side (constant hydraulic head). On the other hand, pumping wells with a higher pumping rate are more likely to be drilled in parts of the aquifer where there is hydraulic conductivity is low. This tendency of algorithms is because of minimizing aquifer drawdown.

This study could determine the location of injection wells that have the greatest effect on aquifer. And other limitations can be added to the problem and checked again. If accurate information is available from the actual aquifer. We can investigated and compared.