1 Introduction

In this Big Data era, massive data are generated, processed, transmitted, and stored in various field [4, 6, 19]. Industrial control systems are no exception. Advanced control approaches are generally based on mathematical models which are usually data-driven models obtained from the input and output data of dynamic systems through system identification methods. Subspace identification methods (SIMs) [13, 17, 21, 25] are attractive since a state-space realization is estimated directly from input-output data, without non-linear optimization as generally required by the prediction error methods (PEMs) [15]. Moreover, SIMs have a better numerical reliability and a modest computational complexity compared with PEMs, particularly when the number of outputs and states is large. If the available data records exceed hundreds of thousands or even millions of samples, cloud computing can be adopted to solve the system identification problem [2, 7, 18], since cloud computing has rapidly emerged as an accepted big data computing paradigm in many areas such as smart city [29], smart medical [1], smart transportation [30] and image processing [28].

However, most of the SIM algorithms only consider output errors and assume the input variables are noise-free. This assumption is far from being satisfactory since all variables contain noise in practice. The effect of disturbances can be eliminated by appropriate selection of the instrument variables that are independent of disturbances. Chou and Verhaegen [3] developed an instrumental variable subspace method which can be applied to errors-in-variables (EIV) and closed-loop identification problem, but it handles white-noise input differently from correlated input. Gustaffson [9] investigated an alternative IV-approach to subspace identification and proposed an improvement of EIV-algorithm of [3].

In parallel, Wang and Qin [26] proposed the use of parity space and principal component analysis (SIMPCA) for errors-in-variables identification with colored input excitation, which can also be applied to closed-loop identification. Huang et al. [11] developed a new closed-loop subspace identification algorithm (SOPIM) by adopting the EIV model structure of SIMPCA, and proposed a revised instrumental variable method to avoid identifying the parity space of the feedback controller. Wang and Qin [27] introduced appropriate column weighting for SIMPCA which seemed to improve the accuracy of the estimation, and pointed out that the parameter estimates from this method (SIMPCAw) is equivalent to that from SOPIM.

In this paper, by adopting the EIV model structure, closed-loop subspace identification methods are proposed based on instrumental variables using orthogonal projection. It is shown that the existing subspace identification methods via instrumental variables for EIV problems yield biased solution in closed-loop at least under the condition that the external excitation is white noise. Therefore a remedy is proposed to eliminate the bias. Compared with the subspace methods using PCA, the present methods using orthogonal projection are quite simple and easy to extend.

The rest of this paper is organized as follows. In Section 2, the problem formulation and assumptions are presented. Section 3 addresses the subspace algorithms based on instrumental variables under a unified framework–for convenience, called SIV framework– which includes the methods proposed in [3, 9]. Besides, an easier SIV method is proposed in terms of implementation in Section 2. Under the SIV framework, Section 4 presents new closed-loop subspace methods which yield unbiased estimation for EIV problems. In Section 5, two numerical examples are illustrated. The final section concludes the paper.

2 Problem Formulation

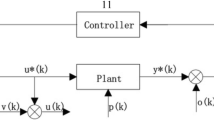
Suppose that the plant depicted in Fig. 1 can be described by the following discrete time linear time-invariant system:

$$ \begin{array}{ll} x(k+1) &= A x(k)+ B \tilde{u}(k)+ w(k)\\ \tilde{y}(k) &=C x(k)+D \tilde{u}(k) \end{array} $$
(1)

where \(x(k) \in \mathbb {R}^{n}\), \(\tilde {u}(k) \in \mathbb {R}^{m}\) and \(\tilde {y}(k) \in \mathbb {R}^{l}\) are the state variables, noise-free inputs and noise-free outputs, respectively. \(w(k)\in \mathbb {R}^{n}\) is the process noise term. A, B, C and D are system matrices with appropriate dimensions. The available observations for identification are the measured input signals u(k) and output signals y(k):

$$ \begin{array}{ll} u(k) &= \tilde{u}(k)+ o(k)\\ y(k) &= \tilde{y}(k)+ v(k) \end{array} $$
(2)

where \(o(k)\in \mathbb {R}^{m}\) and \(v(k)\in \mathbb {R}^{l}\) are input and output noise.

Figure 1
figure 1

EIV model structure.

Full size image

We introduce the following assumptions:

  • A1. The system is asymptotically stable, i.e. the eigenvalues of A are strictly inside the unit circle.

  • A2. w(k),v(k),o(k) are zero-mean white noises, and

    $$ E\left\{\begin{bmatrix}w(k)\\v(k)\\o(k)\end{bmatrix} \begin{bmatrix}w^{T}(j) & v^{T}(j) & o^{T}(j)\end{bmatrix}\right\}=\begin{bmatrix}R_{w} & R_{wv} & R_{wo}\\R_{vw} & R_{v} & R_{vo}\\R_{ow} & R_{ov} & R_{o} \end{bmatrix}\delta_{kj} $$
    (3)

    here, E{⋅} denotes statistical expectation, Rw denotes the autocorrelation function of the random variable v, Rwv denotes the cross-correlation function of the random variables w and v, and similar definition for the other R(⋅). δkj is the Kronecker delta function, i.e.,

    $$ \delta_{kj}=\begin{cases} 0, & \text{if $k \neq j $}\\ 1, & \text{if $k = j $} \end{cases} $$
    (4)

  • A3. \(\tilde {u}(k)\) is a quasi-stationary deterministic sequence and satisfy the persistence of excitation condition [15].

  • A4. The pair (A,C) is observable, and the pair \((A,[B \quad R_{w}^{1/2}]\) is reachable [5].

3 Notations and the SIV Framework

Firstly, we define the stacked past and future output vectors and the block Hankel output matrices as the following:

$$ \begin{array}{@{}rcl@{}} y_{p}(k)&=\begin{bmatrix} y(k-p)\\ y(k-p+1)\\ \vdots\\ y(k-1) \end{bmatrix}, y_{f}(k)=\begin{bmatrix} y(k)\\ y(k+1)\\ \vdots\\ y(k+f-1) \end{bmatrix} \end{array} $$
(5)
$$ \begin{array}{@{}rcl@{}} Y_{p}&=\begin{bmatrix} y_{p}(k) & y_{p}(k+1) & {\cdots} & y_{p}(k+L-1) \end{bmatrix} \end{array} $$
(6)
$$ \begin{array}{@{}rcl@{}} Y_{f}&=\begin{bmatrix} y_{f}(k) & y_{f}(k+1) & {\cdots} & y_{f}(k+L-1) \end{bmatrix} \end{array} $$
(7)

where subscript p,f are user-defined integers (p ≥ f > n) and stand for past horizon and future horizon, respectively. The input and noise block Hankel matrices Up,Uf,Of,Wf,Vf are defined similarly to Yp,Yf.

Through the iteration of Eqs. 1 and 2, we can derive the following subspace matrix equation

$$ Y_{f} = {\varGamma}_{f} X_{k}+ H_{f} U_{f} -H_{f} O_{f} + G_{f} W_{f} +V_{f} $$
(8)

where

$$ X_{k}=\begin{bmatrix} x(k) & x(k+1) & {\cdots} & x(k+L-1) \end{bmatrix} $$
(9)

is the state sequence,

$$ {\varGamma}_{f} :=\begin{bmatrix}C\\CA\\\vdots\\CA^{f-1}\end{bmatrix} $$
(10)

is the extended observability matrix with rank n,

$$ H_{f} :=\begin{bmatrix} D & 0 & {\cdots} & 0 \\ CB & D & {\ddots} & 0\\ {\vdots} & & {\ddots} & \vdots\\ CA^{f-2}B & {\cdots} & CB & D\\ \end{bmatrix} $$
(11)

and

$$ G_{f} :=\begin{bmatrix} 0 & 0 & {\cdots} & 0 \\ C & 0 & {\ddots} & 0\\ {\vdots} & & {\ddots} & \vdots\\ CA^{f-2} & {\cdots} & C & 0\\ \end{bmatrix} $$
(12)

are two block Toeplitz matrices.

Unlike traditional subspace identification methods [16, 20, 23, 24], SIV first eliminates the effect of the noises via instrumental variables (IV). Suppose the IV vector \(\xi (k) \in \mathbb {R}^{n_{\xi }}\) is available, for example, a natural choice is \(\xi (k)=[{u_{p}^{T}}(k) {y_{p}^{T}}(k)]^{T}\) in the EIV case. Construct the IV matrix

$$ {\varXi} :=\begin{bmatrix} \xi(k) & \xi(k+1) & {\cdots} & \xi(k+L-1) \end{bmatrix} $$
(13)

such that

$$ \underset{L \rightarrow \infty}{\lim} \frac{1}{L}[W_{f} \quad V_{f} \quad O_{f}] {\varXi}^{T}=0 \quad \text{w.p.1} $$
(14)

For notational convenience, all noise terms are collected in Nf = Vf − HfOf + GfWf. Postmultiplying both sides of Eq. 8 by ΞT, we get

$$ \hat{R}_{y_{f} \xi}={\varGamma}_{f} \hat{R}_{x \xi}+H_{f} \hat{R}_{u_{f} \xi}+ \hat{R}_{n_{f} \xi} $$
(15)

where \( \hat {R}_{y_{f} \xi }:= \frac {1}{L}Y_{f} {\varXi }^{T}\), \(\hat {R}_{x \xi }:= \frac {1}{L}X_{k} {\varXi }^{T}\), and \(\hat {R}_{u_{f} \xi },\hat {R}_{n_{f} \xi }\) are defined conformably with \(\hat {R}_{y_{f} \xi }\). From the condition Eq. 14,

$$ \hat{R}_{y_{f} \xi}={\varGamma}_{f} \hat{R}_{x \xi}+H_{f} \hat{R}_{u_{f} \xi} \quad \text{w.p.1 as} L\rightarrow \infty $$
(16)

Next SIV removes the effect of the future input on the future output by orthogonal projection.

$$ \hat{R}_{y_{f} \xi} {\varPi}_{u_{f} \xi}^{\bot}={\varGamma}_{f} \hat{R}_{x \xi}{\varPi}_{u_{f} \xi}^{\bot} \quad \text{w.p.1 as} L\rightarrow \infty $$
(17)

where \({\varPi }_{u_{f} \xi }^{\bot }\) denotes the orthogonal projection matrix onto the nullspace of \(\hat {R}_{u_{f} \xi }\). Assuming that \(\hat {R}_{u_{f} \xi }\) has full rank,

$$ {\varPi}_{u_{f} \xi}^{\bot}=I-\hat{R}_{u_{f} \xi}^{T}(\hat{R}_{u_{f} \xi}\hat{R}_{u_{f} \xi}^{T})^{-1}\hat{R}_{u_{f} \xi} $$
(18)

Then like other subspace identification methods [10, 12, 14, 22], SIV uses SVD to obtain the extended observability matrix

$$ {\varOmega}:=\hat{R}_{y_{f} \xi} {\varPi}_{u_{f} \xi}^{\bot} W_{2}=\begin{bmatrix} U_{1} & U_{2} \end{bmatrix} \begin{bmatrix} S_{1} & 0 \\0 & S_{2} \end{bmatrix} \begin{bmatrix} {V_{1}^{T}} \\{V_{2}^{T}} \end{bmatrix} $$
(19)

where W2 is a weighting matrix. The matrix U1 consists of the n principal left singular vectors of Ω, S1 and S2 are diagonal matrices with the non-increasing singular values of Ω. Due to the existing of noises, S2≠ 0 and a decision on the order of the system must be made. The extended observability matrix is obtained as Γf = U1T, T is a non-singular matrix and typical choices are T = I or \(T=S_{1}^{1/2}\).

For numerical implementation, the first step of SIV is to compute the following QR factorization [8]

$$ \frac{1}{L}\begin{bmatrix} U_{f} \\ Y_{f} \end{bmatrix}{\varXi}^{T}=\begin{bmatrix} R_{11} & 0 \\ R_{21} & R_{22} \end{bmatrix}\begin{bmatrix} {Q_{1}^{T}} \\ {Q_{2}^{T}} \end{bmatrix} $$
(20)

From Eq. 20 it is clear that \(\hat {R}_{y_{f} \xi } {\varPi }_{u_{f} \xi }^{\bot }=R_{22}{Q_{2}^{T}}\), so Γf can be obtained by performing SVD on R22. Once Γf has been estimated, the system matrices A,B,C,D can be computed as in [13, 21].

Suppose \(Z_{p}=[{U_{p}^{T}} {Y_{p}^{T}}]^{T}\), W2 = I, and the instruments are chosen as Ξ = Zp, then SIV boils down to the method proposed in [3]. Gustafsson [9] found an improvement to this method by modifying the instruments as \({\varXi }=(\frac {1}{L}Z_{p} {Z_{p}^{T}})^{-1/2}Z_{p}\). For simplicity, these two methods are referred to as SIV and SIVw.

On the other side, we choose the instruments as \({\varXi }={\varPi }_{Z_{p}}^{\bot }={Z_{p}^{T}}(Z_{p} {Z_{p}^{T}})^{-1}Z_{p}\), and call the corresponding method SIVp. In terms of the estimation accuracy, SIVp is equivalent to SIVw, because

$$ \begin{array}{@{}rcl@{}} [Z_{f} {\varPi}_{Z_{p}}^{\bot}][Z_{f} {\varPi}_{Z_{p}}^{\bot}]^{T}&=&[Z_{f} {Z_{p}^{T}} (Z_{p} {Z_{p}^{T}})^{-1/2}]\\&&[Z_{f} {Z_{p}^{T}} (Z_{p} {Z_{p}^{T}})^{-1/2}]^{T} \end{array} $$
(21)

However, SIVp, which uses the orthogonal projection as the instruments, is easier to implement. Up to now, it seems that these three methods can work under closed-loop conditions, because they avoid projecting out Uf directly. However, simulation results indicate that this is not always the case for closed-loop systems.

4 New Closed-Loop Subspace Methods Under SIV Framework

To find the problem, let us consider the controller described by the following state space model:

$$ \begin{array}{ll} x^{c}(k+1)&=A_{c} x^{c}(k)+B_{c} (r(k)-y(k))\\ u(k)&=C_{c} x^{c}(k)+D_{c} (r(k)-y(k) ) \end{array} $$
(22)

where r(k) is the setpoint excitation. Based on Eq. 22, we can derive the following subspace matrix equation

$$ U_{f}={{\varGamma}_{f}^{c}} {X_{k}^{c}}+ {H_{f}^{c}} (R_{f}-Y_{f}) $$
(23)

Post-multiplying both sides of Eq. 23 by ΞT,

$$ \hat{R}_{u_{f} \xi}={{\varGamma}_{f}^{c}} \hat{R}_{x^{c} \xi}-{H_{f}^{c}} \hat{R}_{y_{f} \xi}+ {H_{f}^{c}} \hat{R}_{r_{f} \xi} $$
(24)

If the following condition

$$ \underset{L \rightarrow \infty}{\lim} R_{f} {\varXi}^{T}=0 $$
(25)

is satisfied, then

$$ \hat{R}_{u_{f} \xi}={{\varGamma}_{f}^{c}} \hat{R}_{x^{c} \xi}-{H_{f}^{c}} \hat{R}_{y_{f} \xi} \qquad \text{w.p.1 as} L\rightarrow \infty $$
(26)

Combining Eqs. 16 and 26 gives

$$ \begin{bmatrix} I & -H_{f} \\ {H_{f}^{c}} & I \end{bmatrix}\begin{bmatrix} R_{y_{f} \xi} \\ R_{u_{f} \xi} \end{bmatrix}=\begin{bmatrix} {\varGamma}_{f} R_{x \xi}\\ {{\varGamma}_{f}^{c}} R_{x^{c} \xi} \end{bmatrix} $$
(27)

Consequently, both the row space of Rxξ and \(R_{x^{c} \xi }\) fall in the row space of \(\begin {bmatrix} R_{y_{f} \xi } \\ R_{u_{f} \xi } \end {bmatrix}\). This means \(\begin {bmatrix} R_{y_{f} \xi } \\ R_{u_{f} \xi } \end {bmatrix}\), which is used to identify the process model, contains also the controller information. In order to exclude the controller information, the IV matrix Ξ must satisfy the following conditions:

$$ \begin{array}{@{}rcl@{}} \underset{L \rightarrow \infty}{\lim} \frac{1}{L}[W_{f} \quad V_{f} \quad O_{f}] {\varXi}^{T} & = 0 \end{array} $$
(28)
$$ \begin{array}{@{}rcl@{}} \underset{L \rightarrow \infty}{\lim} \frac{1}{L} R_{f} {\varXi}^{T} & \neq 0 \end{array} $$
(29)

Suppose

$$ \tilde{{\varXi}}=\begin{bmatrix} R_{f} \\ Z_{p} \end{bmatrix} $$
(30)

It is natural to choose the IV matrix as follows:

$$ {\varXi}=\begin{cases} \tilde{{\varXi}} & \text{CSIV}\\ {\varPi}_{\tilde{{\varXi}}}& \text{CSIVp} \end{cases} $$
(31)

With this modification, all the computation procedures discussed in the last section are valid for closed-loop identification. We call the modified algorithms as CSIV and CSIVp.

5 Numerical Examples

In this section a simulation study is presented to demonstrate the performance of the new algorithms proposed in this paper.

5.1 Example 1: A First Order System

The simulation example is a first order SISO system under closed-loop operation,

$$ y(k)-0.9y(k-1)=u(k-1)+e(k)+0.9e(k-1) $$
(32)

The feedback has the following structure:

$$ u(k)=-0.6 y(k)+r(k) $$
(33)

where r(k) is the excitation signal and is generated as

$$ r(k)=(1+0.8 q^{-1}+0.6 q^{-2})r_{0} $$
(34)

where r0(k) is zero mean white noise with unit variance. The innovation process e(k) is zero mean white noise with variance Re = 1.44. Monte-Carlo simulations are conducted with 30 runs. Each simulation generates 2000 data points. In addition, the input and the output are contaminated with zero mean white noises whose variances are tuned so as for the signal to noise ratios (SNR)

$$ \begin{array}{@{}rcl@{}} \text{Input SNR} & = \frac{\text{var}(\tilde{u}(k))}{\text{var}(o(k))} \end{array} $$
(35)
$$ \begin{array}{@{}rcl@{}} \text{Output SNR} & =\frac{\text{var}(\tilde{y}(k))}{\text{var}(v(k))} \end{array} $$
(36)

to be 10.

For this example, we will apply the following subspace identification methods: SIMPCA in [26], the three methods (SOPIM, CSIMPCA, CSOPIM) in [11], SIV in [3], and the proposed methods (SIVp, CSIV, CSIVp) in this paper. The horizons are chosen as f = p = 2.

Table 1 shows some Monte-Carlo simulation results. From the table, we can see that the results of the methods using the same weighting matrix are close, for example, SIV and SIMPCA, SIVp and SOPIM, CSIV and CSIMPCA, CSIVp and CSOPIM respectively. For the methods in which Rf is introduced into the weighting matrix, i.e., CSIV, CSIVp, CSIMPCA and CSOPIM, the estimate of b1 are better than that of the other methods. Figure 2 gives the visual representation in Bode plots. It is very different for the four methods (SIV, SIVp, CSIV and CSIVp) in the low frequency estimates.

Table 1 Simulation results for the first order model P(z) = (b1z + b2)/(z − a), where the means and standard deviations(s.d.) are computed based on 30 Monte-Carlo runs. Both SNRs are 10, and the setpoint signal is colored noise.
Full size table
Figure 2
figure 2

Bode plots of the first order model by four different methods: SIV, SIVp, CSIV and CSIVp. The solid lines (red) are true values and the dashed lines (blue) are estimated values of 30 Monte-Carlo runs.

Full size image

If we enhance the effects of the measurement noises by reducing both SNRs to 5, the simulation results are showed in Table 2. The methods in which Rf is introduced into the weighting matrix, give good results, and the other methods yield somewhat biased estimates.

Table 2 Simulation results for the first order model P(z) = (b1z + b2)/(z − a), where the means and standard deviations (s.d.) are computed based on 30 Monte-Carlo runs. Both SNRs are 5, and the setpoint signal is colored noise.
Full size table

If the setpoint signal is white noise, Table 3 shows the simulation results. The methods in which Rf is introduced into the weighting matrix, give consistent results while the other methods yield biased estimates.

Table 3 Simulation results for the first order model P(z) = (b1z + b2)/(z − a), where the means and standard deviations(s.d.) are computed based on 30 Monte-Carlo runs. Both SNRs are 10, and the setpoint signal is white noise.
Full size table

5.2 Example 2: A Fifth Order System

The system to be considered is expressed in the innovation state space form:

$$ A = \begin{bmatrix} 4.40 & 1 & 0 & 0 & 0\\ -8.09 & 0 & 1 & 0 & 0\\ 7.83 & 0 & 0& 1 & 0 \\ -4.00 & 0 & 0 & 0 & 1\\ 0.86 & 0 & 0 & 0 & 0 \end{bmatrix} B = \begin{bmatrix} 0.00098\\ 0.01299\\ 0.01859\\ 0.0033\\ -0.00002 \end{bmatrix} C^T = \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0\\ 0 \end{bmatrix} K = \begin{bmatrix} 2.3\\ -6.64\\ 7.515\\ -4.0146\\ 0.86336 \end{bmatrix} $$
(37)

and D = 0. The state space model of the controller is:

$$ A_{c} = \begin{bmatrix} 2.65 & -3.11 & 1.75 & -0.39 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} B_{c} = \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} {C_{c}^{T}} = \begin{bmatrix} -0.4135 \\ 0.8629 \\ -0.7625\\ 0.2521 \end{bmatrix} $$
(38)

and Dc = 0.61. The block diagram of this example is shown in Fig. 3.

Figure 3
figure 3

The block diagram of Example 2.

Full size image

The simulation conditions are exactly the same as those used in [11]: the reference signal r is Gaussian white noise with variance 1; the innovation e is Gaussian white noise with variance 1/9. Monte-Carlo simulations are conducted with 30 runs. Each simulation generates 1200 data points. Moreover, we add zero mean white noises with variance 0.2 to the input and the output measurements.

Fig. 4 shows the pole plots of the fifth order system by SIV and SIVp. It is obvious that the results are biased due to the correlation between the input and the unmeasured disturbance under feedback control. When the IV matrix is contained Rf, the corresponding methods CSIV and CSIVp give consistent pole results which are shown in Fig. 5(a). Nevertheless, the bode plots in Fig. 5(b) show that the low frequency responses of CSIVp are much better than that of CSIV which confirms CSIVp is more efficient than CSIV without column weighting.

Figure 4
figure 4

Pole estimates of the fifth order system by SIV and SIVp, where the true poles are denoted by (red) +.

Full size image
Figure 5
figure 5

Simulation results of the fifth order system by CSIV and CSIVp. The left column is pole estimates, and the true poles are denoted by (red) +. The right column is Bode magnitude plots, and the true bode plot (red, solid) is covered by 30 curves.

Full size image

In this example, we will explore the effect of different IV matrices. Besides the IV matrices abovementioned, we also consider the following IV matrices:

$$ \begin{array}{@{}rcl@{}} &&\begin{array}{llll} (1) \tilde{{\varXi}}&=\begin{bmatrix} R_{f} \\ Y_{p} \end{bmatrix} ~(2) \tilde{{\varXi}}&= \begin{bmatrix} R_{f} \\ U_{p} \end{bmatrix} ~~(3) \tilde{{\varXi}}&=\begin{bmatrix} R_{f} \\ R_{p} \end{bmatrix} \end{array} \end{array} $$
(39a)
$$ \begin{array}{@{}rcl@{}} &&\begin{array}{llll} (4) \tilde{{\varXi}}&=\begin{bmatrix} R_{f} \\ R_{p} \\Y_{p} \end{bmatrix} (5) \tilde{{\varXi}}&=\begin{bmatrix} R_{f} \\ R_{p} \\ U_{p} \end{bmatrix} (6) \tilde{{\varXi}}&=\begin{bmatrix} R_{f} \\ R_{p} \\ Z_{p} \end{bmatrix} \end{array} \end{array} $$
(39b)

The resulting methods called CSIVx or CSIVpx, where x denotes the number corresponding to the IV matrix. For example, CSIV1 uses the IV matrix \( \left [ \begin {smallmatrix} R_{f} \\ Y_{p} \end {smallmatrix} \right ] \) and CSIVp1 uses the projection form of the IV matrix. For all methods, the horizons are chosen as f = p = 20.

Figure 6 displays the pole plots of the fifth order system by CSIV1, CSIV2, CSIV3, CSIV4, CSIV5 and CSIV6. The simulation results of the fifth order system by

Figure 6
figure 6

Pole estimates of the fifth order system by CSIV1, CSIV2, CSIV3, CSIV4, CSIV5 and CSIV6, and the true poles are denoted by (red) +.

Full size image

CSIVp1, CSIVp2, CSIVp3, CSIVp4, CSIVp5 and CSIVp6 are shown in Figs. 7 and 8. As for the pole estimates, the methods using the projection IV matrices give slightly better results. For this example, the methods using the projection IV matrices which contain Yp yield better results not only for pole estimates but also for the low frequency responses. However, it is not always the case for other systems.

Figure 7
figure 7

Simulation results of the fifth order system by CSIVp1, CSIVp2 and CSIVp3. The left column is pole estimates, and the true poles are denoted by (red) +. The right column is Bode magnitude plots, and the true bode plot (red, solid) is covered by 30 curves.

Full size image
Figure 8
figure 8

Simulation results of the fifth order system by CSIVp4, CSIVp5 and CSIVp6. The left column is pole estimates, and the true poles are denoted by (red) +. The right column is Bode magnitude plots, and the true bode plot (red, solid) is covered by 30 curves.

Full size image

6 Conclusions

In this paper, closed-loop subspace identification methods for EIV problems are developed using orthogonal projection as instrumental variables. They can provide consistent estimates regardless of whether the reference signal is white noise. In addition, the effect of different IV matrices is explored. Compared with the subspace methods based on PCA, the methods proposed here are simple to implement and easy to extend. Two simulation examples are given to illustrate the performance of the proposed methods in closed-loop EIV identification and the effect of instrumental variables.