1 Introduction

In the past two decades, the subspace identification method (SIM) has undergone rapid development in both theory and practice [1,2,3,4,5,6,7]. In the actual industrial process, because of factors such as safety, economical efficiency and operation stability, the system should be operated under closed loop conditions; biased estimation may be obtained when identifying the system model through the method of open-loop subspace identification. This is a result of feedback when identifying models in the closed loop, causing the “future” inputs to be relevant to the “past” noise in the system; thus, the method of orthogonal projection applied by open-loop subspace identification will not be able to eliminate noise. Scholars have proposed different solutions in the field of closed-loop identification. Verhaege [8] applied the method of MOESP (Multivariable Output Error State Space) in closed-loop identification with the input and output state space model. However, a model order reduction process should be required in this method. Ljung and McKelvey [9] regarded the high-order ARX models obtained from the input and output data as a multi-step forward output predictor, assuming that the vector of the multi-step output prediction can be obtained when the input is zero and that system parameters are obtained by the state space regression equation. However, only the output noise is considered in these methods, and the input variables are noise free. Obviously, the assumption is not consistent with reality because all the observed variables will be affected by noise pollution.

For the EIV (errors-in-variables) model structure, namely, the input and output, both are affected by noise pollution. Chou and Verhaegen [10] put forward a new method of subspace identification. The method eliminates noise effects by regarding the past input/output data as auxiliary variables. Gustafsson and Tony [11] changed the steps of the traditional SIM and proposed a new subspace auxiliary variable method (Subspace-based Identification using Instrumental Variables, SIVs). The algorithm presented in literature [12] was included, and the identification precision was improved after the algorithm was modified. In terms of the algorithm itself, the input being independent of noise assumption is not involved in the two methods; thus, it seems that they can be applied for identification in a closed-loop system. However, this is not the case based on simulation examples; these two types of algorithms used in closed-loop identification do not obtain consensus estimates in some cases.

On the other hand, Wang and Qin [13,14,15] introduced the concept of parity space, i.e., considering the input and output variables at the same time. The EIV mode was identified in subspace through Principal Component Analysis, PCA, called SIMPCA. On the basis of this, through the model combining input/output, Huang [16,17,18] analysed the reason why the deviation exists in SIMPCA when the external excitation signal is white noise in closed-loop identification and then proposed the improvement on the new auxiliary variables. In the process of algorithm implementation, SVD should be applied twice to solve the orthogonal complement space in the two methods [19, 20]. It is difficult to determine the dimensions of the orthogonal complement space when the system order is unknown. According to the theory of stochastic implementation with external input, Katayama [20,21,22] decomposed the signal into a deterministic part and a random part by using orthogonal decomposition; thus, the system model can be estimated through the deterministic part.

This article first proposed auxiliary variables based on orthogonal projection in the framework of SIVs as an improved strategy of the SIM. Compared with the existing SIM based on instrumental variables, on the premise of ensuring high identification, the algorithm of this method is simpler and the computational complexity is lower. Through the analysis of the closed-loop identification problem, this article explains the cause of the possible errors in estimation through the method under the condition of closed-loop identification. To eliminate the deviation of the identification, it can be improved by new auxiliary variables proposed in this paper, and in addition, it is compared with PCA and methods of auxiliary variable subspace identification. The method proposed in this paper only depends on the choice of auxiliary variables; the algorithm is simpler and direct and is easy to implement. In the process of identification, SVD was implemented only once; the amount of the computation for derived matrix dimensions can be greatly reduced under the condition of unknown system order time. In addition, one should discuss the mode of choosing a variety of secondary variables and simultaneously validating the results with numerical simulation.

2 Description of the problem and assumptions

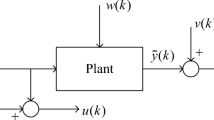
Assuming the system is defined as shown in Fig. 1, the discrete-time linear time-invariant model can be represented as the following state space form:

Fig. 1
figure 1

EIV model structure

Full size image
$$\begin{aligned} x(k) &= Ax(k) + Bu^{\ast}(k) + p(k) \hfill \\ y^{\ast}(k) &= Cx(k) + Du^{\ast}(k) \hfill \\ \end{aligned}$$
(1)

\(x(k) \in \Re^{n},u^{\ast}(k) \in \Re^{l},y^{\ast}(k) \in \Re^{m}\) are state variables, noise-free input, and noise-free output; \(p(k) \in \Re^{n}\) is the process noise. The observable input u(k) and output y(k) are used for identification:

$$\begin{aligned} y(k) = y^{\ast}(k) + o(k) \hfill \\ u(k) = u^{\ast}(k) + v(k) \hfill \\ \end{aligned}$$
(2)

We assume that \(v(k) \in \Re^{l} ,o(k) \in \Re^{m}\) denote the input noise and output noise. They are considered according to the description based on the method of symmetry [10].

Here, the following assumptions are introduced:

  1. A1

    The system is asymptotically stable, for example, all the eigenvalues of A are strictly inside the unit circle.

  2. A2

    (A,C) is observable.

  3. A3

    Process noise p(k), measurement noise o(k) and v(k) are white noise, and they have past statistical independence from the noise input u*(k), e.g.,

    $$E\left\{ {u^{\ast}\left( k \right)\left[ \begin{aligned} p\left( j \right) \hfill \\ o\left( j \right) \hfill \\ v\left( j \right) \hfill \\ \end{aligned} \right]^{T} } \right\} = 0\;j \ge k$$
    (3)
  4. A4

    v(k) and o(k) are independent input noise and output noise, respectively, of the state sequence x(k); process noise p(k) (k ≥ 1) is independent of the initial state x(1), for example [10],

    $$E\left[ {x ^{\ast} \left( k \right)p^{T} \left( j \right)} \right],\;{\text{for}}\;j \ge k \ge 0$$
  5. A5

    Three white noise sequences are relevant, and their covariance is determined by the following unknown matrix:

    $$E\left\{ {\left[ {\begin{array}{*{20}c} {p(k)} \\ {o(k)} \\ {v(k)}\\ \end{array} } \right][\begin{array}{*{20}c} {p(j)^{T} } & {o(j)^{T} } & {v(j)^{T} } \\ \end{array} ]} \right\} = \left[ {\begin{array}{*{20}c} {R_{{pp}} } & {R_{{po}} } & {R_{{pv}} } \\ {R_{{po}}^{T} } & {R_{{oo}} } & {R_{{ov}} } \\ {R_{{pv}}^{T} } & {R_{{ov}}^{T} } & {R_{{vv}}} \\ \end{array} } \right]\delta _{{kj}}$$
    (4)

δkj is the Kronecker delta function. Noise-free input u*(k) meets the condition of “persistent excitation”.

Because of the dynamics of system modelling, we apply the extended state space model, e.g., stacking relationships between continuous variables. Regarding any time k as the current time, define the past and the future output vectors and the Hankel matrix output in the following form:

$$y_{p} (k) = \left[ \begin{aligned} y\left( {k - p} \right) \hfill \\ y\left( {k - p + 1} \right) \hfill \\ \vdots \hfill \\ y\left( {k - 1} \right) \hfill \\ \end{aligned} \right] \in \Re^{mp}$$
(5)
$$y_{f} (k) = \left[ \begin{aligned} y\left( k \right) \hfill \\ y\left( {k + 1} \right) \hfill \\ \vdots \hfill \\ y\left( {k + f - 1} \right) \hfill \\ \end{aligned} \right] \in \Re^{mf}$$
(6)
$$Y_{p} = \left[ {y_{p} \left( k \right)\;\;\;\;y_{p} \left( {k + 1} \right)\;\; \ldots \;\;y_{p} \left( {k + N - 1} \right)} \right] \in \Re^{mp \times N}$$
(7)
$$Y_{f} = \left[ {y_{f} \left( k \right)\;\;\;\;y_{f} \left( {k + 1} \right)\;\; \ldots \;\;y_{f} \left( {k + N - 1} \right)} \right] \in \Re^{mf \times N}$$
(8)
$$p \ge f > n$$

Iterating formulas (1) and (2), there exists

$$y_{f} (k) = \Upgamma_{f} x(k) + H_{f} u_{f} (k) - H_{f} v_{f} (k) + G_{f} p_{f} (k) + o_{f} (k)$$
(9)
$$y_{f} (k) = \Upgamma_{f} x(k) + H_{f} u_{f} (k) - H_{f} v_{f} (k) + G_{f} p_{f} (k) + o_{f} (k)$$
(10)

which is an extended observable matrix with rank n.

$$H_{f} = \left[ {\begin{array}{*{20}c} D & 0 & \cdots & 0 \\ {CB} & D & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ {CA^{{f - 2}} } & {CA^{{f - 3}} B} & \cdots & D \\ \end{array} } \right] \in \Re ^{{mf \times lf}}$$
(11)
$$G_{f} = \left[ {\begin{array}{*{20}c} 0 & 0 & \cdots & 0 \\ C & D & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ {CA^{{f - 2}} } & {CA^{{f - 3}} B} & \cdots & 0 \\ \end{array} } \right] \in \Re ^{{mf \times nf}}$$
(12)

are Toeplitz matrices with two blocks;

vectors \(v_{f} (k) \in \Re^{lf} ,o_{f} (k) \in \Re^{mf} ,p_{f} (k) \in \Re^{nf} ,y_{f} (k)\) and yf(k) have similar definitions.

Define

$$z_{f} (k) = \left[ \begin{aligned} y_{f} (k) \hfill \\ u_{f} (k) \hfill \\ \end{aligned} \right] \in \Re^{(lf + mf)}$$
(13)

Formula (9) is rewritten as

$$\begin{aligned} \left[ {I\;|\; - H_{f} } \right]z_{f} (k) & = \Upgamma_{f} x(k) - H_{f} v_{f} (k) + G_{f} p_{f} (k) + o_{f} (k) \\ & = \Upgamma_{f} x(k) + \varepsilon_{f} (k) \\ \varepsilon_{f} (k) & = - H_{f} v_{f} (k) + G_{f} p_{f} (k) + o_{f} (k) \\ \end{aligned}$$
(14)

Once Hankel matrix data are used to replace the data vector, the extended model can be rewritten as follows:

$$Y_{f} = \Upgamma_{f} X(k) + H_{f} U_{f} + E_{f}$$
(15)
$$X(k) = \left[ {x\left( k \right)\;\;\;x\left( {k + 1} \right)\;\; \cdots \;\;x\left( {k + N - 1} \right)} \right] \in \Re^{n \times N}$$

Uf, Ef and Yf have the same structure, and formula (15) can be converted to formula (16) and augmented data matrix Zf:

$$\left[ {I\;|\; - H_{f} } \right]Z_{f} = \Upgamma_{f} X_{f} + E_{f}$$
(16)
$$Z_{f} \equiv \left[ \begin{aligned} Y_{f} \hfill \\ U_{f} \hfill \\ \end{aligned} \right] \in \Re^{(lf + mf) \times N}$$

Based on orthogonal subspace projection (ORT), the problem of EIV model identification is converted into giving input and output data of the noise disturbance,{u(k)}, {y(k)}, and setting point signal data if necessary; thus, the consensus estimates of the rank of the system and the system matrices for A, B, C, and D can be obtained.

3 Subspace Variable Method based on Orthogonal projection (ORT)

Stacking the vector in formulas(9)-(12)and replacing the block Hankel matrix, we can obtain

$$Y_{f} = \Upgamma_{f} X_{k} + H_{f} U_{f} - H_{f} O_{f} + G_{f} P_{f} + V_{f}$$
(17)

The key point in the method of subspace identification is to estimate the first term on the right side of formula (17); the extended observable matrix Γf or the state sequence Xk can be estimated after SVD. Therefore, we can estimate the parameter matrix in the system generally in the method of subspace identification. First, the second term of formula (17) (future input) can be eliminated by projection; then, the last three terms on the right side of formula (17) can also be eliminated by auxiliary variables, which is applicable in terms of the open-loop system. However, for the closed-loop system, a correlation exists between the input and output future noise; results may appear as a deviation caused by these identification steps. This situation can be improved if we change these two steps.

Step 1 Eliminate the noise terms. Suppose \(Z_{p} \equiv \left[ \begin{aligned} Y_{p} \hfill \\ U_{p} \hfill \\ \end{aligned} \right] \in \Re^{(lp + mp) \times N}\) then, make an orthogonal projection for Zp on both sides of formula (17),

$$Y_{f} /Z_{p} = \Upgamma_{f} X_{k} /Z_{p} + H_{f} U_{f} /Z_{p} { + }{\mathcal{K}}_{f} /Z_{p}$$
(18)

Define \({\mathcal{K}}_{f} = G_{f} P_{f} + V_{f} - H_{f} O_{f}\)

$$Y_{f} /Z_{p} = Y_{f} \Uppi_{Z_{p}} = Y_{f} Z_{p}^{T} (Z_{p} Z_{p}^{T} )^{ - 1} Z_{p}$$

This definition is similar to the rest because input in the past is irrelevant to output in the future; therefore,

$${\mathcal{K}}_{f} /Z_{p} = \frac{1}{j}{\mathcal{K}}_{f} Z_{p}^{T} \left( {\frac{1}{j}Z_{p} Z_{p}^{T} } \right)^{ - 1} Z_{p} \to 0\;\;\;w.p.l\;\;as\;\;j \to \infty$$
(19)

When \(j \to \infty ,\) formula (18) can be rewritten as

$$Y_{f} \Uppi_{Z_{p}} \approx \Upgamma_{f} X_{k} /Z_{p} + H_{f} U_{f} /Z_{p}$$
(20)

Suppose \(\Uptheta = \Uppi_{Z_{p}}\); obviously \(\Uptheta^{T} = \Uptheta ,\) so

$$\begin{aligned} \widehat{{\mathcal{Q}}}_{{y_{f} \xi }} = \Upgamma_{f} \widehat{{\mathcal{Q}}}_{x\xi } + H_{f} \widehat{{\mathcal{Q}}}_{{u_{f} \xi }} \;\;\;\;\;w.p.l\;\;\;as\;\;j \to \infty \hfill \\ \widehat{{\mathcal{Q}}}_{{y_{f} \xi }} = \frac{1}{j}Y_{f} \Uptheta^{T} ,\widehat{{\mathcal{Q}}}_{x\xi } = \frac{1}{j}X_{k} \Uptheta^{T} ,\widehat{{\mathcal{Q}}}_{{u_{f} \xi }} = \frac{1}{j}U_{f} \Uptheta^{T} \hfill \\ \end{aligned}$$
(21)

In fact, Θ is an auxiliary variable matrix.

Step 2 Eliminate the impact of future input data by orthogonal projection.

Project formula (21) onto the null space of \(\widehat{{\mathcal{Q}}}_{{u_{f} \xi }}\)

$$\begin{aligned} \widehat{{\mathcal{Q}}}_{{y_{f} \xi }} \Uppi_{{u_{f} \xi }}^{ \bot }& = \Upgamma_{f} \widehat{{\mathcal{Q}}}_{x\xi } \Uppi_{{u_{f} \xi }}^{ \bot } \;\;\;\;\;w.p.l\;\;\;as\;\;j \to \infty \hfill \\ \Uppi_{{u_{f} \xi }}^{ \bot }& = I - {\mathcal{Q}}_{{u_{f} \xi }}^{T} \left( {{\mathcal{Q}}_{{u_{f} \xi }} {\mathcal{Q}}_{{u_{f} \xi }}^{T} } \right)^{ - 1} {\mathcal{Q}}_{{u_{f} \xi }} \hfill \\ \end{aligned}$$
(22)

Obviously,

$$R{\text{ange}}(\Upgamma_{f} ) = R{\text{ange}}(\widehat{{\mathcal{Q}}}_{{y_{f} \xi }} \Uppi_{{u_{f} \xi }}^{ \bot } \;)$$

Range(*) stands for range space.

The next steps are similar to the method of typical subspace identification; first, obtain the augmented matrix through singular value decomposition (SVD), and then, the system matrix can be calculated.

$$\widehat{{\mathcal{Q}}}_{{y_{f} \xi }} \Uppi_{{u_{f} \xi }}^{ \bot } = \left[ {U_{1} \;\;\;\;U_{2} } \right]\left[ \begin{aligned} \Upsigma_{1} \;\;\;\;\;\;0 \hfill \\ 0\;\;\;\;\;\;\;\Upsigma_{2} \hfill \\ \end{aligned} \right]\left[ \begin{aligned} V_{1}^{T} \hfill \\ V_{2}^{T} \hfill \\ \end{aligned} \right]$$
(23)

Thus, we can obtain Γf = U1T, where T stands for a non-singular transformation matrix, usually a valued unit matrix or \(T = \Upsigma_{1}^{1/2}\) (Table 1).

Table 1 Available forms of auxiliary variables in the sub-space identification method
Full size table

Obviously, there are many other forms of auxiliary variables available; here, we choose the form based on the orthogonal projection called SIVort,

$$\begin{aligned} U = \left[ {U_{p}^{T} \;\;\;U_{f}^{T} } \right]^{T} ,\bar{Z} = \left[ {U_{p}^{T} \;\;\;U_{f}^{T} \;\;\;\;Y_{p}^{T} } \right]^{T} ,\widehat{{\mathcal{Q}}}_{u} = \frac{1}{j}UU^{T} \hfill \\ \widehat{{\mathcal{Q}}}_{{\bar{z}}} = \frac{1}{j}\bar{Z}\bar{Z}^{T} ,\widehat{{\mathcal{Q}}}_{{z_{p} }} = \frac{1}{j}Z_{p} Z_{p}^{T} \hfill \\ \end{aligned}$$

The above four algorithms are proposed in terms of the EIV model structure. Thus, the auxiliary variables in CSIV are the most simple and direct; the CSIV algorithm can be obtained by standardizing the method of CSIV. Literature [11] has described that the estimation accuracy can be further improved by these changes.

$$\left[ {Z_{f} \Uppi_{{Z_{p} }}^{ \bot } } \right]\left[ {Z_{f} \Uppi_{{Z_{p} }}^{ \bot } } \right]^{T} = \left[ {Z_{f} Z_{p}^{T} \left( {Z_{p} Z_{p}^{T} } \right)^{ - 1/2} } \right]\left[ {Z_{f} Z_{p}^{T} \left( {Z_{p} Z_{p}^{T} } \right)^{ - 1/2} } \right]^{T}$$
(24)

Therefore, in terms of estimates of the augmented observable matrix, the two algorithms SIV and SIVort are essentially the same. However, from the perspective of algorithm development, the inverse square root needs to be solved if we want to use standardized auxiliary variables, which requires a large calculation. Apparently, using the auxiliary variables in the form of orthogonal projection is much simpler.

In the algorithm, first perform RQ decomposition for the three algorithms:

$$\left[ {\begin{array}{*{20}c} {U_{f} } \\ {Y_{f} } \\ \end{array} } \right]\Theta ^{T} = \left[ {\begin{array}{*{20}c} {R_{{11}} } & 0 \\ {R_{{21}} } & {R_{{22}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {Q_{1}^{T} } \\ {Q_{2}^{T} } \\ \end{array} } \right]$$
(25)

Thus, we can obtain \(\widehat{{\mathcal{Q}}}_{{y_{f} \xi }} \Uppi_{{u_{f} \xi }}^{ \bot } = R_{22} Q_{2}^{T} R{\text{ange(}}\Upgamma_{f} ) {\text{ = Range(R}}_{22} ).\)

The estimation of R22 can be obtained based on SVD, so we can estimate the system matrix.

To date, it seems that the structure of EIV algorithms, such as CSIV, CSOPIM and CSIVort, can be applied for data in closed-loop identification because they do not require the input signal be independent of noise. However, some simulation results show that these algorithms may be inconsistent with the closed-loop estimation in some cases. Next, this issue will be specifically analysed.

4 Method of subspace identification based on auxiliary variable orthogonal projection

4.1 Analysis of the closed-loop solutions

Since the above algorithm performed well in open-loop system identification, the problem must be generated by the controller because both of them performed well in an open-loop condition. To determine the problem, the controller state-space model is as follows:

$$x^{c} (k + 1) = A_{c} x^{c} (k) + B_{c} \left( {r(k) - y(k)} \right)$$
(26)
$$u(k) = C_{c} x^{c} (k) + D_{c} \left( {r(k) - y(k)} \right)$$
(27)

r stands for setpoint, and c stands for controller.

We can obtain the controller by subspace symbols as follows:

$$U_{f} = \Upgamma_{i}^{c} X_{f}^{c} + H_{i}^{c} \left( {R_{f} - Y_{f} } \right)$$
(28)
$$U_{p} = \Upgamma_{i}^{c} X_{p}^{c} + H_{i}^{c} \left( {R_{p} - Y_{p} } \right)$$
(29)

Rf and Rp are the Hankel data matrix for set points.

X c p and X c f are the state matrix for the controller, Γ c i is the extended observable matrix, and H c i is a three blocked Toeplitz matrix.

Formula (28) can be rewritten as:

$$\left[ {H_{i}^{c} \;\;\;I} \right]W_{f} = \Upgamma_{i}^{c} X_{f}^{c} + H_{i}^{c} R_{f}$$
(30)

Multiplying ΘT on the right of both sides of formula (28),

$$\widehat{{\mathcal{Q}}}_{{u_{f} \xi }} = \Upgamma_{f}^{c} \widehat{{\mathcal{Q}}}_{{x^{c} \xi }} - H_{f}^{c} \widehat{{\mathcal{Q}}}_{{(y_{f} \xi )}} + H_{f}^{c} \widehat{{\mathcal{Q}}}_{{r_{f} \xi }}$$
(31)

If the condition is satisfied, we can obtain

$$\mathop {\lim }\limits_{L \to \infty } \frac{1}{j}R_{f} \Uptheta^{T} = 0$$
(32)

Thus,

$$\widehat{{\mathcal{Q}}}_{{u_{f} \xi }} = \Upgamma_{f}^{c} \widehat{{\mathcal{Q}}}_{{x^{c} \xi }} - H_{f}^{c} \widehat{{\mathcal{Q}}}_{{y_{f} \xi }} \;\;\;\;\;\;\;\;\;\;\;\;\;\;w.p.l\;\;as\;\;j \to 0$$
(33)

Compared with formula (21), it is obvious that both \(\widehat{{\mathcal{Q}}}_{{x^{c} \xi }}\) and \(\widehat{{\mathcal{Q}}}_{x\xi }\) are included in \(\left[ {\widehat{{\mathcal{Q}}}_{{u_{f} \xi }} \;\;\;\widehat{{\mathcal{Q}}}_{{y_{f} \xi }} } \right]^{T}\) in terms of the row space. The models obtained from identification may be the process model, controller model or mutual interference model. Therefore, to ensure independence between the identified models and controllers, only the dynamics of the process need to be described, i.e., to make the auxiliary variables satisfy both conditions simultaneously:

$$\mathop {\lim }\limits_{L \to \infty } \frac{1}{j}\left[ {W_{f} \;\;\;V_{f} \;\;\;\;{\text{O}}_{f} } \right]^{T} = 0$$
(34)
$$\mathop {\lim }\limits_{L \to \infty } \frac{1}{j}R_{f} \Uptheta^{T} \ne 0$$
(35)

Specifically, the selected auxiliary variables should be irrelevant to the various system noise and should be relevant to pumping signals of the set point at the same time.

4.2 Selection of the auxiliary variables based on orthogonal projection

Since the selection of auxiliary variables has a great impact on the results of recognition, we should treat this issue with caution. Combined with the results of the preceding analysis, it is natural that more information about Rf should be contained in the auxiliary variables.

$${\text{suppose}}\;\tilde{\Uptheta} = \left[ \begin{aligned} R_{f} \hfill \\ R_{p} \hfill \\ Z_{p} \hfill \\ \end{aligned} \right]$$
(36)

Thus, the auxiliary variable matrix can be determined according to the following method:

$$\Theta \left\{ \begin{array}{ll}{\tilde{\Theta }} & {CSOPIM} \\ {(\tilde{\Theta }\tilde{\Theta }^{T} )^{{1/2}} \tilde{\Theta }} & {CSIV} \\ {\Pi _{{\tilde{\Theta }}} } & {CSIV_{{ort}}} \end{array} \right.$$
(37)

To facilitate the description, the auxiliary variables are divided into three categories:

The direct form, e.g., CSOPIM and SOPIM

  1. (1)

    The standard form, e.g., CSIV and SIV

  2. (2)

    The Orthogonal projection form, e.g., CSIVort and SIVort

Given data \(u(k),r(k),y(k),k = 1 \ldots N,\) parameters in the time domain are f,p.

The improved subspace methods are as follows:

  • Step 1 Establish the block Hankel matrix \(U_{p} ,U_{f} ,Y_{p} ,Y_{f} ,R_{f} ,R_{p};\)

  • Step 2 Select the auxiliary variable matrix Θ according to \(\Uppi_{{Z_{p} }}\) or methods in formula (37);

  • Step 3 Perform an RQ decomposition as in formula (25);

  • Step 4 Perform a singular value decomposition in SVD on R22, so \(\Upgamma_{f} = U_{1} ;\)

  • Step 5 Compute system matrices A,B,C,D.

Remark 1 Different algorithms are required because of different auxiliary variables; apart from the previous forms of auxiliary variables, we have many other forms.

Remark 2 We should consider the model of noise, for example, the output forecast; the new system can be introduced in the following form:

$$x(k + 1) = Ax(k) + Bu(k) + Ke(k)$$
(38)
$$y(k) = Cx(k) + Du(k) + e(k)$$
(39)

Here, the variances of the Kalman gain K and new sequence e(k) need to be estimated. After obtaining the estimations for \(\Upgamma_{f} ,H_{f} ,\)K and Re can be obtained by using the method described in the literature [14].

5 Simulation study

In this section, the benchmark will be utilized to evaluate the raised method and compare it with a type of existing SIM. We will use the representative subspace algorithms described in the following literature: subspace identification algorithms in the EIV model proposed in the literature [1, 8, 10, 11, 14, 15], e.g., CSOPIM, CSIV, CSIMPCA and CSIVort. To follow the practice in the literature for subspace identification [10, 15], Monte Carlo simulations are performed and plotted with averaged Bode values. The estimated error variance can be presented by a scatter plot of estimated poles.

Consider the system described in literature [8], which is also a comparison of a benchmark problem used for a closed-loop subspace identification algorithm in literature [15]. In Fig. 1, the block diagram of the original system is displayed. This new model is presented in the form of an information state space represented by formulas (1)–(2), with values as follows:

$$A = \left( \begin{array}{*{20}c} {4.40} & 1 & 0 & 0 & 0 \\ { - \,8.09} & 0 & 1 & 0 & 0 \\ {7.83} & 0 & 0 & 1 & 0 \\ { - \,4.00} & 0 & 0 & 0 & 1 \\ {0.86} & 0 & 0 & 0 & 0 \\ \end{array} \right),\quad B = \left( \begin{array}{*{20}c} {0.00098} \\ {0.01299} \\ {0.01859} \\ {0.0033} \\ { - \,0.00002} \\ \end{array} \right)$$
$$C^{T} = \left( \begin{array}{l} 1 \\ 0 \\ 0 \\ 0 \\ 0 \end{array} \right), \quad K = \left( \begin{array}{l} 2.3 \\ -\,6.64\\ 7.515\\ - 4.0146 \\ 0.86336 \end{array} \right)$$

The state space models of feedback control are as follows:

$$A_{c} = \left( {\begin{array}{*{20}c} {2.65} & { - \,3.11} & {1.75} & { - \,0.39} \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{array} } \right)$$
$$B_{c} = \left( \begin{array}{l} 1 \\ 0 \\ 0 \\ 0 \\ \end{array} \right), \quad C_{c}^{T} = \left( \begin{array}{l} { - \,0.4135} \\ {0.8629} \\ { - \,0.7625} \\ {0.2521} \\ \end{array} \right)$$
$$D_{c} = 0.61$$

The conditions of simulation are exactly the same as those previously published (15); et is a Gaussian white noise sequence with a variance of \(\frac{1}{9}.\) The input reference r(k) denotes Gaussian white noise with a variance of 1. The simulation carried out at each time generates 1500 data points, and Monte Carlo simulation is performed 100 times by using the same input reference r(k) but a different noise sequence e(k).

In this simulation, we will reproduce the results previously described in literature [10,11,12, 14, 15] and compare them with the proposed CSIVort algorithms; the simulation results are depicted in Figs. 2 and 5. In terms of bias and variance, we find that the proposed CSIVort algorithm achieves better performance than the CSIMPCA algorithm. However, the proposed algorithm only needs to perform SVD once during the identification process, greatly reducing the amount of calculation for the dimension of the matrix derived under the condition of an unknown system. To determine the advantages of the proposed algorithm, we should consider the EIV cases of measured input ut and output yt with white noise. We ran the Monte Carlo simulation twice for EIV using a measured noise variance of 0.2 and 0.5. According to Figs. 3 and 5, if there is measured noise, it can be concluded that the proposed algorithm performed better than the CSOPIM algorithm and that there is a certain bias in CSOPIM.

Fig. 2
figure 2

Comparison between simulation results of CSIMPCA and real object

Full size image
Fig. 3
figure 3

Comparison between simulation results of CSIV and real object

Full size image

The proposed algorithm can be applied to open-loop identification because it is a closed-loop identification algorithm. There is a problem in its application method for open-loop identification. Therefore, we ran the Monte Carlo simulation using an open-loop device without feedback control. The results and other auxiliary variable subspace identification algorithm results are shown in Figs. 4 and 5; it can be seen that the CSIVort algorithm achieved consistent estimation.

Fig. 4
figure 4

Comparison between simulation results of CSOPIM and real object

Full size image
Fig. 5
figure 5

Comparison between identical results of CSIVort and real object

Full size image

Finally, we verify that when the external pumping signals are white noise, the identification algorithm CSIV with auxiliary variables based on orthogonal subspace projection enables consistent estimates in closed-loop identification, but the deviation will be reduced if the external stimulus is auto-correlative and the bias will be eliminated effectively by the CSIMPCA algorithm, as shown in Fig. 2. Simulation results of closed-loop CSIVort are shown in Fig. 5. In Fig. 5, there is an external excitation of white noise with unit variance; the right column corresponds to the relevant external excitation r, where r is white noise with a filter; the filter is a one rank system, with the pole of 0.9, and the variance of the excitation signal is 1. The results showed that (1) external incentives of auto-relevance can indeed reduce the deviation of CSIMPCA and (2) CSIVort performed significantly better than CSIMPCA.

6 Conclusion

In this paper, we develop an algorithm for subspace orthogonal projection identification based on the EIV model structure. However, when the external excitation signal is white, it will produce a bias for closed-loop identification. With the analysis of deviation in CSOPIM, CSIMPCA, and CSIV, we find that the same deviation is also included in other existing auxiliary variable SIMs in a closed loop, so these methods can only provide a partial solution for closed-loop identification. Based on this, we proposed an algorithm of closed-loop subspace with auxiliary variable identification (CSIVort) based on orthogonal decomposition; in addition, the calculation has been reduced effectively. Simulation of the benchmark allowed comparison of the proposed algorithm with several typical subspace auxiliary variable algorithms and verified its feasibility and closed-loop adaptability.