1 Introduction

Under shear, granular materials exhibit fascinating properties such as sustaining stress as a solid or flowing as a fluid [1,2,3]. Granular flow has motivated many studies over the past decades, since the rheological properties of dense granular materials play an important role in various natural phenomena and industrial applications such as geographical faults, powder metallurgy, three-body friction, and particle flow lubrication [4,5,6,7,8,9,10]. Generally, three different granular flow regimes are categorized according to the flow rate, including the quasi-static regime, inertial regime, and collisional regime [11,12,13,14]. In the inertial regime, when a dense granular system is subjected to continuous shear, a local flow near the boundary is first generated after the initial static equilibrium is broken, and gradually a global flow is achieved and ultimately maintained at steady state [15, 16]. Moreover, the evolution of the flow state is accompanied by dilatancy, which represents the volume expansion of the granular system [17,18,19,20]. Two representative quantities, i.e., the macroscopic friction coefficient \(\mu\) and the solid fraction \(\phi\), are most commonly employed to characterize the rheological properties of dense granular flow [21,22,23,24,25]. Depending on the calculation method, the macroscopic friction coefficient \(\mu\) can be referred to three different meanings, namely, the interfacial friction coefficient \({\mu }^{^{\prime}}\), the effective friction coefficient \({\mu }_\text{e}\), and the internal shear strength \({\mu }^{*}\). The interfacial friction coefficient \({\mu }^{^{\prime}}\) can be understood as the driving strength provided by the boundary for maintaining the particle flow, which is defined as the ratio of the shear stress to the normal stress on the shear boundary [23,24,25,26,27,28]. The effective friction coefficient \({\mu }_\text{e}\) and the internal shear strength \({\mu }^{*}\) represent the shear resistance to the flow of the system. When the granular system is assumed to be a continuous medium for stress analysis [29], the effective friction coefficient \({\mu }_\text{e}\) is expressed as the ratio of the deviatoric stress to the average stress in the system [30, 31]. The internal shear strength \({\mu }^{*}\) is derived from the anisotropies of the microstructure formed by contacts [21, 32]. In the steady state, the boundary driving strength and the system’s shear resistance are in equilibrium, and these three coefficients \({\mu }^{^{\prime}}\), \({\mu }_\text{e}\) and \({\mu }^{*}\) are approximately equal and can be unified as the macroscopic friction coefficient \(\mu\).

The interfacial friction characteristics could be influenced by several geometric factors, including the boundary surface structure, the thickness of particle layers, and the shape and constrained extent of particles [33,34,35,36,37,38]. Most experimental studies on the interfacial friction characteristics address local shear deformation, where stick–slip or particle flow occurs only near the boundary due to either the small shear velocity or the short shear strain. However, when the boundary cumulative shear strain is large enough in the inertial regime, the system reaches a steady flow state eventually. In this case, the interfacial friction coefficient \({\mu }^{^{\prime}}\) tends to be a constant value independent on the initial filling state of the dense granular system. Moreover, the interfacial friction coefficient \({\mu }^{^{\prime}}\) has a significant dependence on the flow rate, which is determined by the shear velocity and the applied normal stress [39,40,41]. For rigid dry granular materials, the flow rate can be measured by the dimensionless inertial number I, which represents the ratio of the inertial force to the confining pressure [14, 42, 43]. Numerous experimental and simulation results have confirmed that in the inertial regime, the interfacial friction coefficient \({\mu }^{^{\prime}}\) monotonically increases as a function of the inertial number I [23,24,25, 43,44,45]. It is a familiar feature of granular rheology that the interfacial friction coefficient \({\mu }^{^{\prime}}\) is closely related to the system’s flow rate during the shear process.

On the other hand, the interparticle contact and contact forces exhibit anisotropy, which are the microscopic origins of the system’s shear resistance [12, 21, 46,47,48]. At the microscopic scale, particles transfer forces through interparticle contacts. The variation in the flow state changes the contact status and the force transmission paths between particles, thereby altering the topology and mechanical properties of the microscopic contact force network [47,48,49,50]. As a result, the internal shear strength significantly changes during inertial flow due to the temporal and spatial variations in the microstructure of the contact force network between particles. Much work has been carried out on analyzing the internal shear strength under static filling or steady inertial flow situations. For the stationary granular system, the internal shear strength is independent of the size polydispersity of the filled particles [51,52,53]. In addition, the influences of the different particle shapes on the internal shear strength were also investigated [12, 33, 34, 38, 54,55,56,57,58]. For the steady inertial flow state, Azéma et al. [12] compared the rheological properties of a frictionless granular system between pentagonal particles and circular discs. Binaree et al. [34] further explored the integrated effects of interparticle friction and particle shape on the internal shear strength. In addition, the rheological properties and microstructure characteristics of some cohesive granular systems were investigated [59,60,61], where the effect of viscosity on the internal shear strength was discussed.

By virtue of the abovementioned studies, the steady rheological properties of dense granular materials have been well studied under equilibrium conditions. Under some circumstances, it is necessary to study the transient behaviors, for example, whether a steady flow can be obtained for a particular granular system, and how long it takes for a static system to achieve the steady flow state. To answer these questions, we should understand how the equilibrium is gradually established, and figure out which factors could affect the evolution process. To this end, it is essential to perform a dedicated investigation into the transient evolution of the rheological properties. Here we choose one of the most commonly studied granular flow models—the plane shear model, as our research target. The composing structure and motion manner of this model are simple. Additionally, under the steady flow state, the flow velocity linearly increases along the height, which can be used as a direct criterion for judging whether the system reaches steady state [62]. The particle flow of this model is still a hot topic very recently [39, 59, 63]. Discrete element method (DEM) serves as a powerful tool for studying the mechanical properties of granular materials because it can extract the microscopic information of individual particles and also analyze the macroscopic behaviors of the whole granular system [64, 65]. Therefore, this paper employs DEM simulations to analyze the evolution flow process of a plane shear system by carefully characterizing the evolution principles of the flow state, the mechanical behaviors, and the microstructure characteristics at different moments. Moreover, we clarify the influences of the flow state on the interfacial friction coefficient, the effective friction coefficient and the internal shear strength and finally reveal the equilibrium mechanism between the boundary driving strength and the system’s shear resistance. In addition, the influences of the shear velocity are explored.

2 DEM Model and Basic Theories

2.1 DEM Model of Plane Shear

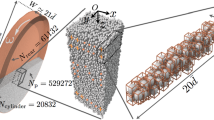
In the two-dimensional DEM model, the granular material is described as a collection of discrete discs. The contact force dependent on the force–displacement relationship between particles is defined by the soft contact method. The motion information of each particle is derived from its own unbalanced force using Newton’s second law. As shown in Fig. 1a, the dense granular system consists of \({N}_\text{p}=2\times {10}^{4}\) cohesionless rigid disc particles with an average diameter of \(d=1 \, \text{mm}\). The solid fraction \(\phi\) of the system is 0.84. Initially, the system’s width along x-axis is \(L=200d\), and the height along y-axis is \(H=96d\). Compared with similar studies, the number of particles included in this simulation model is large enough to ensure the statistical confidence of the analysis results. The particle size distribution polydispersity is set as 20% to avoid crystallization. The top and bottom plates are rough boundaries formed by the bonding monodisperse particles with diameter \(d\), while the sidewalls are periodic boundaries. During shear, the bottom plate is fixed, and the top plate slides tangentially at a constant velocity Vs and applies a constant normal stress \(P\) to the granular system.

Fig. 1
figure 1

a Two-dimensional DEM model of a dense granular system under plane shear, b linear contact model between particles

Full size image

For cohesionless rigid particles, a linear contact model (spring-dashpot model) is used to define the contact forces between particles, as shown in Fig. 1b. The linear model consists of two parts, namely, a stiffness model and a slip model. The stiffness model provides a linear elastic relationship between the contact force and the relative displacement. The normal contact force \({f}_\text{c}^{n}\) is composed of the normal linear force \({f}_\text{cl}^{n}\) and the normal damping force \({f}_\text{cd}^{n}\), written as \({f}_\text{c}^{n}\) = \({f}_\text{cl}^{n}+{f}_\text{cd}^{n}\)  = \({k}_{\text{n}}{g}_{\text{s}}+{d}_{\text{n}}\dot{{g}_{\text{s}}}\), where \({k}_{\text{n}}\) is the normal contact stiffness, \({d}_{\text{n}}\) is the normal damping coefficient, \({g}_{\text{s}}\) is the surface gap between particles, and \(\dot{{g}_{\text{s}}}\) is the relative normal translation velocity. For dry granular materials, the normal contact force between particles is always compressive, so the equation \({f}_\text{cl}^{n}+{f}_\text{cd}^{n}\le 0\) is satisfied. The tangential contact force \({f}_\text{c}^{t}\) is incrementally updated using \({f}_\text{c}^{t}={f}_\text{c}^{ot}+\Delta {f}_\text{c}^{t}\), \(\Delta {f}_\text{c}^{t}={k}_\text{t}\Delta {\delta }_\text{s}+{d}_\text{t}\Delta {\dot{\delta }}_\text{s}\), where \({f}_\text{c}^{ot}\) is the tangential contact force before updating, \({k}_\text{t}\) is the tangential stiffness, \(\Delta {\delta }_{\text{s}}\) is the relative tangential displacement increment, \({d}_{\text{t}}\) is the tangential damping coefficient, and \(\Delta {\dot{\delta }}_{\text{s}}\) is the relative tangential translation velocity. The relative motion between particles follows the Coulomb relationship \(\left|{f}_\text{c}^{t}\right|\le {\mu }_\text{c}{f}_\text{c}^{n}\), where \({\mu }_{\text{c}}\) is the sliding friction coefficient between particles, dictating that relative sliding between particles is allowed only when the equal sign is satisfied.

2.2 Parameters Setup of DEM Model

A series of dimensionless parameters related to the particle material properties and the shear conditions are set according to references [38, 43], which mainly include the contact stiffness coefficient \(k\), the stiffness ratio \(s\), and the restitution coefficient \(e\). The dimensionless contact stiffness coefficient \(k={k}_\text{n}/P\) measures the rigidity of particles and limits the maximum deformation of particles under external load, where \(P\) is the applied normal stress, and \({k}_\text{n}\) is the normal contact stiffness. In detail, a large value of k represents rigid particles, and a small value represents soft particles. Relevant studies have shown that once \(k\) exceeds \({10}^{4}\), it will no longer influence the results because rigid particles are ensured [23, 66]. Therefore, \(k\) is set to \({10}^{4}\) herein. The stiffness ratio \(s={k}_\text{t}/{k}_\text{n}\) takes an empirical value of 0.5. The normal and tangential damping coefficients \({d}_\text{n}\) and \({d}_\text{t}\) are related only to the restitution coefficient \(e\) once the stiffness coefficient \({k}_\text{n}\) and the stiffness ratio \(s\) are determined, that is, \({d}_\text{n}=2{\beta }_\text{n}\sqrt{m{k}_\text{n}}\) and \({d}_\text{t}=2{\beta }_\text{s}\sqrt{ms{k}_\text{n}}\), where \({\beta }_\text{s}\) and \({\beta }_\text{n}\) are normal and shear critical-damping ratios, respectively, and \(\beta _{{\text{s}}} \, = \,\beta _{{\text{n}}} \, = \,{{ - \,{\text{ln}}\left( e \right)} \mathord{\left/ {\vphantom {{ - \,{\text{ln}}\left( e \right)} {\left[ {\pi ^{2} + \left( {{\text{ln}}\left( e \right)} \right)^{2} } \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {\pi ^{2} + \left( {{\text{ln}}\left( e \right)} \right)^{2} } \right]}}\). The restitution coefficient \(e\) determines the threshold value for granular system transformation from dense flow to dilution collision [14]. To broaden the range of inertial flow, e is set as a fixed value of 0.1. The particle–particle and particle–wall friction coefficients are both set to 0.4 and notated as \({\mu }_\text{c}\). A combined set of e = 0.1 and \({\mu }_\text{c}=0.4\) is frequently used in simulations because it results in a strong dissipative granular system that well matches the real situation. Table 1 lists the detailed parameters of the granular system.

Table 1 The detailed parameters of the granular system
Full size table

The inertial number, defined as \(I=\dot{\gamma }d/\sqrt{P/\rho }\), is one of the most important quantities to express constitutive laws [25], where \(\dot{\gamma }\) is the shear rate,\(d\) is the mean particle diameter, \(P\) is the normal stress, and \(\rho\) is the particle density. For a frictional granular material, a small value of I (\(\le\) 10–2) corresponds to the quasi-static regime, while a large value of I (\(\ge\) 10–1) for the collisional regime [22, 24]. In this study, as P is a fixed value of 50 Pa, the shear velocity of the top plate is selected within the range of 0.5–2.5 m/s, fully ensuring an inertial flow with I in the range of 0.033 to 0.133. The DEM simulation adopts an explicit numerical scheme in the calculation process, where Newton’s second law needs to be repeatedly called to update the particle’s position and interparticle contact information. During the simulation process, the instantaneous micromechanical information is obtained by an interval of every 1000 steps, including the particle’s position and velocity, contact position and contact forces, to monitor the evolution of the flow state and multiscale mechanical behaviors.

2.3 Definitions of Mechanical Behavior Quantities

2.3.1 Microscopic Quantities

For a two-dimensional granular system, the solid fraction is defined as \(\phi={A}_\text{p}/A\), where \({A}_\text{p}\) is the area occupied by the particles and \(A\) is the total area of the system. The coordination number \(Z\) is the average number of contacts and is calculated using \(\mathrm{Z}={N}_\text{c}/{N}_\text{p}\), where \({N}_\text{c}\) is the total number of contacts, and \({N}_\text{p}\) is the total number of particles in the system. The existing contacts can be grouped into strong contact and weak contact using the following rule: if the force magnitude \({f}_\text{c}\) of a specific contact is greater than the average magnitude of all the contact forces \(\langle {f}_\text{c}\rangle\), namely, \({f}_\text{c}\ge \langle {f}_\text{c}\rangle\), this contact is defined as a strong one; otherwise, if \({f}_\text{c}<\langle {f}_\text{c}\rangle\), it is regarded as a weak one. The number ratio of strong contacts is defined as \({R}_\text{c}^{s}={N}_\text{c}^{s}/{N}_\text{c}\), where \({N}_\text{c}^{s}\) is the number of strong contacts and \({N}_\text{c}\) is the total number of contacts. Additionally, the bearing ratio of strong contacts is calculated using the sum of the strong contact forces divided by the sum of all the contact forces, given as \(B_{{\text{f}}}^{s} \, = \,{{\sum\limits_{{c \in s}} {f_{{\text{c}}} } } \mathord{\left/ {\vphantom {{\sum\limits_{{c \in s}} {f_{{\text{c}}} } } {\sum {f_{{\text{c}}} } }}} \right. \kern-\nulldelimiterspace} {\sum {f_{{\text{c}}} } }}\), where \(c\in s\) represents the collection of the strong contacts. Likewise, for the remaining weak contacts, the following equations satisfy \({R}_\text{c}^{w}=1.0-{R}_\text{c}^{s}\) and \({B}_\text{f}^{w}=1.0-{B}_\text{f}^{s}\).

2.3.2 Macroscopic Quantities

The strain rate tensor is expressed as the symmetric part of the velocity gradient tensor [67,68,69]:

$${\dot{\varepsilon }}_{\alpha \beta }=\frac{1}{2}\left(\frac{\partial {V}_{\alpha }}{\partial \beta }+\frac{\partial {V}_{\beta }}{\partial \alpha }\right),$$
(1)

where \({V}_{\alpha }\) and \({V}_{\beta }\) are the velocity fields. In our model, since we assume that the flow characteristics of particles in the sliding direction x are homogeneous, \(\partial {V}_\text{x}/\partial x\) and \(\partial {V}_\text{y}/\partial x\) are always 0. Moreover, as the value of \({V}_\text{y}\) is very slight, \(\partial {V}_\text{x}/\partial y\) composes the main variation in the strain rate tensor.

To measure the transient evolution of the global flow in the granular system, a dimensionless equivalent shear strain rate \({\dot{\upvarepsilon }}_\text{xx}^{\mathrm{e}}\) is calculated by averaging the horizontal velocity of particles in the system with area A, given as follows:

$${\dot{\varepsilon }}_\text{xx}^{e}\left(t\right)=\frac{\frac{2}{{N}_\text{p}}\sum_{i\in A}{V}_\text{x}^{i}\left(t\right)}{{V}_\text{s}},$$
(2)

where \({N}_\text{p}\) is the total number of particles, \({V}_\text{s}\) is the constant sliding velocity of the top plate, and \({V}_\text{x}^{i}\) is the horizontal velocity of particle i. In the evolution process, \({\dot{\upvarepsilon }}_\text{xx}^{\mathrm{e}}\)<1.0, and when the system reaches steady state, \({\dot{\upvarepsilon }}_\text{xx}^{\mathrm{e}}\approx 1.0\).

The stress tensor \({\sigma }_{\alpha \beta }\) is the sum of static contact stress and kinetic contact stress [68, 70, 71], given as follows:

$${\sigma }_{\alpha \beta }=\frac{1}{A}\left(\sum_{c\in A}{r}_\text{c}^{\alpha }{f}_\text{c}^{\beta }+\sum_{i\in A}{m}^{i}{\delta V}_{\alpha }^{i}{\delta V}_{\beta }^{i}\right),$$
(3)

where \(A\) is the area of the model, \({r}_\text{c}\) is the contact branch vector, \({f}_\text{c}\) is the contact force, \({m}^{i}\) is the mass of particle \(i\), and \({\delta V}^{i}\) is the velocity fluctuation of particle \(i\) relative to the average velocity of the corresponding layer.

2.3.3 Calculation Methods of Friction Coefficients

For the plane shear system, the interfacial friction coefficient \({\mu }^{^{\prime}}\) is the ratio of the total tangential stress \({\sigma }_\text{t}\) to the total normal stress \({\sigma }_\text{n}\) at all contact points between the top plate and the top layer particles,

$${\mu }^{^{\prime}}=\frac{{\sigma }_\text{t}}{{\sigma }_\text{n}}=\frac{\sum_{c\in B}{\sigma }_\text{c}^{t}}{\sum_{c\in B}{\sigma }_\text{c}^{n}},$$
(4)

where \({\sigma }_\text{c}^{t}\) and \({\sigma }_\text{c}^{n}\) are the tangential stress and the normal stress on a single contact point, respectively, and \(c\in B\) represents the collection of contacts between particles and the top plate. The effective friction coefficient \({\mu }_\text{e}\) is defined as the ratio of internal shear stress to normal stress, and \({\mu }_\text{e}={\sigma }_\text{xy}/{\sigma }_\text{yy}\), where \({\sigma }_\text{xy}\) and \({\sigma }_\text{xy}\) are stress tensor components defined in Eq. (3).

2.4 Stress–Force–Fabric Relationship

The stress–force–fabric relationship provides an effective approach for establishing the quantitative relationship between the macroscopic stress tensor and the microstructure anisotropy parameters [72]. Based on this relationship, we conduct a statistical analysis on the distribution functions of contact orientation, normal contact force, and tangential contact force in polar coordinates, denoted as P(θ), \({f}_\text{n}(\theta )\), and \({f}_\text{t}(\theta )\), respectively, where \(\theta\) is the angle of unit vector \({\varvec{n}}\) along the contact direction. These distribution functions provide abundant micromechanical information for accurately evaluating the anisotropy extent of granular systems. Commonly, low-order Fourier approximations are employed to describe them:

$$P\left( \theta \right) \cong \frac{1}{{2\pi }}\left\{ {1\, + \,a_{{\text{c}}} {\text{cos}}2\left( {\theta \, - \,\theta _{{\text{c}}} } \right)} \right\}$$
(5a)
$${f}_\text{n}\left(\theta \right)\cong \overline{{f }_\text{n}}\left\{1+{a}_\text{n}\mathrm{cos}2\left(\theta -{\theta }_\text{n}\right)\right\}$$
(5b)
$${f}_\text{t}\left(\theta \right)\cong -\overline{{f }_\text{n}}{a}_\text{t}\mathrm{sin}2\left(\theta -{\theta }_\text{t}\right),$$
(5c)

where \(\overline{{f }_\text{n}}\) is the magnitude of average normal contact force over the system, \({a}_\text{c}\) represents the anisotropy in contact orientations, \({a}_\text{n}\) and \({a}_\text{t}\) describe the directional variation of contact forces, \({\theta }_\text{c}\) is the direction of anisotropy in contact orientation, and \({\theta }_\text{n}\) and \({\theta }_\text{t}\) are the preferred directions of contact forces. When the three main principal directions are assumed to be collinear and codirectional, the internal shear strength \({\mu }^{*}\) can be approximately given as follows:

$${\mu }^{*}\cong \frac{1}{2}\left({a}_\text{c}+{a}_\text{n}+{a}_\text{t}\right)$$
(6)

This equation shows the microscopic components of the internal shear strength of the granular system under plane shear.

3 Transient Evolution of the Flow State

In this part, we employ the simulation results of \(P\,=\,50 \, \text{ Pa}\) and \({V}_\text{s}\) = 0.5 m/s as a demo to quantitatively analyze the evolution of flow state. The simulation time is 40 s, which is long enough for the system to reach steady state. The flow state is characterized by the flow features of both horizontal and vertical directions. In detail, the horizontal velocity determining the shear rate is the main movement characteristic of the particles, and the vertical velocity indicates the dilatancy phenomenon.

3.1 Horizontal Flow Characteristics

Figure 2a shows the time history plot of the equivalent shear strain rate \({\dot{\upvarepsilon }}_\text{xx}^{\mathrm{e}}\). Throughout the evolution process, \({\dot{\upvarepsilon }}_\text{xx}^{\mathrm{e}}\) first rapidly increases and then gradually approaches a constant value of 1.0. Figure 2b shows the horizontal velocity distribution contours at six representative moments (\({P}_{1}\)–\({P}_{6}\)) selected in Fig. 2a. Overall, under continuous shear, the local flow near the top plate is transferred downward layer-by-layer and then gradually expands into the whole system; ultimately, a global steady flow is formed. The horizontal velocity decreases from the top layer to the bottom layer, which is the result of energy dissipation caused by interparticle friction and inelastic collisions. In Fig. 2c, the average horizontal velocity of particles in the same layer is plotted in solid line as a function of the vertical height. Additionally, Fig. 2e shows the time history plots of the average horizontal velocity within some representative layers of particles. During the evolution process, we divide the whole granular model into flowing and nonflowing regions, written as \(H(t)={H}_\text{F}(t)+{H}_\text{S}(t)\), where \({H}_\text{F}(t)\) and \({H}_\text{S}(t)\) are the heights of the flowing and non-flowing regions, respectively. Herein, a specific layer is considered flowing only when the average horizontal velocity of particles in this layer is higher than a threshold value, which is set as 1% of the top plate’s sliding velocity. We further normalize the height of the flowing region using \({DH}_\text{F}={H}_\text{F}\left(t\right)/H\left(t\right)\) and present its evolution as a function of \({\dot{\upvarepsilon }}_\text{xx}^{\mathrm{e}}\) in Fig. 2d.

Fig. 2
figure 2

Evolution process of the system’s horizontal flow state under \(P=50 \, \text{Pa}\) and \({V}_\text{s}=0.5 \, \text{m}/\text{s}\), a time history plot of the equivalent shear strain rate \({\dot{\upvarepsilon }}_\text{xx}^{\mathrm{e}}\), b the horizontal velocity distribution contours at six representative moments, c the average horizontal velocity of particles in the same layer (in solid line), d time history plots of the normalized flowing region \({DH}_\text{F}\), e time history plots of the average horizontal velocity at representative layers, the distribution profiles of the normal pressure (f), the scaled gradient of horizontal velocity (g), and the local inertial number (h) along the height

Full size image

The evolution results regarding the horizontal flow characteristics in Fig. 2a–e directly reflect the change in flow states. During the time interval from \({P}_{1}\) (0.5 s) to \({P}_{3}\) (6.5 s), the flowing region expands from the local region near the top plate to the global system, and the horizontal velocity of the already flowing region gradually increases. Correspondingly, \({\dot{\upvarepsilon }}_\text{xx}^{\mathrm{e}}\) increases from 0 to approximately 0.6, and \({DH}_\text{F}\) quickly increases from 0 to 1.0. It is worth mentioning that the system at \({P}_{3}\) (6.5 s) has achieved a global flow since \({DH}_\text{F}=1\) in Fig. 2d. During the time interval from \({P}_{3}\) (6.5 s) to \({P}_{6}\) (27 s), the granular system maintains a global flow state, meanwhile the horizontal velocities gradually increase to constant values for all the selected layers. Moreover, by comparing the evolution characteristics, it is found that the closer to the top plate, the shorter time is required for the particle layer to reach a steady state. In other words, the growth rate of the horizontal velocity decreases from top to bottom, which is caused by the layer-by-layer attenuation of shear momentum. At \({P}_{6}\) (27 s), the system has reached a steady flow state, under which \({\dot{\upvarepsilon }}_\text{xx}^{\mathrm{e}}\) approximately reaches 1.0 (Fig. 2a) and the horizontal velocity profile is almost linearly distributed in the vertical direction (Fig. 2c).

Therefore, according to the evolution characteristics of the horizontal flow, the flow status experiences three stages, namely, transmission (T), adjustment (A), and stabilization (S). As outlined in Fig. 2a and d, in the transmission (T) stage, the flowing region expands from top to bottom. When the flowing region arrives at the bottom surface, i.e., \({DH}_\text{F}=1.0\), the transmission stage ends. In the subsequent adjustment (A) stage, the profile of \({V}_\text{x}\) continues evolving and finally approaches the steady (S) state under which the equivalent shear strain rate \({\dot{\upvarepsilon }}_\text{xx}^{\mathrm{e}}\) reaches 1.0.

In addition, we employ the distribution profile of the local inertial number along the height direction to characterize the flow state. Considering the variation in the shear rate with height, the local inertial number I(y) is calculated as follows:

$$I(y)=\dot{\gamma }\frac{d}{\sqrt{P/\rho }}=\frac{\partial {V}_\text{x}}{\partial y}\frac{d}{\sqrt{P(y)/\rho }}$$
(7)

In Fig. 2f, when gravity is absent, the normal pressures along the height \(P(y)\) fluctuate around 50 Pa, which is caused by the applied normal stress on the top plate. As a result, the profile shapes of the velocity gradient (Fig. 2g) are similar to those of the local inertial number (Fig. 2h). Interestingly, during evolution, I(y) quickly decreases in the top region but gradually increases near the bottom region, clearly indicating the transfer of momentum from top to bottom. Finally, in the steady flow state, the profile of I(y) exhibits a valley shape along the height due to the boundary effect. Except for the top and bottom boundary regions, the values of I(y) fluctuate around the expected value of 0.033 at 0.5 m/s.

3.2 Vertical Velocity and Shear Dilatancy

Dilatancy is the volume expansion observed in granular materials when they are subjected to shear deformation. Figure 3 illustrates the shear dilatancy mechanism of dense granular flow. Initially, the particles are related to each other through contacts and form a dense packing with the maximum solid fraction, as shown in Fig. 3a. When the solid fraction \(\phi\) is larger than a critical value, namely the jamming point, a preliminary dilation is necessary for shear deformation to occur. In other words, for rigid particles, if the system’s height undergoing shear remained fixed, the granular system would be blocked. To avoid blockage, the volume has to be expanded. As shown in Fig. 3b, when sheared by the top plate, particles in the flowing region cross the peaks and valleys formed by the neighboring particles, causing the microscopic arrangement of particles. Whether a particle is crossing a peak or valley is indicated by the sign of the particle’s vertical velocity. It is noteworthy that a particle could repeatedly cross peaks or fall into valleys during evolution, resulting in vertical velocity fluctuations. Moreover, as the horizontal velocity increases, the duration for a particle horizontally moving over a valley is shortened; hence, the vertical distance falling into the valley is reduced, leading to an increase in dilatancy.

Fig. 3
figure 3

Illustration of shear dilatancy in a dense granular system: a the initial dense packing state, and b the movement of particles under shear

Full size image

Figure 4 shows the vertical velocity distribution contours of all the particles at six different moments in the evolution process. Additionally, the average vertical velocity of particles in the same layer along the height direction is plotted on the right side for each moment to quantify the local dilatancy rate. First, from 0.0001 to 4.6 s, it is observed that the upward and downward moving particles randomly coexist within the system, and the vertical movement gradually propagates from top to bottom. At \(t=0.0001\mathrm{ s}\), the average vertical velocity is positive over the entire height, suggesting that the granular system dilates globally. In particular, the particles near the top plate expand rapidly under shear. Soon after that, the global dilatancy is locally replaced as shown at \(t=0.1\mathrm{ s}\). At \(t=1\mathrm{ s}\) and \(t=2.7\mathrm{ s}\), the dilating region mainly resides near the top plate (\(y/d>80\)), as the current dilatancy mainly comes from the local shear flow of particles. At \(t=4.6\mathrm{ s}\), the maximum velocity has been transferred from near the top plate (\(y/d>80\)) to the middle part (y/d = 50–80), which implies that the dilating region is moving down due to the propagation of local flow. Moreover, the sign of the average vertical velocity near the top plate changes from positive to negative. After the granular system enters a global flow state, the profile of vertical velocity along the height approaches zero, and the amount of shear dilatancy reaches the maximum and slightly fluctuates in the subsequent stages.

Fig. 4
figure 4

a The vertical velocity distribution contours at six different moments, and the arithmetic average vertical velocity of particles in the same layer along the height direction under P = 50 Pa and \({V}_\text{s}\) = 0.5 m/s, b time history plot of \({\varepsilon }_\text{yy}\), and c the evolution of \({\varepsilon }_\text{yy}\) as a function of \({\dot{\varepsilon }}_\text{xx}^{e}\)

Full size image

The dilatancy extent is measured by the normal strain in the vertical direction, \({\varepsilon }_\text{yy}=\left({H}_\text{t}-{H}_{0}\right)/{H}_{o}\), where \({H}_{0}\) is the initial height of the system and \({H}_\text{t}\) is the height of the system at time \(t\). Figure 4b and c show the evolution results of \({\varepsilon }_\text{yy}\) as a function of time \(t\) and of equivalent shear strain rate \({\dot{\varepsilon }}_\text{xx}^{e}\), respectively. In the evolution process, \({\varepsilon }_\text{yy}\) gradually increases to the maximum value of approximately 0.05 and then stabilizes. Moreover, the increase in \({\varepsilon }_\text{yy}\) mainly occurs in the transmission stage (\(0\mathrm{ s}\le t\le 6.5\mathrm{ s}, 0\le {\dot{\varepsilon }}_\text{xx}^{e}\le 0.62\)), indicating that shear dilatancy is a prerequisite for particle flow.

4 Evolution of Macroscopic Mechanical Properties

4.1 Interfacial Friction Coefficient

This part continues to use the simulation results under the condition of \(P=50\,\text{ Pa}\) and \({V}_\text{s}=0.5 \,\text{m}/\text{s}\) to analyze the transient evolution of the boundary driving strength. Figure 5 shows the evolution curves of the scaled normal stress \({\sigma }_\text{n}/P\) and the scaled tangential stress \({\sigma }_\text{t}/P\), all of which act upon the top plate. To maintain the applied external normal stress constant throughout the evolution process, the position of the top plate must be dynamically adjusted. In detail, once the scaled normal stress \({\sigma }_\text{n}/P\) on the top plate exceeds 1.0, the top plate moves slightly upward to reduce the normal stress, and vice versa. Therefore, as shown in Fig. 5a, \({\sigma }_\text{n}/P\) always fluctuates around 1.0. Additionally, the fluctuation extent is closely related to the flow state, in the way that the fluctuation is intensive in the transmission stage (T) but mild in the adjustment (A), as shown in Fig. 5a. As previously discussed, the particle flow state near the top plate changes dramatically at the beginning of the shear, and the horizontal and vertical velocities increase rapidly. Under this case, the particles collide violently with the top plate, resulting in large fluctuations in the normal and tangential stresses. Subsequently, the particle flow state changes smoothly, so the fluctuations gradually stabilize.

Fig. 5
figure 5

The evolution curves of the scaled normal stress \({\sigma }_\text{n}/P\) (a), the scaled tangential stress \({\sigma }_\text{t}/P\) (b), the interfacial friction coefficient \({\mu }^{{^{\prime}}}\) (c), and the solid fraction \(\phi\) (d) with the equivalent shear strain rate \({\dot{\varepsilon }}_\text{xx}^{e}\), where \(P=50\,\text{ Pa}\) and \({V}_\text{s}=0.5 \,\text{m}/\text{s}\)

Full size image

In Fig. 5c, the interfacial friction coefficient \({\mu }^{^{\prime}}\) is calculated based on the results of \({\sigma }_\text{n}\) and \({\sigma }_\text{t}\) in Fig. 5a and b. First, it is found that the interfacial friction coefficient \({\mu }^{^{\prime}}\) gradually decreases to a constant value during evolution. In Fig. 5d, as the shear dilatancy extent increases, the solid fraction \(\phi\) decreases; in other words, shear dilatancy makes the system loose. Moreover, \(\phi\) mainly decreases in the transmission stage (T) and remains at the minimum value afterward. In the transmission (T) stage, dilatancy loosens the system’s spatial geometric constraint, thus weakening the tangential load-bearing capacity and making the interfacial friction coefficient \({\mu }^{^{\prime}}\) drop rapidly, which can be understood as the strain softening of granular material. However, in the adjustment (A) and stabilization (S) stages, the flow velocities within the particle layers change very slightly, so the shear dilatancy rate is close to zero, and the interfacial friction coefficient \({\mu }^{^{\prime}}\) also tends to be a constant value.

4.2 Stress–Strain Behavior and Effective Friction Coefficient

Furthermore, as shown in Fig. 6, we analyze the evolution principles of the internal stress components and their ratios. Here, the stress components and their ratios show obvious fluctuations during evolution, which are mainly caused by the microscopic rearrangement of particles. In Fig. 6a, the scaled internal normal stress \({\sigma }_\text{yy}/P\) always fluctuates around 1.0. Moreover, due to the shear flow of the particle system, the internal shear stress \({\sigma }_\text{xy}\) rapidly increases to the maximum value in the beginning (\({\dot{\varepsilon }}_\text{xx}^{e}\le 0.1\)), and then decreases slightly and gradually tends to a constant value, as shown in Fig. 6b. In Fig. 6c, \({\sigma }_\text{xx}/{\sigma }_\text{yy}\) is always close to 1.0, since the plane shear model with a periodic boundary condition is similar to a confined box.

Fig. 6
figure 6

Evolution curves of the scaled internal normal stresses \({\sigma }_\text{xx}/{P}\) and \({\sigma }_\text{yy}/{P}\) (a), the scaled internal shear stress \({\sigma }_\text{xy}/P\) (b), the ratio \({\sigma }_\text{xx}/{\sigma }_\text{yy}\) (c), and the interfacial friction coefficient \({\mu }^{{^{\prime}}}\) and the internal effective friction coefficient \({\mu }_\text{e}={\sigma }_\text{xy}/{\sigma }_\text{yy}\) (d), where \(P=50 \, \text{Pa}\) and \({V}_\text{s}=0.5 \, \text{m}/\text{s}\)

Full size image

As mentioned earlier, the ratio of the internal shear stress to the internal normal stress is defined as the effective friction coefficient \({{\mu }_\text{e}=\sigma }_\text{xy}/{\sigma }_\text{yy}\). Similar to \({\sigma }_\text{xy}\), \({\mu }_\text{e}\) first rapidly increases to the peak and then gradually drops to a constant value. Comparing Figs. 5 and 6, the changes in \({\sigma }_\text{n}/P\) and \({\sigma }_\text{yy}/P\) are basically the same, both fluctuating around 1.0. However, before reaching a steady state, the internal shear stress \({\sigma }_\text{xy}\) is always significantly less than \({\sigma }_\text{t}\). As a result, in Fig. 6d, there is a significant difference in the evolution trend between the effective friction coefficient \({\mu }_\text{e}\) and the interfacial friction coefficient \({\mu }^{^{\prime}}\). Moreover, \({\mu }^{^{\prime}}\) is greater than \({\mu }_\text{e}\) until they become approximately equal in the steady flow state. Therefore, the evolution of the flow state from initially static to finally steady under continuous shear, is essentially realized by achieving the final dynamic balance between the boundary driving strength and the system’s shear resistance.

5 Evolution of Microstructure and Microscopic Mechanical Properties

5.1 Spatial Distribution of the Contact Force Network

The contact force network can indicate the spatial distribution of contact forces and the force transmission paths inside the granular system. Figure 7a clearly presents the contact force network graphs at five different moments under the conditions of \(P=50 \, \text{Pa}\) and \({V}_\text{s}=0.5 \, \text{m}/\text{s}\). Here, the existence of an interparticle contact is represented by a line segment connecting the center of the two contact particles, and the force magnitude \({f}_\text{c}\) is proportional to the line thickness. Initially, the contact force network is dense and uniform. In the evolution process, the contact force network becomes sparsely scattered, and the spatial distribution of strong contacts has a preferred direction.

Fig. 7
figure 7

a The contact force network graphs at initial and four representative moments under the conditions of \(P=50 \, \text{Pa}\) and \({V}_\text{s}=0.5 \, \text{m}/\text{s}\), and the transient evolution of the total contact number \({N}_\text{c}\) and the coordination number Z (b), the strong contact number \({N}_\text{c}^{s}\) and ratio \({R}_\text{c}^{s}\) (c), the weak contact number \({N}_\text{c}^{w}\) and ratio \(R_{\text{c}}^{w}\) (d), and the bearing ratios of strong contact \({B}_\text{f}^{s}\) and weak contact \({B}_\text{f}^{w}\) (e) as a function of \({\dot{\varepsilon }}_\text{xx}^{e}\)

Full size image

We further conduct a quantitative analysis of the contact force network. During the transient process, \({N}_\text{c}\), \({N}_\text{c}^{s}\), and \({N}_\text{c}^{w}\) all gradually decrease with increasing \({\dot{\varepsilon }}_\text{xx}^{e}\) (Fig. 7b–d), which is caused by shear dilatancy. Meanwhile, the coordination number Z slightly decreases from 3.6 to 2.3 during evolution, indicating that the compactness of the filled particles gradually becomes loose. Our data are consistent with the reported data in reference [23]. Although the numbers of both strong contacts \({N}_\text{c}^{s}\) and weak contacts \({N}_\text{c}^{w}\) decrease significantly during evolution, the contact number ratios \({R}_\text{c}^{s}\) and \({R}_\text{c}^{w}\) are basically unchanged at \({R}_\text{c}^{s}\approx 0.37\) and \({R}_\text{c}^{w}\approx 0.63\). In Fig. 7e, the force bearing ratio of strong contacts \({B}_\text{f}^{s}\) gradually increases from 0.68 to 0.73 during evolution, and a clear overshoot in \({B}_\text{f}^{s}\) occurs at the onset moment of shearing movement. Although the number ratio of weak contacts \({R}_\text{c}^{w}\) is always greater than that of the strong contacts \({R}_\text{c}^{s}\), the force bearing ratio of the strong contacts \({B}_\text{f}^{s}\) is much greater than that of the weak contacts \({B}_\text{f}^{w}\), indicating that the strong contact force network carries a larger portion of the external load. Therefore, the evolution of the flow state changes the microstructure characteristics of the contact force network and improves the load-bearing capacity.

5.2 Anisotropies in Microstructure and Internal Shear Strength

Based on the contact force network in Sect. 5.1, we are ready to deduce the internal shear strength and anisotropy parameters using the stress–force–fabric relationship. First, as shown in Fig. 8a–c, the three distribution functions \(P\left(\theta \right)\), \({f}_\text{n}(\theta )\), and \({f}_\text{t}(\theta )\) at four representative moments are compared to those of the initial state. Initially, \(P\left(\theta \right)\) is approximately circular as \({a}_\text{c}\cong 0\), indicating that the contact orientations are distributed isotropically. However, the distributions of both normal and tangential contact forces are anisotropic with \({a}_\text{n}=0.237\) and \({a}_\text{t}=0.075\); particularly, the anisotropy in the normal contact force is very strong. Without flow, the contact forces are mainly used to carry the applied normal stress, while the internal shear strength is relatively weak so that it is easy for the system to flow. In the evolution process, obvious anisotropy is introduced into the distributions of contact orientation and contact forces. Moreover, their preferred directions are collinear, i.e., \({\theta }_\text{c}\approx {\theta }_\text{n}\approx {\theta }_\text{t}\approx\uptheta\), and here, θ ≈ − 45°. As a result, with the increase in \({\dot{\varepsilon }}_\text{xx}^{e}\), \({a}_\text{c}\) first quickly increases from 0 and then gradually reaches a constant value of approximately 0.32 (Fig. 8a). After passing a peak, \({a}_\text{n}\) gradually decreases to a constant value of approximately 0.24 (Fig. 8b). Apart from the initial abrupt drop and rebound, \({a}_\text{t}\) basically fluctuates around a small value of 0.06 (Fig. 8c). In the steady state, the ratio of \({a}_\text{c}\), \({a}_\text{n}\), and \({a}_\text{t}\) is approximately 16:12:3, implying that the anisotropies in the contact orientation and in the normal contact force are the main sources of the internal shear strength.

Fig. 8
figure 8

a–c The transient evolution of anisotropy parameters \({a}_\text{c}\), \({a}_\text{n}\), and \({a}_\text{t}\), as well as the three distribution functions \(P\left(\theta \right)\), \({f}_\text{n}(\theta )\), and \({f}_\text{t}\left(\theta \right)\) at representative moments, and (d) \({\mu }^{*}\) and \({\mu }_\text{e}\) as a function of \({\dot{\varepsilon }}_\text{xx}^{e}\)

Full size image

Next, the reasons for the changes in the anisotropy parameters are explained in combination with the system’s internal micromechanical behaviors. In the beginning of shear, the increase in \({a}_\text{c}\) and \({a}_\text{n}\) could be attributed to the potential shear resistance caused by the spatial geometric constraints. Nevertheless, most particles except a few near the top plate have not undergone shear flow, so the tangential contact force anisotropy parameter \({a}_\text{t}\) changes slightly. Since the horizontal flow is the predominant deformation pattern, the differences in the tangential contact force are slight; thus, \({a}_\text{t}\) is low and makes a small contribution to the internal shear strength. Subsequently, because the occurrence of dilatancy reduces the spatial geometric constraints among particles, the original particles that bear large normal contact forces lose lateral support and cannot maintain stability. Once these particles are out of balance, the breakage of the established contacts causes a decrease in \({a}_\text{n}\). On the other hand, particle flow reduces the number of contacts, especially in the direction of the minimum principal stress, which leads to a gradual increase in the contact number difference between along the direction of the maximum principal stress and along the direction of the minimum principal stress; thus, \({a}_\text{c}\) gradually increases. In short, the increase in \({a}_\text{c}\) leads to a reduction in \({a}_\text{n}\), which damages the system’s stability.

Last, the internal shear strength \({\mu }^{*}\) is obtained according to Eq. 6, as shown in Fig. 8d. When combining the contributions of the anisotropic parameters, \({\mu }^{*}\) first rapidly increases to the peak and then gradually drops to a fixed value. Moreover, the transient evolution curves of \({\mu }^{*}\) and \({\mu }_\text{e}\) are basically consistent, which confirms that the internal shear strength originates from the anisotropies in both contact orientation and contact forces.

6 Effects of Shear Velocity on Rheological Properties

6.1 Effects of Shear Velocity on the Transient Flow State

We select four velocities of the top sliding plate (0.5, 1.0, 1.5, and 2.0 m/s) to study the effects of shear velocity on the rheological properties. The evolution profiles of the horizontal velocity at the other velocities are similar to those of \({V}_\text{s}=0.5 \, \text{m}/\text{s}\). In addition, three distinct stages, i.e., transmission (T), adjustment (A), and stabilization (S), are identified for all velocities. Nevertheless, there still exist differences in the evolution of the flow state among them. As shown in Fig. 9a, with increasing shear velocity, the time required for \({\dot{\varepsilon }}_\text{xx}^{e}\) to reach the maximum value increases, indicating that the evolution rate of the flow state decreases. Under inertial flow, an increase in the shear velocity strengthens the inertial effect and reduces the duration of contact between particles, thereby weakening the momentum transfer between particles. Therefore, the time required for reaching steady state becomes longer with increasing shear velocity. Additionally, in Fig. 9b, the maximum normal strain \({\varepsilon }_\text{yy}\), i.e., the dilatancy extent, increases with shear velocity. Therefore, the shear velocity does not affect the evolution characteristics of particle flow, but changes the momentum transfer rate.

Fig. 9
figure 9

a Time history plots of the dimensionless equivalent shear strain rate \({\dot{\varepsilon }}_\text{xx}^{e}\), and b the evolution curves of \({\varepsilon }_\text{yy}\) as a function of \({\dot{\varepsilon }}_\text{xx}^{e}\) under four different velocities

Full size image

6.2 Effects of Shear Velocity on Macroscopic and Microscopic Mechanical Properties

We present the evolution results of normal stress and shear stress acting on the top plate (\({\sigma }_\text{n}\) and \({\sigma }_\text{t}\) in Fig. 10a and b) and within the granular system (\({\sigma }_\text{yy}\) and \({\sigma }_\text{xy}\) in Fig. 10c and d), respectively. In terms of the evolution characteristics, these stresses fluctuate more intensively as the shear velocity increases, especially for the boundary stresses \({\sigma }_\text{n}\) and \({\sigma }_\text{t}\). In addition, Fig. 10e shows that the internal shear stress \({\sigma }_\text{xy}\) significantly increases with increasing \({\dot{\varepsilon }}_\text{xx}^{e}\) at higher shear velocities. On the other hand, with increasing shear velocity, the magnitudes of shear stresses \({\sigma }_\text{t}\) and \({\sigma }_\text{xy}\) at the same moment significantly increase, while the scaled normal stresses \({\sigma }_\text{n}/P\) and \({\sigma }_\text{yy}/P\) always fluctuate around 1.0. As a result, both the interfacial friction coefficients \({\mu }^{^{\prime}}\) and the effective friction coefficients \({\mu }_\text{e}\) increase as the shear velocity increases, as shown in Fig. 10c and f. This could be explained by the fact that when the overall shear rate increases, the boundary driving strength must be correspondingly improved to overcome more energy dissipation and maintain steady flow.

Fig. 10
figure 10

The transient evolution of the scaled normal stress \({\sigma }_\text{n}/P\) (a), the scaled tangential stress \({\sigma }_\text{t}/P\) (b), the interfacial friction coefficient \({\mu }^{\mathrm{^{\prime}}}\) (c), the scaled internal normal stress \({\sigma }_\text{yy}/\mathrm{P}\) (d), the scaled internal shear stress \({\sigma }_\text{xy}/P\) (e), and the effective friction coefficient \({\mu }_\text{e}\) (f) with \({\dot{\varepsilon }}_\text{xx}^{e}\) under different shear velocities

Full size image

Furthermore, the anisotropy parameters \({a}_\text{c}\),\({a}_\text{n}\), and \({a}_\text{t}\) all increase with increasing shear velocity as shown in Fig. 11a–c. According to Eq. (6), the system’s internal shear strength characterized by \({\mu }^{*}\) is correspondingly improved in Fig. 11d. The changes in these anisotropy parameters could be explained by comparing the contact force network graphs in the steady state. As shown in Fig. 12a, at \({V}_\text{s}=0.5 \, \text{m}/\text{s}\), a dense and continuous contact force network is formed as the particles remain in contact and interact frictionally with neighbors over long durations. By contrast, at \({V}_\text{s}=2 \, \text{m}/\text{s}\), the distribution of contact force is so dispersed that only some local line segments of contact force exist. As a result, the difference in contact number increases between along the maximum principal stress and along the minimum principal stress, leading to an increase in the contact orientation anisotropy parameter \({a}_\text{c}\). As shown in Fig. 12b, in the steady state, both the strong contact number \({N}_\text{c}^{s}\) and the weak contact number \({N}_\text{c}^{w}\) decrease with increasing shear velocity. \({N}_\text{c}^{w}\) is always greater than \({N}_\text{c}^{s}\). Additionally, with increasing shear velocity, the bearing ratio of weak contacts \({B}_\text{f}^{w}\) decreases while the bearing ratio of strong contacts \({B}_\text{f}^{s}\) increases, so the differences in the force magnitudes become more distinct, which explains the increase in the anisotropy parameters of contact forces \({a}_\text{n}\) and \({a}_\text{t}\).

Fig. 11
figure 11

Changes in \({a}_\text{c}\) (a), \({a}_\text{n}\) (b), \({a}_\text{t}\) (c), and \({\mu }^{*}\) (d) as a function of \({\dot{\varepsilon }}_\text{xx}^{e}\) under four different velocities

Full size image
Fig. 12
figure 12

a The contact force network graphs of steady state under different shear velocities, b the strong contact number \({N}_\text{c}^{s}\) and the weak contact number \({N}_\text{c}^{w}\), and c the bearing ratio of strong contacts \({B}_\text{f}^{s}\) and the bearing ratio of weak contacts \({B}_\text{f}^{w}\) as a function of shear velocity

Full size image

Finally, we present and compare the different types of friction coefficients in the steady state, as shown in Fig. 13a. Numerous experimental and simulation results have confirmed that for the inertial regime, the macroscopic friction coefficient \(\mu\) increases with an increasing inertial number I in the following manner:

$${\mu }_\text{e}\left(I\right)={\mu }_\text{s}+\frac{{\mu }_\text{g}-{\mu }_\text{s}}{{I}_{0}/I+1},$$
(8)

where \({\mu }_\text{s}\), \({\mu }_\text{g}\), and \({I}_{0}\) are material-dependent constants. In Fig. 13a, our simulation results can be well fitted using Eq. (8), where the fitting coefficients and confidence are listed in Table 2. These fitting equations form the constitutive laws for the dense granular material under plane shear in this study. The three types of friction coefficients are approximately equal because the boundary driving strength and the system’s shear resistance are dynamically balanced.

Fig. 13
figure 13

a The interfacial friction coefficient \({\mu }^{\mathrm{^{\prime}}}\), the effective friction coefficient \({\mu }_\text{e}\) and the internal shear strength \({\mu }^{*}\), and b the variations in the anisotropy parameter \({a}_\text{c}\), \({a}_\text{n}\), and \({a}_\text{t}\), as a function of the inertial number I

Full size image
Table 2 Fitting coefficients of \({\mu }^{^{\prime}}\), \({\mu }_\text{e}\) and \({\mu }^{*}\) using the form of \(\mu ={\mu }_\text{s}+({\mu }_\text{g}-{\mu }_\text{s})/({I}_{0}/I+1)\)
Full size table

Furthermore, Fig. 13b shows the variations in the anisotropy parameters with the inertial number I. Specifically, the contact orientation anisotropy parameter \({a}_\text{c}\) increases significantly from 0.34 to 0.47, and the normal contact force anisotropy parameter \({a}_\text{n}\) gradually increases from 0.23 to 0.30, while the tangential contact force anisotropy parameter \({a}_\text{t}\) only slightly increases from 0.06 to 0.09. By comparing their increasing extents, it can be concluded that \({a}_\text{c}\) and \({a}_\text{n}\) are the main sources of the system’s shear strength. Moreover, the contribution of \({a}_\text{c}\) becomes more predominant with the increase in the inertial number I.

7 Conclusions

DEM simulations are employed to investigate the transient rheological properties of a dense granular system under plane shear in the inertial regime. Simulation results show that there are three typical stages in the evolution process of the system’s horizontal flow state, namely, transmission, adjustment, and stabilization. The shear dilatancy which is caused by the vertical movement of particles, weakens the system’s tangential load-bearing capacity, decreases the interfacial friction coefficient \({\mu }^{^{\prime}}\) and reduces the boundary driving strength. On the other hand, the shear flow induces variations in the anisotropies of the contact orientation and contact forces, thus improving the system’s internal shear strength \({\mu }^{*}\) and increasing the effective friction coefficient \({\mu }_\text{e}\). As a result, the evolution trends are opposite between \({\mu }^{^{\prime}}\) and \({\mu }_\text{e}\); moreover, \({\mu }^{^{\prime}}\) is greater than \({\mu }_\text{e}\) until approximately equal in the steady flow state. Therefore, the flow evolution from static to steady flow is realized by achieving the final dynamic balance between the boundary driving strength and the system’s shear resistance. In addition, an increase in the shear velocity enhances the rheological evolution rate, but the evolution pattern is not changed. Distinguished from the micromechanical behaviors, the system’s shear strength always mainly originates from the anisotropies in contact orientation and in normal contact force. Moreover, the anisotropy in contact orientation makes more contribution as the shear velocity increases.

Our work comprehensively analyzes the competition between the boundary driving strength and the system’s shear resistance in the evolution process, and thus reveals the shear equilibrium mechanism of dense particle flow. In addition, the effects of shear velocity on the transient evolution are determined, by means of integrated analyses on both the macroscopic quantities and the microstructure characteristics. Together with the previous studies on steady flow, our transient analysis would help supplement a more complete understanding of the flow behaviors of granular materials. In the future, we plan to distinguish the contributions of strong contacts and weak contacts on the granular flow behaviors.